Wind Climate and Wind Power Resource Assessment Based on Gridded Scatterometer Data: A Thracian Sea Case Study
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area Description
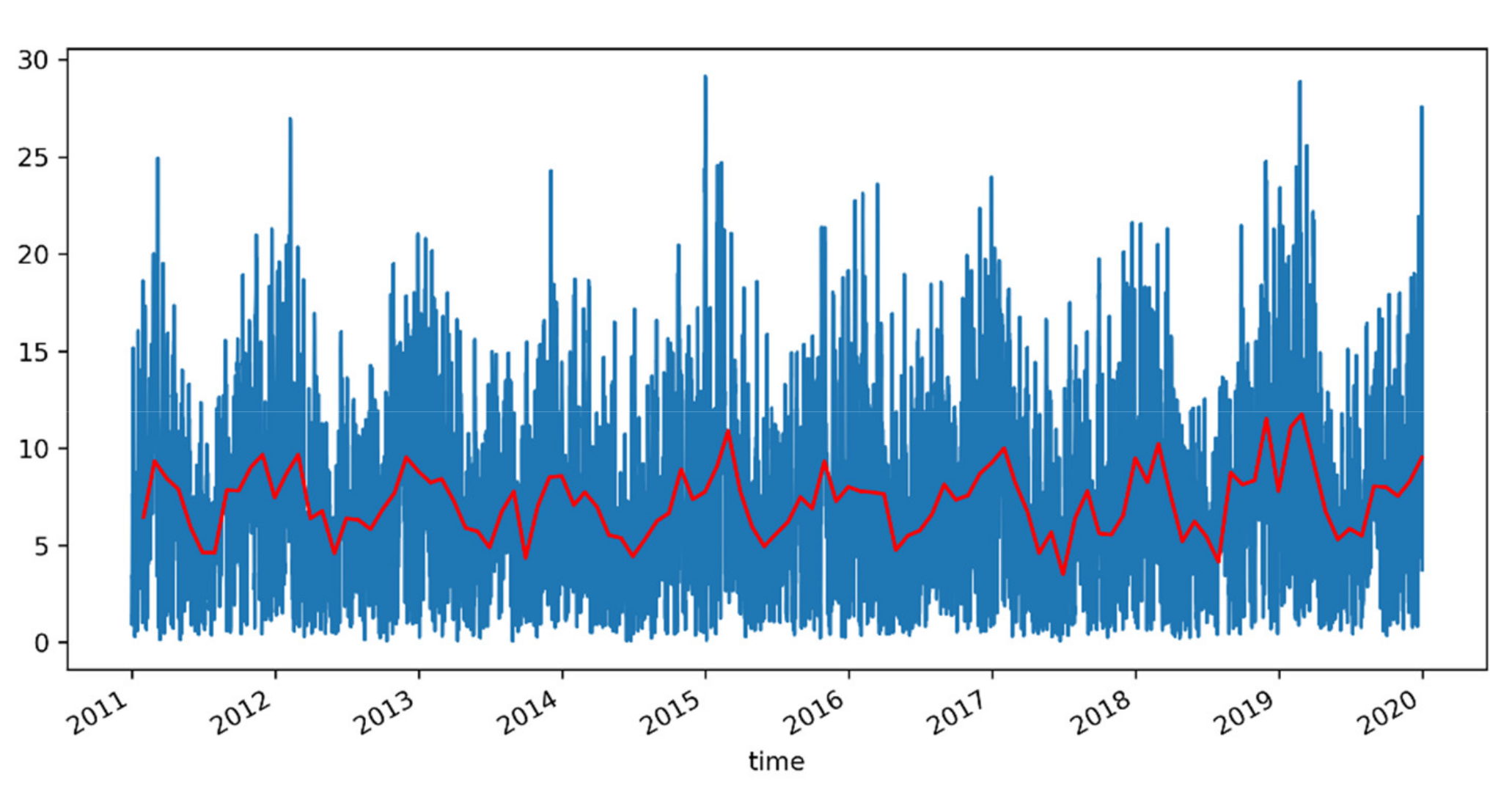
2.2. Wind Data Description
2.3. Qualitative Wind Data Assessment
2.4. Preliminary Data Processing
2.5. Weibull Probability Function
2.6. Wind Energy Content and Power Density
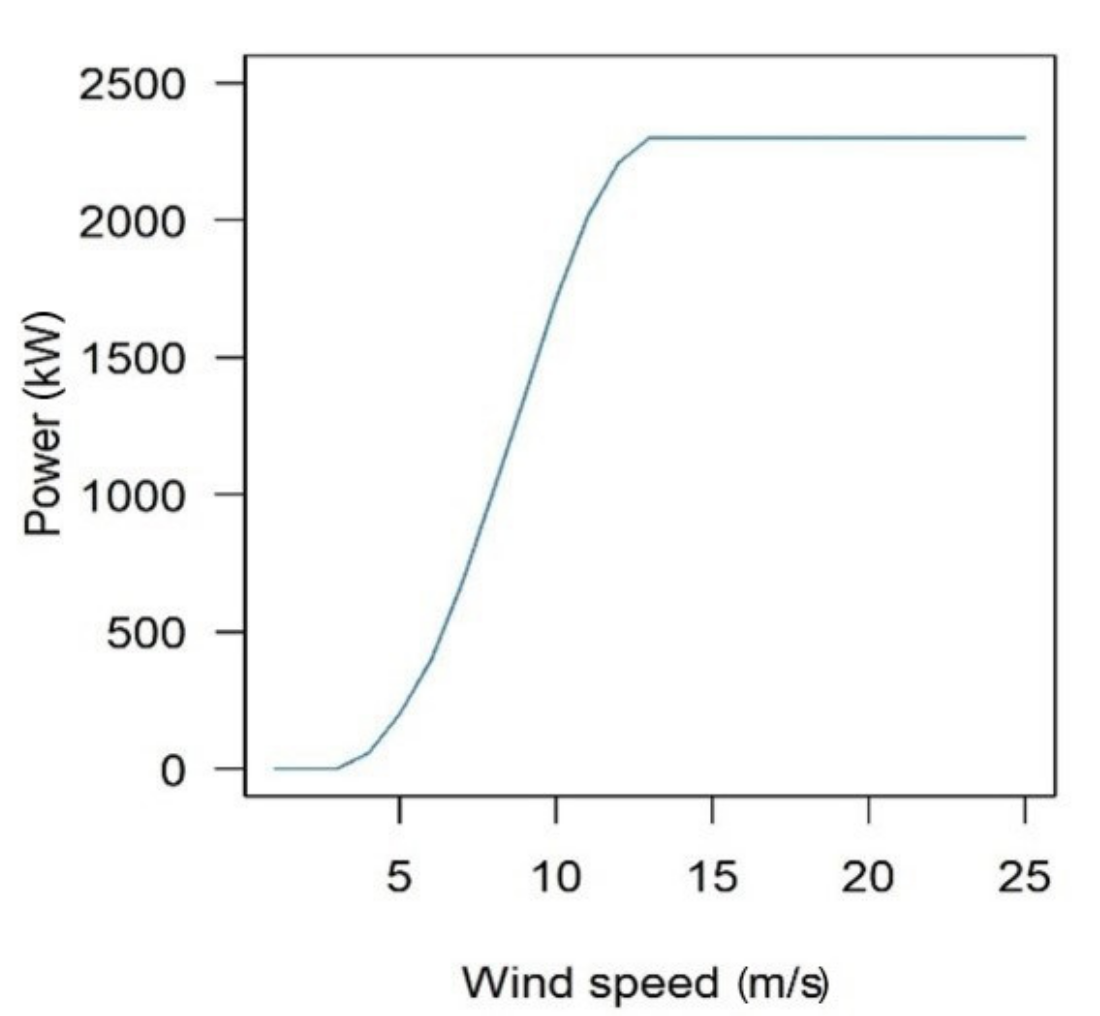
2.7. Annual Wind Energy Production
3. Results
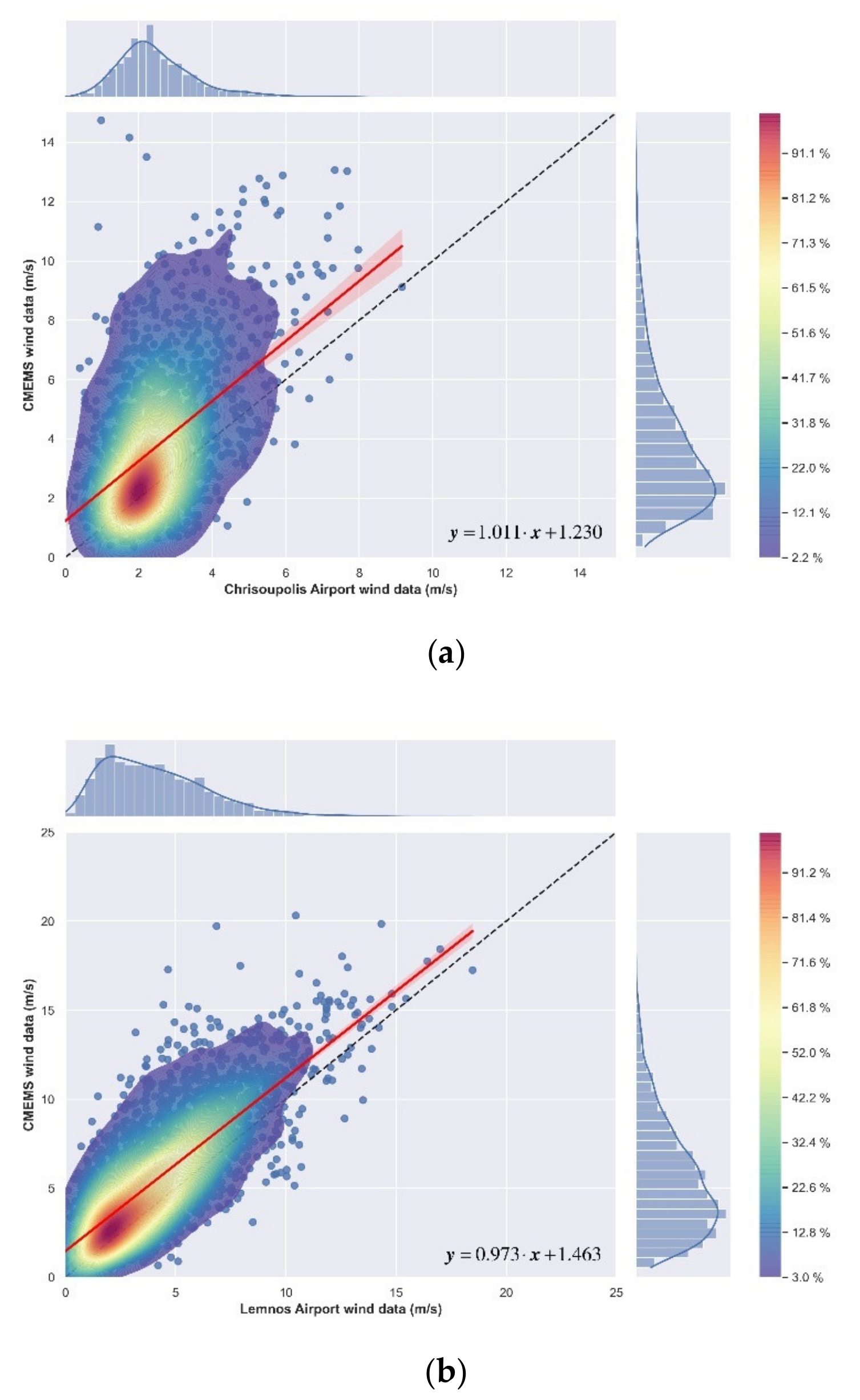
3.1. Assessment in Satellite Wind Analysis Accuracy
3.2. Descriptive Wind Statistics per Sub-Area
3.3. Spatial Variability in Weibull Fitting Function Parameters
3.4. Total Wind Energy Content
3.5. Annual Wind Energy Production
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- European Union. The European Green Deal. Communication from the Commission to the European Parliament, the European Council, the Council, the European Economic and Social Committee and the Committee of the Regions. COM (2019) 640 Final. 2019. Available online: https://ec.europa.eu/info/sites/info/files/european-green-deal-communication_en.pdf (accessed on 10 June 2021).
- International Renewable Energy Agency (IRENA). Future of Wind: Deployment, Investment, Technology, Grid Integration and Socio-Economic Aspects (A Global Energy Transformation Paper). Available online: https://www.irena.org/publications/2019/Oct/Future-of-wind (accessed on 10 June 2021).
- Global Wind Energy Council. Global Offshore Wind Report, 102p. 2020. Available online: https://gwec.net/wp-content/uploads/2020/12/GWEC-Global-Offshore-Wind-Report-2020.pdf (accessed on 10 June 2021).
- European Parliamentary Research Service. Offshore Wind Energy in Europe, by Alex Benjamin Wilson, 2020, PE 659.313, 12 p. Available online: https://www.europarl.europa.eu/RegData/etudes/BRIE/2020/659313/EPRS_BRI(2020)659313_EN.pdf (accessed on 10 June 2021).
- Aslan, A. Comparison based on the technical and economical analysis of wind energy potential at onshore, coastal, and offshore locations in Canakkale, Turkey. J. Renew. Sustain. Energy 2020, 12, 063306. [Google Scholar] [CrossRef]
- American Clean Power Association, U.S. Offshore Wind Industry. In Cleanpower.org. Retrieved from Website. 2021. Available online: https://cleanpower.org/wp-content/uploads/2021/02/ACP_FactSheet-Offshore_Final.pdf (accessed on 10 June 2021).
- Soukissian, T.; Papadopoulos, A.; Skrimizeas, P.; Karathanasi, F.; Axaopoulos, P.; Avgoustoglou, E.; Kyriakidou, H.; Tsalis, C.; Voudouri, A.; Gofa, F.; et al. Assessment of offshore wind power potential in the Aegean and Ionian Seas based on high-resolution hindcast model results. AIMS Energy 2017, 5, 268–289. [Google Scholar] [CrossRef]
- Saleous, N.; Issa, S.; Al Mazrouei, J. GIS-based wind farm site selection model offshore Abu Dhabi Eirate, UAE. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences (ISPRS) Congress, Prague, Czech Republic, 12–16 July 2016; B8. [Google Scholar] [CrossRef]
- Díaz, H.; Fonseca, R.B.; Guedes Soares, C. Site selection process for floating offshore wind farms in Madeira Islands. In Advances in Renewable Energies Offshore; Soares, G., Ed.; Taylor & Francis Group: London, UK, 2018; pp. 729–737. [Google Scholar]
- Latinopoulos, D.; Kechagia, K. A GIS-Based Multi Criteria Evaluation for Wind Farm Site Selection: A Regional Scale Application in Greece. Renew. Energy 2015, 78, 550–560. [Google Scholar] [CrossRef]
- Satir, M.; Murphy, F.; McDonnell, K. Feasibility study of an offshore wind farm in the Aegean Sea, Turkey. Renew. Sustain. Energy Rev. 2018, 81, 2552–2562. [Google Scholar] [CrossRef] [Green Version]
- Majidi Nezhad, M.; Neshat, M.; Groppi, D.; Marzialetti, P.; Heydari, A.; Sylaios, G.; Astiaso Garcia, D. A primary offshore wind farm site assessment using reanalysis data: A case study for Samothraki island. Renew. Energy 2021, 172, 667–679. [Google Scholar] [CrossRef]
- Bagiorgas, H.S.; Mihalakakou, G.; Rehman, S.; Al-Hadhrami, L.M. Wind power potential assessment for seven buoys data collection stations in Aegean Sea using Weibull distribution function. J. Renew. Sustain. Energy 2012, 4, 013119. [Google Scholar] [CrossRef] [Green Version]
- Zafeiratou, E.; Spataru, C.; Bleischwitz, R. Wind offshore energy in the Northern Aegean Sea islanding region. In Proceedings of the IEEE 16th International Conference on Environment and Electrical Engineering (EEEIC), Florence, Italy, 7–10 June 2016. [Google Scholar] [CrossRef]
- Konstantinidis, E.I.; Kompolias, D.G.; Botsaris, P.N. Viability analysis of an offshore wind farm in North Aegean Sea, Greece. J. Renew. Sustain. Energy 2014, 6, 023116. [Google Scholar] [CrossRef]
- Arun Kumar, S.V.V.; Nagababu, G.; Kumar, R. Comparative study of offshore winds and wind energy production derived from multiple scatterometers and met buoys. Energy 2019, 185, 599–611. [Google Scholar] [CrossRef]
- Pimenta, F.; Kempton, W.; Garvine, R. Combining meteorological stations and satellite data to evaluate the offshore wind power resource of Southeastern Brazil. Renew. Energy 2008, 33, 2375–2387. [Google Scholar] [CrossRef]
- Mostafaeipour, A. Feasibility study of offshore wind turbine installation in Iran compared with the world. Renew. Sustain. Energy Rev. 2010, 14, 1722–1743. [Google Scholar] [CrossRef]
- Karamanis, D.; Tsabaris, C.; Stamoulis, K.; Georgopoulos, D. Wind energy resources in the Ionian Sea. Renew. Energy 2011, 36, 815–822. [Google Scholar] [CrossRef]
- Fuverik, B.R.; Sempreviva, A.M.; Cavaleri, L.; Lefèvre, J.-M.; Transerici, C. Eight years of wind measurements from scatterometer for wind resource mapping in the Mediterranean Sea. Wind Energy 2011, 14, 355–372. [Google Scholar] [CrossRef] [Green Version]
- Young, I.R.; Kirezci, E.; Ribal, A. The Global Wind Resource Observed by Scatterometer. Remote Sens. 2020, 12, 2920. [Google Scholar] [CrossRef]
- Sylaios, G. Meteorological influences on the surface hydrographic patterns of the North Aegean Sea. Oceanologia 2011, 53, 57–80. [Google Scholar] [CrossRef] [Green Version]
- Sylaios, G.; Kamidis, N.; Anastasiou, S.; Tsihrintzis, V.A. Hydrodynamic response of Thassos Passage (N. Aegean Sea) to Nestos River discharge and meteorological forcing. Cont. Shelf Res. 2013, 59, 37–51. [Google Scholar] [CrossRef]
- Bentamy, A.; Grodsky, S.A.; Cambon, G.; Tandeo, P.; Capet, X.; Roy, C.; Herbette, S.; Grouazel, A. Twenty-Seven Years of Scatterometer Surface Wind Analysis over Eastern Boundary Upwelling Systems. Remote. Sens. 2021, 13, 940. [Google Scholar] [CrossRef]
- Kumar, M.; Samuel, C. Wind energy potential estimation with prediction of wind speed distribution. Int. J. Intell. Syst. Technol. Appl. 2018, 17, 19–41. [Google Scholar] [CrossRef]
- Delignette-Muller, M.L.; Dutang, C. Fitdistrplus: An R Package for Fitting Distributions. J. Stat. Softw. 2015, 64, 1–34. Available online: https://www.jstatsoft.org/article/view/v064i04 (accessed on 18 April 2021). [CrossRef] [Green Version]
- Carvalho, D.; Rocha, A.; Gómez-Gesteira, M.; Silva Santos, C. Offshore winds and wind energy production estimates derived from ASCAT, OSCAT, numerical weather prediction models and buoys—A comparative study for the Iberian Peninsula Atlantic coast. Renew. Energy 2017, 102, 433–444. [Google Scholar] [CrossRef]
- Alvarez, I.; Gomez-Gesteira, M.; de Castro, M.; Carvalho, D. Comparison of different wind products and buoy wind data with seasonality and interannual climate variability in the southern Bay of Biscay (2000–2009). Deep Res. Part. II Top. Stud. Oceanogr. 2014, 106, 38–48. [Google Scholar] [CrossRef]
- Pryor, S.C.; Shepherd, T.J.; Barthelmie, R.J. Interannual variability of wind climates and wind turbine annual energy production. Wind Energy Sci. 2018, 3, 651–665. [Google Scholar] [CrossRef] [Green Version]
- Fyrippis, I.; Axaopoulos, P.J.; Panayiotou, G. Wind energy potential assessment in Naxos Island, Greece. Appl. Energy 2010, 87, 577–586. [Google Scholar] [CrossRef]
- Wang, Y.-H.; Walter, R.K.; White, C.; Farr, H.; Ruttenberg, B.I. Assessment of surface wind datasets for estimating offshore wind energy along the Central California Coast. Renew. Energy 2019, 133, 343–353. [Google Scholar] [CrossRef]
- Pickett, M.H.; Tang, W.; Rosenfeld, L.K.; Wash, C.H. QuikSCAT satellite comparisons with nearshore buoy wind data off the U.S. West Coast. J. Atmos. Ocean. Technol. 2003, 20, 1869–1879. [Google Scholar] [CrossRef] [Green Version]
- Bagiorgas, H.S.; Mihalakakou, G.; Rehman, S.; Al-Hadhrami, L.M. Offshore wind speed and wind power characteristics for ten locations in Aegean and Ionian Seas. J. Earth Syst. Sci. 2012, 121, 975–987. [Google Scholar] [CrossRef] [Green Version]
- Borhan, Y. Mesoscale interactions on wind energy potential in the northern Aegean region: A case study. Renew. Sustain. Energy Rev. 1998, 2, 353–360. [Google Scholar] [CrossRef]
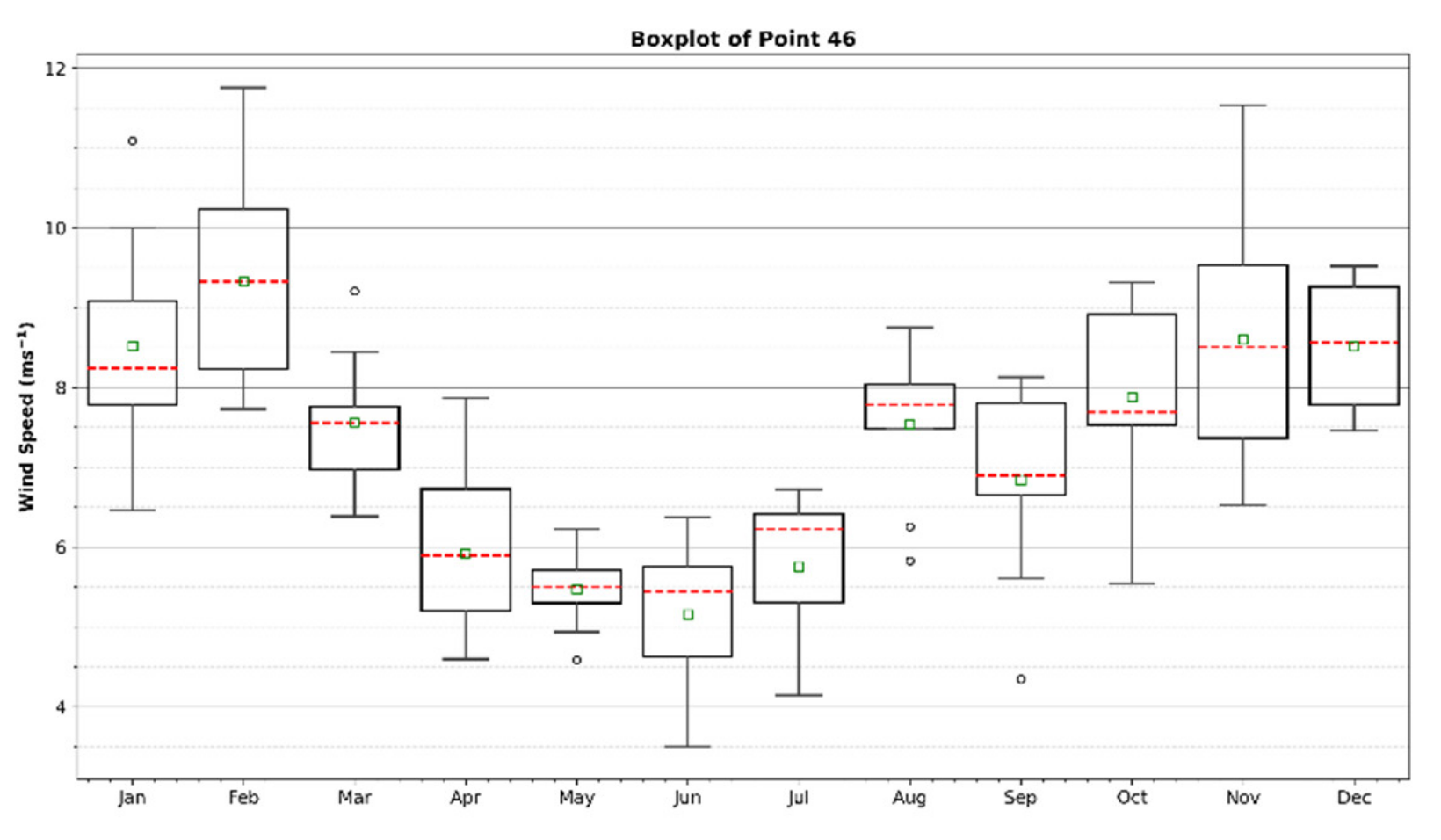
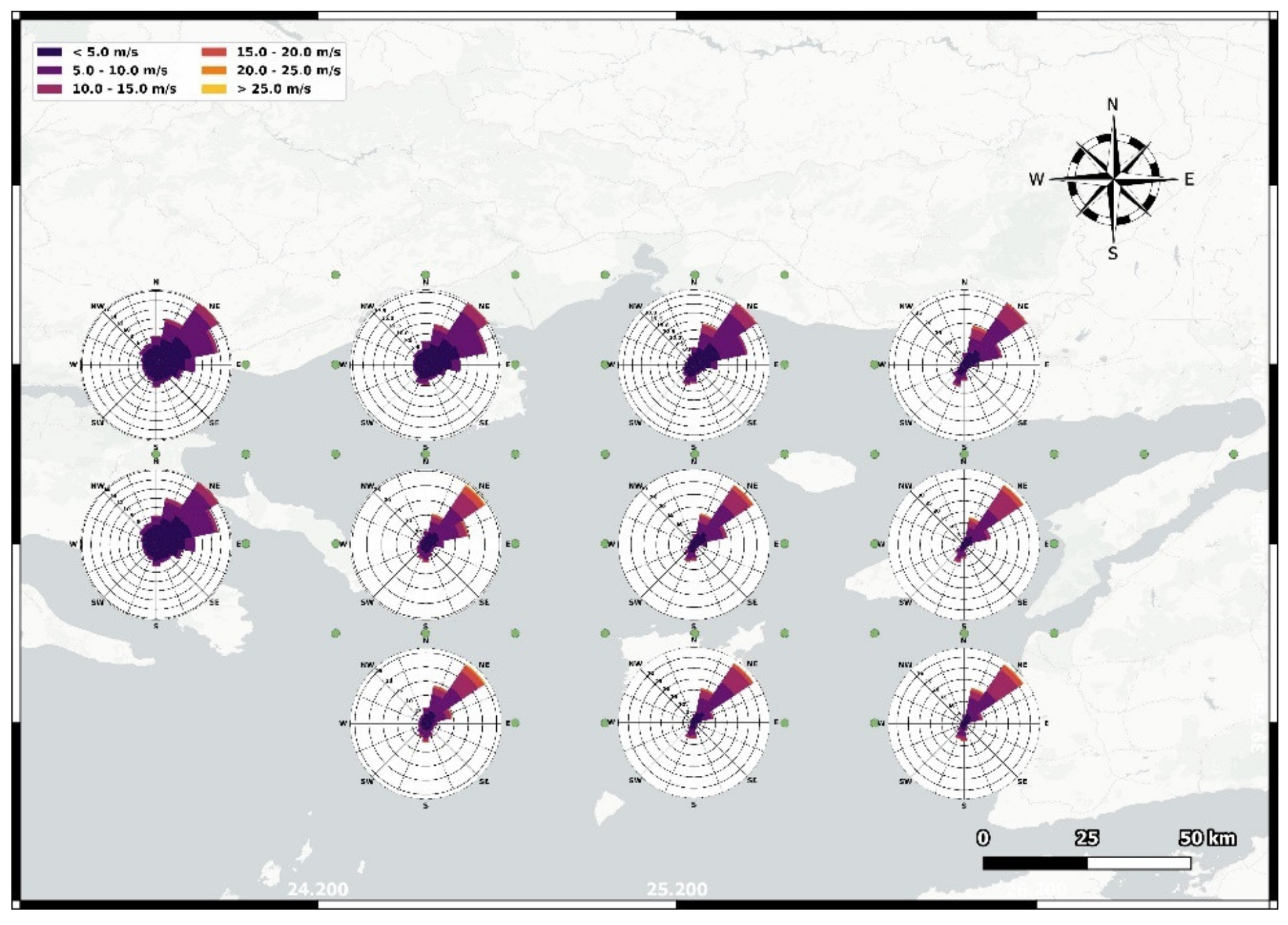
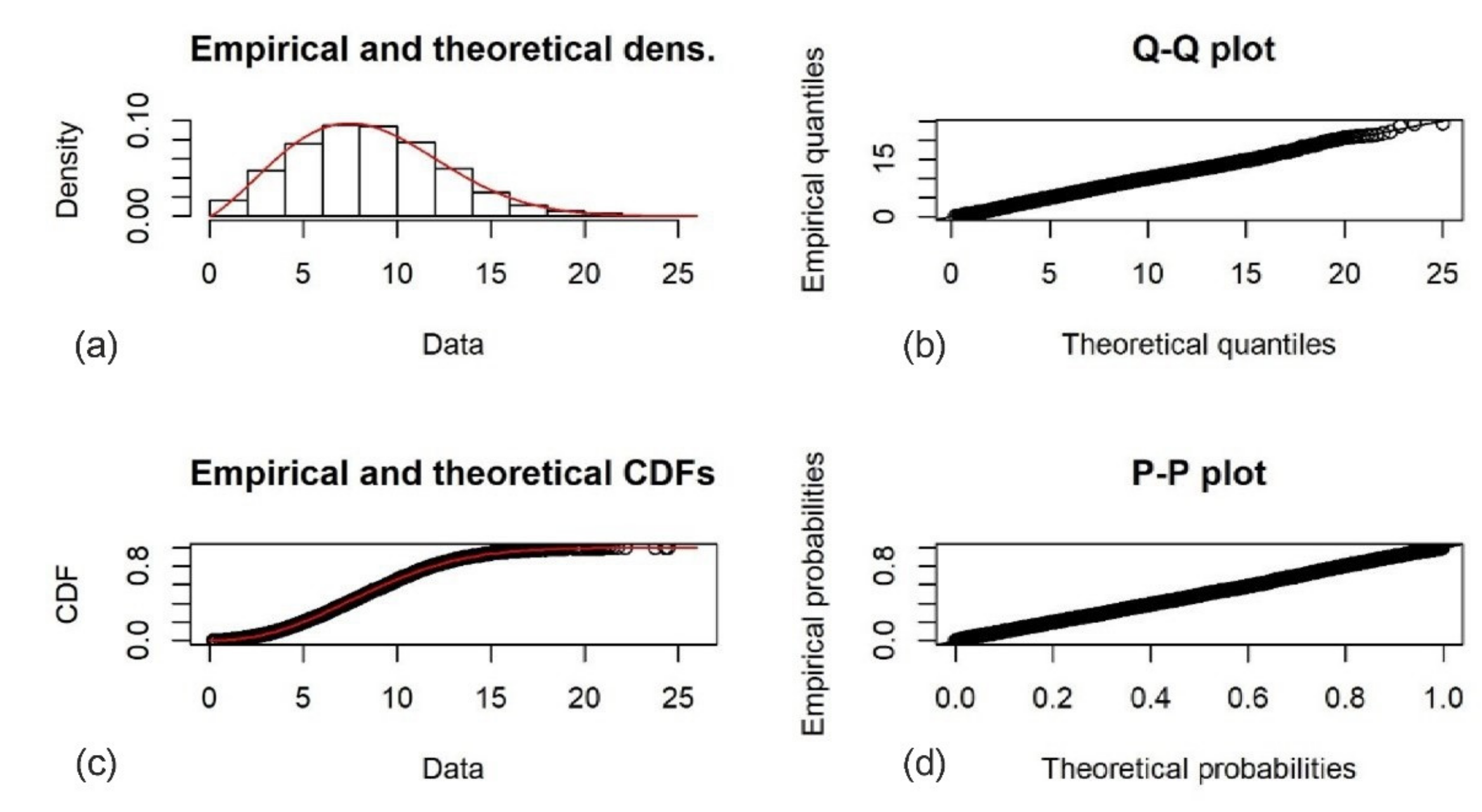
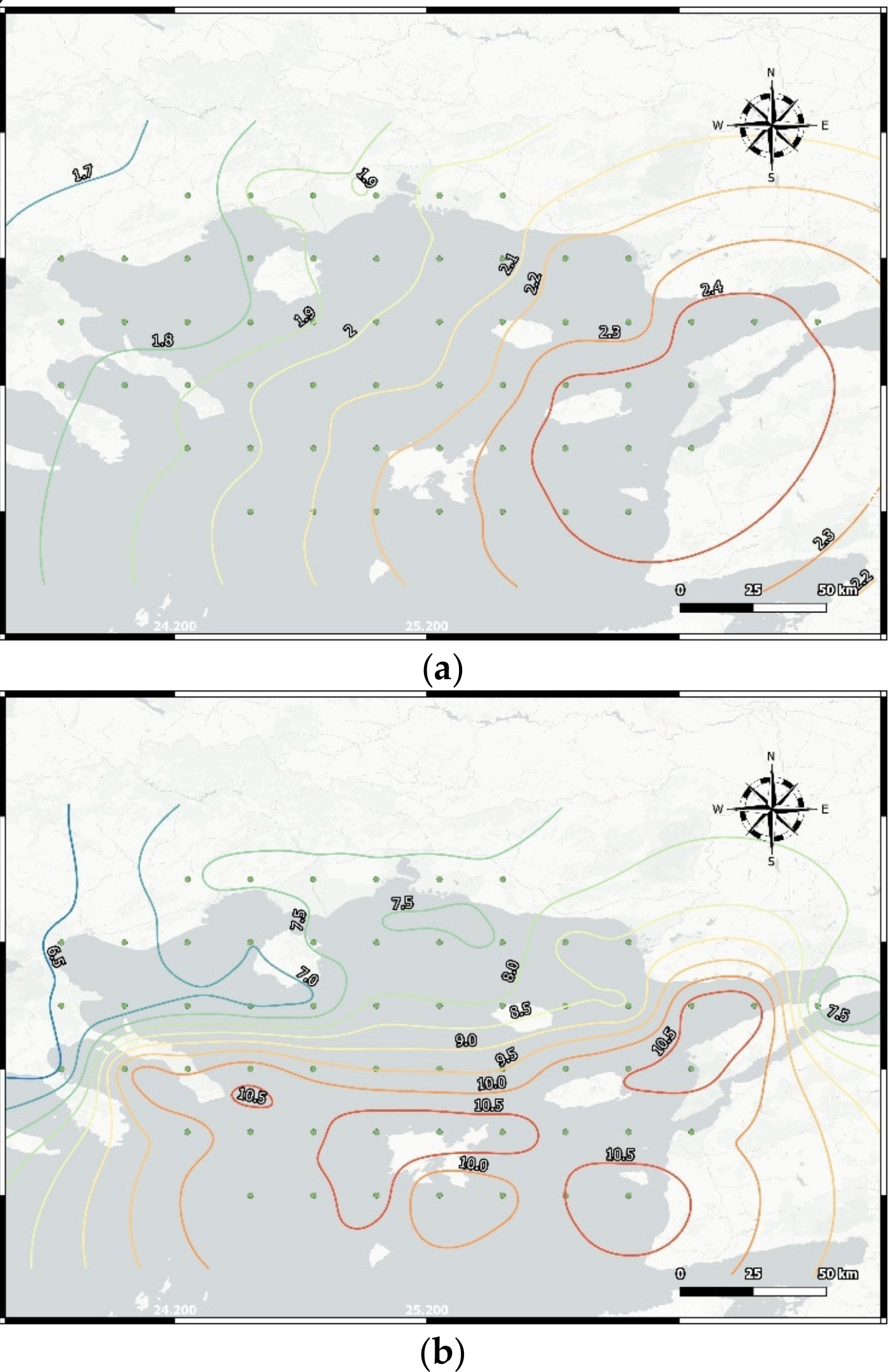
| Sub-Area | Q1 | Median | Mean | Q3 | Max |
|---|---|---|---|---|---|
| West Thracian Sea | 2.16 | 3.65 | 4.37 | 5.86 | 46.88 |
| Central Thracian Sea | 2.45 | 4.14 | 4.90 | 6.62 | 35.19 |
| East Thracian Sea | 3.17 | 5.32 | 6.05 | 8.25 | 29.66 |
| Lemnos Plateau | 3.60 | 6.20 | 6.99 | 9.57 | 32.72 |
| Dardanelles’ Zone of Influence | 3.82 | 6.48 | 7.15 | 9.81 | 29.30 |
| Siggitikos Gulf and Mt Athos | 2.86 | 4.88 | 5.82 | 7.89 | 31.73 |
| Sub-Areas/ Directional Bins | West Thracian Sea | Central Thracian Sea | East Thracian Sea | Lemnos Plateau | Dardanelles | Siggitikos/Mt Athos | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| k | A (m/s) | k | A (m/s) | k | A (m/s) | k | A (m/s) | k | A (m/s) | k | A (m/s) | |
| N | 1.38 | 4.71 | 1.45 | 4.67 | 1.35 | 5.08 | 1.42 | 5.03 | 1.47 | 5.05 | 1.46 | 5.41 |
| NNE | 1.50 | 5.87 | 1.61 | 7.08 | 1.79 | 8.79 | 1.71 | 8.80 | 1.82 | 9.16 | 1.56 | 7.49 |
| NE | 1.75 | 6.84 | 1.93 | 7.50 | 2.27 | 8.75 | 2.23 | 10.42 | 2.45 | 10.39 | 1.88 | 9.23 |
| ENE | 1.74 | 5.70 | 2.00 | 6.00 | 2.17 | 6.57 | 1.87 | 7.61 | 2.02 | 7.25 | 1.77 | 7.58 |
| E | 1.88 | 4.45 | 1.94 | 4.47 | 1.98 | 4.38 | 1.65 | 4.99 | 1.81 | 4.96 | 1.71 | 5.28 |
| ESE | 1.21 | 3.42 | 1.65 | 3.49 | 1.76 | 3.54 | 1.57 | 4.36 | 1.70 | 4.48 | 1.50 | 4.29 |
| SE | 1.50 | 3.32 | 1.28 | 3.24 | 1.60 | 3.81 | 1.46 | 4.75 | 1.55 | 4.56 | 1.51 | 4.23 |
| SSE | 1.48 | 3.62 | 1.38 | 3.79 | 1.51 | 4.38 | 1.57 | 5.89 | 1.65 | 5.76 | 1.46 | 4.81 |
| S | 1.27 | 4.53 | 1.35 | 5.40 | 1.56 | 6.70 | 1.67 | 8.13 | 1.75 | 8.42 | 1.40 | 6.13 |
| SSW | 1.44 | 4.02 | 1.53 | 5.26 | 1.68 | 6.74 | 1.73 | 7.43 | 1.79 | 7.68 | 1.51 | 5.64 |
| SW | 1.31 | 3.35 | 1.59 | 3.99 | 1.89 | 5.01 | 1.84 | 5.69 | 1.82 | 5.86 | 1.61 | 4.79 |
| WSW | 1.61 | 3.63 | 1.76 | 3.74 | 1.60 | 4.14 | 1.60 | 4.95 | 1.52 | 4.57 | 1.62 | 4.75 |
| W | 1.77 | 3.24 | 1.68 | 3.07 | 1.66 | 3.36 | 1.46 | 3.84 | 1.40 | 3.37 | 1.69 | 4.31 |
| WNW | 1.51 | 3.42 | 1.60 | 3.20 | 1.52 | 3.17 | 1.43 | 3.55 | 1.38 | 3.41 | 1.59 | 4.31 |
| NW | 1.45 | 3.87 | 1.40 | 3.33 | 1.34 | 3.31 | 1.31 | 3.95 | 1.19 | 3.41 | 1.40 | 4.68 |
| NNW | 1.50 | 4.09 | 1.29 | 3.29 | 1.30 | 3.50 | 1.56 | 3.93 | 1.59 | 3.54 | 1.48 | 4.81 |
| all | 1.40 | 4.79 | 1.48 | 5.42 | 1.64 | 6.77 | 1.63 | 7.81 | 1.73 | 8.02 | 1.47 | 6.44 |
| Sub-Areas/ Directional Bins | West Thracian Sea | Central Thracian Sea | East Thracian Sea | Lemnos Plateau | Dardanelles | Siggitikos/Mt Athos |
|---|---|---|---|---|---|---|
| N | 82 | 62 | 80 | 73 | 59 | 91 |
| NNE | 214 | 389 | 775 | 887 | 973 | 436 |
| NE | 435 | 664 | 1256 | 2256 | 2206 | 1308 |
| ENE | 222 | 238 | 262 | 353 | 252 | 556 |
| E | 60 | 47 | 30 | 42 | 32 | 96 |
| ESE | 60 | 15 | 9 | 19 | 14 | 45 |
| SE | 18 | 30 | 12 | 27 | 21 | 33 |
| SSE | 23 | 23 | 25 | 72 | 58 | 62 |
| S | 69 | 112 | 183 | 358 | 395 | 168 |
| SSW | 27 | 87 | 227 | 235 | 272 | 89 |
| SW | 42 | 26 | 52 | 56 | 61 | 40 |
| WSW | 14 | 14 | 21 | 29 | 22 | 34 |
| W | 9 | 8 | 6 | 13 | 7 | 21 |
| WNW | 16 | 9 | 5 | 10 | 7 | 24 |
| NW | 29 | 14 | 8 | 17 | 11 | 40 |
| NNW | 36 | 37 | 13 | 15 | 9 | 47 |
| all | 1354 | 1774 | 2964 | 4455 | 4398 | 3091 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kokkos, N.; Zoidou, M.; Zachopoulos, K.; Nezhad, M.M.; Garcia, D.A.; Sylaios, G. Wind Climate and Wind Power Resource Assessment Based on Gridded Scatterometer Data: A Thracian Sea Case Study. Energies 2021, 14, 3448. https://doi.org/10.3390/en14123448
Kokkos N, Zoidou M, Zachopoulos K, Nezhad MM, Garcia DA, Sylaios G. Wind Climate and Wind Power Resource Assessment Based on Gridded Scatterometer Data: A Thracian Sea Case Study. Energies. 2021; 14(12):3448. https://doi.org/10.3390/en14123448
Chicago/Turabian StyleKokkos, Nikolaos, Maria Zoidou, Konstantinos Zachopoulos, Meysam Majidi Nezhad, Davide Astiaso Garcia, and Georgios Sylaios. 2021. "Wind Climate and Wind Power Resource Assessment Based on Gridded Scatterometer Data: A Thracian Sea Case Study" Energies 14, no. 12: 3448. https://doi.org/10.3390/en14123448
APA StyleKokkos, N., Zoidou, M., Zachopoulos, K., Nezhad, M. M., Garcia, D. A., & Sylaios, G. (2021). Wind Climate and Wind Power Resource Assessment Based on Gridded Scatterometer Data: A Thracian Sea Case Study. Energies, 14(12), 3448. https://doi.org/10.3390/en14123448










