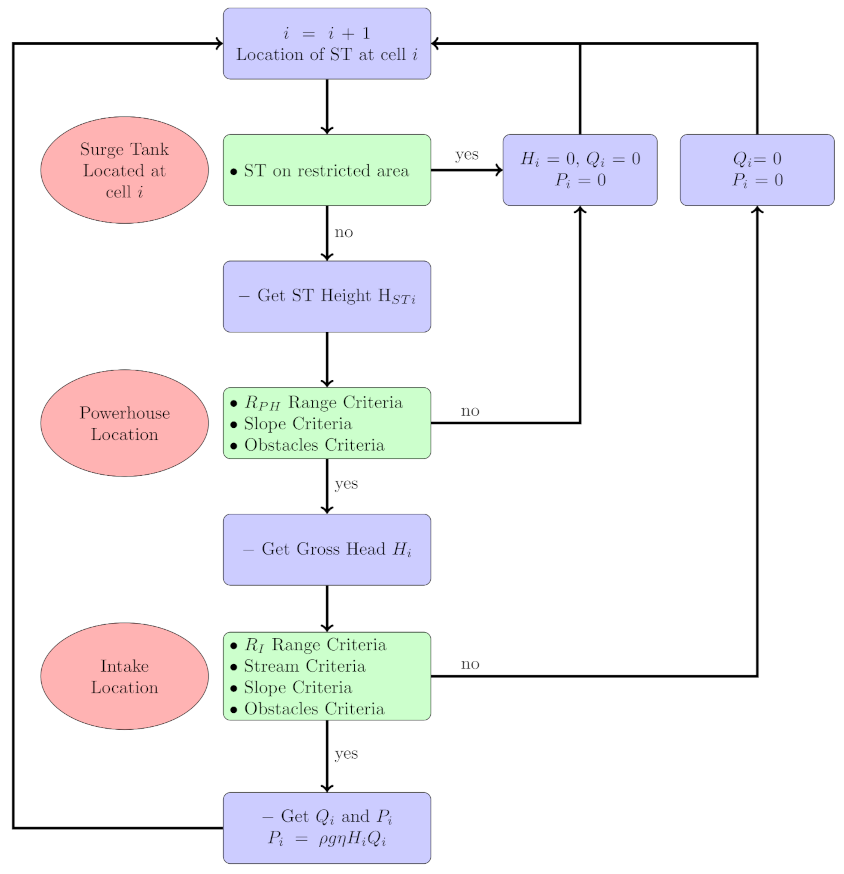
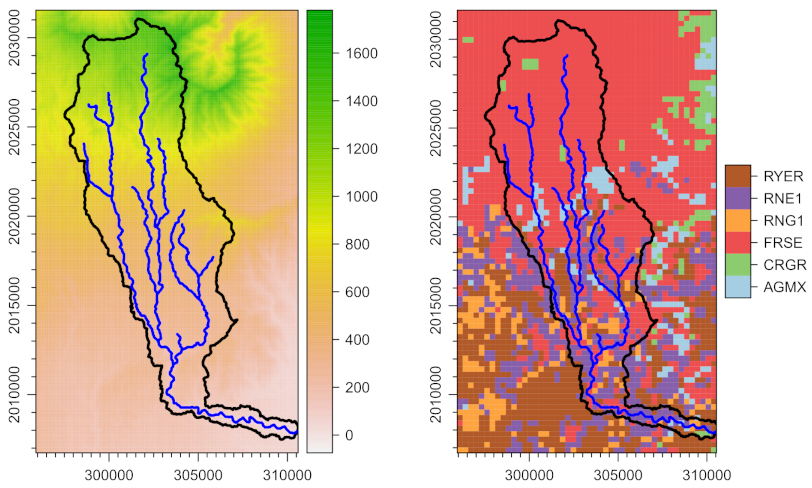
Results are presented as they were utilized in the proposed model. First, the hydrological model calibration and validation were presented along with its performance. Second, the hydrological behavior was exposed in terms of the actual watershed physical conditions and the model parameters. Third, hydro-maps were developed as functions of two more relevant variables, the headrace, and penstock lengths. Thus the hydro-power spatial distribution was shown. Additionally, the contribution of the variables mentioned above is quantified by multiple regression analysis. Lastly, a more comprehensive MSA methodology is illustrated to show its use and potentiality, and limitations.
3.2. SWAT Calibration and Validation
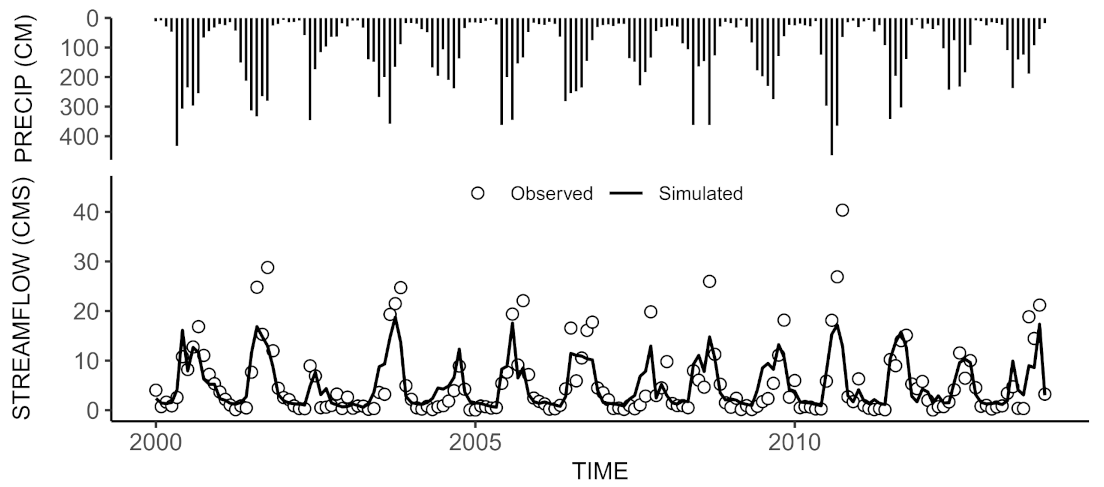
Overall, a good calibration of the proposed model was obtained when compared to the observed flow discharge at the outlet of the Huazuntlan River Watershed.
Figure 7 shows the observed flow discharge and the best simulated flow signal after automatic calibration and validation procedures. The NSE value for the calibration period was 0.69,
was 0.84, whereas PBIAS was 3.1%, which represent a good performance for monthly flow discharge calculations according to [
44]. Similarly, the performance during the validation period NSE was 0.64,
was 0.83, and PBIAS was 12.5%, which are in the range bracketing a good fit between the observed and simulated signals (see
Table 3). The mean, maximum, and minimum observed discharge for the calibration period were 5.28, 28.78, and 0.03 m
/s, respectively. The simulated flow showed a mean, maximum, and minimum of 5.12, 20.75, and 0.55 m
/s, respectively. It can be noticed that similar flow magnitudes were obtained between the predictions and the observations. However, minimum flow conditions were the slightly over-predicted by the model. During the model validation, the mean, maximum, and minimum observed discharge for the calibration period were 5.99, 40.35, and 0.04 m
/s, respectively, while during simulated conditions, the validation period showed mean, maximum, and minimum of 5.30, 17.33, and 0.90 m
/s, respectively. We can see that the mean discharge agreed well with its simulated counterpart. However, several peaks during both calibration and validation were not able to be captured by the model accurately. Similarly to the calibration period, the model slightly overestimated the base-flow conditions, especially for those months with low values of precipitation.
3.3. Hydrological Behavior of the Watershed
The SWAT model proposed in this study performed well and indicated a linear watershed hydrologic response as it presented a rapid response to rainfall events, except for storm events presented during the intense summer rainfall generally preceded by dry conditions. This linearity and rapid response of the watershed is attributed to the response to the subsurface lateral flow [
45]. Evidence of this type of hydrologic behavior is accountable for the relatively high values of ALPHA_BF during the calibration period [
46]. Although non-linearity response assumes that overland flow in steep mountainous catchments is the most significant contribution to the streamflow, surface run-off is unlikely to happen in forested hillslopes due to the high hydraulic conductivities of the soil, which is the case for the mainly forested Huazuntlan River Watershed. As a result, in the shallow soils found in the study area, a preferential flow mechanism is likely to occur within the watershed. This process is common to happen in mostly humid climate and forested watersheds [
47] due to ephemeral and perennial pipes in the soil maintained mainly by subsurface flow and burrowing animals, respectively. This type of preferential flow is quite complex to explain and simulated and it is only possible to discuss by the statistical properties of parameters defining the movement of the subsurface in hydrological models. In addition, in SWAT models, the representation of the water table attributes and position tends to be inadequate. As a result, the parameters controlling shallow groundwater structure will have a large source of uncertainty associated with them [
48]. A more discrete spatial representation of the aquifer characteristics and groundwater systems within sub-watersheds may increase the model accuracy.
The overall hydrologic response of the watershed showed that observed and simulated streamflow outputs presented similar phases and trends, as well as a reasonable match with the observed peaks during humid season (see
Figure 7). However, significant deviations between the simulated and observed peaks were found. These deviations, present during high-intensity rainfall events, might be due to the precipitation heterogeneity within the watershed or the well-known curve number (CN) method limitations. The CN method does not considered neither the storm or precipitation duration and its intensity [
49], which can limit the SWAT model to estimate the magnitude of the flow discharge peaks [
50]. Regardless these limitations, the CN method slightly overestimated streamflow for some large rainfall events and showed some limitations to capture the peak during the high-intensity rainfall season. This peak mismatching, as previously mentioned, is present due to the spatial-temporal variability of the rainfall data, which was heterogeneous by nature. Additionally, peak discharges may be due to changes in land use influencing the hydrological phenomena of the direct run-off. In this study, a increase of 25% of the overall curve number was found during the calibration period. Although the calibration procedure produced a good performance, a more accurate representation of the CN may be obtained from a spatial and dynamic calibration of this parameter.
At large basins, the residence time plays an important role during calibration. These residence time refers to the average time that a certain amount of water travels through a defined river reach. In SWAT model, this variable is affected by the Mannign’s roughness coefficient, which by the definition influences the mean velocity of the flow traveling through streams. This roughness was homogeneously assumed in the proposed SWAT model, having a calibrated value of natural streams (∼0.06 [
51]). Additionally, the hydraulic conductivity of the overall system of streams presented an average value of 476.15 mm/day, which represent a high transmissivity of water from the streams to the hillslope or vice versa, which is consisted with the high rates of lateral flow dominating the flow hydrograph. Overall, the annual average discharge from 2000 to 2013 were 5.49 and 5.17 m
/s for the measured and simulated data, respectively. These values and the performance metrics indicate that the model can be applied for further assessment of the hydrologic response under different land use scenarios. It is carefully noted, that some uncertainty is always introduced into a hydrologic model regardless the agreement between the simulated and observed signals [
52]. The foretold uncertainties may arise from different sources, including the model conceptual structure, assumed initial conditions, observed input data, and selected calibration parameters. The latter have been discussed extensively and although 20 parameters were selected as the most significant, Duan et al. [
52] suggested that more variables are needed for calibration purposes.
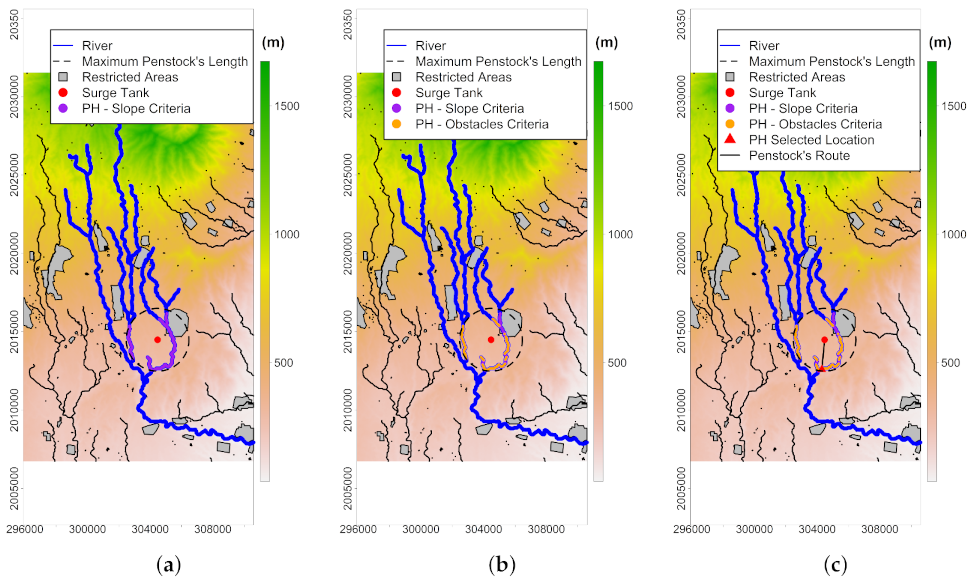
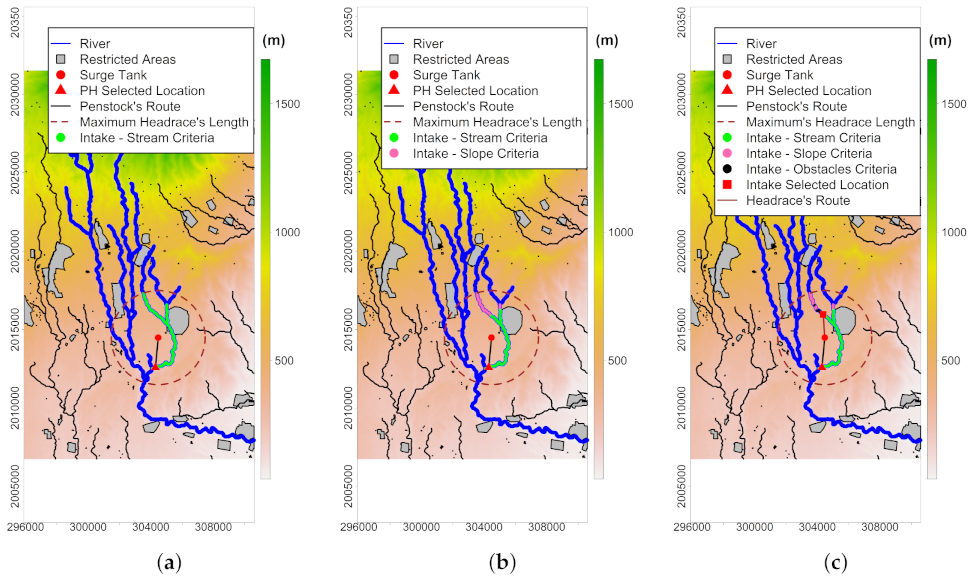
3.4. Hydropower Map
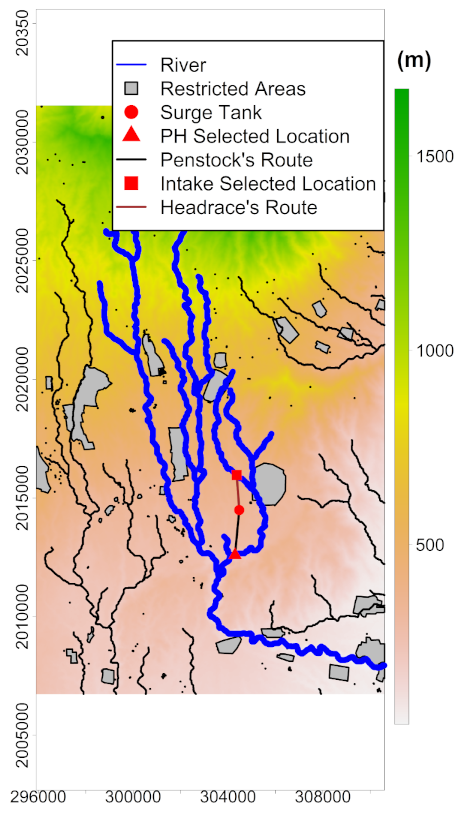
Hydropower maps were obtained by implementing the MSA according to the scheme of
Figure 5 for different pairs of values
representing the headrace’s and penstock’s maximum permissible lengths, respectively. Values of (100, 250, 500, 1000, 1500, 2000, 2500) m were used for
and
to get a more comprehensive understanding of the interaction between both variables. Due to computing access limitations (i.e., HPC account expired), results for
= (2500, 2500) m were not considered. As a result, only 48 simulations were analyzed. Potential sites include mountainous regions with steep geographies, as well as downstream places.
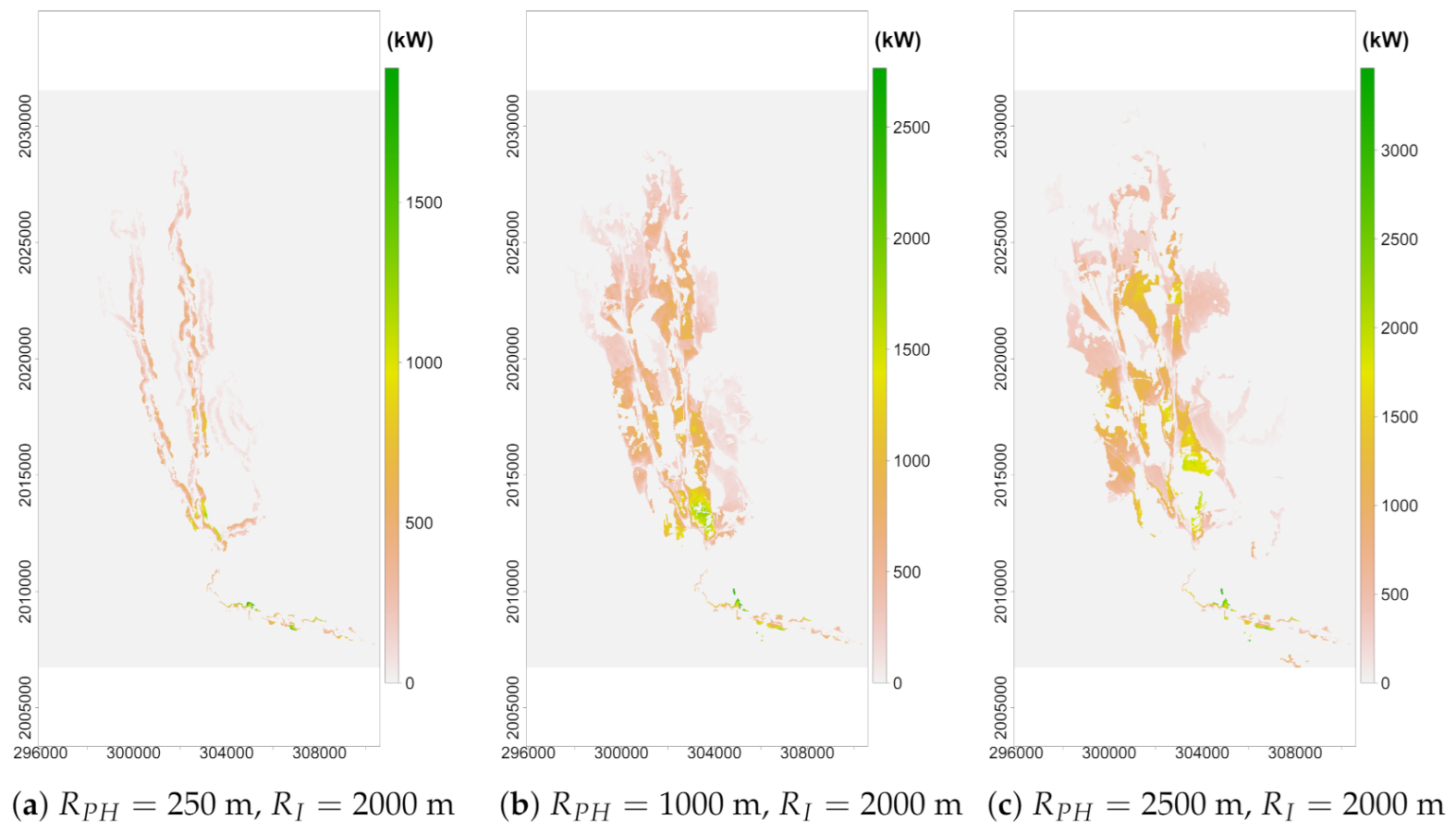
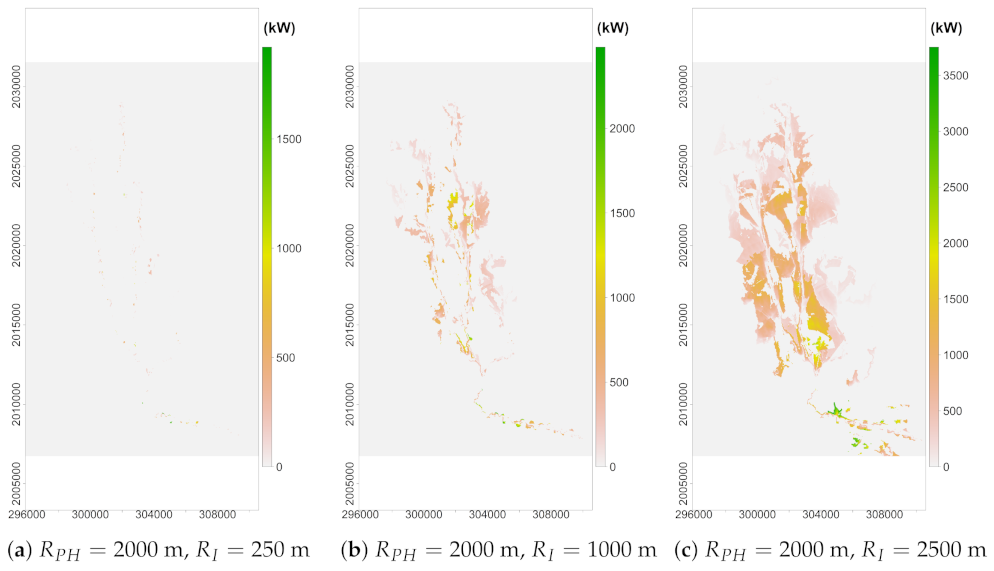
Figure 8 shows hydro-power maps for the three representative
cases,
,
and
m, where
is a fixed value. For the sake of visualization, different scales were used. It can be observed that for all three maps, most of the values are close to zero. The main reason is that places far away from the river were not included within the
or the
radius. For some other cases, it could be that obstacles were obstructing the headrace’s or the penstock’s path, or simply that the study site did not meet the requirements given by the model. Overall, the larger the
values, the more potential sites were found with higher hydro-power. Additionally, spatially speaking, a non-uniform hydro-power distribution was present on all maps. This behavior is due to an implicit balance between discharges
Q and hydraulic heads
H, which is required for hydro-power estimation according to Equation (
1). This translates to flow discharges increasing from downstream to upstream (from north to south), and higher elevation gradients present more commonly at high elevations. For instance, when
were (250, 2000) m, specifically
Figure 8a, potential sites with hydro-power lower than 1500 kW tended to be located within the buffer created along flood plains of the river and dominated by
. Locations with hydro-power higher than 1500 kW were mostly at the junction of the river’s main stem and tributaries and other downstream zones. Similarly, for
Figure 8b,c, increments in hydro-power were due to the magnitude of
. However, whereas the former showed the highest hydro-power values ranging from 1500 to 2500 kW over similar locations as shown in
Figure 8a, the extension increased. Lastly,
Figure 8c shows significant changes in potential locations for hydro-power generations, where the locations with the highest hydro-power (>2000 kW) were located downstream and all over the middle and top sections of the watershed. According to all this, it would be possible to select high potential sites without interfering with other high potential sites.
For fixed values of
and three representative values of
,
Figure 9 shows cases
,
and
m. Once again, different scales were used for each map for the sake of visualization. It can be seen that for the first scenario, there are fewer potential sites for low values of
with the highest hydro-power close to the mouth of the river (
Figure 9a). An increment in
showed that hydro-power ranged from 500 to 2000 kW and was mostly located at the watershed’s headwaters. Additionally, a few locations with
kW were at the junction of the main river and its tributaries and close the watershed’s outlet (
Figure 9b). The last scenario with
and
m showed a similar hydro-power distributions as in
Figure 8c. However, potential locations with moderate hydro-power conditions
kW were located mainly over the middle and top sections of the watershed, whereas the highest hydro-power,
kW, were still located at the river’s junction and near the mouth of the watershed (
Figure 9c). Once again, it can be seen that high potential sites do not interfere with other high potential sites under this approach.
The MSA shares common criteria with other methodologies. Works such as [
3,
16,
17] located the different components of the RoR scheme by fixing maximum distances between surge tank and powerhouse. Then, the head was maximized according to the given criteria. Nevertheless, in these works, hydro-power was assessed by first establishing the position of the weir along the river. Thereafter, the position of the surge tank is conditioned when included in the model. This limits the potential sites to locations along the river and at sub-basin levels. This MSA method, on the other hand, allows multiple potential sites over the entire study area or any raster region (e.g.,
Figure 8 and
Figure 9).
3.5. and Contributions
To observe the effect of the
and
parameters,
Table 4 shows the mean value for the 243 sites with the highest hydro-power. This amounts only to the 0.01% of the total simulated data. The mean values ranged from 103 to 3432 kW. It is important to highlight that considering the mean of all values (100% of the total data) would lead to wrong conclusions since there are plenty of locations with zero potential values. This study was only concerned about the sites with the highest potentials. For the HP values on
Table 4, a multiple linear regression model with interaction effect was estimated as
with a 0.945 value for the
correlation coefficient. The predictors
,
and
were
,
, and
, respectively.
Table 5 shows reasonable contribution of interaction term and the penstock’s length, whereas the strongest contribution to the hydro-power was due to the headrace’s maximum length with a significance level of 0.05. Namely, an increase in 100 m for
is associated with an increase in 35.456 + 0.0221
kW, meanwhile an increase in 100 m for
is associated with an increase in 65.379 + 0.0221
kW. The interception term shows to be not significant in the regression equation with
since neither
or
can be set to zero as this combination makes an irrational arrangement in a hydro-power generation system.
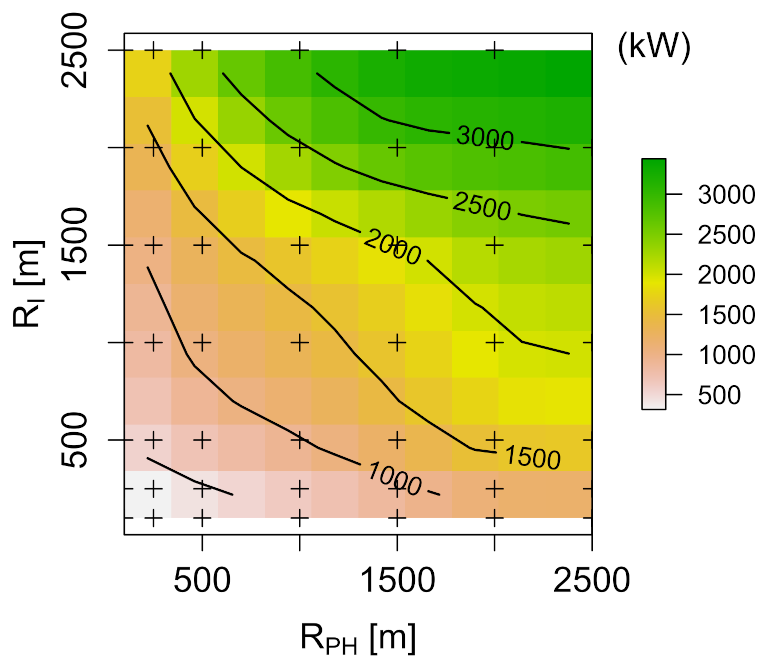
Figure 10 describes the parametric space for
and
through a contour plot for the hydro-power conditions shown in
Table 4. The interpolation was performed using a cubic spline. A thorough analysis of the level plot supports the same conclusion as the one derived from the regression equation. Small increments in
produce a significant increment in hydro-power, especially for high values of
. Besides, this description of the two variables involved in hydro-power production allows the observation of all possible system arrangements, which is an advantage derived from the use of raster information.
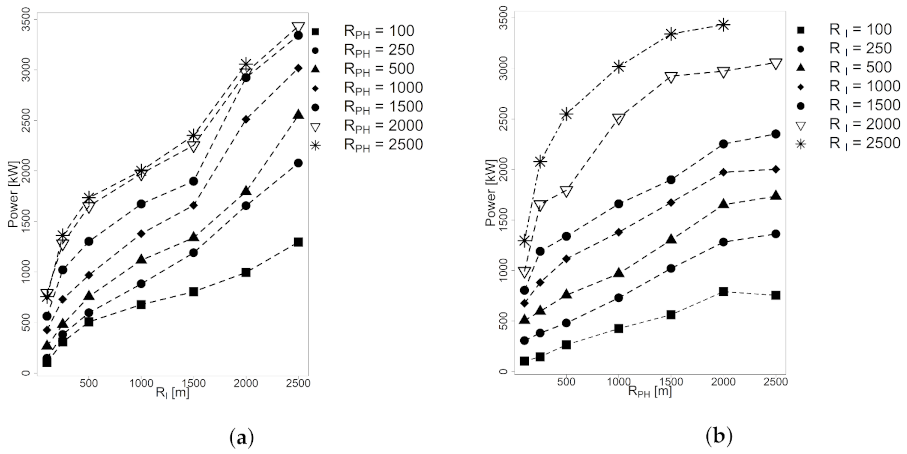
Figure 11a plots the mean HP against the
by fixing the
for different values. It shows a linear increment of the power as the
length increases. Moreover, when
takes values from 1500 to 2000 m, there is a significant increment in power for
values higher than 1000 m. The lines
m and
m show no significant difference for any
value. On the other hand,
Figure 11b plots mean HP against the
by fixing the
for different values. There was an asymptotic trend for
values higher than 1500 observed for all
values. This suggested
values within the range
m behave as a threshold for this parameter, as no significant gains in power were obtained when increasing. The lines
m and
m show no significant difference for low
values.
Table 6 indicates the maximum hydro-power for each run. Maximum HP values range from 608 to 3752 kW for the
m and
m cases, respectively. One could see that this case represented the topmost hydro-power condition, whereas the previous case includes a representative selection of the maxima HP (e.g., 0.01% of the entire raster database). A multiple linear regression model with form
was adjusted to explained the variability of the maximum hydro-power as a function of
and
. The
value was equal to 0.950, which means HP depends linearly on the penstock’s and the headrace’s length. The predictor’s values were 0.714 and 0.823 for
and
, respectively (
Table 7). Although both variables had a significant effect on the maximum HP, headrace’s length
had a slightly stronger effect (
). Once again, the interception term played an important effect on the maximum HP when considering a complete hydro-power generation system. However, it would be meaningless to consider its effect on HP by itself.
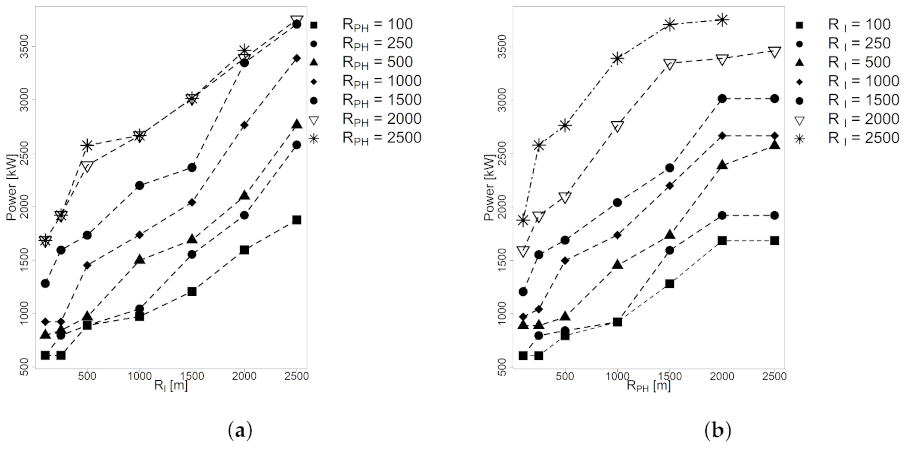
Figure 12a shows a linear increment of the hydro-power as
increases, and a significant increment when increasing from 1500 to 2000 m for
values greater than 1000 m. Once again, the lines corresponding to
m and
had no significant difference for any
value. Additionally, for small
values within the range
m some hydro-power lines for different
values intercept each other, that is the case of
m and
m. There is no guarantee that by increasing
or
by a relatively small amount, HP value will increase. This is because the
and
values stand for the maximum permissible penstock’s and headrace’s length, respectively, but in general, the values for both lengths are lower than permissible ones.
On the other hand,
Figure 12b plots maximum HP against
for different
values. No significant increments were observed for
greater than 2000 m for all
values. There are also cases, where where hydro-power lines intercept, or closely intercept each other. That is the case of
m and
m. Nevertheless, compared with
Figure 12a there are fewer cases since the increment on
has a stronger increment on the HP.
Results indicated that according the MSA the headrace’s length,
, plays an important role on HP assessment and has to be taken into account to generate a more effective hydro-power generation system. However, general studies for hydro-power assessment models mainly focus on the penstock and ignore the headrace contribution in their models [
17,
22,
53].
3.6. Considerations
Although the raster representation associates a hydro-power potential to every position, it does not mean that all sites can be used at the same time, as there could be interference between potential RoR projects. In fact, each cell of the hydro-power map contains additional information such as the powerhouse locations, the intake, the surge tank, and the headrace’s and penstock’s route, the flow discharge as well as the gross head. Therefore, when one selects a location for potential use, not only consider that single location but the complete facilities and a segment of the river, which restricts, in consequence, the selection of other potential locations. Additionally to these considerations, working with a raster representation carries advantages for further data processing and analysis. In fact, implementations such as turbine selection or MCDM analysis becomes a straightforward task [
28,
54]. For instance,
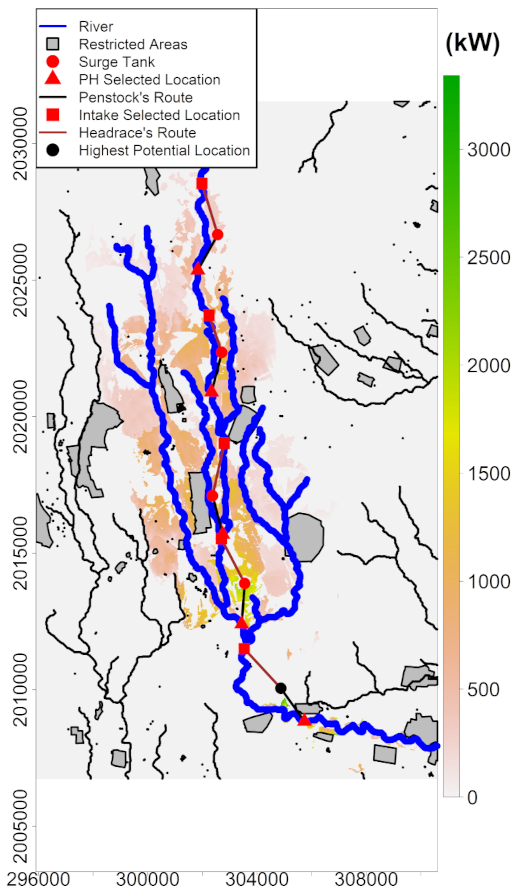
Figure 13 presents a simple scheme of 5 non-overlapping projects by considering the
m and
m. The extent was divided in five equally sized horizontal rectangles from east to west. As a result of the approach used in this study, the highest hydro-power values were 492.61, 1355.98, 1408.47, 2000.90, and 3346.18 kW for sites located from top to bottom of the image or downstream direction. The highest potential location among all the trials is shown in black. More complex optimization procedures could be implemented [
22,
55] as the MSA procedure was designed for further applications and research. That being said, the MSA methodology can be improved or extended without compromising it. An important improvement would be modeling more complex routes for the headrace and the pentsock by incorporating variables such as land use, watershed geomorphology, head losses, and economic costs. It could also be possible to integrate the different scenarios for the different parameters
and
, all in a single raster, in order to provide enough information, and make it open and accessible for the community.