1. Introduction
Lithium-ion batteries have been widely used as the power source of electric vehicles due to their high energy and power density. However, many accidents of electric vehicles have been reported in recent years [
1]. In many cases, the battery cells suffered severe mechanical deformation and got smoked, fired, and even exploded. Research on the mechanical behavior of lithium-ion battery is necessary to achieve better understanding of failure mechanism of the lithium-ion battery under mechanical loading and to develop more safe design of the battery system.
Many studies have been carried out to build up a finite element model to predict the mechanical behavior of lithium-ion battery cells and jellyrolls. There are mainly two categories of modeling methods. One is the detailed finite element model, which includes all components including current collectors, coatings, and separators of the jellyroll [
2,
3,
4,
5]. A well-defined detailed model can predict both the global mechanical behavior and the detailed deformation and failure in battery cells. Zhu et al. [
3] conducted axial compression tests of 18,650 battery cells and developed a detailed finite element model to perform a detailed analysis of the local failure mechanism. Zhang et al. [
4] designed and conducted mechanical tests on constitutive properties of porous electrodes and built up a heterogeneous model for pouch cells. Pan et al. [
5] designed an impact test on a pouch battery cell and built a 3D detailed model to reveal the battery deformation for each part of the cell. However, development of the detailed or heterogeneous models requires a large number of component material tests and onerous calibration processes of material parameters, and the large number of elements (usually more than 100,000 elements in a detailed model [
6,
7]) and the tiny mesh size tend to incur large computational cost. This means that lack of efficiency is a big issue for the detailed model, so it is unsuitable for vehicle or pack level simulation or optimization design.
The other category is the homogenized finite element model. This method simplifies the battery cell or jellyroll as a homogeneous part, and only one constitutive model is required for the equivalent material theoretically. Such a treatment brings the advantage that the model can be easily discretized with larger mesh size owing to relatively simple geometry and composition. Therefore, the homogenized model is usually computationally efficient compared with the detailed model. Sahraei et al. [
8,
9,
10,
11] developed homogenized models based on crushable foam or honeycomb material models in Ls-Dyna as well as the model calibration methods. Those models are applied to predict the load versus displacement responses from a series of indentation tests on 18,650 cells and pouch cells. Xu et al. [
12] carried out the mechanical tests of 18,650 cells under different loading speeds, and developed a homogenized model taking strain-rate effect into consideration. Lian et al. [
13] compared seven failure criteria for Deshpande–Fleck crushable foam model with Abaqus/Explicit in the effort to predict shear crack formation in jellyrolls of pouch cells under rod indentation.
The research on pouch cells and prismatic cells mentioned above mainly focused on the out-of-plane loading cases (i.e., loading is normal to the stacked multilayer of jellyroll in the battery cell). We can notice that the jellyroll of prismatic cell is a winding structure. The structure itself looks highly directional, necessarily corresponding to apparent mechanical anisotropy if the homogenization assumption is made. Li et al. [
14] built a homogenized model for pouch cell considering mechanical anisotropy, damage, strain-rate dependence, and SOC dependence. Kotter et al. [
15] carried out a series of loading tests on large-format prismatic lithium-ion battery cells considering different loading directions and speeds. Zhu et al. [
16] conducted indentation tests on prismatic battery cells and jellyrolls along different directions, and the force-displacement responses and failure intrusions show apparent anisotropy. In realistic accidents, the battery pack may suffer intrusions along different directions. The pack consists of battery modules, which also introduce the second level of structural directionality. Therefore, from cell to pack, there should be at least three levels of directionality, which brings sufficient complexity for the safety assessment or design of the final battery system. From the utmost basic level, cell level, it is important to enable the numerical models to comprehensively capture the deformation responses and failure risks at different directions.
In the present study, a user subroutine of a constitutive model describing anisotropic mechanical behavior is written and implanted in Abaqus/Explicit for a homogenized FE model of the jellyroll in prismatic cell to capture the force versus displacement responses along different loading directions before failure. Then, the model is extended with failure definitions. Two categories of failure criteria, i.e., five single-parameter criteria and two combined criteria, are examined and compared with each other to determine the ones that can be applied to predict the multidirectional failure of jellyroll.
2. Basic Framework of the Constitutive Model
The constitutive relationship for the homogenized equivalence of the jellyroll basically comes from the Modified Honeycomb model (Material Type 126 in Ls-Dyna) [
17]. The model is originally developed for cellular materials with anisotropic behavior, especially aluminum honeycombs. When the deformation is below a certain amount, the normal and shear stress-strain behaviors in all directions are assumed fully uncoupled, and nonlinear elastoplastic material behavior can be defined separately for each stress component. It is similar to the apparently anisotropic mechanical behavior of the jellyroll when it is subjected to compression or indentation from different directions. When the deformation becomes sufficiently large, i.e., the volume of the block decreases to a certain value, the material is fully compacted and becomes isotropic.
Before being full compacted, the behavior of material is orthotropic, and the components of the stress tensor are uncoupled. A material coordinate system (1,2,3) is defined for the orthotropic material model and 1,2,3 represent the major direction. The Cauchy stress and the total strain tensors follow the Voigt notation:
and
. For each component of Cauchy stresses
, the relationship with the total strains is given by:
Einstein’s summation convention is not used in this paper, i.e., no summation over . The relationship means that for each component , it is only related to the corresponding component of total strain .
The detailed implementation process is described as below. The elastic moduli vary from the initial values to the fully compacted values linearly with the relative volume:
where
, and
and
are the elastic modulus and shear modulus along different direction, respectively, for the uncompacted state.
and
are the elastic modulus and shear modulus for the fully compacted state, while
and
are initial values of the elastic modulus and shear modulus.
is the relative volume (i.e., the ratio of the current volume to the initial volume), and
is the fully compacted volume.
The model adopts six load curves
to define the normal stress and shear stress values during deformation along different direction. For the uncompacted state, at the beginning the trial, stress values are updated as:
Each component of the updated stress tensor is checked to make sure that it does not exceed the permissible value determined from the load curve. If
then
where
represents the scale factor defining strain-rate effect. For the quasi-static cases,
.
When
, corresponding to the fully compacted state, the material behavior is isotropic elastic-perfectly plastic, which means that there is no work hardening. The Cauchy stress
and the elastic strain
tensors follow the Voigt notation:
and
. The relationship with Cauchy stresses and the elastic strains is given by:
is the elastic stiffness matrix, and there are only two individual parameters determined by Young’s modulus and Poisson’s ratio .
The trial deviatoric stress components are updated as:
where the deviatoric strain increment is defined as:
The effective trial stress is defined as:
It is checked to see if the yield stress is exceeded. If the effective trial stress exceeds the yield stress, we need to scale back the stress components to the yield surface:
The pressure is updated as:
where
is the elastic bulk modulus and the stress is calculated by:
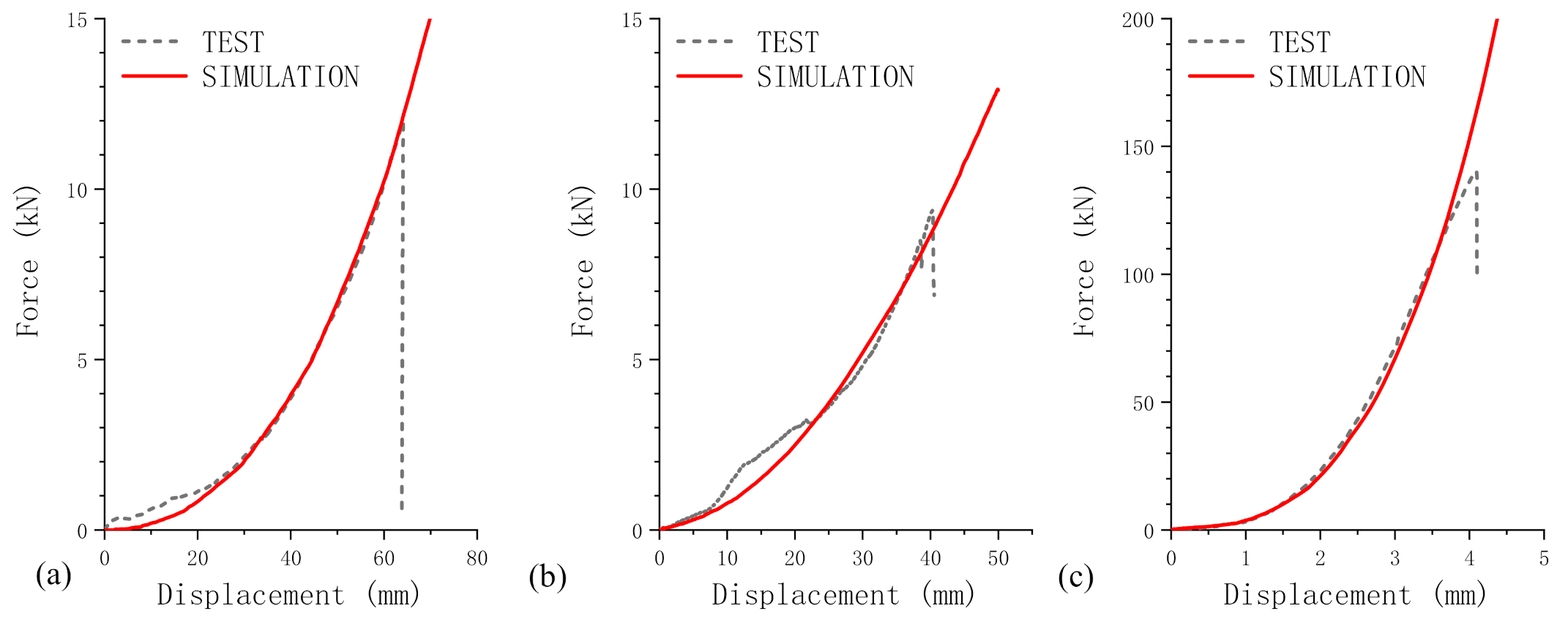
The framework described above is written as a user subroutine and implanted in Abaqus/Explicit. Key inputs for the mechanical anisotropy of the jellyroll contain the elastic modulus and the load curves along different directions.
3. Experiments and Experimental Results
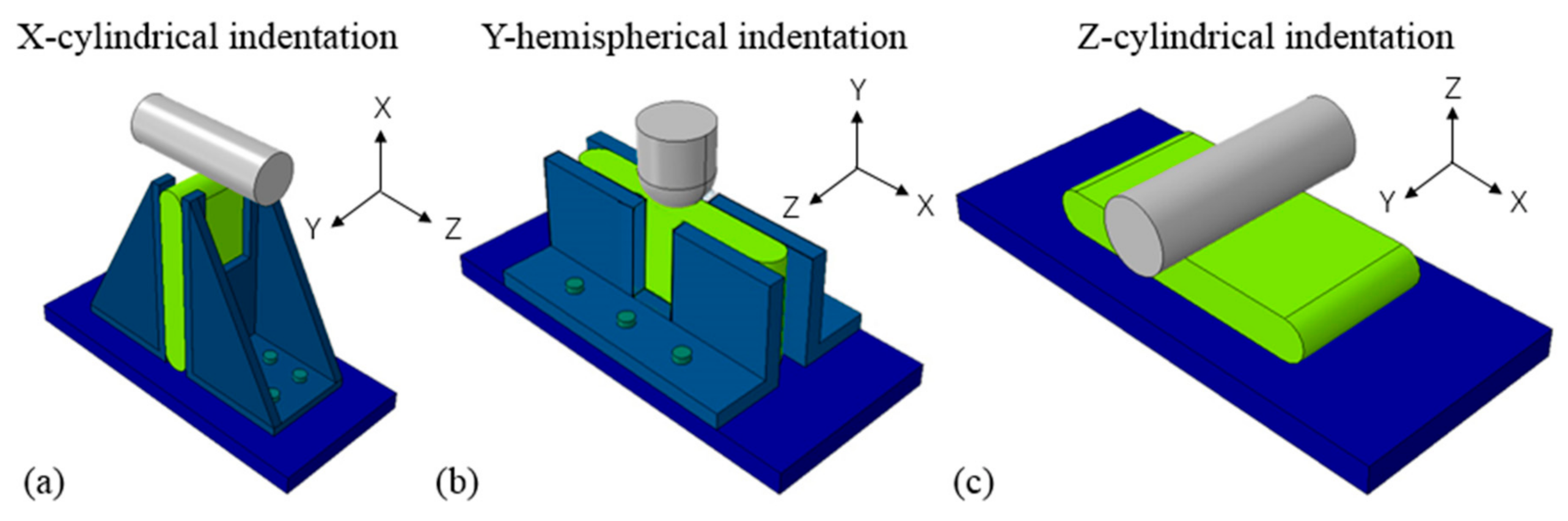
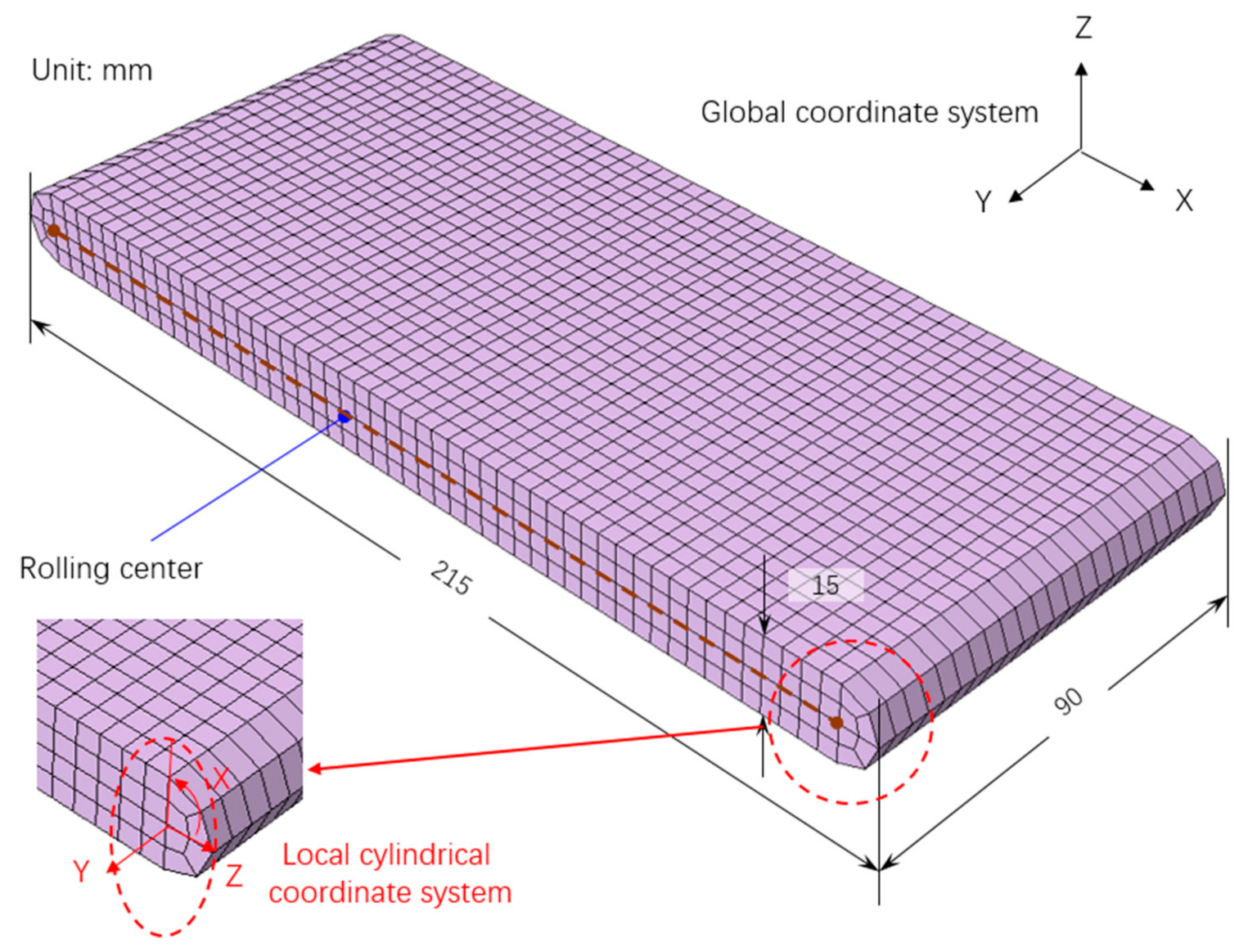
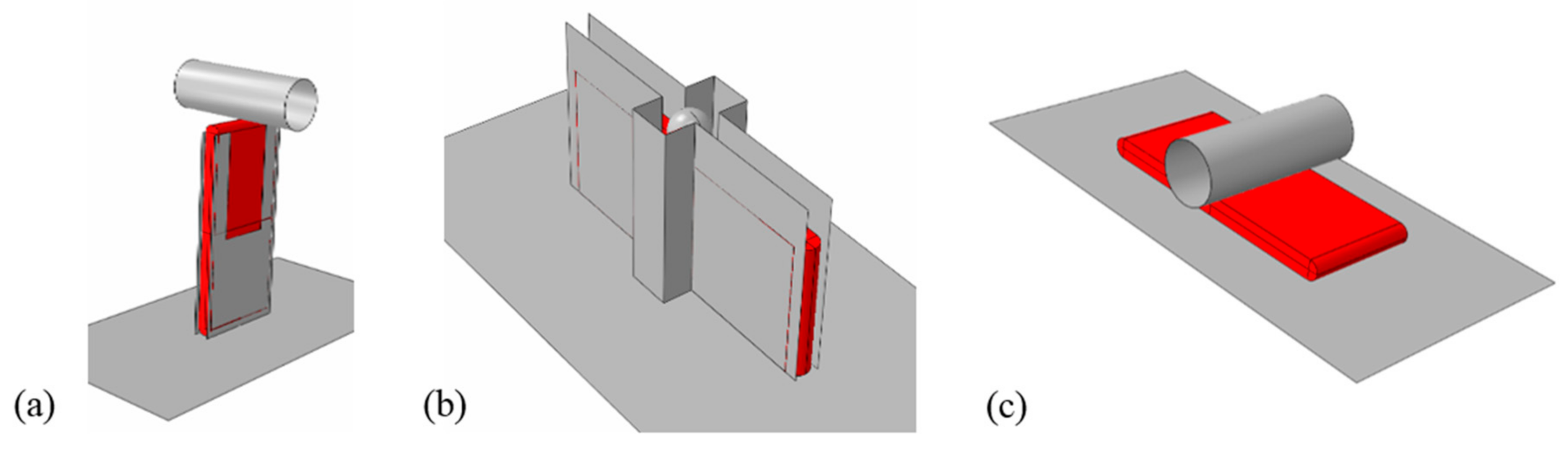
To validate the homogenized FE model in this study, jellyrolls from a large format commercial prismatic lithium-ion battery cell for electric vehicles are tested. The jellyroll dimensions are 215 mm, 90 mm, and 15 mm (length, width and thickness). Three types of quasi-static indentation tests are conducted on the jellyrolls along three directions. Along the length (X) and thickness (Z) direction, the indentation object is a cylindrical bar with a diameter of 50 mm. Along the width (Y) direction, the indentation object is a hemispherical head with a diameter of 25 mm. To keep the jellyroll from unstable deformation along X and Y directions, the fixtures for side constraint are designed and applied in these two experiments. The loading setup of jellyroll experiments and the fixtures are shown in
Figure 1. The quasi-static tests with a speed of 2 mm/min were conducted on a universal test machine. A CCD camera with a frame of 10 fps was used to record the intrusion in the quasi-static tests. The intrusion distance of the impactor is calculated by the digital image correlation (DIC) method. The contact force was collected with a 200 kN force sensor.
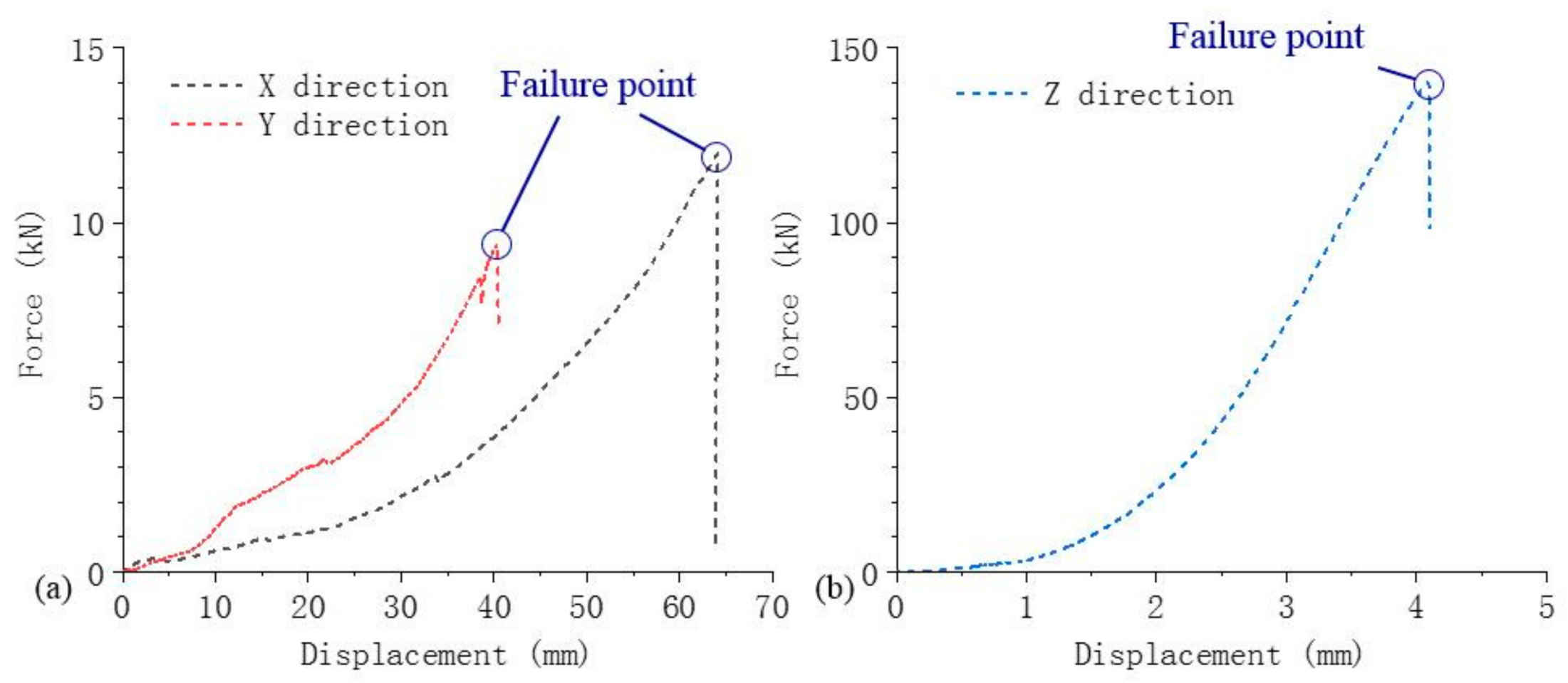
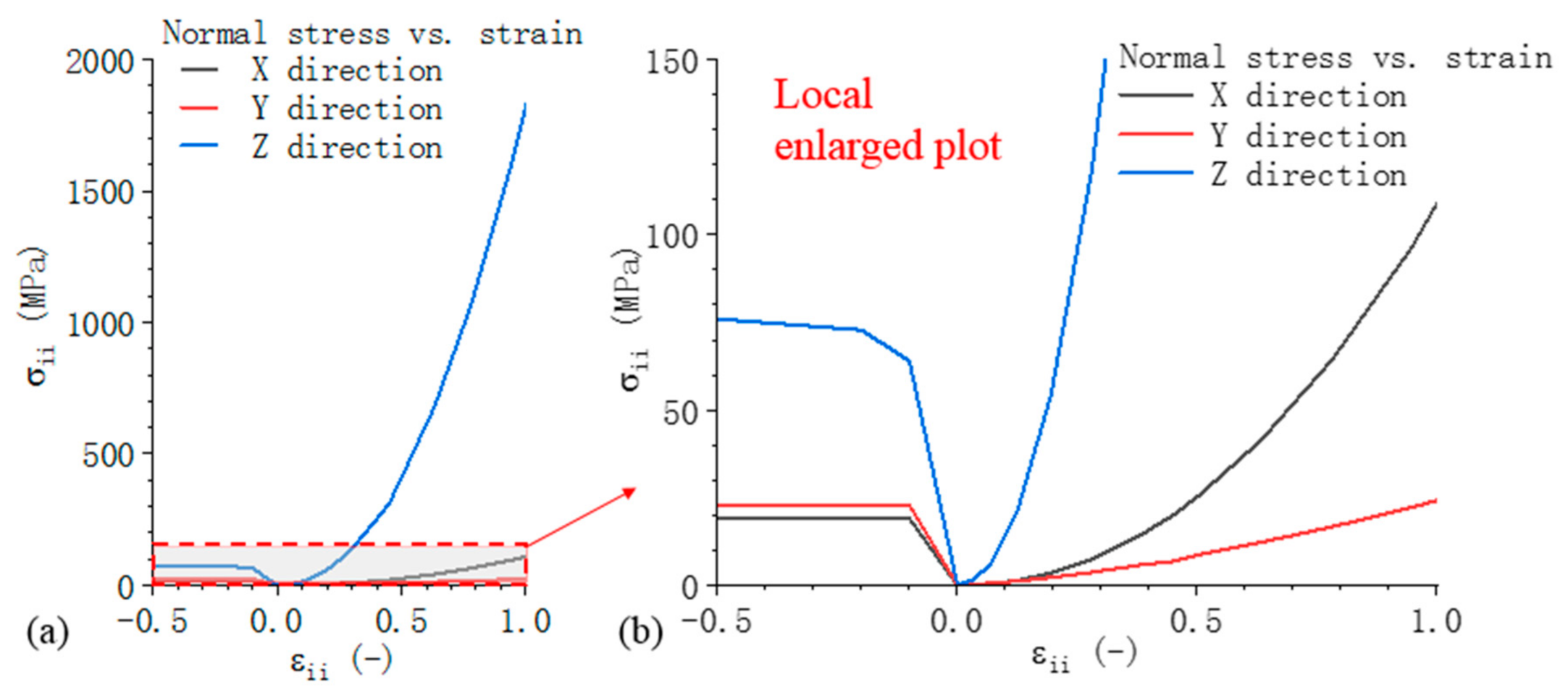
The force-displacement responses and the failure intrusions are shown in
Figure 2. The experimental results indicate remarkably different deformation responses and failure tolerances along different directions of the jellyroll in prismatic cell. For detailed information about the cells and the experimental setup, the readers can refer to Zhu et al. [
16].
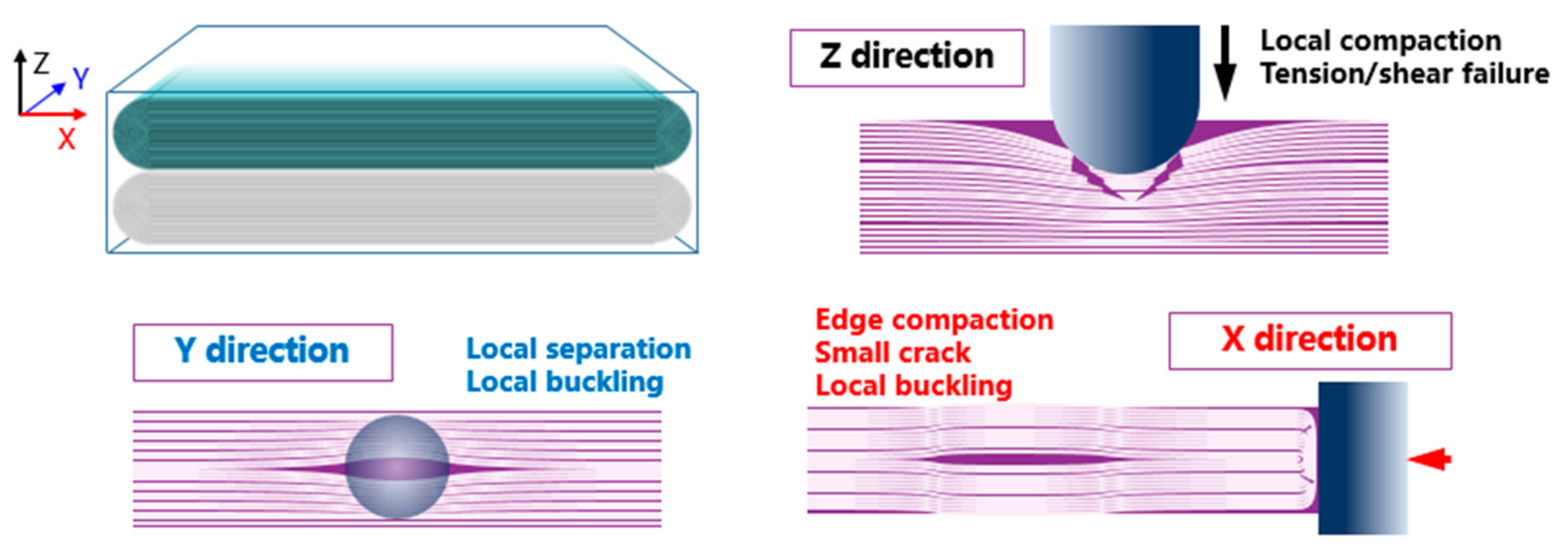
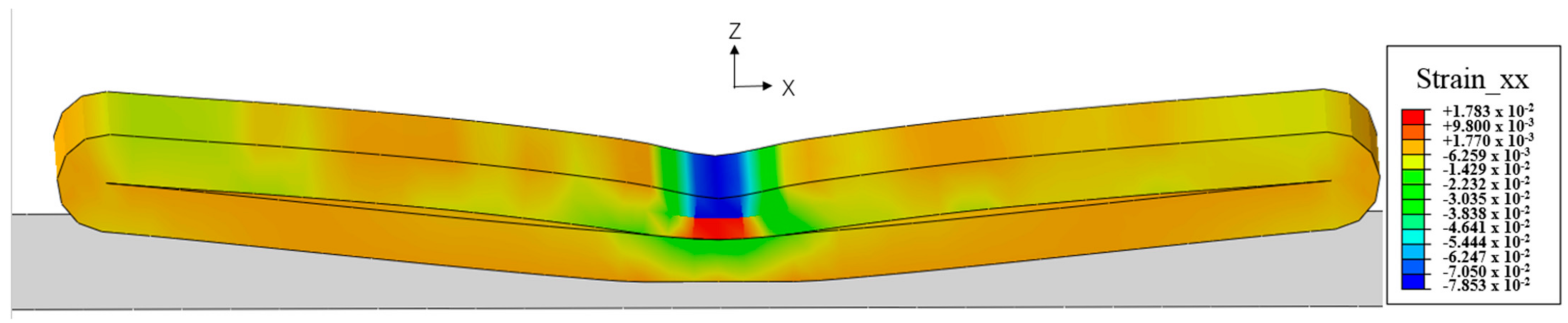
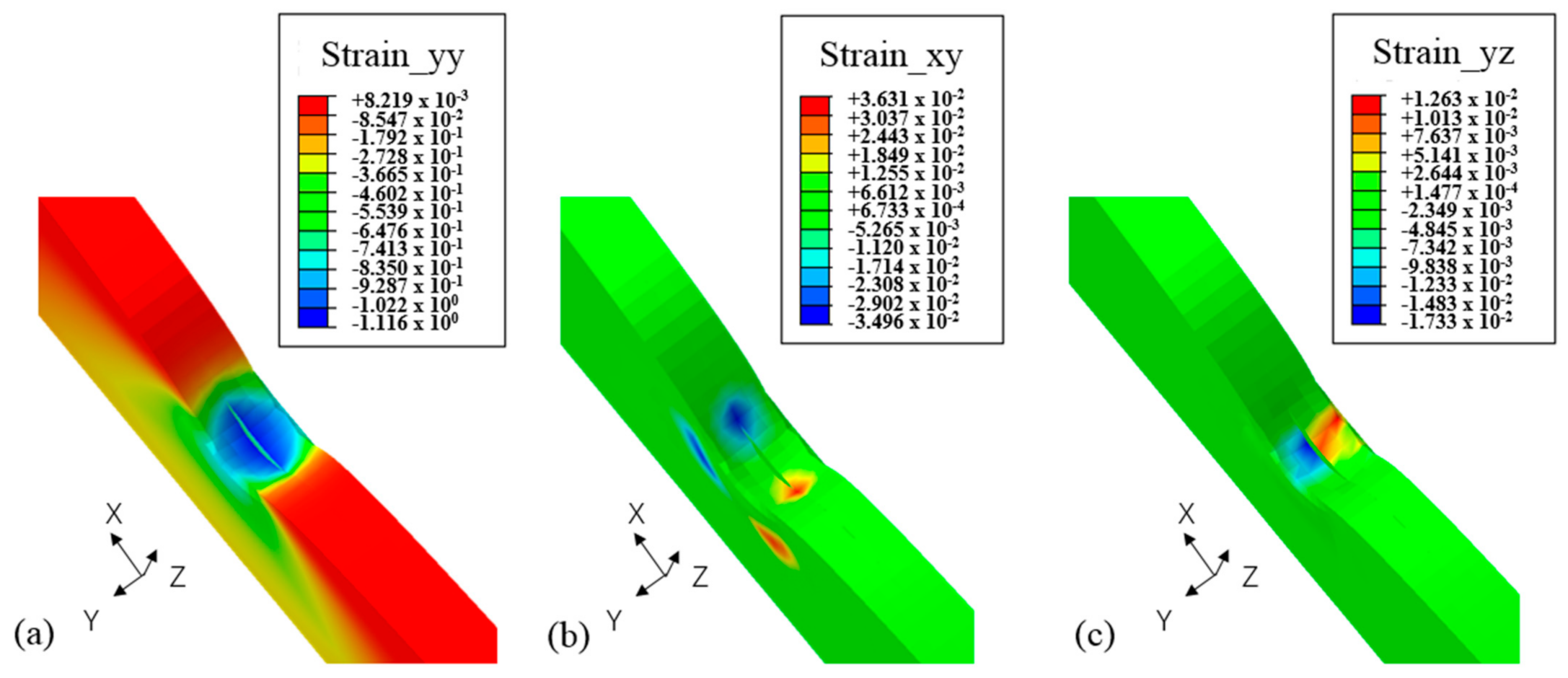
During the tests, we noticed that in the indentation test along Z direction, a crack penetrated the whole sample below the indenter and the jellyroll was divided into two parts. Inclined shear zones were found at both sides of the crack (as shown in the figure with purple line) and the jellyroll deformed more seriously between the shear zones. At this area, the components of jellyroll suffered tensile and shear deformation. As for the samples along X and Y directions, no apparent crack across the layers was found after the tests and the deformation type of the jellyrolls was mainly the buckling of the layer structures. Under the indentation test along Y direction, the indenter tended to separate the layer structures of jellyroll and local buckling was found. For the indentation test along X direction, the edge of the jellyroll was compacted, and small crack occurred under the indenter. The shape of small crack was similar to the crack along Z direction impact. Local buckling was also found in the middle of jellyroll. The two parts of jellyroll on the either side of the rolling center tends to disperse to the sides of itself, and this phenomenon reduces the contact stiffness and the risk of internal short circuit. The deformation and failure/buckling modes are shown in
Figure 3.
6. Conclusions
The aim of the study is to produce a homogenized FE model for the jellyroll in the prismatic battery cell that can capture the multidirectional failure behaviors. Based on the framework of a modified honeycomb material model, a user subroutine is implanted in Abaqus to fulfill the homogenized equivalence of the jellyroll. This model can correctly describe the anisotropic mechanical response as shown in the experiments, providing a reliable basis for further modeling of failure onsets along different directions.
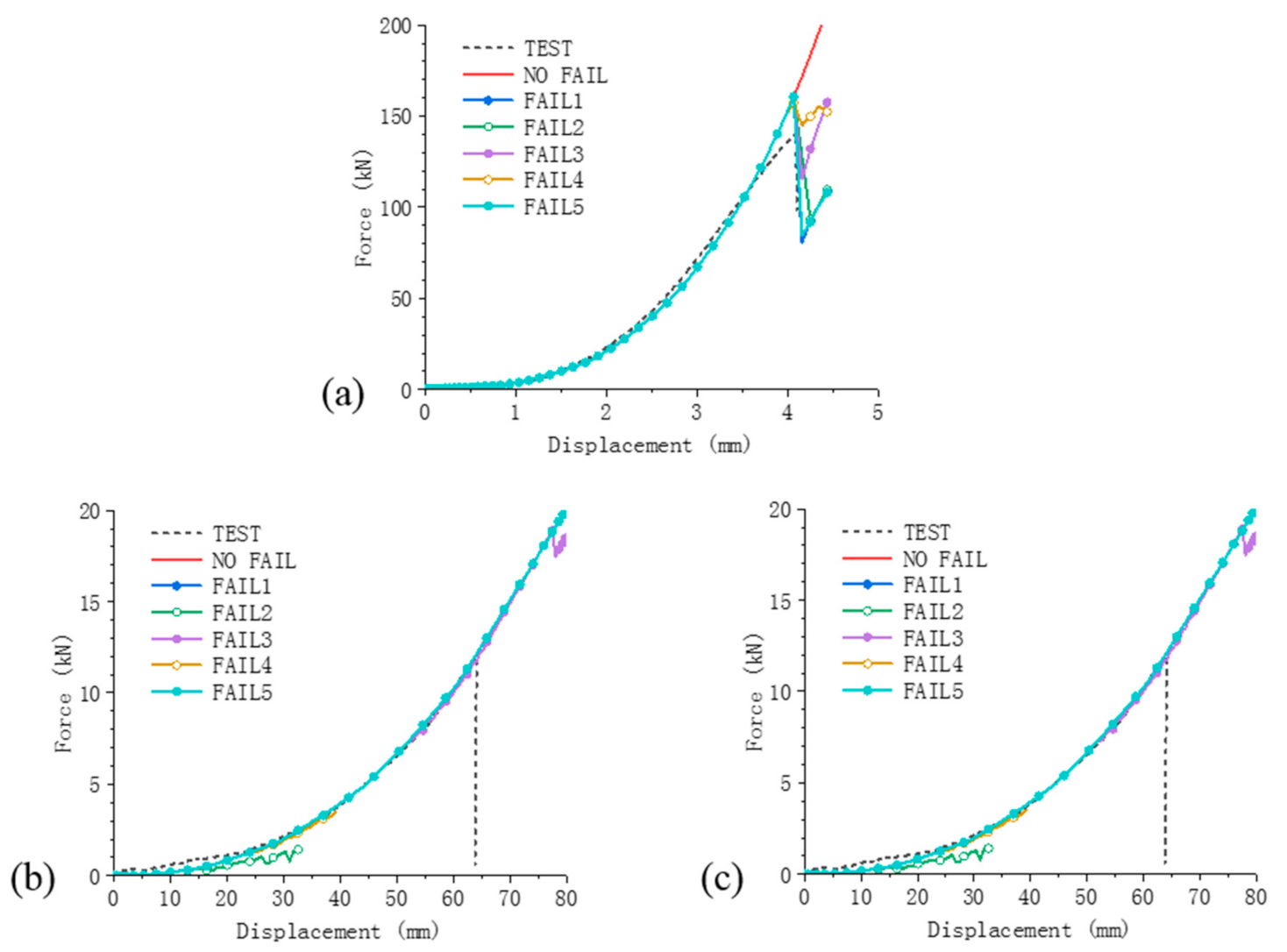
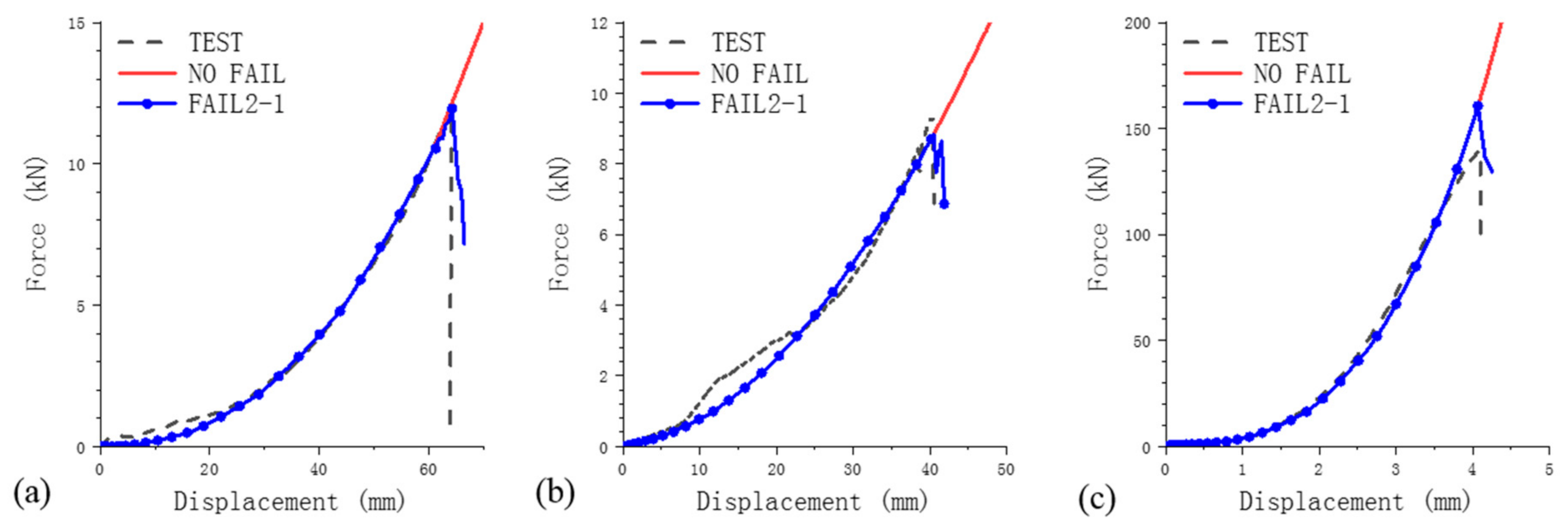
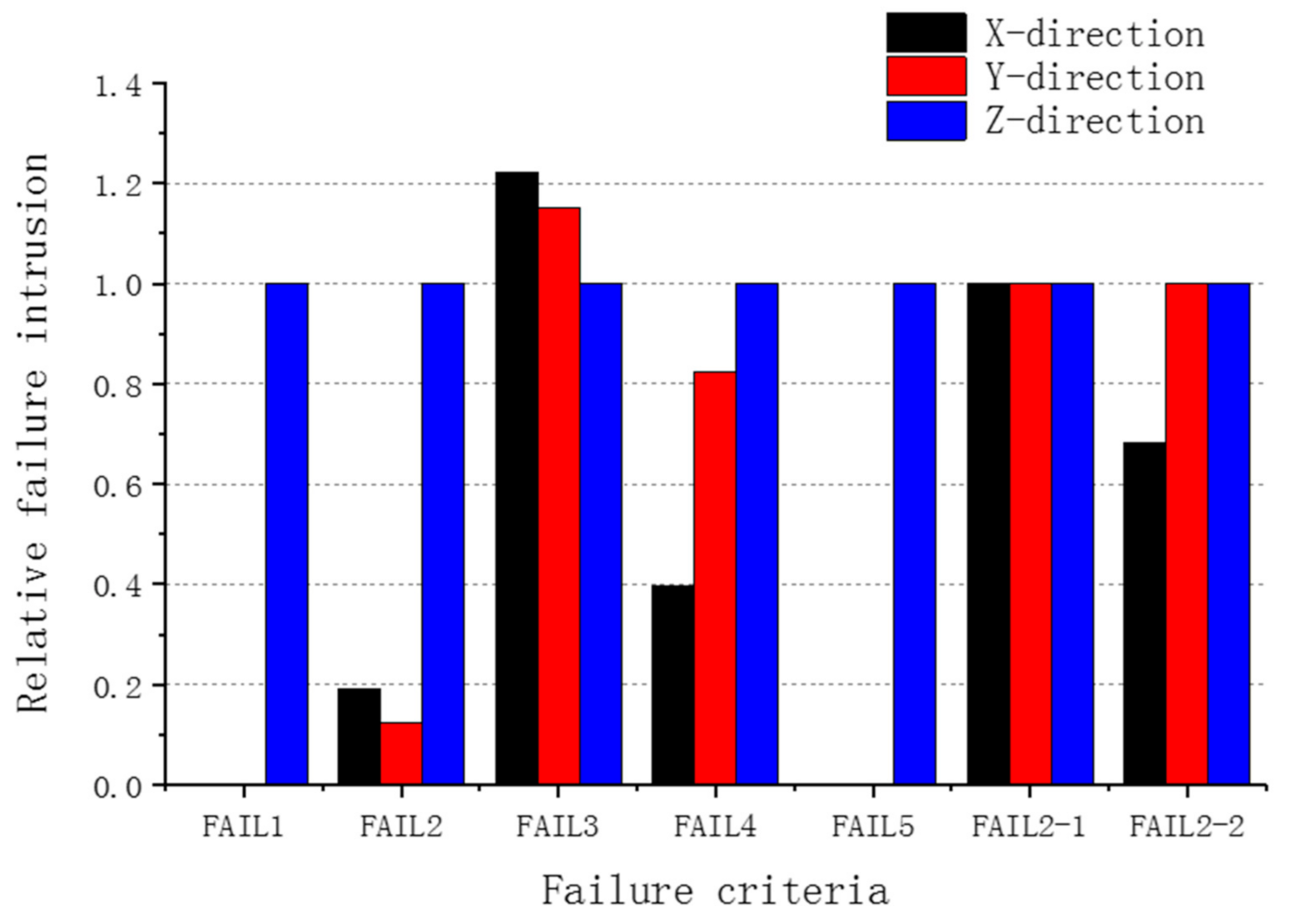
To extend the current jellyroll model for failure simulation, five single-parameter failure criteria are examined at first. With the same calibration and validation process, all the five criteria with failure parameter values identified, from the Z direction, that the loading case failed to properly predict the failure onsets of jellyroll in the other two loading cases along different directions.
Analysis of the indentation process and deformation concentration mode under various cases suggests that introducing a certain combined criterion is promising to address the highly directional failure behavior for jellyroll structures. Two specific combined failure criteria are then proposed based on observation of the local strain evolution in different loading cases. Calibration and validation results indicate that both combined criteria are able to accurately predict the failure onsets in all the indentation tests along three different directions.
The homogenized FE model developed in the present paper achieves high computational efficiency and accuracy, and it comes up with effective combined failure criteria for predicting directional failure onsets of jellyroll. These features enable the extended model to meet the requirements in modeling batteries in large-scale structures and under complex loading conditions. On the other hand, we have to mention the limitations of the current model, as it still has the common shortcoming of the homogenized model category and the failure criterion is still an empirical definition. We cannot count on such a model to accurately predict details of the local damage or failure occurrence and evolution. In those aspects, detailed FE models and other characterization approaches like XCT image analysis have irreplaceable advantages.