Swarm-Inspired Algorithms to Optimize a Nonlinear Gaussian Adaptive PID Controller
Abstract
1. Introduction
2. Optimization Algorithms
2.1. Particle Swarm Optimization (PSO)
- : the current particle velocity;
- : the inertia constant, set at ;
- : the position of all particle from previously looping;
- : the cognitive coefficient;
- : the social coefficient;
- and : the randomness factors generated from a uniform distribution, in the range between 0 and 1;
- : the best position of each particle (personal best); and
- : the best global position among all particles (global best).
| Algorithm 1 Particle Swarm Optimization-Pseudocode |
| 1: Randomly initialize a population of particles 2: Calculate the fitness of each particle through the position 3: for do 4: for each particle do 5: Update using Equation (2) 6: Update particle position using Equation (1) 7: Evaluate the fitness 8: if better than then 9: 10: end if 11: if better than then 12: 13: end if 14: end for 15: end for 16: return Adapted from [35] |
2.2. Artificial Bee Colony (ABC)
2.2.1. Initialization Stage
2.2.2. Employed Bee Stage
2.2.3. Onlooker Bee Stage
2.2.4. Scout Bee Stage
| Algorithm 2 Artificial Bee Colony-Pseudocode |
|
1: Initialize a bee swarm with N employed and onlooker bees 2: Initialize a random clustering for employed bees and compute the cluster center matrix. 3: Compute fitness values. 4: If the number of scouts exceeds , make the employed bees with the worst fitness as scouts and the rest as employed. 5: Apply random update to employed bee. If fitness has improved, update the cluster centers. 6: Set the solution (cluster center matrix) for each onlooker bee by choosing a solution from the employed bees with probability proportional to its fitness. 7: Apply random update to each onlooker. If the fitness improves, update cluster centers. 8: Make the employed bees scouts for which has been reached. 9: Remember the best solution. 10: Go to 3 and repeat MCN times. Adapted from [39] |
2.3. Whale Optimization Algorithm (WOA)
2.3.1. Encircling Prey
2.3.2. Bubble-Net
- Spiral updating position: The following steps perform the simulation for this behavior:
- The distance between the current position and the best solution is calculated;
- The propeller-shaped movement of humpback whales is imitated by creating a spiral equation as in (10) [44]:where indicates the distance of the i-th whale to the prey or best solution obtained so far, b is a constant to define the shape of the logarithmic spiral, l is a random value drawn in the interval [−1,1], and is the element-by-element multiplication.
2.3.3. Search for Pray
| Algorithm 3 Whale Optimization Algorithm-Pseudocode |
|
1: Initialize the whale population 2: Calculate the fitness of each search agent 3: 4: for do 5: if () then 6: if ( then 7: Update the position of the current search agent by Equation (6) 8: else 9: if then 10: Select random search agent () 11: Update the position of the current search agent by Equation (13) 12: end if 13: end if 14: else 15: if () then 16: Update the position of the current search agent by (10) 17: end if 18: end if 19: 20: end for 21: Check if any search agent goes beyond the search space and amend it 22: Calculate the Fitness of each search agent 23: Update if there is a better solution 24: return Adapted from [40] |
3. Gaussian PID Controller
4. Buck Converter
5. Computational Results
5.1. Performance Evaluation Metric and Coding
5.2. Buck Converter Response to a Linear PID
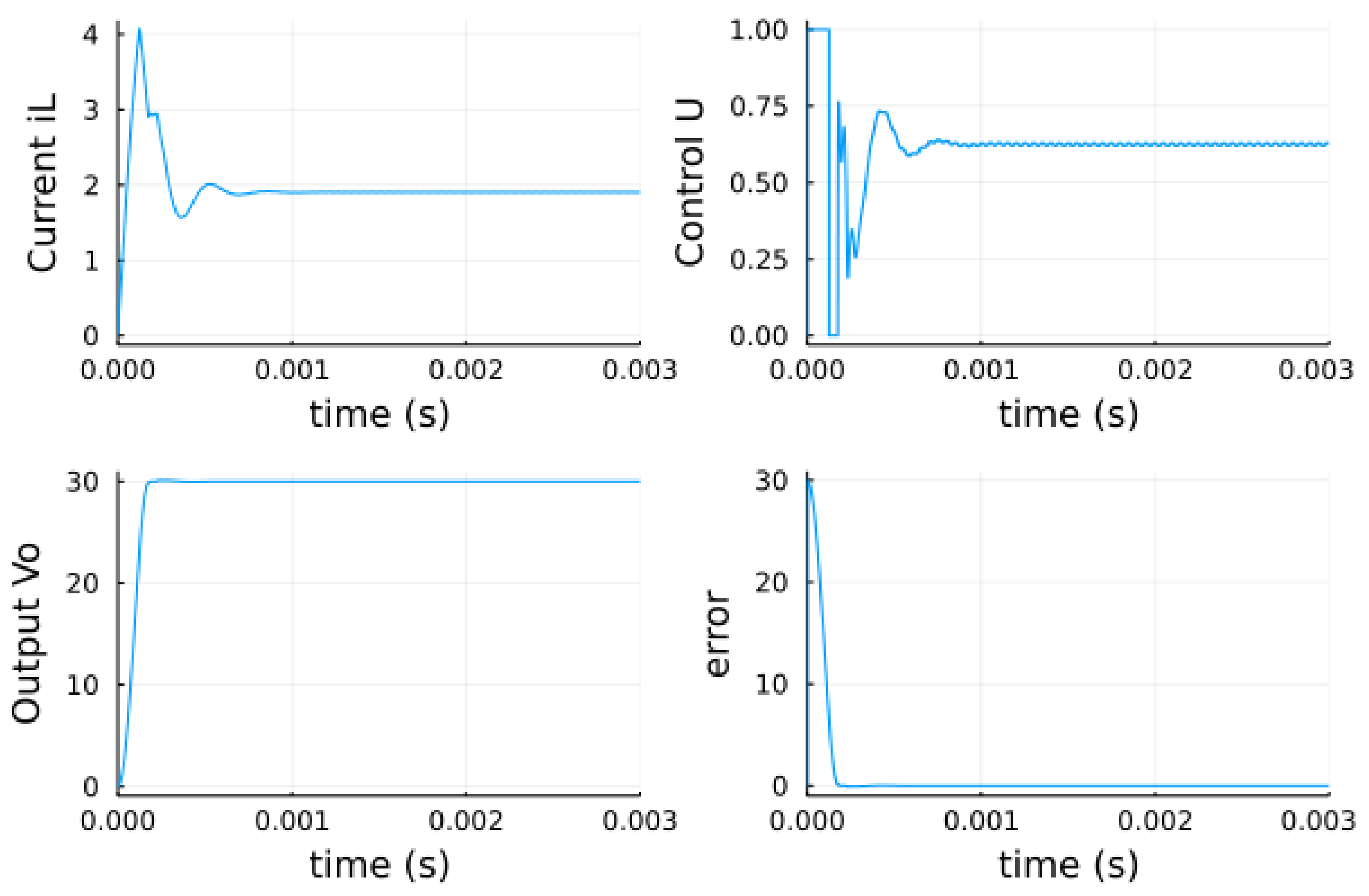
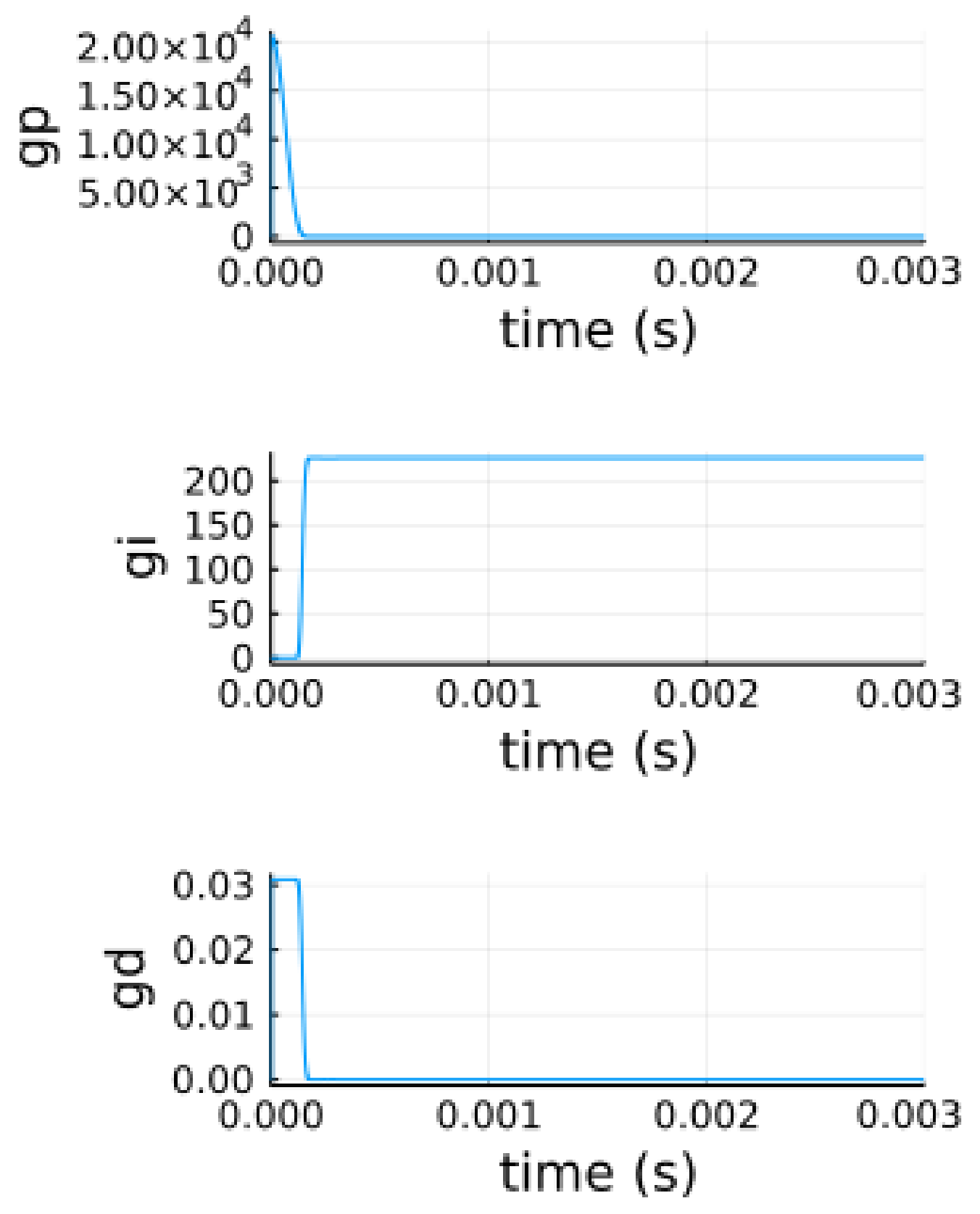
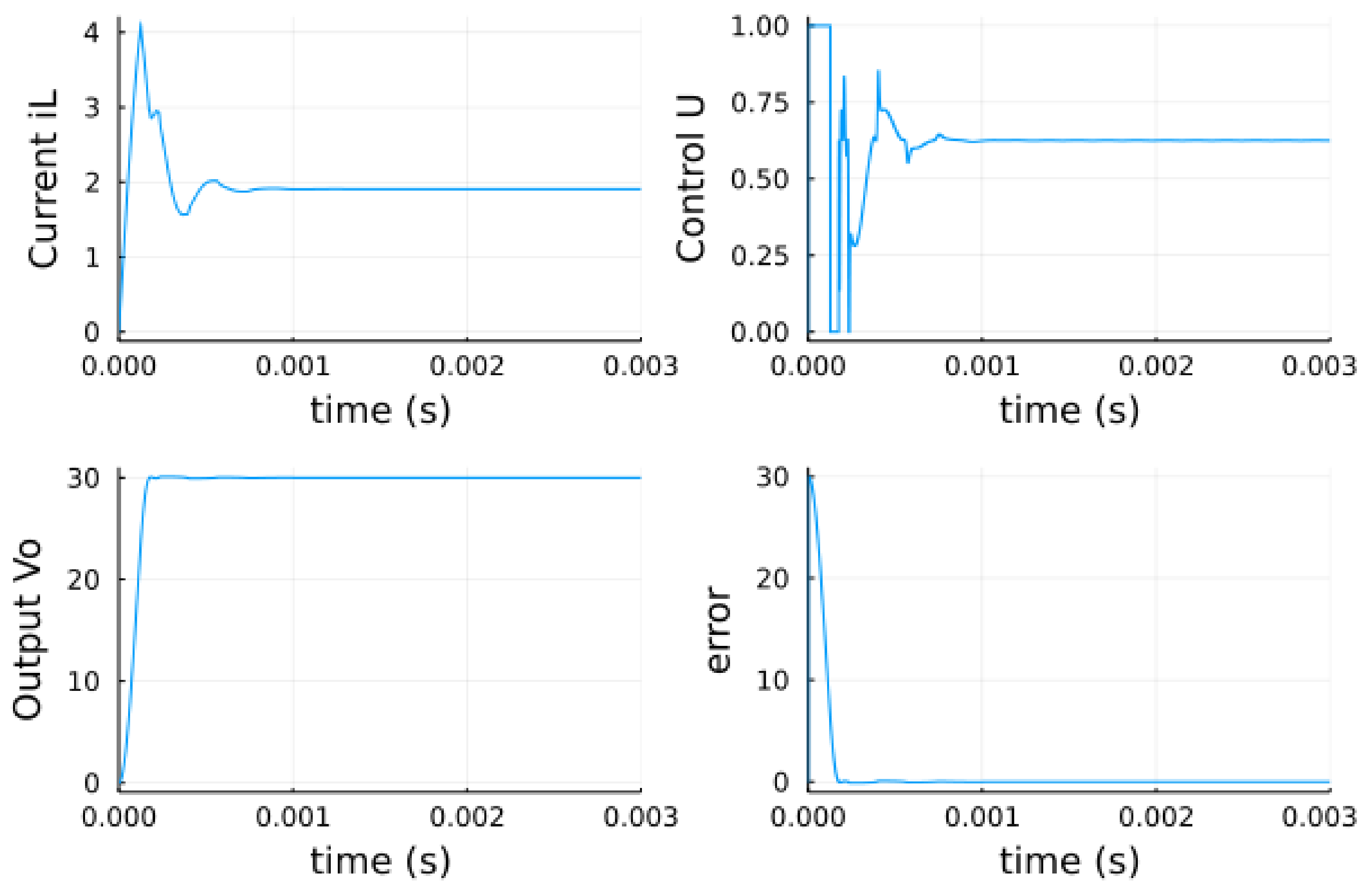
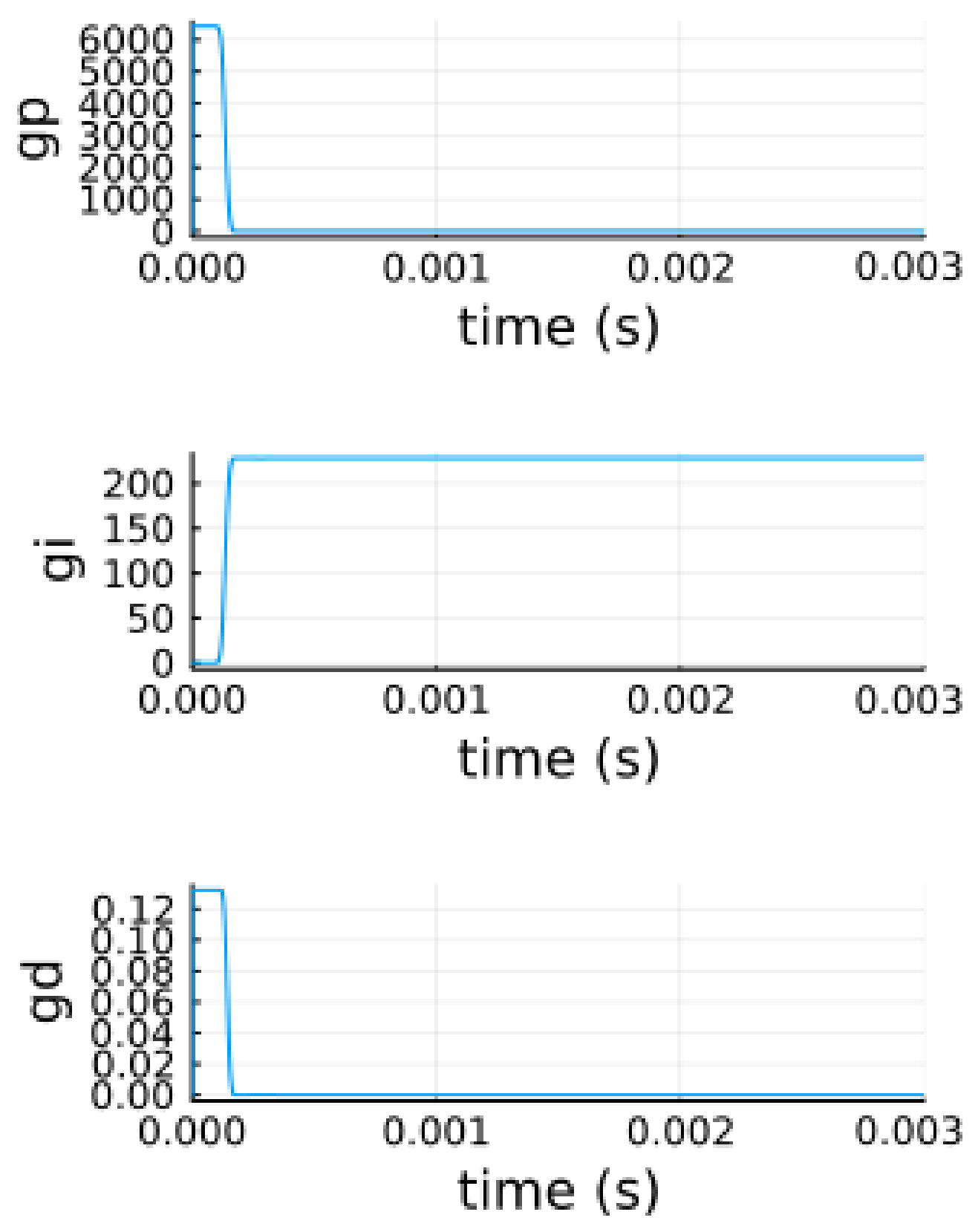
5.3. Optimization by Bioinspired Algorithms
5.3.1. Parameter Optimization Using PSO
5.3.2. Parameters Optimization Using ABC
5.3.3. Parameter Optimization Using WOA
5.4. Analysis of the Results
- PSO × ABC: p-value = ;
- PSO × WOA: p-value = ;
- ABC × WOA: p-value = .
5.5. Future Research
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ABC | Artificial Bee Colony |
| PSO | Partcile Swarm Optimization |
| WOA | Whale Optimization Algorithm |
| PID | Proportional, Integral and Derivative |
| GAPID | Gaussian Adaptive PID |
References
- Gong, Y.J.; Chen, W.N.; Zhan, Z.H.; Zhang, J.; Li, Y.; Zhang, Q.; Li, J.J. Distributed evolutionary algorithms and their models: A survey of the state-of-the-art. Appl. Soft Comput. 2015, 34, 286–300. [Google Scholar] [CrossRef]
- Figueiredo, E.; Macedo, M.; Siqueira, H.V.; Santana, C.J., Jr.; Gokhale, A.; Bastos-Filho, C.J. Swarm intelligence for clustering—A systematic review with new perspectives on data mining. Eng. Appl. Artif. Intell. 2019, 82, 313–329. [Google Scholar] [CrossRef]
- de Souza Tadano, Y.; Siqueira, H.V.; Alves, T.A. Unorganized machines to predict hospital admissions for respiratory diseases. In Proceedings of the 2016 IEEE Latin American Conference on Computational Intelligence (LA-CCI), Cartagena, Spain, 2–4 November 2016; pp. 1–6. [Google Scholar]
- Miao, Z.; Yong, P.; Mei, Y.; Quanjun, Y.; Xu, X. A discrete PSO-based static load balancing algorithm for distributed simulations in a cloud environment. Future Gener. Comput. Syst. 2021, 115, 497–516. [Google Scholar] [CrossRef]
- Santos, P.; Macedo, M.; Figueiredo, E.; Santana, C.J.; Soares, F.; Siqueira, H.; Maciel, A.; Gokhale, A.; Bastos-Filho, C.J. Application of PSO-based clustering algorithms on educational databases. In Proceedings of the 2017 IEEE Latin American Conference on Computational Intelligence (LA-CCI), Arequipa, Peru, 8–10 November 2017; pp. 1–6. [Google Scholar]
- Siqueira, H.; Figueiredo, E.; Macedo, M.; Santana, C.J.; Santos, P.; Bastos-Filho, C.J.; Gokhale, A.A. Double-swarm binary Particle Swarm Optimization. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Santana, C.J., Jr.; Macedo, M.; Siqueira, H.; Gokhale, A.; Bastos-Filho, C.J. A novel binary Artificial Bee Colony algorithm. Future Gener. Comput. Syst. 2019, 98, 180–196. [Google Scholar] [CrossRef]
- Devi, S.; Geethanjali, M. Application of modified bacterial foraging optimization algorithm for optimal placement and sizing of distributed generation. Expert Syst. Appl. 2014, 41, 2772–2781. [Google Scholar] [CrossRef]
- Siqueira, H.; Figueiredo, E.; Macedo, M.; Santana, C.J.; Bastos-Filho, C.J.; Gokhale, A.A. Boolean binary cat swarm optimization algorithm. In Proceedings of the 2018 IEEE Latin American Conference on Computational Intelligence (LA-CCI), Gudalajara, Mexico, 7–9 November 2018; pp. 1–6. [Google Scholar]
- Siqueira, H.; Santana, C.; Macedo, M.; Figueiredo, E.; Gokhale, A.; Bastos-Filho, C. Simplified binary cat swarm optimization. Integr. Comput. Aided Eng. 2020, 28, 35–50. [Google Scholar] [CrossRef]
- Tang, J.; Ma, Y.; Guan, J.; Yan, C. A max–min ant system for the split delivery weighted vehicle routing problem. Expert Syst. Appl. 2013, 40, 7468–7477. [Google Scholar] [CrossRef]
- Siqueira, H.; Macedo, M.; Tadano, Y.D.S.; Alves, T.A.; Stevan, S.L.; Oliveira, D.S.; Marinho, M.H.; Neto, P.S.; de Oliveira, J.F.; Luna, I.; et al. Selection of temporal lags for predicting riverflow series from hydroelectric plants using variable selection methods. Energies 2020, 13, 4236. [Google Scholar] [CrossRef]
- Santana, C.J.; Bastos-Filho, C.J.; Macedo, M.; Siqueira, H. SBFSS: Simplified binary fish school search. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 2595–2602. [Google Scholar]
- Purushothama, G.; Jenkins, L. Simulated annealing with local search-a hybrid algorithm for unit commitment. IEEE Trans. Power Syst. 2003, 18, 273–278. [Google Scholar] [CrossRef]
- Gholizadeh, S.; Danesh, M.; Gheyratmand, C. A new Newton metaheuristic algorithm for discrete performance-based design optimization of steel moment frames. Comput. Struct. 2020, 234, 106250. [Google Scholar] [CrossRef]
- Belotti, J.T.; Castanho, D.S.; Araujo, L.N.; da Silva, L.V.; Alves, T.A.; Tadano, Y.S.; Stevan, S.L., Jr.; Corrêa, F.C.; Siqueira, H.V. Air pollution epidemiology: A simplified Generalized Linear Model approach optimized by bio-inspired metaheuristics. Environ. Res. 2020, 191, 110106. [Google Scholar] [CrossRef]
- Puchta, E.D.P.; Lucas, R.; Ferreira, F.R.V.; Siqueira, H.V.; Kaster, M.S. Gaussian adaptive PID control optimized via genetic algorithm applied to a step-down DC-DC converter. In Proceedings of the 12th IEEE International Conference on Industry Applications (INDUSCON 2016), Curitiba, Brazil, 20–23 November 2016. [Google Scholar] [CrossRef]
- Borges, F.G.; Itaborahy, M.A.; Siqueira, H.V.; Correa, F.C.; Kaster, M.S. Comparison of several Genetic Algorithm strategies on a nonlinear GAPID controller optimization applied to a Buck converter. In Proceedings of the Congresso Brasileiro de Automática, Sociedade Brasileira de Automática, João Pessoa, Brazil, 9–12 September 2018. [Google Scholar]
- Borges, F.G.; MOnteiro, L.F.; Martins, M.S.R.; Correa, F.C.; Siqueira, H.V.; Kaster, M.S. Performance Comparison of Particle Swarm optimization Strategies to Adjust a Nonlinear GAPID Controller. In Proceedings of the 2018 13th IEEE International Conference on Industry Applications (INDUSCON), Sao Paulo, Brazil, 12–14 November 2018; pp. 685–691. [Google Scholar]
- Puchta, E.D.P.; Siqueira, H.V.; dos Santos Kaster, M. Optimization tools based on metaheuristics for performance enhancement in a Gaussian adaptive PID controller. IEEE Trans. Cybern. 2019, 50, 1185–1194. [Google Scholar] [CrossRef]
- Savran, A.; Kahraman, G. A fuzzy model based adaptive PID controller design for nonlinear and uncertain processes. ISA Trans. 2014, 53, 280–288. [Google Scholar] [CrossRef]
- Anderson, K.; Blankenship, G.; Lebow, L. A rule-based adaptive PID controller. In Proceedings of the 27th IEEE Conference on Decision and Control, Austin, TX, USA, 7–9 December 1988; Volume 1, pp. 564–569. [Google Scholar] [CrossRef]
- Benaskeur, A.; Desbiens, A. Backstepping-based adaptive PID control. IEE Proc. Control. Theory Appl. 2002, 149, 54–59. [Google Scholar] [CrossRef]
- Poulin, É.; Pomerleau, A.; Desbiens, A.; Hodouin, D. Development and evaluation of an auto-tuning and adaptive PID controller. Automatica 1996, 32, 71–82. [Google Scholar] [CrossRef]
- Radke, F.; Isermann, R. A parameter-adaptive PID-controller with stepwise parameter optimization. Automatica 1987, 23, 449–457. [Google Scholar] [CrossRef]
- Delavari, H.; Ghaderi, R.; Ranjbar, N.A.; HosseinNia, S.H.; Momani, S. Adaptive Fractional PID Controller for Robot Manipulator. In Proceedings of the FDA’10 the 4th IFAC Workshop Fractional Differentiation and Its Applications, Badajoz, Spain, 18–20 October 2010. [Google Scholar]
- Lin, C.M.; Lin, M.H.; Chen, C.W. SoPC-Based Adaptive PID Control System Design for Magnetic Levitation System. IEEE Syst. J. 2011, 5, 278–287. [Google Scholar] [CrossRef]
- Srivastava, V.; Srivastava, S. Whale Optimization algorithm (WOA) based control of nonlinear systems. In Proceedings of the 2019 2nd International Conference on Power Energy, Environment and Intelligent Control (PEEIC), Greater Noida, India, 18–19 October 2019; pp. 402–406. [Google Scholar]
- Kumar, A.A.; Kumar, S.G. Application of Whale Optimization Algorithm for tuning of a PID controller for a drilling machine. In Proceedings of the ICAARS 2018, Coimbatore, India, 14–15 December 2018. [Google Scholar]
- Fan, Q.; Chen, Z.; Li, Z.; Xia, Z.; Yu, J.; Wang, D. A new improved Whale Optimization algorithm with joint search mechanisms for high-dimensional global optimization problems. Eng. Comput. 2020, 1–28. [Google Scholar] [CrossRef]
- Niknam, T. A new fuzzy adaptive hybrid Particle Swarm Optimization algorithm for non-linear, non-smooth and non-convex economic dispatch problem. Appl. Energy 2010, 87, 327–339. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Siqueira, H.; Belotti, J.T.; Boccato, L.; Luna, I.; Attux, R.; Lyra, C. Recursive linear models optimized by bioinspired metaheuristics to streamflow time series prediction. Int. Trans. Oper. Res. 2021. [Google Scholar] [CrossRef]
- Elloumi, W.; El Abed, H.; Abraham, A.; Alimi, A.M. A comparative study of the improvement of performance using a PSO modified by ACO applied to TSP. Appl. Soft Comput. 2014, 25, 234–241. [Google Scholar] [CrossRef]
- Xiao, G.; Juan, Z.; Gao, J. Travel mode detection based on neural networks and particle swarm optimization. Information 2015, 6, 522–535. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical Report; Citeseer: University Park, PA, USA, 2005. [Google Scholar]
- Awadallah, M.A.; Al-Betar, M.A.; Bolaji, A.L.; Alsukhni, E.M.; Al-Zoubi, H. Natural selection methods for Artificial Bee Colony with new versions of onlooker bee. Soft Comput. 2019, 23, 6455–6494. [Google Scholar] [CrossRef]
- Karaboga, D.; Akay, B. A comparative study of Artificial Bee Colony algorithm. Appl. Math. Comput. 2009, 214, 108–132. [Google Scholar] [CrossRef]
- Hussain, S.F.; Pervez, A.; Hussain, M. Co-clustering optimization using Artificial Bee Colony (ABC) algorithm. Appl. Soft Comput. 2020, 97, 106725. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Watkins, W.A.; Schevill, W.E. Aerial observation of feeding behavior in four baleen whales: Eubalaena glacialis, Balaenoptera borealis, Megaptera novaeangliae, and Balaenoptera physalus. J. Mammal. 1979, 60, 155–163. [Google Scholar] [CrossRef]
- Goldbogen, J.A.; Friedlaender, A.S.; Calambokidis, J.; Mckenna, M.F.; Simon, M.; Nowacek, D.P. Integrative approaches to the study of baleen whale diving behavior, feeding performance, and foraging ecology. BioScience 2013, 63, 90–100. [Google Scholar] [CrossRef]
- Tharwat, A.; Moemen, Y.S.; Hassanien, A.E. Classification of toxicity effects of biotransformed hepatic drugs using whale optimized support vector machines. J. Biomed. Inform. 2017, 68, 132–149. [Google Scholar] [CrossRef]
- McCann, S.; Lowe, D.G. Local naive bayes nearest neighbor for image classification. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3650–3656. [Google Scholar]
- Soriano-Sánchez, A.G.; Rodríguez-Licea, M.A.; Pérez-Pinal, F.J.; Vázquez-López, J.A. Fractional-order approximation and synthesis of a PID controller for a buck converter. Energies 2020, 13, 629. [Google Scholar] [CrossRef]
- Ali, N.; Liu, Z.; Armghan, H.; Ahmad, I.; Hou, Y. LCC-S-Based Integral Terminal Sliding Mode Controller for a Hybrid Energy Storage System Using a Wireless Power System. Energies 2021, 14, 1693. [Google Scholar] [CrossRef]
- Ogata, K. Modern Control Engineering; Prentice Hall: Englewood Cliffs, NJ, USA, 2010. [Google Scholar]
- Kaster, M.; Cunha, G.; Burgardt, I.; Nascimento, C. Análise do uso de controle pid não linear aplicado a conversor buck. In Proceedings of the X Conferência Brasileira de Dinâmica, Controle e Aplicações, Aguas de Londoia, Brazil, 29 August–2 September 2011. [Google Scholar]
- Yfoulis, C.; Papadopoulou, S.; Voutetakis, S. Robust Linear Control of Boost and Buck-Boost DC-DC Converters in Micro-Grids with Constant Power Loads. Energies 2020, 13, 4829. [Google Scholar] [CrossRef]
- Siqueira, H.; Luna, I. Performance comparison of feedforward neural networks applied to streamflow series forecasting. Math. Eng. Sci. Aerosp. (MESA) 2019, 10, 41–53. [Google Scholar]

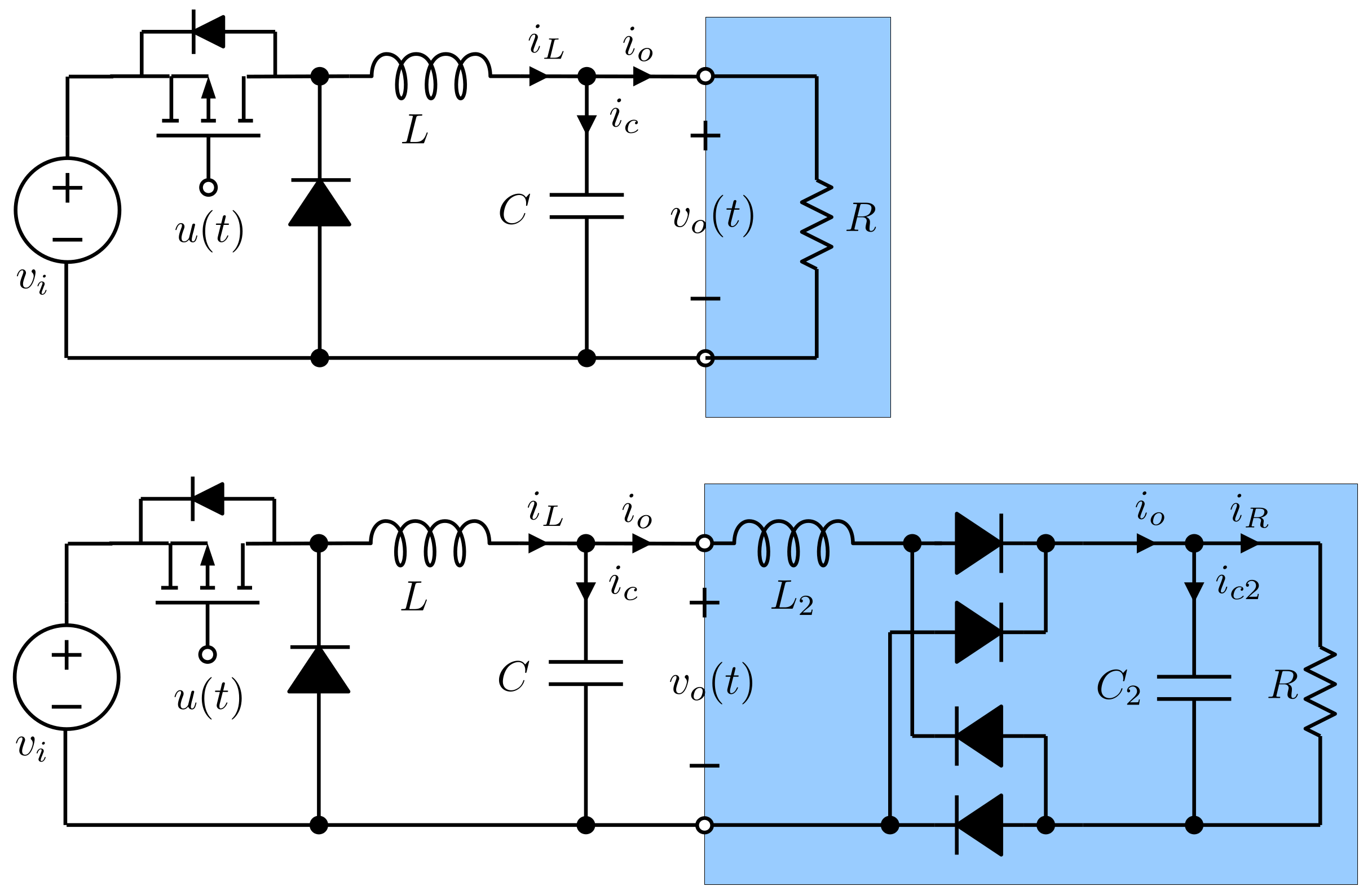
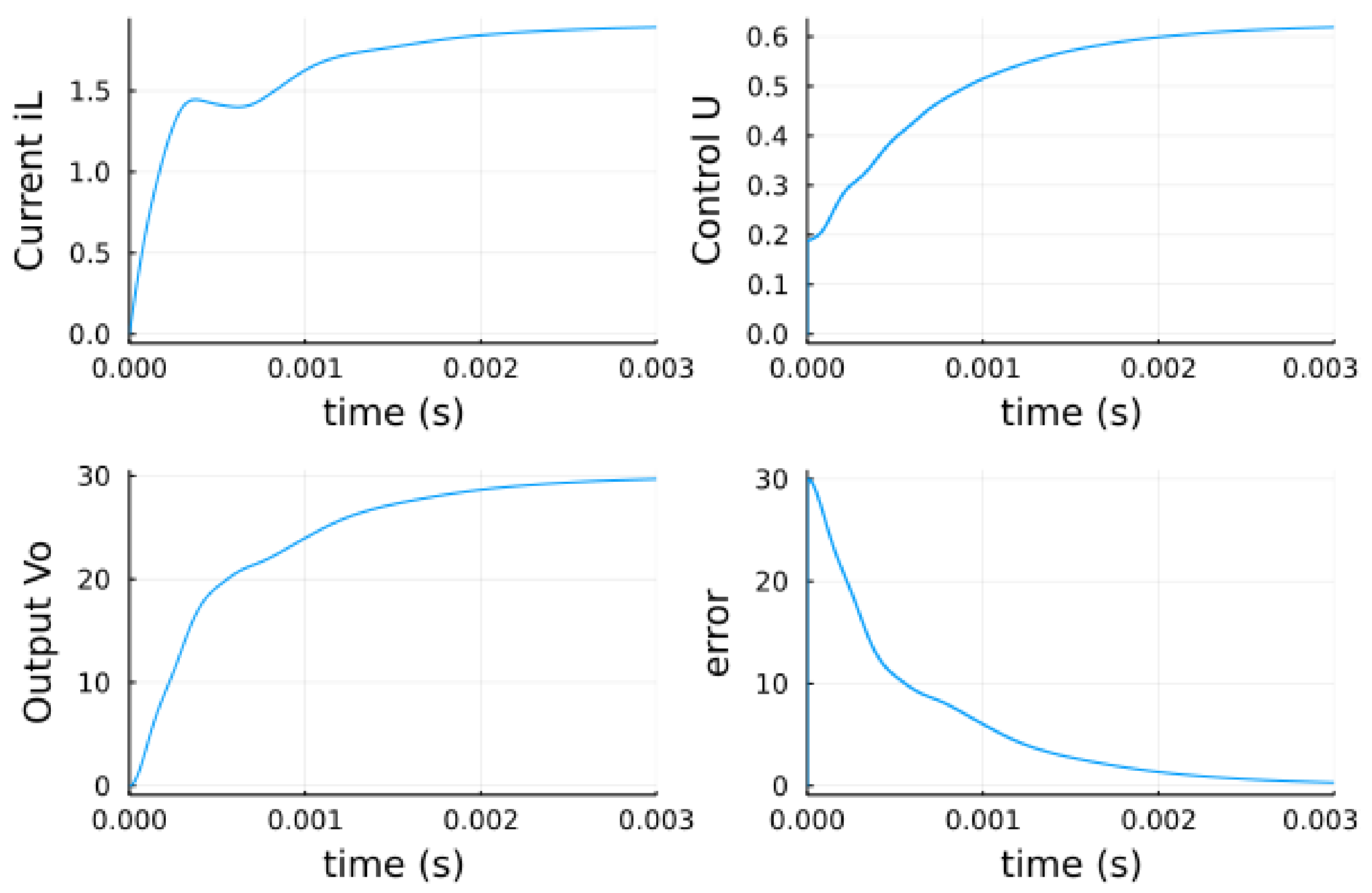

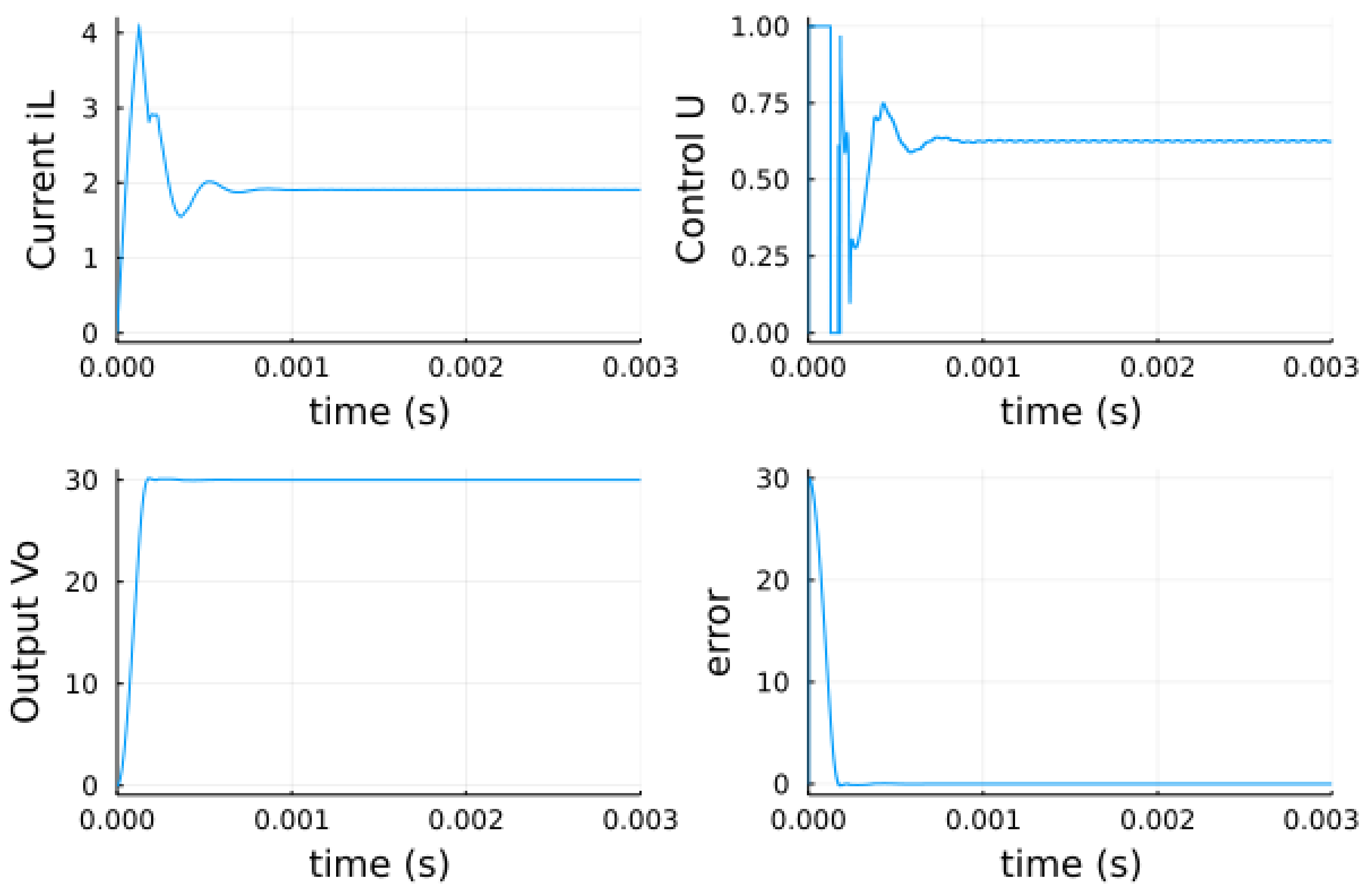
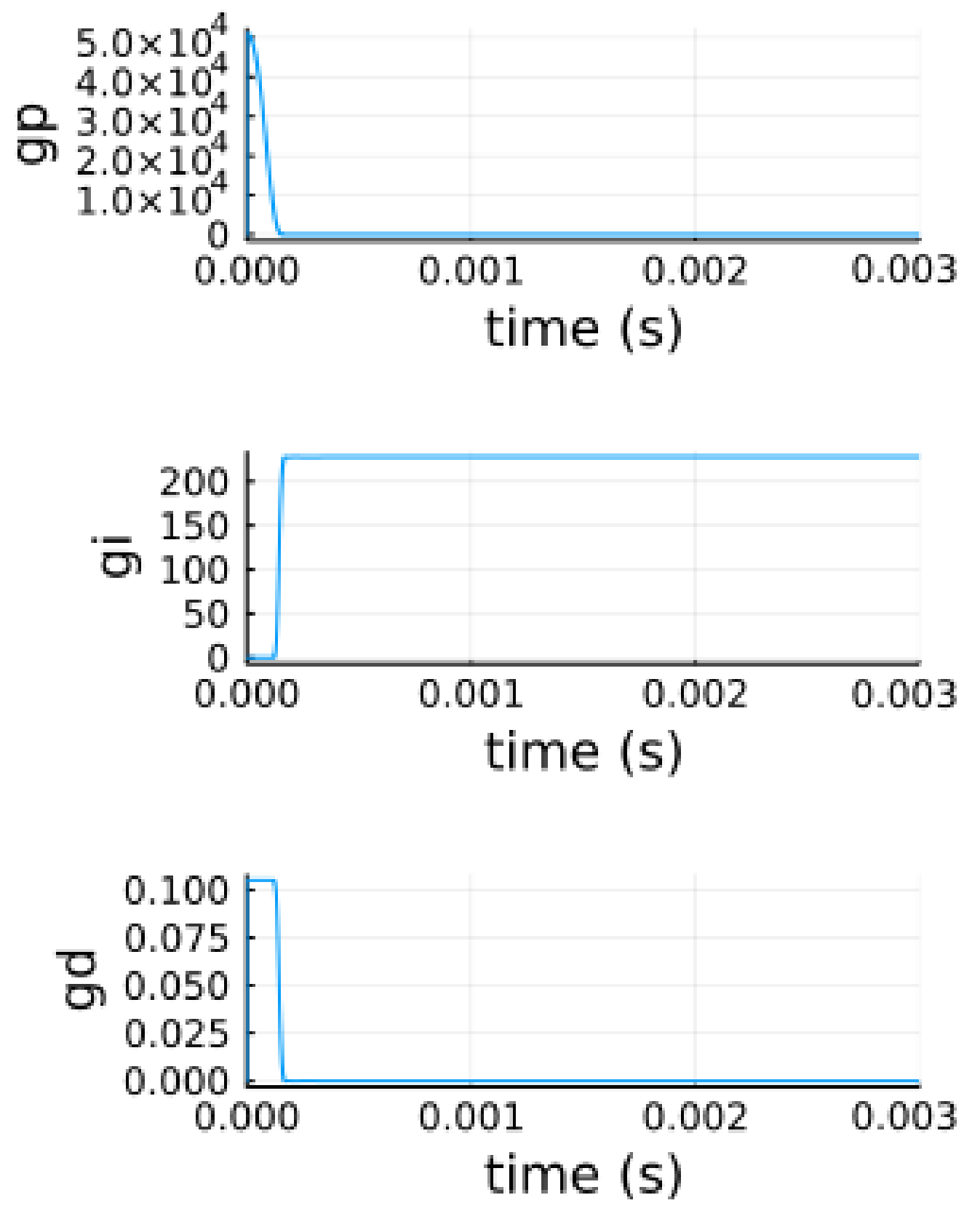

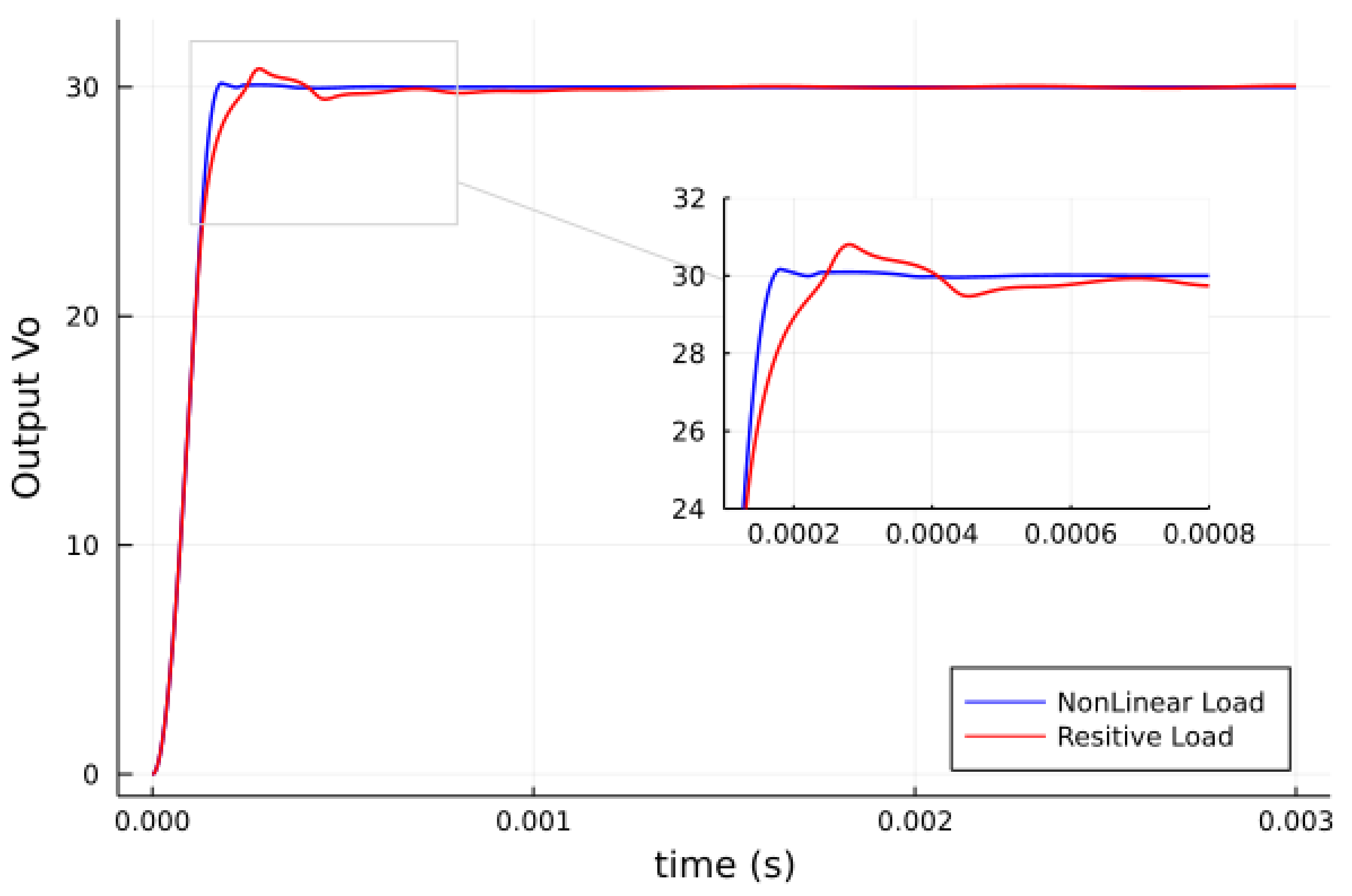

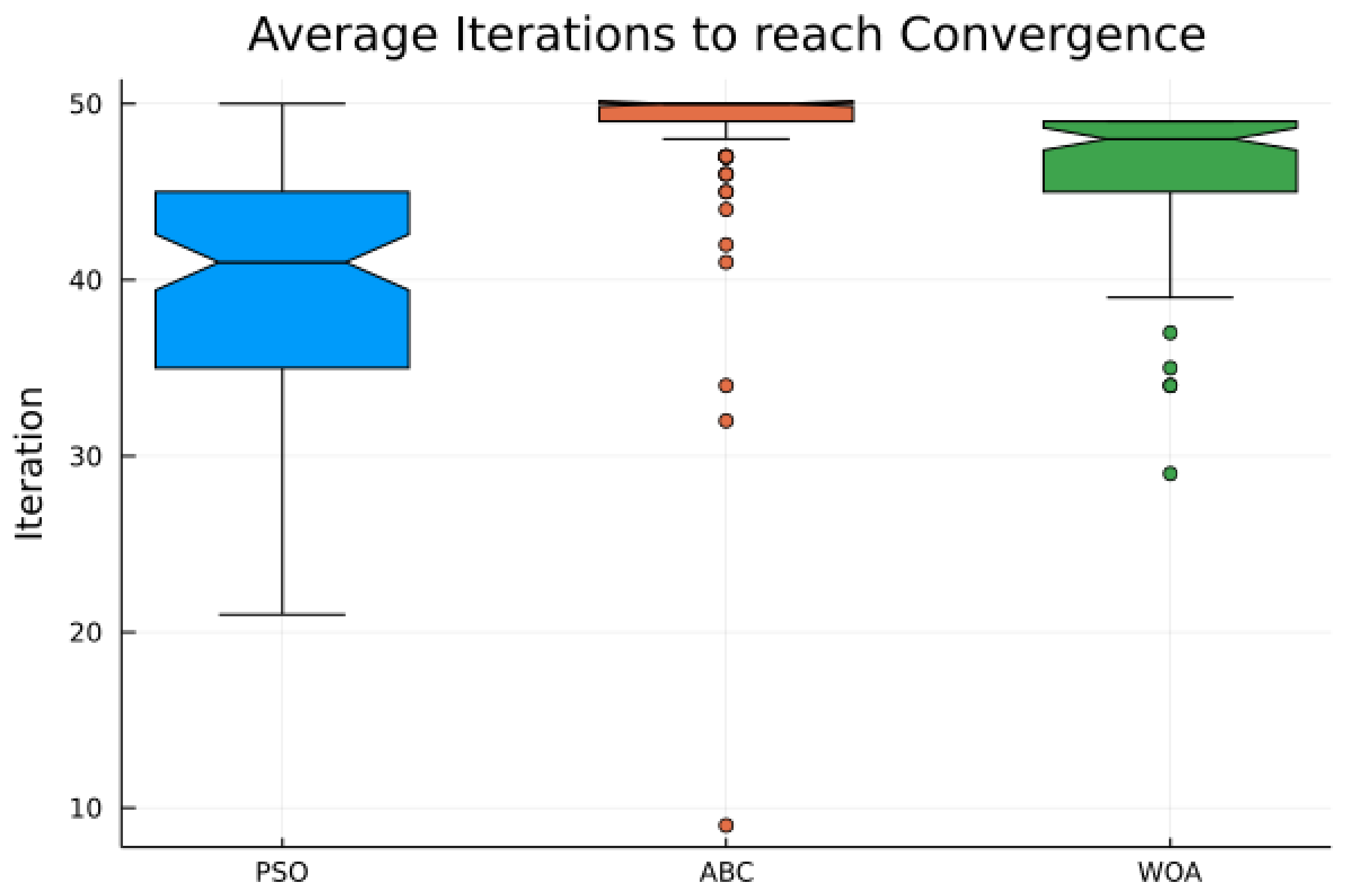
| Description | Symbol | Value |
|---|---|---|
| Input voltage | 48 V | |
| Output voltage | 30 V | |
| Converter Capacitor | C | 10 F |
| Converter Inductor | L | 1.2 mH |
| Load Resistance | R | 15 |
| Load Capacitor | 4.7 F | |
| Load Inductor | 0.5 mH |
| Parameters | PSO | ABC | WOA |
|---|---|---|---|
| 0.000541 | 3.93096 | 0.246775 | |
| 14.077712 | 1.02262e5 | 6419.73 | |
| 0.1 | 0.000249032 | 0.0384613 | |
| 208.560244 | 225.662 | 228.545 | |
| 0.170253 | 0.184214 | 0.186567 | |
| 0.01 | 0.09 | 0.0374831 | |
| 0.000570 | 0.0308419 | 0.132381 | |
| 0.1 | 0.09 | 0.0882509 |
| Results | PSO | ABC | WOA |
|---|---|---|---|
| Best | |||
| Mean | |||
| Standard Deviation |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Puchta, E.D.P.; Bassetto, P.; Biuk, L.H.; Itaborahy Filho, M.A.; Converti, A.; Kaster, M.d.S.; Siqueira, H.V. Swarm-Inspired Algorithms to Optimize a Nonlinear Gaussian Adaptive PID Controller. Energies 2021, 14, 3385. https://doi.org/10.3390/en14123385
Puchta EDP, Bassetto P, Biuk LH, Itaborahy Filho MA, Converti A, Kaster MdS, Siqueira HV. Swarm-Inspired Algorithms to Optimize a Nonlinear Gaussian Adaptive PID Controller. Energies. 2021; 14(12):3385. https://doi.org/10.3390/en14123385
Chicago/Turabian StylePuchta, Erickson Diogo Pereira, Priscilla Bassetto, Lucas Henrique Biuk, Marco Antônio Itaborahy Filho, Attilio Converti, Mauricio dos Santos Kaster, and Hugo Valadares Siqueira. 2021. "Swarm-Inspired Algorithms to Optimize a Nonlinear Gaussian Adaptive PID Controller" Energies 14, no. 12: 3385. https://doi.org/10.3390/en14123385
APA StylePuchta, E. D. P., Bassetto, P., Biuk, L. H., Itaborahy Filho, M. A., Converti, A., Kaster, M. d. S., & Siqueira, H. V. (2021). Swarm-Inspired Algorithms to Optimize a Nonlinear Gaussian Adaptive PID Controller. Energies, 14(12), 3385. https://doi.org/10.3390/en14123385








