This section is divided into three subsections, and the first provides some of the details and methods used to simulate the depletion of the PWR lattice model. Following this, a subsection is given on the structure of depletion calculations necessary to perform this analysis. Finally, a formulation of the sensitivity analysis method is presented.
2.2. Sampling Approach
A random-sampling based approach is used to generate the dataset for the sensitivity analysis. Four state variables are selected:
For any coolant density incorporated into a model, a corresponding coolant temperature will be used according to the isobaric properties of water at a pressure of 15.5 MPa. These parameters were selected both because they are known to have a large effect on lattice characteristics, and they are commonly used in other studies [
13,
26,
27]. However, this methodology is certainly general and scalable enough to include any number of other lattice parameters providing there is the computational capability to generate a sufficient number of samples and those lattice parameters have a reasonably linear relationship with the homogenized cross-sections.
It is well known in the community that the Doppler-coefficient—which describes the effect on HXS from changes in fuel temperature—varies linearly with the square root of the fuel temperature [
28]. The methodology used in this study relies on linearity in the relationships between the HXS and state variables for both the values of the state variables at which the HXS is calculated as well as past values of the state variables leading up to the state for which the HXS is calculated. It is expected that the relationship between the
historical values of fuel temperature, and HXS is not necessarily more linear with respect to the square root of the fuel temperature than with respect to fuel temperature alone. Therefore, it was decided that the fuel temperature, without the square root, will be used for this analysis. Work was done to ensure that, in the range of fuel temperatures used for analysis, the linear models based on the fuel temperature performed comparatively to linear models based on the square root of the fuel temperature.
In this context, the building blocks for the sampling process are single lattice burnup sequences. For constant burnup spacing in each history, a new set of state variables are independently selected according to their distributions listed in
Table 1. In order to obtain accurate results for the state variable history considered, substeps may be taken in the burnup calculation where the lattice does not change state, but the Boltzman and Bateman equations are still solved. In other studies for HXS construction, there may be branch states considered from each burnup state, but, in this study, none are considered because a full lattice history is sampled.
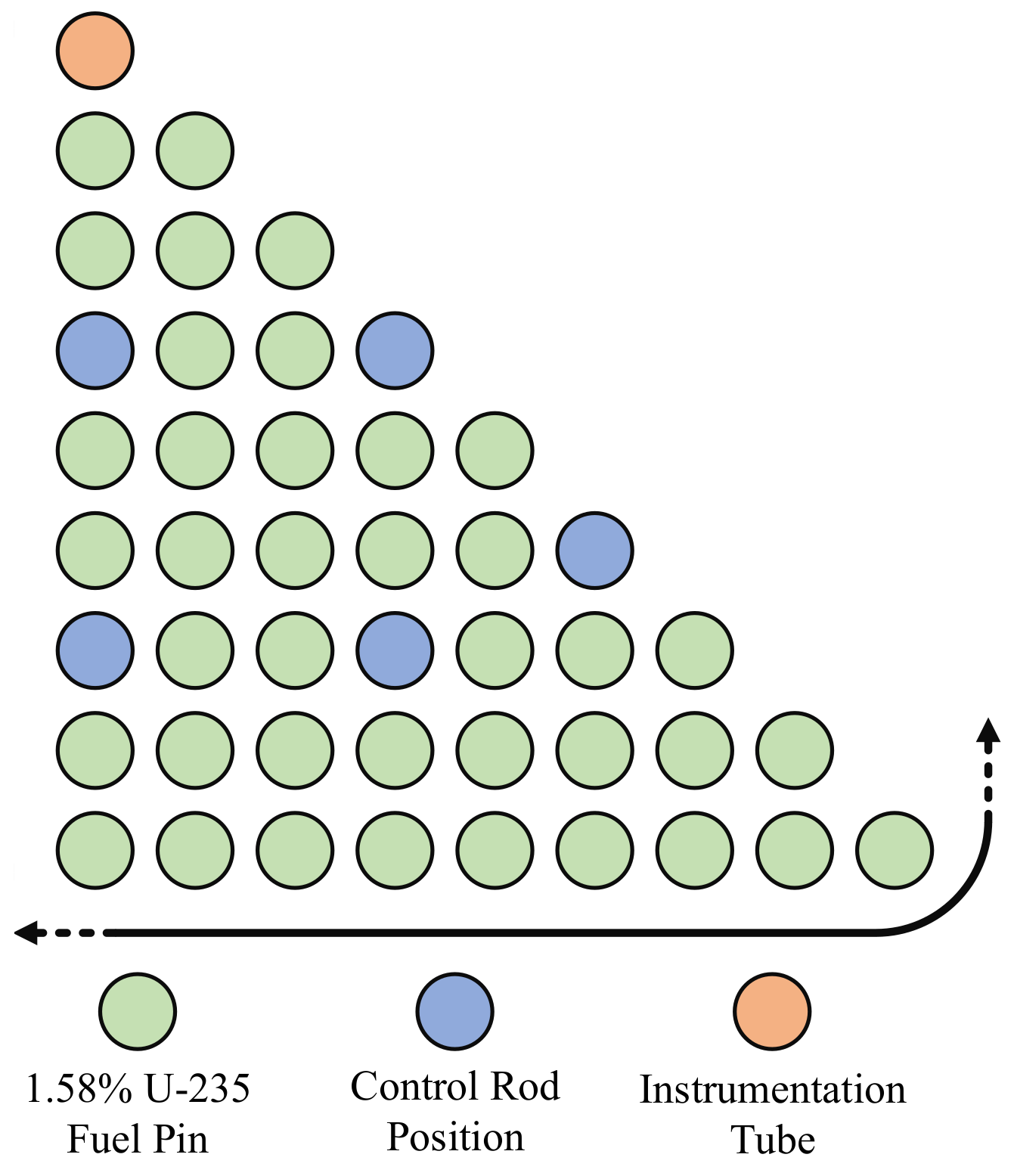
Figure 2 is included to give the reader an understanding of the structure of the burnup sequence.
Figure 2a shows the progression of fuel temperature and coolant temperature of a single lattice through a potential burnup sequence. Boron concentration and control rod insertion are not shown. Blue points depict states where HXS are calculated, and they are intentionally placed after burnup at state
and before the transition to the next state. It is expected that, for a short time after a transition, the lattice may undergo nontrivial changes in its fuel composition as it adjusts to the new neutron energy spectrum. By calculating HXS at the the end of these periods, instead of the beginning, it is thought that a more representative HXS for the fuel composition of that burnup during the segment will be obtained. Solid blue lines show depletion states, and dashed lines show transitions from the current depletion state to the next sampled state.
Figure 2b shows the structure of the burnup sequences and some mathematical notation that will be used in
Section 2.3. A state vector, denoted by
, is composed of values of state parameters at burnup point
n. The state vector is fixed during some burnup period
.
will be used to indicate the value of the burnup at the end of increment
n. Following the lattice depletion calculation reaching burnup increments of
, a new
is independently sampled according to the distribution of its components. In this application, the four parameters given in
Table 1 are used. In this study, the ranges were chosen to reflect a wide range of possible operating conditions to explore the extent of the linearity in the relationship between the state variables and the HXS for an exaggerated range of operating conditions. One practical consideration is that, in realistic operation, fuel temperature is closely related to reactor power, which in turn is related to burnup. This leads to an interaction between
and burnup that is not considered in this sampling approach. In addition, there are no covariances considered in the sampling process so sampled state values may not reflect realistic operational conditions. However, given the strong linear relationships observed between these state variables and the HXS, the results obtained for this wider domain should be applicable to any other domain that one may find to be realistic given that it falls within the operational ranges specified. In specific applications, care should be taken to ensure that these ranges are appropriate. In datasets where some state variables are held constant, they are held at the value in the “Nominal Value” column of the table.
In these results, a of 3 GW/MTU is used up to a maximum burnup of 60 GWD/MTU. For low burnups, 1 GWD/MTU substeps are taken where the reactor state does not undergo any parametric transition, but the code still calculates the change in fuel composition. Although in practical scenarios it is unlikely that a lattice would frequently undergo such radical changes in its operational state, this approach allows for a more flexible methodology that can generate sensitivities for any lattice independent of operational data availability.
In
Section 2.3, a method for the sensitivity analysis is described which relies on burnup-averaged values of the state variables as independent parameters for analysis. This leads to distributions of burnup-averaged values that have lower variances than the instantaneous distributions of those parameters. This effect is formally described by the central limit theorem. In the end, scenarios with some nonlinearities may result in biased estimates for the global sensitivity. This study sought to maintain the number of burnup levels at a reasonably low level to minimize this effect.
2.3. Sensitivity Analysis
Here, a description of the method for sensitivity quantification for the effect of both instantaneous and historical values of state variables on HXS. In this context, burnup is not used as a lattice state variable and is instead treated similarly to the temporal axis in conventional time-series analysis. Some general HXS, denoted as
at burnup set
n, is calculated with a physics-based computer simulation and can be written as some explicit function of the instantaneous value of the state vector as well as all historical values of the state vectors during burnup as is shown in Equation (1). In this equation,
refers to a vector of state variables, with the subscript referring to which burnup step in the simulation those state variables correspond to. For example, if the boron concentration in the coolant and fuel temperature are the two state variables for which sensitivities are to be computed,
if the reactor can be approximated to have a boron concentration of 2000 ppm and a fuel temperature of 600 K at the first portion of the cycle. Throughout this paper, the instantaneous state vector will refer to the state vector which describes the reactor state at the time in which the HXS is calculated. For now, notation indicating reaction type in
will be forgone:
It is the aim of the methods described in [
13,
14,
15,
16,
18,
21] to best approximate
f using reduced-order methods based on the pre-calculated relationships between
and
. This is not the aim of our current study. Instead, as a sensitivity study, the gradient of
is the quantity of interest, as shown in Equation (2). The exact form of the gradient operator will be described in more detail later in this section; however, its form is given in Equation (10):
From here, an approximate linear model for
can be written according to Equation (3).
denotes an estimated value of
. The subscript on
functions identically to the subscript on
, and it describes the burnup step. The vector
and scalar
are fitted model parameters estimated using ordinary least squares (OLS). The subscripts on each
indicate how many burnup steps back in the history from
n a set of fitted coefficients correspond to.
does not have any subscript because there will only be one fitted
parameter for any model used to predict
. Full physics-code calculations will be performed to get data to perform this fit. Proceeding forward, this model will be referred to as the complete history model (CHM). This name is assigned because the expression for
contains all reactor states present in the history of the reactor. No averaging is performed across multiple states in the history. The origin of the model is assumed to be that the homogenized cross-section is a linear function of each state variable at each burnup step across the entire history. The fitting calculation will be demonstrated later in this section:
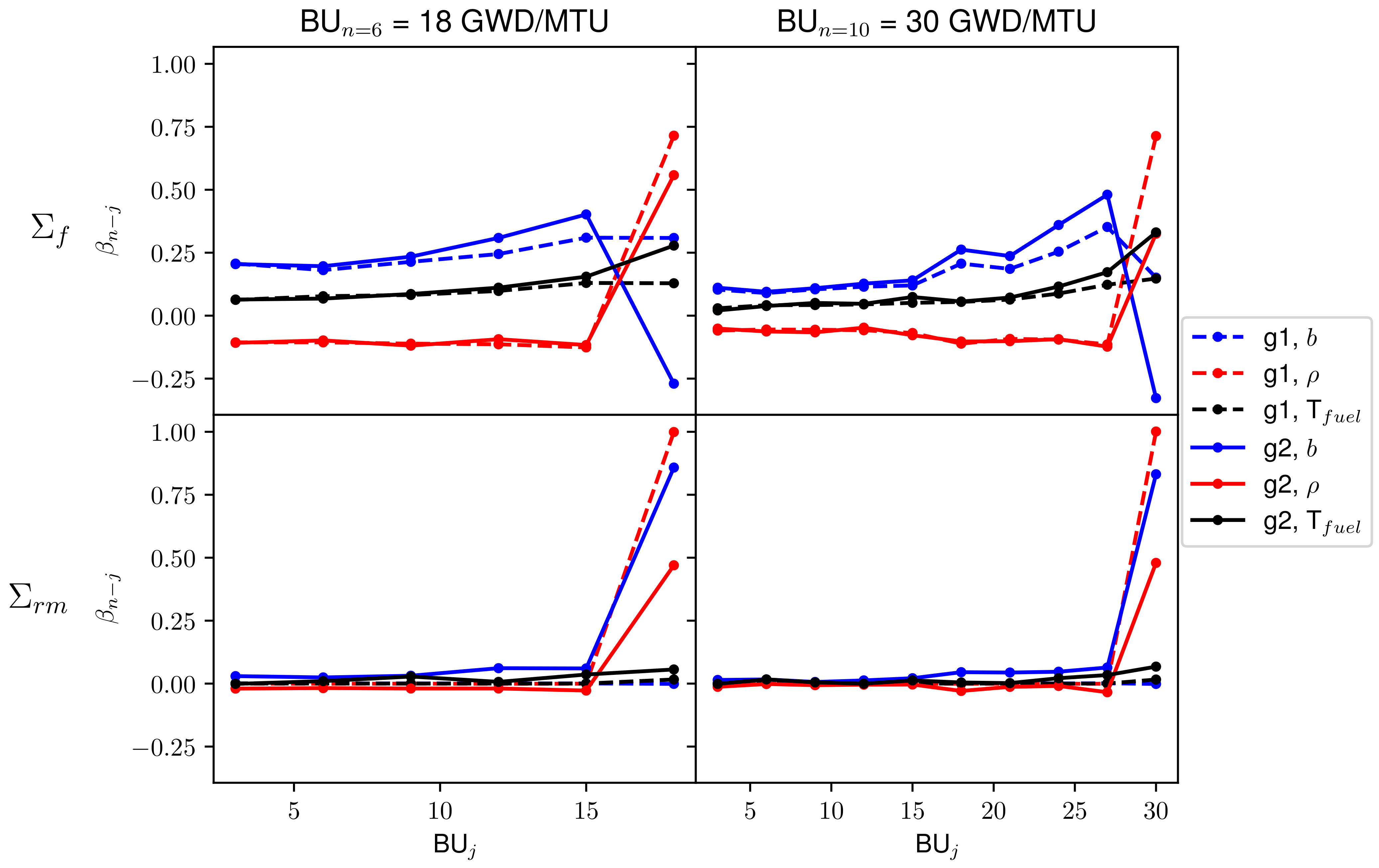
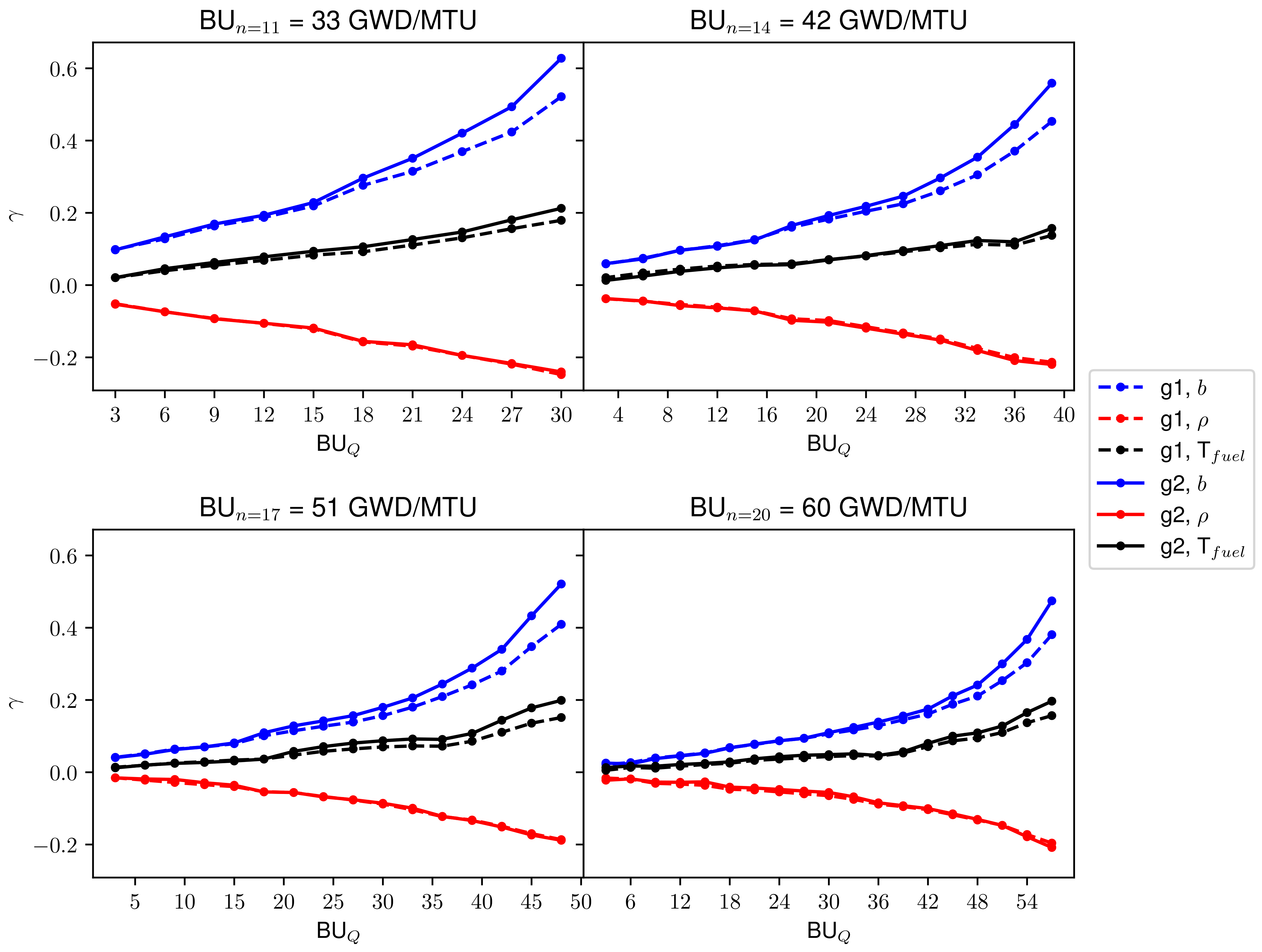
Although the previous formulation can lead to sensitivity estimates for every state parameter for every burnup step leading to state n, the number of fitted parameters becomes very large. An alternative model, featuring some model reduction parameter Q, can be used to include burnup-weighted average state vectors. This model will be referred to as the reduced history model (RHM). In this model, a fitted vector, , is used to capture the effect from the historical values of the state vector for previous steps greater than Q without assigning fitted parameters to each of these historic states individually. is assigned to the historic average of these state variables. Q can be selected to balance the interpretability and precision of the results. Higher Q values will result in sensitivity measures for the state variable values for more states in a burnup sequence to be reported. Lower Q values will provide less sensitivity measures by averaging the initial portions of the burnup sequence. Instead, the averages of these historic states are used. The equation for the RHM is shown in Equation (4). This equation can be obtained by considering a state vector that is the element-wise average of all state vectors in the history greater than Q steps back. This new state vector is also assigned a vector of fitted parameters. For this equation, there are two limiting cases worth mentioning:
: This is the largest allowable value for Q. In this case, the RHM and CHM become identical in that the fitted parameter operates on the single , functioning identically as in the CHM.
: This is the smallest possible value for Q. In this case, only the current value of the state vector is assigned an individual fitted vector. The remaining state vectors are averaged and assigned a single fitted vector:
In order to fit the RHM model, OLS is used with a number of sampled burnup sequences. Each burnup sequence yields
N relationships between HXS and historical and instantaneous values of the state vectors, where
N is the total number of burnup steps in the sequence. A linear system of equations can be formulated according to Equation (5). This equation is used to estimate the linear model parameters. Here,
is the state vector at burnup step
n in burnup sequence
i and
is the computed homogenized cross-section at burnup step
n for burnup sequence
i. The goal of the OLS fit is to find some optimal set of linear model parameters that best predicts the result vector
. Therefore, there are no superscripts on the
and
fitted parameters because they will have the same values across all sampled burnup sequences.
I is the total number of burnup sequences generated by the lattice physics code. This can be understood as the specific number of realized operational histories that get randomly sampled. The subscripts on the matrices are used to indicate the values of
n and
Q that can be used to form the matrices.
where
With this formulation, the fitted model parameters can be found using the normal equations according to Equation (6). The total number of fitted parameters (including the individual components of
and
) in
for these models is
; therefore, for large
Q, there is a need for a large number of sampled burnup histories to get an adequate estimate for
. However, as mentioned previously, an estimate for the sensitivity is the true desired quantity of interest that may help inform the creation of more accurate surrogate models for HXS interpolation:
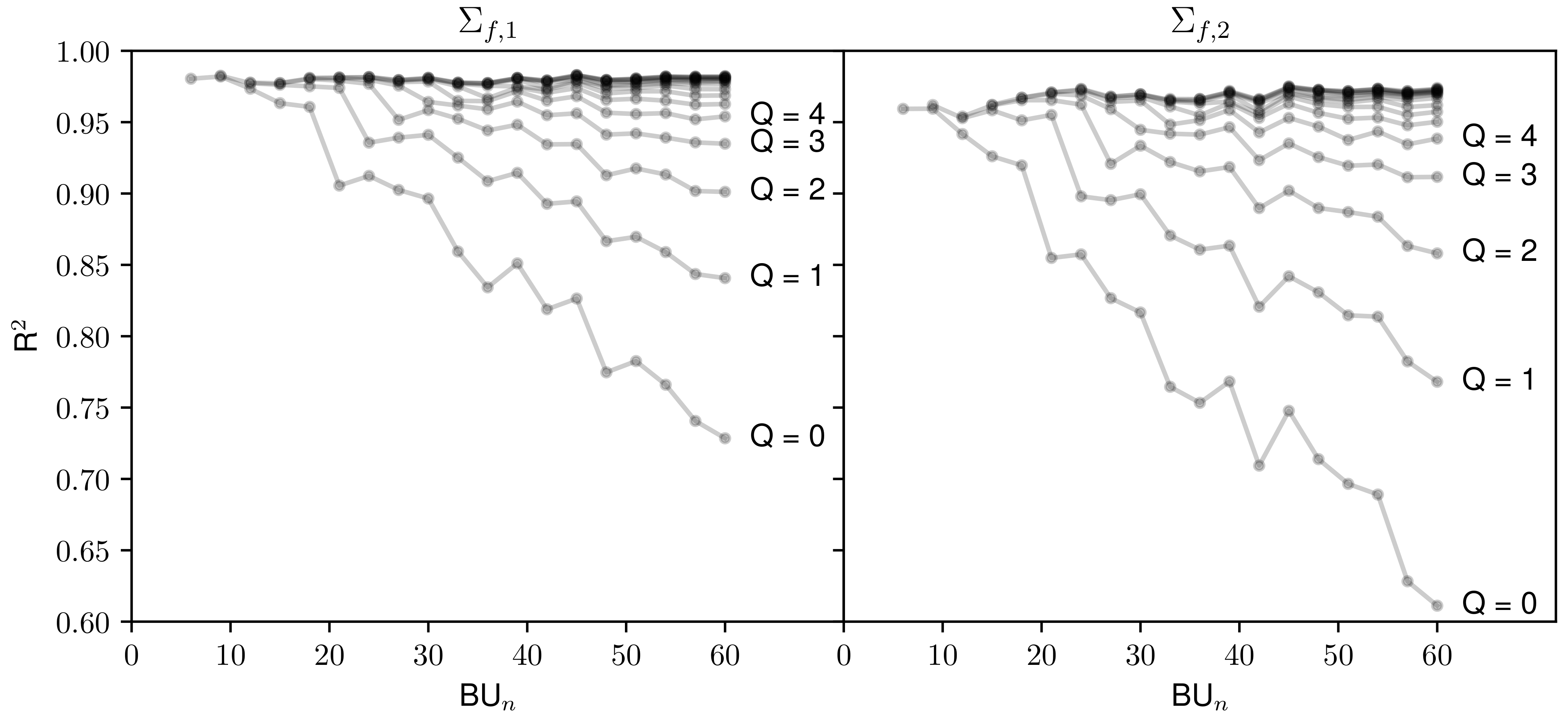
Furthermore, this model can only capture linear relationships between the state variables and the HXS. The validity of this assumption will be explored later in this study in
Section 3. One useful definition for linear model evaluation is the coefficient of determination, often referred to as
. This quantity describes the fraction of variance in the result that can be explained by the model and can be calculated using Equation (
7), where the definition for
is simply the HXS averaged across all burnup sequences at step
n. Here, the subscripts of
n and
Q are maintained to indicate the form of model that corresponds to some computed
:
Moving on, one important technique used in sensitivity analysis is “data standardization”. This is a linear transformation which scales the mean and variance of the input and output parameter distributions to 0 and 1, respectively. This has the benefit of non-dimensionalizing the data according to the range of its variation. After fitting the linear model, the resulting sensitivity measures will account for both the magnitude of impact a particular state variable has on the HXS as well as the range of variation of that parameter. Formally, this is often referred to as the standardized regression coefficient method [
29] for sensitivity analysis. Often in statistical analysis, one of the first steps is for the analyst to standardize the data. However, in this application, the standardization transformation should only be performed after the formation of the
matrix where each column should be standardized. As mentioned previously, by performing burnup-averaging, the distributions of the parameters in the linear models are changed. By standardizing the columns of
, it ensures that the standardization transformation is applied after the narrowing of the burnup-averaged state variable distributions has occurred. Furthermore, this transformation loses its usefulness if applied to binary state variables, such as control rod insertion. Nevertheless, to perform this transformation on
, Equation (8) can be used. Here, the mean of the elements in
(
) at burnup step
n is subtracted and then this quantity is further divided by the standard deviation (
) to yield the normalized vector
. An identical operation can be preformed column-wise on
according to Equation (9). Here,
indicates the element in
that corresponds to row
r and column
c,
denotes the average of column
c of
,
denotes the standard deviation of column
c of
, and
refers to the column-standardized form of
:
To compute sensitivities for the model form given in Equation (4), an expression for ∇ is needed. This is given in Equation (10), which yields a measure of the sensitivity of the HXS to the desired parameters. This sensitivity estimate will be global with respect to the various state parameters but local to the burnup step
n; hence, the subscript on each of the derivatives:
If this gradient operator is applied to the linear model given in Equation (4), the result vector is given in Equation (11). Here, the subscripts on the ∇ can be inferred from the subscripts on
. This form provides a clear mathematical definition for the sensitivity coefficients used in this study. If the standardization transformation is performed on
and
,
aligns with the definition for sensitivity measures from the standardized regression coefficient (SRC) method [
29] where instantaneous, historical, and burnup-averaged state variables are considered parameters of interest. To explain further, without the standardization transformation, the fitted linear model coefficients can be interpreted as the change in HXS for some unit change in the state variable. Although this sensitivity measure may be useful in many analyses, if the goal is to compare the sensitivities of
different state variables, these coefficients are not as useful. At the simplest level, some state variables will have different units because they represent different quantities, making a comparison between those values meaningless. However, the more fundamental problem is that these state variables may have wildly different ranges of variation that will not be accounted for. For example, in more generalized applications, if two parameters have the same unit and vary at different orders of magnitude, it is possible that, despite having the same dimensionalized sensitivity coefficient, the outcome of the system is significantly more influenced by the parameter with the larger range of variation. The standardization transformation scales the ranges of all parameters to be unity, which allows for the magnitude of influence as well as the range of variability to be accounted for in a single sensitivity measure:
To summarize the two models used for sensitivity analysis:
Full History Model (FHM): Uses every reactor state variable in the history leading up to the burnup at which the HXS is calculated to calculate sensitivities.
Reduced History Model (RHM): Uses a reduction parameter to use burnup-averaged state variable values instead of considering the reactor state at every burnup step.
2.4. Workflow Summary
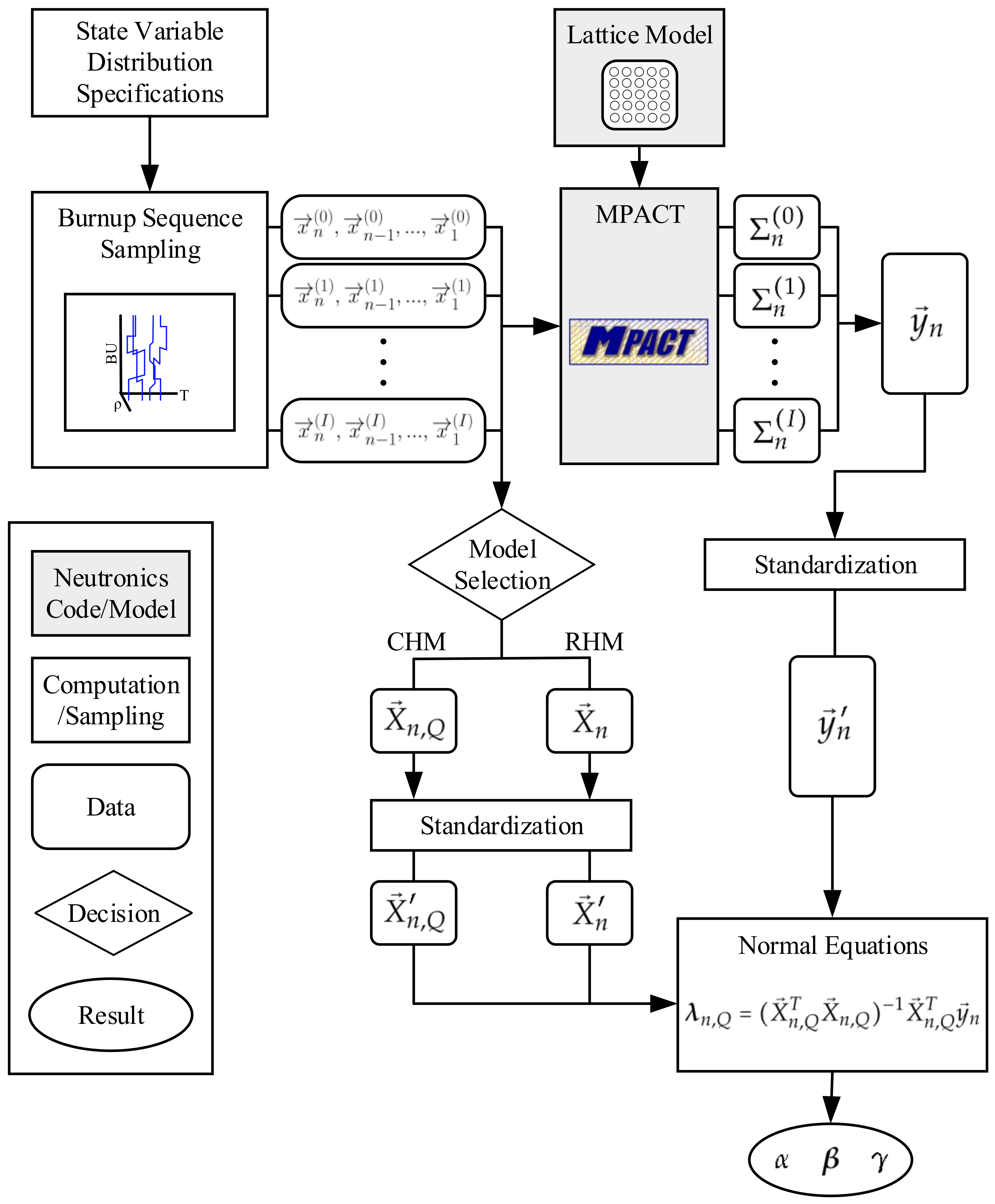
This section will help to summarize the previous content and provide a logical progression for how a sensitivity analysis following the proposed methodology can be performed. Mainly, the discussion will be centered around the flow chart provided in
Figure 3. To begin, the ranges and distributions of the state variables used in the analysis should be carefully considered. These ranges should cover the reasonable ranges for the reactor in some specific application and no more. Wider operational ranges lead to weaker linearity between state variables and HXS. Separate analysis can be done for multiple application states, but including these operational ranges in an analysis intended for an operating reactor can skew the reported sensitivities to reflect undesired states. Following this, burnup sequences should be sampled according to these distributions. This sampling is represented by the “Burnup Sequence Sampling" box in the flowchart. These processes are described in more detail in
Section 2.2. The result of this sampling procedure is represented by the “Data” boxes containing
. Here, the subscripts indicate the burnup step that the state vector
corresponds to. The superscript
i indicates which of the
I total samples the burnup sequence corresponds to.
Moving on with the burnup sequences, an MPACT depletion calculation must be performed on each sample. Of course, the lattice geometry and materials must also be provided for this calculation to be performed—as indicated by the box titled “Lattice Model”. The result of these calculations is a series HXSs at burnup step n for each sample i, denoted as . This analysis can be performed with any HXS so the reaction type is neglected in the notation. The set of HXS can then be compiled into the vector as described by Equation (5).
Separately from the MPACT calculations, the
matrices can be formed directly from the sampled burnup sequences as described in Equation (5). Prior to this formation, however, the analyst must first select whether the CHM or RHM will be used—as indicated by the “Decision” diamond labeled “Model Selection” in
Figure 3. This decision should be made based on the complexity of the desired result. For a complete understanding of the sensitivity of an HXS to every historic value of a state variable, the CHM should be used. For more interpretable results, smaller values of
Q can be used for the RHM. The formation of the
matrix in the case of the CHM is identical to the RHM case where
.
From here, both and can be standardized according to Equations (8) and (9). With the standardized versions of these quantities, the normal equations can be solved to obtain . From Equation (5), it can be seen that is composed of the sensitivity measures that align with the definition from Equation (11) that can be used for further analysis.