Optimization of Architectural Form for Thermal Comfort in Naturally Ventilated Gymnasium at Hot and Humid Climate by Orthogonal Experiment
Abstract
1. Introduction
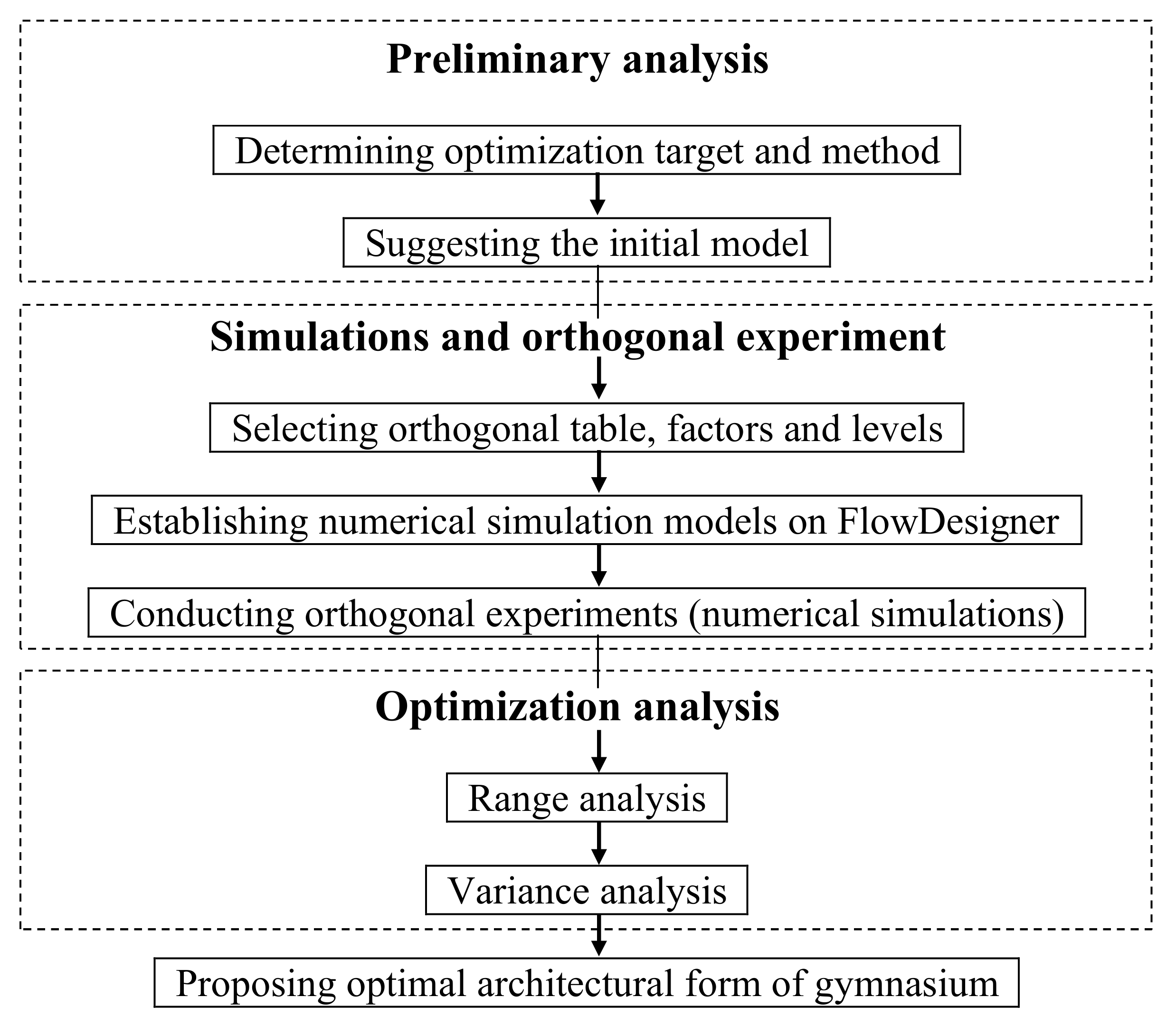
2. Materials and Methods
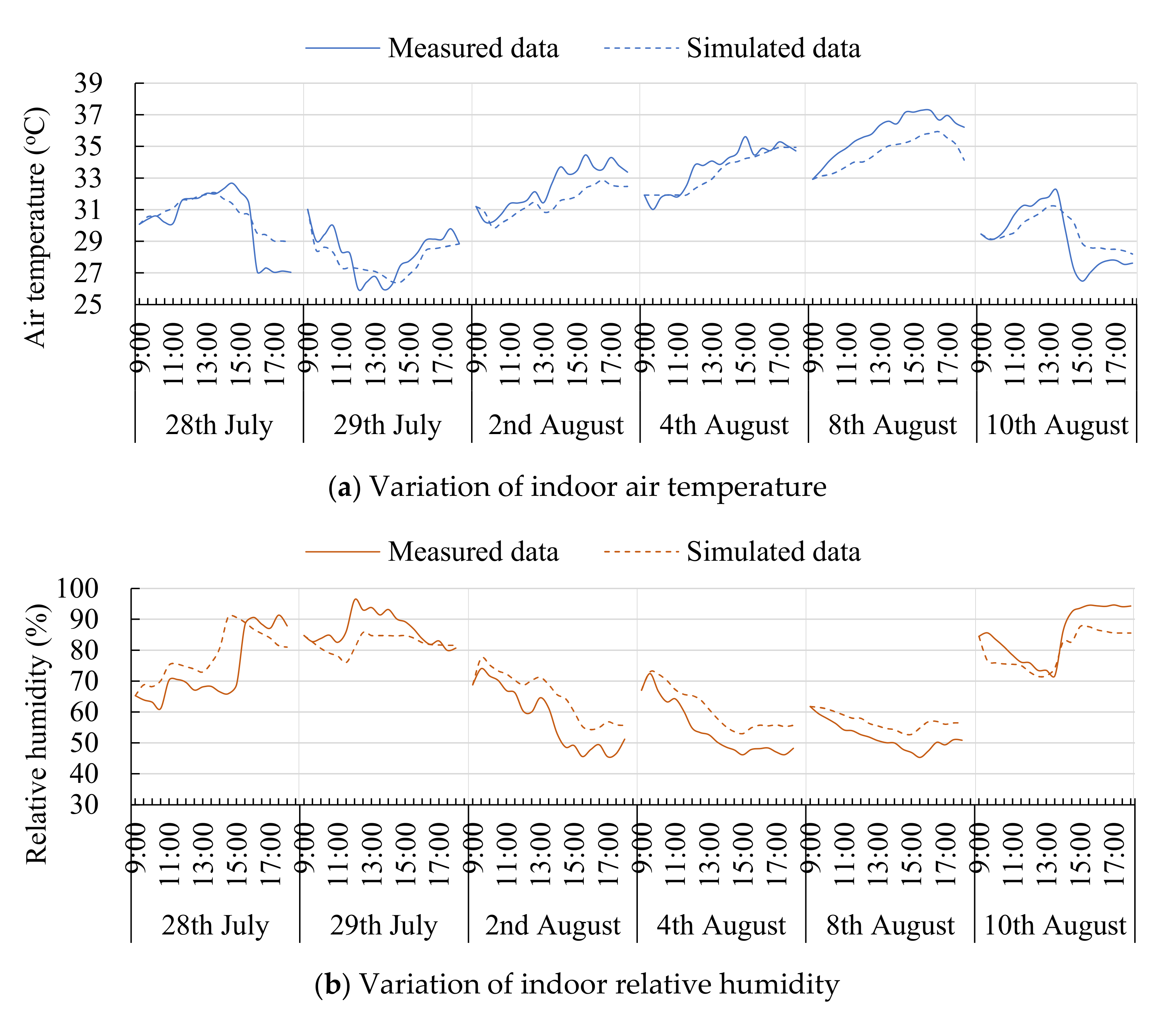
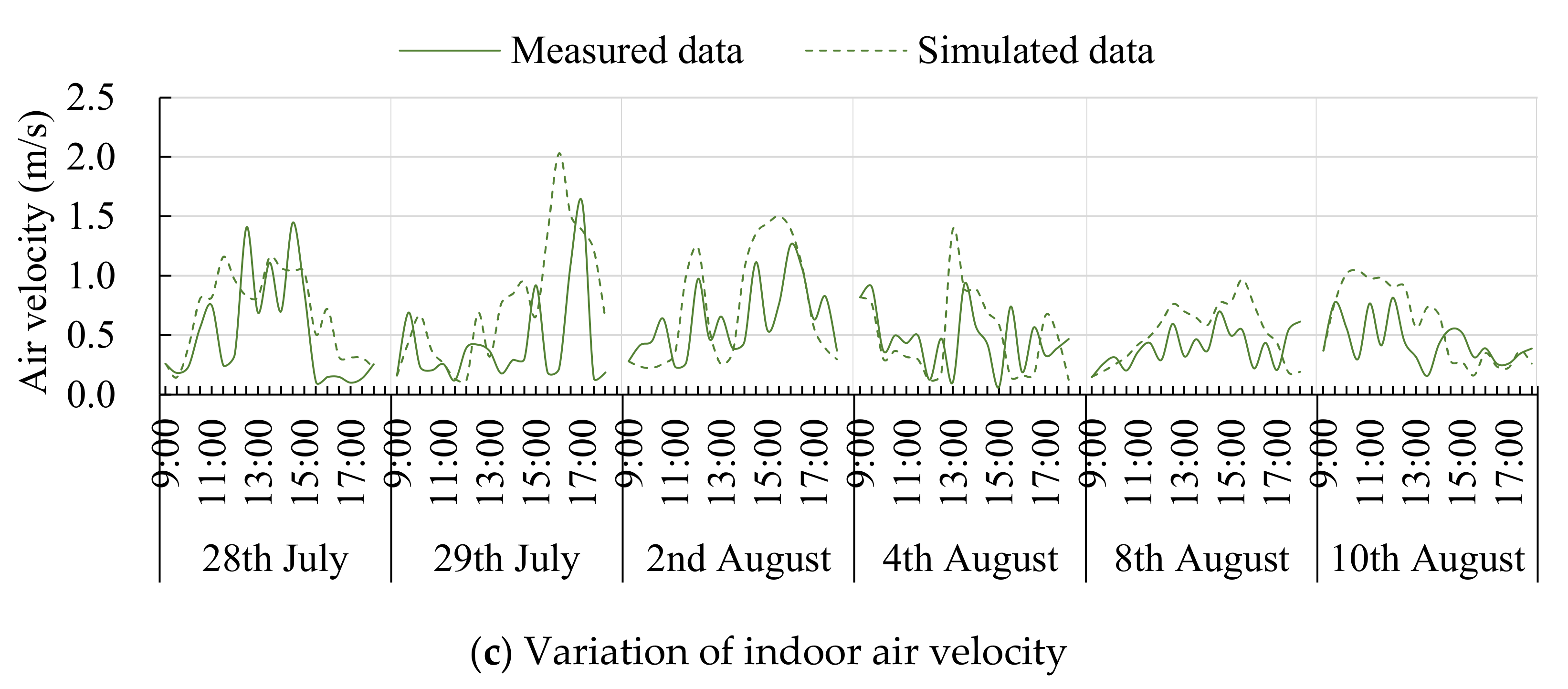
2.1. Simulation Tool and Its Validation
2.2. Selection of Thermal Comfort Model
2.3. Principle of Orthogonal Experiment
2.3.1. Range Analysis
2.3.2. Variance Analysis
2.4. Statistical Analysis
3. The Initial Model of Gymnasium in Hot and Humid Area
3.1. The Situation of Gymnasiums in Guangzhou City
3.2. Plan Layout of the Initial Model of Gymnasium
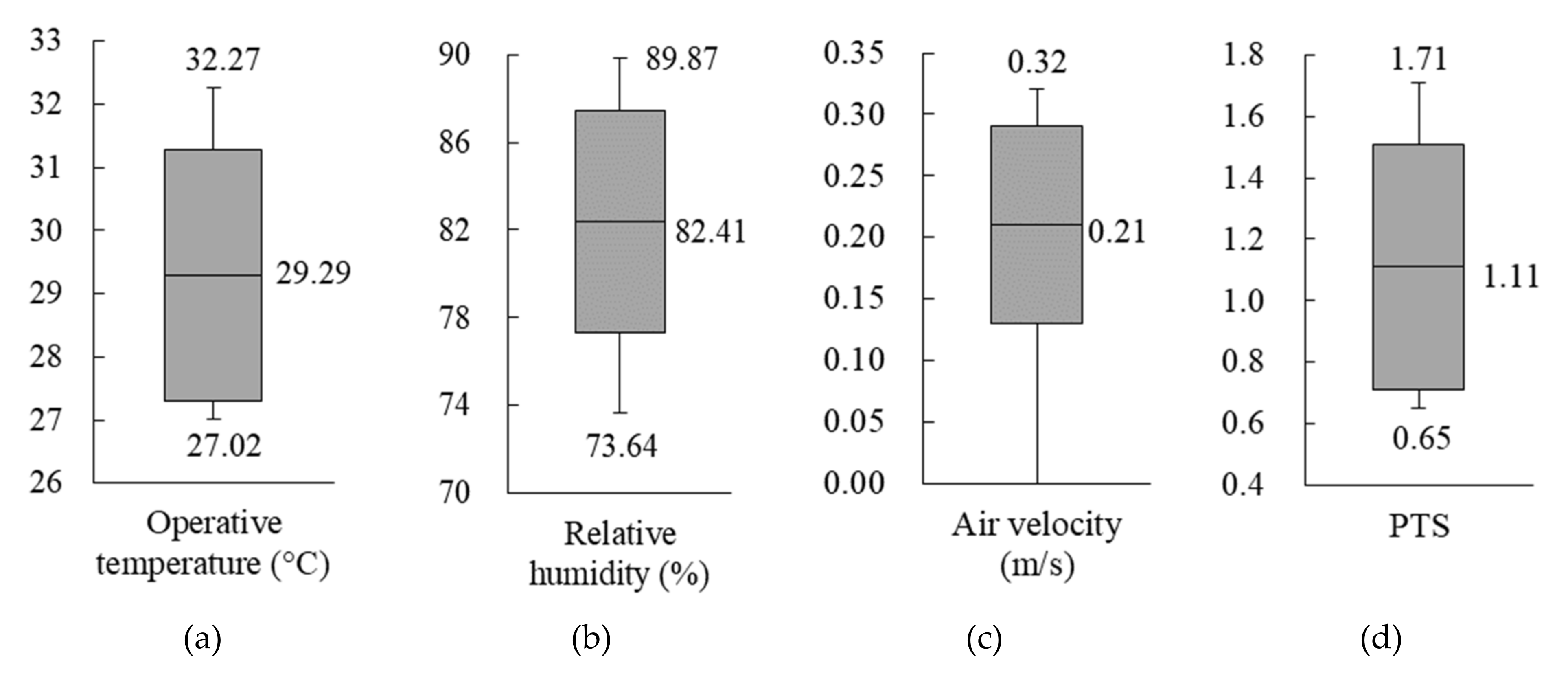
3.3. Simulation of the Initial Model of Gymnasium
4. Simulation Results and Optimization Analysis
4.1. Simulation Factors and Levels of Orthogonal Experiment
- Factor A: The window position affects the natural ventilation and thermal comfort, as well as even energy consumption. In previous research, Prakash [35] identified a new set of strategies to locate the window openings which could reduce the PMV by 0.12%. Kim et al. [36] demonstrated that the buildings achieve the lowest energy consumption when the windows were located in the middle height in all orientations. As the wind direction in Guangzhou is mainly from southeast to northwest, the window position on south and north is more valuable to study than that on east and west. The three levels in factor A in this study are different positions of main windows that were selected from the result of investigation and the relevant research.
- Factor B and C: As a significant factor affecting on indoor thermal environment, the WWR plays an important role in architectural design. There are extensive research and efforts focused on the WWR up to now. Kahsay et al. [37] tried to analyze the optimization of window configuration for a high-rise building to minimize its energy consumption, and he obtained the optimum WWR of 30%, 48%, and 30% for a room located on the 2nd, 15th, and 29th floor, respectively. Wen et al. [38] took the indoor air temperature as the parameter to evaluate the optimal WWR and proposed a WWR maps for the architectural design in the early stages. According to the relevant research and regulations of China, as well as the investigation in Guangzhou, the WWR in the study are chosen in three levels, 10%, 20%, and 30%.
- Factor D: The heat gain from the solar radiation is a key problem in the buildings in south of China. Since the roof surfaces are the main positions absorbing radiant heat, the insulation measures of roofs are critical. Zingre et al. [39] compared the thermal performances between the double skin roof and the insulated roof in Singapore, found that the double roof performs better in reducing heat gain into the building during daytimes. Yang et al. [15] analyzed the correlations between indoor thermal comfort and Double-Skin Façades in different climatic conditions and found that the solar heat gain coefficient of the external window of the Double-Skin Façades possessed the highest importance affecting indoor thermal comfort. In this study, three types of roof are selected to discuss the optimum for the gymnasiums in hot and humid climate. The single skin roof is the ordinary reinforced concrete roof without any passive cooling; the double skin roof is with an air cavity of 500 mm thickness inside; the insulated roof composes of reinforced concrete and an insulation board of 20 mm thickness.
- Factor E: Roof slope can regulate the natural ventilation and cooling effect. Mao and Yang [40] investigated the heat transfer performance of double-slope hollow glazed roof with different slope angles in hot summer and cold winter regions, and the results indicate that the inner surface temperature of the roof reduced obviously with the roof slope decreases. Since the wind direction in Guangzhou is southeast-to-northwest, the three levels of roof slope in this study are mainly consider the south-north direction.
- Factor F: The overhanging eave influences natural ventilation and shading, as well as heat insulation. Li [11] simulated the symmetrical and asymmetrical models of a gymnasium in Guangzhou and recommended adjusting the width and angle of the overhanging eaves of the gymnasiums to improve the thermal performance. Due to most of the investigated gymnasiums in Guangzhou own overhanging eaves on the roofs, the three levels of factor F are different in the depth of overhanging eave.
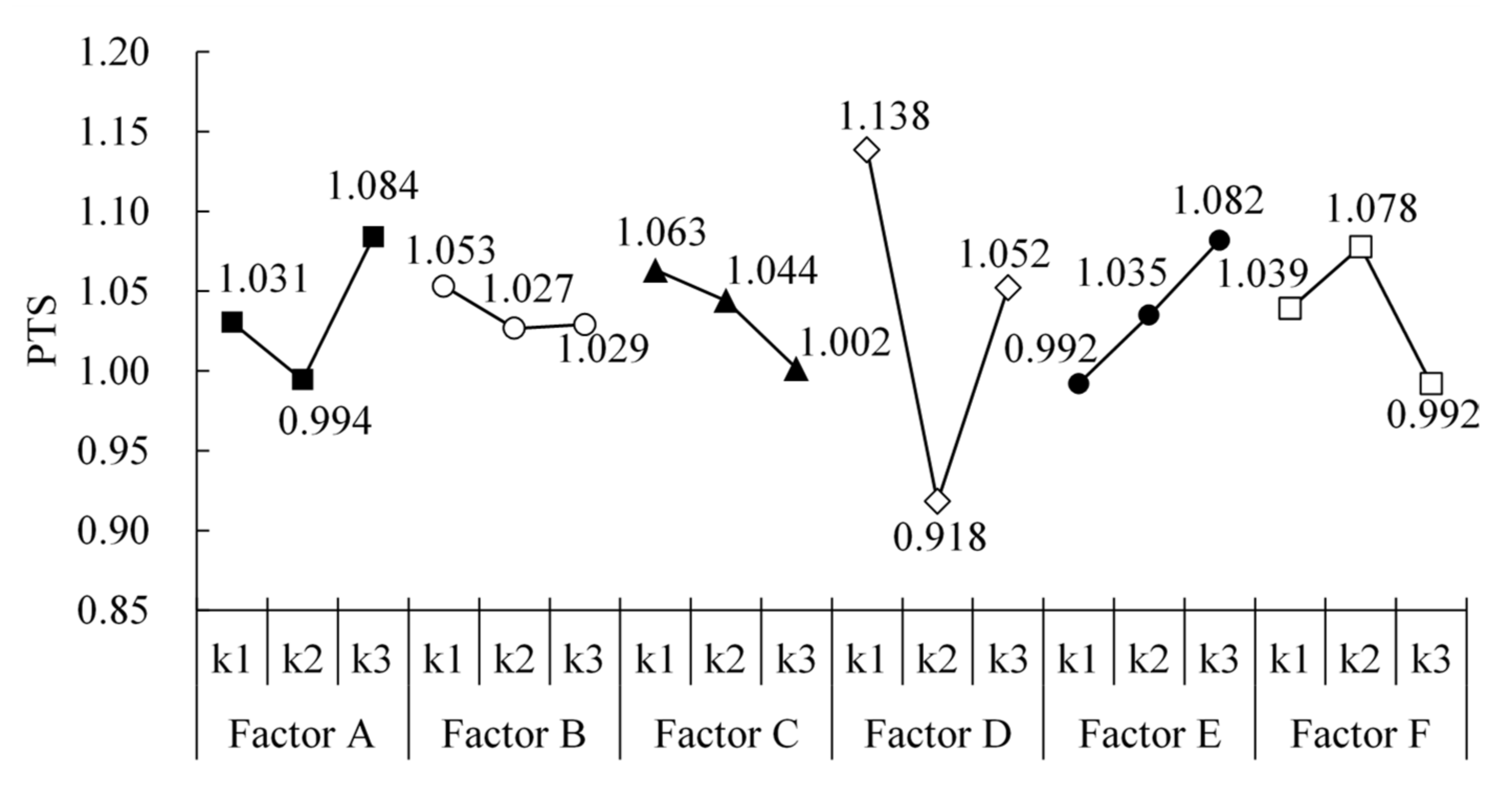
4.2. Range Analysis
4.3. Correlations between Factors and Indicator
4.4. Variance Analysis
5. Discussion on the Optimization Effects
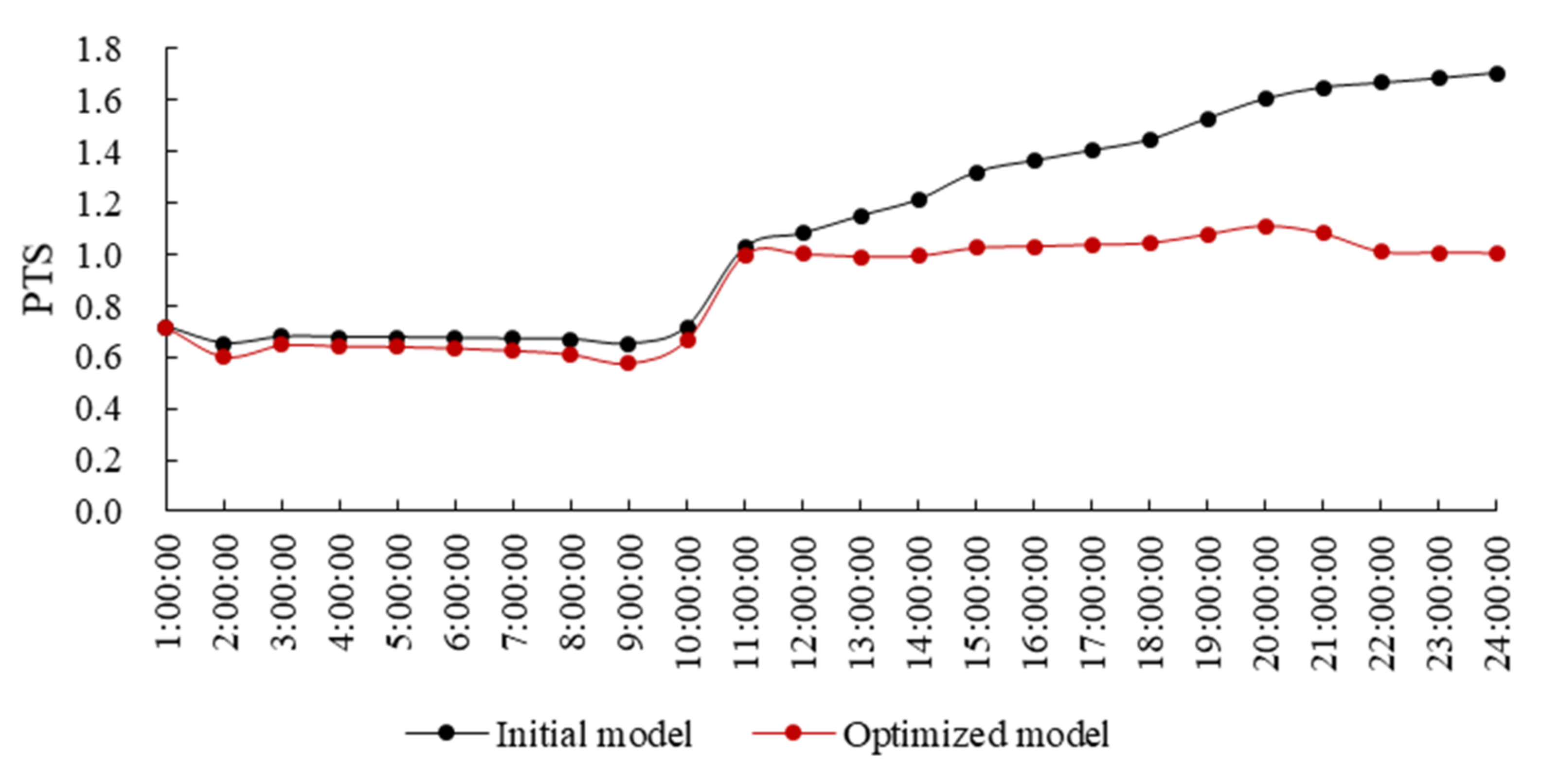
5.1. Optimized Model vs. Initial Model
5.2. Comparing with Other Studies
5.3. Practical Implication
5.4. Limitations
6. Conclusions
- (1)
- Seven hundred and twenty-nine experiments have been dramatically decreased to 18 tests by the method of orthogonal experiment.
- (2)
- The range analysis and variance analysis demonstrate that the influence of the six factors on PTS (Predicted Thermal Sensation) are ranked as: Roof insulation type > Main window position = Roof slope > Depth of overhanging eave > North window-to-wall ratio > South window-to-wall ratio.
- (3)
- In terms of thermal comfort of gymnasiums, the optimized architectural form turns out to be the combination of the windows at the low position and high position on the south and north wall, respectively; the south and north window-to-wall ratio of 20% and 30%, respectively; a horizontal roof with double skin and the overhanging eave with the depth of 9 m.
- (4)
- The PTS (Predicted Thermal Sensation) value decreases from 1.11 (slightly hot) to 0.86 (comfortable) via optimization on the gymnasium forms, and the gap of PTS value between initial model and optimized model is mainly reflected in the afternoon.
- (5)
- The findings benefit designers and researchers to determine the key parameters in the gymnasium architectural design and to optimize the thermal comfort, as well as energy efficiency.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Title | Unit of Measure |
| A | A coefficient as a function of the air velocity | / |
| df | Degree of freedom | / |
| F | Statistic for test | / |
| Fp-N | Angle factor between a person (p) and surface (N) | / |
| fs | Saturated water vapor pressure | Pa |
| Icl | Static clothing insulation | clo |
| k | Number of factors in orthogonal experiment | / |
| Kji | Sum of the experimental results | / |
| kji | Average value of Kji | / |
| L | Symbol of the orthogonal table | / |
| M | Metabolic rate | W/m2 |
| m | Number of levels in orthogonal experiment | / |
| n | Number of trials in orthogonal experiment | / |
| p | Atmospheric pressure | Pa |
| PTS | Predicted Thermal Sensation | / |
| Rj | Range of values between the maximum and minimum values of kji | / |
| RH | Relative humidity | % |
| SS | Sum of the squared deviation | / |
| TSV | Thermal Sensation Vote | / |
| Top | Operative temperature | °C |
| Ta | Air temperature | °C |
| Tr | mean radiant temperature | °C |
| Tk | Surface temperature | °C |
| TN | Surface temperature of surface (N) | °C |
| V | Variance of the factor | / |
| v | Air velocity | m/s |
| WWR | Window-to-wall ratio | / |
| Wk | Results of each trial (k, k = 1, 2, 3, ……, n) | / |
| Wa | Humidity ratio | g/kg’ |
| w | Arithmetic average of Wk | / |
References
- Chen, L.; Ng, E. Outdoor thermal comfort and outdoor activities: A review of research in the past decade. Cities 2012, 29, 118–125. [Google Scholar] [CrossRef]
- Yao, J.W.; Yang, F.; Zhuang, Z.; Shao, Y.; Yuan, P.F. The effect of personal and microclimatic variables on outdoor thermal comfort: A field study in a cold season in Lujiazui CBD, Shanghai. Sustain. Cities Soc. 2018, 39, 181–188. [Google Scholar] [CrossRef]
- ASHRAE. ASHRAE Standard 55-2020. In Thermal Environmental Conditions for Human Occupancy; American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc.: Atlanta, GA, USA, 2020. [Google Scholar]
- ASHRAE. Chapter 9, Thermal Comfort, ASHRAE Handbook—Fundamentals; American Society of Heating, Refrigerating and Air Conditioning Engineers, Inc.: Atlanta, GA, USA, 2017. [Google Scholar]
- De Dear, R.; Brager, G.S. Towards an adaptive model of thermal comfort and preference. ASHRAE Trans. 1998, 104, 145–167. [Google Scholar]
- Humphreys, M.A.; Nicol, J.F. Outdoor temperature and indoor thermal comfort: Raising the precision of the relationship for the 1998 ASHRAE database of field studies. ASHRAE Trans. 2000, 106, 485–492. [Google Scholar]
- Fanger, P.O. Thermal Comfort—Analysis and Application in Environmental Engineering; Danish Technology Press: Copenhagen, Denmark, 1970; pp. 142–155. [Google Scholar]
- ISO. ISO: International Standard 7730. In Ergonomics of the Thermal Environment—Analytical Determination and Interpretation of Thermal Comfort Using Calculation of the PMV and PPD Indices and Local Thermal Comfort Criteria; International Organization for Standardization: Geneva, Switzerland, 2005. [Google Scholar]
- Wei, Z. Research on the Construction of Green and Environmental Protection Modern Gymnasium. J. Physics Conf. Ser. 2021, 1802, 022050. [Google Scholar] [CrossRef]
- Yang, L.; Fu, R.; He, W.; He, Q.; Liu, Y. Adaptive thermal comfort and climate responsive building design strategies in dry–hot and dry–cold areas: Case study in Turpan, China. Energy Build. 2020, 209, 1–16. [Google Scholar] [CrossRef]
- Li, J. Effect of Form Asymmetry of Gymnasium on Natural Ventilation and Thermal Comfort of Exercise Site. J. South China Univ. Technol. 2013, 41, 83–89. (In Chinese) [Google Scholar]
- Huang, X.; Ma, X.; Zhang, Q. Effect of building interface form on thermal comfort in gymnasiums in hot and humid climates. Front. Arch. Res. 2019, 8, 32–43. [Google Scholar] [CrossRef]
- Sayadi, S.; Hayati, A.; Salmanzadeh, M. Optimization of Window-to-Wall Ratio for Buildings Located in Different Climates: An IDA-Indoor Climate and Energy Simulation Study. Energies 2021, 14, 1974. [Google Scholar] [CrossRef]
- Gupta, R.; Gregg, M. Assessing the Magnitude and Likely Causes of Summertime Overheating in Modern Flats in UK. Energies 2020, 13, 5202. [Google Scholar] [CrossRef]
- Yang, S.; Fiorito, F.; Prasad, D.; Sproul, A.; Cannavale, A. A sensitivity analysis of design parameters of BIPV/T-DSF in relation to building energy and thermal comfort performances. J. Build. Eng. 2021, 41, 102426. [Google Scholar] [CrossRef]
- Amini, R.; Ghaffarianhoseini, A.; Ghaffarianhoseini, A.; Berardi, U. Numerical investigation of indoor thermal comfort and air quality for a multi-purpose hall with various shading and glazing ratios. Therm. Sci. Eng. Prog. 2021, 22, 100812. [Google Scholar] [CrossRef]
- Rawat, M.; Singh, R.N. A study on the comparative review of cool roof thermal performance in various regions. Energy Built Environ. 2021, 23, 26. [Google Scholar] [CrossRef]
- Albatayneh, A. Optimisation of building envelope parameters in a semi-arid and warm Mediterranean climate zone. Energy Rep. 2021, 7, 2081–2093. [Google Scholar] [CrossRef]
- Shao, N.; Zhang, J.; Ma, L. Analysis on indoor thermal environment and optimization on design parameters of rural residence. J. Build. Eng. 2017, 12, 229–238. [Google Scholar] [CrossRef]
- Li, H.X.; Li, Y.; Jiang, B.; Zhang, L.; Wu, X.; Lin, J. Energy performance optimization of building envelope retrofit through integrated orthogonal arrays with data envelopment analysis. Renew. Energy 2020, 149, 1414–1423. [Google Scholar] [CrossRef]
- Lv, W.; Li, A.; Ma, J.; Cui, H.; Zhang, X.; Zhang, W.; Guo, Y. Relative importance of certain factors affecting the thermal environment in subway stations based on field and orthogonal experiments. Sustain. Cities Soc. 2020, 56, 102107. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, H. Typical Meteorological Database Handbook for Buildings; China Architecture & Building Press: Beijing, China, 2012; p. 202. (In Chinese) [Google Scholar]
- The Historical Changes of Winds above Open Spaces and the Surroundings of Nanjing. Urban. Plan. Forum. 2018, 2, 81–88. (In Chinese)
- Rowe, P.G.; Forsyth, A.; Kan, H.Y. China’s Urban Communities: Concepts, Contexts, and Well-Being; Birkhäuser: Boston, MA, USA, 2016; pp. 172–198. [Google Scholar]
- Advanced Knowledge Laboratory, Inc. CFD Simulation for Architectural Design. Available online: http://www.akl.co.jp/en/ (accessed on 1 April 2020).
- China Architecture & Building Press. JGJ/T347: 2014. In Standard of Test Methods for Thermal Environment of Building; China Architecture & Building Press: Beijing, China, 2014. [Google Scholar]
- NCEI. Integrated Surface Database (ISD). Available online: https://www.ncdc.noaa.gov/isd (accessed on 1 April 2020).
- ISO. International Standard 7243. In Ergonomics of the Thermal Environment—Assessment of Heat Stress Using the WBGT (Wet Bulb Globe Temperature) Index; International Organization for Standardization: Geneva, Switzerland, 2017. [Google Scholar]
- Huang, X.; Zhang, Q.; Wang, Z.; Ma, X. Thermal sensation under high-intensive exercise in naturally ventilated gymnasiums in hot-humid areas of China: Taking basketball players for example. Indoor Built Environ. 2020. [Google Scholar] [CrossRef]
- Oliveira, A.V.M.; Raimundo, A.M.; Gaspar, A.R.; Quintela, D.A. Globe Temperature and Its Measurement: Requirements and Limitations. Ann. Work Expo. Health 2019, 63, 743–758. [Google Scholar] [CrossRef]
- ISO. International Standard 8996. In Ergonomics of the Thermal Environment—Determination of Metabolic Rate; International Organization for Standardization: Geneva, Switzerland, 2004. [Google Scholar]
- China Architecture & Building Press. GB50189-2015. In Design Standard for Energy Efficiency of Public Buildings; China Architecture & Building Press: Beijing, China, 2015. (In Chinese) [Google Scholar]
- Energy Plus. Weather Data by Region. Available online: https://energyplus.net/weather-region/asia_wmo_region_2 (accessed on 1 April 2020).
- China Architecture & Building Press. JGJ31-2003. In Design Code for Sports Building; China Architecture & Building Press: Beijing, China, 2003. (In Chinese) [Google Scholar]
- Prakash, D.; Ravikumar, P. Analysis of thermal comfort and indoor air flow characteristics for a residential building room under generalized window opening position at the adjacent walls. Int. J. Sustain. Built Environ. 2015, 4, 42–57. [Google Scholar] [CrossRef]
- Kim, S.; Zadeh, P.A.; Staub-French, S.; Froese, T.; Cavka, B.T. Assessment of the Impact of Window Size, Position and Orientation on Building Energy Load Using BIM. Procedia Eng. 2016, 145, 1424–1431. [Google Scholar] [CrossRef]
- Kahsay, M.T.; Bitsuamlak, G.T.; Tariku, F. Thermal zoning and window optimization framework for high-rise buildings. Appl. Energy 2021, 292, 116894. [Google Scholar] [CrossRef]
- Wen, L.; Hiyama, K.; Koganei, M. A method for creating maps of recommended window-to-wall ratios to assign appropriate default values in design performance modeling: A case study of a typical office building in Japan. Energy Build. 2017, 145, 304–317. [Google Scholar] [CrossRef]
- Zingre, K.T.; Yang, E.H.; Wan, M.P. Dynamic thermal performance of inclined double-skin roof: Modeling and experimental investigation. Energy 2017, 133, 900–912. [Google Scholar] [CrossRef]
- Mao, Q.; Yang, M. Experimental and numerical investigation on heat transfer performance of a solar double-slope hollow glazed roof. Appl. Therm. Eng. 2020, 180, 115832. [Google Scholar] [CrossRef]
- Gagliano, A.; Patania, F.; Nocera, F.; Ferlito, A.; Galesi, A. Thermal performance of ventilated roofs during summer period. Energy Build. 2012, 49, 611–618. [Google Scholar] [CrossRef]
- Omar, A.I.; Virgone, J.; Vergnault, E.; David, D.; Idriss, A.I. Energy Saving Potential with a Double-Skin Roof Ventilated by Natural Convection in Djibouti. Energy Procedia 2017, 140, 361–373. [Google Scholar] [CrossRef]


| −3 | −2 | −1 | 0 | +1 | +2 | +3 |
| Extremely cold | Cold | Slightly cold | Comfortable | Slightly hot | Hot | Extremely hot |
| Parameter | Situation | Percentage |
|---|---|---|
| Size | Medium | 8/15 |
| Small | 7/15 | |
| Audience capacity (seat) | 3000~6000 | 8/15 |
| ≤3000 | 7/15 | |
| Auditorium layout (side) | ≤2 | 9/15 |
| >2 | 6/15 | |
| Building material | Reinforced concrete | 14/15 |
| steel | 1/15 | |
| Building height (meter) | ≤15 | 10/15 |
| >15 | 5/15 | |
| Main window position | Height of the walls | 8/15 |
| Bottom of the walls | 2/15 | |
| Both height and bottom of the walls | 2/15 | |
| On the roof | 3/15 | |
| window-to-wall ratio (WWR) | ≤0.3 | 10/15 |
| 0.3~0.7 | 5/15 | |
| Roof slope | Horizontal roof | 8/15 |
| Single slope | 3/15 | |
| Multi-slope | 4/15 | |
| Overhanging eave | Without overhanging eave | 2/15 |
| With overhanging eave | 13/15 |
| Component | Materials | U-Value (W/ (m2·K)) |
|---|---|---|
| Exterior wall | 13 mm decorative brick + 20 mm lime mortar + 10 mm Expanded Polystyrene (EPS) insulation + 240 mm aerated concrete + 20 mm lime mortar | 0.5 |
| Roof | 40 mm C20 fine aggregate concrete + 20 mm cement mortar + 5 mm waterproof membrane + 30 mm cement mortar + 60 mm Extruded Polystyrene (XPS) insulation + 20 mm cement mortar + 120 mm reinforced concrete + 20 mm cement mortar | 0.35 |
| Window | Aluminium frame + 6 mm clear single glazing | 6.073 |
| Floor | 20 mm cement mortar + 100 mm reinforced concrete + 20 mm cement mortar | 2.813 |
| Foundation | 20 mm cement mortar + 80 mm fine aggregate concrete + 500 mm rammed clay | 0.887 |
| Factor | Level 1 | Level 2 | Level 3 |
|---|---|---|---|
| (A) Main window position | High at the south and north wall | Low at the south wall and high at the north wall | High at the south wall and low at the north wall |
| (B) South WWR | 10% | 20% | 30% |
| (C) North WWR | 10% | 20% | 30% |
| (D) Roof insulation type | Single skin roof | Double skin roof | Insulated roof |
| (E) Roof slope | Horizontal roof | Rise from south to north | Rise from north to south |
| (F) Depth of overhanging eave | 1 m | 5 m | 9 m |
| Test Number | Factor | Result of PTS | |||||
|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | ||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1.110 |
| 2 | 1 | 2 | 2 | 2 | 2 | 2 | 0.924 |
| 3 | 1 | 3 | 3 | 3 | 3 | 3 | 0.984 |
| 4 | 2 | 1 | 3 | 1 | 2 | 2 | 1.119 |
| 5 | 2 | 2 | 1 | 2 | 3 | 3 | 0.892 |
| 6 | 2 | 3 | 2 | 3 | 1 | 1 | 0.965 |
| 7 | 3 | 1 | 2 | 2 | 1 | 3 | 0.913 |
| 8 | 3 | 2 | 3 | 3 | 2 | 1 | 1.065 |
| 9 | 3 | 3 | 1 | 1 | 3 | 2 | 1.299 |
| 10 | 1 | 1 | 2 | 3 | 3 | 2 | 1.182 |
| 11 | 1 | 2 | 3 | 1 | 1 | 3 | 1.022 |
| 12 | 1 | 3 | 1 | 2 | 2 | 1 | 0.961 |
| 13 | 2 | 1 | 3 | 2 | 3 | 1 | 0.907 |
| 14 | 2 | 2 | 1 | 3 | 1 | 2 | 1.03 |
| 15 | 2 | 3 | 2 | 1 | 2 | 3 | 1.053 |
| 16 | 3 | 1 | 1 | 3 | 2 | 3 | 1.087 |
| 17 | 3 | 2 | 2 | 1 | 3 | 1 | 1.227 |
| 18 | 3 | 3 | 3 | 2 | 1 | 2 | 0.912 |
| K1 | 6.183 | 6.318 | 6.379 | 6.830 | 5.952 | 6.235 | |
| K2 | 5.966 | 6.160 | 6.264 | 5.509 | 6.209 | 6.466 | |
| K3 | 6.503 | 6.174 | 6.009 | 6.313 | 6.491 | 5.951 | |
| k1 | 1.031 | 1.053 | 1.063 | 1.138 | 0.992 | 1.039 | |
| k2 | 0.994 | 1.027 | 1.044 | 0.918 | 1.035 | 1.078 | |
| k3 | 1.084 | 1.029 | 1.002 | 1.052 | 1.082 | 0.992 | |
| R | 0.090 | 0.026 | 0.062 | 0.220 | 0.090 | 0.086 | |
| Factor ranking | D > A = E > F > C > B | ||||||
| Factor | SS | df | V | F | F(0.05) | Significance |
|---|---|---|---|---|---|---|
| A | 0.024 | 2 | 0.012 | 0.721 | 3.74 | * |
| B | 0.003 | 2 | 0.002 | 0.090 | 3.74 | |
| C | 0.012 | 2 | 0.006 | 0.361 | 3.74 | |
| D | 0.148 | 2 | 0.074 | 4.446 | 3.74 | ** |
| E | 0.024 | 2 | 0.012 | 0.721 | 3.74 | * |
| F | 0.022 | 2 | 0.011 | 0.661 | 3.74 | |
| Deviation | 0.231 | 14 | 0.016 |
| Parameters | Initial Model | Optimized Model |
|---|---|---|
| Window position | High to the south and north | Low to the south and high to the north |
| WWR | South and north for 10% | South for 20% and north for 30% |
| Roof insulation type | Single skin reinforced concrete | Double skin reinforced concrete |
| Roof slope | Horizontal roof | Horizontal roof |
| Depth of overhanging eave (m) | 1 | 9 |
| Indoor avg. operative temperature (°C) | 29.30 | 28.21 |
| Indoor avg. humidity ratio (g/kg’) | 20.16 | 20.15 |
| Indoor avg. air velocity (m/s) | 0.21 | 0.77 |
| Indoor avg. PTS | 1.11 | 0.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Zhang, Q.; Tanaka, I. Optimization of Architectural Form for Thermal Comfort in Naturally Ventilated Gymnasium at Hot and Humid Climate by Orthogonal Experiment. Energies 2021, 14, 3228. https://doi.org/10.3390/en14113228
Huang X, Zhang Q, Tanaka I. Optimization of Architectural Form for Thermal Comfort in Naturally Ventilated Gymnasium at Hot and Humid Climate by Orthogonal Experiment. Energies. 2021; 14(11):3228. https://doi.org/10.3390/en14113228
Chicago/Turabian StyleHuang, Xiaodan, Qingyuan Zhang, and Ineko Tanaka. 2021. "Optimization of Architectural Form for Thermal Comfort in Naturally Ventilated Gymnasium at Hot and Humid Climate by Orthogonal Experiment" Energies 14, no. 11: 3228. https://doi.org/10.3390/en14113228
APA StyleHuang, X., Zhang, Q., & Tanaka, I. (2021). Optimization of Architectural Form for Thermal Comfort in Naturally Ventilated Gymnasium at Hot and Humid Climate by Orthogonal Experiment. Energies, 14(11), 3228. https://doi.org/10.3390/en14113228





