Multi-Criteria Analysis for the Selection of the Optimal Mining Design Solution—A Case Study on Quarry “Tambura”

Abstract

Mining design is usually evaluated with different multiple-criteria decision-making (MCDM) methods when it comes to large open pit or underground ore mines, but it is not used on quarry sites. Since Croatia is mostly mining stone, the implementation of such methods in decision making of the quarry mine design is imperative but left out. In this paper, the PROMETHEE II and AHP decision-making methods are implemented on the quarry site to find out the best final quarry design contour. By implementing the MCDM methods, the best quarry model was chosen based on 22 different criteria parameters out of three final quarry designs. The chosen model is not only financially sound but also has the least environmental impact.

1. Introduction

Multiple-criteria decision-making (MCDM) methods are used worldwide by scientists and engineers in solving problems with multiple variables and uncertain conditions in different fields of work such as infrastructure [1], railways [2], electricity distribution network planning [3], and so on.

Similar to all other industries, the MCDM has found the practical application in mining industry in solving different challenges in various conditions but is not constantly used. Hudej et al. [4] determined the position of the main mining shaft using multiple criteria analyses simultaneously (PROMETHEE, ELECTRE, AHP, and VIKOR), and the final model was obtained by the weighting method. Dimitrijević et al. [5] used PROMETHEE and ELECTRE methods to select the best land reclamation method of open-pit coal mine between 10 offered alternatives. Multi-criteria analysis was used by Šubaranović et al. [6] to choose between the two variants of the groundwater penetration protection system modification of the surface coal mine Drmno. Özfırat [7] used the FAHP method to determine which machinery can be used in the underground coal mine. Kizil et al. [8] used the AHP method in determining the best position and orientation of the long wall based on geological, geographical, geotechnical, and economic parameters of the underground coal mine. Stojanović et al. [9] used the AHP and ELECTRE methods in determining the optimal exploitation technology of surface coal mine by comparing three different exploitation technologies while defining eight selection method criteria. Bouhedja et al. [10] used the PROMETHEE method in determining the secondary method of crushing oversized stone in the quarry. Aryafar et al. [11] determined the optimal drilling and blasting pattern in the open-pit iron mine by first using AHP method under a fuzzy environment to define the weight of criteria and then applying TOPSIS and PROMETHEE methods to select the most proper alternative. Yari et al. [12] assessed the risks of the exploitation of dimension stone by defining 17 main levels that are ranked using the PROMETHEE method. The optimization of copper and zinc open-pit mine [13] was performed based on the minerals cost data. By integrating multiple mining optimization results, from the price of the mineral raw material, a probability model was obtained. Yari et al. [14], in their work, used a multi-criteria analysis for the evaluation and classification of dimension stone deposits and emphasized the safety parameters. Wang et al. [15] determined the priority order of auxiliary transportation models using the PROMETHEE method. Nolan and Kecojevic [16] used the AHP method on five interrelated modules to improve surface mining practices and reduce negative environmental impact of overburden removal in West Virginia. Aghajani Bazzazi et al. [17] used a combination of fuzzy set theory and AHP method in solving the multi-attribute open-pit mining equipment selection problem. Vujić et al. [18] used PROMETHEE method in selecting technological system in the open-pit clay mine in Serbia. Betrie et al. [19] determined the remedial alternatives for mine sites by implementing the PROMETHEE method in a study along with AHP method for definition of criteria weights. Yakovlev et al. [20] determined the optimal open-pit contour of the diamond mine by determining the ultimate strip ratio based on geological and geotechnical characteristics of the deposit.

In underground mining, multi-criteria analysis was applied extensively by many researchers. Balusa and Singam [21] used a combination of the WPM and PROMETHEE methods to determine an effective exploitation method of the underground bauxite deposit. Chander et al. [22] used improved AHP and VIKOR methods of multi-criteria decision making and defined the Cut and Fill method as the best underground exploitation method of the bauxite deposits based on the assumed criteria. Alpay and Yavuz [23] used the AHP method to support the determination of the underground mining method by analysing different scenarios and criteria. Iphar and Alpay [24] developed a mobile application that allows the designer to use one or more of the offered MCDM methods (TOPSIS, AHP-TOPSIS, PROMETHEE, AHP-PROMETHEE, ELECTRE, AHP-ELECTRE, VIKOR, AHP-VIKOR, FMADM, and AHP-FMADM) in the analysis of input parameters when determining the method of underground exploitation for the analysed case. Yazdani-Chamzini et al. [25] created an integral model for determining the method of underground exploitation of zinc deposits using FAHP and FTOPSIS methods. Gupta and Kumar [26] determined the best underground mining stopping method of the deposit using the AHP method. Naghadehi et al. [27] determined the optimal method of underground bauxite exploitation using the fuzzy analytical hierarchy process (FAHP) method to determine the weight of the criteria and then rank the exploitation methods using the conventional AHP method. Balusa and Mountains [28] used a fuzzy analytical hierarchy process (FAHP) to determine the exploitation method (seven mining methods were analysed) of an underground metal mine based on 16 criteria model consisting of three layers. Balusa and Gorai [29] used TOPSIS, VIKOR, improved ELECTRE, PROMETHEE II, and WPM multi-criteria decision-making methods in selecting the best method of underground exploitation of the underground mine and obtaining non-uniform results when selecting the method of underground exploitation. Javanshirgiv and Safari [30] used the fuzzy TOPSIS method to determine the optimal mining method between the four considered methods of underground exploitation of fluorine mine based on 14 criteria. Asadi Ooriad et al. [31] defined a new approach in determining the method of underground exploitation on the example of coal deposits in Iran using the FTOPSIS method in combination with the AHP method. Ataei et al. [32] used the TOPSIS method of multi-criteria decision-making to determine the optimal method of underground bauxite exploitation on the example of Golbini No. 8 deposit in Iran by comparing six different underground exploitation methods and 13 technical criteria. Yavuz [33] used AHP and FMADM methods to select the best underground mining method for lignite mine near Istanbul. Kabwe [34] used AHP and Yager’s method to determine underground exploitation method of copper ore deposits in Zambia. Bajić et al. [35] defined a set of criteria and, using the FAHP method, determined the optimal method of underground exploitation of copper deposits in Serbia. Bogdanović et al. [36] applied a combination of AHP and PROMETHEE methods to select the method of underground exploitation.

When determining the optimal contour of the open pit or quarry, the methods that are most often used are the floating slopes method, floating cone method/technique, stochastic optimization, Lerchs-Grossman algorithm, and others, in order to primarily observe the spatial placement of the mineral raw materials in the form of block models and the exploitation expenses [37,38,39,40,41].

This work showcases the application of multi-criteria analysis using the analytical hierarchy process (AHP) and the PROMETHEE II method on the example of the quarry “Tambura”, Croatia. AHP and PROMEETHE II methods were used due to the simplicity of application and the possibility of using the proposed methodology when selecting the optimal quarry final contours. The emphasis was given to the selection of project parameters, which must ensure the safety (stability) of the whole quarry, and to ensure the quantity of the mineral raw material reserves that can be obtained with the greatest amount of gain. On the other hand, there is a larger demand and effort for mining to not disturb the environment and the ownership of land where the exploitation is planned. The design solution must be optimal in all aspects, so it is a requirement to analyse all the criteria when selecting the optimal solution. There were three possible quarry contours analysed, and the optimal design solution were used as the final quarry contour.

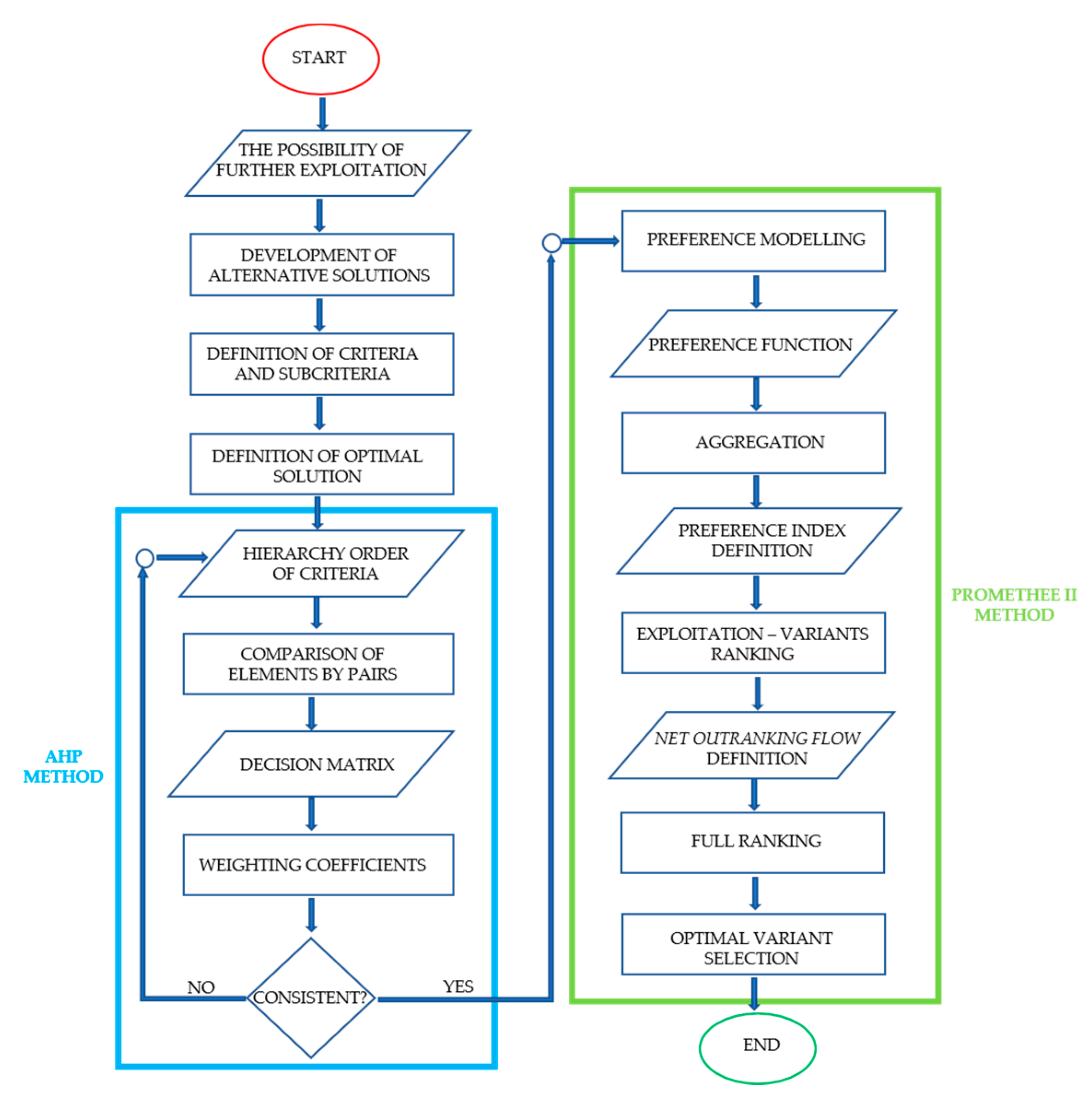
2. Methodology (Methods of Multi-Criteria Decision Making)

According to authors Hwang and Yoon [42], the term multi-criteria decision making refers to making decisions based on multiple criteria which are often contradictory. The authors also state that each problem has four common characteristics: multiple criteria, appearance of conflicting criteria, unmeasurable units, and problem solution.

The optimal contour of the quarry “Tambura” was determined using two MCDM methods. Models were first analysed using the method of analytical hierarchy process (AHP) and then the output results were additionally analysed with the PROMETHEE II method, and further, the optimal solution for the final contour design of quarry “Tambura” was selected (Figure 1).

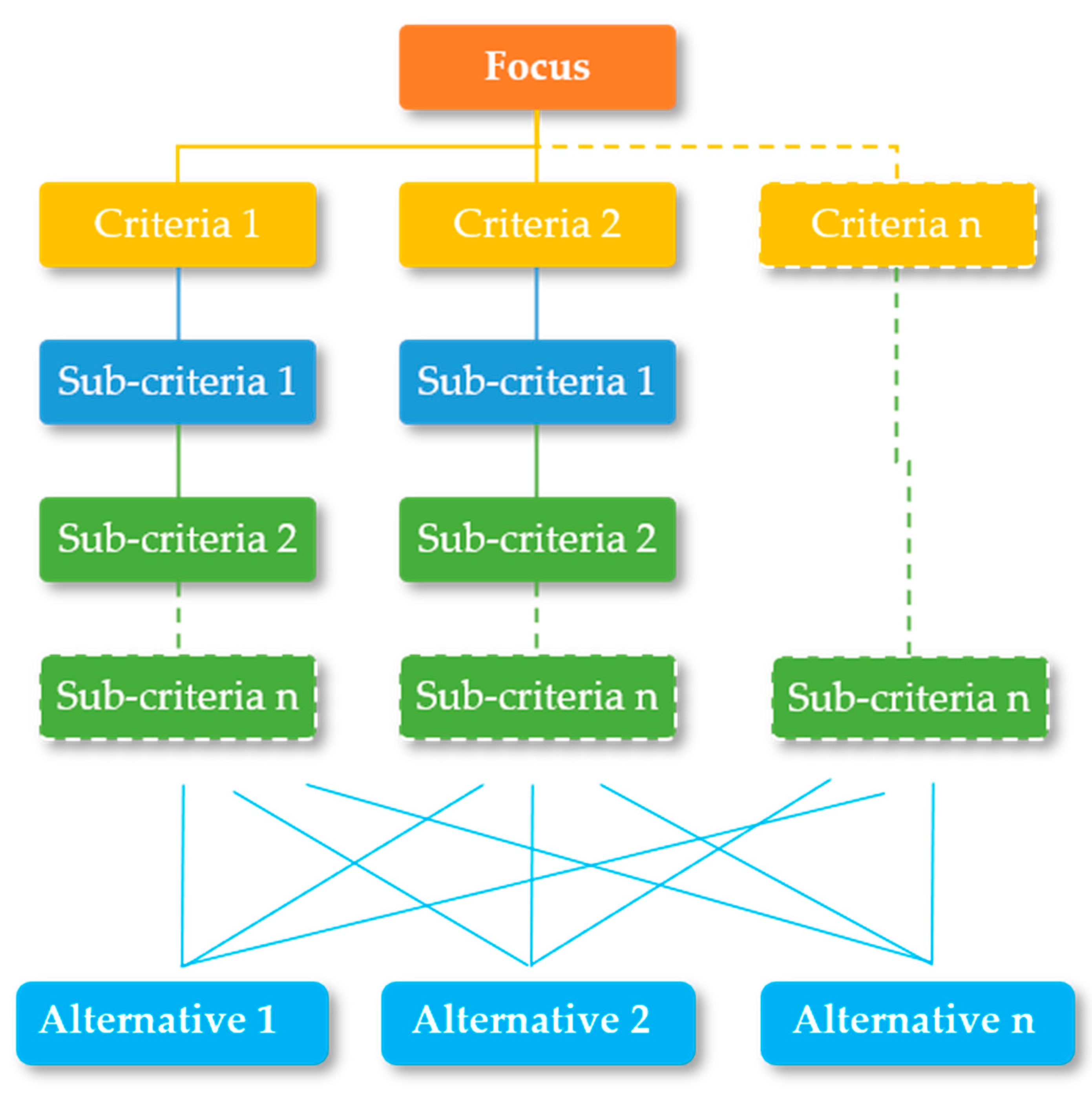
2.1. Analytical Hierarchy Process (AHP)

The method used as the entry point for the analysis and final solution selection is the most commonly used method of multi-criteria decision making—analytical hierarchy process (AHP)—on the basis of which decisions on the optimal solution selection or alternative were made. The method is based on the assessment of relative sizes of certain criteria by comparing them in order to determine their ratio and hierarchal ranking dependent on the importance of each criterion [43] based on their evaluation. The hierarchal process structure is shown in Figure 2 [43,44].

In the analytical hierarchy process, it is necessary to define the following steps [43]:

• Define the problem (the desired optimal solution);
• Create a hierarchy of criteria according to their level of importance, the most important at the top and the least important at the lowest level as they usually represent alternatives;
• Determine/create a square matrix of comparisons where you compare criteria (or alternatives) at the same level with other elements of the same level;
• Select the optimal alternative (solution) based on weighting coefficients.

In order for the elements to be compared and result in the final outcome, namely, ranking of alternatives, it is necessary to add numerical values to the elements in the matrix (criteria and alternatives). According to Saaty [45], the strength/intensity of a certain criterion compared to the other can be described, i.e., criteria are given numerical values from 1, which means two elements of the same importance, to 9, which points to the extreme preference of one element over the other, as shown in

Table 1. AHP scale.

Degree/Intensity of Importance	Definition	Description
1	Equally favourable	2 elements (i and j) have equal value
3	Slightly more favourable	Element (i) is slightly more favourable than element (j)
5	Highly favourable	Element (i) is highly favourable than element (j)
7	Very highly favourable	Element (i) is very highly favourable than element (j)
9	Extremely favourable	Element (i) is extremely favourable than element (j)
2, 4, 6, 8	Median values between two definitions

.

The square matrix of comparisons, or relative importance, is created by comparing two elements in pairs (Equation (1)), one compared to the other where the end result is a matrix of array n with obtained assessment.

$$\left[A\right]=\left[\begin{array}{c}\begin{array}{ccc}{a}_{11}& a_{12}& \dots a_{1n}\\ a_{21}& a_{22}& \dots a_{2n}\\ ⋮& ⋮& \ddots ⋮\end{array}\\ a_{m1 } a_{m2} {\cdots }_{} a_{mn}\end{array}\right].$$

(1)

The relative importance of criterion i (i compared to the relative importance of criterion j) is shown with the element a_ij. In accordance with that, if the criterion i is more important than the criterion j, the importance is shown with the element a_ij > 1, if the criterion j is more important than the criterion I, the importance is shown with the element a_ij < 1, and for the criteria of same importance, the following is valid: a_ij = 1 [46].

The priority, i.e., the weight of each criterion needs to be calculated according to Equation (2) as follows:

$$\left[A\right]·\overrightarrow{p}=\lambda ·\overrightarrow{p},$$

(2)

where

[A]—square matrix of comparisons,

λ—maximum unit value,

$\overrightarrow{p}$—vector of typical values.

The priority of each criterion is approximated with a unit vector and maximum unit value. The maximum unit value λ is attained by the following expression (Equation (3)):

$$det\left(\lambda \left[I\right]-\left[A\right]\right)=0.$$

(3)

In order to obtain the final result, namely, to determine the rank of alternatives, it is necessary to check the consistency of comparisons, in other words, determine the consistency ratio CR (Equation (4))

$$CR=\frac{CI}{RI},$$

(4)

which is derived from the ratio of consistency index CI (Equation (5)) and the value of the random index RI.

The value of the random index RI (

Table 2. Random index RI values.

n	RI
1	0.00
2	0.00
3	0.58
4	0.90
5	1.12
6	1.24
7	1.32
8	1.41
9	1.45
10	1.49

) represents the medium value of consistency index and has different values for matrices of different sizes [44].

Consistency index, CI, is obtained according to the following expression:

$$CI=\frac{\lambda -n}{n-1},$$

(5)

where

λ—maximum unit value (approximated by Equation (6))

n—maximum unit value of consistent matrix.

$$\lambda =\frac{{{\displaystyle \sum }}_{i=1}^{n}c{v}_{ij}}{j}.$$

(6)

The consistency vector, cv, is calculated according to Equation (7) by multiplying the comparison matrix (of relative importance) and weight of the criteria as follows:

$$\left[A\right]·\left[W\right]=\left[\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right]·\left[\begin{array}{c}{W}_{11}\\ W_{12}\\ W_{13}\end{array}\right]=\left[\begin{array}{c}c{v}_{11}\\ c{v}_{12}\\ c{v}_{13}\end{array}\right],$$

(7)

where

[A]—square matrix of comparisons,

[W]—the weight of the criteria (priority vector).

The final rank of alternatives, which is the main goal of this method, is obtained by joining local priorities according to expression (8) as stated in [3]:

$$\begin{gathered} Priority={{\displaystyle \sum }}_i\mathrm{local}\mathrm{priority}\mathrm{of}\mathrm{alternative}\mathrm{A}\mathrm{compared}\mathrm{to}\mathrm{criterion}\mathrm{Ci}· \\ \mathrm{local}\mathrm{priority}\mathrm{of}\mathrm{criterion}\mathrm{Ci}\mathrm{compared}\mathrm{to}\mathrm{goal}i, \end{gathered}$$

(8)

According to Saaty [44], all assessments with CR < 0.1, meaning the mistake with assessments is less than 10%, are considered consistent. Albeit the value of 10% is not the governing factor in making decisions (assessments), which are based on the knowledge and experience of the designer, the discrepancy should not be too big.

2.2. PROMETHEE II Method

The PROMETHEE II method (Preference Ranking Organisation Method for Enrichment Evaluation) [47,48] is also a method of multi-criteria analysis based on comparing alternatives by different criteria in order to establish the strength of one alternative compared to another, namely, it gives a full ranking of alternatives based on their previous assessment by selected criteria [49].

According to a group of authors [2,50], introducing a preference function P(a,b) for alternatives a and b, and after defining the criteria, it is possible to rank the given alternatives.

The decision-making process with the help of PROMETHEE II method can be carried out according to the following steps [50]:

• Preference modelling,
• Aggregation,
• Exploitation.

With preference modelling, the preference function Pi is determined, namely, P(a,b), and it is defined in the following manner according to Equation (9) [47]:

$$P\left(a,b\right)=\{\begin{array}{cc}0& ako je g\left(a\right)\le g\left(b\right)\\ p\left[g\left(a\right),g\left(b\right)\right]& ako je g\left(a\right)\ge g\left(b\right)\end{array},$$

(9)

where

g(a)—estimated value of alternative a according to criteria,

g(b)—estimated value of alternative b according to criteria.

The preference function can have values between 0 and 1, and it is defined for each of the criteria separately, where the following is valid: the smaller the value of preference function, namely, the closer it is to 0, the intensity of the preference is weaker, and vice versa, the closer the value is to 1, the intensity of the preference is stronger. In cases where the preference function acquires extreme values, either indifference occurs (valid for value 0) or strict preference occurs (value of 1) [2,49,50].

The next step is aggregation where the preference index needs to be defined, namely, the index of multi-criteria preference π(a,b), which represents the degree or measure of preference for alternative a compared to alternative b while considering all the criteria [2,49]. The preference index is calculated according to Equation (10):

$$\pi \left(a,b\right)={{\displaystyle \sum }}_{i=1}^k{w}_i·P_i\left(a,b\right),$$

(10)

where

w_i—weight of criteria,

P_i—preference function.

As it is valid for the preference function, it is also valid with the preference index, i.e., the closer the index is to zero, the weaker global preference of alternative a when compared to alternative b, namely, the closer the value gets to 1, the global preference is stronger [49].

The last step of the PROMETHEE II method is exploitation. In order to rank alternatives, PROMETHEE II method was used, which gives the full ranking of alternatives [48], namely, the optimal alternative.

Entering and leaving flow need to be determined as an in-between step. Entering flow ϕ⁻ (a) shows the inclination towards other alternatives in comparison to alternative a, meaning how much weaker alternative a is when compared to other alternatives. The leaving flow ϕ⁺ (a) displays the inclination towards alternative a when compared to other alternatives, i.e., how much better alternative a is [51]. Entering and leaving flows are defined according to the following formula:

$${\mathsf{\varphi }}^{-}\left(a\right)=\frac{1}{n-1}{\displaystyle \sum }_{x\in A}^{}\pi \left(a,x\right)$$

(11)

$${\mathsf{\varphi }}^{+}\left(a\right)=\frac{1}{n-1}{{\displaystyle \sum }}_{x\in A}^{}\pi \left(x,a\right).$$

(12)

Net outranking flow ϕ(a) needs to be calculated for each of the alternatives in order to obtain the full ranking of the alternatives (Equation (13)):

$$\mathsf{\varphi }\left(a\right)={\mathsf{\varphi }}^{+}\left(a\right)-{\mathsf{\varphi }}^{-}\left(a\right).$$

(13)

The ranking of obtained values ϕ(a), from the greatest to the lowest, gives the final ranking of alternative solutions.

3. Selection of the Optimal Final Contour for the Quarry “TAMBURA”—Case Study

The input data (project parameters, mineral deposit reserves, economic indicators, environmental impact, and property legal relations) [52], on the basis of which the multi-criteria decision-making methods were applied, were elaborated in more detail in order to obtain the optimal solution, namely, the selection of the final contour for the continuation of further exploitation.

3.1. Site Location

The quarry “Tambura” is located in Croatia, at the southern part of Istrian peninsula and is part of the administrative district of Fažana. In the pit-shaped quarry “Tambura”, technical building stone is mined from the surface to the lower horizons (Figure 3).

The quarry “Tambura” has been exploited since 1996 and can be reached by a macadam road (approximately, 6 m wide and 292 m long). The quarry is approximately 277 m wide and approximately 184 m long (Figure 3). The lowest quarry point is +80 m ASL (central plateau), and the tallest pit point is 104 m ASL (located at the quarry east side) which makes that a height difference of 24 m. The central plateau can be accessed by two access ramps—main and ancillary. The main ramp is around 90 m long, with average slope of 12% and is located at the north-eastern part of the quarry. The ancillary ramp is located in the north-western part of the quarry and is 107 m long, with an average slope of 13%. In the eastern and southern parts of the quarry two deep benches were created; +80 m ASL (average height of 10 m) and +90 m ASL (maximum height of 14 m). Although +90 m ASL bench can be recognized, it is of irregular height, varying from +87 m ASL to +90 m ASL (Figure 3).

The need to decrease the borders of the exploitation field due to property legal relations and abating the environmental impact of the open pit, the selection of optimal quarry model for the continuation of exploitation was required. The continuing quarry development was only possible in going deeper, and taking that into consideration, three models of the final contour for the quarry “Tambura” were made with different project parameters.

3.2. Criteria Selection for Optimization—Application of the AHP Method

When selecting the optimal solution, three different solutions, i.e., models were proposed, based on different input data for each of them.

Each of the proposed models had to fulfil certain conditions, based on which the criteria for the selection of the optimal model were designed, further processed, and evaluated. According to Hrastov [52], the optimal model needs to fulfil the following conditions:

• Compliance with the relevant Croatian legislation,
• Maximally adapt to the present situation of the previously done mining work,
• Ensure the maximum possible level of safety for people and environment,
• Consider other neighbouring objects and works,
• Enable carrying out of biological reclamation after the exploitation is finished, and
• Enable the settlement of all property legal relations on all cadastral parcels covered by the exploitation field.

In order to select the optimal model of exploitation, five main groups of criteria were selected, as well as the sub-criteria for each of those groups based on the previously stated conditions that need to be fulfilled. Each of the models was evaluated for the total of 21 criteria. Each group of criteria and their subgroup was assigned criteria importance on the basis of the AHP method according to Saaty scale [45].

Table 3. The importance of the main group of criteria.

Criteria Group	Degree/Intensity of Importance	Definition
Project parameters	1	Equally preferred
Mineral deposit reserves	1	Equally preferred
Economic indicators	4	Moderately to strongly preferred
Environmental impact	5	Strongly preferred
Property legal relations	9	Extremely preferred

shows the intensity of importance for the main group of criteria.

As shown in Table 3, each criterion is given a numerical value (degree/intensity of importance) depending on the level of importance of each criterion. In this example, two criteria stand out and were emphasized for further analysis on the basis of which the optimal model for exploitation continuation was selected; the two selected criteria are the environmental impact and property legal relations (possibility of their settlement).

To determine the importance of a criterion, a question needs to be asked for each of them: Is criterion A more or less important than criterion B? Mutually comparing elements (criteria) in such a manner creates a square matrix for criteria of the same level.

Table 4. Comparison matrix of main groups of criteria.

Criteria Group	Project Parameters	Mineral Deposit Reserves	Economic Indicators	Environmental Impact	Property Legal Relations
Project parameters	1.00	1.00	0.25	0.20	0.11
Mineral deposit reserves	1.00	1.00	0.20	0.25	0.11
Economic indicators	4.00	4.00	1.00	0.20	0.33
Environmental impact	5.00	5.00	5.00	1.00	0.33
Property legal relations	9.00	9.00	3.00	3.00	1.00

shows the comparison matrix for the main groups of criteria.

Based on the obtained matrix and element comparison, the weighting coefficient for each of the main group of criteria is determined. The weighting coefficients of the main group of criteria are shown in

Table 5. Weighting coefficients for the main group of criteria.

Criteria Group	Weighting Coefficient	Weighting Coefficient (%)
Project parameters	0.05	5.00
Mineral deposit reserves	0.05	5.00
Economic indicators	0.16	16.00
Environmental impact	0.27	27.00
Property legal relations	0.48	48.00

. The estimation consistency obtained by adding importance to criteria and from the weighting coefficients is 8.50%, which is considered a consistent evaluation according to [44].

In the same way as was shown for the main group of criteria (Table 5), comparison matrices were made for all other sub-criteria, and their weighting coefficients and consistency ratios were calculated and determined.

The obtained weighting coefficients were used as input data for the continuing analysis using the PROMETHEE II method.

3.3. Application of the PROMETHEE II Method

The weighting coefficients obtained with the AHP method (Table 5) represent input data for the application of PROMETHEE II method when selecting the optimal model for continuing the exploitation. The output results of the PROMETHEE II method give the definite ranking of the quarry final contour models.

Before the final ranking was obtained, and pursuantly the optimal model, these were the precedent steps (phases):

• Selection of design solution alternatives (models) for further exploitation,
• Evaluation of models according to the set criteria and their sub-criteria,
• Comparison and ranking of alternative solutions, and
• Selection of the optimal model.

The design parameters of the model’s final design contours (

Table 6. Project parameters for the quarry “Tambura”.

Project Parameters	Models
	Model 1	Model 2	Model 3
Maximum bench height (he), m	20.0	17.0	24.0
Minimum width of bench level (B), m	3.0	5.0	5.0
Angle of inclination of bench slope (αe), °	≤70	≤70	≤70
Angle of inclination of final slope (αz), °	≤60	≤61	≤61
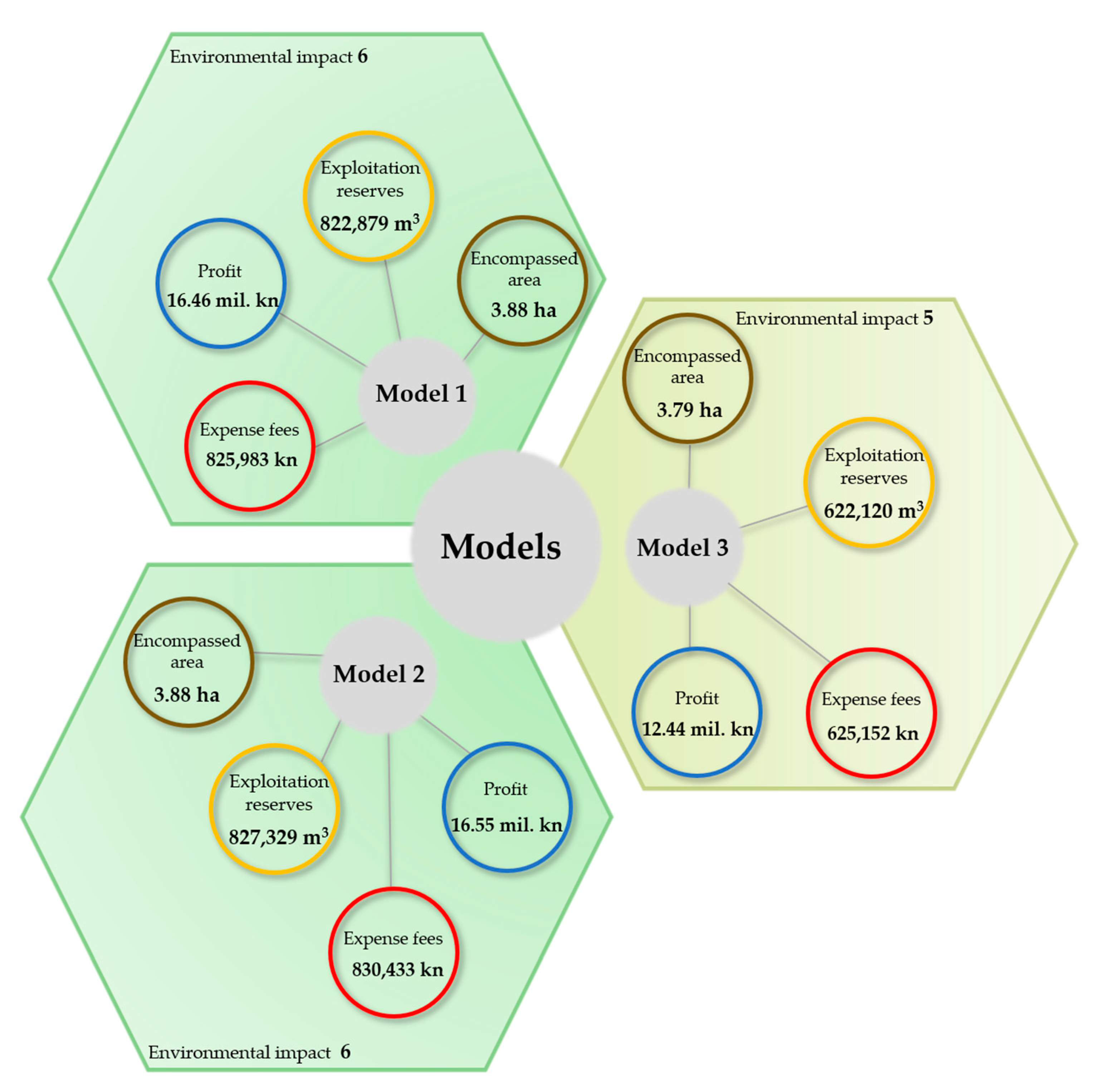
Area of exploitation field, ha	3.88	3.88	3.79

) were determined based on the exploitation field spatial constraint (mining area and property-legal relations within the scope of cadastral parcels) and the possibility of continuing exploitation depending on the quantities of determined mineral reserves. Based on the conducted geomechanical stability analysis, it was confirmed that the design parameters for each model meet the safety standards. The entry data (project parameters) for each of the models are shown in Table 6, on the basis of which mineral deposit reserves and the economic indicators were calculated [52], which were then all used in the calculation, namely, were applied in the PROMETHEE II method.

Each of the main group of criteria (

Table 7. Criteria and sub-criteria for the selection of the optimal model.

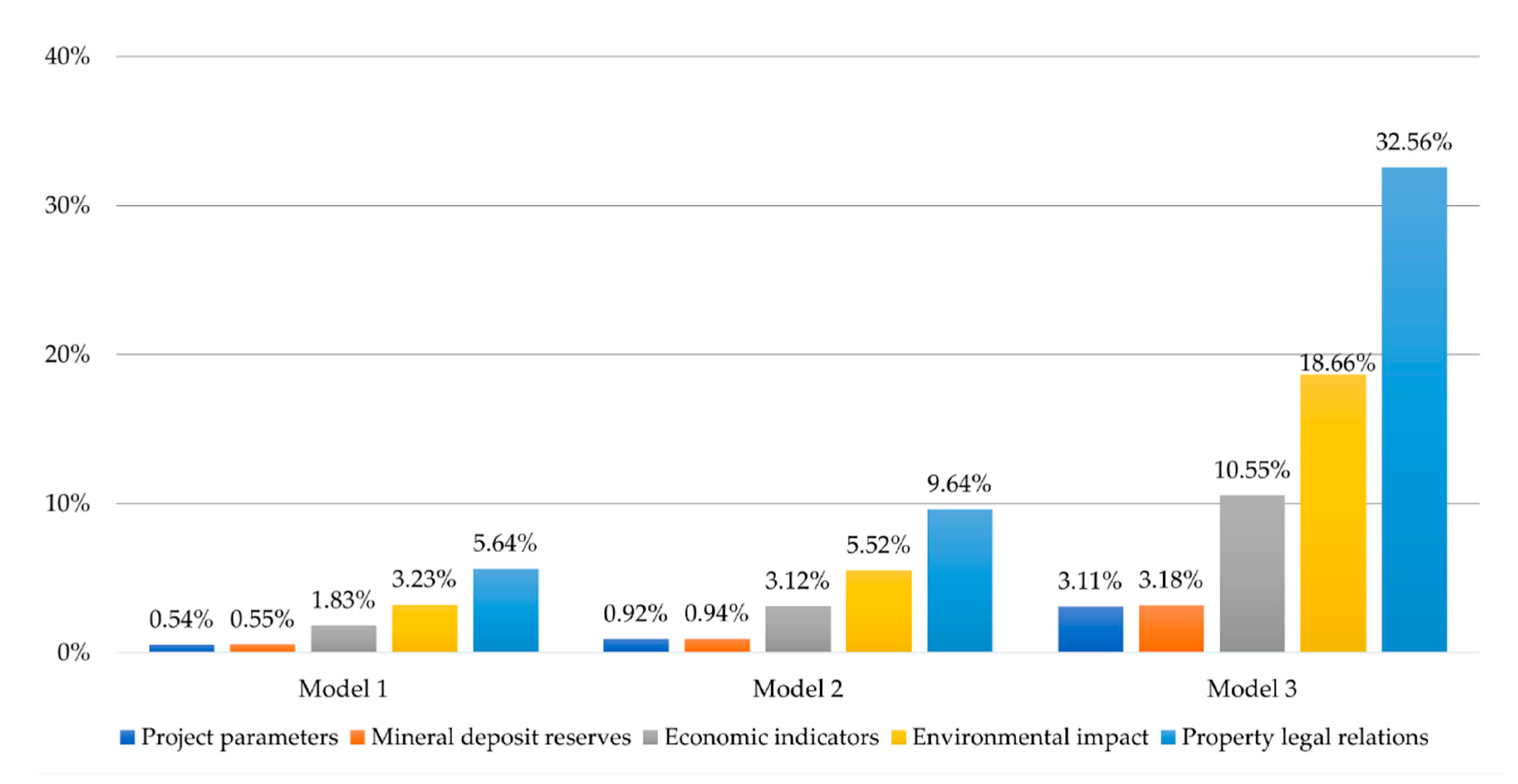
Selection Criteria
Criteria Group	%	Criteria Name			%	Category Mark
Project parameters	5	Maximum bench height (he), m			8	C1
		Minimum width of bench level (B), m			6	C2
		Angle of inclination of bench slope (αe), °			23	C3
		Angle of inclination of final slope (αz), °			43	C4
		Area of exploitation field, ha			19	C5
Mineral deposit reserves	5	Balance reserves, m3			28	C6
		Out of balance reserves, m3			10	C7
		Exploitation reserves, m3			62	C8
Economic indicators	16	Profit, kn			19	C9
		Fee expenses, kn	Fixed fee, kn		17	C10
			Variable fee, kn	Government budget, kn	14	C11
				Local regional unit, kn	24	C12
				Local government unit, kn	27	C13
Environmental impact	27	Biodiversity			7	C14
		Geological and hydrological characteristics			9	C15
		Seismological, pedological, and climatological characteristics			7	C16
		Infrastructural and economic characteristics			16	C17
		Cultural and landscape characteristics			6	C18
		Noise			18	C19
		Blasting			21	C20
		Population			17	C21
Property legal relations	48	Possibility of enabling access to all cadastral parcels			100	C22

) was evaluated by mutual comparison, and thus the weighting criteria was ascertained, which in the end amounts to 100%. In addition, the sub-criteria of each group were evaluated in the same manner. The sub-criteria from the same group were compared among each other and the sum of their weighting criteria is also 100%.

The greatest importance when selecting the optimal model on the basis of the multi-criteria analysis was given to property legal relations, namely, the possibility of enabling access to all cadastral parcels, without which continuing the exploitation is not feasible.

Table 7 gives an overview of obtained weighting factors for all the criteria which were used in the analysis, namely, selection of the optimal model of exploitation continuation for the quarry “Tambura” [52].

After selecting alternatives to be analysed as the possible solution, it is also necessary to evaluate alternatives (models) according to already stated criteria and sub-criteria (

Table 8. Assessment of environmental impact.

Environmental Impact
None	/	Weak	/	Moderate	/	High
7	6	5	4	3	2	1

).

During criteria evaluation, according to Krpan [2], it is necessary to differentiate two manners of evaluation, namely, two sets of criteria:

• Criteria evaluated based on the quantitative data,
• Criteria evaluated on the subjective assessment of the designer.

Project parameters, mineral deposit reserves, and economic indicators were evaluated on the basis of quantitative data [53,54], and environmental impact was evaluated by subjective assessment [55].

The selected criteria have designated marks from C1 to C22 (Table 7) and are either quantitatively evaluated (C1–C13) or subjectively evaluated (C14–C22). The reserves of technical building stone [52] were calculated on the basis of project parameters [53], which resulted in economic indicators. The environmental impact was assessed as none/weak/moderate/high impact [55] and those criteria were given grades from 1 to 7 (Table 8) for the purpose of evaluation, where grade 1 presents significant impact and grade 7 has no environmental impact. The values in between were marked with grades of 2, 4, and 6. The criteria for settlement of property legal relations were evaluated with yes/no, namely, grades 1 and 0.

All main groups of criteria were cumulatively considered (Table 3) for each of the final contour models of the quarry “Tambura” by evaluating criteria for alternative solutions (

Table 9. Evaluation of criteria for alternative solutions.

Selection Criteria				Models
Criteria Group	%	Criteria Mark		Model 1	Model 2	Model 3
Project parameters	5	C1	m max	20	17	24
		C2	m min	3	5	5
		C3	° max	70	70	70
		C4	° max	60	61	61
		C5	ha max	3.88	3.88	3.79
Mineral deposit reserves	5	C6	m3 max	839,672	844,213	634,817
		C7	m3 max	507,177	500,038	553,694
		C8	m3 max	822,879	827,329	622,120
Economic indicators	16	C9	kn min	16,457,578	16,546,579	12,442,405
		C10	kn max	3104	3104	3032
		C11	kn min	411,439	413,664	311,060
		C12	kn min	164,576	165,466	124,424
		C13	kn min	246,864	248,199	186,636
Environmental impact	27	C14	max	4	3	6
		C15	max	5	6	7
		C16	max	4	4	5
		C17	max	6	6	7
		C18	max	6	6	6
		C19	max	4	3	6
		C20	max	3	3	5
		C21	max	5	5	6
Property legal relations	48	C22	yes/no	no	no	yes

).

Model 1 (Figure 4 and Table 9) encompasses the area of 3.88 ha where it is possible to exploit 822,879 m³ of rock mass with the profit of 16,457,578 kn and total expense fees of 825,983 kn. The environmental impact is weak. The settlement of property legal relations is not possible for all cadastral parcels inside the exploitation field.

Model 2 (Figure 4 and Table 9) also encompasses the area of 3.88 ha where it is possible to exploit 827,329 m³ of technical building stone with the profit of 16,546,579 kn and expense fees of 830,433 kn. The environmental impact is weak. The settlement of property legal relations is not possible for all cadastral parcels inside the exploitation field.

Model 3 (Figure 4 and Table 9) encompasses a decreased area which totals 3.79 ha inside of which it is possible to exploit 622,120 m³ of technical building stone with the profit of 12,442,405 kn and expense fees of 625,152 kn. The environmental impact is weak or there is none. The settlement of property legal relations is possible on all cadastral parcels inside the intervention area.

Figure 4 shows all the above-mentioned data: profit, exploitation reserves of the mineral raw material, expense fees, and the intervention area. The encompassed area is shown in brown colour, exploitation reserves of the technical building stone are shown in yellow colour, profit is shown in blue colour, and the expense fees are shown in red colour. Green colour displays the environmental impact (Table 8).

4. Discussion

As previously stated, when selecting the optimal model, namely, the design solution, importance was given to criteria of environmental impact and the settlement of legal property relations, so they were given the greatest weight of criteria. The environmental impact criterion was given 27% and the legal property relations was given 48% (Table 7).

By comparing the models and using the mentioned criteria in PROMETHEE II, the values of entering flow (ϕ⁻ (a)) (Equation (11)) and leaving flow (ϕ⁺ (a)) (Equation (12)) were obtained. The values are shown in

Table 10. Entering and leaving flows.

Flow	Model 1	Model 2	Model 3
ϕ− entering flow	0.2509	0.2940	0.4043
ϕ+ leaving flow	0.2789	0.1924	0.4779

.

On the basis of entering and output flows, the values of net outranking flow ϕ(a) (Equation (13)) (

Table 11. Net outranking flow ϕ(a) and the final ranking of alternative solutions.

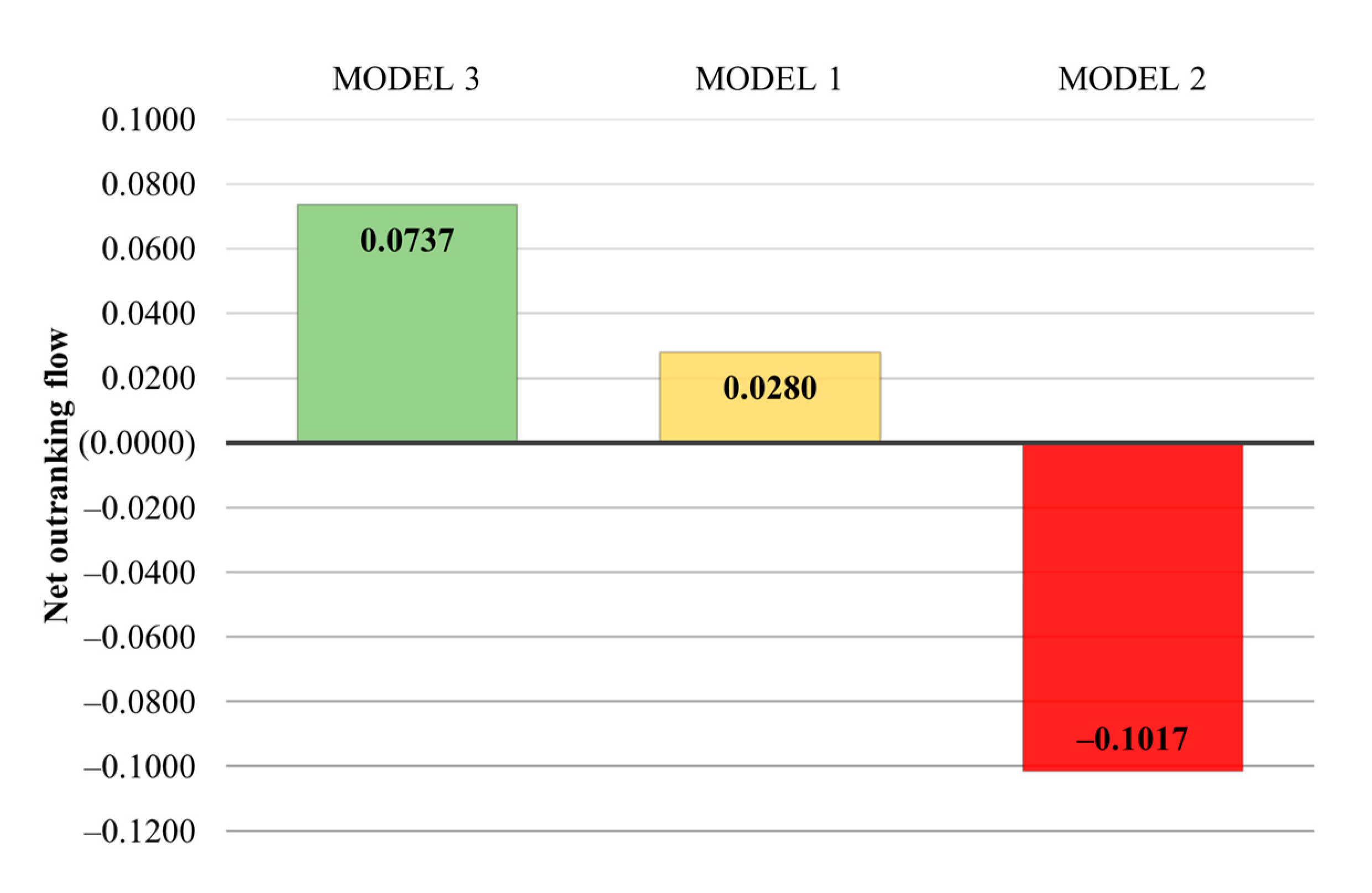
Model	ϕ(a)	Final Ranking
Model 1	0.0280	2
Model 2	−0.1017	3
Model 3	0.0737	1

) were obtained, which were necessary for the ranking of models (alternatives), namely, to get the final ranking of alternative solutions so that the optimal model can be chosen.

Table 11 shows numerical values of the net outranking flow ϕ(a) obtained with PROMETHEE II method and the final ranking of models (alternatives); graphic overview of the final ranking of alternative solutions is shown in Figure 5.

The value of net outranking flow ϕ(a) for Model 3 is 0.0737 and that puts it at the first position in the final ranking. Model 1 has a net outranking flow ϕ(a) value of 0.0280, while Model 2 even has a negative value in the amount of −0.1017, which puts it at the last place.

AHP method was used to determine the structure of each criterion for every alternative (model) (Figure 6). By comparing the alternatives between themselves (Model 1, Model 2, and Model 3) and then comparing them depending on the main group of criteria, the percentage of each criterion in each alternative (model) was determined.

As shown in Figure 6, each of the five main criteria has a different percentage for each alternate model, but their ratios regarding the model are the same in all three cases. It can be observed that the structure of the main groups of criteria is the same for each model.

In addition, the structure of the main groups of criteria for each model is shown cumulatively in Figure 7. It can be observed that the cumulative values for each of the criteria give a weighting criterion calculated with the AHP method (Table 7).

For example, the ratio of project parameters for Model 1 is 0.54%, for Model 2 is 0.92%, and for Model 3 is 3.11%, namely, their sum (cumulatively displayed) is the same as the sum of the weighting criteria and is 5% (Table 7).

The main groups of criteria that had the greatest impact on the selection of the optimal model are seen in Figure 6 and Figure 7. Project parameters and mineral deposit reserves have an equal importance (weighting factor 5%; Table 7), they are followed by economic indicators (weighting factor 17%; Table 7) which is also linked to the previous two criteria. It is clear that the two most important criteria are environmental impact (weighting factor 27%; Table 7) and property legal relations (weighting factor 48%; Table 7) without which it would be impossible to further continue with the exploitation.

5. Conclusions

The selection of the optimal model for the final contour of the quarry was done by analysing three different final contour models and using two methods of multi-criteria analysis, i.e., the analytic hierarchy process method (AHP) and the PROMETHEE II method. By determining the entry parameters, namely, the main group of criteria and sub-criteria for each of the groups, and then adding weighting criteria (application of AHP method), the final ranking of models-alternatives (application of PROMETHEE II method) was obtained.

Subdividing the criteria to main groups and then giving them additional elaboration ensured a more detailed approach to settling the problem of how to continue the exploitation. Using multi-criteria analysis, Model 3 was selected as the optimal model as it meets all the specified criteria. Although the application of Model 1 or Model 2 would allow for greater exploitation of technical building stone, and consequently lead to greater profit, these two models do not meet the criterion of legal property relations settlement. By analysing the structure, namely, the share of each criterion for each of the models and then cumulatively displaying that data, it can be observed that the selection of the optimal model of the final contour mostly depends on the legal property relations.

Further study should be oriented in determining the impact on how much a change in a certain parameter affects the output results and to find out which parameter should be studied in more detail.