MRAS-Based Switching Linear Feedback Strategy for Sensorless Speed Control of Induction Motor Drives
Abstract
1. Introduction
2. SLF-SMC for MRAS Estimator
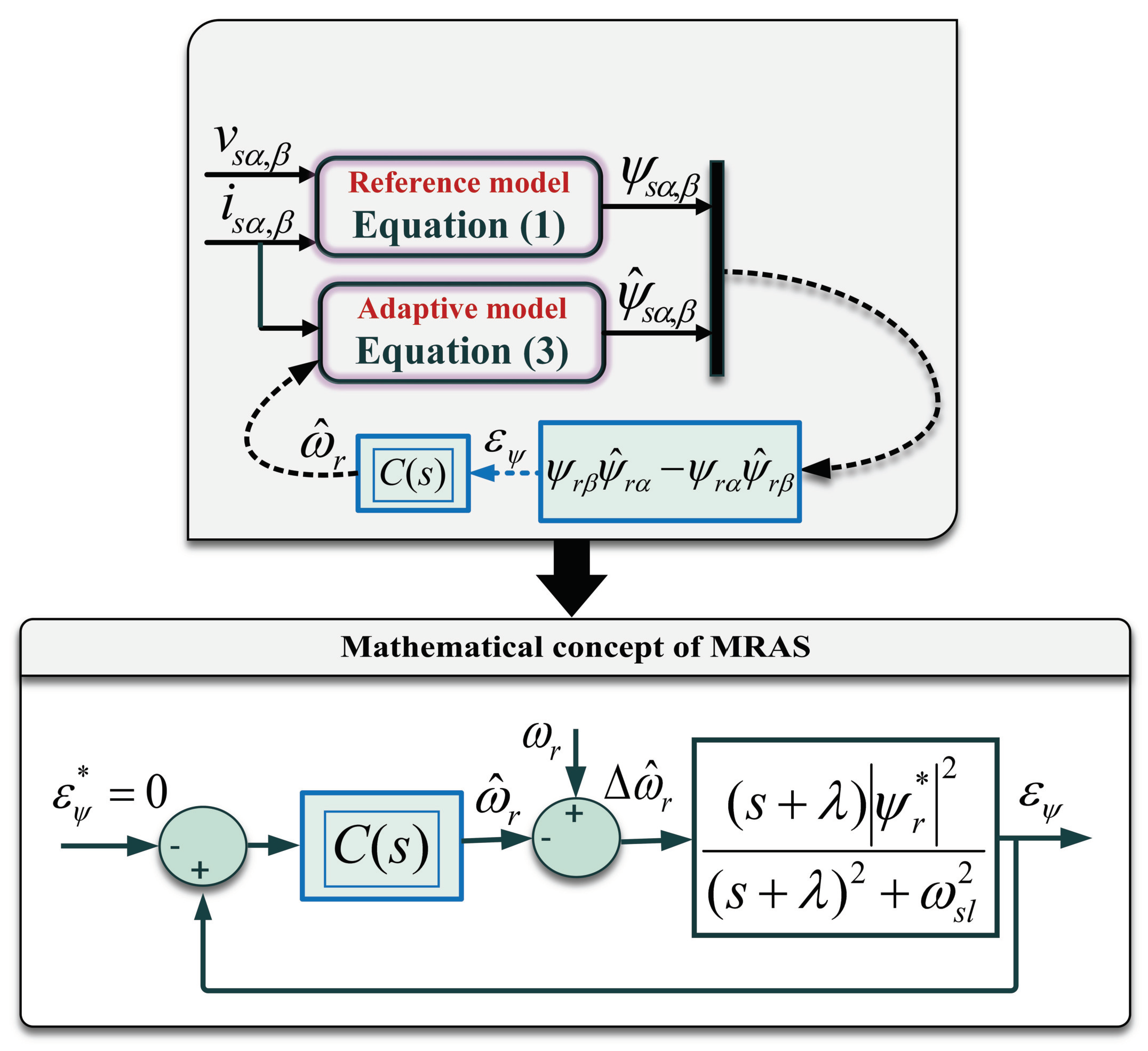
2.1. Preliminaries on MRAS Estimator
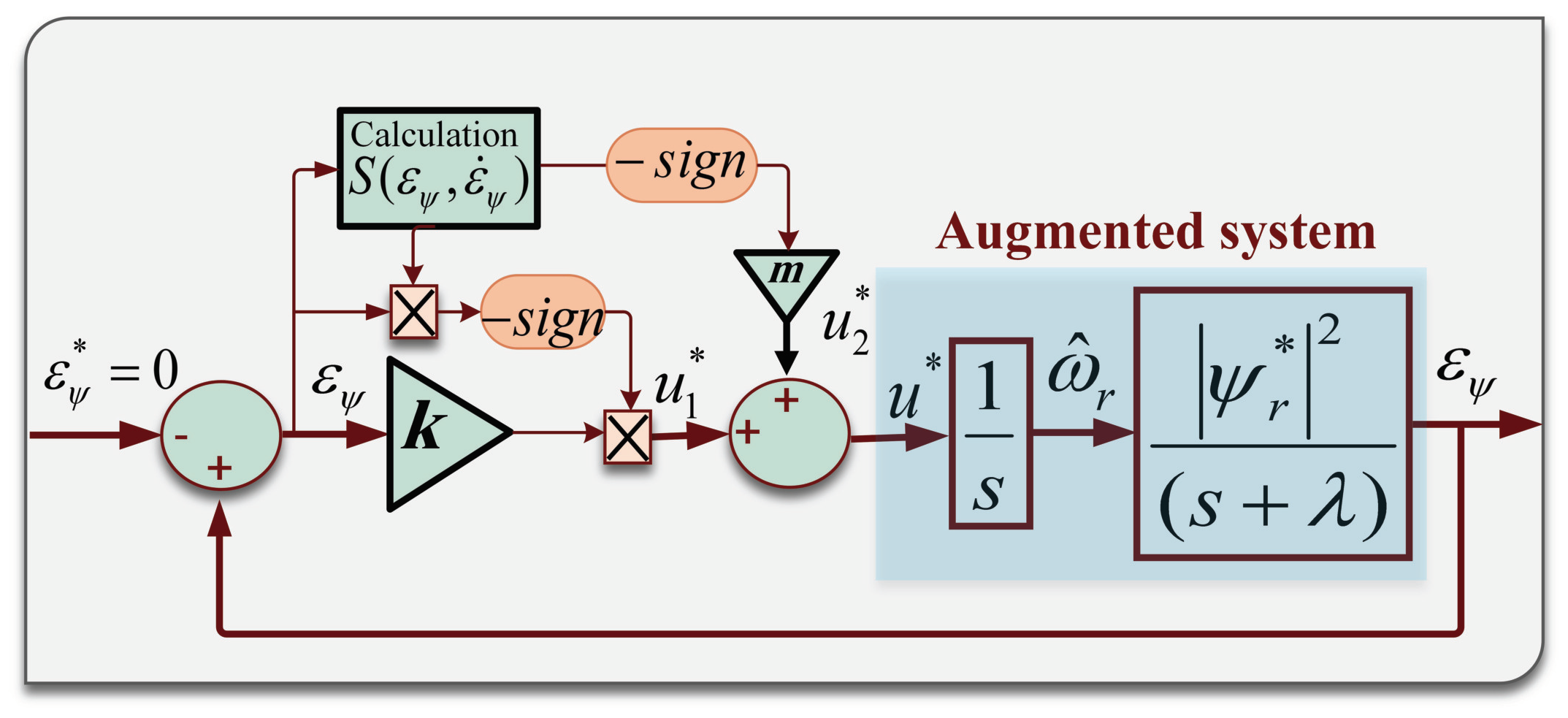
2.2. Design of the SLF-SMC for the MRAS
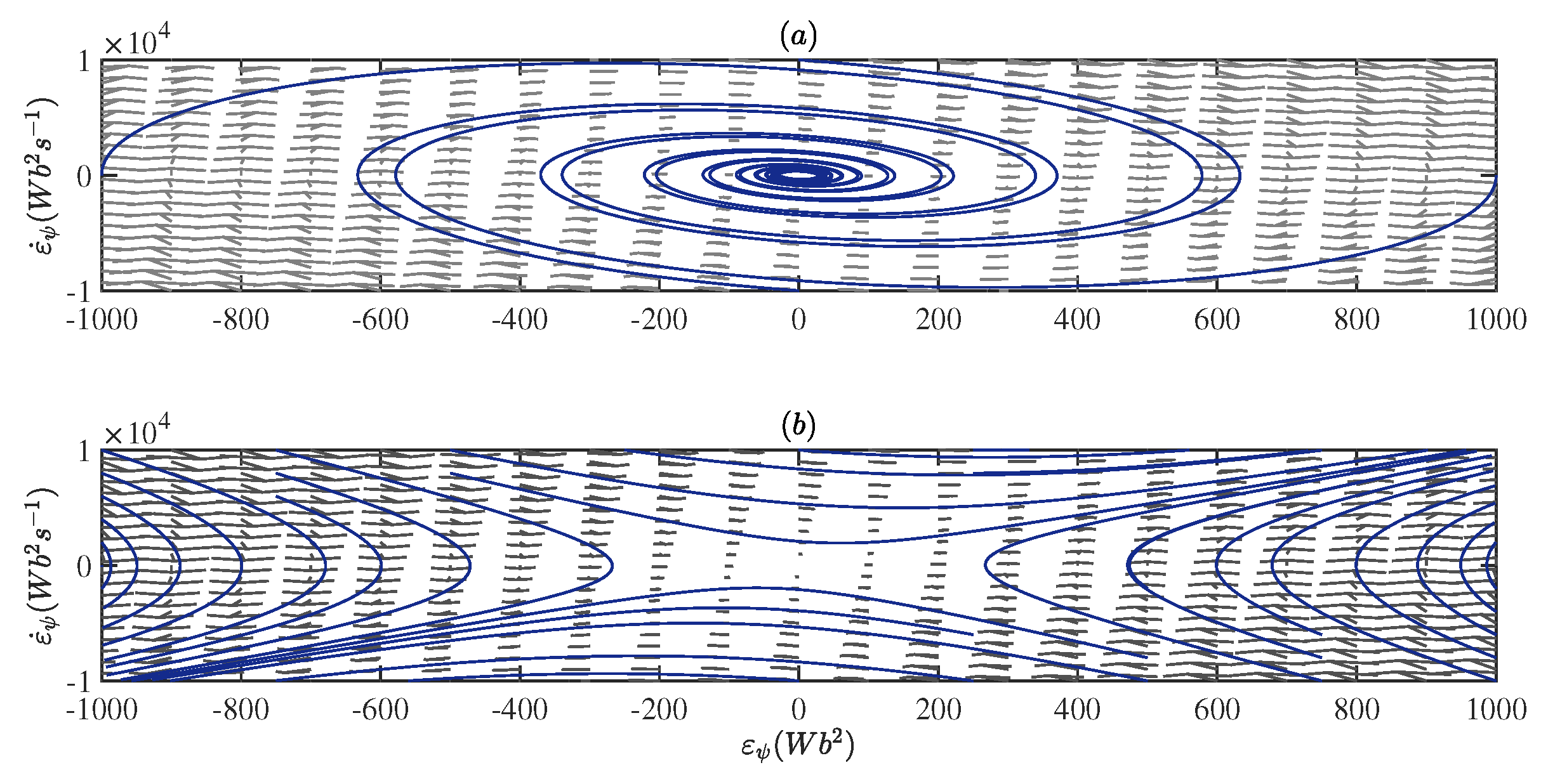
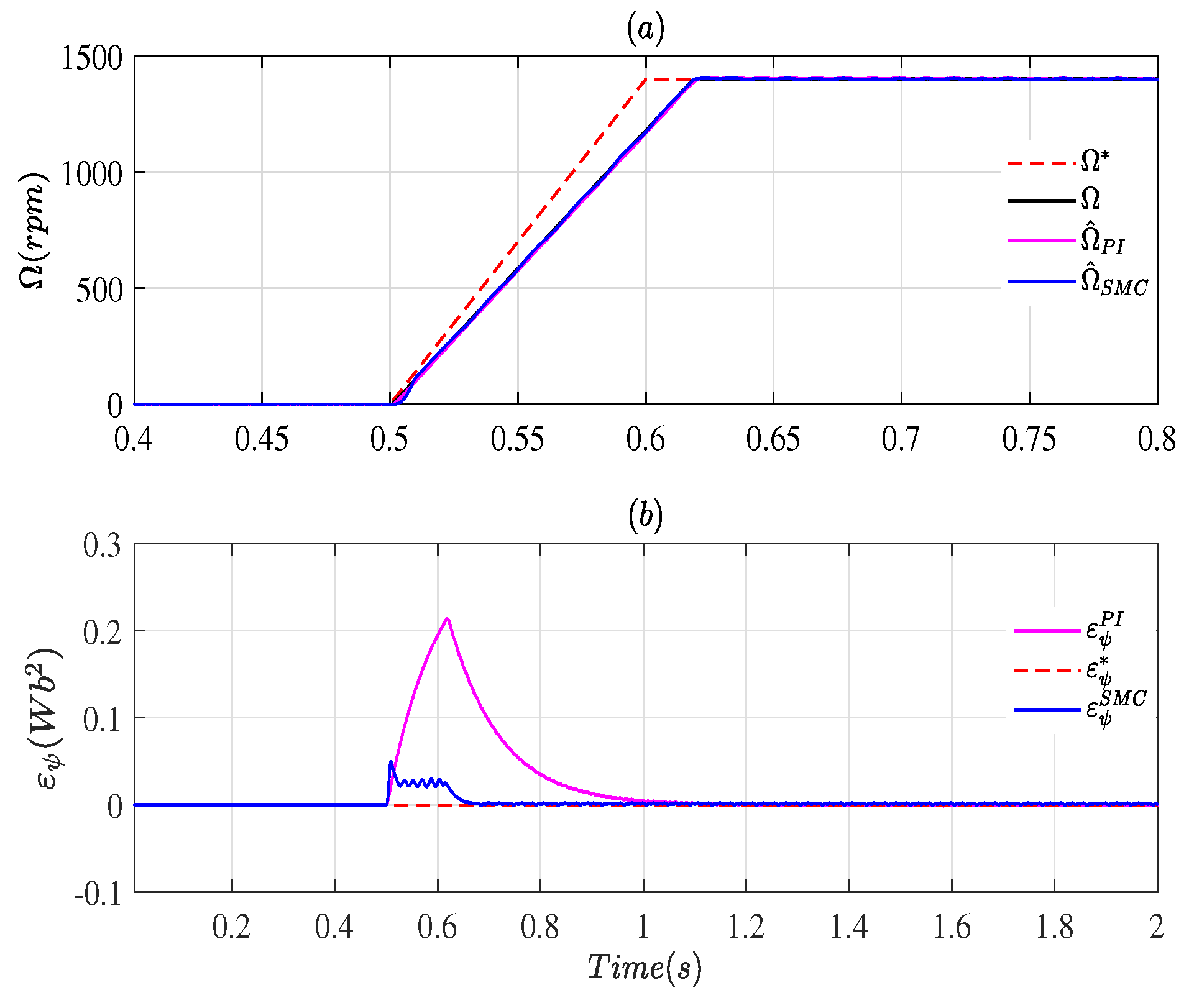
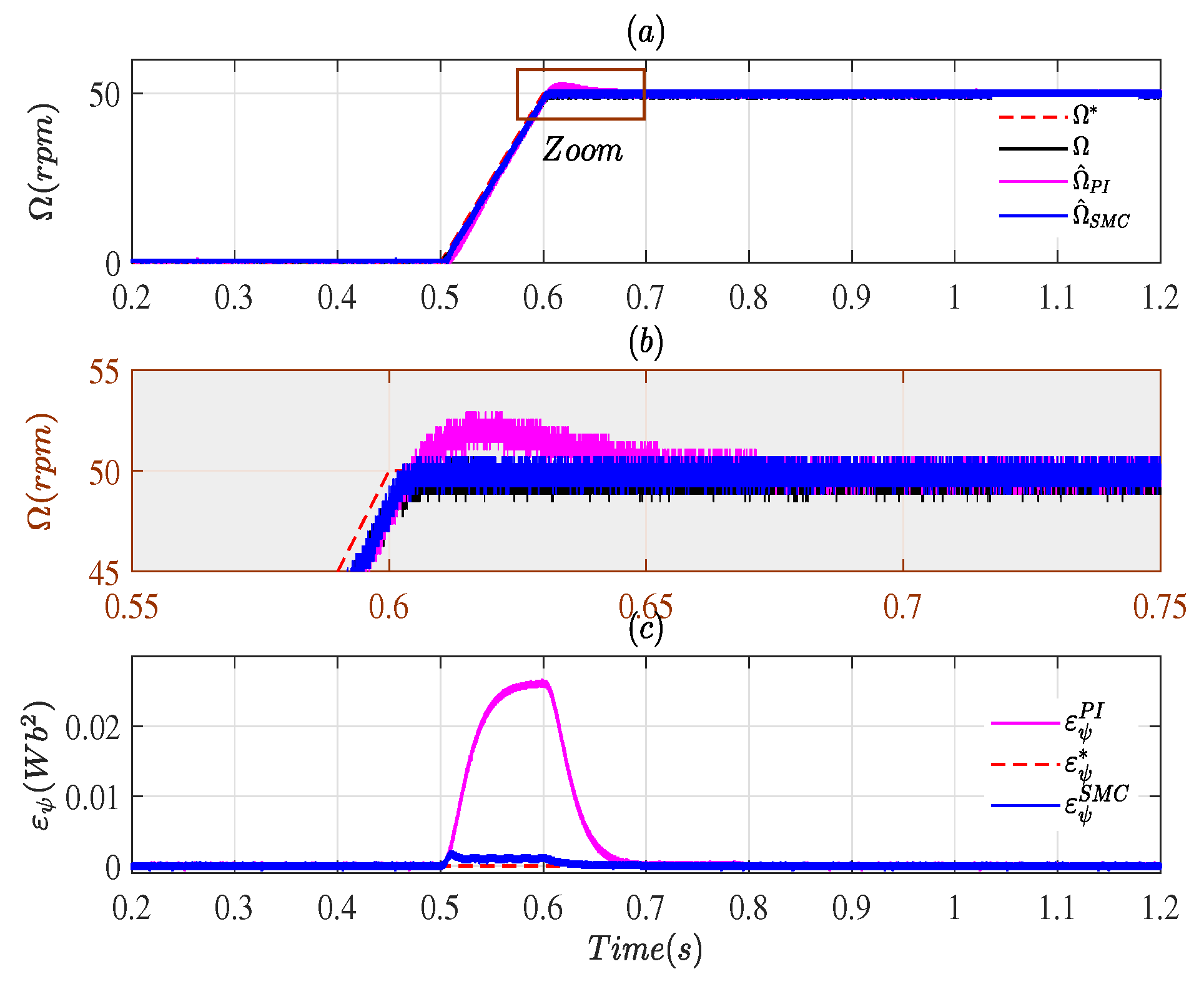
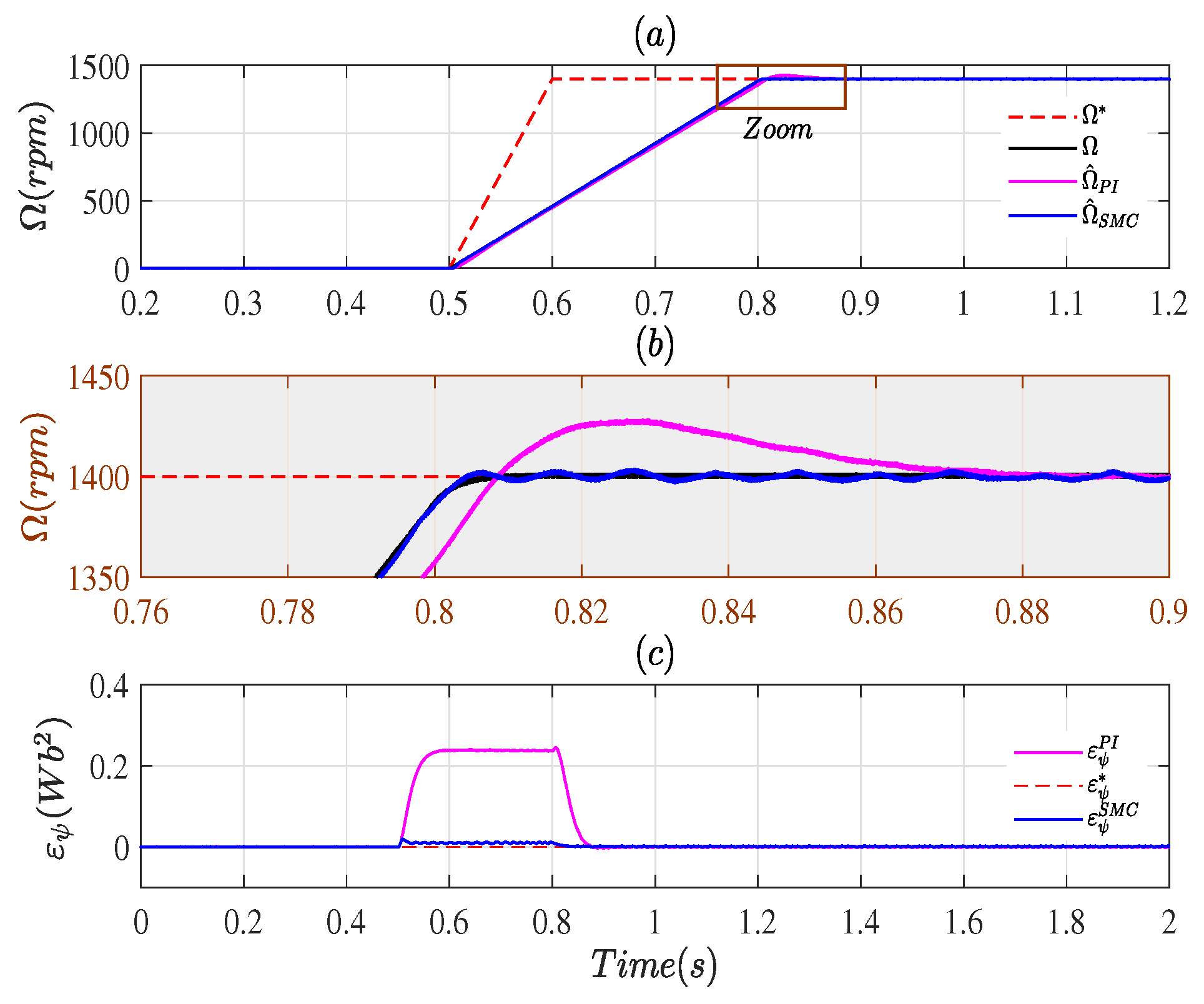
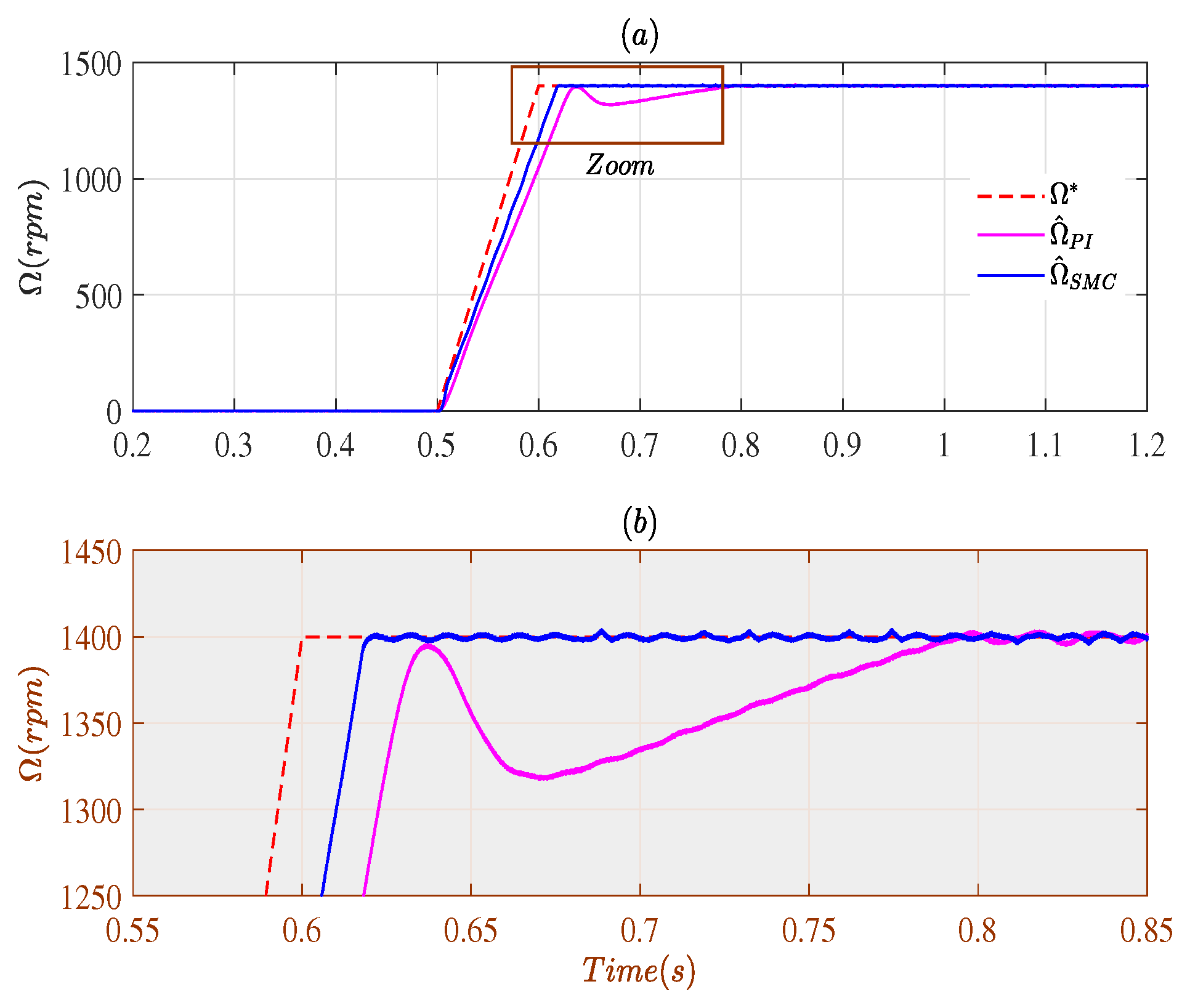
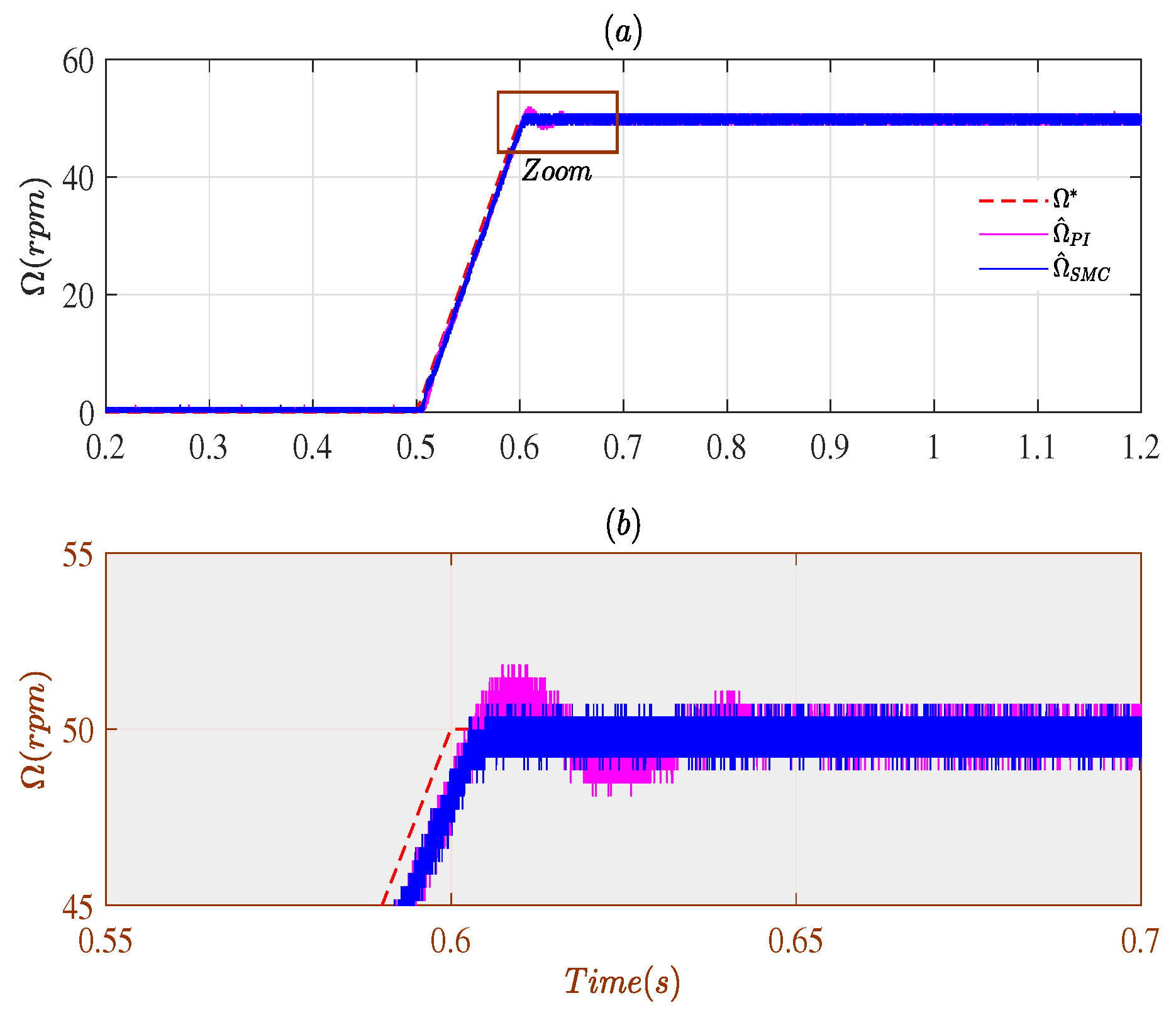
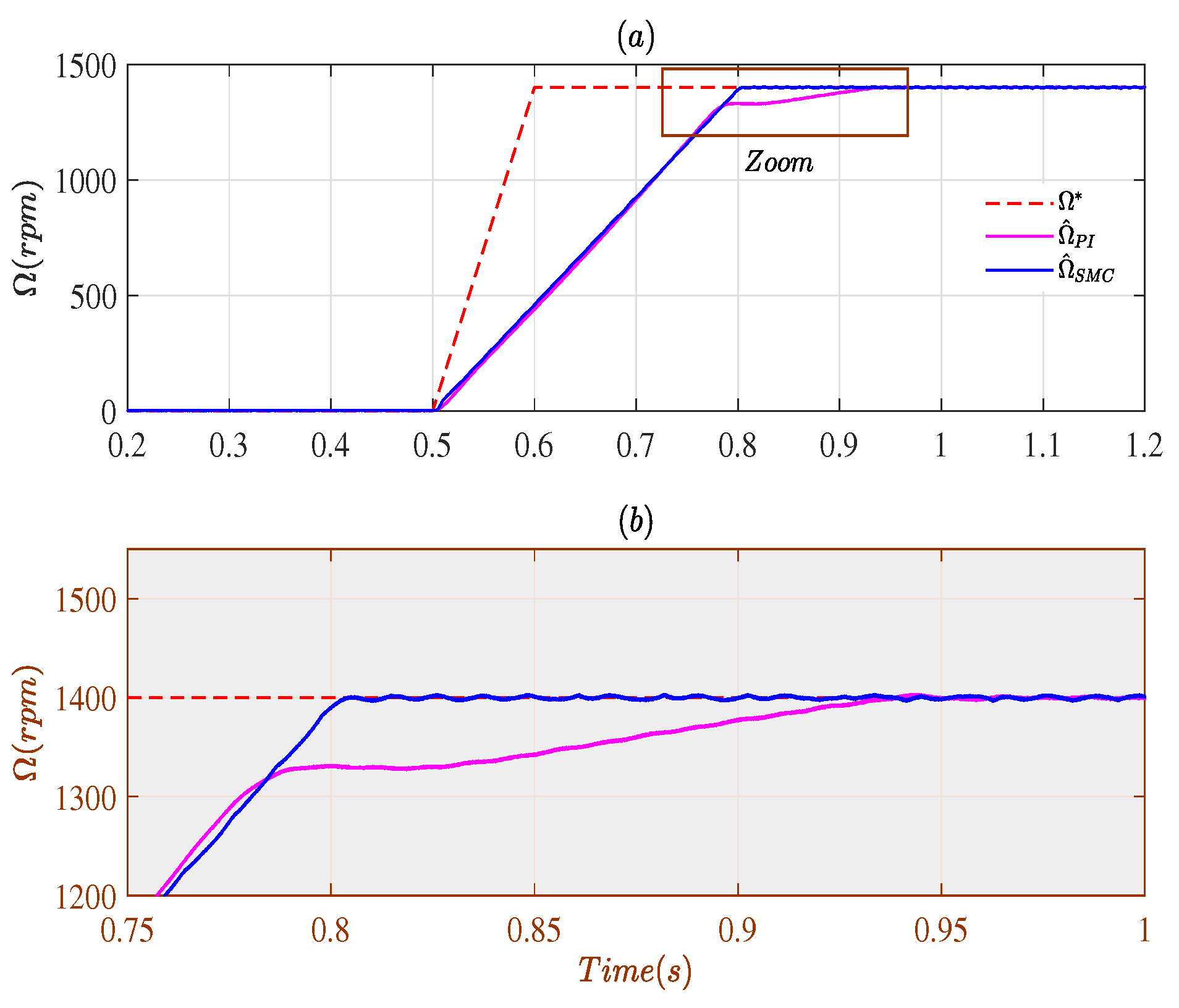
3. Simulation Results
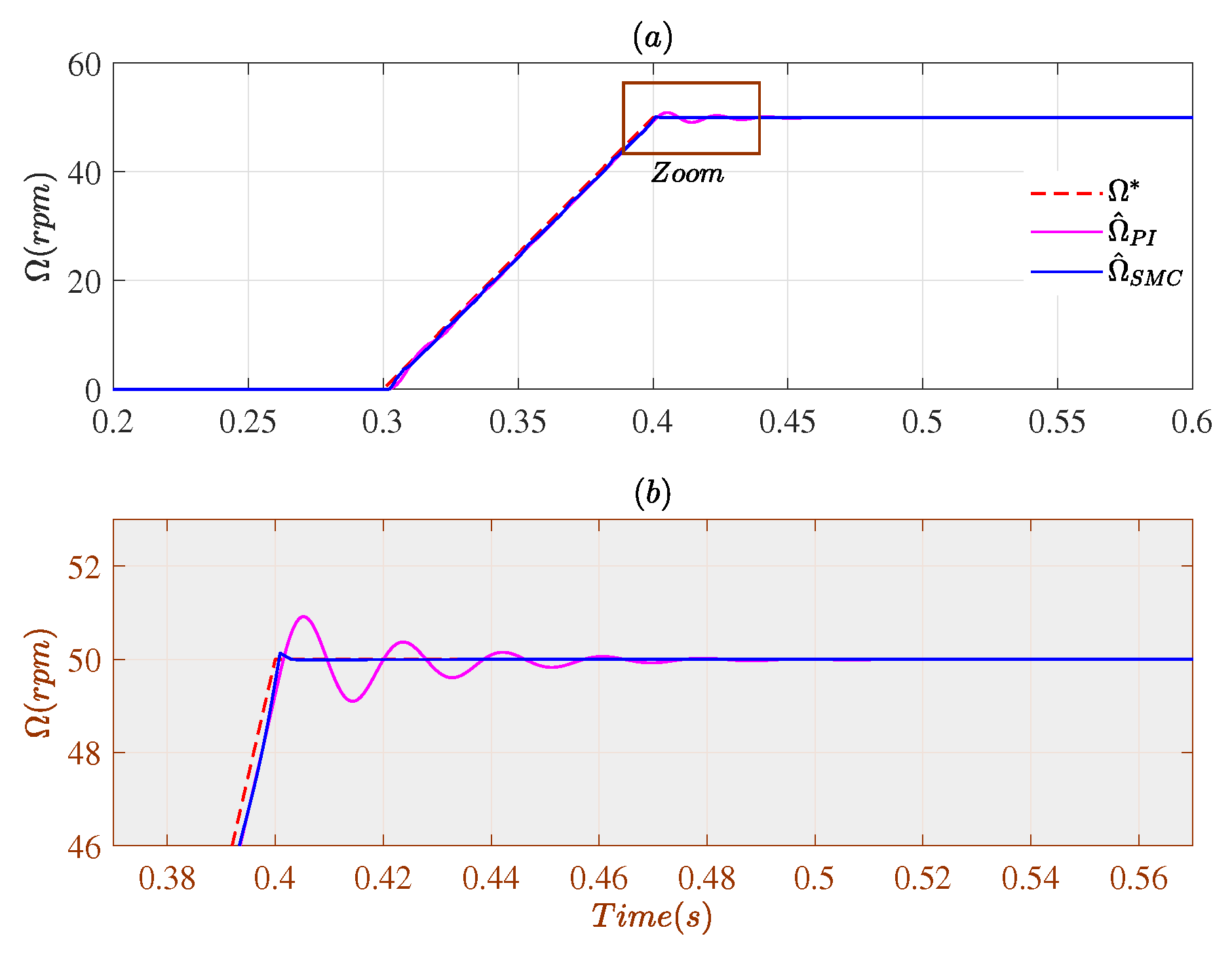
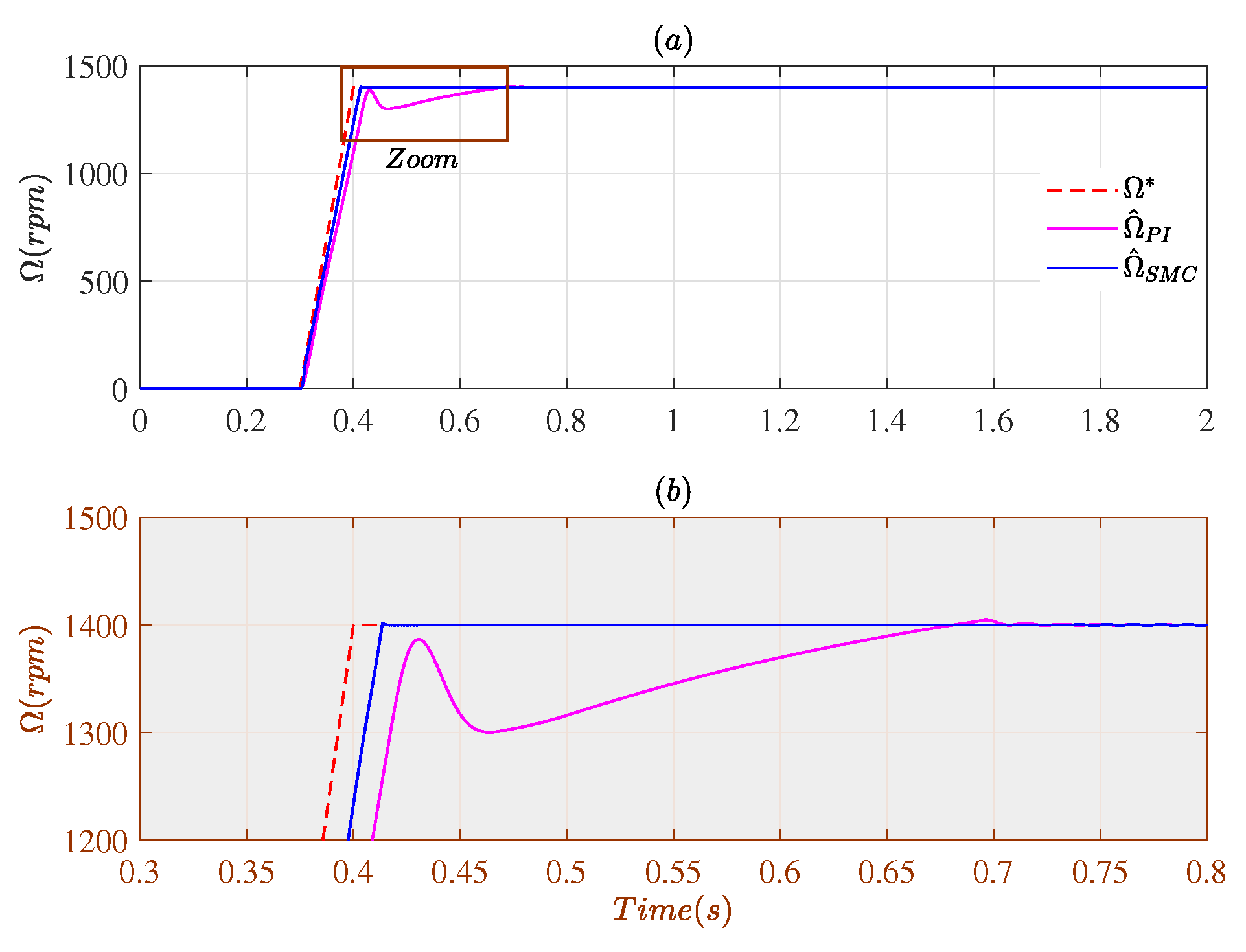
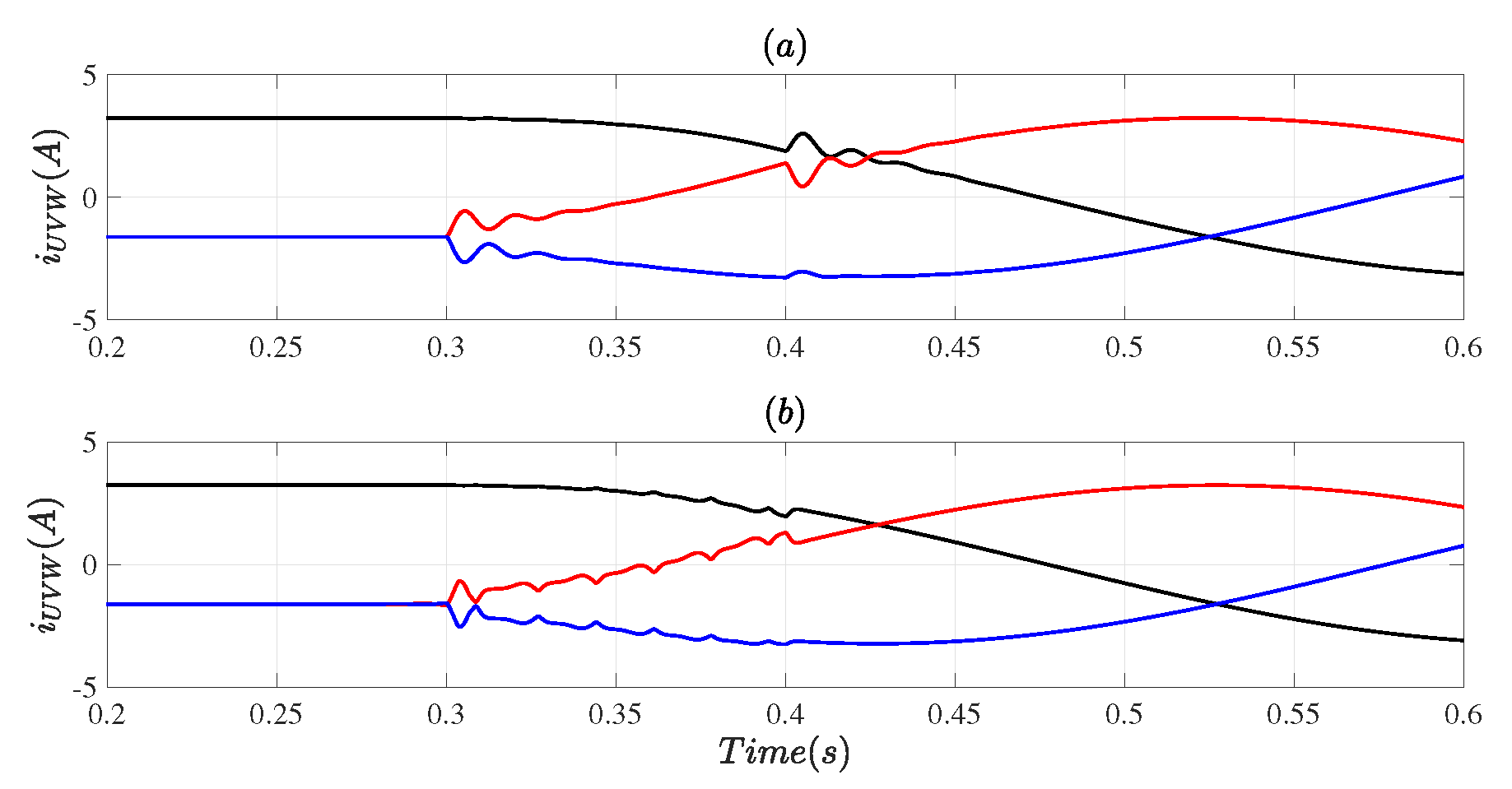
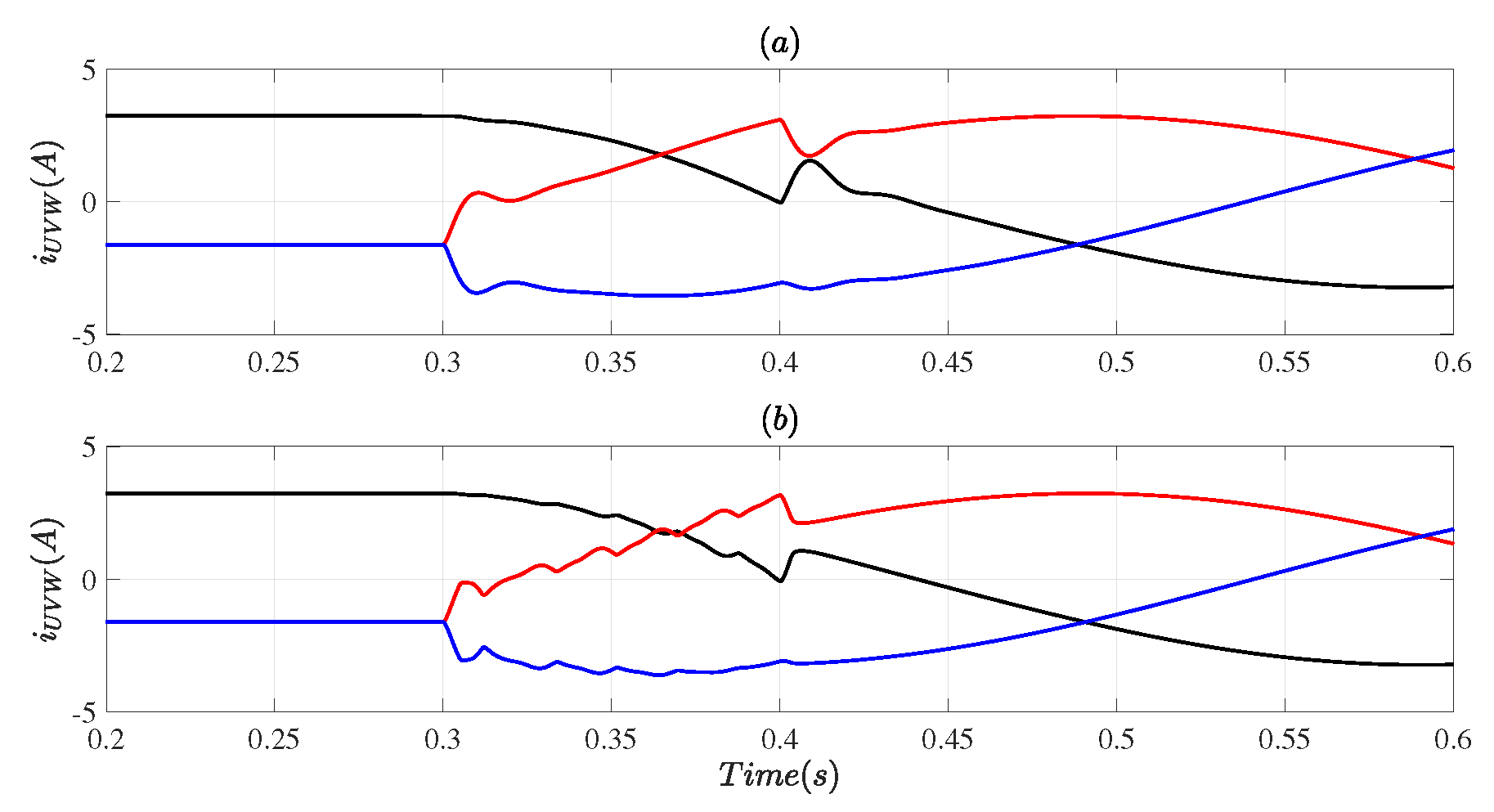
3.1. Case # 1
3.2. Case # 2
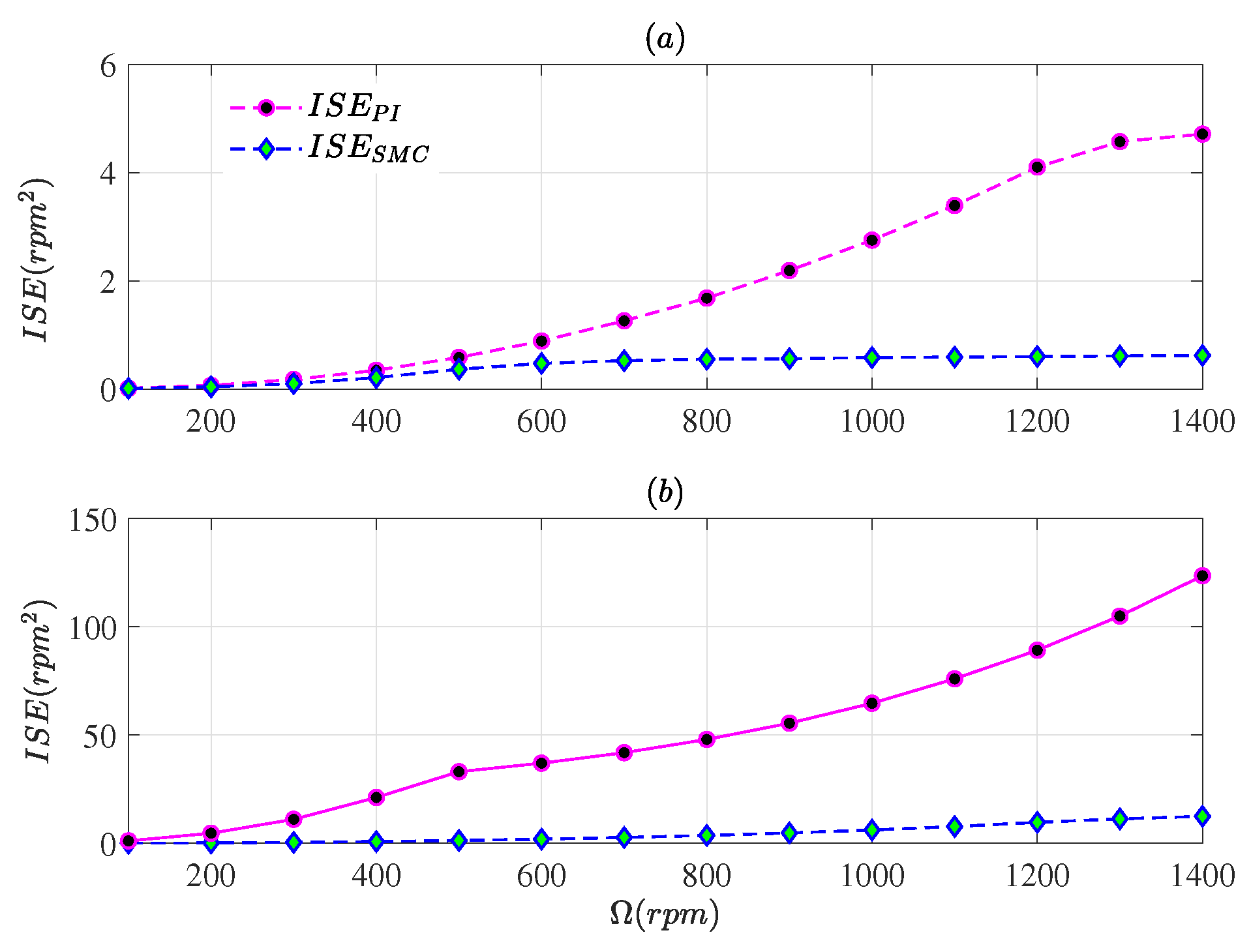
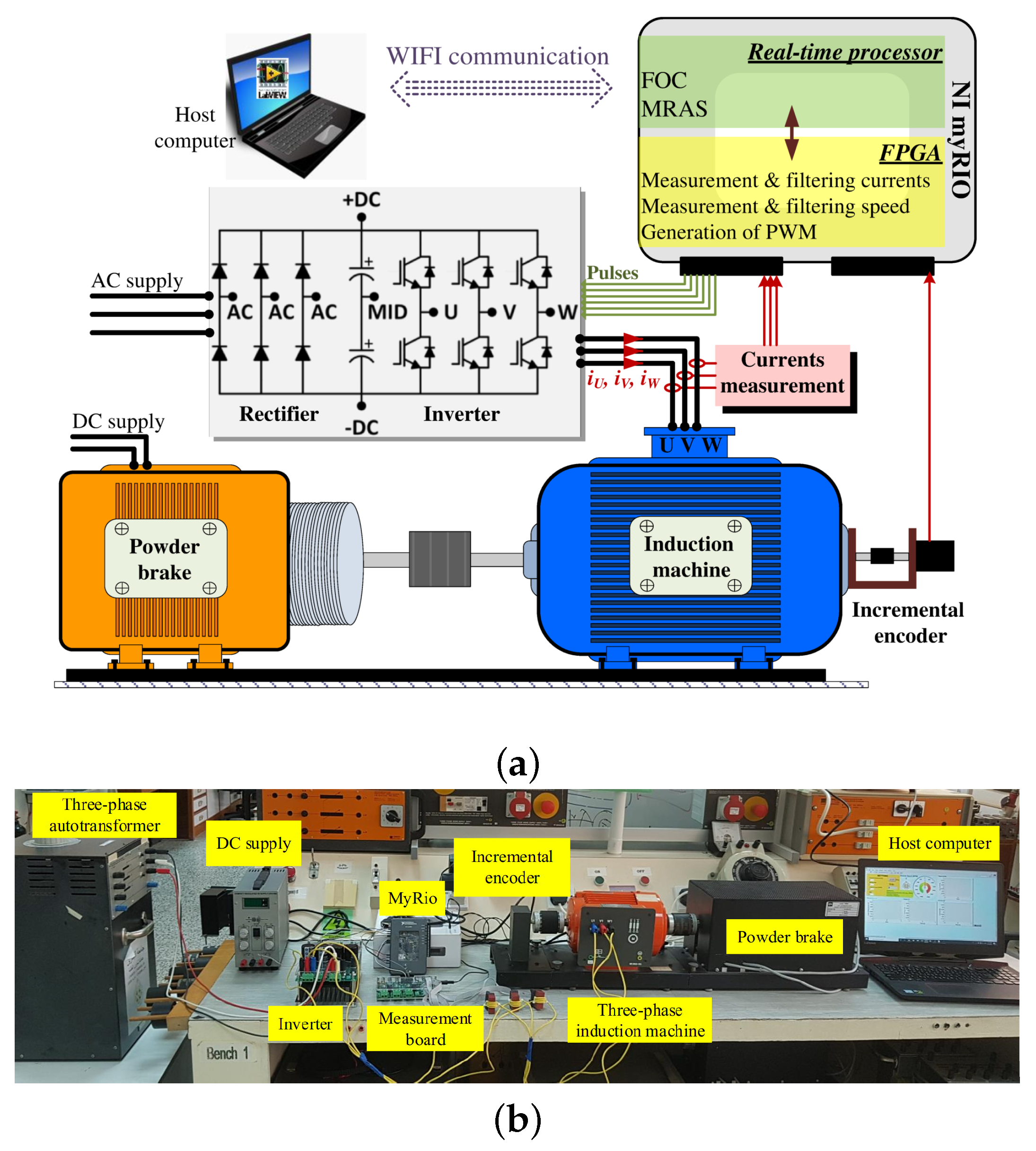
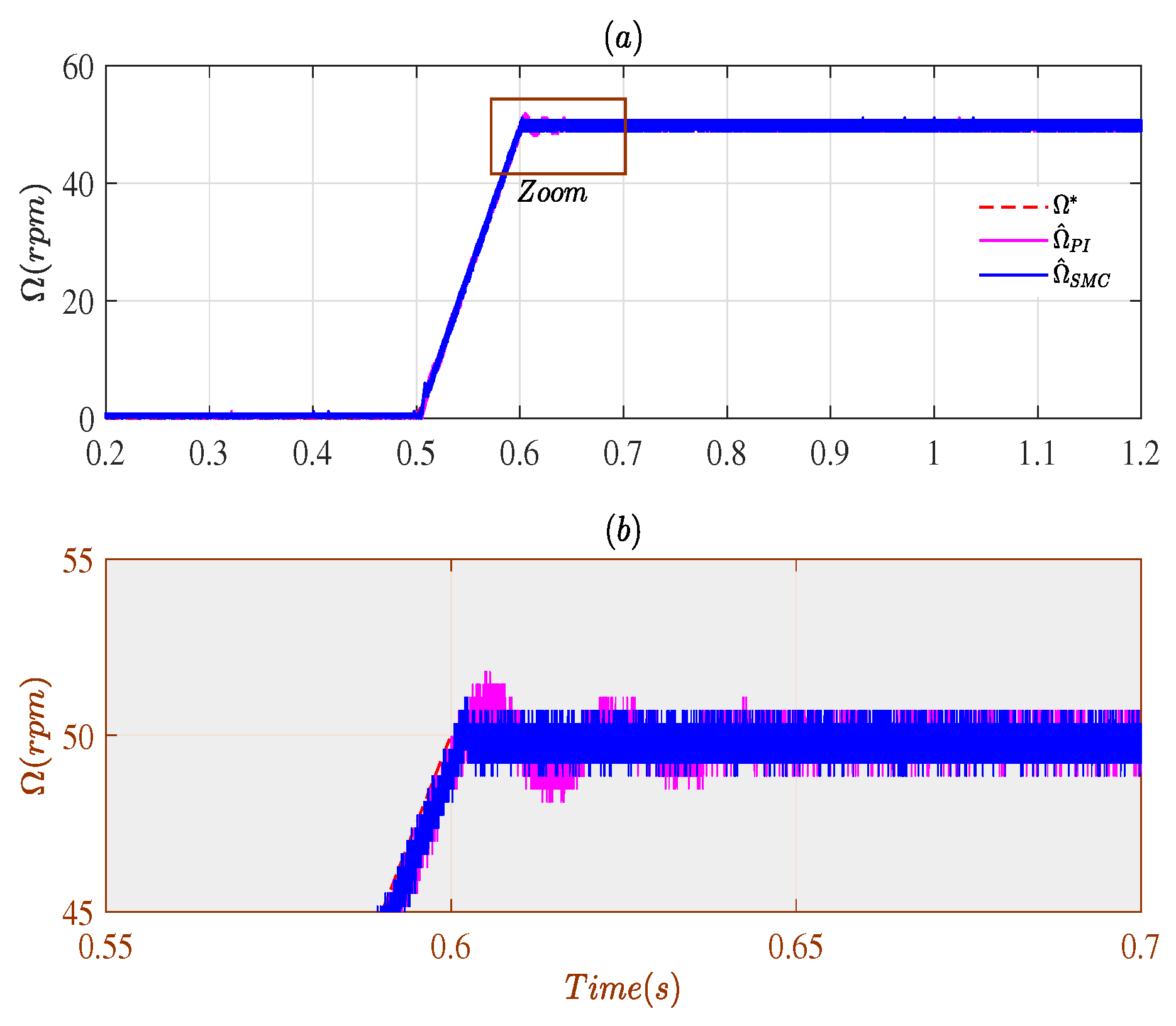
4. Experimental Validation
- Measurement of signals, computations, and transformations;
- FOC structure with PI controllers and MRAS estimator; and
- Application of the calculated control signals.
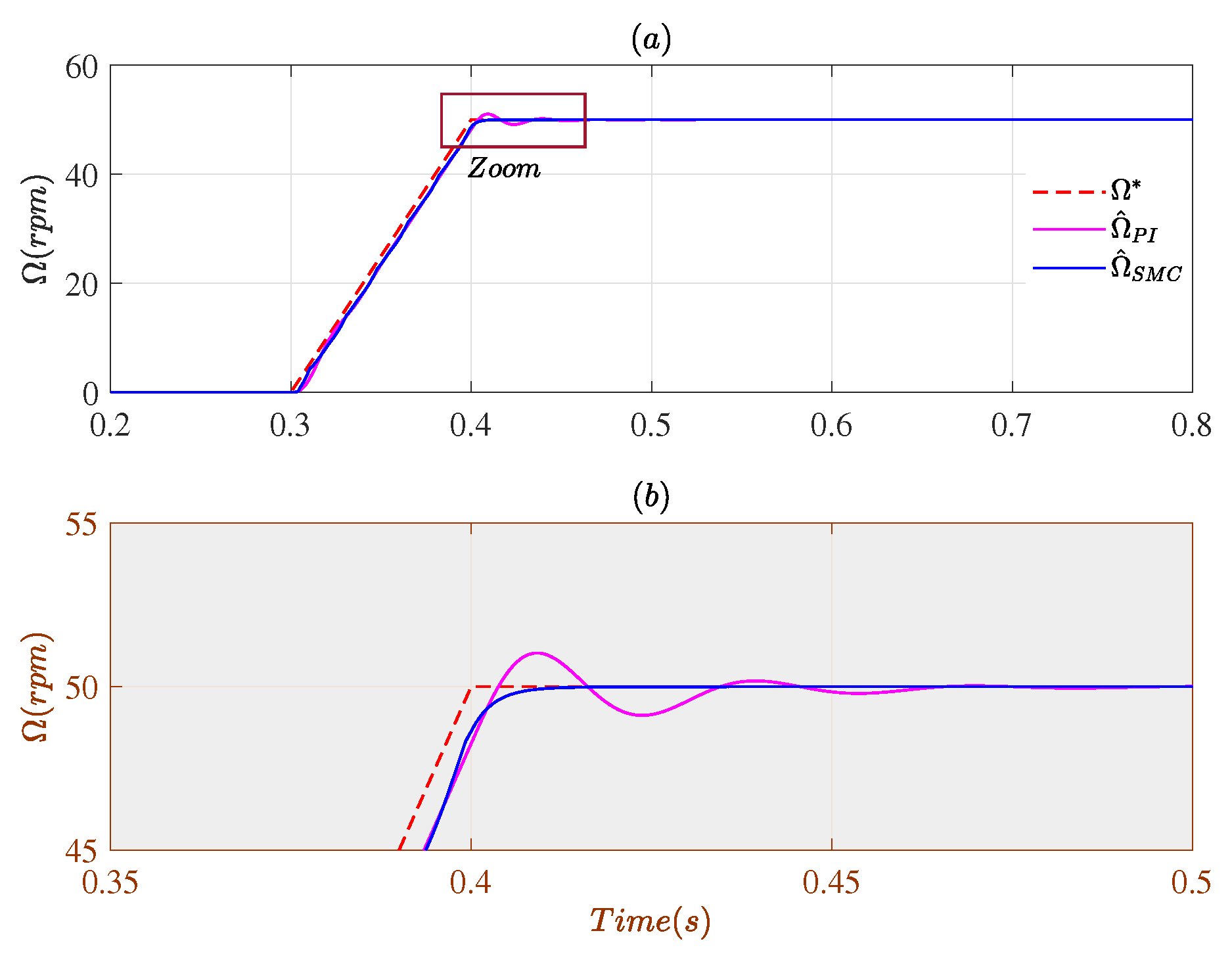
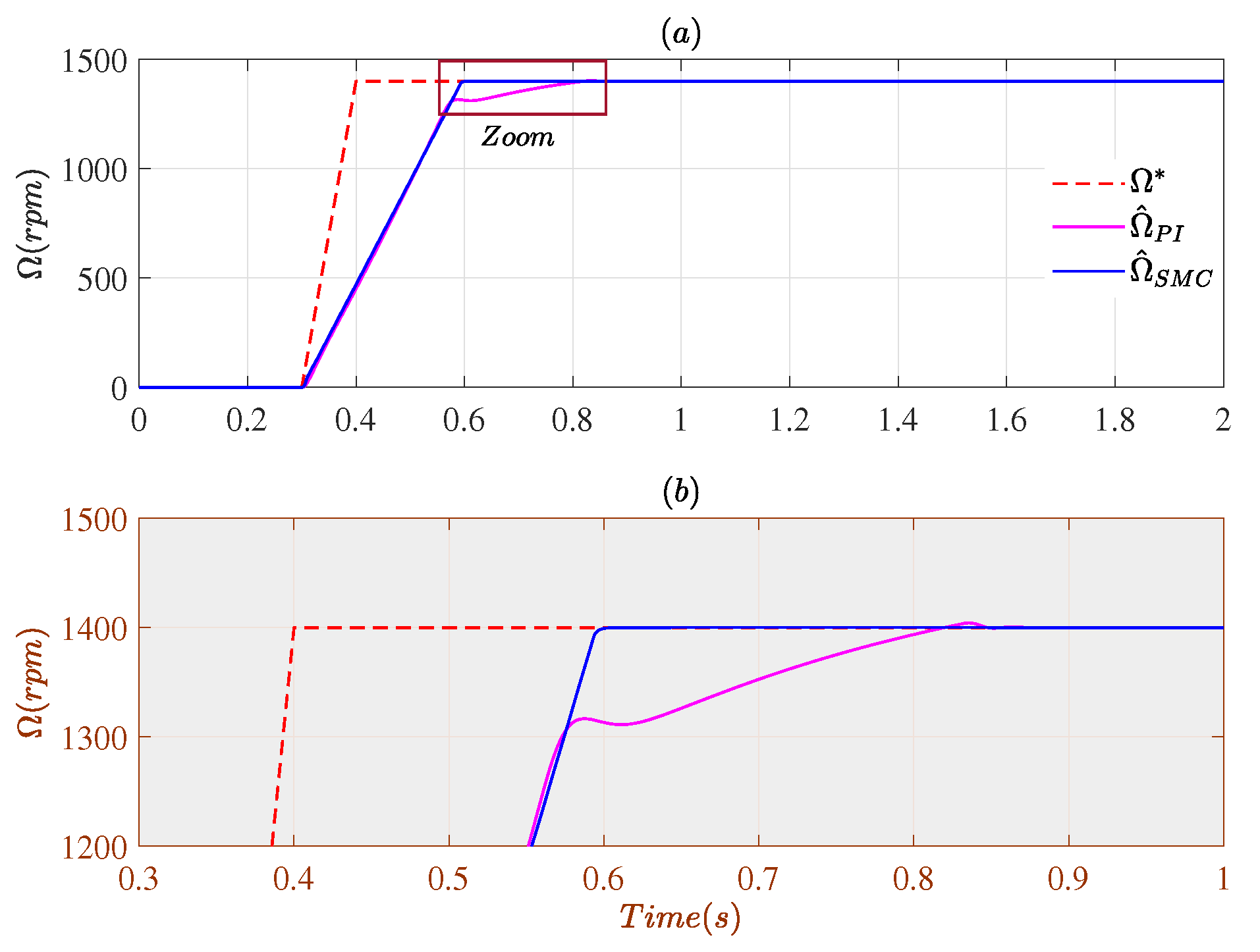
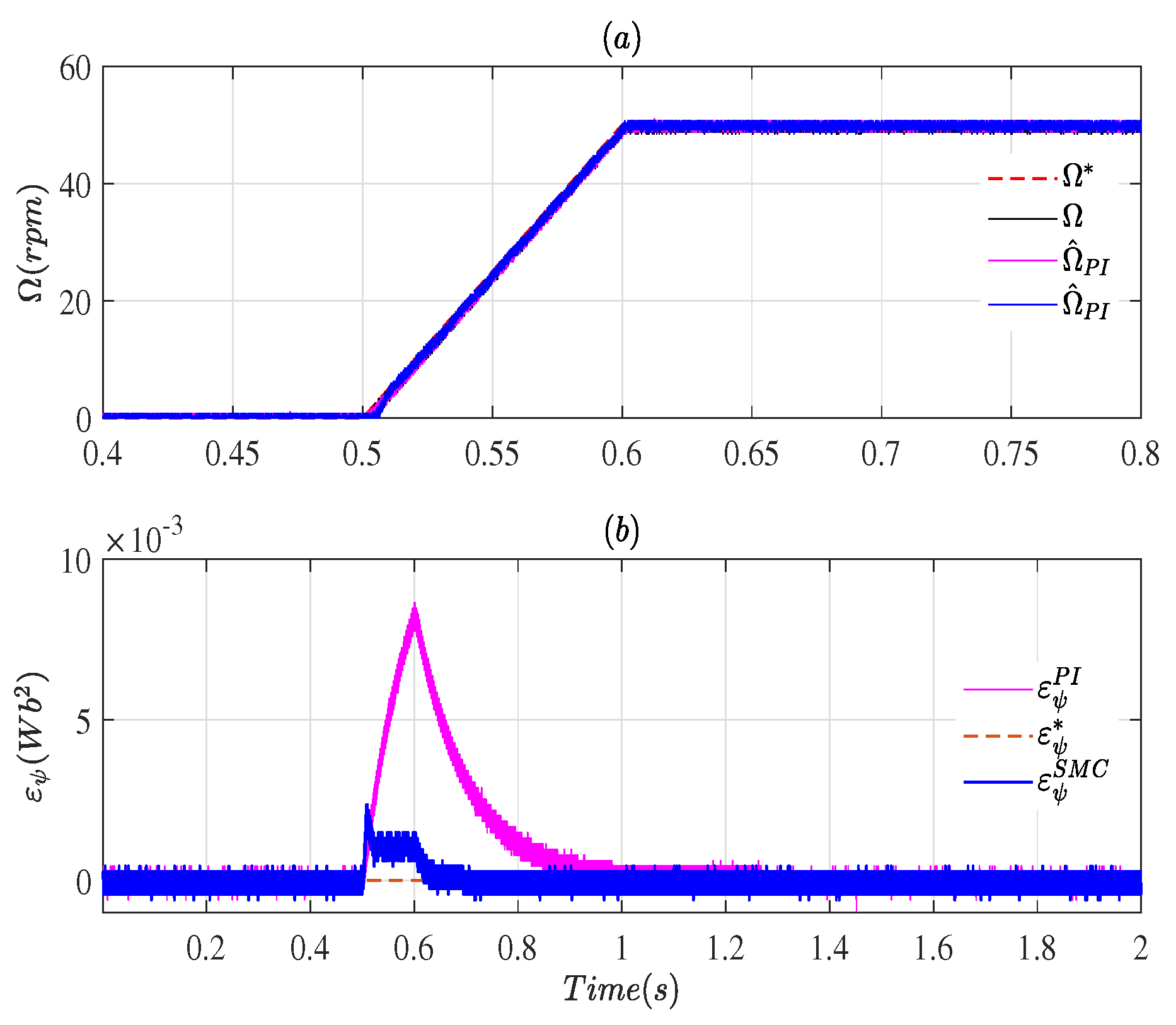
4.1. Closed-Loop Using Measured Speed
4.2. Closed-Loop Using Estimated Speeds
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| IM | Induction machine |
| FOC | Field-oriented control |
| SFOC | Sensorless field-oreinted control |
| MRAS | Model reference adaptive system |
| SMC | Sliding-mode control |
| PI | Proportional-integral controller |
| SLF | Switching linear feedback |
Nomenclature
| Rotor resistance | |
| Rotor inductance | |
| Stator inductance | |
| Main inductance | |
| Inverse of rotor time constant | |
| Total leakage factor | |
| u-v-w Stator voltage components | |
| - Stator voltage components | |
| u-v-w Stator current components | |
| - Stator current components | |
| d-q Stator current components | |
| - Stator flux components | |
| - Rotor flux components | |
| Rotor electrical angular speed | |
| S | Switching surface |
| s | Laplace variable |
| Slip angular speed | |
| P | Number of pole pairs |
| Rotor mechanical shaft speed | |
| Desired value | |
| Estimated value | |
| PARK transformation | |
| Inverse of PARK transformation | |
| Angle of PARK transformation |
References
- Guzinski, J.; Abu-Rub, H. Speed sensorless induction motor drive with predictive current controller. IEEE Trans. Ind. Electron. 2013, 60, 699–709. [Google Scholar] [CrossRef]
- Schauder, C. Adaptive speed identification for vector control of induction motors without rotational transducers. IEEE Trans. Ind. Appl. 1992, 28, 1054–1061. [Google Scholar] [CrossRef]
- Kojabadi, H.; Liuchen, C.; Doraiswami, R. A mras-based adaptive pseudoreduced-order flux observer for sensorless induction motor drives. IEEE Trans. Power Electron. 2005, 20, 930–938. [Google Scholar] [CrossRef]
- Gadoue, S.; Giaouris, D.; Finch, J. Mras sensorless vector control of an induction motor using new sliding-mode and fuzzy-logic adaptation mechanisms. IEEE Trans. Energy Convers. 2010, 25, 394–402. [Google Scholar] [CrossRef]
- Comanescu, M.; Xu, L. Sliding-mode mras speed estimators for sensorless vector control of induction machine. IEEE Trans. Ind. Electron. 2006, 53, 146–153. [Google Scholar] [CrossRef]
- Cirrincione, M.; Accetta, A.; Pucci, M.; Vitale, G. Mras speed observer for high-performance linear induction motor drives based on linear neural networks. IEEE Trans. Power Electron. 2013, 28, 123–134. [Google Scholar] [CrossRef]
- Zbede, Y.B.; Gadoue, S.M.; Atkinson, D.J. Model predictive mras estimator for sensorless induction motor drives. IEEE Trans. Ind. Electron. 2016, 63, 3511–3521. [Google Scholar] [CrossRef]
- Dominguez, J.R. Discrete-time modeling and control of induction motors by means of variational integrators and sliding modespart ii: Control design. IEEE Trans. Ind. Electron. 2015, 62, 6183–6193. [Google Scholar] [CrossRef]
- Hung, J.C.; Gao, W. Variable structure control: A survey. IEEE TTrans. Ind. Electron. 1993, 40, 2–21. [Google Scholar] [CrossRef]
- Levant, A. Principles of 2-sliding mode design. Automtica 2007, 43, 576–586. [Google Scholar] [CrossRef]
- Holakooie, M.; Ojaghi, M.; Taheri, A. Modified dtc of a six-phase induction motor with a second-order sliding-mode mras-based speed estimator. IEEE Trans. Power Electron. 2019, 34, 600–611. [Google Scholar] [CrossRef]
- Wang, H.; Ge, X.; Liu, Y. Second-order sliding-mode mras observerbased sensorless vector control of linear induction motor drives for medium-low speed maglev applications. IEEE Trans. Ind. Electron. 2018, 65, 9938–9952. [Google Scholar] [CrossRef]
- Tarchala, G.; Orlowska-Kowalska, T. Equivalent-signal-based sliding mode speed mras-type estimator for induction motor drive stable in the regenerating mode. IEEE Trans. Ind. Electron. 2018, 65, 6936–6947. [Google Scholar] [CrossRef]
- Benlaloui, I.; Drid, S.; Chrifi-Alaoui, L.; Ouriagli, M. Implementation of a new mras speed sensorless vector control of induction machine. IEEE Trans. Energy Convers. 2015, 30, 588–595. [Google Scholar] [CrossRef]
- Utkin, V. Discussion aspects of high-order sliding mode control. IEEE Trans. Autom. Control. 2016, 61, 829–833. [Google Scholar] [CrossRef]
- Zhao, Z.; Gu, H.; Zhang, J.; Ding, G. Terminal sliding mode control based on super-twisting algorithm. J. Syst. Eng. Electron. 2017, 28, 145–150. [Google Scholar] [CrossRef]
- Ding, S.; Wang, J.; Zheng, W.X. Second-order sliding mode control for nonlinear uncertain systems bounded by positive functions. IEEE Trans. Ind. Electron. 2015, 62, 5899–5909. [Google Scholar] [CrossRef]
- Abu-Rub, H.; Iqbal, A.; Guzinski, J. High Performance Control of AC Drives with Matlab/Simulink Models; A John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Davari, S.A.; Wang, F.; Kennel, R.M. Robust deadbeat control of an induction motor by stable mras speed and stator estimation. IEEE Trans. Ind. Inform. 2018, 14, 200–209. [Google Scholar] [CrossRef]
- Das, S.; Kumar, R.; Pal, A. Mras-based speed estimation of induction motor drive utilizing machines’ d- and q-circuit impedances. IEEE Trans. Ind. Electron. 2019, 66, 4286–4295. [Google Scholar] [CrossRef]
- Cao, P.; Zhang, X.; Yang, S. A unified-model-based analysis of mras for online rotor time constant estimation in an induction motor drive. IEEE Trans. Ind. Electron. 2017, 64, 4361–4371. [Google Scholar] [CrossRef]
- Popov, V.M. Hyperstability of Control Systems; Springer: Berlin/Heidelberg, Germany, 1973. [Google Scholar]
- Pal, A.; Das, S.; Chattopadhyay, A. An improved rotor flux space vector based mras for field-oriented control of induction motor drives. IEEE Trans. Power Electron. 2018, 33, 5131–5141. [Google Scholar] [CrossRef]
- Dehghan-Azad, E.; Gadoue, S.; Atkinson, D.; Slater, H.; Barrass, P.; Blaabjerg, F. Sensorless control of im based on stator-voltage mras for limp-home ev applications. IEEE Trans. Power Electron. 2018, 33, 1911–1921. [Google Scholar] [CrossRef]
- Accetta, A.; Cirrincione, M.; Pucci, M.; Vitale, G. Closed-loop mras speed observer for linear induction motor drives. IEEE Trans. Ind. Appl. 2015, 51, 2279–2290. [Google Scholar] [CrossRef]
- Utkin, V.I. Sliding Mode Control in Discrete-Time and Difference Systems; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Fnaiech, M.A.; Trabelsi, M.; Khalil, S.; Mansouri, M.; Nounou, H.; Abu-Rub, H. Robust sliding mode control for three-phase rectifier supplied by non-ideal voltage. Control Eng. Pract. 2018, 77, 73–85. [Google Scholar] [CrossRef]
- Huber, O.; Acary, V.; Brogliato, B. Lyapunov stability and performance analysis of the implicit discrete sliding mode control. IEEE Trans. Autom. Control 2016, 61, 3016–3030. [Google Scholar] [CrossRef]

| Induction Motor Nominal Parameters | ||
|---|---|---|
| Description | Parameter | Value |
| Power | 1.5 kW | |
| Voltage | 3 × 400 V 50 Hz | |
| Current | 3.5 A | |
| Speed | 1410 rpm | |
| Efficiency | 0.79 | |
| Power coefficient | 0.78 | |
| Torque | 10.16 Nm | |
| Stator resistance | 4.74 | |
| Rotor resistance | 4.75 | |
| Mutual inductance | 303 mH | |
| Stator inductance | 320 mH | |
| Rotor inductance | 320 mH | |
| Inertia | 0.0038 kg m | |
| Modified inertia | 0.007 kg m | |
| Inverter nominal parameters | ||
| Power | 6.1 kW | |
| Voltage | 3 × 420 V 50 Hz | |
| Current | 7.5 A | |
| Switching frequency | 30 kHz | |
| DC Voltage | 600 V | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fnaiech, M.A.; Guzinski, J.; Trabelsi, M.; Kouzou, A.; Benbouzid, M.; Luksza, K. MRAS-Based Switching Linear Feedback Strategy for Sensorless Speed Control of Induction Motor Drives. Energies 2021, 14, 3083. https://doi.org/10.3390/en14113083
Fnaiech MA, Guzinski J, Trabelsi M, Kouzou A, Benbouzid M, Luksza K. MRAS-Based Switching Linear Feedback Strategy for Sensorless Speed Control of Induction Motor Drives. Energies. 2021; 14(11):3083. https://doi.org/10.3390/en14113083
Chicago/Turabian StyleFnaiech, Mohamed Amine, Jaroslaw Guzinski, Mohamed Trabelsi, Abdellah Kouzou, Mohamed Benbouzid, and Krzysztof Luksza. 2021. "MRAS-Based Switching Linear Feedback Strategy for Sensorless Speed Control of Induction Motor Drives" Energies 14, no. 11: 3083. https://doi.org/10.3390/en14113083
APA StyleFnaiech, M. A., Guzinski, J., Trabelsi, M., Kouzou, A., Benbouzid, M., & Luksza, K. (2021). MRAS-Based Switching Linear Feedback Strategy for Sensorless Speed Control of Induction Motor Drives. Energies, 14(11), 3083. https://doi.org/10.3390/en14113083









