Figure 1.
Prediction tools.
Figure 1.
Prediction tools.
Figure 2.
Distance between actual output (Ya) and predicted output (Y).
Figure 2.
Distance between actual output (Ya) and predicted output (Y).
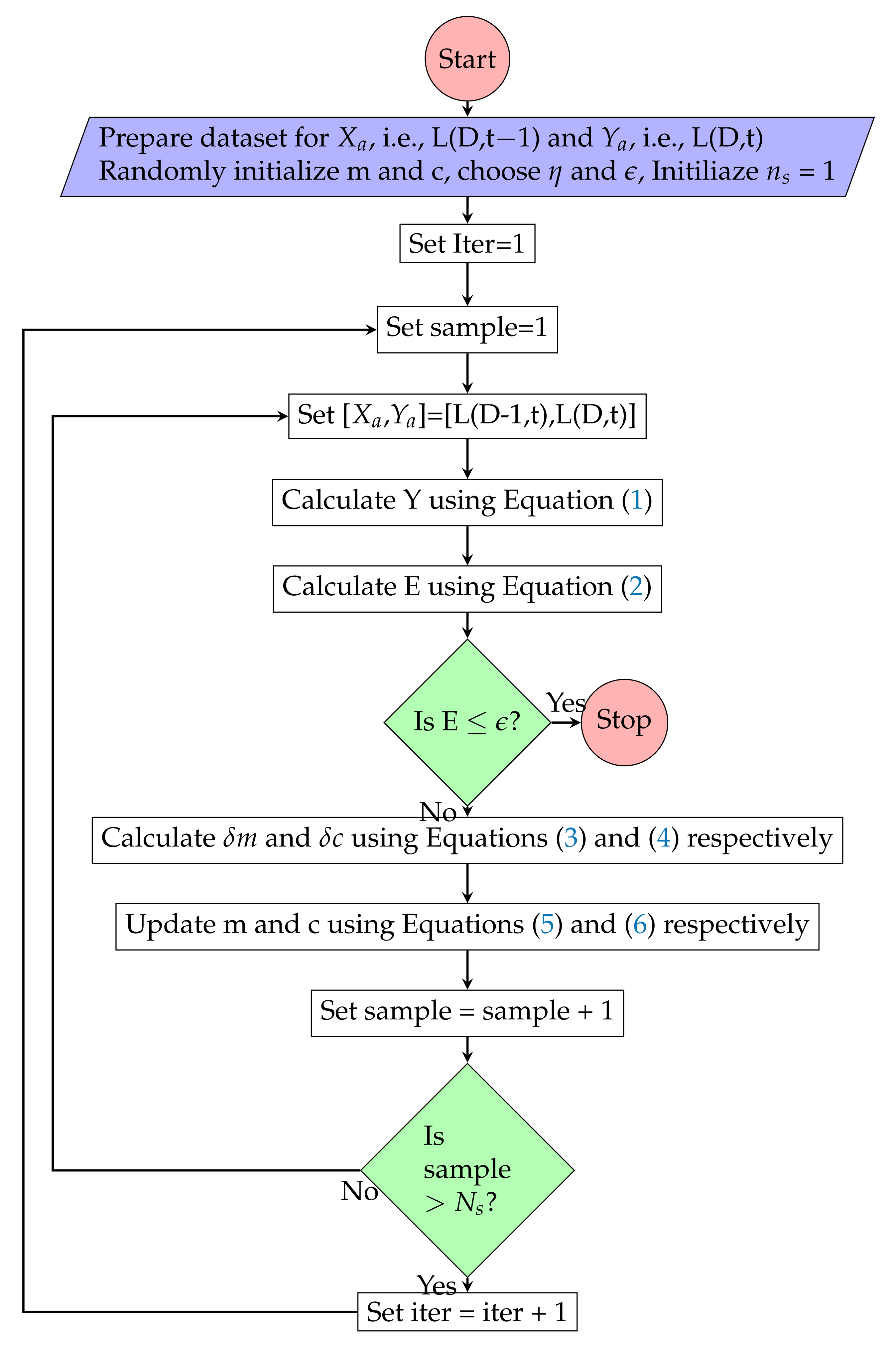
Figure 3.
Simple Linear Regression model training algorithm.
Figure 3.
Simple Linear Regression model training algorithm.
Figure 4.
Distance between actual output (Ya) and predicted output (Y) for MLR.
Figure 4.
Distance between actual output (Ya) and predicted output (Y) for MLR.
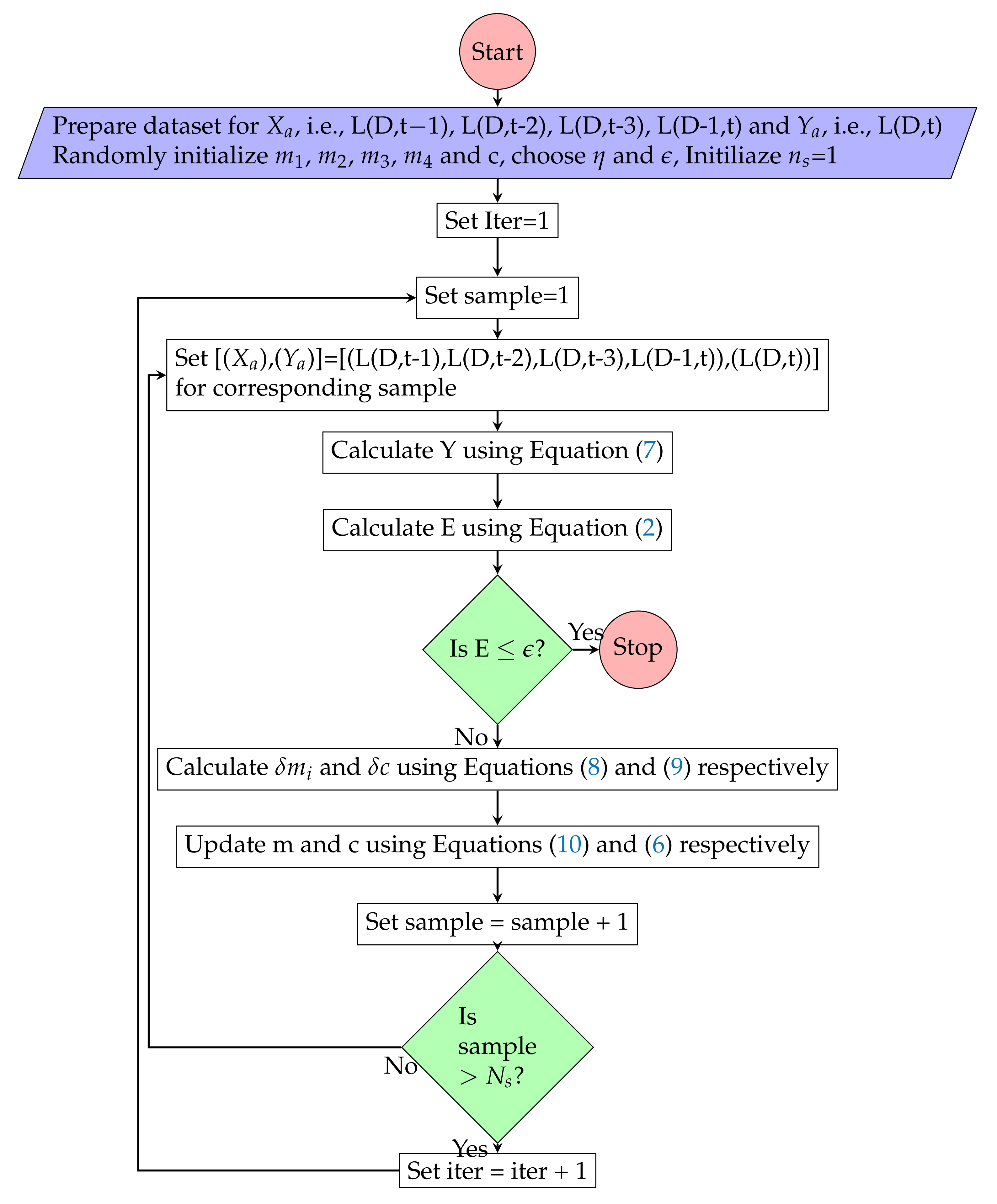
Figure 5.
Multiple linear regression model training algorithm.
Figure 5.
Multiple linear regression model training algorithm.
Figure 6.
Distance between actual output (Ya) and predicted output (Y).
Figure 6.
Distance between actual output (Ya) and predicted output (Y).
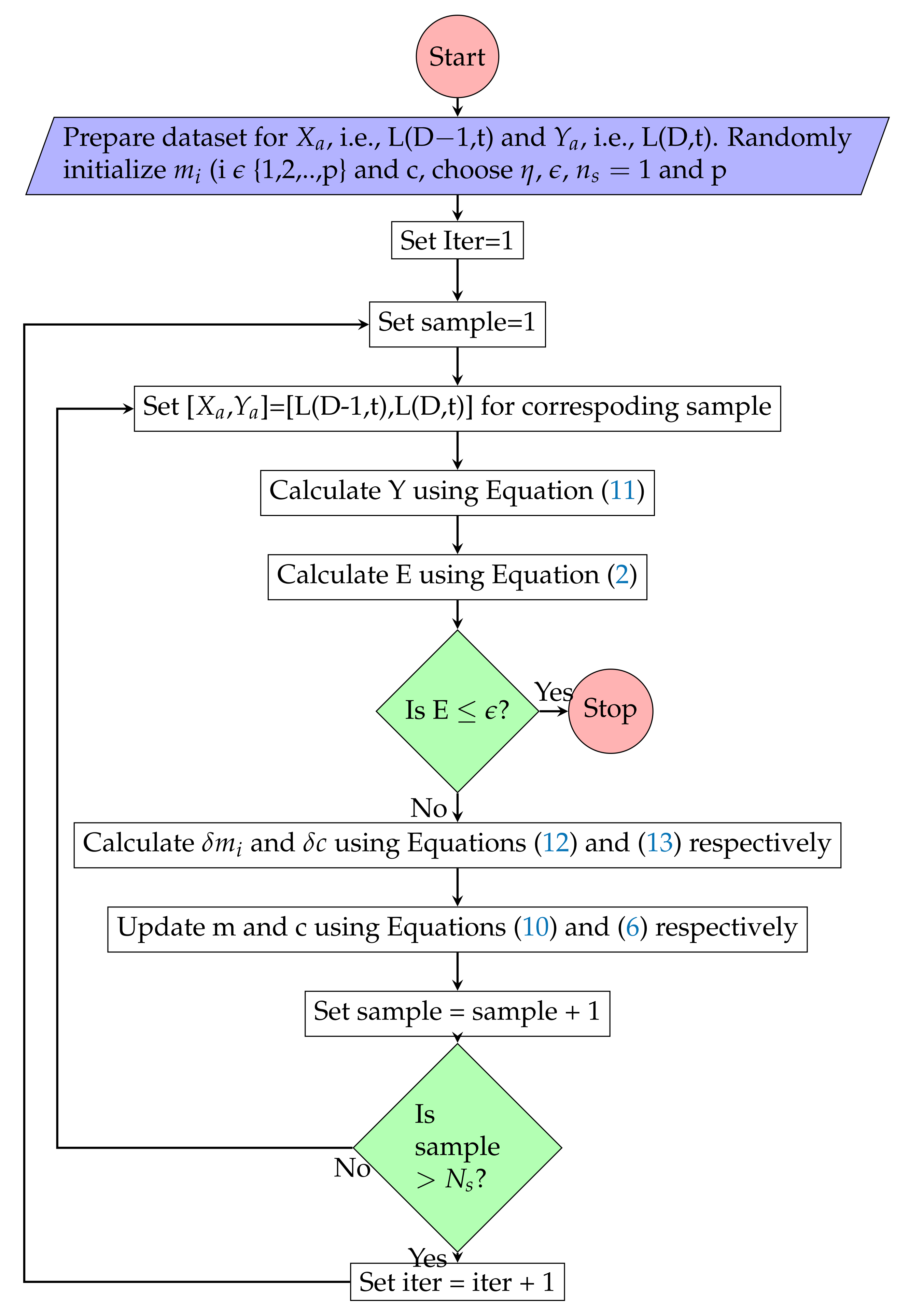
Figure 7.
Polynomial Regression model training algorithm.
Figure 7.
Polynomial Regression model training algorithm.
Figure 8.
Impact of each input feature on output variable.
Figure 8.
Impact of each input feature on output variable.
Figure 9.
SLR: Scattering of data available in the dataset.
Figure 9.
SLR: Scattering of data available in the dataset.
Figure 10.
SLR: Data observation using histogram plot.
Figure 10.
SLR: Data observation using histogram plot.
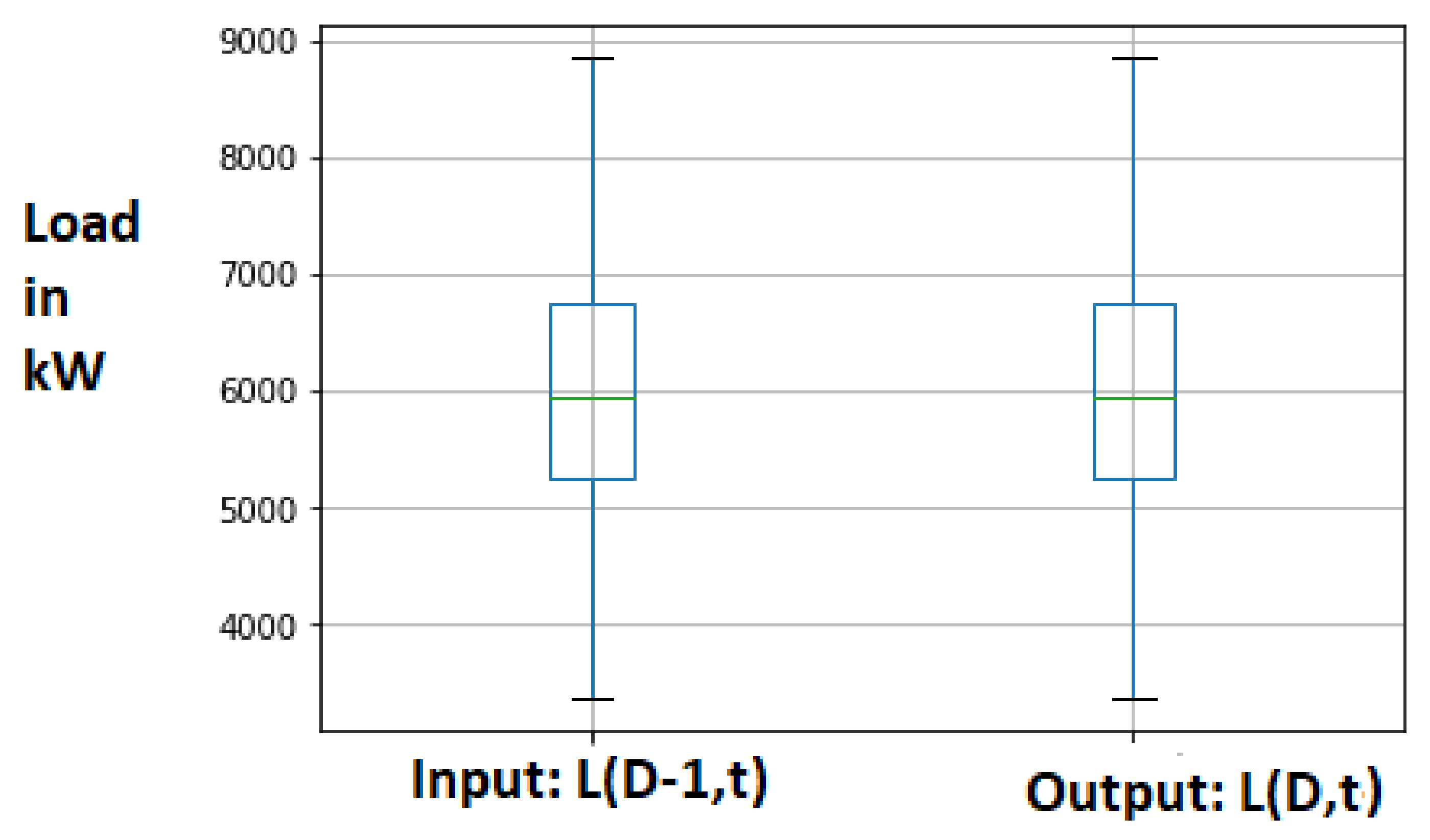
Figure 11.
SLR: Data observation using box plot.
Figure 11.
SLR: Data observation using box plot.
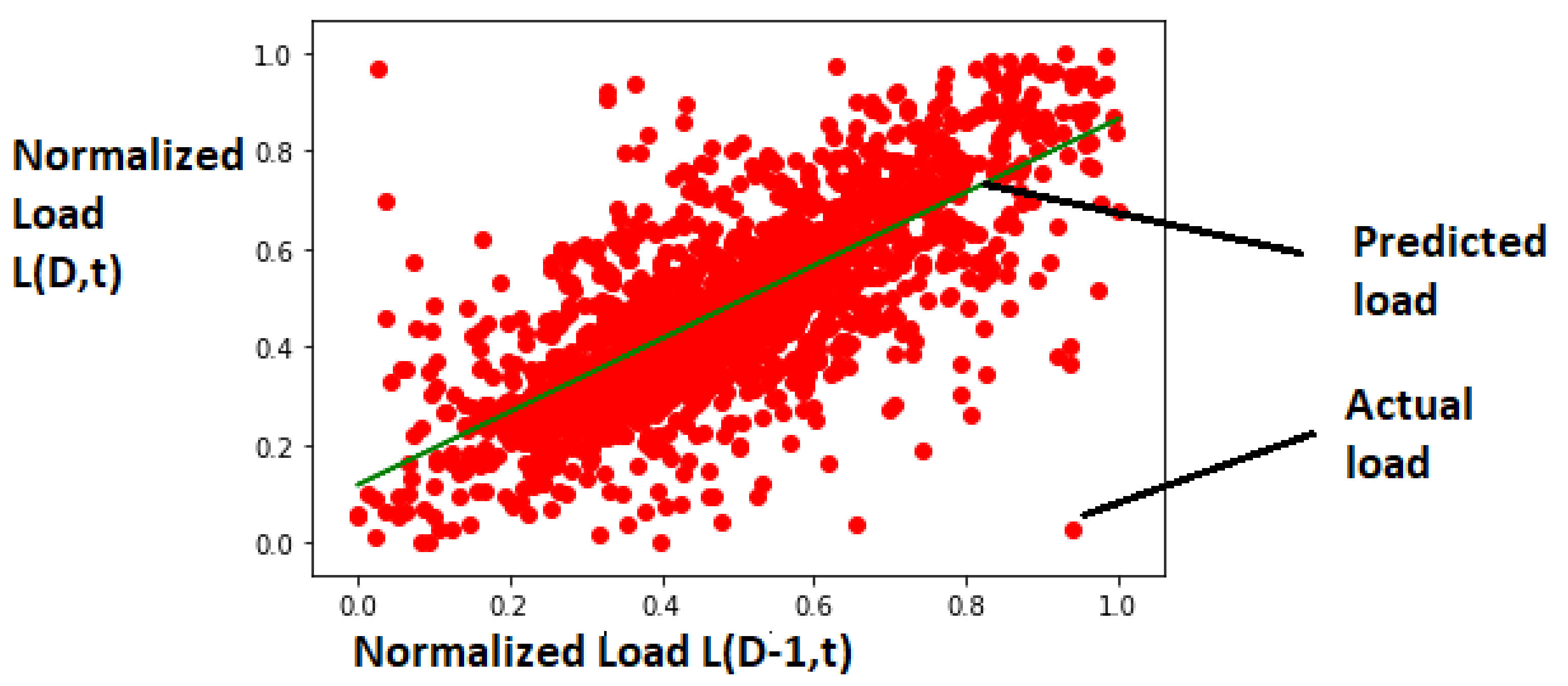
Figure 12.
SLR: Distribution of actual load and predicted load with training dataset and with m = 0.7472 and c = 0.1173.
Figure 12.
SLR: Distribution of actual load and predicted load with training dataset and with m = 0.7472 and c = 0.1173.
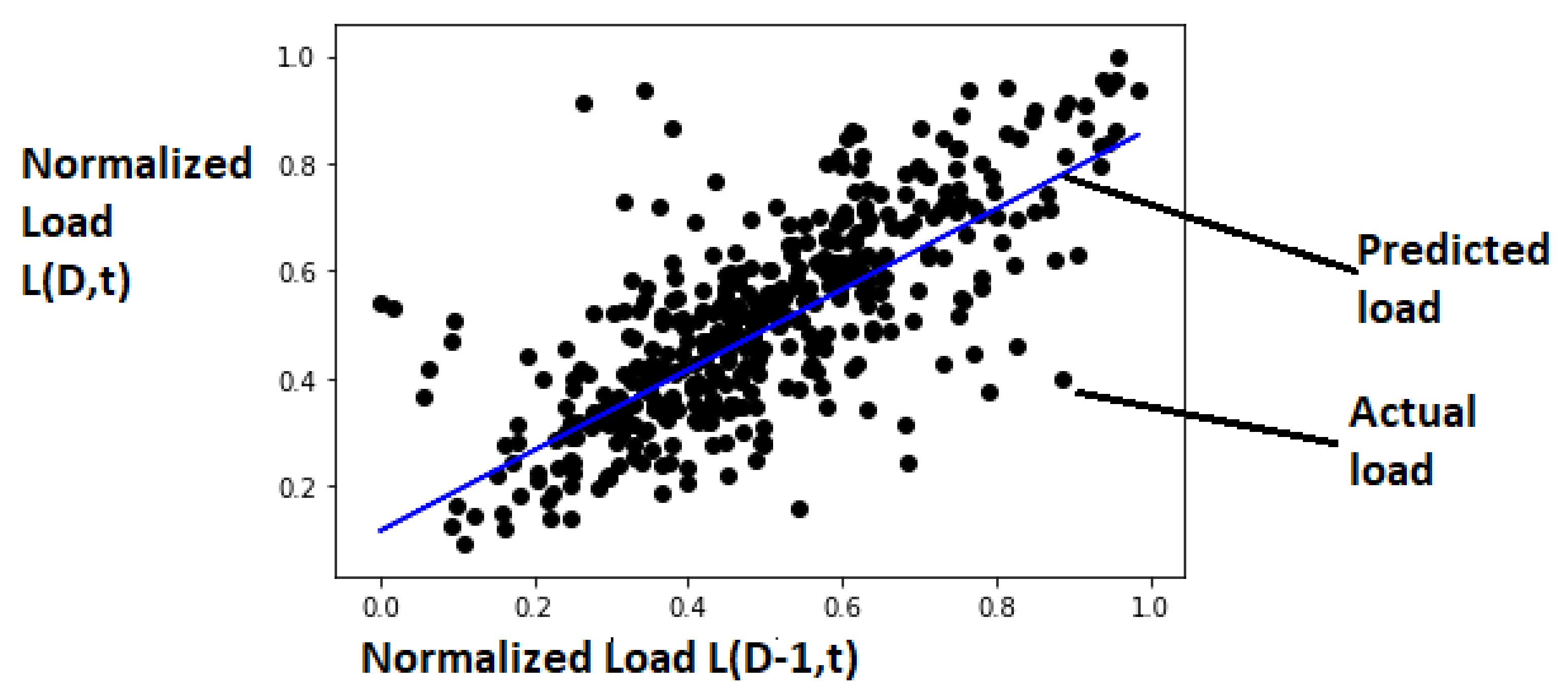
Figure 13.
SLR: Distribution of actual load and predicted load with testing dataset and with m = 0.7472 and c = 0.1173.
Figure 13.
SLR: Distribution of actual load and predicted load with testing dataset and with m = 0.7472 and c = 0.1173.
Figure 14.
SLR: Comparison of actual load and predicted load with trained SLR model.
Figure 14.
SLR: Comparison of actual load and predicted load with trained SLR model.
Figure 15.
MLR: Data observation using histogram plot.
Figure 15.
MLR: Data observation using histogram plot.
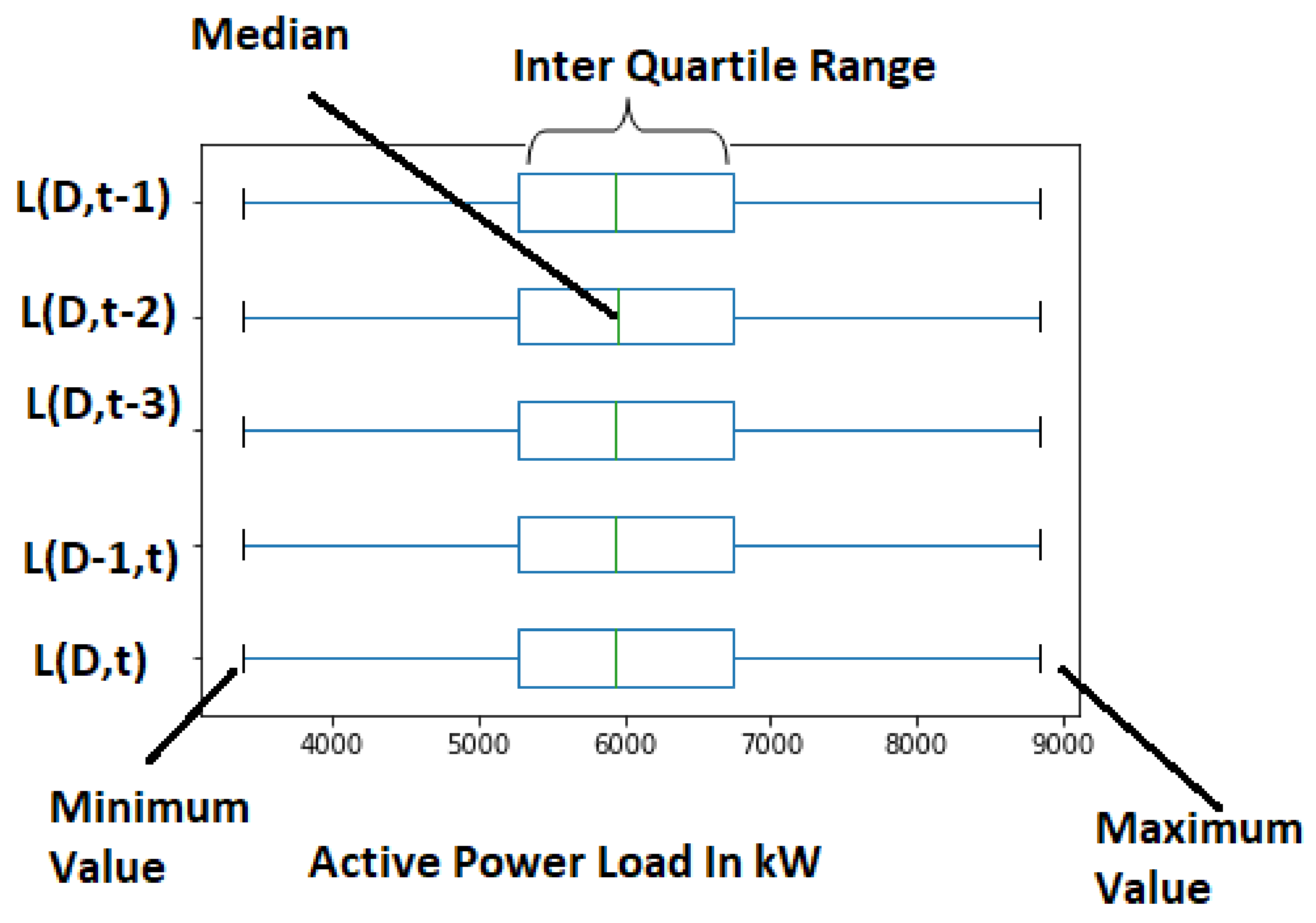
Figure 16.
MLR: Data observation using box plot.
Figure 16.
MLR: Data observation using box plot.
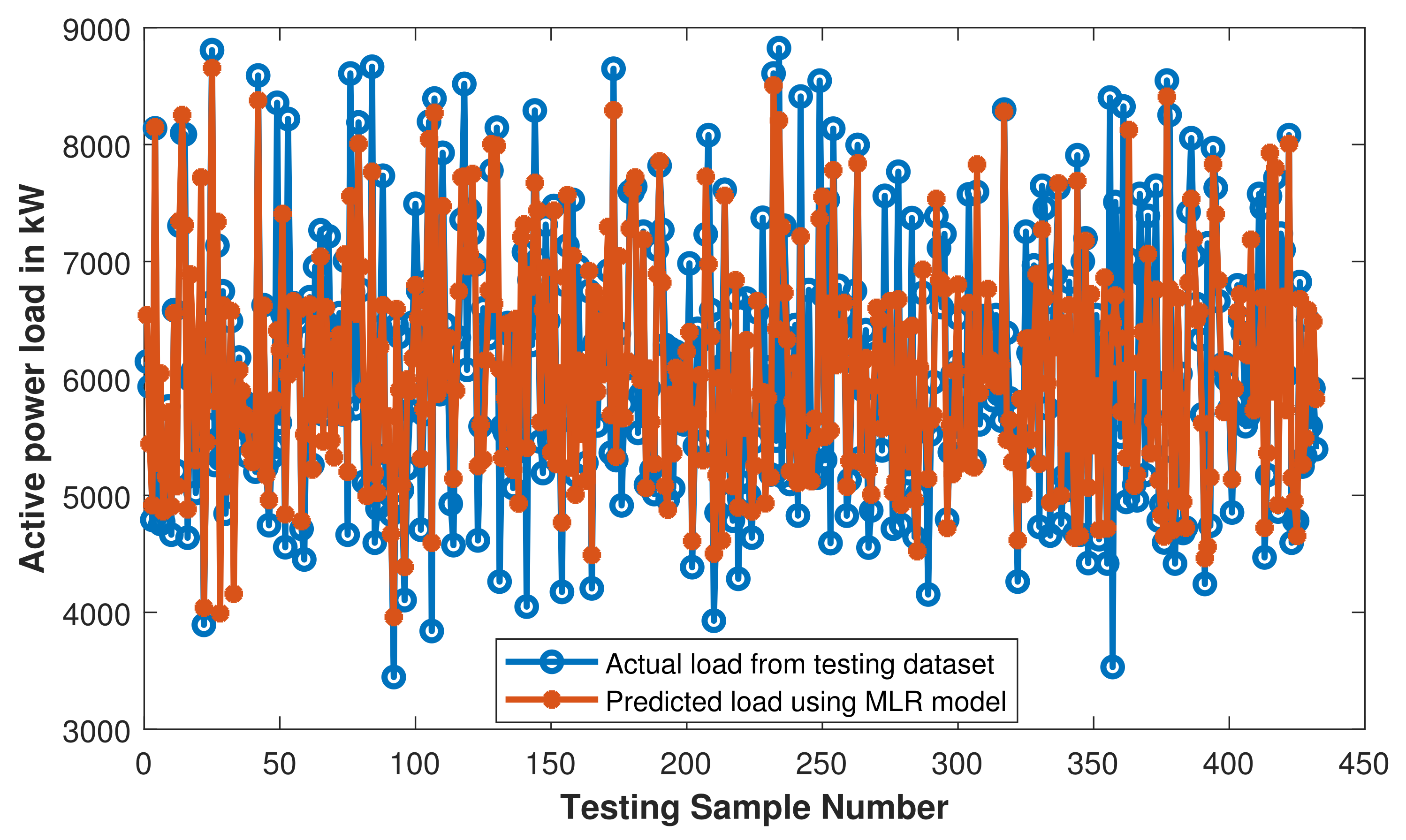
Figure 17.
MLR: comparison of actual load and predicted load with trained MLR model.
Figure 17.
MLR: comparison of actual load and predicted load with trained MLR model.
Figure 18.
MLR With Dimensionality Reduction: comparison of actual load and predicted load with trained MLR model.
Figure 18.
MLR With Dimensionality Reduction: comparison of actual load and predicted load with trained MLR model.
Figure 19.
PR: identification of Optimal PR Model.
Figure 19.
PR: identification of Optimal PR Model.
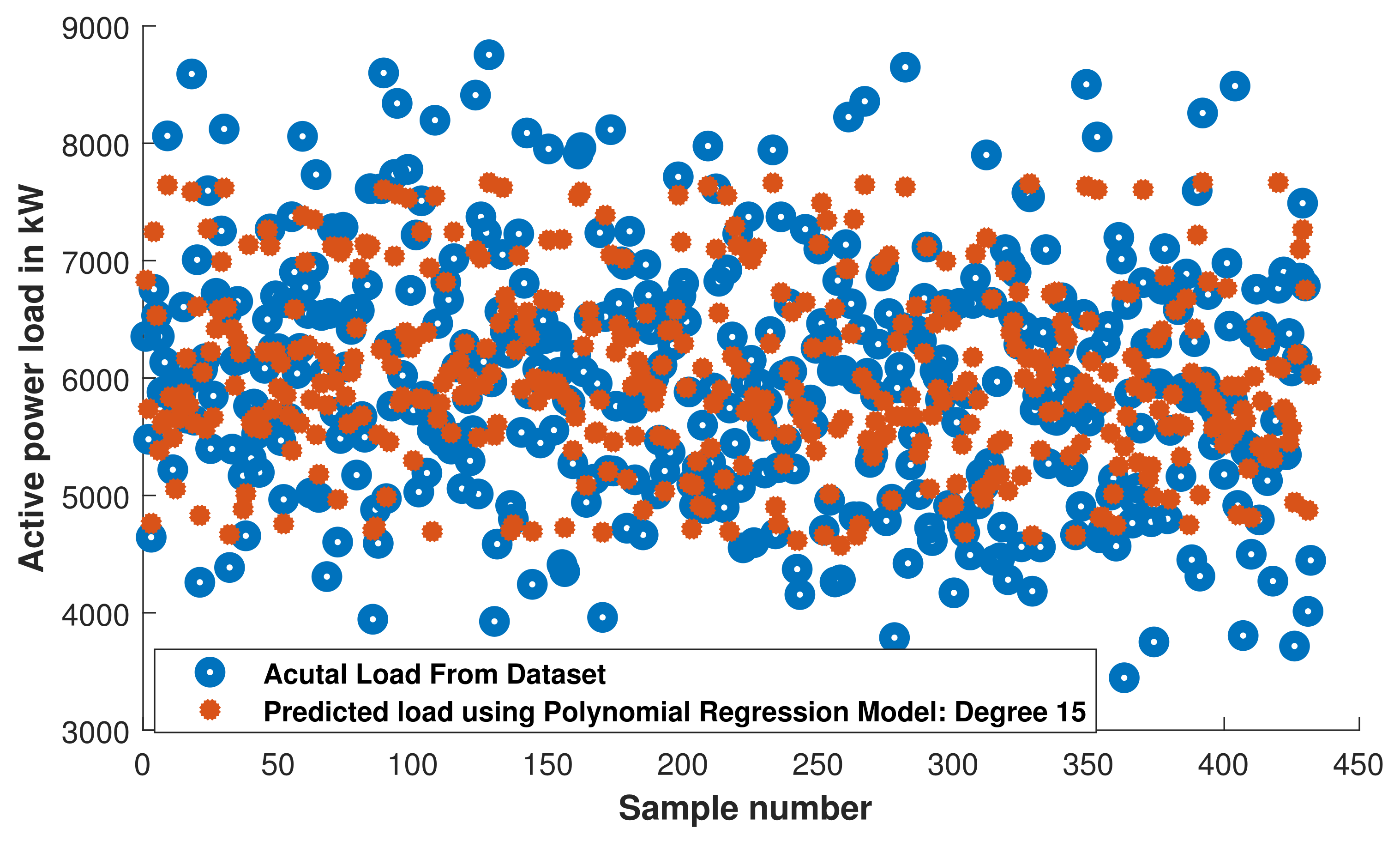
Figure 20.
PR: comparison of actual load and predicted load with trained PR model.
Figure 20.
PR: comparison of actual load and predicted load with trained PR model.
Figure 21.
Model performance to predict load with in threshold limit.
Figure 21.
Model performance to predict load with in threshold limit.
Table 1.
Active power load prediction classification.
Table 1.
Active power load prediction classification.
| Load Prediction Type | Time | Usage |
|---|
| Short term | Few hours to days | Electric power generation and transmission scheduling |
| Medium term | Few weeks to months | Fuel purchase scheduling |
| Long term | 1–10 years | Establishment of power sector entities |
Table 2.
SLR: statistical information of active power load dataset.
Table 2.
SLR: statistical information of active power load dataset.
| Parameter | Input | Output |
|---|
| count | 2160 | 2160 |
| mean | 6037 | 6028 |
| std | 1066 | 1068 |
| min | 3378 | 3378 |
| 25% | 5263 | 5260 |
| 50% | 5950 | 5935 |
| 75% | 6747 | 6739 |
| max | 8842 | 8842 |
Table 3.
MLR: Statistical information of active power load dataset.
Table 3.
MLR: Statistical information of active power load dataset.
| Parameter | L(D,t−1) | L(D,t−2) | L(D,t−3) | L(D−1,t) | L(D,t) |
|---|
| count | 2160 | 2160 | 2160 | 2160 | 2160 |
| mean | 6028 | 6028 | 6029 | 6037 | 6028 |
| std | 1068 | 1068 | 1068 | 1066 | 1068 |
| min | 3378 | 3378 | 3378 | 3378 | 3378 |
| 25% | 5260 | 5260 | 5260 | 5263 | 5260 |
| 50% | 5933 | 5935 | 5936 | 5950 | 5935 |
| 75% | 6739 | 6739 | 6739 | 6747 | 6739 |
| max | 8842 | 8842 | 8842 | 8842 | 8842 |
Table 4.
MLR: coefficients and intercept information.
Table 4.
MLR: coefficients and intercept information.
| | | | c |
|---|
| 0.618733 | −0.00289 | −0.148361 | 0.374255 | 0.07541947 |
Table 5.
MLR: coefficients and intercept information.
Table 5.
MLR: coefficients and intercept information.
| Features | L(D,t−1) | L(D,t−2) | L(D,t−3) | L(D−1,t) |
|---|
| L(D,t−1) | 1 | 0.783398 | 0.547211 | 0.660699 |
| L(D,t−2) | 0.783398 | 1 | 0.783336 | 0.472053 |
| L(D,t−3) | 0.547211 | 0.783336 | 1 | 0.256744 |
| L(D−1,t) | 0.660699 | 0.472053 | 0.256744 | 1 |
Table 6.
MLR with dimensionality reduction: coefficients and intercept information.
Table 6.
MLR with dimensionality reduction: coefficients and intercept information.
| | | c |
|---|
| 0.596832 | −0.137541 | 0.392209 | 0.07235393 |
Table 7.
MLR with dimensionality reduction: performance of the model on training dataset.
Table 7.
MLR with dimensionality reduction: performance of the model on training dataset.
| | MAE | MSE | RMSE |
|---|
| With DR | 0.0748 | 0.0113 | 0.107 |
| Without DR | 0.0723 | 0.0105 | 0.103 |
Table 8.
MLR with dimensionality reduction: performance of the model on testing dataset.
Table 8.
MLR with dimensionality reduction: performance of the model on testing dataset.
| | MAE | MSE | RMSE |
|---|
| With DR | 0.0679 | 0.009 | 0.093 |
| Without DR | 0.0766 | 0.0119 | 0.109 |
Table 9.
PR: coefficients and intercept information.
Table 9.
PR: coefficients and intercept information.
| Degree (p) | | | | | | | | |
|---|
| 2 | 0.6061 | 0.1345 | NA | NA | NA | NA | NA | NA |
| 3 | −0.016 | 1.5525 | −0.936 | NA | NA | NA | NA | NA |
| 4 | −0.235 | 2.4303 | −2.25139 | 0.65556 | NA | NA | NA | NA |
| 5 | −1.458 | 9.886 | −20.92 | 21.1449 | −8.156 | NA | NA | NA |
| 10 | 3.8512 | −90.59 | 857.68 | −3885.2 | 10,407 | 17,572.45 | 19067.9 | 13006.7 |
| 15 | 20.437 | −802.9 | 13357 | −121,706 | 661,929 | −2,132,575 | 3,267,138 | 2,932,709 |
| Degree (p) | | | | | | | | c |
| 2 | NA | NA | NA | NA | NA | NA | NA | 0.15478 |
| 3 | NA | NA | NA | NA | NA | NA | NA | 0.22922 |
| 4 | NA | NA | NA | NA | NA | NA | NA | 0.24466 |
| 5 | NA | NA | NA | NA | NA | NA | NA | 0.30014 |
| 10 | 5113.5 | -888.6 | NA | NA | NA | NA | NA | 0.25182 |
| 15 | −3 × 10 | 7 × 10 | −1 × 10 | 9.2 × 10 | −5 × 10 | 18132030 | −3 × 10 | 0.19706 |
Table 10.
PR: training performance metrics.
Table 10.
PR: training performance metrics.
| Polynomial Degree (p) | Training |
|---|
| MAE | MSE | RMSE |
|---|
| 3 | 0.0973329 | 0.01732 | 0.131609177 |
| 4 | 0.0973174 | 0.01732 | 0.131591693 |
| 10 | 0.0970367 | 0.01717 | 0.131019329 |
| 15 | 0.0969165 | 0.01708 | 0.130697822 |
| 16 | 0.0968882 | 0.01708 | 0.130688064 |
| 18 | 0.0969342 | 0.01707 | 0.130644772 |
| 20 | 0.0970481 | 0.01705 | 0.130574147 |
Table 11.
PR: testing performance metrics.
Table 11.
PR: testing performance metrics.
| Polynomial Degree (p) | Training |
|---|
| MAE | MSE | RMSE |
|---|
| 3 | 0.09289 | 0.015969 | 0.12637 |
| 4 | 0.09276 | 0.015939 | 0.12625 |
| 10 | 0.09274 | 0.015889 | 0.12605 |
| 15 | 0.09295 | 0.015849 | 0.12589 |
| 16 | 0.09292 | 0.015853 | 0.12591 |
| 18 | 0.09308 | 0.015877 | 0.12600 |
| 20 | 0.09311 | 0.015900 | 0.12609 |
Table 12.
Comparison of regression models’ performance on testing dataset.
Table 12.
Comparison of regression models’ performance on testing dataset.
| Regression | |
|---|
| Model
| MAE
| MSE
| RMSE
|
|---|
| SLR | 0.0939 | 0.0163 | 0.1277 |
| PR | 0.0930 | 0.0158 | 0.1259 |
| MLR | 0.0766 | 0.0119 | 0.1092 |
| MLR with DR | 0.0679 | 0.009 | 0.093 |
Table 13.
Performance comparison with existing complex models.
Table 13.
Performance comparison with existing complex models.
| | Mean Square Error |
|---|
| Model | Training | Testing |
| SLR | 0.0973 | 0.0163 |
| PR | 0.0171 | 0.0158 |
| MLR | 0.0723 | 0.0119 |
| MLR with DR | 0.0748 | 0.009 |
| [18] | 0.23 | 0.44 |
| [17] | 0.29 | 1.59 |