A System Dynamics Approach to Comparative Analysis of Biomass Supply Chain Coordination Strategies
Abstract
1. Introduction
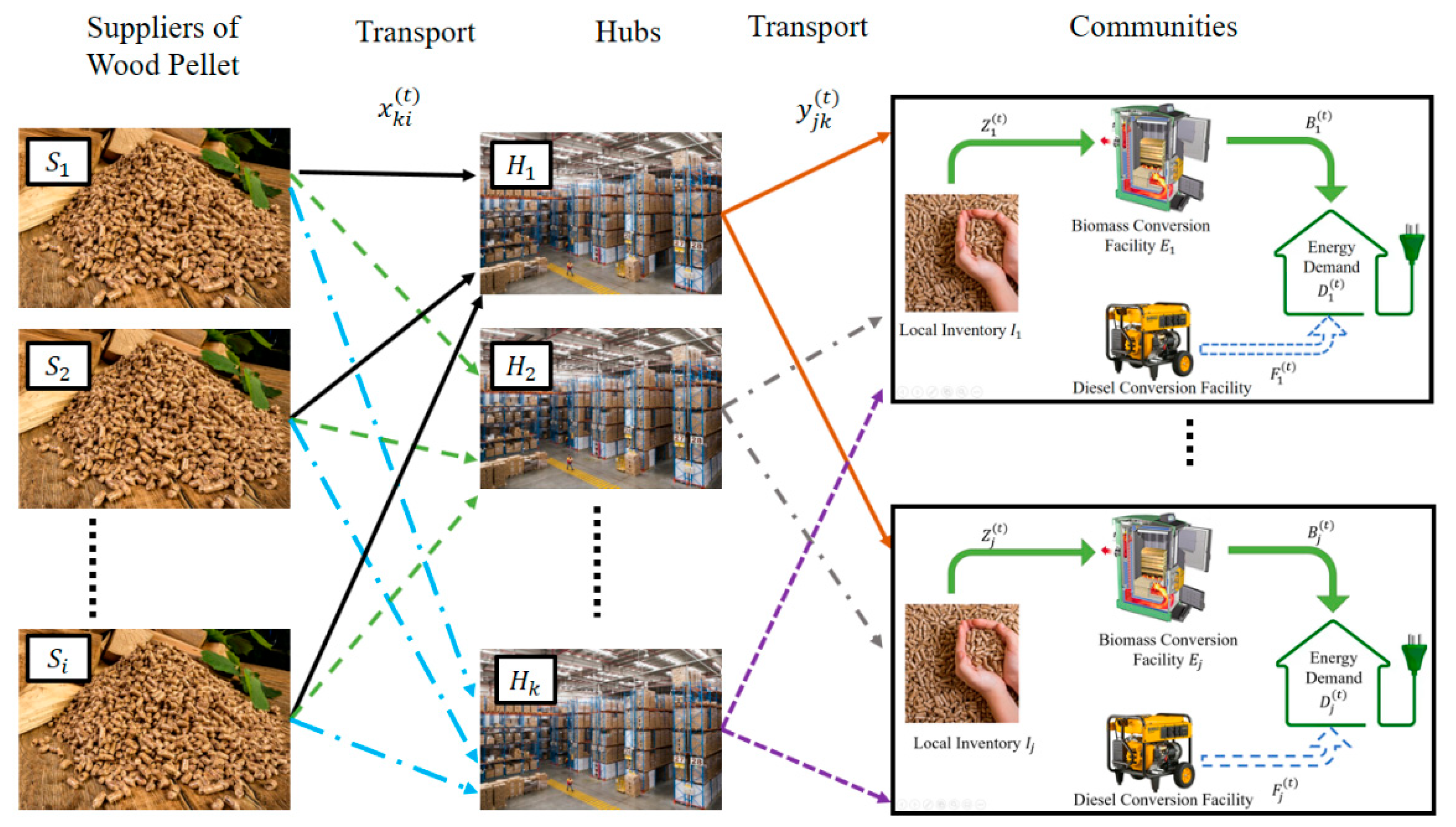
2. Problem Description
3. Methodology
3.1. Causal Relationships
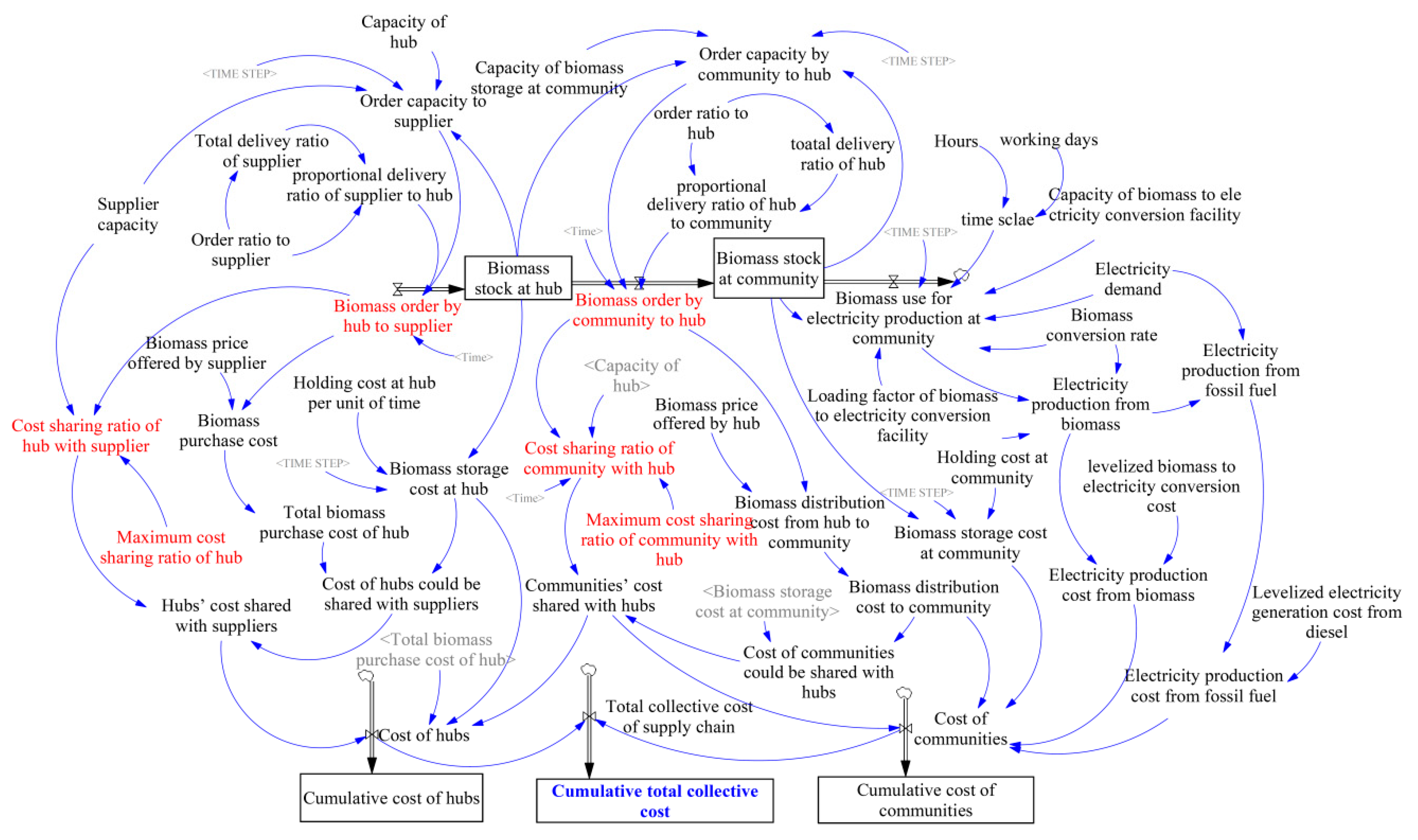
3.2. Model
3.3. Equations
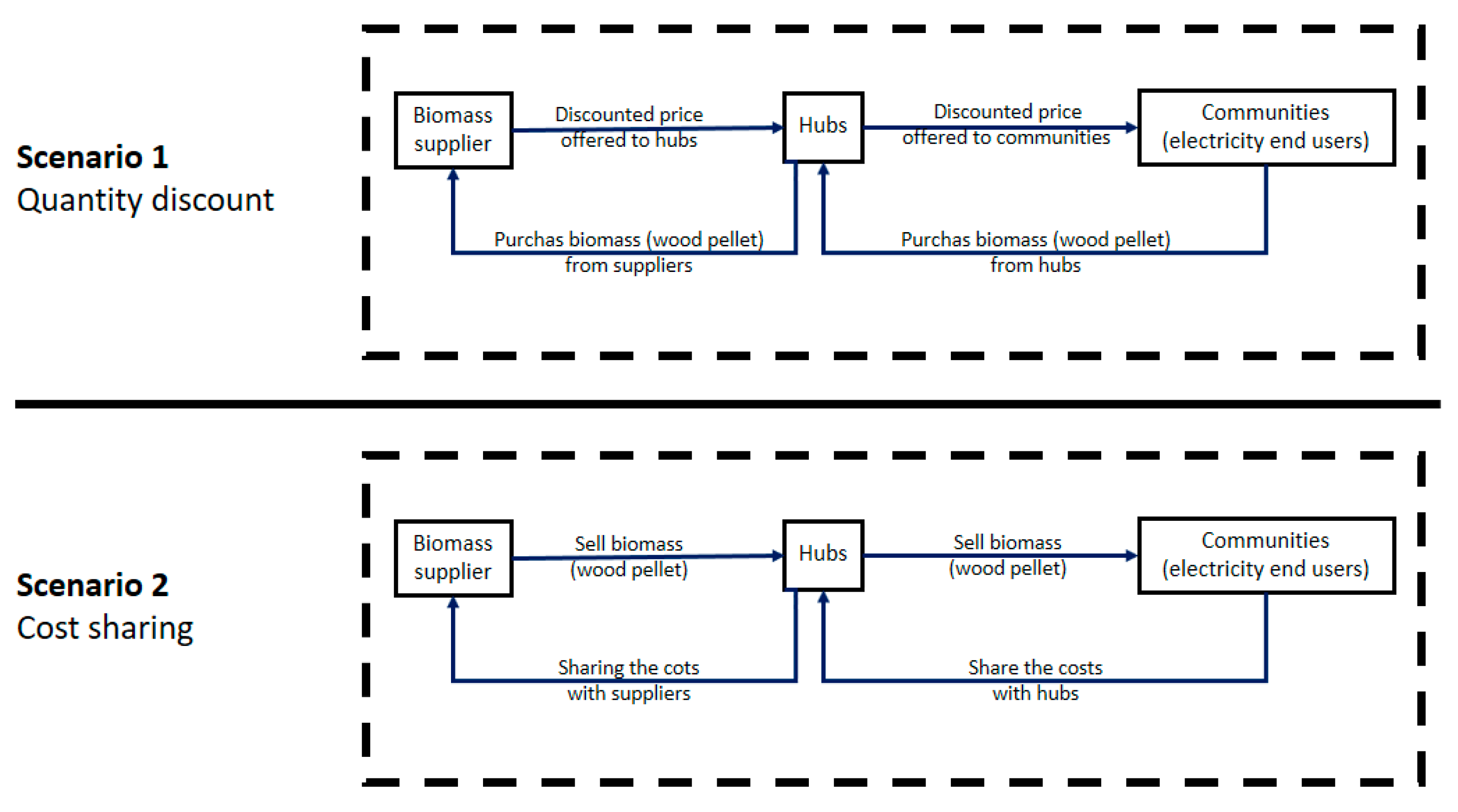
3.3.1. Objective Function for Quantity Discount Scenario
3.3.2. Objective Function for Cost Sharing Scenario
3.3.3. Model Constraints
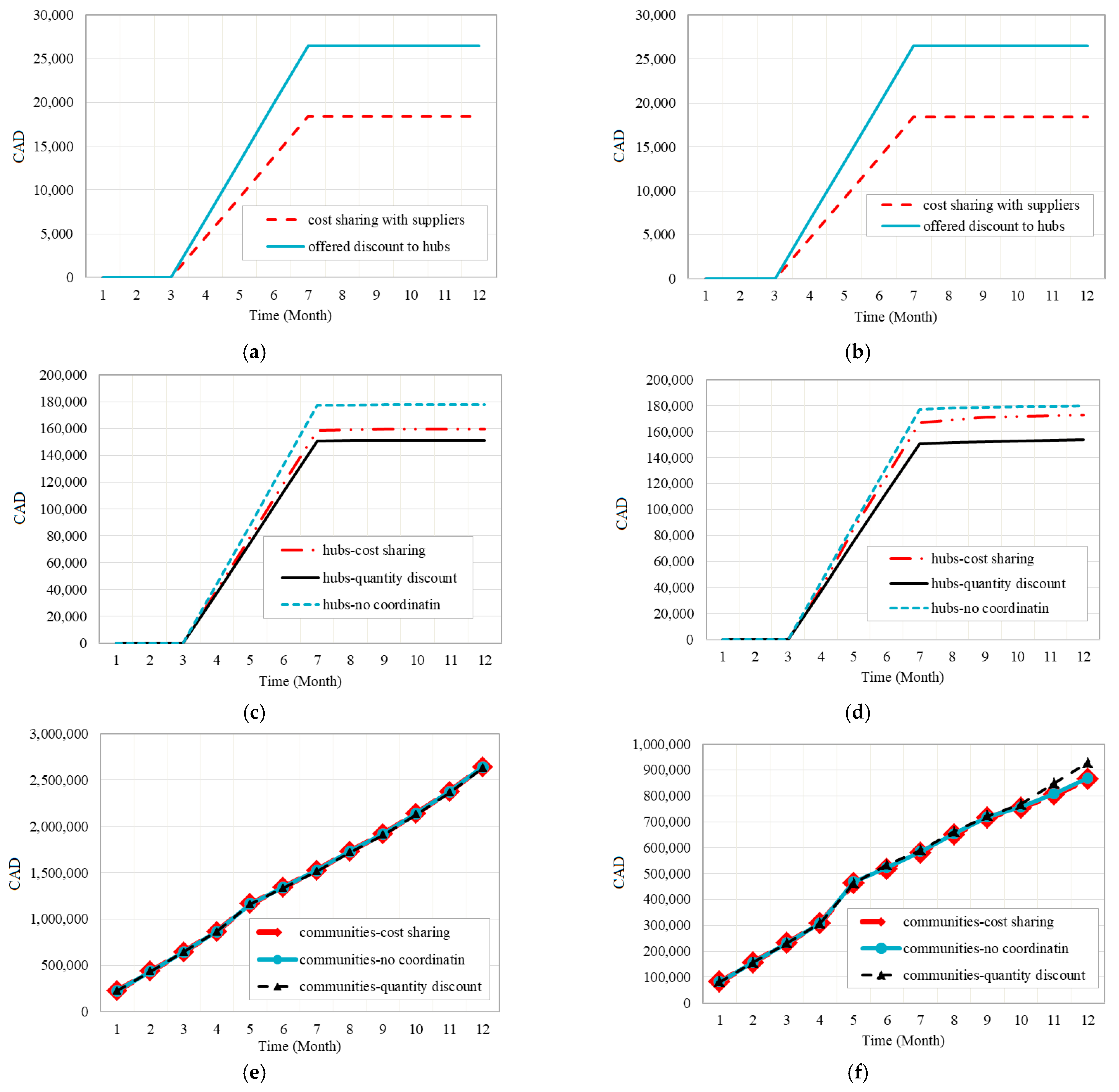
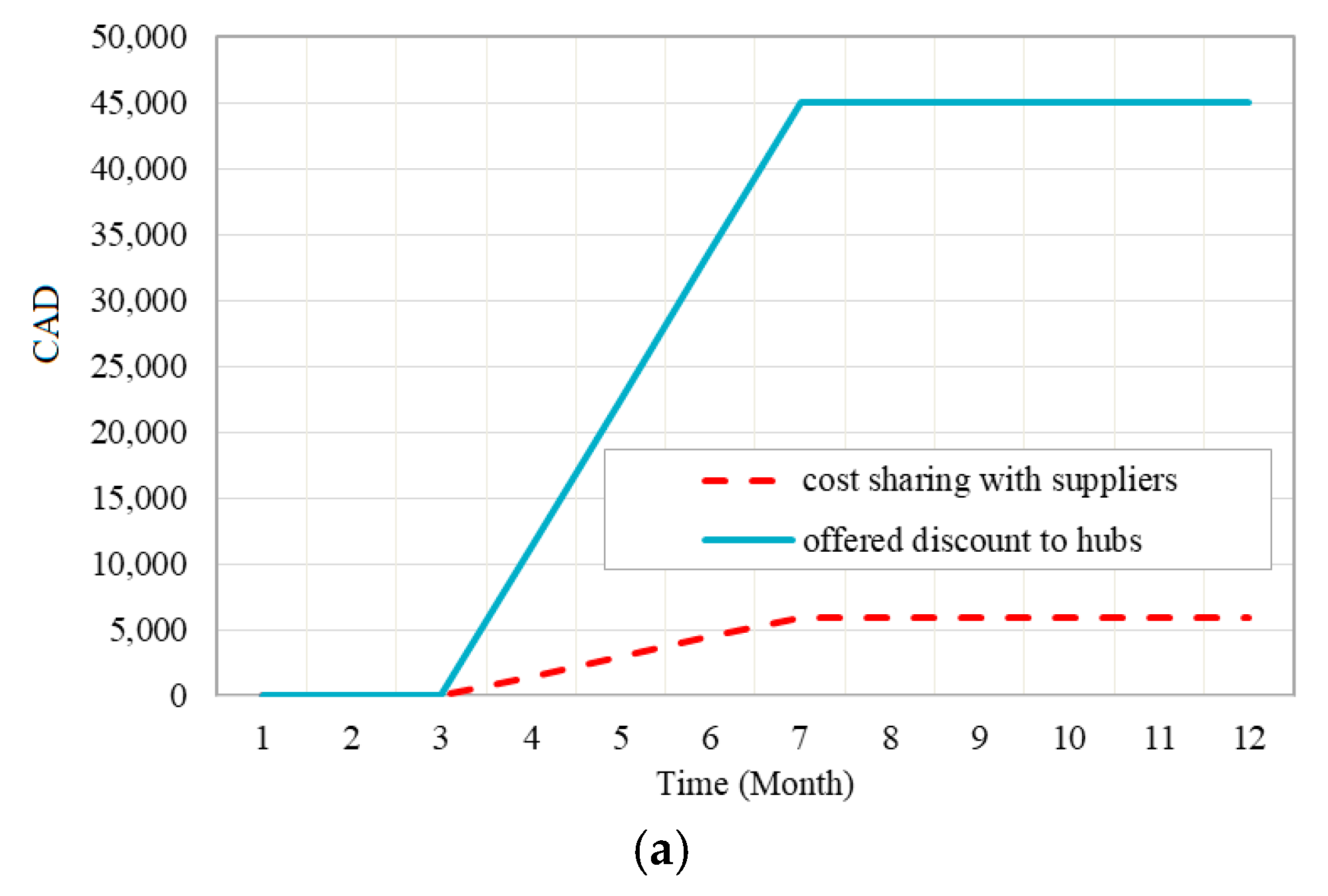
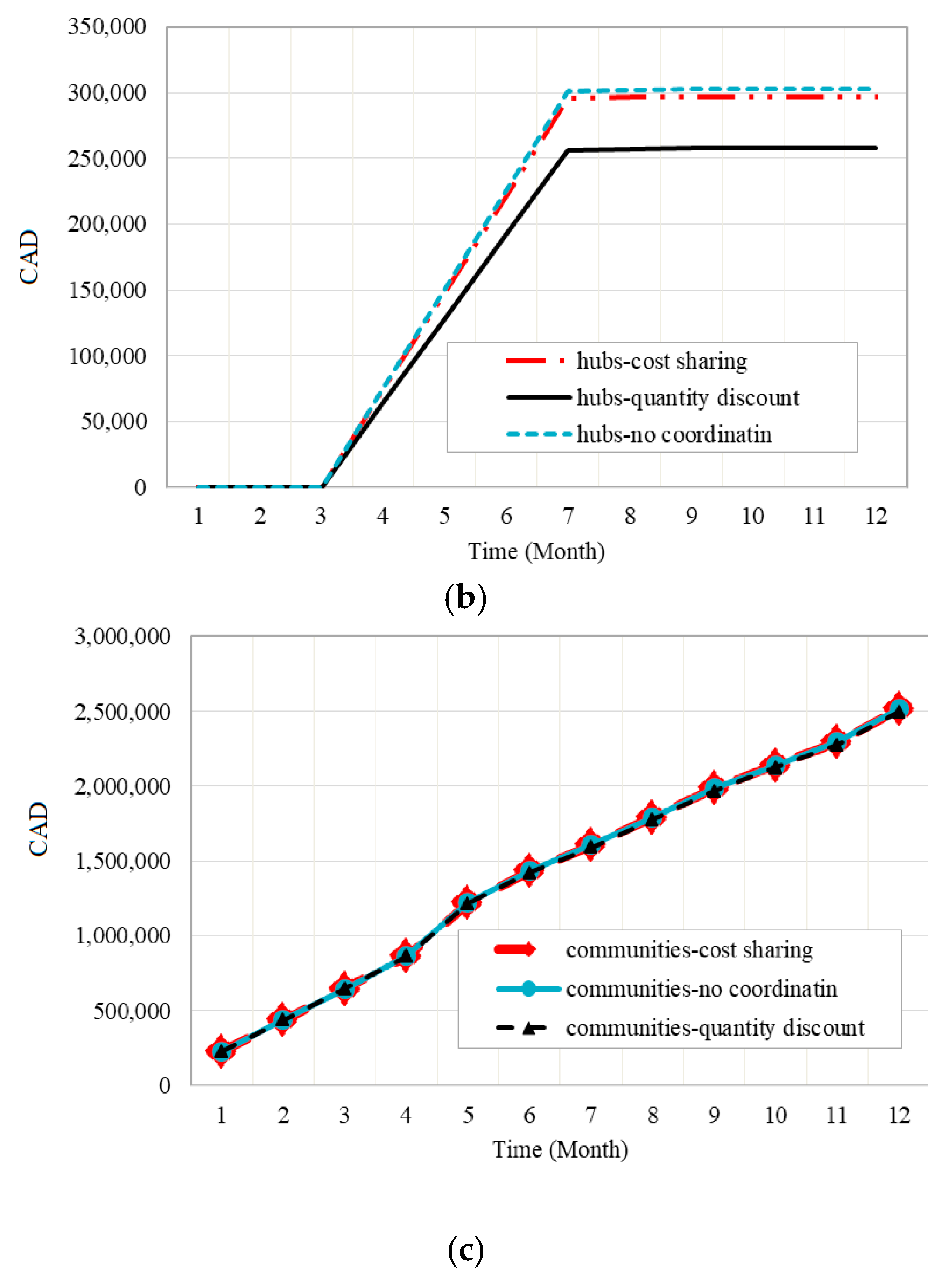
4. Case Study and Results
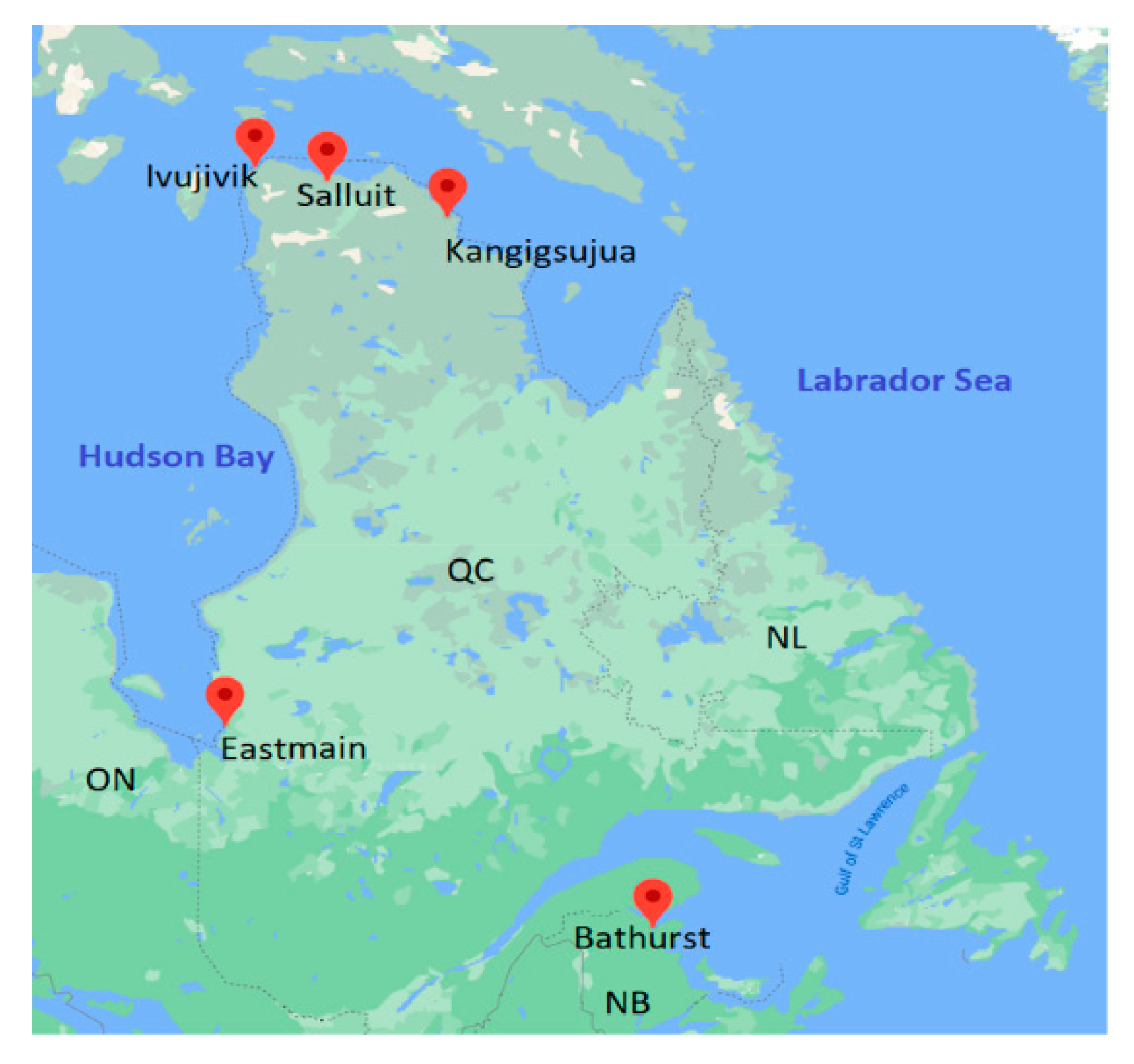
4.1. Case Study
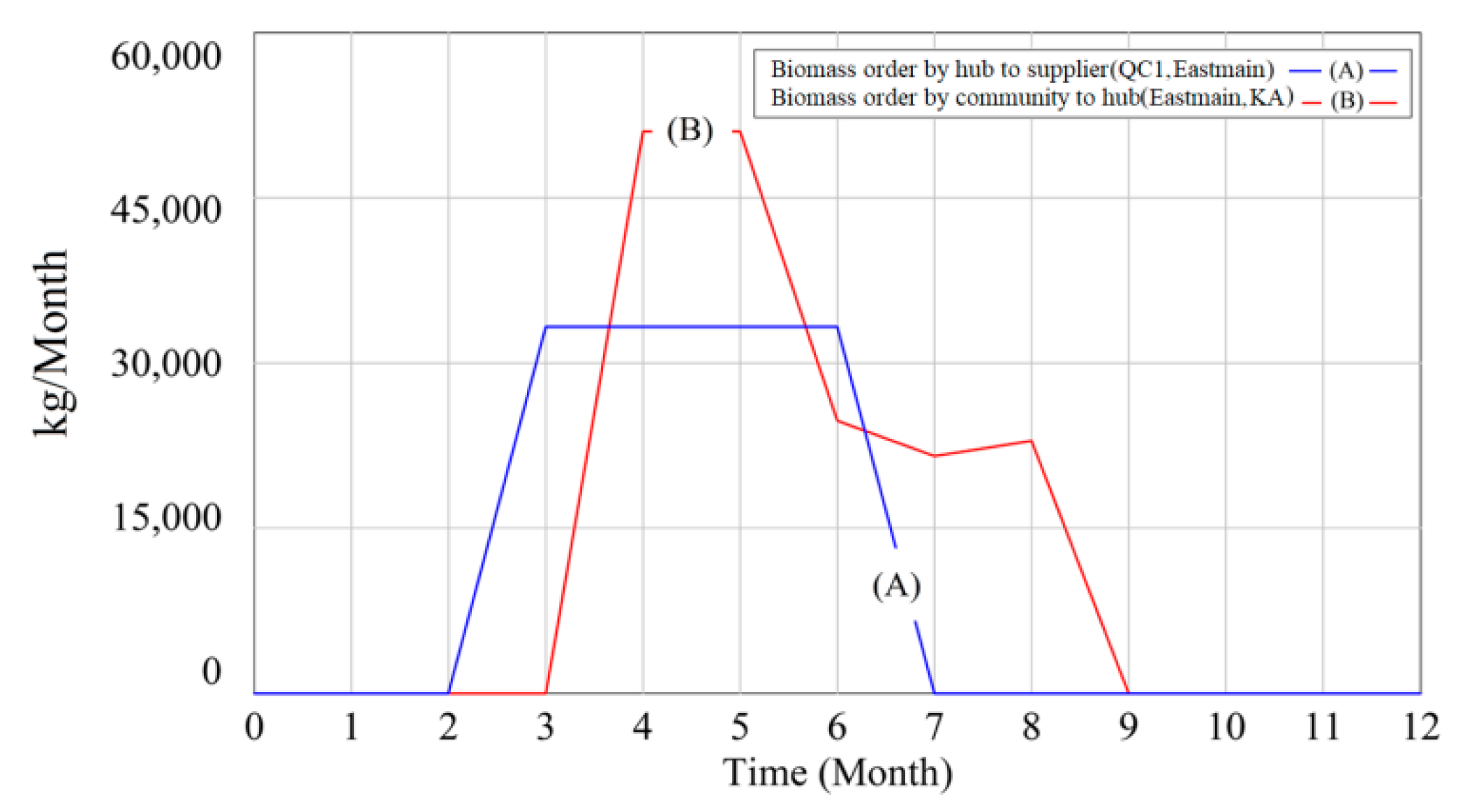
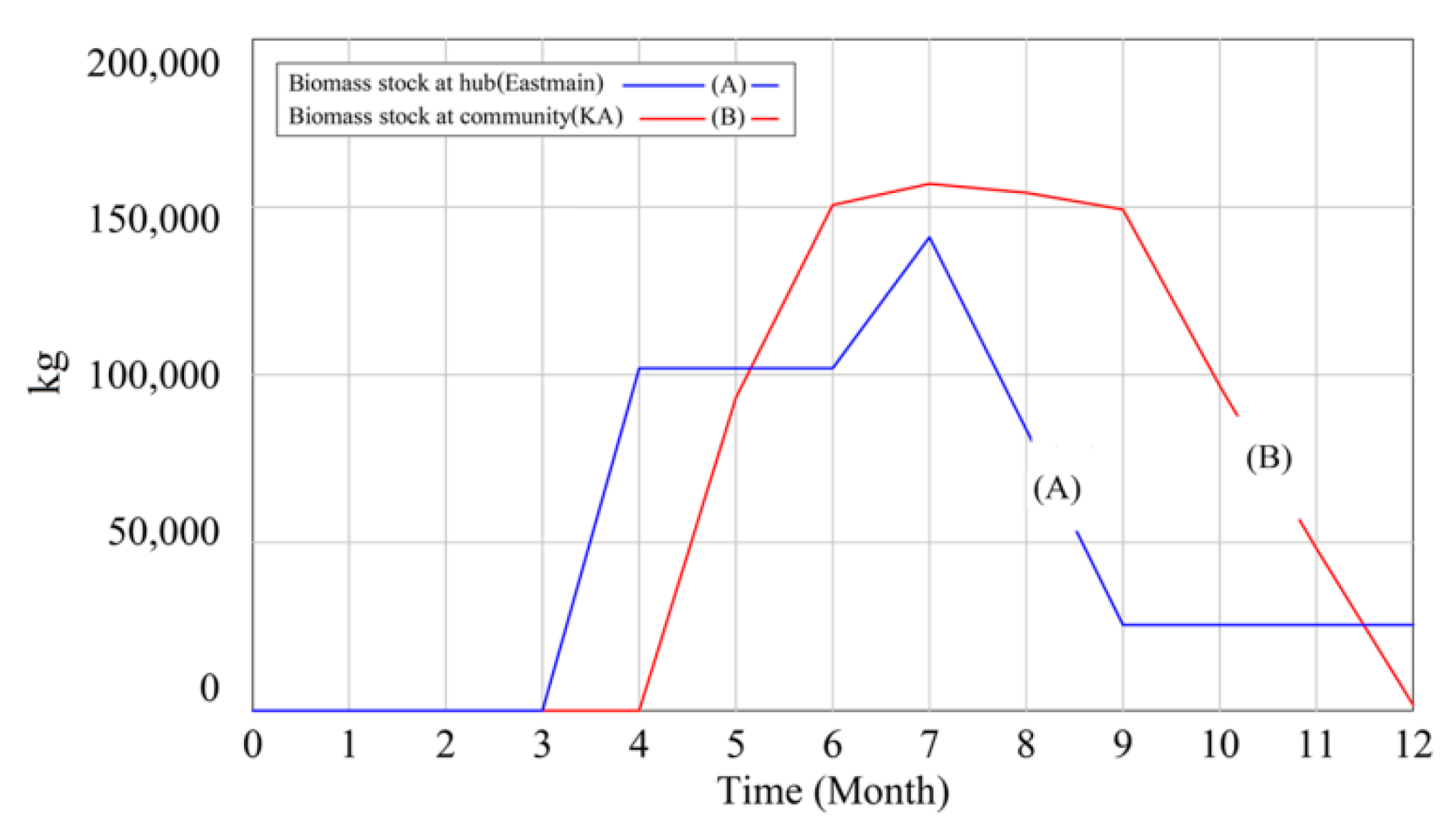
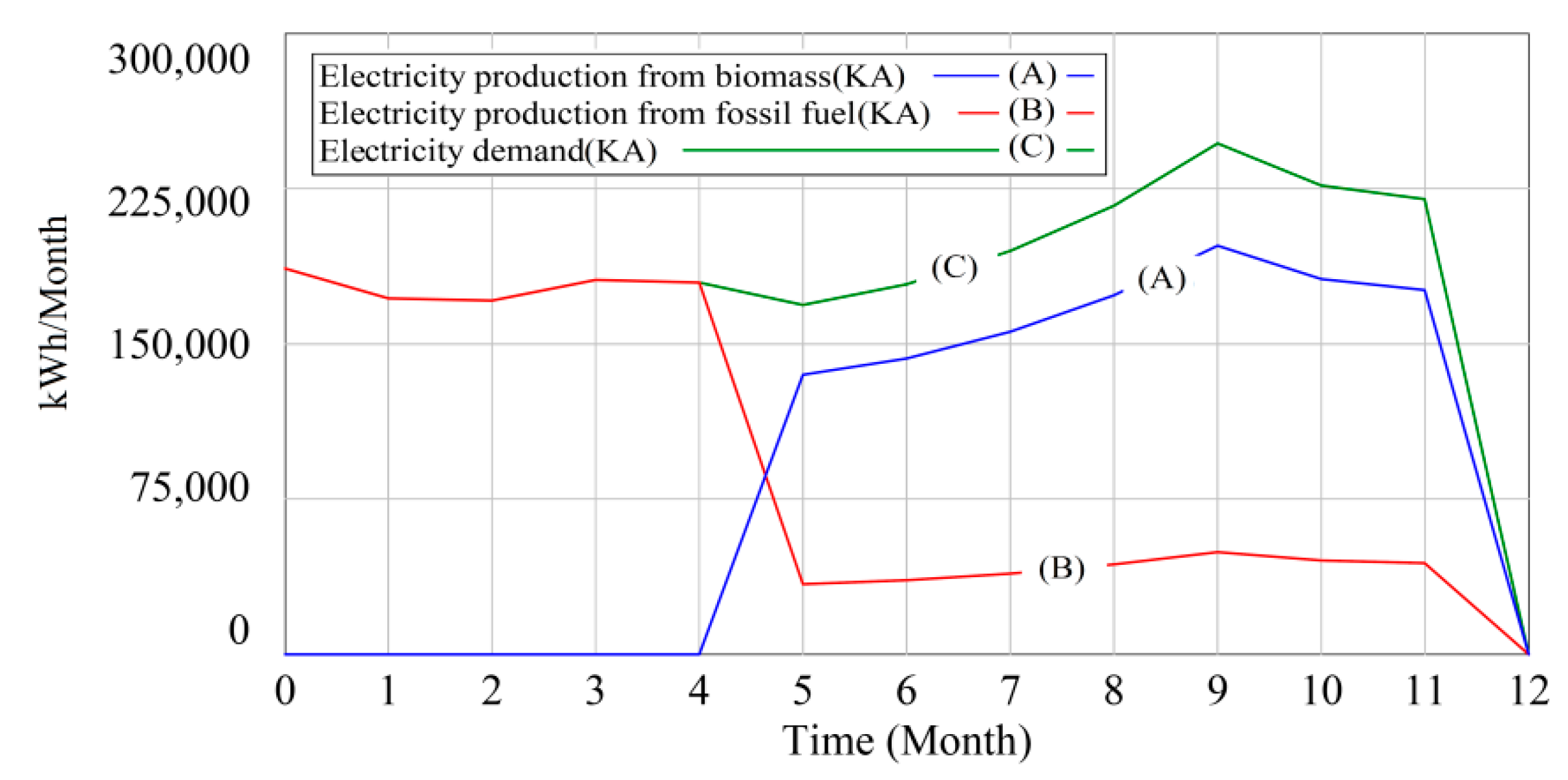
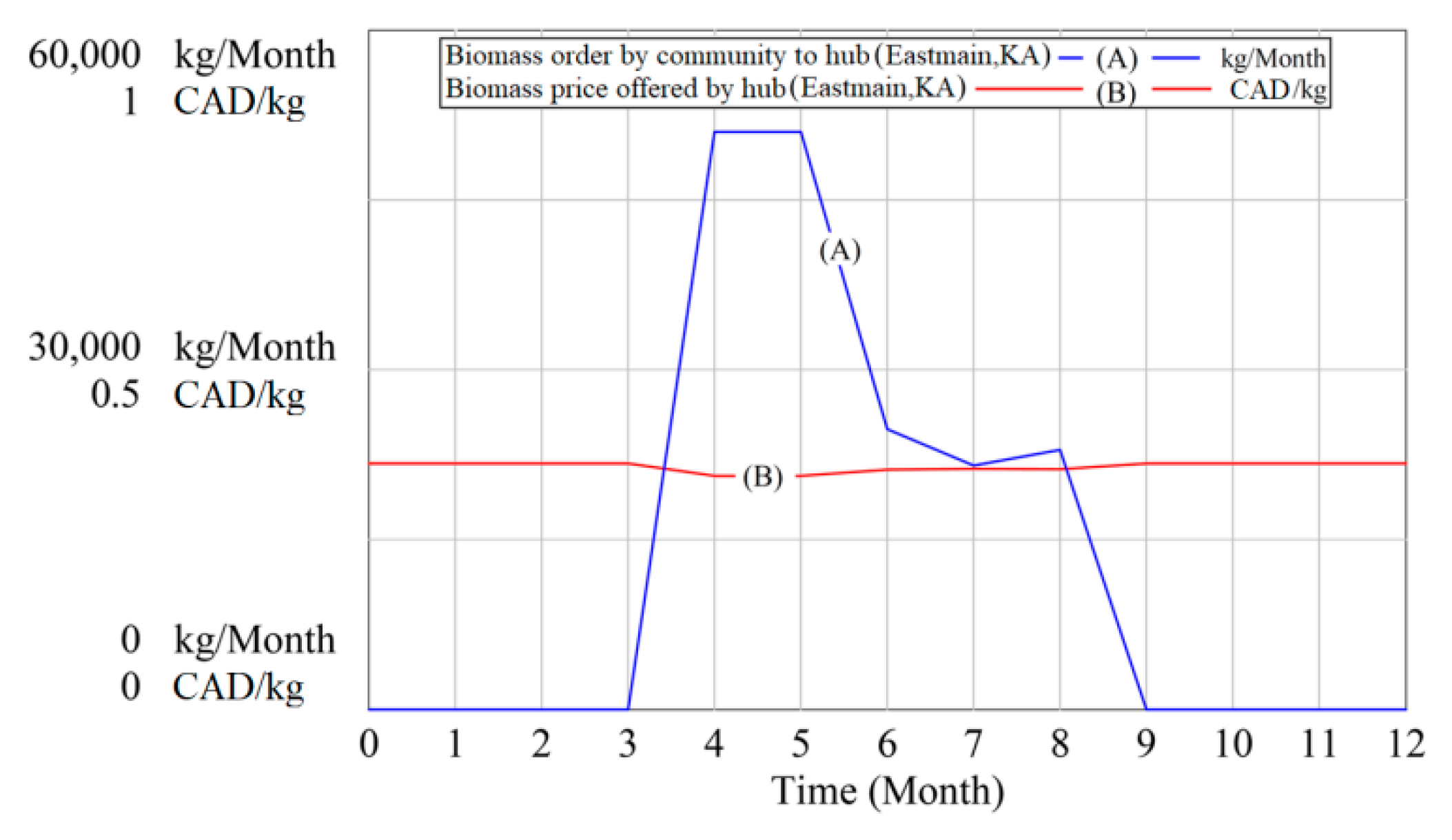
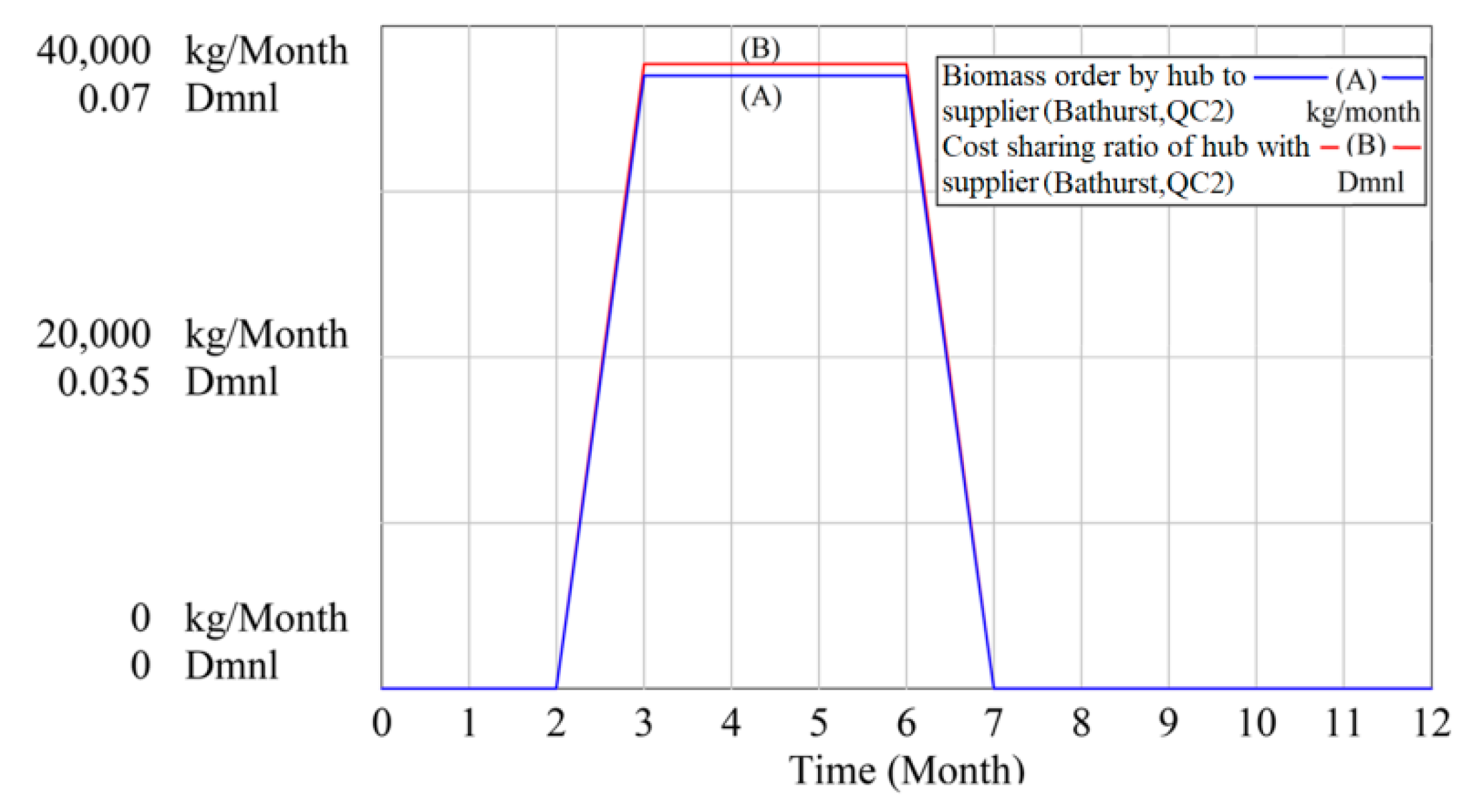
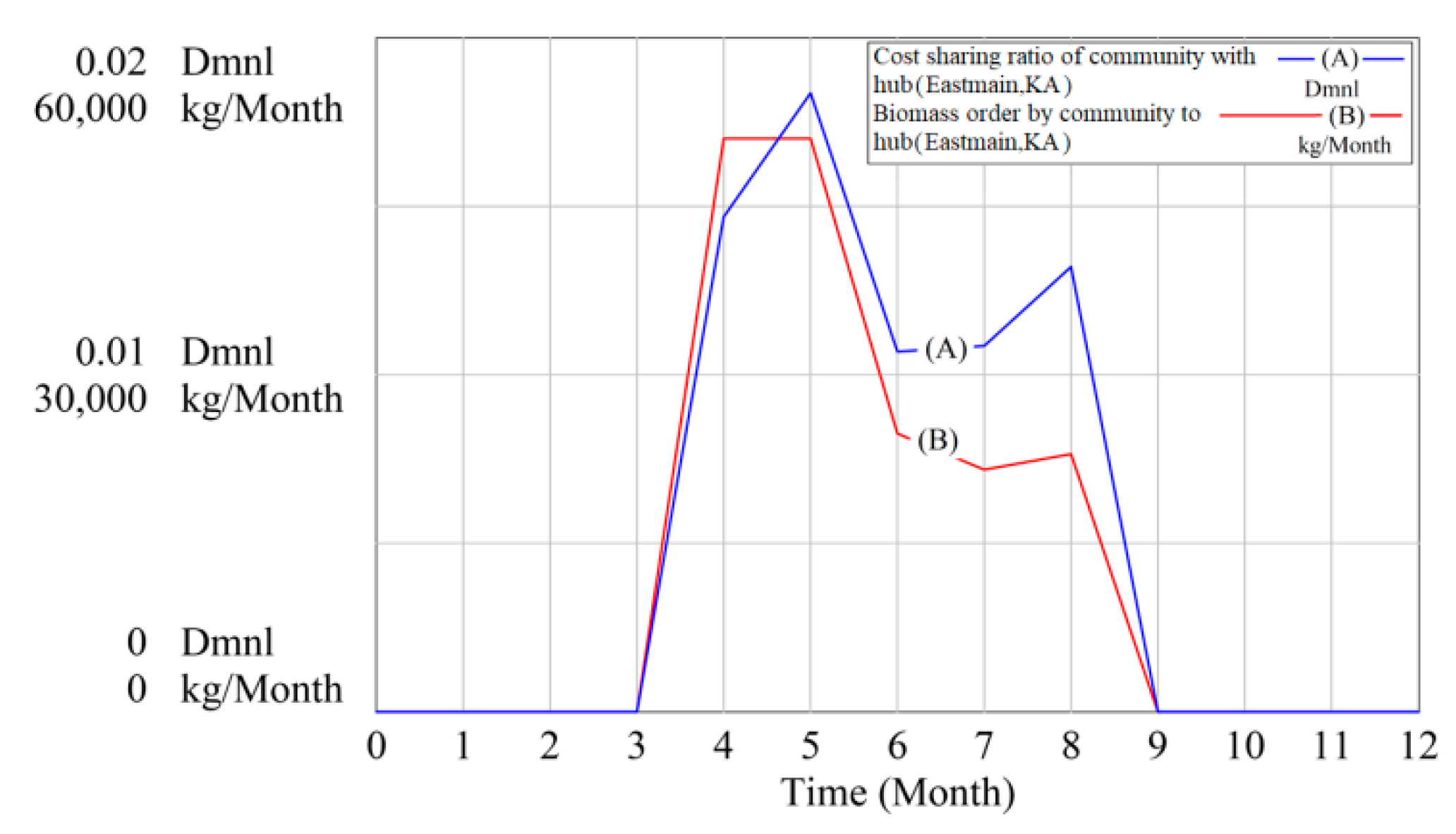
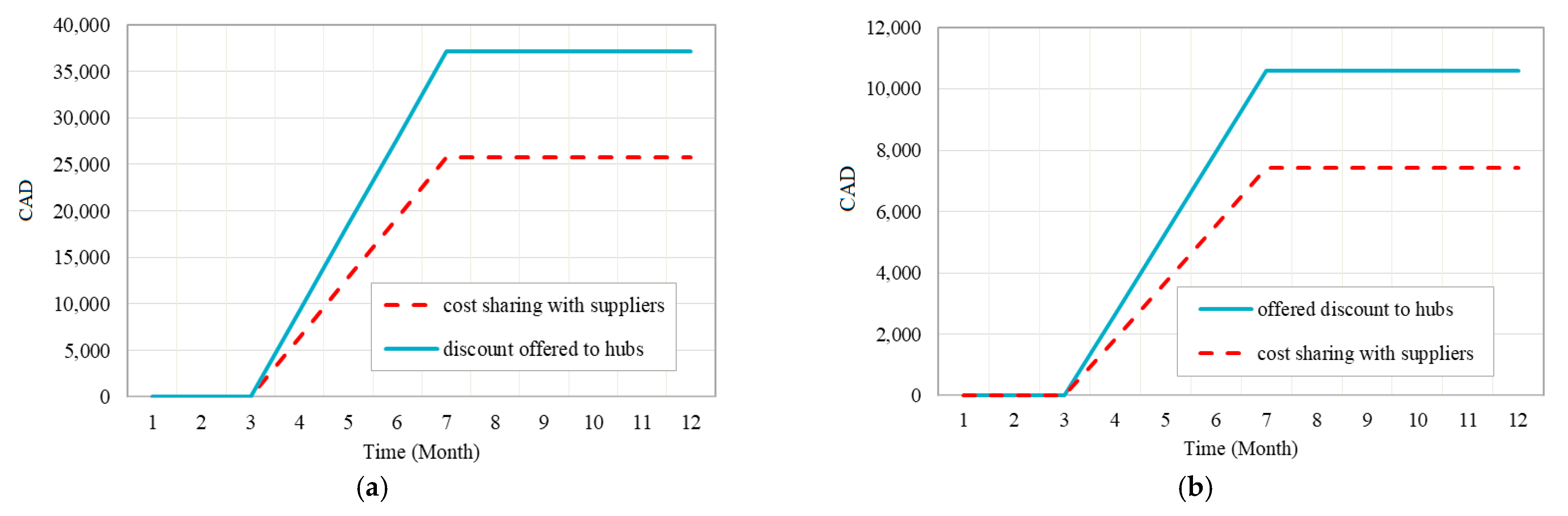
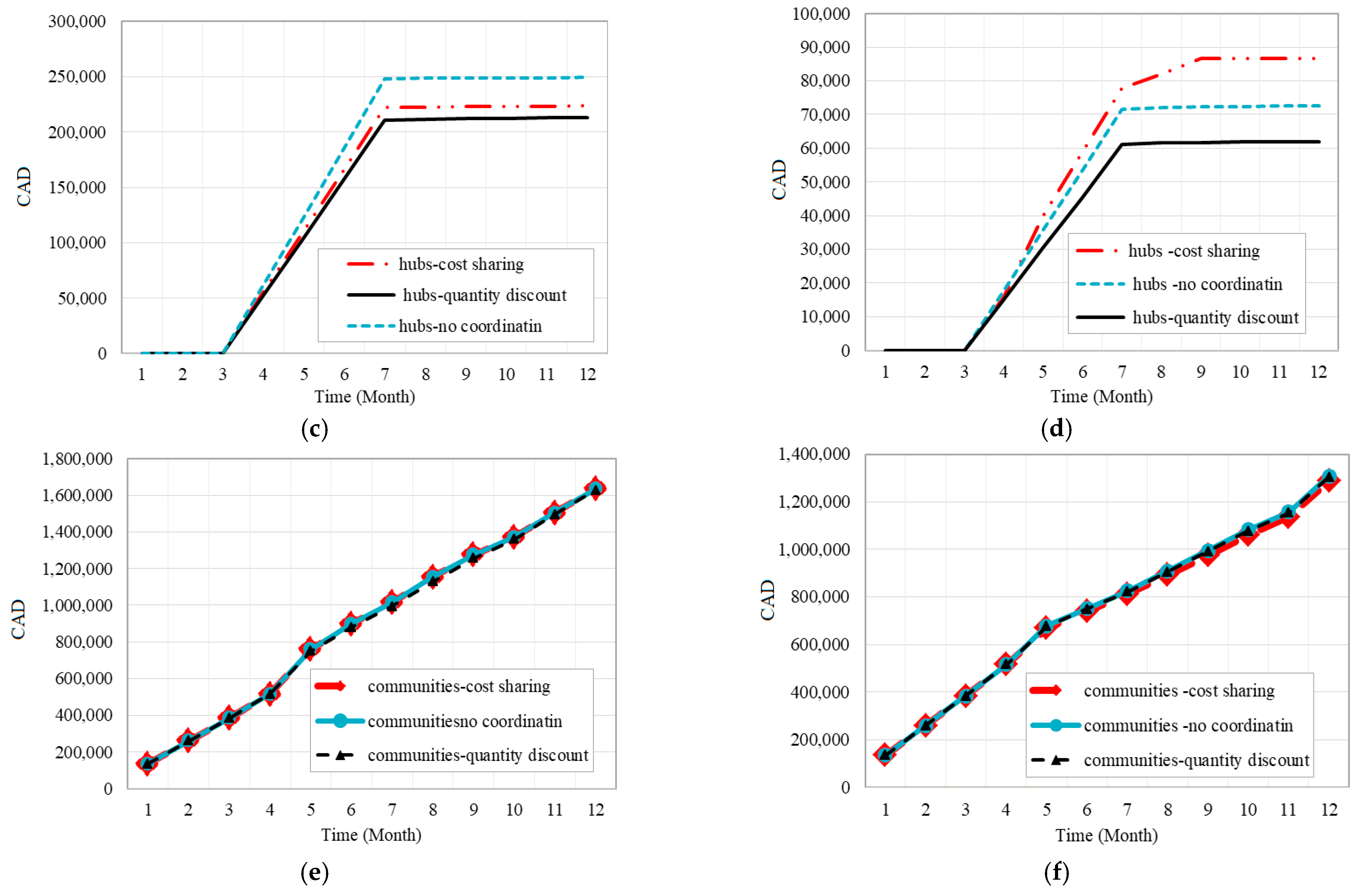
4.2. Results Analysis
4.3. Sensitivity Analysis and Discussion
- Opting for more expensive or cheaper biomass types: to investigate the impact of such scenarios, upper and lower bounds of biomass price (price with full discount and price without discount) are increased up to 40% and then decreased up to 60% while other parameters are kept fixed.
- Having larger or smaller storage capacities at hubs and communities: Storage capacities are increased and decreased by the same rate of 40% while fixing all other parameters to investigate the sensitivity to the capacity assumptions.
- Dealing with larger or smaller communities: Obviously, large communities are expected to demand more electricity compared with smaller communities. Accordingly, electricity demand is increased up to 70% to investigate the effect of larger communities. In addition, electricity demand is decreased by 40% to capture the effect of dealing with smaller communities. Note that all other parameters are kept fixed.
- Increasing the Number of Parties at Each Level of Supply Chain: In case of having more suppliers, total biomass supply amount could increase. Similarly, having more hubs and communities leads to increasing the total storage capacities as well as higher electricity demand.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Sets | Definition |
|---|---|
| i | Set of suppliers |
| j | Set of communities (end users) |
| k | Set of hubs |
| t | Time (months) |
| Stock Variables (and units) with Corresponding Players | |
| Community | |
| : Biomass stock level at community “j” at time “t”—(kg) | |
| : Cumulative cost of communities at time “t”—(CAD) | |
| Hub | |
| : Biomass stock level at hub “k” at time “t”—(kg) | |
| : Cumulative cost of hubs at time “t”—(CAD) | |
| : Cumulative total cost of supply chain at time “t”—(CAD) | |
| Flow Variables (and units) with Corresponding Players | |
| Community | |
| : Cost of communities at time “t”—(CAD/month) | |
| : Biomass order by community “j” to hub “k” at time “t”—(kg/month)—Decision variable | |
| : Biomass use for electricity production at community “j” at time “t”—(kg/month) | |
| Hub | |
| : Cost of hubs at time “t”—(CAD/month) | |
| : Biomass order by hub “k” to supplier “i” at time “t” (kg/month)—Decision variable | |
| : Total collective cost of supply chain at time “t”—(CAD/month) | |
| Auxiliary Variables (and units) with Corresponding Players | |
| Community | |
| : Order capacity to hub “k” by community “j” at time “t”—(kg/month) | |
| : Order ratio to hub “k” by community “j” at time “t”—(Dimensionless) | |
| : Electricity production from fossil fuel at community “j” at time “t”—(kWh/month) | |
| : Electricity production from biomass at community “j” at time “t”—(kWh/month) | |
| : Biomass distribution cost to communities at time “t”—(CAD/month) | |
| : Biomass storage cost at communities at time “t”—(CAD/month) | |
| : Electricity production cost from fossil fuel at time “t”—(CAD/month) | |
| : Fossil-based energy generation cost at time “t“—(CAD/month) | |
| : Biomass-to-electricity conversion cost at time “t”—(CAD/month) | |
| : Maximum cost sharing ratio of community “j” with hub “k”—(Dimensionless)—Decision variable | |
| : Cost sharing ratio of community “j” with hub “k” at time “t”—(Dimensionless)—Decision variable | |
| Hub | |
| : Order capacity to supplier “i” by hub “k” at time “t”—(kg/month) | |
| : Order ratio to supplier “i” by hub “k” at time “t”—(Dimensionless) | |
| : Biomass price offered by hub “k” to community “j” including delivery at time “t”—(CAD/kg)—Decision variable | |
| : Biomass purchasing cost at time “t”—(CAD/month) | |
| : Biomass storage cost at hubs at time “t”—(CAD/month) | |
| : Maximum cost sharing ratio of hub “k” with supplier “i”—(Dimensionless)—Decision variable | |
| : Cost sharing ratio of hub “k” with supplier “i” at time “t”—(Dimensionless)—Decision variable | |
| : Communities’ cost shared with hubs at time “t”—(CAD/month) | |
| Supplier | |
| : Biomass price offered by supplier “i” to hub “k” including delivery at time “t”—(CAD/kg)—Decision variable | |
| : Hubs’ cost shared with suppliers at time “t”—(CAD/month) | |
| Constant Variables (and units) with Corresponding Players | |
| Community | |
| : Capacity of biomass storage at community “j”—(kg) | |
| : Capacity of biomass-to-electricity conversion facility at community “j”—(kW) | |
| : Electricity demand in community “j” at time “t”—(kWh/month) | |
| : Loading factor of biomass-to-electricity conversion facility at community “j”—(Dimensionless) | |
| : holding cost at community “j” per unit of time—(CAD/kg) | |
| : Levelized electricity generation cost from diesel at community “j”—(CAD/kWh) | |
| : Levelized biomass-to-electricity conversion cost at community “j”—(CAD/kWh) | |
| : Biomass conversion ratio in community “j”—(kWh/kg) | |
| : Working hours per day—(h) | |
| : Working days—(day) | |
| : Time scale—(h) | |
| Hub | |
| : Holding cost at hub “k” per unit of time—(CAD/kg) | |
| : Capacity of hub “k”—(kg) | |
| : Biomass price of hub “k” (including delivery) without discount—(CAD/kg) | |
| : Biomass price of hub “k” (including delivery) with full discount—(CAD/kg) | |
| Supplier | |
| : Biomass supply capacity of supplier “i”—(kg) | |
| : Biomass price of supplier “i” with full discount—(CAD/kg) | |
| : Biomass price of supplier “i” with no discount—(CAD/kg) | |
- (1)
- Biomass stock at hub [hub] = INTEG (SUM (Biomass order by hub to supplier [supplier!, hub]) − SUM(Biomass order by community to hub[hub, community!]))
- (2)
- Biomass stock at community [community] = INTEG (SUM (Biomass order by community to hub [hub!, Community]) − Biomass use for electricity production at community[community]
- (3)
- Biomass order by hub to supplier[supplier, hub] = IF THEN ELSE(Time = 3:OR:Time = 4:OR:Time = 5:OR:Time = 6, Proportional delivery ratio of supplier to Biomass order by hub to supplier[supplier, hub] = hub[supplier, hub]*Order capacity to supplier[supplier, hub], 0)
- (4)
- Biomass order by community to hub[hubs, communities] = IF THEN ELSE (Time = 3:OR:Time = 4:OR:Time = 5:OR:Time = 6:OR:Time = 7:OR:Time = 8, Order capacity by community to hub[hub, community]*Proportional delivery ratio of hub to community[hub, community], 0)
- (5)
- Biomass use for electricity production at community[community] = max(min((min((Time scale*Capacity of biomass to electricity conversion facility[community]*Loading factor of biomass to electricity conversion facility[community]), Electricity demand[community])/Biomass conversion ratio[community]), Biomass stock at community[community]/TIME STEP),0)
- (6)
- Proportional delivery ratio of supplier to hub [supplier, hub] = Order ratio to suppliers [supplier, hubs]/Total delivery ratio of suppliers [supplier]
- (7)
- Total delivery ratio of supplier [supplier] = SUM (Order ratio to supplier [supplier, hub!])
- (8)
- 0< = Order ratio to supplier [supplier, hub] < = 1
- (9)
- Initial value of order ratio to supplier [supplier, hub] = 1
- (10)
- Order capacity to supplier [supplier, hub] = max (min ((Capacity of hub [hub] − Biomass stock at hub [hub])/TIME STEP, Supplier capacity [supplier]), 0)
- (11)
- Capacity of hub [hub] = 350,000, 400,000
- (12)
- Supplier capacity [supplier] = 33,300, 34,000, 34,700, 37,000, 35,000, 34,000
- (13)
- Total biomass purchase cost of hub [hub] = SUM (Biomass purchase cost [hub, supplier!])
- (14)
- Biomass purchase cost [hub, supplier] = Biomass price offered by supplier [supplier, hub]*Biomass order by hub to supplier [supplier, hub]
- (15)
- Biomass price offered by supplier [supplier, hub] = Biomass price of supplier with no discount [supplier] − (Biomass price of supplier with no discount [supplier]-Biomass price of supplier with full discount [Supplier])*((Biomass order by hub to supplier [supplier, hub])/Supplier capacity [supplier])
- (16)
- Biomass price of supplier with no discount [supplier] = 0.205, 0.21, 0.2, 0.215, 0.22, 0.22
- (17)
- Biomass storage cost at hub [hub] = (Biomass stock at hub [hub]*Holding cost at hub per unit of time [hub])/TIME STEP
- (18)
- Holding cost at hub per unit of time [hub] = 0.002, 0.0015
- (19)
- Proportional delivery ratio of hub to community [hub, community] = Order ratio to hub [hub, community]/Total delivery ratio of hub [hub]
- (20)
- Total delivery ratio of hub [hub] = SUM (Order ratio to hub [hub, community!])
- (21)
- 0< = Order ratio to hub [hub, community] < = 1
- (22)
- Initial value of Order ratio to hub [hub, community = 1
- (23)
- Order capacity by community to hub [hub, community] = max (min ((Capacity of biomass storage at community [community] − Biomass stock at community [Community]), Biomass stock at hub [hub]), 0)/TIME STEP
- (24)
- Capacity of biomass storage at community [community] = 200,000, 200,000, 1.5 × 106
- (25)
- Biomass distribution cost to community [community] = SUM (Biomass distribution cost from hub to community [hub!, community])
- (26)
- Biomass distribution cost from hub to community [hub, community] = (Biomass price offered by hub [hub, community]*Biomass order by community to hub [hub, community])
- (27)
- Biomass price offered by hub [hub, community] = Biomass price of hub with no discount [hub] − (Biomass price of hub with no discount [hub] − Biomass price of hub with full discount [hub])*(Biomass order by community to hub [hub, community]/(Capacity of hub [hub]/TIME STEP))
- (28)
- Biomass price of hub with full discount [hub] = 0.235, 0.266
- (29)
- Biomass price of hub with no discount [hub] = 0.362, 0.409
- (30)
- Biomass storage cost at community [community] = (Biomass stock at community [community]*Holding cost at community [community])/TIME STEP
- (31)
- Electricity production cost from biomass [community] = Electricity production from biomass [community]*Levelized biomass to electricity conversion cost [community]
- (32)
- Electricity production cost from fossil fuel [community] = Electricity production from fossil fuel [community]*Levelized electricity generation cost from diesel [community]
- (33)
- Electricity production from biomass [community] = Biomass conversion ratio [community]*Biomass use for electricity production at community [community]*Loading factor of biomass to electricity conversion facility [community]
- (34)
- Electricity production from fossil fuel [community] = Electricity demand [community]-Electricity production from biomass [community]
- (35)
- Cumulative cost of hubs = INTEG (SUM (Cost of hubs [hub!]))
- (36)
- Initial value = 0
- (37)
- Cumulative cost of communities = SUM (Cost of communities [community!])
- (38)
- Initial value = 0
- (39)
- Total collective cost of supply chain = SUM (Cost of communities [community!]) + SUM (Cost of hubs [hub!])
- (40)
- Cumulative total cost = INTEG (Total collective cost of supply chain)
- (41)
- Levelized biomass to electricity conversion cost [community] = 0.046, 0.044, 0.048
- (42)
- Levelized electricity generation cost from diesel [community] = 0.208, 0.215, 0.207
- (43)
- Biomass conversion ratio [community] = 4.7, 4.8, 4.6
- (44)
- Capacity of biomass to electricity conversion facility [community] = 500, 500, 500
- (45)
- Working days = 30
- (46)
- Hours = 24
- (47)
- TIME STEP = 1
- (1)
- Biomass stock at hub [hub] = INTEG (SUM (Biomass order by hub to supplier [supplier!, hub]) − SUM(Biomass order by community to hub[hub, community!]))
- (2)
- Biomass stock at community [community] = INTEG (SUM (Biomass order by community to hub [hub!, Community])-Biomass use for electricity production at community[community]
- (3)
- Biomass order by hub to supplier[supplier, hub] = IF THEN ELSE (Time = 3:OR:Time = 4:OR:Time = 5:OR:Time = 6, proportional delivery ratio of supplier to hub[supplier, hub]*Order capacity to supplier[supplier, hub], 0)
- (4)
- Biomass order by community to hub[hub, community] = IF THEN ELSE (Time = 3:OR:Time = 4:OR:Time = 5:OR:Time = 6:OR:Time = 7:OR:Time = 8, Order capacity by community to hub[hub, community]*proportional delivery ratio of hub to community[hub, community] , 0)
- (5)
- Biomass use for electricity production at community [community] = SUM (Biomass order by community to hub [hub!, community]) − Biomass use for electricity production at community[community]
- (6)
- Proportional delivery ratio of supplier to hub [suppliers, hubs] = Order ratio to suppliers [supplier, hubs]/Total delivery ratio of suppliers [supplier]
- (7)
- Total delivery ratio of supplier [supplier] = SUM (Order ratio to supplier [supplier, hub!])
- (8)
- 0< = Order ratio to supplier [supplier, hub] < = 1
- (9)
- Initial value of order ratio to supplier [supplier, hub] = 1
- (10)
- Order capacity to supplier [supplier, hub] = max (min ((Capacity of hub [hub]-Biomass stock at hub [hub])/TIME STEP, Supplier capacity [supplier]), 0)
- (11)
- Capacity of hub [hub] = 350,000, 400,000
- (12)
- Supplier capacity [supplier] = 33,300, 34,000, 34,700, 37,000, 35,000, 34,000
- (13)
- Total biomass purchase cost of hub [hub] = SUM (Biomass purchase cost [hub, supplier!])
- (14)
- Biomass purchase cost [hub, supplier] = Biomass price offered by supplier [supplier]*Biomass order by hub to supplier [supplier, hub]
- (15)
- Biomass price offered by supplier [supplier] = 0.205, 0.21, 0.2, 0.215, 0.22, 0.22
- (16)
- Biomass storage cost at hub [hub] = (Biomass stock at hub [hub]*Holding cost at hub per unit of time [hub])/TIME STEP
- (17)
- Holding cost at hub per unit of time [hub] = 0.002, 0.0015
- (18)
- Cost of hubs could be shared with suppliers [hub] = Biomass storage cost at hub [hub] + Total biomass purchase cost of hub [hub]
- (19)
- Hubs’ cost shared with suppliers [hub, supplier] = Cost of hubs could be shared with suppliers [hub]*Cost sharing ratio between Hub and supplier [hub, supplier]
- (20)
- Cost sharing ratio between Hub and supplier [hub, supplier] = Maximum cost sharing ratio between Hub [hub]*(Biomass order by hub to supplier [supplier, hub]/Supplier capacity [supplier])
- (21)
- 0< = Maximum cost sharing ratio between Hub [hub] < = 1
- (22)
- Initial value in the model = 0
- (23)
- Proportional delivery ratio of hub to community [hub, community] = Order ratio to hub [hub, community]/Total delivery ratio of hub [hub]
- (24)
- Total delivery ratio of hub [hub] = SUM (Order ratio to hub [hub, community!])
- (25)
- 0< = Order ratio to hub [hub, community] < = 1
- (26)
- Initial value of Order ratio to hub [hub, community = 1
- (27)
- Order capacity by community to hub [hub, community] = max (min ((Capacity of biomass storage at community [community] − Biomass stock at community [Community]), Biomass stock at hub [hub]), 0)/TIME STEP
- (28)
- Capacity of biomass storage at community [community] = 200,000, 200,000, 1.5 × 106
- (29)
- Biomass distribution cost to community [community] = SUM (Biomass distribution cost from hub to community [hub!, community])
- (30)
- Biomass distribution cost from hub to community [hub, community] = (Biomass price offered by hub [hub, community]*Biomass order by community to hub [hub, community])
- (31)
- Biomass price offered by hub [hub] = 0.362, 0.409
- (32)
- Biomass storage cost at community [community] = (Biomass stock at community [community]*Holding cost at community [community])/TIME STEP
- (33)
- Electricity production cost from biomass [community] = Electricity production from biomass [community]*Levelized biomass to electricity conversion cost [community]
- (34)
- Electricity production cost from fossil fuel [community] = Electricity production from fossil fuel [community]*Levelized electricity generation cost from diesel [community]
- (35)
- Electricity production from biomass [community] = Biomass conversion ratio [community]*Biomass use for electricity production at community [community]*Loading factor of biomass to electricity conversion facility [community]
- (36)
- Electricity production from fossil fuel [community] = Electricity demand [community] − Electricity production from biomass [community]
- (37)
- Cost of communities could be shared with hubs[community] = Biomass distribution cost to community[community] + Biomass storage cost at community[community] + Electricity production cost from biomass[community] + Electricity production cost from fossil fuel[community]
- (38)
- Cost of communities could be shared with hubs[community] = Biomass distribution cost to community[community] + Biomass storage cost at community[community] + Electricity production cost from biomass[community] + Electricity production cost from fossil fuel[community]
- (39)
- Communities’ cost shared with hubs [community, hub] = Cost of communities could be shared with hubs [community]*Cost sharing ratio between community and hub [community, hub]
- (40)
- Cost sharing ratio between community and hub [community, hub] = (Biomass order by community to hub [hub, community]/Capacity of hub [hub])*Maximum cost sharing ratio between community and hub [community]*Time
- (41)
- 0< = Maximum cost sharing ratio between community and hub [community] < = 1
- (42)
- Initial value of cost sharing ratio between community and hub [community] = 0
- (43)
- Cost of hubs[hub] = Total biomass purchase cost of hub[hub] + Biomass storage cost at hub[hub] + SUM(Communities’ cost shared with hubs[community!, hub])-SUM( Hubs’ cost shared with suppliers[hub, supplier!])
- (44)
- Cumulative cost of hubs = INTEG (SUM (Cost of hubs [hub!]))
- (45)
- Cost of communities [community] = Biomass distribution cost to community[community] + Electricity production cost from biomass[community] + Electricity production cost from fossil fuel[community] + Biomass storage cost at community[community] − SUM(Communities’ cost shared with hubs[community, hub!])
- (46)
- Cumulative cost of communities = INTEG [SUM (Cost of communities [community!])]
- (47)
- Total collective cost of supply chain = SUM (Cost of communities [community!]) + SUM (Cost of hubs [hub!])+SUM (Hubs’ cost shared with suppliers [hub!, supplier!])
- (48)
- Cumulative total collective cost = INTEG (Total collective cost of supply chain)
- (49)
- Initial value = 0
- (50)
- Levelized biomass to electricity conversion cost [community] = 0.046, 0.044, 0.048
- (51)
- Levelized electricity generation cost from diesel [community] = 0.208, 0.215, 0.207
- (52)
- Biomass conversion ratio [community] = 4.7, 4.8, 4.6
- (53)
- Capacity of biomass to electricity conversion facility [community] = 500, 500, 500
- (54)
- Working days = 30
- (55)
- Hours = 24
- (56)
- TIME STEP = 1
References
- Ghaderi, H.; Pishvaee, M.S.; Moini, A. Biomass supply chain network design: An optimization-oriented review and analysis. Ind. Crops Prod. 2016, 94, 972–1000. [Google Scholar] [CrossRef]
- Fan, K.; Li, X.; Wang, L.; Wang, M. Two-stage supply chain contract coordination of solid biomass fuel involving multiple suppliers. Comput. Ind. Eng. 2019, 135, 1167–1174. [Google Scholar] [CrossRef]
- Akhtari, S.; Sowlati, T.; Griess, V.C. Integrated strategic and tactical optimization of forest-based biomass supply chains to consider medium-term supply and demand variations. Appl. Energy 2018, 213, 626–638. [Google Scholar] [CrossRef]
- Mafakheri, F.; Nasiri, F. Modeling of biomass-to-energy supply chain operations: Applications, challenges and research directions. Energy Policy 2014, 67, 116–126. [Google Scholar] [CrossRef]
- Nasiri, F.; Zaccour, G. An exploratory game-theoretic analysis of biomass electricity generation supply chain. Energy Policy 2009, 37, 4514–4522. [Google Scholar] [CrossRef]
- Kaygusuz, K. Climate change and biomass energy for sustainability. Energy Sources Part B Econ. Plan. Policy 2010, 5, 133–146. [Google Scholar] [CrossRef]
- Mafakheri, F.; Adebanjo, D.; Genus, A. Coordinating Biomass Supply Chains for Remote Communities: A Comparative Analysis of Non-cooperative and Cooperative Scenarios. Int. J. Prod. Res. 2020, 1–37. [Google Scholar] [CrossRef]
- Santosh Raikar, S.A. (Ed.) 13-Renewable Energy Finance in the International Context; Renewable Energy Finance, Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Mansuy, N.; Staley, D.; Taheriazad, L. Woody Biomass Mobilization for Bioenergy in a Constrained Landscape: A Case Study from Cold Lake First Nations in Alberta, Canada. Energies 2020, 13, 6289. [Google Scholar] [CrossRef]
- Natural Resources Canada. Clean Energy for Rural and Remote Communities: BioHeat, Demonstration & Deployment Program Streams. 2018. Available online: https://www.nrcan.gc.ca/reducingdiesel (accessed on 12 May 2021).
- Balaman, Ş.Y. Biomass-Based Supply Chains and Logistics Networks. In Decision-Making for Biomass-Based Production Chains; Academic Press: Cambridge, MA, USA, 2019; pp. 55–75. [Google Scholar]
- Ba, B.H.; Prins, C.; Prodhon, C. Models for optimization and performance evaluation of biomass supply chains: An Operations Research perspective. Renew. Energy 2016, 87, 977–989. [Google Scholar] [CrossRef]
- Chan, H.K.; Chan, F.T.S. A review of coordination studies in the context of supply chain dynamics. Int. J. Prod. Res. 2010, 48, 2793–2819. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, J.; Yi, W.; Cai, H.; Li, Y.; Su, Z. A Game-Theoretic Analysis of Incentive Effects for Agribiomass Power Generation Supply Chain in China. Energies 2021, 14, 546. [Google Scholar] [CrossRef]
- Wang, L.; Watanabe, T. A Stackelberg Game Theoretic Analysis of Incentive Effects under Perceived Risk for China’s Straw-Based Power Plant Supply Chain. Energies 2016, 9, 455. [Google Scholar] [CrossRef]
- Ye, F.; Li, Y.; Yang, Q. Designing coordination contract for biofuel supply chain in China. Resour. Conserv. Recycl. 2018, 128, 306–314. [Google Scholar] [CrossRef]
- Chintapalli, P.; Disney, S.M.; Tang, C.S. Coordinating Supply Chains via Advance-Order Discounts, Minimum Order Quantities, and Delegations. Prod. Oper. Manag. 2017, 26, 2175–2186. [Google Scholar] [CrossRef]
- Frascatore, M.R.; Mahmoodi, F. Cost-sharing contracts and efficiency in a two-stage supply chain. Int. J. Integr. Supply Manag. 2011, 6, 3–19. [Google Scholar] [CrossRef]
- Liu, R.; Dan, B.; Zhou, M.; Zhang, Y. Coordinating contracts for a wind-power equipment supply chain with joint efforts on quality improvement and maintenance services. J. Clean. Prod. 2020, 243, 118616. [Google Scholar] [CrossRef]
- Jiang, L.; Wang, Y.; Liu, D. Logistics cost sharing in supply chains involving a third-party logistics provider. Cent. Eur. J. Oper. Res. 2016, 24, 207–230. [Google Scholar] [CrossRef]
- Forrester, J.W. Industrial Dynamics. J. Oper. Res. Soc. 1997, 48, 1037–1041. [Google Scholar] [CrossRef]
- Bala, B.K.; Arshad, F.M.; Noh, K.M. System Dynamics. Modelling and Simulation; Springer: Singapore, 2017. [Google Scholar]
- Angerhofer, B.J.; Angelides, M.C. System Dynamics Modelling in Supply Chain Management: Research Review. In Proceedings of the 2000 Winter Simulation Conference Proceedings (Cat. No. 00CH37165), Orlando, FL, USA, 10–13 December 2000; IEEE: Piscataway, NJ, USA, 2000; pp. 342–351. [Google Scholar]
- Bhushi, U.M.; Javalagi, C.M. System Dynamics application to Supply Chain Management: A review. In Proceedings of the 2004 IEEE International Engineering Management Conference (IEEE Cat. No.04CH37574), Singapore, 18–21 October 2004; pp. 1244–1248. [Google Scholar]
- Bala, B.K.; Bhuiyan, M.G.K.; Alam, M.M.; Arshad, F.M.; Sidique, S.F.; Alias, E.F. Modelling of supply chain of rice in Bangladesh. Int. J. Syst. Sci. Oper. Logist. 2017, 4, 181–197. [Google Scholar] [CrossRef]
- Mafakheri, F.; Nasiri, F. Revenue sharing coordination in reverse logistics. J. Clean. Prod. 2013, 59, 185–196. [Google Scholar] [CrossRef]
- Ahmad, S.; Tahar, R.M.; Muhammad-Sukki, F.; Munir, A.B.; Abdul Rahim, R. Application of system dynamics approach in electricity sector modelling: A review. Renew. Sustain. Energy Rev. 2016, 56, 29–37. [Google Scholar] [CrossRef]
- Ricardo Saavedra, M.M.; Cristiano, C.H.; Francisco, F.G. Sustainable and renewable energy supply chain: A system dynamics overview. Renew. Sustain. Energy Rev. 2018, 82, 247–259. [Google Scholar] [CrossRef]
- Nasiri, F.; Mafakheri, F.; Adebanjo, D.; Haghighat, F. Modeling and analysis of renewable heat integration into non-domestic buildings—The case of biomass boilers: A whole life asset-supply chain management approach. Biomass Bioenergy 2016, 95, 244–256. [Google Scholar] [CrossRef]
- Azadeh, A.; Arani, H.V. Biodiesel supply chain optimization via a hybrid system dynamics-mathematical programming approach. Renew. Energy 2016, 93, 383–403. [Google Scholar] [CrossRef]
- Tama, I.P.; Akbar, Z.; Eunike, A. Implementation of system dynamic simulation method to optimize profit in supply chain network of vegetable product. IOP Conf. Ser. Mater. Sci. Eng. 2018, 337, 012014. [Google Scholar] [CrossRef]
- Feng, Y. System Dynamics Modeling for Supply Chain Information Sharing. Phys. Procedia 2012, 25, 1463–1469. [Google Scholar] [CrossRef]
- Khaji, M.R.; Shafaei, R. A system dynamics approach for strategic partnering in supply networks. Int. J. Comput. Integr. Manuf. 2011, 24, 106–125. [Google Scholar] [CrossRef]
- Rendón-Sagardi, M.A.; Sánchez-Ramirez, C.; Cortás-Robles, G.; Alor-Hernández, G.; Moncayo-Martínez, L.A. Dynamic Evaluation of Production Policies: Improving the Coordination of an Ethanol Supply Chain. J. Appl. Res. Technol. 2014, 12, 724–733. [Google Scholar] [CrossRef]
- Spelter, H.; Toth, D. North America’s Wood Pellet Sector; United States Department of Agriculture: Madison, WI, USA, 2009; Volume FPL-RP-656, p. 23. [Google Scholar]
- Mobini, M.; Meyer, J.C.; Trippe, F.; Sowlati, T.; Fröhling, M.; Schultmann, F. Assessing the integration of torrefaction into wood pellet production. J. Clean. Prod. 2014, 78, 216–225. [Google Scholar] [CrossRef]
- Mobini, M.; Sowlati, T.; Sokhansanj, S. A simulation model for the design and analysis of wood pellet supply chains. Appl. Energy 2013, 111, 1239–1249. [Google Scholar] [CrossRef]
- Forrester, J.W. System dynamics, systems thinking, and soft OR. Syst. Dyn. Rev. 1994, 10, 245–256. [Google Scholar] [CrossRef]
- Bayer, S. Systems Thinking and Modeling for a Complex World; McGraw-Hill Education: New York, NY, USA, 2004; Volume 34. [Google Scholar]
- VENSIM. The Ventana Simulation Environment (VENSIM)—Version 8.1.2; Ventana Syst. Inc.: Harvard, MA, USA, 2020. [Google Scholar]
- National Energy Board. Canada’s Energy Future 2016 Energy Supply and Demand Projections to 2040; National Energy Board: Calgary, AB, Canada, 2016; pp. 1–9. [Google Scholar]
- Besset, D.H. Object-Oriented Implementation of Numerical Methods: An Introduction with Java & Smalltalk; Square Bracket Associates: Kehrsatz, Switzerland, 2001. [Google Scholar]
- Vazifeh, Z.; Mafakheri, F.; An, C. Biomass supply chain coordination for remote communities: A game-theoretic modeling and analysis approach. Sustain. Cities Soc. 2021, 69, 102819. [Google Scholar] [CrossRef]
- International Energy Agency. Options for Increased Use of Ash from Biomass Combustion and Co-firing. 2018. Available online: https://www.ieabioenergy.com/wp-content/uploads/2019/02/IEA-Bioenergy-Ash-management-report-revision-5-november.pdf (accessed on 12 May 2021).












Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khoddami, S.; Mafakheri, F.; Zeng, Y. A System Dynamics Approach to Comparative Analysis of Biomass Supply Chain Coordination Strategies. Energies 2021, 14, 2808. https://doi.org/10.3390/en14102808
Khoddami S, Mafakheri F, Zeng Y. A System Dynamics Approach to Comparative Analysis of Biomass Supply Chain Coordination Strategies. Energies. 2021; 14(10):2808. https://doi.org/10.3390/en14102808
Chicago/Turabian StyleKhoddami, Shohre, Fereshteh Mafakheri, and Yong Zeng. 2021. "A System Dynamics Approach to Comparative Analysis of Biomass Supply Chain Coordination Strategies" Energies 14, no. 10: 2808. https://doi.org/10.3390/en14102808
APA StyleKhoddami, S., Mafakheri, F., & Zeng, Y. (2021). A System Dynamics Approach to Comparative Analysis of Biomass Supply Chain Coordination Strategies. Energies, 14(10), 2808. https://doi.org/10.3390/en14102808







