Fuzzy Logic Approach to Dissolved Gas Analysis for Power Transformer Failure Index and Fault Identification

Abstract

This research focuses on problem identification due to faults in power transformers during operation by using dissolved gas analysis such as key gas, IEC ratio, Duval triangle techniques, and fuzzy logic approaches. Then, the condition of the power transformer is evaluated in terms of the percentage of failure index and internal fault determination. Fuzzy logic with the key gas approach was used to calculate the failure index and identify problems inside the power transformer. At the same time, the IEC three-gas ratio and Duval triangle are subsequently applied to confirm the problems in different failure types covering all possibilities inside the power transformer. After that, the fuzzy logic system was applied and validated with DGA results of 244 transformers as reference cases with satisfactory accuracy. Two transformers were evaluated and practically confirmed by the investigation results of an un-tanked power transformer. Finally, the DGA results of a total of 224 transformers were further evaluated by the fuzzy logic system. This fuzzy logic is a smart, accurate tool for automatically identifying faults occurring within transformers. Finally, the recommendation of maintenance strategy and time interval is proposed for effective planning to minimize the catastrophic damage, which could occur with the power transformer and its network.

1. Introduction

The power transformer is a key component in power transmission and distribution systems. During operation, it might be deteriorated by both normal and abnormal conditions, including overloading, aging, and degradation of paper-oil insulation, internal arcing and partial discharge (PD), short circuit, etc. Survey results [1] show damages within power transformers including on-load tap changer (OLTC), winding and iron core, bushing, tank, and other related damages. Therefore, to prevent failure and to maintain the power transformer in the satisfactorily working condition, several traditional and nontraditional diagnostic methods have been performed to assess the condition [2,3]. The traditional diagnostic methods are dissolved gas analysis, oil quality, power factor testing, winding resistance measurement, turn ratio, and thermography, while the nontraditional diagnostic methods are partial discharge measurement, dielectric spectroscopy, frequency response analysis, tap changer monitoring, and internal temperature measurement. After obtaining the test results from various diagnostic methods mentioned above, the data has been further evaluated to assess the condition of the power transformer, mainly based on health index value by applying a scoring and weighting algorithm [4]. However, this traditional health index determination has some drawbacks because it requires many test results from transformer electrical tests and oil diagnostics to complete the evaluation process, as well as the influence of weight determination on the uncertainty of the obtained health index result [4].

Several defects can occur with a power transformer and lead to a shorter transformer life, malfunction, unplanned outage, etc., which directly affect the increase in the amount of specific gases dissolved in insulating oil within the transformer tank, such as methane (CH₄), ethane (C₂H₆), acetylene (C₂H₂), and ethylene (C₂H₄), as well as other gases such as carbon monoxide (CO), carbon dioxide (CO₂), and hydrogen (H₂). The dissolved gas analysis (DGA) with insulating oil can be implemented to identify the condition, interpret faults, and provide early warning of some problems inside the transformer. Many DGA techniques are widely used to diagnose significant faults; those techniques include electrical discharges, PD, electrical arcing, and thermal fault [5,6,7,8]. Reference [9] proposes the failure analysis based on the dissolved key gas concentration, total dissolved combustible gases (TDCG), and key gas. In [10], the Dörnenburg ratio method was introduced to classify the occurring problem as overheating, electrical discharge, and arcing. In [11], the Rogers ratio method was suggested to identify six fault types occurring in the insulating oil. In [12], IEC gas ratio was proposed to determine PD of high energy, low and high energy discharge, and thermal faults, however, it did not identify failure by paper insulation because it ignored CO and CO₂. In [13,14,15,16], the Duval triangle technique was proposed to investigate the causes of faults and failure causes. In [17,18,19,20,21], most of the methods performed DGA with a simple tool to find out the incipient fault. However, it is inconvenient and time-consuming for industrial applications due to the complex analytical process. Hence, artificial intelligence techniques have been proposed to develop more accurate diagnostic tools based on DGA data [22]. In [23,24,25,26,27,28,29,30,31,32], some artificial intelligence techniques such as fuzzy logic, artificial neural network and support vector machines have been introduced for fault classification with nearly equal performance without determination of problem severity. Moreover, the artificial neural network technique requires a huge amount of data for training to make it recognize the fault types with less knowledge on the evaluation process. The fuzzy logic method is also an effective method developed to determine the answer, where the boundary is not explicit. It operates by designing the membership function and fuzzy sets appropriated to a specific problem. The most important step is tuning on ranges of the proposed fuzzy sets to obtain the correct answer with logical reason leading to a precise output. Therefore, the fuzzy logic has been adopted for DGA and fault severity analysis in this work.

As a result, this paper adopts and purposes the fuzzy logic approach to three DGA methods: key gas, IEC ratio, and Duval triangle methods to identify possible faults inside the power transformer such as overheat oil and paper, partial discharge, and arcing classified precisely into different ranges of severity. Moreover, the proposed fuzzy logic applied to the key gas method is a novelty used to determine failure index (%FI) and to identify the severity of faults, facilitates the specification of the proper maintenance actions to prevent the failure. In addition, the proposed combination of IEC ratio and the Duval triangle method is implemented to improve the ability of fault determination up to ten possible faults inside the power transformer. With these proposed fuzzy logic techniques with simulation software, this power transformer diagnostic system is faster, more accurate, and less time-consuming. The DGA test results of 112 power transformers were examined, while two power transformers were thoroughly investigated concerning their internal components.

2. Dissolved Gas Analysis

Three DGA methods including key gas, IEC ratio, and the Duval triangle method were used to investigate abnormality and fault inside a power transformer. In this paper, three DGA methods were simultaneously applied together to diagnose different faults within power transformers for more accurate and reliable results. However, before applying the three mentioned methods, one of the key gases must fall into condition “2” as a moderate condition of the dissolved key gas concentration limit technique [9] as shown in

Table 1. Dissolved key gas concentration and condition classification.

Condition		Dissolved Key Gas Concentration Limit (ppm)
		H2	CH4	C2H2	C2H4	C2H6	CO	CO2
1	good	0–100	0–120	0–1	0–50	0–65	0–350	0–2500
2	moderate	101–700	121–400	2–9	51–100	66–100	351–570	2500–4000
3	poor	701–1800	401–1000	10–35	101–200	101–150	571–1400	4001–10,000
4	bad	>1800	>1000	>35	>200	>150	>1400	>10,000

, otherwise, the fault investigation will not be requested. The dissolved key gas concentration limit technique can identify the severity of faults as good, moderate, poor, and bad condition.

2.1. Key Gas Analysis

The key gas method [9] was used to identify faults inside the power transformer. Key gases included H₂, C₂H₆, C₂H₂, C₂H₄, CH₄, CO, and CO₂. Pairs of key gases indicated four types of faults, as shown in

Table 2. Fault identification using the key gas method.

Pair No.	Pair of Key Gases	Fault Type
1	CO and CO2	overheat cellulose
2	C2H4 and C2H6	overheat oil
3	CH4 and H2	arcing
4	C2H2 and H2	PD

, such as overheat cellulose, overheat oil, electrical arcing, and PD.

2.2. IEC Ratio Method

IEC ratio method [11,13] applies three gas ratios C₁, C₂, and C_3, as written in Equation (1). The ranges of each ratio are specified taking into account different types of faults, including PD, low energy discharge, high energy discharge, thermal fault temperature lower than 300 °C, thermal fault between 300 to 700 °C, and thermal fault temperature greater 700 °C. The ranges and faults are expressed in

Table 3. Fault Identification Using IEC Ratio Method.

C1	C2	C3	Fault Type
<0.1	0.1–1	<0.1, 0.1–1	PD1; PD of low energy
<0.1	<0.1	<0.1, 0.1–1	PD2; PD of high energy
0.1–1	<0.1	<0.1, 0.1–1	D1; discharge of low energy
>3	0.1–1	1–3	D2; discharge of high energy
<0.1	0.1–1	1–3, >3	T1-1; thermal fault T < 150 °C
<0.1	1–3	<0.1, 0.1–1	T1-2; thermal fault 150 < T < 300 °C
<0.1	1–3	1–3	T2; thermal fault 300 < T < 700 °C
<0.1	1–3	>3	T3; thermal fault T > 700 °C
<0.1	0.1–1	<1	normal

.

$${\mathrm{C}}_1 = \frac{{\mathrm{C}}_2{\mathrm{H}}_2}{{\mathrm{C}}_2{\mathrm{H}}_4}, {\mathrm{C}}_2 = \frac{{\mathrm{CH}}_4}{{\mathrm{H}}_2}, {\mathrm{C}}_3 = \frac{{\mathrm{C}}_2{\mathrm{H}}_4}{{\mathrm{C}}_2{\mathrm{H}}_6}$$

(1)

2.3. Duval Triangle Method

The conventional Duval triangle method [13,14,15,16] applies only three gases, which are CH₄, C₂H₄, and C₂H₂, for determining faults in the transformer by using the percentages of %CH₄, %C₂H₄, and %C₂H₂ as written in Equation (2). The coordination of the three percentages is then plotted on the Duval triangle as presented in Figure 1. For example, %CH₄ is firstly marked along the left-axis while %C₂H₄ is then marked along the right-axis. Finally, %C₂H₂ is marked along the x-axis. The coordination of %CH₄, %C₂H₄ and %C₂H₂ are plotted together to obtain the type of failures.

The area in the Duval triangle is divided into seven zones identifying seven faults such as corona PD, low energy discharge, high energy discharge, thermal fault temperature less than 300 °C, thermal fault temperature between 300 to 700 °C, thermal fault temperature greater than 700 °C, and lastly, mixed thermal and electrical fault as illustrated in

Table 4. Fault identification using Duval triangle method.

Failure	Fault
PD	corona PD
D1	low energy discharge
D2	high energy discharge
T1	thermal fault T < 300 °C
T2	thermal fault 300 < T < 700 °C
T3	thermal fault T > 700 °C
DT	mixed thermal and electrical fault

. This method provides highly accurate results. However, the technique ignores H₂ and C₂H₆, which limits its ability in fault detection when the faults have progressively formed. Consequently, the key gas and IEC method are also needed.

$${\%\mathrm{CH}}_4=\frac{{\mathrm{CH}}_4}{\left({\mathrm{CH}}_4{+\mathrm{C}}_2{\mathrm{H}}_2{+\mathrm{C}}_2{\mathrm{H}}_4\right)}\times 100, {\%\mathrm{C}}_2{\mathrm{H}}_2=\frac{{\mathrm{C}}_2{\mathrm{H}}_2}{\left({\mathrm{CH}}_4{+\mathrm{C}}_2{\mathrm{H}}_2{+\mathrm{C}}_2{\mathrm{H}}_4\right)}\times 100, {\%\mathrm{C}}_2{\mathrm{H}}_4=\frac{{\mathrm{C}}_2{\mathrm{H}}_4}{\left({\mathrm{CH}}_4{+\mathrm{C}}_2{\mathrm{H}}_2{+\mathrm{C}}_2{\mathrm{H}}_4\right)}\times 100$$

(2)

3. Fuzzy Logic for Insulating Oil Condition Assessment

The fuzzy logic approach is a computerized calculation tool [24,25,26,27] generally used to simulate expert knowledge, experience, and automatic judgment without human action. In this paper, fuzzy logic was applied with three DGA methods as key gas, IEC gas ratio, and the Duval triangle method to analyze faults inside power transformers. Fuzzy logic based triangular membership function(trimf) was defined in different levels in the fuzzy logic approaches to the IEC gas ratio and Duval triangle method as written in Equation (3), while fuzzy logic-based two-Gaussian membership function (gauss2mf), as written in Equation (4), approaches to the key gas method. The original input of each technique is amount of key gases in ppm. A fuzzy rule-based system is developed to specify faults. The Mamdani fuzzy inference system was applied to differentiate results by eliminating ambiguity. A defuzzifier based center of gravity (COG) method was used to interpret and display the results into numbers (i.e., 1, 3, 5, …) that were then assigned to different faults (i.e., F1, F2, F3, …).

$$f(x;a,b,c)=\left.\left\{\begin{array}{l}0,x\le a\\ \frac{x-a}{b-a},a\le x\le b\\ \frac{c-x}{c-b},b\le x\le c\\ 0,c\le x\end{array}\right.\right\},$$

(3)

where $f(x;a,b,c)$ is the output curve of the trimf, and x is input gases in ppm. The values of parameters a, b, and c are specified to identify the range of the triangular membership function.

$$f(x;\sigma ,c)=e^{\frac{-{(\chi -c)}^2}{2{\sigma }^2}}$$

(4)

where $f(x;\sigma ,c)$ is the output curve of the gauss2mf, and x is input gases in ppm. Similarly, the values of σ and c are specified to identify the range of the two Gaussian membership functions.

Defuzzification based on the center of gravity (COG) method was used to determine a defuzzified output as written in Equation (5).

$$z*=\frac{{\displaystyle \int z\mu (z)dz}}{{\displaystyle \int \mu (z)dz}}$$

(5)

where z is the output curve applied for both triangular membership function and two Gaussian functions, µ(z) is the membership function of the defuzzification, and z* is the defuzzified fuzzy output.

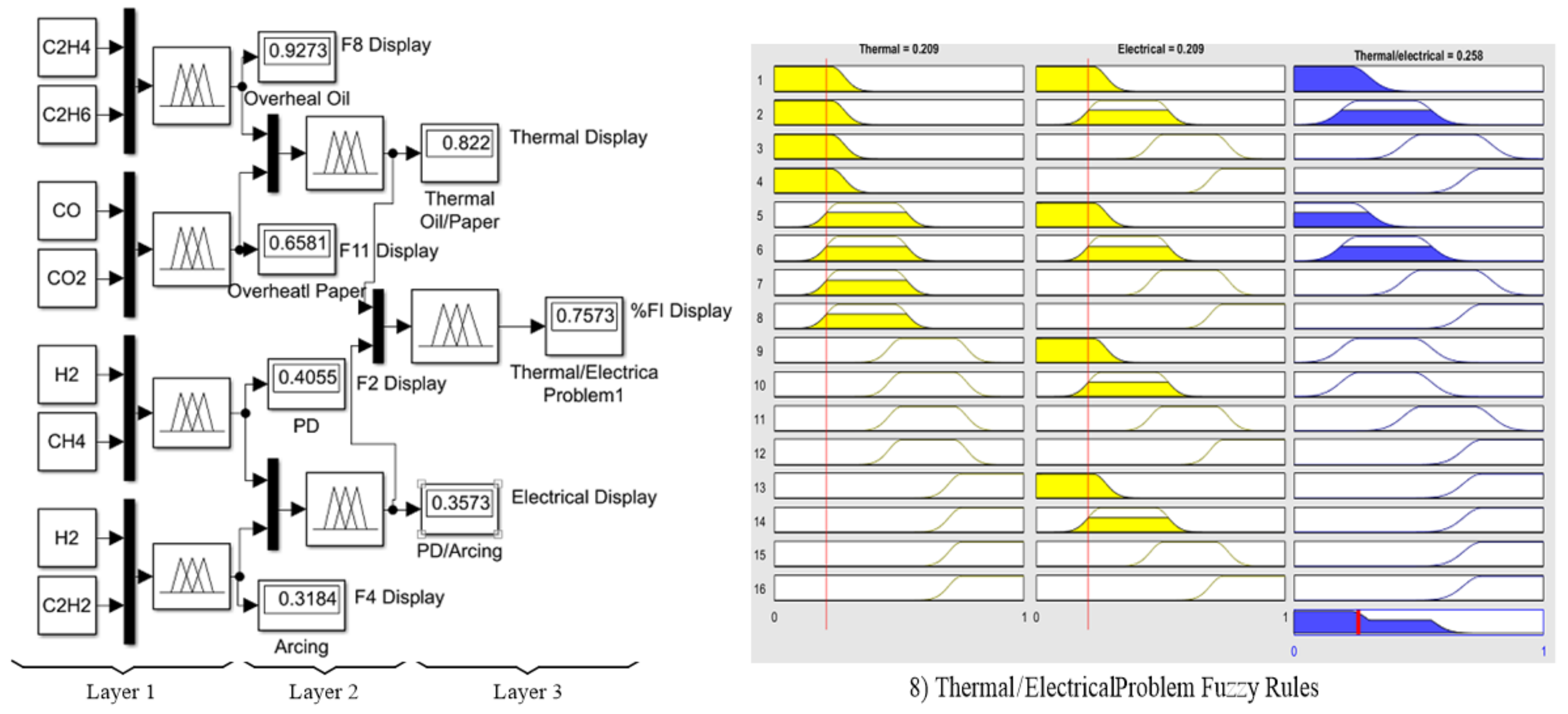
3.1. Application of a Fuzzy Logic Approach to the Key Gas Method

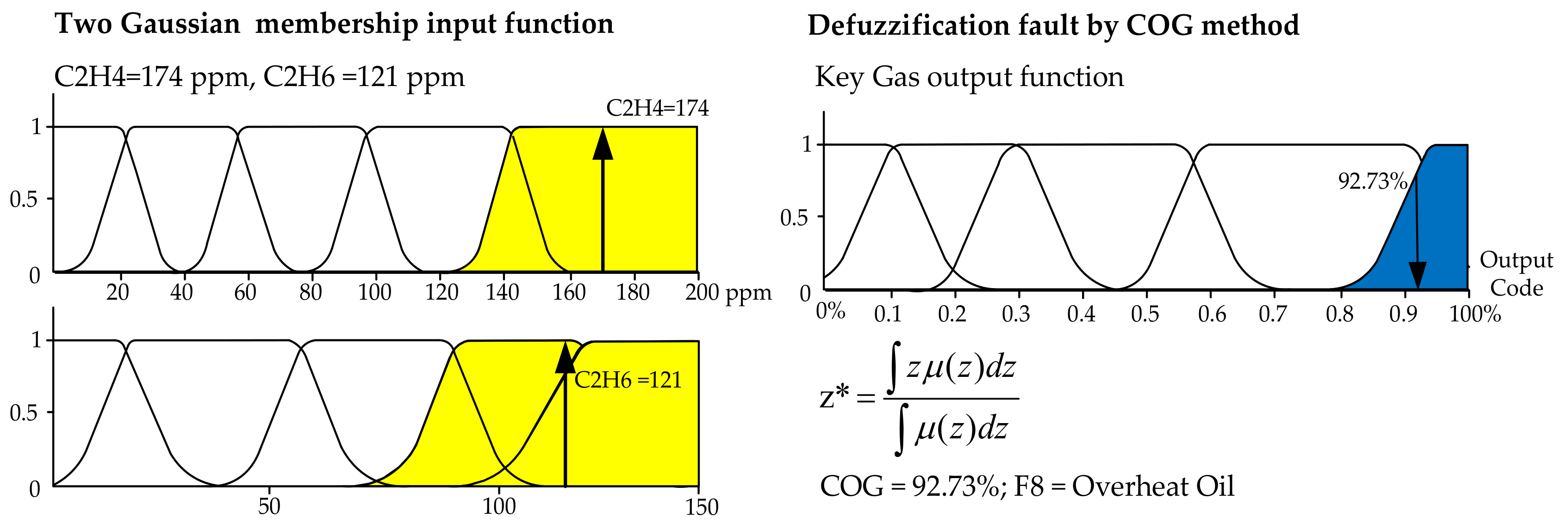
In this paper, a combination of the two-Gaussian membership function in Equation (4) was applied to the DGA using the key gas method [9]. The advantage of this method can be explained by the fact that there are overlapping areas, which are applied to identify the percentage of failure index (%FI). The 3-layer fuzzy logic model with 16 fuzzy rules was proposed and expressed in Figure 2 (left), while the shapes of the 16 fuzzy rules are shown in Figure 2 (right). To obtain a precise result, the input ranges of seven input gases were identified according to Table 2, while four output ranges of the output function were identified in

Table 5. Output ranges of fuzzy membership function of key gases.

Condition	Good	Accept	Caution	Poor
Range	0–30	20–55	45–75	75–100

. The Fuzzy output codes and faults are then determined as written in

Table 6. Fuzzy output codes and faults using the key gas method.

Output Code	Fault Identified by Key Gas Method
3	F2: corona/PD
7	F4: arcing
15	F8: overheat oil
19	F11: overheat cellulose

. Finally, the proposed defuzzification with COG method in Equation (5) was applied to calculate %FI, referring to the power transformer condition as written in

Table 7. %FI and condition determined by the key gas method.

%FI	Condition	Notified Color
0–25	good	green
26–50	acceptable	yellow
51–75	caution	orange
76–100	poor	red

, which can be differentiated into three color bands as red, yellow, and green.

Figure 3 shows the two-Gaussian membership fuzzification and defuzzification procedure according to Equations (3) and (5), respectively. In Figure 3 (left), for the first layer, two couples of key gases as CO and CO₂, C₂H₄ and C₂H₆, CH₄ and H₂, as well as C₂H₂ and H₂ as the inputs were compared to indicate %FI, while all four ranges of inputs are defined. In Figure 3 (right), the types of faults in Table 1 as outputs are defuzzified and decoded as F8 representing an overheating oil problem with 92.73% fault possibility. Similar to the 2nd layer, the couples F2 and F4 as well as F8 and F11 were further compared, resulting to the possibility of 82.2% as a thermal problem and 35.73% as an electrical problem. Finally, in the 3rd layer, %FI was then calculated as equal to 75.73%.

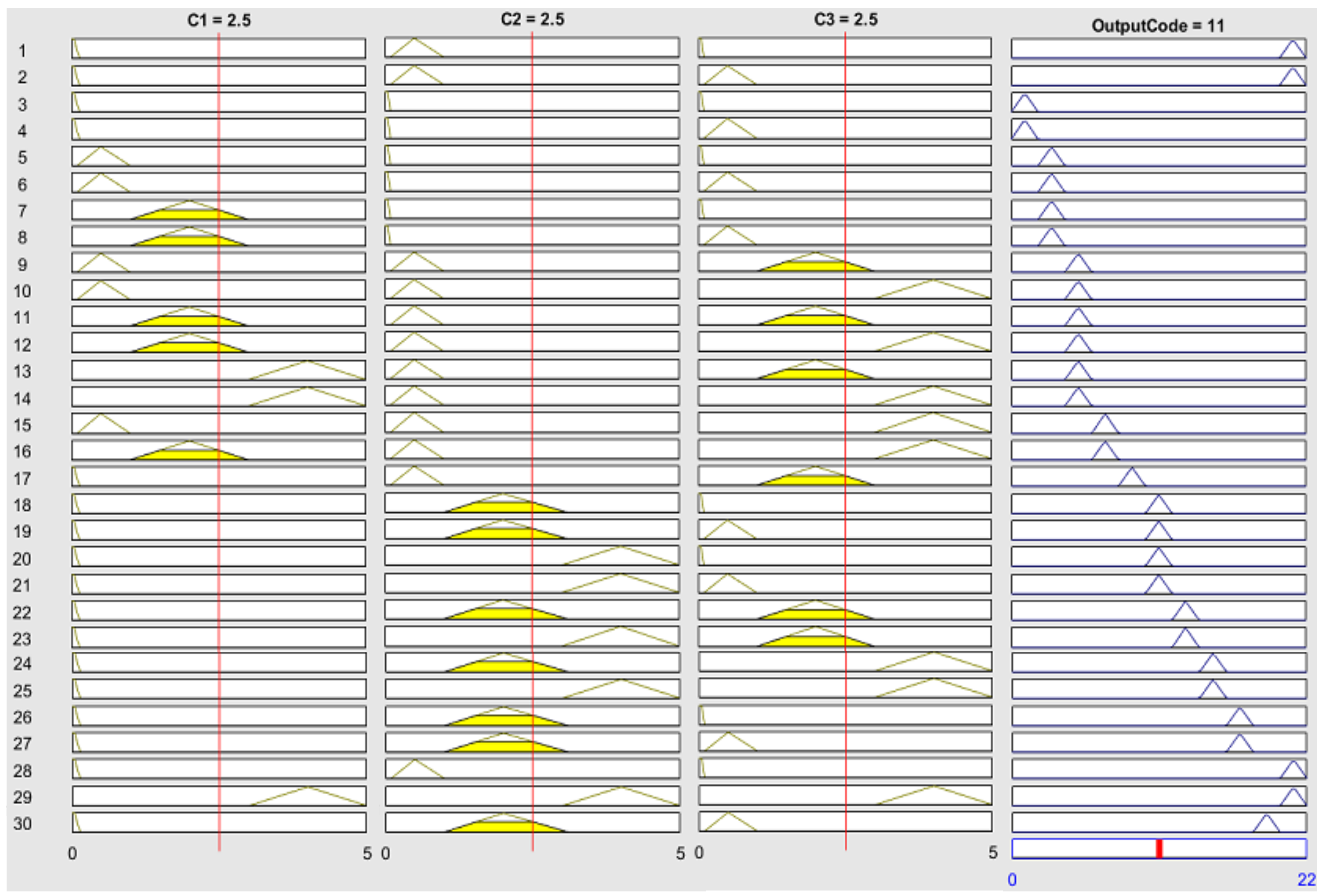
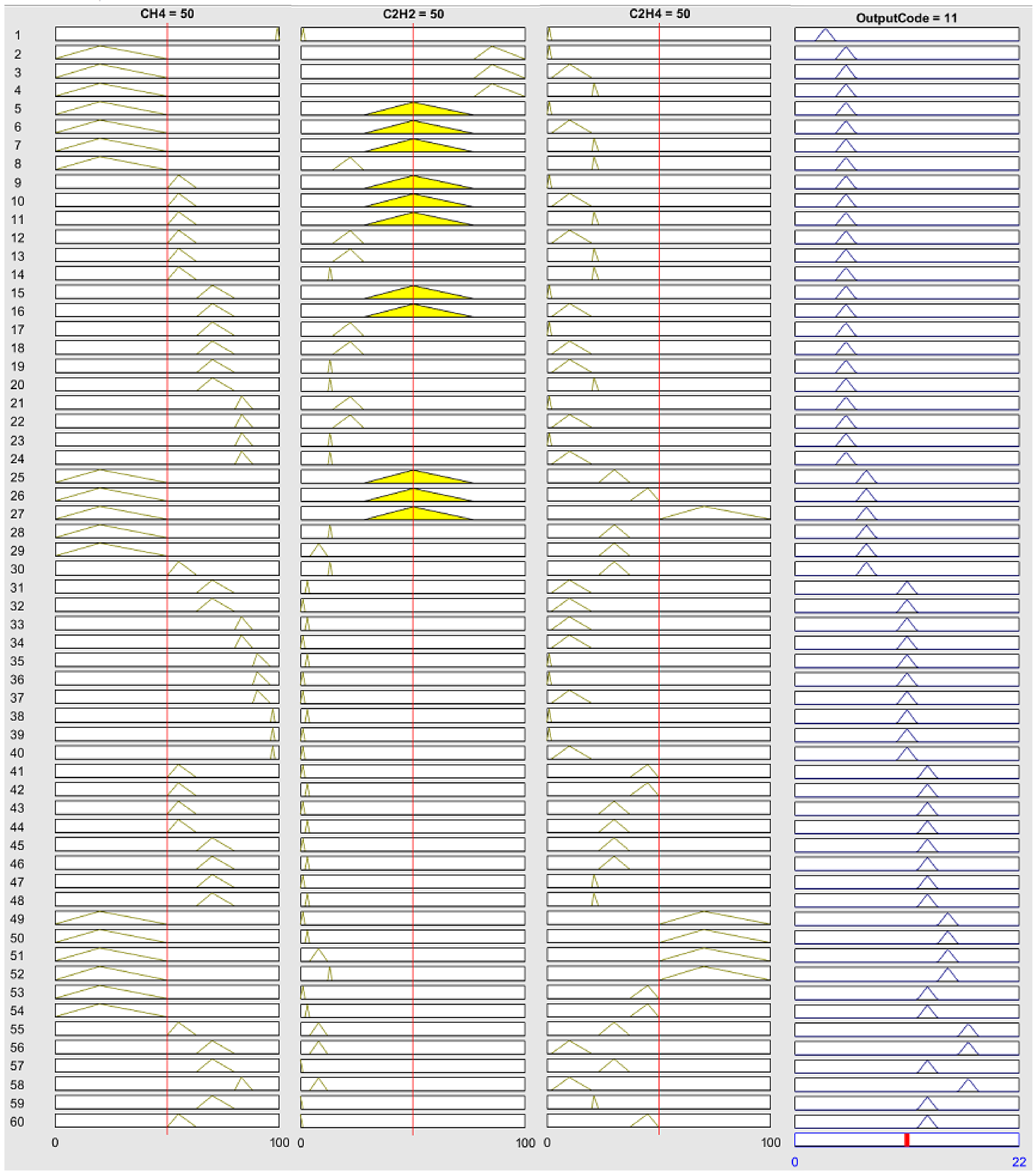
3.2. Application of the Fuzzy Logic Approach to IEC Ratio Method

In this paper, the triangular membership, as in Equation (3) and in Figure 4, was applied to IEC ratio method [13,14,15,16] because of the explicit ranges of input conditions as low, medium, high, and very high resulting in easy interpretation. According to the model, ratios C₁, C₂, and C₃ in Equation (1) were first calculated. Then, the calculated result defined as “$U$” is the input of this membership function, as shown in

Table 8. The input range of triangular membership function for the ICE ratio method.

Condition	Low	Medium	High	Very High
Range	$U<0.1$	$0.1\le U\le 1$	$1\le U\le 3$	$U>3$

. A single-layer fuzzy model was then applied. Thirty fuzzy rules were proposed to identify possible faults, as shown in Figure 4. The output code is represented by the numbers 1 to 21. Similarly, the defuzzification with the COG method is then applied. Nine faults are possible and written in the form of malfunction as given in

Table 9. Fuzzy output code, function, and fault type using the IEC ratio method.

Output Code	Fault Identified by IEC Three-Ratio Method
1	F1: PD of low energy (PD1-1)
3	F2: PD of high energy (PD1-2)
5	F3: low energy discharge (D1-1)
7	F4: high energy discharge (D1-2)
9	F5: thermal fault T < 150 °C (T1-1)
11	F6: thermal fault 150 < T < 300 °C (T1-2)
13	F7: thermal fault 300 < T < 700 °C (T2)
15	F8: thermal fault T > 700 °C (T3)
21	F11: normal

.

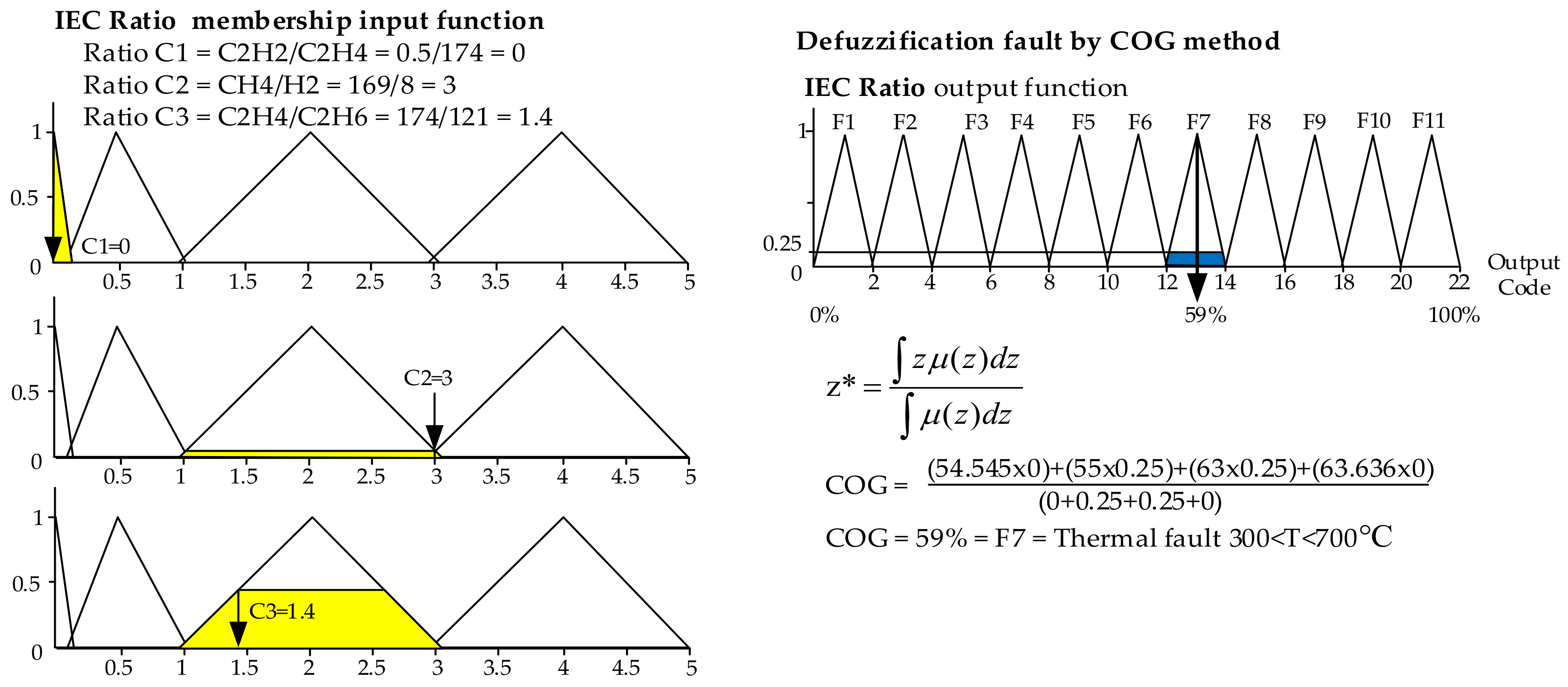
For the IEC Ratio method, Figure 5 shows the first layer of triangle membership function fuzzification and defuzzification procedure according to Equations (3) and (5), respectively. In Figure 5 (left), ratios C₁ = 0, C₂ = 3, and C₃ = 1.4 were calculated by using Equation (1) and represented as inputs in Equation (3). The four ranges of each input were defined, as shown in Figure 5 (left). The types of faults as output are defuzzified as equal to 59% and decoded as F7 representing thermal fault problem (T2; 300 < T < 700 °C) as written in Figure 5 (right).

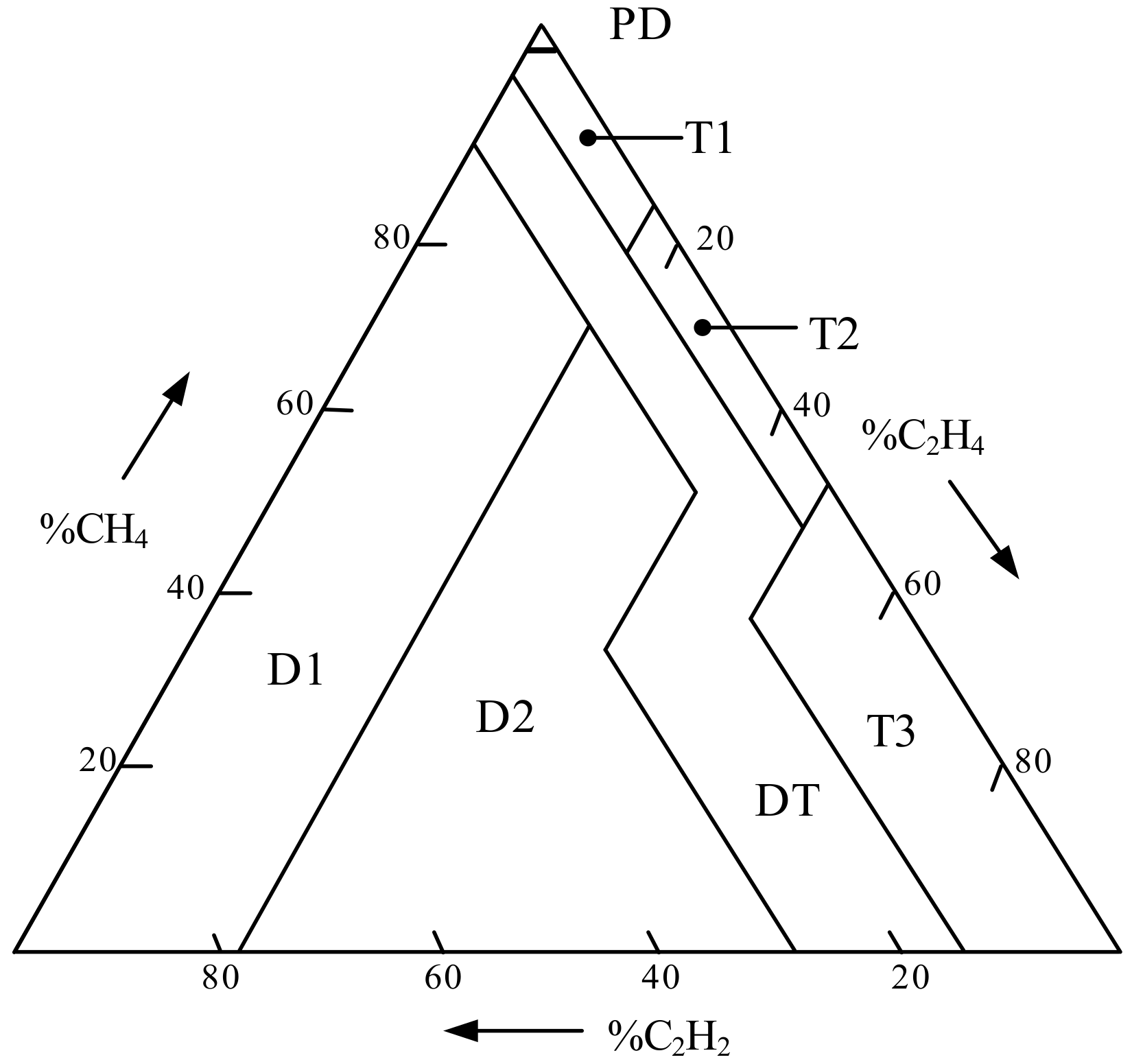
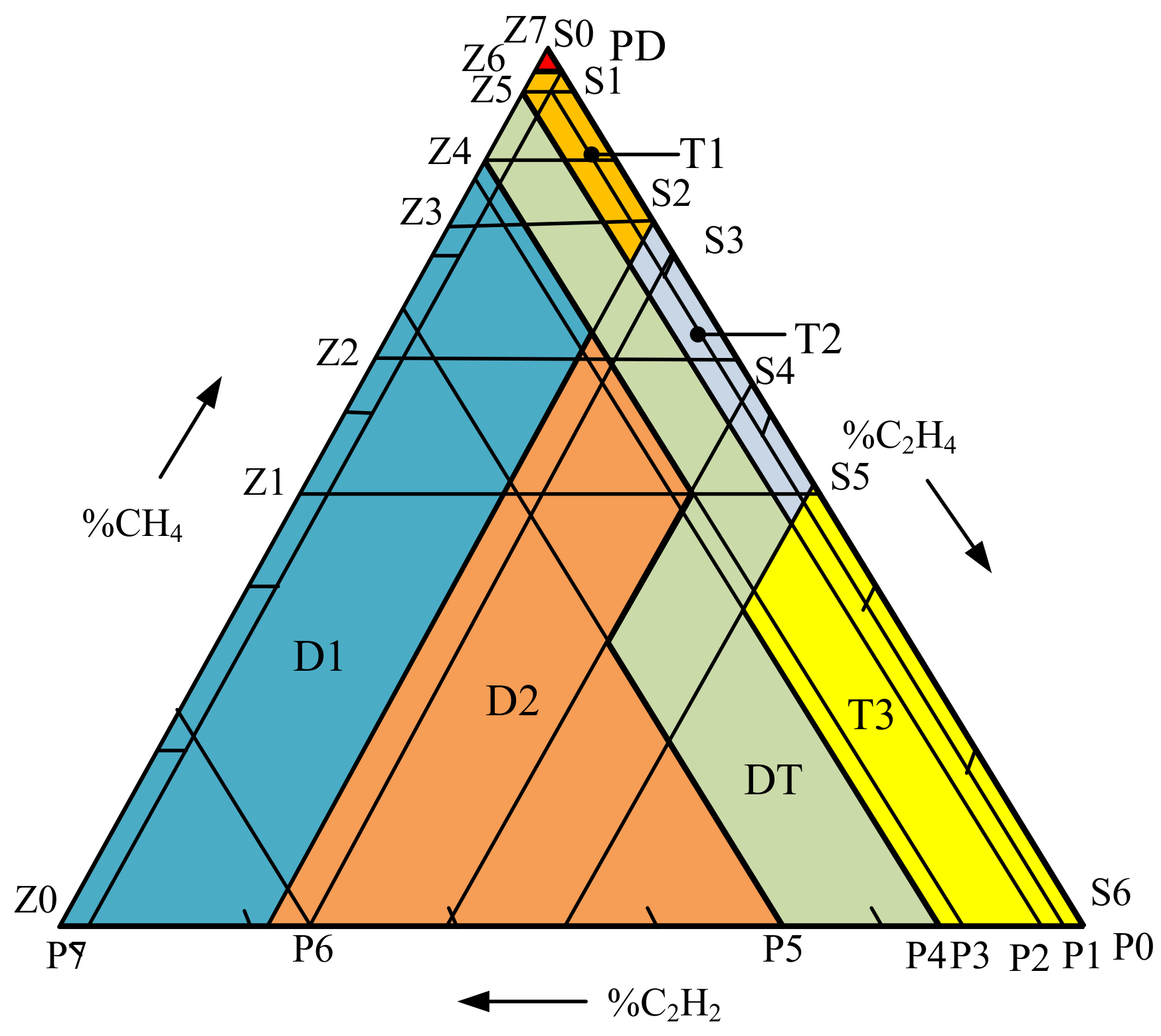
3.3. Fuzzy Logic with Duval Triangle Method

The triangular membership function is applied to the Duval triangle method [11,12,13,14] because of the explicit ranges of the input with the most simple output code interpretation, as written in

Table 10. Fuzzy output code, function and fault type using Duval triangle method.

Output Code	Fault Identified by Duval Triangle Method
3	F2: corona/PD
5	F3: low energy discharge (D1)
7	F4: high energy discharge (D2)
11	F6: low thermal fault T < 300 °C (T1)
13	F7: medium thermal fault 300 < T < 700 °C (T2)
15	F8: high thermal fault T > 700 °C (T3)
17	F9: mixed thermal and electrical fault (DT)
21	F11: normal

. The percentages of ratio %CH₄, %C₂H₄, and %C₂H₂ defined as Z, P, S parameters classified in different zones as written in Equation (6) are the inputs of the membership function for plotting in the Duval triangle as presented in Figure 6. Similarly, a single-layer fuzzy model was applied. Sixty fuzzy rules were identified for possible faults, as shown in Figure 7. Similarly, the output code was represented by numbers (1 to 21). The defuzzification with COG method was then applied. The eight fault types identified by the Duval triangle method are written in Table 10.

$$\%C{H}_4=\left\{\begin{array}{cc}{Z}_1;\hfill & \hfill Z<50\\ Z_2;\hfill & \hfill 50\le Z<63\\ Z_3;\hfill & \hfill 63\le Z<80\\ Z_4;\hfill & \hfill 80\le Z<88\\ Z_5;\hfill & \hfill 88\le Z<98\\ Z_6;\hfill & \hfill Z\ge 98\end{array}\right., \%C_2{H}_2=\left\{\begin{array}{cc}{P}_1;\hfill & \hfill P<2\\ P_2;\hfill & \hfill 2\le P<4\\ P_3;\hfill & \hfill 4\le P<12\\ P_4;\hfill & \hfill 12\le P<14\\ P_5;\hfill & \hfill 14\le P<28\\ P_6;\hfill & \hfill 28\le P<77\\ P_7;\hfill & \hfill P\ge 77\end{array}\right., \%C_2{H}_4=\left\{\begin{array}{cc}{S}_1;\hfill & \hfill S<2\\ S_2;\hfill & \hfill 2\le S<20\\ S_3;\hfill & \hfill 20\le S<23\\ S_4;\hfill & \hfill 23\le S<37\\ S_5;\hfill & \hfill 37\le S<50\\ S_6;\hfill & \hfill S\ge 50\end{array}\right.$$

(6)

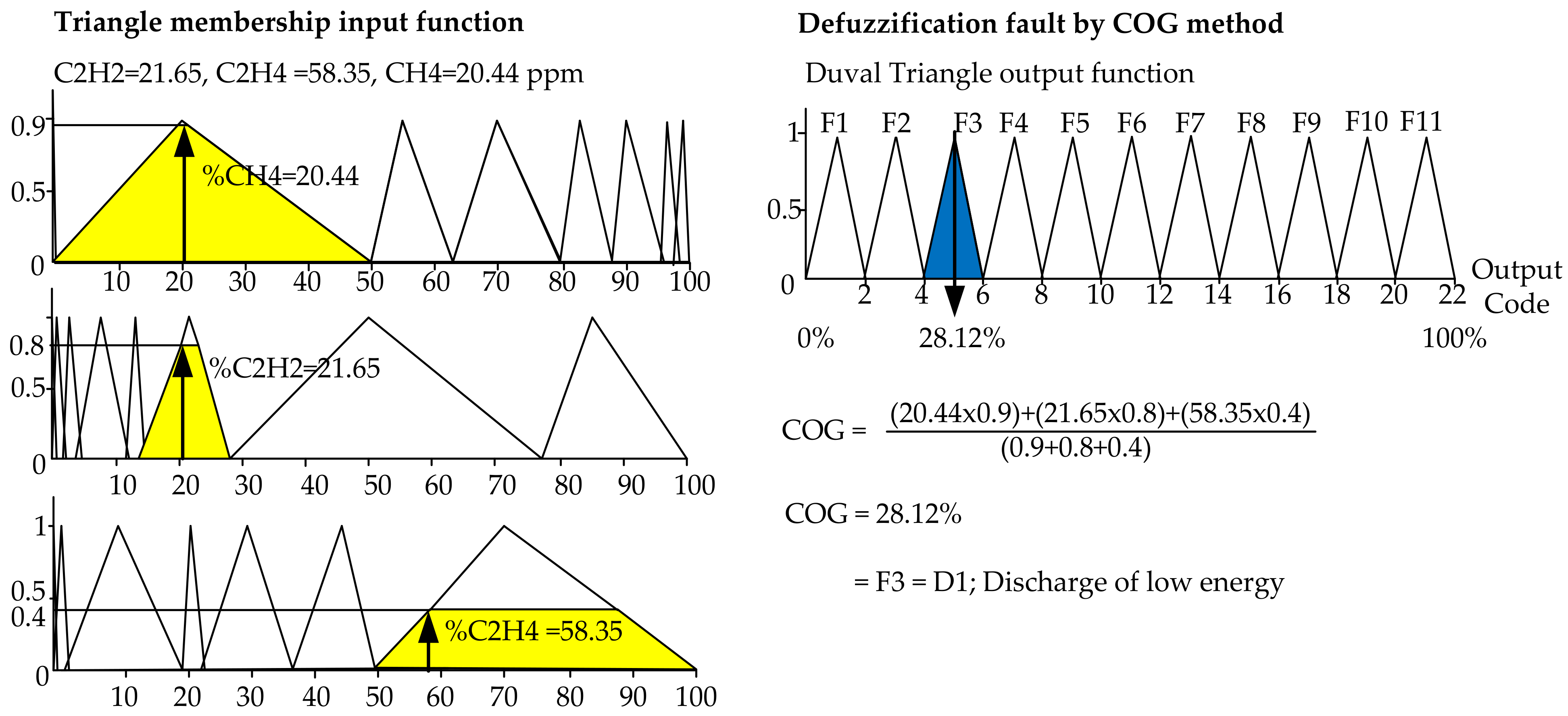
Figure 7 shows the fuzzy logic fuzzification and defuzzification procedure for the Duval triangle method by using Equations (3) and (5), respectively. The %CH₄, %C₂H₄, and %C₂H₂ were calculated as equal to 20.44, and 21.65, 58.35%, which are defined as Z, P, S parameters. The ranges of Z, P, S in Equation (6) are also drawn in Figure 8 (left), while the COG was calculated by using fuzzy logic defuzzification and equal to 28.12% as shown in Figure 8 (right), which falls into F3 decoded to D1 as the discharge of low energy.

3.4. Defuzzified Faults from Three Fuzzy Logic Methods

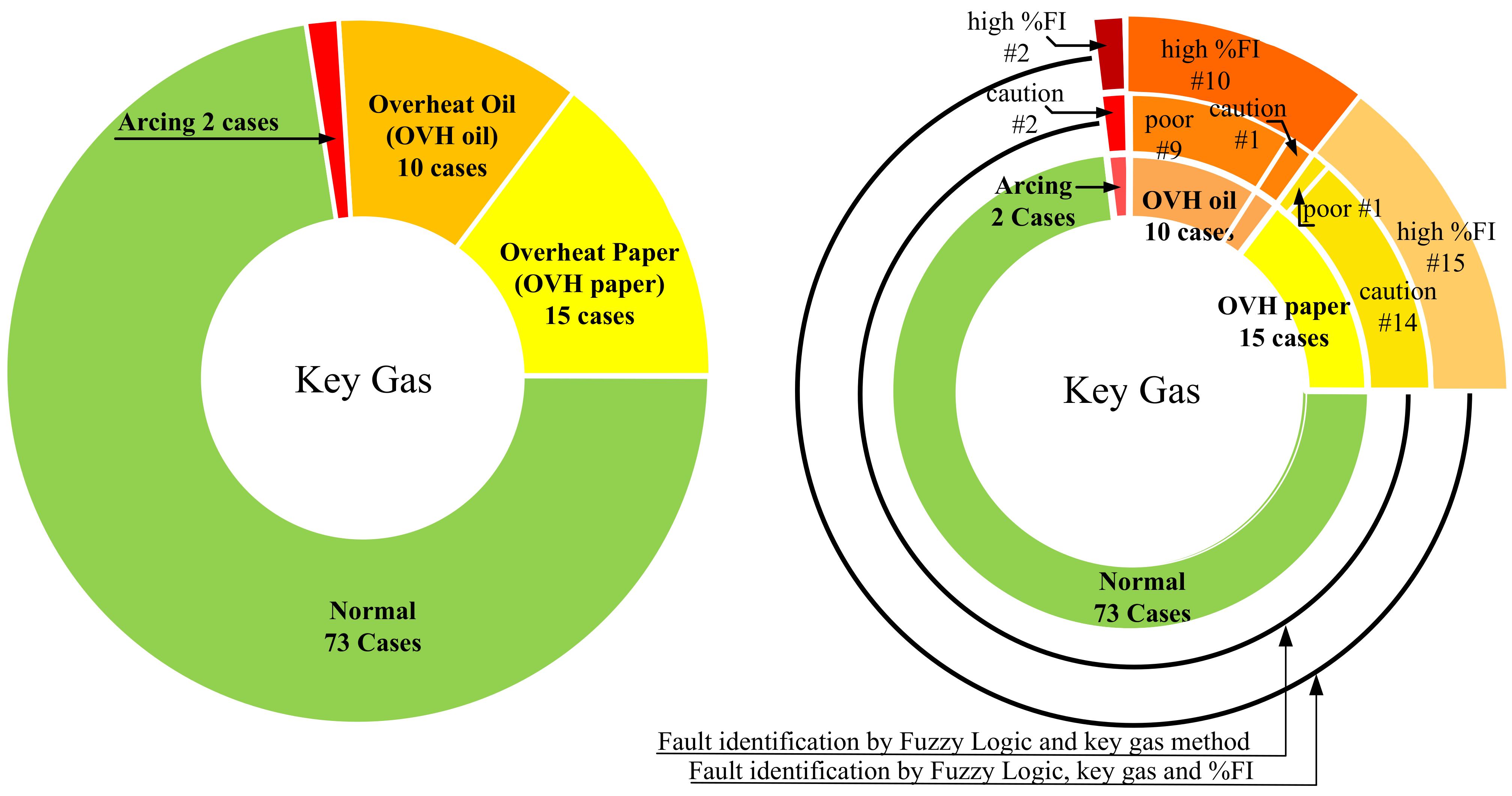
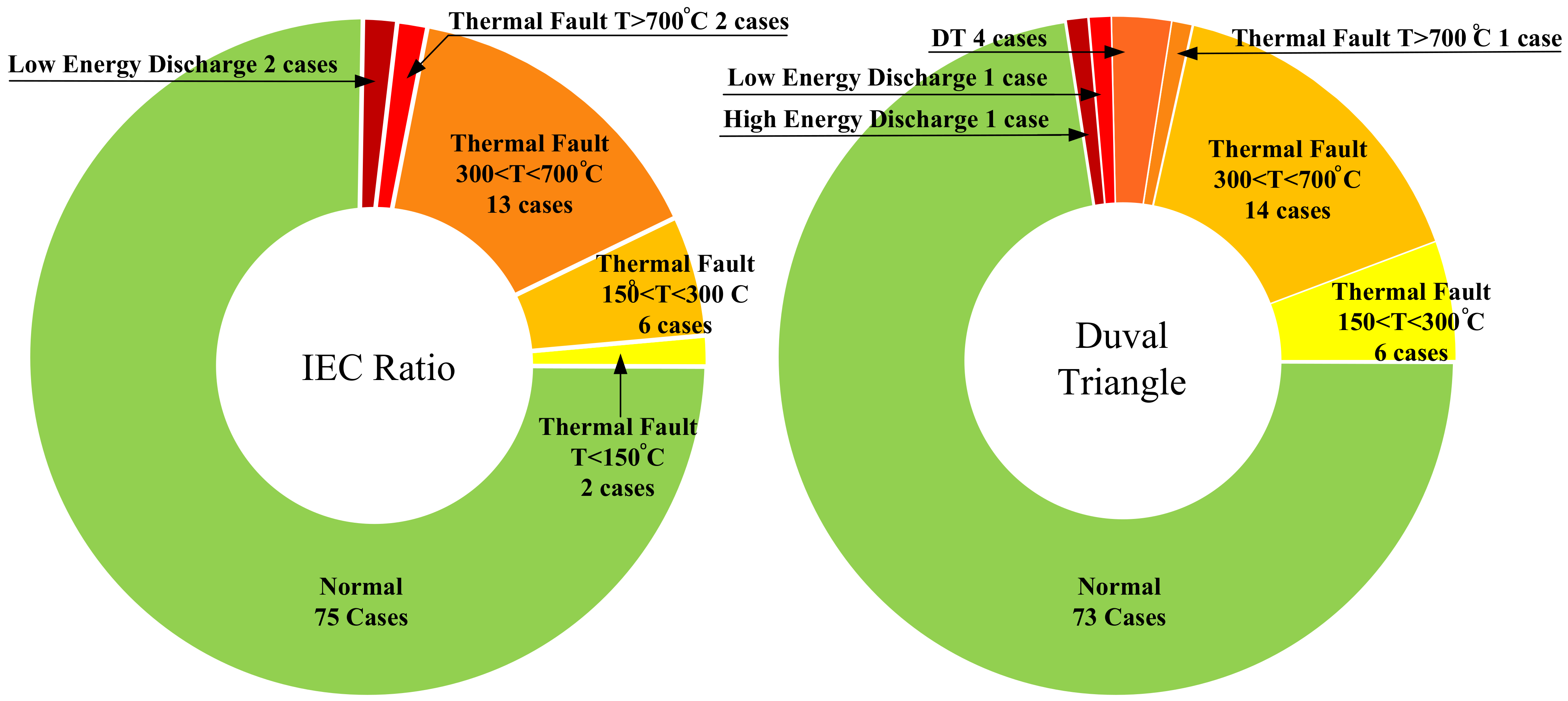
The proposed defuzzified codes from 1–21, representing eleven faults from three fuzzy logic methods and the key gas, IEC Ratio, and the Duval triangle method were compared, as shown in Figure 9. For example, the defuzzified values between range 2–4 shows the faults as PD1-2 as the partial discharge of high energy density, exactly determined by all three methods. All methods should be simultaneously applied to precisely identify the failure inside the power transformer.

4. Results and Discussions

4.1. Fuzzy Logic Implementation to Practical Two Un-Tanked Power Transformers

DGA results of two power transformers named as TR1 and TR2 obtained from certified DGA laboratory with ratings 115/69 kV, 15 MVA and 22 kV/416 V, 3 MVA, respectively with un-tanked investigation after failure [18] were analyzed and interpreted for problems occurring within paper and oil insulation of these transformers, as given in

Table 11. Input gases (ppm) of TR1 and TR2.

Case	Quantity of Gases (ppm)
	H2	CO2	CO	C2H4	C2H6	CH4	C2H2
TR1	602	112	298	97	6	90	262
TR2	5383	3173	465	30,787	4402	19,231	361

. The faults identified by three fuzzy logic approaches are shown in

Table 12. Fuzzy logic results of TR1 and TR2.

Case	%FI	Key Gas	IEC Ratio	Duval Triangle
TR1	87.1	arcing and OVH oil	D2; discharge of high energy	D1; discharge of low energy
TR2	86.8	arcing and PD	T2; thermal fault T > 700 °C	T2; thermal fault T > 700 °C

. All methods by Fuzzy Logic confirmed the arcing inside the power transformer recognized from the abnormal amount of C₂H₂, as well as obvious pictures from the internal investigation, as shown in Figure 10 and Figure 11.

4.2. Fuzzy Logic Implementation to 10 Power Transformers

Similarly,

Table 13. Input gases (ppm) from an on-site test with an additional ten power transformers.

Case	kV Rating * pri/sec/ter	MVA Rating ** ONAN/ONAF	Quantity of Gases (ppm)
			H2	CH4	CO	CO2	C2H4	C2H6	C2H2
TR3	69/12	30/40	32	36	414	4408	16	19	2
TR4	69/12	30/40	36	79	72	1686	10	426	0.5
TR5	69/24	30/40	35	58	91	2362	8	204	0.5
TR6	69/24/12	30/40	79	40	502	3323	33	22	11.1
TR7	69/24/12	30/40	11	10	232	2608	44	19	2
TR8	69/12	36/48/60	31	134	151	2532	12	502	1.5
TR9	69/12	36/48/60	5	85	117	2129	30	784	0
TR10	69/12	30/40	27	0	35	170	739	209	1224
TR11	69/12	36/48/60	70	21	1094	6558	4	16	2.5
TR12	69/24/12	36/48/60	8	169	485	9760	174	121	0.5

* pri/sec/ter means voltage ratings of primary/secondary/tertiary windings. ** ONAN/ONAF are cooling types; i.e., 36/48/60 means ONAN/ONAF/ONAF.

shows practical DGA results of additional ten transformers named as TR3 to TR12 obtained from a certified DGA laboratory. By applying the TDCG method, TR5 encountered condition “2” that a fault could probably occur within the transformer. Transformers TR3 to TR12 (except TR5) encountered condition “3” indicating that some faults were identified. Then, the fuzzy logic was further applied to identify the types of defect.

The results of faults such as corona and PD, arcing, overheated oil, overheated cellulose/paper, and %FI were precisely identified by fuzzy logic with the key gas method as shown in

Table 14. Fault identification by the key gas method.

Case	F2 Corona/PD	F4 Arcing	F8 Overheat Oil	F11 Overheat Paper	%FI	Fault Type
TR3	0.256	0.335	0.226	0.509	58.3	overheat paper
TR4	0.313	0.318	0.927	0.268	86.9	overheat oil
TR5	0.283	0.318	0.927	0.325	87.1	overheat oil
TR6	0.311	0.673	0.249	0.508	70.8	overheat paper
TR7	0.224	0.335	0.264	0.341	36.2	normal
TR8	0.361	0.326	0.927	0.336	86.9	overheat oil
TR9	0.321	0.315	0.927	0.309	86.9	overheat oil
TR10	0.235	0.849	0.5	0.162	70.7	arcing
TR11	0.3	0.345	0.216	0.842	86.8	overheat paper
TR12	0.405	0.318	0.927	0.658	87.0	overheat oil

. Transformer nos. 4, 5, 8, 9, 11, and 12 encountered high severe faults. Similarly, with the fuzzy logic approach to the IEC three-gas ratio and Duval triangle, the results are compared with key gas methods, as shown in

Table 15. Fault identification by key gas, IEC ratio, and Duval triangle method.

Case	Key Gas	IEC Ratio	Duval Triangle
TR3	overheat paper	thermal fault, 150 < T < 300 °C	thermal fault, 300 < T < 700 °C
TR4	overheat oil	thermal fault, 150 < T < 300 °C	thermal fault, T < 300 °C
TR5	overheat oil	thermal fault, 150 < T < 300 °C	thermal fault, T < 300 °C
TR6	overheat paper	discharge of low energy	discharge of high energy
TR7	normal	not analyzed due to normal	not analyzed due to normal
TR8	overheat oil	thermal fault, 150 < T < 300 °C	thermal fault, T < 300 °C
TR9	overheat oil	thermal fault, 150 < T < 300 °C	thermal fault, 300 < T < 700 °C
TR10	arcing	thermal fault 150 < T < 300 °C	discharge of high energy
TR11	overheat paper	thermal fault, 300 < T < 700 °C	thermal fault, T > 700 °C
TR12	overheat oil	thermal fault, 300 < T < 700 °C	thermal fault, T > 700 °C

. The results agree well between both analysis methods.

4.3. Model Validation of the Fuzzy Logic System with Three DGA methods

This paper proposed a fuzzy logic system for power transformer fault assessment based on the three DGA methods; key gas, IEC ratio, and Duval triangle method were validated with a population of 500 power transformers. The diagnosis DGA of 132 transformers taken from [30,33] as reference cases were first validated with accurate results. Then, DGA results of the total 112 power transformers with rating 115/22 kV in sub-transmission system of two electrical utilities were further validated with the developed fuzzy logic system. From these additional 112 cases, the raw DGA data of 2 un-tanked transformers is shown in Table 11 to confirm the obtained results with the evidence found, and 10 example cases are shown in Table 13 to demonstrate result consistency. Moreover, the additional raw DGA data of 100 cases were obtained from a certified DGA laboratory, and the fault types of 100 cases were first analyzed with standard diagnosis methods and subsequently used to validate the results from the developed fuzzy logic system.

Table 16. Comparison of results from fuzzy logic approach to three DGA standard diagnosis methods.

Fault Type	Duval Triangle			IEC Ratio			Key Gas
	* std.	** FL	diff.	* std.	** FL	diff.	* std.	** FL	diff.
normal	77	77	0	77	88	11	77	80	3
overheat celluloseDT; discharge or thermal	10	5	5				40	26	14
T3; thermal fault T > 700 °C	26	27	1	0	12	12
T2; thermal fault 300 < T < 700 °C	24	24	0	17	37	20	41	59	18
T1-2; thermal fault 150 < T < 300 °C	16	14	2	14	20	6
T1-1; thermal fault T < 150 °C				0	2	2
D2; discharge of high energy	56	57	1	16	46	30	72	69	4
D1; discharge of low energy	24	27	3	39	32	7
PD1-2; partial discharge high energy	11	13	2	2	7	5	14	10	4
PD1-1; partial discharge low energy				0	0	0
unable to identify	0	0	0	79	0	n/a	0	0	0
total un-matched units			14			93			43
total matched units			229			n/a			201
total units	244	244	244	244	244	244	244	244	244
error (%)			5.74			38.11			17.63
accuracy (%)			94.26			61.89			82.37
final accuracy after applying sampling theory with 5% error (%)			89.54			58.79			78.26

“* std.” means DGA cases obtained from [30,31,32,33,34] and the laboratory with standard diagnosis methods. “** FL” means DGA analysis using the fuzzy logic system. “diff.” means the number of DGA analysis results using the fuzzy logic system were different from reference cases. “n/a” means unable to calculate because of an unidentified fault by the IEC method.

presents a comparison of results from the fuzzy logic approach to three DGA standard diagnosis methods. The number of transformers was increased to 244 samples to improve the precision of the assessment.

In Table 16, the matched and unmated cases, as well as the percentage accuracy and error are given. The percentage error using fuzzy logic based key gas, IEC ratio, and Duval triangle methods was also calculated by dividing the numbers of unmatched units with the total tested units, which were equal to 82.37, 61.89, and 94.26%, resulting in a percentage accuracy of 80.33, 69.67, and 93.85%, respectively, as shown in Table 16. By applying the sampling theory, the statistical method mentioned in [34] estimated a 5% output error of the system when 244 data was tested out of 500 samples. The overall accuracy was further calculated by multiplying 95% accuracy from sampling theory to the obtained percentage accuracy. Lastly, the final percentage accuracy was calculated as 78.26, 58.79, and 89.54%, accordingly. This implied that the required number of tested DGA data should be more than 244 out of the total 500 populations to improve the accuracy with less than 5% error.

As presented in Table 16, the fuzzy logic approach with the Duval triangle method yielded the most accurate result with 89.54%. It was also clearly seen that the fuzzy logic approach with IEC ratio method could improve the drawbacks of the standard IEC ratio method as the obtained results agreed well with the Duval triangle method. Consequently, 79 fault types, which were unidentified by the conventional IEC method, were better classified by the fuzzy logic system. Moreover, the fuzzy logic approach to the key gas method was able to evaluate both the percentage of failure index and internal fault determination.

4.4. Graphical Circle Using Fuzzy Logic Approach to DGA Results for 100 Power Transformers

A graphical circle was implemented to clearly identify and compare the fault results analyzed by fuzzy logic with three DGA methods when the DGA of 100 power transformers in a utility was investigated. A certified laboratory validated the raw DGA data of these 100 transformers, and the fault types were determined by the standard diagnosis method. In Figure 12 and Figure 13, graphs of a 100 power transformer fleet in Thailand are presented as examples. Figure 12 (left) shows the numbers of four faults as of PD, OVH paper, OVH oil, and arcing, classified by the key gas method using standard diagnosis methods using an excel program. It showed that 15 and 10 transformers encountered OVH paper and oil, respectively. Whereas in Figure 12 (right), the numbers of four faults analyzed by the key gas method with fuzzy logic are given, which were identical to the results obtained from the standard diagnosis method. This shows that fuzzy logic can be simply applied in an easier and less time-consuming manner. Moreover, with this fuzzy logic approach, each type of fault can be deeply identify the severity of each case confirmed by %FI. For example, at the outermost circle in Figure 12 (right), among 15 cases of an OVH paper problem with high %FI, 1 out of 15 was classified as poor. Similarly, 10 cases of an OVH oil problem were classified as high %FI, while 9 out of 10 were classified as poor condition. In Figure 13 (left) and (right), fuzzy logic was applied to the IEC three-gas ratio and Duval triangle method. The results of these two methods were compared and confirmed almost homogeneously. However, the trend and types of faults could be identified correctly.

4.5. Maintenance Strategy

The maintenance task and usage strategy together with the inspection interval are recommended to set up the effective maintenance planning to prevent/minimize the damage and losses occurring in power transformers and electrical networks. %FI is used to identify the conditions and the required maintenance tasks as stipulated in

Table 17. Maintenance tasks and usage strategies corresponding to the accessed conditions.

%FI	Condition	Maintenance Task and Usage Strategies
0–25	good	time-based maintenance: routine visual inspection, dielectric breakdown voltage test, DGA, PD measurement at regular interval (usually once in 2 or 3 years)
26–50	acceptable	time-based maintenance: routine visual inspection, dielectric breakdown voltage test, DGA, PD measurement, electrical test such as turn ratio, power factor, polarization index (usually once a year)
51–75	caution	condition-based maintenance: full electrical and insulating oil test, DGA, PD measurement with localization, shutdown planning for investigation
76–100	poor	shutdown and corrective maintenance: condition monitoring, root caused analysis, maintenance setup and execution, recondition monitoring, usage decision making

. The four different ranges are classified into good, acceptable, caution, and poor condition by a sensitivity check of the power transformer population, as well as experiences of the research group and utility’s experts. The maintenance task and usage strategies are mentioned accordingly.

5. Conclusions

A fuzzy logic approach to three DGA methods; key gas method, IEC three-gas ratio and Duval triangle methods were used to evaluate the condition of power transformers by the percentage of the failure index and the internal fault determination. Moreover, the fuzzy logic with the key gas approach could calculate %FI and identify problems that may occur inside power transformers, while the IEC three-gas ratio and Duval triangle can confirm the problems in different failure types covering all possibilities inside power transformers. Then, the fuzzy logic applied to DGA results of two transformers were evaluated and practically confirmed by an un-tanked power transformer showing arcing at the core in both cases. In addition, the DGA results of ten transformers were further evaluated. The fuzzy logic approach with three DGA methods results were shown and compared. The condition and the internal problems of power transformers could be clearly identified. The graphic circle was introduced to compare the analyzed results of a large number of power transformers. Then, the severity of faults inside the transformers could be deeply identified in terms of the percentage of failure index. This fuzzy logic is a smart, accurate tool for automatically identifying faults occurring within transformers. Then, the recommended maintenance strategy and time interval were proposed for effective planning to minimize the catastrophic damage, which could occur with power transformers and their networks. Finally, the fuzzy logic simulation software with proposed techniques was developed as a low cost, easy, accurate, and less time-consuming tool.