Estimating Energy Forecasting Uncertainty for Reliable AI Autonomous Smart Grid Design
Abstract
1. Introduction
2. Algorithms of Learning Models
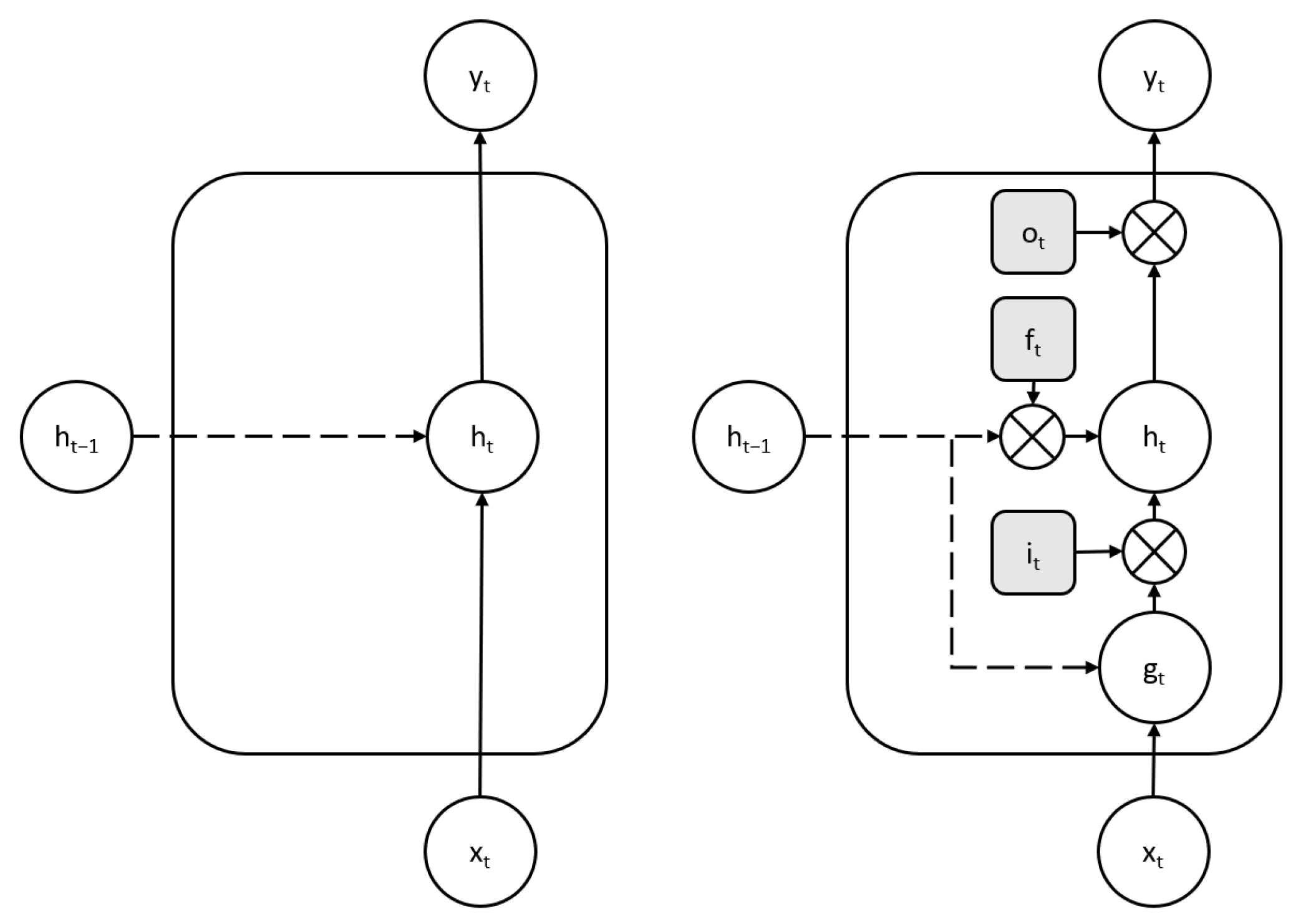
2.1. Long Short-Term Memory
2.2. Uncertainty Estimation for LSTM
2.3. Gradient Tree Boosting
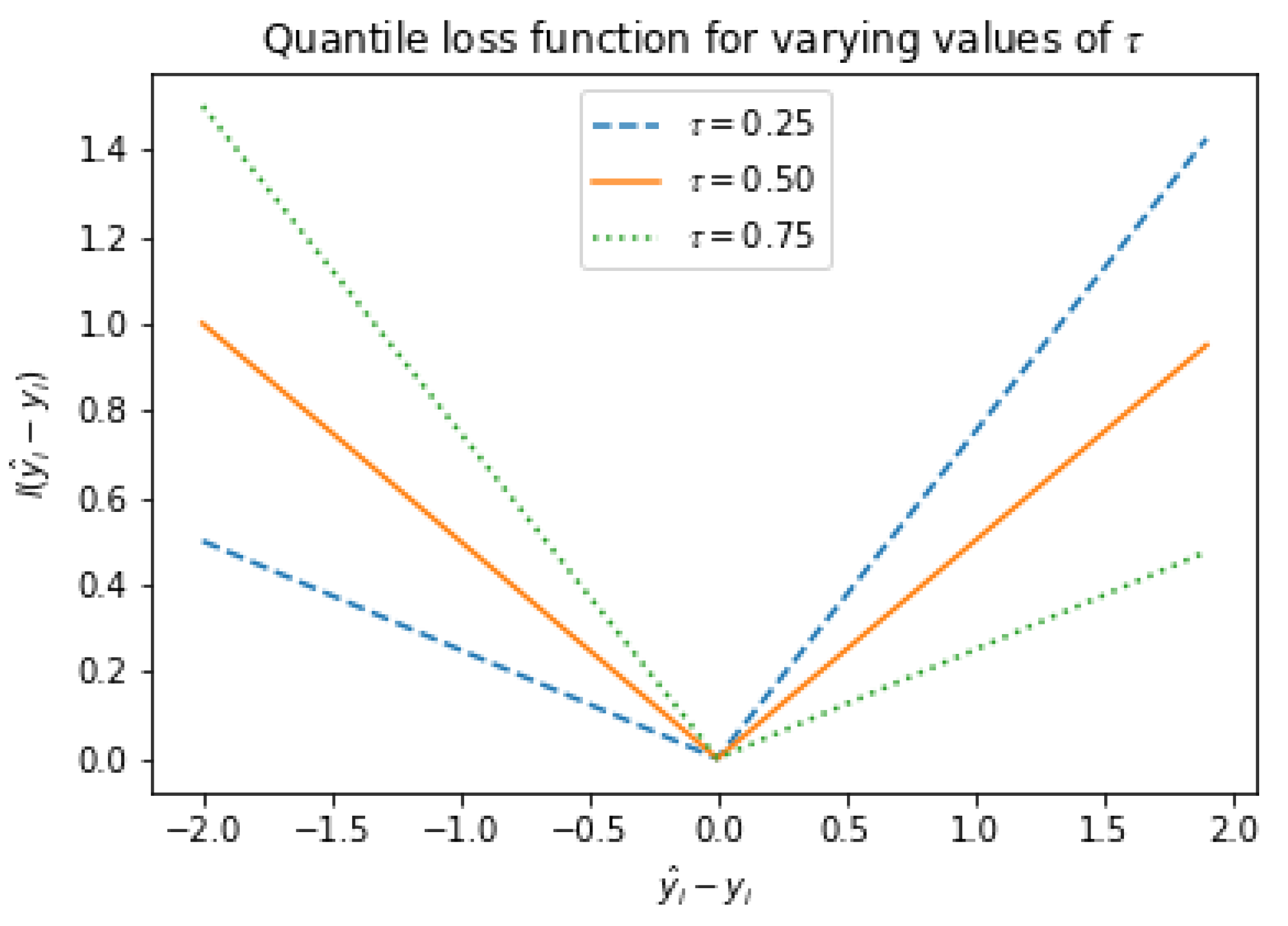
2.4. Uncertainty Estimation for GBR
3. Experiment and Results
3.1. Model Implementation
| Algorithm 1: MC dropout Algorithm for model uncertainty. |
 |
3.2. Data and Feature Selection
3.2.1. Temperature Effects
3.2.2. Weekday Effects
3.2.3. Holiday Effects
3.2.4. Feature Selection
3.2.5. Half-Hourly Load
3.2.6. Average Daily Temperature
3.2.7. Weekday Indicator
3.2.8. Public Holidays
3.2.9. Time Series Modeling
3.2.10. Data Normalization
3.2.11. Convert Data to Input–Output Pairs
3.3. Splitting Data into Train and Test Sets
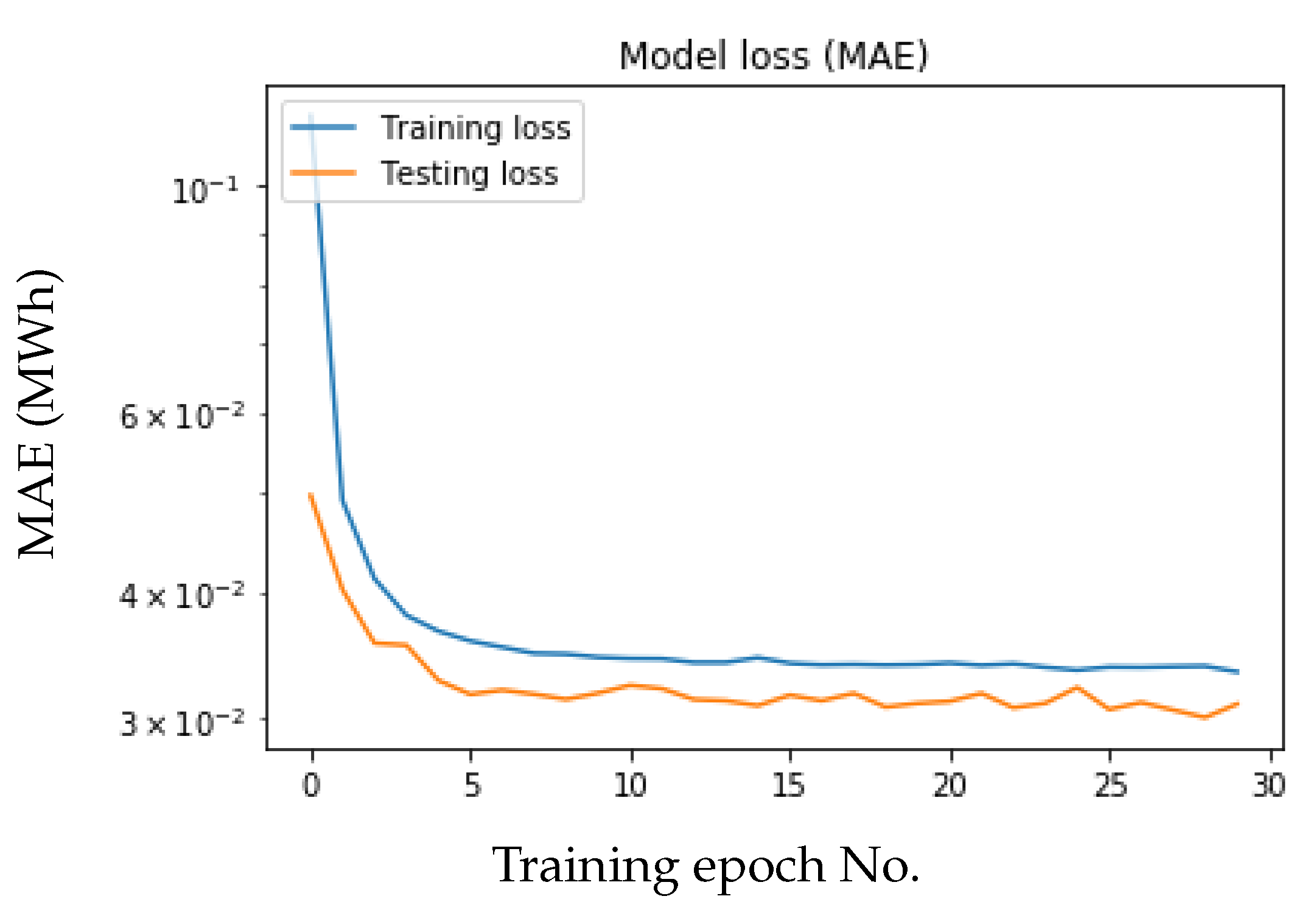
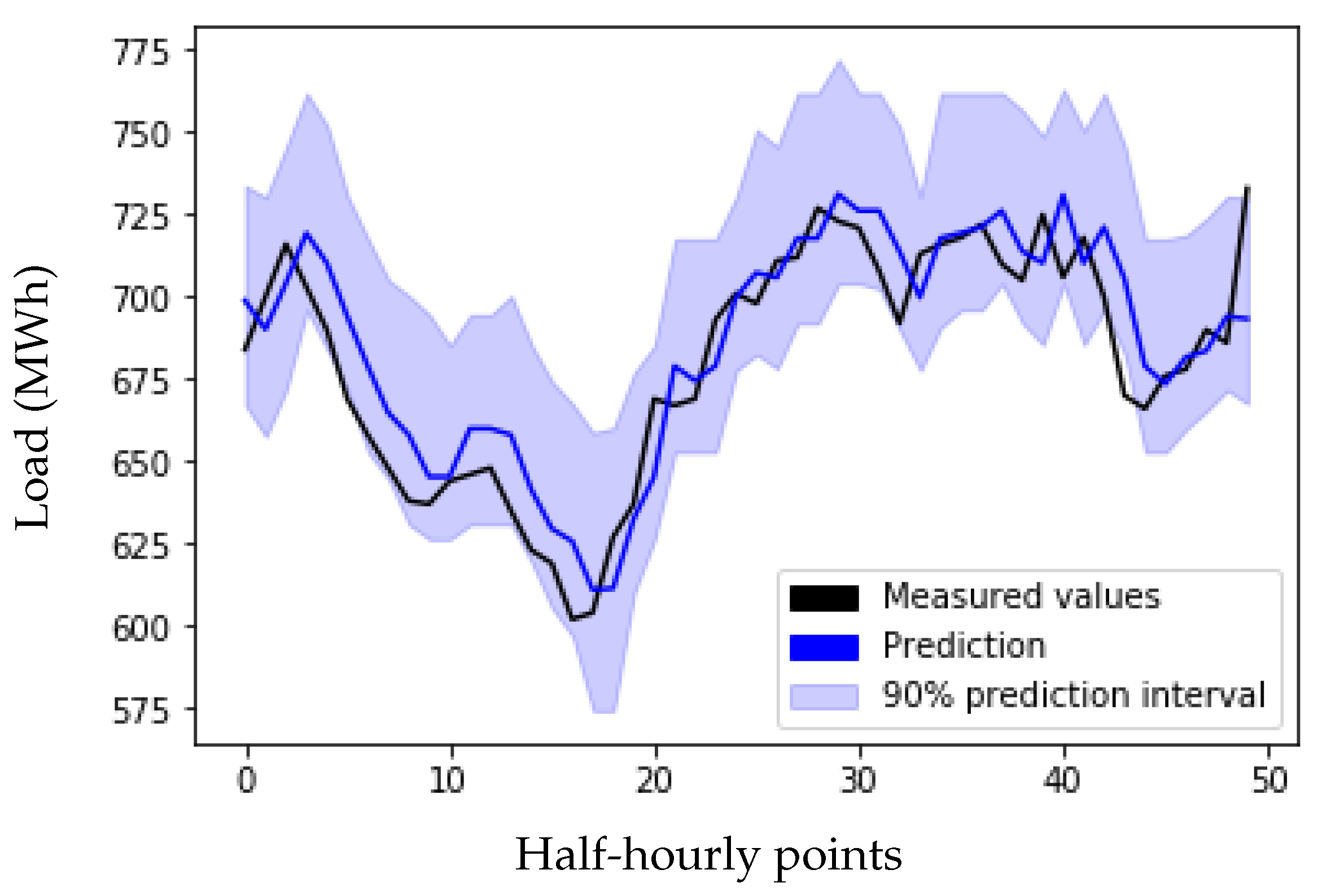
3.4. Experimental Results
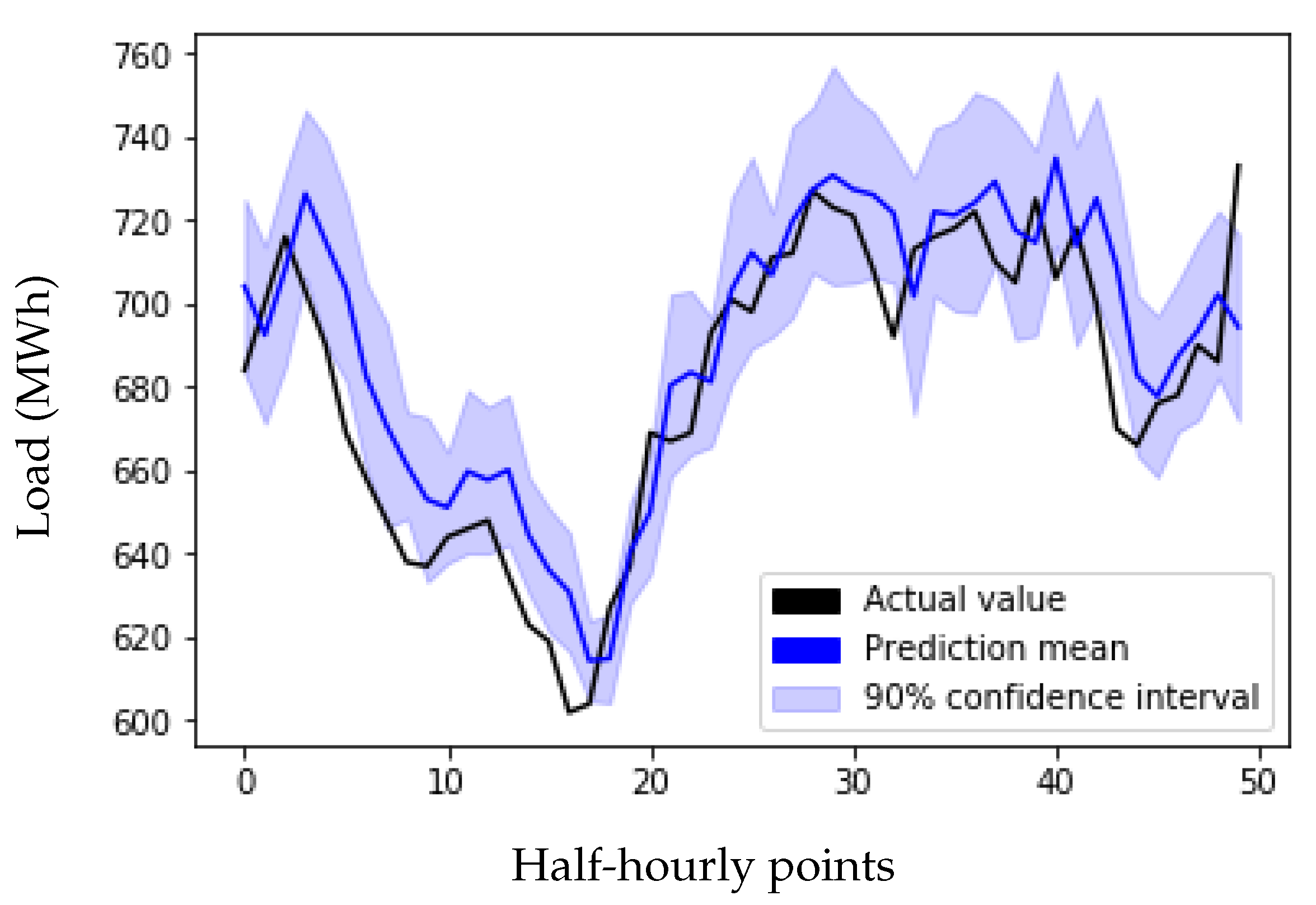
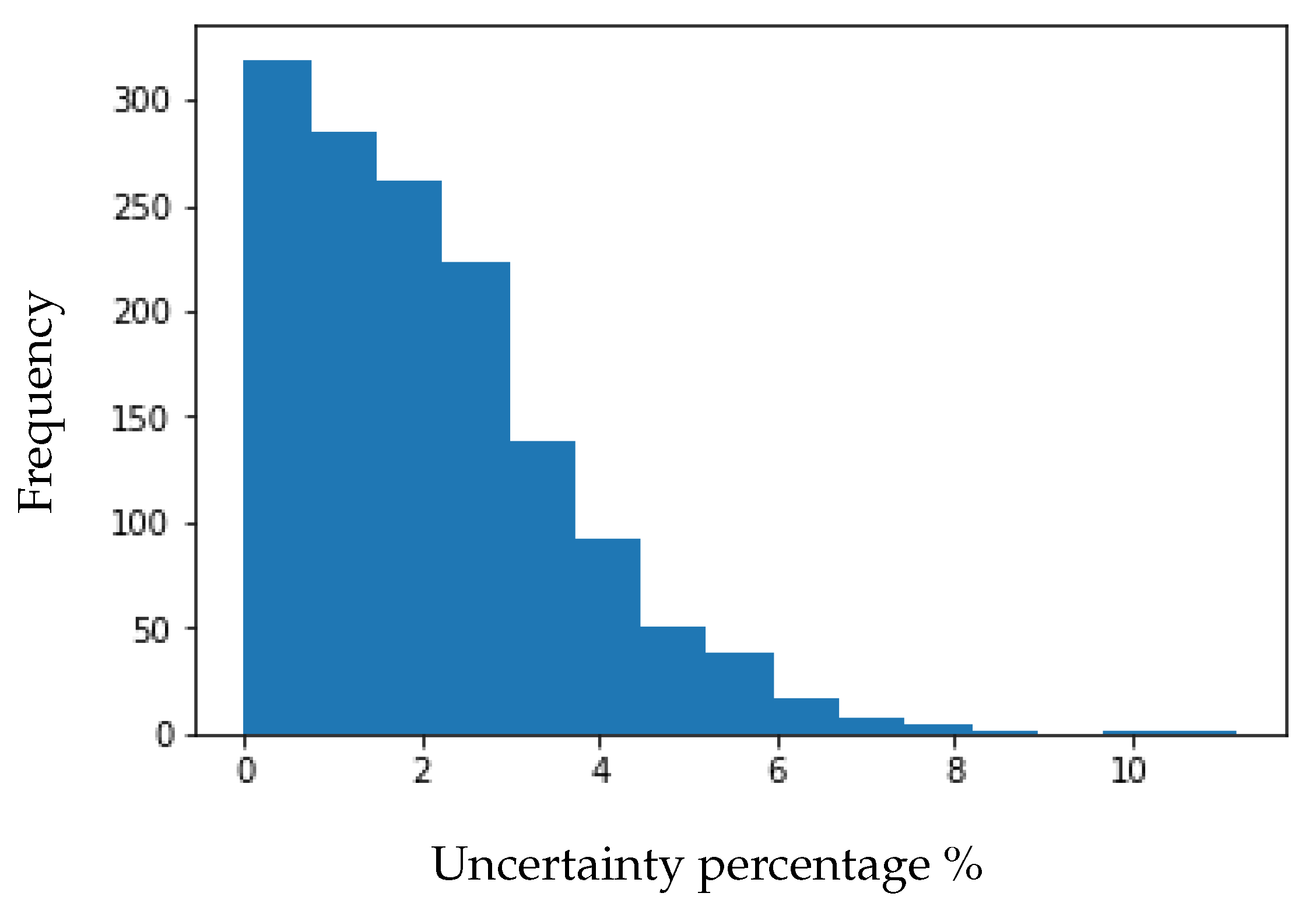
3.5. Uncertainty Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| STELF | Short-Term Electric Load Forecasting |
| AI | Artificial Intelligence |
| LSTM | Long Short-Term Memory |
| ANNs | Artificial Neural Networks |
| SVMs | Support Vector Machines |
| GBR | Gradient Tree Boosting |
| RMSE | Root Mean Square Error |
| MAPE | Mean Absolute Percent Error |
| EUNITE | European Network on Intelligent Technologies |
References
- Hong, Y.Y.; Lai, Y.M.; Chang, Y.R.; Lee, Y.D.; Liu, P.W. Optimizing capacities of distributed generation and energy storage in a small autonomous power system considering uncertainty in renewables. Energies 2015, 8, 2473–2492. [Google Scholar] [CrossRef]
- Toffanin, D. Generation of Customer Load Profiles Based on Smart-Metering Time Series, Building-Level Data and Aggregated Measurements. Ph.D. Thesis, Università degli Studi di Padova, Padova, Italy, 2016. [Google Scholar]
- Saleh, A.I.; Rabie, A.H.; Abo-Al-Ez, K.M. A data mining based load forecasting strategy for smart electrical grids. Adv. Eng. Inform. 2016, 30, 422–448. [Google Scholar] [CrossRef]
- Zhou, K.; Fu, C.; Yang, S. Big data driven smart energy management: From big data to big insights. Renew. Sustain. Energy Rev. 2016, 56, 215–225. [Google Scholar] [CrossRef]
- Bianchi, F.M.; Maiorino, E.; Kampffmeyer, M.C.; Rizzi, A.; Jenssen, R. An overview and comparative analysis of Recurrent Neural Networks for Short Term Load Forecasting. arXiv 2017, arXiv:1705.04378. [Google Scholar]
- Lilliu, F.; Loi, A.; Recupero, D.R.; Sisinni, M.; Vinyals, M. An uncertainty-aware optimization approach for flexible loads of smart grid prosumers: A use case on the Cardiff energy grid. Sustain. Energy Grids Netw. 2019, 20, 100272. [Google Scholar] [CrossRef]
- Kabir, H.D.; Khosravi, A.; Hosen, M.A.; Nahavandi, S. Neural network-based uncertainty quantification: A survey of methodologies and applications. IEEE Access 2018, 6, 36218–36234. [Google Scholar] [CrossRef]
- Kumari, P.A.; Geethanjali, P. Artificial Neural Network-Based Smart Energy Meter Monitoring and Control Using Global System for Mobile Communication Module. In Soft Computing for Problem Solving; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1–8. [Google Scholar]
- McAllister, R.; Gal, Y.; Kendall, A.; Van der Wilk, M.; Shah, A.; Cipolla, R.; Weller, A.V. Concrete problems for autonomous vehicle safety: Advantages of Bayesian deep learning. In Proceedings of the International Joint Conferences on Artificial Intelligence, New York, NY, USA, 9–15 July 2016. [Google Scholar]
- Gal, Y. Uncertainty in Deep Learning. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2017. [Google Scholar]
- Kontokosta, C.E.; Tull, C. A data-driven predictive model of city-scale energy use in buildings. Appl. Energy 2017, 197, 303–317. [Google Scholar] [CrossRef]
- Grolinger, K.; Capretz, M.A.; Seewald, L. Energy consumption prediction with big data: Balancing prediction accuracy and computational resources. In Proceedings of the 2016 IEEE International Congress on Big Data (BigData Congress), San Francisco, CA, USA, 27 June–2 July 2016; pp. 157–164. [Google Scholar]
- Amasyali, K.; El-Gohary, N.M. A review of data-driven building energy consumption prediction studies. Renew. Sustain. Energy Rev. 2018, 81, 1192–1205. [Google Scholar] [CrossRef]
- Browning, L.; Gould, S. ‘Big Data’ Is Solving the Problem of $200 Billion of Wasted Energy; Business Insider: New York, NY, USA, 2015. [Google Scholar]
- Olah, C. Understanding LSTM networks. GITHUB Blog 2015, 2015, 27. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Narayan, A.; Hipel, K.W. Long short term memory networks for short-term electric load forecasting. In Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Banff, AB, Canada, 5–8 October 2017; pp. 1050–1059. [Google Scholar]
- Gamboa, J.C.B. Deep learning for time-series analysis. arXiv 2017, arXiv:1701.01887. [Google Scholar]
- Zhu, L.; Laptev, N. Deep and Confident Prediction for Time Series at Uber. arXiv 2017, arXiv:1709.01907. [Google Scholar]
- Taieb, S.B.; Hyndman, R.J. A gradient boosting approach to the Kaggle load forecasting competition. Int. J. Forecast. 2014, 30, 382–394. [Google Scholar] [CrossRef]
- Ruiz-Abellón, M.; Gabaldón, A.; Guillamón, A. Load forecasting for a campus university using ensemble methods based on regression trees. Energies 2018, 11, 2038. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef] [PubMed]
- Géron, A. Hands-On Machine Learning with Scikit-Learn and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems; O’Reilly Media: Newton, MA, USA, 2017. [Google Scholar]
- Lipton, Z.C.; Berkowitz, J.; Elkan, C. A critical review of recurrent neural networks for sequence learning. arXiv 2015, arXiv:1506.00019. [Google Scholar]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-term residential load forecasting based on LSTM recurrent neural network. IEEE Trans. Smart Grid 2017, 10, 841–851. [Google Scholar] [CrossRef]
- Kendall, A.; Gal, Y. What uncertainties do we need in bayesian deep learning for computer vision? In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5580–5590. [Google Scholar]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; Balcan, M.F., Weinberger, K.Q., Eds.; PMLR: New York, NY, USA, 2016; Volume 48, pp. 1050–1059. [Google Scholar]
- Polson, N.G.; Sokolov, V. Deep Learning: A Bayesian Perspective. Bayesian Anal. 2017, 12, 1275–1304. [Google Scholar] [CrossRef]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R.R. Improving neural networks by preventing co-adaptation of feature detectors. arXiv 2012, arXiv:1207.0580. [Google Scholar]
- Srivastava, N.; Hinton, G.E.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Gal, Y.; Ghahramani, Z. A theoretically grounded application of dropout in recurrent neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 1019–1027. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive logistic regression: A statistical view of boosting (with discussion and a rejoinder by the authors). Ann. Stat. 2000, 28, 337–407. [Google Scholar] [CrossRef]
- Koenker, R.; Bassett, G., Jr. Regression quantiles. Econom. J. Econom. Soc. 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Biau, G.; Patra, B. Sequential quantile prediction of time series. IEEE Trans. Inf. Theory 2011, 57, 1664–1674. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Grus, J. Data Science from Scratch: First Principles with Python; O’Reilly Media: Newton, MA, USA, 2015. [Google Scholar]
- Brownlee, J. Introduction to Time Series Forecasting With Python; Machine Learning Mastery: Victoria, Australia, 2016. [Google Scholar]
- EUNITE Inc. EUNITE Electricity Load Forecast 2001 Competition; EUNITE: Irvine, CA, USA, 2001. [Google Scholar]
- Chen, B.J.; Chang, M.W.; Lin, C.J. Load forecasting using support vector machines: A study on EUNITE competition 2001. IEEE Trans. Power Syst. 2004, 19, 1821–1830. [Google Scholar] [CrossRef]
- Nagi, J.; Yap, K.S.; Nagi, F.; Tiong, S.K.; Ahmed, S.K. A computational intelligence scheme for the prediction of the daily peak load. Appl. Soft Comput. 2011, 11, 4773–4788. [Google Scholar] [CrossRef]
- Bontempi, G.; Taieb, S.B.; Le Borgne, Y.A. Machine learning strategies for time series forecasting. In Business Intelligence; Springer: Berlin/Heidelberg, Germany, 2013; pp. 62–77. [Google Scholar]
- Dietterich, T.G. Machine learning for sequential data: A review. In Joint IAPR International Workshops on Statistical Techniques in Pattern Recognition (SPR) and Structural and Syntactic Pattern Recognition (SSPR); Springer: Berlin/Heidelberg, Germany, 2002; pp. 15–30. [Google Scholar]


| Model | Configuration Parameters |
|---|---|
| LSTM | Input layer, 50 LSTM neurons, 1 neuron output layer |
| loss (mae), optimizer (adam), epochs (300), batch size (72) | |
| Gradient | booster(gbtree), colsample bytree (1), gamma (0) |
| Boosting | learning rate (0.1), delta step (0), max depth (3), No estimators (100) |
| Datetime | Load | Temperture | Weekday | Holidays |
|---|---|---|---|---|
| 1997-01-01 00:30:00 | 797.0 | −7.55 | 2 | 1 |
| 1997-01-01 01:00:00 | 794.0 | −7.55 | 2 | 1 |
| 1997-01-01 01:30:00 | 784.0 | −7.55 | 2 | 1 |
| 1997-01-01 02:00:00 | 787.0 | −7.55 | 2 | 1 |
| 1997-01-01 02:30:00 | 763.0 | −7.55 | 2 | 1 |
| LSTM | MC Dropout | GBR | |
|---|---|---|---|
| Model | LSTM Model | Model | |
| MAPE | 0.023 | 0.025 | 0.023 |
| RMSE | 18.025 | 18.48 | 17.42 |
| Load | Temperature | Weekday | Holiday |
|---|---|---|---|
| −0.05 | 0.03 | 0.00 | 0.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Selim, M.; Zhou, R.; Feng, W.; Quinsey, P. Estimating Energy Forecasting Uncertainty for Reliable AI Autonomous Smart Grid Design. Energies 2021, 14, 247. https://doi.org/10.3390/en14010247
Selim M, Zhou R, Feng W, Quinsey P. Estimating Energy Forecasting Uncertainty for Reliable AI Autonomous Smart Grid Design. Energies. 2021; 14(1):247. https://doi.org/10.3390/en14010247
Chicago/Turabian StyleSelim, Maher, Ryan Zhou, Wenying Feng, and Peter Quinsey. 2021. "Estimating Energy Forecasting Uncertainty for Reliable AI Autonomous Smart Grid Design" Energies 14, no. 1: 247. https://doi.org/10.3390/en14010247
APA StyleSelim, M., Zhou, R., Feng, W., & Quinsey, P. (2021). Estimating Energy Forecasting Uncertainty for Reliable AI Autonomous Smart Grid Design. Energies, 14(1), 247. https://doi.org/10.3390/en14010247







