Acoustic Emission Characteristics and Joint Nonlinear Mechanical Response of Rock Masses under Uniaxial Compression
Abstract
1. Introduction
2. Introduction to Laboratory Tests
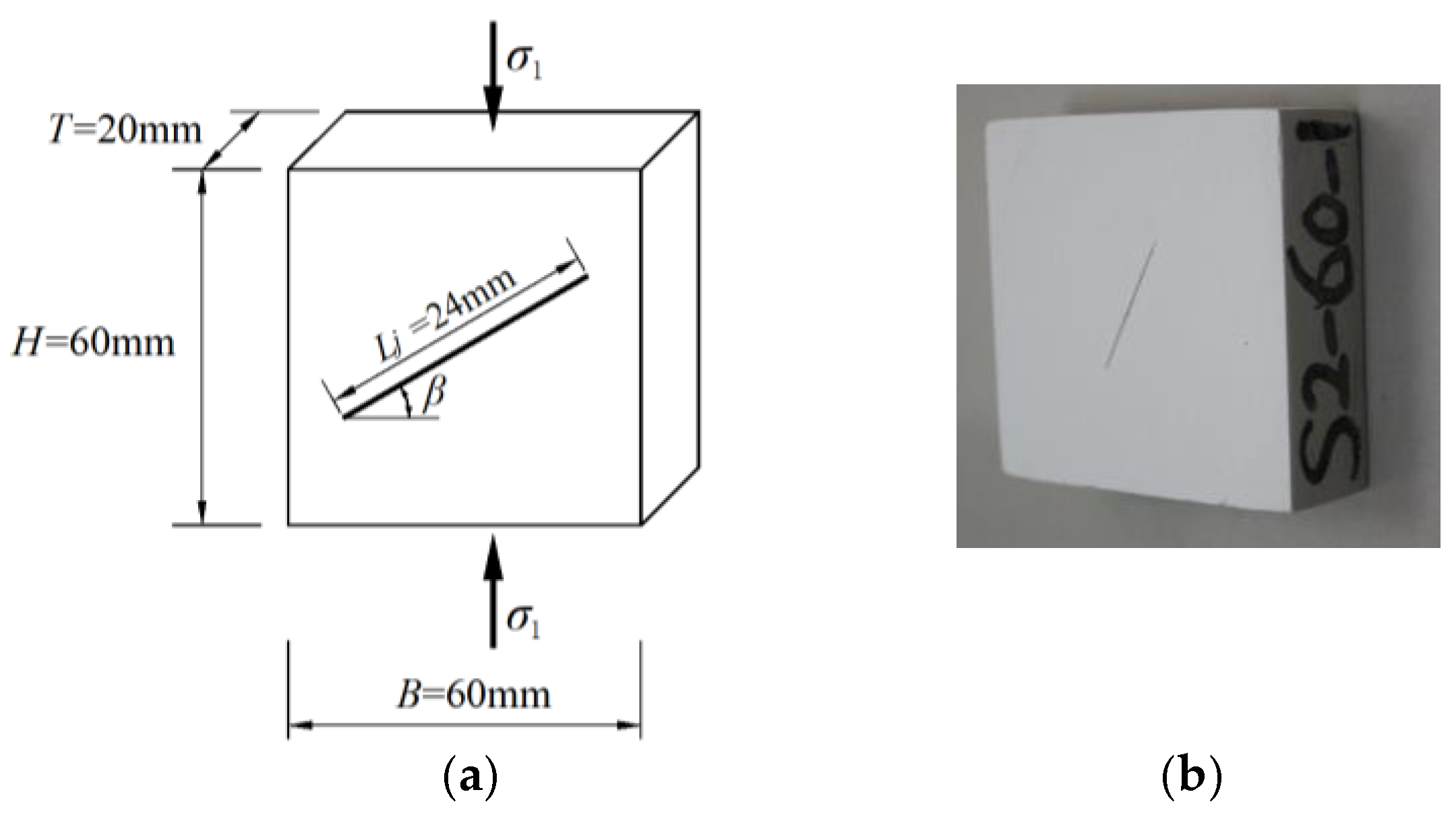
2.1. Specimen Preparation and Mechanical Properties of Materials
2.2. Experimental Setup and Conditions
2.3. AE Parameter Selection
3. Experimental Results
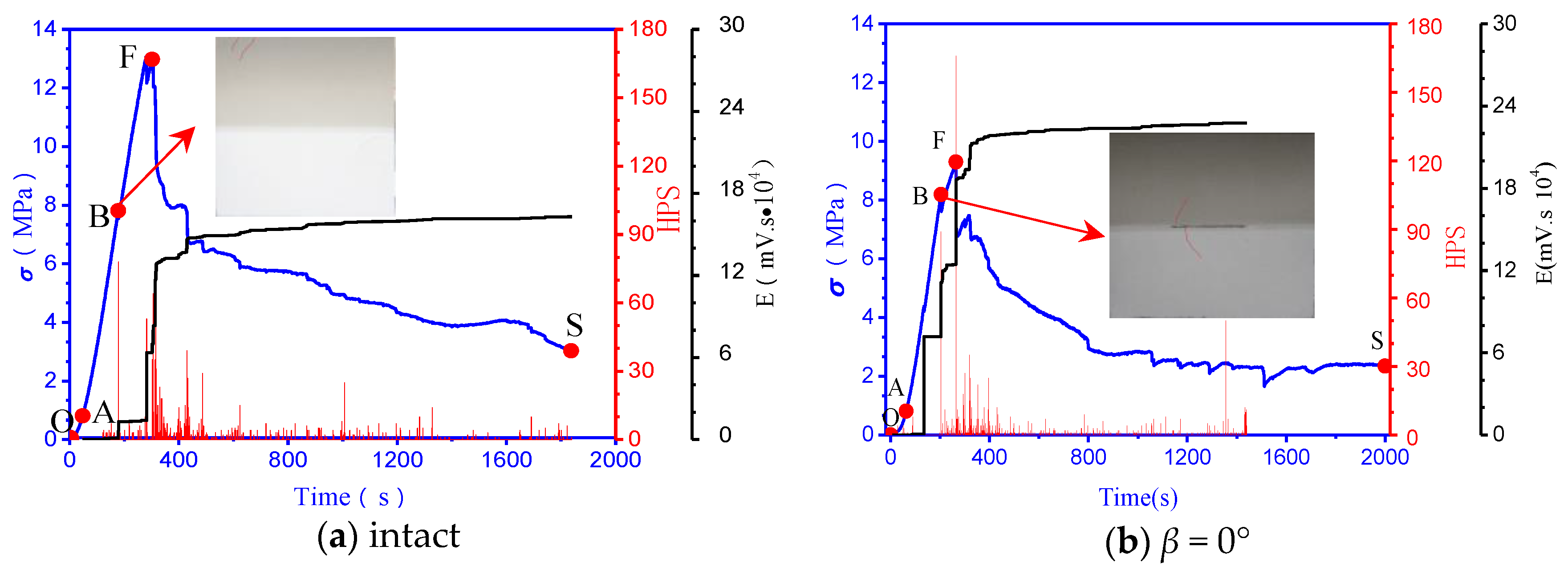
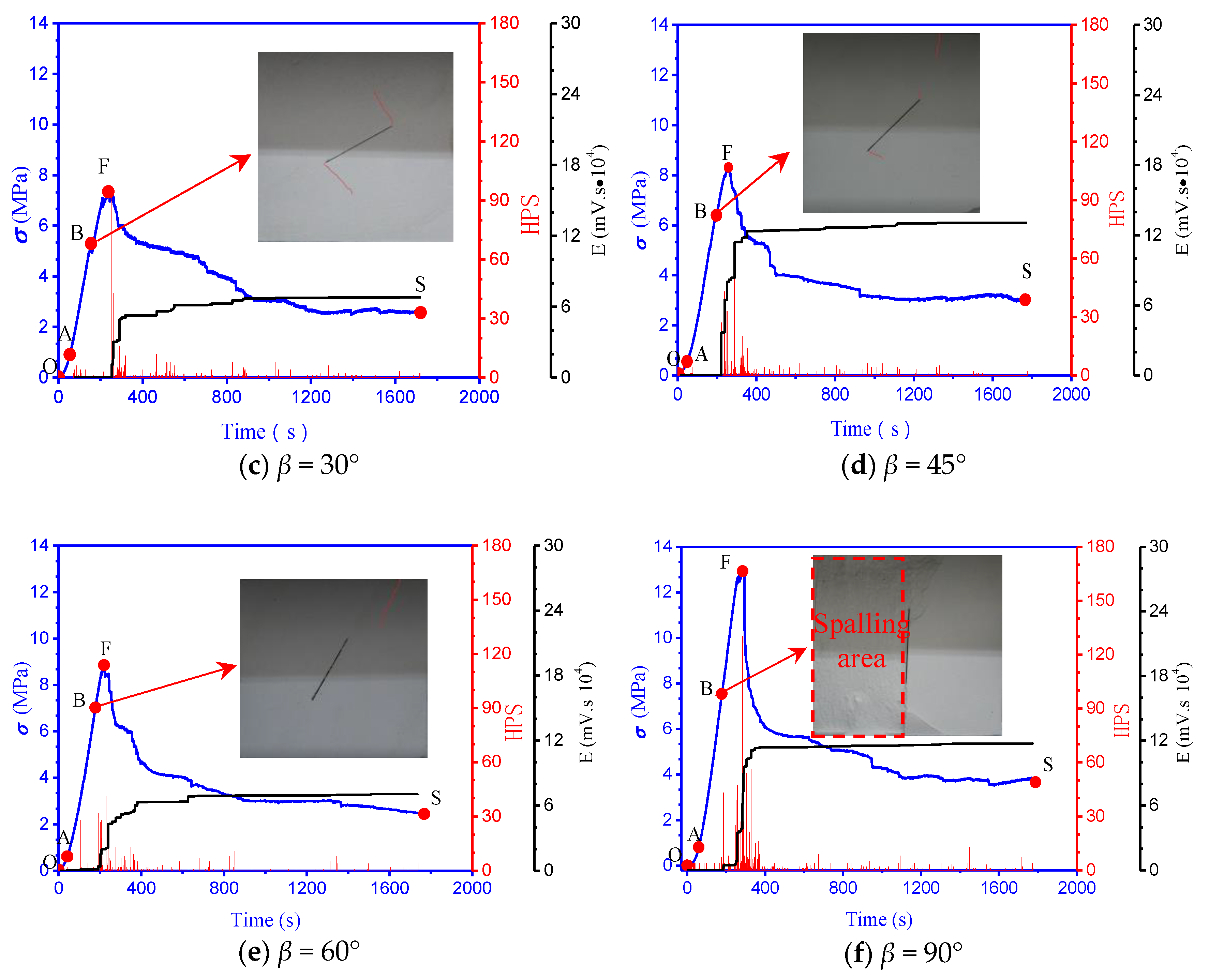
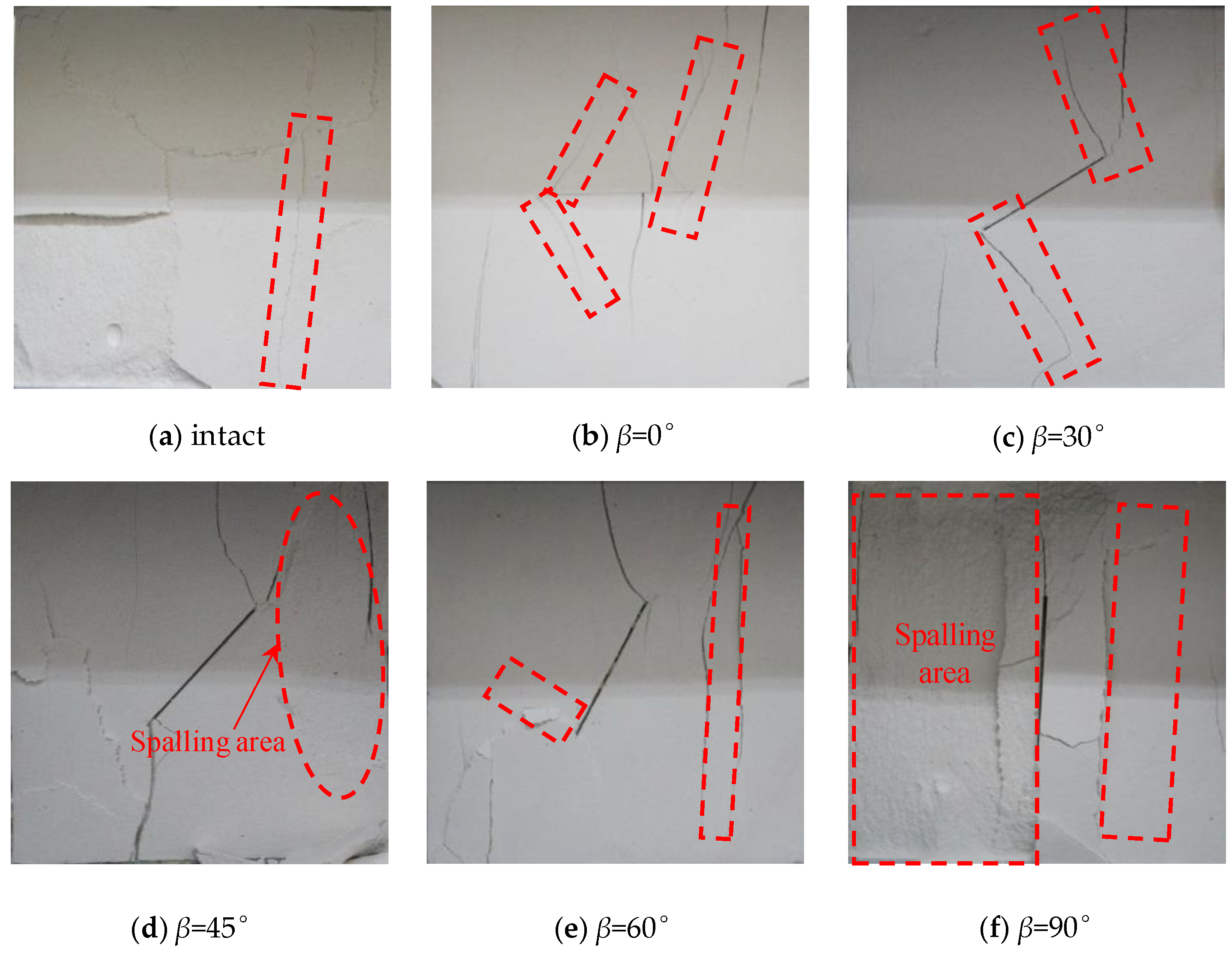
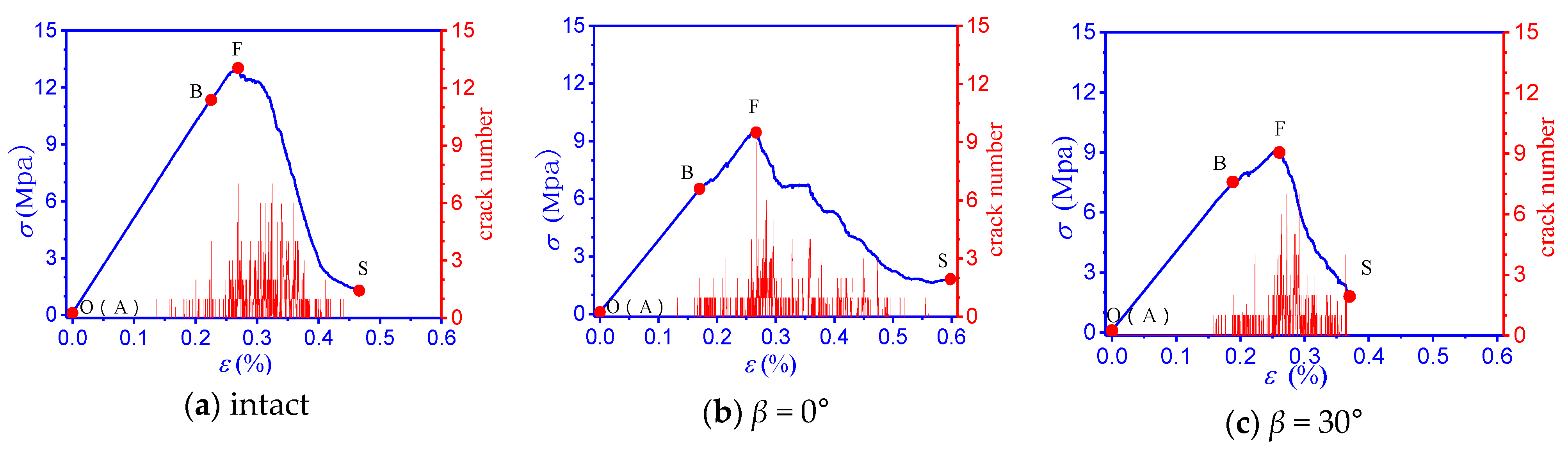
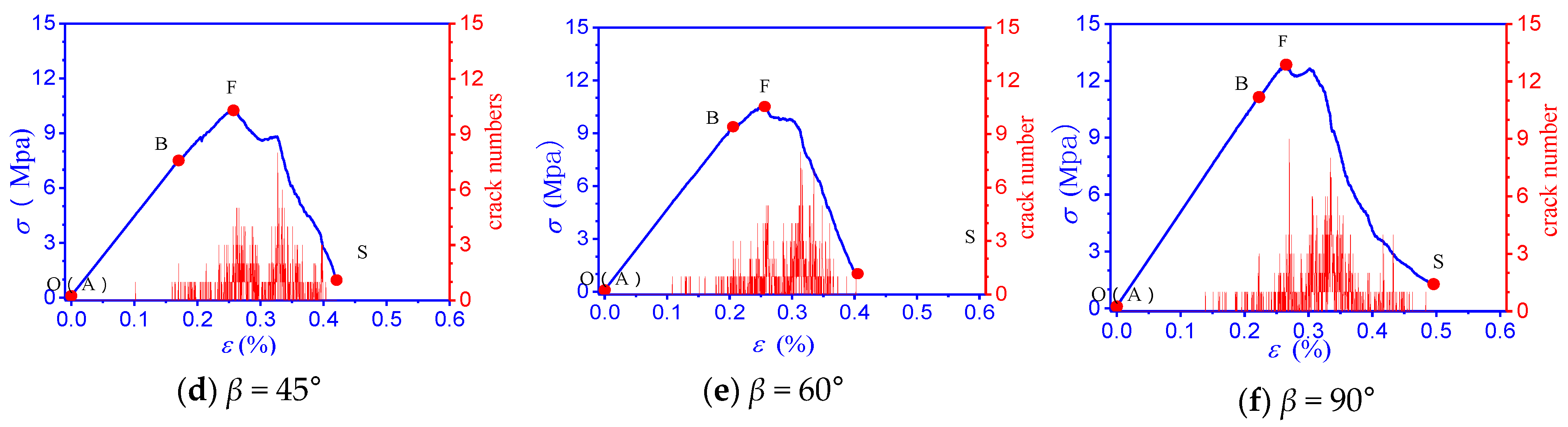
3.1. AE Sequential Characteristics and Failure Modes
- (1)
- For the specimens with low dip angles, for β = 0°, the failure mode was crushing; and in the plastic deformation stage, the propagation and coalescence of several thinner tensile cracks on the surface of the specimens occurred. These cracks were relatively small, the AE activity was dense throughout the entire stage, and the AE level was stable at a low level. For β = 30°, the failure mode was shear failure along the prefabricated joint plane. It had the smallest strength (7.34 MPa) compared with the jointed specimens with other angles, and the matrix damage was the lowest when the unstable failure occurred. Thus, the AE activity was weak and was only concentrated near the peak point.
- (2)
- For the specimens with medium inclination angles (β = 45° and 60°), which had a mixed type failure mode composed of shear failure and axial cleavage failure, the strength of the jointed specimens with inclination angles of 45° and 60° (8.31 MPa and 8.85 MPa, respectively) were between those of the specimens with inclination angles of 0° and 30°. In the plastic deformation stage, a large number of shear cracks formed in the specimens along the prefabricated joint plane. Furthermore, a long tensile crack formed along the loading axis (Figure 4d,e). Thus, the AE activity exhibited a dense rapid increase throughout the entire stage.
- (3)
- For the high joint angle specimens (β = 90°) and intact specimens, the failure mode was axial cleavage failure, which had a high strength compared with the jointed specimens with other angles. The matrix damage was very high when the instability destruction occurred. Thus, the AE activity was denser, and the average value was larger and was near the peak point.
3.2. Strength and Deformation Parameters
4. Numerical Models
4.1. Brief Introduction to the PFC2D Code and AE Simulation
4.2. Calibration of the Microparameters
4.3. Analysis of the AE Test Results of the PFC2D Model
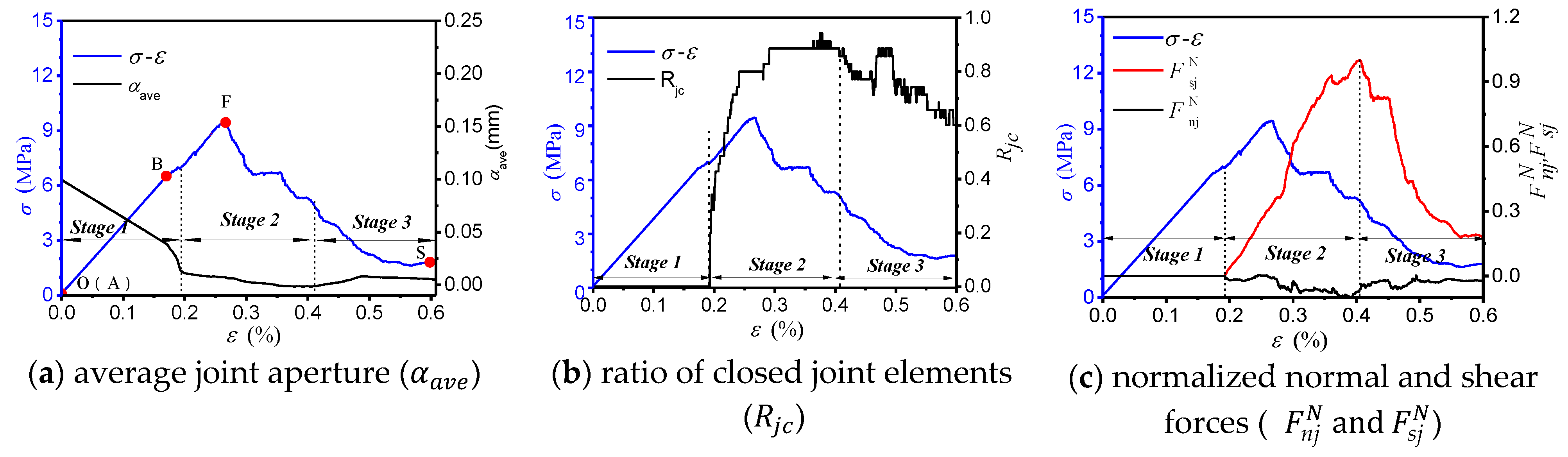
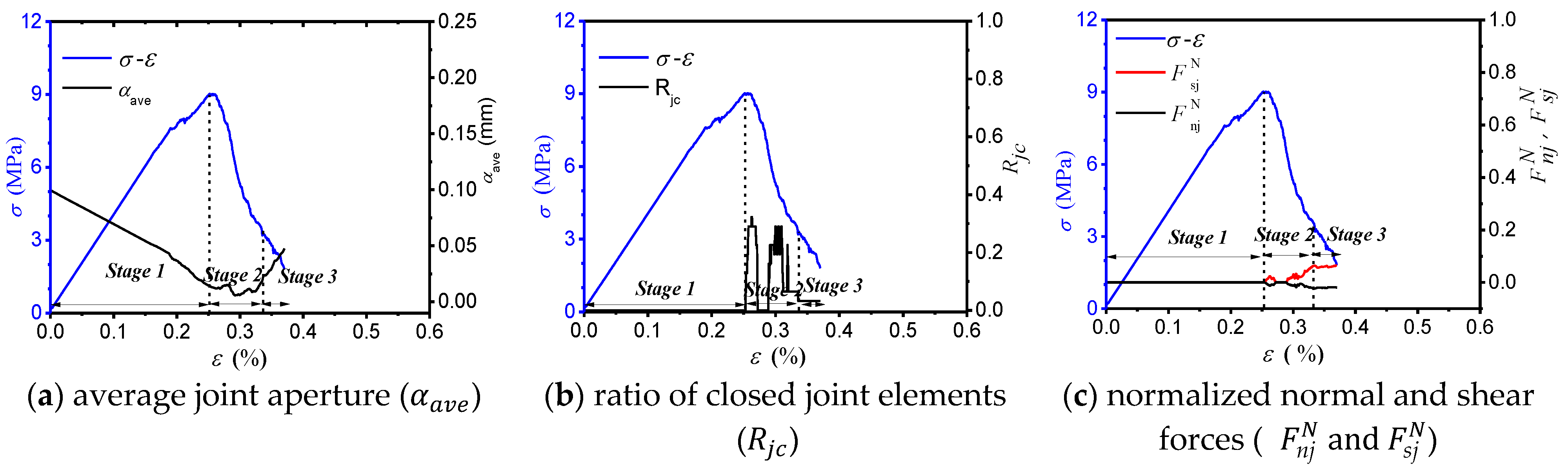
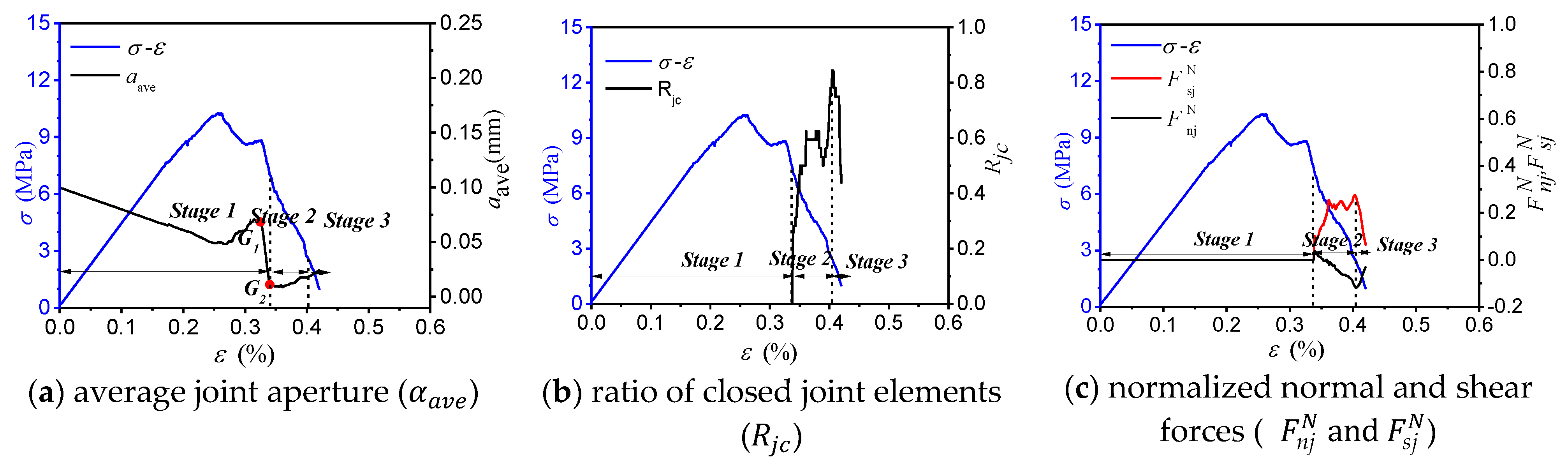
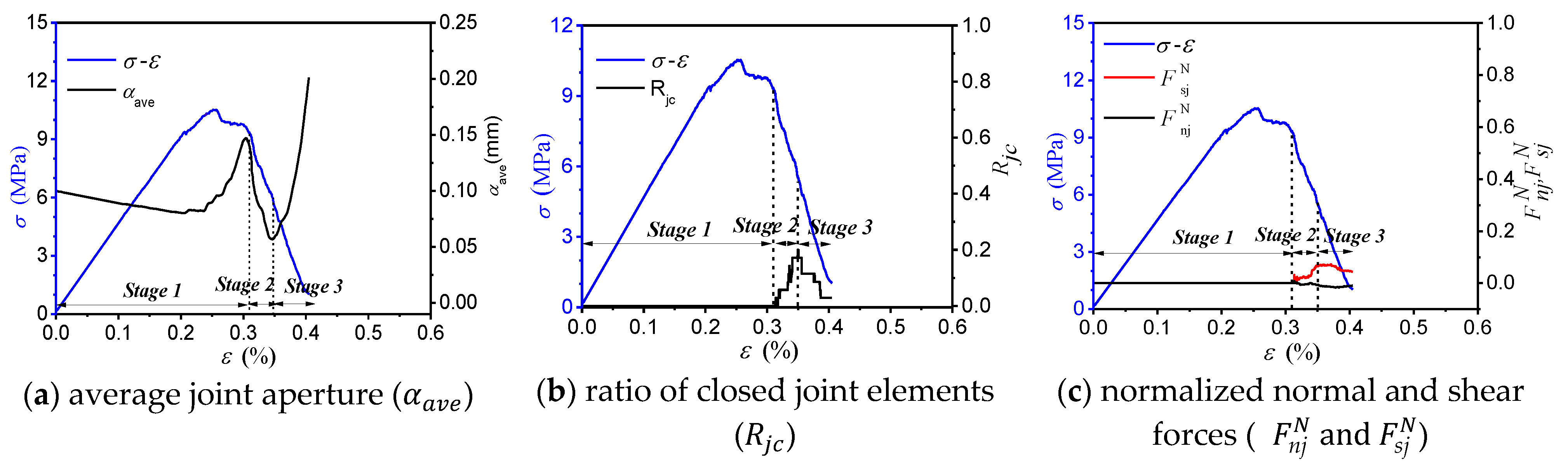
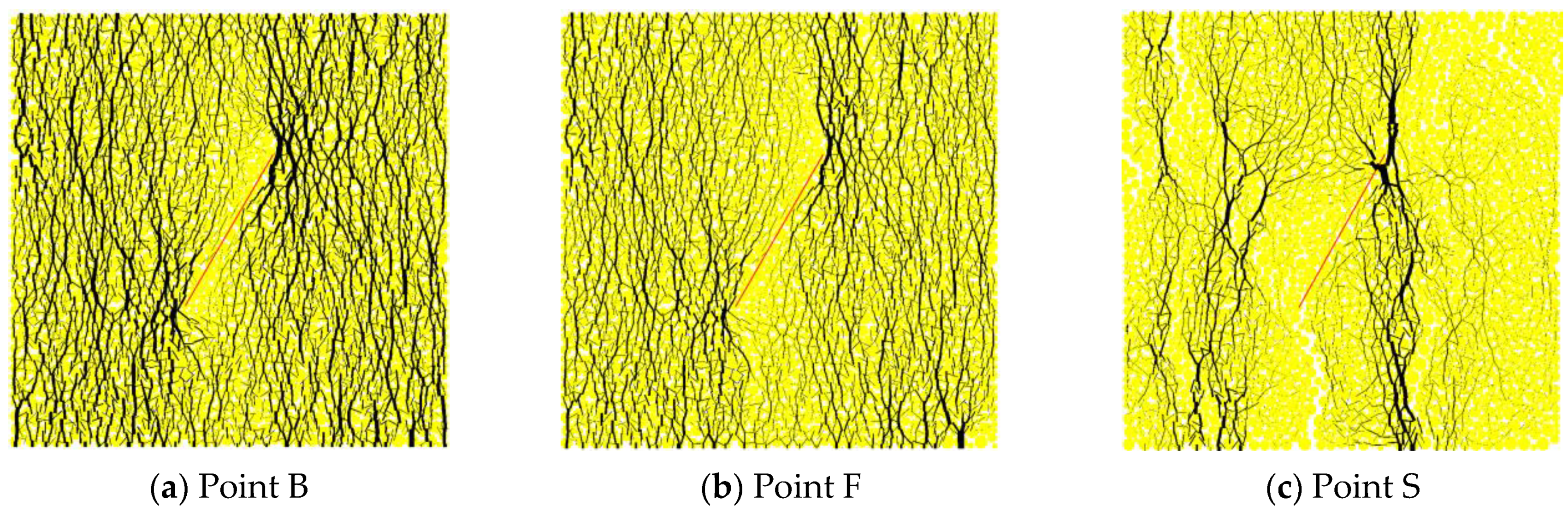
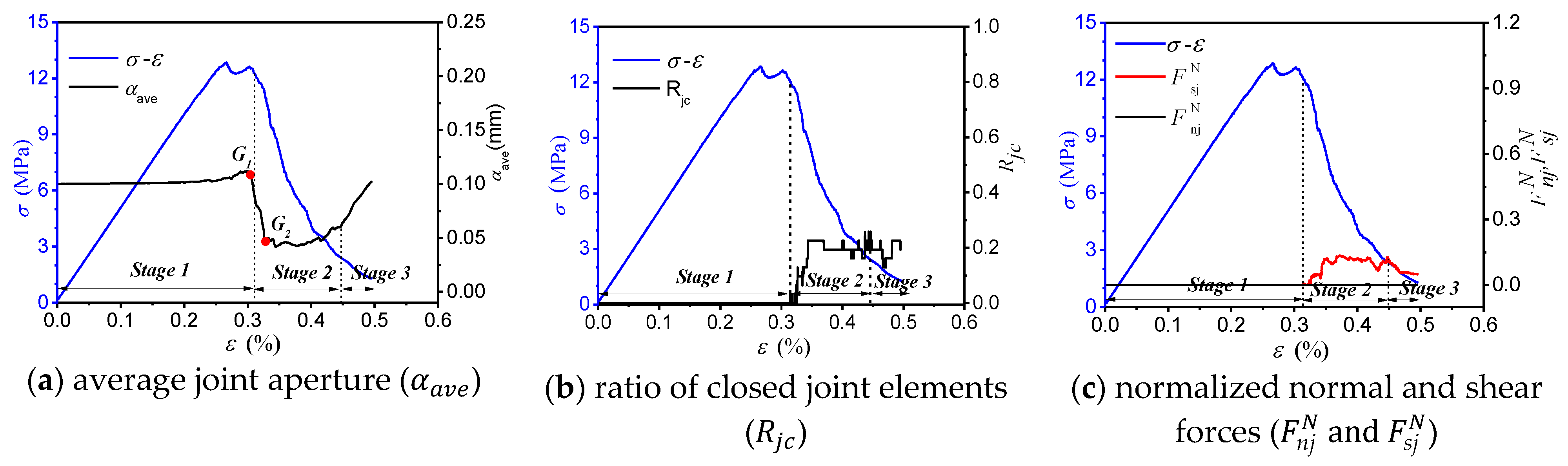
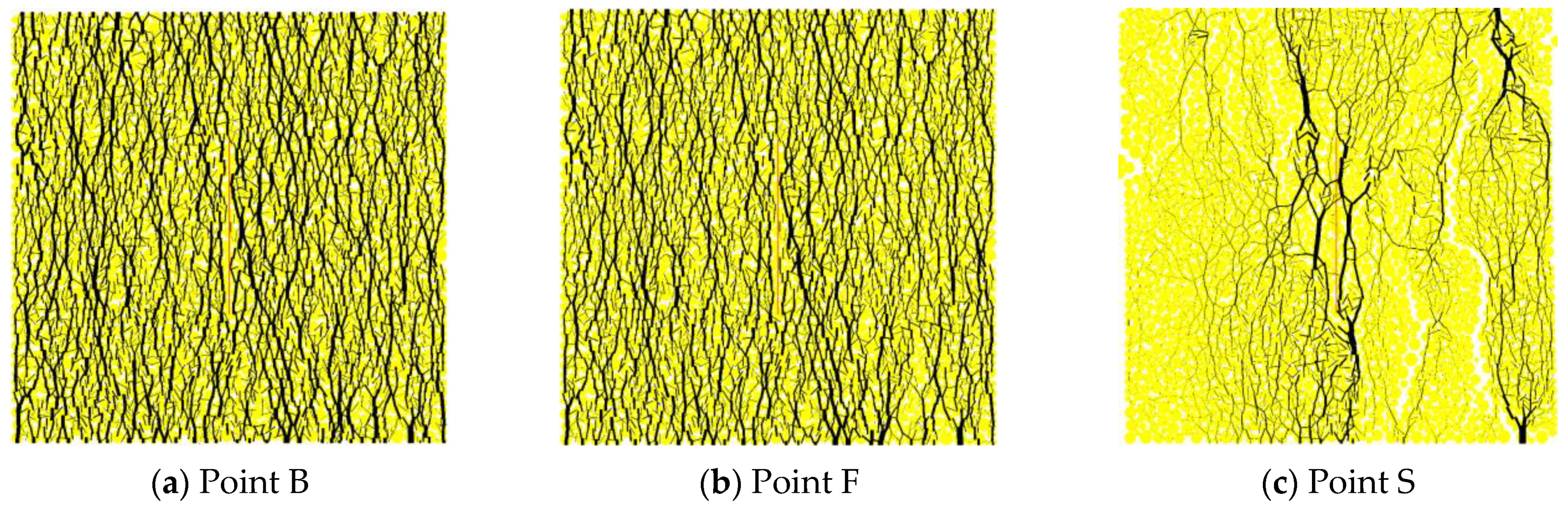
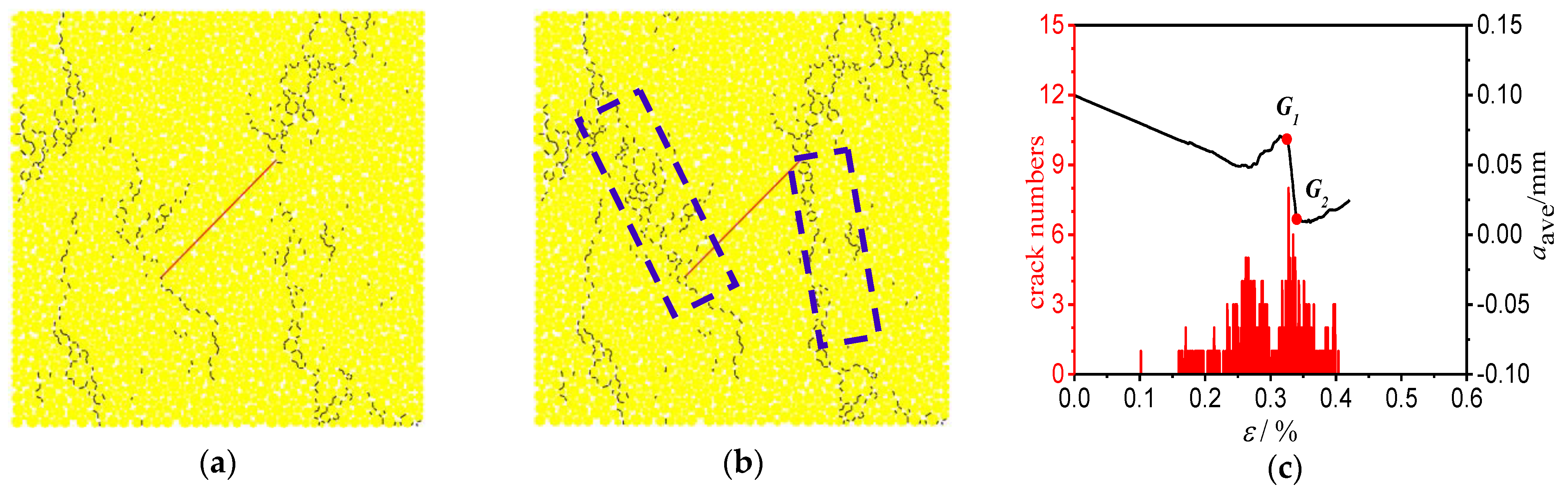
4.4. Response of the Pre-Existing Joint
5. Conclusions
- The AE characteristics have a good correlation with the failure mode of the specimens with different inclination angles. In the plastic deformation stage of the stress–strain curve, for the specimens with small inclination angles (β = 0°, 30°), the AE activity was stable at a low level and lasted for a long time, and the failure modes were crushing (β = 0°) and shear failure (β = 30°). For the specimens with medium inclination angles (β = 45°, 60°), the AE exhibited a dense rapid increase in the form of a pulse throughout the entire stage, and it had a mixed type failure mode consisting of shear failure and axial cleavage failure. For the high joint angle specimens (β = 90°) and intact specimens, the AE distribution was a pulse, which was denser and had a larger average value near the peak point (point F), and the failure mode was axial cleavage failure.
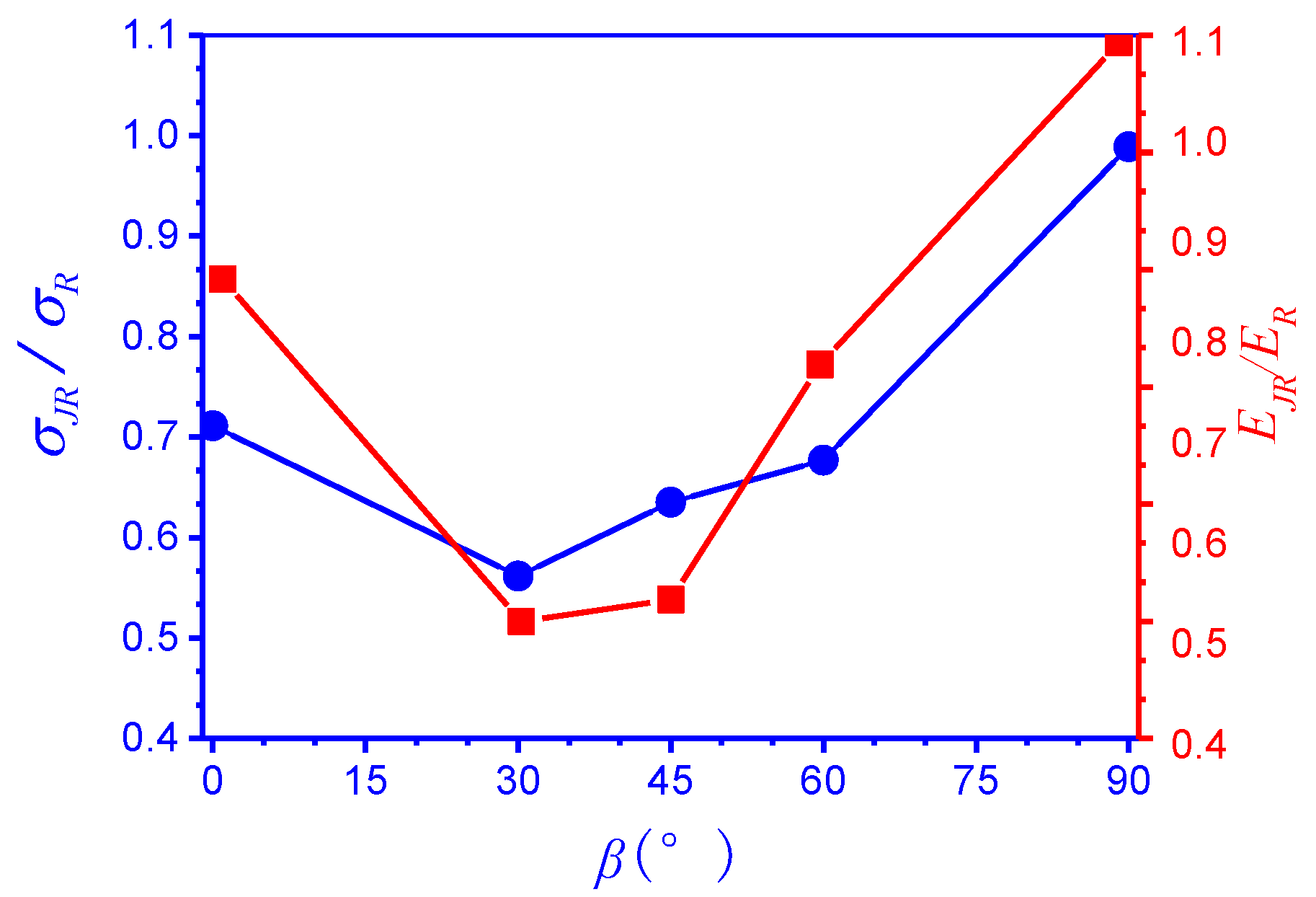
- The variations in the peak strength and the Young’s modulus with β are V-shaped or U-shaped, with a minima and maxima at β = 30° and 90°, respectively.
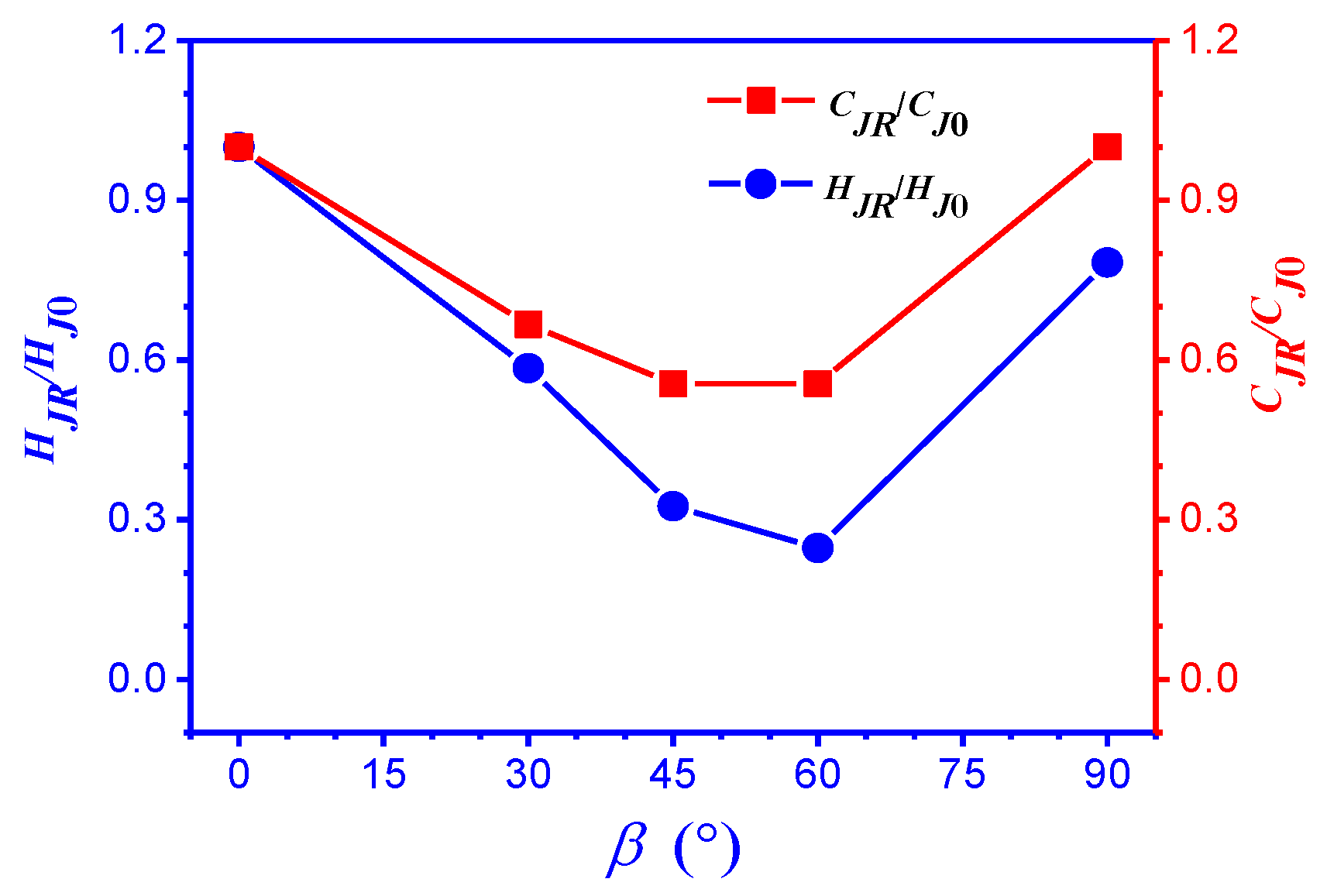
- As the joint inclination angle increased, the AE characteristic evolution curve gradually transformed from a single peak type curve to a double peak type curve. For the specimens with medium and high inclination angles, the generation of the second peak point on the evolution curve of the AE characteristics was closely related to the response of the pre-existing joint.
- In the post-peak failure stage (FS), for the specimens with medium and high inclination angles (β = 45°, 60° and 90°), the stronger AE activity corresponded to an instantaneous decrease in the average joint aperture (), which was related to the failure mode of the specimens.
- The response of the pre-existing joint in the numerical model can be divided into three stages based on the varied mobilization of the joint strength: (I) the closing of the pre-existing joint; (II) the strength mobilization of the pre-existing joint; and (III) the reopening of the pre-existing joint. As the joint inclination angle increased, the strength mobilization stage of the joint system gradually shifted from the pre-peak stage of the stress-strain curve to the post-peak stage.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cai, M.; Kaiser, P.K.; Martin, C.D. Quantification of rock mass damage in underground excavations from microseismic event monitoring. Int. J. Rock Mech. Min. Sci. 2001, 38, 1135–1145. [Google Scholar] [CrossRef]
- Li, S.L.; Tang, H.Y. Acoustic emission characteristics in failure process of rock under different uniaxial compressive loads. Yantu Gongcheng Xuebao Chin. J. Geotech. Eng. 2010, 32, 147–152. [Google Scholar]
- Blake, W. Microseismic Applications for Mining–A Practical Guide; Bureau of Mines: Washington, DC, USA, 1982.
- Kong, B.; Wang, E.; Li, Z.; Wang, X.; Niu, Y.; Kong, X. Acoustic emission signals frequency-amplitude characteristics of sandstone after thermal treated under uniaxial compression. J. Appl. Geophys. 2017, 136, 190–197. [Google Scholar] [CrossRef]
- Han, G.; Jing, H.; Jiang, Y.; Liu, R.; Su, H.; Wu, J. The effect of joint dip angle on the mechanical behavior of infilled jointed rock masses under uniaxial and biaxial compressions. Processes 2018, 6, 49. [Google Scholar] [CrossRef]
- Meng, Q.; Zhang, M.; Han, L.; Pu, H.; Nie, T. Effects of Acoustic Emission and Energy Evolution of Rock Specimens Under the Uniaxial Cyclic Loading and Unloading Compression. Rock Mech. Rock Eng. 2016, 49, 3873–3886. [Google Scholar] [CrossRef]
- Wang, J.; Xie, L.; Xie, H.; Ren, L.; He, B.; Li, C.; Yang, Z.; Gao, C. Effect of layer orientation on acoustic emission characteristics of anisotropic shale in Brazilian tests. J. Nat. Gas. Sci. Eng. 2016, 36, 1120–1129. [Google Scholar] [CrossRef]
- Ishida, T.; Kanagawa, T.; Kanaori, Y. Source distribution of acoustic emissions during an in-situ direct shear test: Implications for an analog model of seismogenic faulting in an inhomogeneous rock mass. Eng. Geol. 2010, 110, 66–76. [Google Scholar] [CrossRef]
- Wang, H.; Liu, D.; Cui, Z.; Cheng, C.; Jian, Z. Investigation of the fracture modes of red sandstone using XFEM and acoustic emissions. Theor. Appl. Fract. Mech. 2016, 85, 283–293. [Google Scholar] [CrossRef]
- Katsuyama, K. Application of AE techniques; Metallurgy Industry Press: Beijing, China, 1996. [Google Scholar]
- Holcomb, D.J.; Costin, L.S. Detecting damage surfaces in brittle materials using acoustic emissions. J. Appl. Mech. Trans. ASME 1986, 53, 536–545. [Google Scholar] [CrossRef]
- Pestman, B.J.; Van Munster, J.G. An acoustic emission study of damage development and stress-memory effects in sandstone. Int. J. Rock Mech. Min. Sci. Geomech. 1996, 33, 585–593. [Google Scholar] [CrossRef]
- Liu, T.; Lin, B.; Yang, W. Mechanical behavior and failure mechanism of pre-cracked specimen under uniaxial compression. Tectonophysics 2017, 712–713, 330–343. [Google Scholar] [CrossRef]
- Jiang, Y.; Luan, H.; Wang, D.; Wang, C.; Han, W. Failure Mechanism and Acoustic Emission Characteristics of Rock Specimen with Edge Crack Under Uniaxial Compression. Geotech. Geol. Eng. 2019, 37, 2135–2145. [Google Scholar] [CrossRef]
- Li, D.; Wang, E.; Kong, X.; Ali, M.; Wang, D. Mechanical behaviors and acoustic emission fractal characteristics of coal specimens with a pre-existing flaw of various inclinations under uniaxial compression. Int. J. Rock Mech. Min. Sci. 2019, 116, 38–51. [Google Scholar] [CrossRef]
- Hazzard, J.F.; Young, R.P. Simulating acoustic emissions in bonded-particle models of rock. Int. J. Rock Mech. Min. Sci. 2000, 37, 867–872. [Google Scholar] [CrossRef]
- Hazzard, J.F.; Young, R.P. Dynamic modelling of induced seismicity. Int. J. Rock Mech. Min. Sci. 2004, 41, 1365–1376. [Google Scholar] [CrossRef]
- Su, H.; Dang, C.H.; Li, Y.J. Study of numerical simulation of acoustic emission in rock of inhomogeneity. Yantu Lixue Rock Soil Mech. 2011, 32, 1886–1890. [Google Scholar] [CrossRef]
- Wang, P.; Yang, T.; Xu, T.; Cai, M.; Li, C. Numerical analysis on scale effect of elasticity, strength and failure patterns of jointed rock masses. Geosci. J. 2016, 20, 539–549. [Google Scholar] [CrossRef]
- Cai, M.; Kaiser, P.K.; Morioka, H.; Minami, M.; Maejima, T.; Tasaka, Y.; Kurose, H. FLAC/PFC coupled numerical simulation of AE in large-scale underground excavations. Int. J. Rock Mech. Min. Sci. 2007, 44, 550–564. [Google Scholar] [CrossRef]
- Shang, J.; Hencher, S.R.; West, L.J. Tensile Strength of Geological Discontinuities Including Incipient Bedding, Rock Joints and Mineral Veins. Rock Mech. Rock Eng. 2016, 49, 4213–4225. [Google Scholar] [CrossRef]
- Wasantha, P.L.P.; Ranjith, P.G.; Xu, T.; Zhao, J.; Yan, Y.L. A new parameter to describe the persistency of non-persistent joints. Eng. Geol. 2014. [Google Scholar] [CrossRef]
- Wong, R.H.C.; Chau, K.T.; Tang, C.A.; Lin, P. Analysis of crack coalescence in rock-like materials containing three flaws—Part I: Experimental approach. Int. J. Rock Mech. Min. Sci. 2001, 38, 909–924. [Google Scholar] [CrossRef]
- Zhang, H.Q.; Zhao, Z.Y.; Tang, C.A.; Song, L. Numerical study of shear behavior of intermittent rock joints with different geometrical parameters. Int. J. Rock Mech. Min. Sci. 2006. [Google Scholar] [CrossRef]
- Gehle, C.; Kutter, H.K. Breakage and shear behaviour of intermittent rock joints. Int. J. Rock Mech. Min. Sci. 2003. [Google Scholar] [CrossRef]
- Halakatevakis, N.; Sofianos, A.I. Strength of a blocky rock mass based on an extended plane of weakness theory. Int. J. Rock Mech. Min. Sci. 2010. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, B.; Yamashita, Y. Simulation of cracking near a large underground cavern in a discontinuous rock mass using the expanded distinct element method. Int. J. Rock Mech. Min. Sci. 2009. [Google Scholar] [CrossRef]
- Kulatilake, P.H.S.W.; Ucpirti, H.; Wang, S.; Radberg, G.; Stephansson, O. Use of the distinct element method to perform stress analysis in rock with non-persistent joints and to study the effect of joint geometry parameters on the strength and deformability of rock masses. Rock Mech. Rock Eng. 1992. [Google Scholar] [CrossRef]
- Ghazvinian, A.; Sarfarazi, V.; Schubert, W.; Blumel, M. A study of the failure mechanism of planar non-persistent open joints using PFC2D. Rock Mech. Rock Eng. 2012. [Google Scholar] [CrossRef]
- Fan, X.; Kulatilake, P.H.S.W.; Chen, X. Mechanical behavior of rock-like jointed blocks with multi-non-persistent joints under uniaxial loading: A particle mechanics approach. Eng. Geol. 2015. [Google Scholar] [CrossRef]
- Sagong, M.; Park, D.; Yoo, J.; Lee, J.S. Experimental and numerical analyses of an opening in a jointed rock mass under biaxial compression. Int. J. Rock Mech. Min. Sci. 2011, 48, 1055–1067. [Google Scholar] [CrossRef]
- Cheng, C.; Chen, X.; Zhang, S. Multi-peak deformation behavior of jointed rock mass under uniaxial compression: Insight from particle flow modeling. Eng. Geol. 2016, 213, 25–45. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, S.; Cheng, C. Numerical study on effect of joint strength mobilization on behavior of rock masses with large nonpersistent joints under uniaxial compression. Int. J. Geomech. 2018, 18, 1–21. [Google Scholar] [CrossRef]
- Shang, J. Rupture of Veined Granite in Polyaxial Compression: Insights From Three-Dimensional Discrete Element Method Modeling. J. Geophys. Res. Solid Earth 2020, 125, e2019JB019052. [Google Scholar] [CrossRef]
- Wang, S.; Liu, Y.; Chen, X.; Yang, Q. Failure analysis of pre-cracked specimen based on acoustic emission technique. Shuili Fadian Xuebao J. Hydroelectr. Eng. 2019, 38, 110–120. [Google Scholar] [CrossRef]
- Song, Y.; Xing, T.; Zhao, T.; Zhao, Z.; Gao, P. Acoustic emission characteristics of deformation field development of rock under uniaxial loading. Yanshilixue Yu Gongcheng Xuebao Chin. J. Rock Mech. Eng. 2017, 36, 534–542. [Google Scholar] [CrossRef]
- Chen, X.; Liao, Z.H.; Peng, X. Cracking process of rock mass models under uniaxial compression. J. Cent. South. Univ. 2013, 20, 1661–1678. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1980, 30, 331–336. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Mas Ivars, D.; Pierce, M.E.; Darcel, C.; Reyes-Montes, J.; Potyondy, D.O.; Paul Young, R.; Cundall, P.A. The synthetic rock mass approach for jointed rock mass modelling. Int. J. Rock Mech. Min. Sci. 2011, 48, 219–244. [Google Scholar] [CrossRef]
- Hazzard, J.F.; Young, R.P.; Maxwell, S.C. Micromechanical modeling of cracking and failure in brittle rocks. J. Geophys. Res. Solid Earth 2000, 105, 16683–16697. [Google Scholar] [CrossRef]
- Yoon, J. Application of experimental design and optimization to PFC model calibration in uniaxial compression simulation. Int. J. Rock Mech. Min. Sci. 2007, 44, 871–889. [Google Scholar] [CrossRef]
- Shang, J.; Zhao, Z.; Hu, J.; Handley, K. 3D Particle-Based DEM Investigation into the Shear Behaviour of Incipient Rock Joints with Various Geometries of Rock Bridges. Rock Mech. Rock Eng. 2018, 51, 3563–3584. [Google Scholar] [CrossRef]






| Unit Weight γ (kN/m3) | UCS (MPa) | Young’s Modulus E (GPa) | Poisson’s Ratio v | Cohesion c (MPa) | Internal Friction Angle φ (°) |
|---|---|---|---|---|---|
| 11.69 | 12.54 | 5.6 | 0.23 | 3.0 | 34 |
| Characteristic Points | Definition |
|---|---|
| O | Start point of test |
| A | Start point of elastic deformation |
| B | Start point of plastic deformation |
| F | Peak strength point |
| S | End point of test |
| Ball Parameters | Value | Parallel Bond Parameters | Value |
|---|---|---|---|
| Ball density [ (kg/m3)] | 1169 | Bond modulus [ (GPa)] | 4.17 |
| Minimum ball radius [ (mm)] | 0.6 | Normal bond strength [ (MPa)] | 9.2 |
| Ball radius ratio () | 1.66 | S.D. normal bond strength [ (MPa)] | 3.78 |
| Contact modulus [ (GPa)] | 4.17 | Cohesion [ (MPa)] | 20 |
| Friction coefficient (μ) | 0.5 | S.D. cohesion [ (MPa)] | 5.0 |
| Normal to shearing stiffness ratio () | 2.5 | Friction angle (°) | 30 |
| Normal to shearing bond stiffness ratio () | 2.5 |
| Macroscopic Properties | Experimental | Numerical |
|---|---|---|
| Uniaxial compressive strength [UCS (MPa)] | 13.08 | 13.20 |
| Young’s modulus [E (GPa)] | 5.03 | 4.38 |
| Smooth-Joint Parameters | Value |
|---|---|
| Joint friction angle (°) | 38 |
| Joint dilation angle (°) | 0 |
| Joint normal stiffness (N/m3) | 1.0 × 1012 |
| Joint shear stiffness (N/m3) | 1.0 × 1012 |
| Joint aperture (mm) | 0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Z.; Chen, X.; Fu, Y.; Qing, S.; Xie, T. Acoustic Emission Characteristics and Joint Nonlinear Mechanical Response of Rock Masses under Uniaxial Compression. Energies 2021, 14, 200. https://doi.org/10.3390/en14010200
Feng Z, Chen X, Fu Y, Qing S, Xie T. Acoustic Emission Characteristics and Joint Nonlinear Mechanical Response of Rock Masses under Uniaxial Compression. Energies. 2021; 14(1):200. https://doi.org/10.3390/en14010200
Chicago/Turabian StyleFeng, Zhongliang, Xin Chen, Yu Fu, Shaoshuai Qing, and Tongguan Xie. 2021. "Acoustic Emission Characteristics and Joint Nonlinear Mechanical Response of Rock Masses under Uniaxial Compression" Energies 14, no. 1: 200. https://doi.org/10.3390/en14010200
APA StyleFeng, Z., Chen, X., Fu, Y., Qing, S., & Xie, T. (2021). Acoustic Emission Characteristics and Joint Nonlinear Mechanical Response of Rock Masses under Uniaxial Compression. Energies, 14(1), 200. https://doi.org/10.3390/en14010200






