Preventive Security-Constrained Optimal Power Flow with Probabilistic Guarantees
Abstract
:1. Introduction
1.1. Literature Review
1.2. Contributions
2. Review of Traditional PSCOPF
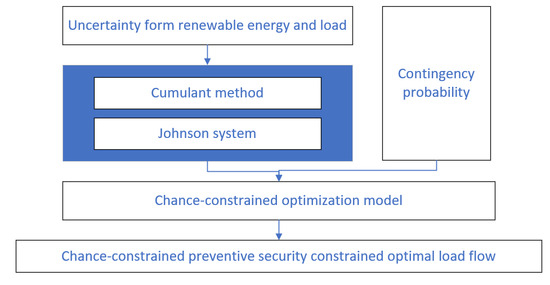
3. Formulation of the Proposed Optimization Model
3.1. Modeling of Uncertainties
3.2. Chance-Constrained Optimization
3.3. Chance-Constrained PSCOPF Model
3.4. Deterministic Reformulation of CC-PSCOPF
3.4.1. The Cumulant
3.4.2. The Johnson System
4. Case Study
4.1. Description of the Test System
4.2. CDF Approximation Performance of the Proposed Method
4.3. Solutions of Different Optimization Formulations
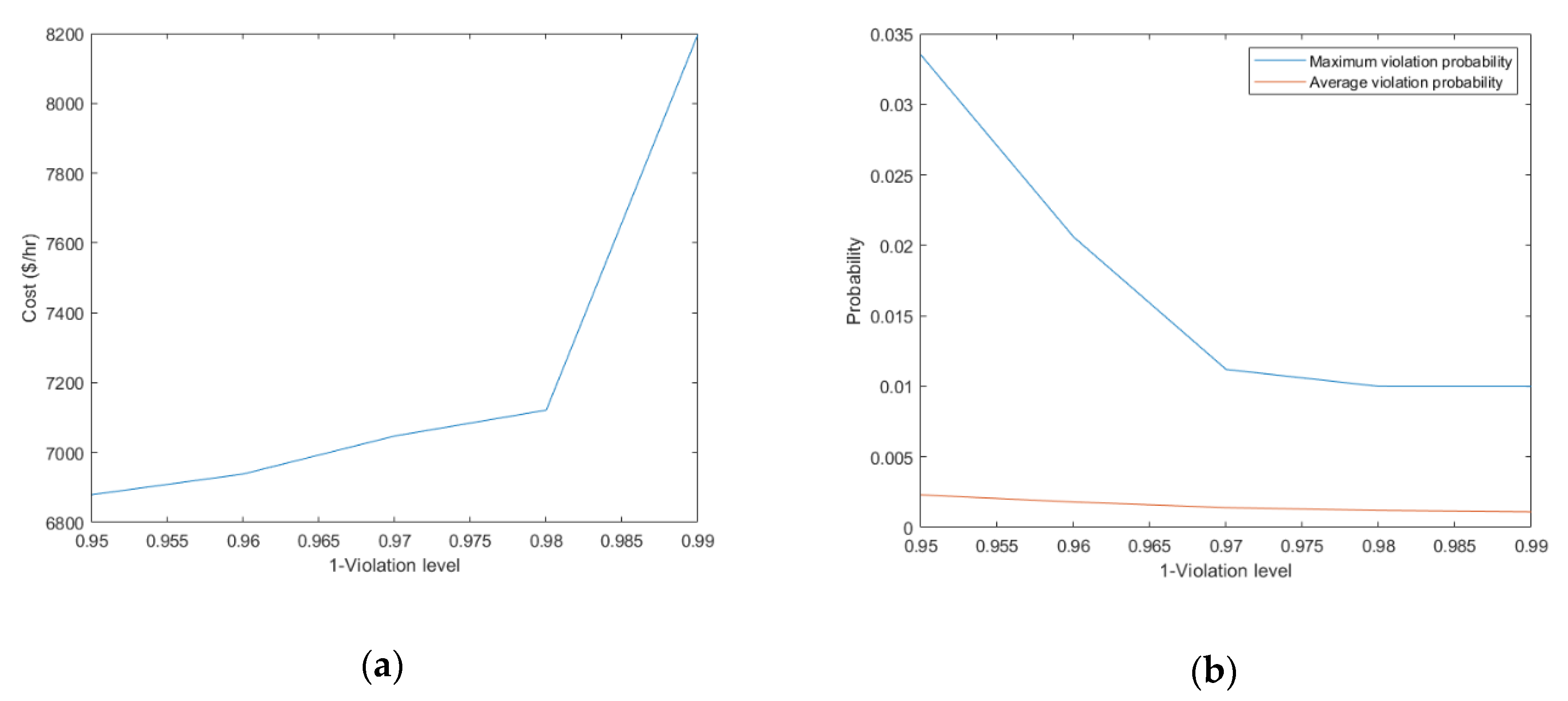
4.4. Influence of the Value of Violation Level
4.5. Efficiency of the Proposed Method
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, X.; Zhang, X.; Wu, L.; Lu, P.; Zhang, S. Transmission Line Overload Risk Assessment for Power Systems with Wind and Load-Power Generation Correlation. IEEE Trans. Smart Grid. 2015, 6, 1233–1242. [Google Scholar] [CrossRef]
- Duan, Y.; Zhang, B. Security risk assessment using fast probabilistic power flow considering static power-frequency characteristics of power systems. Int. J. Electr. Power Energy Syst. 2014, 6, 53–58. [Google Scholar] [CrossRef]
- Da Silva, A.M.L.; De Castro, A.M. Risk Assessment in Probabilistic Load Flow via Monte Carlo Simulation and Cross-Entropy Method. IEEE Trans. Power Syst. 2019, 34, 1193–1202. [Google Scholar] [CrossRef]
- Capitanescu, F. Critical review of recent advances and further developments needed in AC optimal power flow. Electr. Power Syst. Res. 2016, 136, 57–68. [Google Scholar] [CrossRef]
- Monticelli, A.; Pereira, M.V.F.; Granville, S. Security-constrained optimal power flow with post-contingency corrective rescheduling. IEEE Trans. Power Syst. 1987, 2, 175–182. [Google Scholar] [CrossRef]
- Hinojosa, V.H.; Gonzalez-Longatt, F. Preventive Security-Constrained DCOPF Formulation Using Power Transmission Distribution Factors and Line Outage Distribution Factors. Energies 2018, 11, 1497. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Dong, Z.Y.; Zhang, R.; Wong, K.P.; Lai, M.Y. Solving Preventive-Corrective SCOPF by a Hybrid Computational Strategy. IEEE Trans. Power Syst. 2014, 29, 1345–1355. [Google Scholar] [CrossRef]
- Alsac, O.; Bright, J.; Prais, M.; Stott, B. Further developments in LP-based optimal power flow. IEEE Trans. Power Syst. 1990, 5, 697–711. [Google Scholar] [CrossRef]
- Capitanescu, F.; Glavic, M.; Ernst, D.; Wehenkel, L. Contingency filtering techniques for preventive security-constrained optimal power flow. IEEE Trans. Power Syst. 2007, 22, 1690–1697. [Google Scholar] [CrossRef]
- Li, Y.; McCalley, J.D. Decomposed SCOPF for improving efficiency. IEEE Trans. Power Syst. 2009, 24, 494–495. [Google Scholar]
- Fu, Y.; Shahidehpour, M.A.C. Contingency dispatch based on security-constrained unit commitment. IEEE Trans. Power Syst. 2006, 21, 897–908. [Google Scholar] [CrossRef]
- Granville, S.; Lima, M.C.A. Application of decomposition techniques to VAr planning: Methodological and computational aspects. IEEE Trans. Power Syst. 1994, 9, 1780–1787. [Google Scholar] [CrossRef]
- Wang, Q.; McCally, J.D. Risk and “N-1” Criteria Coordination for Real-Time Operations. IEEE Trans. Power Syst. 2013, 28, 3505–3506. [Google Scholar] [CrossRef]
- Wang, Q.; McCally, J.D.; Zheng, T.X.; Litvinov, E. Solving corrective risk-based security-constrained optimal power flow with Lagrangian relaxation and Benders decomposition. Int. J. Electr. Power Energy Syst. 2016, 75, 255–264. [Google Scholar] [CrossRef]
- Roald, L.; Vrakopoulou, M.; Oldewurtel, F.; Andersson, G. Risk-based optimal power flow with probabilistic guarantees. Int. J. Electr. Power Energy Syst. 2015, 72, 66–74. [Google Scholar] [CrossRef] [Green Version]
- Charnes, A.; Cooper, W.; Symonds, G. Cost horizons and certainty equivalents: An approach to stochastic programming of heating oil. Manag. Sci. 1958, 4, 235–263. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W. Deterministic equivalents for optimizing and satisficing under chance constraints. Oper. Res. 1963, 11, 18–39. [Google Scholar] [CrossRef]
- Zhang, Z.S.; Sun, Y.Z.; Gao, D.W.; Lin, J.; Cheng, L. A Versatile Probability Distribution Model for Wind Power Forecast Errors and Its Application in Economic Dispatch. IEEE Trans. Power Syst. 2013, 28, 3114–3125. [Google Scholar] [CrossRef]
- Bienstock, D.; Chertkov, M.; Harnett, S. Chance-Constrained Optimal Power Flow: Risk-Aware Network Control under Uncertainty. SIAM Rev. 2014, 56, 461–495. [Google Scholar] [CrossRef]
- Wang, Z.W.; Shen, C.; Liu, F.; Wu, X.Y.; Liu, C.C.; Gao, F. Chance-Constrained Economic Dispatch With Non-Gaussian Correlated Wind Power Uncertainty. IEEE Trans. Power Syst. 2017, 32, 4880–4893. [Google Scholar] [CrossRef]
- Venzke, A.; Halilbasic, L.; Markovic, U.; Hub, G.; Chatzivasileiadis, S. Convex Relaxations of Chance Constrained AC Optimal Power Flow. IEEE Trans. Power Syst. 2018, 33, 2829–2841. [Google Scholar] [CrossRef] [Green Version]
- Roald, L.; Misra, S.; Krause, T.; Andersson, G. Corrective Control to Handle Forecast Uncertainty: A Chance Constrained Optimal Power Flow. IEEE Trans. Power Syst. 2017, 32, 1626–1637. [Google Scholar]
- Li, Y.; Wang, J.; Ding, T. Clustering-based chance-constrained transmission expansion planning using an improved benders decomposition algorithm. IET Gener. Transm. Distrib. 2018, 12, 935–946. [Google Scholar] [CrossRef]
- Liu, J.; Chen, H.; Zhang, W.; Yurkovich, B.; Rizzoni, G. Energy Management Problems Under Uncertainties for Grid-Connected Microgrids: A Chance Constrained Programming Approach. IEEE Trans. Smart Grid. 2017, 8, 2585–2596. [Google Scholar] [CrossRef]
- Wu, H.; Shahidehpour, M.; Li, Z.; Tian, W. Chance-constrained day-ahead scheduling in stochastic power system operation. IEEE Trans. Power Syst. 2014, 29, 1583–1591. [Google Scholar] [CrossRef]
- Nazir, F.; Pal, B.; Jabr, R. A two-stage chance constrained volt/var control scheme for active distribution networks with nodal power uncertainties. IEEE Trans. Power Syst. 2019, 34, 314–325. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Zhang, B.; Li, H.; Li, Z.; Chen, Y.; Miao, X. Statistical distribution for wind power forecast error and its application to determine optimal size of energy storage system. Int. J. Electr. Power Energy Syst. 2014, 55, 100–107. [Google Scholar] [CrossRef]
- Bludszuweit, H.; Dominguez-Navarro, J.A.; Llombart, A. Statistical analysis of wind power forecast error. IEEE Trans. Power Syst. 2008, 23, 983–991. [Google Scholar] [CrossRef]
- Kaur, A.; Pedro, H.T.C.; Coimbra, C.F.M. Impact of onsite solar generation on system load demand forecast. Energy Convers. Manag. 2013, 75, 701–709. [Google Scholar] [CrossRef]
- Li, Y.; McCally, J.D. Risk-Based Optimal Power Flow and System Operation State. In Proceedings of the Power & Energy Society General Meeting 2009 IEEE, Calgary, BC, Canada, 26–30 July 2009. [Google Scholar]
- Billinton, R.; Singh, G. Application of adverse and extreme adverse weather: Modelling in transmission and distribution system reliability evaluation. IEE Proc. Gener. Transm. Distrib. 2006, 153, 115–120. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhou, J.; Ju, P.; Feuchtwang, J. Probabilistic load flow computation of a power system containing wind farms using the method of combined cumulants and Gram-Charlier expansion. IET Gener. Transm. Distrib. 2011, 5, 448–454. [Google Scholar] [CrossRef]
- Usaola, J. Probabilistic load flow with correlated wind power injections. Electr. Power Syst. Res. 2010, 80, 528–536. [Google Scholar] [CrossRef]
- Zhang, L.B.; Cheng, H.Z.; Zhang, S.X.; Zeng, P.L.; Yao, L.Z. Probabilistic power flow calculation using the Johnson system and Sobol’s quasi-random numbers. IET Gener. Transm. Distrib. 2016, 10, 3050–3059. [Google Scholar] [CrossRef]
- Soukissian, T. Use of multi-parameter distributions for offshore wind speed modeling: The Johnson S-B distribution. Appl. Energy 2013, 111, 982–1000. [Google Scholar] [CrossRef]
- Hill, I.D.; Hill, R.; Holder, R.L. Algorithm AS 99: Fitting Johnson Curves by Moments. Appl. Sci. 1980, 25, 180–189. [Google Scholar] [CrossRef]
- Wachter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2016, 106, 25–57. [Google Scholar] [CrossRef]
- Power System Test Case Archive. Available online: https://labs.ece.uw.edu/pstca/ (accessed on 1 March 2020).
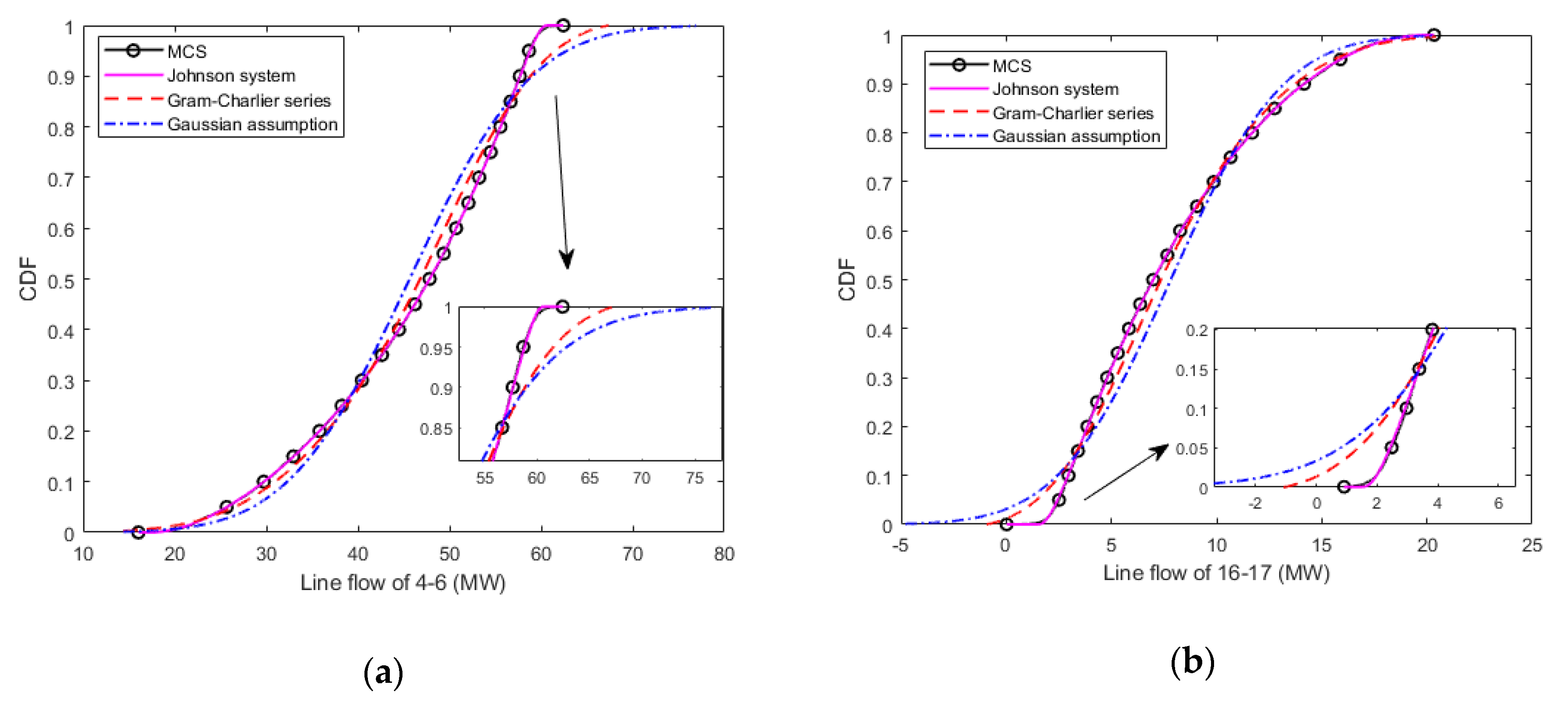

| Lines | ARMS of Cumulant + Johnson System | ARMS of Cumulant + Gram-Charlier | ARMS of Gaussian Assumption |
|---|---|---|---|
| Line 4–6 | 0.0031 | 0.1294 | 0.1312 |
| Line 16–17 | 0.0038 | 0.1288 | 0.1306 |
| PSCOPF | CC-PSCOPF | |
|---|---|---|
| Cost ($/hr) | 7488.1 | 8196.5 |
| PSCOPF | CC-PSCOPF | |
|---|---|---|
| Average violation probability | 0.0045 | 0.0010 |
| Maximum violation probability | 0.0779 | 0.0100 |
| 22 | 6 | |
| 1.95 | 1.5 | |
| 5 | 2 |
| Test System | PSCOPF | CC-PSCOPF | |
|---|---|---|---|
| IEEE-30 | Constraint Numbers | 1600 | 42 |
| Time (s) | 1.23 | 0.13 | |
| IEEE-118 | Constraint Numbers | 33109 | 187 |
| Time (s) | 319.57 | 0.67 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Zhang, Z.; Yin, X.; Zhang, B. Preventive Security-Constrained Optimal Power Flow with Probabilistic Guarantees. Energies 2020, 13, 2344. https://doi.org/10.3390/en13092344
Li H, Zhang Z, Yin X, Zhang B. Preventive Security-Constrained Optimal Power Flow with Probabilistic Guarantees. Energies. 2020; 13(9):2344. https://doi.org/10.3390/en13092344
Chicago/Turabian StyleLi, Hang, Zhe Zhang, Xianggen Yin, and Buhan Zhang. 2020. "Preventive Security-Constrained Optimal Power Flow with Probabilistic Guarantees" Energies 13, no. 9: 2344. https://doi.org/10.3390/en13092344
APA StyleLi, H., Zhang, Z., Yin, X., & Zhang, B. (2020). Preventive Security-Constrained Optimal Power Flow with Probabilistic Guarantees. Energies, 13(9), 2344. https://doi.org/10.3390/en13092344