A Modelica Toolbox for the Simulation of Borehole Thermal Energy Storage Systems
Abstract
1. Introduction
1.1. State-of-the-Art Modeling Approaches for BTES Systems
1.2. Existing BTES Models for Dynamic System Simulation
2. Methods
2.1. MoBTES Modeling Approaches
2.1.1. Borehole Heat Exchanger Models
2.1.2. Local Heat Transport Models
2.1.3. Global Heat Transport Model
2.2. Model Validation
2.2.1. Parameter Study
2.2.2. Case Study
3. Results
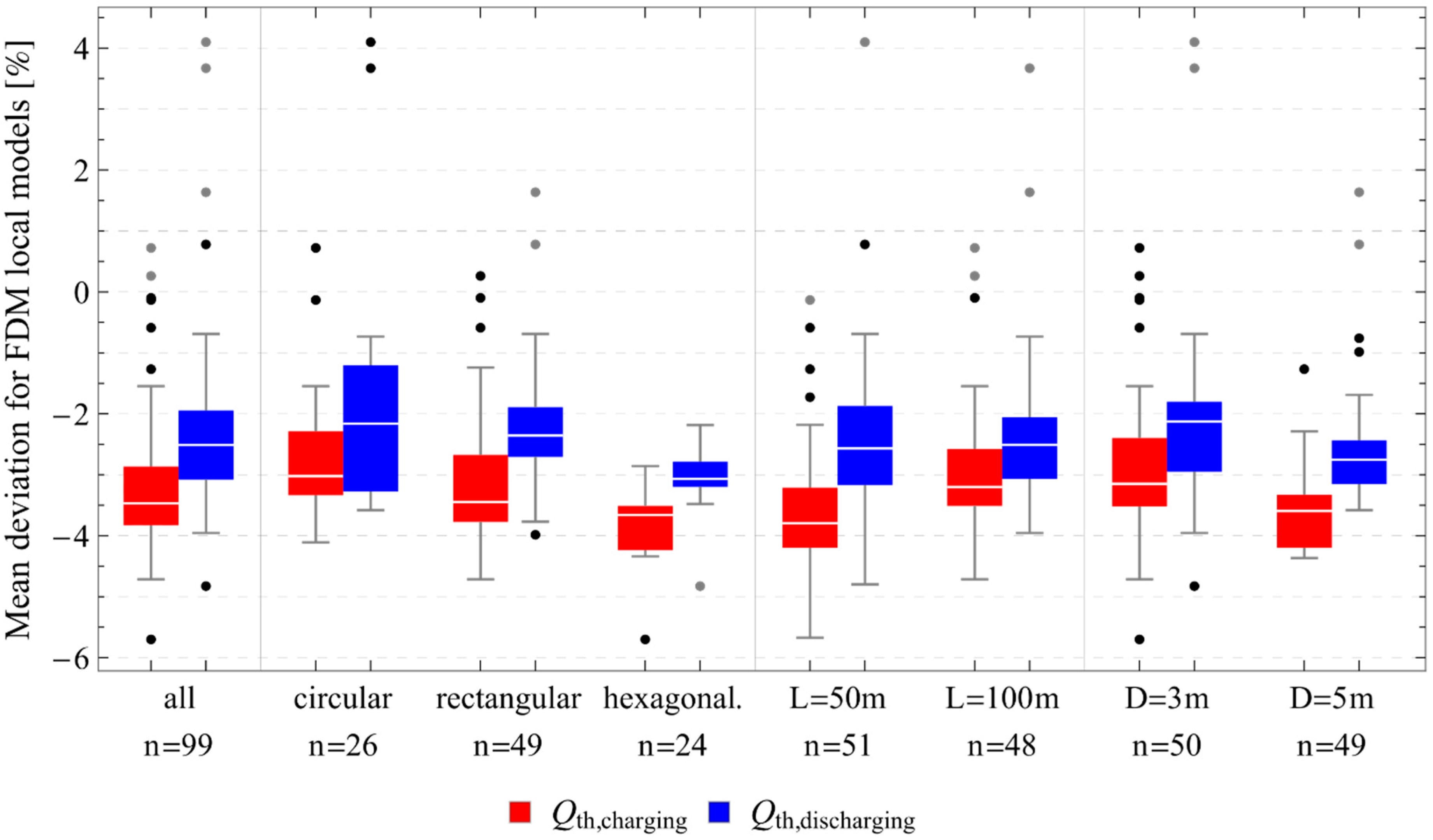
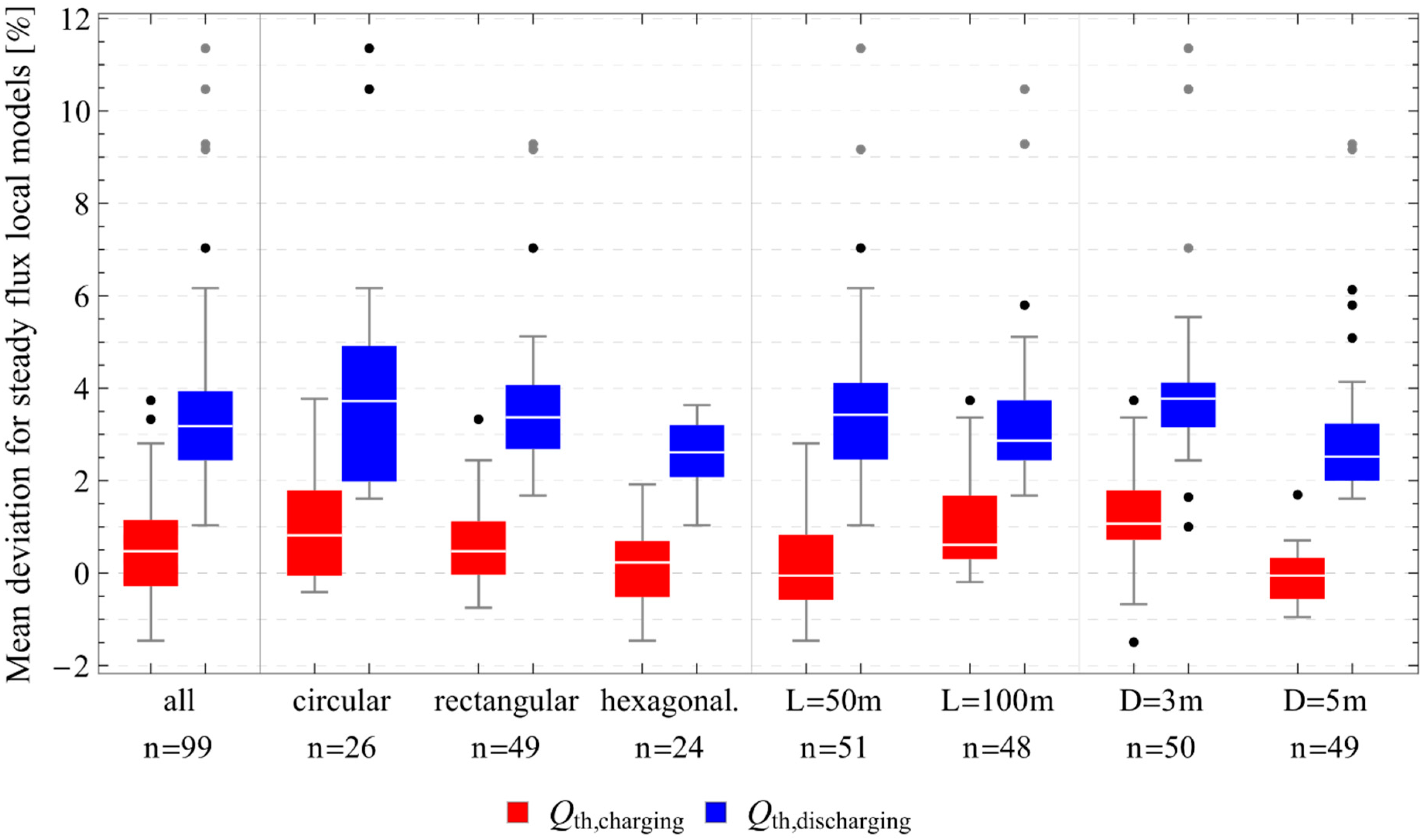
3.1. Parameter Study Results
3.2. Case Study Results
4. Discussion
4.1. Parameter Study
4.2. Case Study
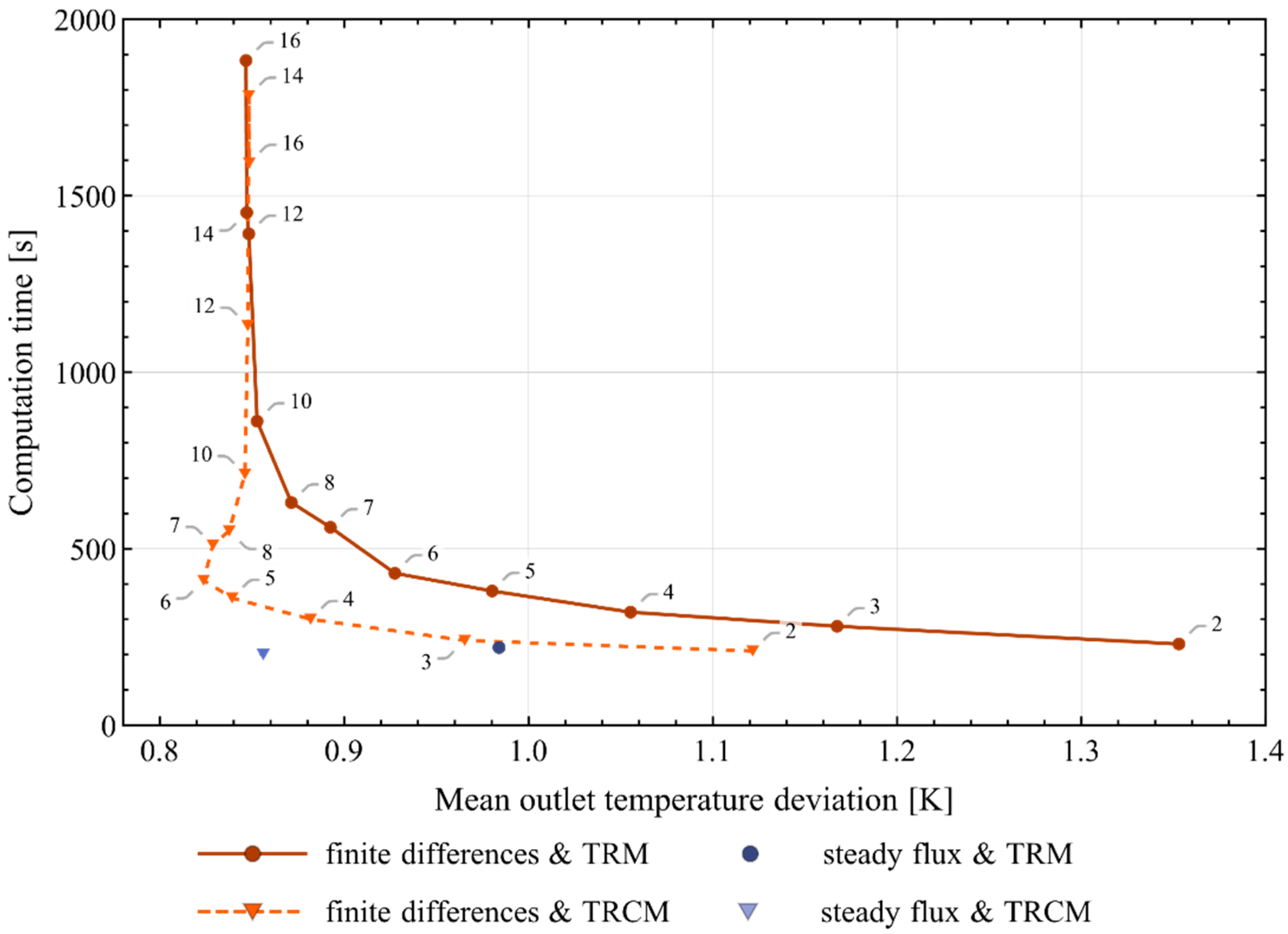
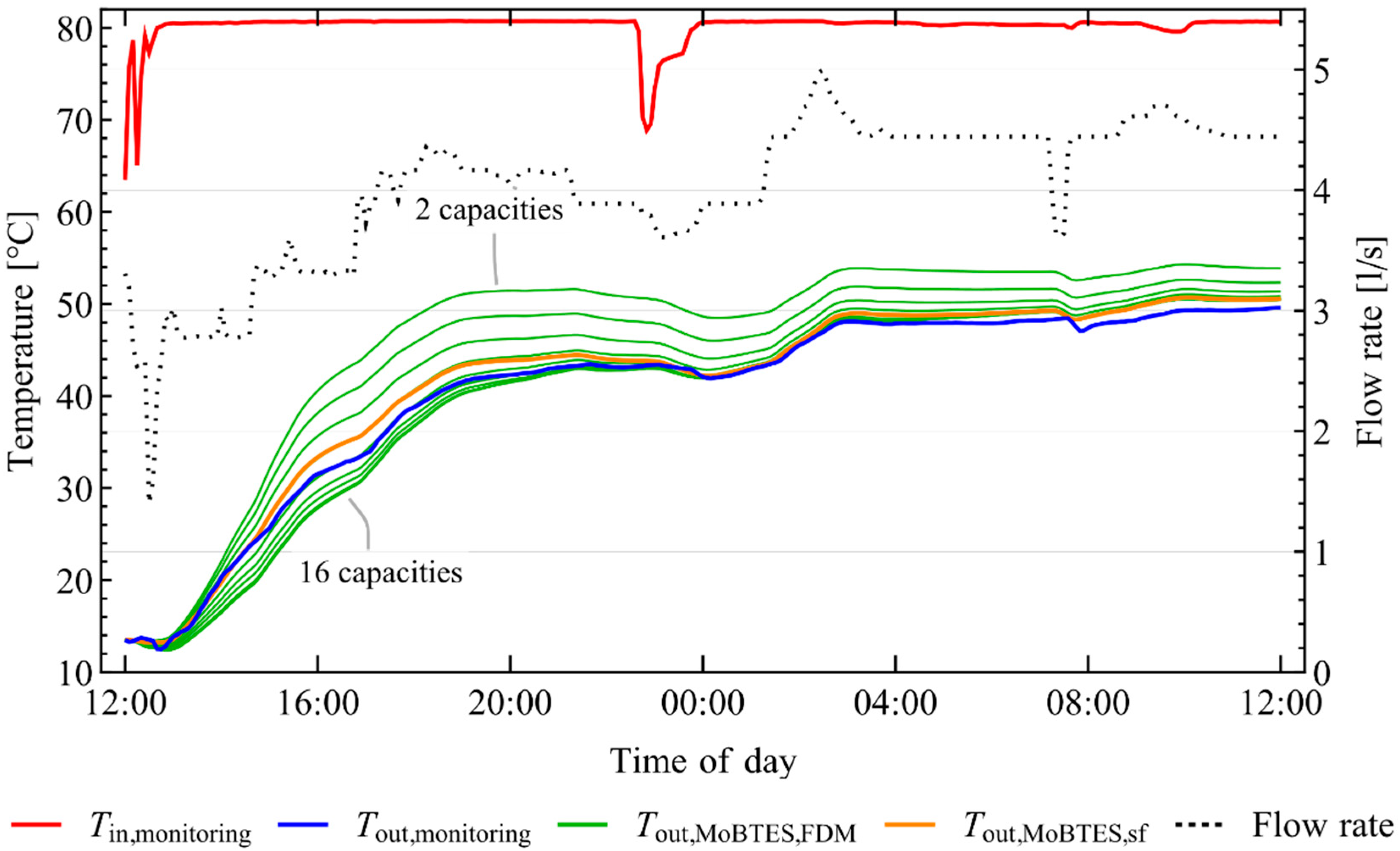
4.2.1. Computational Effort and Mean Outlet Temperature Deviation
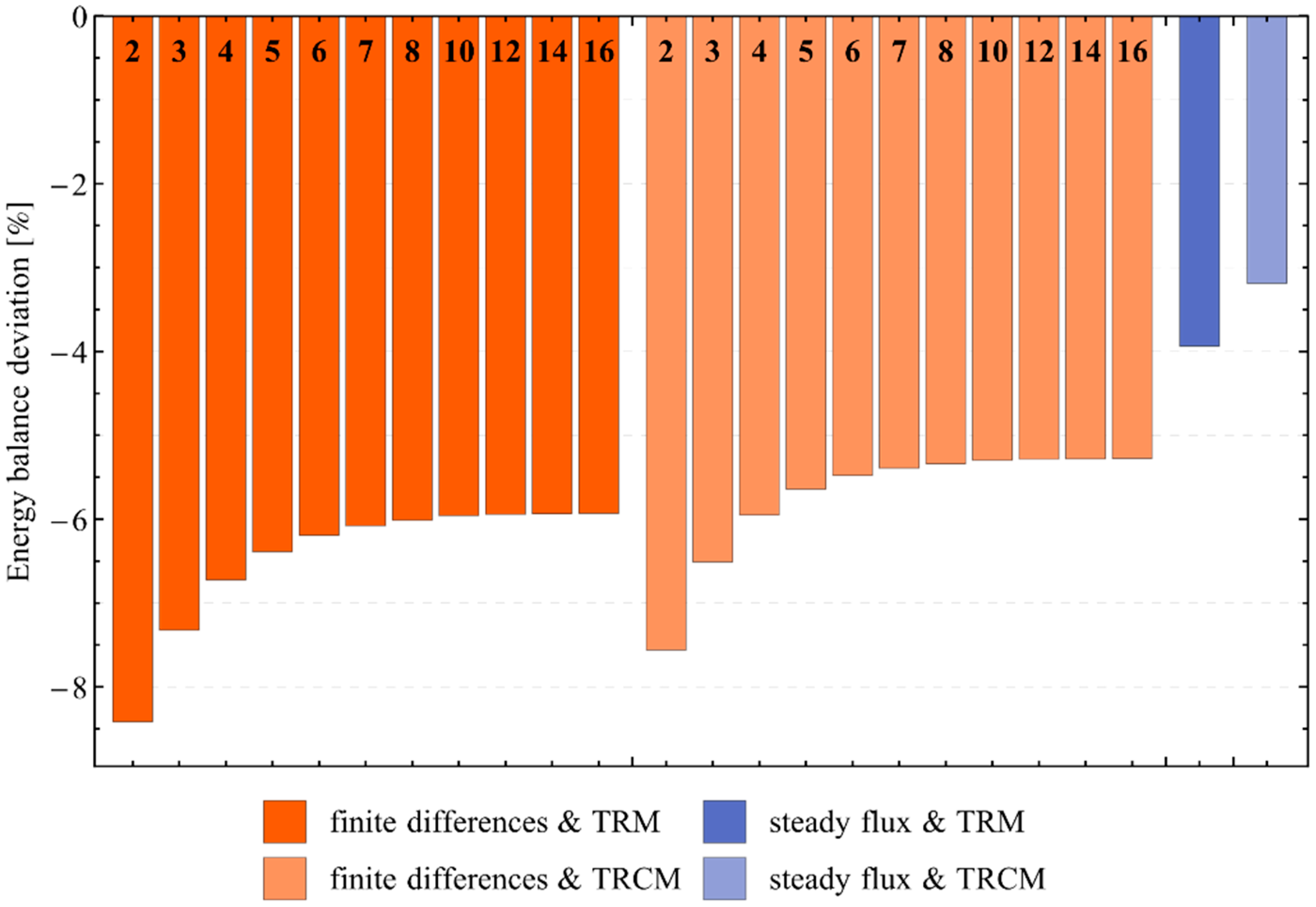
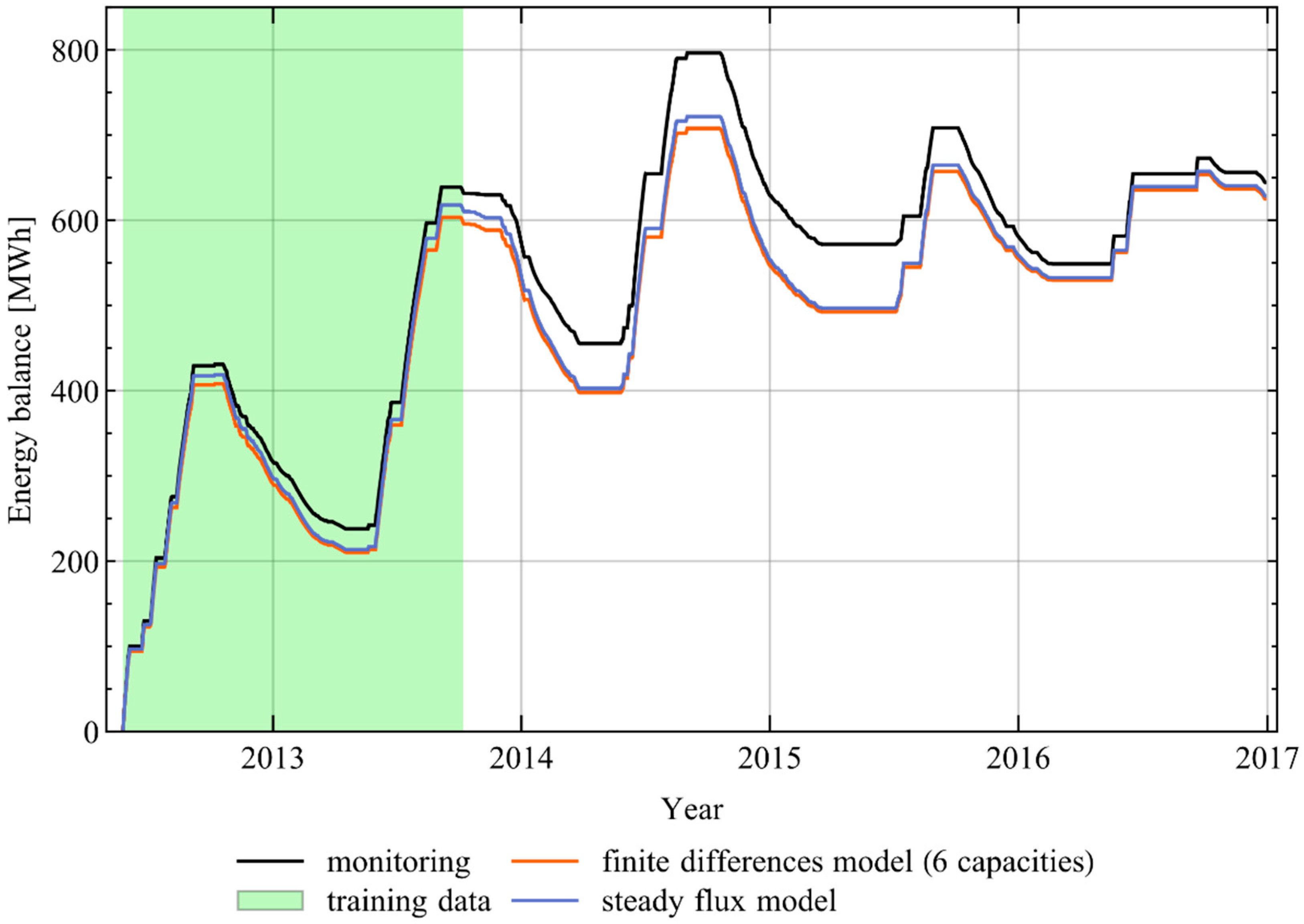
4.2.2. Comparison of Overall Energy Balance Deviations
4.2.3. Short Time Accuracy
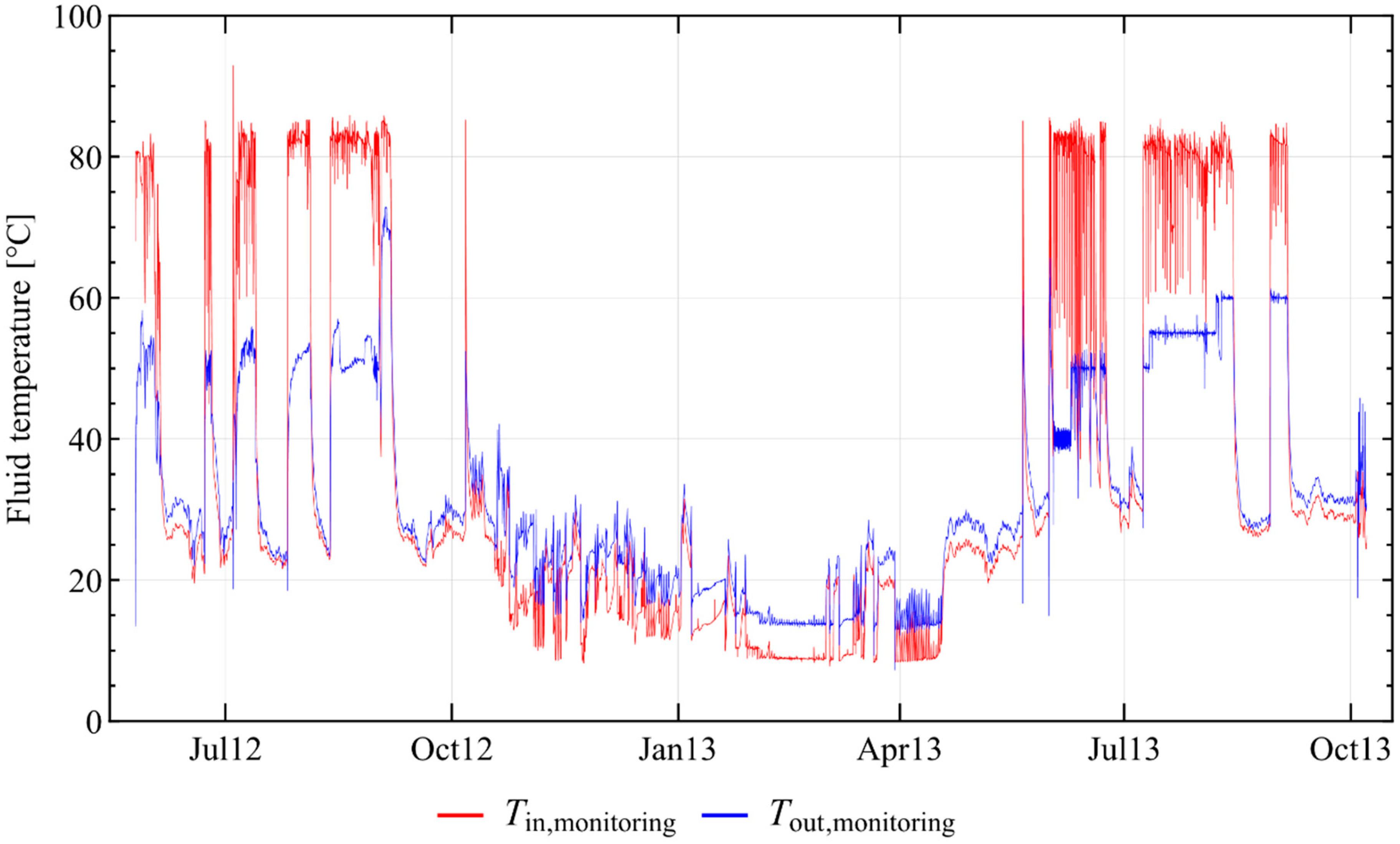
4.2.4. Comparison of Model Results and the Extended Monitoring Data
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| BHE | borehole heat exchanger |
| BTES | borehole thermal energy storage |
| DoF | degrees of freedom |
| FDM | finite differences model |
| HSRM | hybrid step response model |
| MoBTES | Modelica borehole thermal energy storage model |
| SBM | superposition borehole model |
| TRCM | thermal resistance and capacity model |
| TRM | thermal resistance model |
Symbols
| a | thermal diffusivity | m²/s |
| c | gravimetric thermal capacity | kg/m³ |
| C | thermal capacity | J/K |
| D | borehole spacing | m |
| L | Borehole length | m |
| q | specific heat flux | W/m |
| Q | Thermal energy | J |
| heat flux | W | |
| r | radius | m |
| R | thermal resistance | K/W |
| T | temperature | K |
| t | time | s |
| δ | relative deviation | - |
| ρ | density | kg/m³ |
| λ | thermal conductivity | W/(m K) |
| τ | time constant | s |
| indicator function | - |
Subscripts
| b | borehole wall |
| glo | global problem |
| loc | local problem |
| m | mean |
| min | minimum |
| sf | steady flux |
| sim | final simulation time |
| th | thermal |
| 0 | constant temperature profile under steady flux condition |
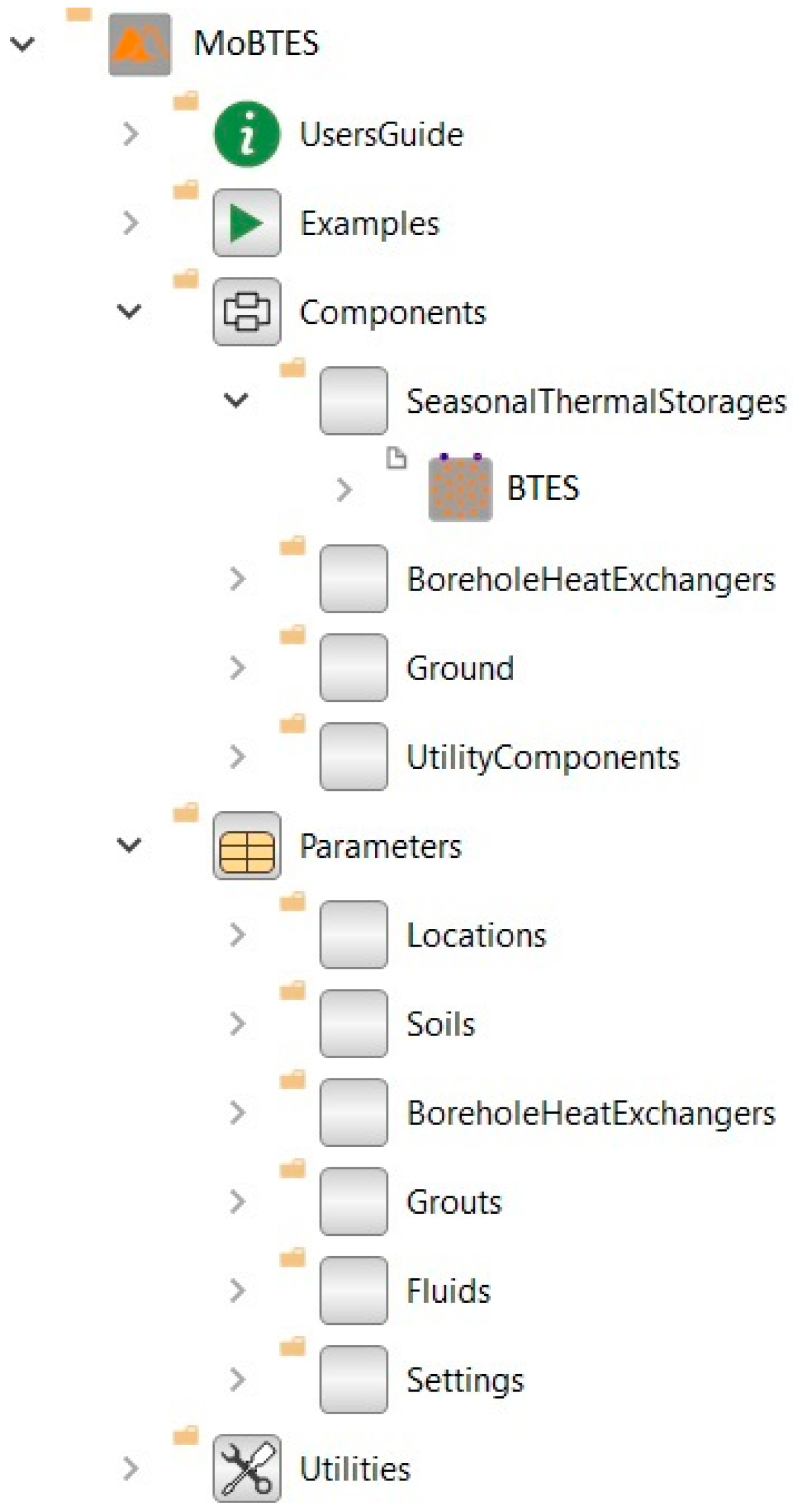
Appendix A. Modelica Library
References
- Reuss, M. The use of borehole thermal energy storage (BTES) systems. In Advances in Thermal Energy Storage Systems: Methods and Applications; Elsevier: Cambridge, UK, 2015; pp. 117–147. ISBN 9781782420965. [Google Scholar]
- Gehlin, S. Borehole thermal energy storage. In Advances in Ground-Source Heat Pump Systems; Elsevier: Duxford, UK, 2016; pp. 295–337. [Google Scholar]
- Welsch, B.; Göllner-Völker, L.; Schulte, D.O.; Bär, K.; Sass, I.; Schebek, L. Environmental and economic assessment of borehole thermal energy storage in district heating systems. Appl. Energy 2018, 216, 73–90. [Google Scholar] [CrossRef]
- Olsson, H. Modelica—A unified object-oriented language for physical systems modeling; Modelica Association. Available online: https://www.modelica.org/documents/ModelicaSpec34.pdf (accessed on 30 April 2020).
- Schweiger, G.; Larsson, P.O.; Magnusson, F.; Lauenburg, P.; Velut, S. District heating and cooling systems—Framework for Modelica-based simulation and dynamic optimization. Energy 2017, 137, 566–578. [Google Scholar] [CrossRef]
- Filonenko, K.; Howard, D.; Buck, J.; Veje, C. Comparison of two simulation tools for district heating applications. In Proceedings of the 9th International Conference on Energy Reliability REMOO-2019, Hong Kong, China, 16–18 April 2019. [Google Scholar]
- Wetter, M. Haugstetter Modelica versus TRNSYS—A Comparison between an equation-based and a procedural modeling language for building energy simulation. Proc. SimBuild 2006, 2, 262–269. [Google Scholar]
- Diersch, H.J.G.; Bauer, D.; Heidemann, W.; Rühaak, W.; Schätzl, P. Finite element modeling of borehole heat exchanger systems. Part 2. Numerical simulation. Comput. Geosci. 2011, 37, 1136–1147. [Google Scholar] [CrossRef]
- Schulte, D.O.; Welsch, B.; Rühaak, W.; Bär, K.; Sass, I. BASIMO—Borehole Heat Exchanger Array Simulation and Optimization Tool. In Proceedings of the European Geosciences Union General Assembly 2017, Vienna, Austria, 23–28 April 2017. [Google Scholar]
- Blocon. Earth Energy Designer (version 4); Windows; Blocon: Lund, Sweden, 2016. [Google Scholar]
- Pahud, D.; Hellström, G. The new duct ground heat model for TRNSYS. In Proceedings of the Eurotherm Seminar no49, Physical models for Thermal Energy Stores, Eindhoven, The Netherlands, 25–27 March 1996; pp. 127–136. [Google Scholar]
- Picard, D.; Helsen, L. A New Hybrid Model For Borefield Heat Exchangers Performance Evaluation. In Proceedings of the 2014 Ashrae Annual Conference, Seattle, WA, USA, 28 June–2 July 2014; pp. 857–866. [Google Scholar]
- Skarphagen, H.; Banks, D.; Frengstad, B.S.; Gether, H. Design Considerations for Borehole Thermal Energy Storage (BTES): A Review with Emphasis on Convective Heat Transfer. Geofluids 2019, 1–26. [Google Scholar] [CrossRef]
- Moradi, A.; Smits, K.M.; Lu, N.; McCartney, J.S. Heat Transfer in Unsaturated Soil with Application to Borehole Thermal Energy Storage. Vadose Zone J. 2016, 15. [Google Scholar] [CrossRef]
- Picard, D. Modeling, Optimal Control and HVAC Design of Large Buildings using Ground Source Heat Pump Systems. Ph.D. Thesis, KU Leuven, Leuven, Belgium, 2017. [Google Scholar]
- Lanahan, M.; Tabares-Velasco, P.C. Seasonal thermal-energy storage: A critical review on BTES systems, modeling, and system design for higher system efficiency. Energies 2017, 10, 743. [Google Scholar] [CrossRef]
- Chio, S.; Miriaiiliosseinabadi, S. Simulation modeling of ground source heat pump systems for the performance analysis of residential buildings. In Proceedings of the BS 2013: 13th Conference of the International Building Performance Simulation Association, Chambéry, France, 26–28 August 2013; pp. 1960–1967. [Google Scholar]
- Hellström, G. Ground Heat Storage: Thermal Analyses of Duct Storage Systems. Ph.D. Thesis, Lund University, Lund, Sweden, 1991. [Google Scholar]
- Eskilson, P.; Claesson, J. Simulation model for thermally interacting heat extraction boreholes. Numer. Heat Transf. 1988, 13, 149–165. [Google Scholar] [CrossRef]
- Javed, S. Thermal Modelling and Evaluation of Borehole Heat Transfer. Ph.D. Thesis, Chalmers University of Technology, Göteborg, Sweden, 2012. [Google Scholar]
- Solar Energy Laboratory. TRNSYS—A Transient System Simulation Program (Version 18); University of Wisconsin-Madison, Solar Energy Laboratory: Madison, WI, USA, 2017. [Google Scholar]
- Bauer, D.; Heidemann, W.; Müller-Steinhagen, H.; Diersch, H.J.G. Thermal resistance and capacity models for borehole heat exchangers. Int. J. Energy Res. 2011, 35, 312–320. [Google Scholar] [CrossRef]
- Schulte, D.O.; Welsch, B.; Boockmeyer, A.; Rühaak, W.; Bär, K.; Bauer, S.; Sass, I. Modelling Insulated Borehole Heat Exchangers. Environ. Earth Sci. 2016, 75, 910. [Google Scholar] [CrossRef]
- ESI ITI. SimulationX (Version 4.1); ESI ITI: Dresden, Germany, 2017. [Google Scholar]
- Bauer, D. Zur thermischen Modellierung von Erdwärmesonden und Erdsonden-Wärmespeichern. Ph.D. Thesis, Universität Stuttgart, Stuttgart, Germany, 2012. [Google Scholar]
- Claesson, J.; Eskilson, P. Conductive heat extraction to a deep borehole: Thermal analyses and dimensioning rules. Energy 1988, 13, 509–527. [Google Scholar] [CrossRef]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids. Phys. Today 1962, 15, 74–76. [Google Scholar] [CrossRef]
- Franke, R. Integrierte Dynamische Modellierung und Optimierung von Systemen mit Saisonaler Wärmespeicherung; Fortschrittberichte VDI: Reihe 6, Energietechnik Nr. 394; VDI-Verlag: Düsseldorf, Germany, 1998; ISBN 3-18-339406-5. [Google Scholar]
- DHI WASY. FEFLOW (version 7.1); Windows; DHI WASY: Berlin, Germany, 2017. [Google Scholar]
- Mielke, P.; Bauer, D.; Homuth, S.; Götz, A.E.; Sass, I. Thermal effect of a borehole thermal energy store on the subsurface. Geotherm. Energy 2014, 2, 5. [Google Scholar] [CrossRef]
- Tordrup, K.W.; Poulsen, S.E.; Bjørn, H. An improved method for upscaling borehole thermal energy storage using inverse finite element modelling. Renew. Energy 2017, 105, 13–21. [Google Scholar] [CrossRef]
- Homuth, S.; Mikisek, P.; Götz, A.E.; Sass, I. Geothermische Langzeitmodellierung eines solargekoppelten Erdsonden-Wärmespeichers in Crailsheim. In Proceedings of the Der Geothermiekongress 2011, Bochum, Germany, 15–17 November 2011. [Google Scholar]
- Sørensen, P.A.; Larsen, J.; Thøgersen, L.; Dannemand Andersen, J.; Østergaard, C.; Schmidt, T. Boreholes in Brædstrup. Final Rep. 2013. [Google Scholar]
- Dassault Systemes. Dymola—Dynamic Modeling Laboratory (version 2020); Windows; Dassault Systèmes AB: Lund, Sweden, 2020. [Google Scholar]
- Fritzson, P.; Aronsson, P.; Lundvall, H.; Nyström, K.; Pop, A.; Saldamli, L.; Broman, D. The OpenModelica Modeling, Simulation, and Development Environment. In Proceedings of the 46th Conference on Simulation and Modelling of the Scandinavian Simulation Society (SIMS2005), Trondheim, Norway, 13–14 October 2005; pp. 83–90. [Google Scholar]


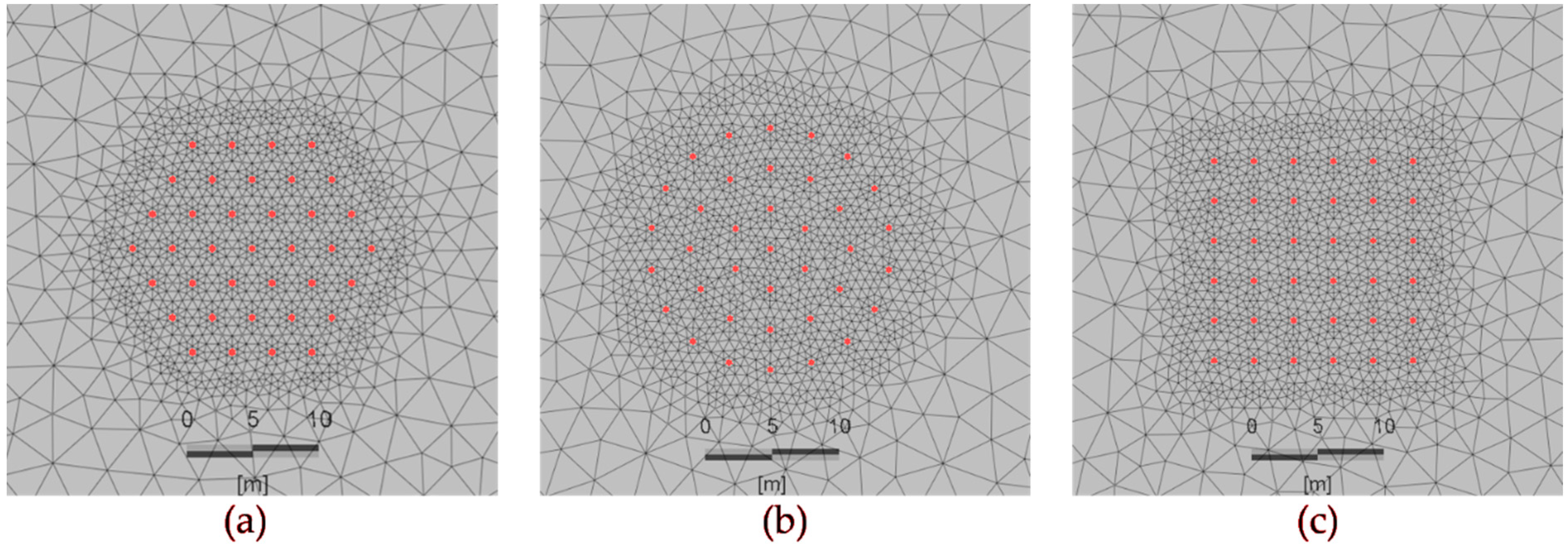

| Parameter | Range |
|---|---|
| Number of BHEs | 4, 7, 9, 16, 19, 25, 36, 37, 49, 61, 62, 64, 81, 91, 93, 100, 121, 127, 130, 144, 169, 173, 196 |
| BHE length | 50 m, 100 m |
| BHE spacing | 3 m, 5 m |
| BTES layout | circular, rectangular, hexagonal |
| Local model variants | steady flux, FDM with 10 capacity nodes |
| Results | MoBTES FDM | MoBTES Steady Flux Model |
|---|---|---|
| Mean storage efficiency MoBTES | 61.4% | 62.5% |
| Mean deviation from FEFLOW: charged energy | −3.2% (±1.1%) | +0.6% (±1.0%) |
| Mean deviation from FEFLOW: discharged energy | −2.3% (±1.3%) | +3.5% (±1.7%) |
| Average computation time MoBTES | 751.8 s | 181.1 s |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Formhals, J.; Hemmatabady, H.; Welsch, B.; Schulte, D.O.; Sass, I. A Modelica Toolbox for the Simulation of Borehole Thermal Energy Storage Systems. Energies 2020, 13, 2327. https://doi.org/10.3390/en13092327
Formhals J, Hemmatabady H, Welsch B, Schulte DO, Sass I. A Modelica Toolbox for the Simulation of Borehole Thermal Energy Storage Systems. Energies. 2020; 13(9):2327. https://doi.org/10.3390/en13092327
Chicago/Turabian StyleFormhals, Julian, Hoofar Hemmatabady, Bastian Welsch, Daniel Otto Schulte, and Ingo Sass. 2020. "A Modelica Toolbox for the Simulation of Borehole Thermal Energy Storage Systems" Energies 13, no. 9: 2327. https://doi.org/10.3390/en13092327
APA StyleFormhals, J., Hemmatabady, H., Welsch, B., Schulte, D. O., & Sass, I. (2020). A Modelica Toolbox for the Simulation of Borehole Thermal Energy Storage Systems. Energies, 13(9), 2327. https://doi.org/10.3390/en13092327







