Forecasting of Day-Ahead Natural Gas Consumption Demand in Greece Using Adaptive Neuro-Fuzzy Inference System
Abstract
1. Introduction
1.1. Indicative Related Work on AI Applied in Natural Gas Consumption Forecasting
1.2. Related Work on ANFIS in Energy Consumption Forecasting
1.3. Related Work on ANFIS in Natural Gas Consumption Forecasting
1.4. Related Work on Fuzzy Cognitive Maps (FCMs) in Energy and Natural Gas Consumption Forecasting
1.5. Research Gap and the Novelty of This Study
- The creation and demonstration of a simple, fast, robust ANFIS prediction tool to forecast NG demand using historical time series data. The proposed model is characterized by high flexibility, especially in large datasets, easiness of use and low execution time requirements.
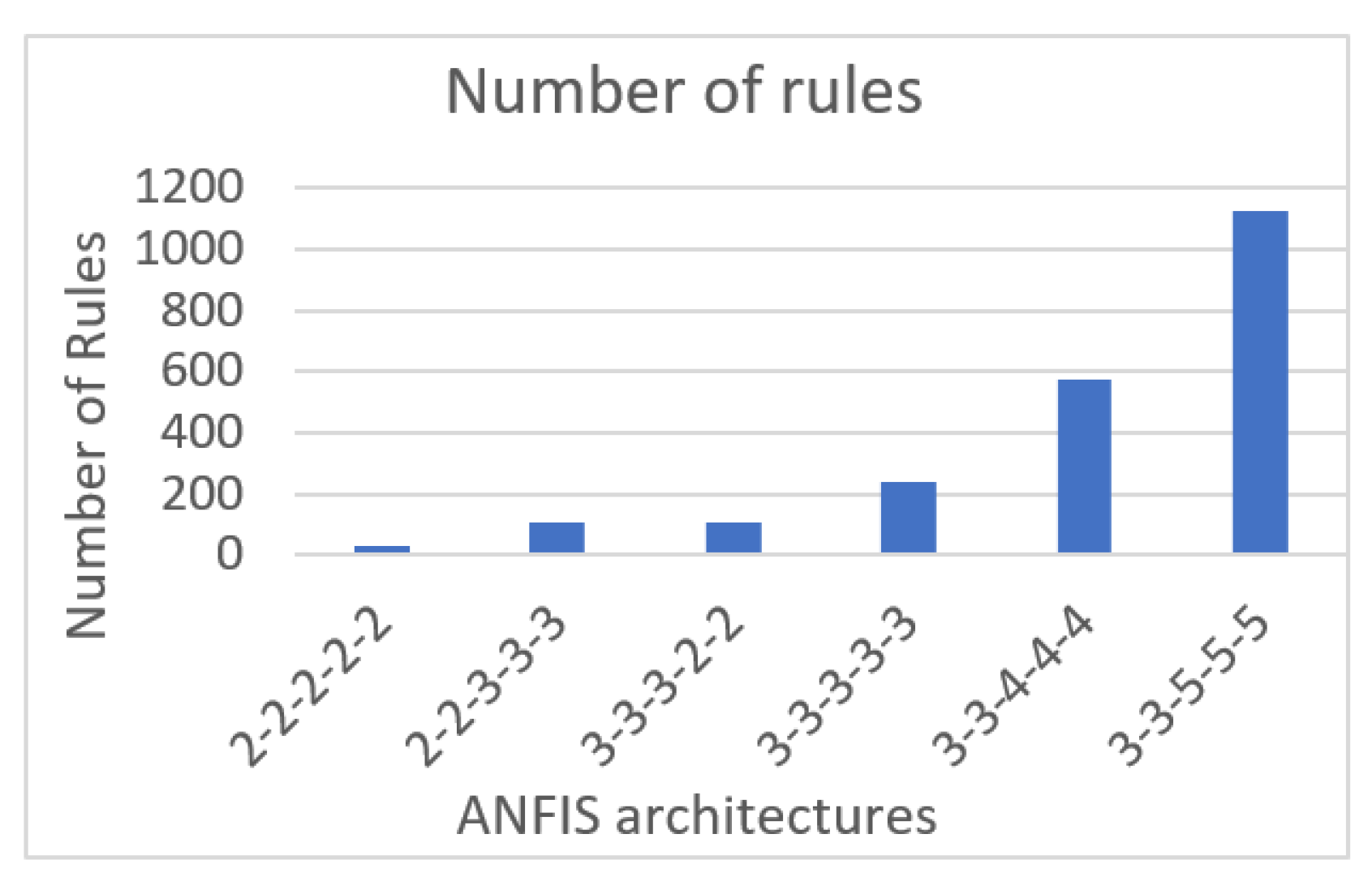
- The rigorous ANFIS fine-tuning for determining the most appropriate architecture for an enhanced prediction performance.
1.6. Aim of This Research Work
- (a)
- To develop a robust ANFIS model to provide accurate short-term forecasts for a number of cities in Greece, using a relatively large dataset. At the same time, the authors perform model fine-tuning that can lead to high accuracy in most distribution points. The proposed model is characterized by high flexibility, easiness of use and low execution time requirements.
- (b)
- To apply FCMs, ANNs and hybrid combinations of them to forecast NG demand in the same dataset, since these approaches have been proved as efficient techniques for NG demand forecasting according to the relevant literature.
- (c)
- To assess the performance of these soft computing methods in terms of prediction accuracy using well-known evaluation metrics.
- (d)
- To compare forecasting accuracy results of the proposed approach with those of the other soft computing and ANN methods that were examined, and finally decide on which model offers the best forecasting accuracy.
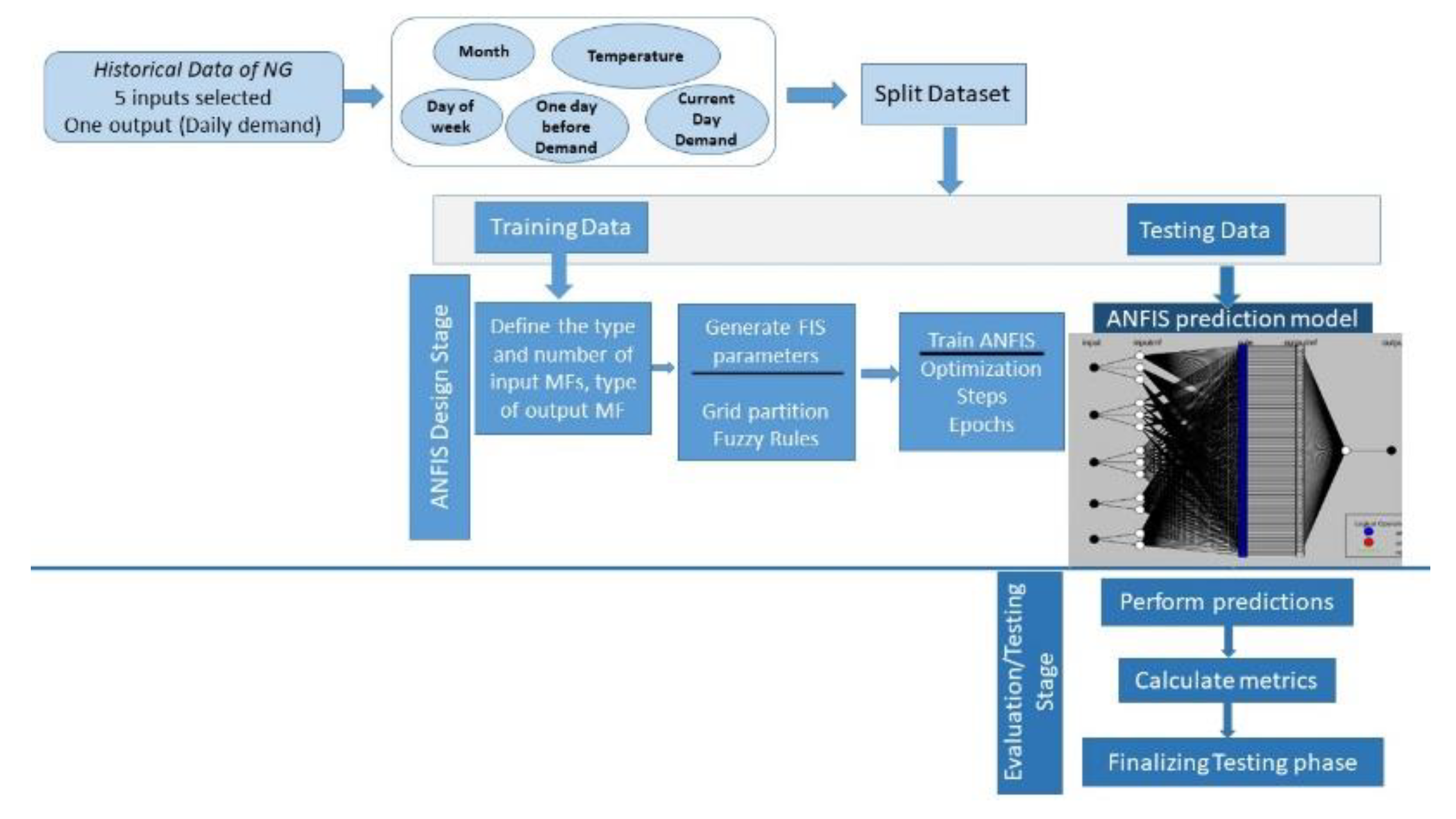
2. Materials and Methods
2.1. Dataset
2.2. Methods
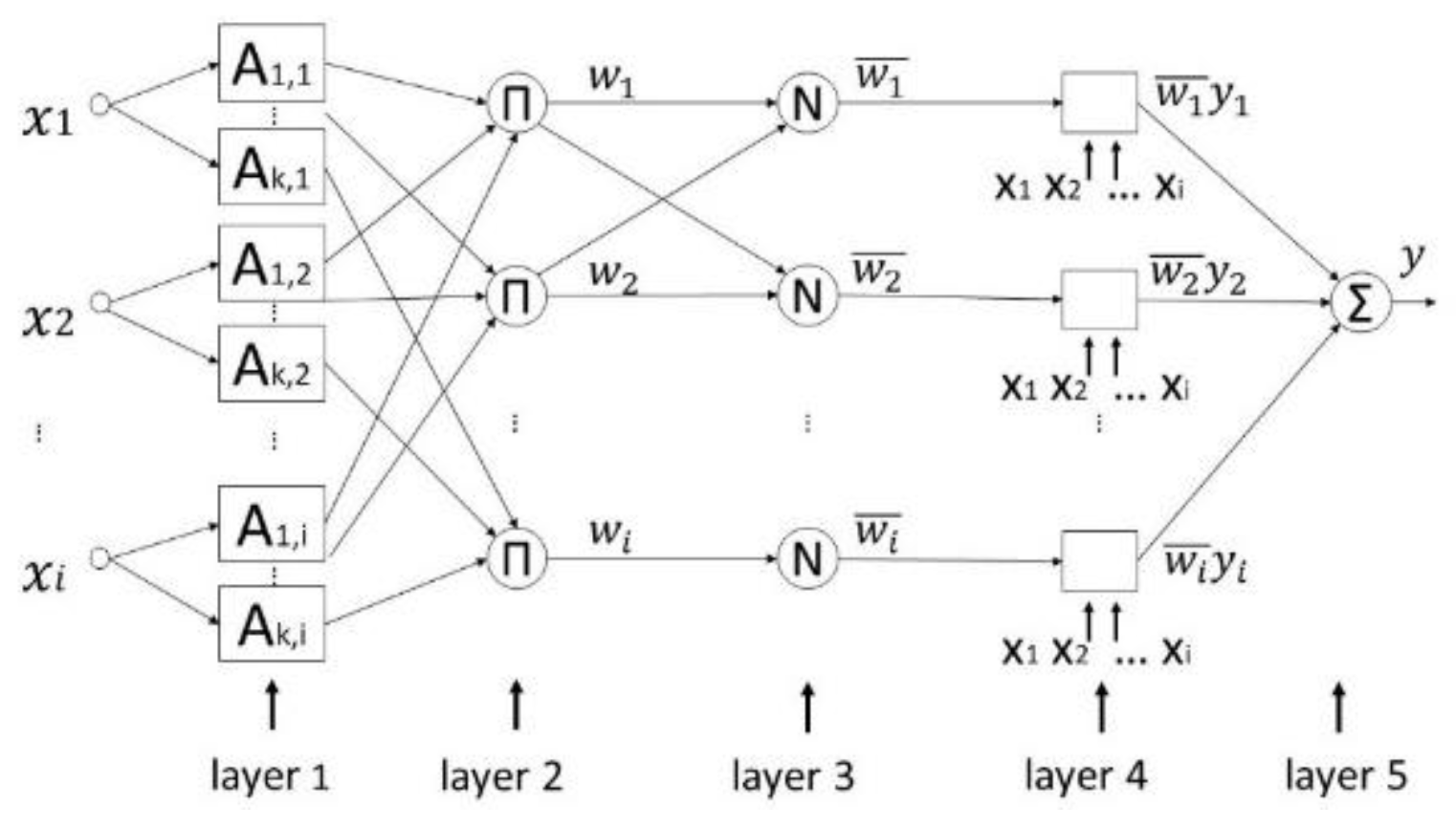
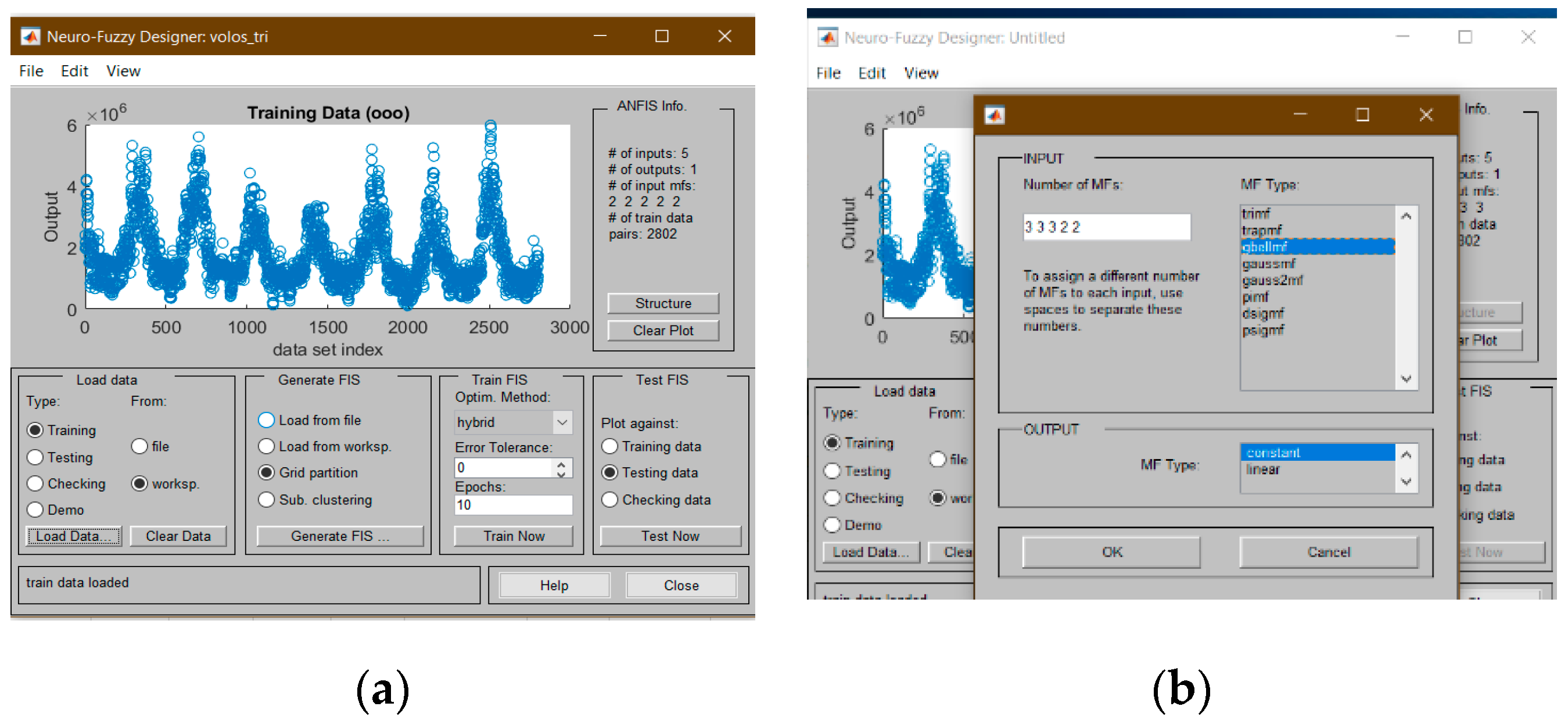
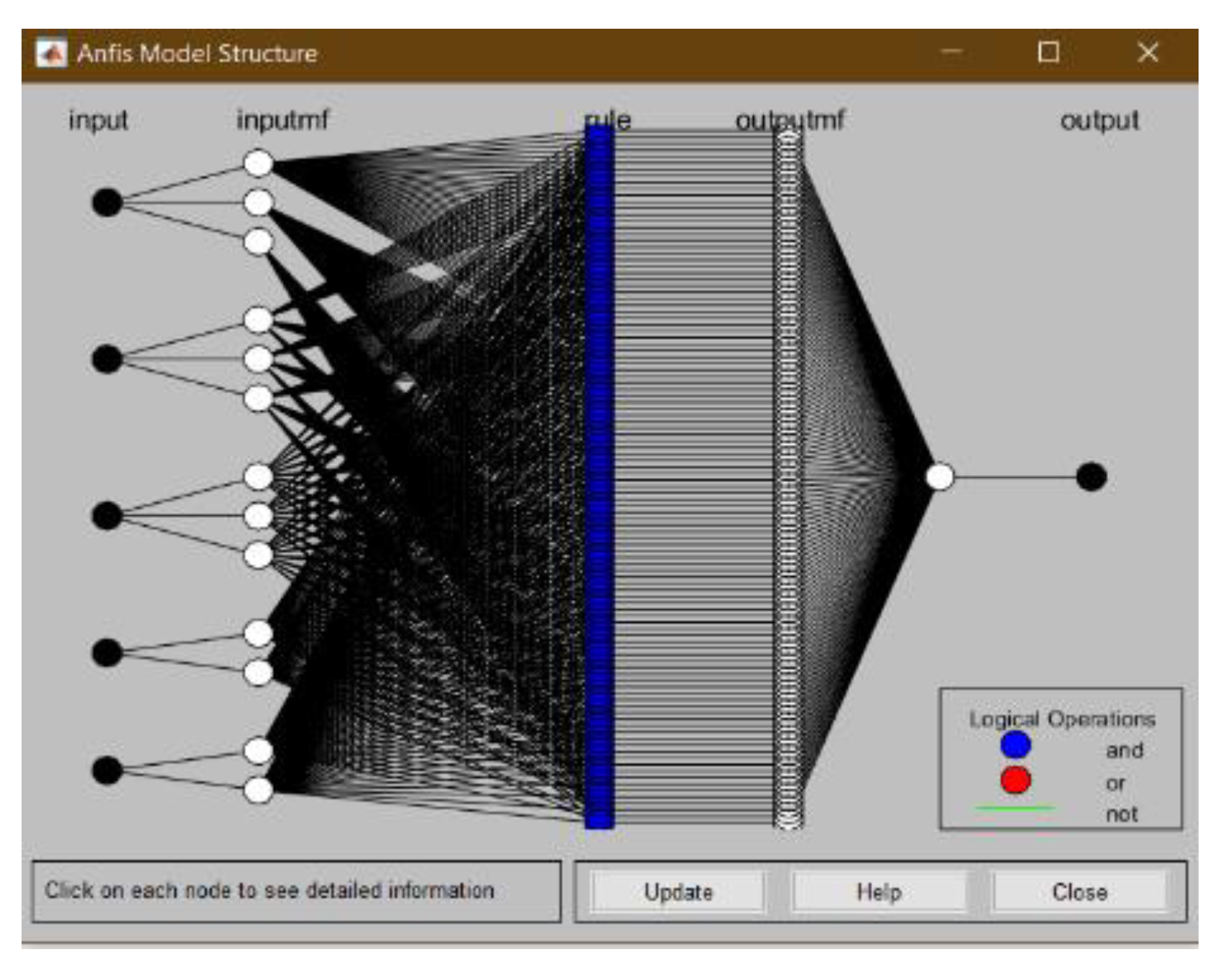
2.2.1. Adaptive Neuro-Fuzzy Inference System (ANFIS)
2.2.2. Proposed ANFIS Architecture Applied in Natural Gas Consumption Forecasting
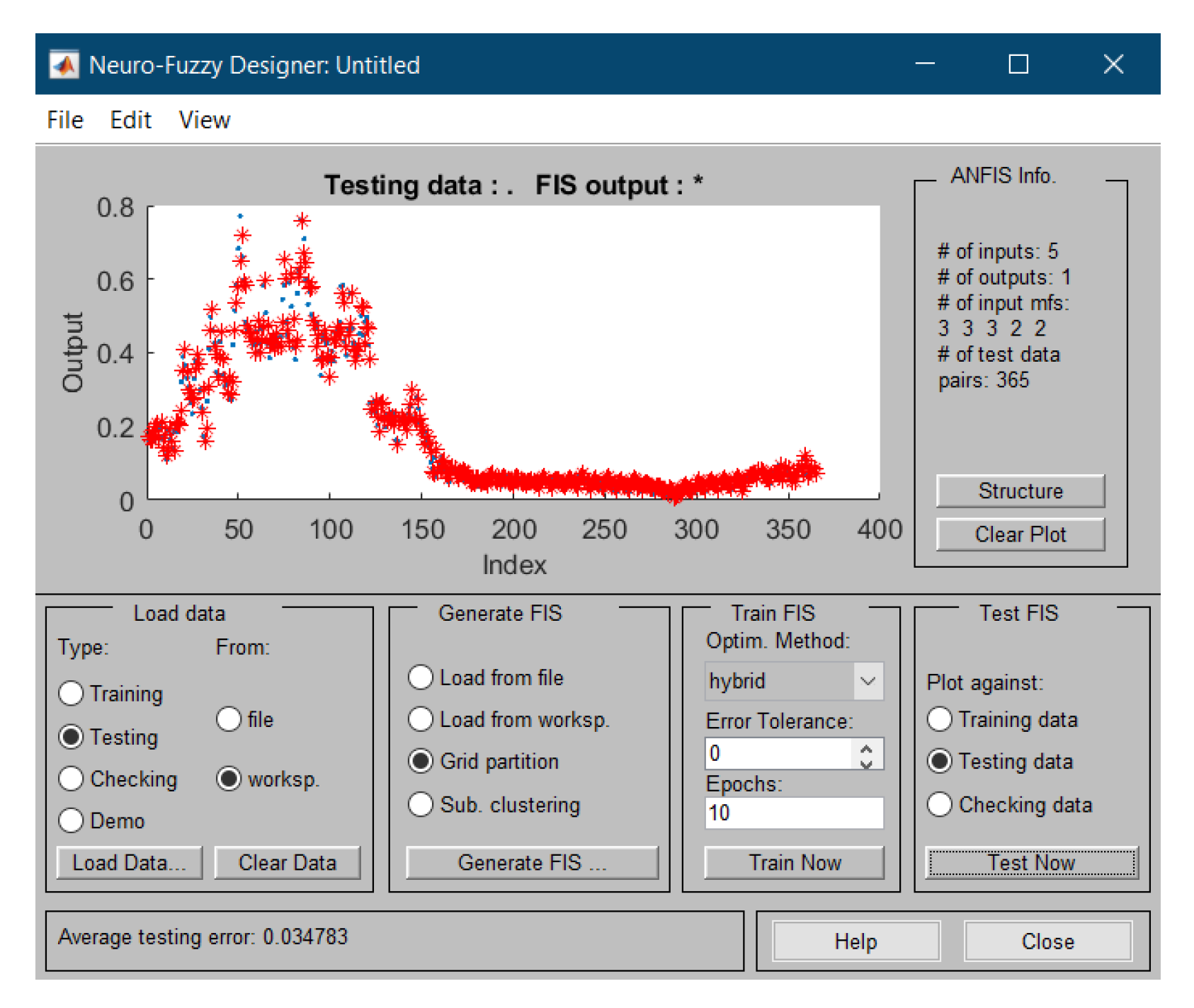
2.2.3. Testing and Evaluation
- Mean squared error:
- Root mean squared error:
- Mean absolute error:
- Mean absolute percentage error:
- Coefficient of determination:where X(t) is the forecasted value of the NG at the t-th iteration, and Z(t) is the actual value of the NG at the t-th iteration, t = 1, …, T, where T is the number of testing records.
3. Results
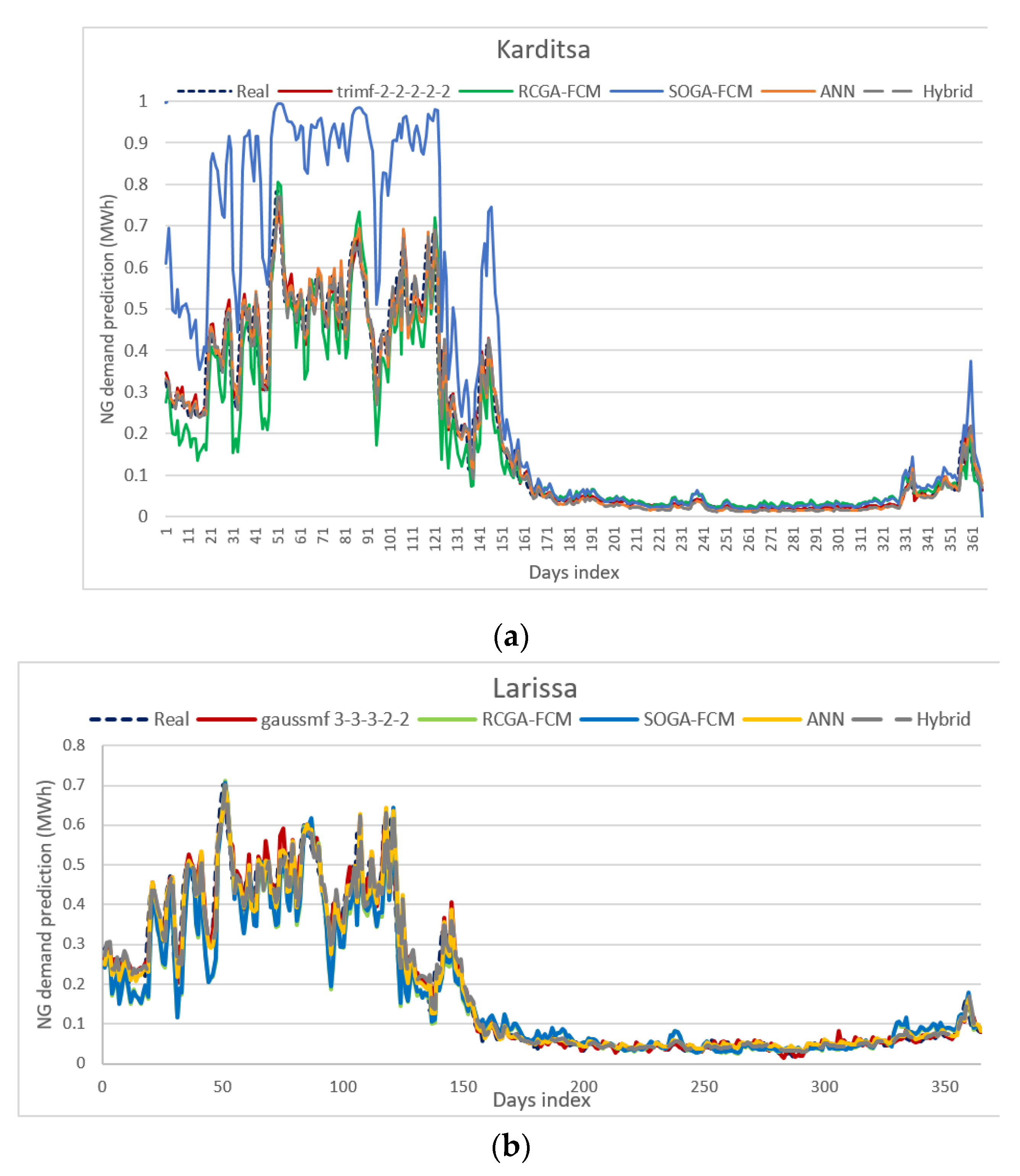
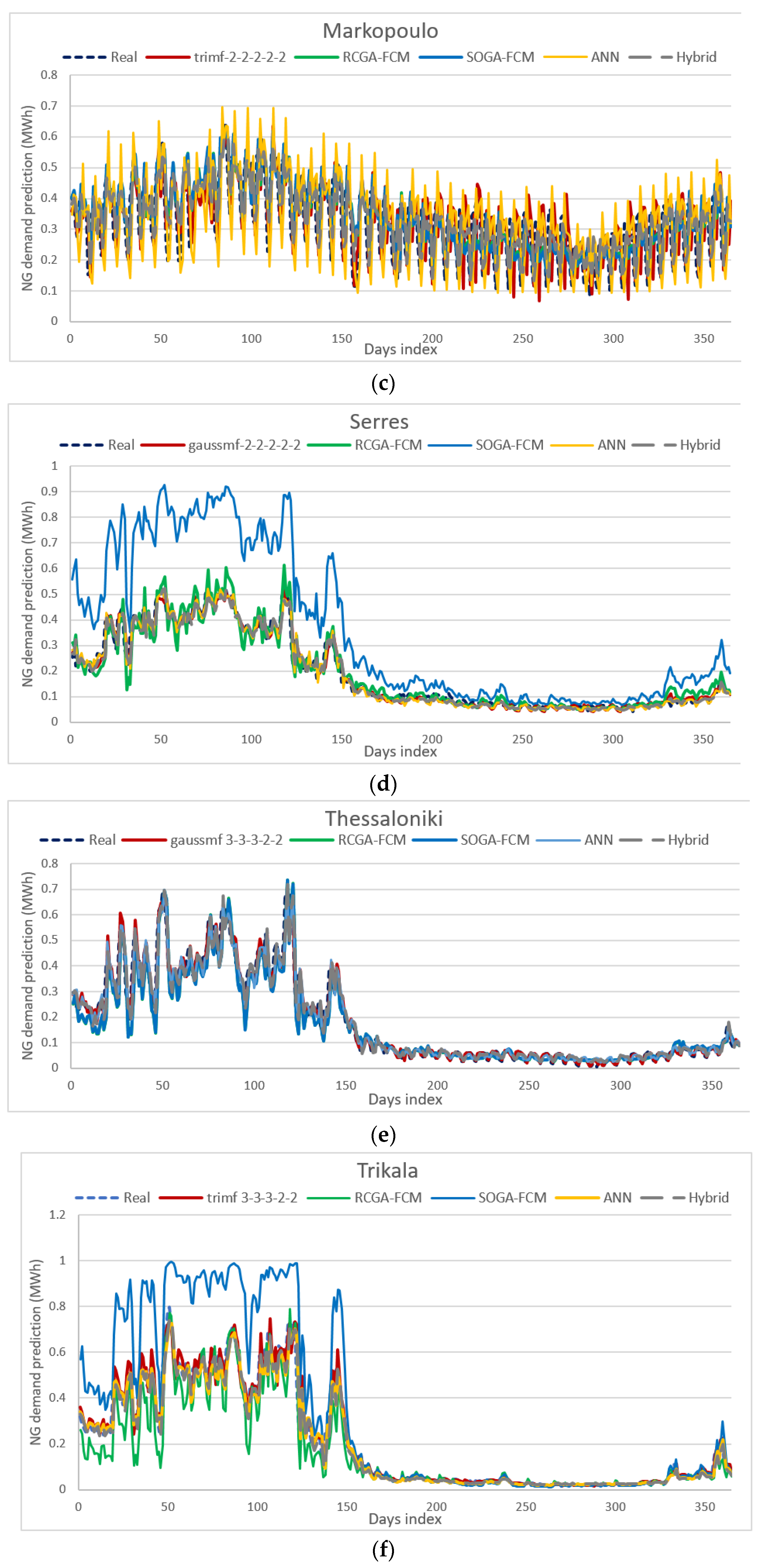
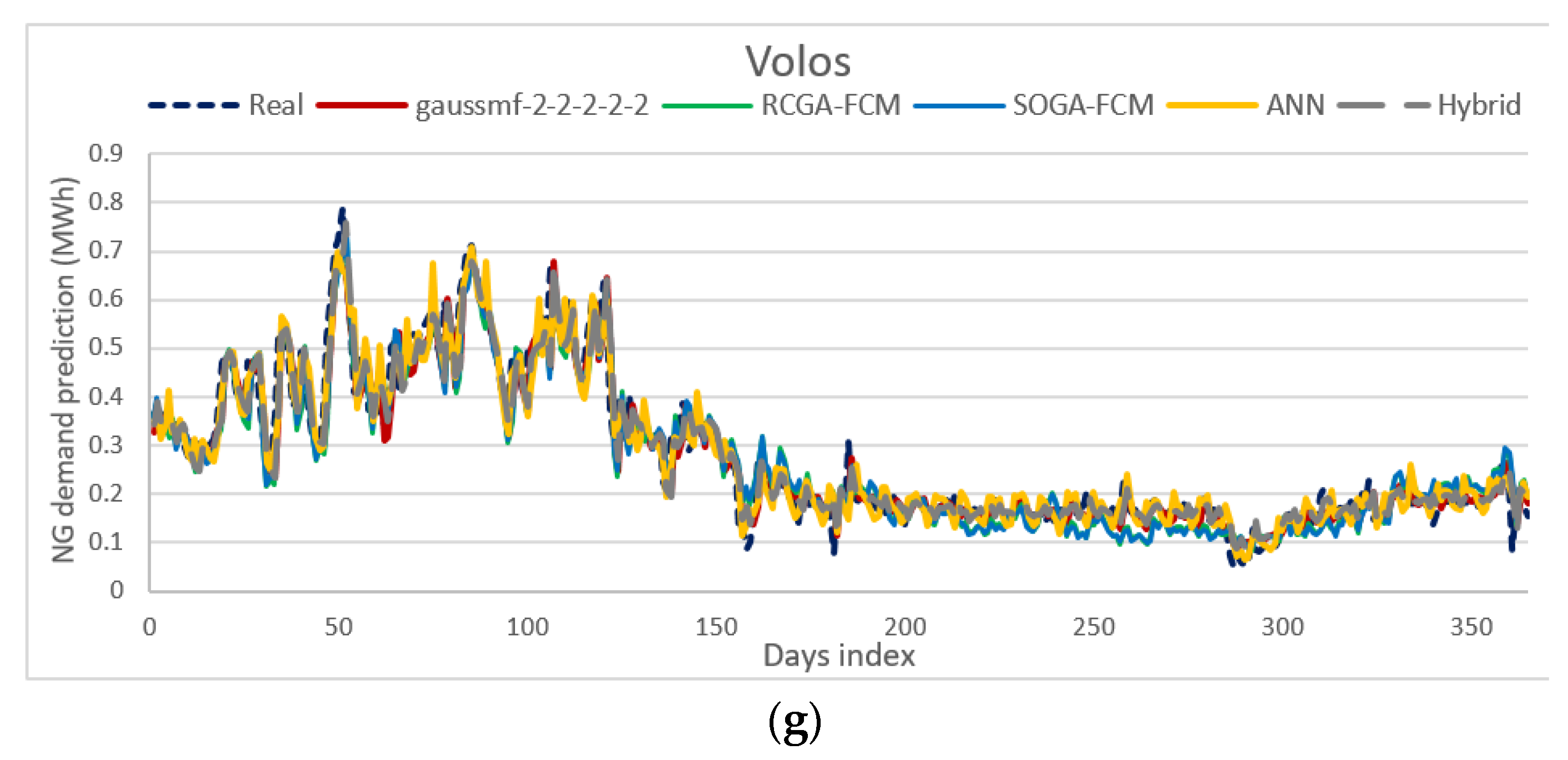
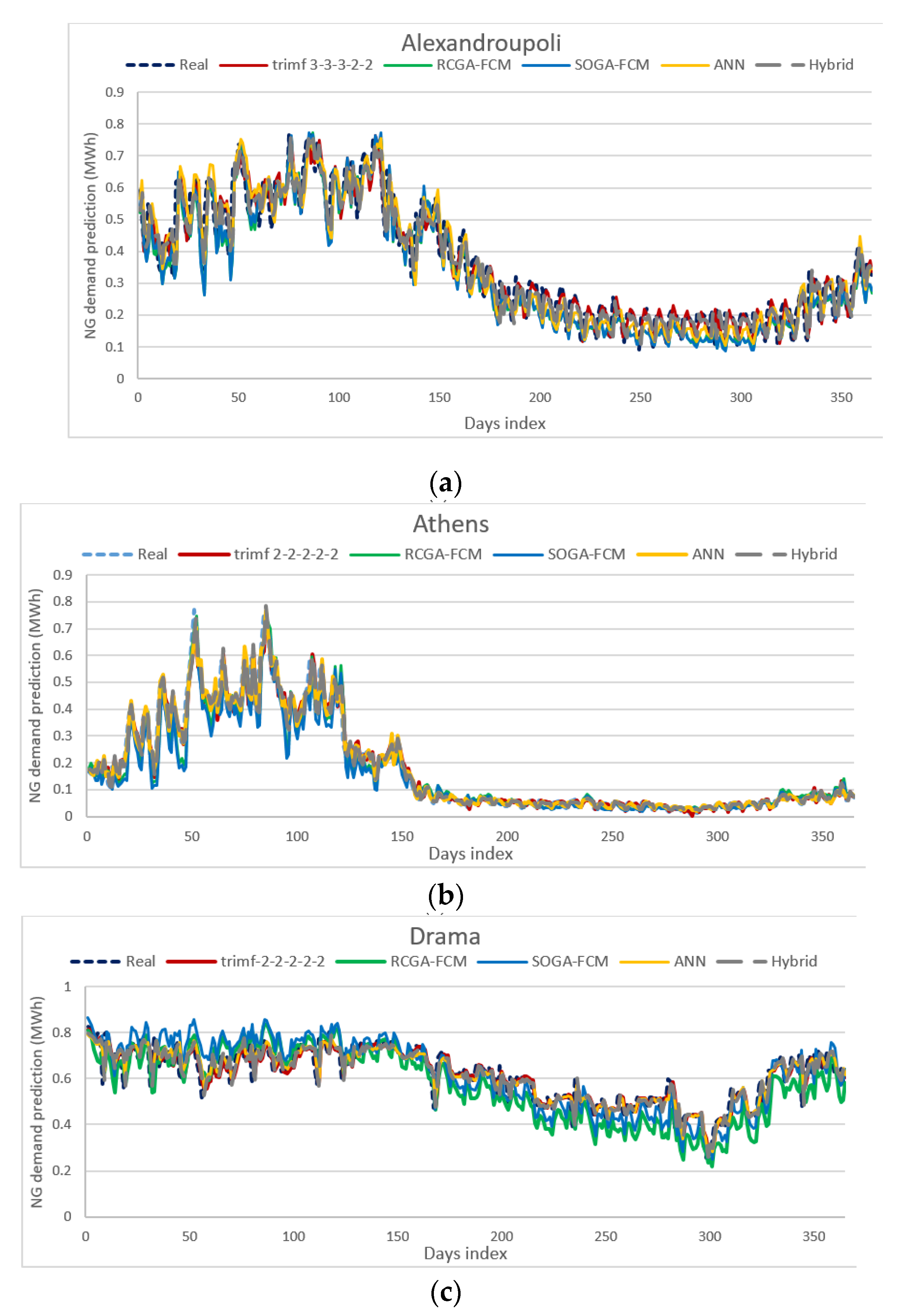
3.1. Comparison with ANNs, FCMs and Hybrid FCM-ANN
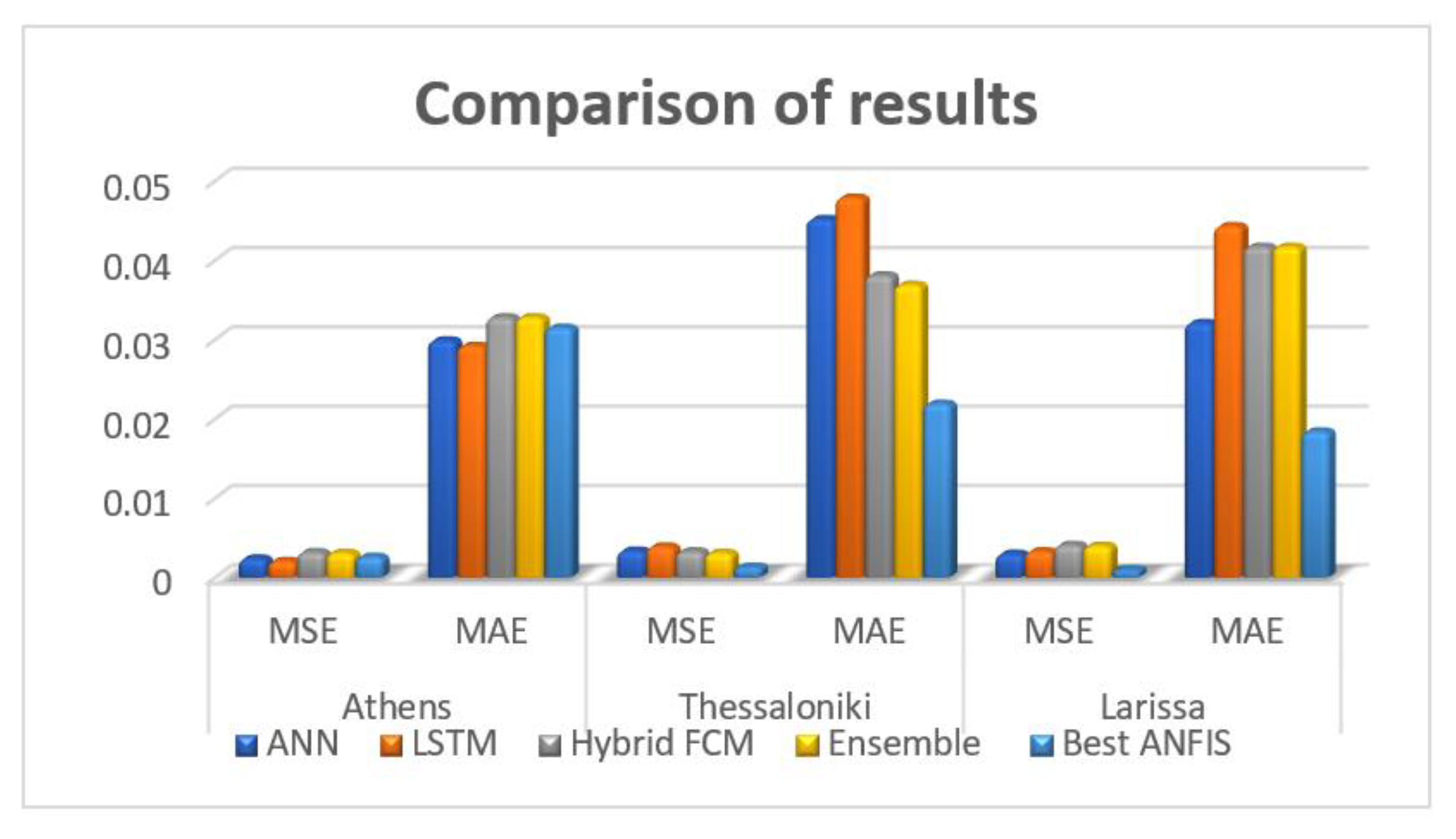
3.2. Discussion of Results
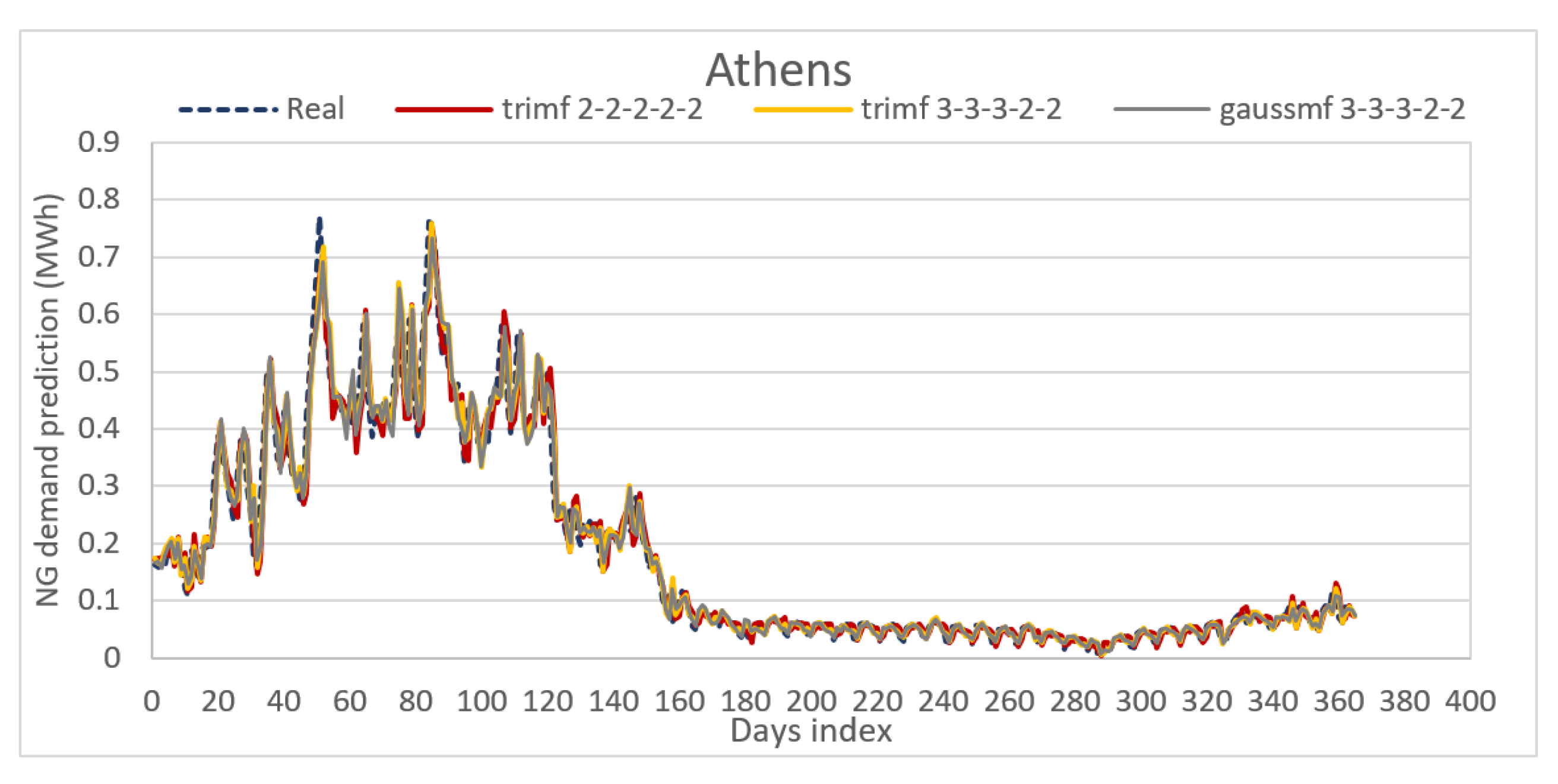
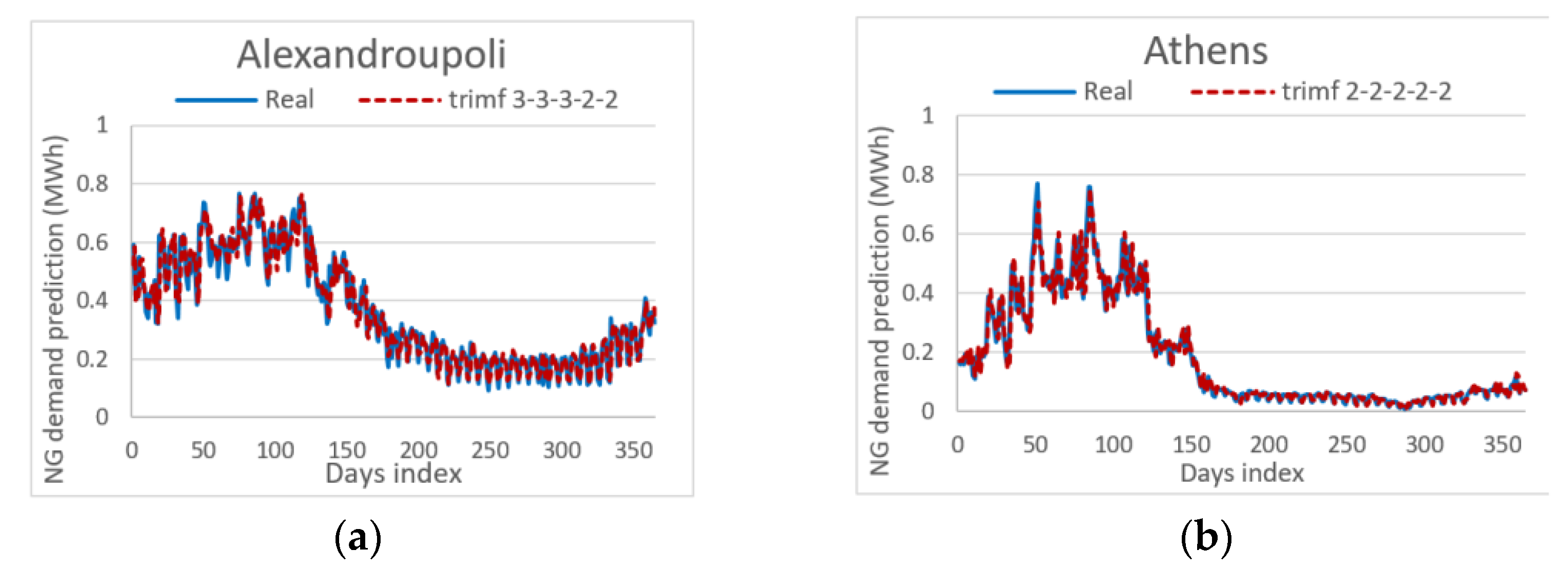
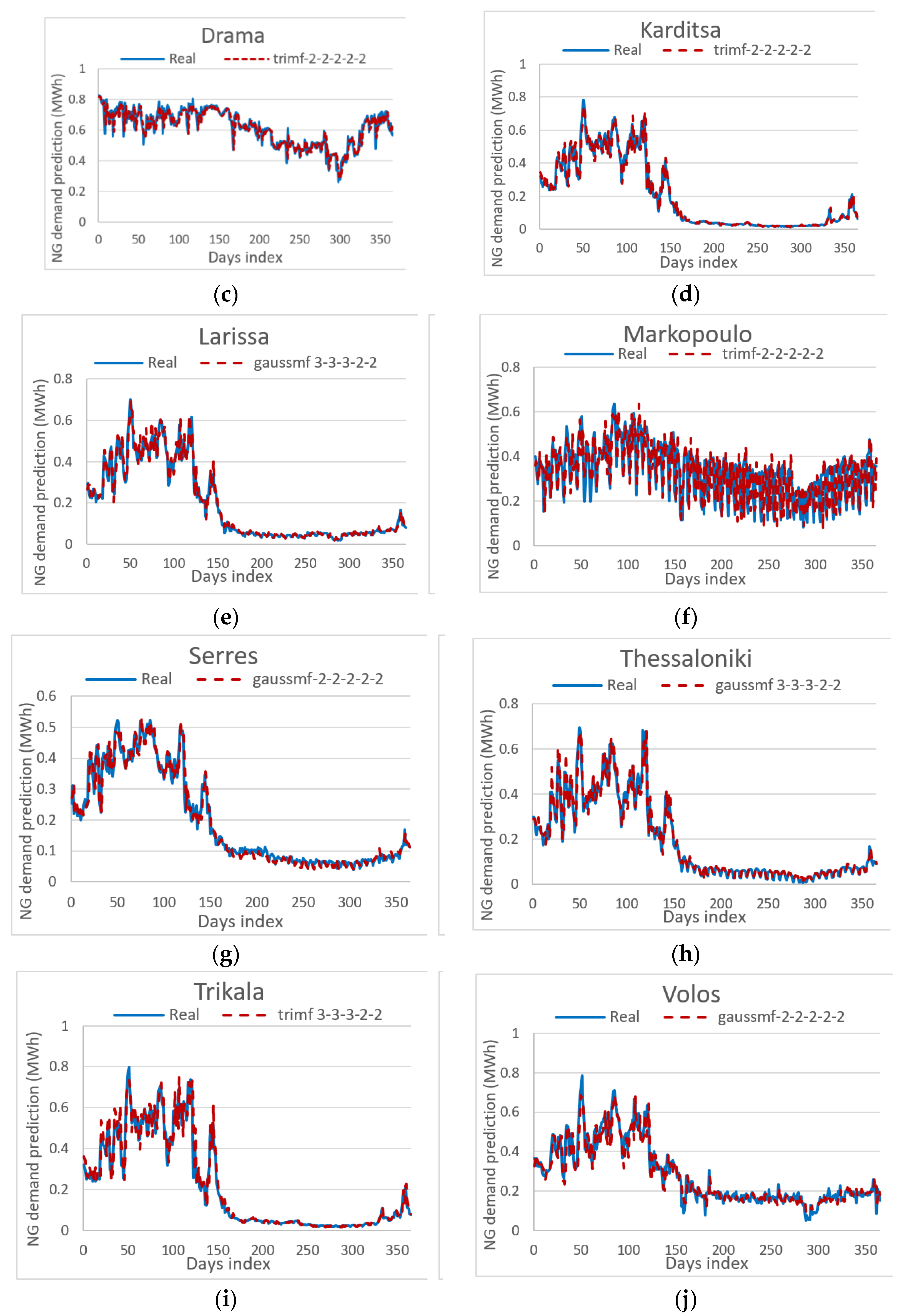
- The proposed ANFIS method exhibits the best performance when certain configuration settings are selected for the examined datasets which are linked to ten cities of Greece. The authors concluded that a certain configuration is best for the examined ANFIS model, after having conducted a number of experiments and following a trial-and error approach. The best ANFIS model is based on a distinct architecture that features a 2-2-2-2-2 triangular or gaussian MF.
- The proposed ANFIS architecture is superior to the four benchmark and well-known ANN and FCM methods (ANN, SOGA-FCM, RCGA-FCM, Hybrid FCM-ANN), which have been efficiently used in NG consumption forecasting. The results presented in Table 7, which gathers various error indicators and the R2, as prediction accuracy indices for all five architectures, show that the best ANFIS model holds the best prediction accuracy among all the methods that were included in this comparative analysis.
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Type of Input MF | Number of MFs | Type of Output MF | Number of Rules | MSE | RMSE | MAE | MAPE | R2 | Time (s) |
|---|---|---|---|---|---|---|---|---|---|
| trimf | 2-2-2-2-2 | Linear | 32 | 0.001195 | 0.034572 | 0.019426 | 11.72180 | 0.982121 | 148 |
| trapmf | 2-2-2-2-2 | Linear | 32 | 0.001358 | 0.036859 | 0.020861 | 12.12378 | 0.979559 | 148 |
| gbellmf | 2-2-2-2-2 | Linear | 32 | 0.001267 | 0.035603 | 0.019921 | 11.46446 | 0.980963 | 148 |
| Gaussmf | 2-2-2-2-2 | Linear | 32 | 0.001298 | 0.036038 | 0.020259 | 11.97794 | 0.980468 | 148 |
| Gauss2mf | 2-2-2-2-2 | Linear | 32 | 0.001406 | 0.037496 | 0.020878 | 11.26382 | 0.978860 | 148 |
| pimf | 2-2-2-2-2 | Linear | 32 | 0.001635 | 0.040442 | 0.022176 | 12.08298 | 0.975405 | 148 |
| dsigmf | 2-2-2-2-2 | Linear | 32 | 0.001423 | 0.037733 | 0.021062 | 11.26721 | 0.978592 | 148 |
| psigmf | 2-2-2-2-2 | Linear | 32 | 0.001423 | 0.037733 | 0.021062 | 11.26722 | 0.978592 | 148 |
| trimf | 2-2-3-3-3 | Linear | 108 | 0.001476 | 0.038430 | 0.020941 | 11.17862 | 0.977773 | 328 |
| Gaussmf | 2-2-3-3-3 | Linear | 108 | 0.002038 | 0.045149 | 0.023286 | 12.71720 | 0.969241 | 328 |
| Type of Input MF | Number of MFs | Type of Output MF | Number of Epochs | Optimization | Number of Rules | Time Run |
|---|---|---|---|---|---|---|
| trimf, trapmf, gbell, gauss, pim, sigm | 2-2-2-2-2 | Constant | 10 | Hybrid | 32 | 7 s |
| trimf, trapmf, gbell, gauss, pim, sigm | 2-2-3-3-3 | Constant | 10 | Hybrid | 108 | 11 s |
| trimf, trapmf, gbell, gauss, pim, sigm | 3-3-3-2-2 | Constant | 10 | Hybrid | 108 | 19 s |
| trimf, trapmf, gbell | 3-3-3-3-3 | Constant | 10 | Hybrid | 243 | 68 s |
| trimf | 3-3-4-4-4 | Constant | 10 | Hybrid | 576 | 10 min 10 s |
| trimf | 3-3-5-5-5 | Constant | 10 | Hybrid | 1125 | 40 min |
| trapmf | 3-3-4-4-4 | Constant | 10 | Hybrid | 576 | 12min |
| trapmf | 3-3-5-5-5 | Constant | 10 | Hybrid | 1125 | 70 min |
| gbellmf | 3-3-4-4-4 | Constant | 10 | Hybrid | 576 | 12 min 35 s |
| gbellmf | 3-3-5-5-5 | Constant | 10 | Hybrid | 1125 | 50 min |
| gaussmf | 3-3-3-3-3 | Constant | 10 | Hybrid | 243 | 4 min |
| gaussmf | 3-3-4-4-4 | Constant | 10 | Hybrid | 576 | 25 min |
| gaussmf | 3-3-5-5-5 | Constant | 10 | Hybrid | 1125 | 47 min |
| gauss2mf | 3-3-3-3-3 | Constant | 10 | Hybrid | 243 | 4 min |
| gauss2mf | 3-3-4-4-4 | Constant | 10 | Hybrid | 576 | 25 min |
| gauss2mf | 3-3-5-5-5 | Constant | 10 | Hybrid | 1125 | 47 min |
| pimf | 3-3-3-3-3 | Constant | 10 | Hybrid | 243 | 3.5 min |
| pimf | 3-3-4-4-4 | Constant | 10 | hybrid | 576 | 20 min |
| pimf | 3-3-5-5-5 | Constant | 10 | hybrid | 1125 | 42 min |
Appendix B
Appendix B.1. Fuzzy Cognitive Maps
References
- Lee, Y.-S.; Tong, L.-I. Forecasting energy consumption using a grey model improved by incorporating genetic programming. Energy Convers. Manag. 2011, 52, 147–152. [Google Scholar] [CrossRef]
- Barak, S.; Sadegh, S.S. Forecasting energy consumption using ensemble ARIMA–ANFIS hybrid algorithm. Int. J. Electr. Power Energy Syst. 2016, 82, 92–104. [Google Scholar] [CrossRef]
- Adedeji, P.; Akinlabi, S.; Madushele, N.; Olatunji, O. Hybrid Adaptive Neuro-fuzzy Inference System (ANFIS) for a Multi-campus University Energy Consumption Forecast. Int. J. Ambient Energy 2020, 41, 1–20. [Google Scholar] [CrossRef]
- Yu, S.; Wei, Y.-M.; Wang, K. A PSO-GA optimal model to estimate primary energy demand of China. Energy Policy 2012, 42, 329–340. [Google Scholar] [CrossRef]
- U.S. Energy Information Administraton. International Energy Outlook. 2016. Available online: https://www.eia.gov/outlooks/ieo/pdf/0484(2016)pdf (accessed on 3 January 2020).
- Wei, N.; Li, C.; Li, C.; Xie, H.; Du, Z.; Zhang, Q.; Zeng, F. Short-Term Forecasting of Natural Gas Consumption Using Factor Selection Algorithm and Optimized Support Vector Regression. J. Energy Res. Technol. 2018, 141, 032701. [Google Scholar] [CrossRef]
- Tamba, J.G.; Ndjakomo, S.; Sapnken, E.; Koffi, F.; Nsouandele, J.L.; Soldo, B.; Njomo, D. Forecasting Natural Gas: A Literature Survey. Int. J. Energy Econ. Policy 2018, 8, 216–249. [Google Scholar]
- Salehnia, N.; Falahi, M.A.; Seifi, A.; Adeli, M.H.M. Forecasting natural gas spot prices with nonlinear modeling using Gamma test analysis. J. Nat. Gas Sci. Eng. 2013, 14, 238–249. [Google Scholar] [CrossRef]
- Xu, G.; Wang, W. Forecasting China’s natural gas consumption based on a combination model. J. Nat. Gas Chem. 2010, 19, 493–496. [Google Scholar] [CrossRef]
- Agbonifo, P.E. Natural Gas Distribution Infrastructure and the Quest for Environmental Sustainability in the Niger Delta: The Prospect of Natural Gas Utilization in Nigeria. Int. J. Energy Econ. Policy 2016, 6, 442–448. [Google Scholar]
- Solarin, S.A.; Ozturk, I. The relationship between natural gas consumption and economic growth in OPEC members. Renew. Sustain. Energy Rev. 2016, 58, 1348–1356. [Google Scholar] [CrossRef]
- Panapakidis, I.P.; Dagoumas, A.S. Day-ahead natural gas demand forecasting based on the combination of wavelet transform and ANFIS/genetic algorithm/neural network model. Energy 2017, 118, 231–245. [Google Scholar] [CrossRef]
- Papageorgiou, K.; Papageorgiou, E.; Poczeta, K.; Gerogiannis, V.; Stamoulis, G. Exploring an Ensemble of Methods that Combines Fuzzy Cognitive Maps and Neural Networks in Solving the Time Series Prediction Problem of Gas Consumption in Greece. Algorithms 2019, 12, 235. [Google Scholar] [CrossRef]
- Ediger, V.Ş.; Akar, S. ARIMA forecasting of primary energy demand by fuel in Turkey. Energy Policy 2007, 35, 1701–1708. [Google Scholar] [CrossRef]
- Šebalj, D.; Mesaric, J.; Dujak, D. Predicting Natural Gas Consumption—A Literature Review. In Proceedings of the Central European Conference on Information and Intelligent Systems, Varaždin, Croatia, 27–29 September 2017. [Google Scholar]
- Gil, S.; Deferrari, J. Generalized Model of Prediction of Natural Gas Consumption. J. Energy Res. Technol. 2004, 126, 90–98. [Google Scholar] [CrossRef]
- Akpınar, M.; Yumuşak, N. Estimating household natural gas consumption with multiple regression: Effect of cycle. In Proceedings of the 2013 International Conference on Electronics, Computer and Computation, ICECCO 2013, Ankara, Turkey, 7–9 November 2013; pp. 188–191. [Google Scholar]
- Akpinar, M.; Yumusak, N. Day-ahead natural gas forecasting using nonseasonal exponential smoothing methods. In Proceedings of the 2017 IEEE International Conference on Environment and Electrical Engineering and 2017 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I CPS Europe), Milan, Italy, 6–9 June 2017; pp. 1–4. [Google Scholar]
- Akpınar, M.; Yumuşak, N. Forecasting household natural gas consumption with ARIMA model: A case study of removing cycle. In Proceedings of the 2013 7th International Conference on Application of Information and Communication Technologies, Baku, Azerbaijan, 23–25 October 2013; pp. 1–6. [Google Scholar]
- Deka, A.; Hamta, N.; Esmaeilian, B.; Behdad, S. Predictive Modeling Techniques to Forecast Energy Demand in the United States: A Focus on Economic and Demographic Factors. In Proceedings of the Journal of Energy Resources Technology, Boston, MA, USA, 2–5 August 2015; Volume 138. [Google Scholar]
- Kaynar, O.; Yilmaz, I.; Demirkoparan, F. Forecasting of natural gas consumption with neural network and neuro fuzzy system. Energy Educ. Sci. Technol. Part A Energy Sci. Res. 2010, 26, 221–238. [Google Scholar]
- Zhu, L.; Li, M.S.; Wu, Q.H.; Jiang, L. Short-term natural gas demand prediction based on support vector regression with false neighbours filtered. Energy 2015, 80, 428–436. [Google Scholar] [CrossRef]
- Yu, F.; Xu, X. A short-term load forecasting model of natural gas based on optimized genetic algorithm and improved BP neural network. Appl. Energy 2014, 134, 102–113. [Google Scholar] [CrossRef]
- Potočnik, P.; Govekar, E.; Grabec, I. Short-term natural gas consumption forecasting. In Proceedings of the IASTED International Conference on Applied Simulation and Modelling, ASM 2011, Palma de Mallorca, Spain, 29–31 August 2007; pp. 353–357. [Google Scholar]
- Merkel, G.D.; Povinelli, R.J.; Brown, R.H. Short-Term Load Forecasting of Natural Gas with Deep Neural Network Regression. Energies 2018, 11, 2008. [Google Scholar] [CrossRef]
- Pedregal, D.J.; Trapero, J.R. Mid-term hourly electricity forecasting based on a multi-rate approach. Energy Convers. Manag. 2010, 51, 105–111. [Google Scholar] [CrossRef]
- Almeshaiei, E.; Soltan, H. A methodology for Electric Power Load Forecasting. Alex. Eng. J. 2011, 50, 137–144. [Google Scholar] [CrossRef]
- Park, D.C.; El-Sharkawi, M.A.; Marks, R.J.; Atlas, L.E.; Damborg, M.J. Electric load forecasting using an artificial neural network. IEEE Trans. Power Syst. 1991, 6, 442–449. [Google Scholar] [CrossRef]
- Pai, P.-F.; Hong, W.-C. Forecasting regional electricity load based on recurrent support vector machines with genetic algorithms. Electr. Power Syst. Res. 2005, 74, 417–425. [Google Scholar] [CrossRef]
- Pai, P.-F.; Hong, W.-C. Support vector machines with simulated annealing algorithms in electricity load forecasting. Energy Convers. Manag. 2005, 46, 2669–2688. [Google Scholar] [CrossRef]
- Hippert, H.S.; Pedreira, C.E.; Souza, R.C. Neural networks for short-term load forecasting: A review and evaluation. IEEE Trans. Power Syst. 2001, 16, 44–55. [Google Scholar] [CrossRef]
- Hong, W.-C. Electric load forecasting by support vector model. Appl. Math. Model. 2009, 33, 2444–2454. [Google Scholar] [CrossRef]
- Nizami, S.J.; Al-Garni, A.Z. Forecasting electric energy consumption using neural networks. Energy Policy 1995, 23, 1097–1104. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Applications of artificial neural networks in energy systems. Energy Convers. Manag. 1999, 40, 1073–1087. [Google Scholar] [CrossRef]
- Aydinalp, M.; Ismet Ugursal, V.; Fung, A.S. Modeling of the appliance, lighting, and space-cooling energy consumptions in the residential sector using neural networks. Appl. Energy 2002, 71, 87–110. [Google Scholar] [CrossRef]
- Hsu, C.-C.; Chen, C.-Y. Regional load forecasting in Taiwan—Applications of artificial neural networks. Energy Convers. Manag. 2003, 44, 1941–1949. [Google Scholar] [CrossRef]
- Roldán-Blay, C.; Escrivá-Escrivá, G.; Álvarez-Bel, C.; Roldán-Porta, C.; Rodríguez-García, J. Upgrade of an artificial neural network prediction method for electrical consumption forecasting using an hourly temperature curve model. Energy Build. 2013, 60, 38–46. [Google Scholar] [CrossRef]
- Raza, M.Q.; Baharudin, Z. A review on short term load forecasting using hybrid neural network techniques. In Proceedings of the 2012 IEEE International Conference on Power and Energy (PECon), Kota Kinabalu, Malaysia, 2–5 December 2012; pp. 846–851. [Google Scholar]
- De Felice, M.; Yao, X. Notes Short-Term Load Forecasting with Neural Network Ensembles: A Comparative Study. Comput. Intell. Mag. 2011, 6, 47–56. [Google Scholar] [CrossRef]
- Kumar, R.; Aggarwal, R.K.; Sharma, J.D. Energy analysis of a building using artificial neural network: A review. Energy Build. 2013, 65, 352–358. [Google Scholar] [CrossRef]
- Sulaiman, S.; Jeyanthy, A.; Devaraj, D. Artificial neural network based day ahead load forecasting using Smart Meter data. In Proceedings of the 2016 Biennial International Conference on Power and Energy Systems: Towards Sustainable Energy (PESTSE), Bangalore, India, 21–23 January 2016; pp. 1–6. [Google Scholar]
- Abdel-Aal, R.E.; Al-Garni, A.Z.; Al-Nassar, Y.N. Modelling and forecasting monthly electric energy consumption in eastern Saudi Arabia using abductive networks. Energy 1997, 22, 911–921. [Google Scholar] [CrossRef]
- Kermanshahi, B. Recurrent neural network for forecasting next 10 years loads of nine Japanese utilities. Neurocomputing 1998, 23, 125–133. [Google Scholar] [CrossRef]
- Ghelardoni, L.; Ghio, A.; Anguita, D. Energy Load Forecasting Using Empirical Mode Decomposition and Support Vector Regression. IEEE Trans. Smart Grid 2013, 4, 549–556. [Google Scholar] [CrossRef]
- Ceylan, H.; Ozturk, H. Estimating energy demand of Turkey based on economic indicators using genetic algorithm approach. Energy Convers. Manag. 2004, 45, 2525–2537. [Google Scholar] [CrossRef]
- Ozturk, H.K.; Ceylan, H.; Canyurt, O.E.; Hepbasli, A. Electricity estimation using genetic algorithm approach: A case study of Turkey. Energy 2005, 30, 1003–1012. [Google Scholar] [CrossRef]
- Azadeh, A.; Ghaderi, S.F.; Tarverdian, S.; Saberi, M. Integration of artificial neural networks and genetic algorithm to predict electrical energy consumption. Appl. Math. Comput. 2007, 186, 1731–1741. [Google Scholar] [CrossRef]
- Daut, M.A.M.; Hassan, M.Y.; Abdullah, H.; Rahman, H.A.; Abdullah, M.P.; Hussin, F. Building electrical energy consumption forecasting analysis using conventional and artificial intelligence methods: A review. Renew. Sustain. Energy Rev. 2017, 70, 1108–1118. [Google Scholar] [CrossRef]
- Ahmad, T.; Chen, H.; Guo, Y.; Wang, J. A comprehensive overview on the data driven and large scale based approaches for forecasting of building energy demand: A review. Energy Build. 2018, 165, 301–320. [Google Scholar] [CrossRef]
- Foucquier, A.; Robert, S.; Suard, F.; Stéphan, L.; Jay, A. State of the art in building modelling and energy performances prediction: A review. Renew. Sustain. Energy Rev. 2013, 23, 272–288. [Google Scholar] [CrossRef]
- Metaxiotis, K.; Kagiannas, A.; Askounis, D.; Psarras, J. Artificial intelligence in short term electric load forecasting: A state-of-the-art survey for the researcher. Energy Convers. Manag. 2003, 44, 1525–1534. [Google Scholar] [CrossRef]
- GORUCU, F.B. Artificial Neural Network Modeling for Forecasting Gas Consumption. Energy Sources 2004, 26, 299–307. [Google Scholar] [CrossRef]
- Karimi, H.; Dastranj, J. Artificial neural network-based genetic algorithm to predict natural gas consumption. Energy Syst. 2014, 5, 571–581. [Google Scholar] [CrossRef]
- Khotanzad, A.; Elragal, H.M. Natural gas load forecasting with combination of adaptive neural networks. In Proceedings of the IJCNN’99. International Joint Conference on Neural Networks. Proceedings (Cat. No.99CH36339), Washington, DC, USA, 10–16 July 1999; Volume 6, pp. 4069–4072. [Google Scholar]
- Khotanzad, A.; Elragal, H.; Lu, T. Combination of artificial neural-network forecasters for prediction of natural gas consumption. IEEE Trans. Neural Netw. 2000, 11, 464–473. [Google Scholar] [CrossRef]
- Kizilaslan, R.; Karlik, B. Combination of neural networks forecasters for monthly natural gas consumption prediction. Neural Netw. World 2009, 19, 191–199. [Google Scholar]
- Kizilaslan, R.; Karlik, B. Comparison neural networks models for short term forecasting of natural gas consumption in Istanbul. In Proceedings of the 2008 First International Conference on the Applications of Digital Information and Web Technologies (ICADIWT), Ostrava, Czech Republic, 4–6 August 2008; pp. 448–453. [Google Scholar]
- Musílek, P.; Pelikán, E.; Brabec, T.; Simunek, M. Recurrent Neural Network Based Gating for Natural Gas Load Prediction System. In Proceedings of the 2006 IEEE International Joint Conference on Neural Network Proceedings, Vancouver, BC, Canada, 16–21 July 2006; pp. 3736–3741. [Google Scholar]
- Soldo, B. Forecasting natural gas consumption. Appl. Energy 2012, 92, 26–37. [Google Scholar] [CrossRef]
- Szoplik, J. Forecasting of natural gas consumption with artificial neural networks. Energy 2015, 85, 208–220. [Google Scholar] [CrossRef]
- Aydinalp-Koksal, M.; Ugursal, V.I. Comparison of neural network, conditional demand analysis, and engineering approaches for modeling end-use energy consumption in the residential sector. Appl. Energy 2008, 85, 271–296. [Google Scholar] [CrossRef]
- Dombayci, Ö. The prediction of heating energy consumption in a model house by using artificial neural networks in Denizli-Turkey. Adv. Eng. Softw. 2010, 41, 141–147. [Google Scholar] [CrossRef]
- Taşpınar, F.; Çelebi, N.; Tutkun, N. Forecasting of daily natural gas consumption on regional basis in Turkey using various computational methods. Energy Build. 2013, 56, 23–31. [Google Scholar] [CrossRef]
- Lago, J.; Ridder, F.D.; Schutter, B.D. Forecasting spot electricity prices: Deep learning approaches and empirical comparison of traditional algorithms. Appl. Energy 2018, 221, 386–405. [Google Scholar] [CrossRef]
- Tonkovic, Z.; Zekic-Susac, M.; Somolanji, M. Predicting natural gas consumption by neural networks. Teh. Vjesn. 2009, 16, 51–61. [Google Scholar]
- Demirel, F.; Zaim, S.; Caliskan, A.; Gokcin Ozuyar, P. Forecasting natural gas consumption in Istanbul using neural networks and multivariate time series methods. Turk. J. Electr. Eng. Comput. Sci. 2012, 20, 695–711. [Google Scholar] [CrossRef]
- Olgun, M.; Ozdemir, G.; Aydemir, E. Forecasting of Turkey’s natural gas demand using artifical neural networks and support vector machines. Energy Educ. Sci. Technol. 2011, 30, 15–20. [Google Scholar]
- Soldo, B.; Potočnik, P.; Šimunović, G.; Šarić, T.; Govekar, E. Improving the residential natural gas consumption forecasting models by using solar radiation. Energy Build. 2014, 69, 498–506. [Google Scholar] [CrossRef]
- Izadyar, N.; Ong, H.C.; Shamshirband, S.; Ghadamian, H.; Tong, C.W. Intelligent forecasting of residential heating demand for the District Heating System based on the monthly overall natural gas consumption. Energy Build. 2015, 104, 208–214. [Google Scholar] [CrossRef]
- Ivezić, D. Short-term natural gas consumption forecast. FME Trans. 2006, 34, 165–169. [Google Scholar]
- Garcia, A.; Mohaghegh, S.D. Forecasting US Natural Gas Production into year 2020: A comparative study. In Proceedings of the SPE Eastern Regional Meeting, Charleston, WV, USA, 15–17 September 2004; Society of Petroleum Engineers: Richardson, TX, USA, 2004; p. 5. [Google Scholar]
- Ma, H.; Wu, Y. Grey Predictive on Natural Gas Consumption and Production in China. In Proceedings of the 2009 Second Pacific-Asia Conference on Web Mining and Web-based Application, Wuhan, China, 6–7 June 2009; pp. 91–94. [Google Scholar]
- Ervural, B.C.; Beyca, O.F.; Zaim, S. Model Estimation of ARMA Using Genetic Algorithms: A Case Study of Forecasting Natural Gas Consumption. Procedia Soc. Behav. Sci. 2016, 235, 537–545. [Google Scholar] [CrossRef]
- Zeng, B.; Li, C. Forecasting the natural gas demand in China using a self-adapting intelligent grey model. Energy 2016, 112, 810–825. [Google Scholar] [CrossRef]
- Liu, G.; Dong, X.; Jiang, Q.; Dong, C.; Li, J. Natural gas consumption of urban households in China and corresponding influencing factors. Energy Policy 2018, 122, 17–26. [Google Scholar] [CrossRef]
- Wang, D.; Liu, Y.; Wu, Z.; Fu, H.; Shi, Y.; Guo, H. Scenario Analysis of Natural Gas Consumption in China Based on Wavelet Neural Network Optimized by Particle Swarm Optimization Algorithm. Energies 2018, 11, 825. [Google Scholar] [CrossRef]
- Hribar, R.; Potočnik, P.; Šilc, J.; Papa, G. A comparison of models for forecasting the residential natural gas demand of an urban area. Energy 2019, 167, 511–522. [Google Scholar] [CrossRef]
- Laib, O.; Khadir, M.T.; Mihaylova, L. Toward efficient energy systems based on natural gas consumption prediction with LSTM Recurrent Neural Networks. Energy 2019, 177, 530–542. [Google Scholar] [CrossRef]
- Chen, Y.; Chua, W.S.; Koch, T. Forecasting day-ahead high-resolution natural-gas demand and supply in Germany. Appl. Energy 2018, 228, 1091–1110. [Google Scholar] [CrossRef]
- Beyca, O.F.; Ervural, B.C.; Tatoglu, E.; Ozuyar, P.G.; Zaim, S. Using machine learning tools for forecasting natural gas consumption in the province of Istanbul. Energy Econ. 2019, 80, 937–949. [Google Scholar] [CrossRef]
- Ding, S. A novel self-adapting intelligent grey model for forecasting China’s natural-gas demand. Energy 2018, 162, 393–407. [Google Scholar] [CrossRef]
- Fan, G.-F.; Wang, A.; Hong, W.-C. Combining Grey Model and Self-Adapting Intelligent Grey Model with Genetic Algorithm and Annual Share Changes in Natural Gas Demand Forecasting. Energies 2018, 11, 1625. [Google Scholar] [CrossRef]
- Brown, R.G.; Matin, L.; Kharout, P.; Piessens, L.P. Development of artificial neural-network models to predict daily gas consumption. In Proceedings of the IECON ′95—21st Annual Conference on IEEE Industrial Electronics, Orlando, FL, USA, 6–10 November 1996; Volume 5, pp. 1–22. [Google Scholar]
- Viet, N.H.; Mandziuk, J. Neural and fuzzy neural networks for natural gas consumption prediction. In Proceedings of the 2003 IEEE XIII Workshop on Neural Networks for Signal Processing (IEEE Cat. No.03TH8718), Toulouse, France, 17–19 September 2003; pp. 759–768. [Google Scholar]
- Ying, L.-C.; Pan, M.-C. Using adaptive network based fuzzy inference system to forecast regional electricity loads. Energy Convers. Manag. 2008, 49, 205–211. [Google Scholar] [CrossRef]
- Akdemir, B.; Çetinkaya, N. Long-term load forecasting based on adaptive neural fuzzy inference system using real energy data. Energy Procedia 2012, 14, 794–799. [Google Scholar] [CrossRef]
- Mordjaoui, M.; Boudjema, B. Forecasting and Modelling Electricity Demand Using Anfis Predictor. J. Math. Stat. 2011, 7, 275–281. [Google Scholar] [CrossRef][Green Version]
- Azadeh, A.; Saberi, M.; Gitiforouz, A.; Saberi, Z. A hybrid simulation adaptive-network-based fuzzy inference system for improvement of electricity consumption estimation. Expert Syst. Appl. 2009, 36, 11108–11117. [Google Scholar] [CrossRef]
- Cheng, C.-H.; Wei, L.-Y. One step-ahead ANFIS time series model for forecasting electricity loads. Optim. Eng. 2010, 11, 303–317. [Google Scholar] [CrossRef]
- Senvar, O.; Ulutagay, G.; Turanoğlu Bekar, E. ANFIS Modeling for Forecasting Oil Consumption of Turkey. J. Mult.-Valued Log. Soft Comput. 2016, 26, 609–624. [Google Scholar]
- Azadeh, A.; Asadzadeh, S.M.; Ghanbari, A. An adaptive network-based fuzzy inference system for short-term natural gas demand estimation: Uncertain and complex environments. Energy Policy 2010, 38, 1529–1536. [Google Scholar] [CrossRef]
- Zhang, Y.; Ling, C. A strategy to apply machine learning to small datasets in materials science. Npj Comput. Mater. 2018, 4, 25. [Google Scholar] [CrossRef]
- Behrouznia, A.; Saberi, M.; Azadeh, A.; Asadzadeh, S.M.; Pazhoheshfar, P. An adaptive network based fuzzy inference system-fuzzy data envelopment analysis for gas consumption forecasting and analysis: The case of South America. In Proceedings of the 2010 International Conference on Intelligent and Advanced Systems, Manila, Philippines, 15–17 June 2010; pp. 1–6. [Google Scholar]
- Azadeh, A.; Saberi, M.; Asadzadeh, S.M.; Hussain, O.K.; Saberi, Z. A neuro-fuzzy-multivariate algorithm for accurate gas consumption estimation in South America with noisy inputs. Int. J. Electr. Power Energy Syst. 2013, 46, 315–325. [Google Scholar] [CrossRef]
- Azadeh, A.; Asadzadeh, S.M.; Saberi, M.; Nadimi, V.; Tajvidi, A.; Sheikalishahi, M. A Neuro-fuzzy-stochastic frontier analysis approach for long-term natural gas consumption forecasting and behavior analysis: The cases of Bahrain, Saudi Arabia, Syria, and UAE. Appl. Energy 2011, 88, 3850–3859. [Google Scholar] [CrossRef]
- Azadeh, A.; Zarrin, M.; Rahdar Beik, H.; Aliheidari Bioki, T. A neuro-fuzzy algorithm for improved gas consumption forecasting with economic, environmental and IT/IS indicators. J. Pet. Sci. Eng. 2015, 133, 716–739. [Google Scholar] [CrossRef]
- Salmeron, J.L.; Froelich, W. Dynamic optimization of fuzzy cognitive maps for time series forecasting. Knowl.-Based Syst. 2016, 105, 29–37. [Google Scholar] [CrossRef]
- Froelich, W.; Salmeron, J.L. Evolutionary learning of fuzzy grey cognitive maps for the forecasting of multivariate, interval-valued time series. Int. J. Approx. Reason. 2014, 55, 1319–1335. [Google Scholar] [CrossRef]
- Papageorgiou, E.I.; Poczeta, K.; Laspidou, C. Application of Fuzzy Cognitive Maps to water demand prediction. In Proceedings of the IEEE International Conference on Fuzzy Systems, Istanbul, Turkey, 2–5 August 2015; Volume 2015. [Google Scholar]
- Poczeta, K.; Yastrebov, A.; Papageorgiou, E.I. Learning fuzzy cognitive maps using structure optimization genetic algorithm. In Proceedings of the 2015 Federated Conference on Computer Science and Information Systems, FedCSIS 2015, Lodz, Poland, 13–16 September 2015. [Google Scholar]
- Papageorgiou, E.I.; Poczeta, K. A two-stage model for time series prediction based on fuzzy cognitive maps and neural networks. Neurocomputing 2017, 232, 113–121. [Google Scholar] [CrossRef]
- Poczeta, K.; Papageorgiou, E.I. Implementing Fuzzy Cognitive Maps with Neural Networks for Natural Gas Prediction. In Proceedings of the 2018 IEEE 30th International Conference on Tools with Artificial Intelligence (ICTAI), Volos, Greece, 5–7 November 2018; pp. 1026–1032. [Google Scholar]
- Hellenic Gas Transmission System Operator S.A. (DESFA). Available online: https://www.desfa.gr/en/ (accessed on 1 March 2020).
- Dudek, G. Multilayer perceptron for short-term load forecasting: From global to local approach. Neural Comput. Appl. 2020, 32, 3695–3707. [Google Scholar] [CrossRef]
- Azadeh, A.; Ghaderi, S.F.; Sohrabkhani, S. A simulated-based neural network algorithm for forecasting electrical energy consumption in Iran. Energy Policy 2008, 36, 2637–2644. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, SMC-15, 116–132. [Google Scholar] [CrossRef]
- Jang, J.-R. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Rosadi, D.; Subanar, T. Suhartono Analysis of Financial Time Series Data Using Adaptive Neuro Fuzzy Inference System (ANFIS). Int. J. Comput. Sci. Issues 2013, 10, 491–496. [Google Scholar]
- Jang, J.-S.; Sun, C.-T.; Mizutani, C.T. Neuro-Fuzzy and Soft Computing—A Computational Approach to Learning and Machine Intelligence. In Prentice Hall Upper Saddle River; IEEE: Piscataway, NJ, USA, 1997; Volume 42, pp. 1482–1484. [Google Scholar]
- Jang, J.-S.; Sun, C.-T. Neuro-Fuzzy Modeling and Control. Proc. IEEE 1995, 83, 378–406. [Google Scholar] [CrossRef]
- Yeom, C.-U.; Kwak, K.-C. Performance Comparison of ANFIS Models by Input Space Partitioning Methods. Symmetry 2018, 10, 700. [Google Scholar] [CrossRef]
- Naderloo, L.; Alimardani, R.; Omid, M.; Sarmadian, F.; Javadikia, P.; Torabi, M.Y.; Alimardani, F. Application of ANFIS to predict crop yield based on different energy inputs. Measurement 2012, 45, 1406–1413. [Google Scholar] [CrossRef]
- Papageorgiou, E.I.; Aggelopoulou, K.; Gemtos, T.A.; Nanos, G.D. Development and Evaluation of a Fuzzy Inference System and a Neuro-Fuzzy Inference System for Grading Apple Quality. Appl. Artif. Intell. 2018, 32, 253–280. [Google Scholar] [CrossRef]
- Papageorgiou, E.I.; Groumpos, P.P. Two-stage learning algorithm for fuzzy cognitive maps. In Proceedings of the 2004 2nd International IEEE Conference “Intelligent Systems”—Proceedings, Varna, Bulgaria, 22–24 June 2004; Volume 1. [Google Scholar]
- Papageorgiou, E.I.; Poczȩta, K.; Laspidou, C. Hybrid model for water demand prediction based on fuzzy cognitive maps and artificial neural networks. In Proceedings of the 2016 IEEE International Conference on Fuzzy Systems, FUZZ-IEEE, Vancouver, BC, Canada, 24–29 July 2016. [Google Scholar]
- Poczeta, K.; Kubuś, L.; Yastrebov, A.; Papageorgiou, E.I. Temperature Forecasting for Energy Saving in Smart Buildings Based on Fuzzy Cognitive Map; Springer: Berlin/Heidelberg, Germany, 2018; Volume 743, ISBN 978-3-319-77178-6. [Google Scholar]
- Anagnostis, A.; Papageorgiou, E.; Dafopoulos, V.; Bochtis, D. Applying Long Short-Term Memory Networks for natural gas demand prediction. In Proceedings of the 2019 10th International Conference on Information, Intelligence, Systems and Applications (IISA), Patras, Greece, 15–17 July 2019; pp. 1–7. [Google Scholar]
- Azizi, A. An adaptive neuro-fuzzy inference system for a dynamic production environment under uncertainties. World Appl. Sci. J. 2013, 25, 428–433. [Google Scholar] [CrossRef]
- Raju, G.S.V.P.; Mary Sumalatha, V.; Ramani, K.V.; Lakshmi, K.V. Solving Uncertain Problems using ANFIS. Int. J. Comput. Appl. 2011, 29, 14–21. [Google Scholar] [CrossRef]
- Poczeta, K.; Yastrebov, A.; Papageorgiou, E.I. Forecasting Indoor Temperature Using Fuzzy Cognitive Maps with Structure Optimization Genetic Algorithm; Springer: Berlin/Heidelberg, Germany, 2016; Volume 655. [Google Scholar]
| City | Time Period of the Examined Data | City | Time Period of the Examined Data |
|---|---|---|---|
| Alexandroupoli | 2/2013–10/2018 | Markopoulo | 3/2010–10/2018 |
| Athens | 3/2010–10/2018 | Serres | 6/2013–10/2018 |
| Drama | 9/2011–10/2018 | Thessaloniki | 3/2012–10/2018 |
| Karditsa | 5/2014–10/2018 | Trikala | 9/2012–10/2018 |
| Larissa | 3/2010–10/2018 | Volos | 3/2010–10/2018 |
| Type | Parameter | Unit |
|---|---|---|
| Input | Demand of a day before | MWh |
| Input | Current day demand | MWh |
| Input | Daily average temperature | Celsius degrees |
| Input | Month indicator | K = 1/12, 2/12, …, 1 |
| Input | Day indicator | l = 1/7, 2/7, …, 1 |
| Output | A day ahead NG demand | MWh |
| ANFIS Run | Type of Input MF | Number of MFs | Type of Output MF | Number of Epochs | Learning Method |
|---|---|---|---|---|---|
| 1 | trimf | 2-2-2-2-2 | Constant | 10 | Hybrid |
| 2 | trapmf | 2-2-2-2-2 | Constant | 10 | Hybrid |
| 3 | gbellmf | 2-2-2-2-2 | Constant | 10 | Hybrid |
| 4 | Gaussmf | 2-2-2-2-2 | Constant | 10 | Hybrid |
| 5 | Gauss2mf | 2-2-2-2-2 | Constant | 10 | Hybrid |
| 6 | pimf | 2-2-2-2-2 | Constant | 10 | Hybrid |
| 7 | dsigmf | 2-2-2-2-2 | Constant | 10 | Hybrid |
| 8 | psigmf | 2-2-2-2-2 | Constant | 10 | Hybrid |
| 9 | trimf | 2-2-3-3-3 | Constant | 10 | Hybrid |
| 10 | trapmf | 2-2-3-3-3 | Constant | 10 | Hybrid |
| 11 | gbellmf | 2-2-3-3-3 | Constant | 10 | Hybrid |
| 12 | Gaussmf | 2-2-3-3-3 | Constant | 10 | Hybrid |
| 13 | Gauss2mf | 2-2-3-3-3 | Constant | 10 | Hybrid |
| 14 | pimf | 2-2-3-3-3 | Constant | 10 | Hybrid |
| 15 | dsigmf | 2-2-3-3-3 | Constant | 10 | Hybrid |
| 16 | psigmf | 2-2-3-3-3 | Constant | 10 | Hybrid |
| 17 | trimf | 3-3-3-2-2 | Constant | 10 | Hybrid |
| 18 | trapmf | 3-3-3-2-2 | Constant | 10 | Hybrid |
| 19 | gbellmf | 3-3-3-2-2 | Constant | 10 | Hybrid |
| 20 | Gaussmf | 3-3-3-2-2 | Constant | 10 | Hybrid |
| 21 | trimf | 3-3-3-3-3 | Constant | 10 | hybrid |
| 22 | trimf | 3-3-3-3-3 | Constant | 10 | backpropa |
| 23 | trapmf | 3-3-3-3-3 | Constant | 10 | hybrid |
| 24 | trapmf | 3-3-3-3-3 | Constant | 10 | backpropa |
| 25 | gbellmf | 3-3-3-3-3 | Constant | 10 | hybrid |
| 26 | gbellmf | 3-3-3-3-3 | Constant | 10 | backpropa |
| 27 | trimf | 3-3-3-3-3 | Constant | 30 | hybrid |
| 28 | trimf | 3-3-3-3-3 | Constant | 50 | hybrid |
| 29 | trapmf | 3-3-3-3-3 | Constant | 30 | hybrid |
| 30 | trapmf | 3-3-3-3-3 | Constant | 50 | hybrid |
| 31 | gbellmf | 3-3-3-3-3 | Constant | 30 | hybrid |
| 32 | gbellmf | 3-3-3-3-3 | Constant | 50 | hybrid |
| 33 | trimf | 3-3-4-4-4 | Constant | 10 | hybrid |
| 34 | trimf | 3-3-5-5-5 | Constant | 10 | hybrid |
| 35 | trapmf | 3-3-4-4-4 | Constant | 10 | hybrid |
| 36 | trapmf | 3-3-5-5-5 | Constant | 10 | hybrid |
| 37 | gbellmf | 3-3-4-4-4 | Constant | 10 | hybrid |
| 38 | gbellmf | 3-3-5-5-5 | Constant | 10 | hybrid |
| 39 | gaussmf | 3-3-3-3-3 | Constant | 10 | hybrid |
| 40 | gaussmf | 3-3-4-4-4 | Constant | 10 | hybrid |
| 41 | gaussmf | 3-3-5-5-5 | Constant | 10 | hybrid |
| 42 | gauss2mf | 3-3-3-3-3 | Constant | 10 | hybrid |
| 43 | gauss2mf | 3-3-4-4-4 | Constant | 10 | hybrid |
| 44 | gauss2mf | 3-3-5-5-5 | Constant | 10 | hybrid |
| 45 | pimf | 3-3-3-3-3 | Constant | 10 | hybrid |
| 46 | pimf | 3-3-4-4-4 | Constant | 10 | hybrid |
| 47 | pimf | 3-3-5-5-5 | Constant | 10 | hybrid |
| Anfis Run | Type of Input MF | Number of MFs | Type of Output MF | Number of Epochs | Optimization | MSE | RMSE | MAE | MAPE | R2 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | trimf | 2-2-2-2-2 | Constant | 10 | Hybrid | 0.0010 | 0.0320 | 0.0192 | 12.6882 | 0.9849 |
| 2 | trapmf | 2-2-2-2-2 | Constant | 10 | Hybrid | 0.0013 | 0.0366 | 0.0245 | 19.8878 | 0.9806 |
| 3 | gbellmf | 2-2-2-2-2 | Constant | 10 | Hybrid | 0.0011 | 0.0335 | 0.0209 | 14.7498 | 0.9834 |
| 4 | Gaussmf | 2-2-2-2-2 | Constant | 10 | Hybrid | 0.0011 | 0.0326 | 0.0201 | 13.8422 | 0.9842 |
| 5 | Gauss2mf | 2-2-2-2-2 | Constant | 10 | Hybrid | 0.0011 | 0.0324 | 0.0197 | 13.5785 | 0.9845 |
| 6 | pimf | 2-2-2-2-2 | Constant | 10 | Hybrid | 0.0015 | 0.0389 | 0.0254 | 19.5486 | 0.9782 |
| 7 | dsigmf | 2-2-2-2-2 | Constant | 10 | Hybrid | 0.0014 | 0.0378 | 0.0244 | 18.7851 | 0.9794 |
| 8 | psigmf | 2-2-2-2-2 | Constant | 10 | Hybrid | 0.0014 | 0.0378 | 0.0244 | 18.7851 | 0.9794 |
| 9 | trimf | 2-2-3-3-3 | Constant | 10 | Hybrid | 0.0015 | 0.0388 | 0.0232 | 15.8840 | 0.9774 |
| 10 | trapmf | 2-2-3-3-3 | Constant | 10 | Hybrid | 0.0020 | 0.0448 | 0.0269 | 19.2727 | 0.9698 |
| 11 | gbellmf | 2-2-3-3-3 | Constant | 10 | Hybrid | 0.0014 | 0.0379 | 0.0227 | 15.5056 | 0.9785 |
| 12 | Gaussmf | 2-2-3-3-3 | Constant | 10 | Hybrid | 0.0014 | 0.0379 | 0.0226 | 15.7640 | 0.9784 |
| 13 | Gauss2mf | 2-2-3-3-3 | Constant | 10 | Hybrid | 0.0017 | 0.0410 | 0.0241 | 15.8227 | 0.9747 |
| 14 | pimf | 2-2-3-3-3 | Constant | 10 | Hybrid | 0.0130 | 0.1141 | 0.0347 | 21.6717 | 0.8552 |
| 15 | dsigmf | 2-2-3-3-3 | Constant | 10 | Hybrid | 0.0020 | 0.0448 | 0.0254 | 16.7809 | 0.9698 |
| 16 | psigmf | 2-2-3-3-3 | Constant | 10 | Hybrid | 0.0020 | 0.0448 | 0.0254 | 16.7809 | 0.9698 |
| 17 | trimf | 3-3-3-2-2 | Constant | 10 | Hybrid | 0.0012 | 0.0348 | 0.0210 | 14.6116 | 0.9819 |
| 18 | trapmf | 3-3-3-2-2 | Constant | 10 | Hybrid | 0.0018 | 0.0430 | 0.0297 | 27.0255 | 0.9723 |
| 19 | gbellmf | 3-3-3-2-2 | Constant | 10 | Hybrid | 0.0013 | 0.0355 | 0.0212 | 14.4247 | 0.9810 |
| 20 | Gaussmf | 3-3-3-2-2 | Constant | 10 | Hybrid | 0.0011 | 0.0337 | 0.0198 | 12.8988 | 0.9829 |
| 21 | trimf | 3-3-3-3-3 | Constant | 10 | hybrid | 0.0021 | 0.0455 | 0.0242 | 15.4964 | 0.9698 |
| 22 | trimf | 3-3-3-3-3 | Constant | 10 | backpropa | 0.0559 | 0.2365 | 0.1610 | 74.9654 | 0.7447 |
| 23 | trapmf | 3-3-3-3-3 | Constant | 10 | hybrid | 0.0031 | 0.0556 | 0.0281 | 21.5814 | 0.9562 |
| 24 | trapmf | 3-3-3-3-3 | Constant | 10 | backpropa | 0.0501 | 0.2238 | 0.1527 | 72.2629 | 0.7404 |
| 25 | gbellmf | 3-3-3-3-3 | Constant | 10 | hybrid | 0.0014 | 0.0374 | 0.0217 | 14.6538 | 0.9791 |
| 26 | gbellmf | 3-3-3-3-3 | Constant | 10 | backpropa | 0.0015 | 0.0392 | 0.0265 | 25.1796 | 0.9793 |
| 27 | trimf | 3-3-3-3-3 | Constant | 30 | hybrid | 0.0016 | 0.0403 | 0.0224 | 13.3194 | 0.9759 |
| 28 | trimf | 3-3-3-3-3 | Constant | 50 | hybrid | 0.0017 | 0.0417 | 0.0224 | 13.2276 | 0.9745 |
| 29 | trapmf | 3-3-3-3-3 | Constant | 30 | hybrid | 0.0029 | 0.0539 | 0.0245 | 17.2238 | 0.9590 |
| 30 | trapmf | 3-3-3-3-3 | Constant | 50 | hybrid | 0.0017 | 0.0416 | 0.0233 | 16.4612 | 0.9745 |
| 31 | gbellmf | 3-3-3-3-3 | Constant | 30 | hybrid | 0.0013 | 0.0366 | 0.0213 | 13.2077 | 0.9799 |
| 32 | gbellmf | 3-3-3-3-3 | Constant | 50 | hybrid | 0.0019 | 0.0432 | 0.0236 | 13.4445 | 0.9724 |
| 33 | trimf | 3-3-4-4-4 | Constant | 10 | hybrid | 0.0023 | 0.0479 | 0.0251 | 15.4225 | 0.9662 |
| 34 | trimf | 3-3-5-5-5 | Constant | 10 | hybrid | 0.0078 | 0.0884 | 0.0320 | 17.3158 | 0.9006 |
| 35 | trapmf | 3-3-4-4-4 | Constant | 10 | hybrid | 0.0021 | 0.0454 | 0.0275 | 23.1769 | 0.9695 |
| 36 | trapmf | 3-3-5-5-5 | Constant | 10 | hybrid | 0.0098 | 0.1084 | 0.0450 | 19.3158 | 0.8806 |
| 37 | gbellmf | 3-3-4-4-4 | Constant | 10 | hybrid | 0.0022 | 0.0472 | 0.0256 | 16.1637 | 0.9669 |
| 38 | gbellmf | 3-3-5-5-5 | Constant | 10 | hybrid | 0.0044 | 0.0660 | 0.0307 | 18.0977 | 0.9376 |
| 39 | gaussmf | 3-3-3-3-3 | Constant | 10 | hybrid | 0.0013 | 0.0365 | 0.0212 | 13.8235 | 0.9800 |
| 40 | gaussmf | 3-3-4-4-4 | Constant | 10 | hybrid | 0.0019 | 0.0431 | 0.0241 | 14.7715 | 0.9720 |
| 41 | gaussmf | 3-3-5-5-5 | Constant | 10 | hybrid | 0.0056 | 0.0746 | 0.0314 | 17.5307 | 0.9185 |
| 42 | gauss2mf | 3-3-3-3-3 | Constant | 10 | hybrid | 0.0017 | 0.0409 | 0.0235 | 16.2626 | 0.9755 |
| 43 | gauss2mf | 3-3-4-4-4 | Constant | 10 | hybrid | 0.0040 | 0.0632 | 0.0260 | 17.3863 | 0.9407 |
| 44 | gauss2mf | 3-3-5-5-5 | Constant | 10 | hybrid | 0.0072 | 0.0847 | 0.0290 | 17.7331 | 0.9048 |
| 45 | pimf | 3-3-3-3-3 | Constant | 10 | hybrid | 0.1224 | 0.3499 | 0.0482 | 26.0901 | 0.3608 |
| 46 | pimf | 3-3-4-4-4 | Constant | 10 | hybrid | 0.0026 | 0.0510 | 0.0307 | 24.7626 | 0.9615 |
| 47 | pimf | 3-3-5-5-5 | Constant | 10 | hybrid | 0.0022 | 0.0466 | 0.0285 | 22.3553 | 0.9678 |
| City | Anfis Run | Type of Input MF | Number of MFs | Number of Rules | Time (s) | MSE | RMSE | MAE | MAPE | R2 |
|---|---|---|---|---|---|---|---|---|---|---|
| Alexandroupoli | 17 | trimf | 3-3-3-2-2 | 72 | 5 | 0.0024 | 0.0494 | 0.0351 | 10.5278 | 0.9638 |
| 39 | gaussmf | 3-3-3-3-3 | 243 | 47 | 0.0031 | 0.0557 | 0.0355 | 10.1556 | 0.9538 | |
| 20 | gaussmf | 3-3-3-2-2 | 72 | 5 | 0.0023 | 0.0480 | 0.0341 | 10.1123 | 0.9659 | |
| Athens | 1 | trimf | 2-2-2-2-2 | 32 | 7 | 0.0021 | 0.0457 | 0.0295 | 20.1799 | 0.9825 |
| 17 | trimf | 3-3-3-2-2 | 108 | 19 | 0.0026 | 0.0511 | 0.0315 | 19.7972 | 0.9786 | |
| 20 | gaussmf | 3-3-3-2-2 | 108 | 19 | 0.0022 | 0.0467 | 0.0306 | 21.2929 | 0.9818 | |
| Drama | 17 | trimf | 3-3-3-2-2 | 108 | 19 | 0.0026 | 0.0511 | 0.0363 | 6.2547 | 0.8997 |
| 1 | trimf | 2-2-2-2-2 | 32 | 5 | 0.0026 | 0.0513 | 0.0361 | 6.2235 | 0.8975 | |
| 20 | gaussmf | 3-3-3-2-2 | 108 | 13 | 0.0026 | 0.0508 | 0.0371 | 6.4071 | 0.8995 | |
| Karditsa | 17 | trimf | 3-3-3-2-2 | 108 | 12 | 0.0019 | 0.0434 | 0.0242 | 13.8394 | 0.9789 |
| 1 | trimf | 2-2-2-2-2 | 32 | 4 | 0.0018 | 0.0421 | 0.0236 | 11.6196 | 0.9801 | |
| 4 | gaussmf | 2-2-2-2-2 | 32 | 4 | 0.0019 | 0.0431 | 0.0248 | 13.3841 | 0.9792 | |
| Larissa | 1 | trimf | 2-2-2-2-2 | 32 | 4 | 0.0012 | 0.0352 | 0.0203 | 10.9568 | 0.9817 |
| 4 | gaussmf | 2-2-2-2-2 | 32 | 4 | 0.0012 | 0.0352 | 0.0204 | 10.9833 | 0.9817 | |
| 20 | gaussmf | 3-3-3-2-2 | 108 | 19 | 0.0010 | 0.0314 | 0.0184 | 10.5236 | 0.9858 | |
| Markopoulo | 1 | trimf | 2-2-2-2-2 | 32 | 5 | 0.0091 | 0.0956 | 0.0728 | 25.0887 | 0.6593 |
| 4 | gaussmf | 2-2-2-2-2 | 32 | 5 | 0.0096 | 0.0980 | 0.0755 | 26.7510 | 0.6364 | |
| 17 | trimf | 3-3-3-2-2 | 108 | 19 | 0.0259 | 0.1609 | 0.1087 | 36.7174 | 0.5126 | |
| Serres | 1 | trimf | 2-2-2-2-2 | 32 | 5 | 0.0007 | 0.0271 | 0.0176 | 10.4721 | 0.9839 |
| 4 | gaussmf | 2-2-2-2-2 | 32 | 5 | 0.0008 | 0.0279 | 0.0185 | 11.2421 | 0.9831 | |
| 39 | gaussmf | 3-3-3-3-3 | 243 | 45 | 0.0008 | 0.0285 | 0.0194 | 12.1163 | 0.9824 | |
| Thessaloniki | 17 | trimf | 3-3-3-2-2 | 108 | 13 | 0.0015 | 0.0382 | 0.0229 | 16.1046 | 0.9773 |
| 20 | gaussmf | 3-3-3-2-2 | 108 | 13 | 0.0013 | 0.0363 | 0.0219 | 14.1944 | 0.9795 | |
| 39 | gaussmf | 3-3-3-3-3 | 243 | 45 | 0.0021 | 0.0459 | 0.0256 | 15.2032 | 0.9672 | |
| Trikala | 1 | trimf | 2-2-2-2-2 | 32 | 4 | 0.0019 | 0.0433 | 0.0232 | 10.5817 | 0.9815 |
| 4 | gaussmf | 2-2-2-2-2 | 32 | 4 | 0.0020 | 0.0450 | 0.0245 | 11.1412 | 0.9800 | |
| 20 | gaussmf | 3-3-3-2-2 | 108 | 13 | 0.0028 | 0.0530 | 0.0271 | 11.7631 | 0.9708 | |
| Volos | 1 | trimf | 2-2-2-2-2 | 32 | 4 | 0.0021 | 0.0459 | 0.0317 | 13.2520 | 0.9564 |
| 4 | gaussmf | 2-2-2-2-2 | 32 | 4 | 0.0021 | 0.0460 | 0.0314 | 13.1629 | 0.9563 | |
| 20 | gaussmf | 3-3-3-2-2 | 108 | 12 | 0.0020 | 0.0445 | 0.0323 | 13.9710 | 0.9588 |
| Title 1 | Anfis Run | Type of Input MF | Number of MFs | Type of Output MF | Optimization | MSE | RMSE | MAE | MAPE | R2 |
|---|---|---|---|---|---|---|---|---|---|---|
| Alexandroupoli | 20 | gaussmf | 3-3-3-2-2 | Constant | Hybrid | 0.0023 | 0.0480 | 0.0341 | 10.1123 | 0.9659 |
| Athens | 17 | trimf | 3-3-3-2-2 | Constant | Hybrid | 0.0026 | 0.0511 | 0.0315 | 19.7972 | 0.9786 |
| Drama | 1 | trimf | 2-2-2-2-2 | Constant | Hybrid | 0.0026 | 0.0513 | 0.0361 | 6.2235 | 0.8975 |
| Karditsa | 1 | trimf | 2-2-2-2-2 | Constant | Hybrid | 0.0018 | 0.0421 | 0.0236 | 11.6196 | 0.9801 |
| Larissa | 20 | gaussmf | 3-3-3-2-2 | Constant | Hybrid | 0.0010 | 0.0314 | 0.0184 | 10.5236 | 0.9858 |
| Markopoulo | 1 | trimf | 2-2-2-2-2 | Constant | Hybrid | 0.0091 | 0.0956 | 0.0728 | 25.0887 | 0.6593 |
| Serres | 4 | gaussmf | 2-2-2-2-2 | Constant | Hybrid | 0.0008 | 0.0279 | 0.0185 | 11.2421 | 0.9831 |
| Thessaloniki | 20 | gaussmf | 3-3-3-2-2 | Constant | Hybrid | 0.0013 | 0.0363 | 0.0219 | 14.1944 | 0.9795 |
| Trikala | 4 | gaussmf | 2-2-2-2-2 | Constant | Hybrid | 0.0020 | 0.0450 | 0.0245 | 11.1412 | 0.9800 |
| Volos | 4 | gaussmf | 2-2-2-2-2 | Constant | Hybrid | 0.0021 | 0.0460 | 0.0314 | 13.1629 | 0.9563 |
| City | Method | MSE | RMSE | MAE | MAPE | R2 |
|---|---|---|---|---|---|---|
| Alexandroupoli | RCGA-FCM | 0.0047 | 0.0684 | 0.0538 | 17.6233 | 0.9450 |
| SOGA-FCM | 0.0045 | 0.0672 | 0.0526 | 17.1707 | 0.9484 | |
| ANN | 0.0042 | 0.0645 | 0.0505 | 16.1131 | 0.9439 | |
| Hybrid FCM-ANN | 0.0034 | 0.0579 | 0.0427 | 14.3034 | 0.9498 | |
| Best ANFIS | 0.0023 | 0.0480 | 0.0341 | 10.1123 | 0.9659 | |
| Athens | RCGA-FCM | 0.0022 | 0.0473 | 0.0303 | 23.5985 | 0.9676 |
| SOGA-FCM | 0.0029 | 0.0539 | 0.0337 | 22.7453 | 0.9646 | |
| ANN | 0.0010 | 0.0323 | 0.0198 | 14.2464 | 0.9844 | |
| Hybrid FCM-ANN | 0.0014 | 0.0374 | 0.0230 | 17.5418 | 0.9790 | |
| Best ANFIS | 0.0026 | 0.0511 | 0.0315 | 19.7972 | 0.9786 | |
| Drama | RCGA-FCM | 0.0080 | 0.0894 | 0.0749 | 12.9942 | 0.8691 |
| SOGA-FCM | 0.0056 | 0.0748 | 0.0600 | 10.1766 | 0.8796 | |
| ANN | 0.0025 | 0.0501 | 0.0357 | 6.1657 | 0.9025 | |
| Hybrid FCM-ANN | 0.0028 | 0.0526 | 0.0363 | 6.2502 | 0.8941 | |
| Best ANFIS | 0.0026 | 0.0513 | 0.0361 | 6.2235 | 0.8975 | |
| Karditsa | RCGA-FCM | 0.0039 | 0.0624 | 0.0379 | 27.5914 | 0.9591 |
| SOGA-FCM | 0.0488 | 0.2210 | 0.1397 | 50.2112 | 0.9711 | |
| ANN | 0.0016 | 0.0405 | 0.0245 | 17.4579 | 0.9819 | |
| Hybrid FCM-ANN | 0.0017 | 0.0407 | 0.0245 | 18.4095 | 0.9817 | |
| Best ANFIS | 0.0018 | 0.0421 | 0.0236 | 11.6196 | 0.9801 | |
| Larissa | RCGA-FCM | 0.0027 | 0.0515 | 0.0331 | 22.2481 | 0.9638 |
| SOGA-FCM | 0.0025 | 0.0505 | 0.0328 | 22.9579 | 0.9649 | |
| ANN | 0.0013 | 0.0355 | 0.0209 | 13.2479 | 0.9812 | |
| Hybrid FCM-ANN | 0.0013 | 0.0356 | 0.0215 | 13.1974 | 0.9811 | |
| Best ANFIS | 0.0010 | 0.0314 | 0.0184 | 10.5236 | 0.9858 | |
| Markopoulo | RCGA-FCM | 0.0075 | 0.0868 | 0.0726 | 26.0003 | 0.6975 |
| SOGA-FCM | 0.0078 | 0.0883 | 0.0739 | 26.3345 | 0.6955 | |
| ANN | 0.0172 | 0.1310 | 0.1048 | 34.8594 | 0.4765 | |
| Hybrid FCM-ANN | 0.0070 | 0.0836 | 0.0667 | 23.7166 | 0.7094 | |
| Best ANFIS | 0.0091 | 0.0956 | 0.0728 | 25.0887 | 0.6593 | |
| Serres | RCGA-FCM | 0.0017 | 0.0409 | 0.0274 | 16.5199 | 0.9648 |
| SOGA-FCM | 0.0495 | 0.2225 | 0.1632 | 72.9785 | 0.9772 | |
| ANN | 0.0008 | 0.0275 | 0.0179 | 10.9948 | 0.9842 | |
| Hybrid FCM-ANN | 0.0008 | 0.0289 | 0.0190 | 11.5000 | 0.9821 | |
| Best ANFIS | 0.0008 | 0.0279 | 0.0185 | 11.2421 | 0.9831 | |
| Thessaloniki | RCGA-FCM | 0.0029 | 0.0541 | 0.0339 | 29.9713 | 0.9565 |
| SOGA-FCM | 0.0029 | 0.0539 | 0.0340 | 30.1471 | 0.9568 | |
| ANN | 0.0017 | 0.0412 | 0.0262 | 23.8748 | 0.9735 | |
| Hybrid FCM-ANN | 0.0019 | 0.0441 | 0.0266 | 23.8835 | 0.9696 | |
| Best ANFIS | 0.0013 | 0.0363 | 0.0219 | 14.1944 | 0.9795 | |
| Trikala | RCGA-FCM | 0.0059 | 0.0770 | 0.0453 | 21.9722 | 0.9528 |
| SOGA-FCM | 0.0433 | 0.2082 | 0.1287 | 42.7427 | 0.9715 | |
| ANN | 0.0020 | 0.0443 | 0.0258 | 14.1183 | 0.9804 | |
| Hybrid FCM-ANN | 0.0019 | 0.0432 | 0.0251 | 13.9034 | 0.9815 | |
| Best ANFIS | 0.0020 | 0.0450 | 0.0245 | 11.1412 | 0.9800 | |
| Volos | RCGA-FCM | 0.0028 | 0.0526 | 0.0397 | 17.8195 | 0.9436 |
| SOGA-FCM | 0.0027 | 0.0520 | 0.0395 | 17.8988 | 0.9445 | |
| ANN | 0.0020 | 0.0444 | 0.0319 | 13.2504 | 0.9588 | |
| Hybrid FCM-ANN | 0.0020 | 0.0446 | 0.0307 | 12.7881 | 0.9587 | |
| Best ANFIS | 0.0021 | 0.0460 | 0.0314 | 13.1629 | 0.9563 |
| Architectures | Parameters for Athens City | Average Running Time |
|---|---|---|
| ANN | Multilayer feed forward network, six inputs, 10 neurons, one output, sigmoidal activation function, Levenberg-Marquardt learning, epochs = 20 | 16–20 s |
| RCGA-FCM | Uniform crossover with probability 0.4, Mühlenbein’s mutation with probability 0.4, ranking selection, elite strategy, population size 200, maximum number of generations 200 | 808 s |
| SOGA-FCM | Uniform crossover with probability 0.4, Mühlenbein’s mutation with probability 0.4, ranking selection, elite strategy, population size 200, maximum number of generations 200, learning parameters b1 = b2 = 0.01 | 799 s |
| Hybrid FCM-ANN | Multilayer feed forward network, four inputs selected by SOGA-FCM (month, temperature, demand of a day before, current demand), one hidden layer with 10 neurons, one output, sigmoidal activation function, Levenberg-Marquardt learning, epochs = 20 | 811 s |
| Best ANFIS | Triangular mf, 2-2-2-2-2 or 3-3-3-2-2, Constant output, epochs = 10, Hybrid optimization | 4–19 s |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papageorgiou, K.; I. Papageorgiou, E.; Poczeta, K.; Bochtis, D.; Stamoulis, G. Forecasting of Day-Ahead Natural Gas Consumption Demand in Greece Using Adaptive Neuro-Fuzzy Inference System. Energies 2020, 13, 2317. https://doi.org/10.3390/en13092317
Papageorgiou K, I. Papageorgiou E, Poczeta K, Bochtis D, Stamoulis G. Forecasting of Day-Ahead Natural Gas Consumption Demand in Greece Using Adaptive Neuro-Fuzzy Inference System. Energies. 2020; 13(9):2317. https://doi.org/10.3390/en13092317
Chicago/Turabian StylePapageorgiou, Konstantinos, Elpiniki I. Papageorgiou, Katarzyna Poczeta, Dionysis Bochtis, and George Stamoulis. 2020. "Forecasting of Day-Ahead Natural Gas Consumption Demand in Greece Using Adaptive Neuro-Fuzzy Inference System" Energies 13, no. 9: 2317. https://doi.org/10.3390/en13092317
APA StylePapageorgiou, K., I. Papageorgiou, E., Poczeta, K., Bochtis, D., & Stamoulis, G. (2020). Forecasting of Day-Ahead Natural Gas Consumption Demand in Greece Using Adaptive Neuro-Fuzzy Inference System. Energies, 13(9), 2317. https://doi.org/10.3390/en13092317









