Transient Behavior of Vertical Commingled Well in Vertical Non-Uniform Boundary Radii Reservoir

Abstract

Transient behavior analysis, including rate transient analysis (RTA) and pressure transient analysis (PTA), is a powerful tool to investigate the production performance of the vertical commingled well from long-term production data and capture the formation parameters of the multilayer reservoir from transient well testing data. Current transient behavior analysis models hardly consider the effect of vertical non-uniform boundary radii (VNBR) on transient performances (rate decline and pressure response). The VNBR may cause an obvious novel radial flow regime and rate decline type, which can easily be mistaken as a radial composite reservoir. In this paper, we present a VNBR transient behavior analysis model, the extended vertical uniform boundary radii (VUBR), to investigate the rate decline behavior and pressure response characteristics through diagnostic type curves. Results indicate that the dimensionless production integral derivative curve or pressure derivative curve can magnify the differences so that we can diagnose the outer-convex shape and size of the VNBR. Therefore, it is significant to incorporate the effects of VNBR into the transient behavior analysis models of the vertical commingled well, and the model proposed in this paper enables us to better evaluate well performance, capture formation characteristics and diagnose flow regimes based on rate/pressure transient data.

1. Introduction

With the depletion of conventional oil and gas resources, more and more complex, multilayer oil and gas reservoirs have been discovered with the improvement of exploration technology. The well production performance and reservoir evaluation are of great significance for enhancing recovery in multilayer oil and gas field development [1,2,3]. Both production decline analysis and well testing analysis are important dynamic technologies for petroleum engineers to evaluate well performance [4,5,6]. During the past years, many researchers have investigated the production decline behavior and pressure response characteristics of the vertical commingled well. Their main focus was four types of analysis: transient behavior analysis (including pressure transient analysis (PTA) [7,8,9,10,11,12] and rate transient analysis (RTA) [12,13,14,15]), vertical-heterogeneity analysis [16,17,18] and boundary effect analysis [19,20,21], for a commingled well in a multilayer reservoir.

For the PTA and RTA for the vertical commingled production well, Satman used the discontinuous inner boundary radii to characterize the front of the displacement fluid during the enhanced recovery processes, such as steam flooding and gravity override effect [7,8]. Tariq and Ramey presented a PTA model considering the wellbore storage and skin factor in the multilayer reservoir [9]. Anbarci et al. presented a PTA model to determine the front location in a multilayer reservoir [10]. Ehlig-Economides and Joseph validated a general analytical solution of PTA for an n-layer, composite, crossflow reservoir system [11]. Fetkovich et al. conducted studies on the RTA and PTA for a two-layer non-communicating reservoir, and the pressure response curves showed that these layers can be combined into one layer if the layers have the same physical properties [12]. El-Banbi and Wattenbarger developed an RTA model to match the gas well production data for a three-layer tight gas reservoir [13]. Villanueva-Triana and Civan developed an RTA model for three-layer commingled reservoirs involving formation crossflow and general external flow boundaries [14]. Milad simulated a commingled well RTA model for multilayer shale gas reservoirs, in which the pressures and flow rates are not constant in various zones [15].

For the vertical-heterogeneity of the multilayer reservoir, Aly et al. examined the effect of unequal initial layer pressure on RTA and PTA models [16]. However, their objective was the permeability and skin factor rather than boundary radii of an individual layer. Jordan and Mattar compared the PTA curves of the composite reservoir with that of the multilayer reservoir [17]. His modified composite reservoir demonstrated that the composite reservoir pressure behavior would be like that of a multilayer reservoir if the vertical permeability is very small. Lodon et al. provided a two-layer semi-analytical PTA model of a commingled reservoir with different boundary distances of each layer, and their model shows that the PTA curve of the two-layer reservoir is located between that of the two-layer reservoir with the same minimum and maximum boundary distance [18]. However, their research is limited to the two-layer reservoir and cannot provide a quantitative relation of pressure behavior between the total reservoir and individual layers.

For the boundary effect of the reservoir, Larsen generated an exact Laplace-transformed solution including a great variety of boundary configurations. Results show the PTA of a square boundary reservoir is the same as that of a circle boundary reservoir [19]. For a well near a liner leaky boundary in the two-layer reservoir, Boussila et al. revealed that there is a quantitative relationship between the pressure derivative and the mobility ratio during the boundary flow stage [20]. For the tidal flat layered carbonate reservoir in Sichuan Basin, Shi et al. characterized the pressure transient behavior by a layered reservoir with the vertical inhomogeneous closed boundary [21]. Their results showed that the shape of the closed boundary has an intuitive inverse proportional relationship on the pressure derivative curve during the radial flow regime.

The existing research mainly focuses on the analysis and acquisition of the parameters of layered reservoirs from the production data, and few works discuss the equivalence and substitutability of the boundary effect of multilayer reservoirs [22]. The objective of this paper is to investigate the influence of vertical non-uniform boundary radii (VNBR) on transient behavior and explore the corresponding relation between them. This paper extends the boundaries issues of the multilayer reservoir by a VNBR transient behavior analysis method. Some interesting and valuable phenomena, such as the “equivalent seepage volume effect” and the “equivalent composite zone effect”, are identified, which give a new perspective on the flow regimes of the vertical commingled well in a VNBR reservoir and provide a quick approach to capturing the formation parameters from transient well test data. The transient behavior analysis model presented in this paper provides a tool to characterize the production performance and rate decline type from the long-term production data.

2. Methodology

2.1. Physical Model

Figure 1a shows a vertical commingled well in the VNBR reservoir. The following assumptions are considered to yield the mathematical model:

• A vertical production well is located at the center of a multilayer reservoir formation with constant initial reservoir pressure (p_i) in any layer (j). The formation has a circular-closed boundary with non-uniform boundary radii in the vertical direction, but any layer j has an individual constant thickness (h_j) and boundary radius (r_ej).
• The formation is considered to be isotropic and homogeneous. Any layer has individual physical parameters, including the permeability (k_j), porosity (φ_j) and total compressibility (ctj).
• The formation is fully penetrated by the vertical production well with height (ht) and radius (rw). During the production stage, both the pressure (p_j) and rate (q_j) of any layer are different. The bottom-hole pressure (p_w) and wellbore rate (q) are variable with the production time.
• The porosity of the formation is filled with a single-phase fluid with constant viscosity (μ). Radial flow regime is assumed in any layer (see Figure 1b,c). The isothermal volume factor (B) is descript the volume change of the natural gas from the wellbore to the wellhead.
• The gravity and temperature effects are ignored.

2.2. Mathematical Model

The dimensionless flow equations of any layer j in Laplace domain are (see the detailed derivation in Appendix A):

$$\frac{1}{r_D}\frac{\partial }{\partial r_D}(r_D\frac{{\partial }^2{\overline{p}}_{jD}}{\partial r_D{}^2})={\sigma }_j{\overline{p}}_{jD}$$

(1)

The definition of the parameters is provided in

Table A1. Summary of the dimensionless variables in the model.

Defined Parameters	Expressions
	Constant Production Pressure (RTA Model)	Constant Production Rata (PTA Model)
Dimensionless pressure	pD = 2πkaht(pi − p)/(qμB)	pD = (pi − p)/(pi − pw)
Dimensionless wellbore flow rate	qD = 1	qD = qμB/[2πkaht(pi − pw)]
Dimensionless bottom-hole pressure	pWd = 2πkaht(pi − pw)/(qμB)	pwD = 1
Dimensionless thickness of layer j	hjD = hj/ht
Average reservoir permeability	ka = ∑(kjhjD)
Average reservoir storability coefficient	(φct)a = ∑[(φct)jhjD]
Dimensionless radial distance	rD = r/rw
Dimensionless time	tD = kat/[μ(φct)arw2]
Dimensionless wellbore storage coefficient	CD = C/[2πht(φct)arw2]
Mobility thickness product ratios in layer j	χj = kjhjD/ka
Storability ratios in layer j	ωj = hjD(φct)j/(φct)a

, and the boundary conditions are presented in Appendix A.

Substituting A_j & B_j, obtained by solving Equation (A11) into Equation (A12), the dimensionless rate solution of RTA model is obtained as:

$${\overline{q}}_D(u)={\displaystyle \sum _{j=1}^n\{{\chi }_j\sqrt{{\sigma }_j}[A_j{I}_1(\sqrt{{\sigma }_j})-B_j{K}_1(\sqrt{{\sigma }_j})]}\}$$

(2)

where the parameters are presented in Appendix B.

Stehfest provides the mathematical relationship of a dimensionless solution between Laplace domain and real-time domain [23]. Blasingame et al. defined three parameters to characterize dimensionless transient rate as follows [24]:

$$\{\begin{array}{l}{q}_{Dd}=q_D\cdot b_{Dpss}\\ q_{Ddi}=\frac{1}{t_{Dd}}{\displaystyle {\int }_0^{t_{Dd}}{q}_{Dd}(\tau )}d\tau \\ q_{Ddid}=t_{Dd}\frac{d{q}_{Ddi}}{d{t}_{Dd}}\end{array}$$

(3)

where qDd denotes the normalized dimensionless decline rate, qDdi represents the normalized dimensionless decline rate integral and qDdid is the normalized dimensionless decline rate integral derivative. tDd is the normalized dimensionless decline time, which can be calculated by:

$$t_{Dd}=\frac{\alpha }{b_{Dpss}}{t}_D$$

(4)

where

$$\{\begin{array}{c}\alpha =\frac{2}{{\displaystyle \sum {\omega }_j{r}_{eDj}^2}}\\ b_{Dpss}=\frac{{\alpha }^2}{4}{\displaystyle \sum [\frac{{\omega }_j}{{\chi }_j}{r}_{eDj}^4(\ln r_{ejD}-0.75)]}\end{array}$$

(5)

According to the research results of Van-Everdingen and Hurst, the dimensionless pressure solution of PTA mode can be obtained through the dimensionless rate solution of the RTA model in Laplace domain [25]:

$${\overline{p}}_{wD}(u)=\frac{1}{u^2{\overline{q}}_D(u)}$$

(6)

Based on Duhamel’s superposition principle, the dimensionless pressure solution of the PTA model in Laplace domain with the effects of skin factor and wellbore storage is [25]:

$${\overline{p}}_{wD}(u,S,C_D)=\frac{u{\overline{p}}_{wD}(u)+S}{u+C_D{u}^2[u{\overline{p}}_{wD}(u)+S]}$$

(7)

The dimensionless pressure solution of the PTA model can be obtained in the real-time domain by Stehfest inversion [23]. In the double logarithmic coordinate system, the dimensionless pressure derivative can zoom the characteristics of the dimensionless pressure features, and the dimensionless pressure derivative is:

$${p^{\prime }}_{wD}(t_D)=t_D\frac{d{p}_{wD}(t_D)}{d{t}_D}$$

(8)

3. Results and Discussion

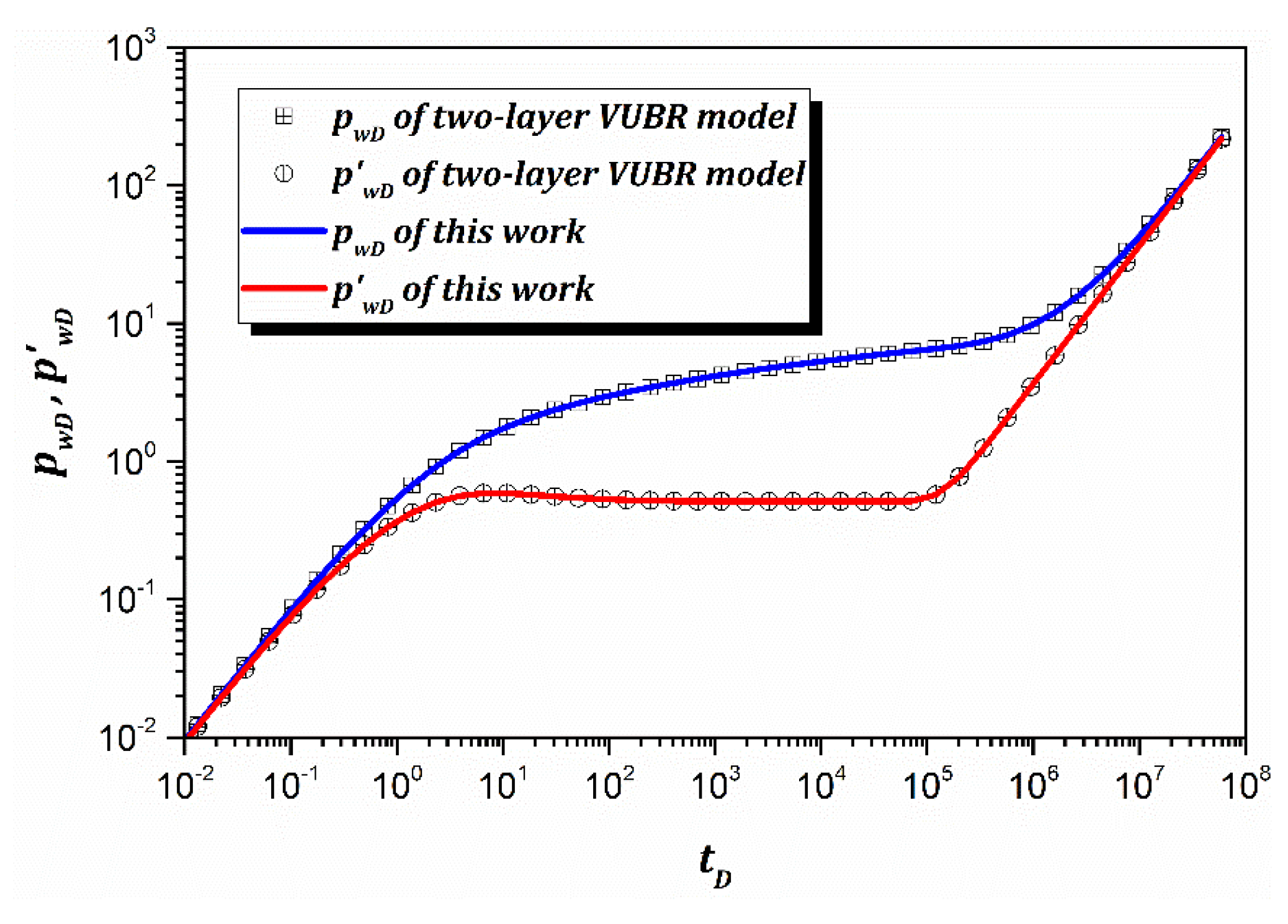
3.1. Solution Validation

The dimensionless pressure solution of the PTA model in a two-layer reservoir with the same boundary radii is [26]:

$${\overline{p}}_{wD}(u)=\frac{1}{u[u+{\chi }_1{\sigma }_1\frac{K_1({\sigma }_1)}{K_0({\sigma }_1)}+{\chi }_2{\sigma }_2\frac{K_1({\sigma }_2)}{K_0({\sigma }_2)}]}$$

(9)

where

$${\sigma }_j=\sqrt{\frac{{\omega }_{j}u}{{\chi }_j{C}_D{e}^{2S}}}$$

(10)

Setting n = 2 and r_e1D = r_e2D = 1000, other parameters are listed in

Table 1. The input parameters of validation cases (constant for Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7).

Parameters	Value
	VNBR	VUBR
Dimensionless wellbore storage (CD)	1.0	1.0
skin factor (S)	0.3	0.3
Mobility thickness product ratio (χ1)	1/n	0.5
Storability ratio (ω1)	1/n	0.5

, the n-layer VNBR reservoir becomes a two-layer vertical uniform boundary radii (VUBR) reservoir. Figure 2 shows that the simplified VNBR PTA model matches that of the two-layer VUBR reservoir perfectly, which proves our model is reliable.

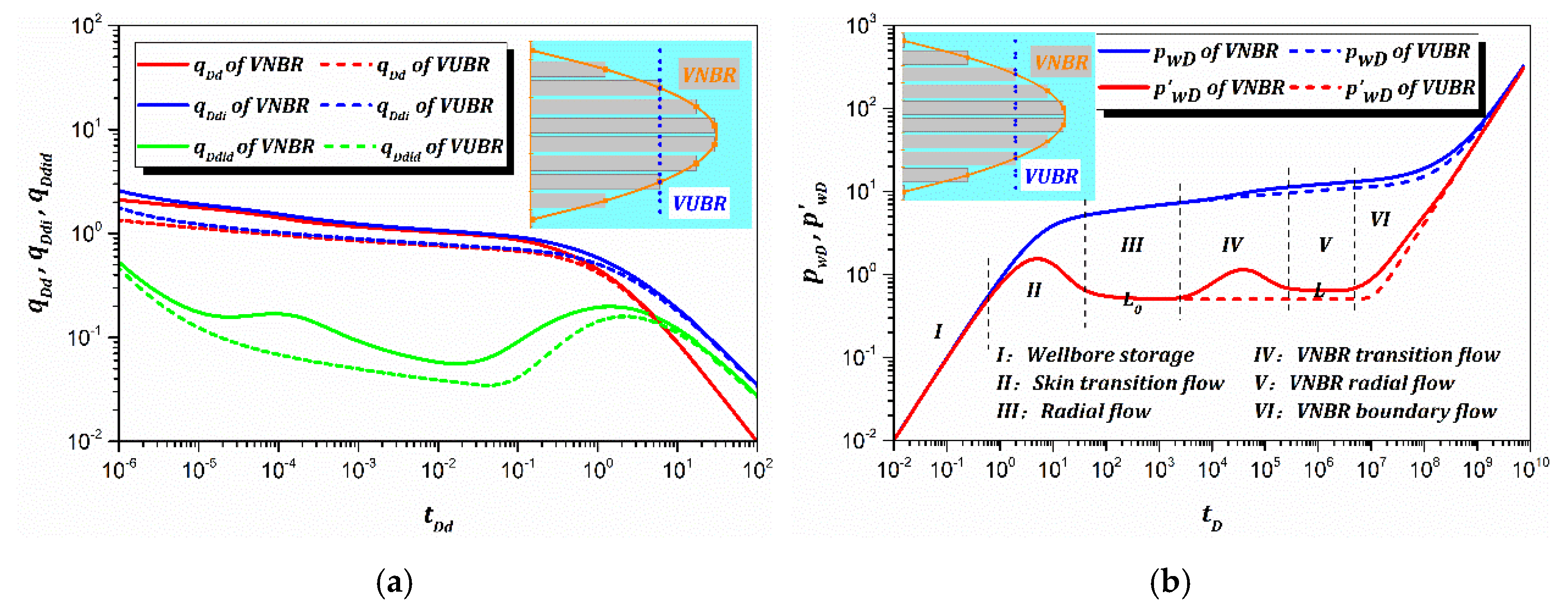
3.2. Combined Type Curve

To characterize the effect of vertical non-uniform boundary radii (VNBR) on rate decline behavior and pressure response, we developed the combined type curves of VNBR and equivalent vertical uniform boundary radii (VUBR). The parameters of VNBR and equivalent VUBR for the combined type curves can be found in

Table 2. The parameters of the combined type curve of VNBR and equivalent VUBR.

Parameters	Value
	VNBR	VUBR
Number of layers (n)	10	10
Dimensionless thickness of any layer (hjD)	1/n	1/n
Dimensionless boundary radii (reD)	(100,10,000)	7030.0

. The outer-convex VNBR, parabolic interpolation from 100 to 1000, is only a typical case of analysis. Based on the equivalent seepage volume (ESV) [21], the value of the equivalent VUBR can be calculated by the following equation:

$$r_{eD\_VUBR}=\sqrt{{\displaystyle \sum _{j=1}^n(\frac{{\chi }_j}{{\omega }_j}{h}_{jD}{r}_{ejD}^2)}}$$

(11)

As shown in Figure 3a, the RTA combined type curves (including the normalized dimensionless decline rate curve (qDd), the normalized dimensionless decline rate integral curve (qDdi) and the normalized dimensionless decline rate integral derivative curve (qDdid)) show the PTA combined type curves of VNBR and VUBR are different, especially before the boundary-dominated flow. The RTA combined curves are much higher than the VUBR case even if the parameters are the same. The deployment of the dimensionless production integral derivative curve magnifies the differences so that we can capture the effect of VUBR. As shown in Figure 3b, the PTA combined type curves (including the dimensionless pressure curve (pwD) and dimensionless pressure derivative curve (p’wD)) show the flow of the VNBR reservoir can be divided into six flow regimes. Flow regime I is caused by wellbore storage. Flow regime II is induced by the skin effect near the wellbore. The pressure derivative is constant (L₀ = 0.5) in flow regime III. In the early stage of flow regime IV, the pressure derivative begins to increase due to the pressure drop having reached the closest boundary. In the late stage of flow regime IV, the pressure derivative begins to decrease as the pressure drop propagates far through other layers. The pressure derivative curve appears a second constant value (L) during flow stage V. The pressure and its derivative increase and eventually coincide into the unit-slope line in flow regime VI.

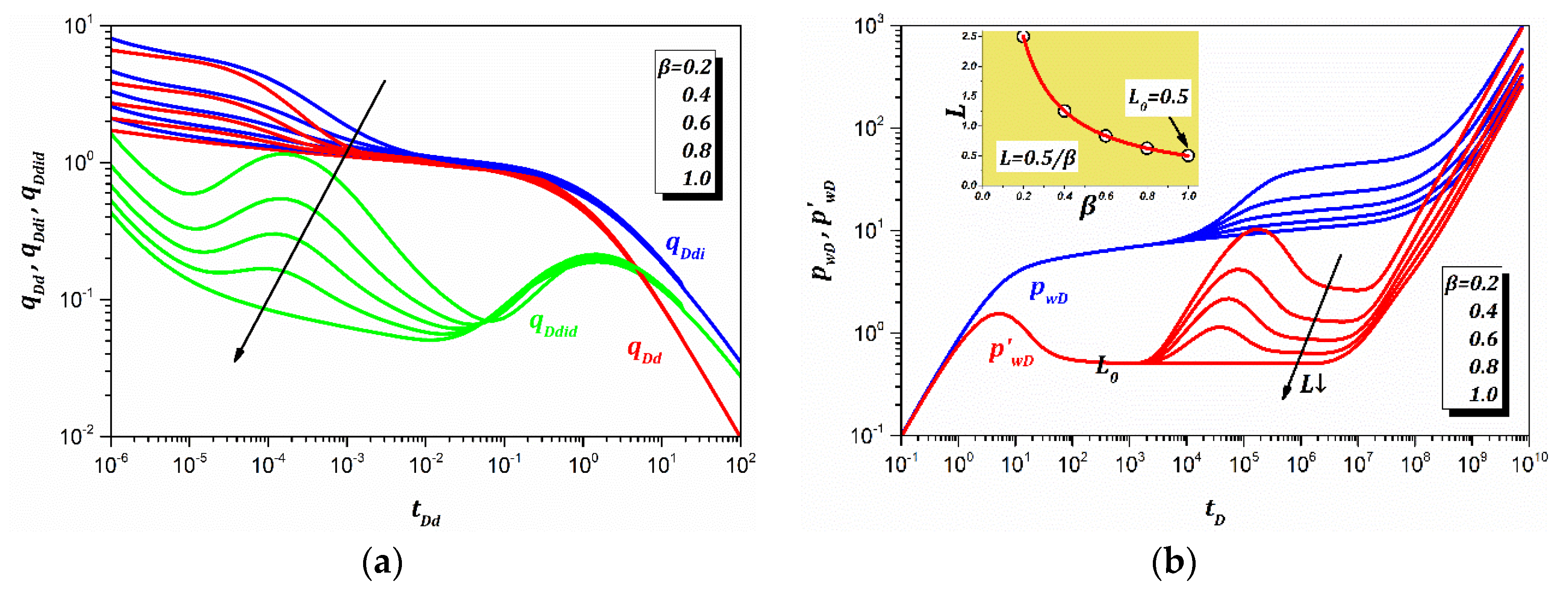
3.3. Sensitivity Analysis

The β is introduced to represent the outer-convex relative thickness. In Case 1 (see Figure 4a), the outer-convex thickness is increasing but the maximum radius is constant. In Case 2 (see Figure 4b), the outer-convex number increases but each outer-convex thickness is the same. In Case 3 (see Figure 4c), the outer-convex positions are different but the each outer-convex is the same.

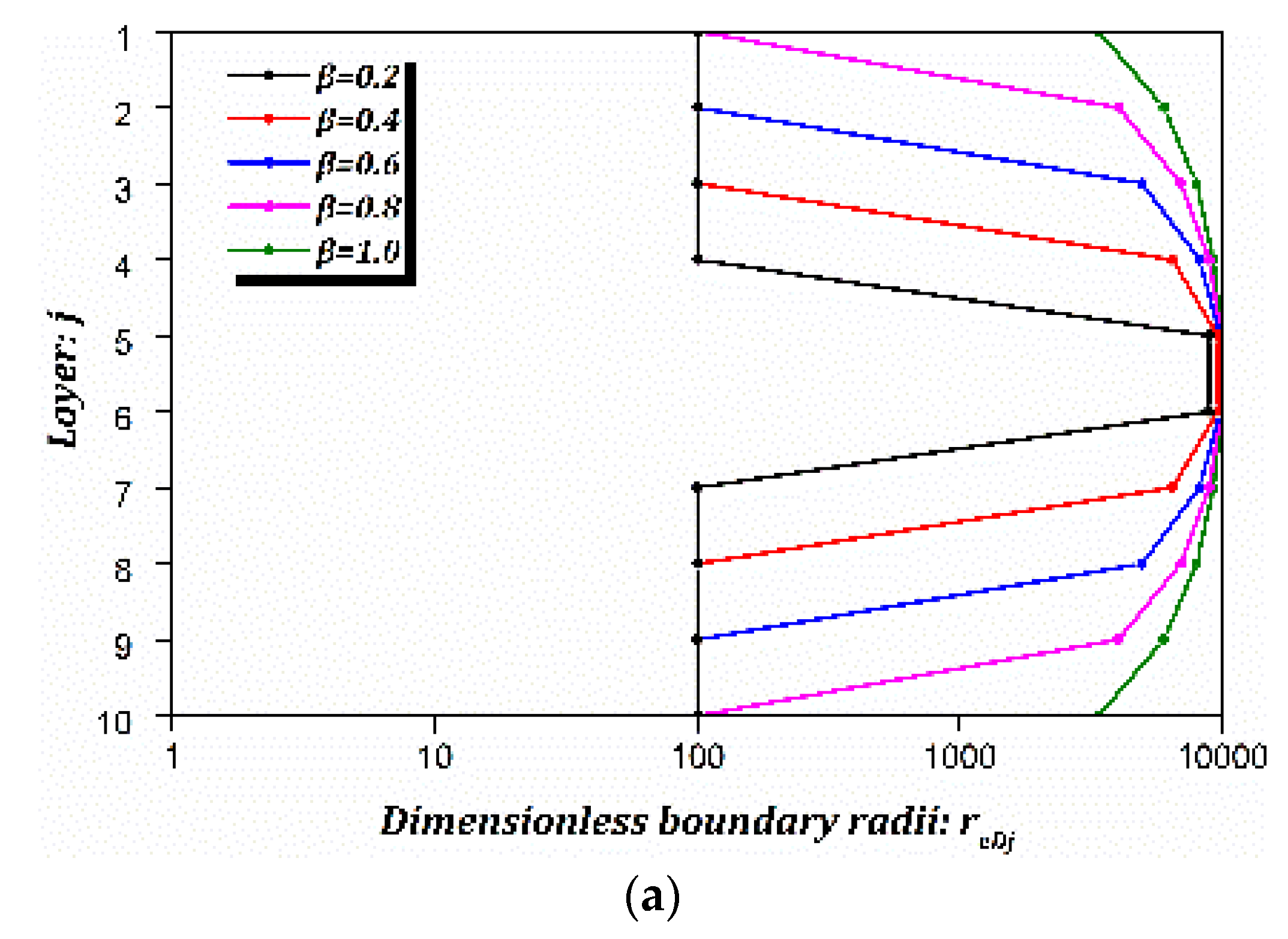
3.3.1. Outer-Convex Thickness

As shown in Figure 5a, the RTA combined type curves of the VNBR move down and closer to that of the VUBR as the β increases. Therefore, the outer-convex thickness can be captured through the combined type curves. As shown in Figure 5b, L approaches L₀ as the β increases, and the mathematical relationship is L = L₀/β. This mathematical relationship clarifies the seepage physical meanings of β and provides a fast way to obtain the outer-convex thickness just from the pressure derivative curve.

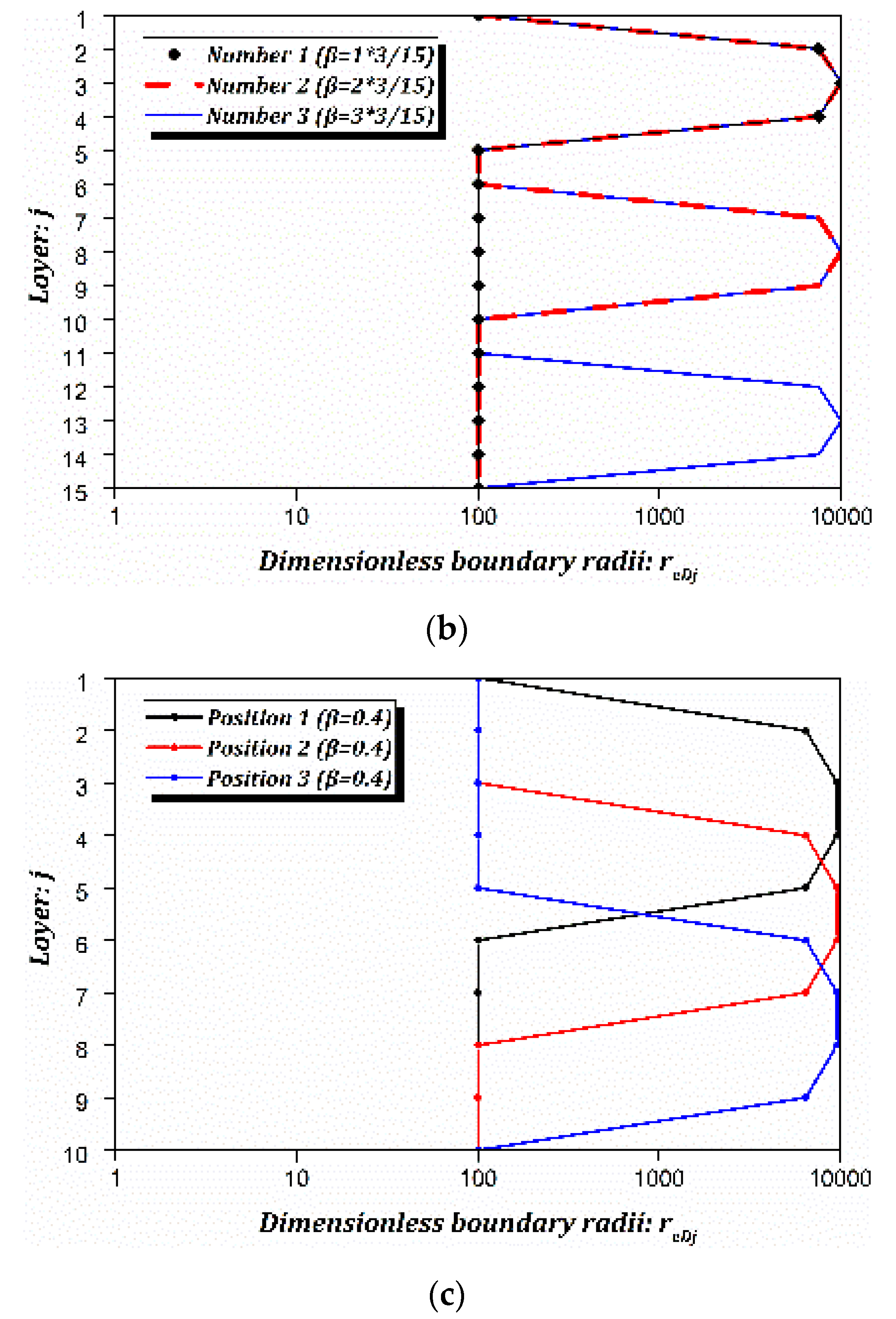
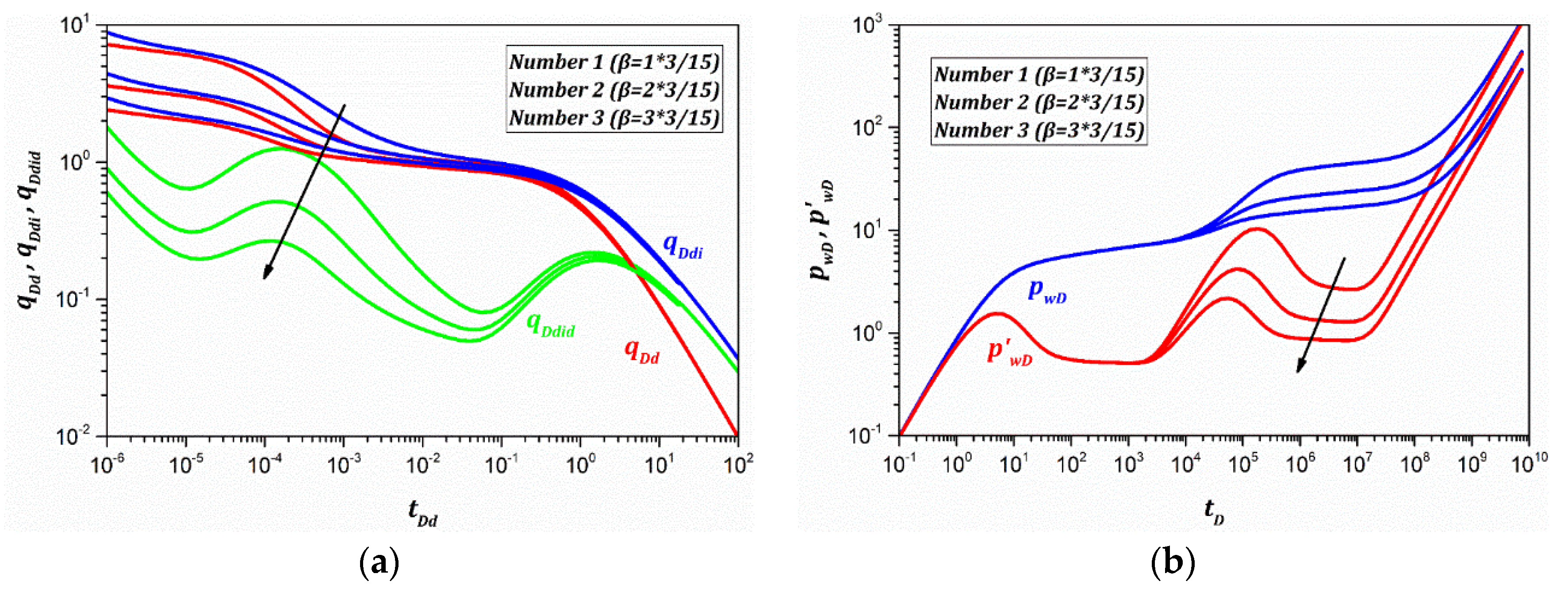
3.3.2. Outer-Convex Number

As shown in Figure 4b, the β is 3/15 when a single outer-convex is located at the top, the β is 6/15 when the double outer-convex is distributed in the top and middle and the β is 9/15 when the triple outer-convex is distributed in the top, middle and bottom. As shown in Figure 6a, the RTA combined curves move down due to the total thickness of outer-convex increasing from single to triple outer-convex as the outer-convex number is increasing. As shown in Figure 6b, the PTA combined type curves move down due to the outer-convex total thicknesses increasing. On the one hand, the start time of the VNBR transition flow regime is the same, as the minimum VNBR is unchanged. On the other hand, the start time of the VNBR boundary flow regime is later, since the equivalent VUBR becomes larger.

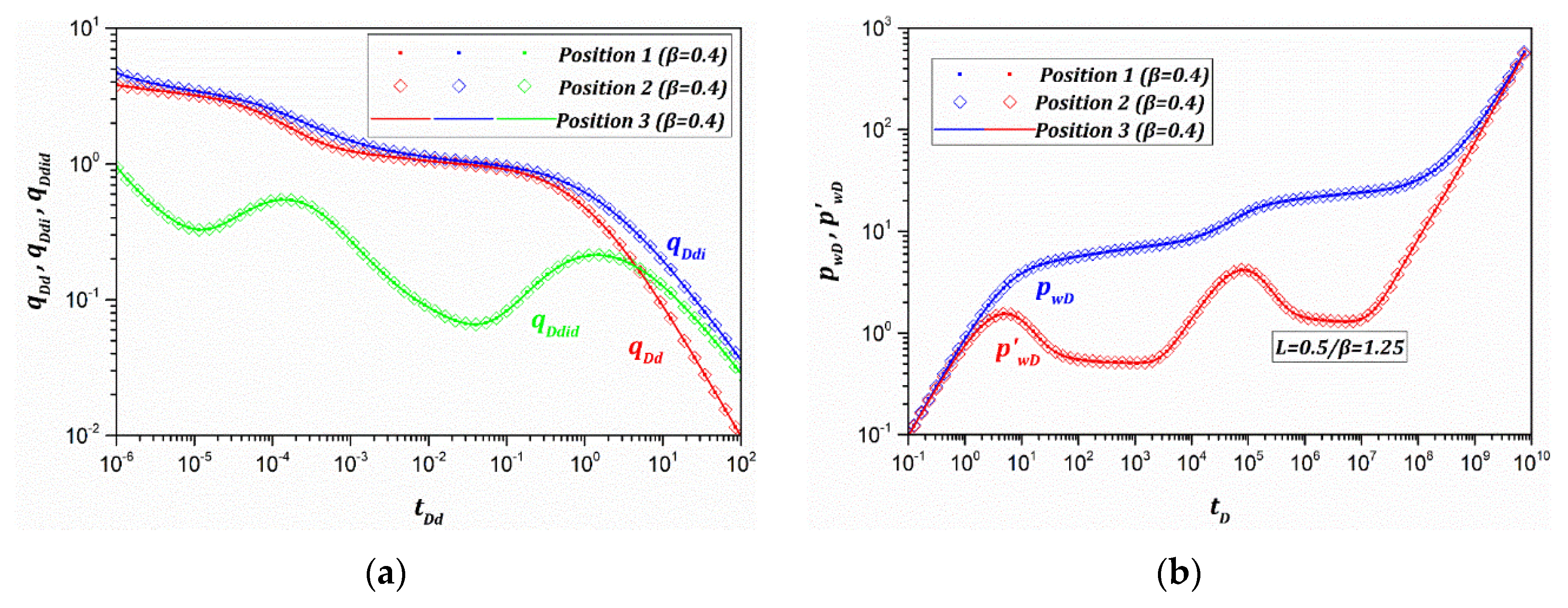
3.3.3. Outer-Convex Position

The outer-convex position refers to the outer-convex located at the top, middle and bottom of the reservoir (see Figure 4c). The ESV and β are unchanged due to the outer-convex thickness and outer-convex number being constant. Therefore, the rate decline curves (see Figure 7a) or pressure response curves (see Figure 7b) are completely coincident, regardless of the outer-convex position. The phenomenon indicates that the outer-convex position cannot be captured only from long-term production data or transient well test data.

4. Conclusions

This paper presents the extended RTA and PTA models of a vertical well in the VNBR reservoir by Laplace transform, Shehfest inverse and Duhamel’s superposition principles, and further develops the rate and pressure combined type curves to capture the production decline behavior and flow regimes’ characteristics. Several conclusions and suggestions are obtained from this work.

(1)

The production decline behavior of the VNBR reservoir is different from that of the VUBR reservoir, and the normalized dimensionless decline rate integral derivative can magnify the differences in the RTA combined type curves.

(2)

A new radial flow regime is identified in the VNBR reservoir that is captured by the PTA combined type curves. This behavior can be easily misinterpreted by a radial composite model as it has two stabilizations of the pressure derivative. Thus, the well testing analyst should be aware of the “equivalent composite zone effect”.

(3)

The outer-convex thickness and outer-convex number of the VNBR can be quickly obtained from the second level of pressure derivative in the PTA combined type curve. The equivalent VUBR can be obtained from the boundary radius corresponding to the boundary flow regime based on the “equivalent seepage volume effect”.

(4)

The actual exact outer-convex position of the VNBR, especially the VNBR with multiple outer-convexes, can neither be identified by RTA nor PTA combined type curves when the outer-convex total thickness and equivalent distance of the VNBR are unchanged.

In conclusion, the proposed RTA model enables petroleum engineers to better evaluate the production performance of a vertical well in the VNBR reservoir and interpret reservoir and well parameters more accurately based on the long-term production data. The PTA model can be used to analyze the pressure response of the VNBR reservoir, and quickly capture the flow regime characteristics from transient well test data.