Advanced PV Performance Modelling Based on Different Levels of Irradiance Data Accuracy
Abstract
1. Introduction
2. Data accuracy and Models
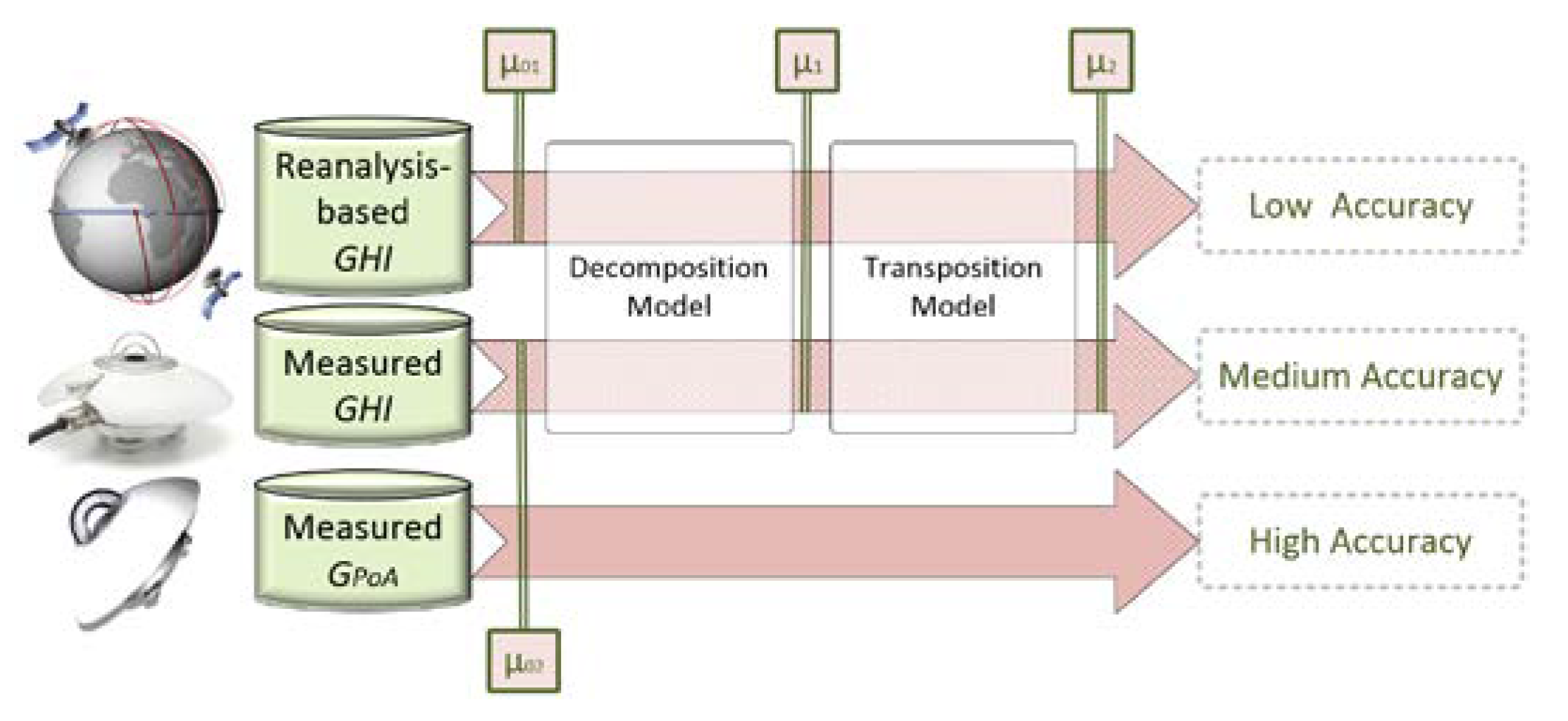
2.1. Definition of Data Accuracy Levels
- Low accuracy: the solar global horizontal irradiance () is extracted from a satellite-based or reanalysis-based dataset without post-processing (uncertainty “μ01”) and estimated at the PoA using decomposition (uncertainty “μ1”) and transposition (uncertainty ”μ2”) models.
- Medium accuracy: the GHI is measured using a pyranometer (uncertainty “μ02”) and estimated using decomposition and transposition models (uncertainties “μ1” and “μ2”).
- High accuracy: the is measured using a pyranometer in the plane of array (uncertainty “μ02”).
2.2. Definition of Empirical Models
- Empirical #1—Modified PVGIS model: An empirical model combining logarithmic regressions of normalized irradiance and PV module temperature with six empirical coefficients has been reported to provide excellent results over large geographical regions [27,28] (e.g., used in the PVGIS online tool [29]). In our simulations, we are using the measured ambient temperature () and measured/modelled plane-of-array irradiance without normalization as an input. Equation (1) shows the mathematical expression.
- Empirical #2—SRCL2014 model: developed by S. Ransome et al. [30], combines first and second-order regressions with logarithmical functions and four empirical coefficients to estimate the output power from the irradiance. The mathematical expression is presented in Equation (2).
- Empirical #3—Polynomial model: a polynomial function of the irradiance can achieve a simple mathematical approximation of the output power. We are using a 4th order polynomial function.
2.3. Machine Learning Approaches
- Artificial neural networks (ANN): are machine learning models inspired by biological neural networks. They consist of mathematical units called neurons and connections between them called weights. For ANN to learn a task, weights have to be optimized. This is usually done through gradient-based optimization techniques [31].
- Support vector machine (SVM): a supervised learning model that can be used for regression as well as classification tasks. SVM separates the data linearly, and by using a kernel trick, it transforms the data into higher dimensional feature space where a linear separation with a hyperplane is performed [32].
- Gradient boosting machines and LightGBM: gradient boosting decision tree (GBDT) [33,34] is a widely used machine learning algorithm, which achieves state-of-the-art results in many tasks and offers interpretability. The GBDT is an ensemble model in which predictors are trained sequentially. In each iteration, a weak prediction model, such as one level tree, fits the residual errors of the previous model. The main computational cost of such algorithm originates from the learning of decision trees, where the bottleneck is to find optimal split points with the highest information gain. LightGBM is a novel GBDT model that involves two novel techniques to deal with the problems of finding the optimal split point: gradient-based one-side sampling (GOSS) and exclusive feature bundling (EFB). The GOSS is applied to reduce the number of data instances, and EFB is used to reduce the feature space. Applying the LightGBM, the time processing can be reduced considerably in comparison to the ANN and SVM approaches.
2.4. Characteristics of the Photovoltaic (PV) System Used
3. Methodology of PV Energy Yield Modelling
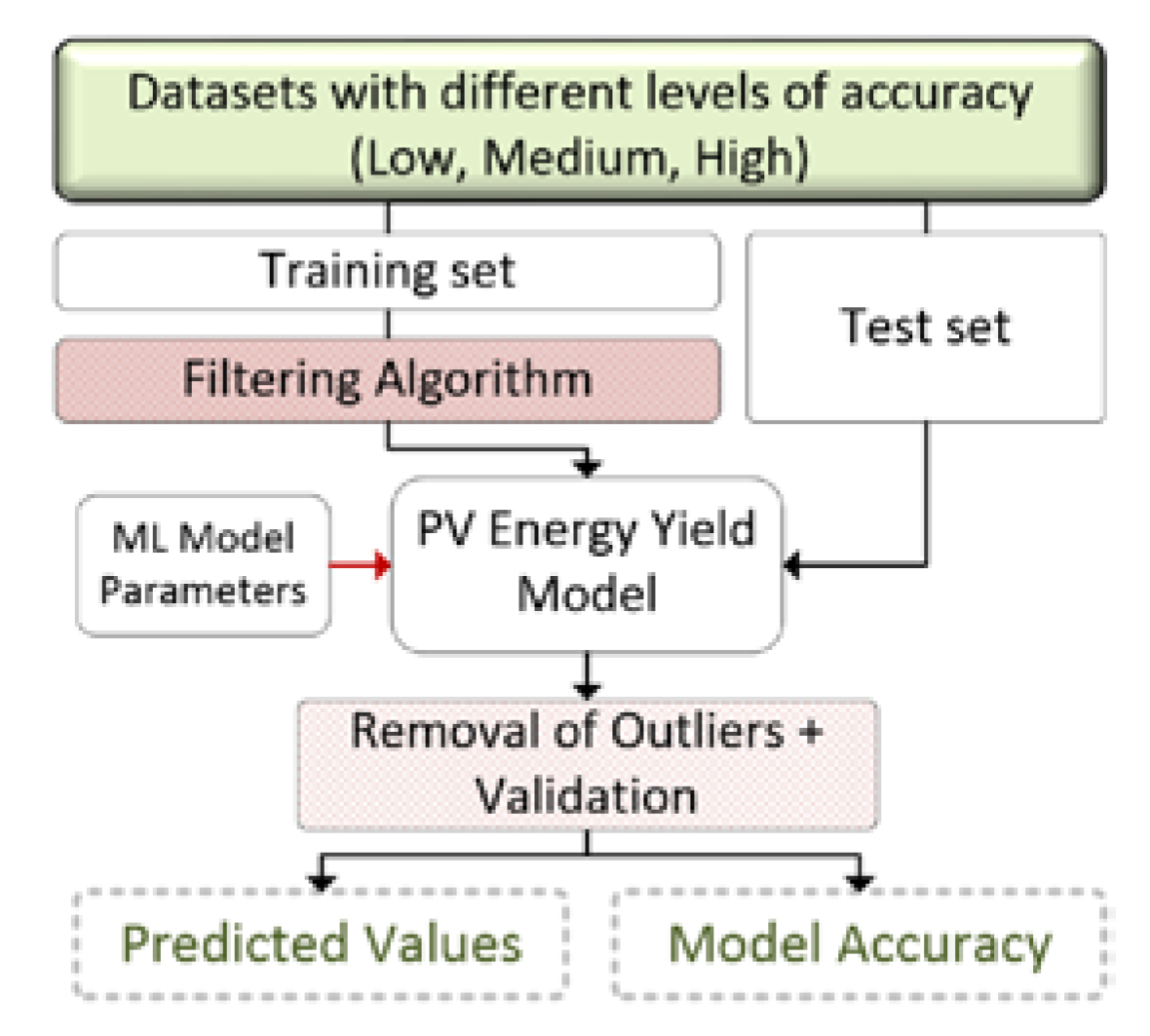
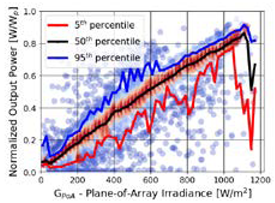
3.1. Data Filtering Process
3.2. PV Energy Yield Modelling Procedure
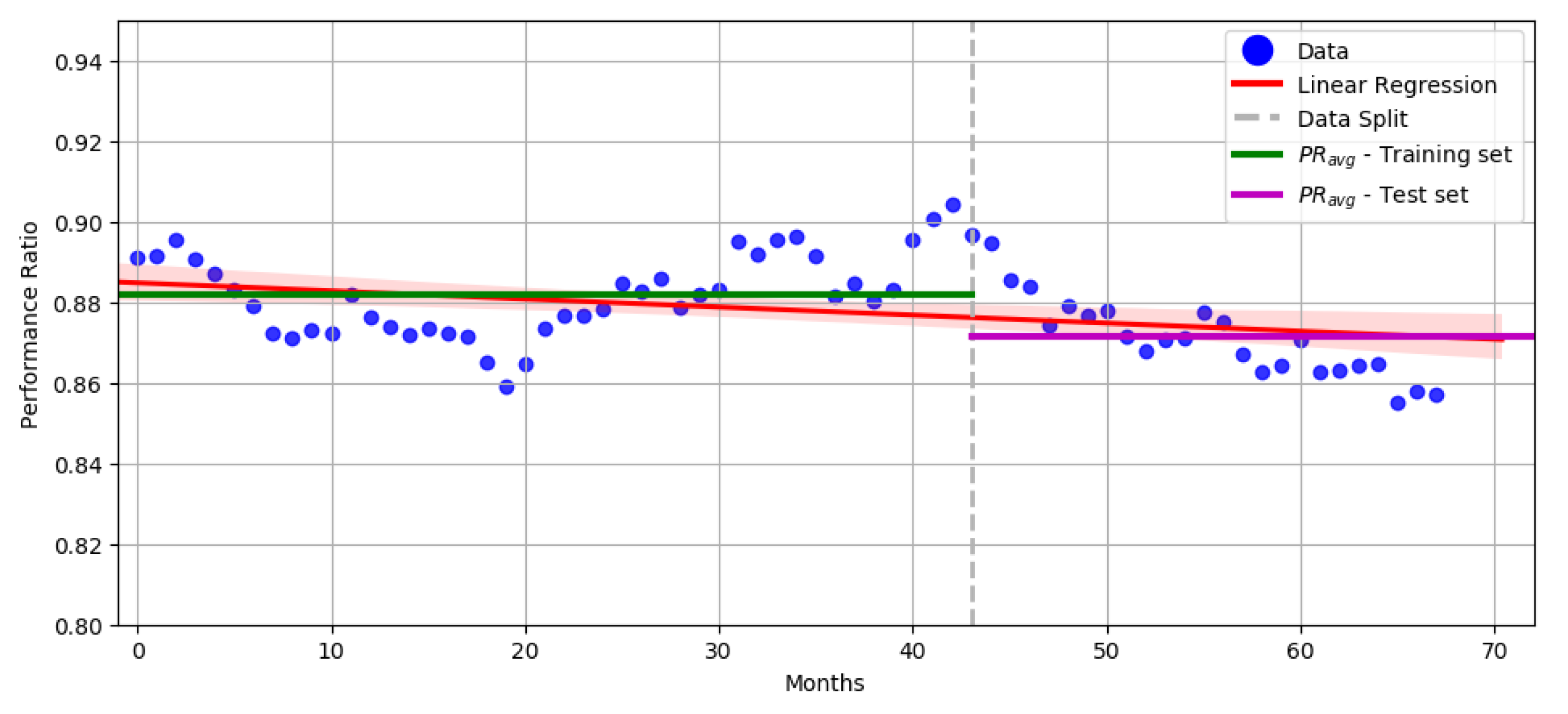
3.3. Uncertainty Indicators
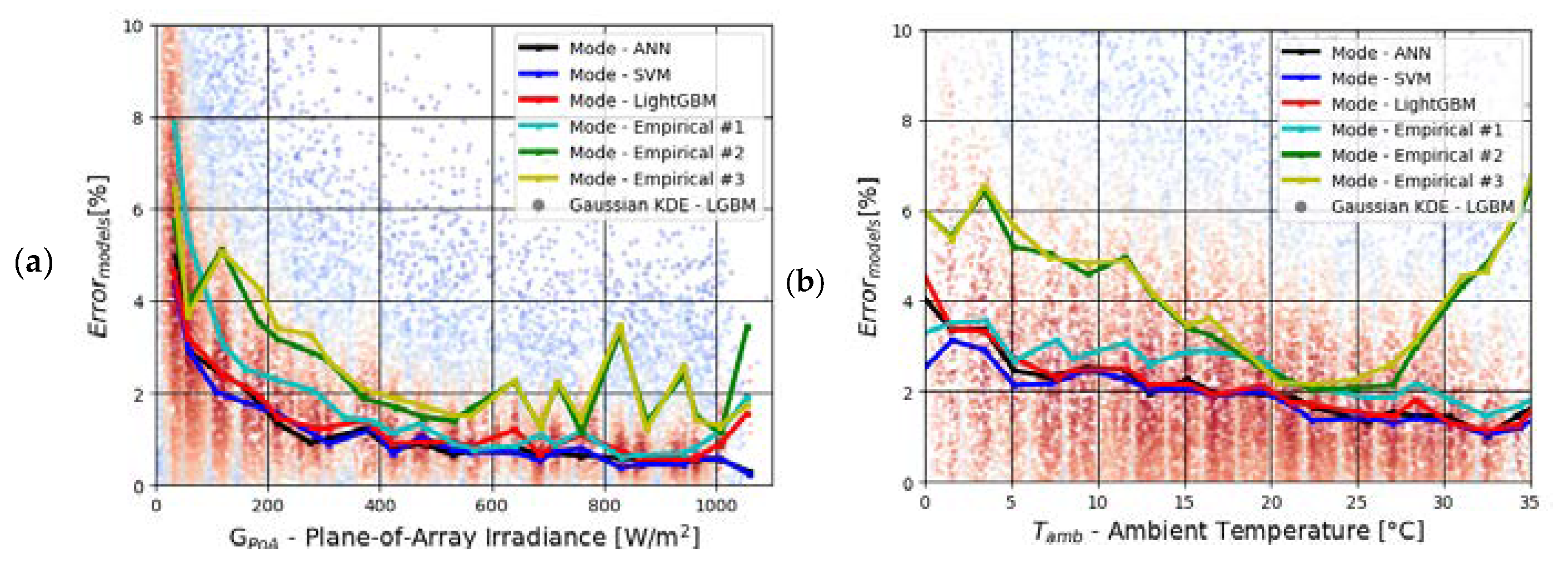
4. Results
5. Discussions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
List of Symbols and Abbreviations
| Ambient Temperature (°C) | |
| ANN | Artificial Neural Networks |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| EFB | Exclusive Feature Bundling |
| GBDT | Gradient Boosting Decision Tree |
| Global horizontal irradiance (W/m2) | |
| GOSS | Gradient-based One-Side Sampling |
| Global PoA irradiance (W/m2) | |
| HW | Holt-Winters |
| KGPV | Köppen-Geiger-Photovoltaic |
| LightGBM | Light Gradient Boosting Machine |
| nRMSE | normalized Root-Mean-Square-Error (%) |
| PoA | Plane-of-Array |
| Performance Ratio | |
| PV | Photovoltaic |
| nMBE | normalized Mean Bias Error (%) |
| SVM | Support Vector Machines |
References
- ETIP PV: The European Technology and Innovation Platform for Photovoltaics Photovoltaic Solar Energy: Big and Beyond. Sustainable Energy to Reach the 1.5 Degrees Climate Target. Available online: https://etip-pv.eu/news/other-news/photovoltaic-solar-energy-big-and-beyond-etip-pv-publishes-vision-for-future-energy-supply/ (accessed on 31 January 2020).
- Urraca, R.; Gracia-Amillo, A.M.; Huld, T.; Martinez-de-Pison, F.J.; Trentmann, J.; Lindfors, A.V.; Riihelä, A.; Sanz-Garcia, A. Quality control of global solar radiation data with satellite-based products. Sol. Energy 2017, 158, 49–62. [Google Scholar] [CrossRef]
- Palmer, D.; Koubli, E.; Cole, I.; Betts, T.; Gottschalg, R. Satellite or ground-based measurements for production of site specific hourly irradiance data: Which is most accurate and where? Sol. Energy 2018, 165, 240–255. [Google Scholar] [CrossRef]
- Urraca, R.; Huld, T.; Gracia-Amillo, A.; Martinez-de-Pison, F.J.; Kaspar, F.; Sanz-Garcia, A. Evaluation of global horizontal irradiance estimates from ERA5 and COSMO-REA6 reanalyses using ground and satellite-based data. Sol. Energy 2018, 164, 339–354. [Google Scholar] [CrossRef]
- Ascencio-Vásquez, J.; Brecl, K.; Topič, M. Methodology of Köppen-Geiger-Photovoltaic climate classification and implications to worldwide mapping of PV system performance. Sol. Energy 2019, 191, 672–685. [Google Scholar] [CrossRef]
- Copernicus Climate Change Service (C3S) ERA5: Fifth generation of ECMWF atmospheric reanalyses of the global climate. In Copernicus Climate Change Service Climate Data Store (CDS); Copernicus Climate Change Service (C3S), 2017.
- Ascencio-Vásquez, J.; Kaaya, I.; Brecl, K.; Weiss, K.A.; Topič, M. Global Climate Data Processing and Mapping of Degradation Mechanisms and Degradation Rates of PV Modules. Energies 2019, 12, 4749. [Google Scholar] [CrossRef]
- Camargo, L.R.; Schmidt, J. Simulation of Long-Term Time Series of Solar Photovoltaic Power: Is the ERA5-Land Reanalysis the Next Big Step? Available online: https://arxiv.org/abs/2003.04131 (accessed on 6 March 2020).
- Babar, B.; Graversen, R.; Boström, T. Solar radiation estimation at high latitudes: Assessment of the CMSAF databases, ASR and ERA5. Sol. Energy 2019, 182, 397–411. [Google Scholar] [CrossRef]
- Jiang, H.; Yang, Y.; Bai, Y.; Wang, H. Evaluation of the Total, Direct, and Diffuse Solar Radiations From the ERA5 Reanalysis Data in China. IEEE Geosci. Remote Sens. Lett. 2020, 17, 47–51. [Google Scholar] [CrossRef]
- Lave, M.; Hayes, W.; Pohl, A.; Hansen, C.W. Evaluation of Global Horizontal Irradiance to Plane-of-Array Irradiance Models at Locations Across the United States. IEEE J. Photovolt. 2015, 5, 597–606. [Google Scholar] [CrossRef]
- Mosavi, A.; Salimi, M.; Faizollahzadeh Ardabili, S.; Rabczuk, T.; Shamshirband, S.; Varkonyi-Koczy, A. State of the Art of Machine Learning Models in Energy Systems, a Systematic Review. Energies 2019, 12, 1301. [Google Scholar] [CrossRef]
- Kirn, B.; Brecl, K.; Topič, M. A new PV module performance model based on separation of diffuse and direct light. Sol. Energy 2015, 113, 212–220. [Google Scholar] [CrossRef]
- Livera, A.; Theristis, M.; Makrides, G.; Sutterlueti, J.; Ransome, S.; Georghiou, G.E. Performance Analysis of Mechanistic and Machine Learning models for Photovoltaic energy yield prediction. In Proceedings of the 36th European Photovoltaic Solar Energy Conference and Exhibition, Marseille, France, 9–13 September 2019; pp. 1272–1277. [Google Scholar]
- Fernández, Á.; Gala, Y.; Dorronsoro, J.R. Machine Learning Prediction of Large Area Photovoltaic Energy Production. In Data Analytics for Renewable Energy Integration; Woon, W.L., Aung, Z., Madnick, S., Eds.; Springer International Publishing: Cham, Switzerland, 2014; Volume 8817, pp. 38–53. ISBN 978-3-319-13289-1. [Google Scholar]
- Mellit, A.; Massi Pavan, A.; Ogliari, E.; Leva, S.; Lughi, V. Advanced Methods for Photovoltaic Output Power Forecasting: A Review. Appl. Sci. 2020, 10, 487. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIP 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Daoud, E.A. Comparison between XGBoost, LightGBM and CatBoost Using a Home Credit Dataset. Int. J. Comput. Inf. Eng. 2019, 13. [Google Scholar] [CrossRef]
- Minastireanu, E.-A.; Mesnita, G. Light GBM Machine Learning Algorithm to Online Click Fraud Detection. J. Inf. Assur. Cybersecur. 2019, 2019, 15. [Google Scholar] [CrossRef]
- Machado, M.R.; Karray, S.; de Sousa, I.T. LightGBM: An Effective Decision Tree Gradient Boosting Method to Predict Customer Loyalty in the Finance Industry. In Proceedings of the 2019 14th International Conference on Computer Science & Education (ICCSE), Toronto, ON, Canada, 19–21 August 2019; pp. 1111–1116. [Google Scholar]
- Song, Y.; Jiao, X.; Qiao, Y.; Liu, X.; Qiang, Y.; Liu, Z. Prediction of Double-High Biochemical Indicators Based on LightGBM and XGBoost. In Proceedings of the 2019 International Conference on Artificial Intelligence and Computer Science—AICS 2019, Wuhan, Hubei, China, 12–13 July 2019; pp. 189–193. [Google Scholar]
- Zhang, J.; Mucs, D.; Norinder, U.; Svensson, F. LightGBM: An Effective and Scalable Algorithm for Prediction of Chemical Toxicity–Application to the Tox21 and Mutagenicity Data Sets. J. Chem. Inf. Model. 2019, 59, 4150–4158. [Google Scholar] [CrossRef]
- Zeng, H.; Yang, C.; Zhang, H.; Wu, Z.; Zhang, J.; Dai, G.; Babiloni, F.; Kong, W. A LightGBM-Based EEG Analysis Method for Driver Mental States Classification. Comput. Intell. Neurosci. 2019, 2019, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Zhang, Y.; Zhao, Y. LightGBM: An Effective miRNA Classification Method in Breast Cancer Patients. In Proceedings of the 2017 International Conference on Computational Biology and Bioinformatics—ICCBB 2017, Newark, NJ, USA, 18–20 October 2017; pp. 7–11. [Google Scholar]
- Reba, K.; Bevc, J.; Ascencio-Vásquez, J.; Jankovec, M.; Topič, M. Photovoltaic Energy Production Forecasting using LightGBM. In Proceedings of the 55rd International Conference on Microelectronics, Devices and Materials, Bled, Slovenia, 22–27 September 2019. [Google Scholar]
- Mariottini, F.; Belluardo, G.; Bliss, M.; Isherwood, P.J.M.; Cole, I.R.; Betts, T.R. Assessment and improvement of thermoelectric pyranometer measurements. In Proceedings of the 36th European Photovoltaic Solar Energy Conference and Exhibition, Marseille, France, 9–13 September 2019. [Google Scholar]
- Huld, T.; Amillo, A. Estimating PV Module Performance over Large Geographical Regions: The Role of Irradiance, Air Temperature, Wind Speed and Solar Spectrum. Energies 2015, 8, 5159–5181. [Google Scholar] [CrossRef]
- Huld, T.; Gottschalg, R.; Beyer, H.G.; Topič, M. Mapping the performance of PV modules, effects of module type and data averaging. Sol. Energy 2010, 84, 324–338. [Google Scholar] [CrossRef]
- European Commission, Joint Research Centre Photovoltaic Geographical Information System (PVGIS), Online Tool. Available online: https://ec.europa.eu/jrc/en/pvgis (accessed on 3 December 2019).
- Ransome, S.; Sutterlueti, J. How to Choose the Best Empirical Model for Optimum Energy Yield Predictions. In Proceedings of the 2017 IEEE 44th Photovoltaic Specialist Conference (PVSC), Washington, DC, USA, 25–30 June 2017; pp. 652–657. [Google Scholar]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press, Inc.: Oxford, UK, 1995; ISBN 0-19-853864-2. [Google Scholar]
- Drucker, H.; Burges, C.J.C.; Kaufman, L.; Smola, A.; Vapnik, V. Support Vector Regression Machines. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Denver, CO, USA, 1–6 December 1997; pp. 155–161. [Google Scholar]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2000, 29, 1189–1232. [Google Scholar] [CrossRef]
- Anghel, A.; Papandreou, N.; Parnell, T.; De Palma, A.; Pozidis, H. Benchmarking and Optimization of Gradient Boosting Decision Tree Algorithms. arXiv 2019, arXiv:1809.04559. [Google Scholar]
- Tsafarakis, O.; Sinapis, K.; van Sark, W. PV System Performance Evaluation by Clustering Production Data to Normal and Non-Normal Operation. Energies 2018, 11, 977. [Google Scholar] [CrossRef]
- Theristis, M.; Stein, J.S. PV Degradation Modeling, PV Performance Modeling Collaborative, Sandia National Laboratories, SAND2019-15366 W. Available online: https://pvpmc.sandia.gov/pv-research/pv-lifetime-project/pv-degradation-modeling/ (accessed on 12 February 2020).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]

| Definitions: |
| class_size: Size of each class |
| PGi: Power output values per cluster |
| Lxth: Lower percentile used as threshold |
| Uxth: Upper percentile used as threshold |
| PGi-Lxth: Lxth percentile of PGi |
| PGi-50th: 50th percentile of PGi |
| PGi-Uxth: Uxth percentile of PGi |
| PGi-50th {Gi}: 50th percentile of output power per class Gi |
| Functions: |
| polyfit(x) = ax + bx2 + cx3 + dx4 + e |
| fGaussian: Gaussian distribution |
| • Clustering by Irradiance |
| for Gi range from class_size to 1300 in steps of class_size |
| Gi = {Gi–class_size, Gi} |
| PGi = Poutput{Gi} |
| • Calculate thresholds per class (Gi) |
| PGi-Lxth = fGaussian(Lxth) |
| PGi-50th = fGaussian(50th) |
| PGi-Uxth = fGaussian(Uxth) |
| • Filtering the 50th percentile curve |
| Pshift{Gi} = |PGi-50th {Gi}–PGi-50th {Gi-2}|2 + |PGi-50th {Gi}–PGi-50th {Gi−1}|+ |
| |PGi-50th {Gi} - PGi-50th {Gi+1}| + |PGi-50th {Gi}–PGi-50th {Gi+2}|2 |
| PGi-50th-Filter{Gi} = PGi-50th {Gi} > Pshift {90th percentile} |
| • Polynomial Fitting the 50th percentile curve |
| Pfit-50th{Gi} = polyfit{PGi-50th-Filter} |
| • Filtering the Lxth and Uxth percentile curves |
| DiffLxth{Gi} = Pfit-50th{Gi} - PGi-Uxth |
| DiffUxth{Gi} = Pfit-50th{Gi} - PGi-Uxth |
| PGi-Lxth-Filter{Gi} = PGi-Lxth < DiffLxth {75th percentile} |
| PGi-Uxth-Filter{Gi} = PGi-Uxth > DiffUxth {25th percentile} |
| • Fitting the Lxth and Uxth percentile curves |
| Pfit-Lxth{Gi} = polyfit{PGi-Lxth-Filter} |
| Pfit-Uxth{Gi} = polyfit{PGi-Uxth-Filter} |
| High Accuracy Data | Medium Accuracy Data | Low Accuracy Data |
|---|---|---|
| (1) Measured Power Output (2) On-site measured GPoA | (1) Measured Power Output (2) On-site measured GHI (3) Estimated GPoA from GHI | (1) Measured Power Output (2) Reanalysis GHI (3) Estimated GPoA from GHI |
| Parameters: Lxth = 5th, Uxth= 95th | Parameters: Lxth = 5th, Uxth= 95th | Parameters: Lxth = 20th, Uxth = 80th |
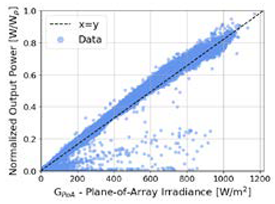 | 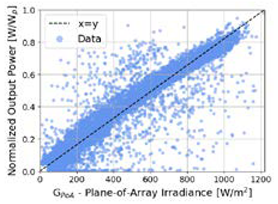 | 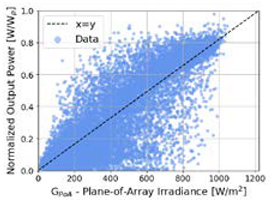 |
 |  | 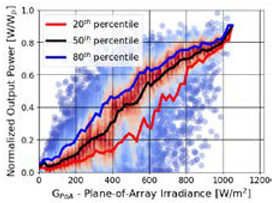 |
 | 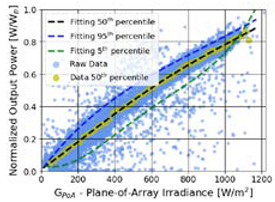 |  |
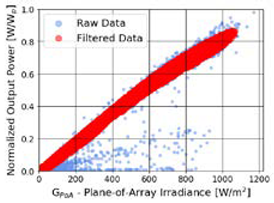 |  |  |
| Model | Low Accuracy (%, s) | Medium Accuracy (%, s) | High Accuracy (%, s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | Speed | (1) | (2) | (3) | Speed | (1) | (2) | (3) | Speed | |
| LightGBM | 11.64 | 12.19 | 4.58 | 0.031 | 5.93 | 5.89 | 2.47 | 0.047 | 1.98 | 1.45 | 0.99 | 0.047 |
| ANN | 11.55 | 12.08 | 4.52 | 75.69 | 6.11 | 6.03 | 2.45 | 85.43 | 2.27 | 1.46 | 1.01 | 133.09 |
| SVM | 12.05 | 12.18 | 4.59 | 4.33 | 5.92 | 5.98 | 2.49 | 15.47 | 1.44 | 1.45 | 1.01 | 38.74 |
| Empirical #1 | 12.07 | 12.26 | 5.05 | 0.031 | 6.41 | 6.32 | 2.99 | 0.031 | 2.33 | 1.60 | 1.18 | 0.031 |
| Empirical #2 | 11.91 | 12.18 | 4.98 | 0.078 | 6.40 | 6.52 | 3.41 | 0.047 | 2.03 | 2.13 | 1.46 | 0.063 |
| Empirical #3 | 11.91 | 12.23 | 4.86 | 0.125 | 6.36 | 6.57 | 3.40 | 0.203 | 2.02 | 2.12 | 1.45 | 0.188 |
| Input Features | GPoA | GPoA + Tamb | GPoA + Tamb +SP |
|---|---|---|---|
| LightGBM | 1.49 % | 1.10 % | 0.99 % |
| ANN | 1.44 % | 1.16 % | 1.01 % |
| SVM | 1.52% | 1.19% | 1.01% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ascencio-Vásquez, J.; Bevc, J.; Reba, K.; Brecl, K.; Jankovec, M.; Topič, M. Advanced PV Performance Modelling Based on Different Levels of Irradiance Data Accuracy. Energies 2020, 13, 2166. https://doi.org/10.3390/en13092166
Ascencio-Vásquez J, Bevc J, Reba K, Brecl K, Jankovec M, Topič M. Advanced PV Performance Modelling Based on Different Levels of Irradiance Data Accuracy. Energies. 2020; 13(9):2166. https://doi.org/10.3390/en13092166
Chicago/Turabian StyleAscencio-Vásquez, Julián, Jakob Bevc, Kristjan Reba, Kristijan Brecl, Marko Jankovec, and Marko Topič. 2020. "Advanced PV Performance Modelling Based on Different Levels of Irradiance Data Accuracy" Energies 13, no. 9: 2166. https://doi.org/10.3390/en13092166
APA StyleAscencio-Vásquez, J., Bevc, J., Reba, K., Brecl, K., Jankovec, M., & Topič, M. (2020). Advanced PV Performance Modelling Based on Different Levels of Irradiance Data Accuracy. Energies, 13(9), 2166. https://doi.org/10.3390/en13092166








