A Finite Element Analysis Model for Partial Discharges in Silicone Gel under a High Slew Rate, High-Frequency Square Wave Voltage in Low-Pressure Conditions
Abstract
1. Introduction
2. Impact of Pressure
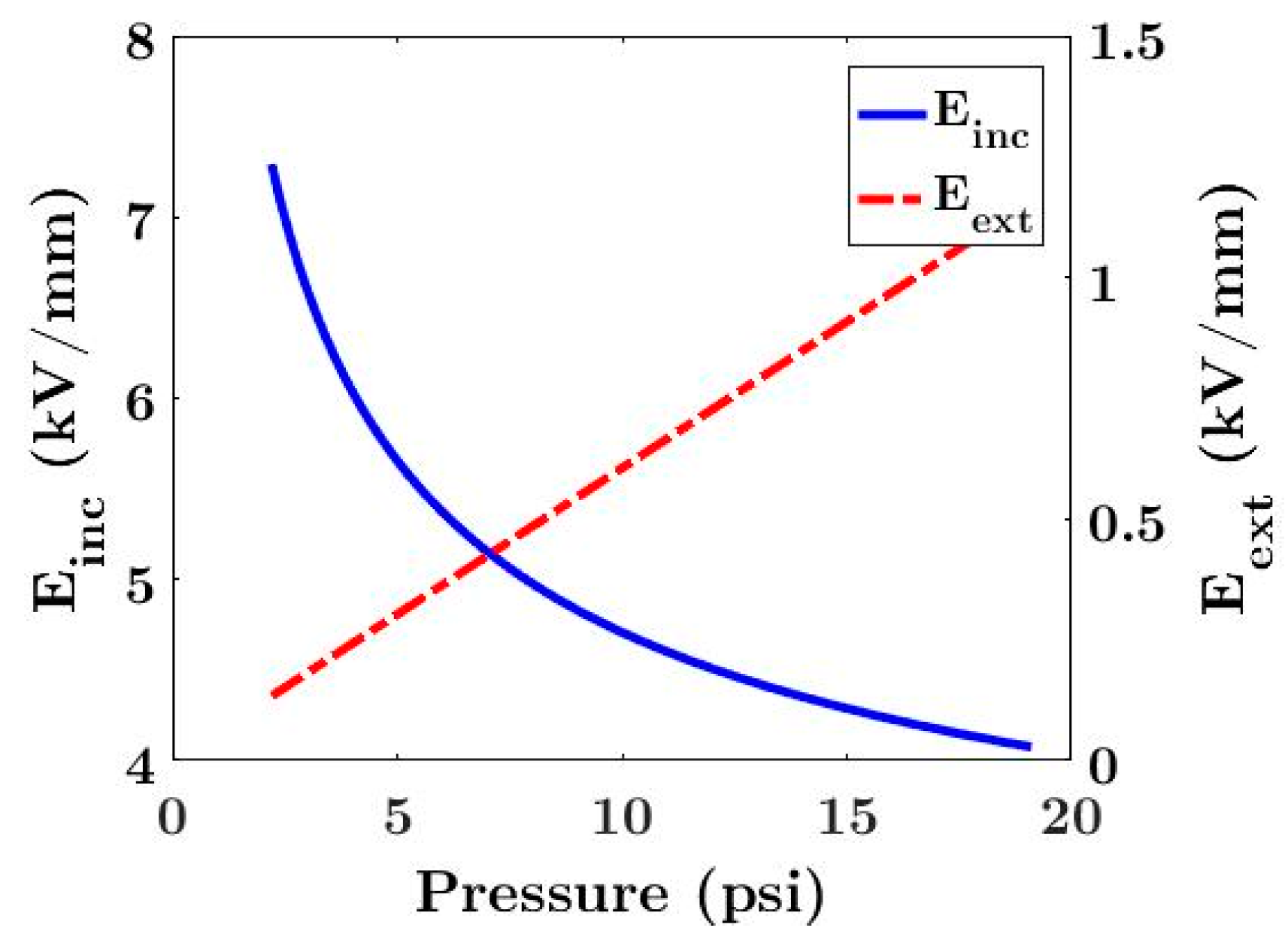
2.1. PD Inception
2.2. PD Extinction
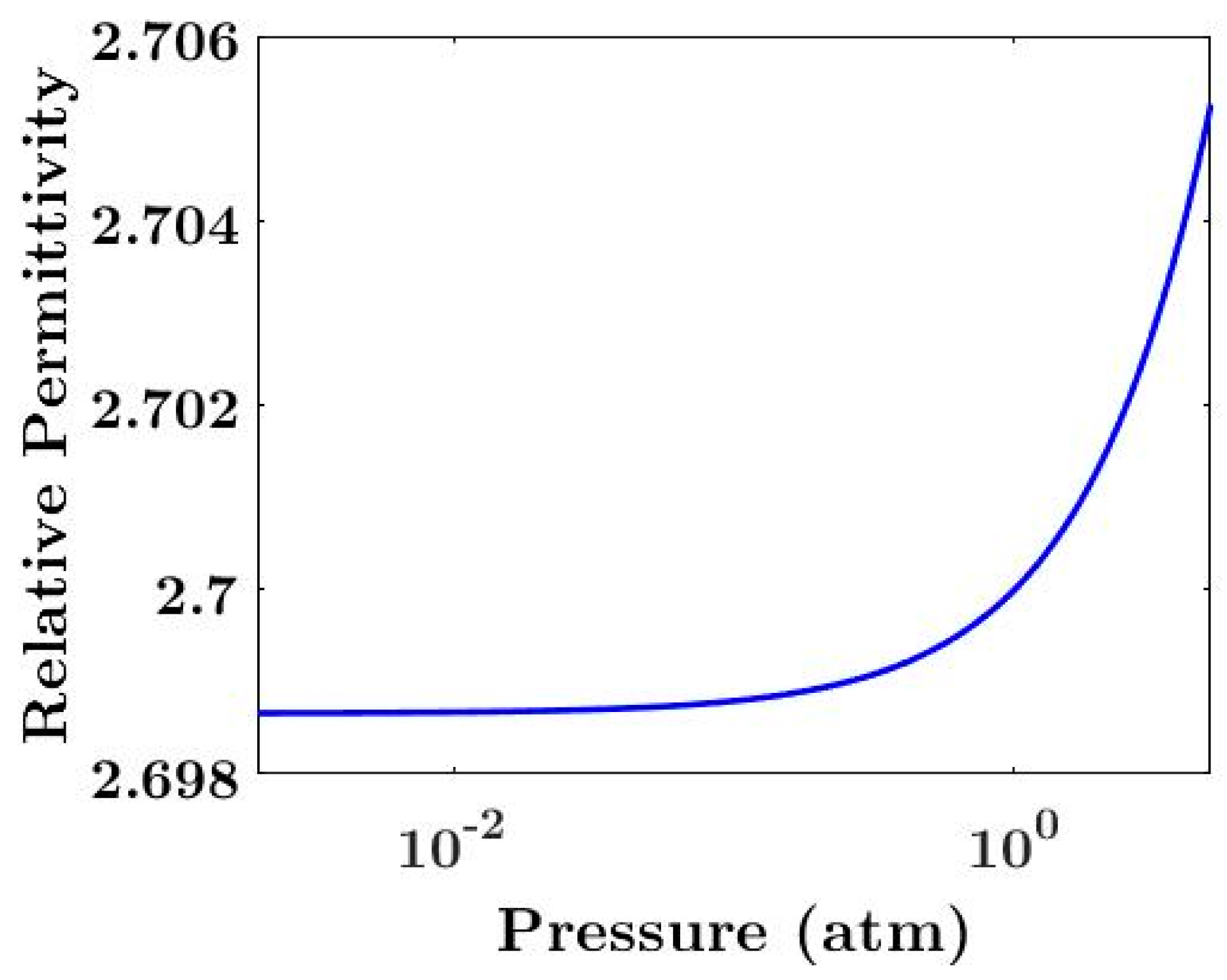
2.3. Dielectric Constant (Relative Permittivity)
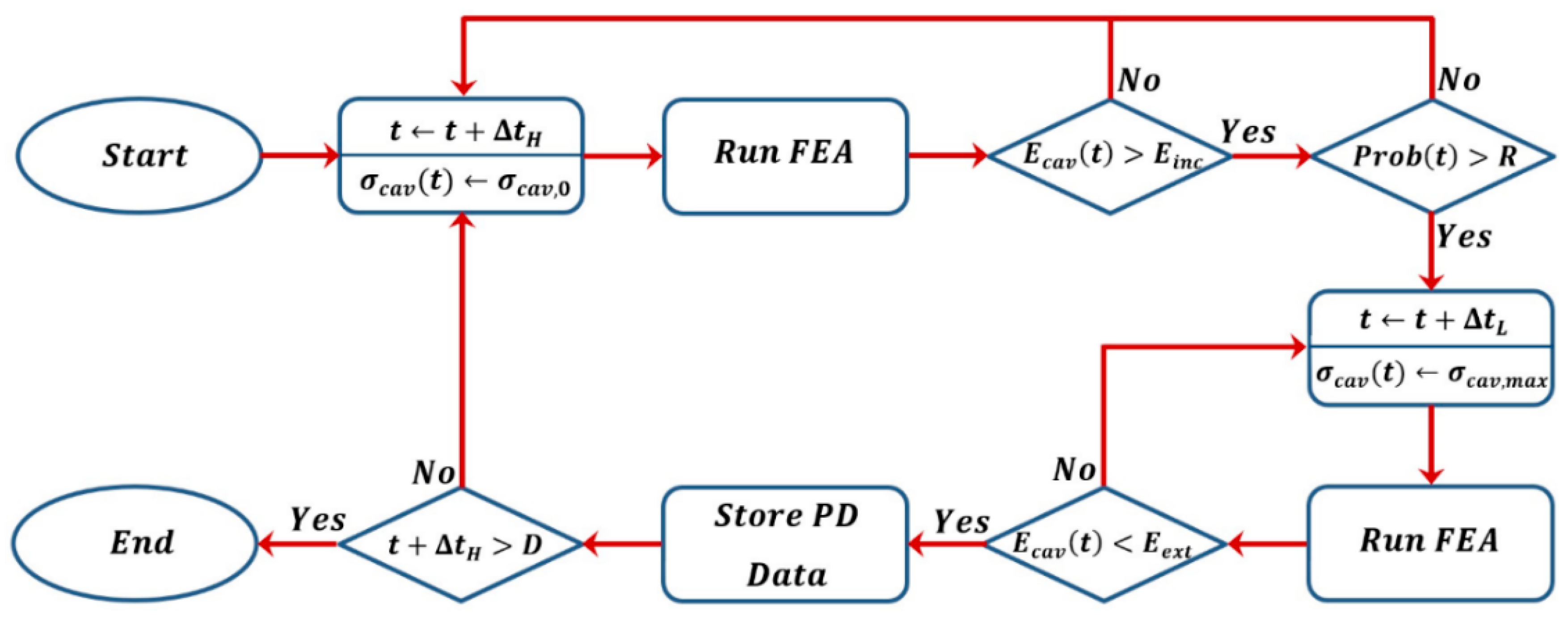
3. PD Modeling
4. Results and Key Challenges
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Advisory Council for Aeronautics Research in Europe. Aeronautics and Air Transport: Beyond Vision 2020 (Towards 2050); Publications Office of the EU: Brussels, Belgium, 2010.
- Advisory Council for Aeronautics Research in Europe. Strategic Research & Innovation Agenda-2017 Update; ACARE: Brussels, Belgium, 2017. [Google Scholar]
- U.S. Environmental Protection Agency (EPA): Fast Facts on Transportation Greenhouse Gas Emissions. 2019. Available online: https://www.epa.gov/greenvehicles/fast-facts-transportation-greenhouse-gas-emissions (accessed on 15 June 2019).
- U.S. Energy Information Administration (EIA): Monthly Energy Review. 2020. Available online: https://www.eia.gov/totalenergy/data/monthly/pdf/sec3_9.pdf (accessed on 15 March 2020).
- Ghassemi, M. Accelerated Insulation Aging due to Fast, Repetitive Voltages: A Review Identifying Challenges and Future Research Needs. IEEE Trans. Dielectr. Electr. Insul. 2019, 26, 1558–1568. [Google Scholar] [CrossRef]
- Muslim, D.J.; Lesaint, O.; Hanna, R.; Reboud, J.L.; Sinisuka, N.I. Electrical characterization of Dibenzyltoluene liquid at high temperatures up to 350_C. In Proceedings of the IEEE Annual Report Conference on Electrical Insulation and Dielectric Phenomena. (CEIDP), Cancun, Mexico, 21–24 October 2018; pp. 58–61. [Google Scholar]
- Muslim, J.; Lesaint, O.; Hanna, R.; Sinisuka, N.I. Streamer generation and propagation in Dibenzyltoluene and Ester liquids under high temperature. In Proceedings of the IEEE International Conference Dielectric Liquids (ICDL), Roma, Italy, 23–27 June 2019; pp. 1–4. [Google Scholar]
- Muslim, J.; Lesaint, O.; Hanna, R.; Sinisuka, N.I. Partial discharge measurements on Dibenzyltoluene for high temperature encapsulant application up to 350 °C. In Proceedings of the IEEE International Conference Dielectric Liquids (ICDL), Roma, Italy, 23–27 June 2019; pp. 1–4. [Google Scholar]
- Ghassemi, M. PD Measurements, Failure Analysis and Control in High Power IGBT Modules. High. Volt. 2018, 3, 170–178. [Google Scholar] [CrossRef]
- Ghassemi, M. Electrical insulation weaknesses in wide bandgap devices. In Simulation and Modelling of Electrical Insulation Weaknesses in Electrical Equipment; Albarracin, R., Ed.; InTechOpen: London, UK, 2018; pp. 129–149. [Google Scholar]
- Wang, N.; Cotton, I.; Robertson, J.; Follmann, S.; Evans, K.; Newcombe, D. Partial Discharge Control in a Power Electronic Module Using High Permittivity Non-Linear Dielectrics. IEEE Trans. Dielectr. Electr. Insul. 2010, 17, 1319–1326. [Google Scholar] [CrossRef]
- Tousi, M.M.; Ghassemi, M. Electric field control by nonlinear field dependent conductivity dielectrics characterization for high voltage power module packaging. In Proceedings of the IEEE International Workshop on Integrated Power Packaging (IWIPP), Toulouse, France, 24–26 April 2019; pp. 54–58. [Google Scholar]
- Tousi, M.M.; Ghassemi, M. Nonlinear field dependent conductivity materials for electric field control within next-generation wide bandgap power electronics modules. In Proceedings of the 2019 IEEE Electrical Insulation Conference (EIC), Calgary, AB, Canada, 16–19 June 2019; pp. 63–66. [Google Scholar]
- Tousi, M.M.; Ghassemi, M. The effect of type of voltage (sinusoidal and square waveform) and the frequency on the performance of nonlinear field-dependent conductivity coatings for electric field control in power electronic modules. In Proceedings of the IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Richland, DC, USA, 20–23 October 2019; pp. 601–604. [Google Scholar]
- Tousi, M.M.; Ghassemi, M. Electrical insulation packaging for a 20 kV high density wide bandgap power module. In Proceedings of the IEEE Energy Conversion Congress & Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 4162–4166. [Google Scholar]
- Tousi, M.M.; Ghassemi, M. Nonlinear resistive electric field grading in high-voltage, high-power wide bandgap power module packaging. In Proceedings of the IEEE Energy Conversion Congress & Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 7124–7129. [Google Scholar]
- Tousi, M.M.; Ghassemi, M. Combined Geometrical Techniques and Applying Nonlinear Field Dependent Conductivity Layers to Address the High Electric Field Stress Issue in High Voltage High-Density Wide Bandgap Power Modules. IEEE Trans. Dielectr. Electr. Insul. 2020, 27, 305–313. [Google Scholar] [CrossRef]
- Tousi, M.M.; Ghassemi, M. Characterization of Nonlinear Field Dependent Conductivity Layer Coupled with Protruding Substrate to Address High Electric Field Issue within High Voltage High-Density Wide Bandgap Power Modules. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 343–350. [Google Scholar] [CrossRef]
- Tousi, M.M.; Ghassemi, M. Effects of Frequency and Temperature on Electric Field Mitigation Method via Protruding Substrate Combined with Applying Nonlinear FDC Layer in Wide Bandgap Power Modules. Energies 2020, 13, 2022. [Google Scholar] [CrossRef]
- Ghassemi, M. Geometrical techniques for electric field control in (ultra) wide bandgap power electronics modules. In Proceedings of the IEEE Electrical Insulation Conference (EIC), San Antonio, TX, USA, 17–20 June 2018; pp. 589–592. [Google Scholar]
- Crichton, G.C.; Karlsson, P.W.; Pedersen, A. Partial Discharges in Ellipsoidal and Spheroidal Voids. IEEE Trans. Electr. Insul. 1989, 24, 335–342. [Google Scholar] [CrossRef]
- Pedersen, A.; Crichton, G.C.; McAllister, I.W. The Theory and Measurement of Partial Discharge Transients. IEEE Trans. Electr. Insul. 1991, 26, 487–497. [Google Scholar] [CrossRef]
- Achillides, Z.; Danikas, M.G.; Kyriakides, E. Partial discharge modeling and induced charge concept: Comments and criticism of Pedersen’s model and associated measured transients. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 1118–1122. [Google Scholar] [CrossRef]
- Callender, G.; Tanmaneeprasert, T.; Lewin, P.L. Simulating Partial Discharge Activity in a Cylindrical Void Using a Model of Plasma Dynamics. J. Appl. Phys. 2019, 52, 169501. [Google Scholar] [CrossRef]
- Callender, G.; Golosnoy, I.O.; Rapisarda, R.; Lewin, P.L. Critical Analysis of Partial Discharge Dynamics in Air Filled Spherical Voids. J. App. Phys. 2018, 51, 125601. [Google Scholar] [CrossRef]
- Borghei, M.; Ghassemi, M.; Rodríguez-Serna, J.M.; Albarracín-Sánchez, R. A Finite Element Analysis and an Improved Induced Charge Concept for Partial Discharge Modeling. IEEE Trans. Power Del. 2020. accepted and to be published. [Google Scholar]
- Borghei, M.; Ghassemi, M. Partial discharge finite element analysis under fast, repetitive voltage pulses. In Proceedings of the IEEE Electric Ship Technologies Symposium (ESTS), Arlington, VA, USA, 13–19 August 2019; pp. 324–328. [Google Scholar]
- Borghei, M.; Ghassemi, M. Partial Discharge Analysis Under High-Frequency, Fast-Rise Square Wave Voltages in Silicone Gel: A Modeling Approach. Energies 2019, 12, 4543. [Google Scholar] [CrossRef]
- Wang, P.; Cavallini, A.; Montanari, G.C. The Influence of Repetitive Square Wave Voltage Parameters on Enameled Wire Endurance. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 1276–1284. [Google Scholar] [CrossRef]
- Illias, H.A.; Bakar, A.H.A.; Mokhlis, H.; Tunio, M.A.; Chen, G.; Lewin, P.L.; Ariffin, A.M. Simulation of partial discharge within a void under square waveform applied voltage. In Proceedings of the IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Montreal, QC, Canada, 14–17 October 2012; pp. 76–79. [Google Scholar]
- Wang, P.; Cavallini, A.; Montanari, G.C.; Wu, G. Effect of Rise Time on PD Pulse Features under Repetitive Square Wave Voltages. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 245–254. [Google Scholar] [CrossRef]
- Meyer, D.R.; Cavallini, A.; Lusuardi, L.; Barater, D.; Pietrini, G.; Soldati, A. Influence of Impulse Voltage Repetition Frequency on RPDIV in Partial Vacuum. IEEE Trans. Dielectr. Electr. Insul. 2018, 25, 873–882. [Google Scholar] [CrossRef]
- Borghei, M.; Ghassemi, M. Finite element modeling of partial discharge activity within a spherical cavity in a solid dielectric material under fast, repetitive voltage pulses. In Proceedings of the IEEE Electrical Insulation Conference (EIC), Calgary, AB, Canada, 16–19 June 2019; pp. 34–37. [Google Scholar]
- Niemeyer, L. A Generalized Approach to Partial Discharge Modeling. IEEE Trans. Dielectr. Electr. Insul. 1995, 2, 510–528. [Google Scholar] [CrossRef]
- Gutfleisch, F.; Niemeyer, L. Measurement and Simulation of PD in Epoxy Voids. IEEE Trans. Dielectr. Electr. Insul. 1995, 2, 729–743. [Google Scholar] [CrossRef]
- Owen, B.B.; Brinkley, S.R. The Effect of Pressure upon the Dielectric Constants of Liquids. Phys. Rev. 1943, 64, 32–36. [Google Scholar] [CrossRef]
- Schornack, L.G.; Eckert, C.A. Effect of Pressure on the Density and Dielectric Constant of Polar Solvents. J. Phys. Chem. 1970, 74, 3014–3020. [Google Scholar] [CrossRef]
- Ebke, T.; Khaddour, A.; Peier, D. Degradation of silicone gel by partial discharges due to different defects. In Proceedings of the IEEE International Conference on Dielectric Materials, Measurements and Applications, Edinburgh, UK, 17–21 September 2000; pp. 202–207. [Google Scholar]
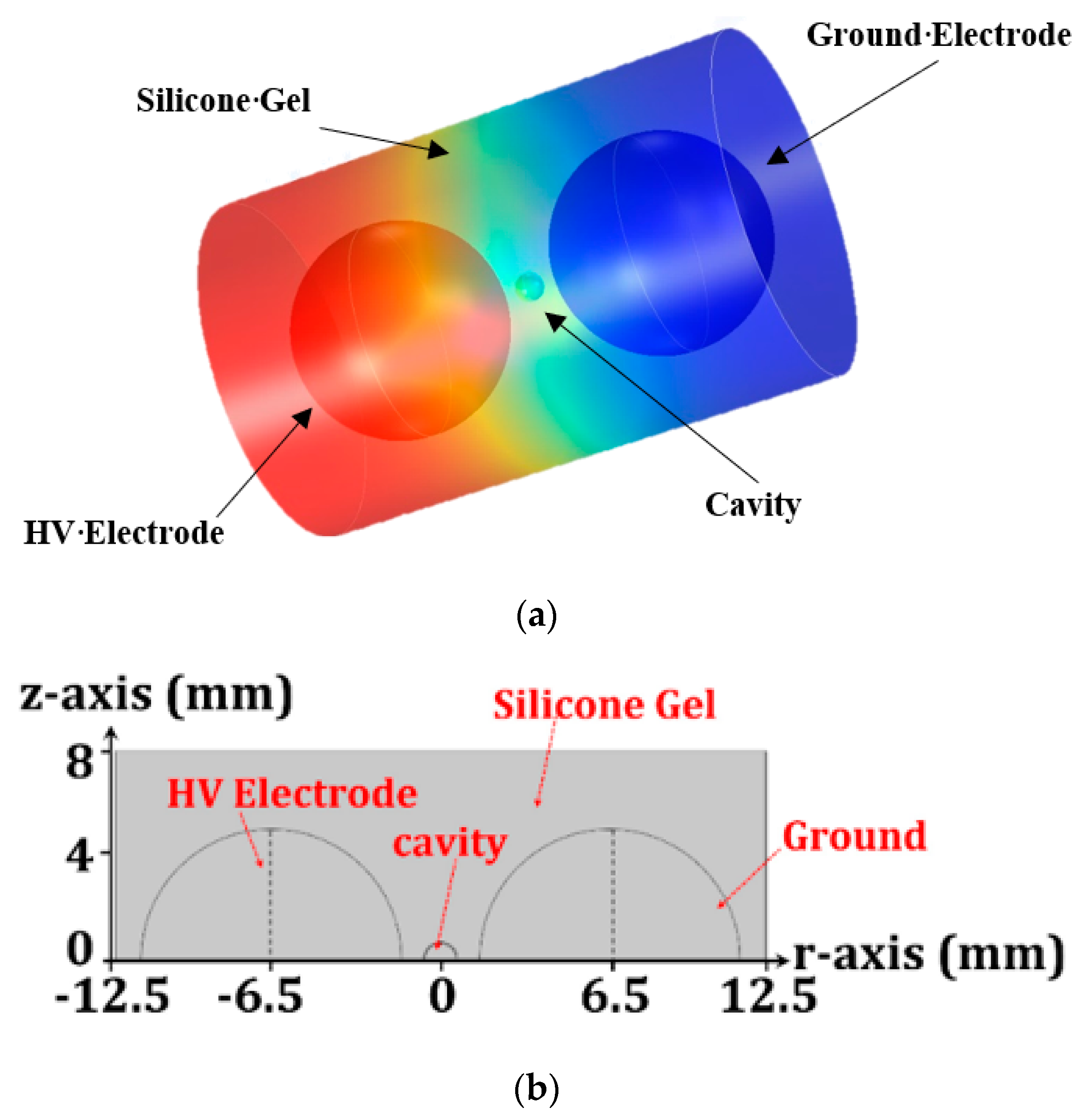

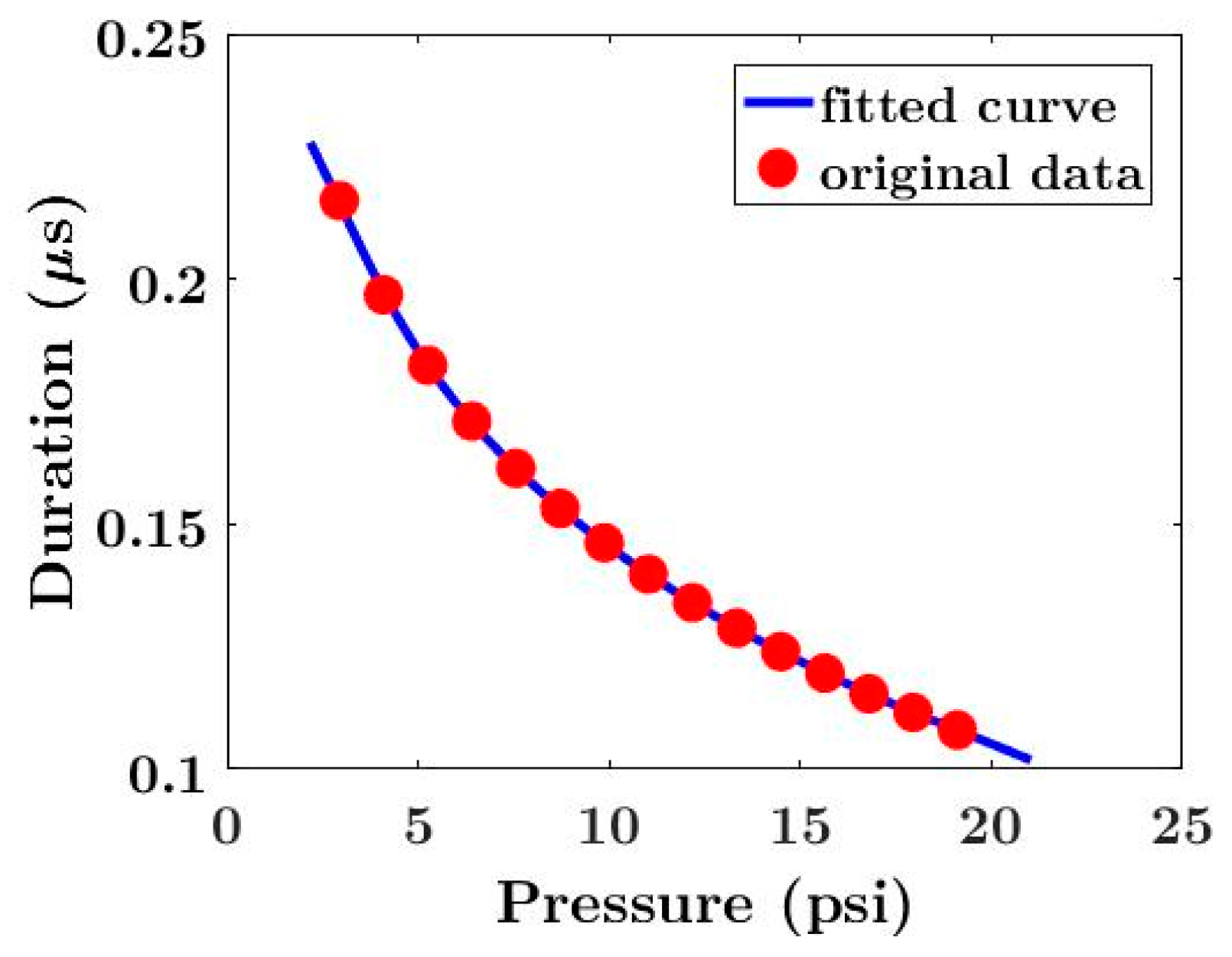
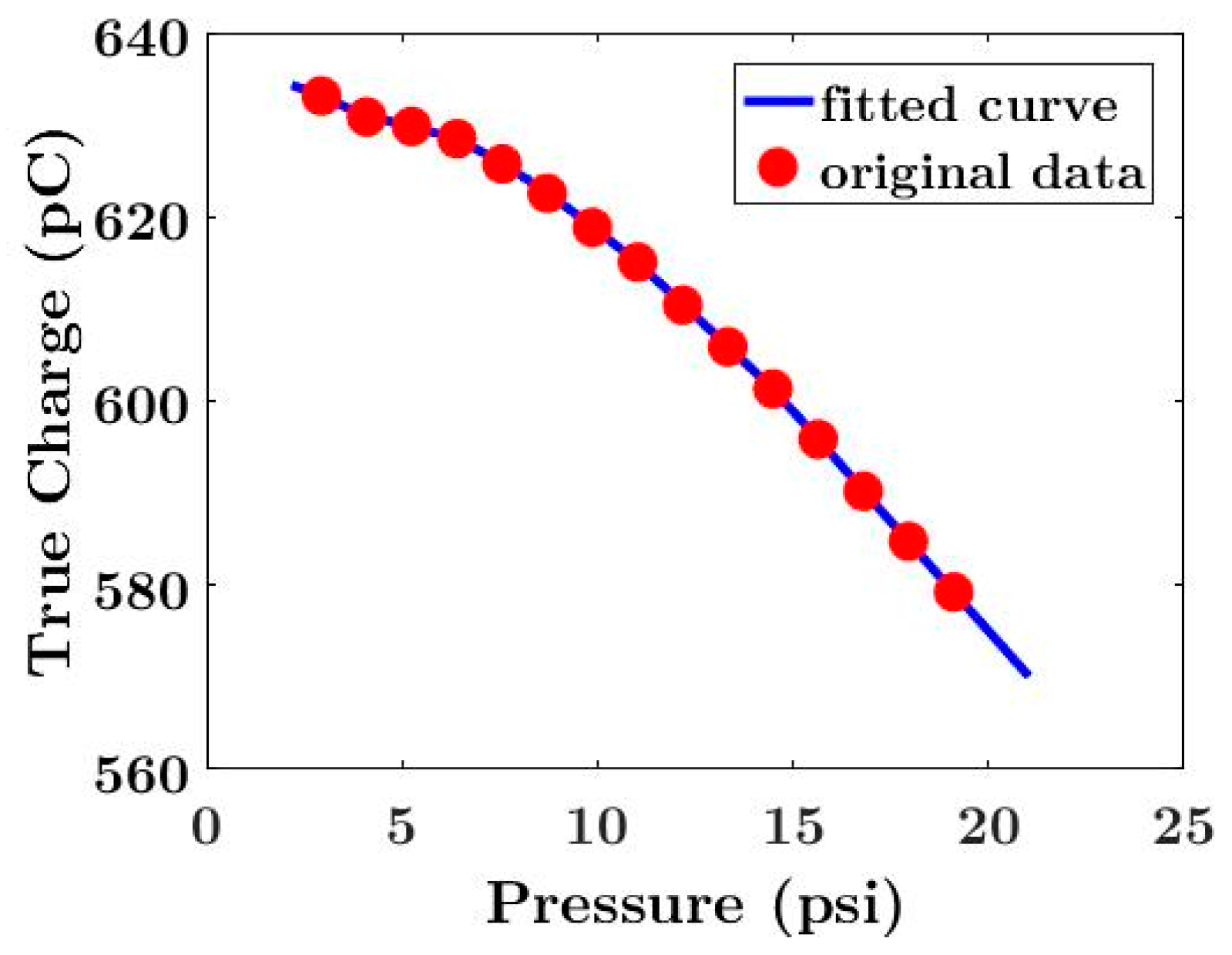
| Parameter | Dielectric Block Height | Dielectric Radius | Cavity Diameter | Electrode Diameter |
|---|---|---|---|---|
| Value | 25 mm | 8 mm | 1.2 mm | 10 mm |
| Parameter | Umax | f | Rise Time | Duty Cycle |
|---|---|---|---|---|
| Value | 18 kV | 10 kHz | 50 ns | 50% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borghei, M.; Ghassemi, M. A Finite Element Analysis Model for Partial Discharges in Silicone Gel under a High Slew Rate, High-Frequency Square Wave Voltage in Low-Pressure Conditions. Energies 2020, 13, 2152. https://doi.org/10.3390/en13092152
Borghei M, Ghassemi M. A Finite Element Analysis Model for Partial Discharges in Silicone Gel under a High Slew Rate, High-Frequency Square Wave Voltage in Low-Pressure Conditions. Energies. 2020; 13(9):2152. https://doi.org/10.3390/en13092152
Chicago/Turabian StyleBorghei, Moein, and Mona Ghassemi. 2020. "A Finite Element Analysis Model for Partial Discharges in Silicone Gel under a High Slew Rate, High-Frequency Square Wave Voltage in Low-Pressure Conditions" Energies 13, no. 9: 2152. https://doi.org/10.3390/en13092152
APA StyleBorghei, M., & Ghassemi, M. (2020). A Finite Element Analysis Model for Partial Discharges in Silicone Gel under a High Slew Rate, High-Frequency Square Wave Voltage in Low-Pressure Conditions. Energies, 13(9), 2152. https://doi.org/10.3390/en13092152







