Three-Dimensional Mathematical Model of the Liquid Film Downflow on a Vertical Surface
Abstract
1. Introduction
2. Material and Methods
- -
- The liquid is incompressible, and the process of its flow is isothermal (ρ = const, and therefore divV = 0);
- -
- The liquid film flow is considered on the vertical surface of the separation channel considering frictional interaction between phases; accordingly, the film does not flow vertically downward, but at some angle to the gravity direction. Therefore, film flow is presented as a two-dimensional case in x- and z-directions. These axes are directed downward and along the wall, respectively. The design scheme is shown in Figure 1;
- -
- liquid flow is stationary , and the film flows without wave formation;
- -
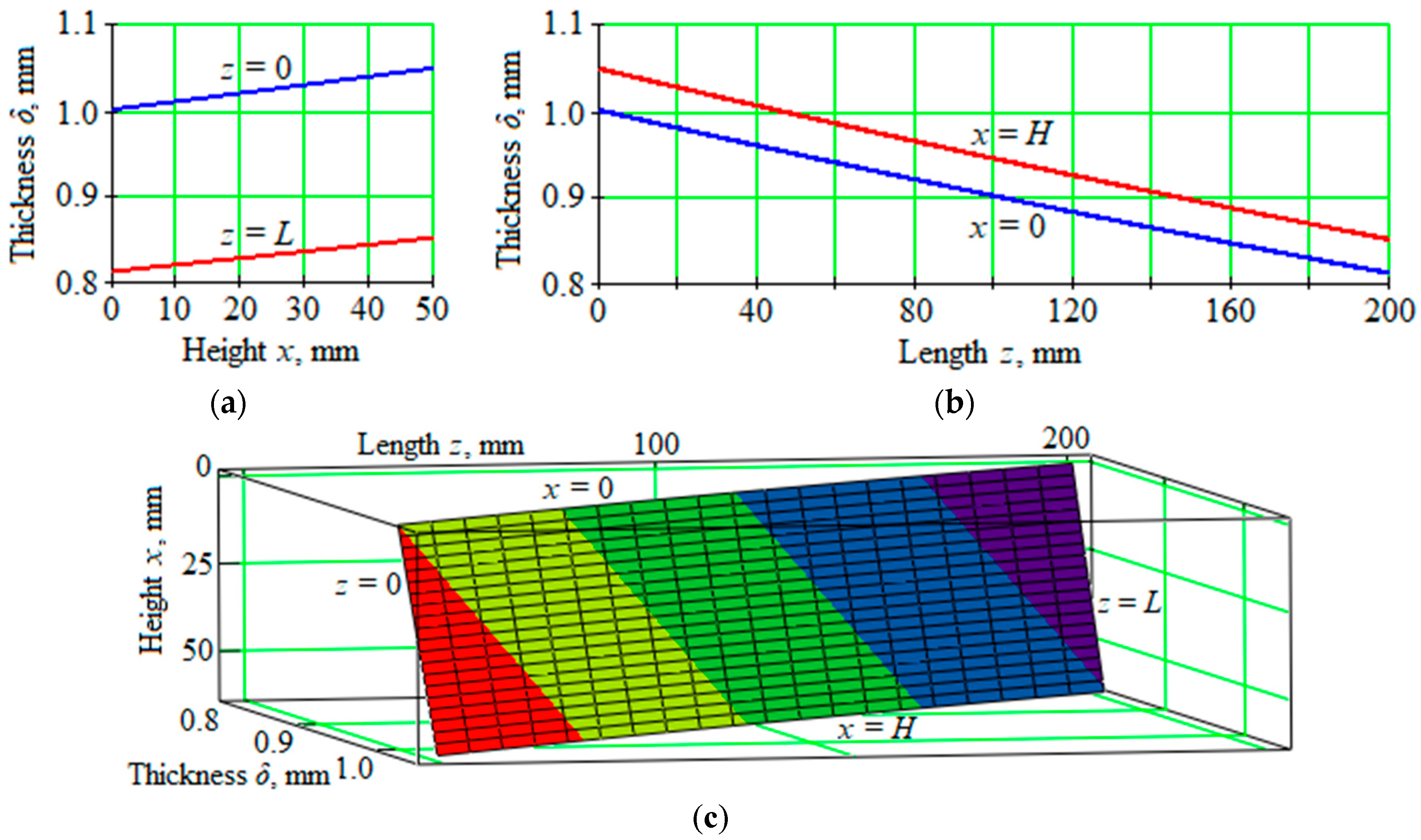
- the liquid film thickness δ varies along the height H and length L of the channel; herewith, it is quite small (δ << L, and δ << H). Due to the abovementioned, the liquid film velocity component in the direction normal to the surface is small in comparison with the components in the main flow directions;
- -
- the pressure change is slow along with the height of the separation channel due to the specific shape of the vane type of the mist extractors (separation devices). It means that .
- -
- comparison of the elements and from the left side of the equation shows that the component can be neglected. The order of magnitude of the following components are the following: film thickness δ () is about 10−3 m, the channel length L() is about 10−1 m. The velocity component directed normal to the wall—10−2 m/s. The above allows for the conclusion that the order of the . Since , the velocity component v can be neglected too.
- -
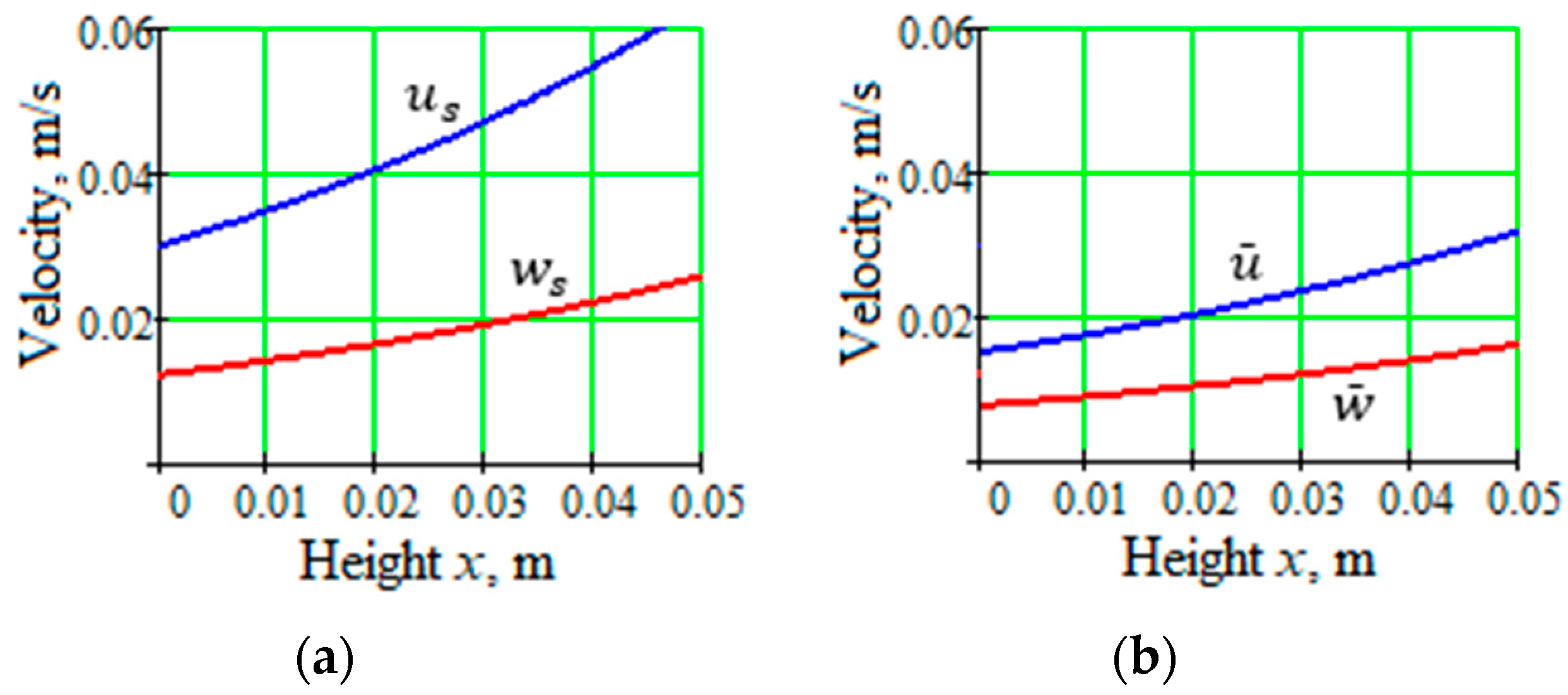
- the components from the right side of the equation are supplemented by replacing the variables with their values on the liquid film surface u → U, v → V, w → W, x → H (the wall height along which the liquid flows), y → δ, z → L. The following values , , are obtained for comparison, has the highest order of them. That is why only stays on the right side of the equation.
- -
- if , the liquid film thickness decreases in the direction of the positive x-coordinate (vertically) and increases in the direction of the positive z-coordinate (horizontally);
- -
- if , the liquid film thickness does not change over the entire surface of its flow δ = δ0;
- -
- if , the fluid film thickness increases in the direction of the positive x coordinate (vertically) and decreases in the direction of the positive z-coordinate (horizontally).
3. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| a, b, c | evaluated functions of coordinates x, z; |
| c0 | initial value of the evaluated function; |
| c3 | evaluated parameter, m−1 |
| cp | liquid volume concentration; |
| B, H, L | width, height, and length of the channel, m; |
| Cr | dimensionless criterion; |
| g | gravitational acceleration, m/s2; |
| k | dimensionless density ratio; |
| p | dynamic pressure of a liquid, Pa; |
| Q0 | flow rate of the air blower, m3/s; |
| Qn | nominal flow rate of the air blower, m3/s; |
| Qu0, Qw0 | initial flow rates, m3/s; |
| Qu1, Qw1, | final flow rates, m3/s; |
| ΔQu, ΔQw | differences of the flow rates, m3/s; |
| R | error function; |
| U, V, W | orders of magnitudes for velocity components, m/s; |
| U(x), W(z) | auxiliary functions; |
| u, v, w | velocity components, m/s; |
| , | average velocity components, m/s; |
| av, av | average velocity components on the interfacial surface, m/s; |
| us, ws | velocity components on the interfacial surface, m/s; |
| V(u, v, w) | total velocity, m/s; |
| the nominal value of the average velocity component, m/s; | |
| x, y, z | coordinates, m; |
| α | inclination angle, rad; |
| δ | film thickness, m; |
| initial film thickness, m; | |
| εw | relative error, %; |
| µ | dynamic viscosity of the liquid, Pa·s; |
| ν | kinematic viscosity, m2/s; |
| ρ | liquid density, kg/m3; |
| ρmix | gas–liquid mixture density, kg/m3; |
| τ | shear stress, N/m2. |
References
- Wellner, N.; Siebeneck, K.; Scholl, S. Continuous dehydration of ionic liquids in a falling film evaporator. Sep. Purif. Technol. 2015, 150, 44–51. [Google Scholar] [CrossRef]
- Plyatsuk, L.D.; Ablieieva, I.Y.; Vaskin, R.A.; Yeskendirov, M.; Hurets, L.L. Mathematical modeling of gas-cleaning equipment with a highly developed phase contact surface. J. Eng. Sci. 2018, 5, F19–F24. [Google Scholar] [CrossRef]
- He, H.; Pan, L.-M.; Huang, H.-J.; Yan, R.-G. Rupture of thin liquid film based premature critical heat flux prediction in microchannel. Int. J. Heat Mass Transf. 2018, 125, 933–942. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, T.; Lv, L.; Chen, Y.; Yang, Y.; Tang, S. Intensification of the liquid side mass transfer in double-side falling film microchannels by micro-mixing structures. Chem. Eng. Sci. 2019, 193, 264–275. [Google Scholar] [CrossRef]
- Nazari, M.; Sani, H.M.; Kayhani, M.H.; Daghighi, Y. Different stages of liquid film growth in a microchannel: Two-phase Lattice Boltzmann study. Braz. J. Chem. Eng. 2018, 35, 977–994. [Google Scholar] [CrossRef]
- Cai, J.; Huai, X.; Liu, B.; Cui, Z. Numerical prediction of thin liquid film near the solid wall for hydraulic cavitating flow in microchannel by a multiphase Lattice Boltzmann model. Int. Heat Mass Transf. 2018, 127, 107–115. [Google Scholar] [CrossRef]
- Gao, H.; Luo, X.; Cui, D.; Liang, Z.; Hu, X.; Hartono, A.; Svendsen, H.F. A study of film thickness and hydrodynamic entrance length in liquid laminar film flow along a vertical tube. Process Syst. Eng. 2018, 64, 2078–2088. [Google Scholar] [CrossRef]
- Yu, Y.Q.; Cheng, X. Three-dimensional simulation on behavior of water film flow with and without shear stress on water-air interface. Int. J. Heat Mass Transf. 2014, 79, 561–572. [Google Scholar] [CrossRef]
- Bo, S.; Ma, X.; Lan, Z.; Chen, H.; Chen, J. Numerical simulation on wave behaviour and flow dynamics of laminar-wavy falling films: Effect of surface tension and viscosity. Can. J. Chem. Eng. 2012, 90, 61–68. [Google Scholar] [CrossRef]
- Min, J.K.; Park, I.S. Numerical study for laminar wavy motions of liquid film flow on vertical wall. Int. J. Heat Mass Transf. 2011, 54, 3256–3266. [Google Scholar] [CrossRef]
- Haeri, S.; Hashemabadi, S.H. Three dimensional CFD simulation and experimental study of power law fluid spreading on inclined plates. Int. Commun. Heat Mass Transf. 2008, 35, 1041–1047. [Google Scholar] [CrossRef]
- Hantsch, A.; Gross, U. Numerical simulation of falling liquid film flow on a vertical plane by two-phase Lattice Boltzmann method. J. Eng. 2012, 2013, 484137. [Google Scholar] [CrossRef][Green Version]
- Klyuev, N.I. Mathematical model of the liquid film flow on the flat surface. Am. J. Aerosp. Eng. 2017, 4, 1–5. [Google Scholar] [CrossRef][Green Version]
- Bender, A.; Stephan, P.; Gambaryan-Roisman, T. Numerical investigation of the evolution and breakup of an evaporating liquid film on a structured wall. Int. J. Heat Fluid Flow 2018, 70, 104–113. [Google Scholar] [CrossRef]
- Lukashov, V.K.; Kostiuchenko, Y.V.; Timofeev, S.V. Hydrodynamics of a liquid film downflow on a flat surface in evaporation conditions into a flow of neutral gas. J. Eng. Sci. 2019, 6, F19–F24. [Google Scholar] [CrossRef]
- Meza, C.E.; Balakotaiah, V. Modeling and experimental studies of large amplitude waves on vertically falling films. Chem. Eng. Sci. 2008, 63, 4704–4734. [Google Scholar] [CrossRef]
- Trifonov, Y.Y. Stability and bifurcations of the wavy film flow down a vertical plate: The results of integral approaches and full-scale computations. Fluid Dyn. Res. 2012, 44, 19. [Google Scholar] [CrossRef]
- Prokudina, L.A.; Salamatov, Y.A. Mathematical modelling of wavy surface of liquid film falling down a vertical plane at moderate Reynolds’ numbers. Bull. South Ural State Univ. Math. Model. Program. Comput. Soft. 2015, 8, 30–39. [Google Scholar] [CrossRef]
- Albijanic, B.; Zhou, Y.; Tadesse, B.; Dyer, L.; Xu, G.; Yang, X. Influence of bubble approach velocity on liquid film drainage between a bubble and a spherical particle. Powder Technol. 2018, 338, 140–144. [Google Scholar] [CrossRef]
- Eichinger, S.; Storch, T.; Grab, T.; Fieback, T.; Gross, U. Investigations of the spreading of falling liquid films in inclined tubes. Int. J. Heat Mass Transf. 2017, 119, 586–600. [Google Scholar] [CrossRef]
- Hasan, N.; Naser, J. Determining the thickness of liquid film in laminar condition on a rotating drum surface using CFD. Chem. Eng. Sci. 2009, 64, 919–924. [Google Scholar] [CrossRef]
- Abdulkadir, M.; Samson, J.N.; Zhao, D.; Okhiria, D.U.; Hernandez-Perez, V. Annular liquid film thickness prediction in a vertical 180° return bend. Exp. Thermal Fluid Sci. 2018, 96, 205–215. [Google Scholar] [CrossRef]
- Bhuiyan, A.A.; Naser, J. Development of 3D transient wall filming mechanism during combustion by coupling Eulerian–Lagrangian approach and particle-wall interaction model. Appl. Thermal Eng. 2017, 112, 911–923. [Google Scholar] [CrossRef]
- Liaposhchenko, O.; Pavlenko, I.; Demianenko, M.; Starynskyi, O.; Pitel, J. The methodology of numerical simulations of separation process in SPR-separator. In Proceedings of the 2nd International Workshop on Computer Modeling and Intelligent Systems, CMIS 2019, Zaporizhzhia, Ukraine, 15–19 April 2019; Volume 2353, pp. 822–832. [Google Scholar]
- Liaposhchenko, O.; Pavlenko, I.; Ivanov, V.; Demianenko, M.; Starynskyi, O.; Kuric, I.; Khukhryanskiy, O. Improvement of parameters for the multi-functional oil-gas separator of “Heater-Treater” type. In Proceedings of the IEEE 6th International Conference on Industrial Engineering and Applications (ICIEA), Tokyo, Japan, 26–29 April 2019; pp. 66–71. [Google Scholar] [CrossRef]
- Liaposchenko, O.; Pavlenko, I.; Nastenko, O. The model of crossed movement and gas–liquid flow interaction with captured liquid film in the inertial-filtering separation channels. Sep. Purif. Technol. 2017, 173, 240–243. [Google Scholar] [CrossRef]
- Pavlenko, I.; Liaposhchenko, O.; Sklabinskyi, V.; Ivanov, V.; Gusak, O. Hydrodynamic features of gas–liquid flow movement in a separation device plane channel with an oscillating wall. Probl. Energ. Reg. 2018, 3, 62–70. [Google Scholar] [CrossRef]
- Sklabinskyi, V.; Liaposhchenko, O.; Pavlenko, I.; Lytvynenko, O.; Demianenko, M. Modelling of liquid’s distribution and migration in the fibrous filter layer in the process of inertial-filtering separation. In Advances in Design, Simulation and Manufacturing; Ivanov, V., Rong, Y., Trojanowska, J., Venus, J., Liaposhchenko, O., Zajac, J., Pavlenko, I., Edl, M., Peraković, D., Eds.; DSMIE 2018; Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2019; pp. 489–497. [Google Scholar] [CrossRef]
- Pylypaka, S.; Nesvidomin, V.; Zaharova, T.; Pavlenko, O.; Klendiy, M. The investigation of particle movement on a helical surface. In Advances in Design, Simulation and Manufacturing II; Ivanov, V., Trojanowska, J., Machado, J., Liaposhchenko, O., Zajac, J., Pavlenko, I., Edl, M., Perakovic, D., Eds.; DSMIE 2019; Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2020; pp. 671–681. [Google Scholar] [CrossRef]
- Pavlenko, I.; Liaposhchenko, A.; Ochowiak, M.; Demyanenko, M. Solving the stationary hydroaeroelasticity problem for dynamic deflection elements of separation devices. Vib. Phys. Syst. 2018, 29, 2018026. [Google Scholar]
- Liaposhchenko, O.; Pavlenko, I.; Monkova, K.; Demianenko, M.; Starynskyi, O. Numerical simulation of aeroelastic interaction between gas–liquid flow and deformable elements in modular separation devices. In Advances in Design, Simulation and Manufacturing II; Ivanov, V., Trojanowska, J., Machado, J., Liaposhchenko, O., Zajac, J., Pavlenko, I., Edl, M., Perakovic, D., Eds.; DSMIE 2019; Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2020; pp. 765–774. [Google Scholar] [CrossRef]
- Goufo, E.F.D.; Mugisha, S. On analysis of fractional Navier-Stokes equations via nonsingular solutions and approximation. Math. Prob. Eng. 2014, 2015, 212760. [Google Scholar] [CrossRef]
- Han, Y.; Yang, S.-Q.; Sivakumar, M.; Qiu, L.-C. Investigation of velocity distribution in open channel flows based on conditional average of turbulent structures. Math. Prob. Eng. 2017, 2017, 1458591. [Google Scholar] [CrossRef]
- Facci, A.L.; Ubertini, S. Numerical assessment of similitude parameters and dimensional analysis for water entry problems. Math. Prob. Eng. 2015, 2015, 324961. [Google Scholar] [CrossRef]
- Chernyshenko, S.I.; Goulart, P.; Huang, D.; Papachristodoulou, A. Polynomial sum of squares in fluid dynamics: A review with a look ahead. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372, 20130350. [Google Scholar] [CrossRef]
- Raees, A.; Xu, H. Explicit solutions of a gravity-induced film flow along a convectively heated vertical wall. Sci. World J. 2013, 2013, 475939. [Google Scholar] [CrossRef] [PubMed]
- Gokhale, S.J.; Plawsky, J.L.; Wayner, P.C. Inferred pressure gradient and fluid flow in a condensing sessile droplet based on the measured thickness profile. Phys. Fluids 2004, 16, 1942–1955. [Google Scholar] [CrossRef]
- Lioumbas, J.S.; Paras, S.V.; Karabelas, A.J. Co-current stratified gas–liquid downflow—Influence of the liquid flow field on interfacial structure. Int. J. Multiph. Flow 2005, 31, 869–896. [Google Scholar] [CrossRef]
- Caughey, D.A.; Hafez, M.M. Frontiers in Computational Fluid Dynamics; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2006. [Google Scholar]
- Munira, S.; Heikalb, M.R.; Azizb, A.R.A.; Muthuvalua, M.S.; Jaafarb, A.; Israr, M. Dynamical analysis of turbulent liquid phase in two-phase pipe flow. ScienceAsia 2014, 40, 63–68. [Google Scholar] [CrossRef]
- Pylypaka, S.F.; Klendii, M.B.; Nesvidomin, V.M.; Trokhaniak, V.I. Particle motion over the edge of an inclined plane that performs axial movement in a vertical limiting cylinder. Acta Polytech. 2019, 59, 67–76. [Google Scholar] [CrossRef]
- Alfonsi, G. Reynolds-averaged Navier–Stokes equations for turbulence modeling. Appl. Mech. Rev. 2009, 62, 040802. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pavlenko, I.; Liaposhchenko, O.; Ochowiak, M.; Olszewski, R.; Demianenko, M.; Starynskyi, O.; Ivanov, V.; Yanovych, V.; Włodarczak, S.; Doligalski, M. Three-Dimensional Mathematical Model of the Liquid Film Downflow on a Vertical Surface. Energies 2020, 13, 1938. https://doi.org/10.3390/en13081938
Pavlenko I, Liaposhchenko O, Ochowiak M, Olszewski R, Demianenko M, Starynskyi O, Ivanov V, Yanovych V, Włodarczak S, Doligalski M. Three-Dimensional Mathematical Model of the Liquid Film Downflow on a Vertical Surface. Energies. 2020; 13(8):1938. https://doi.org/10.3390/en13081938
Chicago/Turabian StylePavlenko, Ivan, Oleksandr Liaposhchenko, Marek Ochowiak, Radosław Olszewski, Maryna Demianenko, Oleksandr Starynskyi, Vitalii Ivanov, Vitalii Yanovych, Sylwia Włodarczak, and Michał Doligalski. 2020. "Three-Dimensional Mathematical Model of the Liquid Film Downflow on a Vertical Surface" Energies 13, no. 8: 1938. https://doi.org/10.3390/en13081938
APA StylePavlenko, I., Liaposhchenko, O., Ochowiak, M., Olszewski, R., Demianenko, M., Starynskyi, O., Ivanov, V., Yanovych, V., Włodarczak, S., & Doligalski, M. (2020). Three-Dimensional Mathematical Model of the Liquid Film Downflow on a Vertical Surface. Energies, 13(8), 1938. https://doi.org/10.3390/en13081938












