Novel Control Approach for a Hybrid Grid-Forming HVDC Offshore Transmission System
Abstract
1. Introduction
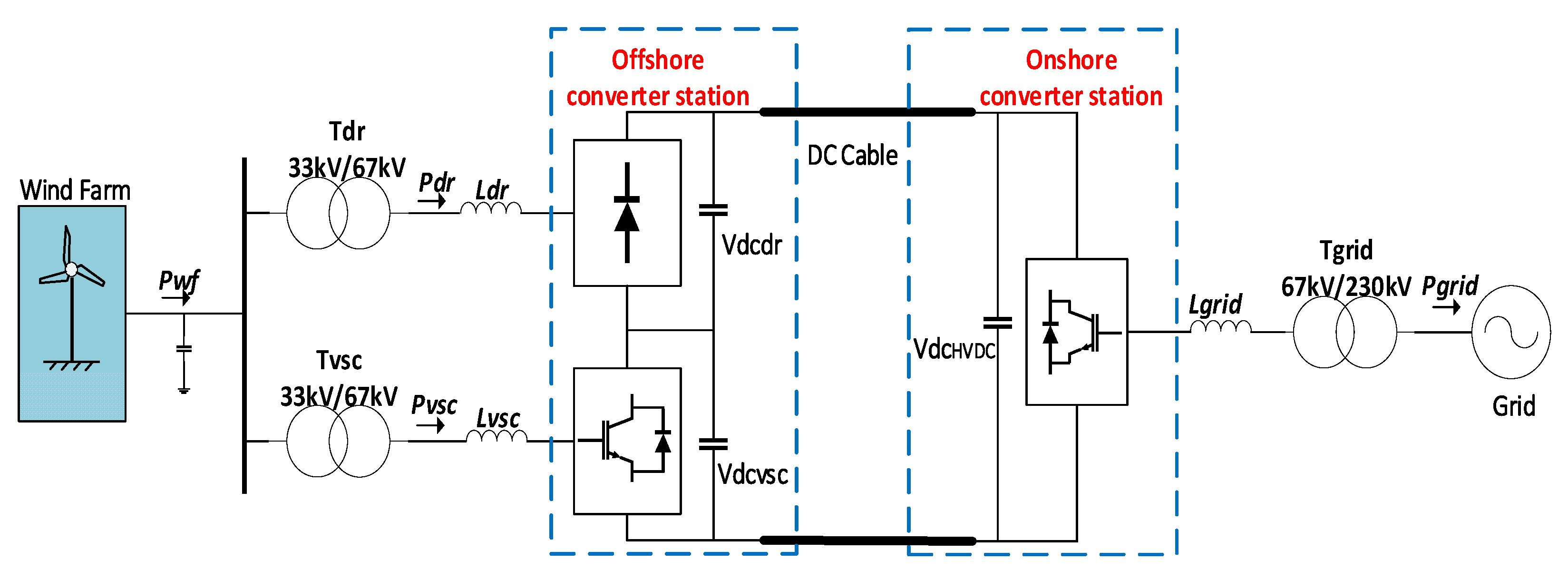
2. Proposed Offshore Hybrid HVDC Converter System
3. Control of the Hybrid HVDC Converter System
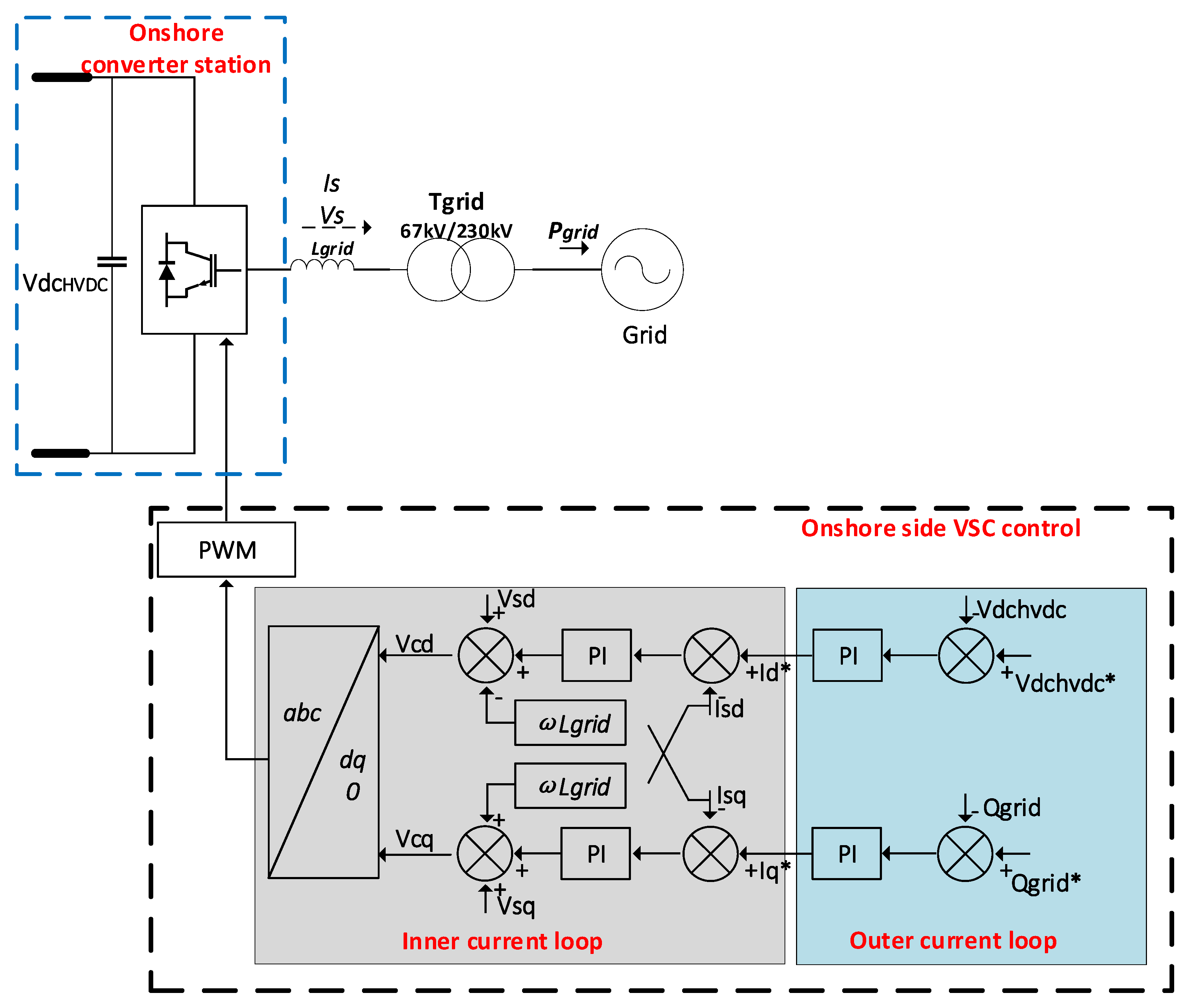
3.1. Control of the Onshore Converter
3.1.1. Inner Current Control
3.1.2. Outer Control Loop
- Active power control mode;
- DC voltage control mode;
- Reactive power control mode;
- AC voltage control mode.
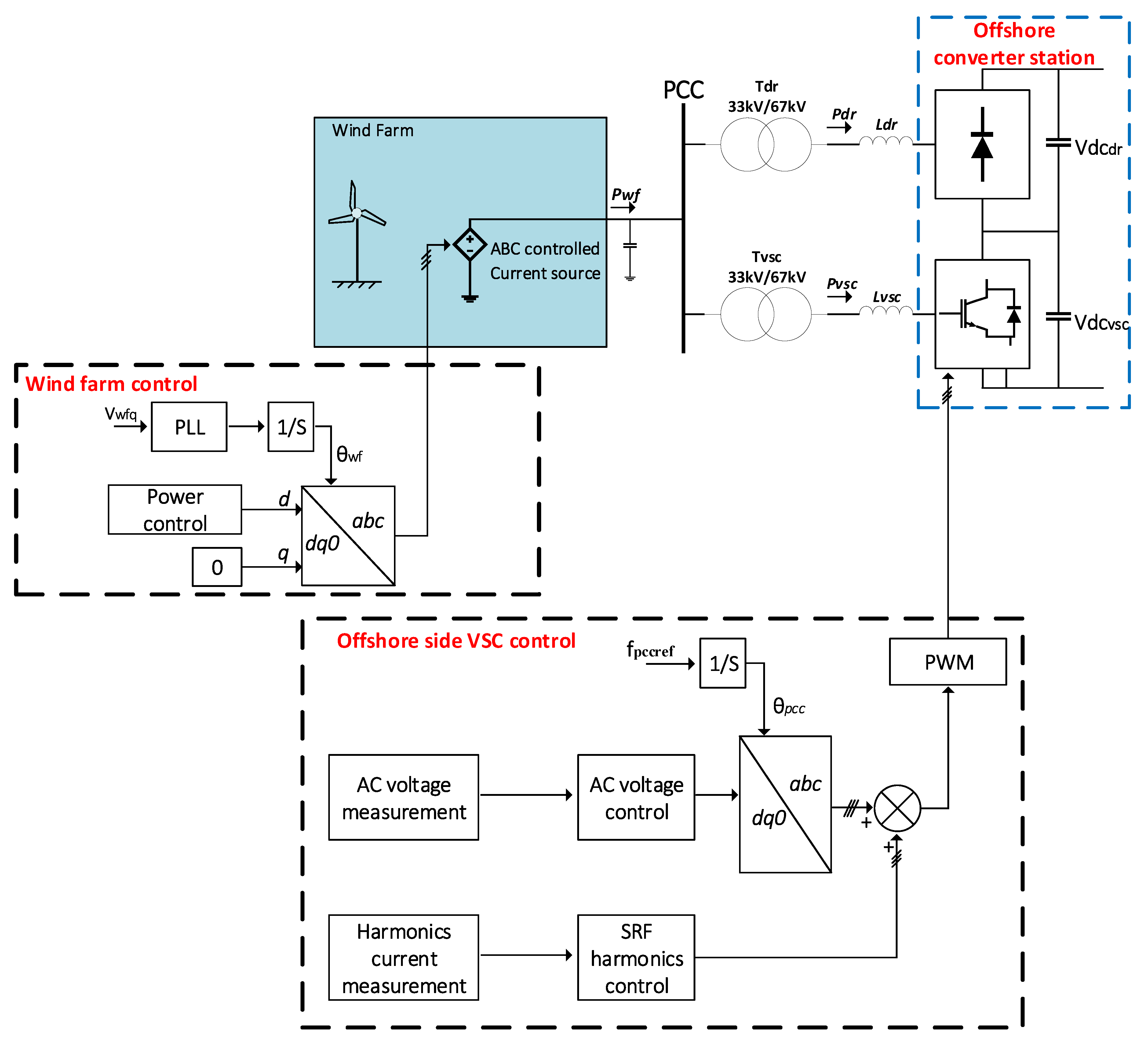
3.2. Offshore Converter Control
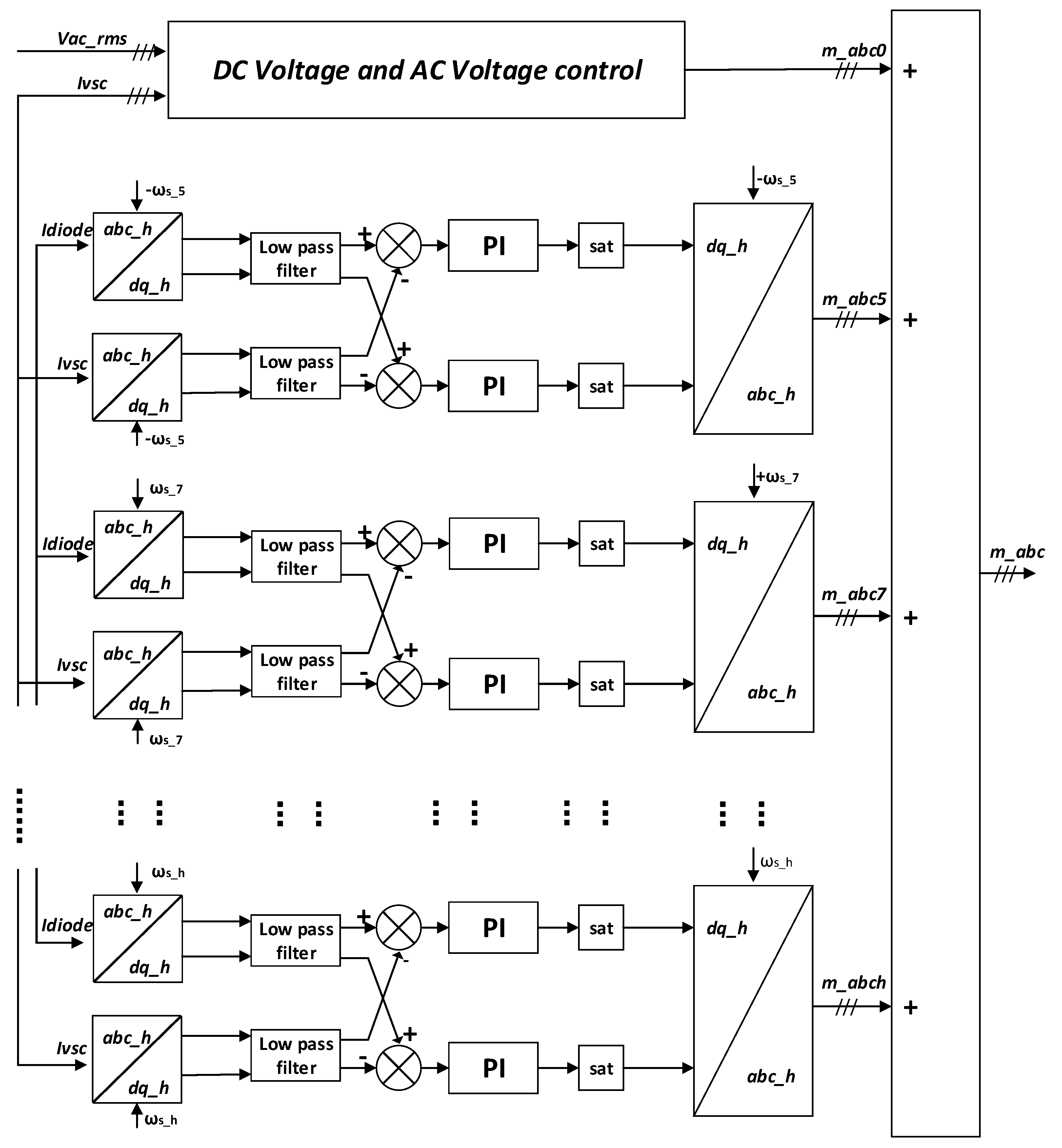
3.3. Harmonic Mitigation Using SRF-Based Controller
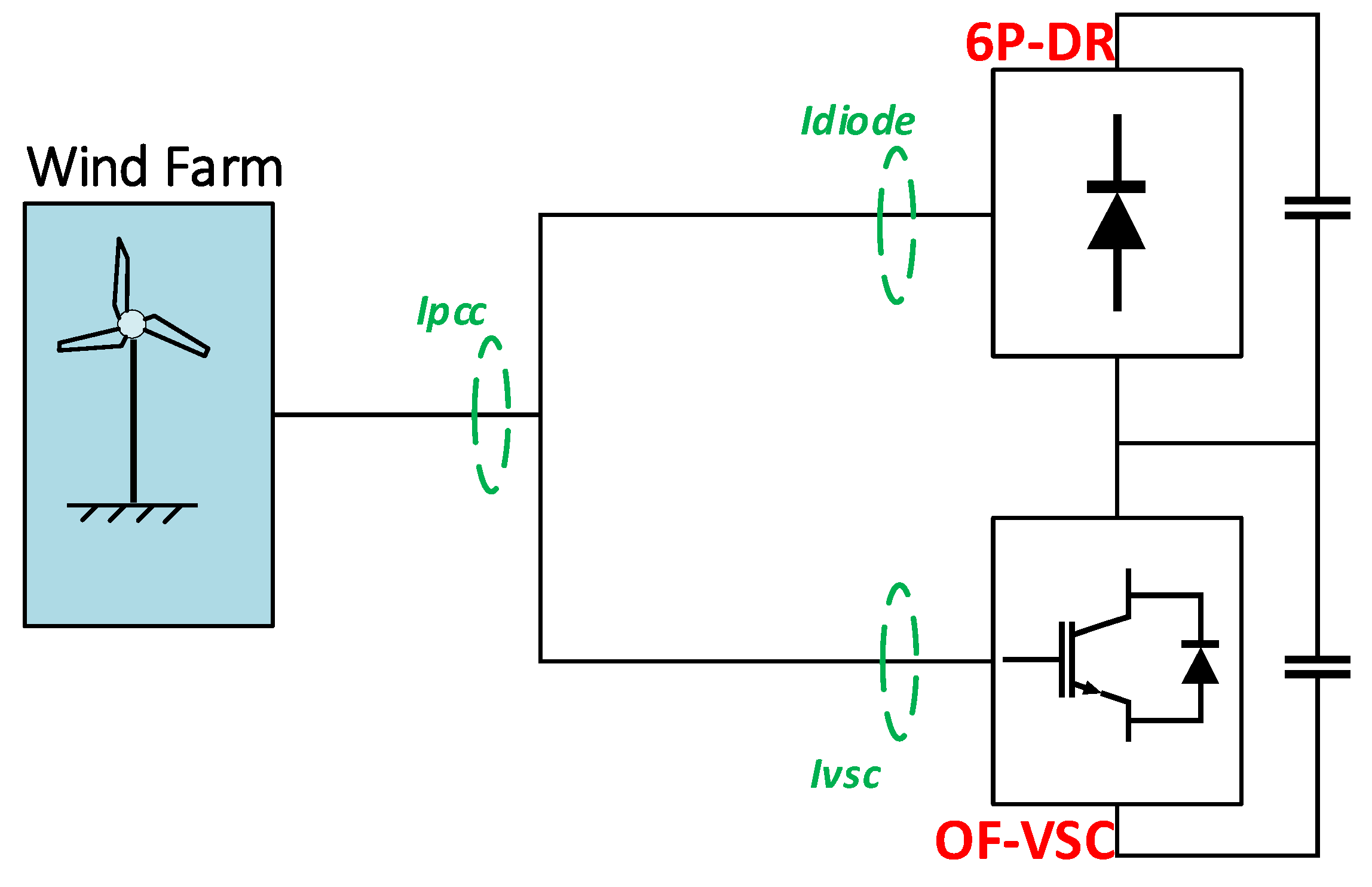
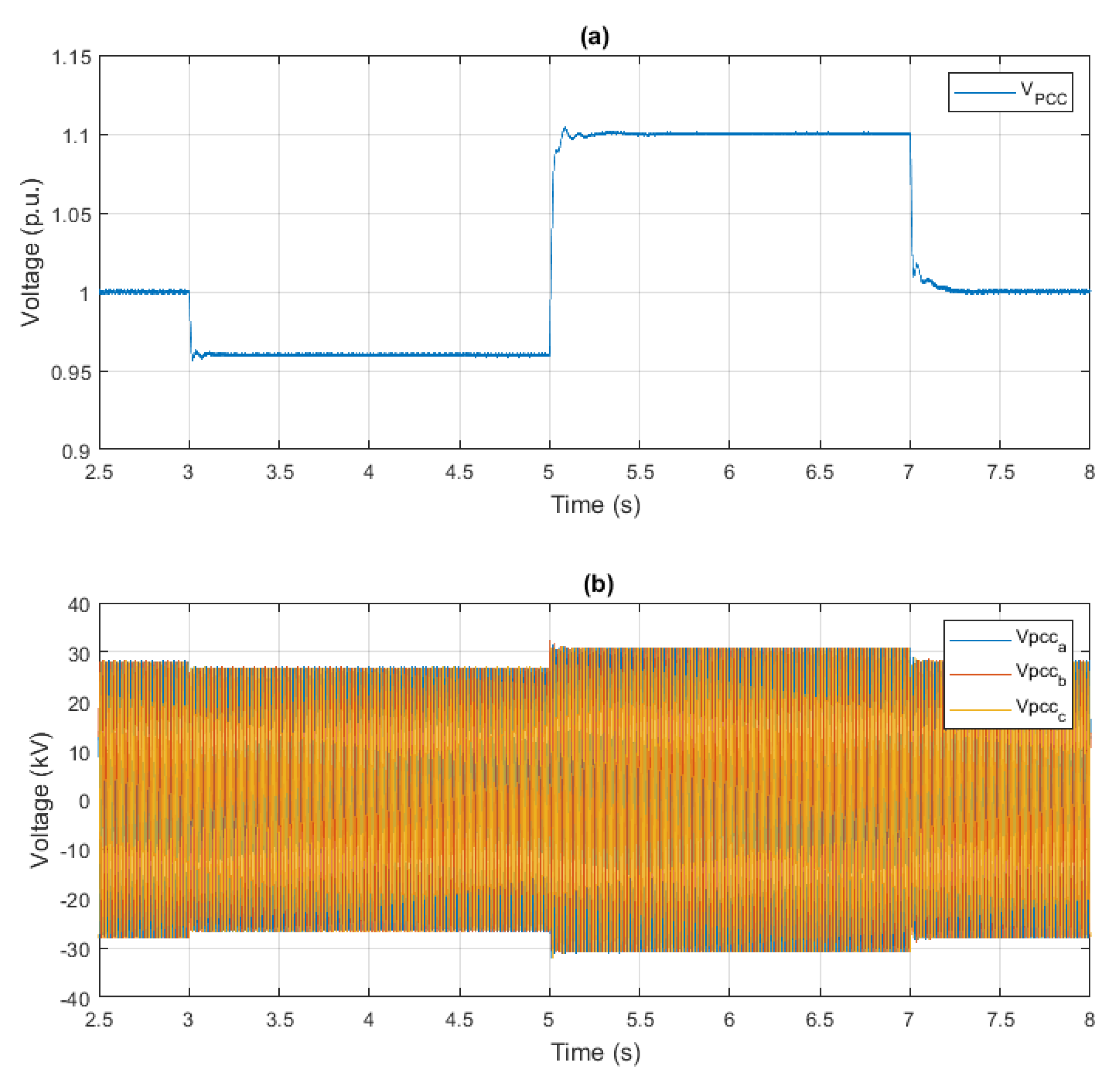
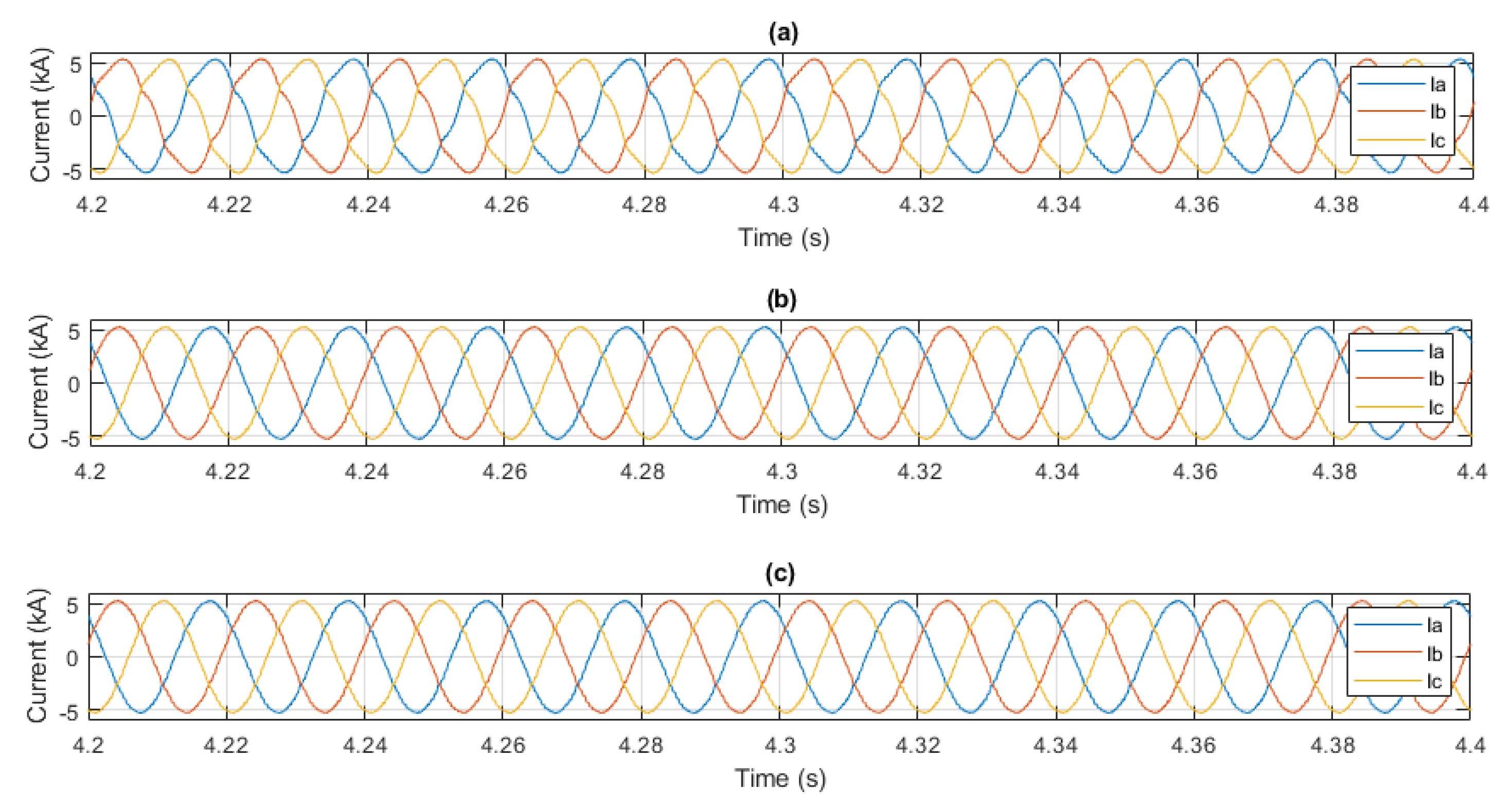
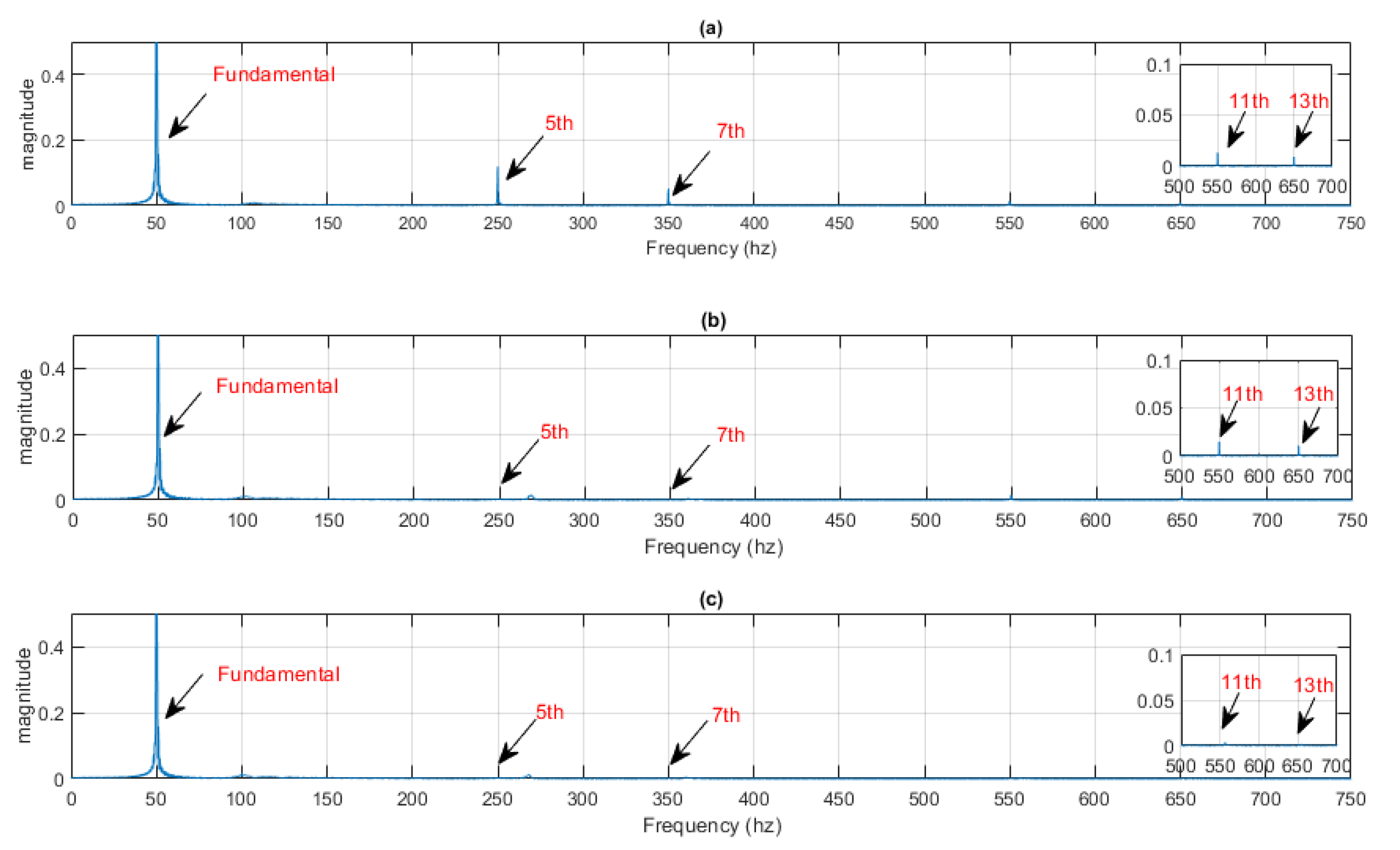
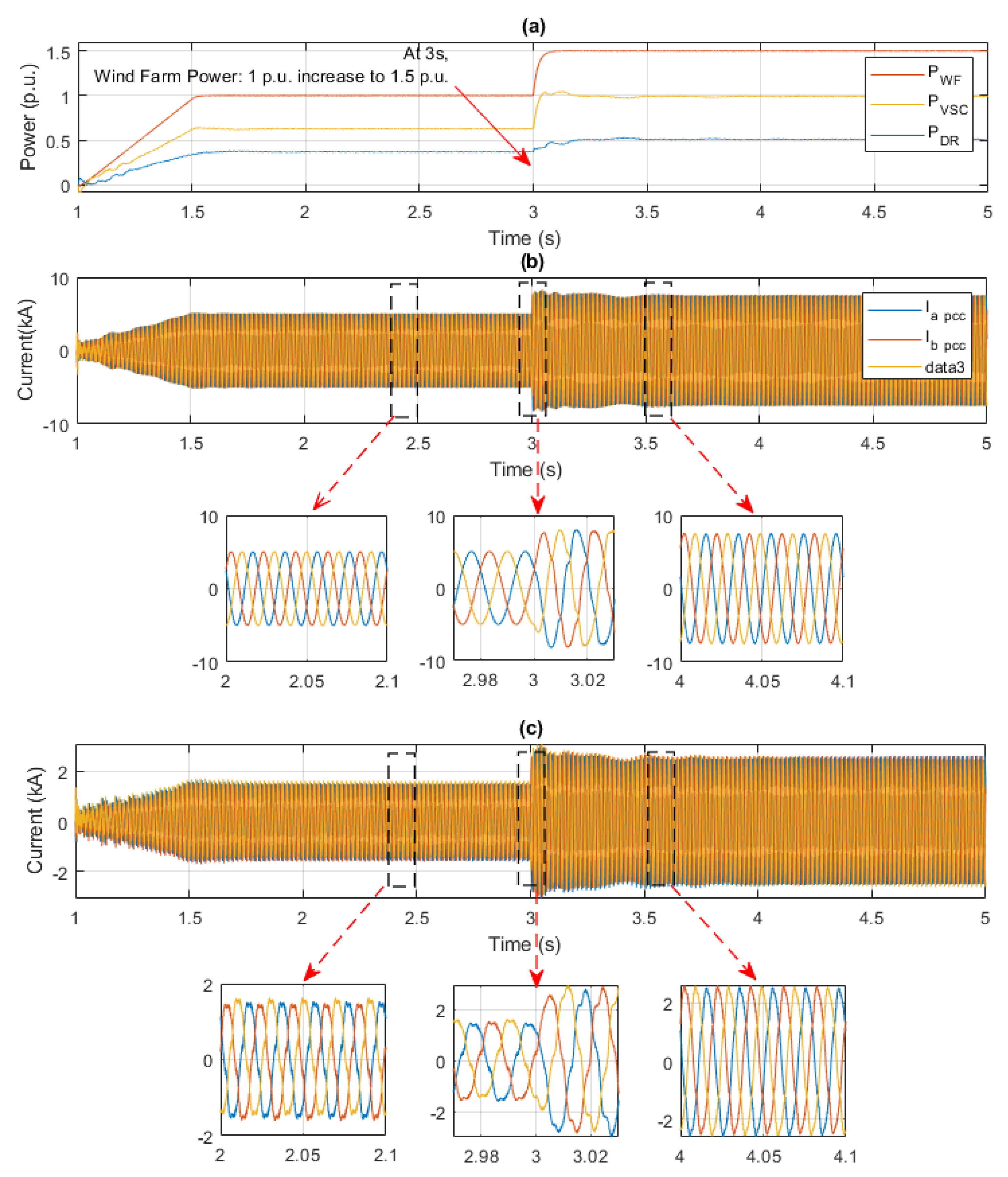
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kalair, A.; Abas, N.; Khan, N. Comparative study of HVAC and HVDC transmission systems. Renew. Sustain. Energy Rev. 2016, 59, 1653–1675. [Google Scholar] [CrossRef]
- Power, B. Offshore Wind Energy Generation: Control, Protection, and Integration to Electrical; John Wiley & Sons: Hoboken, NJ, USA, 2014; pp. 138–140. [Google Scholar]
- Korompili, A.; Wu, Q.; Zhao, H. Review of VSC HVDC connection for offshore wind power integration. Renew. Sustain. Energy Rev. 2016, 59, 1405–1414. [Google Scholar] [CrossRef]
- Blasco-Gimenez, R.; Añí-Villalba, S.; Rodríguez-D’Derlée, J.; Bernal-Perez, S.; Morant, F. Diode-based HVdc link for the connection of large offshore wind farms. IEEE Trans. Energy Convers. 2011, 26, 615–626. [Google Scholar] [CrossRef]
- Bernal-Perez, S.; Ano-Villalba, S.; Blasco-Gimenez, R.; Rodriguez-D’Derlee, J. Efficiency and fault ride-through performance of a diode-rectifier-and VSC-inverter-based HVDC link for offshore wind farms. IEEE Trans. Ind. Electron. 2013, 60, 2401–2409. [Google Scholar] [CrossRef]
- Yu, L.; Li, R.; Xu, L. Distributed PLL-based Control of Offshore Wind Turbine Connected with Diode-Rectifier based HVDC Systems. IEEE Trans. Power Deliv. 2017, 33, 1328–1336. [Google Scholar] [CrossRef]
- Yu, L.; Li, R.; Xu, L. Hierarchical control of offshore wind farm connected by parallel diode-rectifier-based HVDC and HVAC links. IET Renew. Power Gener. 2019, 13, 1493–1502. [Google Scholar] [CrossRef]
- Yu, L.; Li, R.; Xu, L. Parallel operation of diode-rectifier based HVDC link and HVAC link for offshore wind power transmission. J. Eng. 2019, 2019, 4713–4717. [Google Scholar] [CrossRef]
- Seman, S.; Trinh, N.T.; Zurowski, R.; Kreplin, S. Modelling of the Diode-Rectifier Based HVDC Transmission Solution for Large Offshore Wind Power Plants Grid Access. In Proceedings of the International Workshop on Large-Scale Integration of Wind Power into Power Systems, Vienna, Austria, 15–17 November 2016. [Google Scholar]
- Ramachandran, R.; Poullain, S.; Benchaib, A.; Bacha, S.; Francois, B.; de Lille, E.C. AC Grid Forming by Coordinated Control of Offshore Wind Farm connected to Diode Rectifier based HVDC Link–Review and Assessment of Solutions Acknowledgments Keywords. In Proceedings of the 2018 20th European Conference on Power Electronics and Applications (EPE’18 ECCE Europe), Riga, Latvia, 17–21 September 2018; pp. 1–10. [Google Scholar]
- Nguyen, T.H.; Lee, D.C.; Kim, C.K. A series-connected topology of a diode rectifier and a voltage-source converter for an HVDC transmission system. IEEE Trans. Power Electron. 2014, 29, 1579–1584. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Le, Q.A.; Lee, D.C. A Novel HVDC-Link based on Hybrid Voltage-Source Converters. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 3338–3343. [Google Scholar]
- Nguyen, T.H.; Lee, D.C.; Kim, C.K. A Cost-Effective Converter System for HVDC Links Lntegrated with Offshore Wind Farms. In Proceedings of the IECON 2013-39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 7978–7983. [Google Scholar]
- Li, S.; Haskew, T.A.; Swatloski, R.P.; Gathings, W. Optimal and direct-current vector control of direct-driven PMSG wind turbines. IEEE Trans. Power Electron. 2012, 27, 2335–2337. [Google Scholar] [CrossRef]
- Monroy-Morales, J.L.; Campos-Gaona, D.; Hernández-Ángeles, M.; Peña-Alzola, R.; Guardado-Zavala, J.L. An active power filter based on a three-level inverter and 3D-SVPWM for selective harmonic and reactive compensation. Energies 2017, 10, 297. [Google Scholar] [CrossRef]
- Wu, G. Analysis and design of vector control for VSC-HVDC connected to weak grids. CSEE J. Power Energy Syst. 2017, 3, 115–124. [Google Scholar] [CrossRef]
- Liserre, M.; Teodorescu, R.; Blaabjerg, F. Multiple harmonics control for three-phase grid converter systems with the use of PI-RES current controller in a rotating frame. IEEE Trans. Power Electron. 2006, 21, 836–841. [Google Scholar] [CrossRef]
- Asiminoaei, L.; Blaabjerg, F.; Hansen, S. Evaluation of Harmonic Detection Methods for Active Power FilterApplications. In Proceedings of the Twentieth Annual IEEE Applied Power Electronics Conference and Exposition, Austin, TX, USA, 6–10 March 2005; Volume 1, pp. 635–641. [Google Scholar]
- Herman, L.; Papic, I.; Blazic, B. A proportional-resonant current controller for selective harmonic compensation in a hybrid active power filter. IEEE Trans. Power Deliv. 2014, 29, 2055–2065. [Google Scholar] [CrossRef]
- Campos-Gaona, D.; Pena-Alzola, R.; Monroy-Morales, J.L.; Ordonez, M.; Anaya-Lara, O.; Leithead, W.E. Fast selective harmonic mitigation in multifunctional inverters using internal model controllers and synchronous reference frames. IEEE Trans. Ind. Electron. 2017, 64, 6338–6349. [Google Scholar] [CrossRef]
- Chen, G.; Zhu, M.; Cai, X. Medium-voltage level dynamic voltage restorer compensation strategy by positive and negative sequence extractions in multiple reference frames. IET Power Electron. 2014, 7, 1747–1758. [Google Scholar] [CrossRef]
- Morales, J.L.M.; Ángeles, M.H.; Campos-Gaona, D.; Peña-Alzola, R. Control Design of a Neutral Point Clamped Converter based Active Power Filter for the Selective Harmonic Compensation. In Proceedings of the 2016 IEEE PES Transmission & Distribution Conference and Exposition-Latin America (PES T&D-LA), Morelia, Mexico, 20–24 September 2016. [Google Scholar]

| Components | Parameters | Value |
|---|---|---|
| Wind Farm | Power rating | 200 MW |
| Offshore 6-PD | Input inductance (Ldr) | 46.5 mH |
| Offshore 6-PD | DC filter capacitance | 200 µF |
| Offshore 6-PD | Transformer Tdr (Y/D) | 33/67 kV; 0.1 p.u. |
| Offshore 2L-VSC | Input inductance (Lvsc) | 46.5 mH |
| Offshore 2L-VSC | DC filter capacitance | 200 µF |
| Offshore 2L-VSC | Transformer Tvsc (Y/D) | 33/67 kV; 0.1 p.u. |
| Onshore 2L-VSC | Input inductance (Lgrid) | 46.5 mH |
| Onshore 2L-VSC | DC filter capacitance | 400 µF |
| Onshore 2L-VSC | Transformer Tgrid (D/Y) | 67/230 kV; 0.1 p.u. |
| Time | Events |
|---|---|
| 0 s | Onshore station enabled, provides DC link voltage to offshore station |
| 1 s–1.5 s | Offshore station and WF enabled, establishes AC voltage and frequency |
| Harmonics Compensation | %Total Harmonic Distortion (THD) |
|---|---|
| None | 8.43% |
| 5th and 7th | 1.71% |
| 5th, 7th, 11th, and 13th | 0.06% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, S.; Campos-Gaona, D.; A. Lacerda, V.; Torres-Olguin, R.E.; Anaya-Lara, O. Novel Control Approach for a Hybrid Grid-Forming HVDC Offshore Transmission System. Energies 2020, 13, 1681. https://doi.org/10.3390/en13071681
Tian S, Campos-Gaona D, A. Lacerda V, Torres-Olguin RE, Anaya-Lara O. Novel Control Approach for a Hybrid Grid-Forming HVDC Offshore Transmission System. Energies. 2020; 13(7):1681. https://doi.org/10.3390/en13071681
Chicago/Turabian StyleTian, Shangen, David Campos-Gaona, Vinícius A. Lacerda, Raymundo E. Torres-Olguin, and Olimpo Anaya-Lara. 2020. "Novel Control Approach for a Hybrid Grid-Forming HVDC Offshore Transmission System" Energies 13, no. 7: 1681. https://doi.org/10.3390/en13071681
APA StyleTian, S., Campos-Gaona, D., A. Lacerda, V., Torres-Olguin, R. E., & Anaya-Lara, O. (2020). Novel Control Approach for a Hybrid Grid-Forming HVDC Offshore Transmission System. Energies, 13(7), 1681. https://doi.org/10.3390/en13071681







