Numerical and Experimental Study of an Asymmetric CPC-PVT Solar Collector
Abstract
1. Introduction
2. Materials and Methods
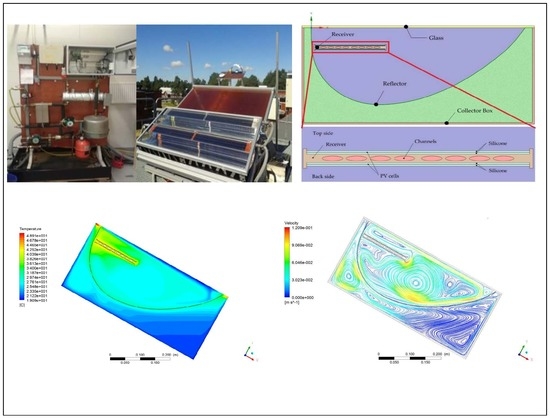
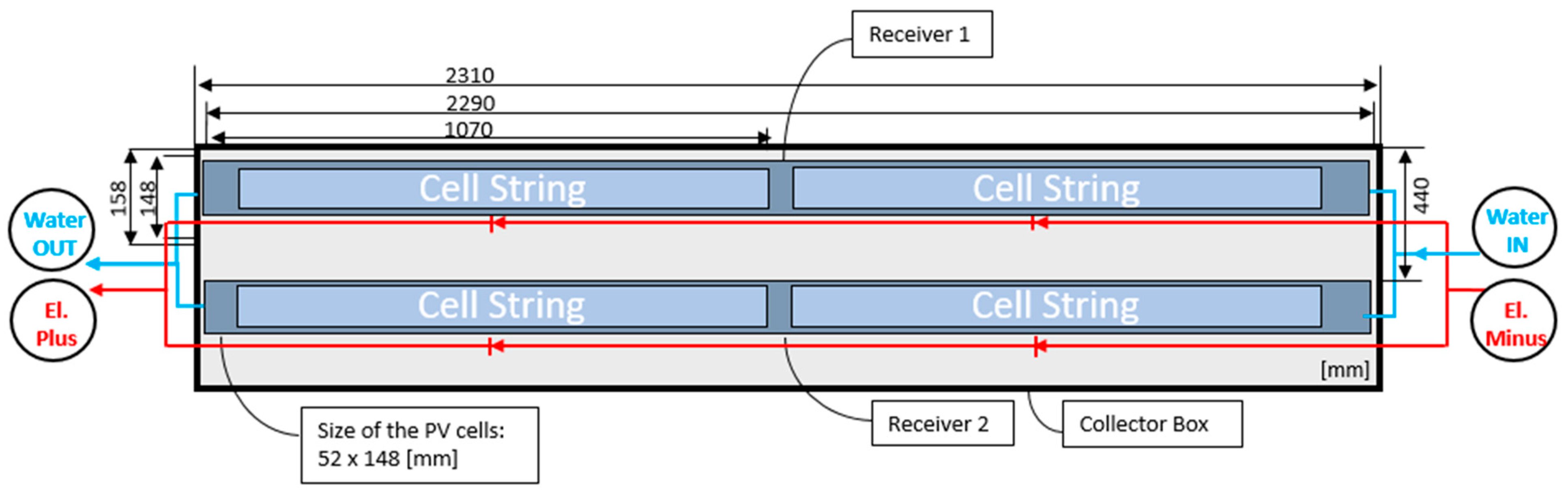
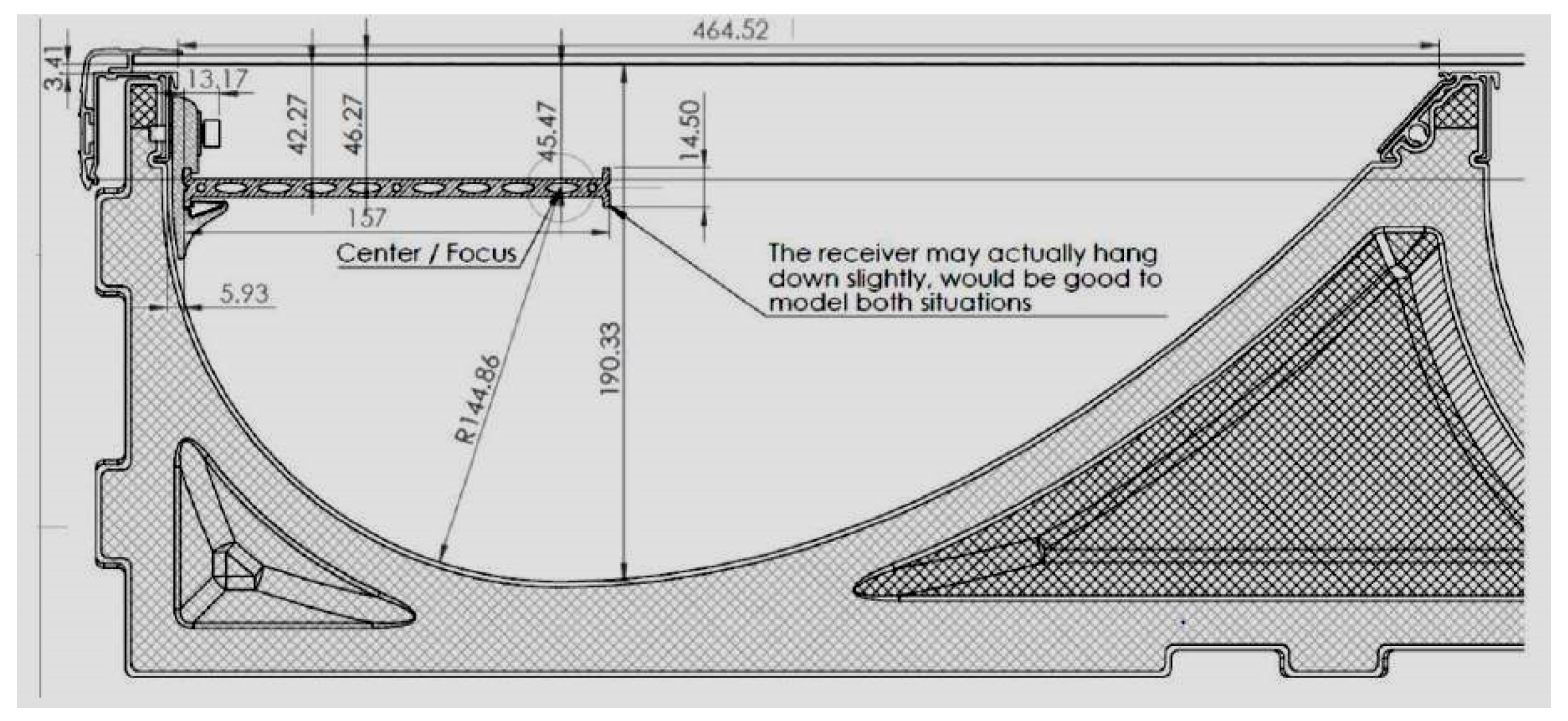
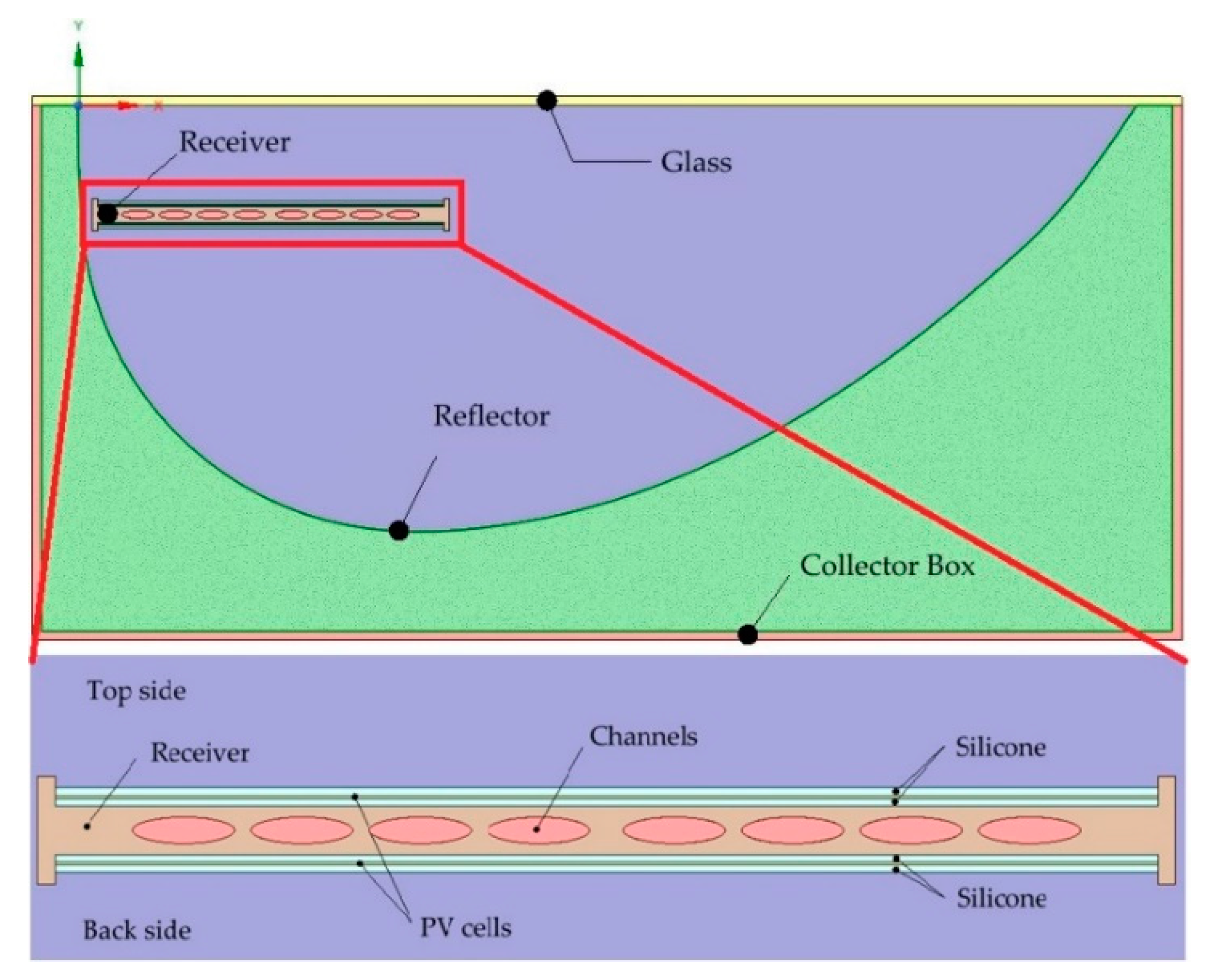
2.1. Description of the Collector and the Properties of its Components
2.2. CFD Model of the Collector
2.2.1. Simulation Procedure
2.2.2. Geometry and Mesh of the Collector
2.2.3. Solution Methods
2.2.4. Material Parameter
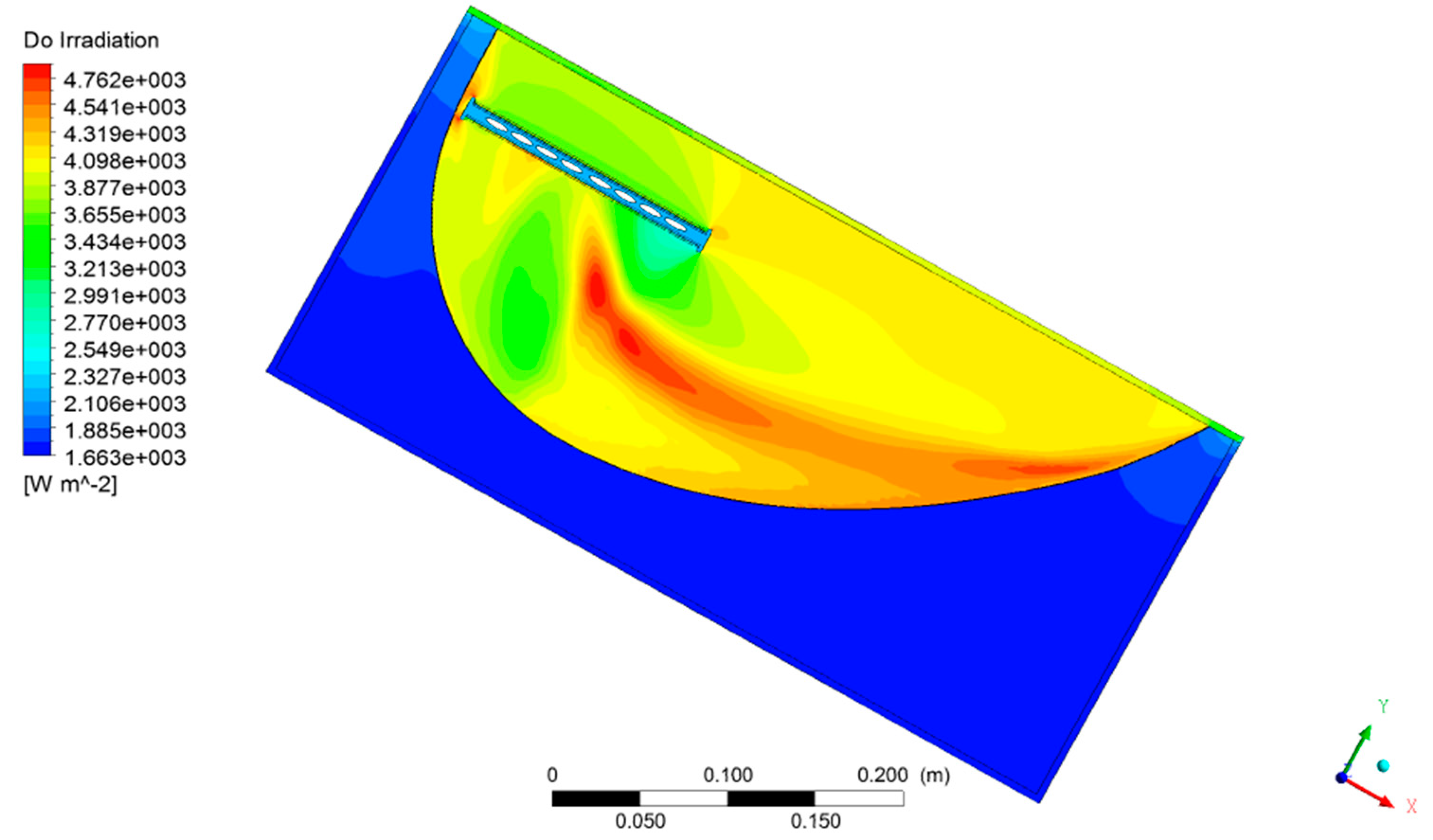
2.2.5. Radiation Model
2.2.6. Boundary Conditions
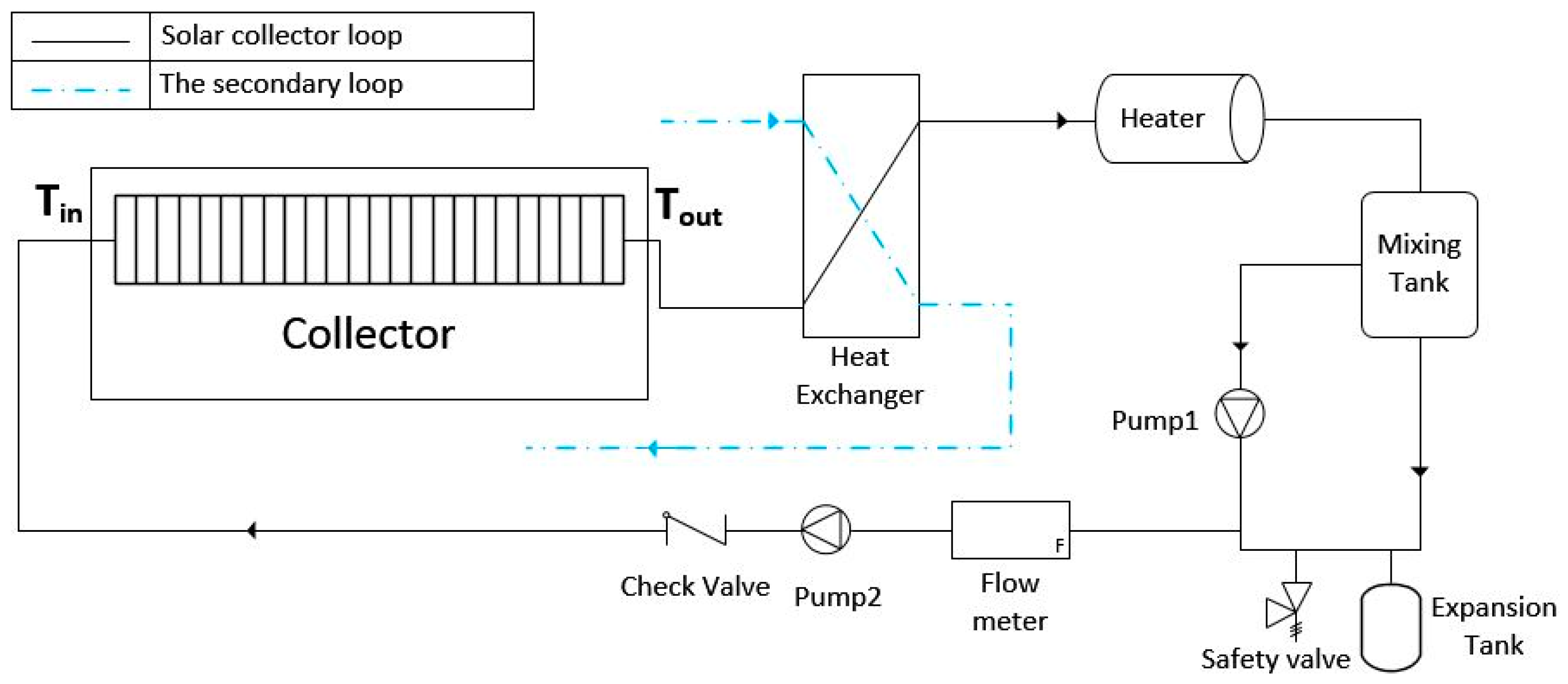
2.3. Experimental Test Method and Equipment Description
- KippZonen CMP3 and CMP6 pyrometers were used to measure solar direct and diffuse radiation.
- PT100 thermal resistances were used to measure the inlet and outlet fluid temperature and ambient temperature.
- K-type thermocouples were used for measuring the PV cells’ temperature.
- 2 Omega FMG80 flowmeters were used to measure the flow rate in each trough.
- A PicoLog USB TC08 datalogger was used to collect the data from the K-type thermocouples.
- A datalogger CR1000 from Campbell Scientific was used to visualize/store the parameters obtained by the PT100 ambient and water flow temperature sensors, the CMP3 and CMP6, and flowmeters.
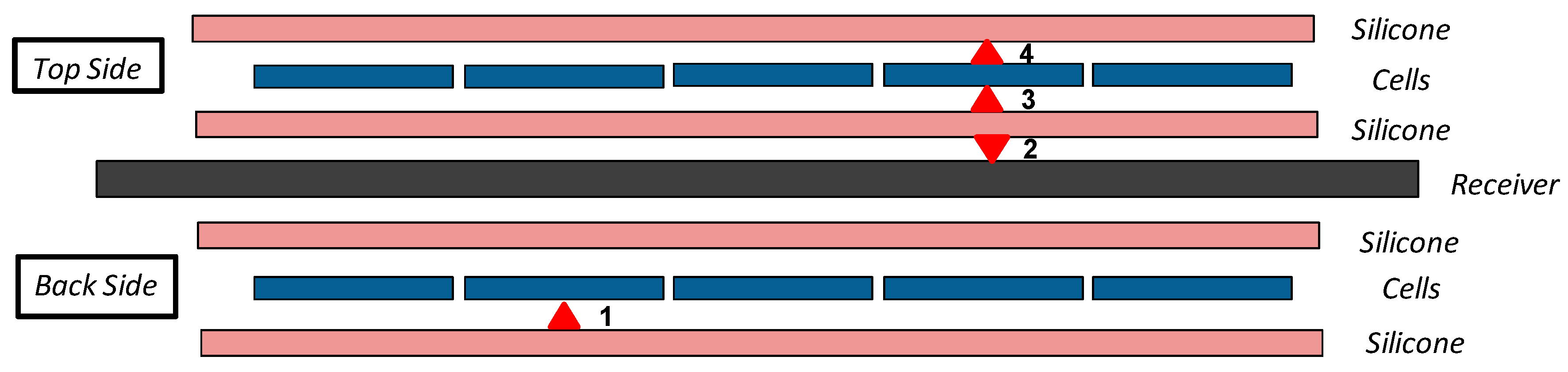
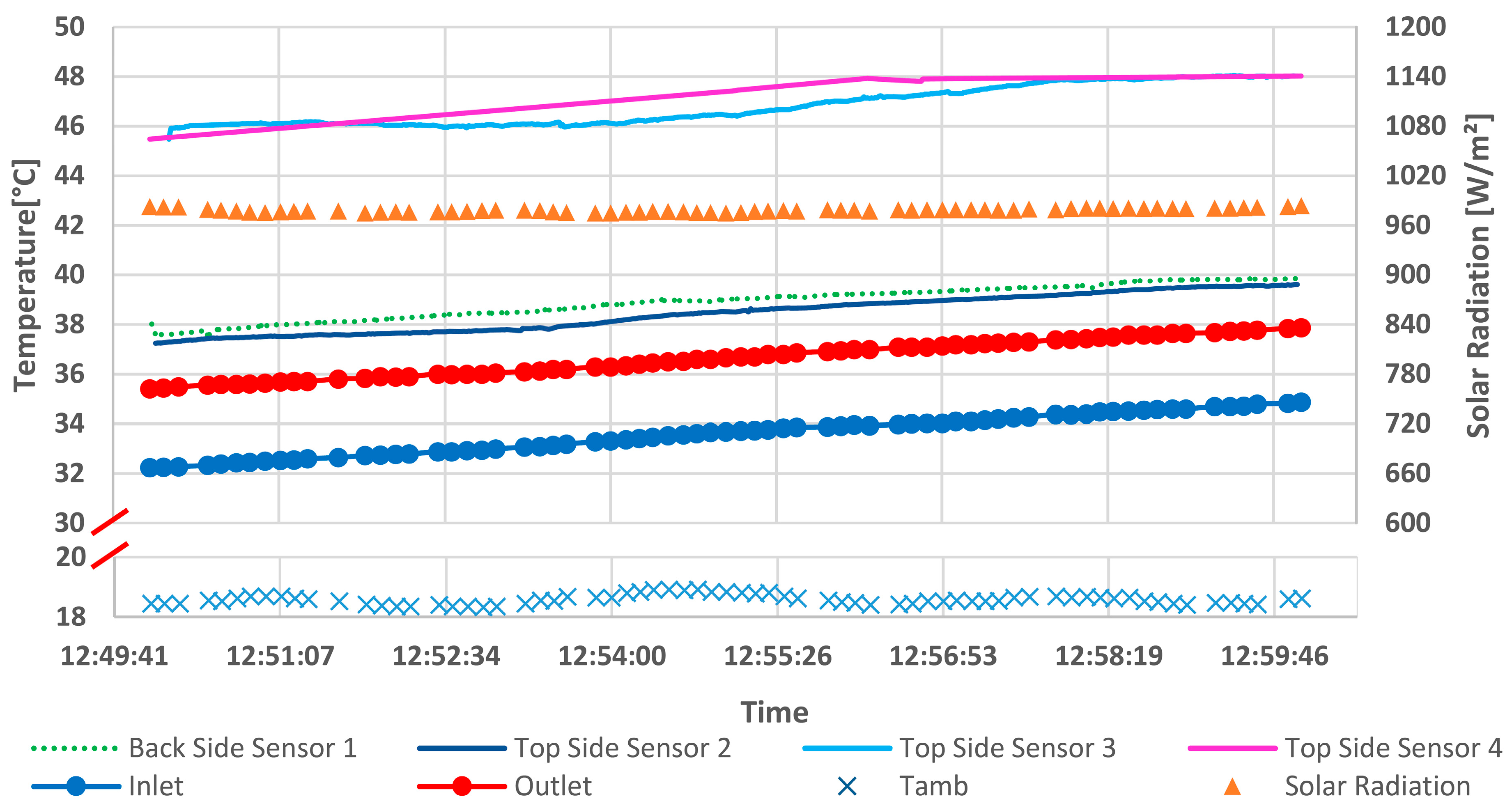
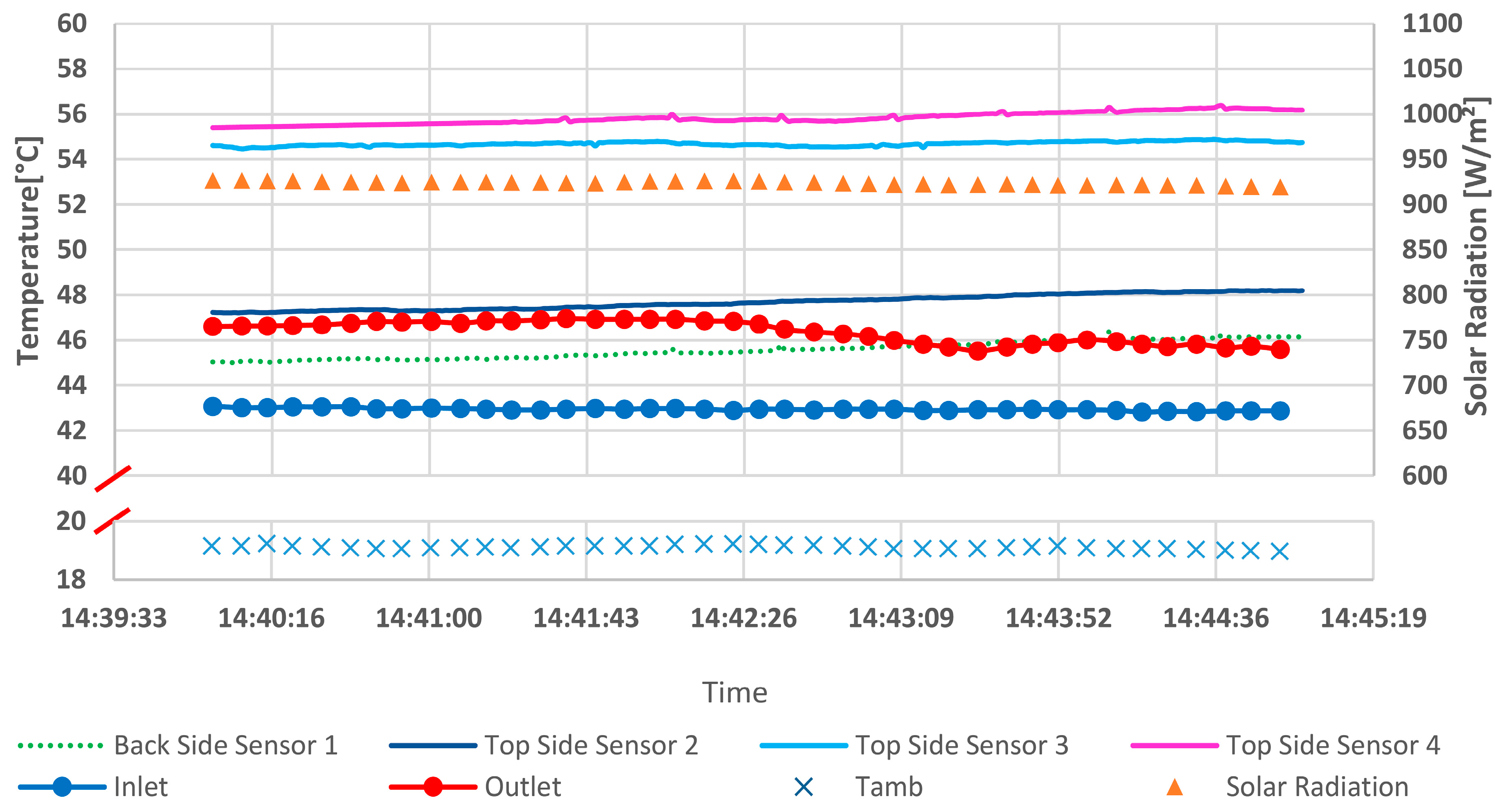
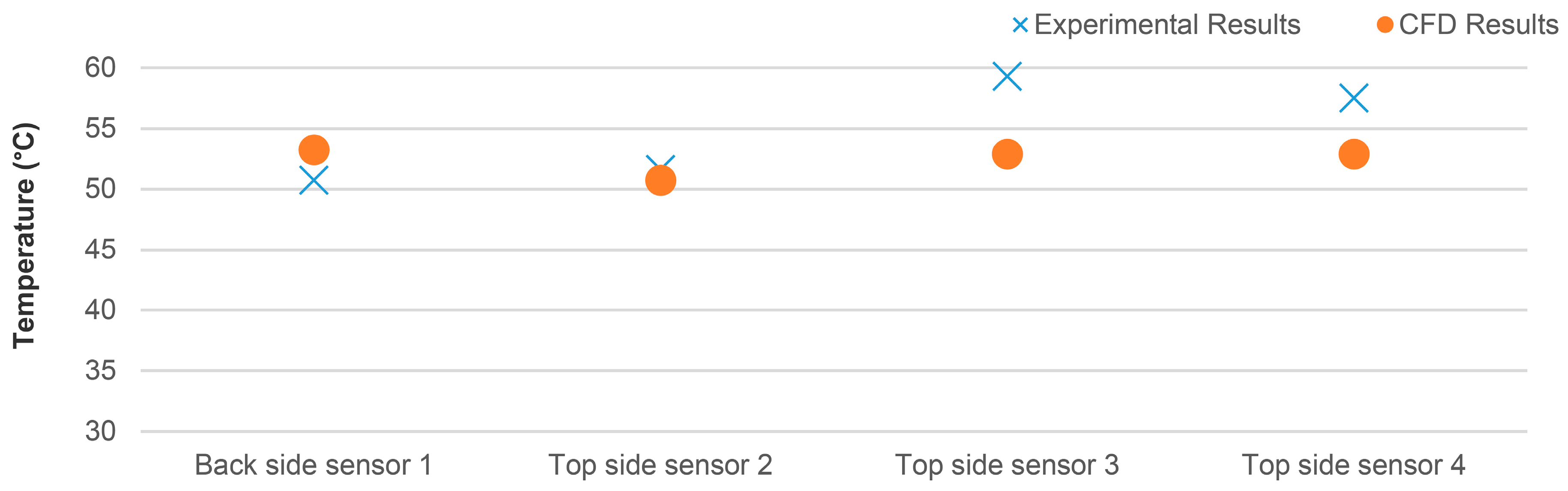
- Back side sensor 1: Temperature over the cell (second cell).
- Top side sensor 2: Temperature on the receiver (fourth cell).
- Top side sensor 3: Temperature under the cell (fourth cell).
- Top side sensor 4: Temperature over the cell (fourth cell).
3. Results and Discussion
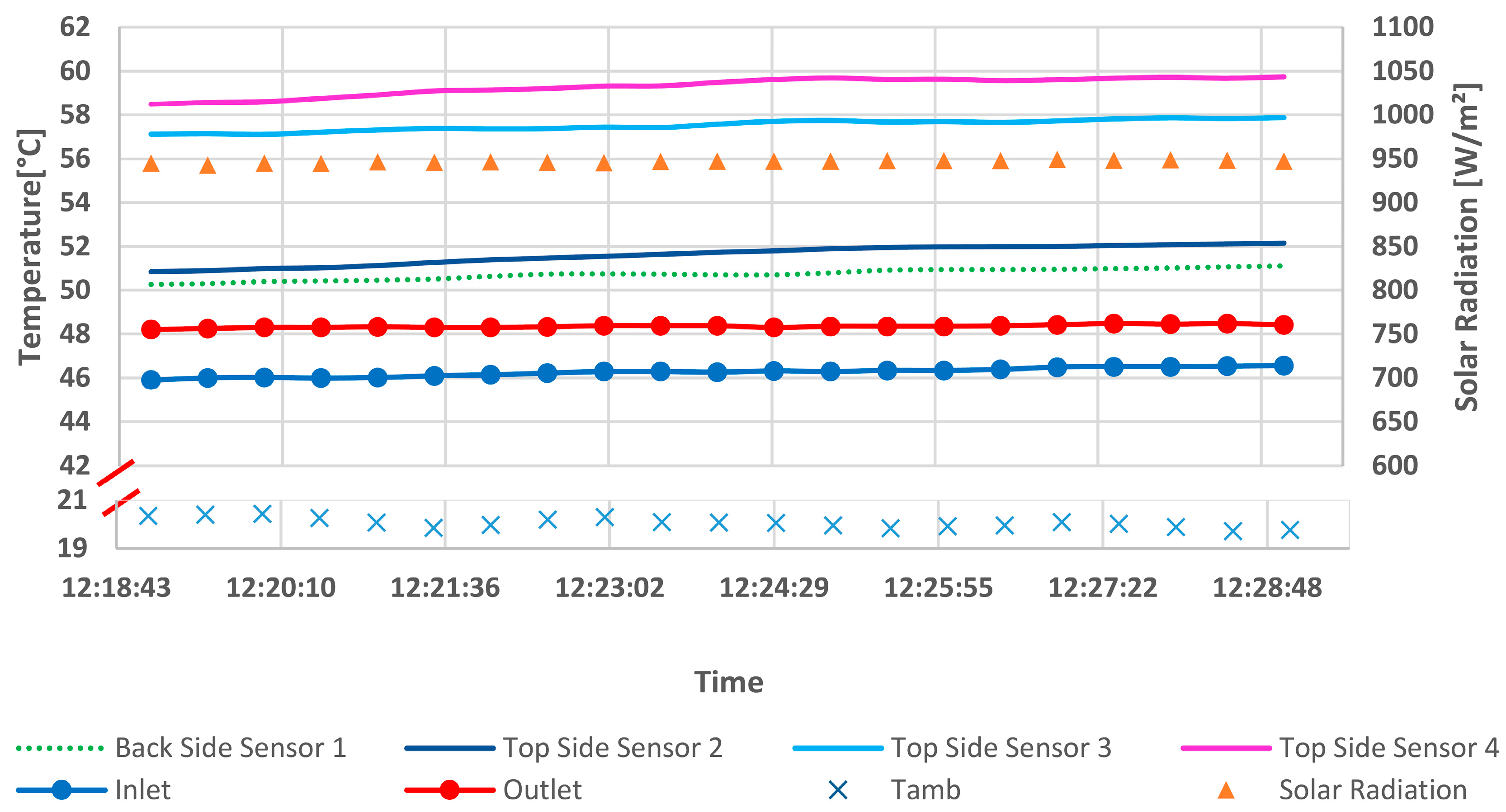
3.1. Experimental Results
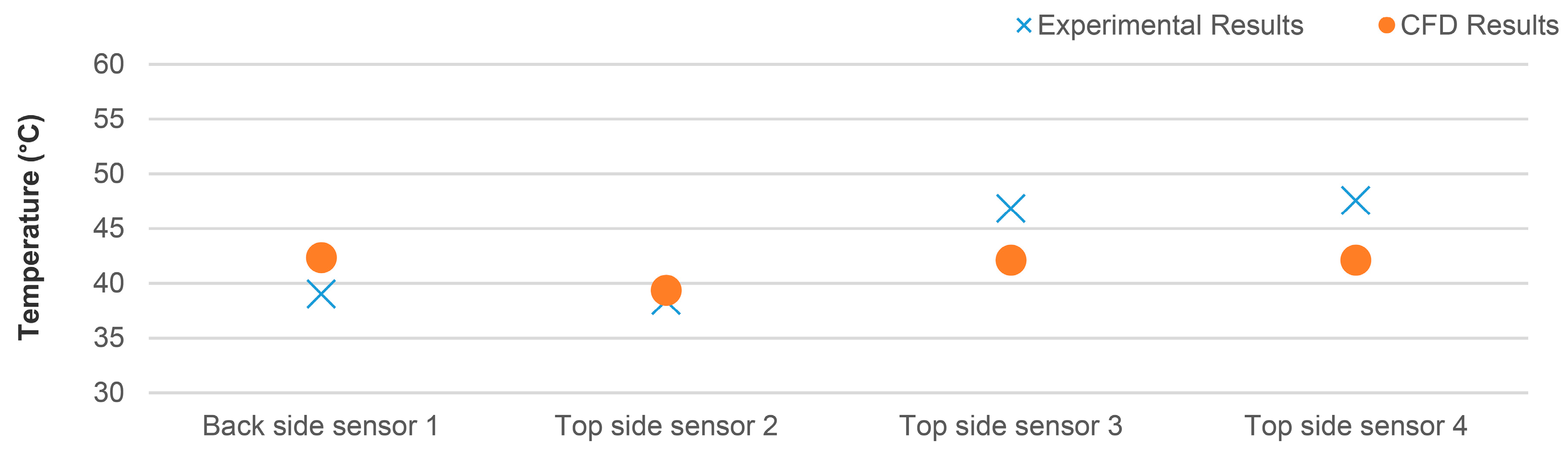
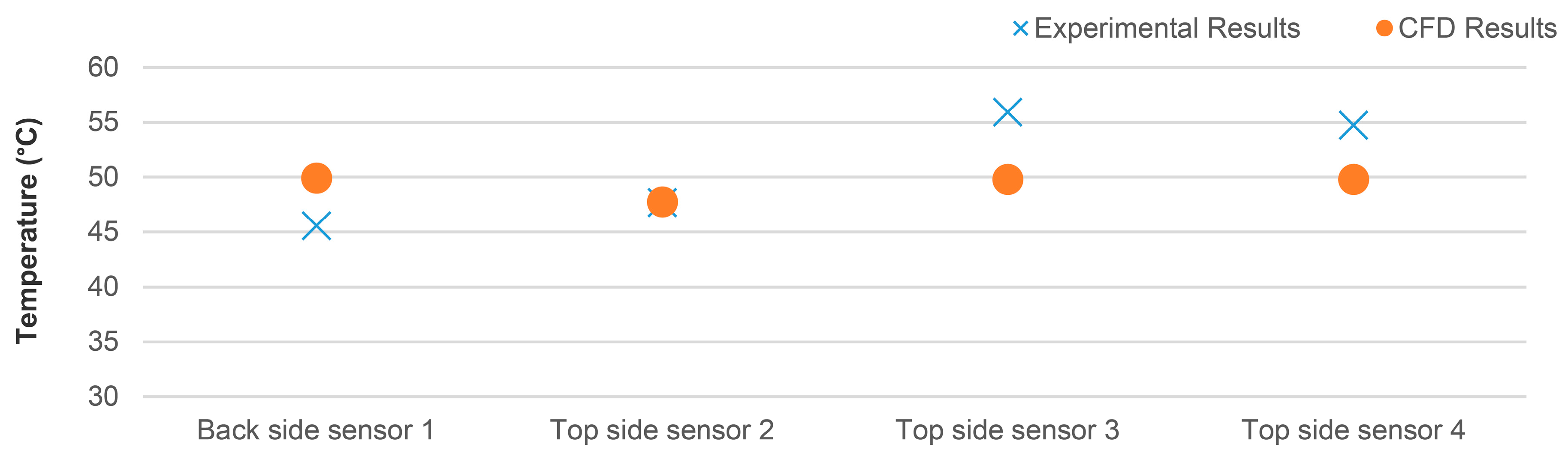
3.2. Validation of the CFD Model
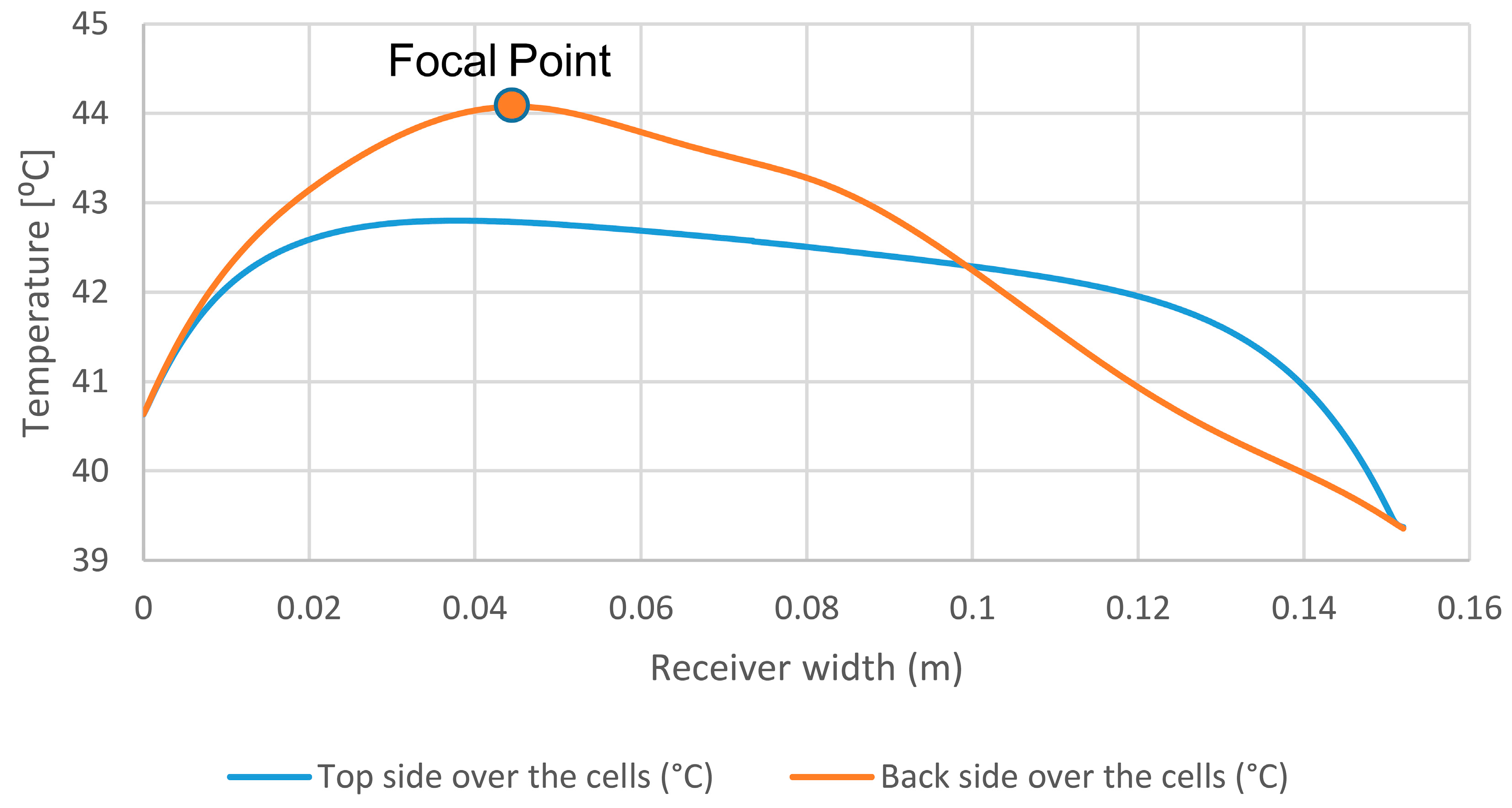
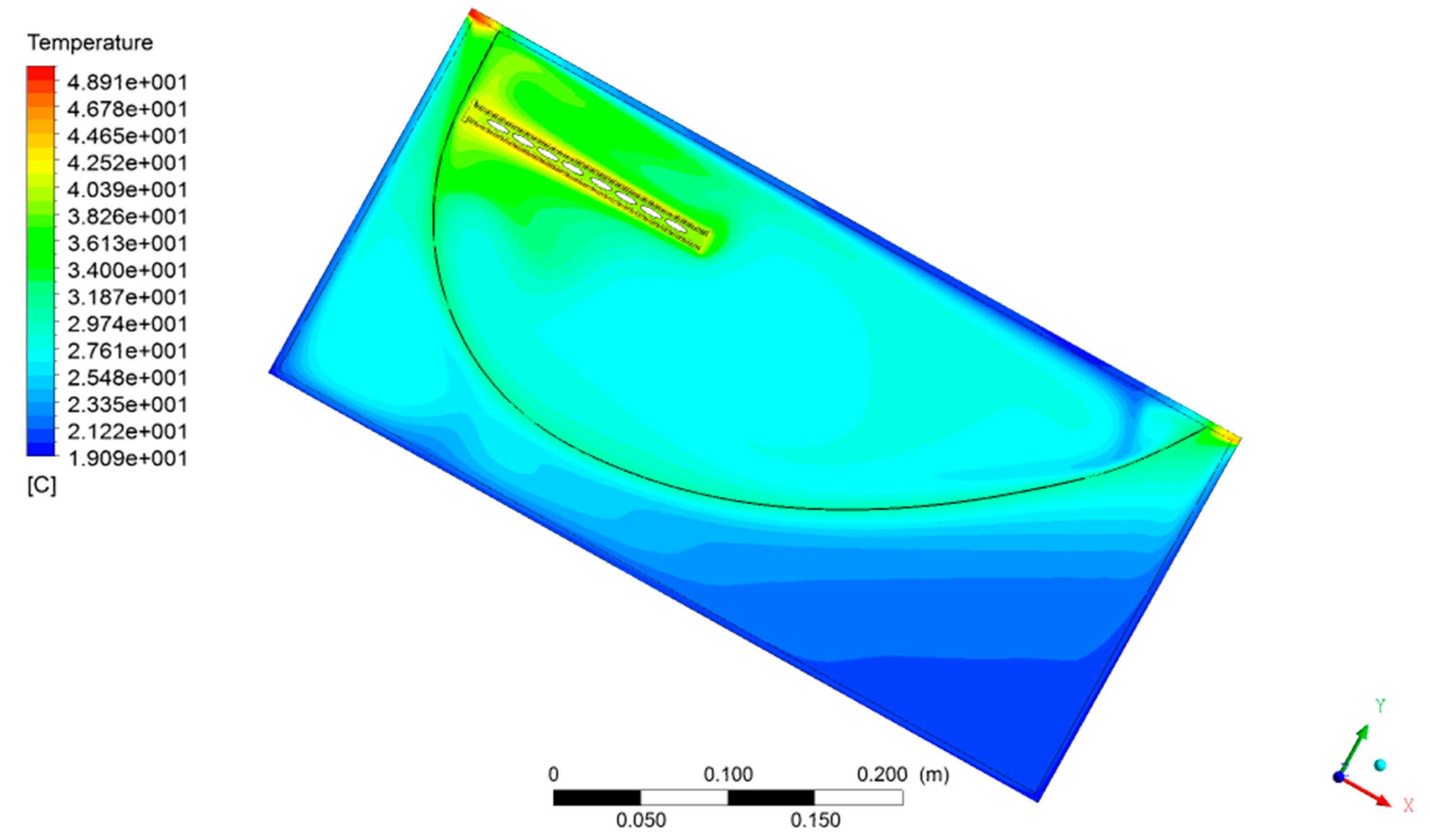
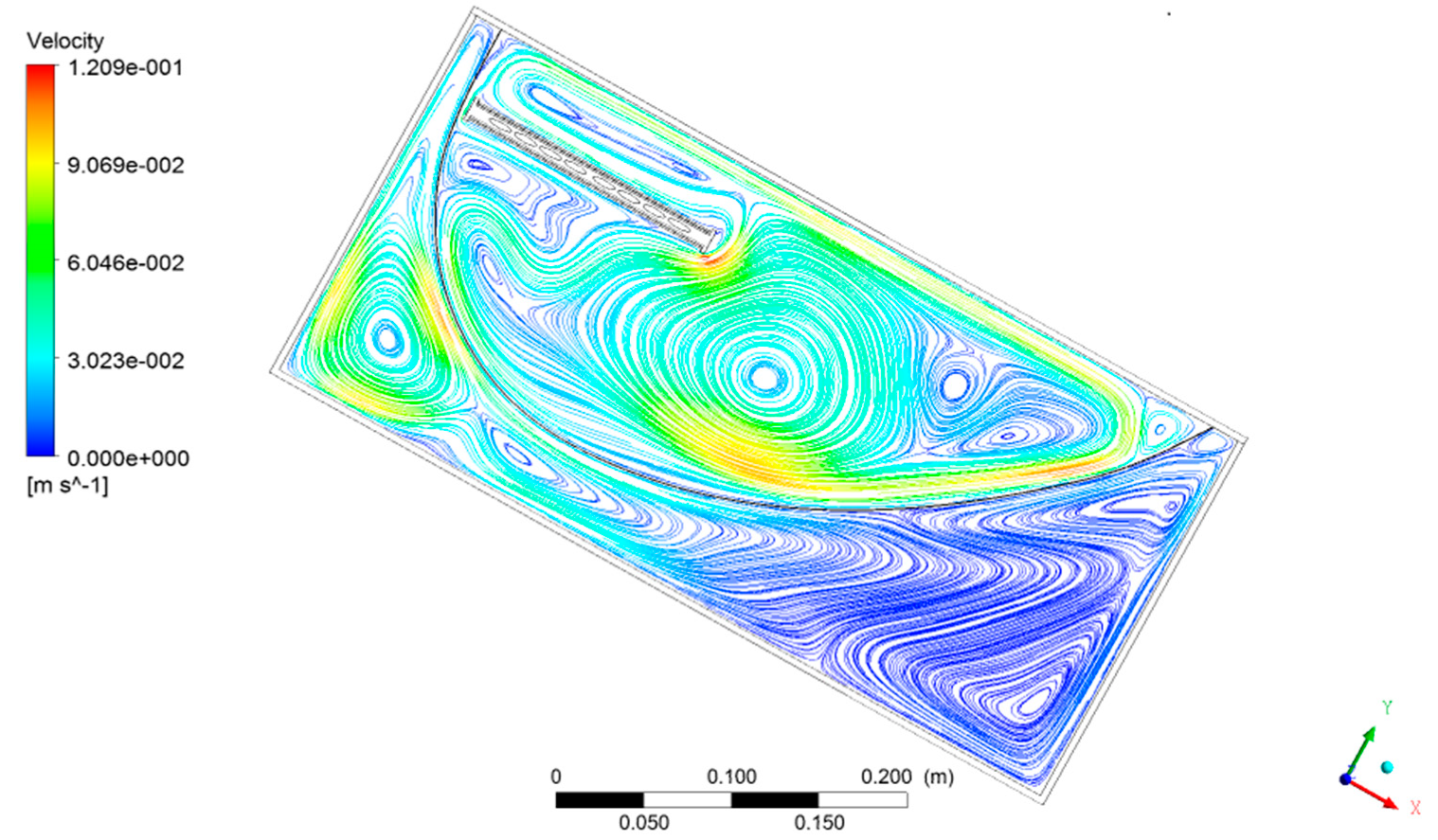
3.3. CFD Results
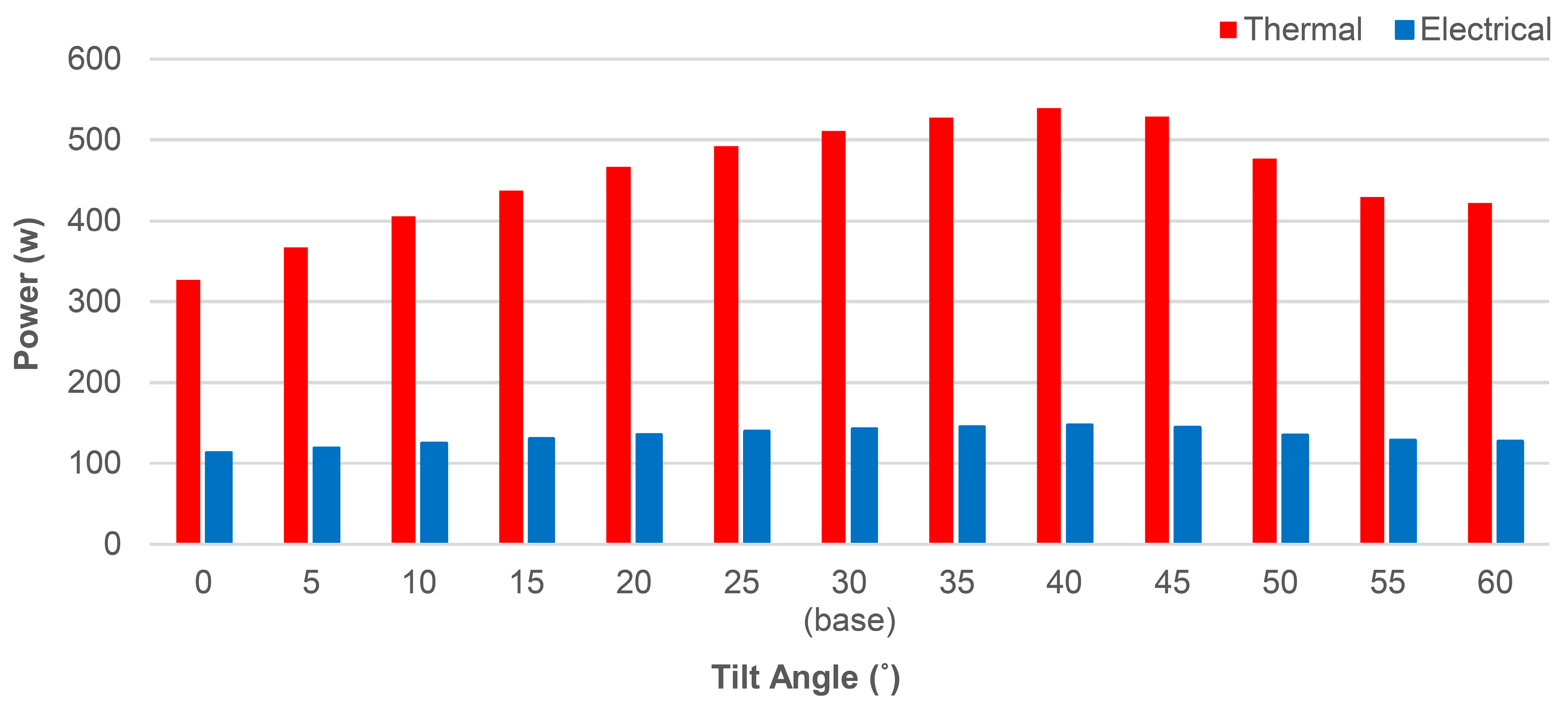
3.3.1. Collector Tilt Angle Variation
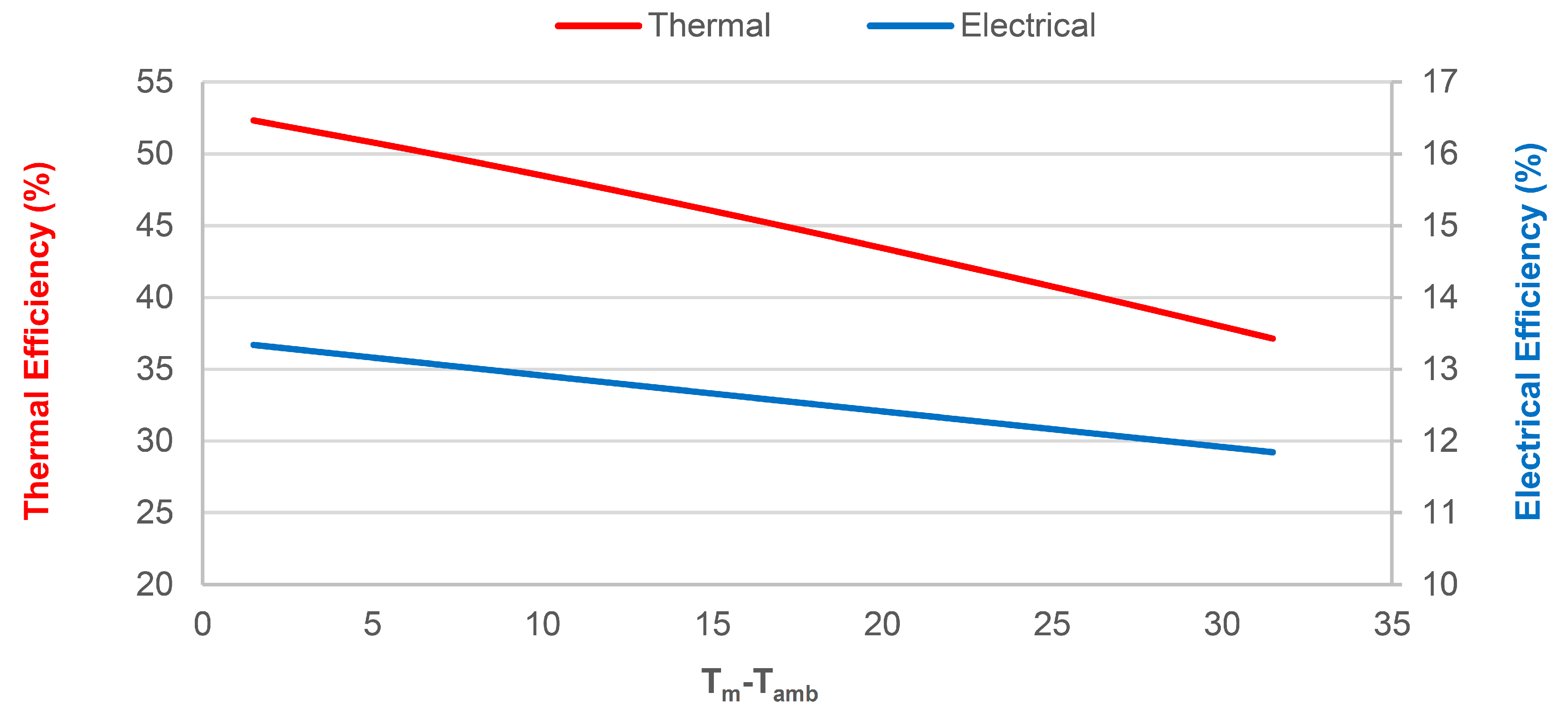
3.3.2. HTF Temperature Variation
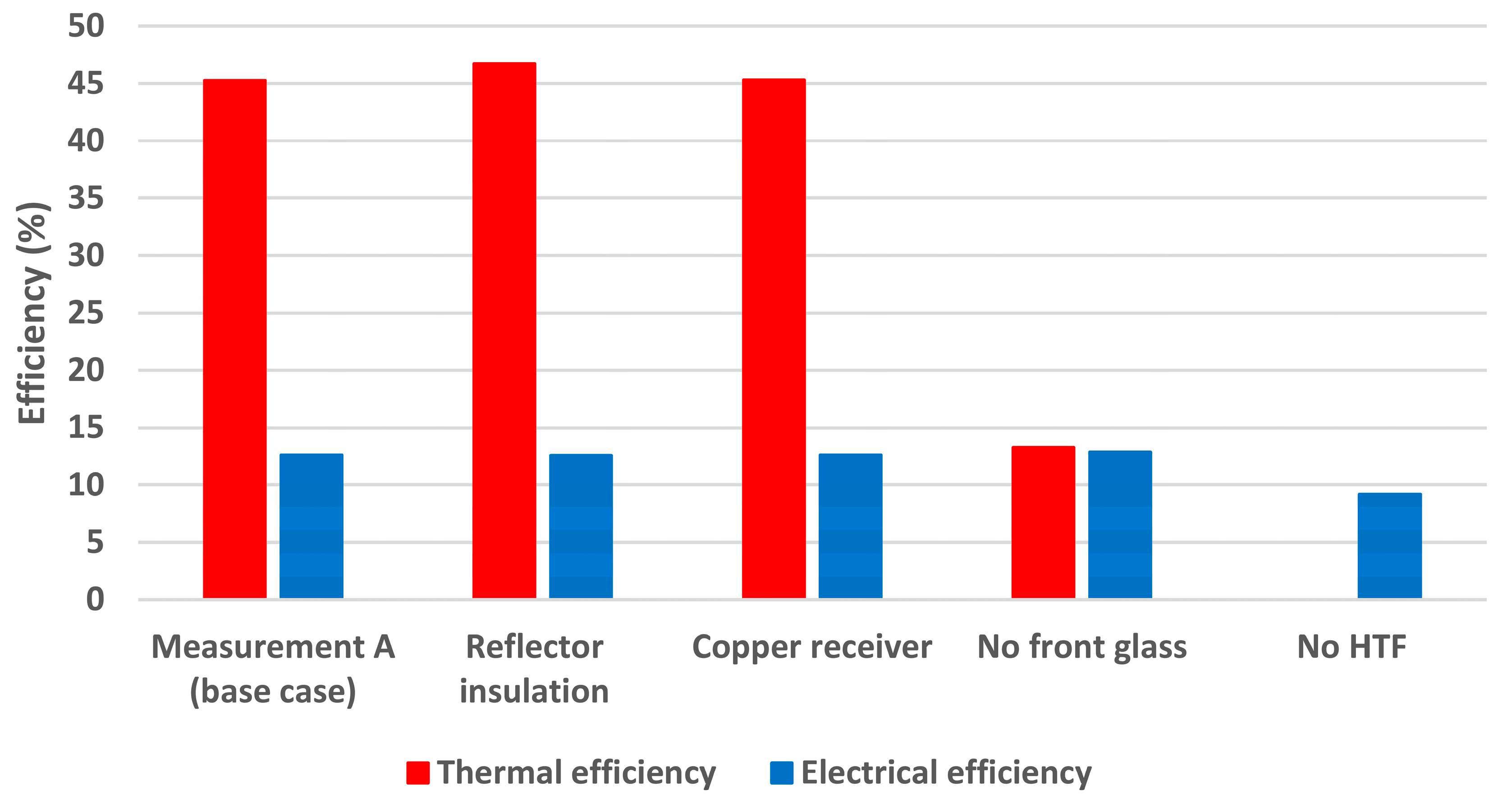
3.3.3. Collector Modification
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Description, (Unit) | Acronyms | |
| κ | Absorption coefficient, (1/m) | CPC | Compound Parabolic Collector |
| Tamb | Ambient temperature, (°C) | CFD | Computational Fluid Dynamics |
| A | Area, (m2) | CPV | Concentrating Photovoltaic |
| L | Characteristic length of the collector, (m) | CPVT | Concentrating Photovoltaic-Thermal |
| ρ | Density, (kg/m3) | CT | Concentrating Thermal |
| L, W | Dimensions of the PV, (m) | DOM | Discrete Ordinate Method |
| Ƞ0 | Efficiency of the PV cell operating at STC, (--) | DHW | Domestic Hot Water |
| Ƞcell | Efficiency of the PV cell, (--) | HTF | Heat Transfer Fluid |
| E | Electrical production of the PV cell, (W) | MCRT | Monte Carlo Ray Tracing |
| ϵ | Emissivity, (--) | PVT | Photovoltaic-Thermal |
| F | External forces, (N) | RTE | Radiative Transfer Equation |
| Kf | Fluid Conductivity, (W/m.K) | STC | Standard Test Condition |
| P | Fluid Pressure, (Pa) | UDF | User-Defined Function |
| Tf | Fluid temperature, (°C) | ||
| u | Fluid velocity, (m/s) | ||
| Q | Heat generation, (W/m3) | ||
| U | Heat loss coefficient, (W/m2.K) | ||
| T’ | Highest operating temperature of the PV cells, (°C) | ||
| Dh | Hydraulic diameter, (m) | ||
| ϒG | Intensity of the PV cell, (--) | ||
| Tm | Mean water temperature, (°C) | ||
| Nud | Nusselt number, (--) | ||
| Position and direction vector, (m) | |||
| I | Radiation intensity, (W/m2) | ||
| Ra | Rayleigh number, (--) | ||
| n | Refraction index, (--) | ||
| σs | Scattering coefficient, (1/m) | ||
| Φ | Scattering phase function, (--) | ||
| Tsky | Sky temperature, (°C) | ||
| G | Solar radiation, (W/m2) | ||
| Cp | Specific Heat Capacity, (J/kg.K) | ||
| T0 | Standard temperature, (25 °C) | ||
| σ | Stefan–Boltzmann constant, (5.669 *10-8 W/m2.K4) | ||
| βPV | Temperature coefficient of the PV cell, (%/K) | ||
| Tpv | Temperature of PV cell, (°C) | ||
| Tw | Temperature of the receiver channels, (°C) | ||
| k | Thermal Conductivity, (W/m.K) | ||
| Qth | Thermal production of the collector, (W) | ||
| β | Tilt angle, (degree) | ||
| t | Time, (s) | ||
| Vcell | Volume of the PV cell, (m3) | ||
| hw forced | Water convection heat transfer, (W/m2.k) | ||
| hwind | Wind convection heat transfer, (W/m2.k) | ||
| V | Wind speed, (m/s) |
References
- Masson-Delmotte, V.; Zhai, P.; Pörtner, H.-O.; Roberts, D.; Skea, J.; Shukla, P.R.; Pirani, A.; Moufouma-Okia, W.; Péan, C.; Pidcock, R.; et al. Global Warming of 1.5 °C. An IPCC Special Report on the Impacts of Global Warming of 1.5 °C; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2018. [Google Scholar]
- Paris, 2015, Sustainable Innovation Forum. Available online: www.cop21paris.org (accessed on 17 November 2019).
- Miller, O.D.; Yablonovitch, E.; Kurtz, S.R. Strong internal and external luminescence as solar cells approach the Shockley-Queisser limit. IEEE J. Photovolt. 2012, 2, 303–311. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Solar Energy Engineering: Processes and Systems, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Miljkovic, N.; Wang, E.N. Modeling and optimization of hybrid solar thermoelectric systems with thermosyphons. Sol. Energy 2011, 85, 2843–2855. [Google Scholar] [CrossRef]
- Zondag, H.A. Flat-plate PV-Thermal collectors and systems: A review. Renew. Sustain. Energy Rev. 2008, 12, 891–959. [Google Scholar] [CrossRef]
- Stylianou, S. Thermal Simulation of Low Concentration PV/Thermal System Using a Computational Fluid Dynamics Software. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2016. [Google Scholar]
- Chow, T.T. A review on photovoltaic/thermal hybrid solar technology. Appl. Energy 2010, 87, 365–379. [Google Scholar] [CrossRef]
- Mbewe, D.J.; Card, H.C.; Card, D.C. A model of silicon solar cells for concentrator photovoltaic and photovoltaic/thermal system design. Sol. Energy 1985, 35, 247–258. [Google Scholar] [CrossRef]
- Garg, H.P.; Adhikari, R.S. Conventional hybrid photovoltaic/thermal (PV/T) air heating collectors: Steady-state simulation. Renew. Energy 1997, 11, 363–385. [Google Scholar] [CrossRef]
- Zondag, H.A.; De Vries, D.D.; Van Helden, W.G.J.; van Zolingen, R.C.; Van Steenhoven, A.A. The thermal and electrical yield of a PV-thermal collector. Sol. Energy 2002, 72, 113–128. [Google Scholar] [CrossRef]
- Coventry, J.S. Performance of a concentrating photovoltaic/thermal solar collector. Sol. Energy 2005, 78, 211–222. [Google Scholar] [CrossRef]
- Reichl, C.; Hengstberger, F.; Zauner, C. Heat transfer mechanisms in a compound parabolic concentrator: Comparison of computational fluid dynamics simulations to particle image velocimetry and local temperature measurements. Sol. Energy 2013, 97, 436–446. [Google Scholar] [CrossRef]
- Buonomano, A.; Calise, F.; Vicidomini, M. Design, Simulation and Experimental Investigation of a Solar System Based on PV Panels and PVT Collectors. Energies 2016, 9, 497. [Google Scholar] [CrossRef]
- Tyto, A. Performance Analysis of the Thermal Absorber of Solarus Photovoltaic-Thermal Collector. Master’s Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2017. [Google Scholar]
- Li, W.; Paul, M.C.; Sellami, N.; Mallick, T.K.; Knox, A.R. Natural convective heat transfer in a walled CCPC with PV cell. Case Stud. Therm. Eng. 2017, 10, 499–516. [Google Scholar] [CrossRef]
- Yi, S.P. Advanced Integrated Numerical Model for a Concentrated Photovoltaic-Thermal (CPVT) Collector. Master’s Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2018. [Google Scholar]
- Campos, C.S.; Torres, J.P.N.; Fernandes, J.F.P. Effects of the Heat Transfer Fluid Selection on the Efficiency of a Hybrid Concentrated Photovoltaic and Thermal Collector. Energies 2019, 12, 1814. [Google Scholar] [CrossRef]
- Tiemessen, M. Thermal Modelling and Experimenting on Solarus’ PowerCollector. Master’s Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2019. [Google Scholar]
- Gomes, J. Assessment of the Impact of Stagnation Temperatures in Receiver Prototypes of C-PVT Collectors. Energies 2019, 12, 2967. [Google Scholar] [CrossRef]
- Solarus Sunpower Sweden. Available online: www.solarus.se (accessed on 17 November 2019).
- Adsten, M.; Helgesson, A.; Karlsson, B. Evaluation of CPC-collector designs for stand-alone, roof-or wall installation. Sol. Energy 2005, 79, 638–647. [Google Scholar] [CrossRef]
- Rönnelid, M.; Perers, B.; Karlsson, B. Construction and testing of a large-area CPC-collector and comparison with a flat plate collector. Sol. Energy 1996, 57, 177–184. [Google Scholar] [CrossRef]
- Bernardo, R.; Davidsson, H.; Gentile, N.; Gomes, J.; Gruffman, C.; Chea, L.; Mumba, C.; Karlsson, B. Measurements of the electrical incidence angle modifiers of an asymmetrical photovoltaic/thermal compound parabolic concentrating-collector. Engineering 2013, 5, 37. [Google Scholar]
- Bergman, T.L.; Incropera, F.P.; DeWitt, D.P.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 7th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Fluent, A.N.S.Y.S. User’s Guide Release 16.2; Ansys Inc.: Pittsburgh, PA, USA, 2015. [Google Scholar]
- Guarracino, I. Hybrid Photovoltaic and Solar Thermal (PVT) Systems for Solar Combined Heat and Power. Ph.D. Thesis, Imperial College London, London, UK, 2017. [Google Scholar]
- Howell, J.R.; Menguc, M.P.; Siegel, R. Thermal Radiation Heat Transfer, 4th ed.; Taylor & Francis: Milton Park, UK, 2002. [Google Scholar]
- García-Gil, Á.; Casado, C.; Pablos, C.; Marugán, J. Novel procedure for the numerical simulation of solar water disinfection processes in flow reactors. Chem. Eng. J. 2019, 376, 120194. [Google Scholar] [CrossRef]




| Photovoltaics | Solar Thermal | Concentration | |
|---|---|---|---|
| CPV | ☑ | ☑ | |
| CT | ☑ | ☑ | |
| PVT | ☑ | ☑ | |
| CPVT | ☑ | ☑ | ☑ |
| Features | Values/Units |
|---|---|
| Collector production (nominal) | 1350W thermal, 270W electrical |
| Collector total area | 2.2 m2 |
| Receiver area | 0.362 m2 |
| Concentration ratio | 1.52 |
| Reflector reflectivity | 96% for the full spectrum and 92% for the visible spectrum |
| Receiver channel area | 8 channels with 154 mm2 (one channel) |
| Silicone thickness | 1 mm on both side of PV cells |
| Solar cell efficiency | 18.7% (STC) |
| Solar cell Temperature coefficient | 0.4%/C |
| Glass transmittance | 95% |
| Thermal Conductivity (W/m.K) | Density (kg/m3) | Specific Heat Capacity (J/kg.K) | |
|---|---|---|---|
| Front Glass | 1 | 2500 | 720 |
| Reflector | 200 | 2700 | 901 |
| Receiver | 210 | 2700 | 901 |
| Silicon | 0.2 | 970 | 1550 |
| PV cell | 124 | 2320 | 678 |
| Collector Box | 0.033 | 500 | 100 |
| Measurement | Ambient Temperature (°C) | Inlet Water Temperature (°C) | Outlet Water Temperature (°C) | Direct Radiation (W/m2) | Diffuse Radiation (W/m2) | Incident Angle (⁰) | Solar Altitude(⁰) | Solar Azimuth (⁰) | Flow Rate (L/min) | Duration of Measurement (min) |
|---|---|---|---|---|---|---|---|---|---|---|
| A | 18.6 | 33.6 | 36.6 | 978.3 | 93.1 | 18.5 | 48.5 | 199.4 | 2.2 | 10 |
| B | 19.1 | 42.9 | 46.2 | 922.8 | 77.2 | 26.4 | 56.3 | 231.9 | 1 | 5 |
| C | 20.1 | 46.3 | 48.4 | 946.0 | 77.2 | 17.9 | 47.8 | 189.4 | 2.2 | 10 |
| D | 20.8 | 44.7 | 47.5 | 892.9 | 76.4 | 28.1 | 58.1 | 235.7 | 1.2 | 5 |
| E | 21.6 | 36.2 | 39.0 | 757.8 | 145.5 | 21.4 | 51.4 | 200.9 | 2.1 | 3 |
| F | 23.1 | - | - | 422.5 | 114.6 | 29.2 | 59.2 | 231.8 | 0 | 3 |
| Back Side Cell Temperature (°C) | Top Side Cell Temperature (°C) | Thermal Power (w) | Electrical Power (w) | |
|---|---|---|---|---|
| Measurement A (base case) | 42.4 | 42.2 | 511 | 142.2 |
| Reflector insulation | 42.6 | 42.4 | 528 | 142.1 |
| Copper receiver | 42.3 | 42.1 | 512 | 142.3 |
| No front glass | 38.2 | 36.5 | 150 | 145.2 |
| No HTF | 105.7 | 105.2 | 0 | 103.6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nasseriyan, P.; Afzali Gorouh, H.; Gomes, J.; Cabral, D.; Salmanzadeh, M.; Lehmann, T.; Hayati, A. Numerical and Experimental Study of an Asymmetric CPC-PVT Solar Collector. Energies 2020, 13, 1669. https://doi.org/10.3390/en13071669
Nasseriyan P, Afzali Gorouh H, Gomes J, Cabral D, Salmanzadeh M, Lehmann T, Hayati A. Numerical and Experimental Study of an Asymmetric CPC-PVT Solar Collector. Energies. 2020; 13(7):1669. https://doi.org/10.3390/en13071669
Chicago/Turabian StyleNasseriyan, Pouriya, Hossein Afzali Gorouh, João Gomes, Diogo Cabral, Mazyar Salmanzadeh, Tiffany Lehmann, and Abolfazl Hayati. 2020. "Numerical and Experimental Study of an Asymmetric CPC-PVT Solar Collector" Energies 13, no. 7: 1669. https://doi.org/10.3390/en13071669
APA StyleNasseriyan, P., Afzali Gorouh, H., Gomes, J., Cabral, D., Salmanzadeh, M., Lehmann, T., & Hayati, A. (2020). Numerical and Experimental Study of an Asymmetric CPC-PVT Solar Collector. Energies, 13(7), 1669. https://doi.org/10.3390/en13071669