CFD Simulation of Aeration and Mixing Processes in a Full-Scale Oxidation Ditch
Abstract
1. Introduction
2. Materials and Methodology
2.1. Computational Geometry
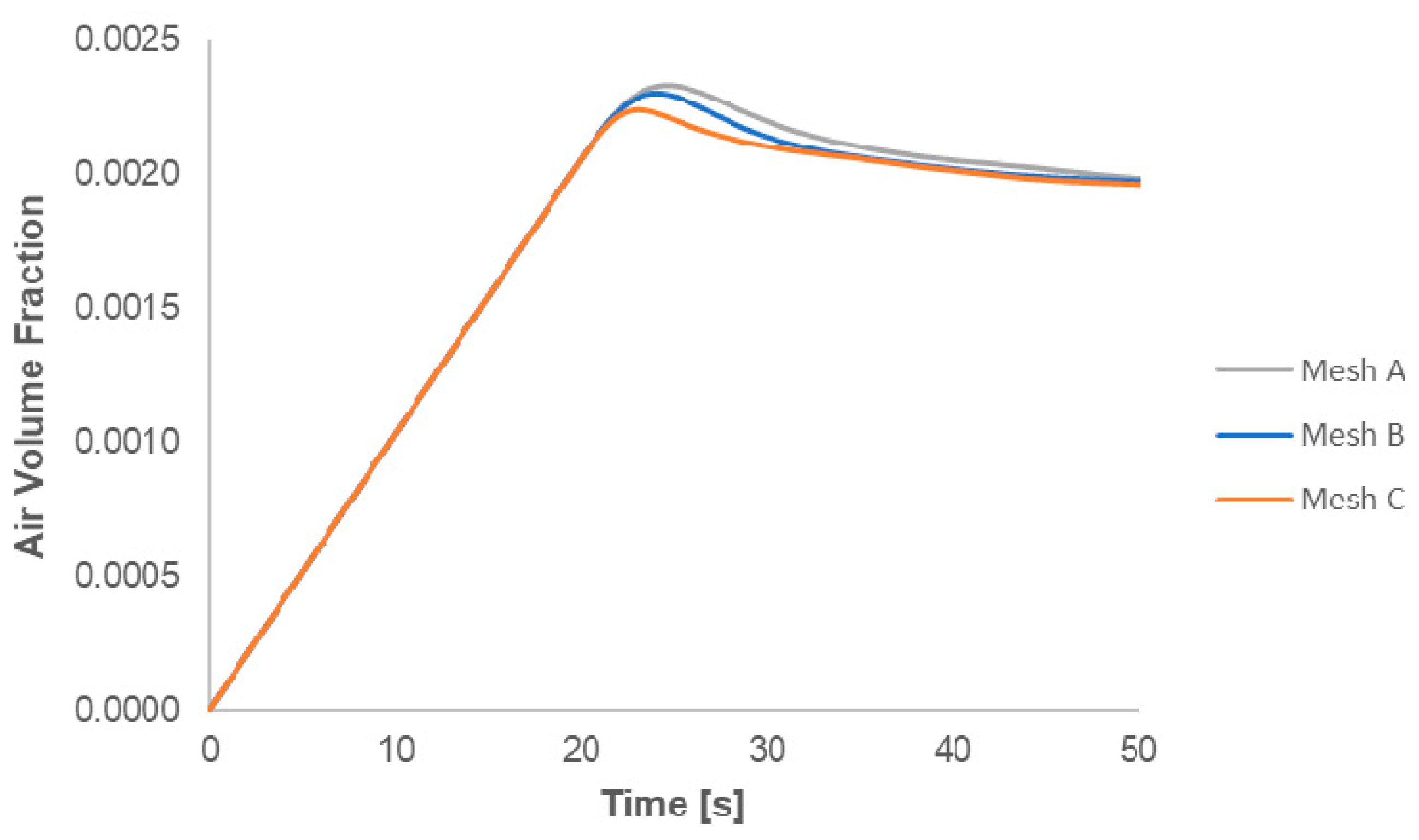
2.2. Mesh Grid
2.3. Boundary Conditions
2.4. Simulation of Submerged Agitators
2.5. Setting Up the Multiphase Flow Model
3. Results and Discussions
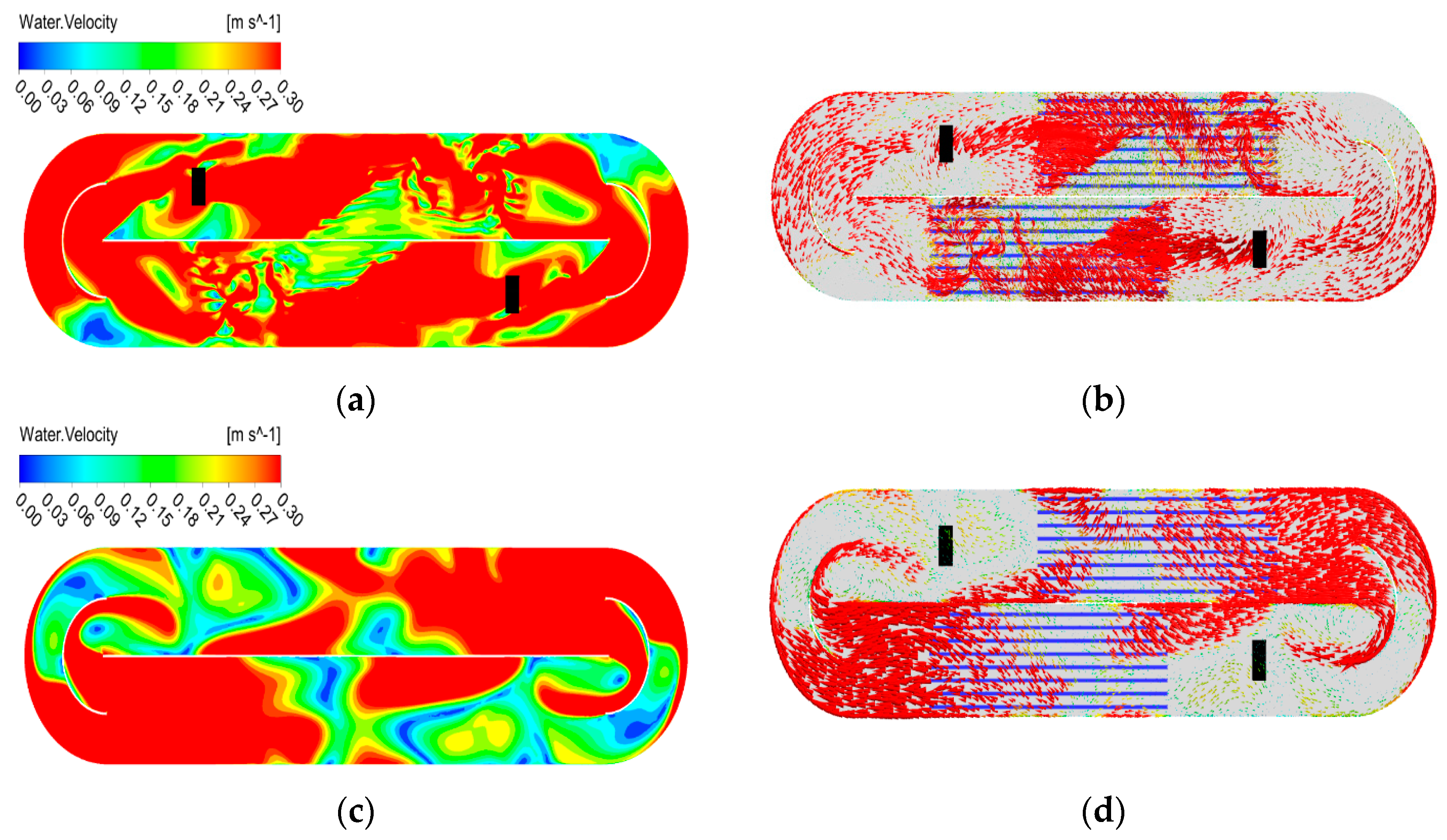
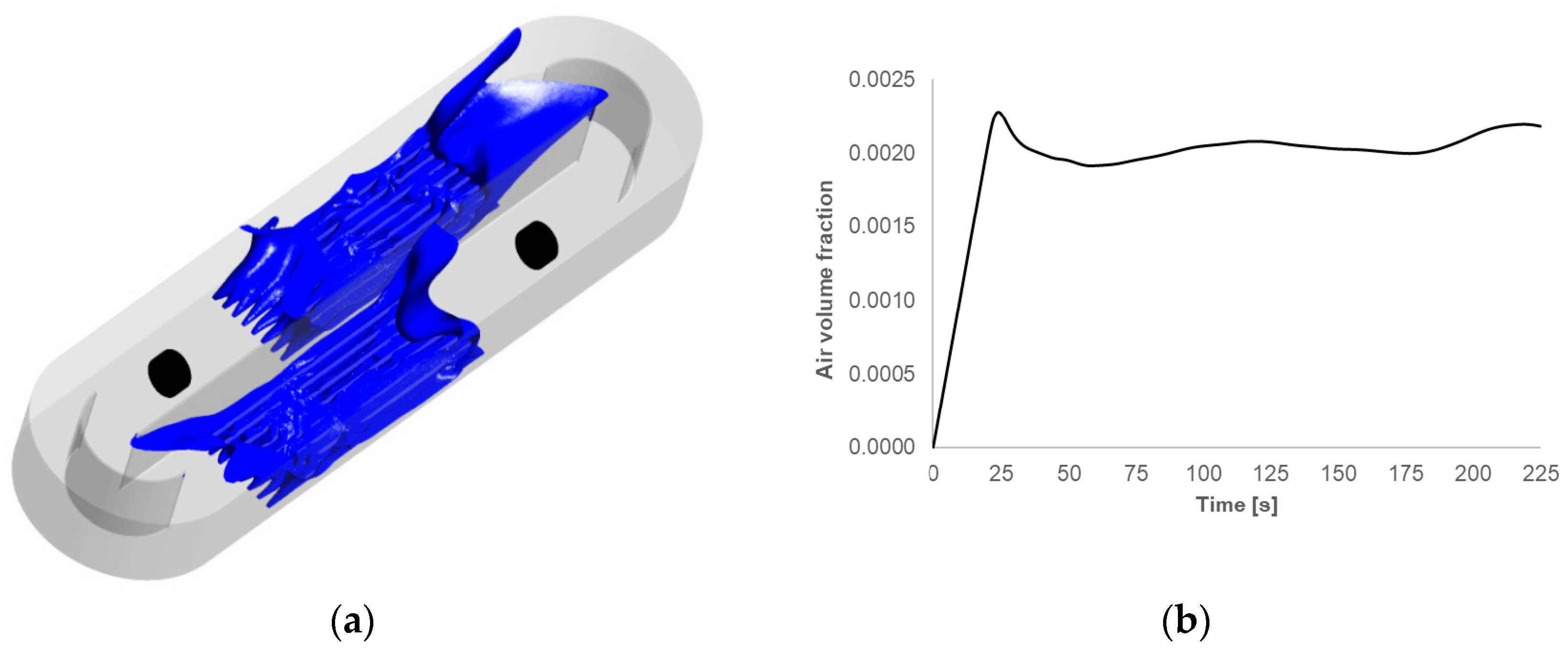
3.1. Momentum Source Term Approach
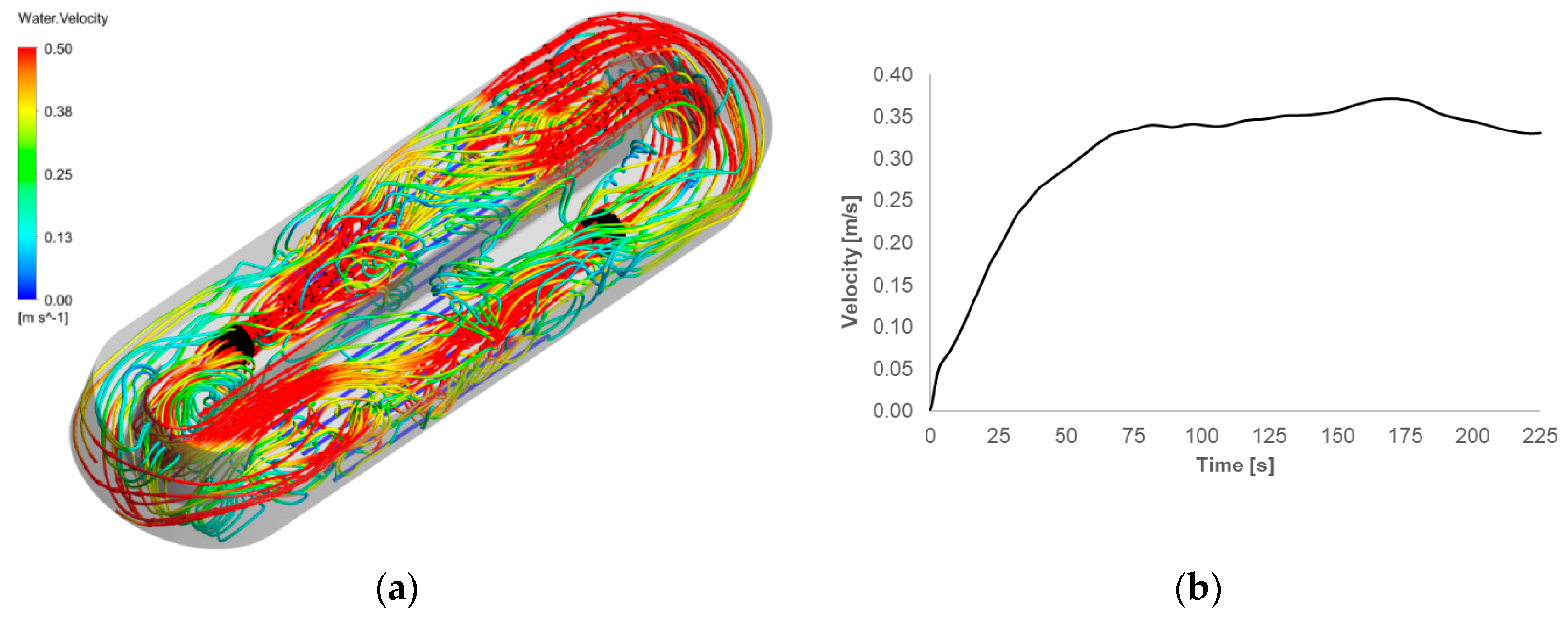
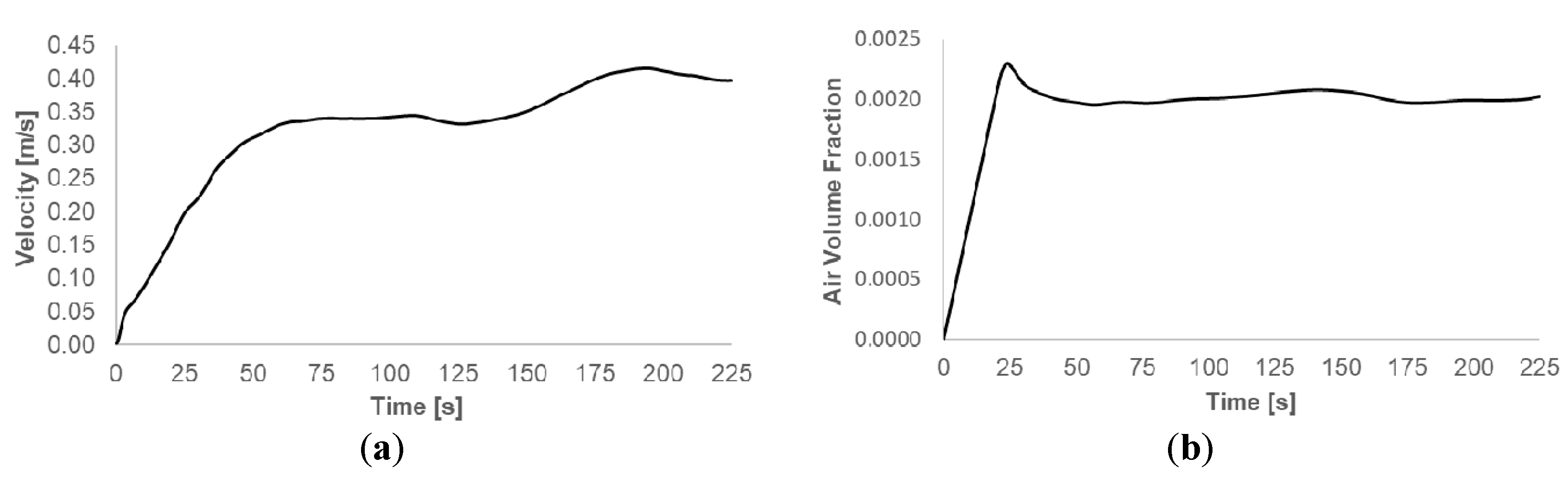
3.2. Transient Rotor-Stator Model
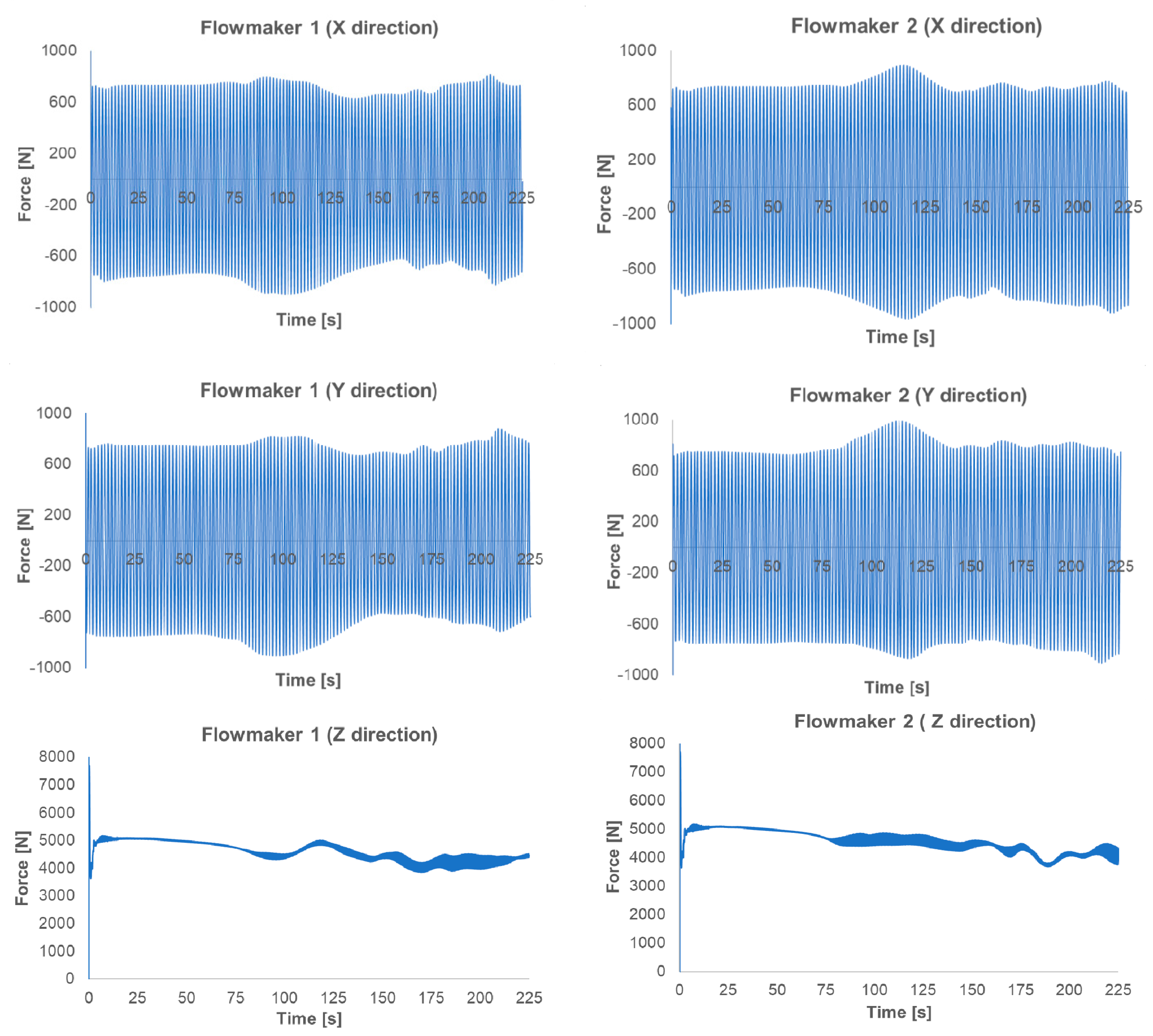
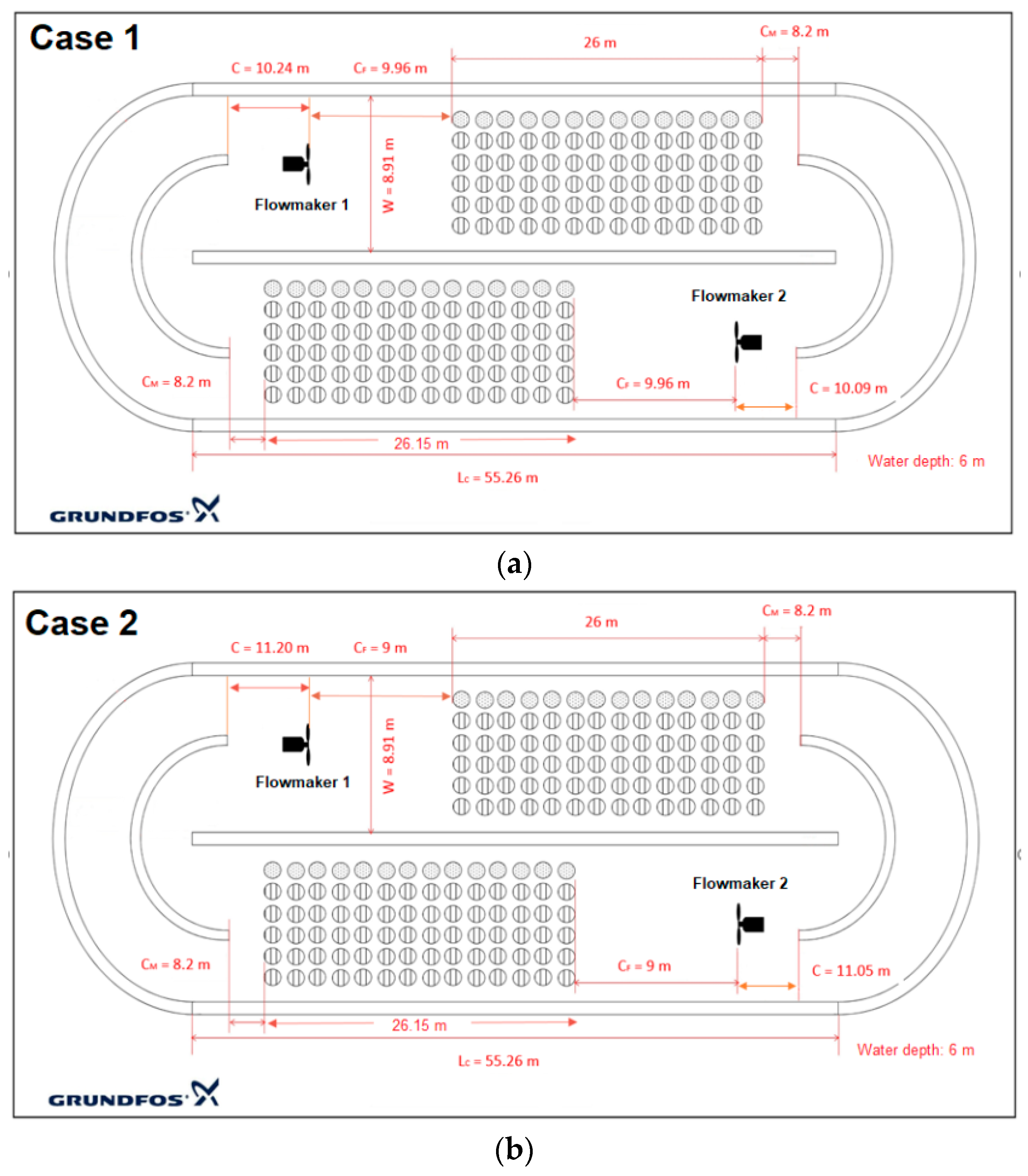
3.3. Positioning of the Flowmakers
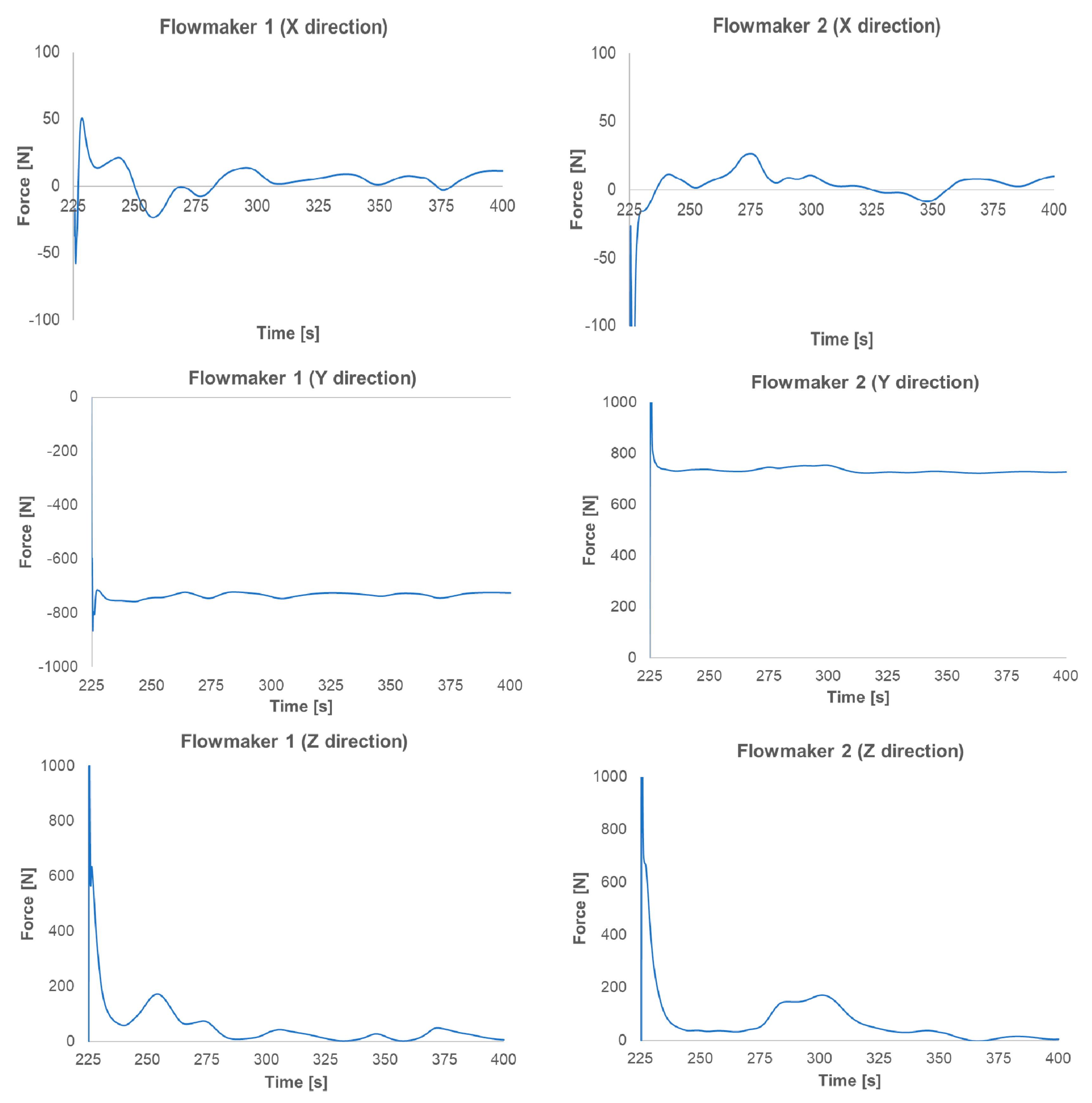
3.4. Contribution of Aeration to the Mixing Process without Flowmakers
4. Summary and Conclusions
- The momentum source term approach was used due to its reliability and high computing speed. The minimum required liquid velocity was reached with this model and adequate mixing was determined. This approach predicts lower water velocity in comparison with the transient rotor-stator model. This is due to the fact that the tangential velocity components were not considered during flowmaker modelling.
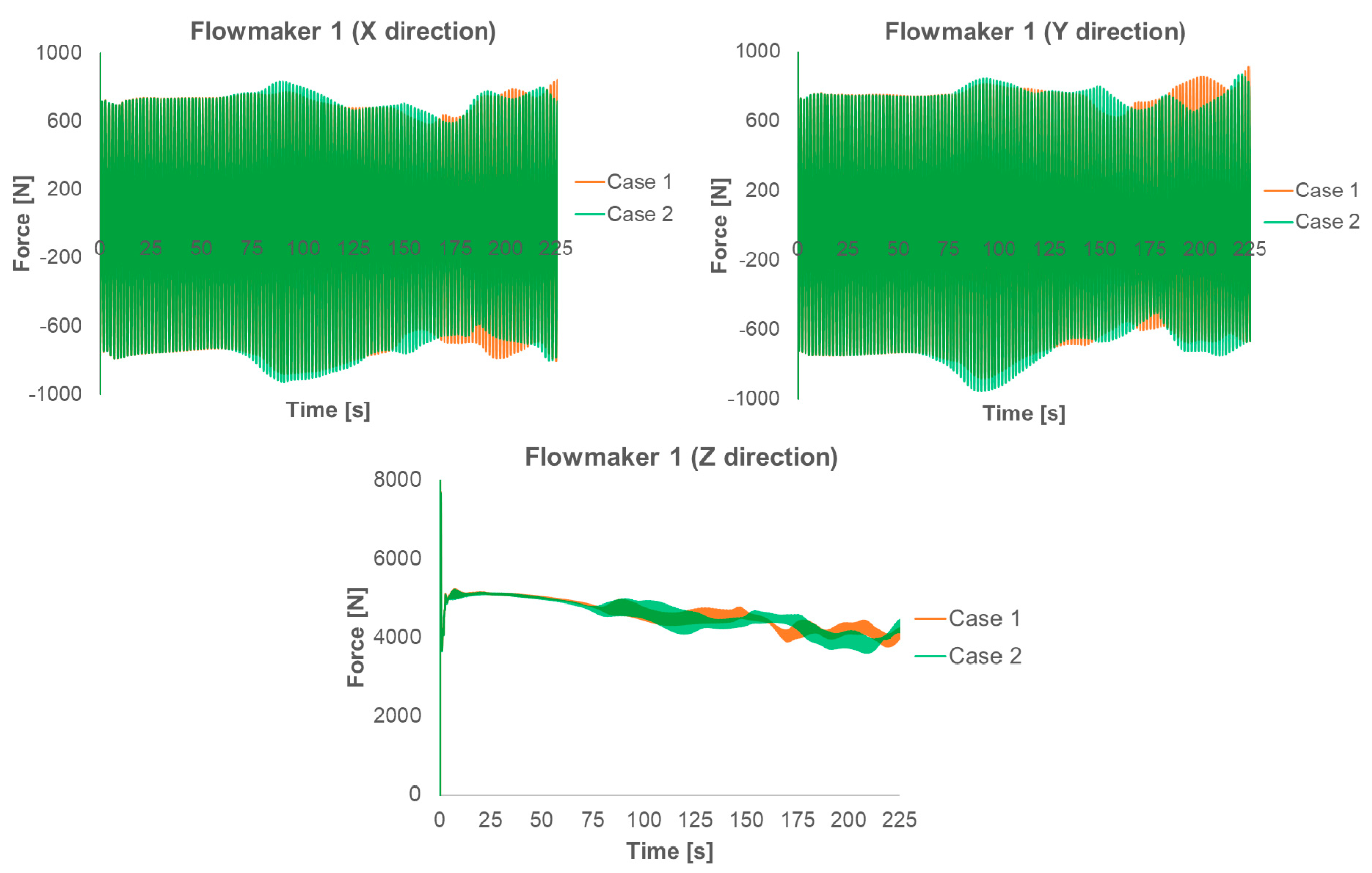
- Despite the excessive computing resource requirements, the transient rotor-stator model accurately predicted the fluid flow pattern in the OD. The flowmakers were able to generate the required thrust in order to obtain sufficient bulk flow. Better mixing performance was determined with this model. Also, the normal forces that act on the blades were monitored and the normal force fluctuations were in the allowed range during the simulation.
- Grundfos best practice guidelines were taken into account for the correct positioning of the flowmakers. Higher thrust fluctuations were determined when the flowmaker position was close to the first row of the diffuser grid. Meanwhile, the uneven distribution of water velocity was observed due to the tank curves and it might be dangerous for the blades. Therefore, the rear clearance is also an important parameter for the correct positioning of the flowmakers. When the distance between the flowmaker and the diffuser grid was 9.96 m, relatively low thrust fluctuations were monitored. As a result, it is the recommended position of the flowmaker for this study.
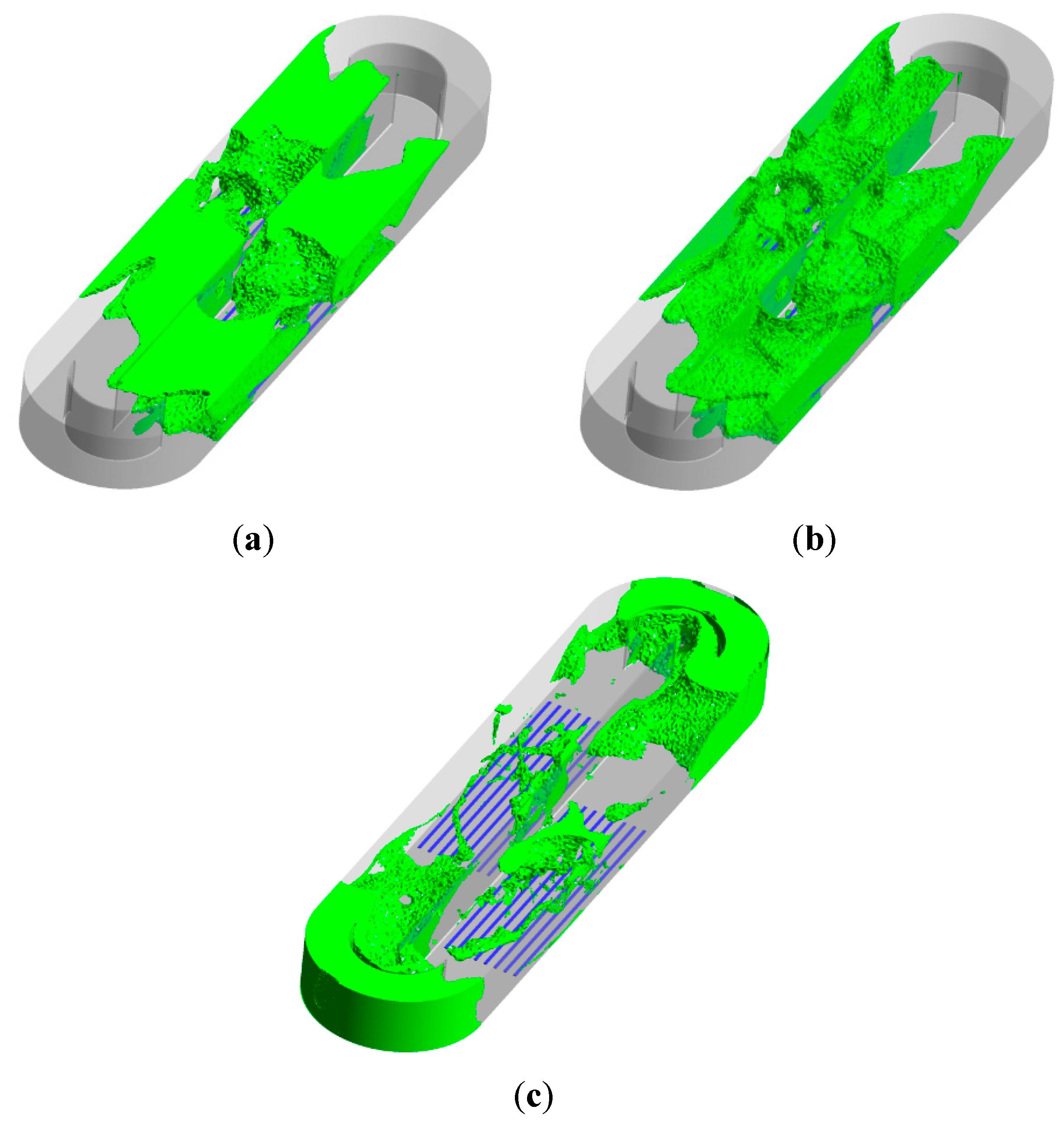
- The contribution of the aeration process to the mixing was also investigated by removing the flowmakers. Inadequate mixing was monitored throughout the OD due to the recirculation zones. Zones of recirculation were determined due to the high aeration rate. There were dead zones around the rounded ends of the oxidation ditch. Also, the diffuser grid arrangement was not suitable to get adequate mixing without the flowmakers. Therefore, it is necessary to use the flowmaker in order to achieve effective bulk flow.
- Fine bubble diffusers were used instead of the more energy-intensive surface aerators and approximately 57% reduction of energy consumption was achieved in the aeration process.
Author Contributions
Funding
Conflicts of Interest
References
- Grady, L. Daigger and Lim, Biological Wastewater Treatment., 2nd ed.; Marcel Dekker: New York, NY, USA, 1999. [Google Scholar]
- Fayolle, Y.; Arnaud, C.; Sylvie, G.; Michel, R.; Alain, H. Oxygen transfer prediction in aeration tanks using CFD. Chem. Eng. Sci. 2007, 62, 7163–7171. [Google Scholar] [CrossRef]
- Karpinska, A.M.; John, B. CFD-aided modelling of activated sludge systems—A critical review. Water Res. 2015, 88, 861–879. [Google Scholar] [CrossRef] [PubMed]
- Tchobanoglous, G.; Burton, F.L.; Stensel, H.D.; Metcalf & Eddy, Inc. Wastewater Engineering: Treatment and Reuse, 4th ed.; McGraw-Hill: New York, NY, USA, 2003. [Google Scholar]
- Grundfos, Fixed Bottom Aeration Grid and Agitators. Available online: https://www.grundfos.com/ (accessed on 27 March 2020).
- Rosa, L.M.; Koerich, D.M.; Giustina, S.V. The Use of CFD in Design and Optimization of Wastewater Treatment Units: A Review. 2017. Available online: https://www.researchgate.net/publication/317771587_The_use_of_CFD_in_design_and_optimization_of_wastewater_treatment_units_A_review (accessed on 10 January 2020).
- Yang, Y.; Yang, J.; Zuo, J.; Li, Y.; He, S.; Yang, X.; Zhang, K. Study on two operating conditions of a full-scale oxidation ditch for optimization of energy consumption and effluent quality by using CFD model. Water Res. 2011, 45, 3439–3452. [Google Scholar] [CrossRef] [PubMed]
- Motivation and Strategy, “www.hzdr.de” HZDR-WebCMS, 21 August 2019. Available online: https://www.hzdr.de/db/Cms?pOid=50658&pNid=121 (accessed on 28 February 2020).
- Climent, J.; Martinez-Cuenca, R.; Carratala, P.; Gonzalez-Ortega, M.J.; Abellan, M.; Monros, G.; Chiva, S. A comprehensive hydrodynamic analysis of a full-scale oxidation ditch using Population Balance Modelling in CFD simulation. Chem. Eng. J. 2019, 374, 760–775. [Google Scholar] [CrossRef]
- Vermande, S.; Essemiani, K.; Meinhold, J.; Traversay, C.D.; Fonande, C. Trouble shooting of agitation in an oxidation ditch: Applicability of hydraulic modeling. In Proceedings of the 76th Annual Technical Exhibition and Conference WEFTEC’03, Los Angeles, CA, USA, 11–15 October 2003. [Google Scholar]
- Xie, H.; Yang, J.; Hu, Y.; Zhang, H.; Yang, Y.; Zhang, K.; Zhu, X.; Li, Y.; Yang, C. Simulation of flow field and sludge settling in a full-scale oxidation ditch by using a two-phase flow CFD model. Chem. Eng. Sci. 2014, 109, 296–305. [Google Scholar] [CrossRef]
- Stamou, A.I. Prediction of hydrodynamic characteristics of oxidation ditches using the k-e turbulence model. In Proceedings of the Second International Symposium on Engineering Turbulence Modelling and Measurements, Florence, Italy, 31 May–2 June 1993. [Google Scholar]
- Karcz, J.; Kacperski, L. An effect of the grid quality on the result of numerical simulations of the fluid flow field in an agitated vessel. In Proceedings of the 14th European Conference on Mixing, Warszawa, Poland, 10–13 September 2012. [Google Scholar]
- Brannock, M. Computational Fluid Dynamics Tools for the Design of Mixed Anoxic Wastewater Treatment Vessels. Ph.D. Thesis, Department of Environmental Engineering, University of Queensland, Brisbane, Australia, 2003. [Google Scholar]
- ANSYS CFX-Solver Modeling Guide; ANSYS Inc.: Canonsburg, PA, USA, 2009.
- Andersson, B.; Andersson, R.; Hakansson, L.; Mortensen, M.; Sudiyo, R.; Van Wachem, B. Computational Fluid Dynamics for Engineers; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar]
- Ratkovich, N. Understanding Hydrodynamics in Membrane Bioreactor Systems for Wastewater Treatment: Two-phase Empirical and Numerical Modelling and Experimental Validation. Ph.D. Thesis, Ghent University, Belgium, Ghent, 2010. [Google Scholar]
- Ishii, M.; Zuber, N. Drag Coefficient and Relative Velocity in Bubbly, Droplet or Particulate Flows. AIChE J. 1979, 25, 843–855. [Google Scholar] [CrossRef]
- Dean, J.A. Lange–s Handbook of Chemistry, 15th ed.; McGraw-Hill: New York, NY, USA, 1999. [Google Scholar]
- Burns, A.D.; Frank, T.; Hamill, I.; Shi, J.-M. The Favre Averaged Drag Model for Turbulent Dispersion in Eulerian Multi-Phase Flows. In Proceedings of the 5th International Conference on Multiphase Flow, Yokohama, Japan, 30 May–4 June 2004. [Google Scholar]
- Karpinska, A.M.; Bridgeman, J. CFD as a tool to optimize aeration tank design and operation. J. Environ. Eng. 2018, 144, 05017008. [Google Scholar] [CrossRef]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Grundfos, “Design Recommendations for Mixing,” 2014. Available online: https://www.grundfos.com/campaigns/download-mixer-handbook.html (accessed on 26 March 2020).

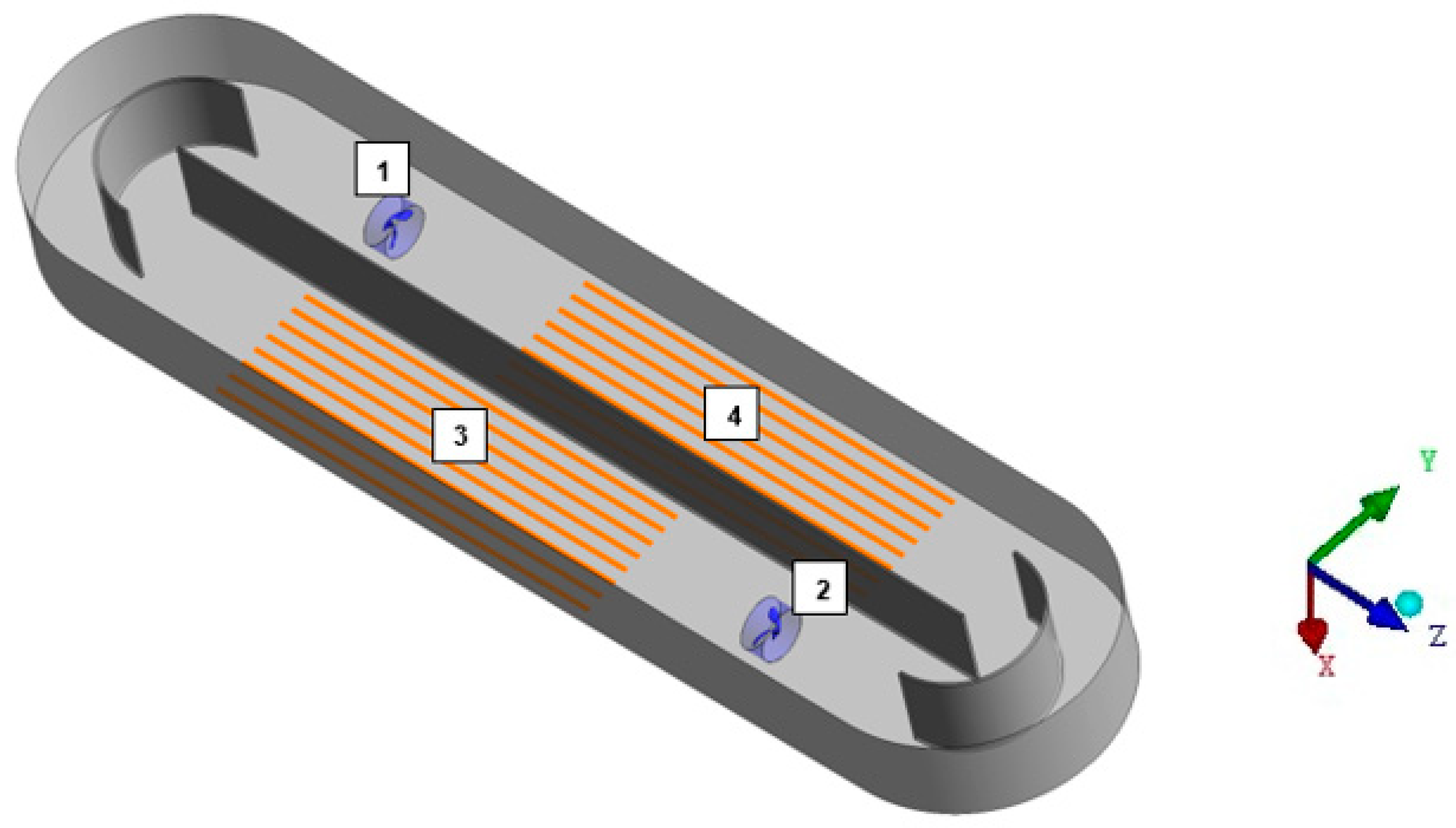


| Computational Geometry | Number of Nodes | Number of Elements |
|---|---|---|
| Tank | 1,557,159 | 7,083,099 |
| Agitator | 440,350 | 2,306,427 |
| Mesh Independence Study | Total Number of Elements (Millions) |
|---|---|
| Mesh A | 8.41 |
| Mesh B | 11.63 |
| Mesh C | 20.47 |
| Parameters | Case 1 | Case 2 | ||
|---|---|---|---|---|
| Flowmaker 1 | Flowmaker 2 | Flowmaker 1 | Flowmaker 2 | |
| 9.96 m | 9.96 m | 9 m | 9 m | |
| C | 10.24 m | 10.09 m | 11.20 m | 11.05 m |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Höhne, T.; Mamedov, T. CFD Simulation of Aeration and Mixing Processes in a Full-Scale Oxidation Ditch. Energies 2020, 13, 1633. https://doi.org/10.3390/en13071633
Höhne T, Mamedov T. CFD Simulation of Aeration and Mixing Processes in a Full-Scale Oxidation Ditch. Energies. 2020; 13(7):1633. https://doi.org/10.3390/en13071633
Chicago/Turabian StyleHöhne, Thomas, and Tural Mamedov. 2020. "CFD Simulation of Aeration and Mixing Processes in a Full-Scale Oxidation Ditch" Energies 13, no. 7: 1633. https://doi.org/10.3390/en13071633
APA StyleHöhne, T., & Mamedov, T. (2020). CFD Simulation of Aeration and Mixing Processes in a Full-Scale Oxidation Ditch. Energies, 13(7), 1633. https://doi.org/10.3390/en13071633





