Optimal Reconfiguration of Distribution Networks Using Hybrid Heuristic-Genetic Algorithm
Abstract
1. Introduction
- Efficient initial topology generation, which is achieved by a combing heuristic approach in combination with a stochastic Kruskal algorithm. The Kruskal algorithm is modified in a way which links the branch weights with physical power flows in the network.
- Efficient utilization of BIBC (bus injection—branch current) matrix to detect different parts of the cycle relevant to analytical expression in the heuristic branch exchange algorithm. Additionally, the proposed algorithm defines the universal BIBC matrix for the meshed network, from which another BIBC matrix can be easily derived utilizing Kron’s reduction method, in case of network topology modification. This proves to be numerically efficient, given that this matrix is also used in the load flow calculation process.
- Modification of the crossover and mutation processes in the genetic algorithm which assure network radial topology and the transfer of good genetic materials (different parts of network structure) through evolution epochs. These modifications eliminate the possibility of unfeasible solutions usually present in other approaches and assure a relatively fast convergence rate, in relation to similar approaches.
- Possibility of applying proposed method on large scale distribution networks, while obtaining equal or better solution quality for all test cases with significantly lower computational time. Lower computational time is especially pronounced on larger distribution networks, with computational times smaller by the order of magnitude in relation to results from references surveyed. In addition to this, the proposed solution approach is suitable for the parallelization on multicore CPU, giving the opportunity for even shorter computational times.
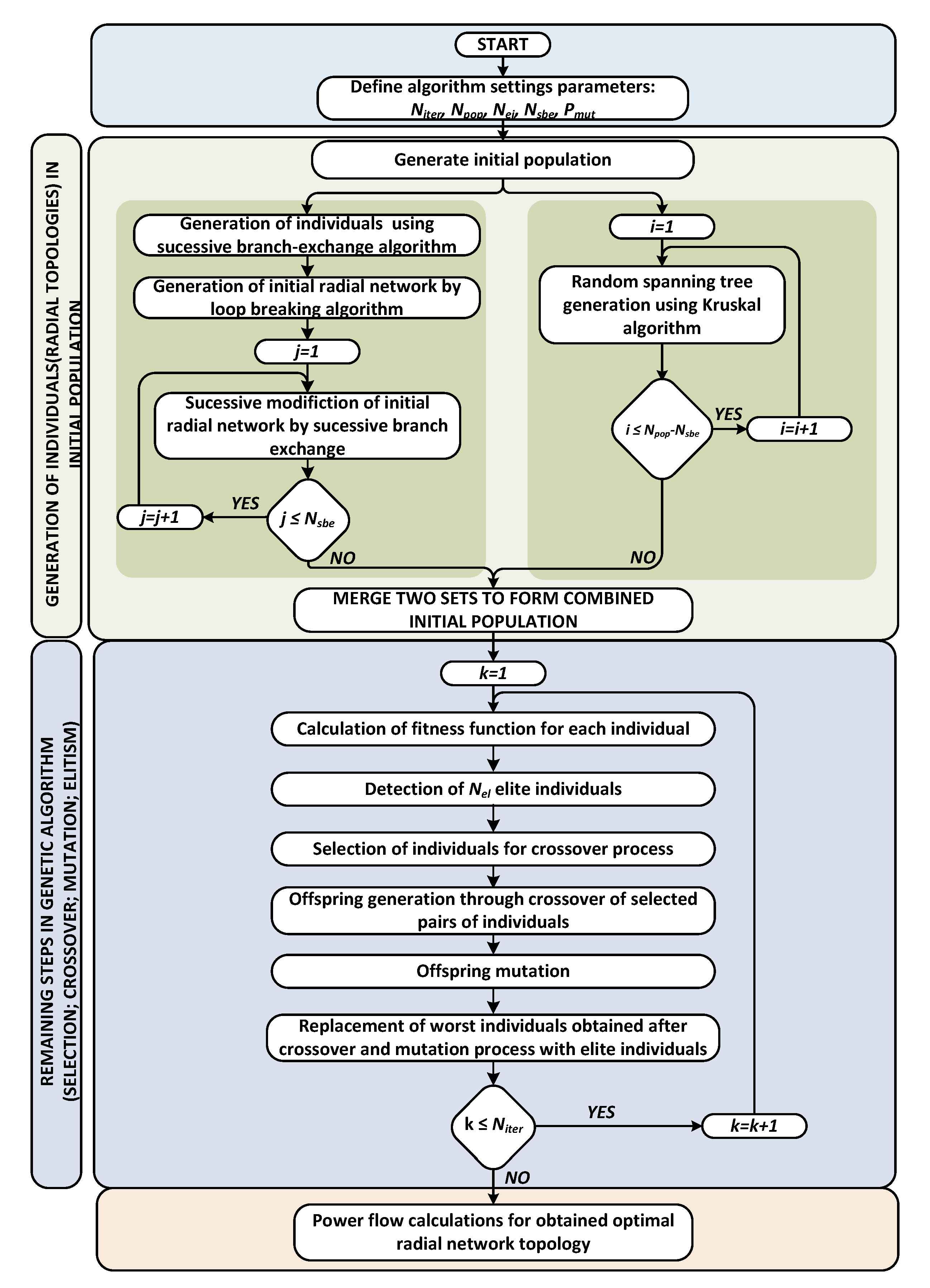
2. Optimal Reconfiguration of Distribution Networks Using Hybrid Heuristic-Genetic Algorithm
- Minimization of total network active power losses:where:
- —total active power losses in network
- Nbr —set of online branches in the distribution network,
- gk —conductance of kth branch that connects bus i and bus j,
- Ui —voltage magnitude of bus i,
- ϑij —voltage angle difference between bus i and bus j.
- Optimal element load balancing:where:
- —network loading index,
- Pk—active power flow through branch k (connecting bus i and bus j),
- Qk—reactive power flow through branch k (connecting bus i and bus j),
- —rated power of branch k,
- wk—weight factor assigned to branch k.
- Niter—number of evolution cycles
- Npop—population size
- Nei—number of elite individuals in each population
- Nsbe—number of individuals generated by successive branch exchange algorithm
- Pmut—mutation probability.
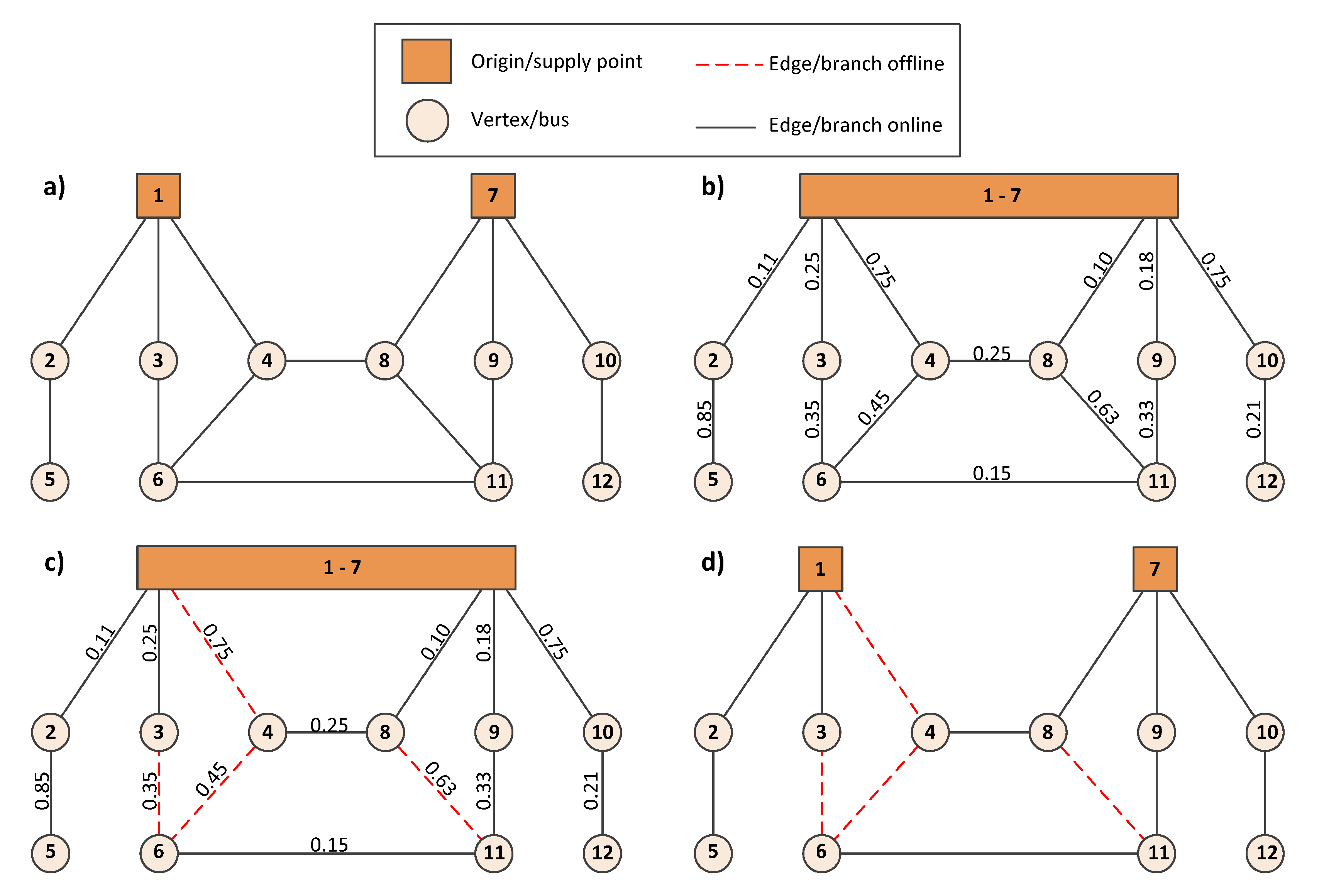
3. Initial Population (Feasible Radial Network Topologies) Generation
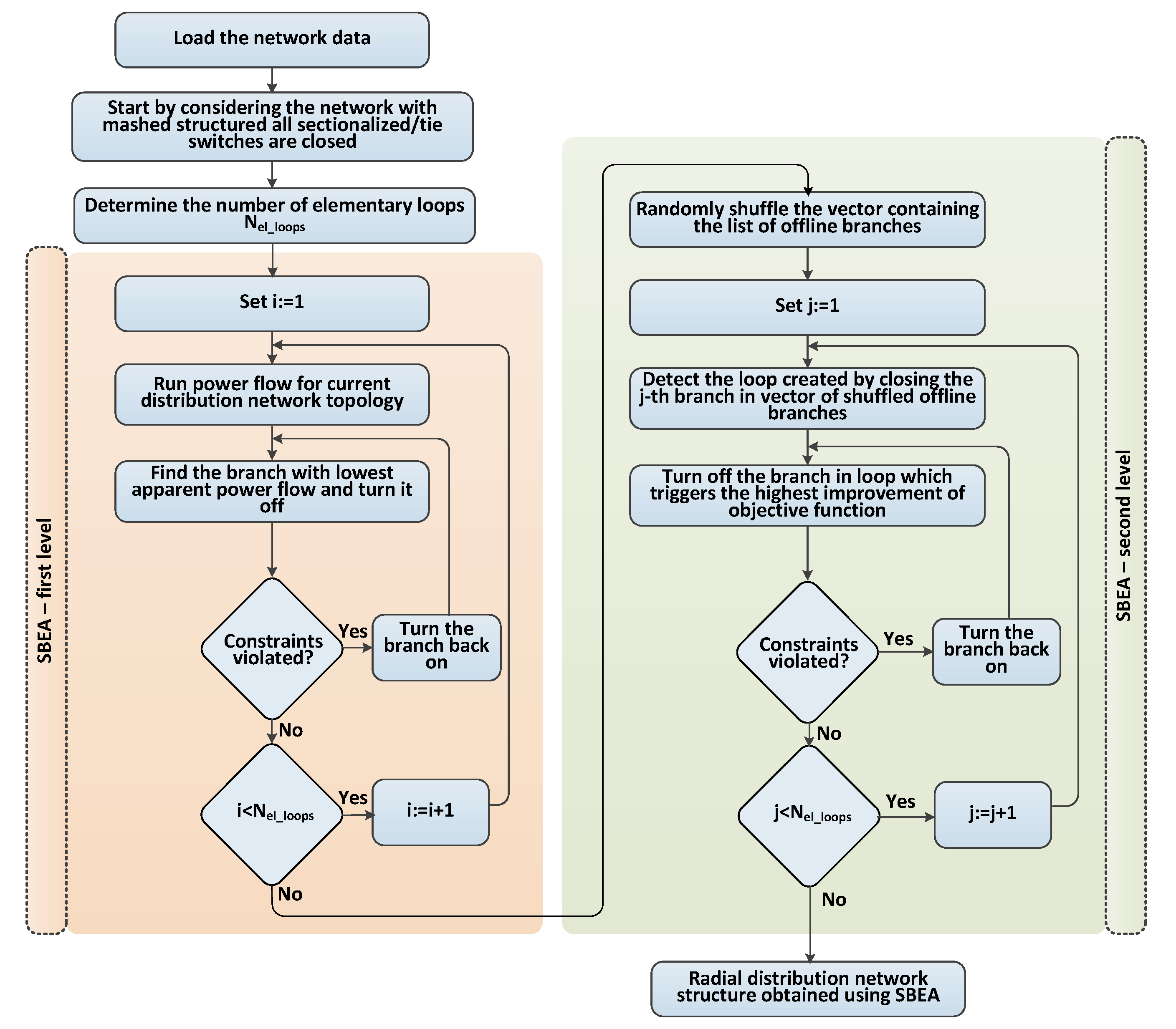
3.1. Heuristic Method—Successive Branch-Exchange Algorithm (SBEA)
- ➢
- The first level determines the initial spanning tree (initial radial distribution network structure), which is further improved in the second level. The first level starts with the mashed distribution network, in which all the sectionalizing and tie switches are closed. After creating the meshed distribution network, we conduct Nel_cycles power flow calculations, each time opening the branch (or sectionalizing/tie switch) with the lowest power flow, while avoiding such operation results with isolated parts of the network or unwanted grid operating conditions. Nel_cycles represents the number of elementary cycles in the mashed distribution network, which can be calculated as:where NSP is a number of supply points.Nel_cycles = Nbr − (Nbus − NSP)The detection of the branch to be opened in each step, while avoiding isolation of a certain part of the network, can be performed by applying the Kruskal’s [25] or Prim’s [26] algorithm, for a minimum spanning tree, in which each branch has weight reversely proportional to power flow running through it. If the distribution network has multiple supply points, we can merge them into a single supply point, reducing the problem of the minimum spanning forest to the problem of a minimum spanning tree. This way, using Kruskal’s or Prim’s algorithm, we get the set of branches (the number of which is reduced in each iteration), not comprising the spanning tree, and we simply choose to open the line with the highest weight from the obtained set. Using this procedure, we sequentially switch-off Nel_cycles branches, obtaining, after this step, the initial radial fully connected distribution network. This way, we least interfere in power flows that would normally flow in mashed distribution network and assure a good power flow pattern for the initial radial distribution network, with low system losses.After this step, we get the vector containing the lists of branches (or sectionalizing/tie switches) that are offline in the initially generated radial distribution network.
- ➢
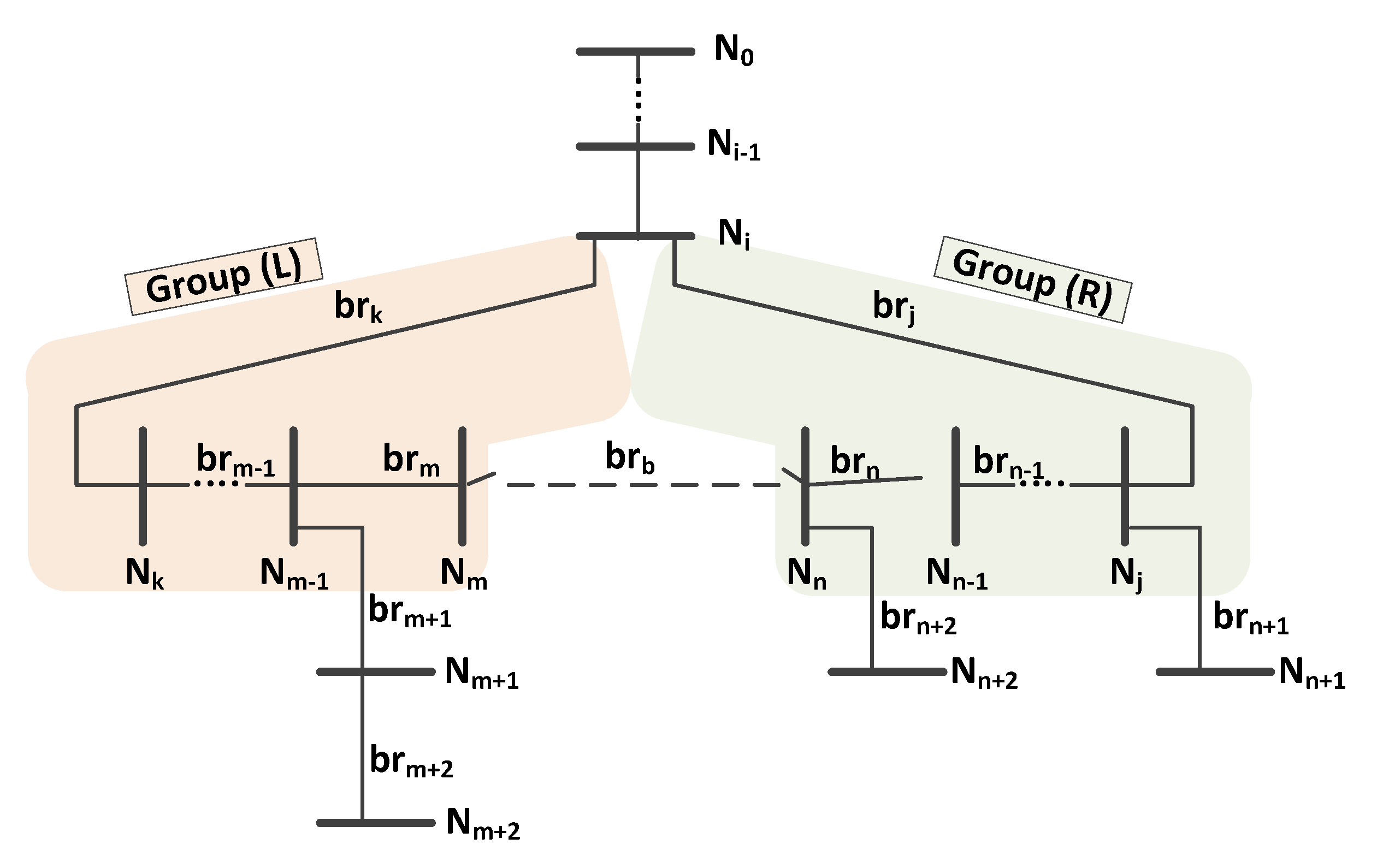
- The second level includes further improvements of the network topology obtained after the first level of SBEA. This involves the generation of a random mask vector obtained by the random shuffling of vector , indicating offline branches. For example, the shuffled vector [br60, br3, …] indicates that we first form a cycle by closing branch 60, and try to find the branch to open in a newly formed cycle that improves the objective function in the best way. If such a branch exists, we replace branch 60 with that branch in the vector containing the list of offline branches. After that, we close branch 3, and try to find the branch to open in that single newly formed cycle, in order to improve objective function, and we repeat this process according to the generated random mask vector. In this step, we use approximate equations for load flow calculations in radial distribution networks, which facilitate the generation of individuals using SBEA in a small fraction of time.Figure 2 shows the simplified distribution network with a single cycle, in which branch (b) is opened to fulfil radiality constraint. In each second loop step in SBEA, we fictively close a single branch and form a single cycle. By opening any branch in that cycle, we mainly change power flows along branches forming that cycle, with minor influence on power flows along other branches in the distribution network. If we use the approximate linearized power flows equation, we can reformulate objective functions as follows:
- Minimization of total network active power losses:The linearization of active power losses is conducted by neglecting the higher order terms related to voltages in branch power loss expressions appearing in denominator:This approximation of branch power losses is used only in population initialization to create a set of initial candidate solutions based on a heuristic approach, which uses an analytical expression derived from the linearized power loss expression to approximate loss change or loading index change in the branch exchange process. All other steps (calculation of fitness function, voltage conditions, power flows) in the algorithm use the exact full non-linear load flow expressions.
- Optimal network loading:Now, consider the branch exchange between branches b (which is originally opened) and m (which is originally closed) in Figure 2. As a result of the simplifying assumptions made above, power flow will change only in the branches, constituting the cycle shown in Figure 2. Let the branches in the cycle that extends between nodes [i, k, …, m-1, m] be denoted by the set L and the ones on the other side between nodes [i, j, … , n-1, n] by the set R.
- —reduction of total active energy losses due to branch exchange between branches b and m over period of time T
- —reduction of network loading index for set of time periods T due to branch exchange between branches b and m
- —active/reactive power flow through branch i for time period t
- —duration of time period t in hours
- T—set of time periods
- (1)
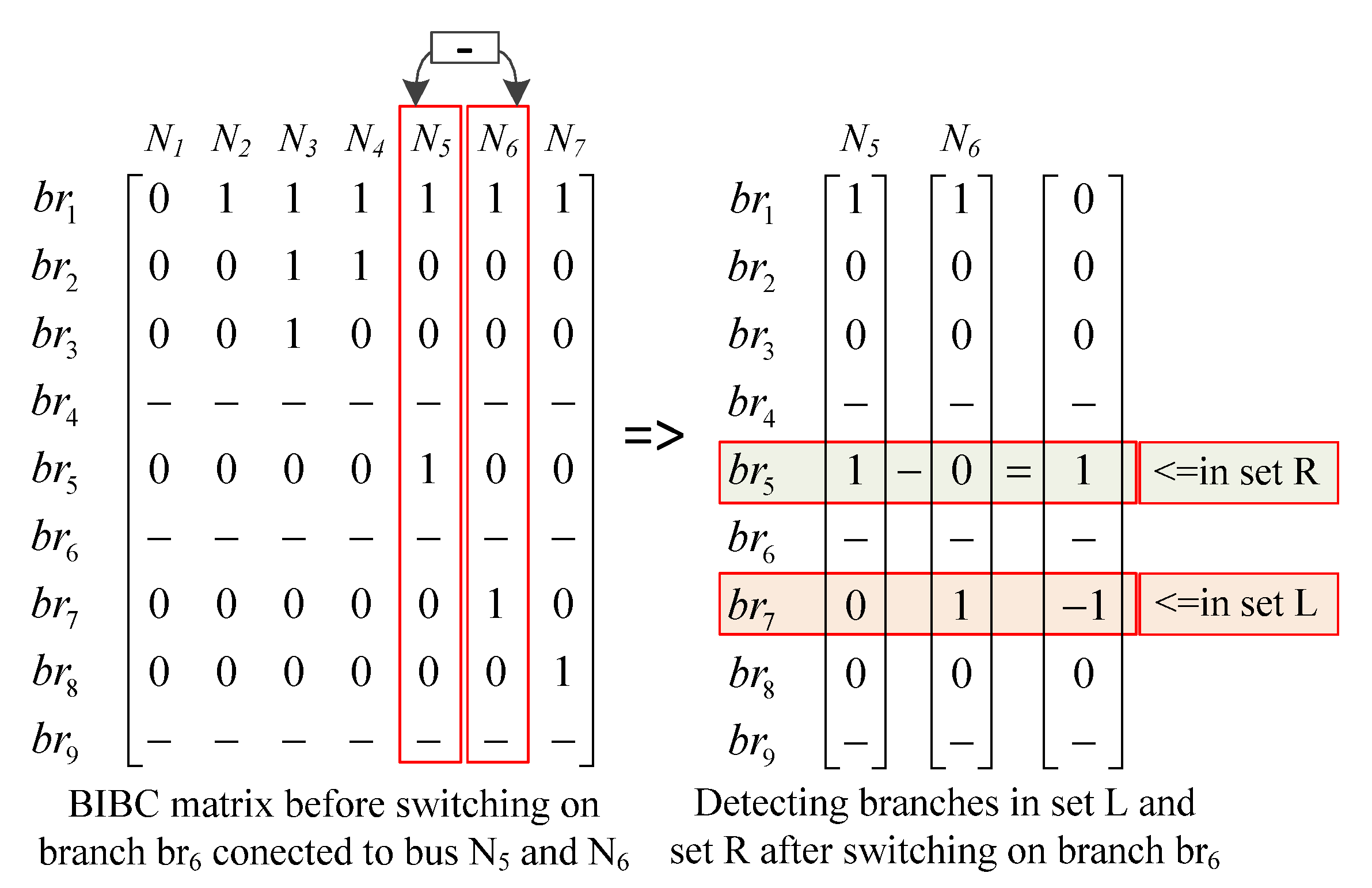
- For the distribution system with Nbr branches and Nbus buses, start by creating a zero BIBC matrix with the dimension Nbr x Nbus.
- (2)
- If a branch brk connecting bus i and bus j does not form a cycle in the network, copy the column of the i -th bus of the BIBC matrix to the column of the j -th bus and fill a +1 to the position of the k -th row and the j -th bus column. Otherwise, if branch brk forms a cycle in the network proceed to step (3).
- (3)
- If a branch brk located between bus i and bus j forms a cycle in the network, in k-th, the column places the elements of the i-th bus column, subtracted by the j-th bus column. In addition to that, fill a +1 value to the position of the k-th row and the j-th column.
- (4)
- Repeat the procedure from step (2), until all branches are included in the BIBC matrix.
- (5)
- Using the steps described above, we can form the BIBC matrix for the mashed distribution network, in which all cycles are closed. To obtain the BIBC matrix for the radial distribution network, we can use modified Krons reduction to eliminate offline branches. This way, we obtain the BIBC matrix for the radial distribution network.
3.2. Stochastic Method—Kruskal’s Algorithm
|
|
|
|
|
|
| If u and v don’t belong to set T: |
| Add (u,v) to T; |
| Add edge (u,v) to the set of online edges; |
| Return T and set of online edges; |
|
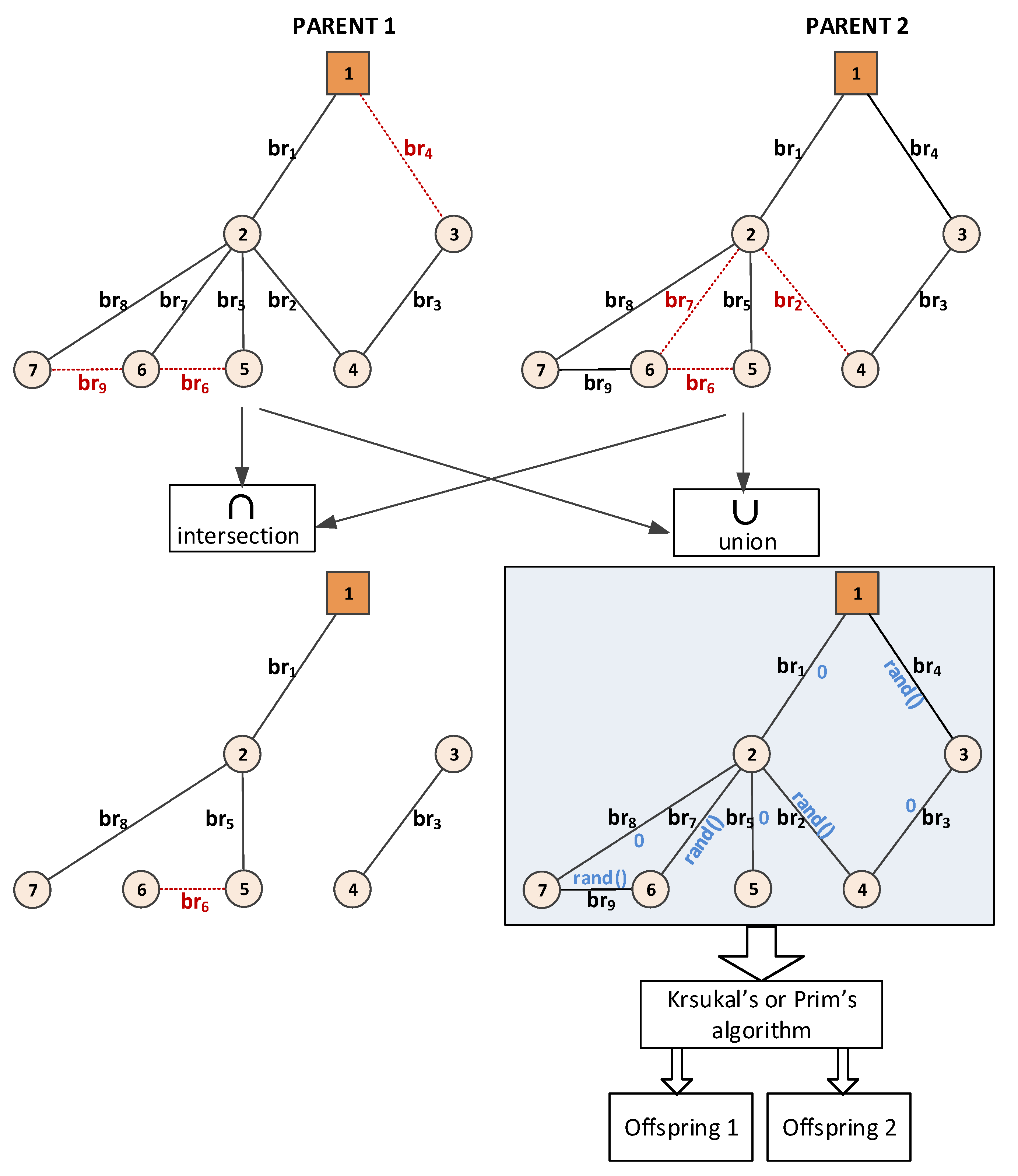
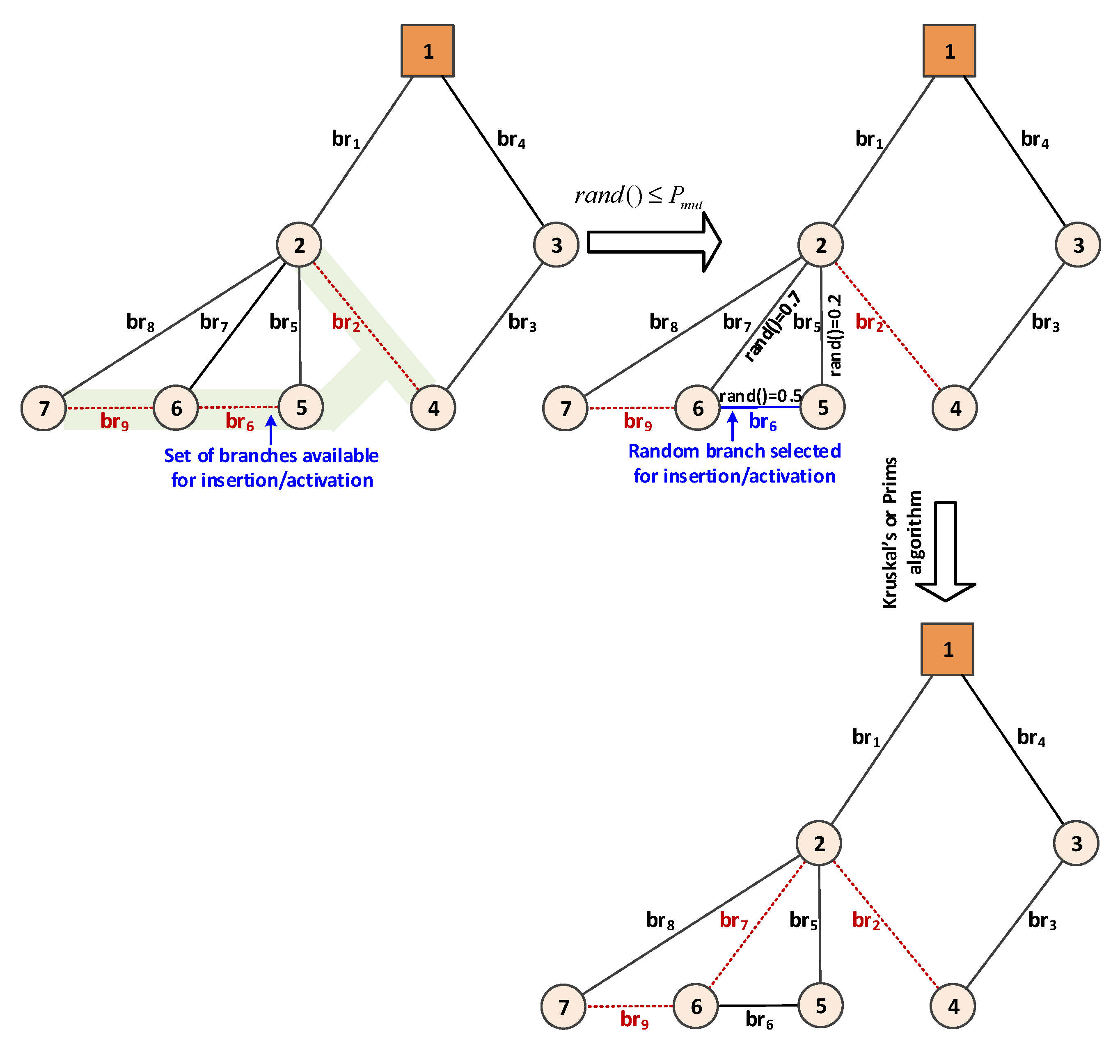
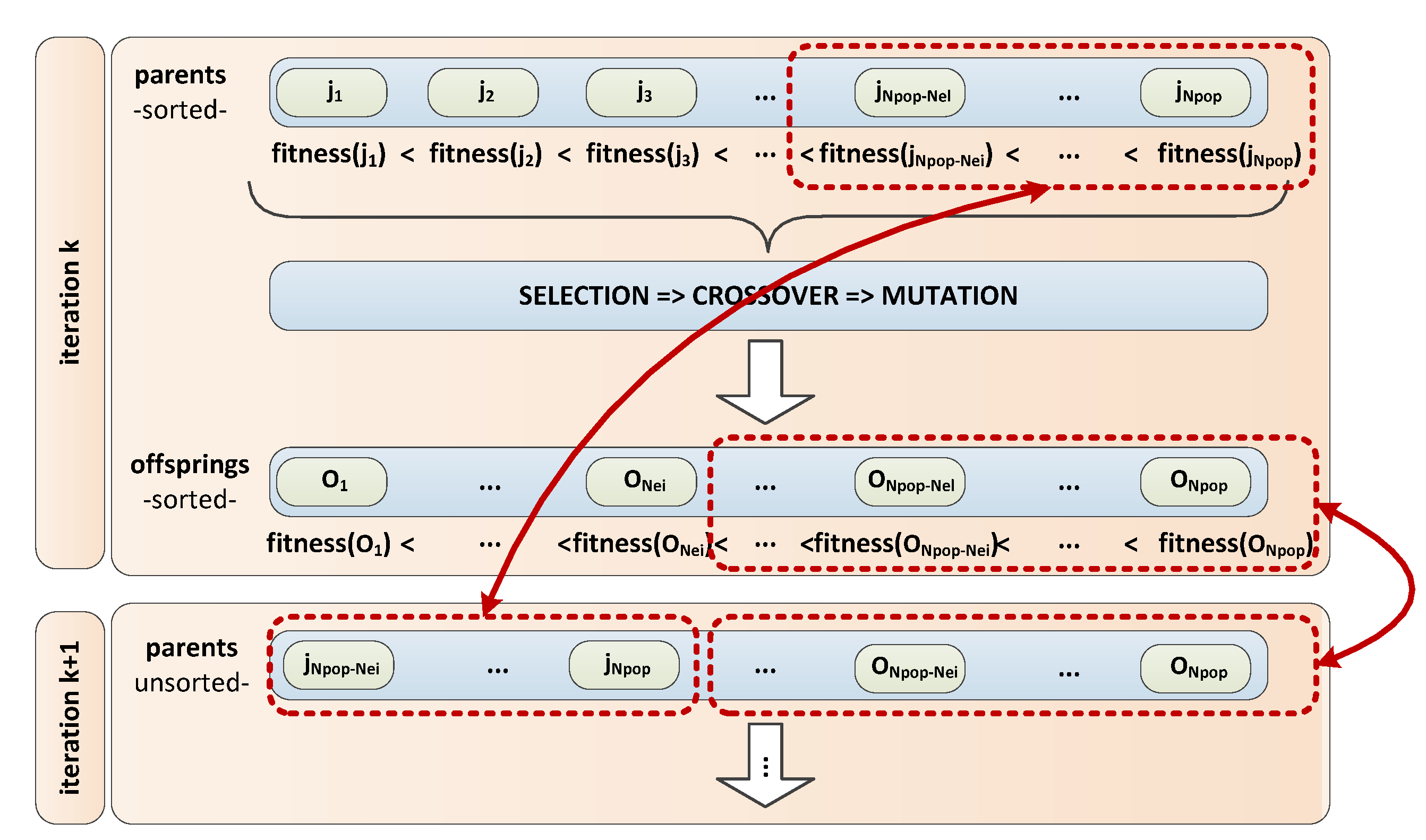
4. Adaption of Other Steps in Genetic Algorithm
4.1. Fitness Function Calculation and Separation of Elite Individuals
4.2. Crossover Process
4.3. Mutation Process
4.4. Elitism
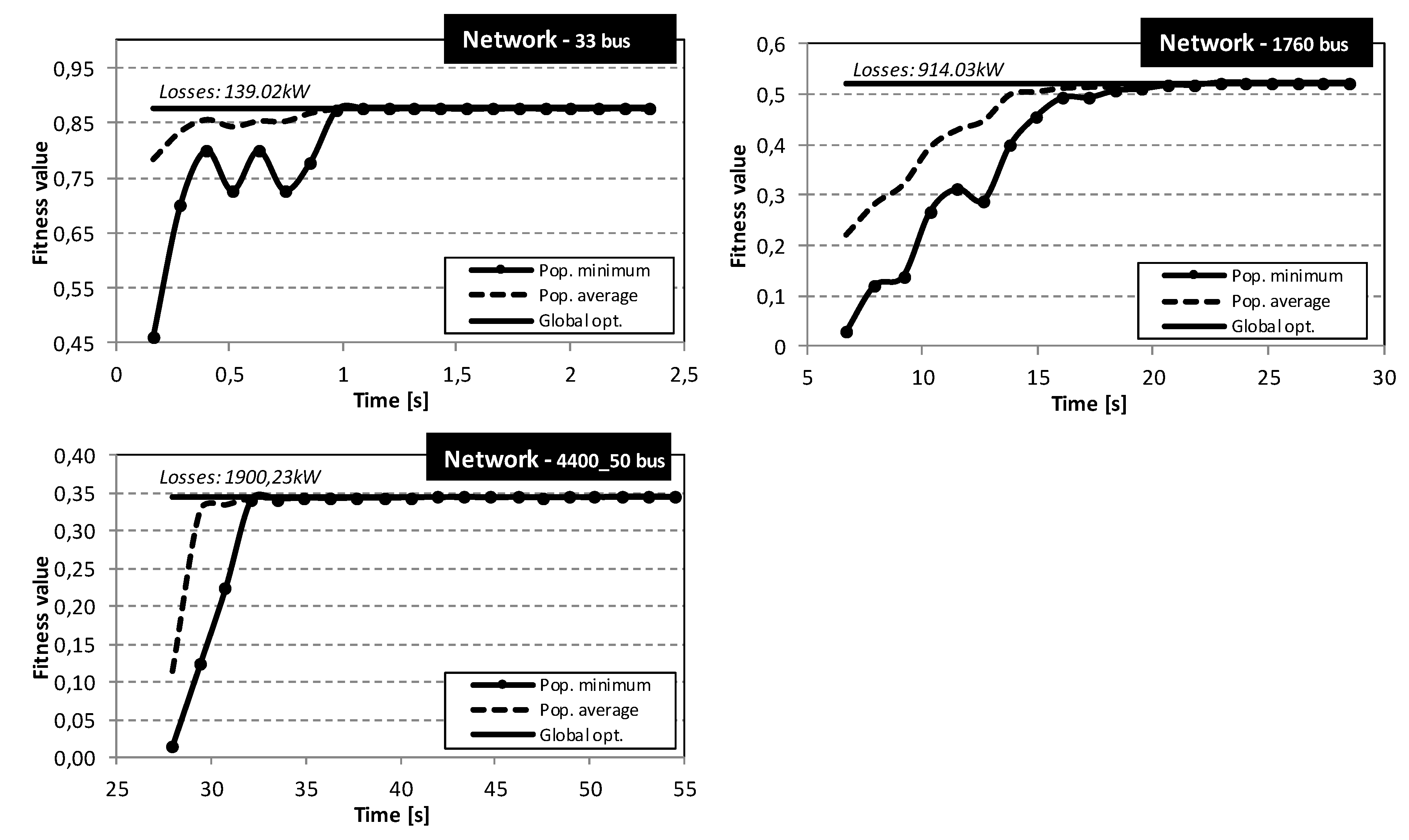
5. Case Study
- Network I—33 bus: The test system is a hypothetical 12.66 kV system with a single supply point, 33 busses and 5 elementary cycles (tie lines). The system data is given in [3], and this system is usually referred to as “Baran’s test case”. The total system load equals 5084.26 kW and 2547.32 kVAr. For the base case network topology, the total system losses equal to 210.99 kW. With the application of the proposed algorithm, the total system losses were reduced to 139.2 kW, which represents a 34.03% loss reduction in relation to the base case topology.
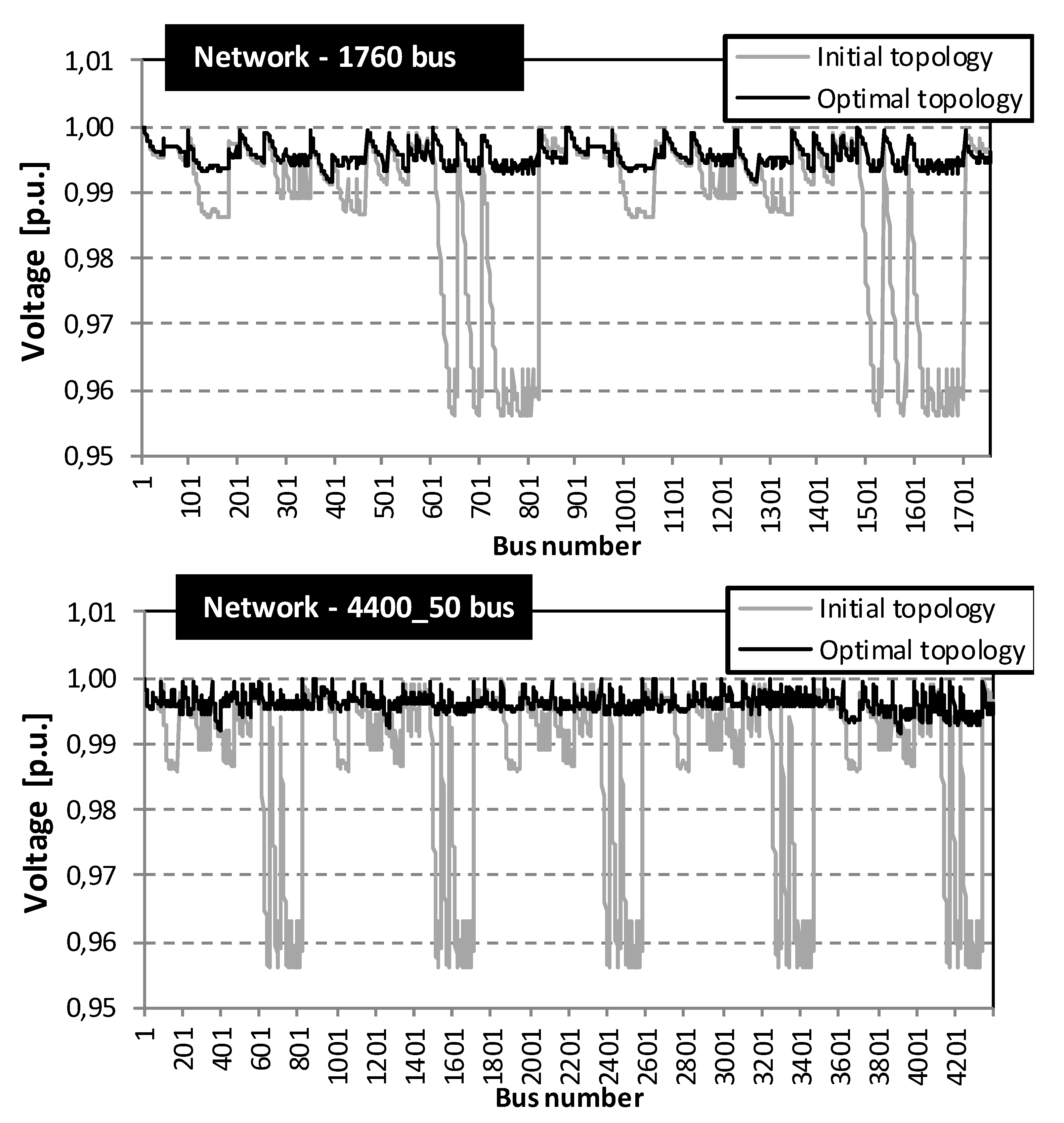
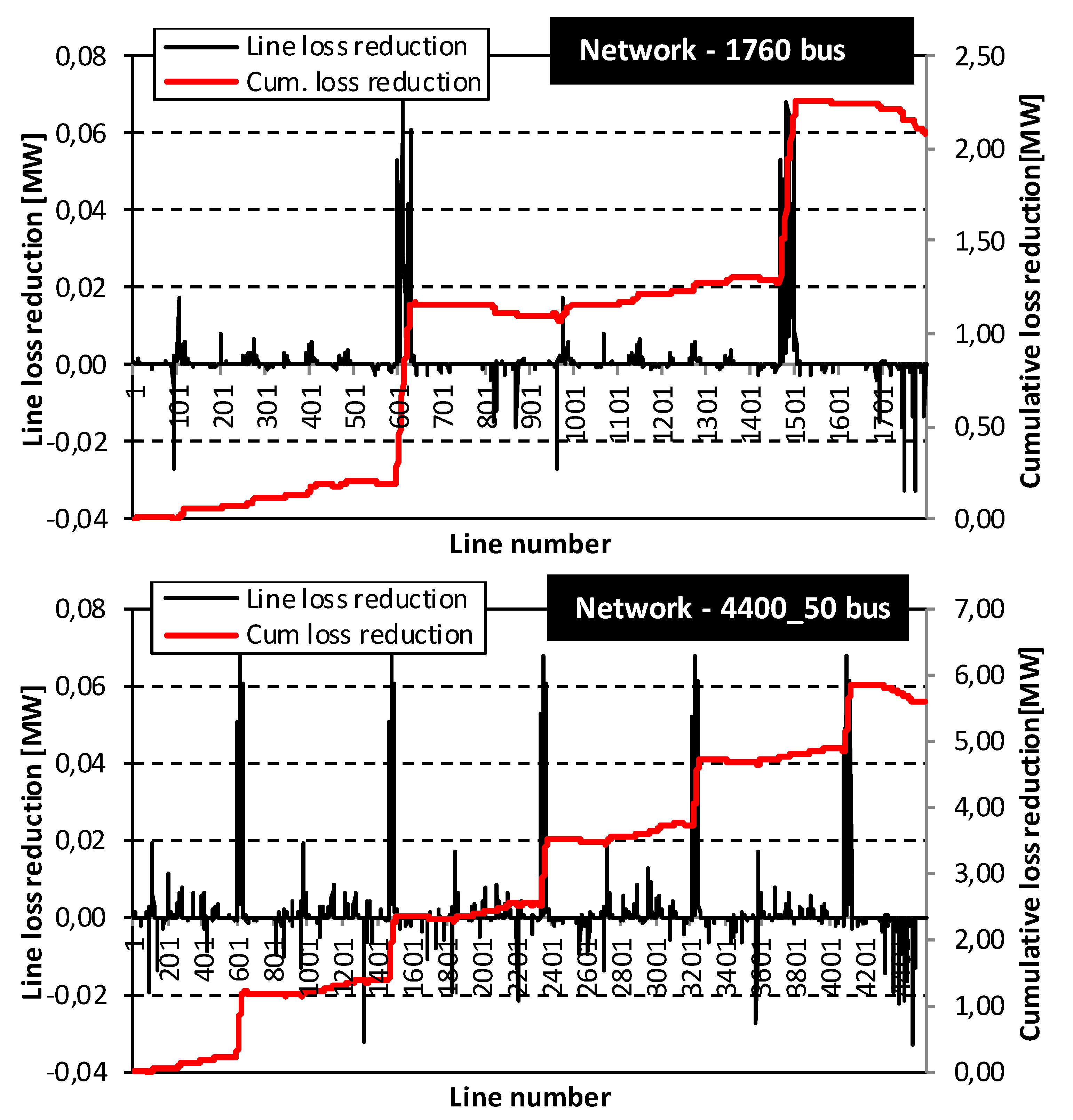
- Network II—1760 bus: The test system is a 130.8 kV system with 14 supply points, 1760 buses and 54 elementary cycles. The system data is given in [27]. The total system load equals 249.73 MW and 148.72 MVAr. For the base case network topology, the total system losses equal to 2.992 MW. With the application of the proposed algorithm, the total system losses were reduced to 914.02 kW, which represents a 69.46% loss reduction, in relation to the base case topology.
- Network III—4400_50 bus: The test system is a 130.8 kV system with 35 supply points, 4400 buses and 185 elementary cycles. The system data is given in [27]. The total system load equals 624.34 MW and 371.80 MVAr. The total system losses for the initial network topology is equal to 7.481 MW. With the application of the proposed algorithm, the total system losses were reduced to 1.9 kW, which represents a 74.6% loss reduction, in relation to the initial network topology.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Civanlar, S.; Grainger, J.J.; Yin, H.; Lee, S.S.H. Distribution feeder reconfiguration for loss reduction. IEEE Trans. Power Deliv. 1988, 3, 1217–1223. [Google Scholar] [CrossRef]
- Abul’Wafa, A.R. A new heuristic approach for optimal reconfiguration in distribution systems. Electr. Power Syst. Res. 2011, 81, 282–289. [Google Scholar] [CrossRef]
- Baran, M.E.; Wu, F.F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 1989, 4, 1401–1407. [Google Scholar] [CrossRef]
- Rosseti, G.J.S.; de Oliveira, E.J.; de Oliveira, L.W.; Silva, I.C.; Peres, W. Optimal allocation of distributed generation with reconfiguration in electric distribution systems. Electr. Power Syst. Res. 2013, 103, 178–183. [Google Scholar] [CrossRef]
- Bahadoorsingh, S.; Milanović, J.V.; Zhang, Y.; Gupta, C.P.; Dragovic, J. Minimization of voltage sag costs by optimal reconfiguration of distribution network Using genetic algorithms. IEEE Trans. Power Deliv. 2007, 22, 2271–2278. [Google Scholar] [CrossRef]
- Kashem, M.A.; Ganapathy, V.; Jasmon, G.B. Network reconfiguration for enhancement of voltage stability in distribution networks. IEE Proc. Gener. Transm. Distrib. 2000, 147, 171. [Google Scholar] [CrossRef]
- Arun, M.; Aravindhababu, P. A new reconfiguration scheme for voltage stability enhancement of radial distribution systems. Energy Convers. Manag. 2009, 50, 2148–2151. [Google Scholar] [CrossRef]
- Zou, B.C.; Gong, Q.W.; Li, X.; Chen, D.J. Reconfiguration in distribution systems based on refined genetic algorithm for improving voltage quality. In Proceedings of the 2011 Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 25–28 March 2011; pp. 1–4. [Google Scholar]
- Roytelman, I.; Melnik, V.; Lee, S.S.H.; Lugtu, R.L. Multi-objective feeder reconfiguration by distribution management system. IEEE Trans. Power Syst. 1996, 11, 661–667. [Google Scholar] [CrossRef]
- Montoya, D.P.; Ramirez, J.M.; Zuluaga, J.R. Multi-objective optimization for reconfiguration and capacitor allocation in distribution systems. In Proceedings of the 2014 North American Power Symposium (NAPS), Pullman, WA, USA, 7–9 September 2014; pp. 1–6. [Google Scholar]
- Tomoiagă, B.; Chindriş, M.; Sumper, A.; Sudria-Andreu, A.; Villafafila-Robles, R. Pareto optimal reconfiguration of power distribution systems using a genetic algorithm based on NSGA-II. Energies 2013, 6, 1439–1455. [Google Scholar] [CrossRef]
- Morton, A.B.; Mareels, I.M.Y. An efficient brute-force solution to the network reconfiguration problem. IEEE Trans. Power Deliv. 2000, 15, 996–1000. [Google Scholar] [CrossRef]
- Taylor, J.A.; Hover, F.S. Convex models of distribution system reconfiguration. IEEE Trans. Power Syst. 2012, 27, 1407–1413. [Google Scholar] [CrossRef]
- Llorens-Iborra, F.; Riquelme-Santos, J.; Romero-Ramos, E. Mixed-integer linear programming model for solving reconfiguration problems in large-scale distribution systems. Electr. Power Syst. Res. 2012, 88, 137–145. [Google Scholar] [CrossRef]
- Abdelaziz, M. Distribution network reconfiguration using a genetic algorithm with varying population size. Electr. Power Syst. Res. 2017, 142, 9–11. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, F.; Zhang, Y. Distribution network reconfiguration based on simulated annealing immune algorithm. Energy Procedia 2011, 12, 271–277. [Google Scholar] [CrossRef]
- Tomoiagă, B.; Chindriş, M.; Sumper, A.; Villafafila-Robles, R.; Sudria-Andreu, A. Distribution system reconfiguration using genetic algorithm based on connected graphs. Electr. Power Syst. Res. 2013, 104, 216–225. [Google Scholar] [CrossRef]
- Queiroz, L.M.O.; Lyra, C. Adaptive hybrid genetic algorithm for technical loss reduction in distribution networks under variable demands. IEEE Trans. Power Syst. 2009, 24, 445–453. [Google Scholar] [CrossRef]
- Alemohammad, S.H.; Mashhour, E.; Saniei, M. A market-based method for reconfiguration of distribution network. Electr. Power Syst. Res. 2015, 125, 15–22. [Google Scholar] [CrossRef]
- Tahboub, A.M.; Pandi, V.R.; Zeineldin, H.H. Distribution system reconfiguration for annual energy loss reduction considering variable distributed generation profiles. IEEE Trans. Power Deliv. 2015, 30, 1677–1685. [Google Scholar] [CrossRef]
- Montoya, D.P.; Ramirez, J.M.; Theory, A.G. A minimal spanning tree algorithm for distribution networks configuration. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–7. [Google Scholar]
- Wu, O.; Cheng, H.; Zhang, X.; Yao, L.; Bazargan, M. Random Spanning Tree Based Improved GA for Distribution Reconfiguration. In Proceedings of the 2009 Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 27–31 March 2009; pp. 1–4. [Google Scholar]
- Zhang, J.; Yuan, X.; Yuan, Y. A novel genetic algorithm based on all spanning trees of undirected graph for distribution network reconfiguration. J. Mod. Power Syst. Clean Energy 2014, 2, 143–149. [Google Scholar] [CrossRef]
- Swarnkar, A.; Gupta, N.; Niazi, K.R. A novel codification for meta-heuristic techniques used in distribution network reconfiguration. Electr. Power Syst. Res. 2011, 81, 1619–1626. [Google Scholar] [CrossRef]
- Kruskal, J.B. On the shortest spanning subtree of a graph and the traveling salesman problem. Proc. Am. Math. Soc. 1956, 7, 48–50. [Google Scholar] [CrossRef]
- Prim, R.C. Shortest connection networks and some generalizations. Bell Syst. Tech. J. 1957, 36, 1389–1401. [Google Scholar] [CrossRef]
- Distribution Feeder Reconfiguration (DFR) Test Cases. Available online: http://roberge.segfaults.net/joomla/index.php/dfr (accessed on 15 March 2020).
| Buses (Nbus) | Supply Points (NSP) | Lines (Nbr) | Sectionalizing Switches | Tie Switches | Initial Losses (kW) |
|---|---|---|---|---|---|
| 33 | 1 | 37 | 32 | 5 | 210.99 |
| 1760 | 14 | 1800 | 1746 | 54 | 2992.00 |
| 4400_50 | 35 | 4550 | 4365 | 185 | 7481.70 |
| Test Network | Losses (Kw) | Losses Reduction (%) | Computational Time(s) | |||
|---|---|---|---|---|---|---|
| Hybrid Heur.-Gen. | MIQP | MIQCP | MISOCP | |||
| Offline Branches | ||||||
| Network I (33bus) | 139.2 | 34.03% | 0.396 | 0.57 (r.g. = 2%) | 2.14 (r.g. = 2%) | 2.801 (r.g. = 2%) |
| 7; 9; 14; 32; 37 | ||||||
| Network II (1760bus) | 914.1 | 69.46% | 9.18 | >36,000 (r.g. = 2%) | >36,000 (r.g. = 2%) | >36,000 (r.g. = 2%) |
| 84; 130; 141; 159; 190; 282; 288; 306; 312; 409; 411; 452; 494; 596; 616; 630; 631; 637; 698; 815; 844; 957; 1003; 1014; 1032; 1063; 1155; 1161; 1179; 1185; 1282; 1284; 1325; 1367; 1469; 1489; 1503; 1504; 1510; 1571; 1688; 1717; 1758; 1761; 1762; 1763; 1769; 1773; 1785; 1788; 1789; 1790; 1796; 1800 | ||||||
| Network III (4400_50bus) | 1900.2 | 74.60% | 30.77 | >36,000 (r.g. = 2%) | >36,000 (r.g. = 2%) | >36,000 (r.g. = 2%) |
| 81; 84; 117; 136; 168; 190; 232; 239; 282; 284; 288; 334; 399; 406; 424; 434; 447; 453; 494; 558; 613; 616; 627; 634; 639; 645; 647; 794; 812; 843; 916; 953; 958; 992; 1003; 1018; 1041; 1062; 1101; 1113; 1154; 1158; 1179; 1184; 1187; 1198; 1280; 1283; 1307; 1357; 1427; 1466; 1485; 1501; 1504; 1509; 1513; 1518; 1571; 1667; 1691; 1716; 1730; 1744; 1794; 1829; 1865; 1880; 1919; 1961; 1990; 2028; 2032; 2052; 2071; 2076; 2089; 2129; 2152; 2162; 2190; 2198; 2204; 2237; 2241; 2300; 2305; 2341; 2360; 2361; 2374; 2378; 2382; 2385; 2394; 2427; 2444; 2564; 2590; 2609; 2693; 2742; 2752; 2762; 2786; 2811; 2860; 2897; 2907; 2925; 2931; 2934; 3000; 3012; 3028; 3030; 3066; 3069; 3076; 3110; 3115; 3193; 3198; 3215; 3232; 3240; 3249; 3261; 3265; 3268; 3309; 3431; 3463; 3576; 3622; 3633; 3651; 3682; 3774; 3780; 3798; 3804; 3901; 3903; 3944; 3986; 4088; 4108; 4122; 4123; 4129; 4190; 4307; 4336; 4377; 4378; 4383; 4385; 4392; 4407; 4411; 4419; 4421; 4435; 4446; 4450; 4473; 4485; 4488; 4489; 4490; 4496; 4500; 4506; 4513; 4520; 4523; 4524; 4527; 4528; 4530; 4537; 4539; 4541; 4550; | ||||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jakus, D.; Čađenović, R.; Vasilj, J.; Sarajčev, P. Optimal Reconfiguration of Distribution Networks Using Hybrid Heuristic-Genetic Algorithm. Energies 2020, 13, 1544. https://doi.org/10.3390/en13071544
Jakus D, Čađenović R, Vasilj J, Sarajčev P. Optimal Reconfiguration of Distribution Networks Using Hybrid Heuristic-Genetic Algorithm. Energies. 2020; 13(7):1544. https://doi.org/10.3390/en13071544
Chicago/Turabian StyleJakus, Damir, Rade Čađenović, Josip Vasilj, and Petar Sarajčev. 2020. "Optimal Reconfiguration of Distribution Networks Using Hybrid Heuristic-Genetic Algorithm" Energies 13, no. 7: 1544. https://doi.org/10.3390/en13071544
APA StyleJakus, D., Čađenović, R., Vasilj, J., & Sarajčev, P. (2020). Optimal Reconfiguration of Distribution Networks Using Hybrid Heuristic-Genetic Algorithm. Energies, 13(7), 1544. https://doi.org/10.3390/en13071544






