Sensitivity Analysis of the Impact of the Sub- Hourly Stochastic Unit Commitment on Power System Dynamics
Abstract
1. Introduction
1.1. Motivation
1.2. Literature Review
1.3. Contributions
- A cosimulation framework that allows to assess the effect that different subhourly SUC models have on the long-term dynamic behaviour of power systems.
- A thorough sensitivity analysis with respect to the interaction between different subhourly SUC models, different frequency control/machine parameters and power system dynamics.
- Show through the aforementioned analysis that synchronous machine inertia has little effect on the standard deviation of the frequency. This result is in accordance with the discussion provided in [4].
- Show that the gain of automatic generation control (AGC) is (most of the time) the main parameter affecting the standard deviation of the frequency.
1.4. Organization
2. Modeling
2.1. Stochastic Long-Term Power System Model
2.2. Wind Power Modeling
2.3. Primary and Secondary Frequency Controllers of Conventional Power Plants
2.4. Stochastic Unit Commitment
2.5. Simplified SUC Formulation
2.6. Alternative SUC Formulation
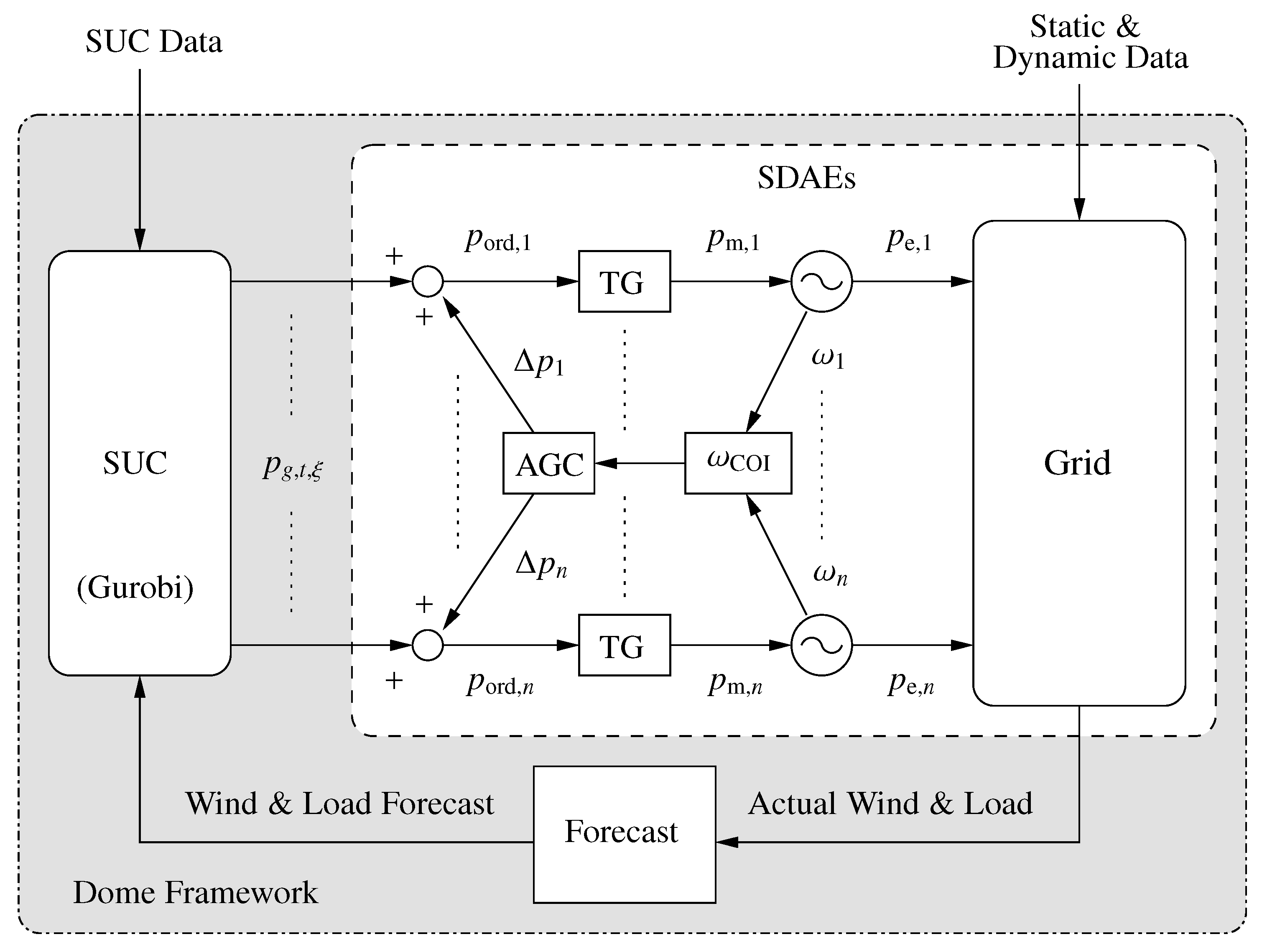
2.7. Cosimulation Framework
3. Case Study
3.1. Sensitivity Analysis of the Impact of Different Frequency Controllers/Machine Parameters
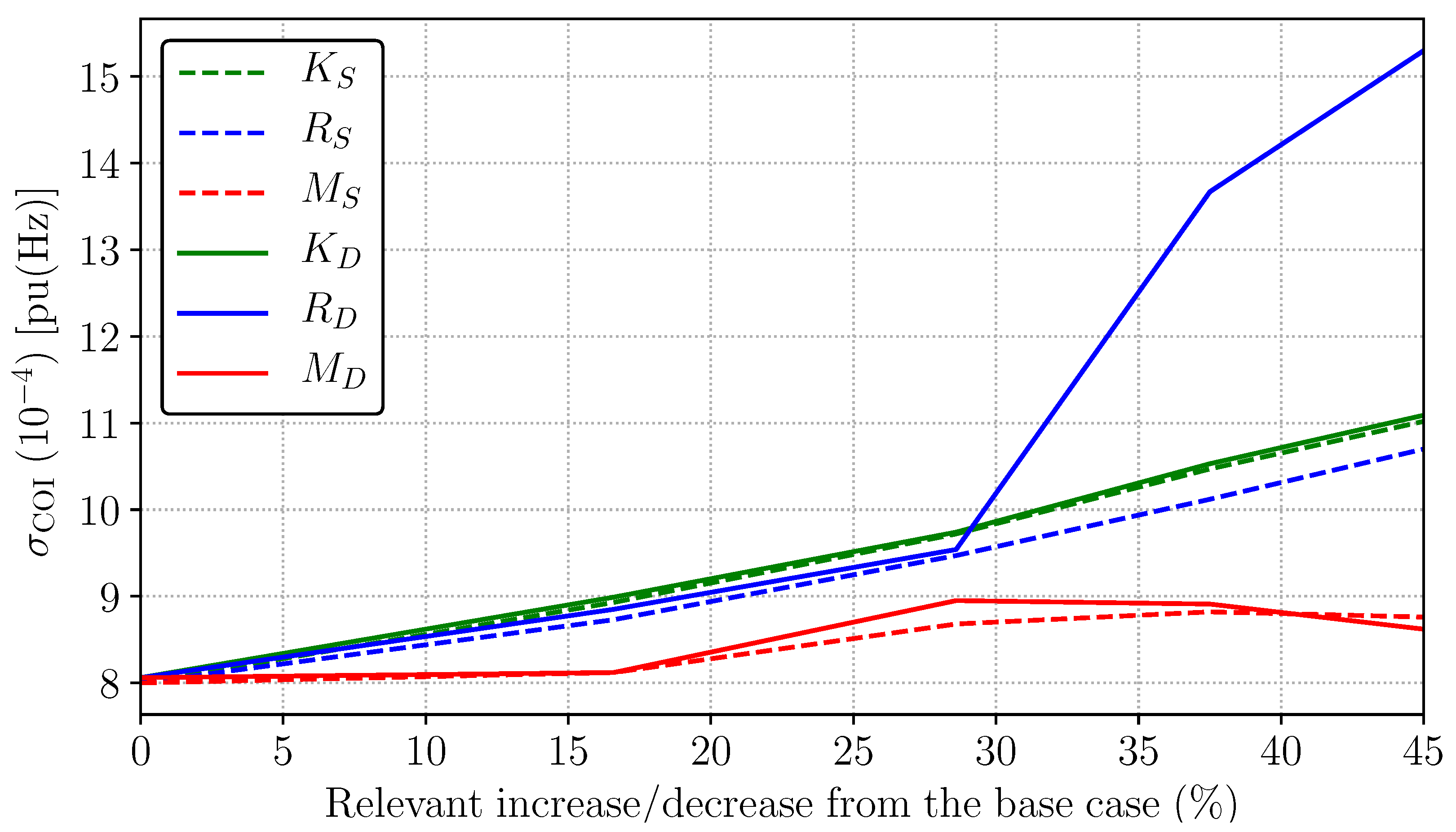
3.1.1. SUC with 15-min Time Period
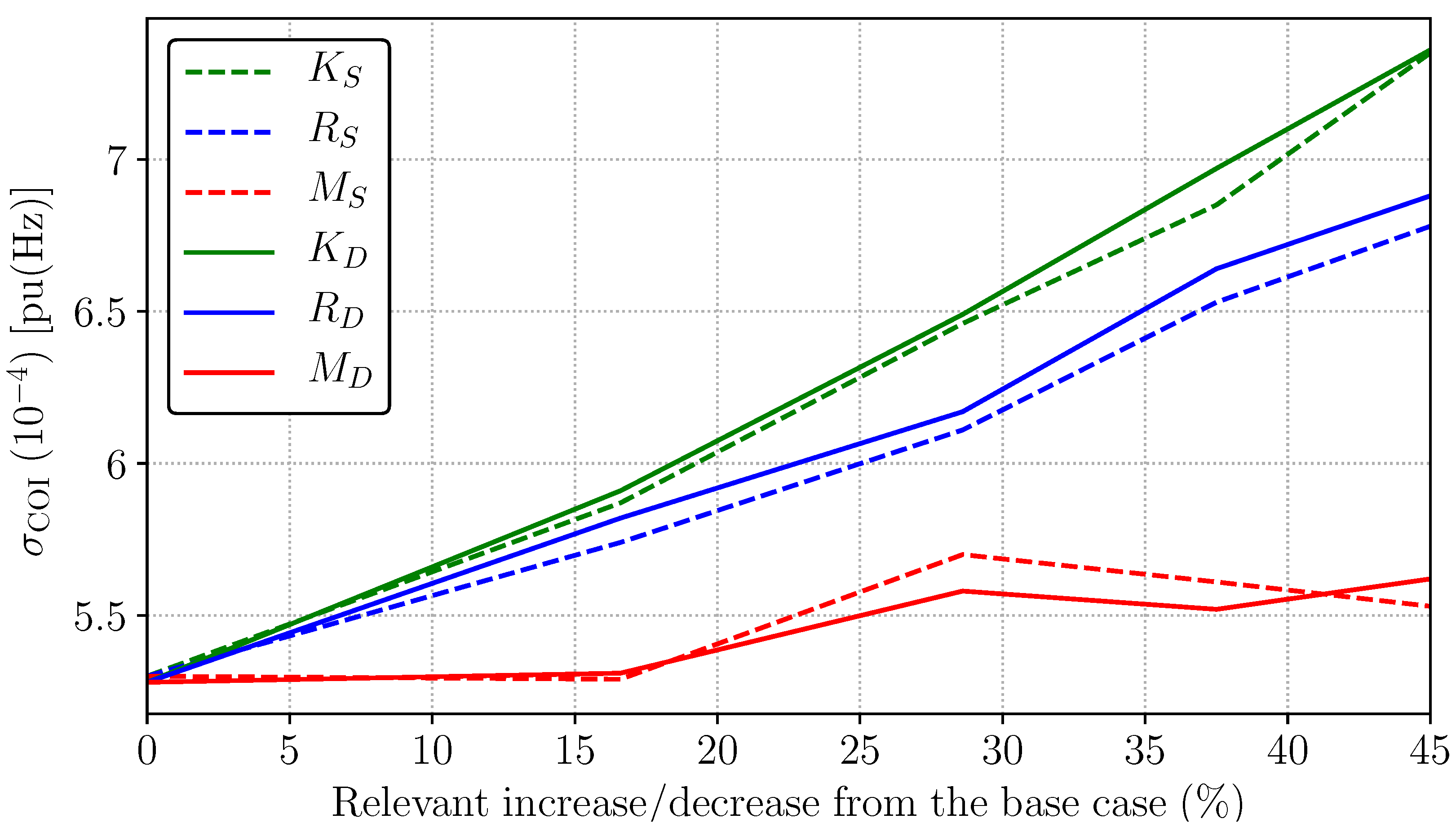
3.1.2. DUC with 15-min Time Period
3.1.3. Sensitivity Analysis Using the Simplified and Alternative SUC, and 15-min Time Period
3.1.4. SUC with 5-min Time Period
3.1.5. DUC with 5-min Time Period
3.2. Comparison of Different SUC Models
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- ENTSO-E. Continental Europe Significant Frequency Deviations January 2019. Available online: https://www.entsoe.eu (accessed on 17 February 2020).
- Kundur, P.; Paserba, J.; Ajjarapu, V.; Andersson, G.; Bose, A.; Cañizares, C.; Hatziargyriou, N.; Hill, D.; Stankovic, A.; Taylor, C.; et al. Definition and classification of power system stability IEEE/CIGRE joint task force on stability terms and definitions. IEEE Trans. Power Syst. 2004, 19, 1387–1401. [Google Scholar]
- Kërçi, T.; Milano, F. A framework to embed the unit commitment problem into time domain simulations. In Proceedings of the 2019 IEEE International Conference on Environment and Electrical Engineering, Genova, Italy, 11–14 June 2019. [Google Scholar]
- Vorobev, P.; Greenwood, D.M.; Bell, J.H.; Bialek, J.W.; Taylor, P.C.; Turitsyn, K. Deadbands, droop, and inertia impact on power system frequency distribution. IEEE Trans. Power Syst. 2019, 34, 3098–3108. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.; Liu, C.; Ruiz, J.P. Stochastic unit commitment with sub-hourly dispatch constraints. Appl. Energy 2013, 105, 418–422. [Google Scholar] [CrossRef]
- Gangammanavar, H.; Sen, S.; Zavala, V.M. Stochastic optimization of sub-hourly economic dispatch with wind energy. IEEE Trans. Power Syst. 2016, 31, 949–959. [Google Scholar] [CrossRef]
- Wang, B.; Hobbs, B.F. Real-time markets for flexiramp: A stochastic unit commitment-based analysis. IEEE Trans. Power Syst. 2016, 31, 846–860. [Google Scholar] [CrossRef]
- Gu, Y.; Xie, L. Stochastic look-ahead economic dispatch with variable generation resources. IEEE Trans. Power Syst. 2017, 32, 17–29. [Google Scholar] [CrossRef]
- Milano, F.; Dörfler, F.; Hug, G.; Hill, D.J.; Verbič, G. Foundations and challenges of low-inertia systems (invited paper). In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018. [Google Scholar]
- Ahmadi, H.; Ghasemi, H. Security-Constrained Unit Commitment With Linearized System Frequency Limit Constraints. IEEE Trans. Power Syst. 2014, 29, 1536–1545. [Google Scholar] [CrossRef]
- Singh Parmar, K.P.; Majhi, S.; Kothari, D.P. Load frequency control of a realistic power system with multi-source power generation. Int. J. Electr. Power Energy Syst. 2012, 42, 426–433. [Google Scholar] [CrossRef]
- Kërçi, T.; Milano, F. Sensitivity Analysis of the Interaction between Power System Dynamics and Unit Commitment. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019. [Google Scholar]
- Kërçi, T.; Giraldo, J.; Milano, F. Analysis of the impact of sub-hourly unit commitment on power system dynamics. Int. J. Electr. Power Energy Syst. 2020, 119, 105819. [Google Scholar] [CrossRef]
- Yuan, B.; Zhou, M.; Li, G.; Zhang, X. Stochastic Small-Signal Stability of Power Systems With Wind Power Generation. IEEE Trans. Power Syst. 2015, 30, 1680–1689. [Google Scholar] [CrossRef]
- Wang, X.; Chiang, H.; Wang, J.; Liu, H.; Wang, T. Long-Term Stability Analysis of Power Systems With Wind Power Based on Stochastic Differential Equations: Model Development and Foundations. IEEE Trans. Power Syst. 2015, 30, 1534–1542. [Google Scholar] [CrossRef]
- Milano, F.; Zárate-Miñano, R. A Systematic Method to Model Power Systems as Stochastic Differential Algebraic Equations. IEEE Trans. Power Syst. 2013, 28, 4537–4544. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Milano, F. Power System Modeling and Scripting; Springer: London, UK, 2010. [Google Scholar]
- IEA-WIND. Design and Operation of Power Systems with Large Amounts of Wind Power. Available online: https://community.ieawind.org (accessed on 17 February 2020).
- Morales, J.; Conejo, A.; Madsen, H.; Pinson, P.; Zugno, M. Integrating Renewables in Electricity Markets: Operational Problems; Springer: Berlin, Germany, 2013. [Google Scholar]
- Conejo, A.; Carrión, M.; Morales, J. Decision Making Under Uncertainty in Electricity Markets; Springer: Berlin, Germany, 2010. [Google Scholar]
- Blanco, I.; Morales, J.M. An Efficient Robust Solution to the Two-Stage Stochastic Unit Commitment Problem. IEEE Trans. Power Syst. 2017, 32, 4477–4488. [Google Scholar] [CrossRef]
- Håberg, M. Fundamentals and recent developments in stochastic unit commitment. Int. J. Electr. Power Energy Syst. 2019, 109, 38–48. [Google Scholar] [CrossRef]
- Zheng, Q.P.; Wang, J.; Liu, A.L. Stochastic Optimization for Unit Commitment—A Review. IEEE Trans. Power Syst. 2015, 30, 1913–1924. [Google Scholar] [CrossRef]
- Gómez Expósito, A.; Conejo, A.; Cañizares, C. Electric Energy Systems: Analysis and Operation; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Palensky, P.; Van Der Meer, A.A.; Lopez, C.D.; Joseph, A.; Pan, K. Cosimulation of Intelligent Power Systems: Fundamentals, Software Architecture, Numerics, and Coupling. IEEE Ind. Electron. Mag. 2017, 11, 34–50. [Google Scholar] [CrossRef]
- Milano, F. A Python-based software tool for power system analysis. In Proceedings of the IEEE PES General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- Gurobi Optimization, LLC. Gurobi Optimizer Reference Manual; Gurobi Optimization, LLC: Houston, TX, USA, 2018. [Google Scholar]
- Illinois Center for a Smarter Electric Grid (ICSEG). IEEE 39-Bus System. Available online: https://icseg.iti.illinois.edu/ieee-39-bus-system/ (accessed on 17 February 2020).
- Carrión, M.; Arroyo, J.M. A computationally efficient mixed-integer linear formulation for the thermal unit commitment problem. IEEE Trans. Power Syst. 2006, 21, 1371–1378. [Google Scholar] [CrossRef]
- Costley, M.; Feizollahi, M.J.; Ahmed, S.; Grijalva, S. A rolling-horizon unit commitment framework with flexible periodicity. Int. J. Electr. Power Energy Syst. 2017, 90, 280–291. [Google Scholar] [CrossRef]
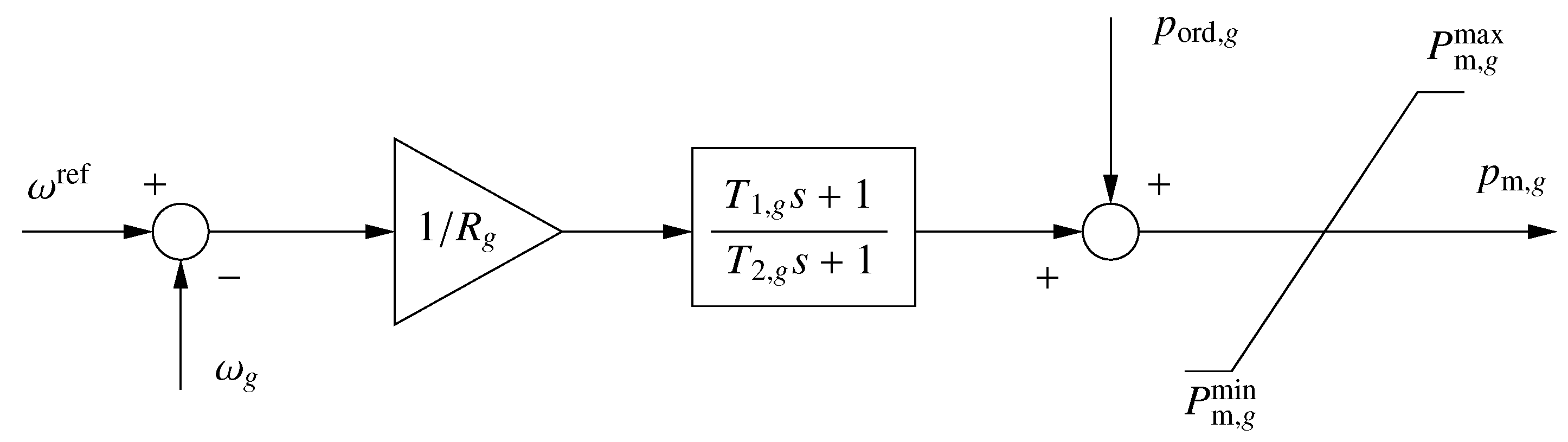


| Model | Total Operation Cost ($) |
|---|---|
| SUC (Complete) | 412,000 |
| SUC (Simplified) | 398,000 |
| SUC (Alternative) | 339,470 |
| DUC | 411,580 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kërçi, T.; Giraldo, J.S.; Milano, F. Sensitivity Analysis of the Impact of the Sub- Hourly Stochastic Unit Commitment on Power System Dynamics. Energies 2020, 13, 1468. https://doi.org/10.3390/en13061468
Kërçi T, Giraldo JS, Milano F. Sensitivity Analysis of the Impact of the Sub- Hourly Stochastic Unit Commitment on Power System Dynamics. Energies. 2020; 13(6):1468. https://doi.org/10.3390/en13061468
Chicago/Turabian StyleKërçi, Taulant, Juan S. Giraldo, and Federico Milano. 2020. "Sensitivity Analysis of the Impact of the Sub- Hourly Stochastic Unit Commitment on Power System Dynamics" Energies 13, no. 6: 1468. https://doi.org/10.3390/en13061468
APA StyleKërçi, T., Giraldo, J. S., & Milano, F. (2020). Sensitivity Analysis of the Impact of the Sub- Hourly Stochastic Unit Commitment on Power System Dynamics. Energies, 13(6), 1468. https://doi.org/10.3390/en13061468







