Energy-Efficient 3D Navigation of a Solar-Powered UAV for Secure Communication in the Presence of Eavesdroppers and No-Fly Zones

Abstract

Unmanned Aerial Vehicles (UAVs) have been regarded as a promising means to reshape future wireless communication systems. In this paper, we consider how to plan the trajectory of a solar-powered UAV under a cloudy condition to secure the communication between the UAV and a target ground node against multiple eavesdroppers. We propose a new 3D UAV trajectory optimization model by taking into account the UAV energy consumption, solar power harvesting, eavesdropping and no-fly zone avoidance. A Rapidly-exploring Random Tree (RRT) method is developed to construct the UAV trajectory. Computer simulations and comparisons with a baseline method demonstrate that the proposed method is able to produce trajectories to ensure the valid wireless communication link with the ground node and prevent eavesdropping.

1. Introduction

With rapidly growing demand for energy and decreasing fossil fuel reserves, renewable energy has attracted great of attention worldwide in the last few decades. Solar power is an important source of renewable energy, and various solar-powered products have become part of our daily-life, such as solar-powered cars [1] and solar-powered Unmanned Aerial Vehicles (UAVs) [2]. Powering UAVs by solar energy is a promising solution to overcome the bottleneck of the limited flight time of UAVs powered by onboard battery. Harvesting solar energy while flying allows UAVs to fly longer in the sky, which enables the UAVs to provide uninterrupted service in different applications such as monitoring and surveillance [3,4], disaster management [5], infrastructure inspection [6,7], parcel delivery [8] and wireless communications [9].

The application of UAVs in wireless communications is a hot topic. Compared to conventional wireless communication systems based on stationary infrastructures, UAV-based communication systems can provide timely and economical services in temporary hotspots, disaster areas, and complex terrains [9,10], thanks to their maneuverability. Many research articles relevant to UAV-enabled wireless communication systems have been published, and the UAVs assist existing communication systems by offloading the traffic demand of the stationary access points [9,11,12] and acting as relays to connect remote users to network [13].

UAVs have also been used to protect wireless communications. Wang et al. [14] maximized the non-zero secrecy capacity of a UAV-node link in the presence of an eavesdropper by optimally deploying the UAV. Wang et al. [15] considered a four-entity system with a transmitter, a receiver, an eavesdropper and a UAV relay. They optimized the transmit power of the transmitter and the UAV to maximize the secrecy rate of the system. Li et al. [16] used a UAV as a jammer that interferes with eavesdroppers. They focused on optimizing the trajectory and the jamming power of the UAV and the transmit power of the transmitter to maximize the average achievable secrecy rate. Cai et al. [17] studied a protection scheme using two UAVs: one transmits information, and the other interferes with eavesdroppers. The method jointly optimizes the UAVs’ trajectories and the user transmission schedule. Li et al. [18] investigated a scenario where two UAVs transmit confidential messages to specified ground nodes using the same spectrum in the presence of an eavesdropper. Although the mutual co-channel interferences arising from spectrum sharing may lower the spectral efficiency, the eavesdropping effect can be reduced as the two UAVs act in essence as cooperative jammers for each other. The authors of [19,20] secured the wireless data communication between a ground transmitter and a UAV by jointly optimizing the trajectory of the UAV and the transmit power of the ground transmitter to maximize the average secrecy rate over a given period of time. One common setting in [14,15,16,17,18,19,20] is that the UAV is powered by an onboard capacity-limited battery. Therefore, these designs may not ensure a sustainable defence against eavesdropping.

This paper considers using a solar-powered UAV to secure wireless communications with a ground node in the presence of collaborative eavesdroppers. By securing wireless communication, we mean that the ground node can recover the data sent by the UAV and the eavesdroppers cannot do this at any time. This is a new scenario which has not been considered comprehensively in the literature. Firstly, in light of the method in [21], we consider a solar-powered UAV which is possible to operate for a longer time than the onboard battery-powered UAVs. Secondly, unlike the methods in [16,18,19,20], which optimize the integrated jamming or eavesdropping performance, we target on the instantaneous communication protection. Thirdly, in light of the method in [22], the eavesdroppers can collaborate by combining the collected signals to get a better understanding of the information sent by the UAV. Obviously, this can make it more difficult for the UAV to optimize its trajectory. Moreover, different from most existing publications, which assume that the UAV flies in free space, we consider no-fly zones. The no-fly zones may be tall buildings or areas with high risks of being targeted by ground-to-air missiles [23,24,25]. These different considerations make the problem considered in this paper more general, challenging and practical.

In this paper, we focus on a new trajectory optimization problem for a UAV by taking into account solar power harvesting, instantaneous communication protection, collaborative eavesdropping and no-fly zones. We propose a new optimization model to minimize the energy expenditure of a UAV with a solar-powered rechargeable battery, while securing communications between the UAV and a ground node, avoiding no-fly zones, satisfying the aeronautic maneuverability and preventing depletion of the battery. This is a realistic problem but needs a nonconvex optimization technique, as the solar power is non-smooth and the UAV dynamic model is non-linear. We propose a scheme to plan the UAV trajectory based on Rapidly-exploring Random Tree (RRT). In the proposed method, an RRT can be constructed to capture the non-linear UAV motion model and the secure communication requirements. From the RRT, we can randomly select a set of possible trajectories which end in a pre-defined destination set. (The final position of the UAV is in the destination set.) We verify the energy storage along each possible trajectory and choose the one with the minimum energy expenditure while satisfying all the constraints. Our key contributions include the new problem formulation and the new RRT-based trajectory planning method, which is computational efficient and can quickly explore the flight space to construct UAV trajectory. Computer simulations demonstrate the effectiveness of the proposed approach. By comparing to a baseline method which is unaware of eavesdropping, the proposed method is shown to guarantee the valid wireless communication link with the ground node and prevent eavesdropping. Although a static environment setting is demonstrated in the paper, the proposed RRT-based method can be potentially applied to dynamic environments thanks to its computational efficiency.

RRT falls into the category of sampling-based path planning algorithms. A similar algorithm is the Probabilistic Roadmap (PRM). It first builds up a dense enough roadmap (graph) and finds a path from the start to the destination by a graph search algorithm [26]. By contrast, the RRT method achieves the best feasible path to the goal all by its own processing procedure, which is more suitable for dynamic cases. Another category of path planning methods is the node-based algorithms such as Dijkstra’s algorithm [27]. They grid the solution space and need a specific metric to characterize the cost of moving from one grid to another. These algorithms cannot handle the mobility constraints of UAVs, such as the non-holonomic constraints, as they generally regard the robot as a point in the graph [27]. However, the RRT-based method can account for the mobility constraint in the process of constructing the tree. Furthermore, as shown below, it is not straightforward to define the cost of moving from one grid to another needed for the node-based algorithms. From these discussions, the RRT-based method well suits the considered problem.

The remainder of the paper is organized as follows. In Section 2, we present the system models and state the problem under investigation. In Section 3, we present the proposed 3D trajectory optimization method to minimize the energy consumption subject to the constraints of the UAV maneuverability, communication security, battery lifetime and no-fly zones. Computer simulations are presented in Section 4 to show the performance of the proposed navigation algorithm. Finally, a conclusion is given in Section 5.

2. Problem Statement

In this section, we first present the system model and then formulate the problem of interest.

2.1. UAV Dynamics

We consider a UAV flying in a 3D space. Let $p\left(t\right)=\left[x\right(t),y(t),z(t\left)\right]$ be the coordinates of the UAV at time t, where $x\left(t\right)$ and $y\left(t\right)$ are the coordinates on the horizontal plane parallel to the ground and $z\left(t\right)$ is the altitude of the UAV. We consider the following well-known model of the UAV’s motion, (This 3D UAV motion model is extended from a 2D model [28] where a forward speed and an angular speed are the control inputs. Beyond these two control inputs, we consider the vertical speed such that the UAV can adjust its altitude.)

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & \dot{x}\left(t\right)=v\left(t\right)cos\left(\theta \left(t\right)\right),\hfill \\ \hfill & \dot{y}\left(t\right)=v\left(t\right)sin\left(\theta \left(t\right)\right),\hfill \\ \hfill & \dot{\theta }\left(t\right)=\omega \left(t\right),\hfill \\ \hfill & \dot{z}\left(t\right)=u\left(t\right),\hfill \\ \hfill & 0\le v\left(t\right)\le V^{max},\hfill \\ \hfill & -{\Omega }^{max}\le \omega \left(t\right)\le {\Omega }^{max},\hfill \\ \hfill & -U^{max}\le u\left(t\right)\le U^{max},\hfill \end{array}\right.\end{array}$$

(1)

where $\theta \left(t\right)$ is the heading of the UAV with respect to the x-axis; $v\left(t\right)$, $\omega \left(t\right)$ and $u\left(t\right)$ are its linear horizontal, angular and vertical speeds, respectively; and $V^{max},{\Omega }^{max}$ and $U^{max}$ are given positive constants indicating the maximum linear, angular and vertical speeds, respectively. The linear horizontal speed $v\left(t\right)$, angular speed $\omega \left(t\right)$ and vertical speed $u\left(t\right)$ are considered as the control inputs of the model in Equation (1). The UAV altitude $z\left(t\right)$ should satisfy the constraints:

$$Z^{min}\le z\left(t\right)\le Z^{max}$$

(2)

where $Z^{min}>0$ is the lower bound of the UAV altitude and $Z^{max}>0$ is the upper bound. Furthermore, the horizontal position of the UAV must be outside no-fly zones $\mathcal{Z}$:

$$\left(x\right(t),y(t\left)\right)\notin \mathcal{Z}.$$

(3)

We assume that the set of no-fly zones $\mathcal{Z}$ consists of r no-fly zones ${\mathcal{Z}}_1,\dots ,{\mathcal{Z}}_r$ where ${\mathcal{Z}}_1,\dots ,{\mathcal{Z}}_r$ are bounded and connected planar sets. These no-fly zones may be urban areas where flights of UAVs are prohibited, or, in military applications, they may represent areas with high risks of being targeted by ground-to-air missiles [23,24,25].

2.2. Harvesting Solar Energy

The UAV can harvest solar energy, and the harvesting rate depends on the cloud condition if there is any. We consider a cloudy weather, and there is a cloud layer with the altitude ranging from $H_l$ to $H_u$. The output power of the solar panel ($P_{solar}\left(t\right)$) can be modeled by a function of the altitude ($z\left(t\right)$) [29]:

$$\begin{array}{c}\hfill P_{solar}\left(t\right)=\left\{\begin{array}{c}\eta SG,z\left(t\right)\ge H_u,\hfill \\ \eta SG{e}^{-\beta (H_u-z\left(t\right))},H_l\le z\left(t\right)\le H_u,\hfill \\ \eta SG{e}^{-\beta (H_u-H_l)},z\left(t\right)<H_l,\hfill \end{array}\right.\end{array}$$

(4)

where $\eta$ is a constant representing the energy transfer efficiency of solar energy harvesting, S is the area of the solar panels, G is the average solar radiation intensity on the earth and $\beta$ is the absorption coefficient of the solar panels. From Equation (4), we see that, when the UAV is above the cloud, the solar energy harvesting power $P_{solar}\left(t\right)$ is the largest; when it is below the cloud, $P_{solar}\left(t\right)$ is the lowest; and when it is inside the cloud, $P_{solar}\left(t\right)$ increases exponentially with the altitude. Equation (4) is a piecewise function of $z\left(t\right)$. The non-smoothness makes the problem under consideration complex to solve.

2.3. UAV Energy Consumption

The energy consumption of the UAV depends on the velocity vector $\nu \left(t\right)=(\dot{x}\left(t\right),\dot{y}\left(t\right),\dot{z}\left(t\right))$ [21] and can can be modeled as the summation of the induced power for level flight, the power for vertical flight and the profile power related the blade drag.

The induced power for level flight is modeled as:

$$P_{lf}\left(t\right)=\frac{W^2}{\sqrt{2}\rho A}\frac{1}{\sqrt{\parallel (\dot{x}\left(t\right),\dot{y}\left(t\right)){\parallel }^2+\sqrt{\parallel (\dot{x}\left(t\right),\dot{y}\left(t\right)){\parallel }^4+4V_h^4}}},$$

(5)

where W is the UAV weight, $\rho$ is the air density, A is the total area of the UAV rotor disks, and $V_h=\sqrt{\frac{W}{2\rho A}}$.

The power for vertical flight is modeled as:

$$P_{vf}\left(t\right)=W\dot{z}\left(t\right).$$

(6)

The profile power related to the blade drag is modeled as:

$$P_{bg}\left(t\right)=\frac{1}{8}{C}_{D0}\rho A{\parallel (\dot{x}\left(t\right),\dot{y}\left(t\right))\parallel }^3.$$

(7)

where $C_{D0}$ is the profile drag coefficient depending on the geometry of the rotor blades.

Thus, at any time t, the power consumption of the for movement is:

$$P_{UAV}\left(t\right)=P_{lf}\left(t\right)+P_{vf}\left(t\right)+P_{bg}\left(t\right).$$

(8)

Moreover, let $P_0$ be the static power consumed for maintaining the operation of the UAV and $P_t$ be the constant transmit power. Let $q\left(t\right)$ denote the energy stored in the on-board battery. Then, the dynamics of the stored energy of the battery is characterized by:

$$\dot{q}\left(t\right)=P_{solor}\left(t\right)-P_{UAV}\left(t\right)-P_0-P_t.$$

(9)

Let $q_c$ denote the battery capacity. Then, the following constraint should be satisfied:

$$q\left(t\right)\le q_c.$$

(10)

2.4. Securing Communication

We consider that the UAV communicates with a stationary ground node $\mathcal{N}$. Let $(x_n,y_n)$ be the position of the node. Moreover, there are M stationary eavesdroppers on the ground, which attempt to eavesdrop on the communication between the UAV and the node $\mathcal{N}$. Let $(x_i^e,y_i^e)$ be the position of an eavesdropper i, $i=1,\dots ,M$.

Let $d\left(t\right)$ denote the Euclidean distance between the UAV and the node $\mathcal{N}$ at time t, and $d_i\left(t\right)$ be the Euclidean distance between the UAV and the eavesdropper i at time t:

$$\begin{array}{c}\hfill d\left(t\right)=\sqrt{{(x\left(t\right)-x_n)}^2+{(y\left(t\right)-y_n)}^2+z{\left(t\right)}^2},\\ \hfill d_i\left(t\right)=\sqrt{{(x\left(t\right)-x_i^e)}^2+{(y\left(t\right)-y_i^e)}^2+z{\left(t\right)}^2}.\end{array}$$

We introduce a function $f\left(d\right)$ which measures the communication/eavesdropping performance from the distance d. Clearly, $f\left(d\right)$ is a decreasing function of d. For example, in the well-known Friis formula [30], when the transmitter and receiver are d apart with dominating line-of-sight, the received signal-to-noise ratio (SNR) is $f\left(d\right)=\frac{\varphi }{d^2}$, where $\varphi >0$ is a given parameter depending on the transmit power, the gains of the transmitter and receiver and the noise power.

To guarantee secure communication between the UAV and the ground node, a set of constraints are considered below. The first requirement is that the received power at the ground node needs to be no lower than a threshold ${\gamma }_c$:

$$\begin{array}{c}\hfill f\left(d\left(t\right)\right)\ge {\gamma }_c,\forall t\ge 0.\end{array}$$

(11)

This is to ensure that the node can successfully recover the received data. Secondly, the received power at each eavesdropper needs to be no larger than a threshold ${\gamma }_e$:

$$\begin{array}{c}\hfill f\left(d_i\left(t\right)\right)\le {\gamma }_e,\forall t\ge 0,\end{array}$$

(12)

for all $i=1,\dots ,M$. This is to ensure that any eavesdropper i cannot recover the captured data. Lastly, the following constraint is satisfied to avoid eavesdropping when the eavesdroppers collaborate:

$$\begin{array}{c}\hfill \sum _{i=1}^{m}f\left(d_i\left(t\right)\right)\le {\gamma }_{ce},\forall t\ge 0,\end{array}$$

(13)

where ${\gamma }_{ce}\le m{\gamma }_e$. The constraint in Equation (13) ensures that, when the eavesdroppers collaborate, they cannot recover the combined data. When they carry out maximal ratio combining (MRC) [30], Equation (13) can take the equality. General speaking, the constraints in Equations (12) and (13) require the UAV to be far enough from the eavesdroppers, whereas Equation (11) expects the UAV to be close to the node $\mathcal{N}$. We note that constraints in Equations (11)–(13) specify stringent instantaneous security rate requirement. We also note that in cases where several eavesdroppers are located closely, they may block the path for the UAV, and there may not exist a feasible trajectory satisfying Equations (11)–(13). To avoid being eavesdropped, we assume that the UAV stops transmitting in these cases.

2.5. Problem Statement

Let $T>0$ be the time the UAV can use to fly to a destination set $\mathcal{D}$. We assume that the destination set $\mathcal{D}$ is a bounded and connected planar set which does not overlap with the set of no-fly zones $\mathcal{Z}$. During the period $[t_0,t_0+T]$, the UAV keeps transmitting confidential data to the stationary ground node. The problem of interest is formulated as follows:

$$\begin{array}{c}\hfill \underset{v\left(t\right),\omega \left(t\right),u\left(t\right)}{min}{\int }_{t_0}^{t_0+T}{P}_{UAV}\left(t\right)dt\end{array}$$

(14)

subject to

$$0<q\left(t\right)\le q_c,$$

(15)

$$(x(t_0+T),y(t_0+T))\in \mathcal{D},$$

(16)

subject to Equations (2), (3), (11), (12) and (13).

In other words, this problem is to develop a navigation law for the UAV (Equation (1)) that minimizes Equation (14) subject to the constraints in Equations (2), (3), (11)–(13), (15) and (16).

3. Navigation Law

The problem under consideration cannot be solved using convex optimization tools, because of the non-convexity of the objective function in Equation (14), especially the part for level flight in Equation (5), the non-smoothness of the solar power harvesting model in Equation (4) and the non-linearity of the UAV dynamic model in Equation (1). We propose an RRT-based trajectory planning scheme to solve the problem heuristically and efficiently. The RRT method can tackle the non-linear dynamic model, secure communication requirements and no-fly zones by generating random samples in the searching space and only keeping the samples satisfying all the constraints.

We assume that the UAV knows the locations of the node and the eavesdroppers. We divide $[t_0,t_0+T]$ into L equal intervals (each interval lasts $\delta =\frac{T}{L}$) and assume that the control inputs $v\left(t\right),\omega \left(t\right)$ and $u\left(t\right)$ are updated at time instants $t_0,t_0+\delta ,\dots ,t_0+(L-1)\delta$ and remain constant at any interval $[t_0+j\delta ,t_0+(j+1)\delta ]$, $j=0,1,\dots ,L-1$. The control inputs of the UAV dynamic model are simplified as follows:

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill & w\left(j\right)=V^{max},\hfill \\ \hfill & w\left(j\right)\in \{-{\Omega }^{max},0,{\Omega }^{max}\},\hfill \\ \hfill & u\left(j\right)\in \{-U^{max},0,U^{max}\},\hfill \end{array}\hfill \end{array}\right.$$

(17)

for $j=0,1,\dots ,L-1$. Compared to Equation (1), the input $v\left(j\right)$ keeps the maximum value $V^{max}$, and $\omega \left(j\right)$ and $u\left(j\right)$ in Equation (17) either take 0 or the corresponding maximum value, respectively. Although this simplification sacrifices the maneuverability of the UAV, it is still realizable since the selected control inputs are all within the allowed ranges. More importantly, this simplification makes the UAV easy to control and also narrows down the solution space significantly. It is not hard to see that this method can be easily extended to include some more feasible control inputs.

Based on Equation (17), the models in Equations (4) and (11)–(13) can be discretized directly as they are functions of the UAV position $p\left(j\right)$. To discretize the energy consumption model of the UAV, we rewrite the velocity vector $\nu \left(j\right)$ as $(\frac{x(j+1)-x\left(j\right)}{\delta },\frac{y(j+1)-y\left(j\right)}{\delta },\frac{z(j+1)-z\left(j\right)}{\delta })$. Then, the discrete forms of Equations (8) and (14) can be obtained. Accordingly, the relationship of Equation (9) is rewritten as:

$$q(j+1)=q\left(j\right)+\delta (P_{solor}\left(j\right)-P_{UAV}\left(j\right)-P_0-P_t).$$

(18)

Considering the battery capacity $q_c$, Equation (18) should be corrected by:

$$q(j+1)=max\{q\left(j\right),q_c\}.$$

(19)

The trajectory of the UAV for the interval $[t_0,t_0+T]$ can be found by solving the discrete version of the considered problem. Specifically, having the position and heading of the UAV at $t_0$, we can construct an RRT with a certain number of vertices based on Equations (2), (3), (11)–(13) and (17). Then, any vertex of the RRT that is reachable from the root via a sequence of control inputs defined in Equation (17) is within the allowed altitudes, is outside the no-fly zones and can avoid both the individual and collaborative eavesdropping. However, not all the vertices in the RRT are feasible for the UAV to visit due to the constraints in Equations (15) and (16). From the RRT, we can randomly select a trajectory with L consecutive vertices starting from the root. If the last vertex falls into the destination set $\mathcal{D}$, then the constraint in Equation (16) holds. Furthermore, for each vertex of this trajectory, we verify the constraint in Equation (15). If Equation (15) also holds, we finally compute the energy consumption of the UAV along this trajectory according to Equation (14). We can randomly select a set of trajectories as above, and the one with the minimum energy consumption can be identified. This algorithm is summarized in

Table 1. UAV 3D Trajectory Planning Algorithm.

1. Construct an RRT rooted at the initial position of the UAV with a certain number of vertices falling into the destination set $\mathcal{D}$ and all the vertices satisfy Equations (2), (3), (11)–(13) and (17).

2. Randomly select a certain number of trajectories with no more than N consecutive vertices from the RRT which start from the root and end at a vertex belonging to $\mathcal{D}$.

3. For each of the selected trajectories, verify whether constraints in Equations (15) and (16) are satisfied.

4. Among the trajectories satisfying Equations (15) and (16), identify the one with the minimum energy consumption according to Equation (14).

.

The RRT-based method can quickly explore the solution space. It belongs to the group of sampling-based algorithms. Another sampling-based method is the probabilistic roadmap (PRM). This method builds up a roadmap (graph) first which should be dense enough such that a path exists between the start and the destination. Then, a path can be obtained by a shortest path query. Different from RRT-based method, which achieves the best feasible path to the goal all by its own processing procedure, PRM generally calls a graph searching algorithm [26]. Another group of path planning methods is the node-based algorithms. The Dijkstra’s algorithm and its variants are the typical ones. As node-based, they require to grid the solution space, and a specific metric is needed to characterize the cost of moving from one grid to another [27]. These algorithms cannot handle the mobility constraints of UAVs such as the non-holonomic constraints. Specifically, in the gridded space, moving from one node to another may be impossible for a UAV having the limited angular speed. If possible, the computation of the feasible linear, angular and vertical speeds is required. However, the developed RRT-based method accounts the mobility constraint in the process of constructing the tree. Thus, the obtained can be tracked directly without any later adjustment. Furthermore, for the problem under consideration, it is not straightforward to define the cost of moving from one grid to another needed for the node-based algorithms. From these discussions, the RRT-based method well suits the considered problem.

4. Simulation Results

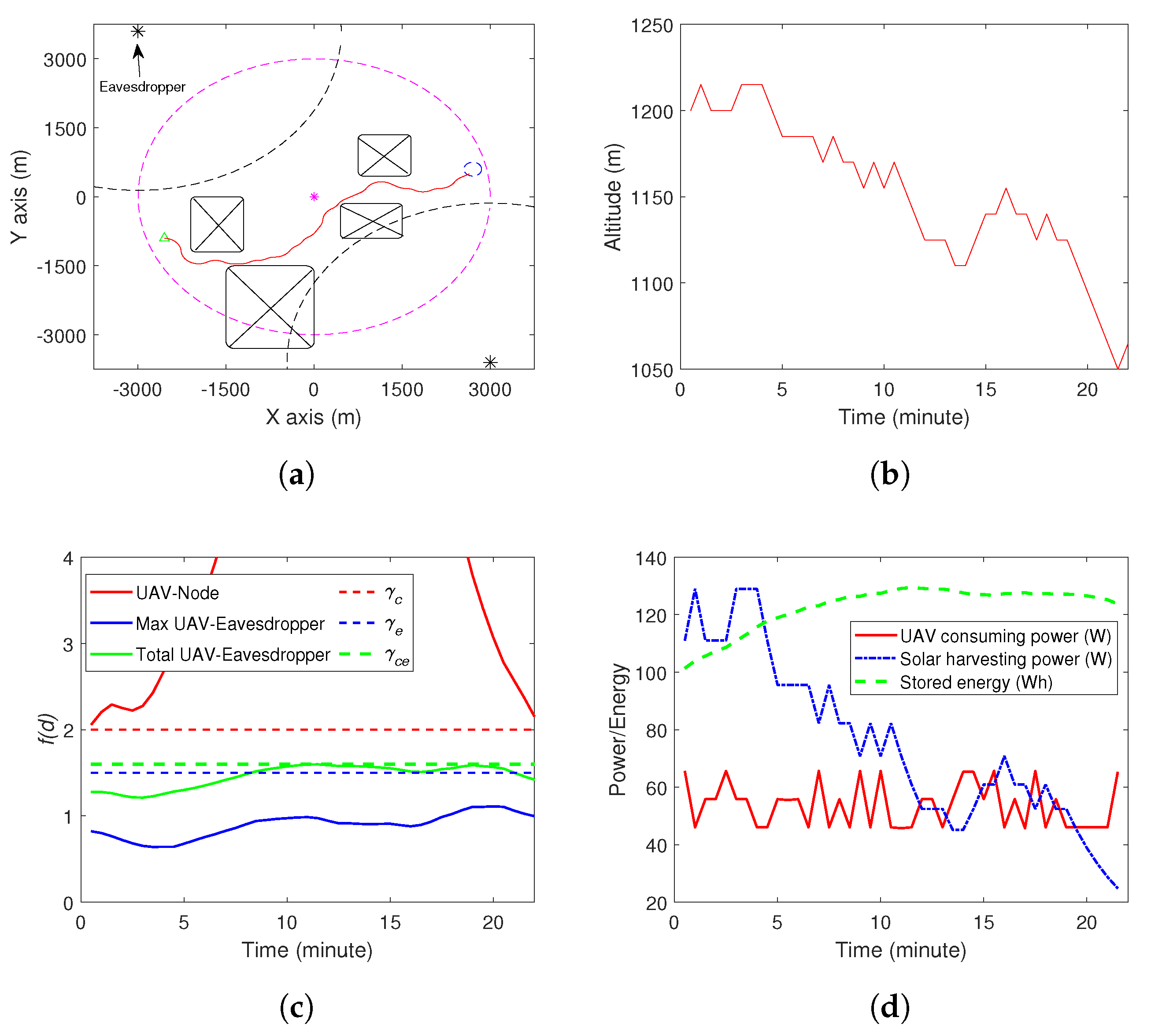
In this section, we demonstrate the effectiveness of the proposed method via computer simulations. The parameters used are summarized in

Table 2. Parameters and values.

Parameter	Value	Parameter	Value	Parameter	Value	Parameter	Value
S	1 m${}^2$	G	1367 W/m${}^2$	$\eta$	0.6	$\beta$	0.01
$H_l$	700 m	$H_u$	1400 m	$\rho$	1.225 kg/m${}^3$	A	0.5 m${}^2$
W	18.4 N	$C_{D0}$	0.08	$P_0$	5 W	$q\left(0\right)$	100 wh
$q_c$	150 wh	$V^{max}$	5 m/s	${\Omega }^{max}$	0.5 rad/s	$U^{max}$	0.5 m/s
$Z^{min}$	100 m	$Z^{max}$	1600 m	$\varphi$	$1.8\times {10}^6$	${\gamma }_c$	2
${\gamma }_e$	1.5	${\gamma }_{ce}$	1.6	$\delta$	1 min	T	30 min

. We considered two simulation environments, as shown in Figure 1 and Figure 2. In Figure 1, there are two eavesdroppers and four no-fly zones, while, in Figure 2, there are three eavesdroppers and five zo-fly zones. The ground node locates at (0,0). The UAV starts from the initial position, which is shown by the green triangle in Figure 1a and Figure 2a. The destination set is shown by a blue circle on the right side of Figure 1a and Figure 2a. In Figure 1a and Figure 2a, we also demonstrate some dash lines on the plane of $z=0$, i.e., the ground. The purple one indicates the area within which the ground node can effectively recover the sent data by the UAV. The black dash lines represent the area within which the eavesdroppers (marked by the black squares) can recover the captured data. Starting from the initial position, the UAV moves along the red trajectory and reaches the destination set in 22 min in environment 1 and 23.5 min in environment 2, which are before the due time. The altitude of the UAV during the movement is shown in Figure 1b and Figure 2b. The communication between the UAV and the ground node is good, as shown in Figure 1c and Figure 2c, and this trajectory avoids the individual and collaborative eavesdropping (see Figure 1c and Figure 2c). Finally, the energy consumption of the UAV, the solar energy harvesting and the stored amount of energy are shown in Figure 1d and Figure 2d. Note that the simulations were conducted on a normal PC with Inter(R) Core(TM) i7-8565U CPU @ 1.8GHz, 1.99GHz and 8G RAM. The average time to find the trajectory was about 3–5 s. Specifically, for the simulation in Environment 1, the algorithm generated about 800–1000 samples. The number of samples generated changed in each simulation as the RRT-based algorithm is a random method. For Environment 2, the algorithm generated more samples, i.e, 10,000–13,000. The reason is that Environment 2 (three eavesdroppers and five no-fly zones) is more complex than Environment 1 (two eavesdroppers and four no-fly zones). Thus, there were more infeasible samples generated in Environment 2.

For comparison, we applied a baseline method to the considered case. This baseline method only considers effectively transmitting data to the ground node while ignoring the eavesdroppers. All the parameters were the same as above. The simulation results are shown in Figure 3 and Figure 4. The trajectories of the UAV are shown in Figure 3a and Figure 4b. Comparing Figure 3a and Figure 1a (Figure 4a and Figure 2a), we see that this trajectory is closer to the eavesdropping boundary of one of the eavesdroppers. Although this does not lead to the successful individual eavesdropping by the top eavesdroppers, the two eavesdroppers can recover the captured data by analyzing the combined data. This is shown in Figure 3c. Between 5 and 13 min, the eavesdropping performance is above the threshold ${\gamma }_{ce}$. A similar finding can be observed in Figure 4c. From this comparison, we can see that the proposed method can construct a safe trajectory, which ensures the communication with the ground node, avoids eavesdropping and avoids collision with no-fly zones.

5. Conclusions

In this paper, we consider a problem of securing wireless communication between a solar-powered UAV and a stationary ground node in the presence of stationary eavesdroppers that can carry out the eavesdropping task independently and collaboratively. We developed a 3D UAV trajectory optimization model which minimizes the UAV flight energy expenditure, subject to that the communication between the UAV and the ground node is reliable and secure, and the UAV does deplete battery during the flight. An RRT trajectory planning scheme was developed. Computer simulations showed that the proposed method guarantees the valid wireless communication link with the ground node, prevents eavesdropping and avoids no-fly zones.