Assessment of Methods for the Real-Time Simulation of Electronic and Thermal Circuits
Abstract
1. Introduction
2. Numerical Methods
2.1. Formulation of the Problem as a System of ODEs
2.2. Solvers for Systems of DAE
2.3. Implementation
3. Benchmark Problems
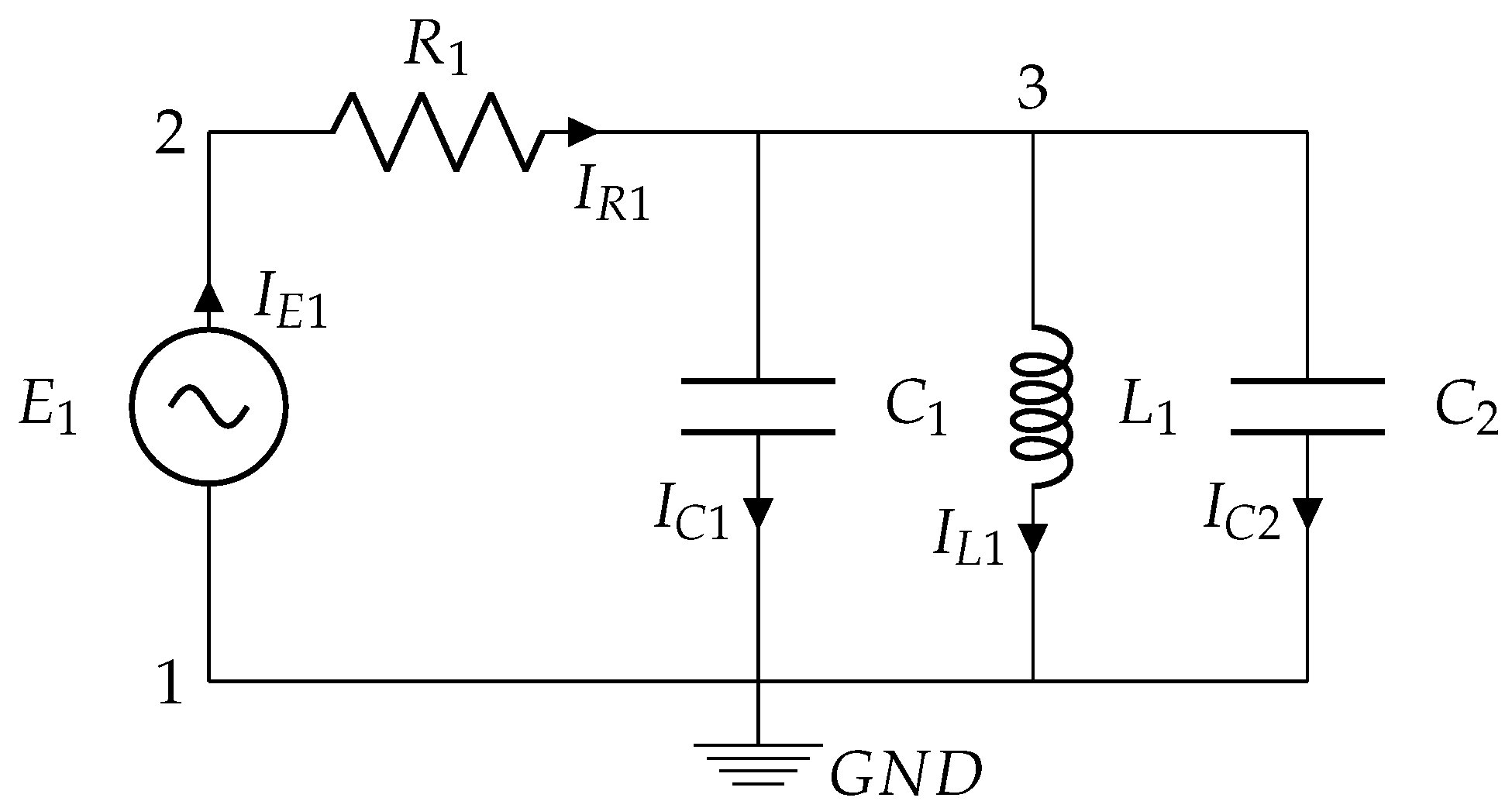
3.1. RLC Circuit
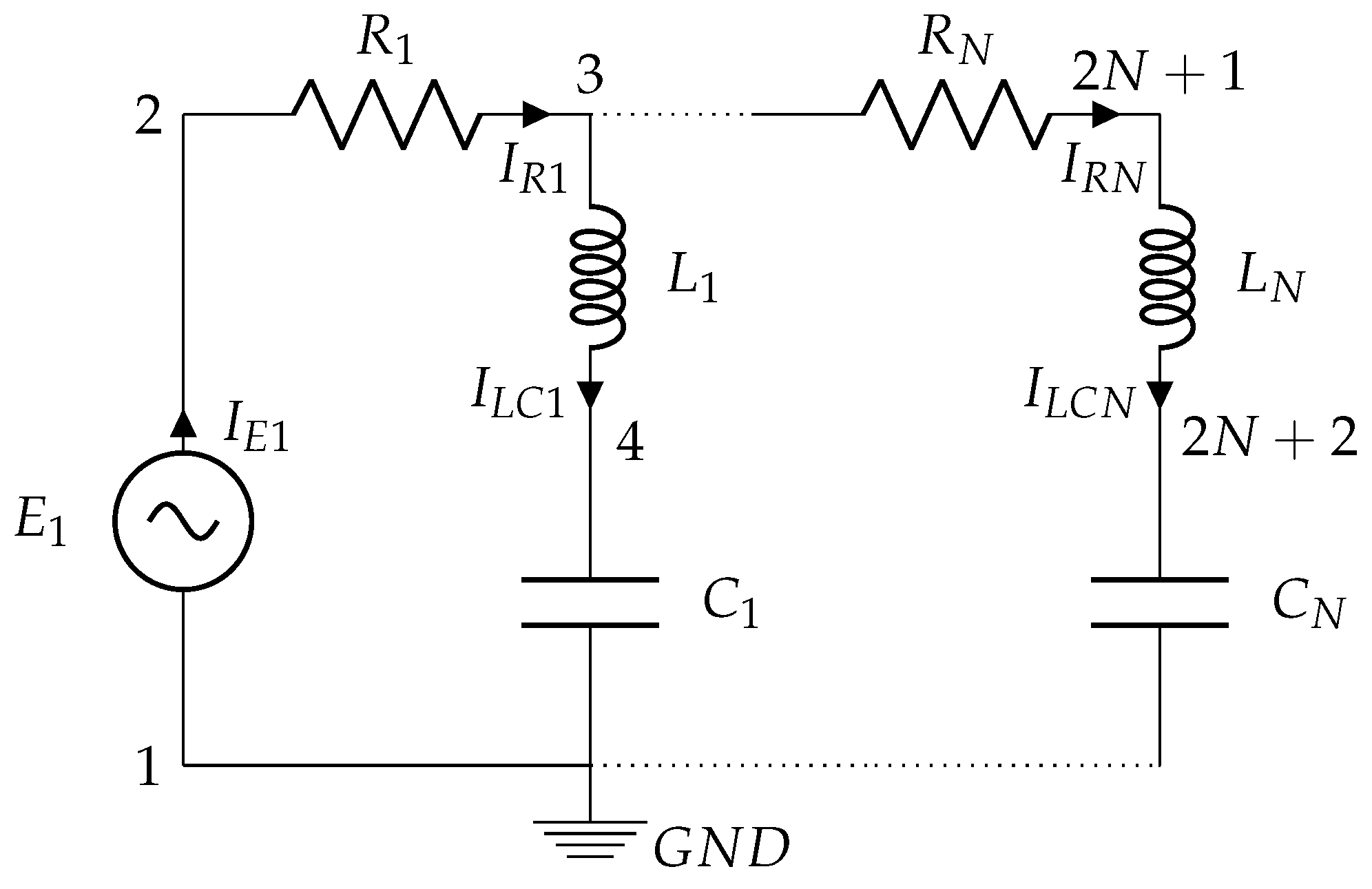
3.2. Scalable RLC Circuit
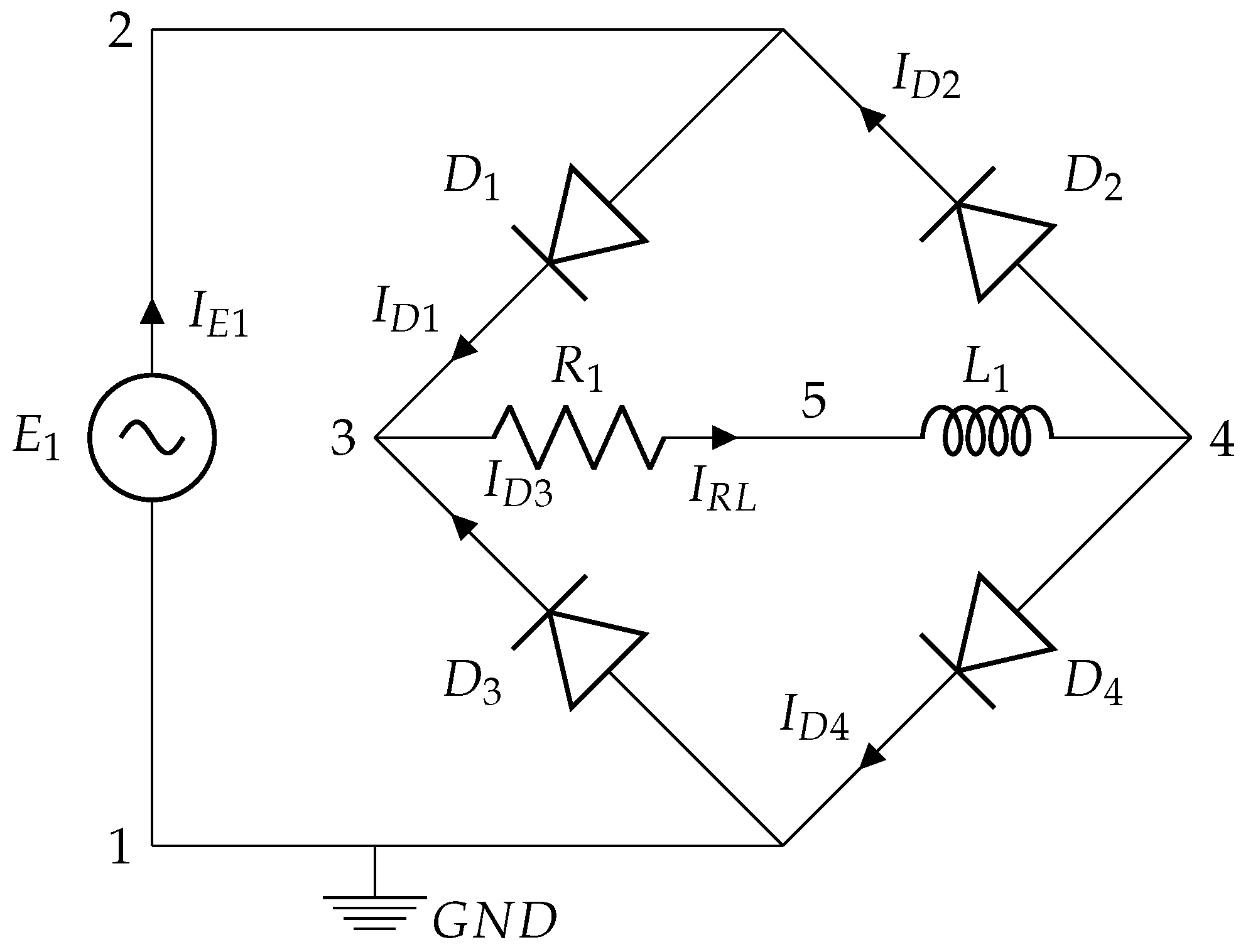
3.3. Full Wave Rectifier
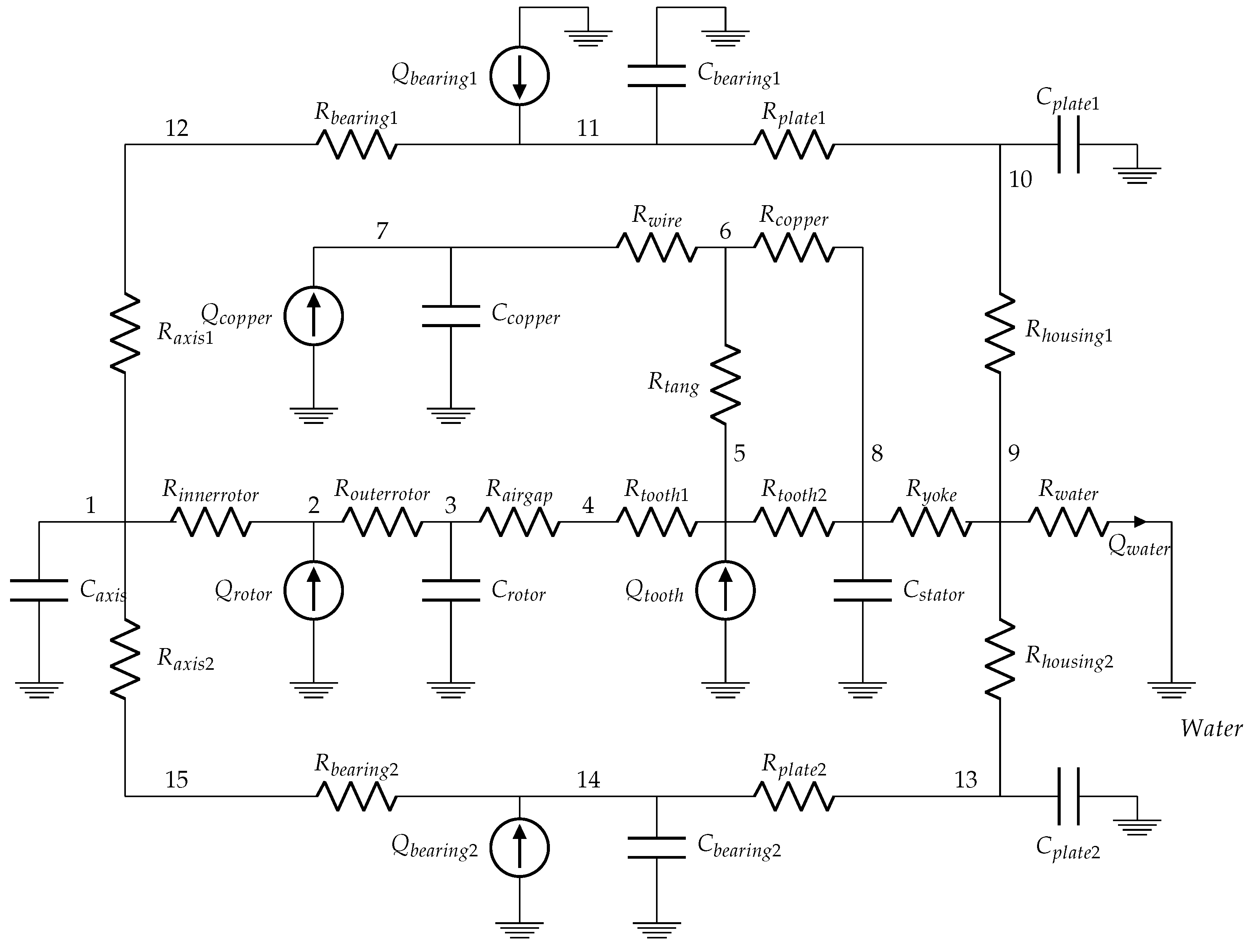
3.4. Synchronous Motor Thermal Equivalent Circuit
3.5. Reference Solutions
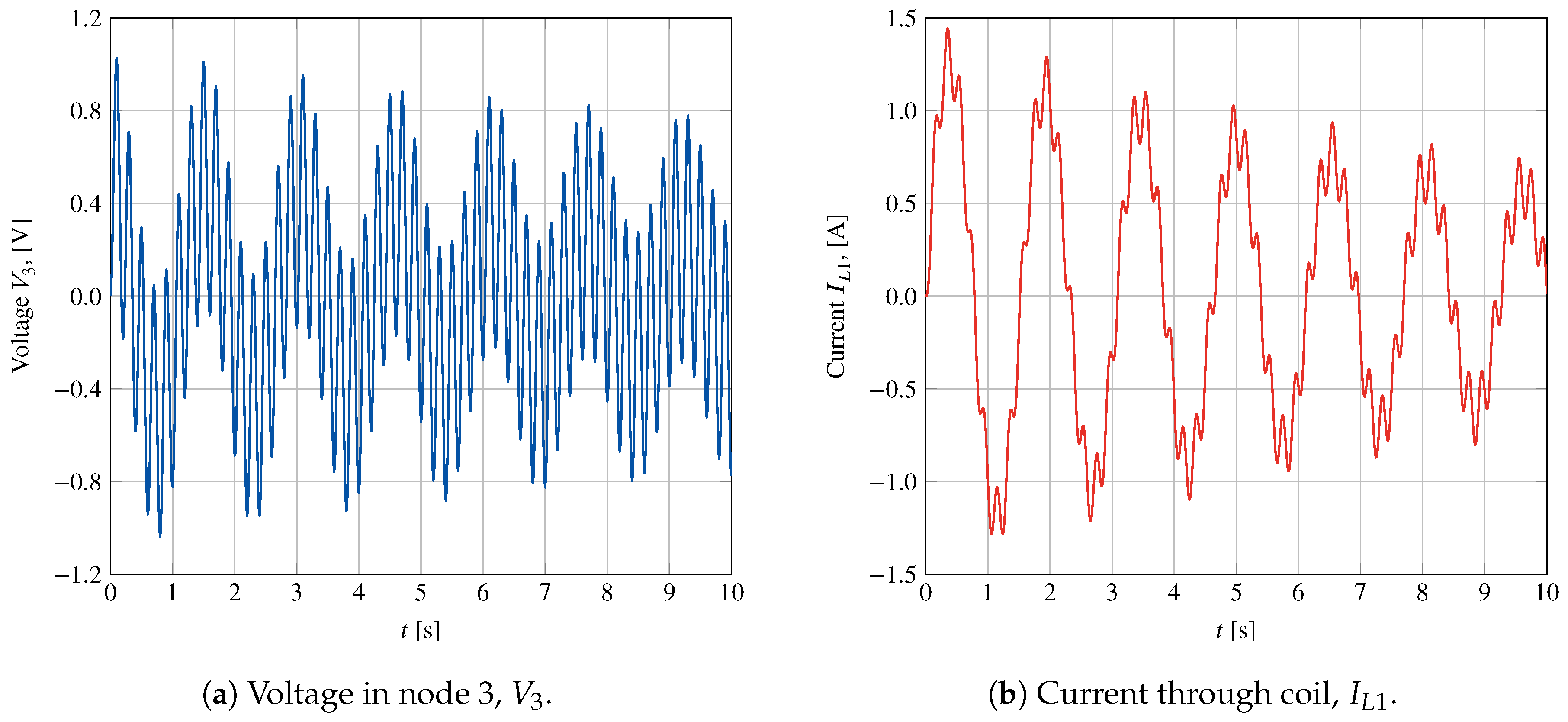
3.5.1. RLC Circuit
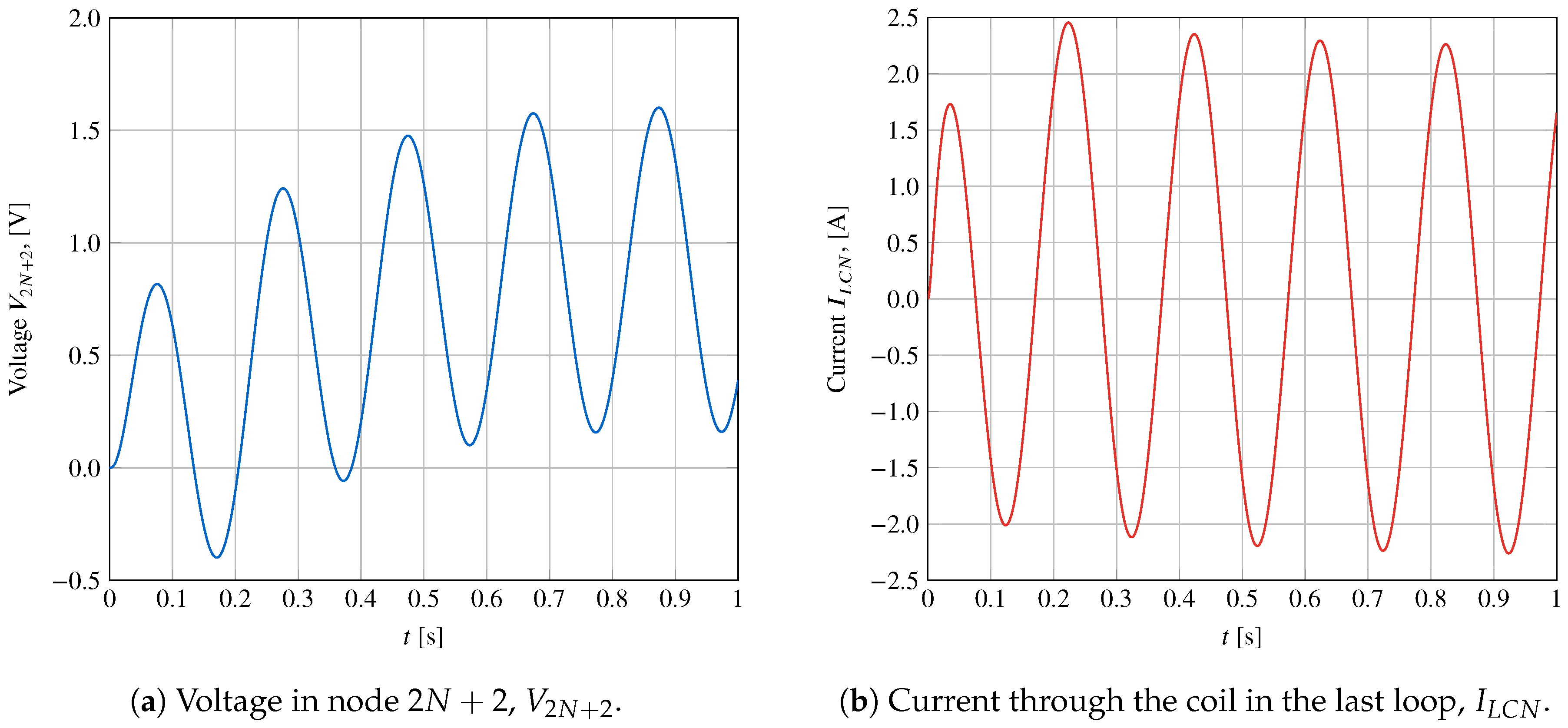
3.5.2. Scalable RLC Circuit
3.5.3. Full Wave Rectifier
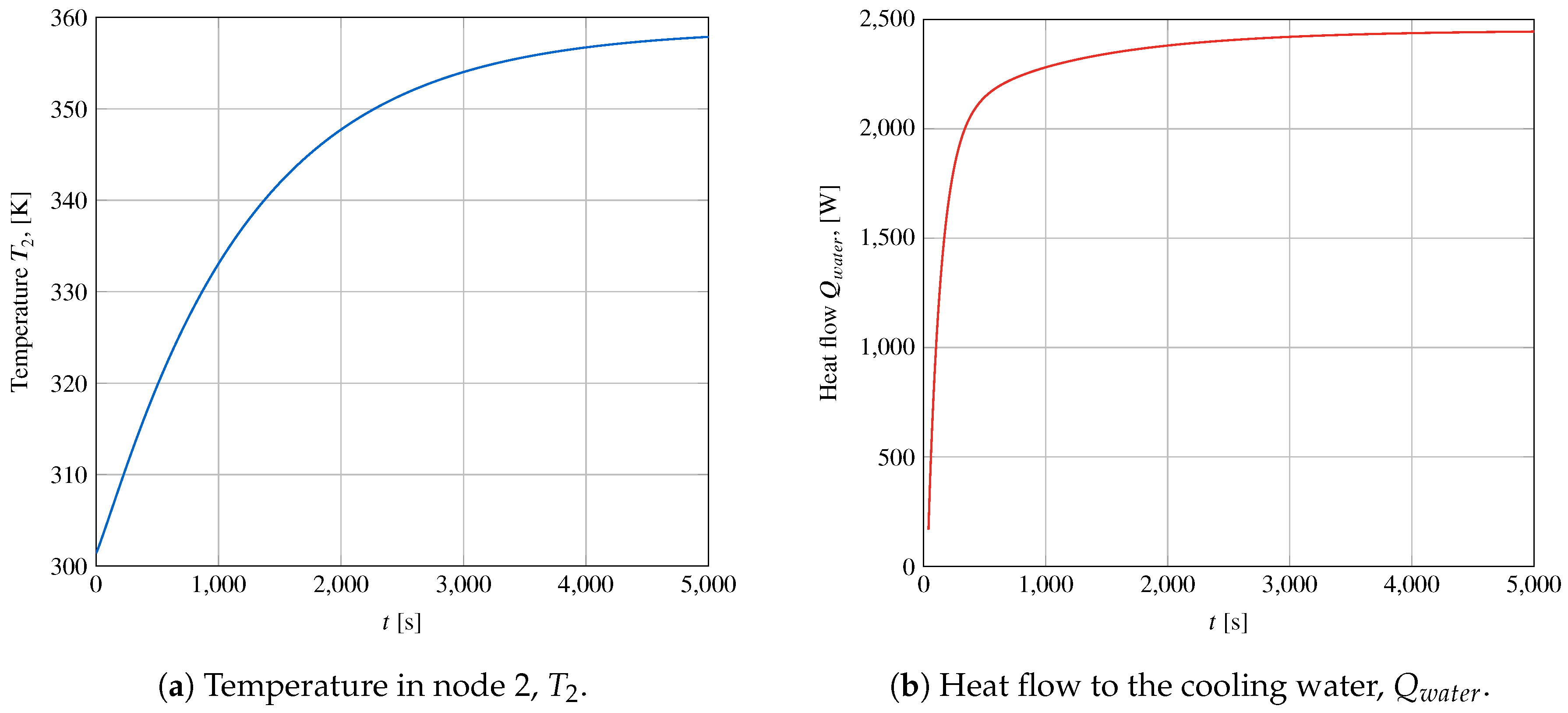
3.5.4. Synchronous Motor
3.6. Error Measurement and Performance Evaluation
4. Numerical Experiments
4.1. Simulation Environments
- a conventional desktop PC,
- a Beaglebone Black, and
- a Raspberry Pi 4.
4.2. Numerical Results
4.2.1. RLC Circuit
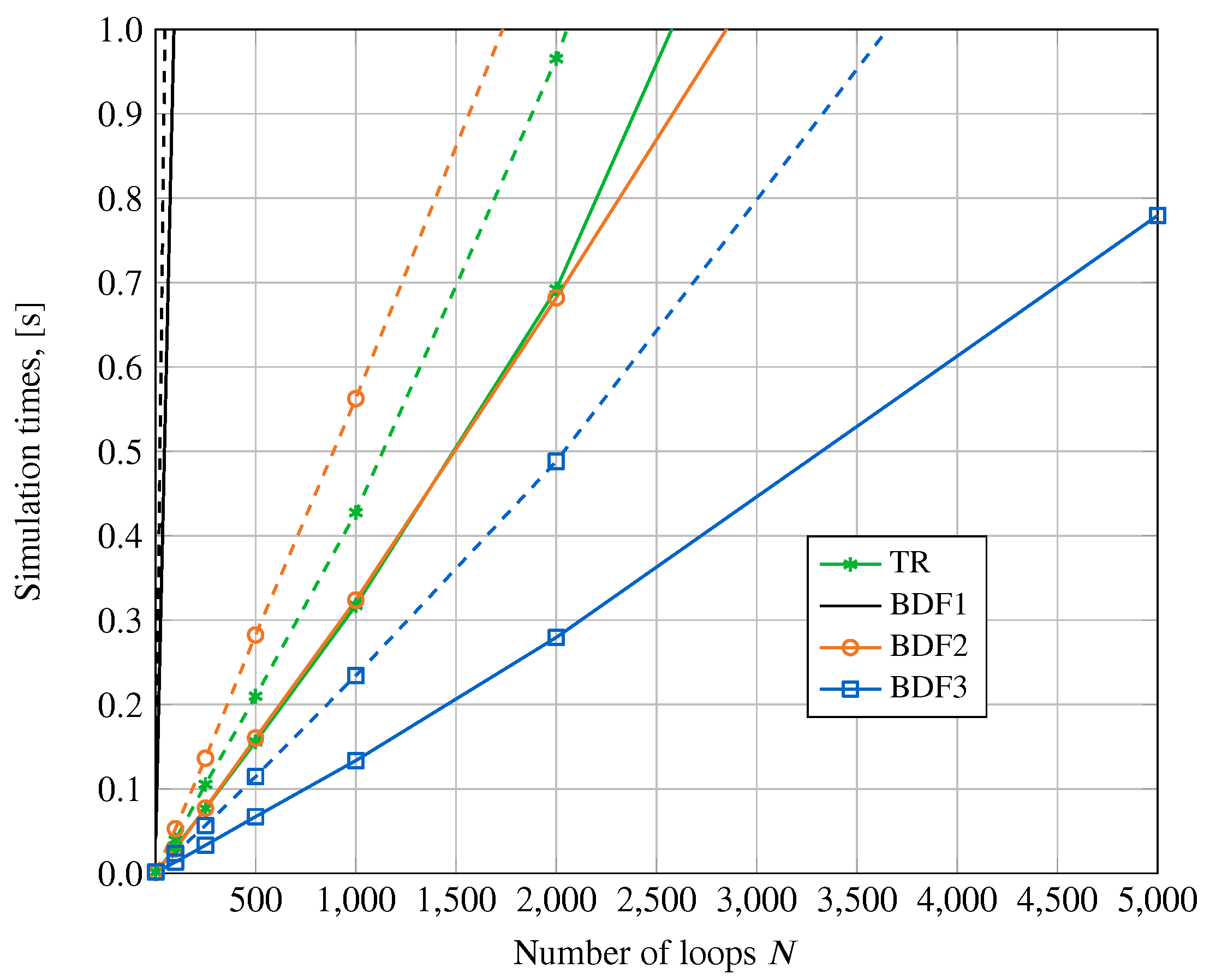
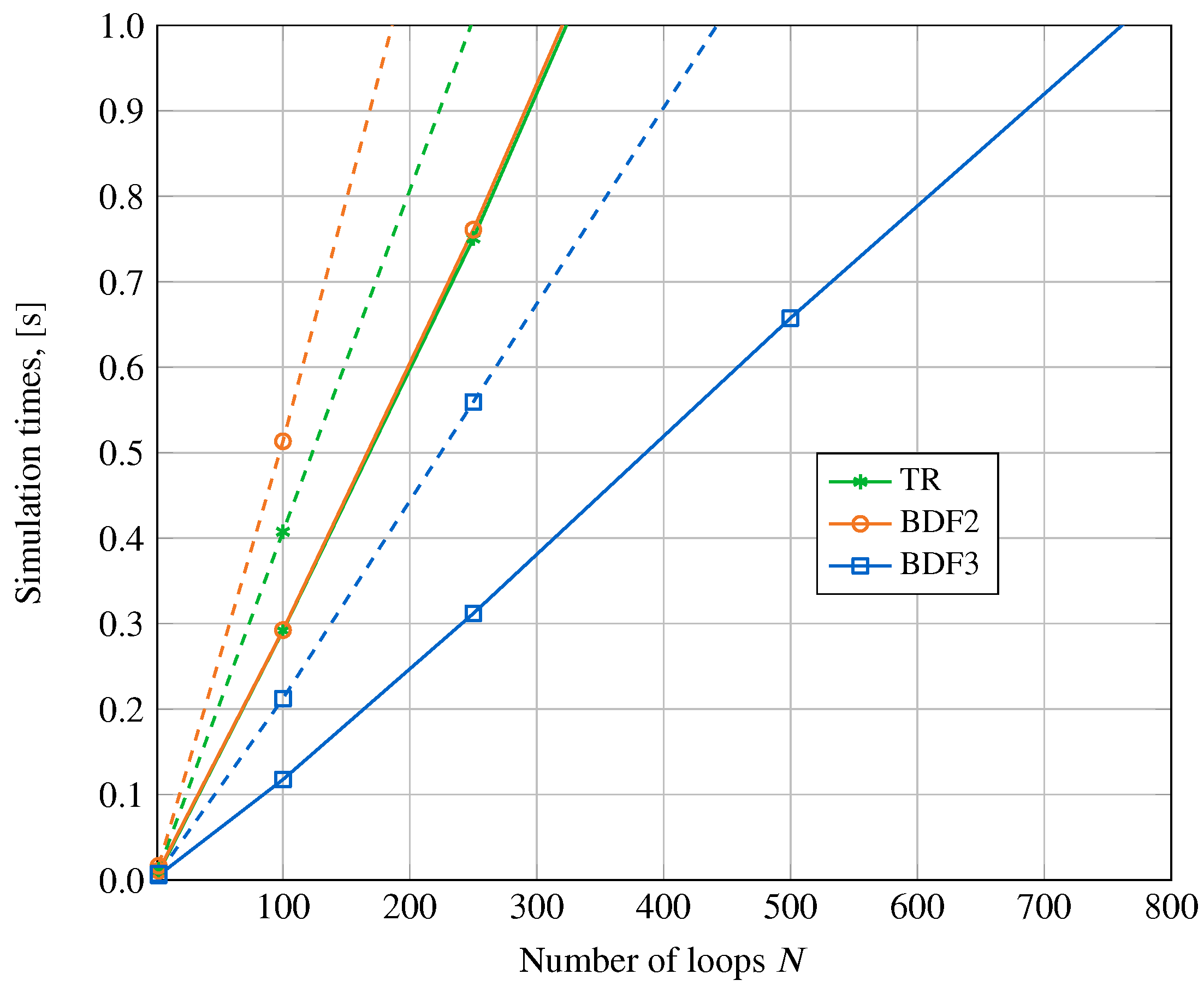
4.2.2. Scalable RLC Circuit
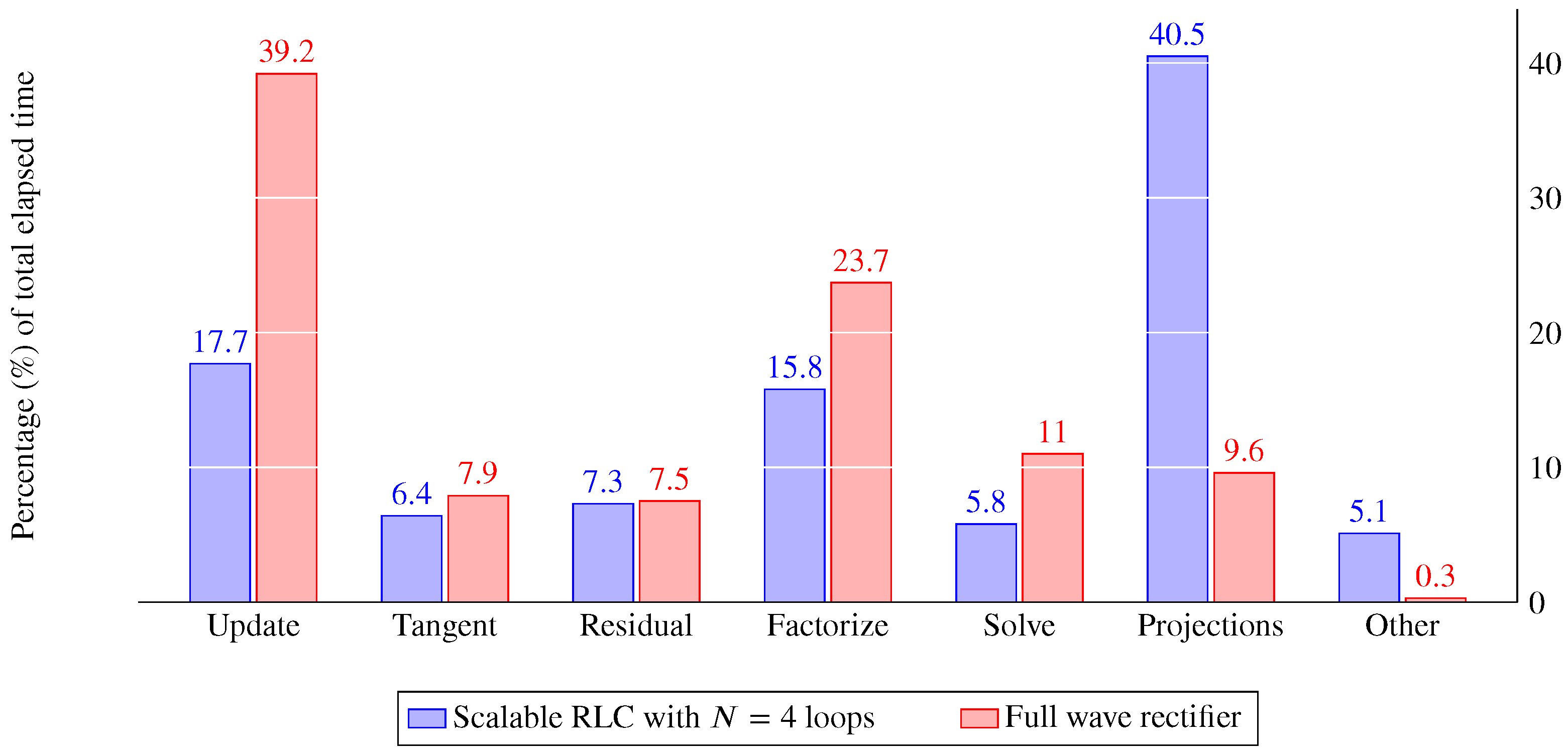
4.2.3. Full Wave Rectifier
- the update of the dynamic terms , , , and their derivatives;
- the evaluation of the residual and the tangent matrix in Equation (7);
- the factorization and backsubstitution of the linear solver in Equation (7);
- the projections in Equation (16); and
- other operations, such as the update of variables and regulation of code execution.
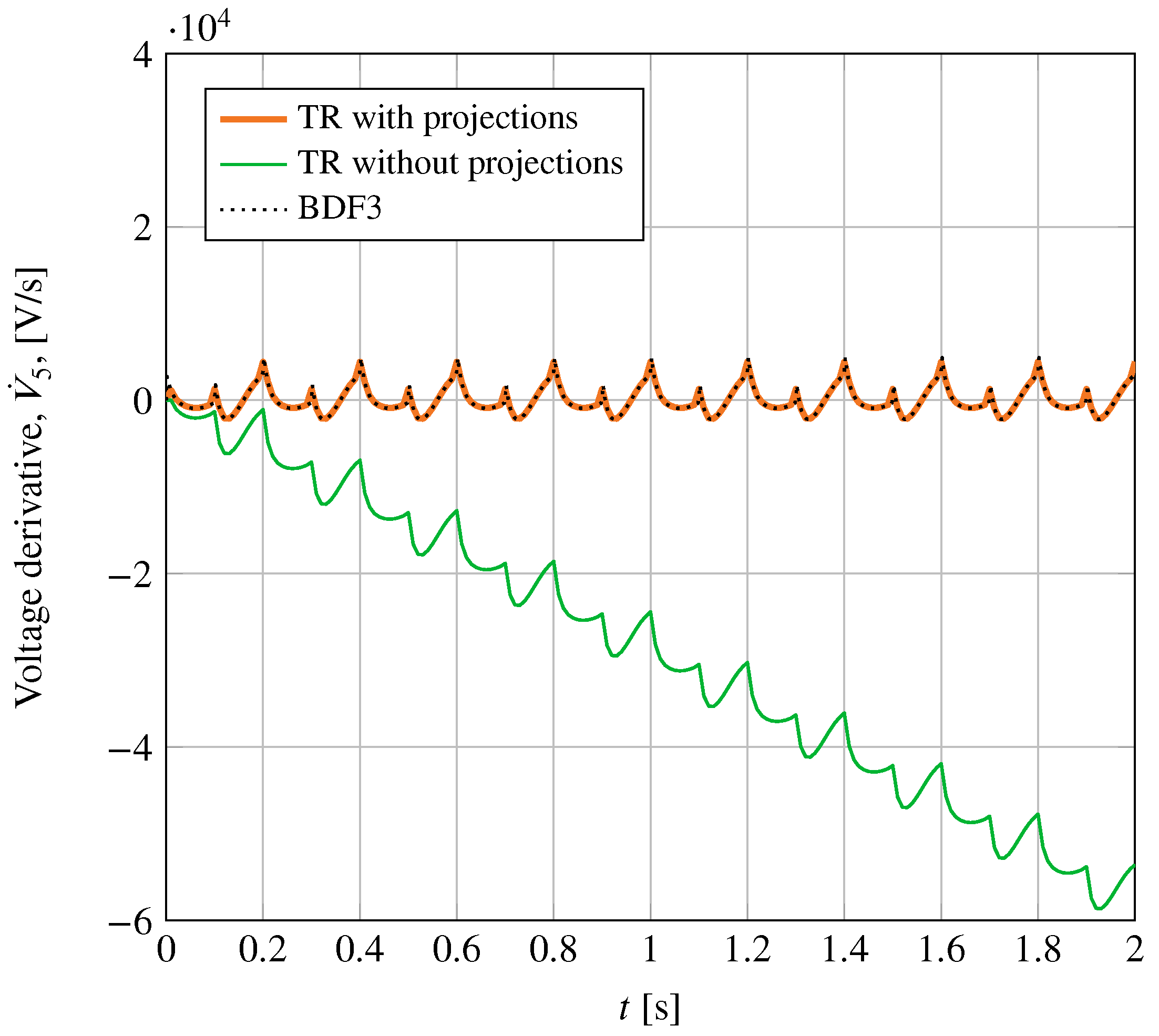
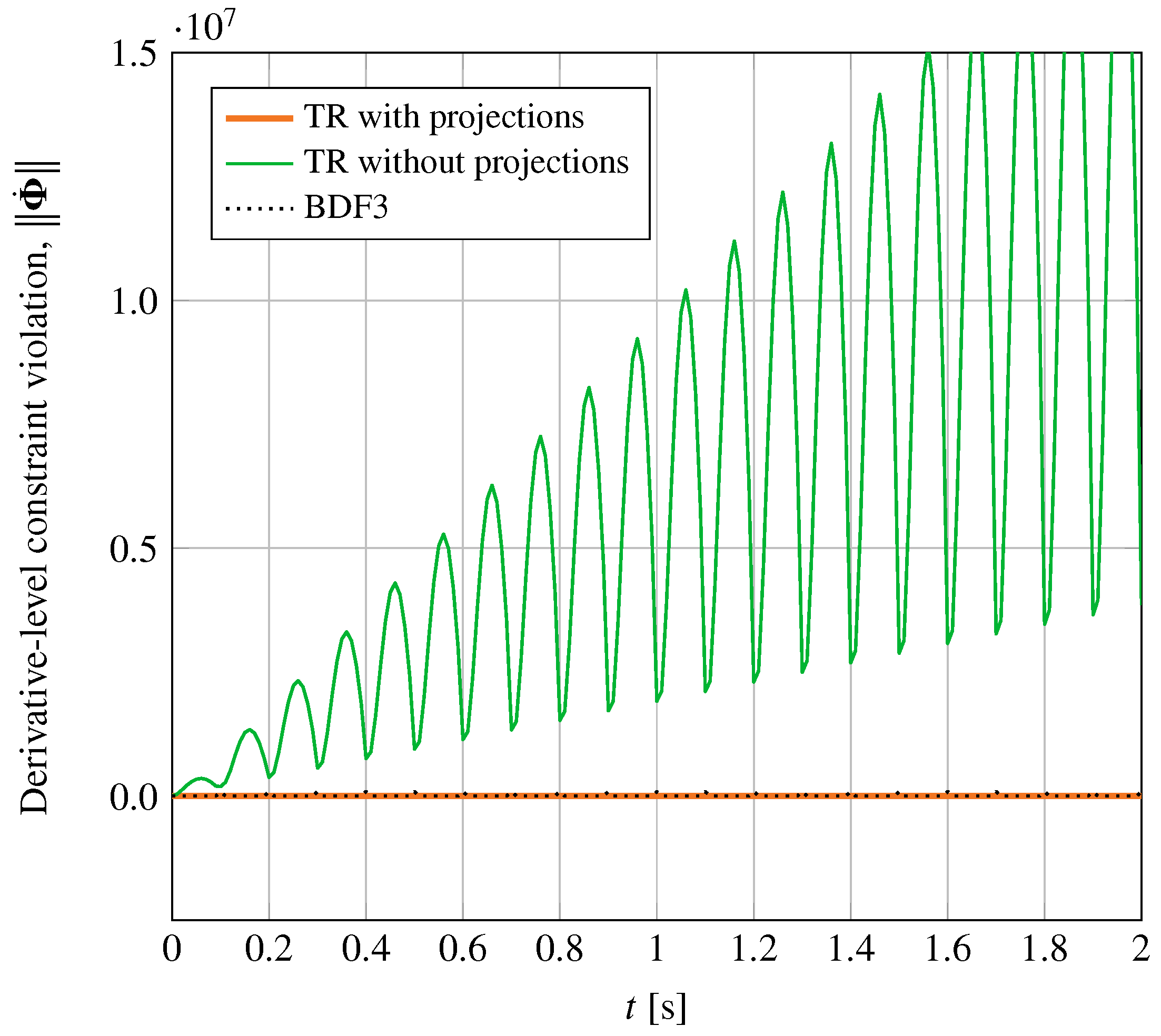
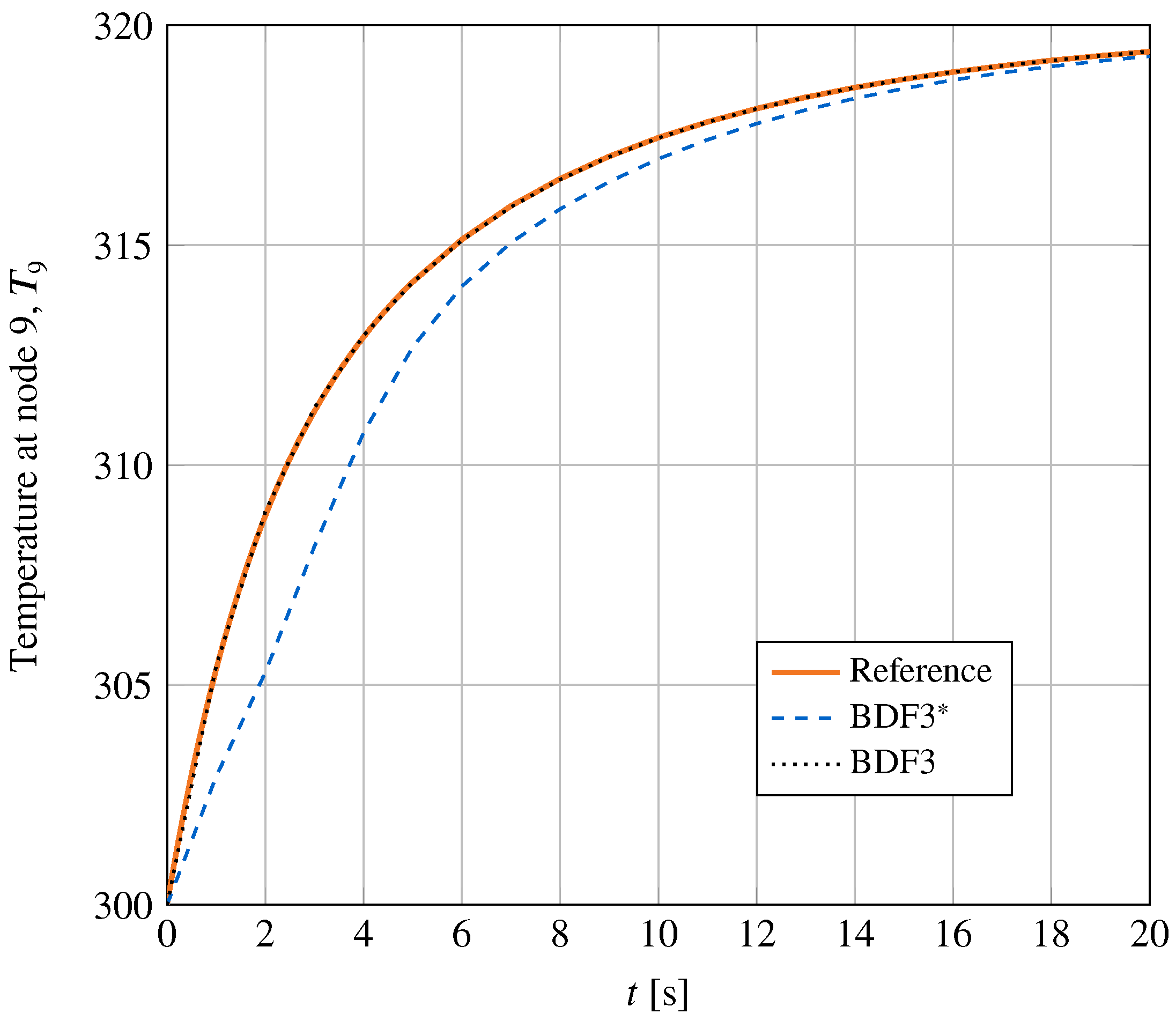
4.2.4. Synchronous Motor
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BDF | Backward Differentiation Formula |
| CCS | Column-Compressed Storage |
| DAE | Differential-Algebraic Equation |
| HiL | Hardware-in-the-Loop |
| ODE | Ordinary Differential Equation |
| PMSM | Permanent-Magnet Synchronous Motor |
| RT | Real Time |
| SITL | System-in-the-Loop |
| TR | Trapezoidal Rule |
Appendix A. Airgap Resistor
References
- Pastorino, R.; Cosco, F.; Naets, F.; Desmet, W.; Cuadrado, J. Hard real-time multibody simulations using ARM-based embedded systems. Multibody Syst. Dyn. 2016, 37, 127–143. [Google Scholar] [CrossRef]
- Andersson, H.; Nordin, P.; Borrvall, T.; Simonsson, K.; Hilding, D.; Schill, M.; Krus, P.; Leidermark, D. A co-simulation method for system-level simulation of fluid–structure couplings in hydraulic percussion units. Eng. Comput. 2017, 33, 317–333. [Google Scholar] [CrossRef]
- Nguyen, V.; Besanger, Y.; Tran, Q.; Nguyen, T. On conceptual structuration and coupling methods of co-simulation frameworks in cyber-physical energy system validation. Energies 2017, 10, 1977. [Google Scholar] [CrossRef]
- Gomes, C.; Thule, C.; Broman, D.; Larsen, P.G.; Vangheluwe, H. Co-simulation: A survey. ACM Comput. Surv. 2018, 51, 49:1–49:33. [Google Scholar] [CrossRef]
- Sadjina, S.; Pedersen, E. Energy conservation and coupling error reduction in non-iterative co-simulations. Eng. Comput. 2019. [Google Scholar] [CrossRef]
- Rodríguez, B.; González, F.; Naya, M.A.; Cuadrado, J. A test framework for the co-simulation of electric powertrains and vehicle dynamics. In Proceedings of the ECCOMAS Thematic Conference on Multibody Dynamics, Duisburg, Germany, 15–18 July 2019. [Google Scholar]
- Stettinger, G.; Benedikt, M.; Tranninger, M.; Horn, M.; Zehetner, J. Recursive FIR-filter design for fault-tolerant real-time co-simulation. In Proceedings of the 2017 25th Mediterranean Conference on Control and Automation (MED), Valletta, Malta, 3–6 July 2017. [Google Scholar] [CrossRef]
- Rahikainen, J.; González, F.; Naya, M.Á. An automated methodology to select functional co-simulation configurations. Multibody Syst. Dyn. 2020, 48, 79–103. [Google Scholar] [CrossRef]
- Nagel, L.W.; Pederson, D.O. Simulation program with integrated circuit emphasis. In Proceedings of the sixteenth Midwest Symposium on Circuit Theory, Waterloo, ON, Canada, 12 April 1973. [Google Scholar]
- Chua, L.O.; Li, P.M. Computer-Aided Analysis of Electronic Circuits; Prentice-Hall: Englewood Cliffs, NJ, USA, 1975. [Google Scholar]
- Newmark, N.M. A method of computation for structural dynamics. J. Eng. Mech. Div. ASCE 1959, 85, 67–94. [Google Scholar]
- Hairer, E.; Nørsett, S.P.; Wanner, G. Solving Ordinary Differential Equations I; Springer: Berlin, Germany, 1993. [Google Scholar] [CrossRef]
- Fijnvandraat, J.G.; Houben, S.H.M.J.; ter Maten, E.J.W.; Peters, J.M.F. Time domain analog circuit simulation. J. Comput. Appl. Math. 2006, 185, 441–459. [Google Scholar] [CrossRef]
- Maffezzoni, P.; Codecasa, L.; D’Amore, D. Time-domain simulation of nonlinear circuits through implicit Runge-Kutta methods. IEEE Trans. Circuits Syst. I Regul. Pap. 2007, 54, 391–400. [Google Scholar] [CrossRef]
- Yuan, F.; Opal, A. Computer methods for switched circuits. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2003, 50, 1013–1024. [Google Scholar] [CrossRef]
- Acary, V.; Bonnefon, O.; Brogliato, B. Time-stepping numerical simulation of switched circuits within the nonsmooth dynamical systems approach. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2010, 29, 1042–1055. [Google Scholar] [CrossRef]
- Ebert, F.; Bächle, S. Element-based index reduction in electrical circuit simulation. PAMM 2006, 6, 731–732. [Google Scholar] [CrossRef]
- Steinbrecher, A.; Stykel, T. Model Order Reduction of Electrical Circuits with Nonlinear Elements. In Progress in Industrial Mathematics at ECMI 2010; Springer: Berlin/Heidelberg, Germany, 2012; pp. 169–177. [Google Scholar] [CrossRef]
- Davoudi, A.; Jatskevich, J.; Chapman, P.L.; Bidram, A. Multi-resolution modeling of power electronics circuits using model-order reduction techniques. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 810–823. [Google Scholar] [CrossRef]
- Dufour, C.; Abourida, S.; Bélanger, J. Real-time simulation of electrical vehicle motor drives on a PC cluster. In Proceedings of the 10th European Conference on Power Electronics and Applications (EPE-2003), Toulouse, France, 2–4 September 2003. [Google Scholar]
- Almaguer, J.; Cárdenas, V.; Espinoza, J.; Aganza-Torres, A.; González, M. Performance and control strategy of real-time simulation of a three-phase solid-state transformer. Appl. Sci. 2019, 9, 789. [Google Scholar] [CrossRef]
- Zhang, B.; Jin, X.; Tu, S.; Jin, Z.; Zhang, J. A new FPGA-based real-time digital solver for power system simulation. Energies 2019, 12, 4666. [Google Scholar] [CrossRef]
- González, M.; Dopico, D.; Lugrís, U.; Cuadrado, J. A benchmarking system for MBS simulation software: Problem standardization and performance measurement. Multibody Syst. Dyn. 2006, 16, 179–190. [Google Scholar] [CrossRef]
- González, M.; González, F.; Luaces, A.; Cuadrado, J. A collaborative benchmarking framework for multibody system dynamics. Eng. Comput. 2010, 26, 1–9. [Google Scholar] [CrossRef]
- Hu, Z.; Du, M.; Wei, K.; Hurley, W.G. An adaptive thermal equivalent circuit model for estimating the junction temperature of IGBTs. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 392–403. [Google Scholar] [CrossRef]
- Bayo, E.; Ledesma, R. Augmented Lagrangian and mass–orthogonal projection methods for constrained multibody dynamics. Nonlinear Dyn. 1996, 9, 113–130. [Google Scholar] [CrossRef]
- Dopico, D.; González, F.; Cuadrado, J.; Kövecses, J. Determination of holonomic and nonholonomic constraint reactions in an index-3 augmented Lagrangian formulation with velocity and acceleration projections. J. Comput. Nonlinear Dyn. 2014, 9. [Google Scholar] [CrossRef]
- Davis, T.A.; Natarajan, E.P. Algorithm 907: KLU, a direct sparse solver for circuit simulation problems. ACM Trans. Math. Softw. 2010, 37, 1–17. [Google Scholar] [CrossRef]
- González, M.; González, F.; Dopico, D.; Luaces, A. On the effect of linear algebra implementations in real-time multibody system dynamics. Comput. Mech. 2008, 41, 607–615. [Google Scholar] [CrossRef]
- Sah, C.; Noyce, R.; Shockley, W. Carrier generation and recombination in P-N junctions and P-N junction characteristics. Proc. IRE 1957, 45, 1228–1243. [Google Scholar] [CrossRef]
- Touhami, S.; Bertin, Y.; Lefèvre, Y.; Llibre, J.F.; Henaux, C.; Fénot, M. Lumped Parameter Thermal Model of Permanent Magnet Synchronous Machines; Technical Report; LAPLACE-LAboratoire PLasma et Conversion d’Energie: Toulouse, France, 2017. [Google Scholar]
- Chen, Q.; Zou, Z.; Cao, B. Lumped-parameter thermal network model and experimental research of interior PMSM for electric vehicle. CES Trans. Electr. Mach. Syst. 2017, 1, 367–374. [Google Scholar] [CrossRef]
- Incropera, F.P.; Dewitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
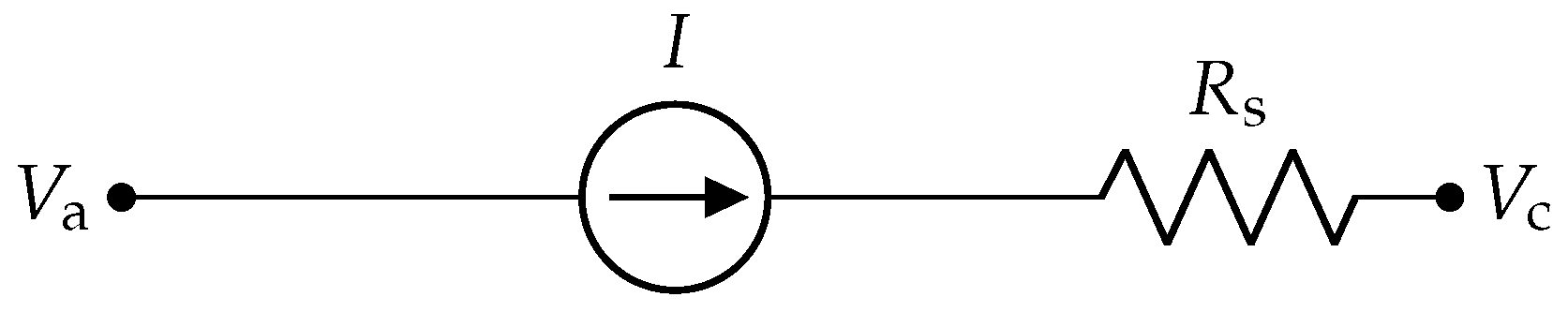

| 1 | 1 | - | - | |
| 2 | 2 | - | ||
| 3 | 3 |
| Resistor | Value | Capacitor | Value | Loss | Value |
|---|---|---|---|---|---|
| [K/W] | [J/K] | [W] | |||
| 1 | 2000 | 150 | |||
| 1 | 5000 | 2000 | |||
| 0.025 | 2000 | 200 | |||
| 0.015 | 1500 | 50 | |||
| 0.025 | 3000 | 50 | |||
| 0.01 | 300 | ||||
| 0.01 | 300 | ||||
| 0.001 | 500 | ||||
| 0.05 | 500 | ||||
| 0.0025 | |||||
| 0.25 | |||||
| 0.25 | |||||
| 0.001 | |||||
| 0.5 | |||||
| 0.5 | |||||
| 3 | |||||
| 3 |
| Problem | Variables | Algebraic ctr. | Differential ctr. |
|---|---|---|---|
| RLC | 8 | 5 | 3 |
| Sc. RLC | |||
| Rectifier | 20 | 19 | 1 |
| Thermal | 49 | 40 | 9 |
| Circuit | Simulation Time [s] | Sample Points |
|---|---|---|
| RLC | 10 | 1000 |
| Sc. RLC | 1 | 100 |
| Rectifier | 1 | 1000 |
| Thermal | 5000 | 5000 |
| Circuit | Precision | Error V or T | Error I or Q |
|---|---|---|---|
| RLC / Sc. RLC | Low | 1 mV | 1 mA |
| High | 10 μV | 10 μA | |
| Rectifier | Low | 1 mV | 1 mA |
| High | 10 μV | 10 μA | |
| Thermal | Low | 0.1 K | 1 W |
| High | 0.01 K | 0.1 W |
| Platform | CPU | Clock Freq. | Cores/ | RAM | L1 Cache | L2 Cache | L3 Cache | OS |
|---|---|---|---|---|---|---|---|---|
| [GHz] | Threads | [GB] | [kB] | [MB] | [MB] | |||
| PC | Intel i7-8700K | 3.7 | 6/12 | 8 | 192/192 | 1.5 | 12 | Win10 |
| RPi4 | ARM A-72 | 1.5 | 4/4 | 4 | 48/32 | 1 | 0 | Raspbian 4.19.57 |
| BBB | ARM A-8 | 1.0 | 1/1 | 0.5 | 32/32 | 0.25 | 0 | Debian 9.9 IoT |
| Method | h | Error V | Error I | |
|---|---|---|---|---|
| [ms] | [mV] | [mA] | ||
| TR | 2 | |||
| BDF1 | 1 | |||
| BDF2 | 2 | |||
| BDF3 | 2 |
| Method | h | Error V | Error I | |
|---|---|---|---|---|
| [ms] | [μV] | [μA] | ||
| TR | 2 | |||
| BDF1 | 1 | |||
| BDF2 | 1 | |||
| BDF3 | 1 |
| Method | Prec. | Elapsed Time | Elapsed Time | Elapsed Time |
|---|---|---|---|---|
| PC [ms] | BBB [ms] | RPi [ms] | ||
| TR | Low | |||
| TRnP | ||||
| BDF1 | ||||
| BDF2 | ||||
| BDF3 | ||||
| TR | High | |||
| TRnP | ||||
| BDF1 | 16,764.9 | 496,852.0 | 77,287.4 | |
| BDF2 | ||||
| BDF3 |
| Method | h | Error V | Error I | |
|---|---|---|---|---|
| [ms] | [mV] | [mA] | ||
| TR | 2 | |||
| BDF1 | 1 | |||
| BDF2 | 1 | 2 | ||
| BDF3 | 2 |
| Method | h | Error V | Error I | |
|---|---|---|---|---|
| [ms] | [μV] | [μA] | ||
| TR | 2 | |||
| BDF1 | 1 | |||
| BDF2 | 2 | |||
| BDF3 | 2 |
| Method | Prec. | Elapsed Time | Elapsed Time | Elapsed Time |
|---|---|---|---|---|
| PC [ms] | BBB [ms] | RPi [ms] | ||
| TR | Low | |||
| TRnP | ||||
| BDF1 | ||||
| BDF2 | ||||
| BDF3 | ||||
| TR | High | |||
| TRnP | ||||
| BDF1 | 65,542.3 | |||
| BDF2 | ||||
| BDF3 |
| Method | Precision | Loops | System Size |
|---|---|---|---|
| [] | [] | ||
| TR | Low | 2053 | 10,268 |
| BDF1 | 48 | 243 | |
| BDF2 | 1790 | 8953 | |
| BDF3 | 3661 | 18,308 | |
| TR | High | 248 | 1243 |
| BDF1 | - | - | |
| BDF2 | 186 | 933 | |
| BDF3 | 447 | 2238 |
| Method | h | Error V | Error I | |
|---|---|---|---|---|
| [ms] | [mV] | [mA] | ||
| TR | 16 | |||
| BDF1 | 3 | |||
| BDF2 | 7 | |||
| BDF3 | 9 |
| Method | h | Error V | Error I | |
|---|---|---|---|---|
| [ms] | [μV] | [μA] | ||
| TR | 6 | |||
| BDF1 | 1 | |||
| BDF2 | 9 | |||
| BDF3 | 9 |
| Method | Prec. | Elapsed Time | Elapsed Time | Elapsed Time |
|---|---|---|---|---|
| PC [ms] | BBB [ms] | RPi [ms] | ||
| TR | Low | |||
| TRnP | ||||
| BDF1 | ||||
| BDF2 | ||||
| BDF3 | ||||
| TR | High | |||
| TRnP | ||||
| BDF1 | 14,009.5 | 141,564.0 | 61,429.0 | |
| BDF2 | ||||
| BDF3 |
| Method | h | Error T | Error Q | |
|---|---|---|---|---|
| [ms] | [K] | [W] | ||
| TR | 500 | 2 | ||
| BDF1 | 25 | 2 | ||
| BDF2 | 250 | 2 | ||
| BDF3 | 500 | 2 |
| Method | h | Error T | Error Q | |
|---|---|---|---|---|
| [ms] | [K] | [W] | ||
| TR | 100 | 2 | ||
| BDF1 | 2 | |||
| BDF2 | 100 | 2 | ||
| BDF3 | 250 | 2 |
| Method | Prec. | Elapsed Time | Elapsed Time | Elapsed Time |
|---|---|---|---|---|
| PC [s] | BBB [s] | RPi [s] | ||
| TR | Low | |||
| TRnP | ||||
| BDF1 | ||||
| BDF2 | ||||
| BDF3 | ||||
| TR | High | |||
| TRnP | ||||
| BDF1 | ||||
| BDF2 | ||||
| BDF3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez, B.; González, F.; Naya, M.Á.; Cuadrado, J. Assessment of Methods for the Real-Time Simulation of Electronic and Thermal Circuits. Energies 2020, 13, 1354. https://doi.org/10.3390/en13061354
Rodríguez B, González F, Naya MÁ, Cuadrado J. Assessment of Methods for the Real-Time Simulation of Electronic and Thermal Circuits. Energies. 2020; 13(6):1354. https://doi.org/10.3390/en13061354
Chicago/Turabian StyleRodríguez, Borja, Francisco González, Miguel Ángel Naya, and Javier Cuadrado. 2020. "Assessment of Methods for the Real-Time Simulation of Electronic and Thermal Circuits" Energies 13, no. 6: 1354. https://doi.org/10.3390/en13061354
APA StyleRodríguez, B., González, F., Naya, M. Á., & Cuadrado, J. (2020). Assessment of Methods for the Real-Time Simulation of Electronic and Thermal Circuits. Energies, 13(6), 1354. https://doi.org/10.3390/en13061354







