Abstract
Scheduled charging offers the potential for electric vehicles (EVs) to use renewable energy more efficiently, lowering costs and improving the stability of the electricity grid. Many studies related to EV charge scheduling found in the literature assume perfect or highly accurate knowledge of energy demand for EVs expected to arrive after the scheduling is performed. However, in practice, there is always a degree of uncertainty related to future EV charging demands. In this work, a Model Predictive Control (MPC) based smart charging strategy is developed, which takes this uncertainty into account, both in terms of the timing of the EV arrival as well as the magnitude of energy demand. The objective of the strategy is to reduce the peak electricity demand at an EV parking lot with PVarrays. The developed strategy is compared with both conventional EV charging as well as smart charging with an assumption of perfect knowledge of uncertain future events. The comparison reveals that the inclusion of a 24 h forecast of EV demand has a considerable effect on the improvement of the performance of the system. Further, strategies that are able to robustly consider uncertainty across many possible forecasts can reduce the peak electricity demand by as much as 39% at an office parking space. The reduction of peak electricity demand can lead to increased flexibility for system design, planning for EV charging facilities, deferral or avoidance of the upgrade of grid capacity as well as its better utilization.
1. Introduction
Globally, road transportation accounts for 17% of all emissions of carbon dioxide (CO) [1]. Electric vehicles (EVs) offer a solution for the reduction of emissions in the road transport sector, particularly for passenger vehicles. Two characteristics of EVs already make a convincing case for their adoption: (1) the high efficiencies of electric propulsion and (2) lower or zero tailpipe emissions.
The net CO emissions per kilometer driven by Battery Electric Vehicles (BEVs), however, depend on the energy mix used for electricity generation. Based on Well-to-Wheel comparison, the use of BEVs can greatly reduce transport-related net emissions when they are powered by electricity generated from renewable sources [2]. There is thus a need both to shift road transportation toward electric propulsion as well as to simultaneously increase the renewable fraction of the electricity used to power it.
Currently, the charging of the majority of EVs is uncoordinated or unscheduled, i.e., they begin charging at the moment when they are plugged in. Unscheduled charging of electric vehicles can cause increased demand for electricity at peak times. These peaks are expected to increase to over 50% even at 30% EV penetration in the Netherlands [3]. Higher peak loads lead to local issues such as overloading of transformers and other infrastructure in distribution networks, increased grid congestion, power imbalances and voltage dips [4,5]. At a more global level, higher peak loads can result in higher electricity costs and greater carbon emissions [6].
Scheduled or smart charging of EVs can greatly reduce the peak demand for electricity and avoid local congestion in electrical power systems [7]. This reduces the costs for the provision of ubiquitous and affordable EV charging facilities. In this manner, it lowers one of the main barriers to EV adoption: a lack of accessible charge points. In addition, by matching EV charging with the availability of locally produced renewable energy (such as that produced by solar photovoltaics), smart charging can also result in increasing the penetration of renewables in the mobility sector. EV charge scheduling strategies, which aim to reduce local peak demands and congestion, require knowledge of future electricity demands and renewable energy production. However, this uncertainty remains either neglected or seldom addressed in the literature on smart charging.
In [8], the impact of EV charging on residential distribution grids is investigated, but although the household demands are forecasted stochastically, the arrival of other EVs in the future are not considered. The power demand of a single EV is considerably larger than the loads in the household profiles considered in the study and the energy required for a daily charging session is in the range of a household daily energy demand [9]. The lack of EV load forecasting is thus a considerable oversight—particularly from a peak shaving perspective. In [10], a fleet of V2G compatible EVs is considered, whose scheduling is to be optimized for the purpose of providing spinning reserves. Although the formulation acknowledges and accounts for the unexpected departure of EVs, it assumes that the aggregator has accurate information on both the EV driving patterns as well as their States of Charge (SoCs), based on which demands are calculated.
In [11], EVs are scheduled for peak reduction and self-consumption within a microgrid. A car-sharing setup is considered, where the users reserve vehicles in advance for the trips they plan. In such a case, the deviation from the planned schedule is small, assumed to be always less than an hour. EVs that are not used in such a car-sharing scheme are not considered. Similarly, in [12], fuel cell electric vehicles are scheduled for V2G energy dispatch in a microgrid. However, although load forecasting is performed with an assumption of accuracy, mobility-related uncertainty associated with the future arrival of vehicles remains unaddressed.
Neglect or incomplete consideration of future EV demand in these models can cause smart charging strategies to perform worse than expected. When designing an optimal strategy, it is critical that uncertainty of vehicle charging demand (both in terms of timing as well as magnitude) is taken into account. This work investigates and quantifies the effect of this uncertainty. It is taken into consideration to develop strategies based on Model Predictive Control (MPC) for scheduling EV charging.
The paper is divided into sections as follows: Section 2 describes the physical system considered i.e., the solar parking lot, EVs and Electric Vehicle Supply Equipment (EVSE) and its modeling. Section 3 introduces the proposed methods of charge scheduling based on MPC methodology and their formulation. Section 4 illustrates the results obtained from running the simulations and discusses their relevance. Finally, Section 5 provides the conclusions and insights provided by the paper together with interesting directions for future research.
2. System Description
The system considered in this work is a solar charging carport for the charging of electric vehicles as seen in Figure 1. It was modeled in MATLAB and was used to generate inputs for the scheduling strategy. It includes a solar photovoltaic (PV) array, stationary storage and LED lighting connected to a DC bus, coupled bidirectionally with a grid-connected AC bus, which also enables AC charging.
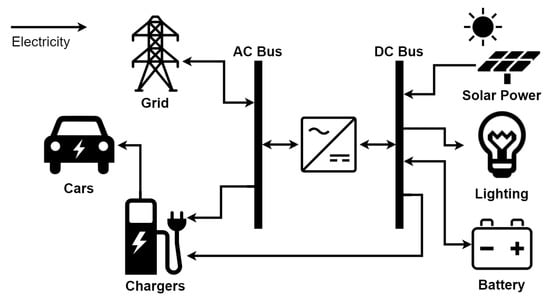
Figure 1.
System configuration of a smart solar parking lot.
2.1. Solar Parking Lots
A solar array that was roof-mounted over the parking lot to generate electricity was considered. The total solar PV array generation capacity of 120 kWp was distributed over 40 parking spaces, corresponding to 3 kWp of generation per parking space. Power generation was simulated based on weather data from the Cabauw weather station located in the province of Utrecht in The Netherlands [13]. The data was used to simulate the typical power of the solar power array for one year with a time resolution of 15 min. Solar power generation was modeled using PVLib, a validated open-source tool developed by Sandia National Labs [14]. Table 1 describes the solar PV array characteristics used in the model.

Table 1.
Description of solar photovoltaic array characteristics.
2.2. Batteries
The electric vehicle batteries using the parking lot for charging were assumed to be representative of the current Dutch EV fleet, including BEVs and Plug-in Hybrid Electric Vehicles (PHEVs). The battery energy capacities considered therefore range from the 8.8 kWh Audi A3 PHEV to the 100 kWh Tesla Model X BEV. The solar parking lot also included a stationary Li-ion based battery storage system, for storing excess energy to further reduce the peak demand. The battery had a rated power of 50 kW and a capacity of 50 kWh, of which 80% was usable. The total number of batteries, , is at all times less than 41, since the maximum occupancy of the parking lot is 40 EVs and there is always the stationary battery.
The charging efficiency, , and discharging efficiency, , in the battery, were each assumed to be 95%, leading to overall roundtrip losses of 9.75%. Coulomb counting was used to infer the state of charge (SoC) of the battery and changes to it. The rectification stage in the vehicle was assumed to lead to losses of about 6% in charging [15].
2.3. Electric Vehicle Supply Equipment
The system includes 40 charge points, each rated at 32 A (7.4 kW) for both AC and DC. While this rating is commonly found as AC level 2 charging [16], it is a lower current capacity than commercial DC charge points. The reason for this choice was to enable the slow charging of EV batteries on the DC bus without multiple rectification-inversion stages, as is expected in the future. The losses in the EVSE, which are primarily resistive in nature, were assumed to be around 0.2% [15].
2.4. Electric Vehicle Load Profile
The electric vehicle load profile was built based on two submodels—first, the EV arrival and departure model and the second, the estimation of the state of charge at the point of entry. In addition, the load is also determined by the extent to which the battery is to be charged by the time of departure. In this work, it is assumed that the EV drivers wish for their EVs to be charged to 100% SoC whenever possible.
2.4.1. EV Arrival and Departure
Direct Use of Observed Activity-Travel Schedule (DUOATS) models are a common method applied in smart charging and demand response studies [17]. Such a model was used in this work, whereby observed vehicle patterns were used to simulate EV behavior. The parking location considered was a workplace, and the model was based on data from the EV Project, a project run by the United States Department of Energy. It included data related to 8228 electric vehicles and hundreds of thousands of trips and charging events [18]. Since the data was collected from a large number of participants and geographical locations across the USA, it was assumed to be generalizable.
This historical parking data was used to determine the arrival and departure rates at both parking lots for each timestep of the day, considering weekdays and weekends separately. Based on these rates, a Monte Carlo approach was taken to determine the number of EV arrivals in each timestep. The duration of parking and the time of day were used to determine the number of departures in each timestep, after which an occupancy profile was built. A representative week of occupancy of vehicles at the workplace is shown in Figure 2. There are noticeable daily patterns of arrivals and departures during weekdays, with weekends having lower arrival rates.
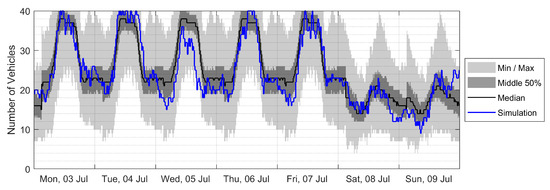
Figure 2.
Simulated occupancy at the workplace parking lot over a week.
2.4.2. EV State of Charge on Arrival
Truncated normal distributions were used for assigning the SoCs on arrival. The coefficients for the normal distribution were inferred by fitting data from the EV Project [18], which collected data for over 8000 EVs in the USA. They are shown in Table 2.

Table 2.
Coefficients describing the assignment of EV battery states of charge on arrival.
The lower mean SoC and greater standard deviation for PHEVs are explained by the lower concern of PHEV drivers about depleted batteries in comparison with BEV drivers.
Based on the time of arrival of an individual EV, the battery capacity of the EV and its SoC at the time of arrival, the expected charging demand of the EV was calculated. This demand (or as high a fraction as possible) needed to be met within the plug-in duration. The control system was informed about the time of departure at the time of arrival in all cases.
With knowledge of the available solar energy, the forecasted solar energy over the forecast horizon and the EV charging demand, the optimal charging of EVs in the parking space was to be determined in a manner that minimized the peak electricity demand in the solar parking lot. The following section describes the methods used for this scheduling.
3. Methods for Charge Scheduling
For an investigation into the effect of uncertainty of EV demand on peak loads, two reference cases and three scenarios are considered. One reference case is unscheduled charging, where EVs charge at maximum power as soon as they are plugged in. In addition, a case is simulated with perfect forecasting of solar production and EV demand, which may be considered as another reference case. The three scenarios investigated lie between these two extreme cases:
- No EV demand forecast: EV charging is scheduled without a forecast of energy demand for EVs arriving in the future
- Average EV demand forecast: EV charging is scheduled with a single forecast of energy demand for EVs arriving in the future which is based on average values.
- Robust EV demand forecast: EV charging is scheduled to be robust across a range of possible energy demands for EVs arriving in the future
In all these three scenarios, the schedule was designed to be robust across a range of possible solar forecasts. These scenarios thus differ only in their approach to EV demand forecasting. The objective function for peak reduction under perfectly accurate forecasts is described in Section 3.1. The introduction of uncertainty in the forecasts is described in Section 3.2, after which each of the three scenarios and its optimization formulations are described. The commercial solver, Gurobi, was used with MATLAB in each case on a Windows PC with an Intel i5 1600 MHz quad-core processor and 32GB RAM.
3.1. Problem Formulation with Perfect Forecasting
In the scenario with perfect forecasting, the future solar production, as well as future electric vehicle demand over the 24 h horizon in the future, are assumed to be accurately known in advance. This is not a practically feasible scenario since neither of these can be accurately known in advance. However, this scenario clearly defines the best possible performance of the scheduling approach, with reference to which other scenarios may be compared. In addition, it also provides an idea of the performance of the scheduling algorithm independent of the degree of accuracy of the forecast.
To optimize the scheduling of EVs within the carport, we apply Model Predictive Control (MPC). MPC is a control technique used for determining the optimal behavior of complex multivariate problems. The control action is determined at each time step by solving an open-loop optimal control problem over a finite time horizon. MPC is used to solve problems during the operation of the system, taking the state of the system into account at each time step. These characteristics make MPC suitable for the control of EV charge scheduling at the solar parking lot.
The goal of the scheduling of EV charging is to reduce the peak demand of the solar parking lot over the time horizon under consideration. Thus, the objective function is:
where is the net energy exchange between the parking lot and the grid at time k and is the time horizon, which is 24 h. A sensitivity analysis on the duration of the horizon revealed that longer forecasts had no increased benefits to the simulation. Further, with reducing the accuracy of the length of the simulation, the reliability of longer horizon forecasts is lower upon the introduction of forecasting uncertainty. An auxiliary variable, is introduced, which represents the local maxima or peak in grid exchange of the parking lot with batteries and lighting load, over the considered horizon, .
The objective function is thus rewritten as:
with the decision variables
subject to a number of constraints, described below.
At any given time, t, the energy exchanged with the grid, , depends on the PV production, , the lighting load, , and summed load of each battery, . It is ensured that the energy exchange peak, which is subject to minimization, is the highest peak within the considered horizon both in purchase as
as well as in feed in as
The stored energy in the battery in the timestep, the state variable, , is described as
In order to formulate the battery behavior linearly, the Mixed Logical Dynamics (MLD) formalism is used [19]. A binary decision variable is introduced, defined as:
and leads to the constraint:
This binary decision variable, , is then used to reformulate Equation (6) as
However, this formulation is still nonlinear because it contains the product of two decision variables, and . An additional set of continuous decision variables is introduced as
The minimum energy, which can be stored in the , battery in the timestep, is limited by the lowest possible energy which can be delivered to it with the objective of maximimizing the SoC at departure. This is formulated as
The maximum energy which can be stored in the i-th, battery in the -th timestep is limited by the physical constraints on the battery capacity and the power rating of the chargepoints. It is formulated as
The constraints on the energy exchanged with the battery in each time step is given as
where is the maximum allowable value of and is the minimum allowable value. An overestimate of or an underestimate of is acceptable, but values close to the true maximum and minimum are preferred to lower computational time. These values are taken as
where and are the power limits of the battery and is the length of the time step i.e., 15 min. The tolerance, is a small value, typically the machine precision of the solver.
The following constraints then limit the auxiliary MLD variables and to ensure they will be equivalent to their stated definitions [20]
3.2. Inclusion of Uncertainty in Forecasting
Since historic data of the PV yield and modeled data for the EV demand were used, the values of the future PV yield and EV demand were known. In order to simulate an inaccurate forecast, errors were introduced to the known PV production and the EV demand over the relevant horizon.
3.2.1. Uncertainty in PV Forecasting
is known to be the PV production over the relevant horizon at the timestep, t. The forecasted value of PV production is the sum of and an additional solar forecasting error term, , as
Monte Carlo methods are used in this case to generate a finite but large number of error vectors, , which are then considered.
where is the number of error vectors considered. If is large enough, may be considered to be a reasonably good approximation of , the set of all possible error vectors. 10,000 is chosen for in this case. Though forecasting error is normally distributed, for robust optimization, a bounded distribution is required. The distribution is therefore truncated such that
for all t in and j in . The upper and lower bounds are determined by (t) the standard deviation of the forecasting error at time, t. The forecasting error is also truncated so that the forecasted power generation cannot be less than zero or greater than the clear sky generation. The choice of three standard deviations as a limit, rather than more conservative values of five or seven, is justified based on simulation results.
3.2.2. Uncertainty in EV Forecasting
Two approaches were considered here—the average approach and the Monte Carlo approach, as used in the PV uncertainty introduction. In the average approach, the terms and , defined in Equations (12) and (13) are taken to be their average values based on data collected from EVs in the parking lot at the timestep, t. Thus, uncertainty in a number of variables like arrival time and numbers, departure times, the energy capacity of the vehicle, the SoC of the vehicle on arrival are all clustered together to be dealt with through the optimization formulation. The nature of the formulation implies a single forecast is available in each timestep, which is based upon average values in the past, thus satisfying the aim of this method of introduction of uncertainty.
In the second approach, error terms are introduced through Monte Carlo simulation, as with the errors in PV generation forecasts. However, as in the average case, the errors are introduced in the terms and , influencing the state constraints rather than the state variables. This formulation thus considers a range of possible forecasts, treated as equally probable, over which the problem needs to be solved.
3.3. No EV Demand Forecast
No EV forecasting is the simplest strategy where the charging of EVs plugged-in at the parking lot at the current time step are optimized over the period they are expected to be plugged in. The arrival of additional EVs in the near future and their demands are not considered—a drawback of the approach.
The schedule is designed to deal with uncertainty in the PV forecast. It does this by considering a range of possible PV forecasts, over all of which it reduces peaks. In other words, it operates robustly over a range of PV uncertainties.
To ensure robustness, we use min max optimization, which minimizes the cost function over the decision variables for the worst case i.e., highest peak load. In this case, the objective function is
where is a vector representing a random possible value for the forecasting errors at each time step t, and is the bounded set of all possible forecasting errors. The errors at each time step are therefore drawn randomly from the uniform distribution given by
A new auxiliary variable, T, is now defined as the maximum value for the objective function under all the forecasting errors considered. Because the objective function is not directly dependant on the forecasting uncertainty, T can simply be defined as being equal to the original objective function. If J is the maximum peak in each case of forecasting error considered, and the decision variables, T is given by
where is independent of the uncertainty variables.
The objective function is redefined as
with the decision variables:
The optimization problem is then solved to be robust across the errors in PV forecast, , which lie within the bounded range of uncertainty . As proven in [20], a constraint cannot be active at some intermediate value of the disturbance without violating the constraint at the extreme value. In this model, the greater-than constraint will be active only at the maximum value of the disturbance and a less-than constraint will be active only at the minimum. Hence, only the minimum value, , and maximum value, , of the errors were considered, which are sufficient for the all intermediate error values.
Although there is no EV forecasting, vehicles which are not plugged in at the charging station at the relevant timestep, would still begin charging at some point in the future. These limits are then included in constraints in Equations (12) and (13), which are modified to
and
The constraints in Equation (15) through Equation (21) remain unchanged.
3.4. Average EV Demand Forecast
The objective function with robust solar PV forecast and a single average EV forecast remains the same as Equation (28). The stored energy terms, and in the constraints in Equations (12) and (13) are replaced by average values of these variables. The new constraints are therefore:
where and are the average values for the variables and respectively.
3.5. Robust EV Demand Forecast
The system is meant to be robust in the sense of reducing peak grid exchange across a wide range of EV forecasting errors as well as errors in the solar forecast. The maximum value, and minimum value, , in the range of errors introduced in the EV demand forecast through the Monte Carlo simulation, as described in Section 3.2.2, were used to define the state constraints for and as
However, constraints risk making the problem infeasible if , which is highly likely. In order to enable a feasible solution to the problem, the state constraints for vehicles which are forecasted to arrive, are expressed as soft constraints:
for all , . The slack variables and correspond respectively to the constraints for the minimum and maximum stored energy, and are added to the optimization problem as an auxiliary decision variables. For the stationary battery as well as the vehicles plugged in at the parking lot at a given timestep, k, the state constraints remain hard since the minimum and maximum stored energies are known with certainty.
The complete optimization formulation is then given by:
where and are penalty constants. The values and were found empirically to lead to lowest values of peak demand. Increasing the penalty constant values did not however lead to large changes in peak demand. The decision variables are:
with the additional constraint
4. Results and Discussion
A year of operation of the solar parking lot was simulated for each of the three described scenarios to determine the performance of the system at peak reduction in each case. During the comparison, the reference cases of unscheduled charging and perfect forecasts are also included to provide additional insights.
4.1. Example Simulations
Figure 3 shows the energy flows within the system over a representative period, in this case, a week. The two reference cases, unscheduled charging and charging with perfect forecasting, are compared. The characteristics of the scheduling seen here are also valid for longer simulations over the year.
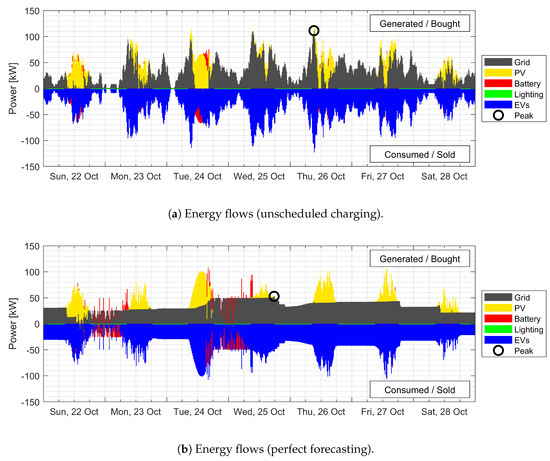
Figure 3.
Comparison of energy flows in the solar parking lot with unscheduled charging as opposed to charging with perfect forecasts.
In accordance with thermodynamic system conventions, the energy entering the electrical system (PV production, grid purchase and battery discharge) is taken as positive and energy leaving the system (EV and battery charging, lighting load and feed-in to the grid) as negative. The shape of the positive and negative sides are similar, showing the energy balance in each timestep, excluding losses. The solar energy production is shown in yellow, battery charge and discharge in red and EV charging in blue. The lighting loads, which are very small in comparison with the others, are shown in green and residual grid load (after solar self-consumption and battery charge/discharge) in gray. The highest peak in the week is highlighted in each figure.
The largest peak in the residual grid load (110 kW) as a result of unscheduled charging, seen on Thursday in Figure 3a, is considerably reduced in magnitude to 50 kW as a result of scheduled charging with perfect forecasts. In addition, the frequency of these peaks is found to decrease considerably and a uniformly flat load profile achieved. The arrivals of many EVs on Tuesday, Wednesday and Thursday mornings, all of which lead to peaks in energy demand if unscheduled are all adequately shaved. Although the perfect forecasting scenario is not an applicable case, it demonstrates the success of the method at reducing the peak residual load in the week considered.
Figure 4, similarly, shows the energy flows in the system for the three scenarios. As seen in Figure 4a, where no EV forecast is available, the magnitude of the highest peak in this case (100 kW) is lower than that in the unscheduled case. Relative to the perfectly forecasted case, though, the peaks are considerably higher. A drawback of the scenario can be seen in the situation leading to the Wednesday afternoon peak. The EVs in the parking lot on Tuesday night was charged slowly to reduce the peak load at night. This led to a larger number of vehicles in need of simultaneous charging on Wednesday morning, leading to a high peak in electricity demand in the afternoon. On the other hand, the Thursday peak seen in the unscheduled charging case was effectively shifted.
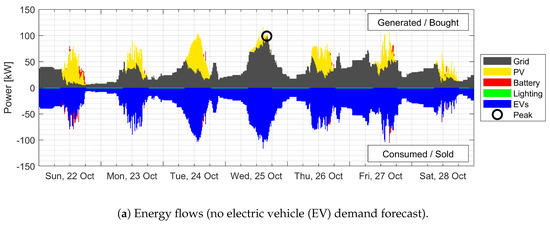
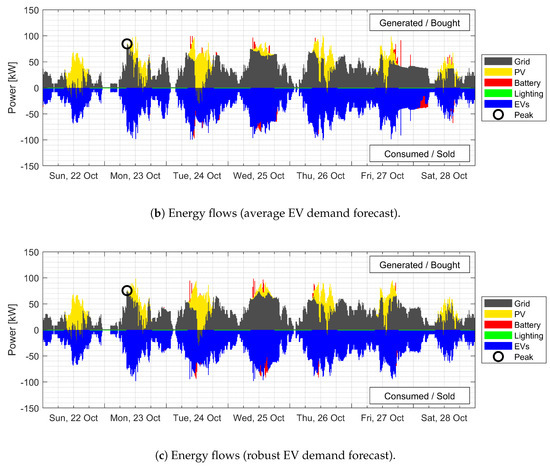
Figure 4.
Comparison of energy flows in the solar parking lot with no EV demand forecast, a single average EV demand forecast and a robust consideration of EV demand forecasting.
The single average forecast seen in Figure 4b already provides a considerable reduction in the magnitude of the highest peak (85 kW) relative to the case without an EV forecast. On the same Wednesday, the vehicles parked overnight are charged in the morning in anticipation of future arrivals, thus lowering the peak on Wednesday. However, a drawback of the system is seen on Monday, which has a lower than average EV charging demand. A large number of EVs are charged in the morning in anticipation of demand later in the day. However, the demand in the afternoon was lower than expected, making the morning peak unnecessary in hindsight. This leads to Monday having the highest peak in the week.
The robust treatment of forecasting seen in Figure 4c results in even further reduction in the magnitude of the highest peak in the week, which is about 75 kW. The Wednesday load is lowered even more, and there is a better performance in the case of the lower demand on Monday. Similar to the average forecast, there are many peaks with similar magnitude across the week, but the height of the highest one is lower than in the case without the demand forecast.
It can be seen that in the system, the peak loads on the grid are always the result of EV charging and never the result of solar feed-in. While solar peaks did occur under low occupancy of the parking lot during summer when the stationary battery was full, they were generally lower than the EV charging peaks. Further, it was assumed that curtailment would be the strategy for peak shaving of solar feed-in peaks.
The power flows also reveal that the use of fixed storage remains low in all cases. A sensitivity analysis was conducted on the battery size used. It revealed that small batteries had a considerable impact on peak reduction, but the returns diminished with increasing battery size. Increasing the battery size beyond 50 kWh had no further effect on peak reduction.
4.2. Maximum Annual Peak Exchange with the Grid
The scenarios are compared in terms of a few metrics, which provide insight into the simulation results. The first metric considered is the highest annual peak in each scenario. These peaks have a magnitude which is generally close to the transformer rated capacity and occur rarely—a few times in the transformer lifetime. They lead to a type of transformer loading known as short term emergency loading, involving a very high demand occurring for periods of half an hour or less. However, despite the short duration and relative rarity of their occurrence, these overloads can cause considerable damage. Increased hot-spot temperatures, resulting in the evolution of free gas from insulation and insulating fluid, reduced mechanical strength and deformation of conductors and structural insulation, and high internal pressures resulting in leaking gaskets or loss of oil can all be results of short term emergency loading. These loads can considerably shorten the lifespan of these assets [21]. A reduction in the highest annual peak indicates a reduction in the intensity of these events. Figure 5 illustrates the peak annual power demand compared across the three scenarios and the two reference cases.
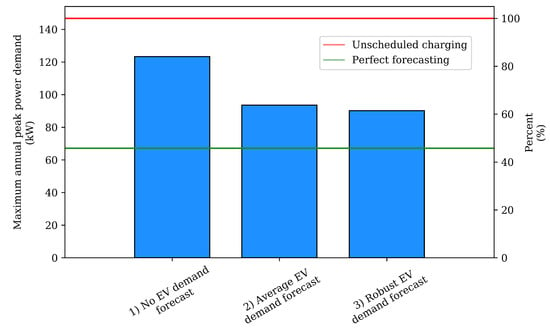
Figure 5.
Comparison of annual peak power exchange with the grid.
The comparison shows that smart charging for peak reduction in the absence of EV demand forecasting is effective at the reduction of short term peak loads, but this effect is limited (about 16% peak reduction relative to unscheduled charging). Further, the magnitude of peak reduction in the absence of EV demand forecasting is considerably less than that possible with perfect forecasting of future EV demand (about 54% reduction), which is the case often assumed in the literature. The availability of single forecasts based on average demands in the past result in an increase in the effectiveness of reducing short term peak loads. Peaks are reduced by an additional 20% relative to unscheduled charging. Consideration of multiple possible forecasts across which the system works in a robust manner further reduces the peak power exchange of the system. Such a system had an annual peak of 39% lower than that found in unscheduled charging.
4.3. Duration of Peak Loads
While the previous metric considered short term load intensity, it did not consider the frequency of occurrence of peaks of marginally smaller magnitude, whose impact is similar to that of the annual peak. A comparison of load duration curves can provide further insight. Figure 6 focuses on the leftmost section of the curve, where high peaks are visualized:
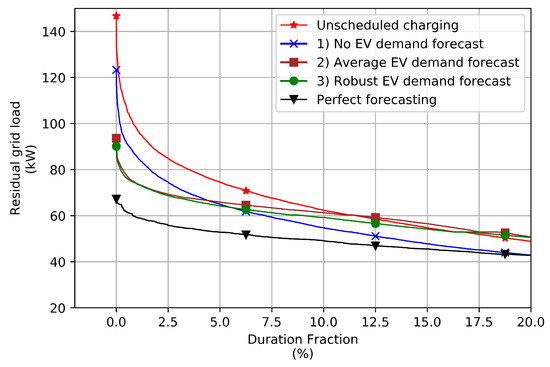
Figure 6.
Load duration curves.
The downward shift of the y-intercept through smart charging represents the reduction in the magnitude of annual peak loads, whereas the leftward shift near the y-intercept represents the reduction in the number of peaks. Smart charging without EV demand forecasting, in addition to lowering the magnitude of peaks, is also found to reduce the number of peaks. The curve reveals that the times for which loads are greater than 100 kW are reduced by more than half while the times for which loads are greater than 80 kW are reduced by about half.
The provision of EV demand forecasting further reduces these durations. Loads above 100 kW are avoided altogether and the number of peaks greater than 80kW are greatly reduced. There is no clear advantage of robust forecasting over average forecasting in this case, with both methods providing similar reductions in the number of peaks that the asset is exposed to.
5. Conclusions
The goal of this work was to quantify the peak load increase when uncertainty is involved in charge scheduling of electric vehicles at a solar parking lot. It further aimed to develop strategies for scheduling charging in a manner that minimized the peak electricity load at the point of common coupling of the parking lot while taking this uncertainty into account. Since short duration high peaks have the maximum impact on transformer aging, these were the peaks that were focused on.
The set up considered included a solar parking lot with 40 spaces located at a workplace. It included a 120 kWp solar array, 40 EV charge points and a 50 kWh stationary battery. The arrival and departure of EVs, which were parked and plugged in at the parking lot, were simulated over a year. Model Predictive Control (MPC) was the method used to optimally schedule the charging of EVs in the parking lot over the year. The operation of the system was simulated over a year in terms of the energy exchanged by the parking lot with the grid.
The system was considered in three scenarios:
- No EV demand forecast: EV charging is scheduled without a forecast of energy demand for EVs arriving in the future
- Average EV demand forecast: EV charging is scheduled with a single forecast of energy demand for EVs arriving in the future which is based on average values.
- Robust EV demand forecast: EV charging is scheduled to be robust across a range of possible energy demands for EVs arriving in the future
with a and a schedule that was robust across multiple possible EV demand forecasts. The scheduling for each scenario was formulated as an optimization problem. The operation of the solar carport was simulated in each scenario for a year based on the solution of the optimization problem. The scenarios were compared with two reference cases—unscheduled charging, which is the current norm, and charging with perfect forecasting of EV demand, which represents the limits of the effectiveness of the system at peak reduction.
The results show that for parking locations with charging, which are currently close to peak load capacity, scheduling of EVs can be used to reduce both the magnitude as well as the frequencies of peak loading on distribution level assets. The magnitude of the peak reduction is however considerably less than the peak reduction possible with perfect forecasting of future EV demand, which is often considered in the literature. Table 3 displays the results of annual peak reduction in the scenarios considered:

Table 3.
Annual peak power across scenarios.
Without EV demand forecasting, the maximum annual peak load of the solar carport was reduced by 16% in our case relative to unscheduled charging. This was, however, considerably less effective than in the reference case with perfect forecasting, where the magnitude of the annual peak was reduced by 54%. The inclusion of a single 24 h horizon EV forecast reduced the peak in the solar parking lot by 36%, increasing the effectiveness of the scheduled charging by an additional 20%. Consideration of multiple forecasts of possible EV demand and robust adjustment of the schedule for the performance of the worst possible forecast marginally improved the effectiveness of the scheduling, reducing the peak by 39%.
In addition to reducing the magnitude of peak loads, scheduling of EV charging also has the effect of reducing the number of peaks that distribution level assets were subject to. The use of EV demand forecasting was found to have the effect of considerably reducing this number. However, in this case, the consideration of multiple forecasts provides no clear advantage over a single forecast.
An economic analysis of the system was considered out of the scope of this work. As such, the cost-benefit analysis of scheduling EV charging versus upgrade of the grid connection was not performed. However, preliminary investigation indicates that there is considerable value for the parking lot owner through the implementation of the system described in this work. In the USA, capacity charges for the grid connection at EV charging sites can be higher than $2000/month, causing the electricity utility bills of some businesses to increase by a factor of four [22]. Similarly, in the Netherlands, the grid capacity cost is €190/year per charge point or 37% of the annual operational costs for the charge point excluding energy costs and about 20% of the costs including energy [23]. Although case-specific, peak reduction does have considerable economic value for system operators. This is expected to be addressed in future work.
Additionally, future research work also involves the investigation of the dependence of the scheduling on the location of the parking lot i.e., on whether the parking patterns have an influence on the choice of the objective of the charging schedule. The use of scheduling for off-grid or constrained grid capacity design of longterm parking lots for EVs may be considered. Improved methods for EV scheduling for other objectives will also be addressed in future works.
Author Contributions
R.G. wrote the final draft, performed some of the analysis and managed the project. Y.S. conceptualized the methodology, performed the investigation and wrote the first draft. S.F. provided guidance with the formulation of the optimization problems and their solution. Z.L. provided supervision and edited the final draft. A.v.W. provided supervision, edited the final draft and acquired funding for this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European Funds for Regional Development through the Kansen voor West program grant 00113 for the project, Powerparking, as well as the Netherlands Organization for Scientific Research as part of the Uncertainty Reduction in Smart Energy Systems (URSES+) grant for the project ‘Car as Power Plant-LIFE’.
Acknowledgments
The authors would like to thank Tomás Pippia for helpful discussions that contributed to this work.
Conflicts of Interest
The authors declare no conflict of interest.
List of Symbols
| Symbol | Definition | Unit | Note |
| Forecasted PV generation: | kWh | ||
| kWh | |||
| Max energy that can be sent to the grid | kWh | 32 kWh = 120 kW | |
| Grid exchange: | kWh | ||
| Energy to (+) or from (-) battery i at time t | kWh | ||
| Load from lighting at time t | kWh | ||
| Generation from solar power at time t | kWh | ||
| i | Index for each battery, 1–40 = EVs, 41 = fixed storage | - | |
| k | Current time step | - | |
| Max possible value of | kWh | ||
| Min possible value of : | kWh | ||
| Total number of batteries | - | 41 = 40 EVs + 1 battery | |
| Number of errors in the bounded set | - | 10,000 | |
| Number of time steps in MPC time horizon | - | ||
| Number of time steps in one full simulation | - | 34,944 = 24 · 4 · 364 | |
| Maximum power to or from battery i | kW | EVs 7.4 kW, battery 50 kW | |
| Energy stored in battery i at time t | kWh | ||
| Maximum energy allowed in battery i at time t | kWh | ||
| Minimum energy allowed in battery i at time t | kWh | ||
| Average value for the max energy in battery i at time t | kWh | ||
| Average value for the min energy in battery i at time t | kWh | ||
| t | time step within MPC horizon | - | |
| kWh | |||
| Length of a single time step | h | 15 min = 0.25 h | |
| For battery i at time t: 0 if discharging, 1 if charging | |||
| Charging efficiency of battery i | - | ||
| Discharging efficiency of battery i | - | ||
| Bounded set of PV forecasting errors | - | ||
| PV forecasting error at time t | kWh | ||
| Max PV forecasting error in set | kWh | ||
| Min PV forecasting error in the set | kWh | ||
| Uncertainty in the value of | kWh | ||
| Uncertainty in the value of | kWh |
References
- Olivier, J.; Schure, K.; Peters, J. Trends in Global CO2 and Total Greenhouse Gas Emissions—2017 Report; Technical Report 2674; PBL Netherlands Environmental Assessment Agency: The Hague, The Netherlands, 2017. [Google Scholar]
- Van Mierlo, J.; Messagie, M.; Rangaraju, S. Comparative environmental assessment of alternative fueled vehicles using a life cycle assessment. Transp. Res. Procedia 2017, 25, 3435–3445. [Google Scholar] [CrossRef]
- Van Vliet, O.; Brouwer, A.S.; Kuramochi, T.; van den Broek, M.; Faaij, A. Energy use, cost and CO2 emissions of electric cars. J. Power Sources 2011, 196, 2298–2310. [Google Scholar] [CrossRef]
- Dubey, A.; Santoso, S. Electric Vehicle Charging on Residential Distribution Systems: Impacts and Mitigations. IEEE Access 2015, 3, 1871–1893. [Google Scholar] [CrossRef]
- Verzijlbergh, R.A.; Lukszo, Z.; Slootweg, J.G.; Ilic, M.D. The impact of controlled electric vehicle charging on residential low voltage networks. In Proceedings of the 2011 International Conference on Networking, Sensing and Control, Delft, The Netherlands, 11–13 April 2011; pp. 14–19. [Google Scholar] [CrossRef]
- Uddin, M.; Romlie, M.F.; Abdullah, M.F.; Abd Halim, S.; Abu Bakar, A.H.; Chia Kwang, T. A review on peak load shaving strategies. Renew. Sustain. Energy Rev. 2018, 82, 3323–3332. [Google Scholar] [CrossRef]
- Verzijlbergh, R.A.; De Vries, L.J.; Lukszo, Z. Renewable Energy Sources and Responsive Demand. Do We Need Congestion Management in the Distribution Grid? IEEE Trans. Power Syst. 2014, 29, 2119–2128. [Google Scholar] [CrossRef]
- Clement-Nyns, K.; Haesen, E.; Driesen, J. The Impact of Charging Plug-In Hybrid Electric Vehicles on a Residential Distribution Grid. IEEE Trans. Power Syst. 2010, 25, 371–380. [Google Scholar] [CrossRef]
- PricewaterhouseCoopers. Smart Charging of Electric Vehicles: Institutional Bottlenecks and Possible Solutions; Technical Report; PricewaterhouseCoopers: Utrecht, The Netherlands, 2017. [Google Scholar]
- Sortomme, E.; El-Sharkawi, M.A. Optimal Scheduling of Vehicle-to-Grid Energy and Ancillary Services. IEEE Trans. Smart Grid 2012, 3, 351–359. [Google Scholar] [CrossRef]
- Van der Kam, M.; van Sark, W. Smart charging of electric vehicles with photovoltaic power and vehicle-to-grid technology in a microgrid: A case study. Appl. Energy 2015, 152, 20–30. [Google Scholar] [CrossRef]
- Sarantis, I.; Alavi, F.; Schutter, B.D. Optimal power scheduling of fuel-cell-car-based microgrids. In Proceedings of the 2017 IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, Australia, 12–15 December 2017; pp. 5062–5067. [Google Scholar] [CrossRef]
- Knap, W. Horizon at Station Cabauw; Pangaea: Cabauw, The Netherlands, 2007. [Google Scholar] [CrossRef]
- Stein, J.S.; Holmgren, W.F.; Forbess, J.; Hansen, C.W. PVLIB: Open source photovoltaic performance modeling functions for Matlab and Python. In Proceedings of the 2016 IEEE 43rd Photovoltaic Specialists Conference (PVSC), Portland, OR, USA, 5–10 June 2016; pp. 3425–3430. [Google Scholar] [CrossRef]
- Apostolaki-Iosifidou, E.; Codani, P.; Kempton, W. Measurement of power loss during electric vehicle charging and discharging. Energy 2017, 127, 730–742. [Google Scholar] [CrossRef]
- Shareef, H.; Islam, M.M.; Mohamed, A. A review of the stage-of-the-art charging technologies, placement methodologies, and impacts of electric vehicles. Renew. Sustain. Energy Rev. 2016, 64, 403–420. [Google Scholar] [CrossRef]
- Daina, N.; Sivakumar, A.; Polak, J.W. Modelling electric vehicles use: A survey on the methods. Renew. Sustain. Energy Rev. 2017, 68, 447–460. [Google Scholar] [CrossRef]
- Francfort, J. EV Project Data & Analytic Results; Idaho National Laboratory: Idaho Falls, ID, USA, 2014. [Google Scholar]
- Bemporad, A.; Morari, M. Robust model predictive control: A survey. In Robustness in Identification and Control; Garulli, A., Tesi, A., Eds.; Lecture Notes in Control and Information Sciences; Springer: London, UK, 1999; pp. 207–226. [Google Scholar]
- Bemporad, A.; Morari, M. Control of systems integrating logic, dynamics, and constraints. Automatica 1999, 35, 407–427. [Google Scholar] [CrossRef]
- IEEE. C57.91-2011—IEEE Guide for Loading Mineral-Oil-Immersed Transformers and Step-Voltage Regulators; IEEE: Piscataway, NJ, USA, 2012; pp. 1–123. Available online: https://ieeexplore.ieee.org/document/6166928 (accessed on 18 November 2019). [CrossRef]
- Smith, M.; Castellano, J. Costs Associated with Non-Residential Electric Vehicle Supply Equipment: Factors to Consider in the Implementation of Electric Vehicle Charging Stations; Technical Report DOE/EE-1289; U.S. Department of Energy Vehicle Technologies Office: Washington, DC, USA, 2015.
- Blok, R.F.P. Verslag Benchmark Publiek Laden 2018—Sneller naar een Volwassen Markt; Technical Report; NKL Nederland: Emmen, NL, USA, 2018. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).