Thermal Assessment of Laminar Flow Liquid Cooling Blocks for LED Circuit Boards Used in Automotive Headlight Assemblies
Abstract
1. Introduction
2. Materials and Methods
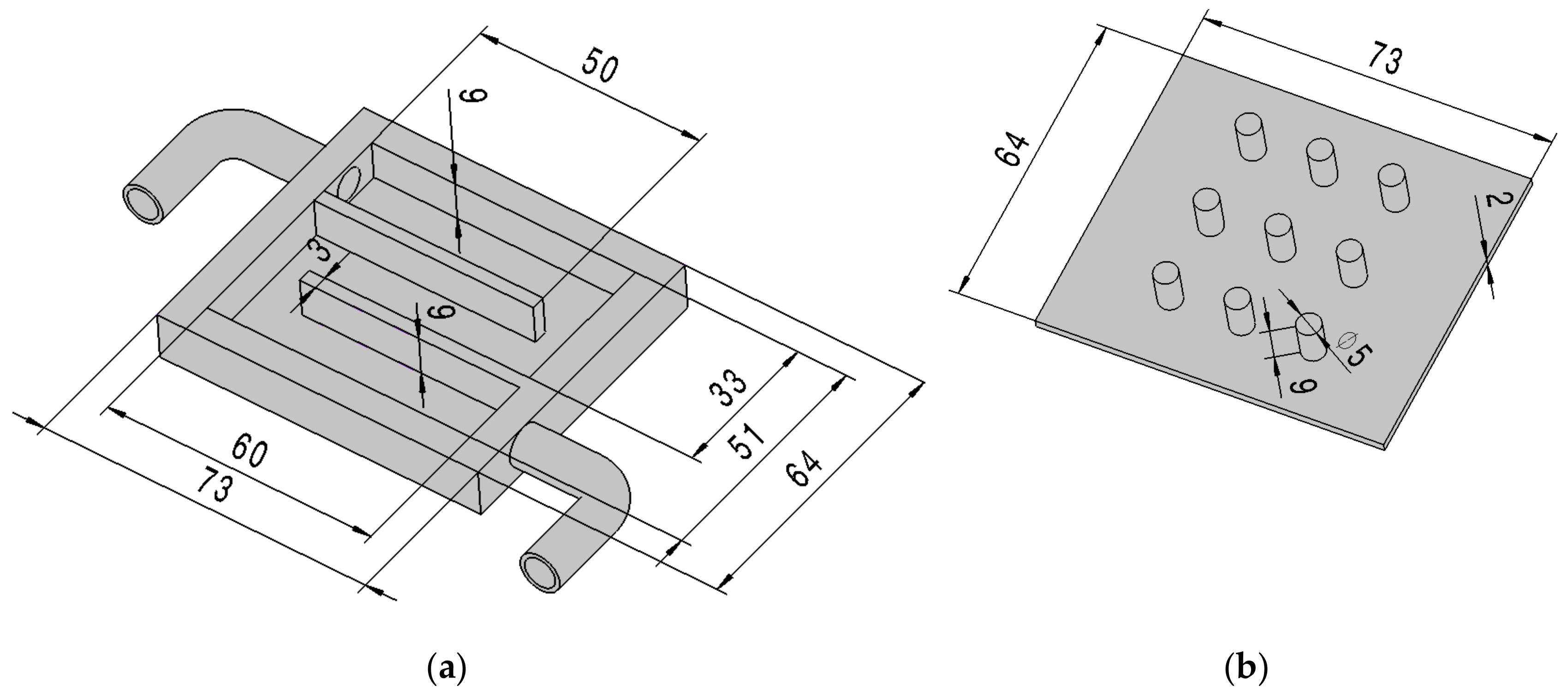
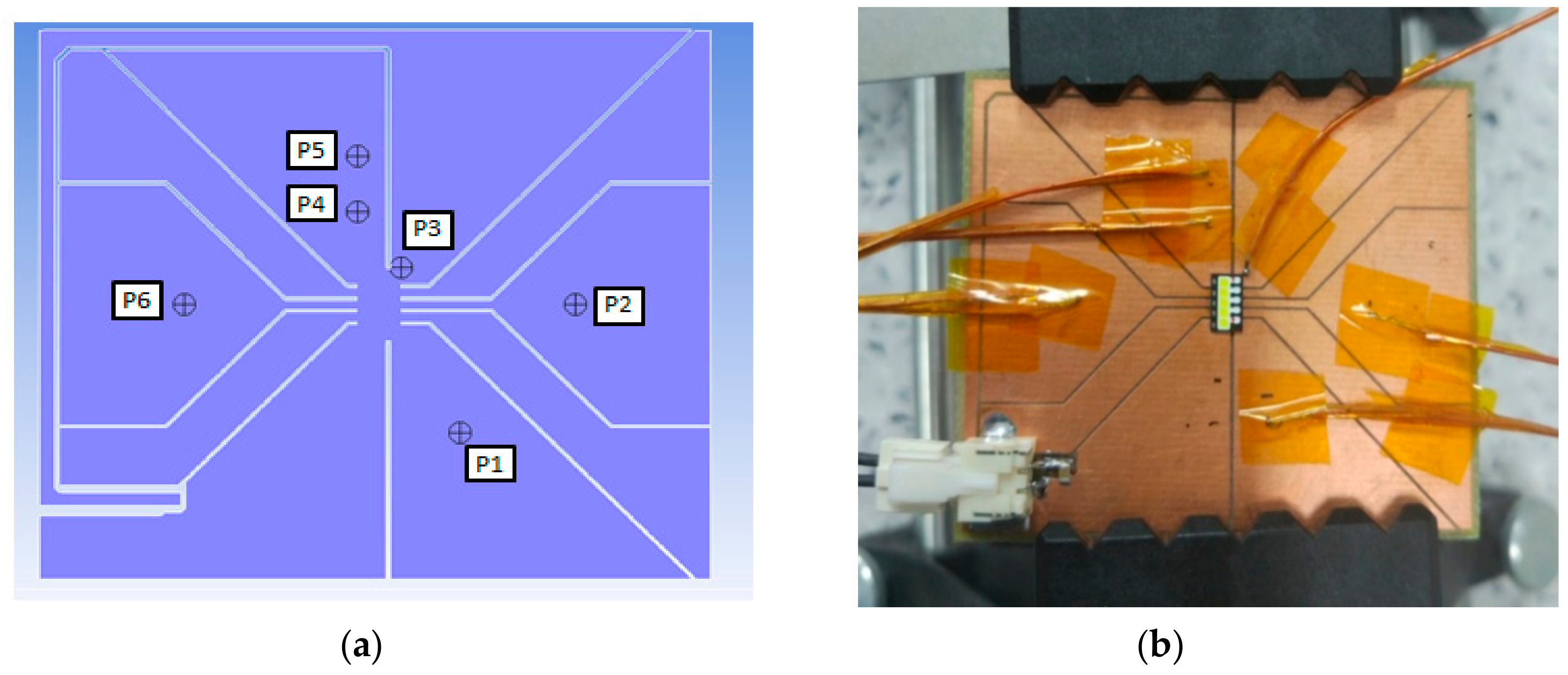
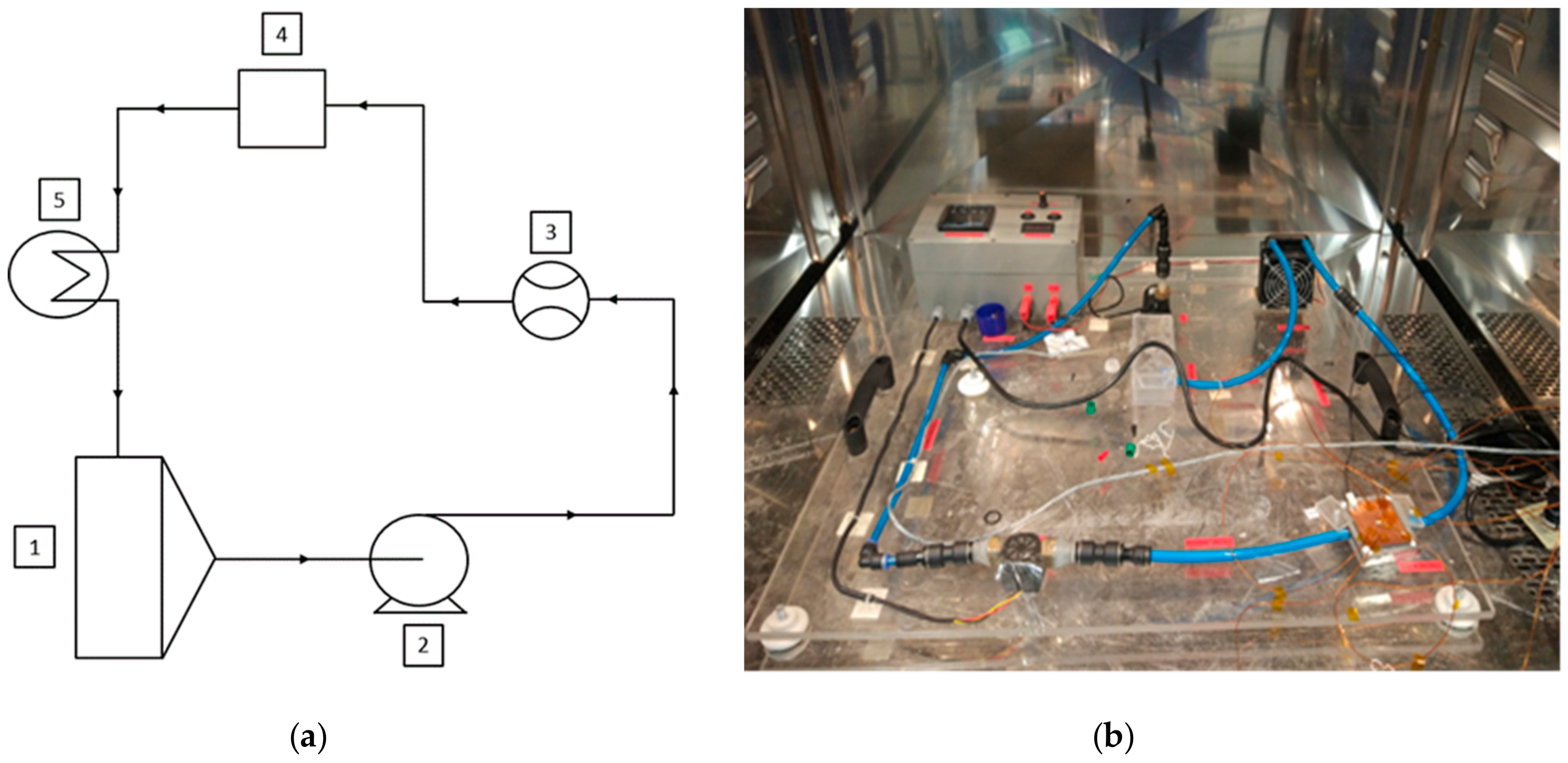
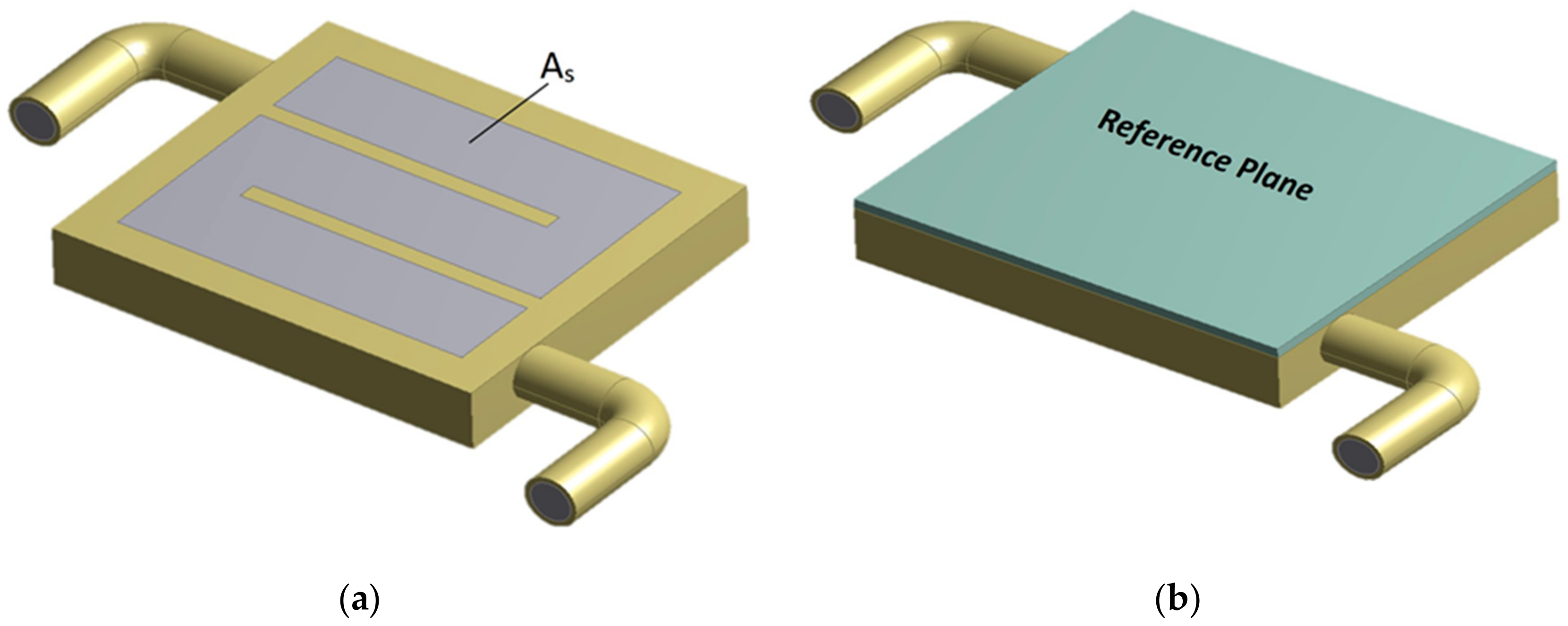
2.1. LED System Design and Experimental Set-up
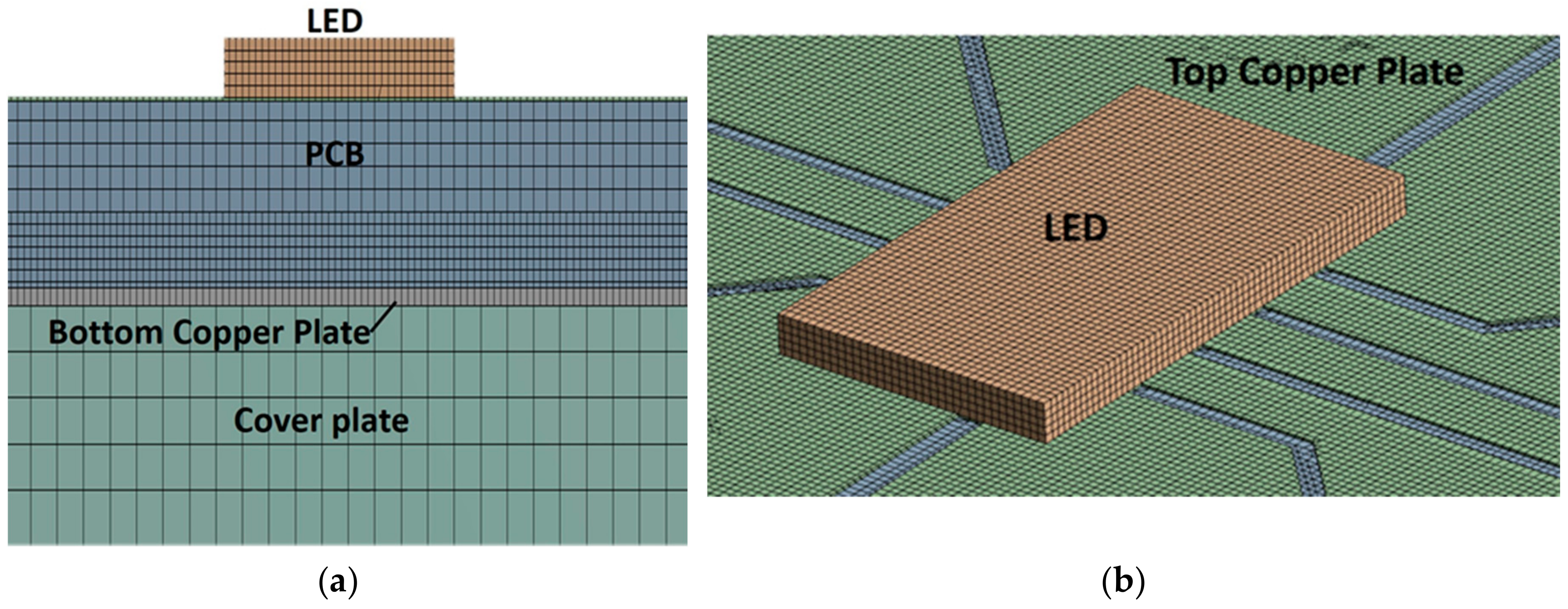
2.2. Numerical Modeling of the Cooling Block with LED PCB
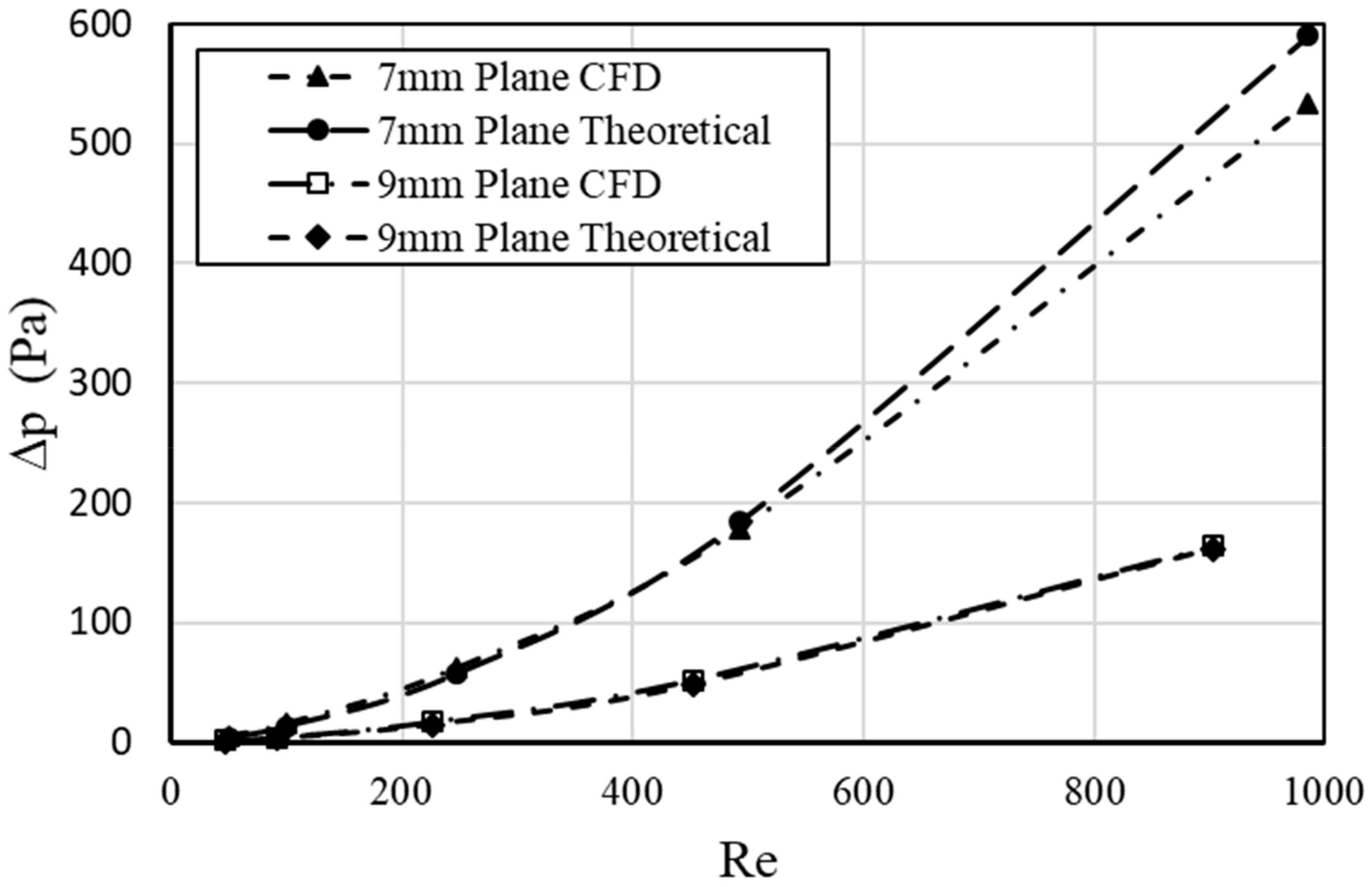
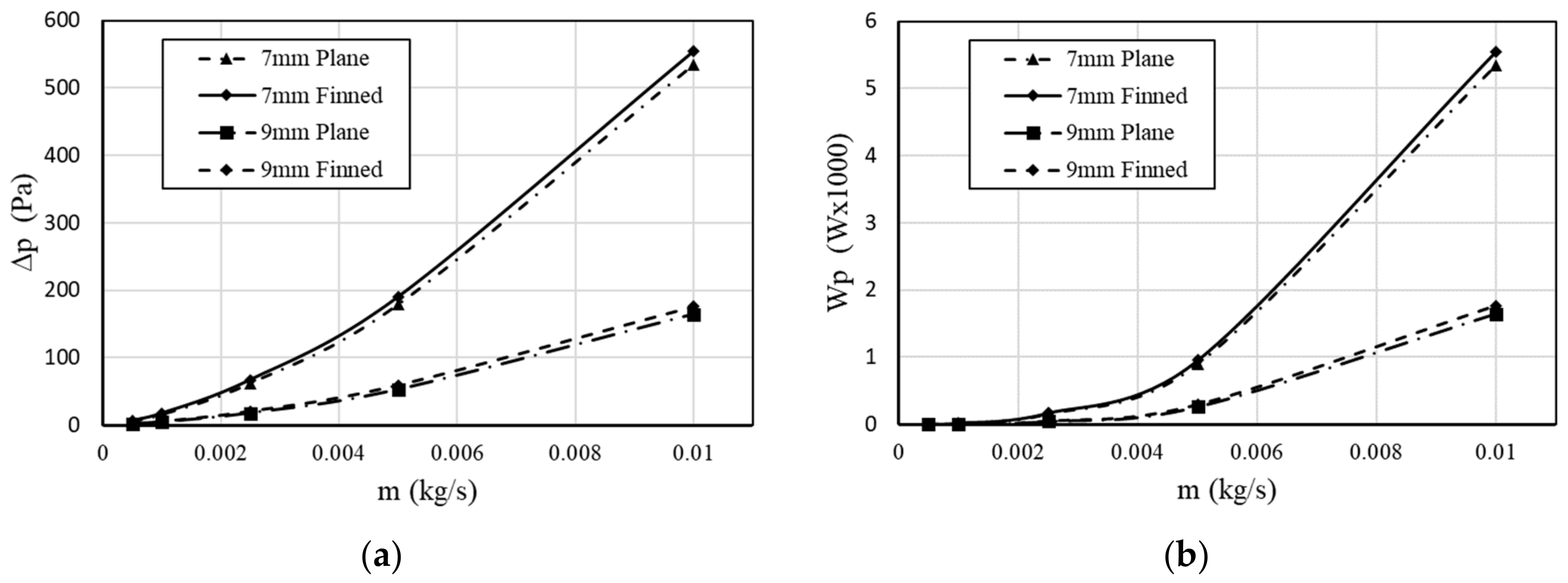
2.3. Friction Coefficient and Pressure Drop Analysis
2.4. Heat Transfer Analysis
2.5. Validation of the Simulation Model
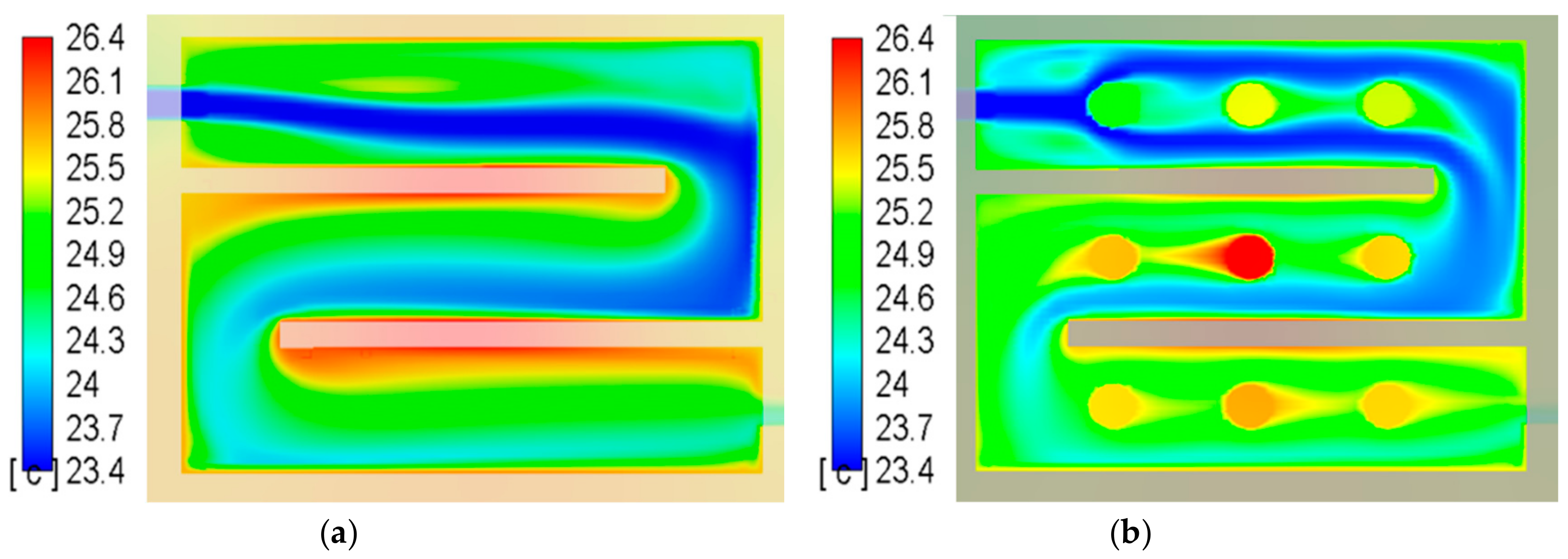
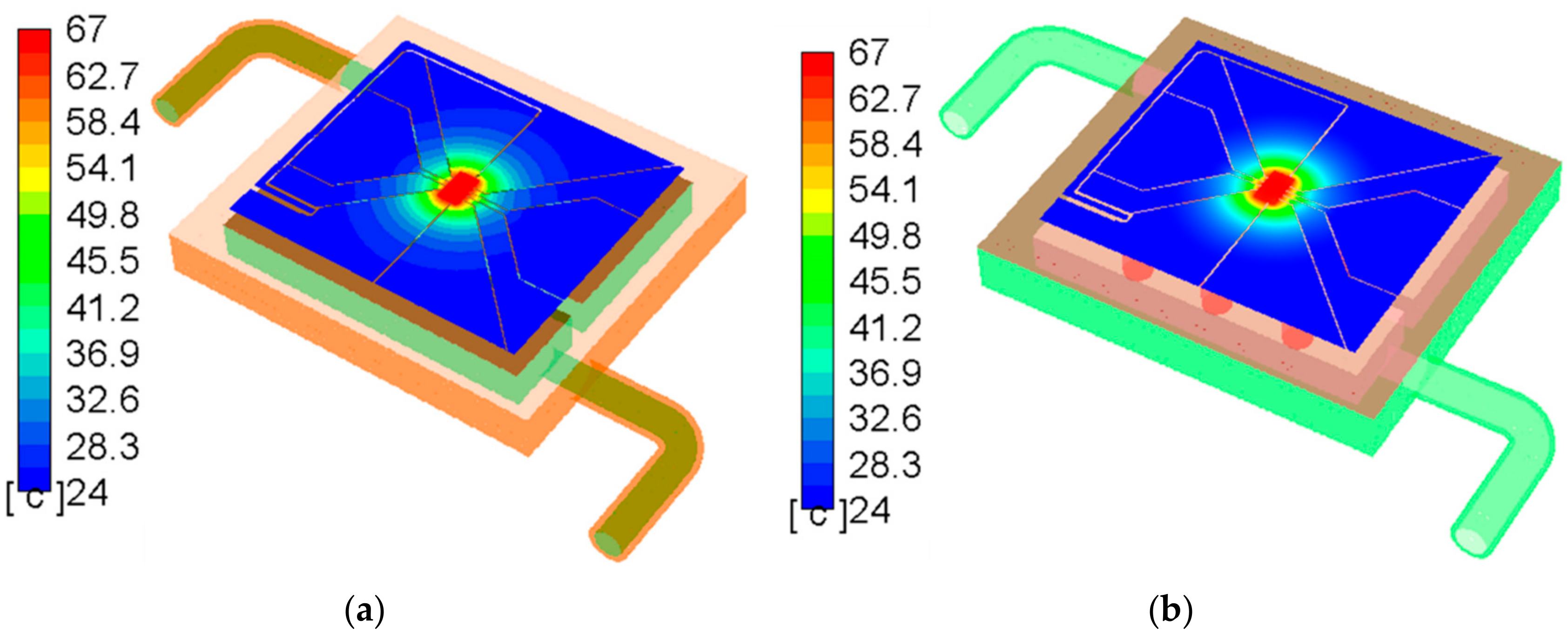
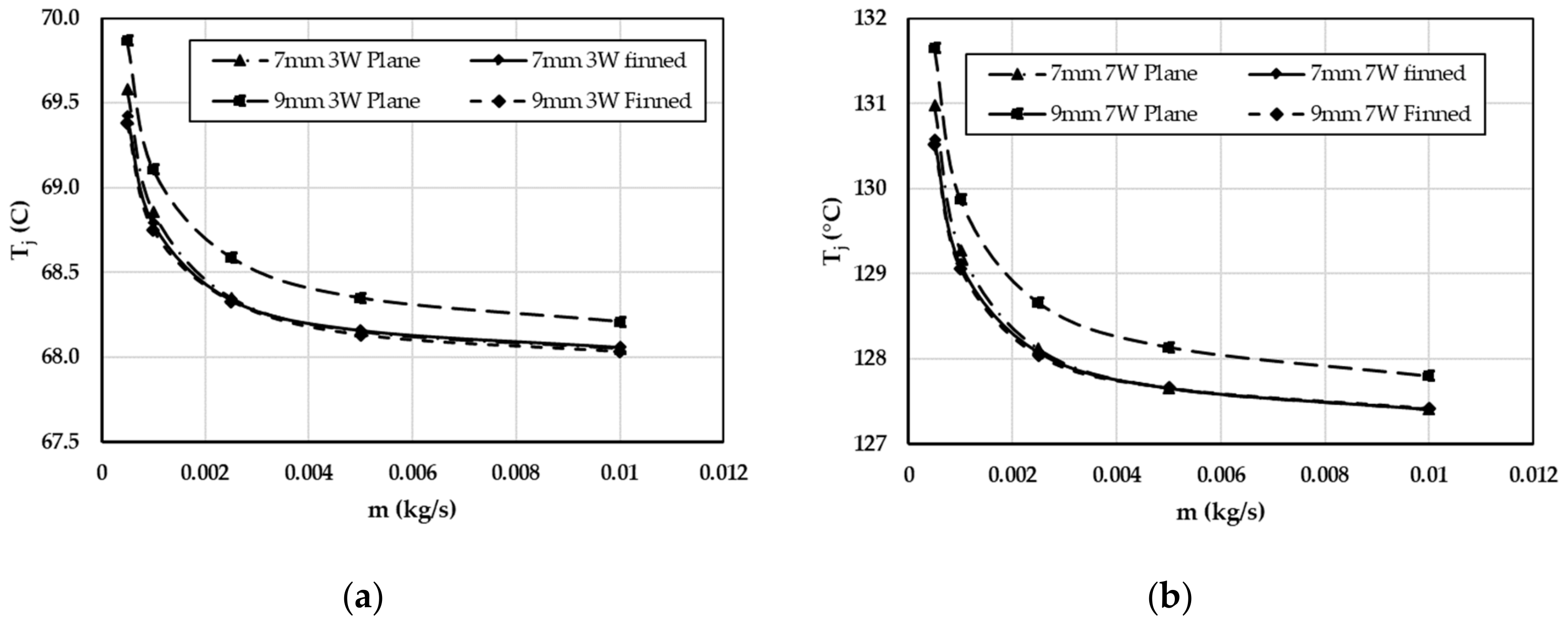
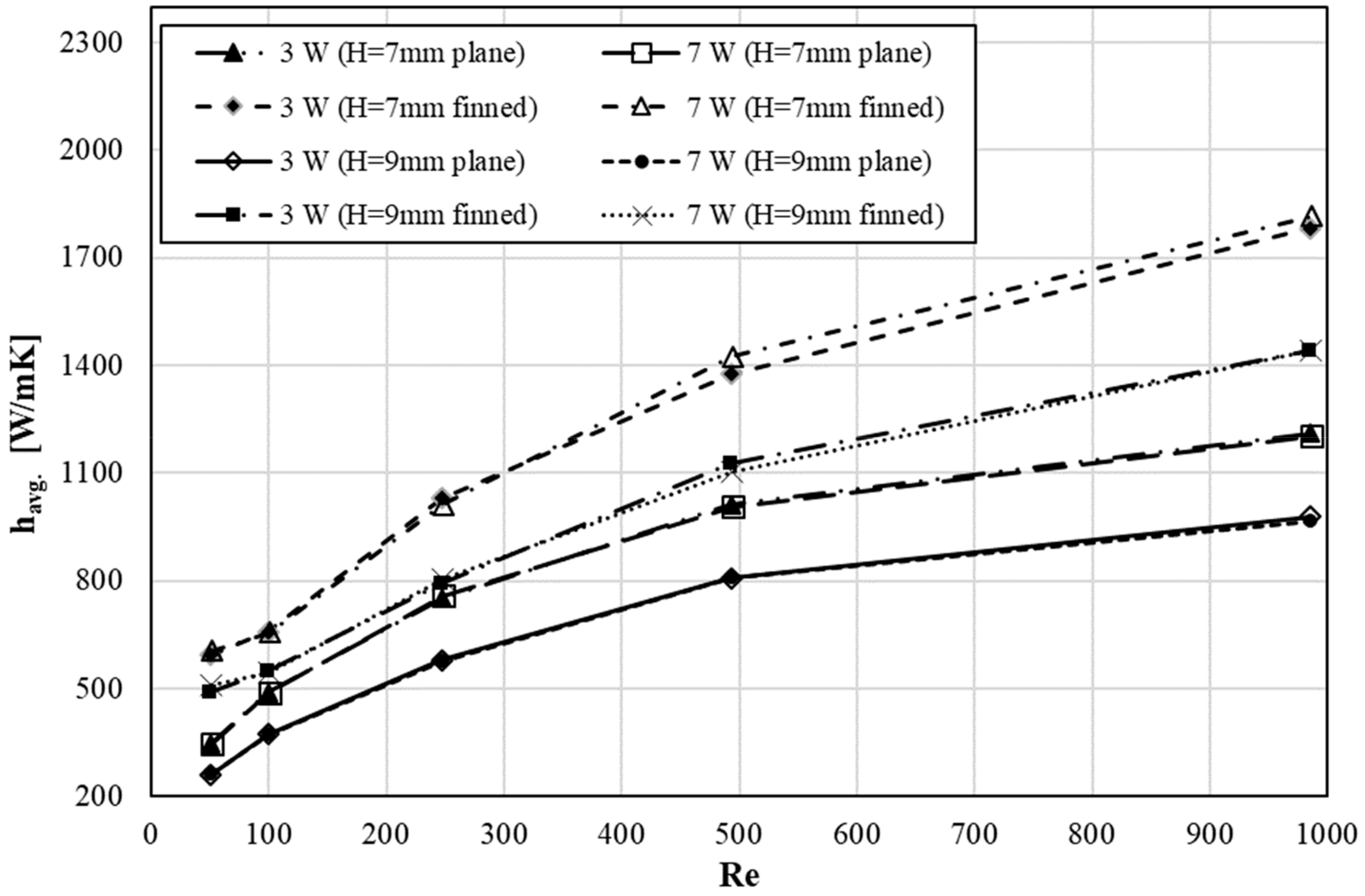
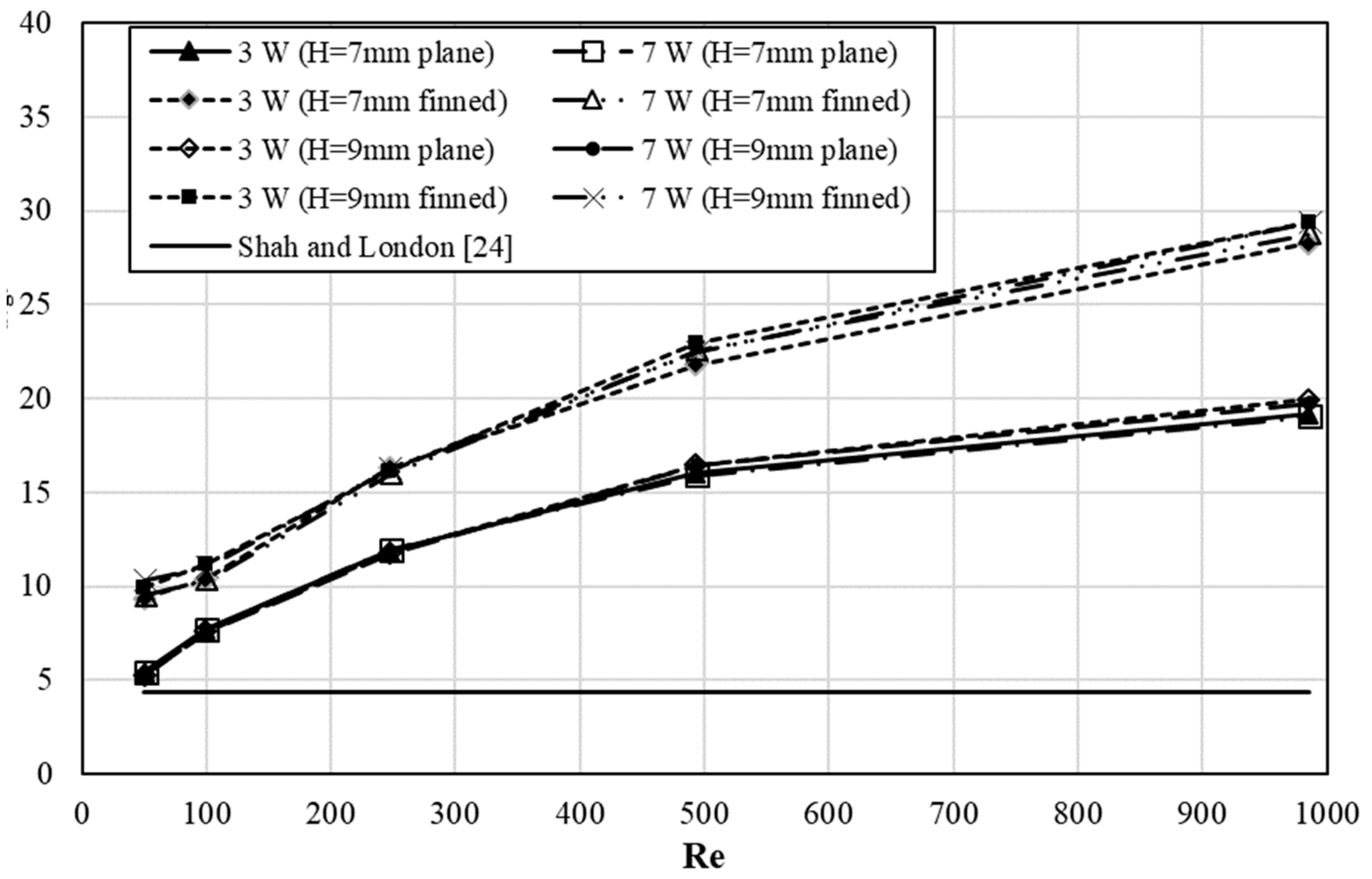
3. Results
4. Discussion
5. Conclusions
- The laminar flow liquid cooling blocks are very effective for the cooling of PCB with LEDs.
- The mass flow rate has a significant effect on the temperature of the LED PCB and the junction temperature values. Increasing mass flow rate up to a certain maximum value presents better cooling with a penalty of rising pressure drop and pumping power.
- Finned cover plates present better thermal performance.
- Two new Nusselt number correlations proposed in the present work can be used to prepare an active energy management system for the LED-based automotive lighting systems.
- The laminar flow cooling blocks can be employed for automotive LED-based headlight assemblies, and the usage of them provide effective energy management on the cooling.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| As | Total heat transfer surface area [m2] |
| Acsa | Cross sectional area of channel [m2] |
| C | Constant |
| cp | Specific heat [J/kg·K] |
| Hydraulic diameter [m] | |
| havg | Average heat transfer coefficient [W/ m2K] |
| Hc | Height of the channel [m] |
| I | Current [A] |
| LED | Light Emitting Diode |
| LMTD | Logarithmic Mean Temperature Difference [°C] |
| k | Thermal conductivity [W/ m2K] |
| Kc | Contraction loss coefficient |
| Ke | Extraction loss coefficient |
| L | Total length of the channel [m] |
| Mass flow rate [kg/s] | |
| Nu | Nusselt number |
| PLED | Power of LED [W] |
| PCB | Printed Circuit Board |
| Total pressure drop [Pa] | |
| Logarithmic Mean Temperature Difference [°C] | |
| Total heat transfer rate occurred in the cooling block [W] | |
| Pr | Prandtl number |
| Re | Reynolds number |
| Thermal resistance of the junction point [°C/W] | |
| S | Source term includes heat generation for LED part [m3/s] |
| T | Temperature [°C] |
| Mean temperature of the fluid at the inlet of the cooling bock | |
| Mean temperature of the fluid at the outlet of the cooling bock | |
| Tj | LED junction temperature [°C] |
| Tmax | Maximum temperature [°C] |
| Average flow velocity [m/s] | |
| V | Voltage [V] |
| Velocity vector [m/s] | |
| Width of the channel [m] | |
| Pump power [W] | |
| Wt | Thickness of the channel wall in the cooling block [m] |
| Greek Symbols | |
| ρ | Density [kg/m3] |
| Bending loss coefficient | |
| ΦV | Luminous flux [Lm] |
| Dynamic viscosity of fluid [Pa.s] | |
| Subscripts | |
| avg | Average |
| b | Block |
| f | Fluid |
| i, in | Inlet |
| o, out | Outlet |
| m | Mean |
| max | Maximum |
| Lm | Lumen |
| s | Solid |
References
- Chang, M.; Das, D.; Varde, P.V.; Pecht, M. Light emitting diodes reliability review. Microelectron. Reliab. 2012, 52, 762–782. [Google Scholar] [CrossRef]
- Tsai, M.; Chen, C.; Kang, C. Thermal measurements and analyses of low-cost high-power LED packages and their modules. Microelectron. Reliab. 2012, 52, 845–854. [Google Scholar] [CrossRef]
- Hu, S.; Yu, G.; Cen, Y. Optimized thermal design of new reflex LED headlamp. Appl. Opt. 2012, 51, 5563–5566. [Google Scholar] [CrossRef] [PubMed]
- Aktaş, M.; Şenyüz, T.; Şenyıldız, T.; Kılıç, M. Liquid cooling applications on automotive exterior LED lighting. AIP Conf. Proc. 2018, 1935, 060003. [Google Scholar]
- Christensen, A.; Graham, S. Thermal effects in packaging high power light emitting diode arrays. Appl. Therm. Eng. 2009, 29, 364–371. [Google Scholar] [CrossRef]
- Yung, K.; Liem, H.; Choy, H.; Lun, W. Thermal performance of high brightness LED array package on PCB. Int. Commun. Heat Mass Transf. 2010, 37, 1266–1272. [Google Scholar] [CrossRef]
- Jang, S.; Shin, W.S. Thermal analysis of LED arrays for automotive head lamp with a novel cooling system. IEEE Trans. Dev. Mater. Reliab. 2008, 8, 561–564. [Google Scholar] [CrossRef]
- Zhao, X.-J.; Cai, Y.-Z.; Wang, J.; Li, X.-H.; Zhang, C. Thermal model design and analysis of the high-power LED automotive headlight cooling device. Appl. Therm. Eng. 2015, 75, 248–258. [Google Scholar] [CrossRef]
- Liu, D.; Yang, H.; Yang, P. Experimental and numerical approach on junction temperature of high-power LED. Microelectron. Reliab. 2014, 54, 926–931. [Google Scholar] [CrossRef]
- Lee, D.; Choi, H.; Jeong, S.; Jeon, C.H.; Lee, D.; Lim, J.; Byon, C.; Choi, J. A study on the measurement and prediction of LED junction temperature. Int. J. Heat Mass Transf. 2018, 127, 1243–1252. [Google Scholar] [CrossRef]
- Cheng, T.; Luo, X.; Huang, S.; Liu, S. Thermal analysis and optimization of multiple LED packaging based on a general analytical solution. Int. J. Therm. Sci. 2010, 49, 196–201. [Google Scholar] [CrossRef]
- Lai, Y.; Cordero, N.; Barthel, F.; Tebbe, F.; Kuhn, J.; Apfelbeck, R.; Würtenberger, D. Liquid cooling of bright LEDs for automotive applications. Appl. Therm. Eng. 2009, 29, 1239–1244. [Google Scholar] [CrossRef]
- Luo, X.; Liu, S. A microjet array cooling system for thermal management of high-brightness LEDs. IEEE Trans. Adv. Packag. 2007, 30, 475–484. [Google Scholar] [CrossRef]
- Liu, S.; Yang, J.; Gan, Z.; Luo, X. Structural optimization of a microjet based cooling system for high power LEDs. Int. J. Therm. Sci. 2008, 47, 1086–1095. [Google Scholar] [CrossRef]
- Li, J.; Ma, B.; Wang, R.; Han, L. Study on a cooling system based on thermoelectric cooler for thermal management of high-power LEDs. Microelect. Reliab. 2011, 51, 2210–2215. [Google Scholar] [CrossRef]
- Deng, Y.; Liu, J. A liquid metal cooling system for the thermal management of high power LEDs. Int. Commun. Heat Mass Transf. 2010, 37, 788–791. [Google Scholar] [CrossRef]
- Wan, Z.M.; Liu, J.; Su, K.L.; Hu, X.H.; M, S.S. Flow and heat transfer in porous micro heat sink for thermal management of high power LEDs. Microelectron. J. 2011, 42, 632–637. [Google Scholar] [CrossRef]
- Sosoi, G.; Vizitiu, R.S.; Burlacu, A.; Galatanu, C.D. A heat pipe cooler for high power LED’s cooling in harsh conditions. Procedia Manuf. 2019, 32, 513–519. [Google Scholar] [CrossRef]
- Seo, J.H.; Lee, M.Y. Illuminance and heat transfer characteristics of high power LED cooling system with heat sink filled with ferrofluid. Appl. Therm. Eng. 2018, 143, 438–449. [Google Scholar] [CrossRef]
- Yenigun, O.; Barisik, M. Electric Field Controlled Heat Transfer through Silicon and Nano-confined Water. Nanosc. Microsc. Therm. 2019, 23, 304–316. [Google Scholar] [CrossRef]
- Hasan, M.R.; Vo, T.Q.; Kim, B. Manipulating thermal resistance at the solid–fluid interface through monolayer deposition. Rsc Adv. 2019, 9, 4948–4956. [Google Scholar] [CrossRef]
- Moffat, R.J. Describing the Uncertainties in Experimental Results. Exp. Therm. Fluid Sci. 1988, 1, 3–17. [Google Scholar] [CrossRef]
- Ansys, Inc. Ansys Fluent Theory Guide; Release 15.0; © ANSYS. Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- Shah, R.K.; London, A.L. Laminar Flow Forced Convection in Ducts; Supplement 1 to Advances in Heat Transfer; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Shah, R.K. A correlation for laminar hydrodynamics entry length solution for circular and noncircular ducts. J. Fluids Eng. 1978, 100, 177–179. [Google Scholar] [CrossRef]
- Mirmanto, M. Developing Flow Pressure Drop and Friction Factor of Water in Copper Microchannels. J. Mech. Eng. Autom. 2013, 3, 641–649. [Google Scholar]

| Type | Measuring Range | Uncertainty |
|---|---|---|
| K-type thermocouple | −40 °C/400 °C | ±0.75% |
| Flowmeter | 0–30 L/min | ±1% |
| Parameter | Symbol | Values | Unit |
|---|---|---|---|
| Operating Temperature | Top | −40–125 | °C |
| Maximum Junction Temperature for short time app.) | Tj,max | 175 | °C |
| Maximum Junction Temperature (for long time app.) | Tj,max | 150 | °C |
| Current | IF | 50–1200 | mA |
| Voltage | VF | 10.90–14.90 | V |
| Luminous Flux (IF = 1000 mA) | ΦV | 1120–1250 | lm |
| Radiating Surface | Acolor | 4.4 | mm2 |
| Junction Point Real Thermal Resistance | Rth,Jp | 1.0 | °C/W |
| Surfaces or Domains | Boundary Conditions |
| Supply temperature of the coolant | Constant temperature value of 23.45 °C |
| Outlet surface of the cooling block | Gauge pressure equals to 0 Pa |
| Mass flow rate of coolant | Between 0.0005 to 0.01 kg/s |
| LED chip | Volumetric heat generation rate |
| Outer surfaces of solid domains | Convection and radiation mixed boundary conditions |
| Material type | Solid domains |
| LED chip | Chip material |
| Top and bottom copper plates | Copper |
| Printed Circuit Board | Glass-reinforced epoxy laminate material (FR4) |
| Cover plate | Aluminum |
| Cooling Block | Aluminum |
| Variables | Value | Unit |
|---|---|---|
| The height of the channel | 7 and 9 | mm |
| Cover plate type | Plane and Finned | − |
| LED power | 3 and 7 | W |
| Cooling fluid mass flow rate | 0.0005, 0.001, 0.0025, 0.005 and 0.01 | kg/s |
| PLED | 3 W LED Power | 7 W LED Power | ||||
|---|---|---|---|---|---|---|
| Point | Simulation T (°C) | Measurement T (°C) | Dif. Ratio % | Simulation T (°C) | Measurement T (°C) | Dif. Ratio % |
| P1 | 28.3 | 27.8 | 1.80 | 34.5 | 34.8 | 0.86 |
| P2 | 24.4 | 24.6 | 0.81 | 25.8 | 25.5 | 1.18 |
| P3 | 40.2 | 41.5 | 3.13 | 60.8 | 62.2 | 2.25 |
| P4 | 36.6 | 37.3 | 1.88 | 52.8 | 51.7 | 2.13 |
| P5 | 28.9 | 28.5 | 1.40 | 35.7 | 36.1 | 1.11 |
| P6 | 24.5 | 24.8 | 1.21 | 26.0 | 25.7 | 1.17 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kilic, M.; Aktas, M.; Sevilgen, G. Thermal Assessment of Laminar Flow Liquid Cooling Blocks for LED Circuit Boards Used in Automotive Headlight Assemblies. Energies 2020, 13, 1202. https://doi.org/10.3390/en13051202
Kilic M, Aktas M, Sevilgen G. Thermal Assessment of Laminar Flow Liquid Cooling Blocks for LED Circuit Boards Used in Automotive Headlight Assemblies. Energies. 2020; 13(5):1202. https://doi.org/10.3390/en13051202
Chicago/Turabian StyleKilic, Muhsin, Mehmet Aktas, and Gokhan Sevilgen. 2020. "Thermal Assessment of Laminar Flow Liquid Cooling Blocks for LED Circuit Boards Used in Automotive Headlight Assemblies" Energies 13, no. 5: 1202. https://doi.org/10.3390/en13051202
APA StyleKilic, M., Aktas, M., & Sevilgen, G. (2020). Thermal Assessment of Laminar Flow Liquid Cooling Blocks for LED Circuit Boards Used in Automotive Headlight Assemblies. Energies, 13(5), 1202. https://doi.org/10.3390/en13051202






