In-Stream Energy by Tidal and Wind-Driven Currents: An Analysis for the Gulf of California
Abstract
1. Introduction
2. Results and Discussion
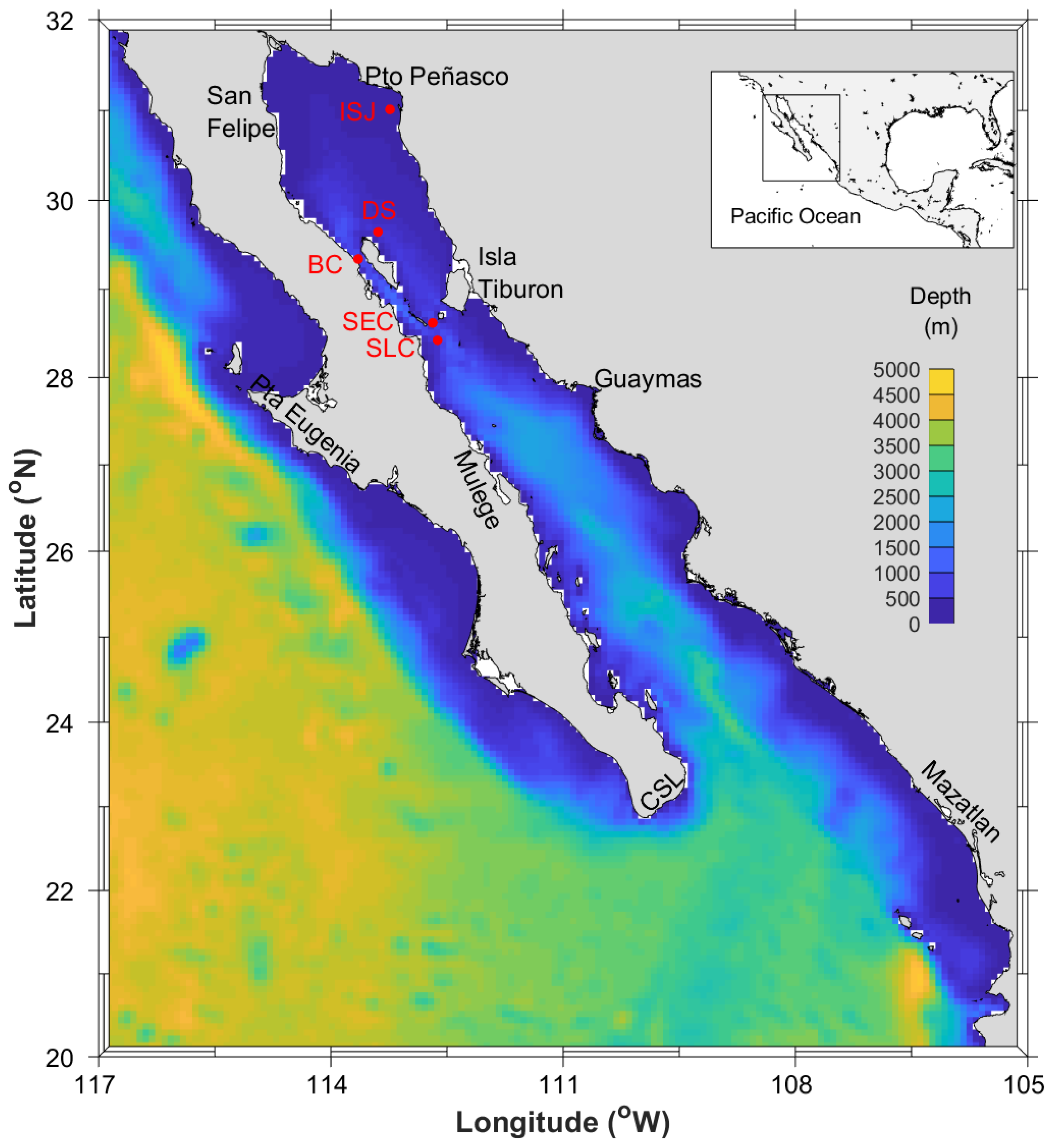
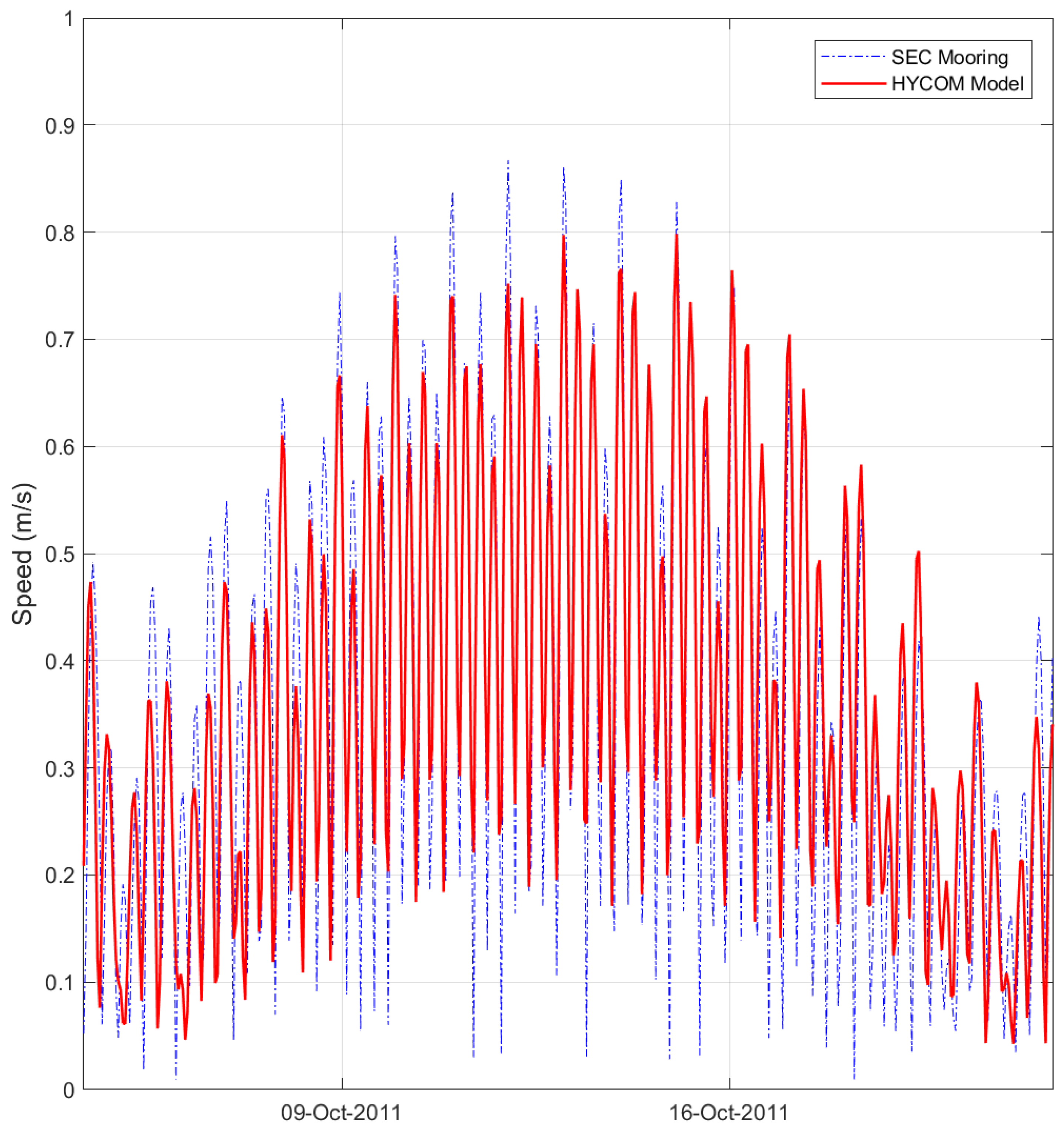
2.1. Verification of Model Predictions against In-Situ Measurements
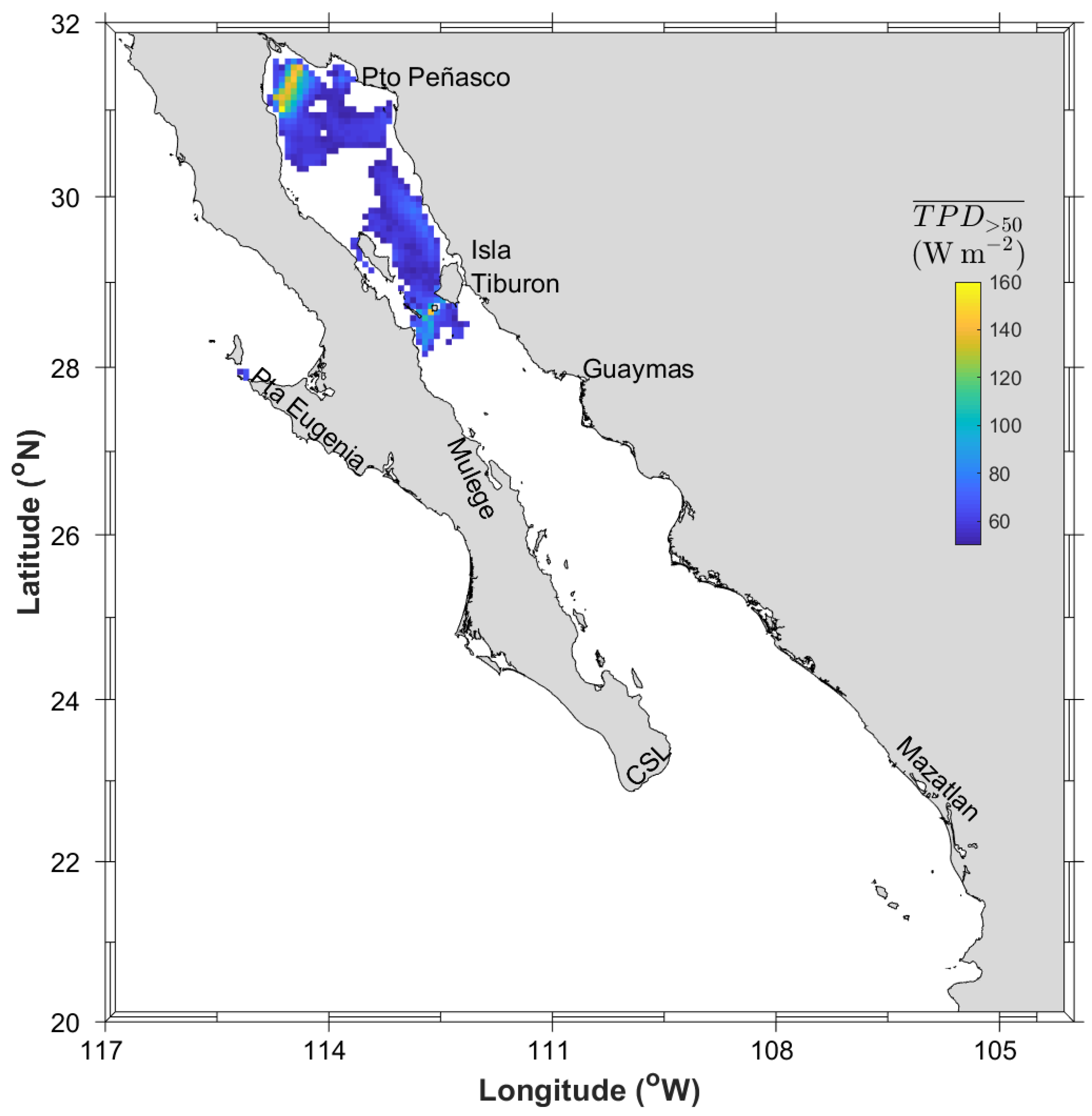
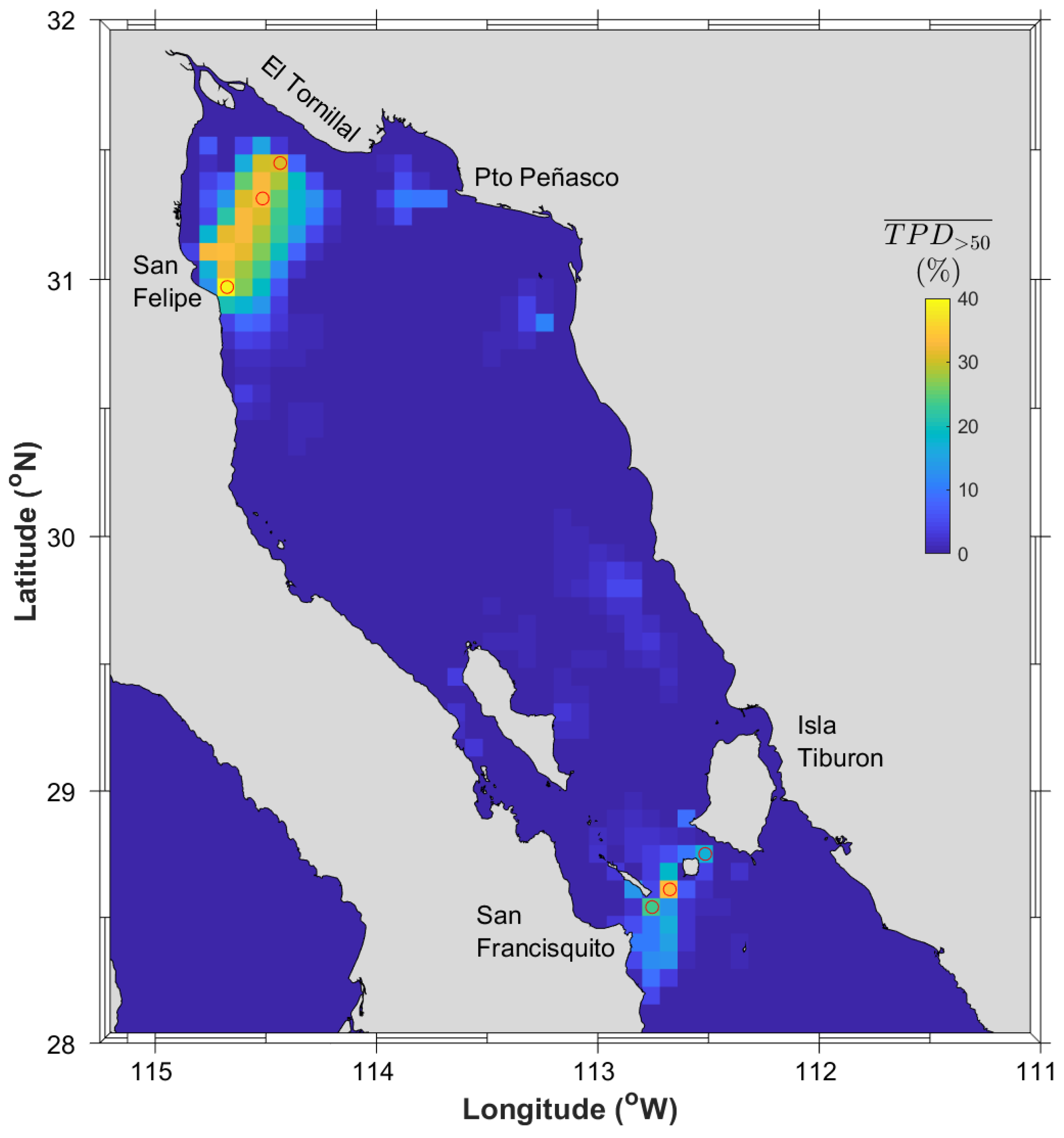
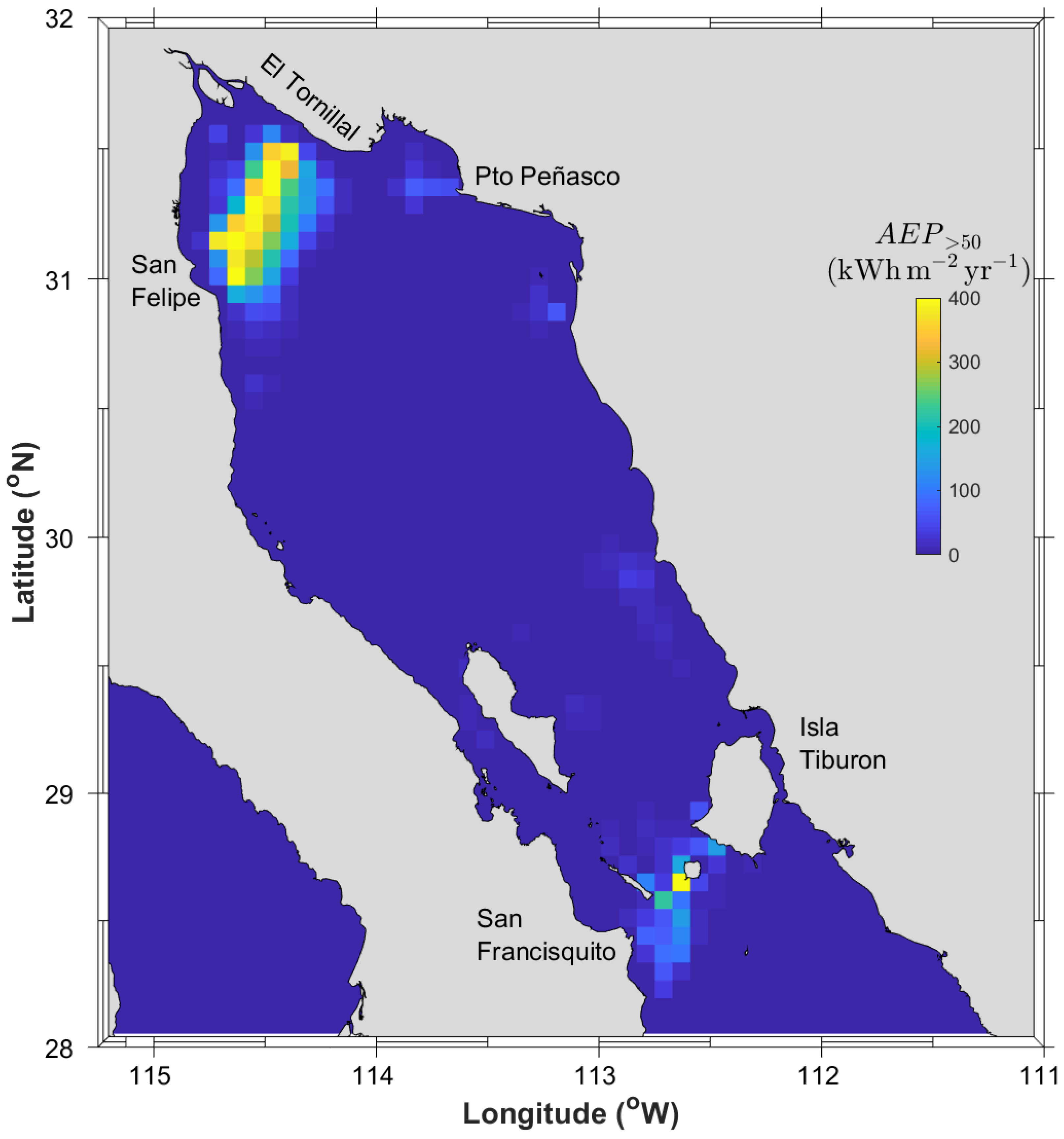
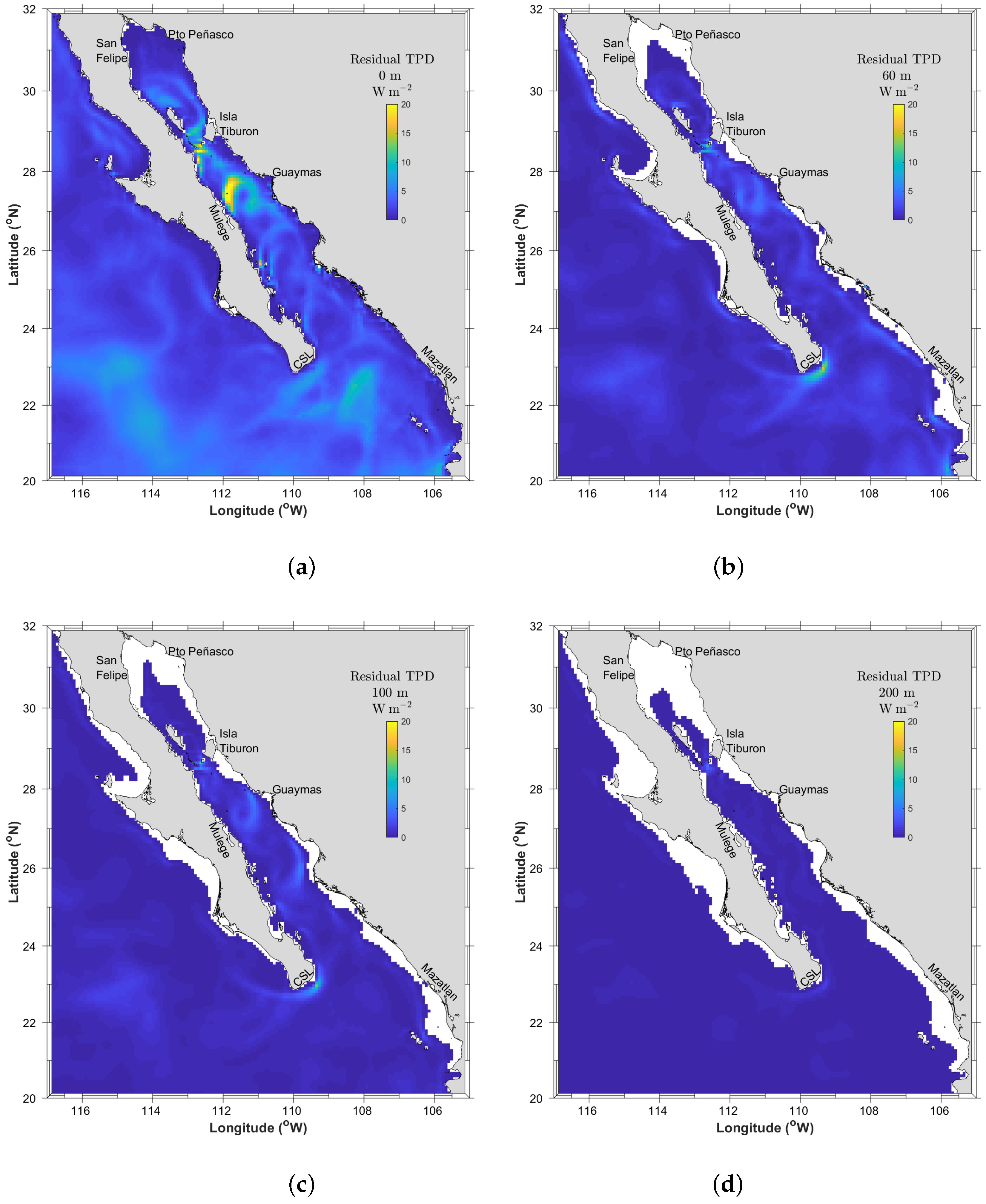
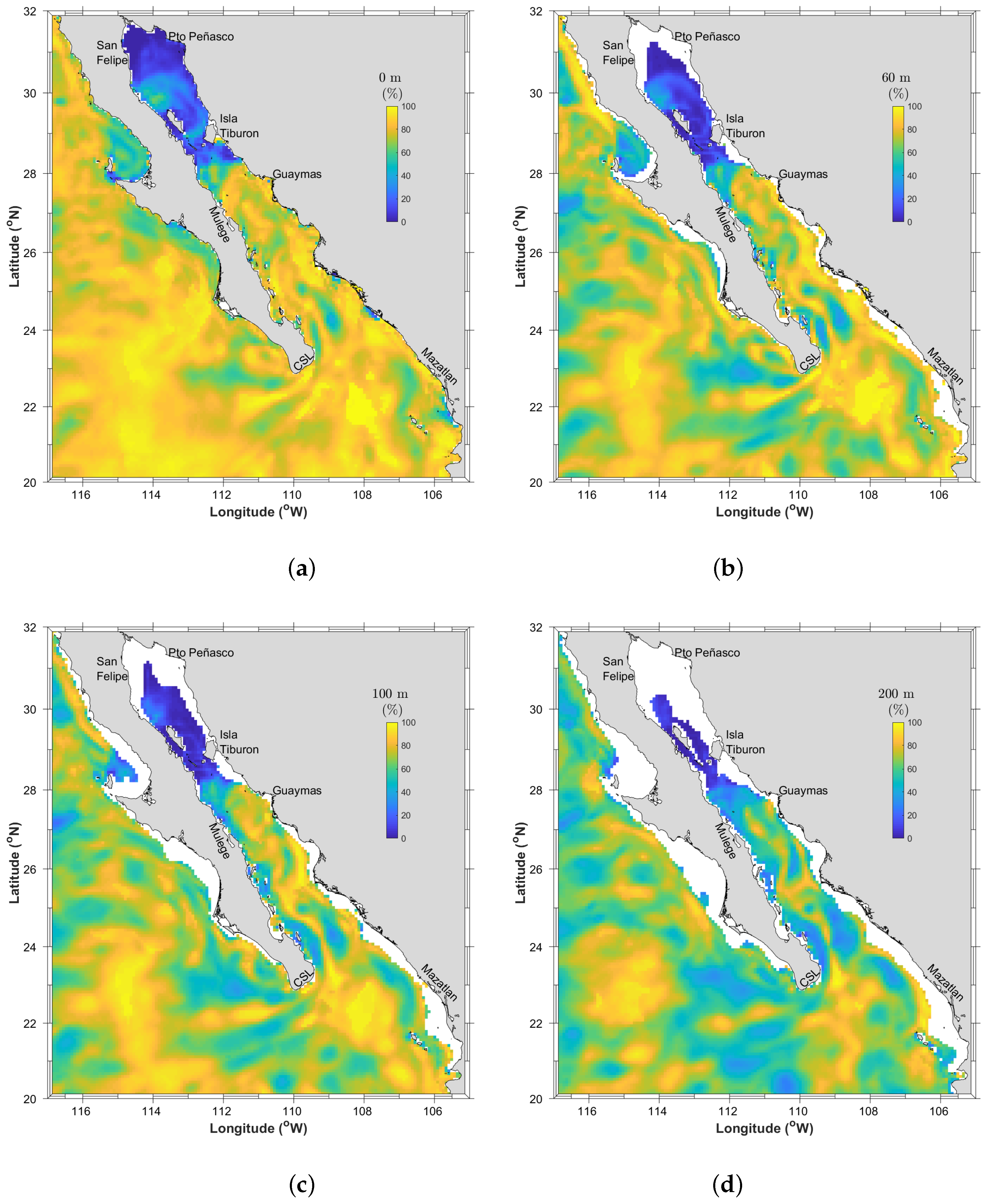
2.2. Analysis of the Barotropic Tidal Signal
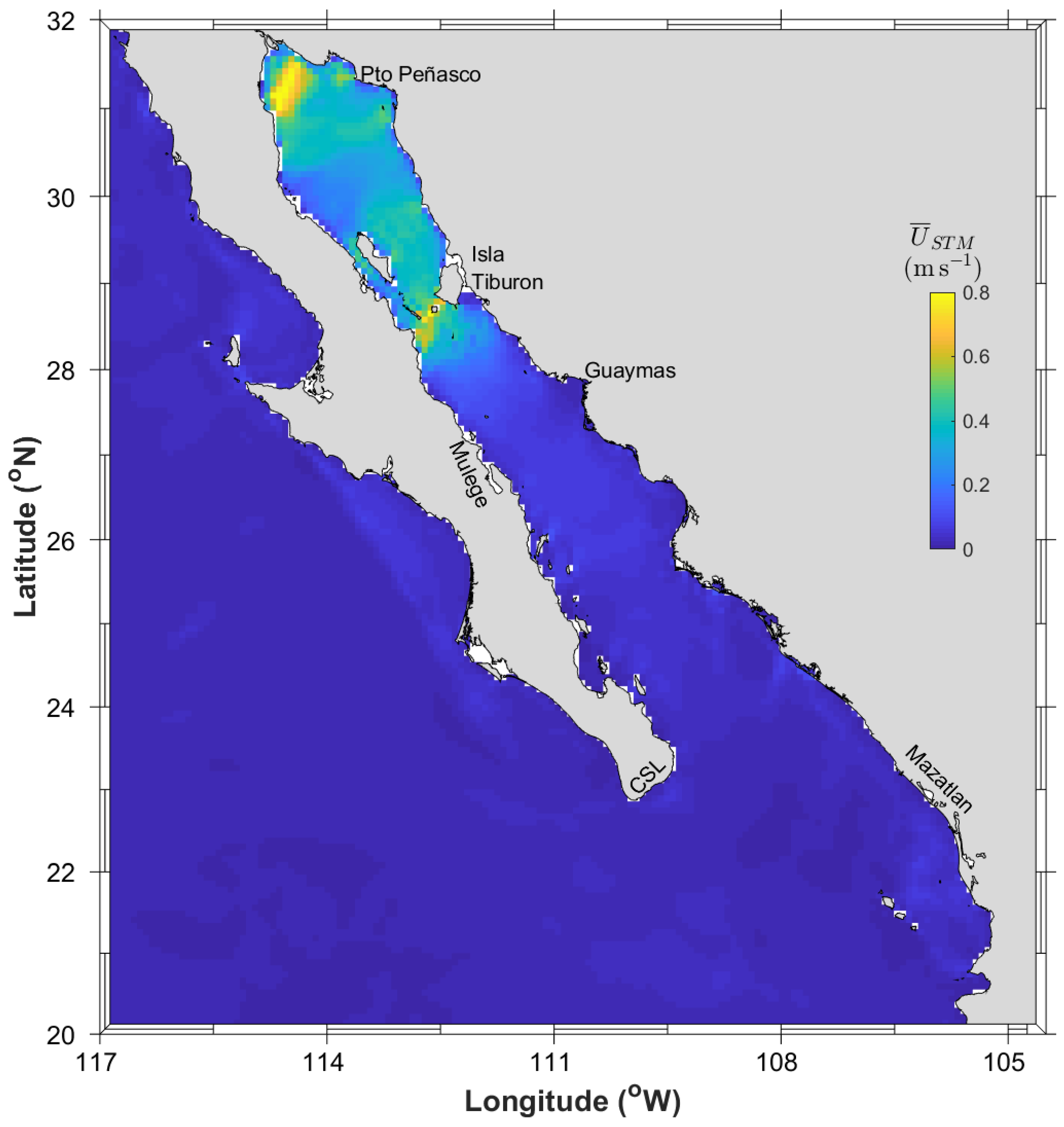
2.3. Analysis of the Wind-Driven In-Stream Energy Resource Contribution
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ADCP | Acoustic Doppler Current Profiler |
| Annual Energy Production | |
| BC | Ballenas Channel |
| DS | Delfin Sill |
| ETOPO1 | Earth topography and bathymetry global relief model, at 1 arc-minute resolution |
| GIR | Great Island Region |
| HYCOM | Hybrid Coordinate Ocean Model |
| ISJ | Isla San Jorge |
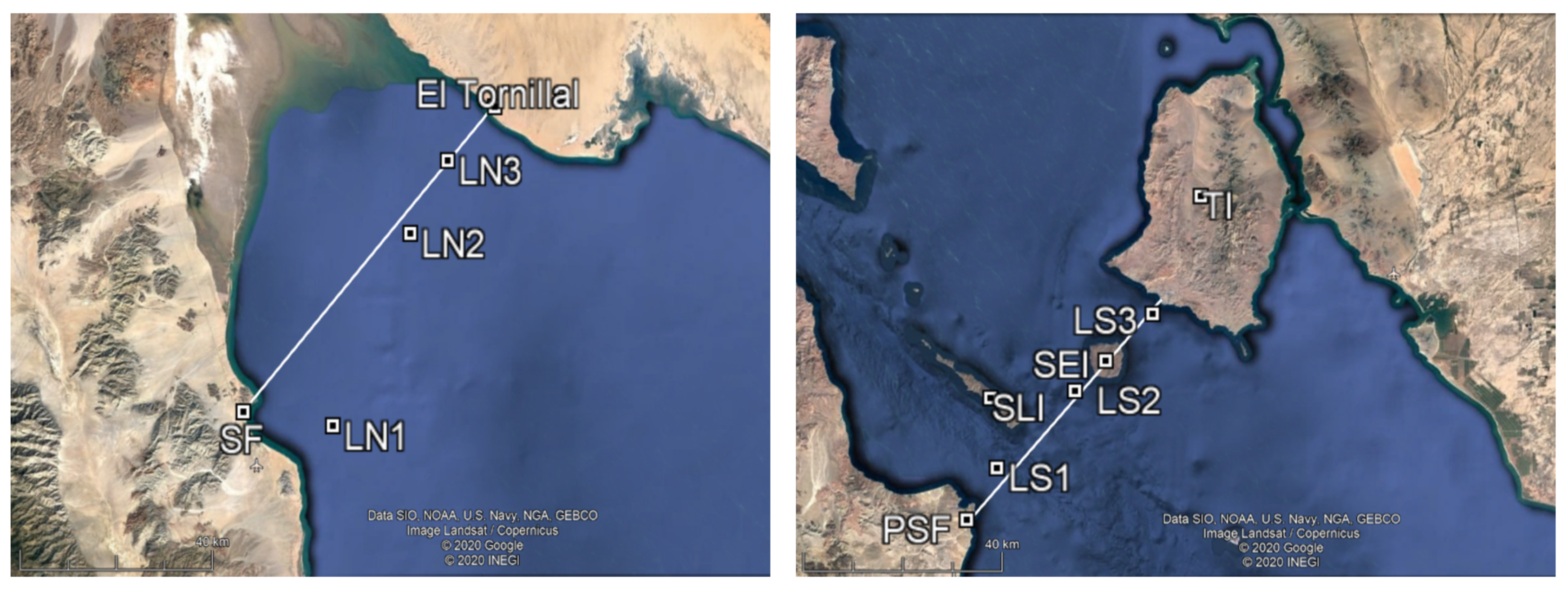
| LN | Location North |
| LS | Location South |
| MICOM | Miami Isopycnic Coordinate Ocean Model |
| MRE | Marine Renewable Energy |
| MUPS | Multi-Use Platforms at Sea |
| NAVGEM | Navy Global Environmental Model |
| NOGAPS | Navy Operational Global Atmospheric Prediction System |
| PSF | Punta San Francisquito |
| SAL | self-attraction and load |
| SEC | San Esteban Channel |
| SF | San Felipe |
| SLC | San Lorenzo Channel |
| TI | Tiburón Island |
| Tidal Power Density | |
| T_TIDE | Tidal Harmonic Analysis Toolbox |
References
- Parker, B.B. (Ed.) Tidal Hydrodynamics; Wiley: Hoboken, NJ, USA, 1991. [Google Scholar]
- Pawlowicz, R.; Beardsley, B.; Lentz, S. Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE. Comput. Geosci. 2002, 28, 929–937. [Google Scholar] [CrossRef]
- Buijsman, M.C.; Arbic, B.K.; Richman, J.G.; Shriver, J.F.; Wallcraft, A.J.; Zamudio, L. Semidiurnal internal tide incoherence in the equatorial Pacific. J. Geophys. Res. Ocean. 2017, 122, 5286–5305. [Google Scholar] [CrossRef]
- Arbic, B.K.; Alford, M.H.; Ansong, J.K.; Buijsman, M.C.; Ciotti, R.B.; Farrar, J.T.; Hallberg, R.W.; Henze, C.E.; Hill, C.N.; Luecke, C.A.; et al. A Primer on Global Internal Tide and Internal Gravity Wave Continuum Modeling in HYCOM and MITgcm. In New Frontiers in Operational Oceanography; GODAE OceanView; Florida Climate Institute: Gainesville, FL, USA, 2018. [Google Scholar] [CrossRef]
- Gross, M.; Magar, V. Wind-Induced Currents in the Gulf of California from Extreme Events and Their Impact on Tidal Energy Devices. J. Mar. Sci. Eng. 2020, 8, 80. [Google Scholar] [CrossRef]
- Dupont, F.; Hannah, C.G.; Greenberg, D. Modelling the sea level of the upper Bay of Fundy. Atmosphere-Ocean 2005, 43, 33–47. [Google Scholar] [CrossRef]
- Hiriart Le Bert, G. Potencial energético del Alto Golfo de California. Boll. Soc. Geológ. Mex. 2009, 61, 143–146. [Google Scholar] [CrossRef]
- Xia, J.; Falconer, R.A.; Lin, B. Hydrodynamic impact of a tidal barrage in the Severn Estuary, UK. Renew. Energy 2010, 35, 1455–1468. [Google Scholar] [CrossRef]
- Carbajal, N.; Backhaus, J.O. Simulation of tides, residual flow and energy budget in the Gulf of California. Oceanol. Acta 1998, 21, 429–446. [Google Scholar] [CrossRef][Green Version]
- Garrett, C.; Cummins, P. The power potential of tidal currents in channels. Proc. R. Soc. A Math. Phys. Eng. Sci. 2005, 461, 2563–2572. [Google Scholar] [CrossRef]
- Defne, Z.; Haas, K.A.; Fritz, H.M. Numerical modeling of tidal currents and the effects of power extraction on estuarine hydrodynamics along the Georgia coast, USA. Renew. Energy 2011, 36, 3461–3471. [Google Scholar] [CrossRef]
- Yang, X.; Haas, K.A.; Fritz, H.M. Theoretical Assessment of Ocean Current Energy Potential for the Gulf Stream System. Mar. Technol. Soc. J. 2013, 47, 101–112. [Google Scholar] [CrossRef]
- Perez-Collazo, C.; Pemberton, R.; Greaves, D.; Iglesias, G. Monopile-mounted wave energy converter for a hybrid wind-wave system. Energy Convers. Manag. 2019, 199, 111971. [Google Scholar] [CrossRef]
- Stuiver, M.; Soma, K.; Koundouri, P.; van den Burg, S.; Gerritsen, A.; Harkamp, T.; Dalsgaard, N.; Zagonari, F.; Guanche, R.; Schouten, J.J.; et al. The Governance of Multi-Use Platforms at Sea for Energy Production and Aquaculture: Challenges for Policy Makers in European Seas. Sustainability 2016, 8, 333. [Google Scholar] [CrossRef]
- Dalton, G.; Bardócz, T.; Blanch, M.; Campbell, D.; Johnson, K.; Lawrence, G.; Lilas, T.; Friis-Madsen, E.; Neumann, F.; Nikitas, N.; et al. Feasibility of investment in Blue Growth multiple-use of space and multi-use platform projects; results of a novel assessment approach and case studies. Renew. Sustain. Energy Rev. 2019, 107, 338–359. [Google Scholar] [CrossRef]
- Tweed, K. Underwater Kite Harvests Energy from Slow Currents—Could Kites be the Secret to Capturing Tidal Energy? 2013. Available online: https://spectrum.ieee.org/energywise/green-tech/geothermal-and-tidal/underwater-kite-harvests-energy-from-slow-currents (accessed on 19 November 2019).
- Minesto. The Future of Renewable Energy. 2019. Available online: https://www.minesto.com/our-technology (accessed on 19 November 2019).
- Magar, V. Tidal Current Technologies. In Sustainable Energy Technologies; CRC Press: New York, NY, USA, 2017; pp. 293–308. [Google Scholar] [CrossRef]
- Byrne, J.V.; Emery, K.O. Sediments of the Gulf of California. Geol. Soc. Am. Bull. 1960, 71, 983. [Google Scholar] [CrossRef]
- Morales Pérez, R.A.; Gutiérrez de Velazco Sanromán, G. Mareas en el Golfo de California. Geofísica Int. 1989, 28, 25–46. [Google Scholar]
- Álvarez, L.G.; Suárez-Vidal, F.; Mendoza-Borunda, R.; González-Escobar, M. Bathymetry and active geological structures in the Upper Gulf of California. Boll. Soc. Geológ. Mex. 2009, 61, 129–141. [Google Scholar] [CrossRef]
- Corsatea, T.D.; Magagna, D. Overview of European Innovation Activities in Marine Energy Technology; Technical report; Environmental Sciences Group: Brussels, Belgium, 2014. [Google Scholar]
- Verdant Power. Technology Advancement. 2019. Available online: https://www.verdantpower.com/technology-adv (accessed on 21 November 2019).
- LeGrand, C. Assessment of Tidal Energy Resource—Marine Renewable Energy Guides; Technical Report; Black and Veatch Ltd.: London, UK, 2009. [Google Scholar]
- Myers, L.; Bahaj, A. Power output performance characteristics of a horizontal axis marine current turbine. Renew. Energy 2006, 31, 197–208. [Google Scholar] [CrossRef]
- Iyer, A.; Couch, S.; Harrison, G.; Wallace, A. Variability and phasing of tidal current energy around the United Kingdom. Renew. Energy 2013, 51, 343–357. [Google Scholar] [CrossRef]
- Oropeza-Perez, I.; Petzold-Rodriguez, A. Analysis of the Energy Use in the Mexican Residential Sector by Using Two Approaches Regarding the Behavior of the Occupants. Appl. Sci. 2018, 8, 2136. [Google Scholar] [CrossRef]
- Magar, V.; Gross, M.; González-García, L. Offshore wind energy resource assessment under techno-economic and social-ecological constraints. Ocean Coast. Manag. 2018, 152, 77–87. [Google Scholar] [CrossRef]
- Bleck, R. An oceanic general circulation model framed in hybrid isopycnic-Cartesian coordinates. Ocean Model. 2002, 4, 55–88. [Google Scholar] [CrossRef]
- Bleck, R.; Rooth, C.; Hu, D.; Smith, L.T. Salinity-driven Thermocline Transients in a Wind- and Thermohaline-forced Isopycnic Coordinate Model of the North Atlantic. J. Phys. Oceanogr. 1992, 22, 1486–1505. [Google Scholar] [CrossRef]
- Hogan, T.F.; Liu, M.; Ridout, J.A.; Peng, M.S.; Whitcomb, T.R.; Ruston, B.C.; Reynolds, C.A.; Eckermann, S.D.; Moskaitis, J.R.; Baker, N.L.; et al. The Navy Global Environmental Model. Oceanography 2014, 27, 116–125. [Google Scholar] [CrossRef]
- Ray, R.D. Ocean self-attraction and loading in numerical tidal models. Mar. Geod. 1998, 21, 181–192. [Google Scholar] [CrossRef]
- Hendershott, M.C. The Effects of Solid Earth Deformation on Global Ocean Tides. Geophys. J. Int. 1972, 29, 389–402. [Google Scholar] [CrossRef]
- Rosmond, T.; Teixeira, J.; Peng, M.; Hogan, T.; Pauley, R. Navy Operational Global Atmospheric Prediction System (NOGAPS): Forcing for Ocean Models. Oceanography 2002, 15, 99–108. [Google Scholar] [CrossRef]
- Argote, M.L.; Amador, A.; Lavín, M.F.; Hunter, J.R. Tidal dissipation and stratification in the Gulf of California. J. Geophys. Res. 1995, 100, 16103. [Google Scholar] [CrossRef]
- López, M.; Candela, J.; Argote, M.L. Why does the Ballenas Channel have the coldest SST in the Gulf of California? Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- López, M.; Candela, J.; García, J. Two overflows in the Northern Gulf of California. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Bermúdez-Romero, A.; Magar, V.; Gross, M.S.; Godínez, V.M.; López-Mariscal, M.; Rivera-Lemus, E. Characterization of in-stream tidal energy resources in the Gulf of California: Implementation, calibration and validation of a hydrodynamic model. In Proceedings of the 13th European Wave and Tidal Energy Conference (EWTEC2019), European Wave and Tidal Energy Conference Series, Napoli, Italy, 1–6 September 2019. [Google Scholar]
- Pearson, K. Mathematical Contributions to the Theory of Evolution. III. Regression, Heredity, and Panmixia. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1896, 187, 253–318. [Google Scholar] [CrossRef]
- Magar, V.; González-García, L.; Gross, M.S. Evaluación Técnico-económica del Potencial de Desarrollo de Parques Eólicos en Mar: El Caso del Golfo de California. BIOtecnia 2017, 19, 3–8. [Google Scholar] [CrossRef]
| Units: U [m s−1], TPD [W m−2], AEP [kWh m−2], RE [%], RMSEU [m s−1], RMSETPD [W m−2] | ||||||||
|---|---|---|---|---|---|---|---|---|
| Mooring | mod/obs | mod/obs | AEP mod/obs | REU | RETPD | RMSEU | RMSETPD | |
| ISJ | 0.202/0.206 | 7.56/10.48 | 66.45/92.07 | 0.71 | 2.0% | 27.8% | 9.1 × 10−2 | 14.13 |
| DS | 0.182/0.182 | 7.44/7.67 | 65.35/67.33 | 0.92 | 0.2% | 3% | 4.8 × 10−2 | 6.05 |
| BC | 0.190/0.360 | 8.69/60.60 | 76.33/532.3 | 0.92 | 47% | 86% | 21 × 10−2 | 98.2 |
| SEC | 0.372/0.417 | 56.28/85.24 | 494.4/748.7 | 0.91 | 10.8% | 34% | 11.7 × 10−2 | 63.98 |
| SLC | 0.263/0.388 | 21.98/72.75 | 193.1/639.1 | 0.92 | 32.2% | 69.8% | 17.3 × 10−2 | 102.0 |
| Units: U [m s−1], TPD [W m−2], RMSEU [m s−1], RMSETPD [W m−2] | ||||||
|---|---|---|---|---|---|---|
| Mooring | mod/obs | mod/obs | REU | RETPD | RMSEU | RMSETPD |
| ISJ | 0.415/0.459 | 38.76/55.80 | 9.8% | 30.6 % | 11.9 × 10−2 | 38.56 |
| DS | 0.417/0.399 | 39.6/35.62 | −4.6% | −11.2% | 4.5 × 10−2 | 12.23 |
| BC | 0.467/0.822 | 54.6/311.1 | 43.2% | 82.5% | 36.7 × 10−2 | 290.2 |
| SEC | 0.866/0.928 | 347.4/437.7 | 6.6% | 20.6% | 8.3 × 10−2 | 119.36 |
| SLC | 0.568/0.918 | 101.7/436.7 | 38.2% | 76.7% | 36.8 × 10−2 | 390.6 |
| Units: U [m s−1] and TPD [W m−2] | |||||
|---|---|---|---|---|---|
| Location | (lat lon) | %T | |||
| LN1 | (31.006–114.64) | 0.899 | 39.00 | 172.8 | 1.11 |
| LN2 | (31.348–114.48) | 0.800 | 33.58 | 145.1 | 1.02 |
| LN3 | (31.480–114.40) | 0.758 | 31.1 | 141.62 | 1.02 |
| LS1 | (28.506–112.80) | 0.733 | 23.54 | 106.7 | 0.89 |
| LS2 | (28.646–112.64) | 0.858 | 33.34 | 145.1 | 1.04 |
| LS3 | (28.786–112.48) | 0.676 | 17.30 | 92.94 | 0.83 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magar, V.; Godínez, V.M.; Gross, M.S.; López-Mariscal, M.; Bermúdez-Romero, A.; Candela, J.; Zamudio, L. In-Stream Energy by Tidal and Wind-Driven Currents: An Analysis for the Gulf of California. Energies 2020, 13, 1095. https://doi.org/10.3390/en13051095
Magar V, Godínez VM, Gross MS, López-Mariscal M, Bermúdez-Romero A, Candela J, Zamudio L. In-Stream Energy by Tidal and Wind-Driven Currents: An Analysis for the Gulf of California. Energies. 2020; 13(5):1095. https://doi.org/10.3390/en13051095
Chicago/Turabian StyleMagar, Vanesa, Victor M. Godínez, Markus S. Gross, Manuel López-Mariscal, Anahí Bermúdez-Romero, Julio Candela, and Luis Zamudio. 2020. "In-Stream Energy by Tidal and Wind-Driven Currents: An Analysis for the Gulf of California" Energies 13, no. 5: 1095. https://doi.org/10.3390/en13051095
APA StyleMagar, V., Godínez, V. M., Gross, M. S., López-Mariscal, M., Bermúdez-Romero, A., Candela, J., & Zamudio, L. (2020). In-Stream Energy by Tidal and Wind-Driven Currents: An Analysis for the Gulf of California. Energies, 13(5), 1095. https://doi.org/10.3390/en13051095






