Turbine Characteristics of Wave Energy Conversion Device for Extraction Power Using Breaking Waves
Abstract
1. Introduction
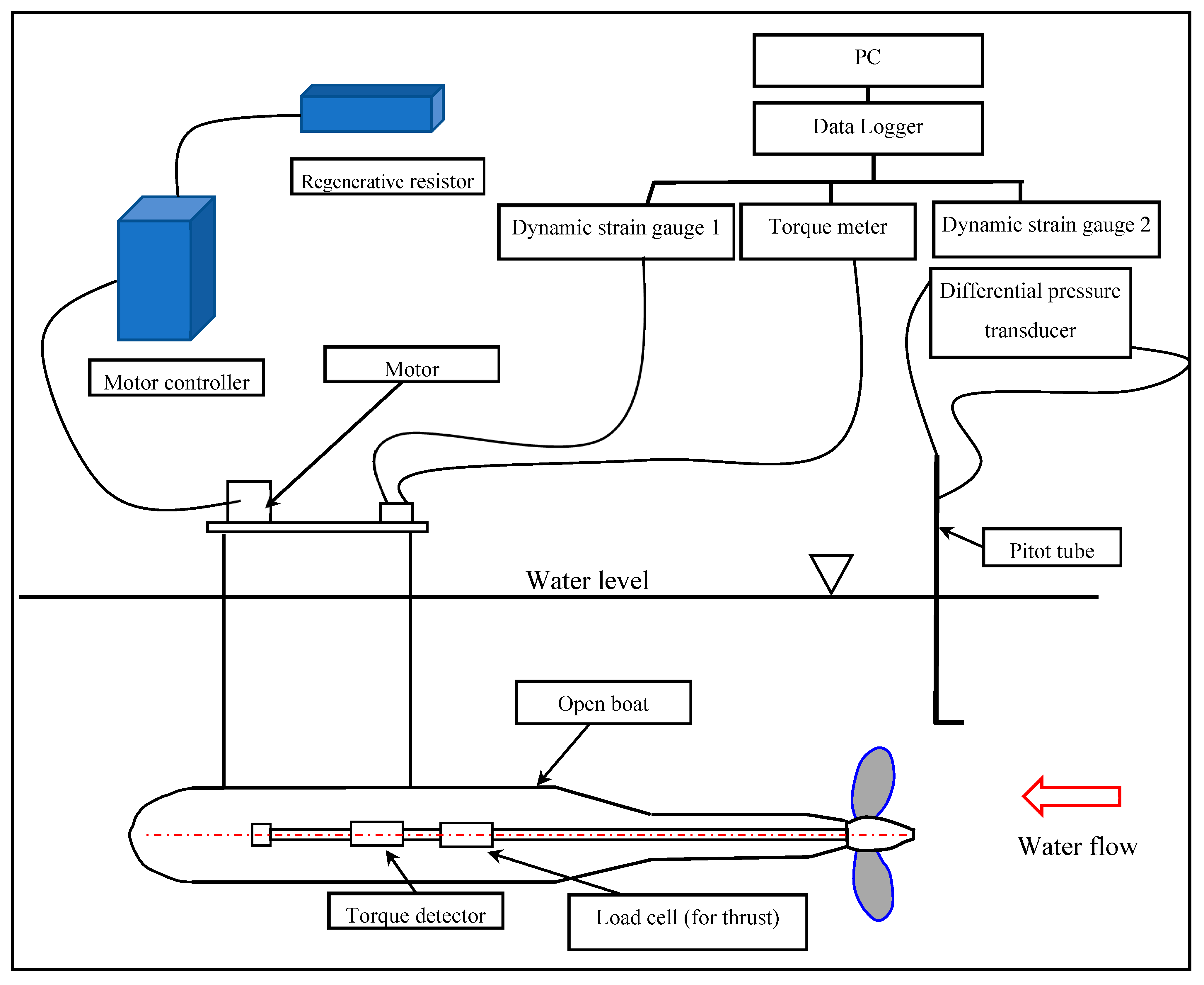
2. Experimental Setup
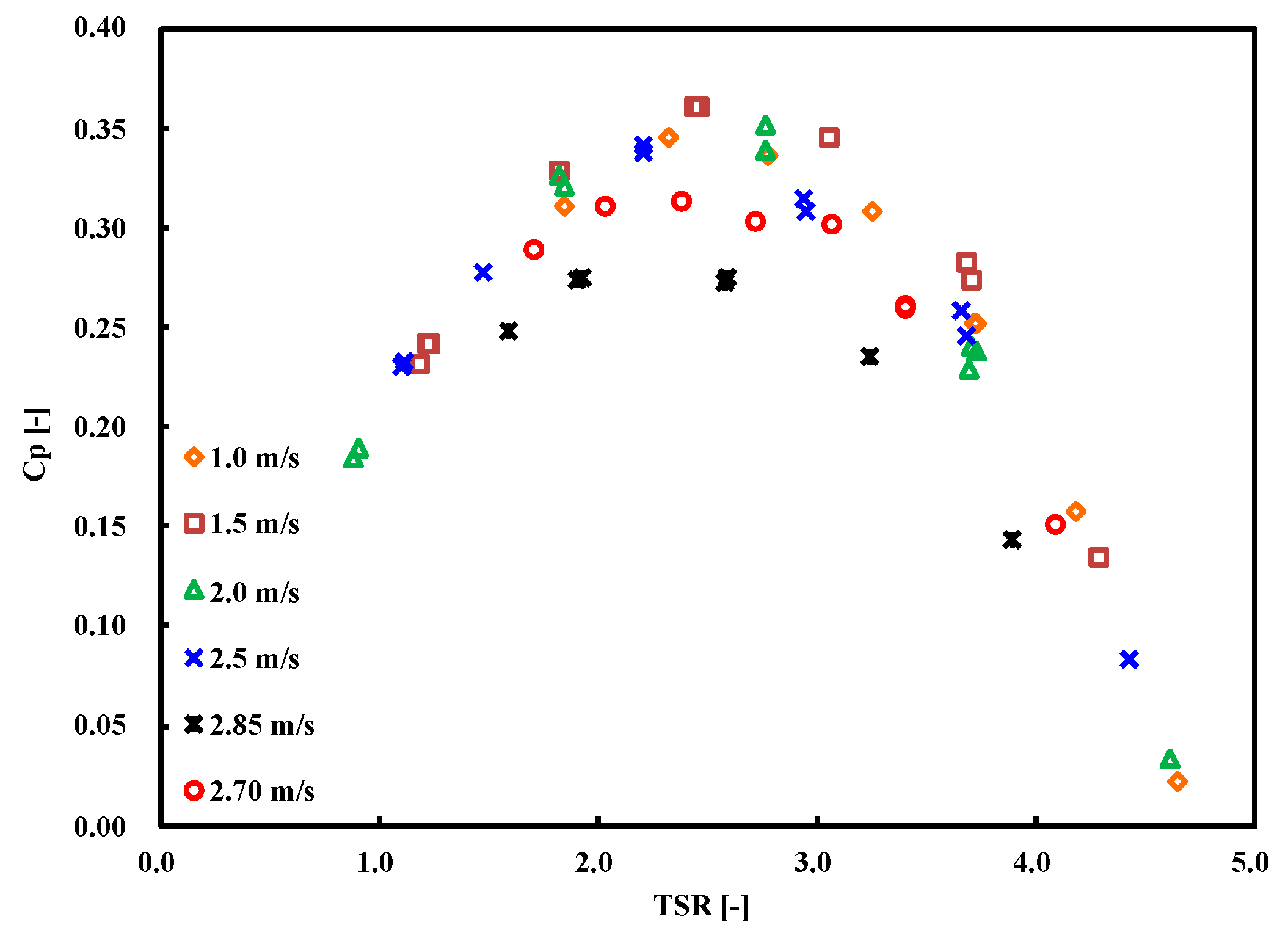
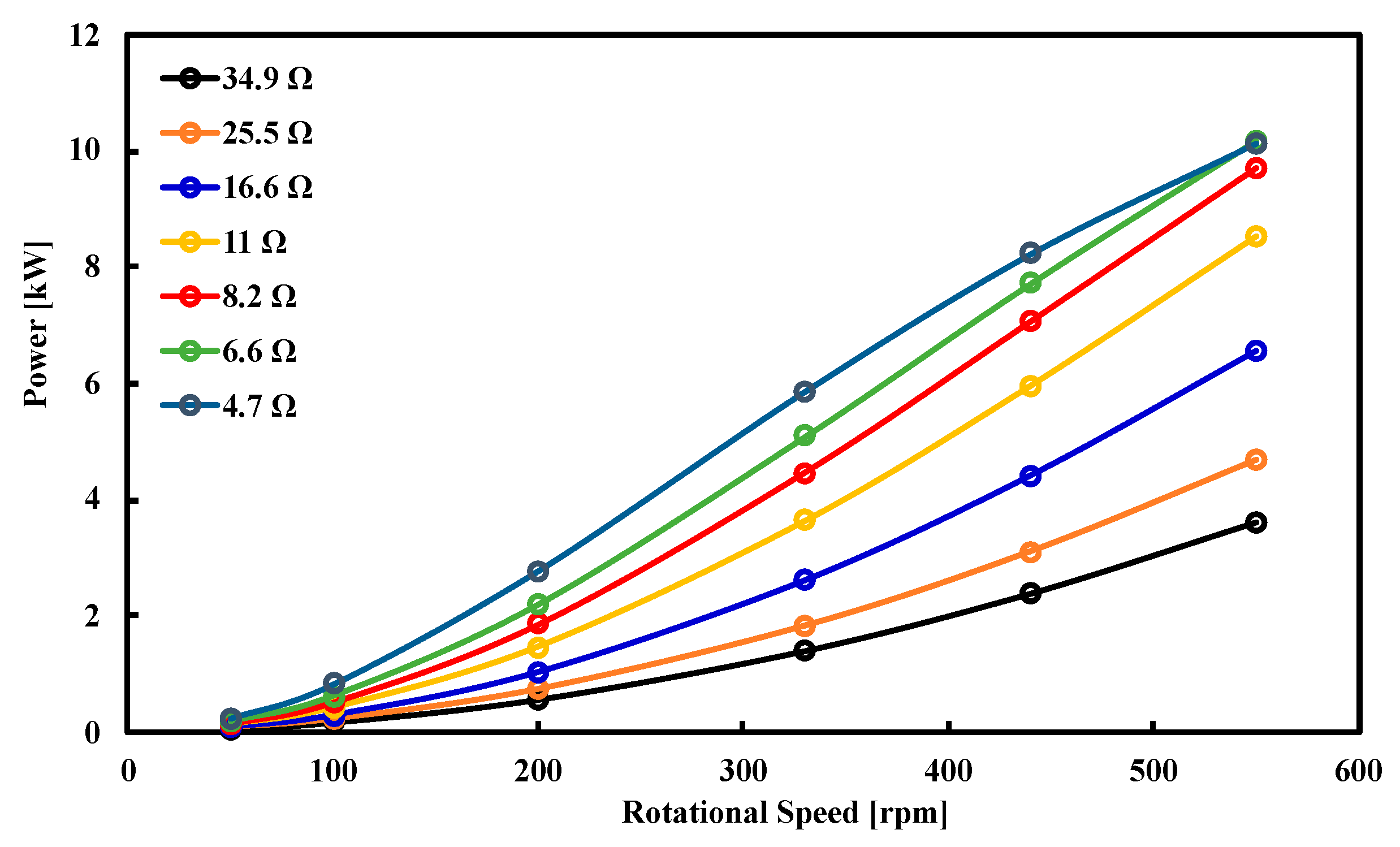
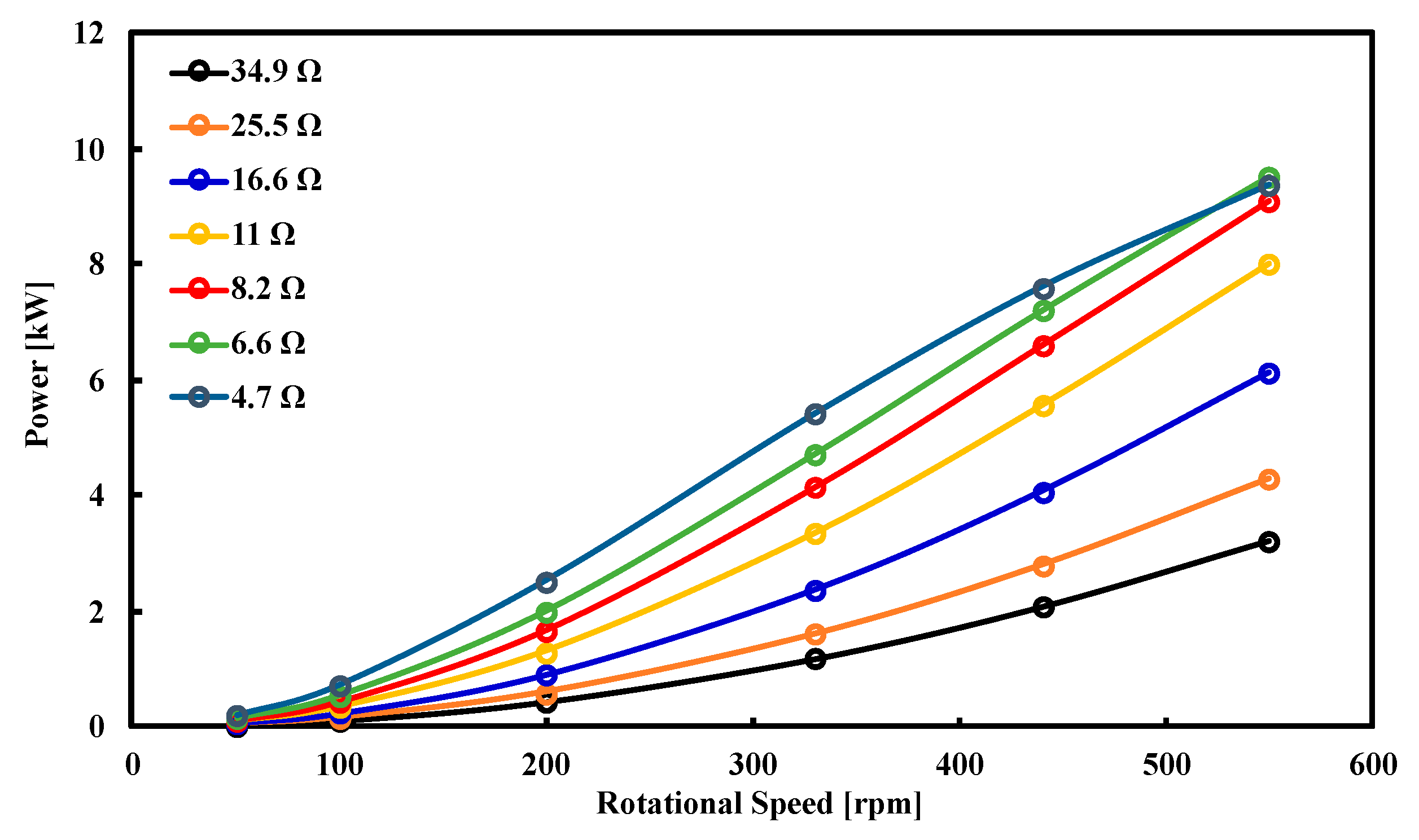
3. Experimental Results
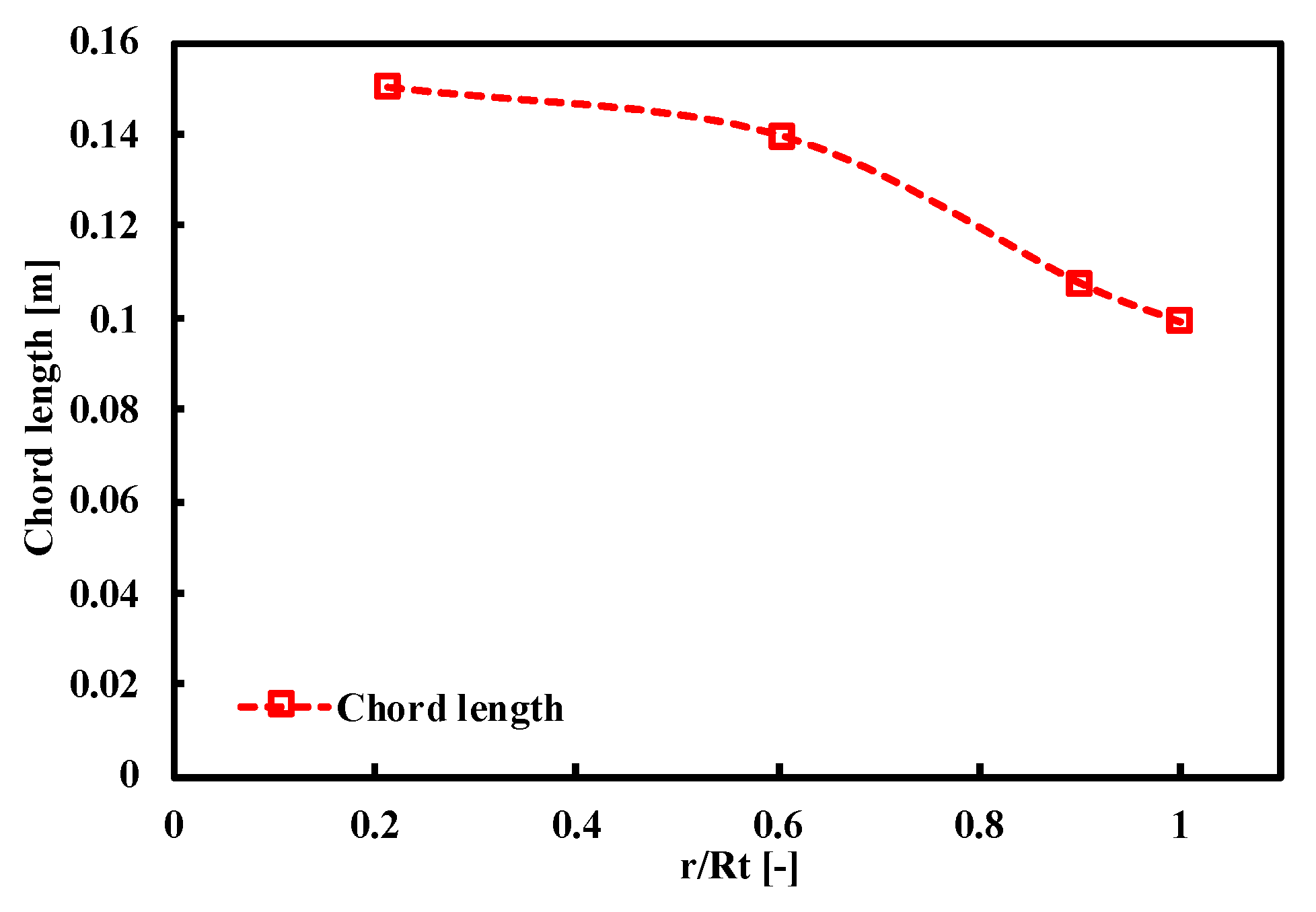
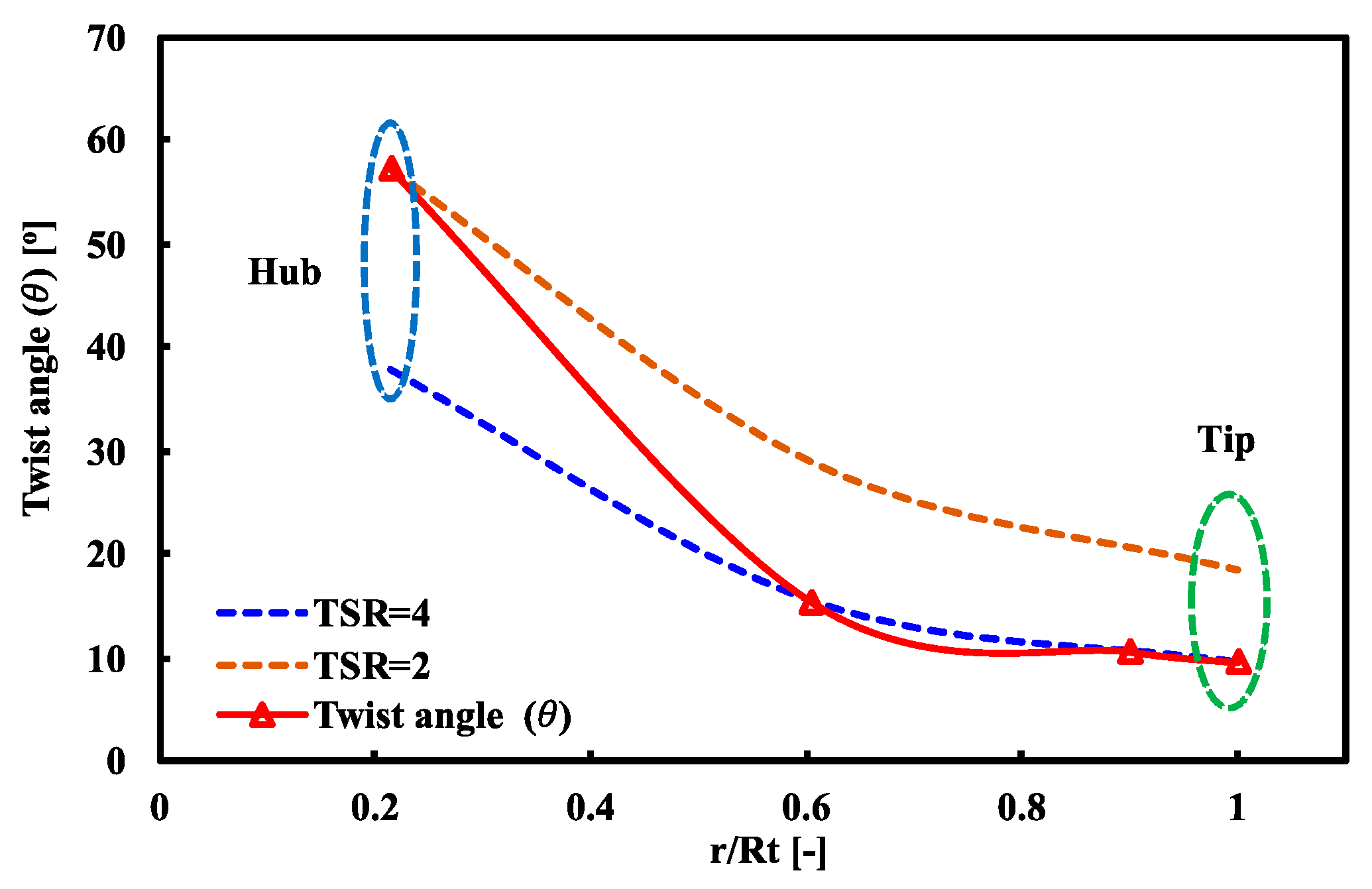
4. Numerical Methodology
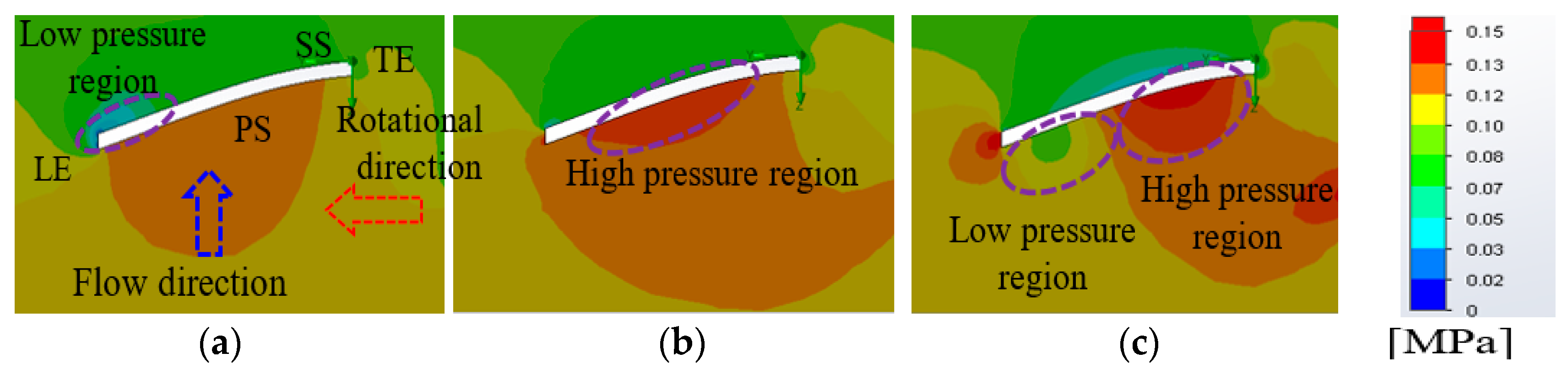
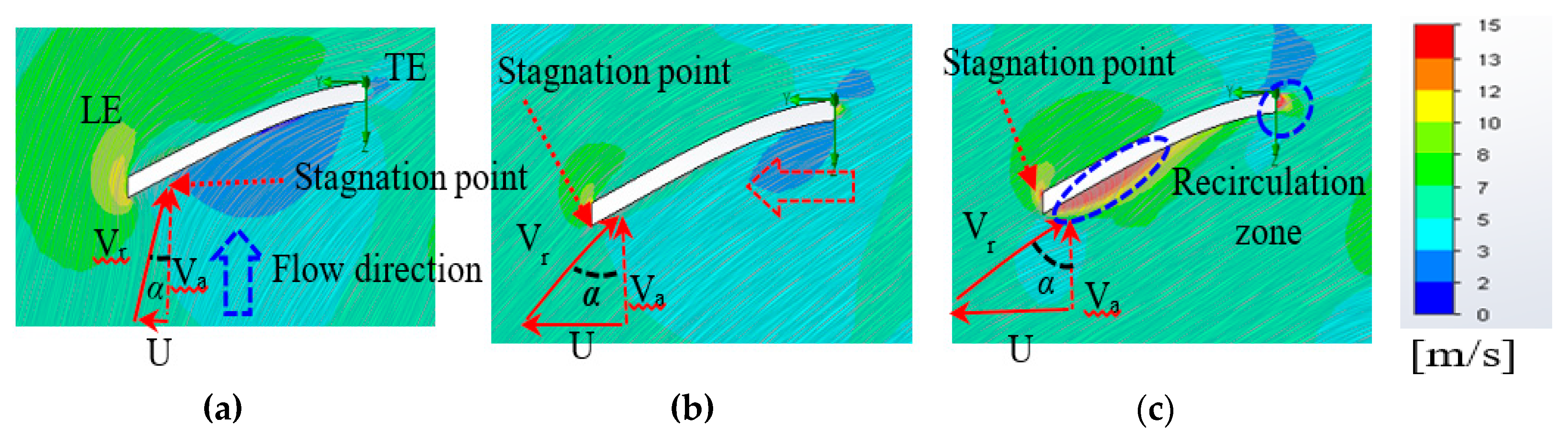
5. Results and Discussion
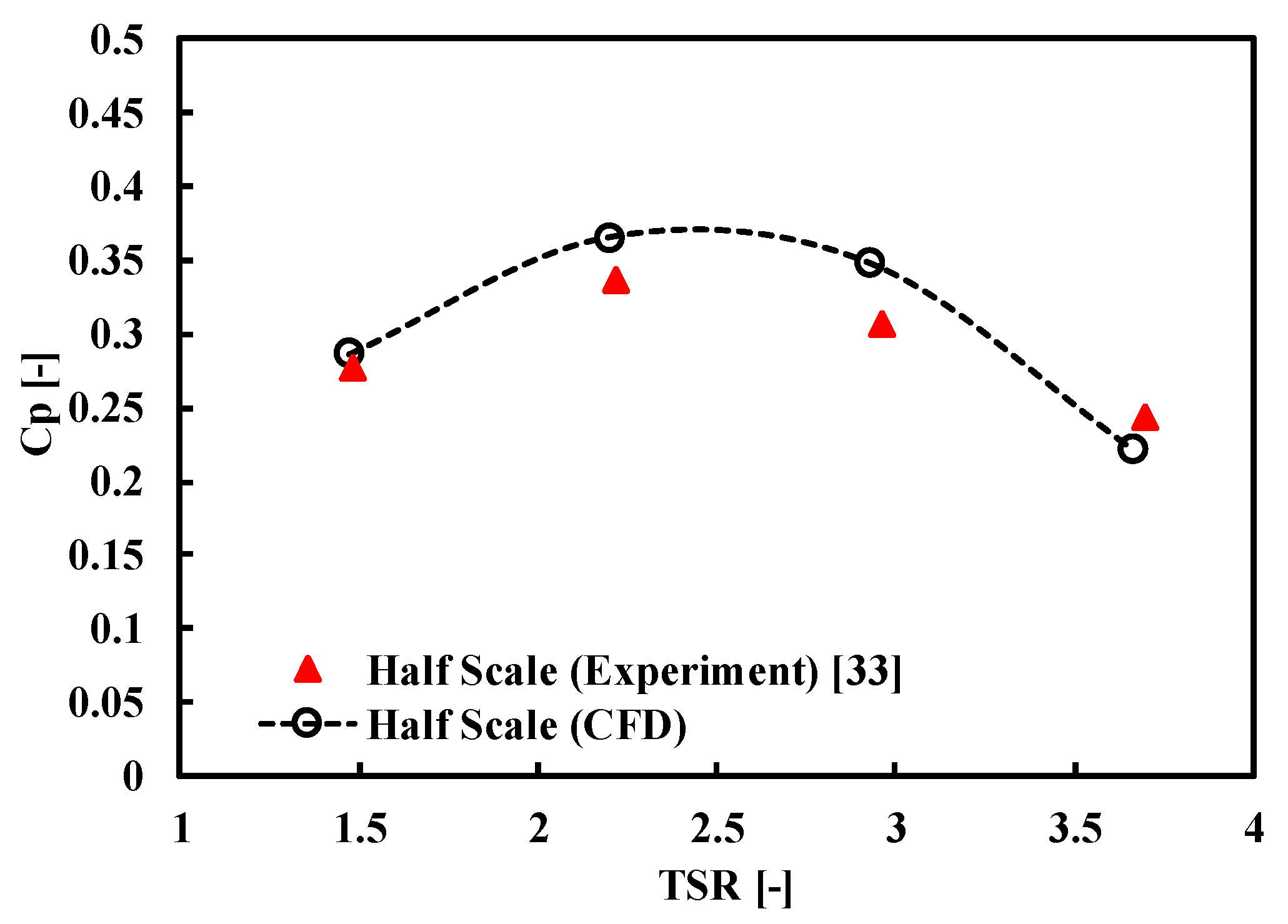
Numerical Validation
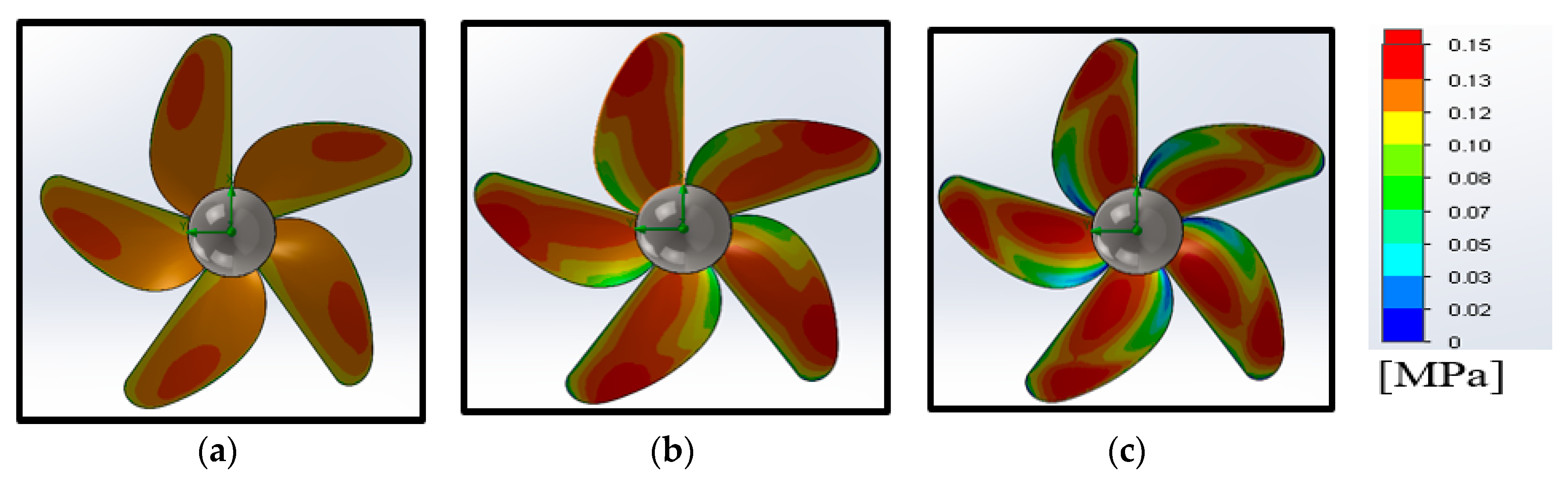
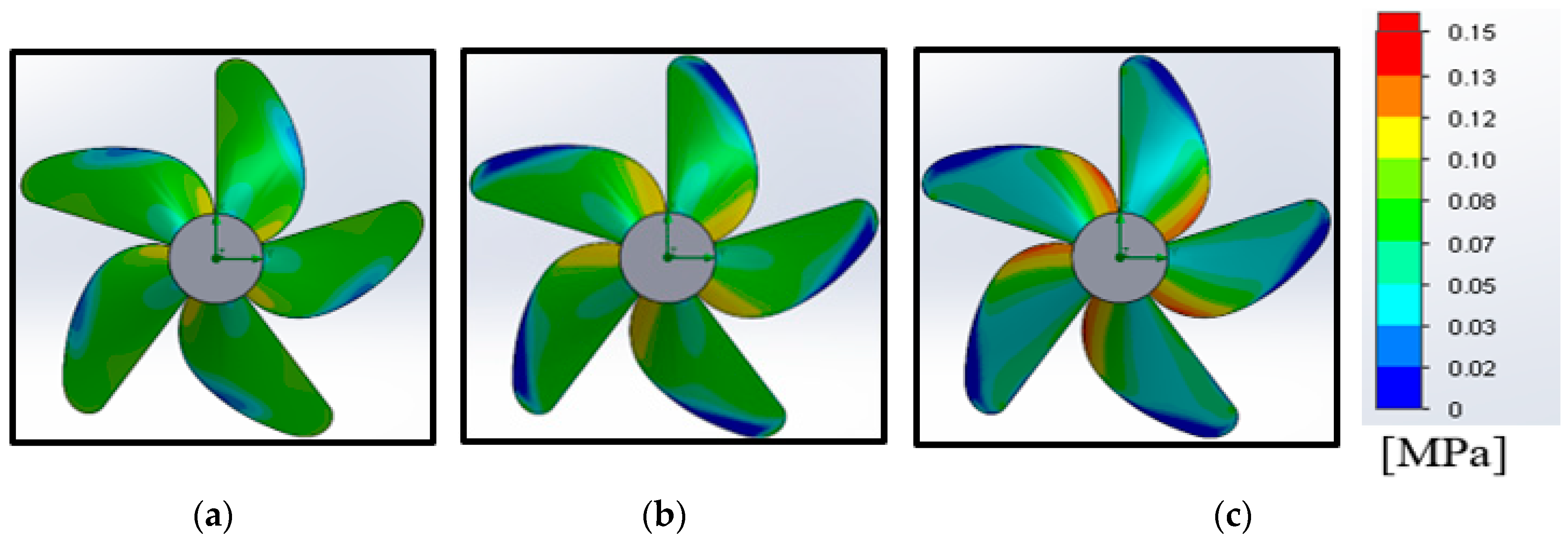
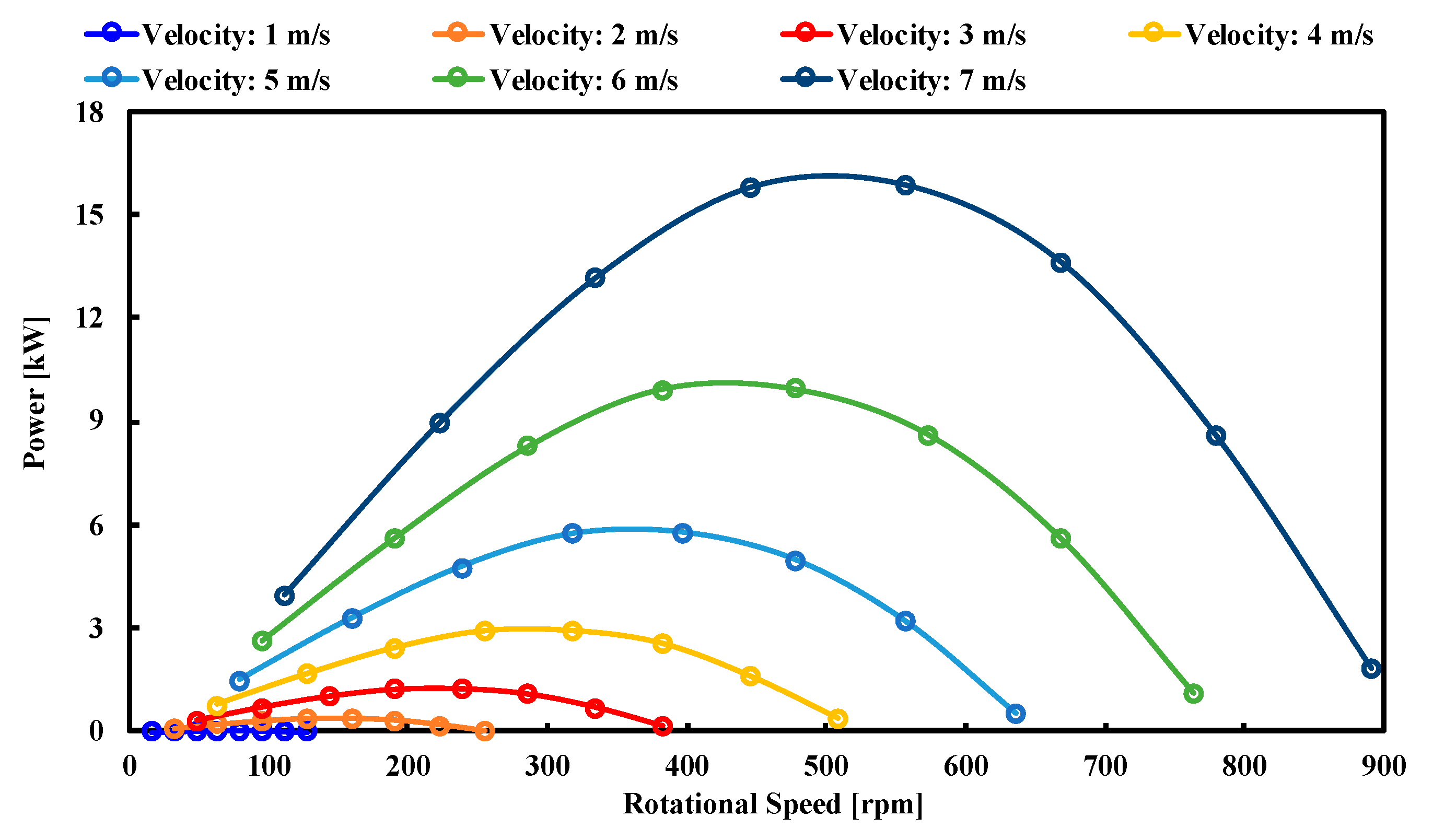
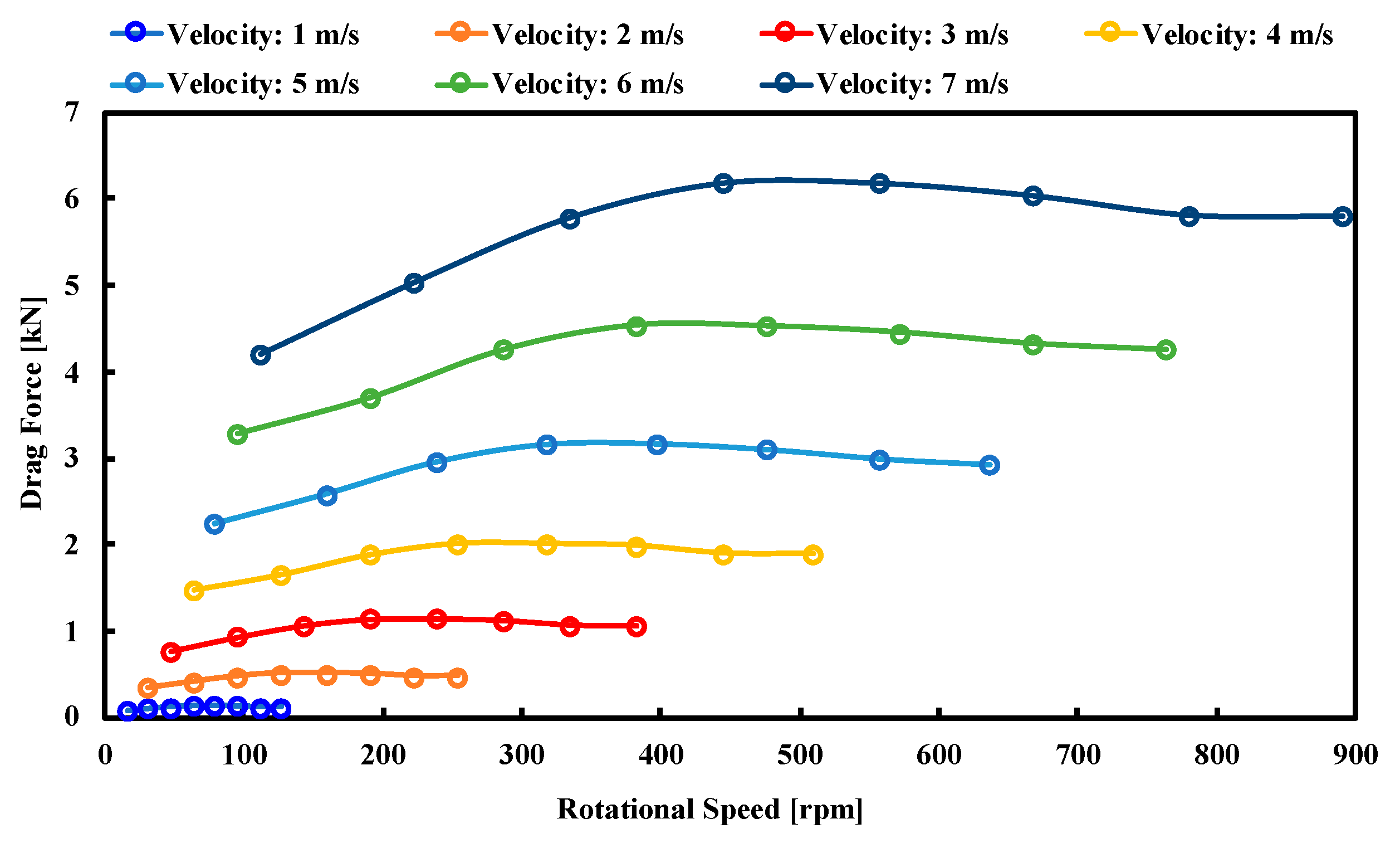
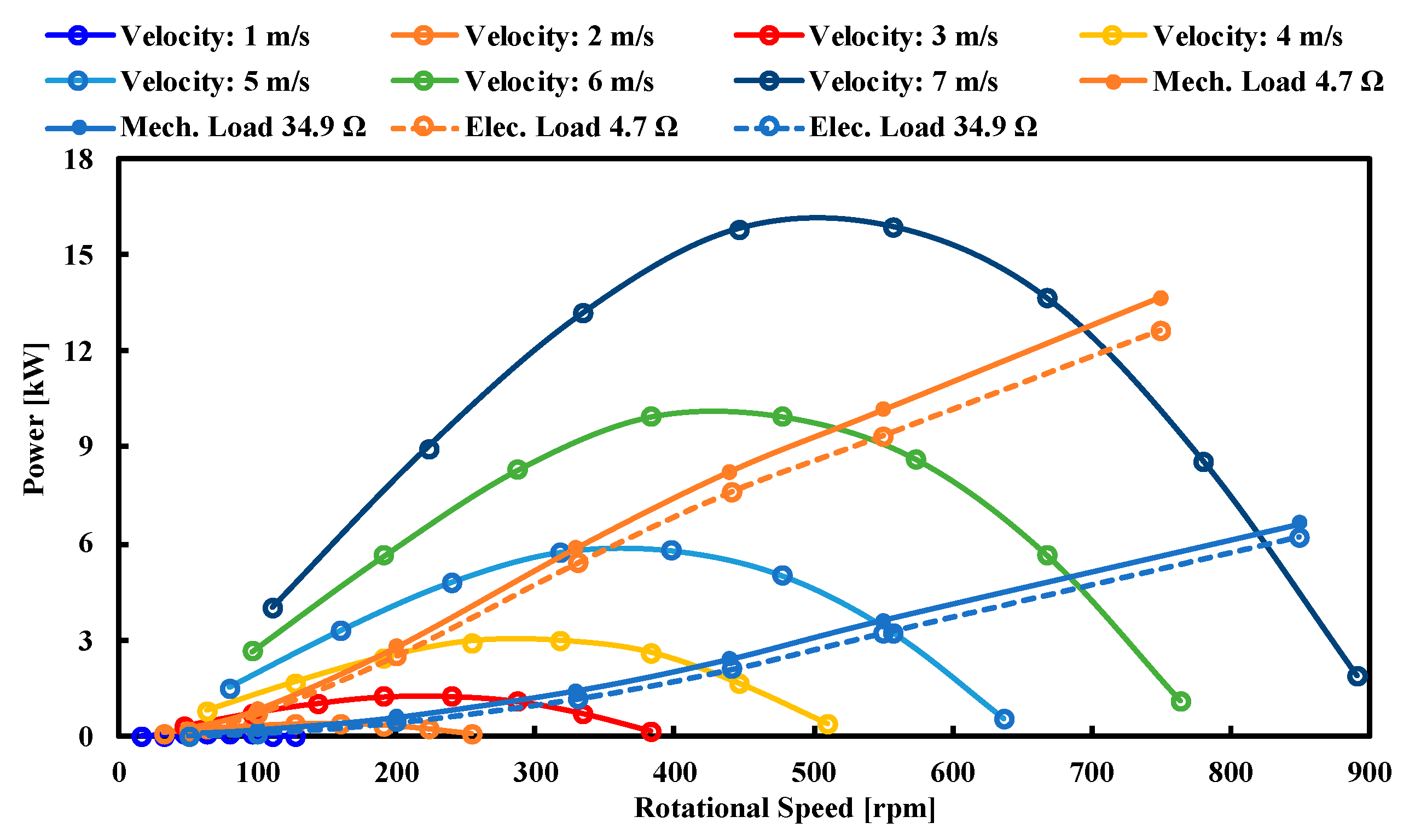
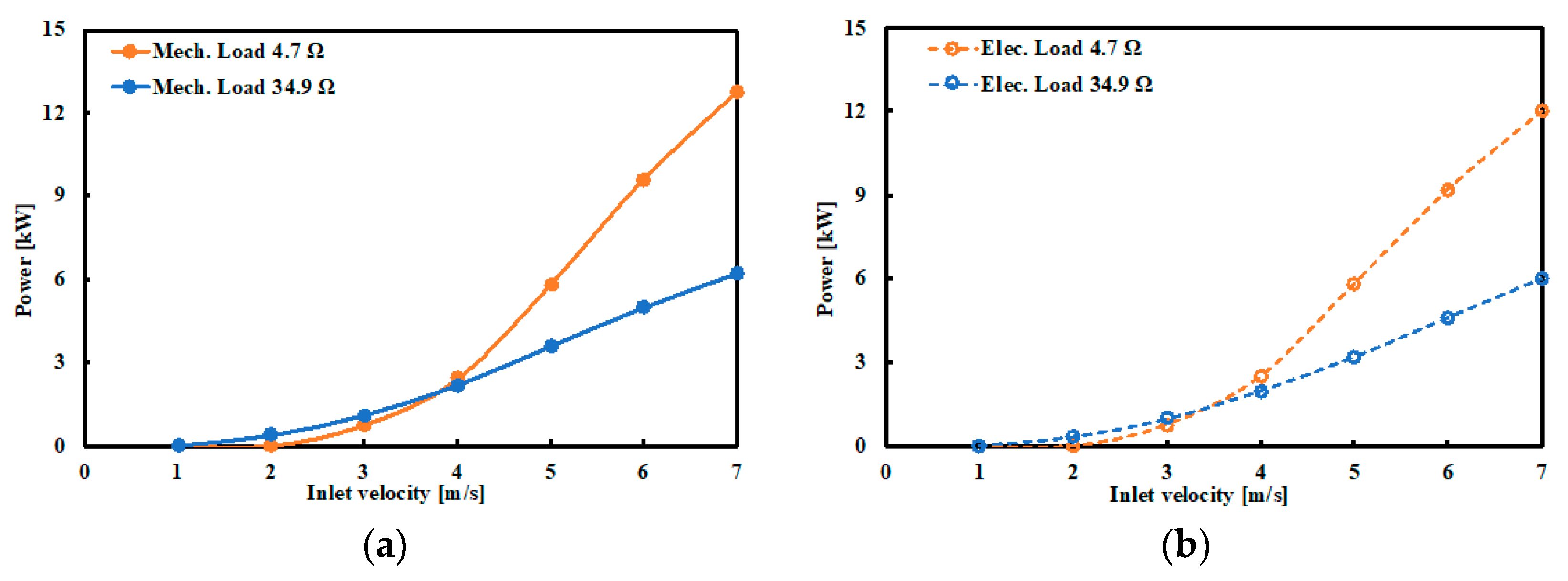
6. Generator and Turbine Running Characteristics
7. Conclusions
- It is observed that the maximum Cp is 0.38 at TSR 2.5.
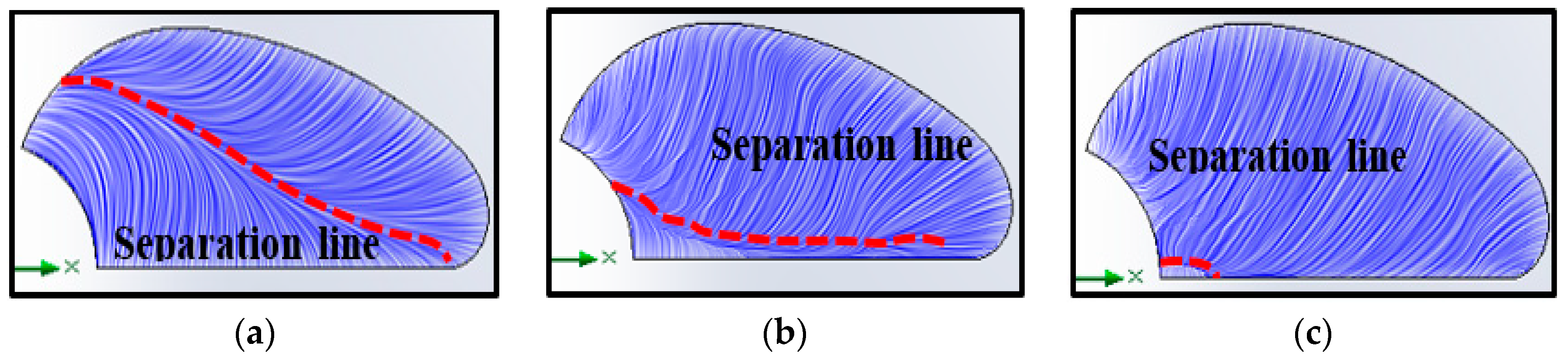
- The separation line moves from leading edge to trailing edge when increase in the TSR is noticed.
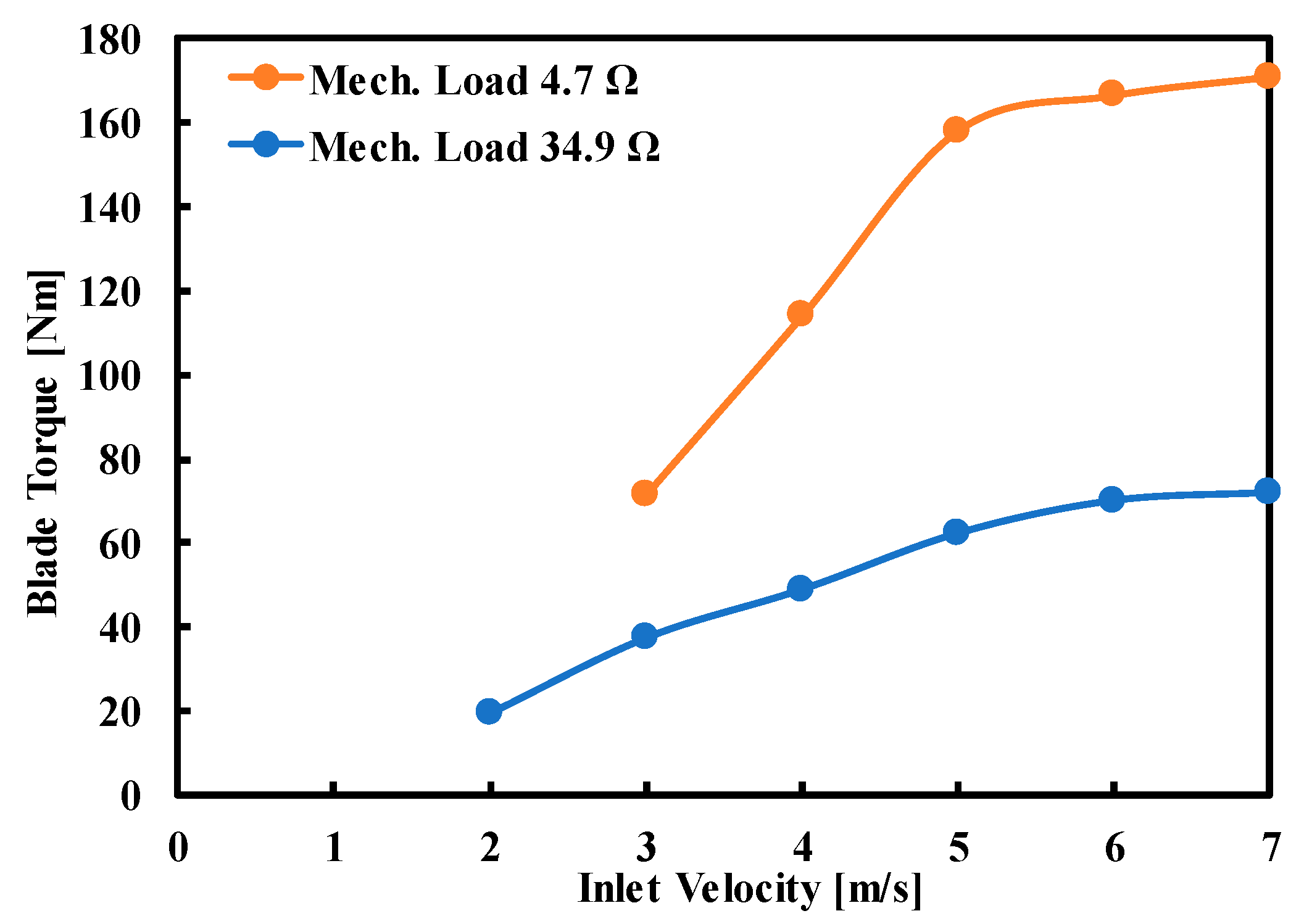
- It can be seen that impedance is a critical factor in determining the turbine starting characteristics.
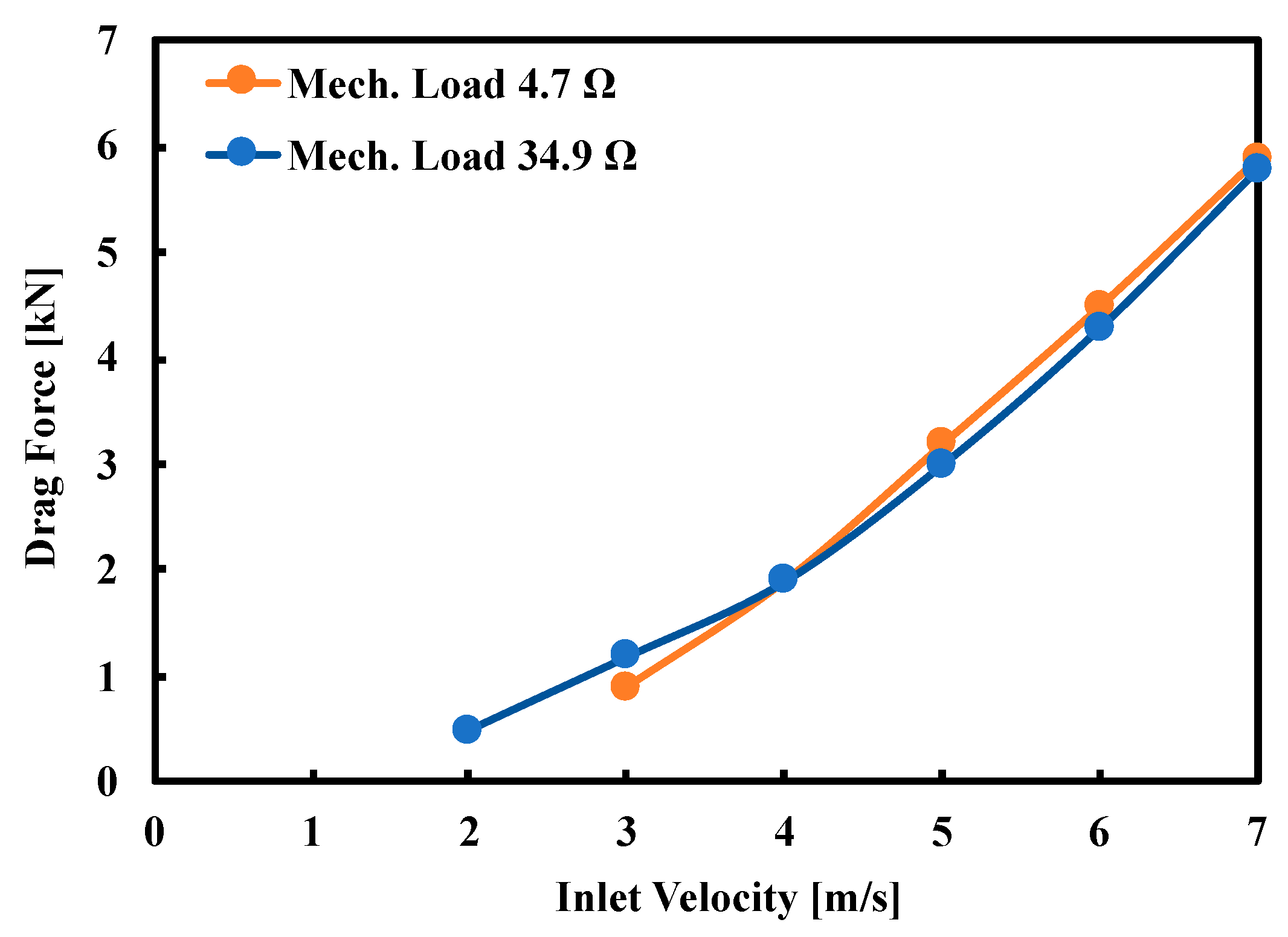
- It is noticed that drag force increases with increase in inlet velocity.
- The running characteristics of the turbine are controlled by wave frequency and incoming velocity.
- It is recommended to investigate the effect of blade shape along with twist angle and chord length on the performance would be a future study.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Abbreviation | Definition |
| AOA | Angle of attack |
| CAD | Computer-aided design |
| CFD | Computational fluid dynamics |
| FVM | Finite volume method |
| LE | Leading edge |
| OIST | Okinawa Institute of Science and Technology Graduate University |
| PS | Pressure side |
| RB | Rotor blade |
| RPM | Revolution per minute |
| RANS | Reynolds-averaged Navier–Stokes equations |
| SIMPLE | Semi-implicit method for pressure linked equations |
| SWFS | Solidworks flow simulation |
| SS | Suction side |
| SETE | Static extended trailing edge |
| TE | Trailing edge |
| TSR | Tip speed ratio |
| WEC | Wave energy converter |
| Symbols | |
| b | Blade span (m) |
| C | Chord length (m) |
| Cl | Lift coefficient (-) |
| Cp | Coefficient of the power (-) |
| Dt | Tip diameter (m) |
| Dh | Hub diameter (m) |
| λ | Tip speed ratio (-) |
| p | Pressure (N/m2) |
| Rt | Tip radius (m) |
| r | Radius (m) |
| S | Blade swept area (m2) |
| T | Torque generated by RB (Nm) |
| t | Blade thickness (m) |
| Va | Axial velocity (m/s) |
| Vr | Relative inlet velocity (m/s) |
| UR | Mean blade speed (m/s) |
| U | Blade tip velocity (m/s) |
| z | Number of RB (-) |
| ɳ | Efficiency (-) |
| ρa | Density of air (g/m3) |
| ϕ | Flow coefficient (-) |
| θ | Blade twist angle (°) |
| α | Angle of attack (°) |
| ω | Angular velocity (rad/s) |
References
- REN21. Renewables Global Status Report; Tech. Rep.; REN21 Secretariat: Paris. France, 2018. [Google Scholar]
- Falcão, A.F.O.; Joao, C.C.H. Oscillating-water-column wave energy converters and air turbines: A review. Renew. Energy 2016, 85, 1391–1424. [Google Scholar] [CrossRef]
- Raghunathan, S.; Tan, C.P. Efficiency Starting Torque and Prevention of Run-Away with Wells Self-Rectifying Turbines. In Proceedings of the 2nd International Symposium on Wave and Tidal Energy, Cambridge, UK, 1981; pp. 207–217. [Google Scholar]
- Raghunathan, S. A methodology for Wells turbine design for wave energy conversion. Proc. Inst. Mech. Eng. Part A J. Power Energy 1995, 209, 221–232. [Google Scholar] [CrossRef]
- Pawitan, K.A.; Dimakopoulos, A.S.; Vicinanza, D.; Allsop, W.; Bruce, T. A loading model for an OWC caisson based upon large-scale measurements. Coast. Eng. 2019, 145, 1–20. [Google Scholar] [CrossRef]
- Brito-Melo, A.; Gato, L.M.C.; Sarmento, A.J.N.A. Analysis of Wells Turbine Design Parameters by Numerical Simulation of the OWC Performance. Ocean. Eng. 2002, 29, 1463–1477. [Google Scholar] [CrossRef]
- Mohamed, M.H.; Janiga, G.; Pap, E.; Thévenin, D. Multi-Objective Optimization of the Airfoil Shape of Wells Turbine Used for Wave Energy Conversion. Energy 2011, 36, 438–446. [Google Scholar] [CrossRef]
- Webster, M.; Gato, L.M.C. The Effect of Rotor Blade Sweep on the Performance of the Wells Turbine. Int. J. Offshore Polar Eng. 2010, 9, 233–240. [Google Scholar]
- Kim, T.H.; Setoguchi, T.; Takao, M.; Kaneko, K.; Santhakumar, S. Study of Turbine with Self-Pitch-Controlled Blades for Wave Energy Conversion. Int. J. Therm. Sci. 2002, 41, 101–107. [Google Scholar] [CrossRef]
- Mohamed, M.H.; Shaaban, S. Optimization of Blade Pitch Angle of an Axial Turbine Used for Wave Energy Conversion. Energy 2013, 56, 229–239. [Google Scholar] [CrossRef]
- Mohamed, M.H.; Sameh, S. Numerical optimization of axial turbine with self-pitch-controlled blades used for wave energy conversion. Int. J. Energy Res. 2014, 38, 592–601. [Google Scholar] [CrossRef]
- Takao, M.; Setoguchi, T.; Kinoue, Y.; Kaneko, K. Wells Turbine with End Plates for Wave Energy Conversion. Ocean. Eng. 2007, 34, 1790–1795. [Google Scholar] [CrossRef]
- Raghunathan, S.; Tan, C.P. Effect of Blade Profile on the Performance of the Wells Self-Rectifing Air Turbine. Int. J. Heat Fluid Flow 1985, 6, 369–379. [Google Scholar]
- Gato, L.M.C.; Webster, M. An Experimental Investigation into the Effect of Rotor Blade Sweep on the Performance of the Variable-Pitch Wells Turbine. Proc. Inst. Mech. Eng. Part. A J. Power Energy 2001, 215, 611–622. [Google Scholar] [CrossRef]
- Suzuki, M.; Arakawa, C. Influence of Blade Profiles on Flow around Wells Turbine. Int. J. Fluid Mach. Syst. 2008, 1, 148–154. [Google Scholar] [CrossRef]
- Takao, M.; Setoguchi, T.; Kinoue, Y.; Kaneko, K. Effect of end plates on the performence of a Wells turbine for wave energy conversion. J. Therm. Sci. 2006, 15, 319–323. [Google Scholar] [CrossRef]
- Kim, T.H.; Takao, M.; Setoguchi, T.; Kaneko, K.; Inoue, M. Performance Comparison of Turbines for Wave Power Conversion. Int. J. Therm. Sci. 2001, 40, 681–689. [Google Scholar] [CrossRef]
- Thakker, A.; Abdulhadi, R. Effect of blade profile on the performance of Wells turbine under unidirectional sinusoidal and real sea flow conditions. Int. J. Rotating Mach. 2007, 2007, 51598. [Google Scholar] [CrossRef]
- Halder, P.; Samad, A.; Kim, J.H.; Choi, Y.S. High performance ocean energy harvesting turbine design—A new casing treatment scheme. Energy 2015, 86, 219–231. [Google Scholar] [CrossRef]
- Halder, P.; Samad, A. Torque and efficiency maximization for a wave energy harvesting turbine: An approach to modify multiple design variables. Int. J. Energy Res. 2017, 41, 1014–1028. [Google Scholar] [CrossRef]
- Halder, P.; Samad, A.; Thevenin, D. Improved design of a Wells turbine for higher operating range. Renew. Energy 2017, 106, 122–134. [Google Scholar] [CrossRef]
- Halder, P.; Mohamed, M.H.; Samad, A. Wave energy conversion: Design and shape optimization. Ocean. Eng. 2018, 150, 337–351. [Google Scholar] [CrossRef]
- Kumar, P.M.; Samad, A. Nature-inspired design of a turbine blade harnessing wave energy. Proceedings of the Institution of Mechanical Engineers. Part. A J. Power Energy 2019. [Google Scholar] [CrossRef]
- Kumar, P.M.; Halder, P.; Husain, A.; Samad, A. Performance enhancement of Wells turbine: Combined radiused edge blade tip, static extended trailing edge, and variable thickness modifications. Ocean. Eng. 2019, 85, 47–58. [Google Scholar] [CrossRef]
- Gomes, R.P.F.; Henriques, J.C.C.; Gato, L.M.C.; Falcão, A.F.O. Multi-point aerodynamic optimization of the rotor blade sections of an axial-flow impulse air turbine for wave energy conversion. Energy 2012, 45, 570–580. [Google Scholar] [CrossRef]
- Badhurshah, R.; Samad, A. Multiple surrogate-based optimization of a bidirectional impulse turbine for wave energy conversion. Renew. Energy 2015, 74, 749–760. [Google Scholar] [CrossRef]
- Ezhilsabareesh, K.; Rhee, S.H.; Samad, A. Shape optimization of a bidirectional impulse turbine via surrogate models. Eng. Appl. Comput. Fluid Mech. 2018, 12, 1–12. [Google Scholar] [CrossRef]
- Badhurshah, R.; Dudhgaonkar, P.; Jalihal, P.; Samad, A. High efficiency design of an impulse turbine used in oscillating water column to harvest wave energy. Renew. Energy 2018, 121, 344–354. [Google Scholar] [CrossRef]
- Shintake, T. Harnessing the Power of Breaking Waves. In Proceedings of the AWTEC 2016, 3rd Asian Wave and Tidal Energy Conference, Singapore, 24–28 October 2016. [Google Scholar]
- Shintake, T.; Shirasawa, K.; Fujita, J.; Misumi, S.; Halder, P.; Nagahama, T.; Shindou, T.; Taggart, H.; Hikaru, K.; Takebe, H. Results of Wave Energy Experiments in the Maldives. In Proceedings of the European Wave and Tidal Energy Conference (EWTEC-2019), Napoli, Italy, 1–6 September 2019. [Google Scholar]
- Takebe, H.; Shirasawa, K.; Fujita, J.; Misumi, S.; Halder, P.; Shintake, T. Wave Power Measurement at Braking Wave Zone in Maldives using Horizontal-Axis Turbine WEC. In Proceedings of the European Wave and Tidal Energy Conference (EWTEC-2019), Napoli, Italy, 1–6 September 2019. [Google Scholar]
- Takebe, H.; Minami, J.; Fujita, J.; Shirasawa, K.; Toda, K.; Shintake, T. Water Speed Measurements at a Wave Energy Converter Test Site. In Proceedings of the EWTEC 2017, Cork, Ireland, 28 August–1 September 2017. [Google Scholar]
- Takebe, H.; Shirasawa, K.; Fujita, J.; Misumi, S.; Shintake, T. Development of OIST Wave Energy Converter Monitoring System for Maldives Island Experiment. J. Energy Power Eng. 2018, 12, 375–384. [Google Scholar]
- Enhanced Turbulence Modeling in Solidworks Flow Simulation; Technical Paper; Dassault Systemes, SolidWorks Corporation: Waltham, MA, USA, 2013; pp. 1–21.
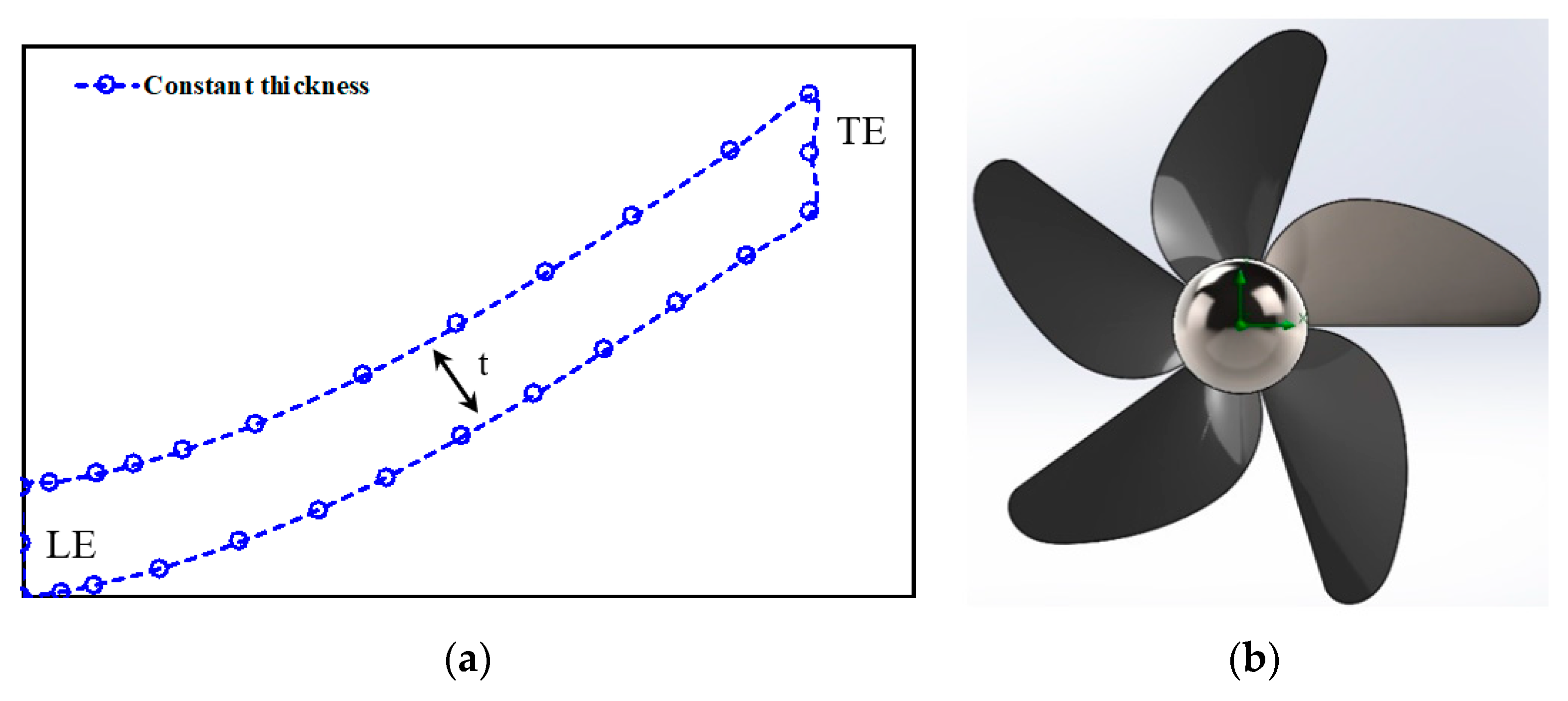
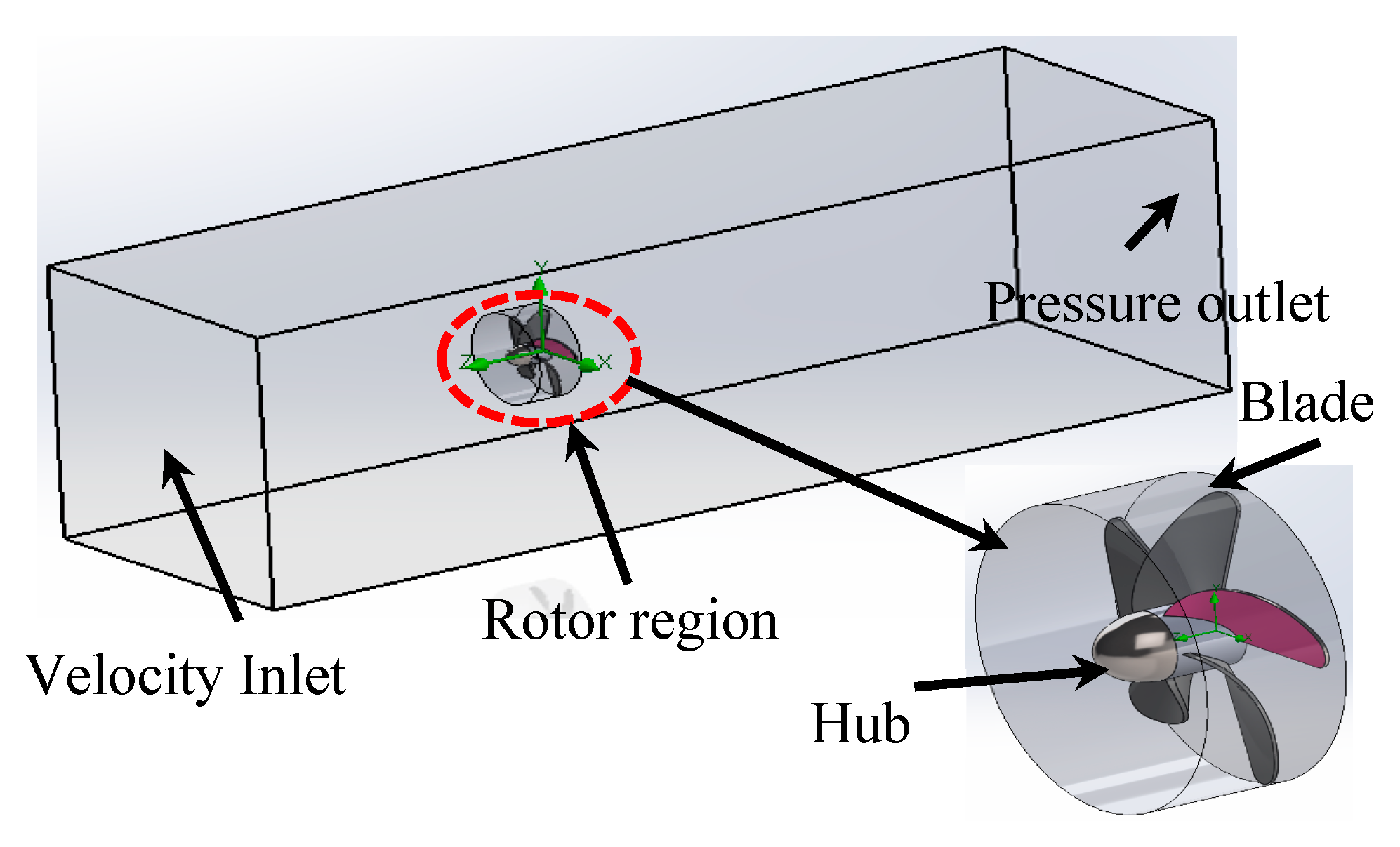
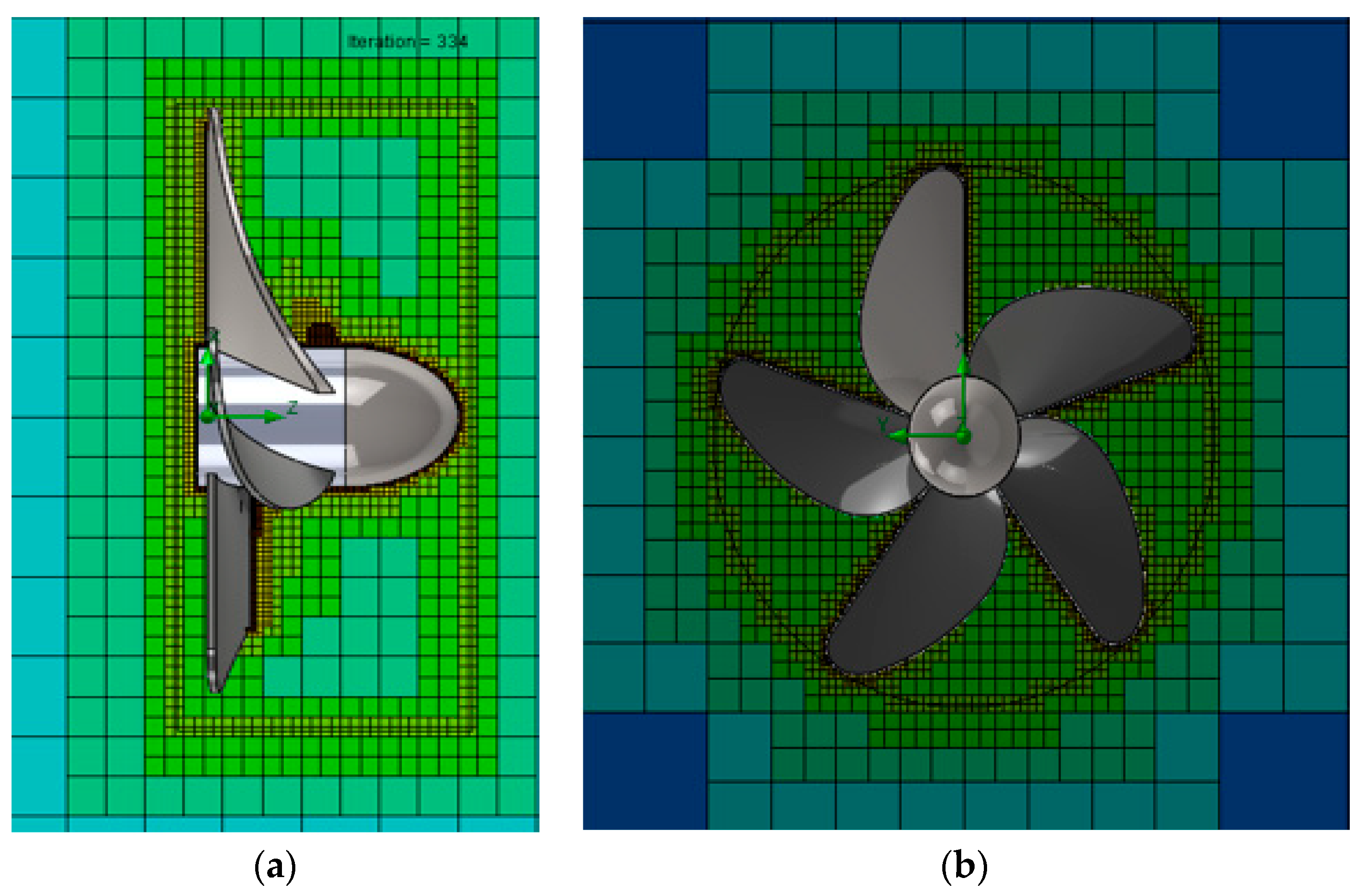
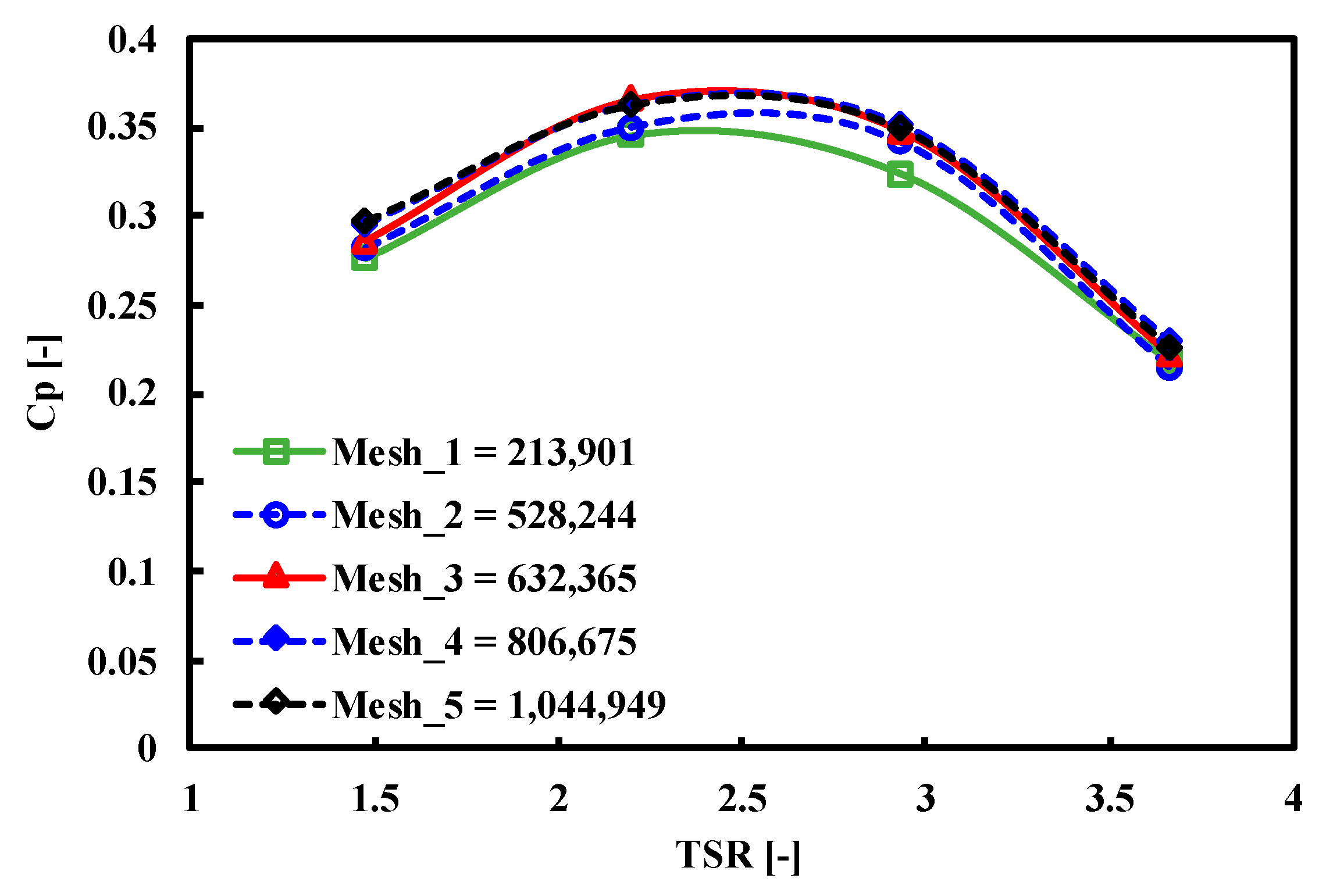
| Wells Turbine | |||
|---|---|---|---|
| Design Modification | Advantage | Description | Profile |
| Sweep with and without guide vane [6] | Higher operating range | Bypass pressure-relief valve produced higher electrical energy. | NACA0015 |
| Aerofoil shape [7] | Increased power output (average relative gain: +11.3% Improved efficiency: 1% | Incident angle varied: 5 to 14° | NACA0021 |
| Blade sweep [8] | Overall efficiency improved | 30° backward sweep | NACA0015 |
| Blade sweep [9] | Improved overall performance | Blade sweep range: 0.25–0.75 | NACA0020 |
| Pitch angle [10] | Improved efficiency: 2.3% and AOP efficiency: 6.2%. | Optimum pitch angle: 0.3° | NACA0021 |
| Pitch angle [11] | Average increase in efficiency: 3.4%, power: 1%. | Optimum pitch angle: 0.6° | NACA0021 |
| Endplate [12] | Improved efficiency by 4% | Endplate thickness: 0.5 mm and plate margin: 0 to 0.3 mm | NACA0020 |
| Blade profile Thickness [13] | The NACA0021 produced peak efficiency. Efficiency drop: ~10% with blade roughened blade. | Thicker and modified aerofoil blades improved the performance of the turbine. | NACA0024, NACA0021, NACA0015H, NACA0015, NACA0012 |
| Blade sweep and pitch angle [14] | Improved turbine performance | 30° backward sweep and blade pitch angle: 0 to 20° | NACA0015 |
| Blade profile [15] | Efficiency improved at an angle of attack < 7°. Stall angle = 10°. | Fan-shaped blades with different sweep angles | NACA0021, NACA0012 |
| Blade profile [16] | Higher peak efficiency | Optimum blade profile: NACA0015 | NACA0015, NACA0020, CA9, HSIM 15-262133-1576 |
| Blade geometry [17] | The stall margin is higher with a higher hub-tip ratio. | Optimum blade sweeps ratio of 0.35 and solidity of ~0.67. | NACA0020 |
| Blade profile [18] | Higher power output | Preferable rotor blade profile CA9 | NACA0015, NACA0020, CA9, HSIM 15-262133-1576 |
| Casing groove [19] | Higher power output and operating range | Introduced circumferential casing groove | NACA0015 |
| Blade sweep and thickness [20] | Stall margin and power enhanced by 22.2% and 33%, respectively. | Optimize the blade sweep and thickness | NACA0015 |
| Blade sweep [21] | Stall margin and power enhanced by 18% and 29%, respectively. | Optimize the blade sweep angle | NACA0015 |
| Sweep, thickness and casing groove [22] | 8% increment efficiency and 17.4% decrement in torque. | Optimize the Blade sweep and thickness along with the casing groove | NACA0015 |
| Static extended trailing edge [23] | Improved relative mean torque by 23.4% and, reduced relative mean efficiency by 5.4%, before stall condition | Static extended trailing edge with 5% chord length | NACA0015 |
| Radiused edge blade tip, static extended trailing edge, and thickness [24] | 22% and 97% relative stall margin and the turbine power. | Fixed SETE at LE and extending TE without altering the original features of the airfoil. Length, thickness, and deflection are fixed as 5% C, 0.25mm and 0°, respectively | NACA0015 |
| Impulse Turbine | |||
| Blade thickness [25] | Improved efficiency. | Camber line iterative design | Circular – elliptical |
| Number of blades and GVs [26] | Enhance efficiency 13% | Surrogate-based optimization | Circular – elliptical |
| Hub and tip thickness [27] | 10.4% efficiency improvement | Surrogate-based optimization | Circular – elliptical |
| Number of blades and GVs along with GV angle and profile. [28] | 24% efficiency enhancement for the entire flow range | Surrogate-based optimization | Circular – elliptical |
| Parameter | Description |
|---|---|
| CAD Model | SolidWorks |
| CFD Package | SolidWorks Flow Simulation (SWFs) |
| Flow domain | Full blade |
| Mesh/Nature | Immersed Boundary Cartesian Meshing Techniques |
| Reference frame | Local averaging frame |
| Working fluid | Water (assume temperature 20 °C) |
| Turbulence Model | Modified κ-ε with two-scale wall function |
| Inlet | Uniform velocity |
| Hub, rotor blade | No-slip wall |
| Outlet | Pressure outlet |
| Goal convergence | 5 |
| Vel. (m/s) | RPM | Power (W) | Ω (rad/s) | T (Nm) | Drag Force (N) |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 |
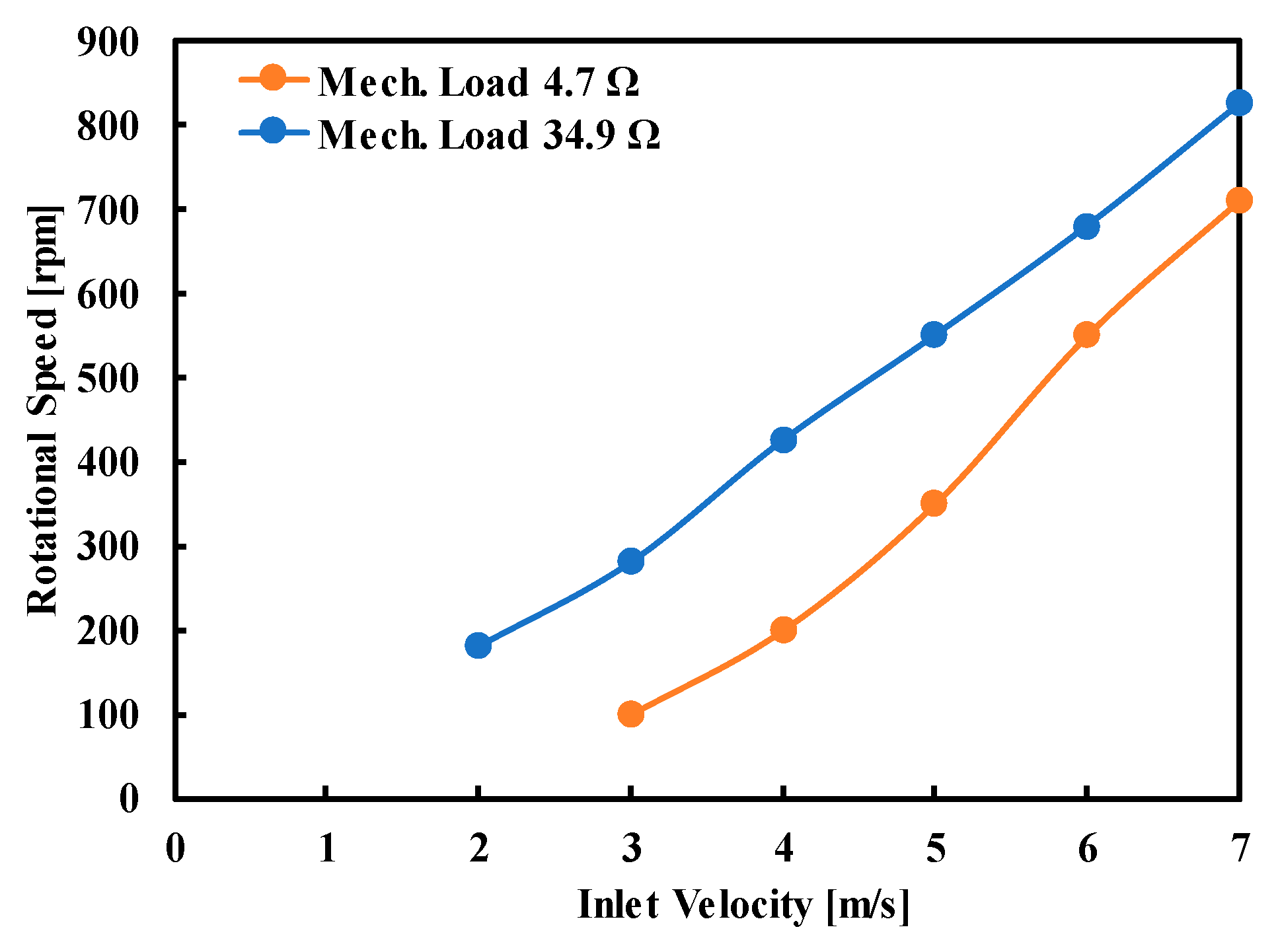
| 3 | 100 | 750 | 10.47 | 71.62 | 900 |
| 4 | 200 | 2390 | 20.94 | 114.11 | 1900 |
| 5 | 350 | 5800 | 36.65 | 158.25 | 3190 |
| 6 | 550 | 9600 | 57.60 | 166.68 | 4500 |
| 7 | 710 | 12,725 | 74.35 | 171.15 | 5900 |
| Vel. (m/s) | RPM | Power (W) | Ω (rad/s) | T (Nm) | Drag Force (N) |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 180 | 370 | 18.85 | 19.63 | 500 |
| 3 | 280 | 1100 | 29.32 | 37.52 | 1190 |
| 4 | 425 | 2180 | 44.51 | 48.98 | 1900 |
| 5 | 550 | 3590 | 57.60 | 62.33 | 3000 |
| 6 | 680 | 4990 | 71.21 | 70.07 | 4300 |
| 7 | 825 | 6220 | 86.39 | 72.00 | 5800 |
| Inlet Velocity | Load 34.9 Ω | Load 4.7 Ω | ||
|---|---|---|---|---|
| Vel. (m/s) | RPM | Power (W) | RPM | Power (W) |
| 1 | 0 | 41 | 0 | 0 |
| 2 | 180 | 350 | 0 | 0 |
| 3 | 280 | 990 | 100 | 760 |
| 4 | 425 | 1990 | 200 | 2500 |
| 5 | 550 | 3200 | 350 | 5820 |
| 6 | 680 | 4610 | 550 | 9200 |
| 7 | 825 | 6000 | 710 | 12,000 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Halder, P.; Takebe, H.; Pawitan, K.; Fujita, J.; Misumi, S.; Shintake, T. Turbine Characteristics of Wave Energy Conversion Device for Extraction Power Using Breaking Waves. Energies 2020, 13, 966. https://doi.org/10.3390/en13040966
Halder P, Takebe H, Pawitan K, Fujita J, Misumi S, Shintake T. Turbine Characteristics of Wave Energy Conversion Device for Extraction Power Using Breaking Waves. Energies. 2020; 13(4):966. https://doi.org/10.3390/en13040966
Chicago/Turabian StyleHalder, Paresh, Hideki Takebe, Krisna Pawitan, Jun Fujita, Shuji Misumi, and Tsumoru Shintake. 2020. "Turbine Characteristics of Wave Energy Conversion Device for Extraction Power Using Breaking Waves" Energies 13, no. 4: 966. https://doi.org/10.3390/en13040966
APA StyleHalder, P., Takebe, H., Pawitan, K., Fujita, J., Misumi, S., & Shintake, T. (2020). Turbine Characteristics of Wave Energy Conversion Device for Extraction Power Using Breaking Waves. Energies, 13(4), 966. https://doi.org/10.3390/en13040966





