The Performance of the BTB-VSC for Active Power Balancing, Reactive Power Compensation and Current Harmonic Filtering in the Interconnected Systems
Abstract
1. Introduction
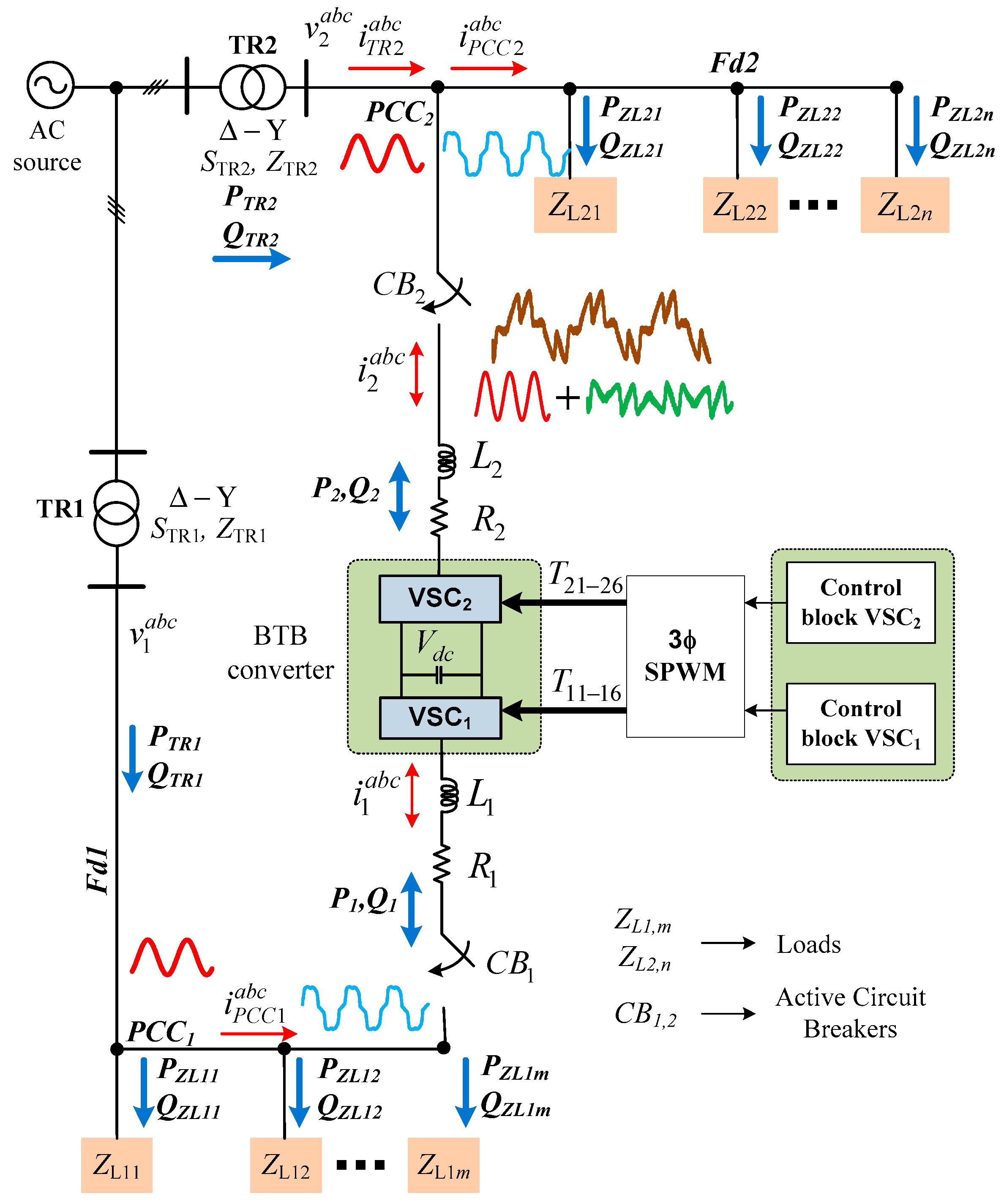
2. System Description and Analysis
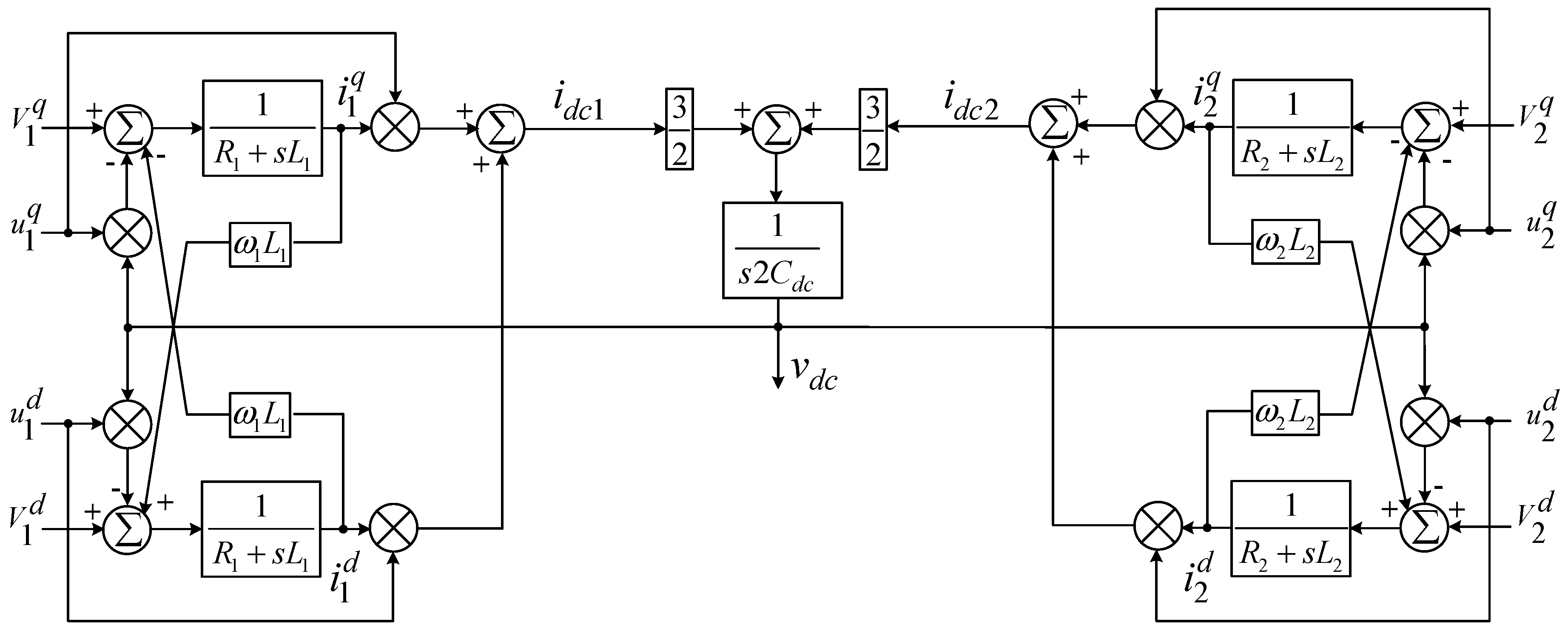
2.1. Modeling of the BTB-VSC Converter
2.2. PQ Operating Modes
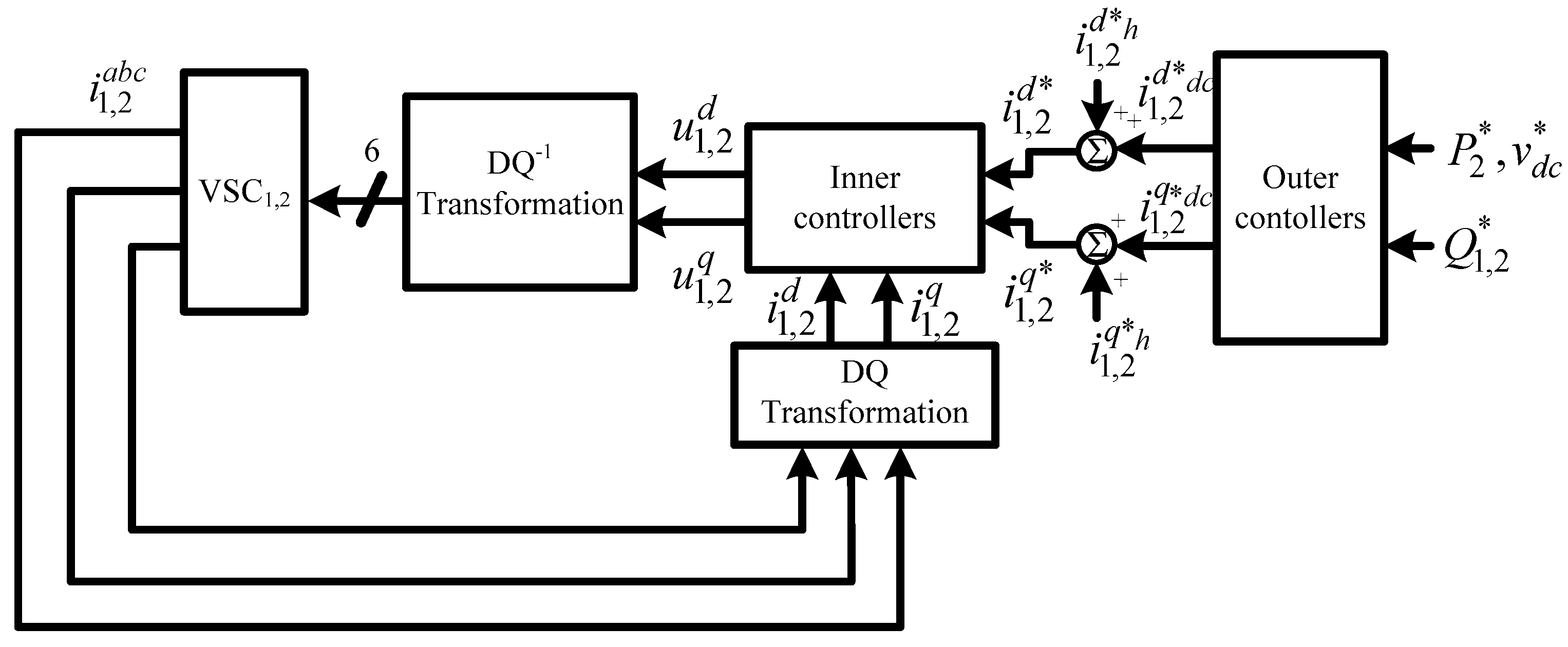
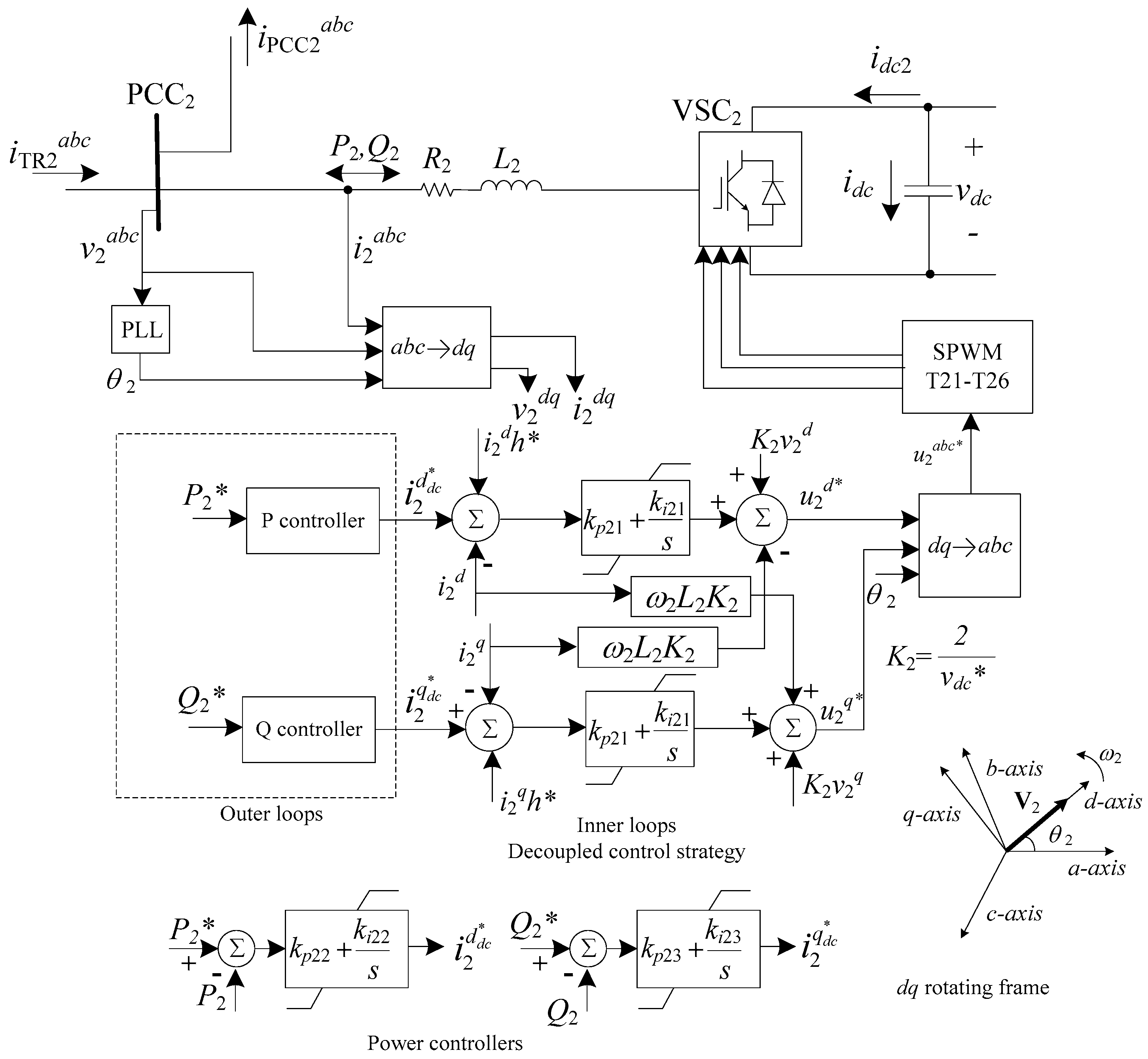
3. Control Strategy
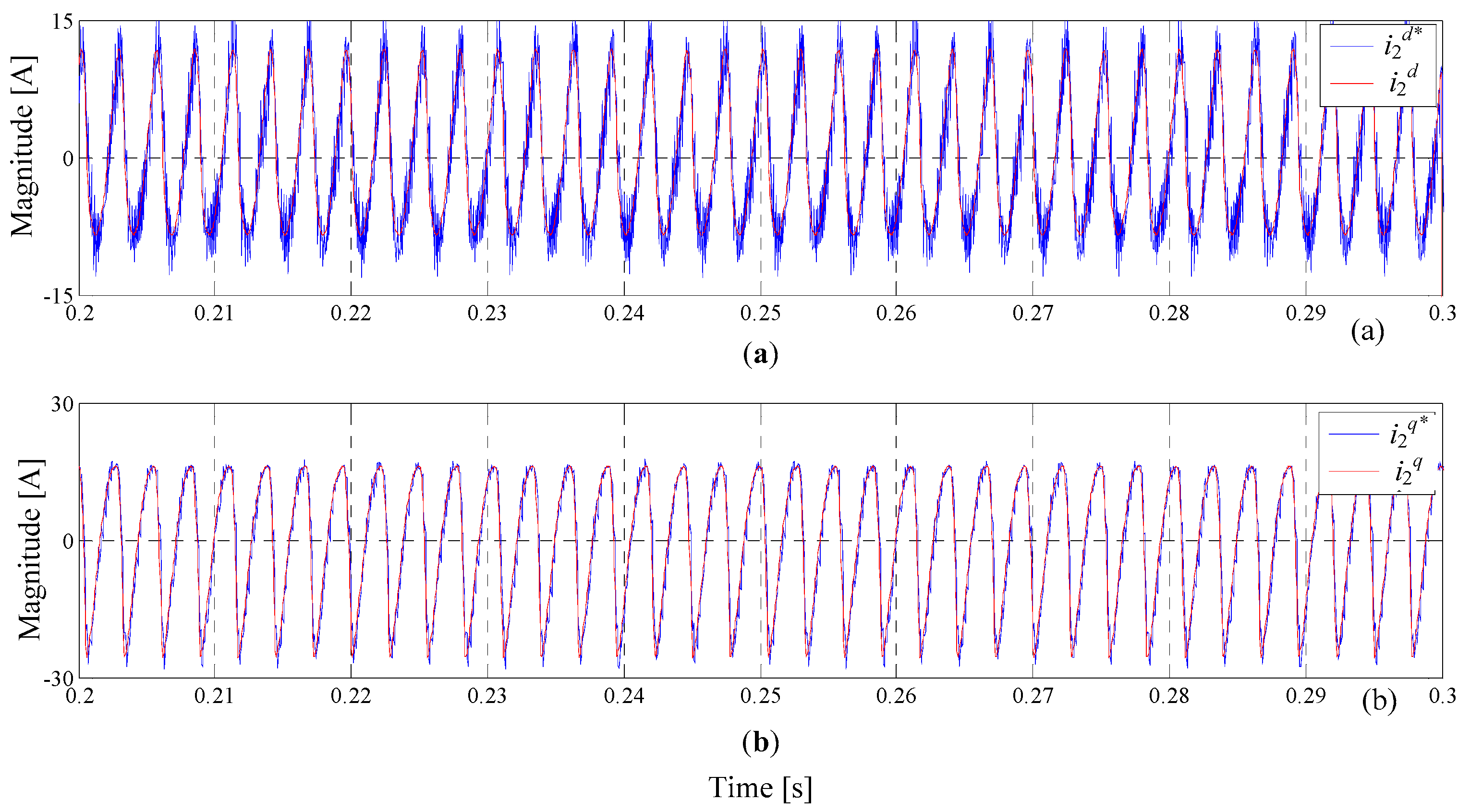
3.1. Controllers Design
3.2. Simulation Results
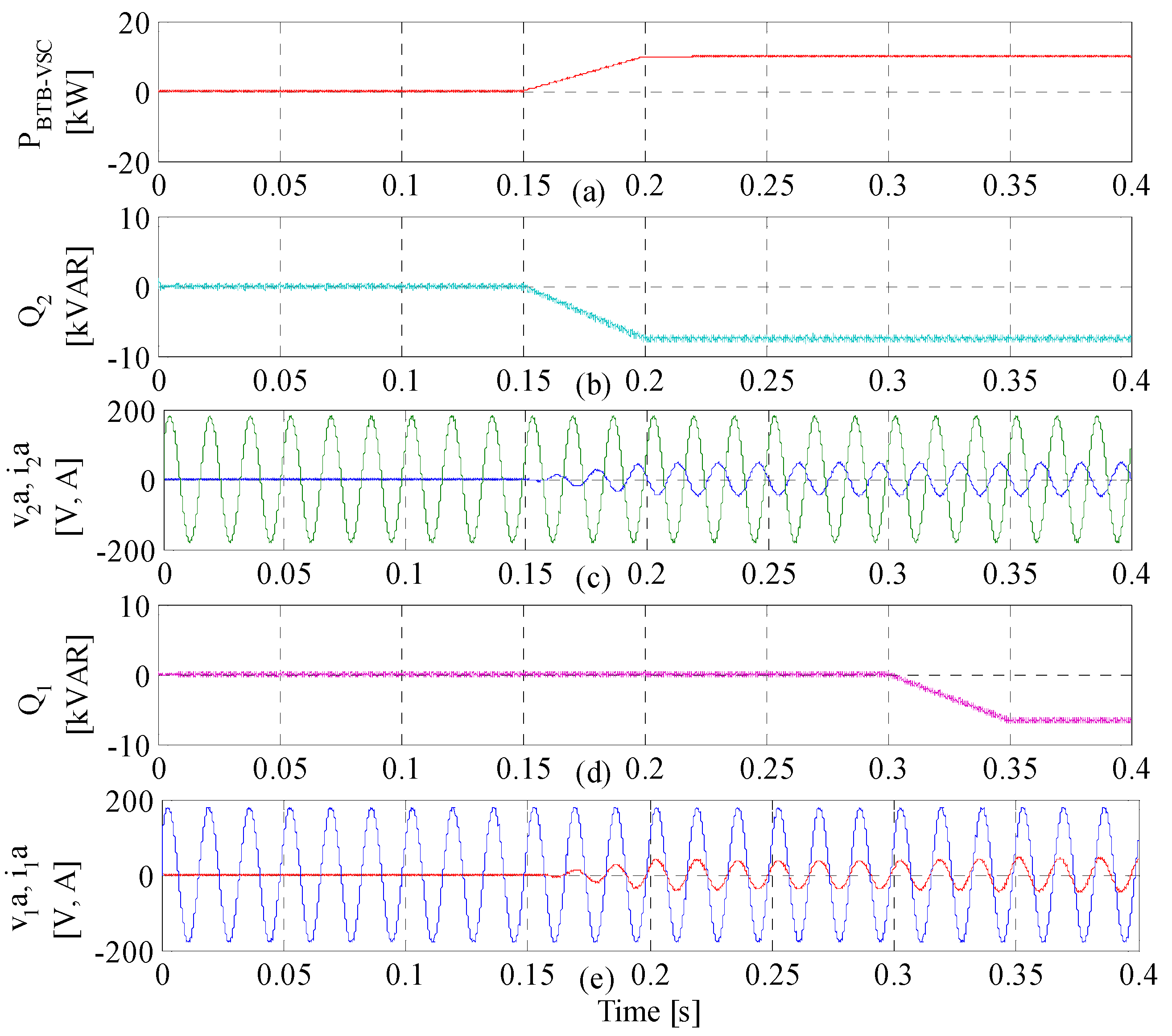
3.2.1. Case 8: Active Power Regulation and Reactive Power Compensation
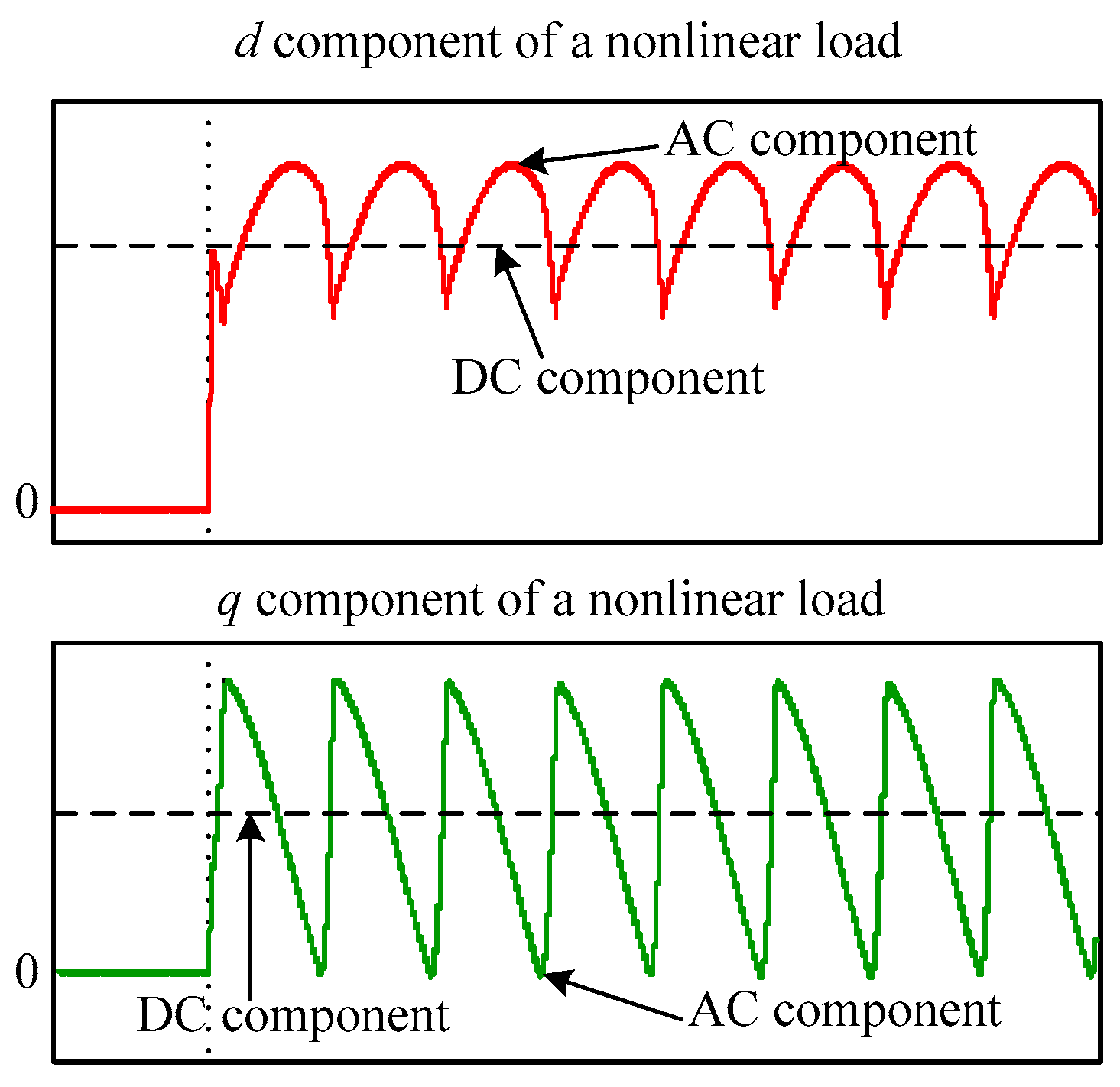
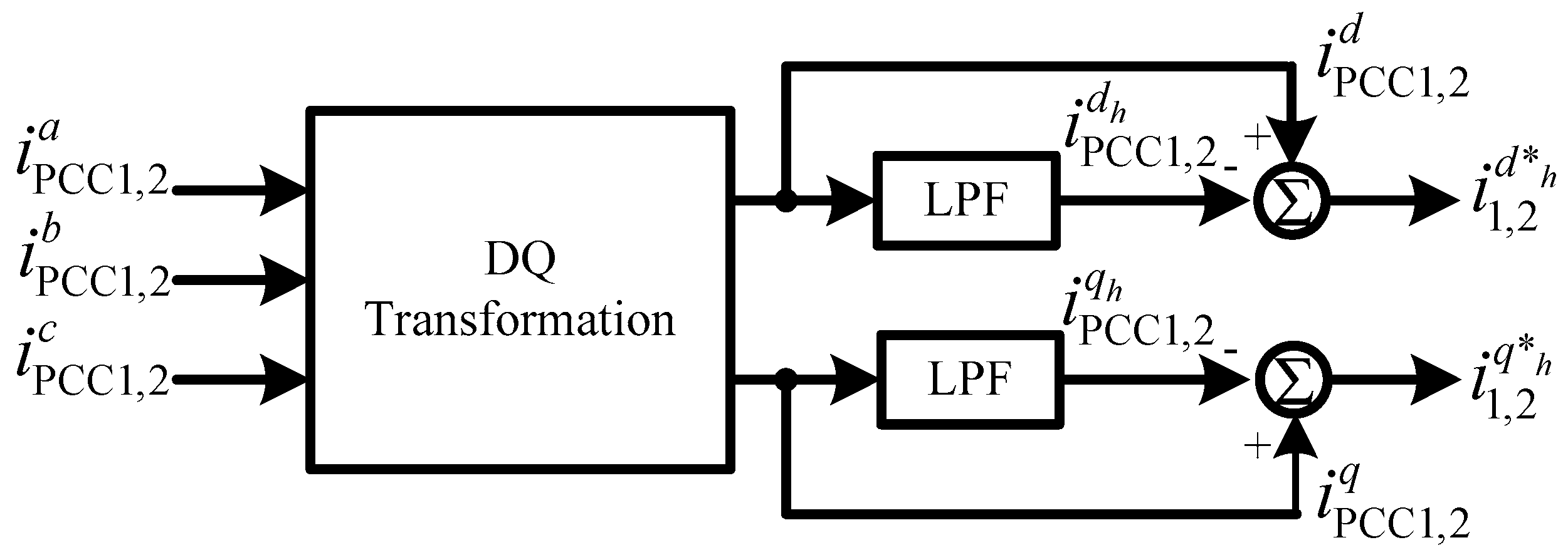
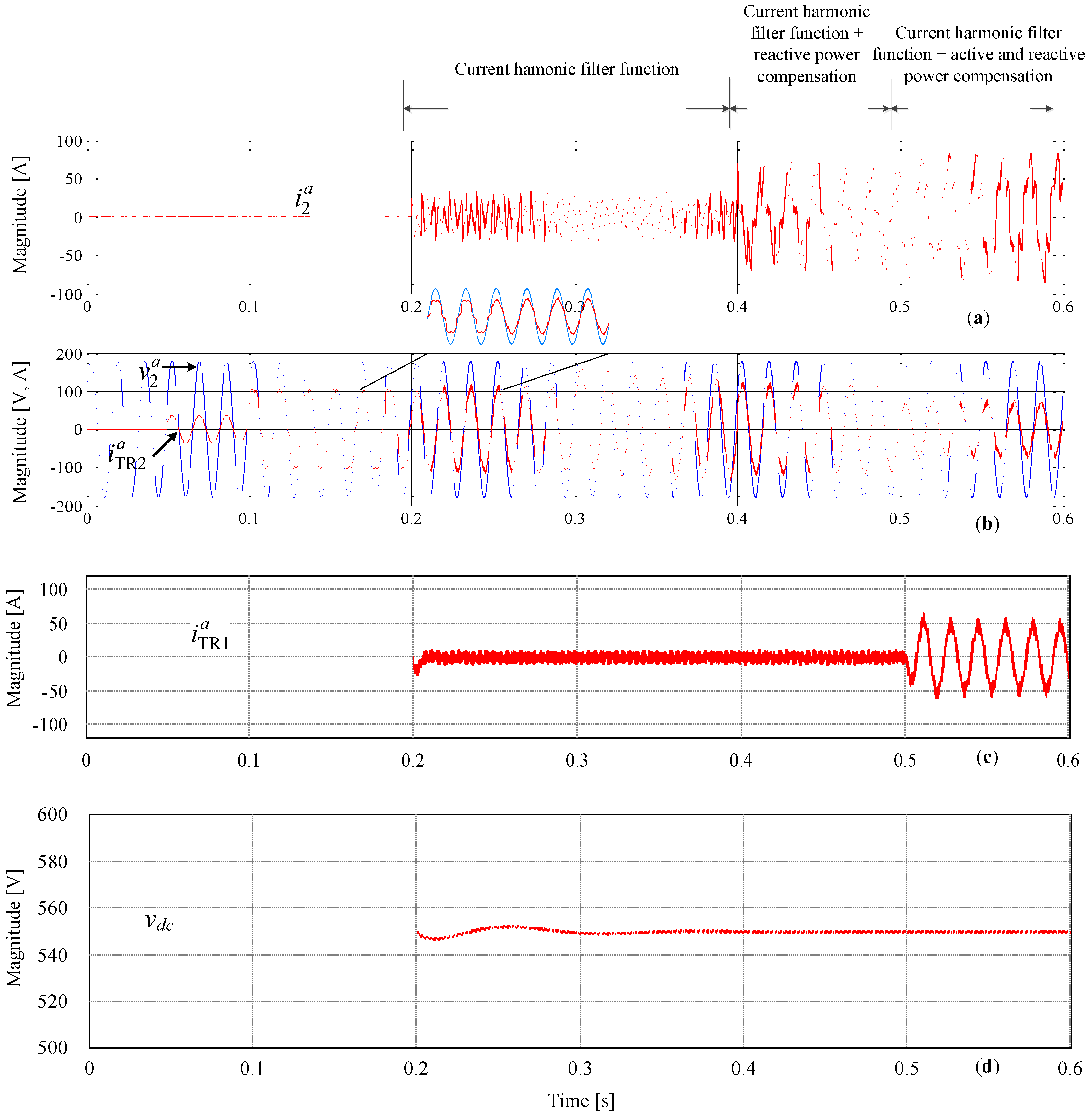
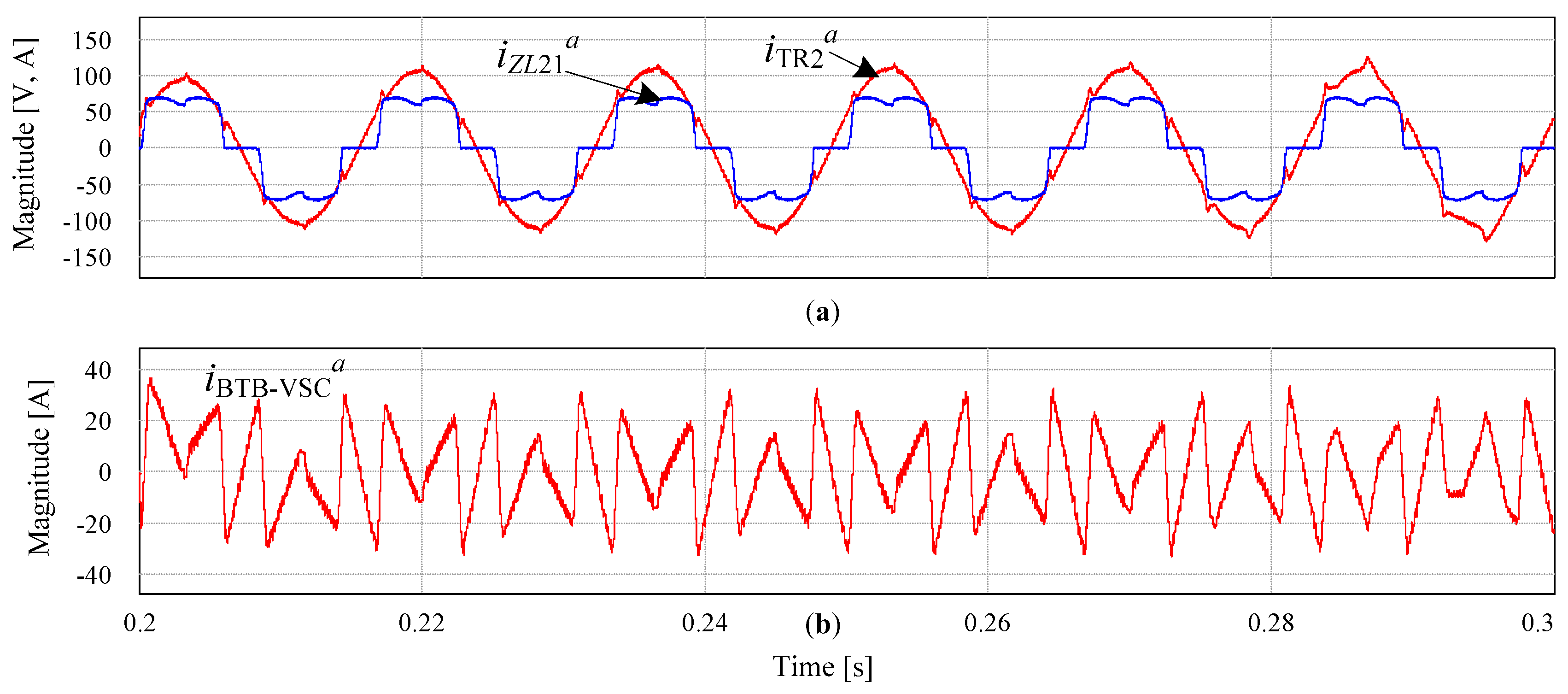
3.2.2. Active Filter Performance
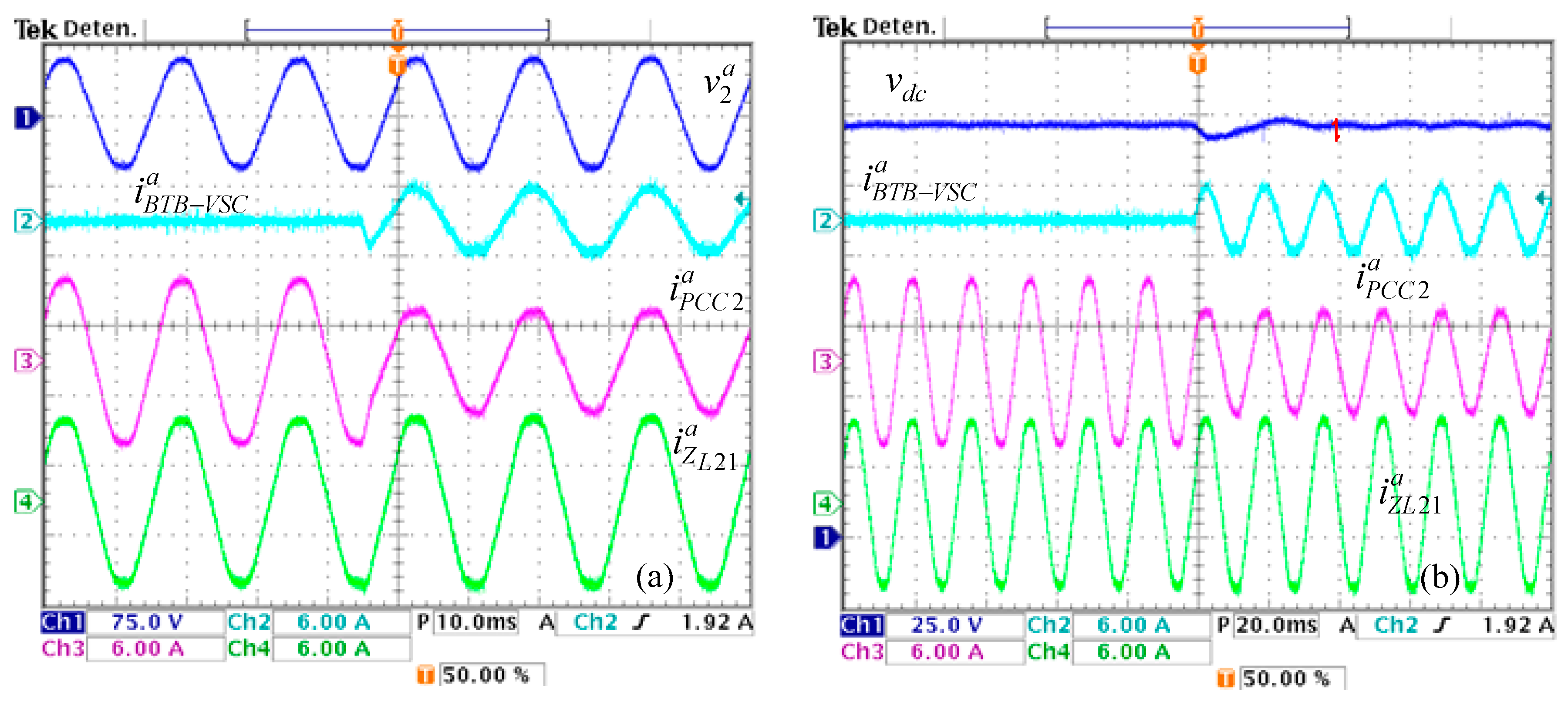
4. Experimental Results
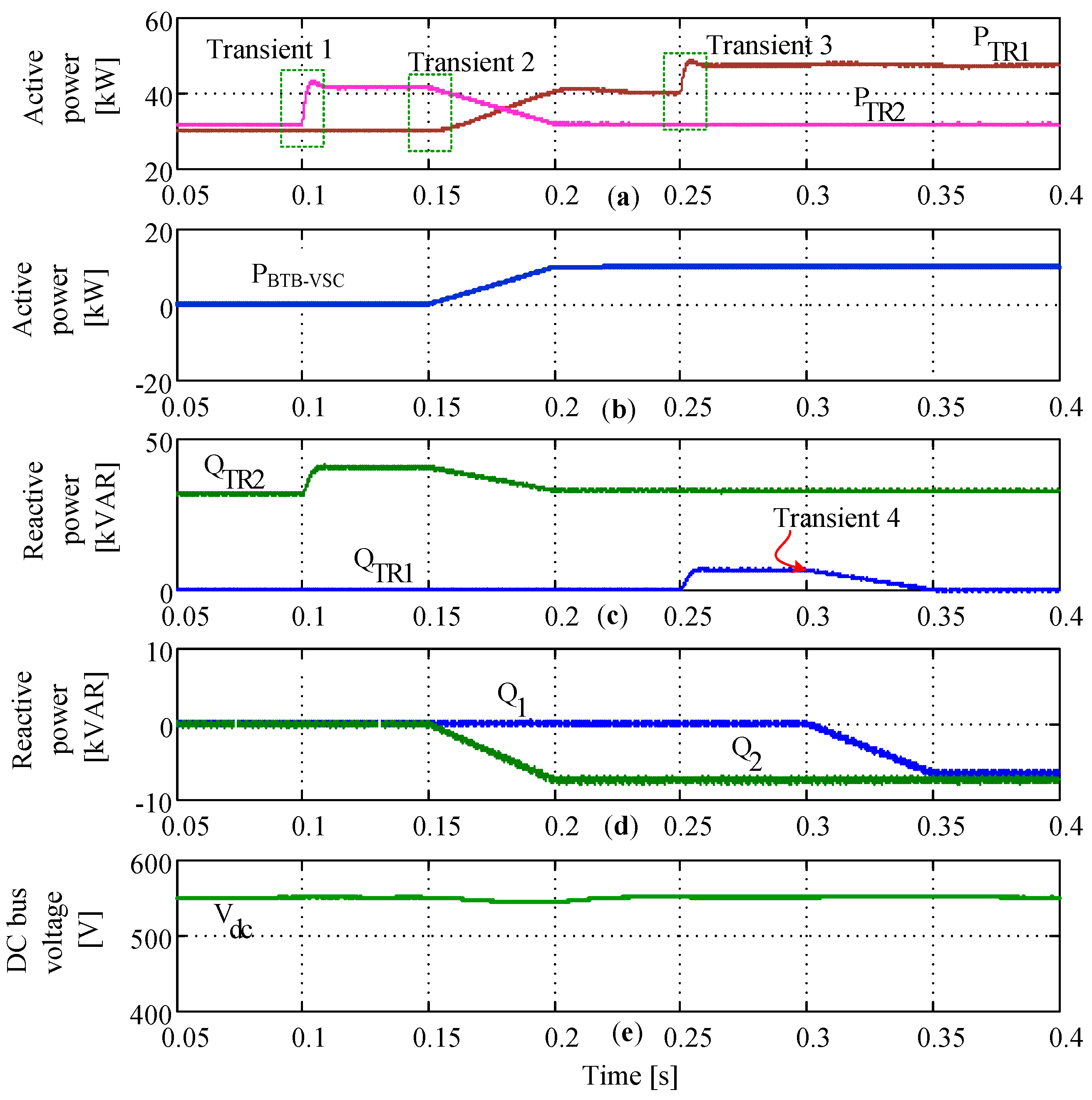
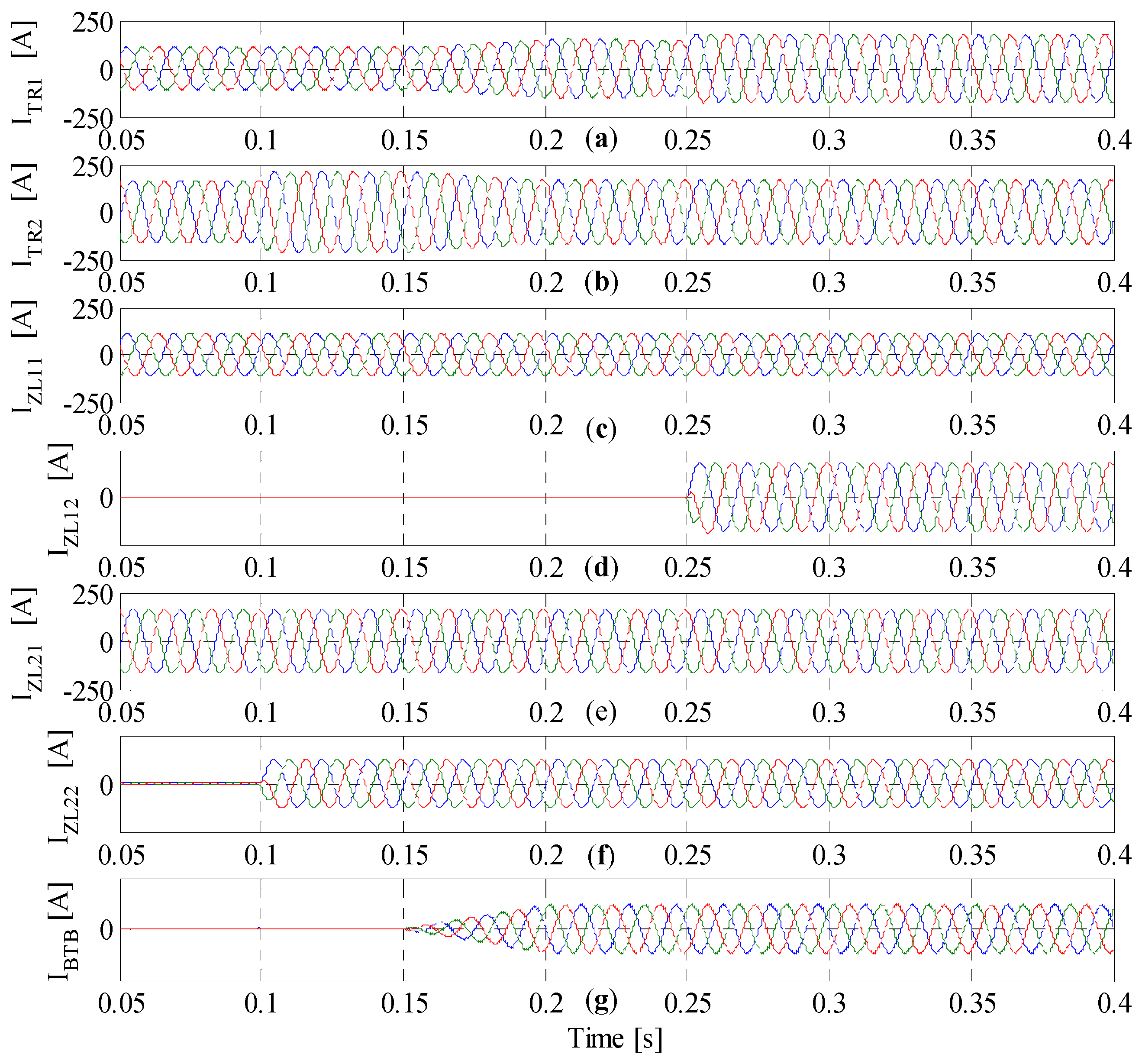
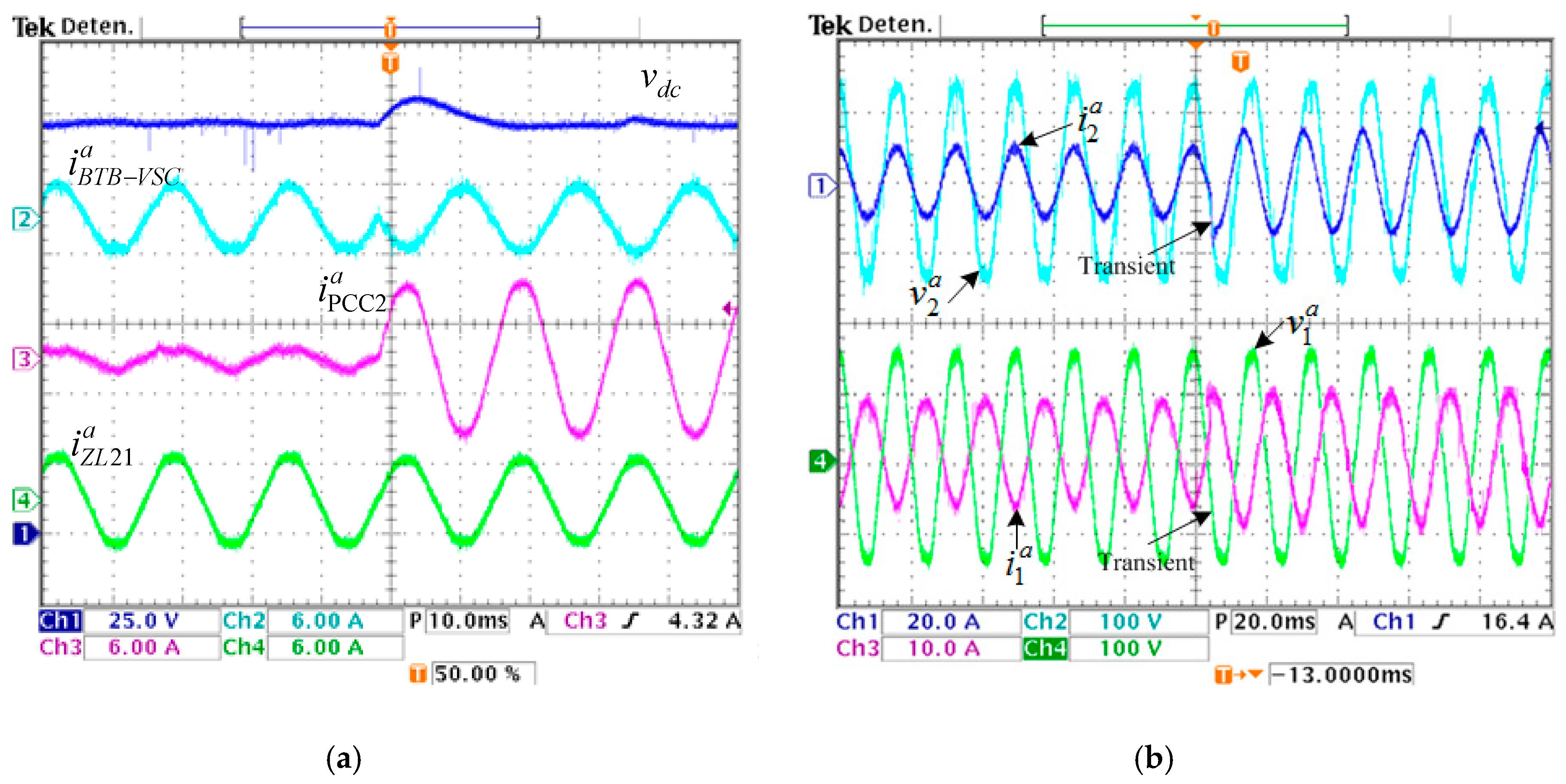
4.1. Active Power Regulation and Reactive Power Compensation
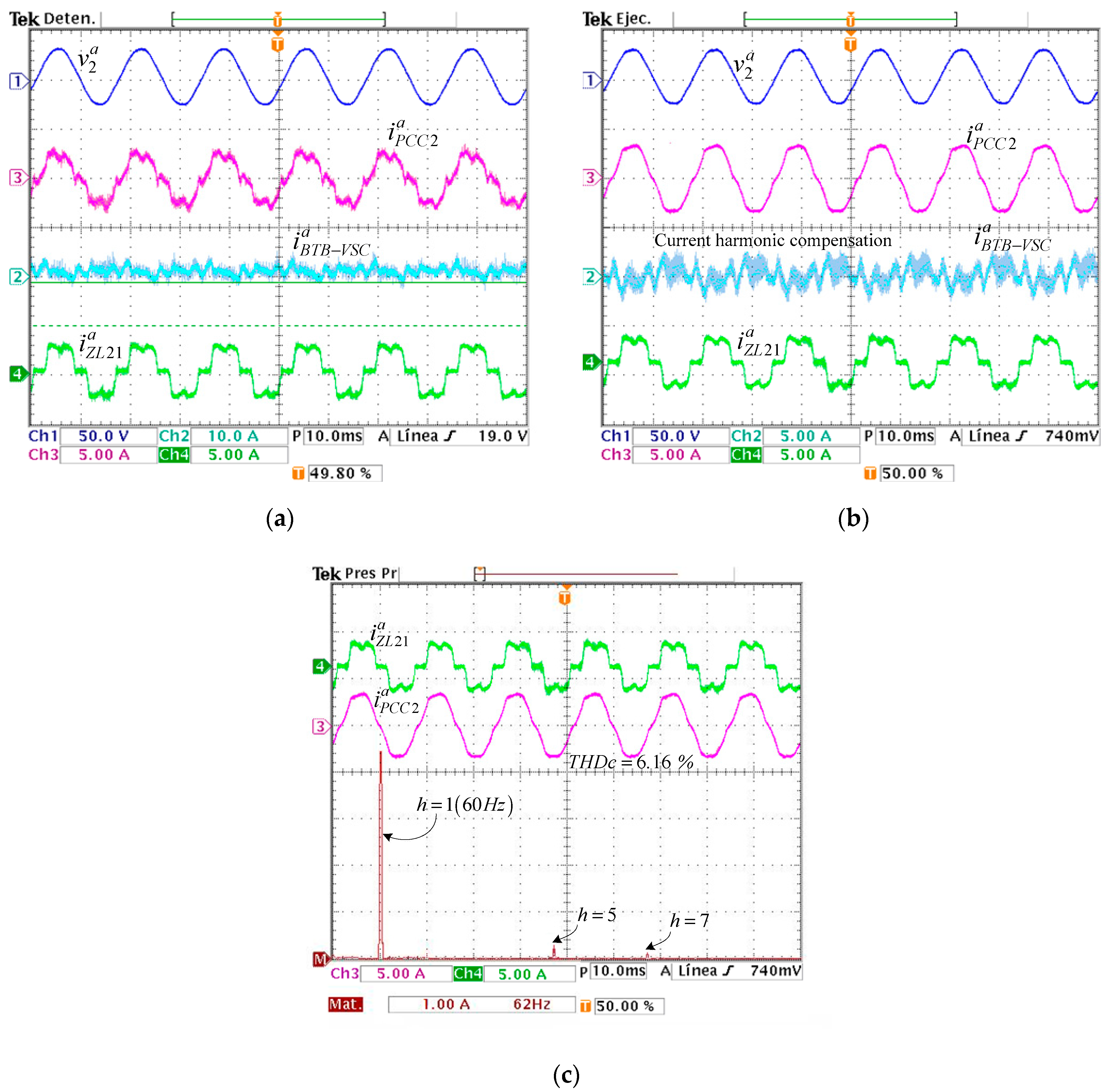
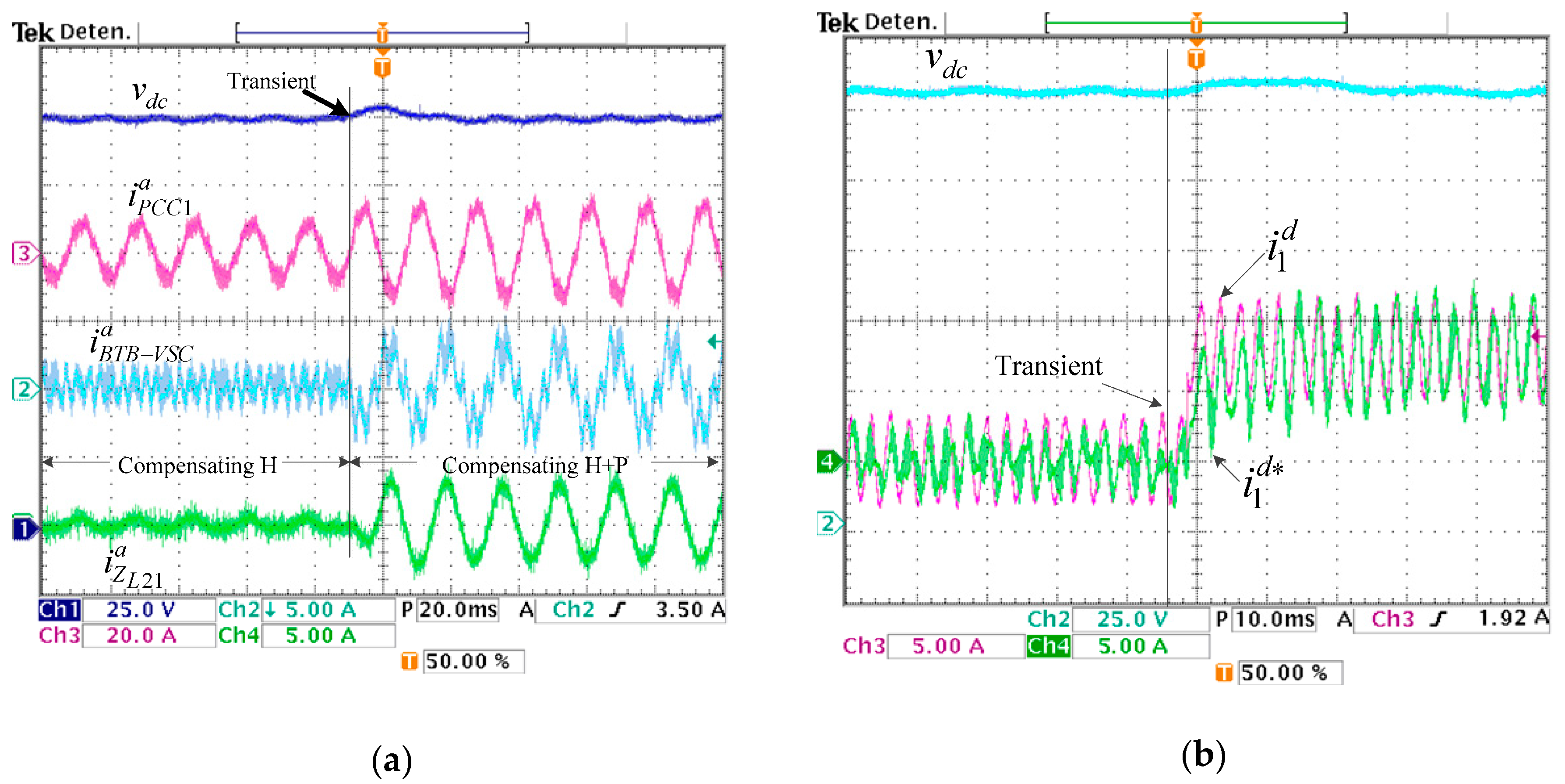
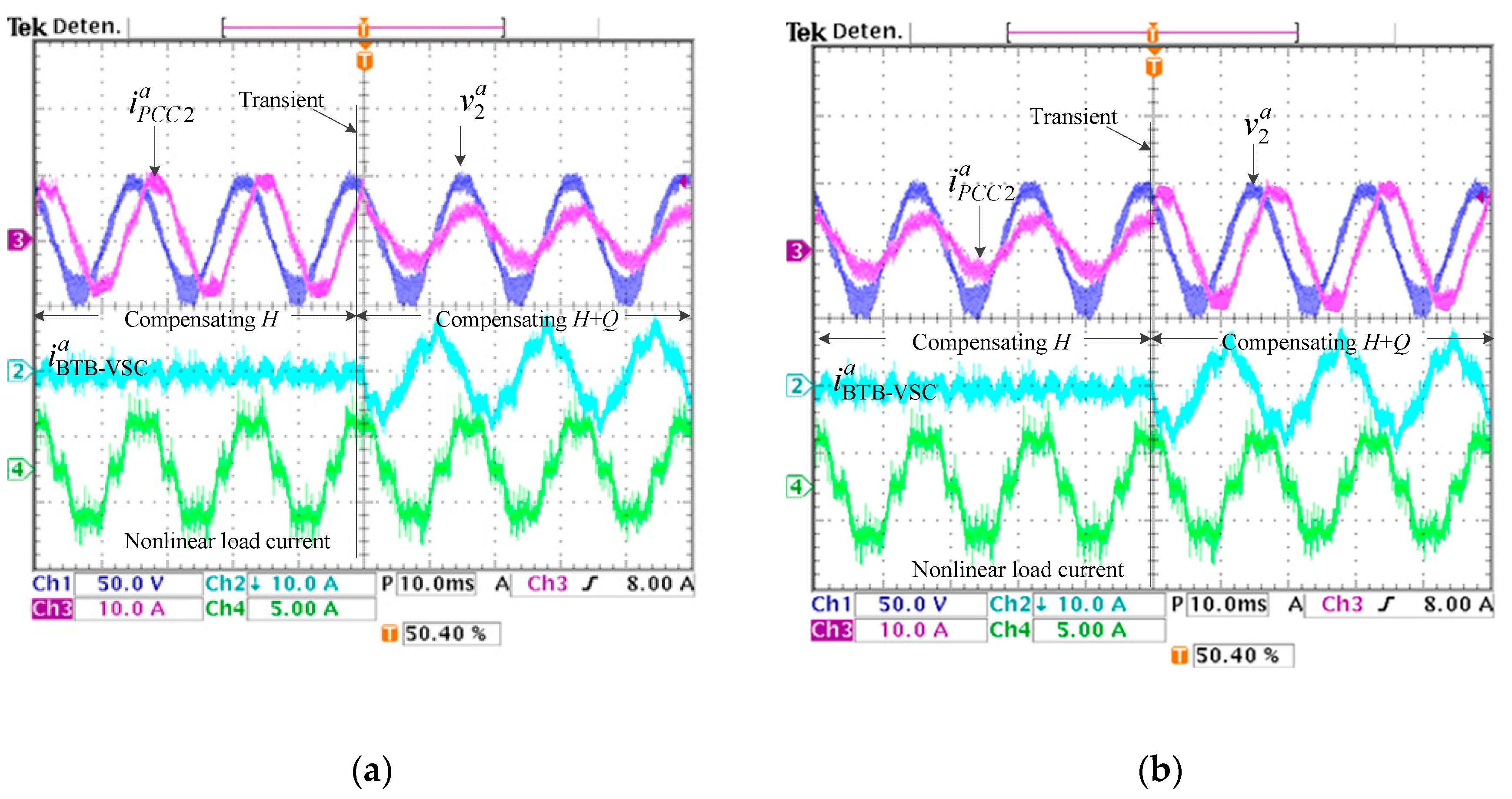
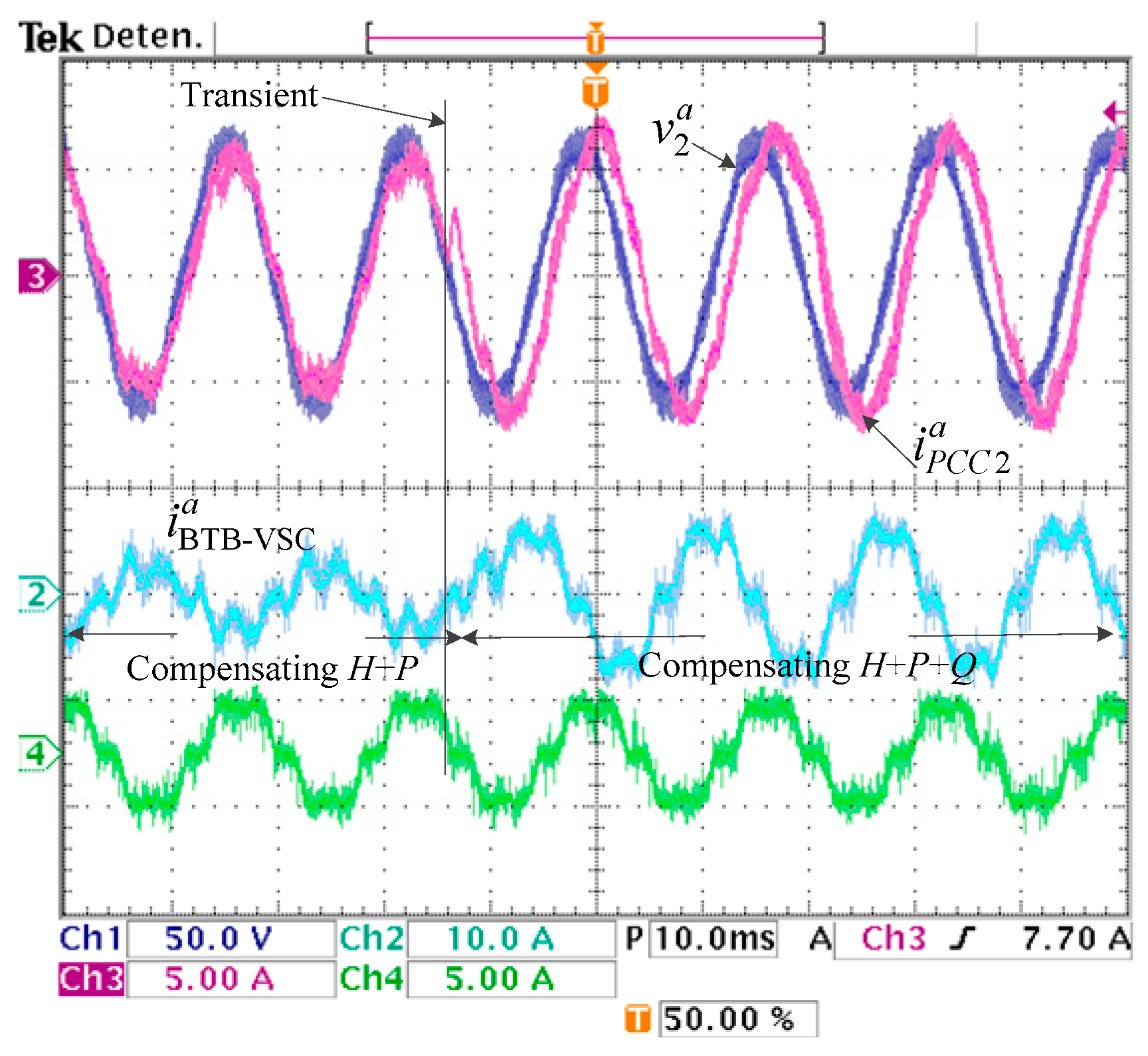
4.2. Active Power and Reactive Power Regulation and Current Harmonic Compensation
5. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Siwakoti, Y.P.; Forouzesh, M.; Pham, N.H. Power Electronics Converters—An Overview. In Control of Power Electronic Converters and Systems, 1st ed.; Blaabjerg, F., Ed.; Academic Press: Cambridge, MA, USA, 2018; Volume 1, pp. 3–29. [Google Scholar] [CrossRef]
- Kolar, J.W.; Friedli, T.; Krismer, F.; Round, S.D. The essence of three-phase AC/AC converter systems. In Proceedings of the 2008 13th International Power Electronics and Motion Control Conference, Poznan, Poland, 1–3 September 2008; pp. 27–42. [Google Scholar] [CrossRef]
- Guidong, Z.; Zhong, L.; Bo, Z.; Wolfgang, H. Power electronics converters: Past, present and future. Renew. Sustain. Energy Rev. 2018, 81, 2028–2044. [Google Scholar] [CrossRef]
- Yaramasu, V.; Wu, B.; Sen, P.C.; Kouro, S.; Narimani, M. High-power wind energy conversion systems: State-of-the-art and emerging technologies. Proc. IEEE 2015, 103, 740–788. [Google Scholar] [CrossRef]
- Alcalá, J.; Cárdenas, V.; Espinoza, J.; Durán, M. Investigation on the limitation of the BTB-VSC converter to control the active and reactive power flow. Electr. Power Syst. Res. 2017, 143, 149–162. [Google Scholar] [CrossRef]
- Ni, K.; Hu, Y.; Lagos, D.T.; Chen, G.; Wang, Z.; Li, X. Highly Reliable Back-to-Back Power Converter without Redundant Bridge Arm for Doubly Fed Induction Generator-Based Wind Turbine. IEEE Trans. Ind. Appl. 2019, 55, 3024–3036. [Google Scholar] [CrossRef]
- Zeng, L.; Yao, W.; Zeng, Q.; Li, D.; Fang, J.; Ai, X.; Wen, J.; He, H. Design and real-time implementation of data-driven adaptive wide-area damping controller for back-to-back VSC-HVDC. Int. J. Electr. Power Energy Syst. 2019, 109, 558–574. [Google Scholar] [CrossRef]
- Spagnuolo, G.; Petrone, G.; Araujo, S.V.; Cecati, C.; Friis-Madsen, E.; Gubia, E.; Hissel, E.; Jasinski, M.; Knapp, W.; Liserre, M.; et al. Renewable Energy Operation and Conversion Schemes: A Summary of Discussions during the Seminar on Renewable Energy Systems. IEEE Ind. Electron. Mag. 2010, 4, 38–51. [Google Scholar] [CrossRef]
- Khorasani, P.G.; Joorabian, M.; Seifossadat, S.G. Smart grid realization with introducing unified power quality conditioner integrated with DC microgrid. Electr. Power Syst. Res. 2017, 151, 68–85. [Google Scholar] [CrossRef]
- Senthilkumar, A.; Raj, P.A. ANFIS and MRAS-PI controllers based adaptive-UPQC for power quality enhancement application. Electr. Power Syst. Res. 2015, 126, 1–11. [Google Scholar] [CrossRef]
- Lee, K.B.; Shin, H.U.; Bak, Y. Basic Control of AC Motor Drives. In Control of Power Electronic Converters and Systems; Blaagjerg, F., Ed.; Academic Press: Cambridge, MA, USA, 2018; Volume 1, pp. 301–329. [Google Scholar] [CrossRef]
- Park, H.S.; Heo, H.J.; Choi, B.S.; Kim, K.C.; Kim, J.M. Speed control for turbine-generator of ORC power generation system and experimental implementation. Energies 2019, 12, 200. [Google Scholar] [CrossRef]
- Hertem, D.V.; Gomis-Bellmunt, O.; Liang, J. HVDC technology overview. In HVDC Grids: For Offshore and Supergrid of the Future; Academic Press: Cambridge, MA, USA, 2016; pp. 47–76. [Google Scholar]
- Nguyen, Q.; Todeschini, G.; Santoso, S. Power Flow in a Multi-Frequency HVac and HVdc System: Formulation, Solution, and Validation. IEEE Trans. Power Syst. 2019, 34, 2487–2497. [Google Scholar] [CrossRef]
- Zeng, L.; Li, D.; Yao, W.; Sun, J.; Wen, J. Dual-loop SFC scheme for BTB-VSC-HVDC interconnecting asynchronous AC grids. J. Eng. 2019, 3, 1020–1026. [Google Scholar] [CrossRef]
- Cai, D.; Zhou, K.; Wang, W.; Liu, H.; Cao, K.; Wang, Y. Influence of back-to-back VSC-HVDC project on the operation characteristics of Hubei power grid. J. Eng. 2017, 801–805. [Google Scholar] [CrossRef]
- Abdelsalam, I.; Adam, G.P.; Williams, B.W. Current source back-to-back converter for wind energy conversion systems. IET Renew. Power Gener. 2016, 10, 1552–1561. [Google Scholar] [CrossRef]
- Nami, A.; Rodríguez Amenedo, J.L.; Arnaltes Gómez, S.; Cardiel Álvarez, M.A. Active Power Filtering Embedded in the Frequency Control of on Offshore Wind Farm Connected to a Diode-Rectifier-Based HVDC Link. Energies 2018, 11, 2718. [Google Scholar] [CrossRef]
- Agheb, E.; Holtsmark, N.; Hoidalen, H.K.; Molinas, M. High frequency wind energy conversion system for offshore DC collection grid—Part I: Comparative loss evaluation. Sustain. Energy Grids Netw. 2016, 5, 167–176. [Google Scholar] [CrossRef]
- López, I.; Andreu, J.; Ceballos, S.; de Alegría, I.M.; Kortabarria, I. Review of wave energy technologies and the necessary power-equipment. Renew. Sustain. Energy Rev. 2013, 25, 413–434. [Google Scholar] [CrossRef]
- Kumar, D.; Zare, F. A Comprehensive Review of Maritime Microgrids: System Architectures, Energy Efficiency, Power Quality, and Regulations. IEEE Access 2019, 7, 67249–67277. [Google Scholar] [CrossRef]
- Müller, N.; Kouro, S.; Malinowski, M.; Rojas, C.A.; Jasinski, M.; Estay, G. Medium-Voltage Power Converter Interface for Multigenerator Marine Energy Conversion Systems. IEEE Trans. Ind. Electron. 2017, 64, 1061–1070. [Google Scholar] [CrossRef]
- Singh, B.; Saha, R.; Chandra, A.; Al-Haddad, K. Static synchronous compensators (STATCOM): A review. IET Power Electron. 2009, 2, 297–324. [Google Scholar] [CrossRef]
- Mete, A.; Çağatay, K. Power flow modeling of Back-to-Back STATCOM: Comprehensive simulation studies including PV curves and PQ circles. Ain Shams Eng. J. 2017, 8, 431–443. [Google Scholar] [CrossRef]
- Baimel, D. Implementation of DQ0 control methods in high power electronics devices for renewable energy sources, energy storage and FACTS. Sustain. Energy Grids Netw. 2019, 18. [Google Scholar] [CrossRef]
- Shu, Z.; Xie, S.; Li, Q. Single-Phase Back-To-Back Converter for Active Power Balancing, Reactive Power Compensation, and Harmonic Filtering in Traction Power System. IEEE Trans. Power Electron. 2011, 26, 334–343. [Google Scholar] [CrossRef]
- Naidu, N.K.S.; Singh, B. Doubly Fed Induction Generator for Wind Energy Conversion Systems with Integrated Active Filter Capabilities. IEEE Trans. Ind. Inform. 2015, 11, 923–933. [Google Scholar] [CrossRef]
- 519-2014—IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems—Redline. 2014. Available online: http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=7047985&isnumber=7047984 (accessed on 13 February 2020).
- Zhang, Z.; Xie, B.; Hu, S.; Li, Y.; Luo, L.; Rehtanz, C.; Krause, O. Reactive Power Compensation and Negative-Sequence Current Suppression System for Electrical Railways with YNvd-Connected Balance Transformer—Part I: Theoretical Analysis. IEEE Trans. Power Electron. 2018, 33, 272–282. [Google Scholar] [CrossRef]
- Zhengyou, H.; Zheng, Z.; Haitao, H. Power quality in high-speed railway systems. Int. J. Rail Transp. 2016, 4, 71–97. [Google Scholar] [CrossRef]
- Kissling, S.; Talon, E.; Biya-Motto, F.; Essimbi, B.; Carpita, M. Control of a Three-Phase to Single Phase Back-to-Back Converter for Electrical Resistance Seam Welding Systems. Energies 2017, 10, 133. [Google Scholar] [CrossRef]
- Zargari, N.R.; Joos, G. Performance investigation of a current-controlled voltage-regulated PWM rectifier in rotating and stationary frames. IEEE Trans. Ind. Electron. 1995, 42, 396–401. [Google Scholar] [CrossRef]
- Abdelhakim, A.; Mattavelli, P.; Boscaino, V.; Lullo, G. Decoupled Control Scheme of Grid-Connected Split-Source Inverters. IEEE Trans. Ind. Electron. 2017, 64, 6202–6211. [Google Scholar] [CrossRef]
- Moran, L.; Dixón, J.; Torres, M. 41-Active Power Filters. In Power Electronics Handbook, 4th ed.; Rashid, M.H., Ed.; Butterworth-Heinemann Elsevier Ltd.: Oxford, UK, 2018; pp. 1341–1379. [Google Scholar] [CrossRef]
- Akagi, H.; Kanazawa, Y.; Nabae, A. Instantaneous Reactive Power Compensators Comprising Switching Devices without Energy Storage Components. IEEE Trans. Ind. Appl. 1984, IA-20, 625–630. [Google Scholar] [CrossRef]
- Khorramabadi, S.S.; Bakhshai, A. Critic-Based Self-Tuning PI Structure for Active and Reactive Power Control of VSCs in Microgrid Systems. IEEE Trans. Smart Grid 2015, 6, 92–103. [Google Scholar] [CrossRef]
- Alcala, J.; Cardenas, V.; Miranda, H.; Perez-Ramirez, J.; Charre, S. A three-phase back to back converter for reactive power compensation, current harmonic filtering and active power compensation. In Proceedings of the Energy Conversion Congress and Exposition (ECCE), Denver, CO, USA, 15–19 September 2013; pp. 2371–2377. [Google Scholar] [CrossRef]
- Yang, W.; Song, Q.; Liu, W. Decoupled Control of Modular Multilevel Converter Based on Intermediate Controllable Voltages. IEEE Trans. Ind. Electron. 2016, 63, 4695–4706. [Google Scholar] [CrossRef]
- Parvez, M.; Elias, M.F.M.; Rahim, N.A.; Osman, N. Current control techniques for three-phase grid interconnection of renewable power generation systems: A review. Sol. Energy 2016, 135, 29–42. [Google Scholar] [CrossRef]
- Meng, X.; Liu, J.; Liu, Z. A Generalized Droop Control for Grid-Supporting Inverter Based on Comparison between Traditional Droop Control and Virtual Synchronous Generator Control. IEEE Trans. Power Electron. 2019, 34, 5416–5438. [Google Scholar] [CrossRef]
- Li, S.; Haskew, T.A.; Swatloski, R.P.; Gathings, W. Optimal and Direct-Current Vector Control of Direct-Driven PMSG Wind Turbines. IEEE Trans. Power Electron. 2012, 27, 2325–2337. [Google Scholar] [CrossRef]
- Ramezani, M.; Li, S.; Sun, Y. Combining droop and direct current vector control for control of parallel inverters in microgrid. IET Renew. Power Gener. 2017, 11, 107–114. [Google Scholar] [CrossRef]
| Case | P | Q1 | Q2 |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 |
| 3 | 0 | 1 | 0 |
| 4 | 0 | 1 | 1 |
| 5 | 1 | 0 | 0 |
| 6 | 1 | 0 | 1 |
| 7 | 1 | 1 | 0 |
| 8 | 1 | 1 | 1 |
| Grid and BTB-VSC Parameters | |||
|---|---|---|---|
| Grid Voltage | 220 Vrms | Vdc | 550 V |
| ω1,2 | 377 rad/s | SBTB-VSC | 30 kVA |
| L1 | 4.1 mH | fsw | 4.86 kHz |
| L2 | 5.3 mH | Cdc | 4700 µF |
| R1 | 30 mΩ | ||
| R2 | 30 mΩ | ||
| Gain | Controller | |||
|---|---|---|---|---|
| vdc | Q1 | P2 | Q2 | |
| kp | 0.514 | 0.010 | 0.010 | 0.010 |
| ki | 102 | −2.9375 | 3.6971 | −2.9375 |
| Harmonic Order | Load [Arms] | BTB-VSC [Arms] | TR2 [Arms] | ||
|---|---|---|---|---|---|
| h | Magnitude | % | Magnitude | Magnitude | % |
| 1 | 52.02 | 100 | 0.01 | 52.01 | 100 |
| 5 | 11.75 | 22.58 | 11.39 | 0.35 | 0.68 |
| 7 | 5.54 | 10.64 | 5.20 | 0.33 | 0.64 |
| 11 | 4.24 | 8.14 | 3.91 | 0.33 | 0.63 |
| 13 | 2.65 | 5.10 | 2.33 | 0.33 | 0.63 |
| 17 | 2.16 | 4.15 | 1.81 | 0.35 | 0.67 |
| 19 | 1.46 | 2.81 | 1.12 | 0.34 | 0.65 |
| THDc | 27.21 | 1.59 | |||
| Grid and BTB-VSC Parameters | |
|---|---|
| V1abc | 127–50 Vrms |
| V2abc | 12–42 Vrms |
| STR1, STR2 | 3 kVA |
| ω1,2 | 377 rad/s |
| L1 | 4.1 mH |
| L2 | 5.3 mH |
| R1 | 284 mΩ |
| R2 | 330 mΩ |
| Vdc | 150 V |
| SBTB-VSC | 3 kVA |
| fsw | 4.81 kHz |
| Cdc | 1050 µF |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alcalá, J.; Cárdenas, V.; Aganza, A.; Gudiño-Lau, J.; Charre, S. The Performance of the BTB-VSC for Active Power Balancing, Reactive Power Compensation and Current Harmonic Filtering in the Interconnected Systems. Energies 2020, 13, 831. https://doi.org/10.3390/en13040831
Alcalá J, Cárdenas V, Aganza A, Gudiño-Lau J, Charre S. The Performance of the BTB-VSC for Active Power Balancing, Reactive Power Compensation and Current Harmonic Filtering in the Interconnected Systems. Energies. 2020; 13(4):831. https://doi.org/10.3390/en13040831
Chicago/Turabian StyleAlcalá, Janeth, Víctor Cárdenas, Alejandro Aganza, Jorge Gudiño-Lau, and Saida Charre. 2020. "The Performance of the BTB-VSC for Active Power Balancing, Reactive Power Compensation and Current Harmonic Filtering in the Interconnected Systems" Energies 13, no. 4: 831. https://doi.org/10.3390/en13040831
APA StyleAlcalá, J., Cárdenas, V., Aganza, A., Gudiño-Lau, J., & Charre, S. (2020). The Performance of the BTB-VSC for Active Power Balancing, Reactive Power Compensation and Current Harmonic Filtering in the Interconnected Systems. Energies, 13(4), 831. https://doi.org/10.3390/en13040831







