A New Lithium-Ion Battery SOH Estimation Method Based on an Indirect Enhanced Health Indicator and Support Vector Regression in PHMs
Abstract
1. Introduction
- (1)
- Dynamic health indicators are extracted from the charging curves. The SOH prediction accuracy is regarded as the fitness of the evolution algorithm. Differential evolution algorithms are used to obtain the weights of the health indicators, and health indicators and their weights are combined to form an enhanced health indicator for the estimation of battery SOH.
- (2)
- A DE algorithm is used to form an enhanced health indicator (HI) and hyperparameters in an improved SVR method. The article also analyzes the improvement in the prediction accuracy of the enhanced health indicator compared to the original health indicators.
2. Related Works
2.1. Description of the SVR Model
2.2. Description of the DE Algorithm
3. New Health Indicator for SOH Estimation
3.1. Definition of SOH
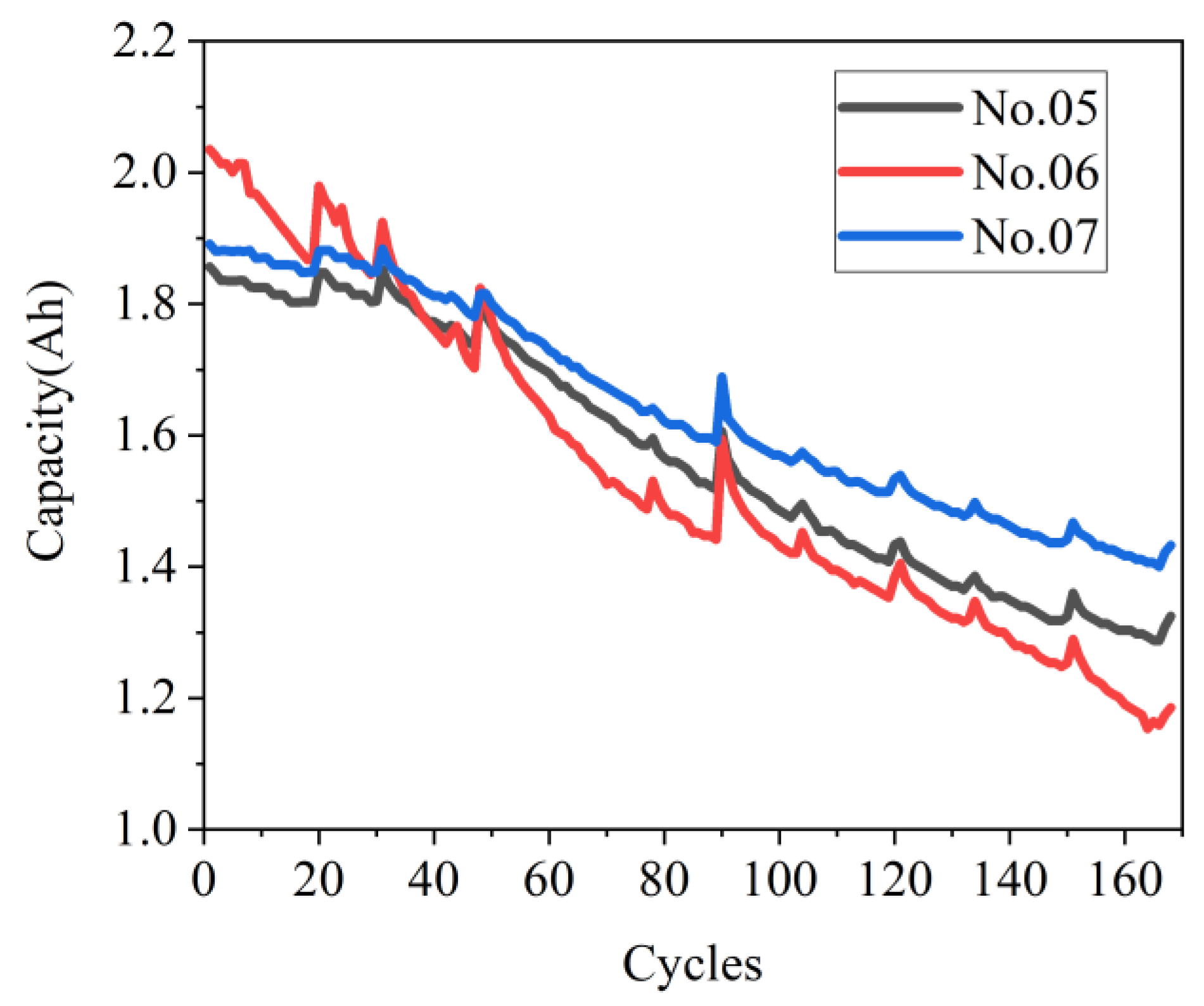
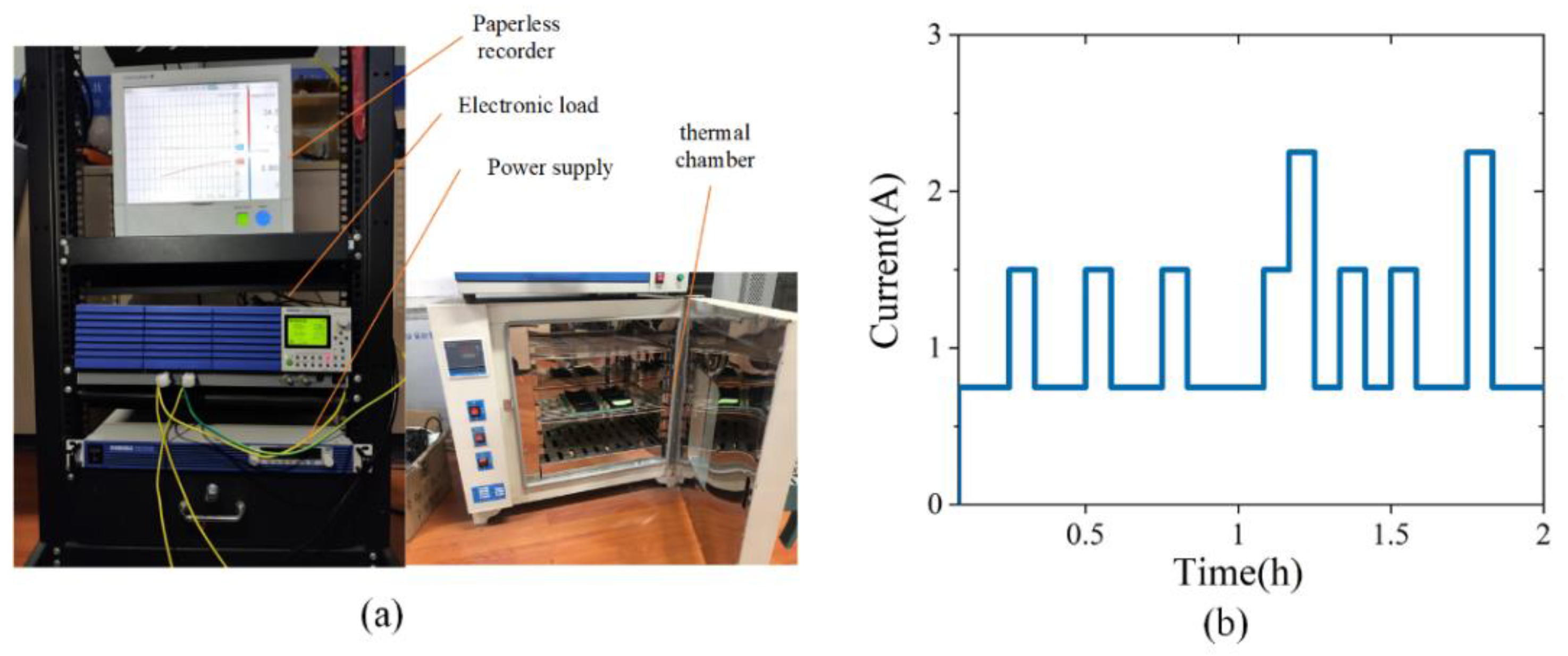
3.2. Experiment Data Analysis
3.3. Electrochemical Reaction Analysis and Features Extraction
- (1)
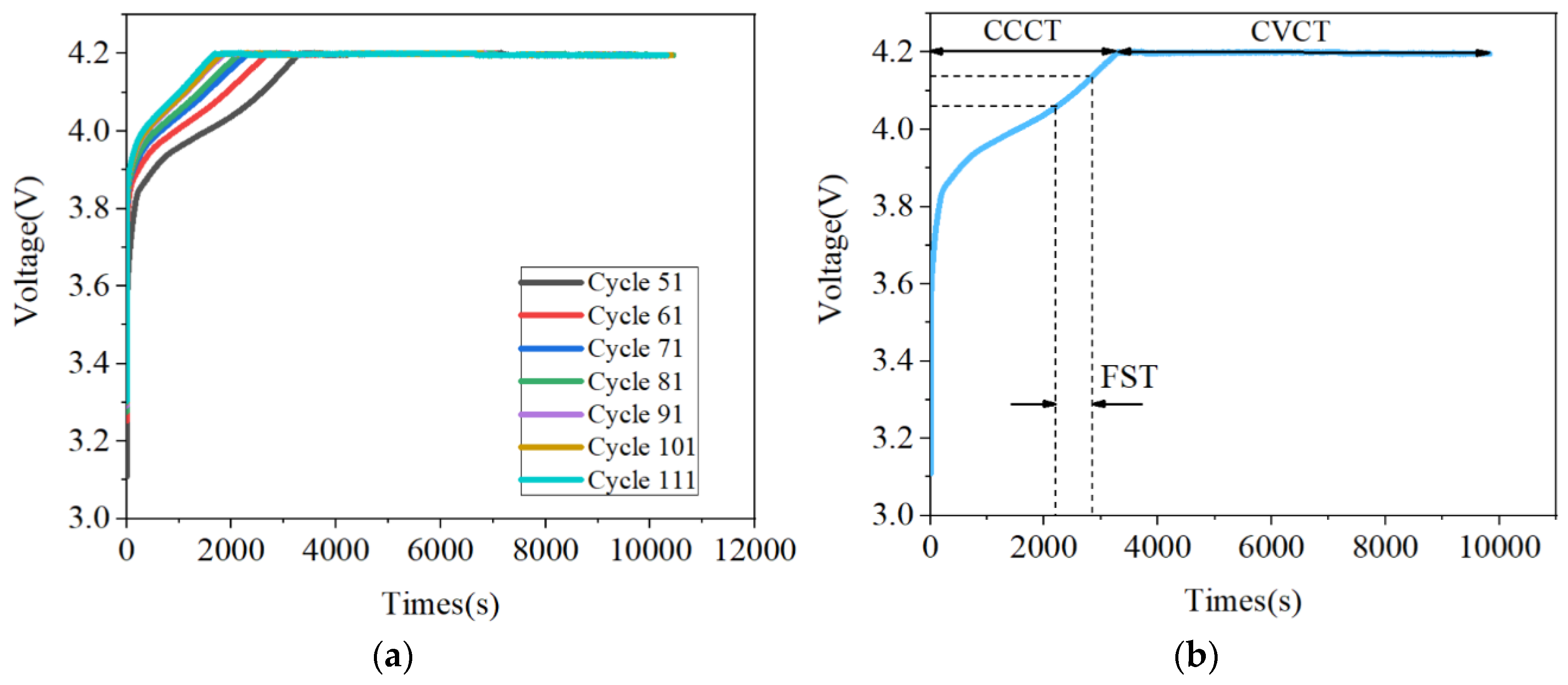
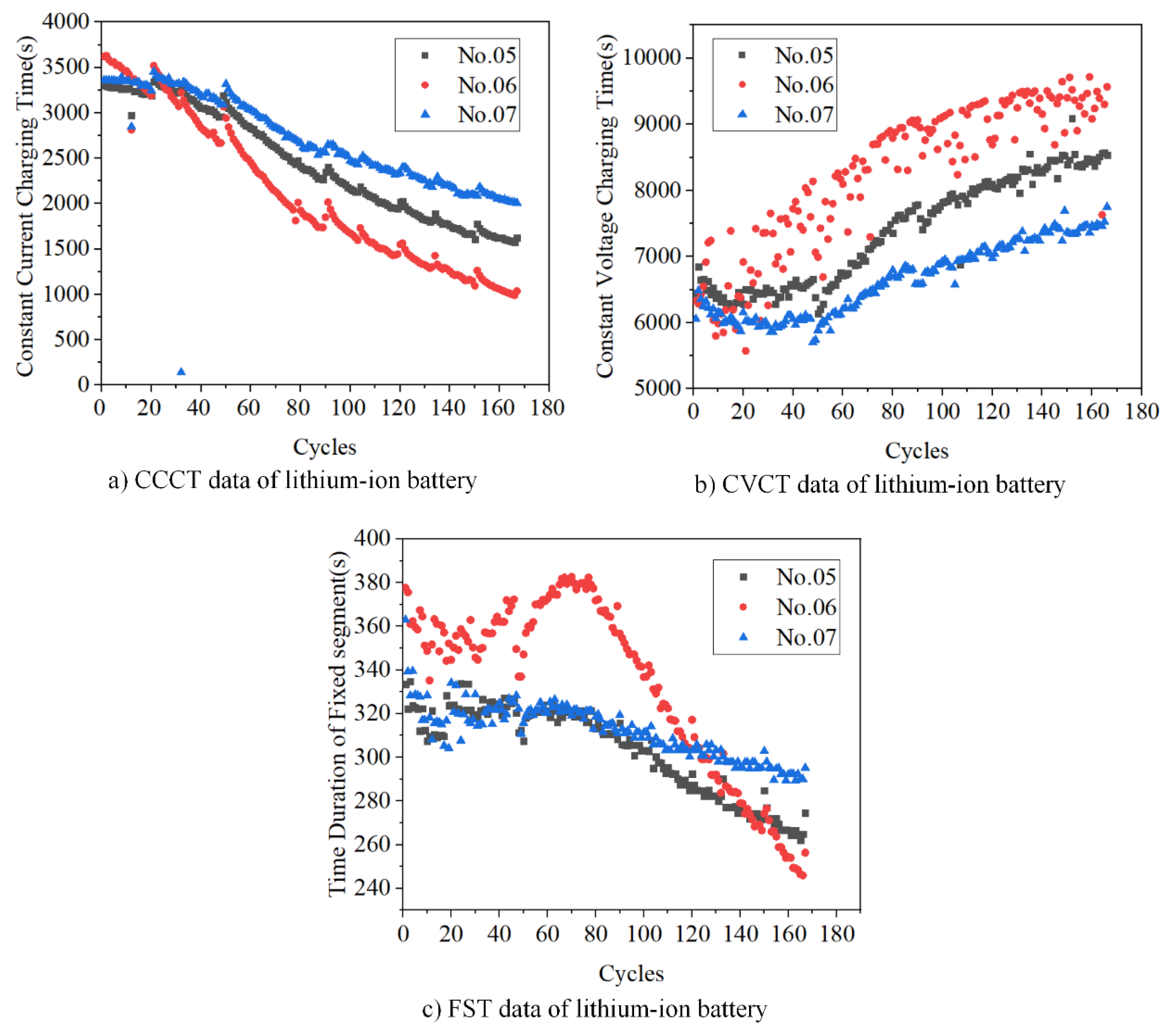
- CCCT: This is the time duration of the CC mode, namely, the amount of time for which the battery is polarized. According to the charging curves of batteries, the CCCT decreases as the cycle life increases.
- (2)
- CVCT: CV mode plays a role in eliminating polarization during the battery charging process. According to Figure 3b, the jitter of the CVCT curve of battery 06 is severe. According to the experimental results, its root means square error (RMSE) is indeed larger than those of the other two batteries, but it is smaller than those of the other compared methods.
- (3)
- FST: This is the time that it takes for a battery to experience a fixed voltage interval during charging process. We focus on the constant current charging process. According to the experimental results, if only the slope of a point on the curve is considered and used as the input of the model, the obtained results will be affected by various factors (current fluctuations, ambient temperature, testing errors, etc.). The selection of this point such that high accuracy of the model is realized will be difficult. In the constant current charging process, the energy that was charged into the battery is proportional to FST. Previous research indicated that FST showed a downward trend as the battery was ageing.
3.4. Feature Analysis Based on GCA and Proposal of the Enhanced Health Indicator
4. Proposed SOH Estimation Algorithm
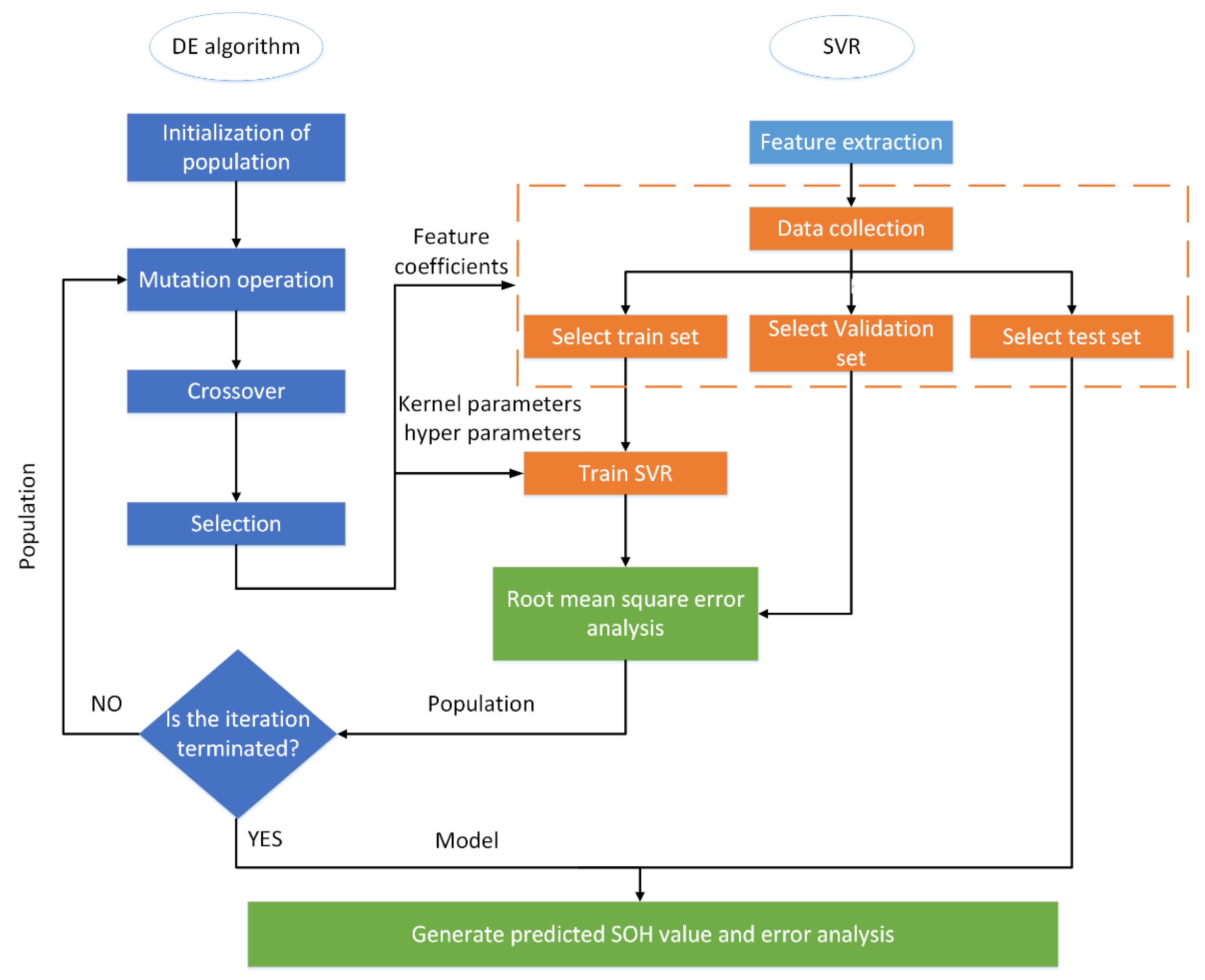
4.1. Framework of the Proposed Method
4.2. Adjustments to the SVR Model
4.3. SOH Estimation Procedure
5. Simulation Analysis
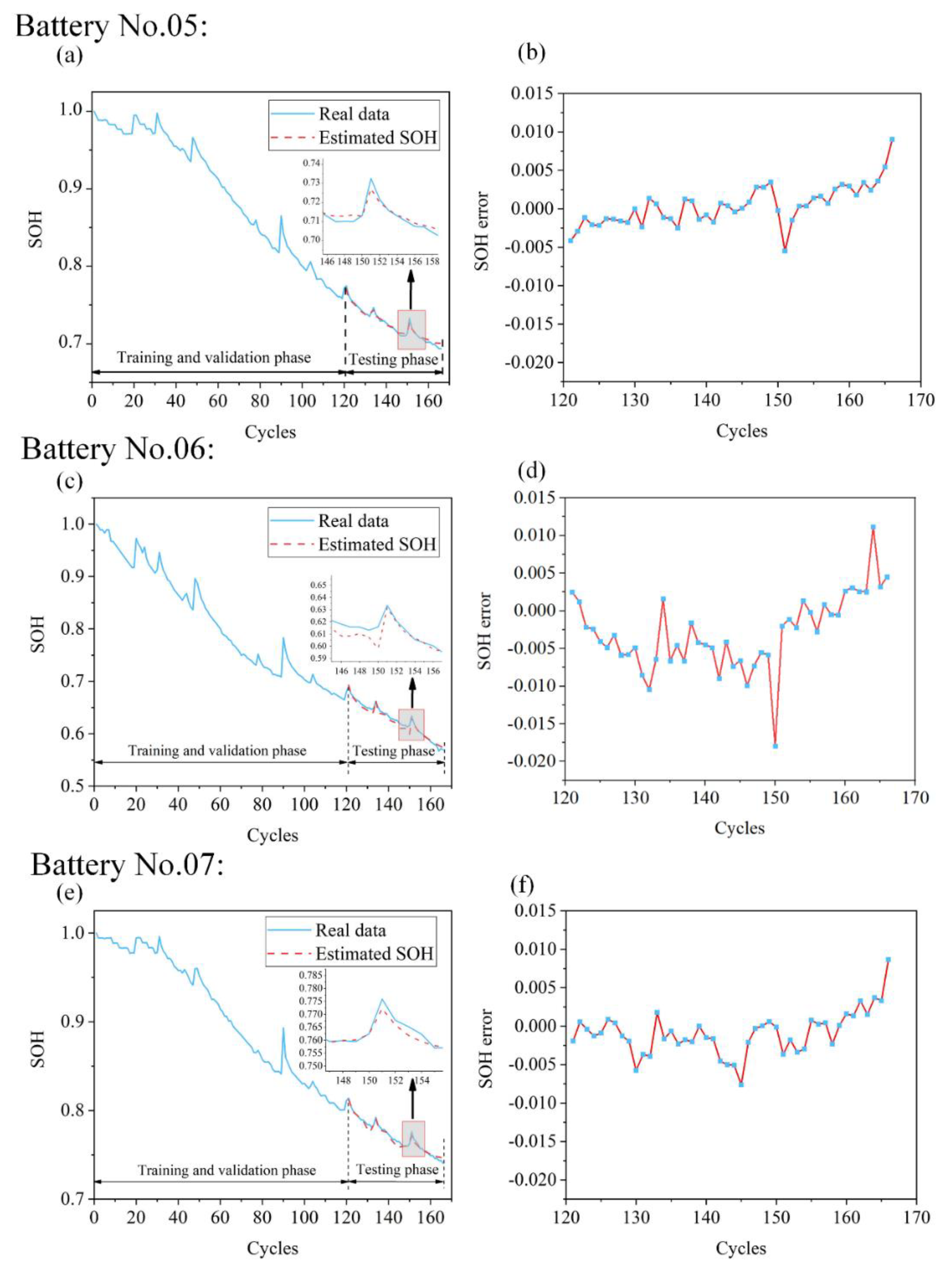
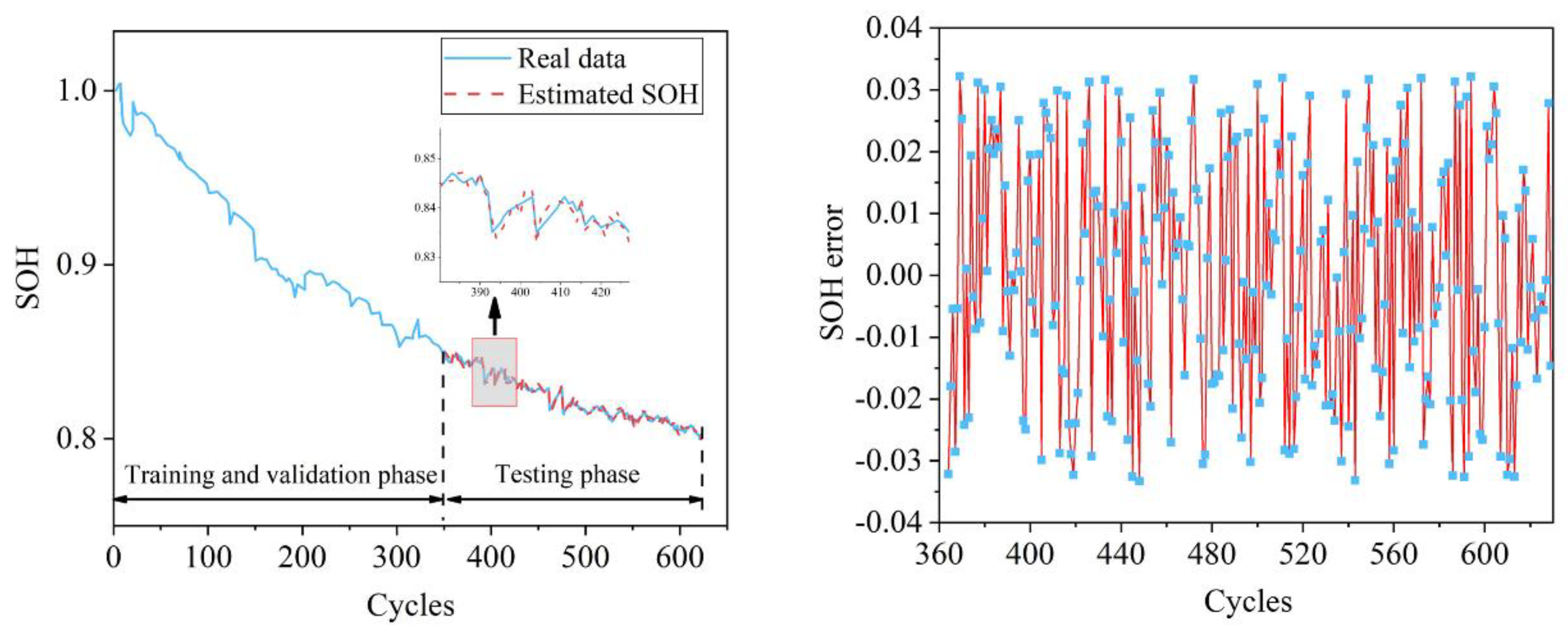
5.1. SOH Estimation Results
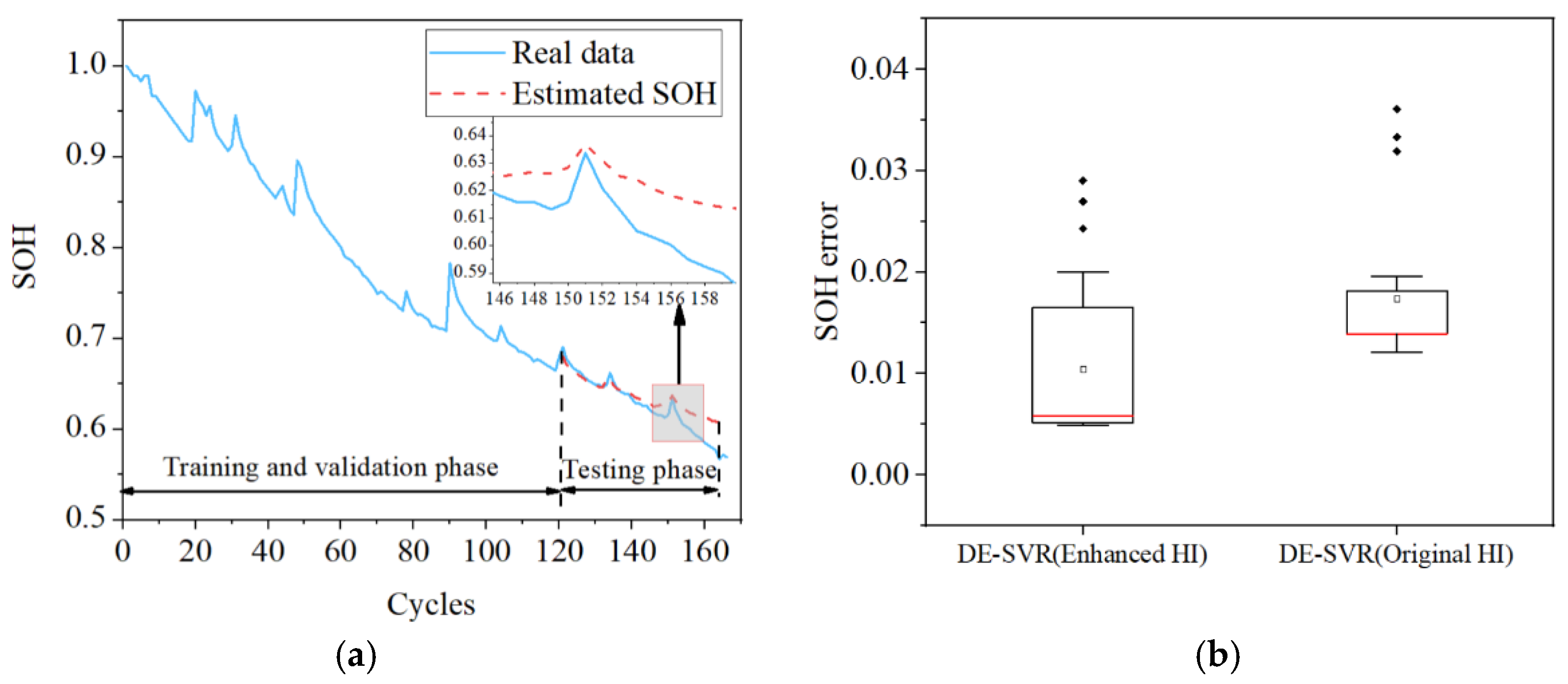
5.2. Increased Accuracy with the Enhanced Health Indicator
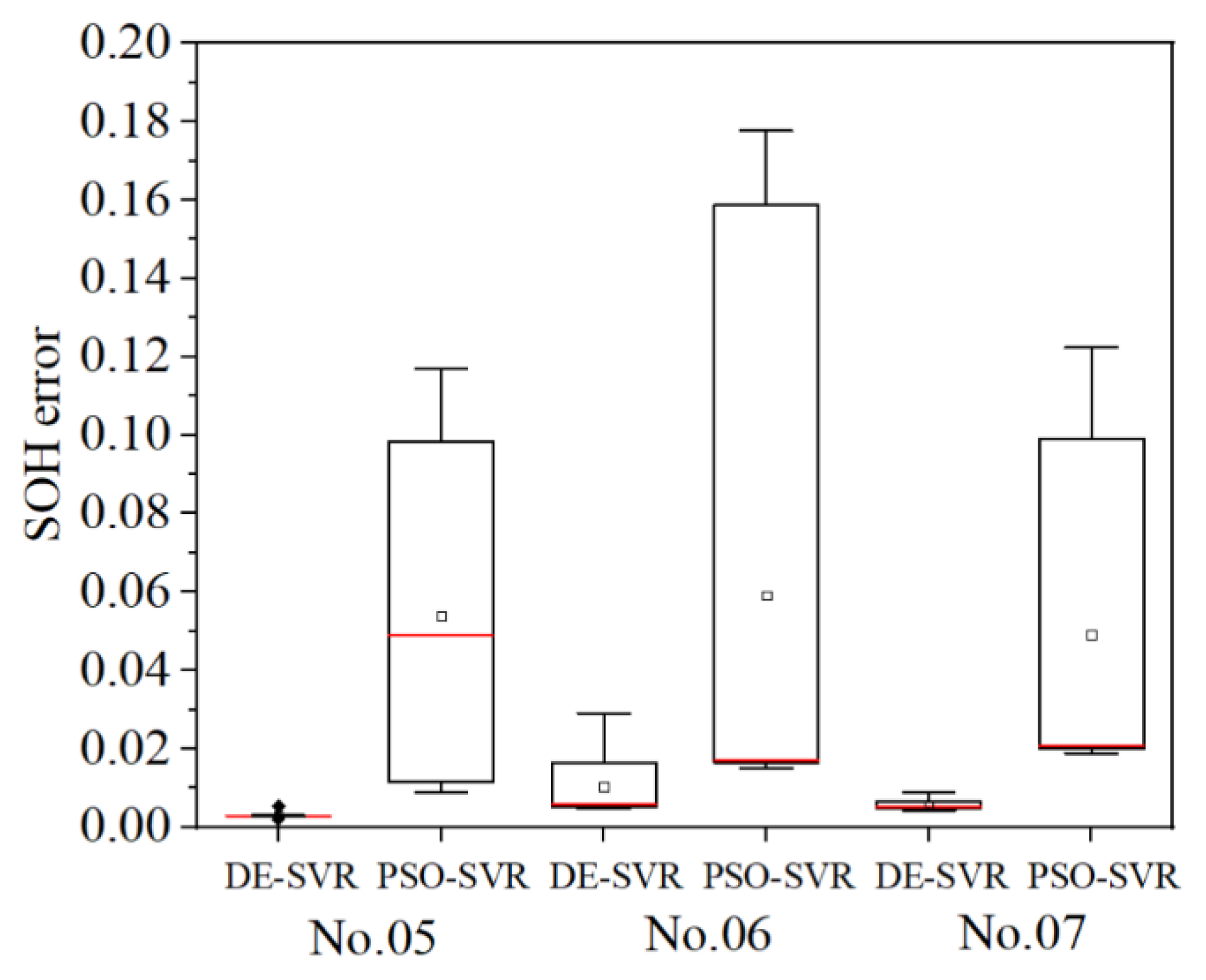
5.3. Comparison with Other Models
5.4. Model Validation under Dynamic Working Conditions
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| SOH | Battery State of Health |
| HIs | Health Indicators |
| SVR | Support Vector Regression |
| SOC | Battery State of Charge |
| RUL | Battery Remaining Useful Life |
| LIB | Lithium-Ion Battery |
| CC | Battery Constant Current Charging Mode |
| CV | Battery Constant Voltage Charging Mode |
| FST | Time Duration of a Fixed Segment |
| GPR | Gaussian Process Regression |
| LGPFR | Linear Gaussian Process Functional Regression |
| QGPFR | Quadratic Polynomial Gaussian Process Functional Regression |
| CLGPRF | Combination Linear Gaussian Process Functional Regression |
| CQGPRF | Combination Quadratic Polynomial Gaussian Process Functional Regression |
| SMK-GPR | Spectral Mixture Kernel Gaussian Process Regression |
| MGPR | Multiscale Gaussian Process Regression |
| RTPF | Real Time Particle Filter |
| EOL | End of Life |
References
- Zhang, X.; Wang, Y.J.; Yang, D.; Chen, Z.H. An on-line estimation of battery pack parameters and state-of-charge using dual filters based on pack model. Energy 2016, 115, 219–229. [Google Scholar] [CrossRef]
- Cheng, Y.J.; Lu, C.; Li, T.Y.; Tao, L.F. Residual lifetime prediction for lithium-ion battery based on functional principal component analysis and bayesian approach. Energy 2015, 90, 1983–1993. [Google Scholar] [CrossRef]
- Rezvanizaniani, S.M.; Liu, Z.C.; Chen, Y.; Lee, J. Review and recent advances in battery health monitoring and prognostics technologies for electric vehicle (ev) safety and mobility. J. Power Sources 2014, 256, 110–124. [Google Scholar] [CrossRef]
- Zhou, Y.P.; Huang, M.H. Lithium-ion batteries remaining useful life prediction based on a mixture of empirical mode decomposition and arima model. Microelectron. Reliab. 2016, 65, 265–273. [Google Scholar] [CrossRef]
- Wang, Y.J.; Zhang, C.B.; Chen, Z.H. A method for joint estimation of state-of-charge and available energy of lifepo4 batteries. Appl. Energy 2014, 135, 81–87. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, C.B.; Chen, Z.H. An online method for lithium-ion battery remaining useful life estimation using importance sampling and neural networks. Appl. Energy 2016, 173, 134–140. [Google Scholar] [CrossRef]
- Hu, C.; Youn, B.D.; Chung, J. A multiscale framework with extended kalman filter for lithium-ion battery soc and capacity estimation. Appl. Energy 2012, 92, 694–704. [Google Scholar] [CrossRef]
- Andre, D.; Appel, C.; Soczka, T.; Sauer, D.U. Advanced mathematical methods of soc and soh estimation for lithium-ion batteries. J. Power Sources 2013, 224, 20–27. [Google Scholar] [CrossRef]
- Hu, C.; Jain, G.; Tamirisa, P.; Gorka, T. Method for estimating capacity and predicting remaining useful life of lithium-ion battery. In Proceedings of the 2014 International Conference on Prognostics and Health Management, Cheney, WA, USA, 22–25 June 2014. [Google Scholar]
- Xian, W.M.; Long, B.; Li, M.; Wang, H.J. Prognostics of lithium-ion batteries based on the verhulst model, particle swarm optimization and particle filter. IEEE Trans. Instrum. Meas. 2013, 63, 2–17. [Google Scholar] [CrossRef]
- Wei, Z.B.; Tseng, K.J.; Wai, N.; Lim, T.M.; Kazacos, M.S. Adaptive estimation of state of charge and capacity with online identified battery model for vanadium redox flow battery. J. Power Sources 2016, 332, 389–398. [Google Scholar] [CrossRef]
- Wei, Z.B.; Zhao, J.Y.; Ji, D.X.; Tseng, K.J. A multi-timescale estimator for battery state of charge and capacity dual estimation based on an online identified model. Appl. Energy 2017, 204, 1264–1274. [Google Scholar] [CrossRef]
- Kim, I.S. A technique for estimating the state of health of lithium batteries through a dual-sliding-mode observer. IEEE Trans. Power Electron. 2009, 25, 1013–1022. [Google Scholar]
- Chen, Z.; Mi, C.C.; Fu, Y.H.; Xu, J.; Gong, X.Z. Online battery state of health estimation based on genetic algorithm for electric and hybrid vehicle applications. J. Power Sources 2013, 240, 184–192. [Google Scholar] [CrossRef]
- Li, J.; Adewuyi, K.; Lotfi, N.; Landers, R.G.; Park, J.H. A single particle model with chemical/mechanical degradation physics for lithium ion battery state of health (soh) estimation. Appl. Energy 2018, 212, 1178–1190. [Google Scholar] [CrossRef]
- Galeotti, M.; Cina, L.; Giammanco, C.; Cordiner, S.; Carlo, A.D. Performance analysis and soh (state of health) evaluation of lithium polymer batteries through electrochemical impedance spectroscopy. Energy 2015, 89, 678–686. [Google Scholar] [CrossRef]
- Torai, S.; Nakagomi, M.; Yoshitake, S.; Yamaguchi, S.; Oyama, N. State-of-health estimation of lifepo4/graphite batteries based on a model using differential capacity. J. Power Sources 2016, 306, 62–69. [Google Scholar] [CrossRef]
- Berecibar, M.; Garmendia, M.; Gandiaga, I.; Crego, J.; Villarreal, I. State of health estimation algorithm of lifepo4 battery packs based on differential voltage curves for battery management system application. Energy 2016, 103, 784–796. [Google Scholar] [CrossRef]
- Wu, J.; Wang, Y.J.; Zhang, X.; Chen, Z.H. A novel state of health estimation method of li-ion battery using group method of data handling. J. Power Sources 2016, 327, 457–464. [Google Scholar] [CrossRef]
- Li, X.Y.; Wang, Z.P.; Zhang, L.; Zou, C.F.; Dorrell, D.D. State-of-health estimation for li-ion batteries by combing the incremental capacity analysis method with grey relational analysis. J. Power Sources 2019, 410, 106–114. [Google Scholar] [CrossRef]
- He, W.; Williard, N.; Osterman, M.; Pecht, M. Prognostics of lithium-ion batteries based on dempster shafer theory and the bayesian monte carlo method. J. Power Sources 2011, 196, 10314–10321. [Google Scholar] [CrossRef]
- Saha, B.; Goebel, K.; Poll, S.; Christophersen, S. Prognostics methods for battery health monitoring using a bayesian framework. IEEE Trans. Instrum. Meas. 2008, 58, 291–296. [Google Scholar] [CrossRef]
- Chen, Z.; Song, X.Y.; Xiao, R.X.; Shen, J.W.; Xia, X.L. State of health estimation for lithium-ion battery based on long short term memory networks. In Proceedings of the International Conference on Energy, Ecology and Environment, Swinburne Univ Technol, Melbourne, Australia, 21–25 November 2018. [Google Scholar]
- Wang, S.; Zhao, L.L.; Su, X.H.; Ma, P.J. Prognostics of lithium-ion batteries based on battery performance analysis and flexible support vector regression. Energies 2014, 7, 6492–6508. [Google Scholar] [CrossRef]
- Liao, R.J.; Zheng, H.B.; Grzybowski, S.; Yang, L.J. Particle swarm optimization-least squares support vector regression based forecasting model on dissolved gases in oil-filled power transformers. Electr. Power Syst. Res. 2011, 81, 2074–2080. [Google Scholar] [CrossRef]
- Wei, J.W.; Dong, G.Z.; Chen, Z.H. Remaining useful life prediction and state of health diagnosis for lithium-ion batteries using particle filter and support vector regression. IEEE Trans. Ind. Electron. 2017, 65, 5634–5643. [Google Scholar] [CrossRef]
- Patil, M.A.; Tagade, P.; Hariharan, K.S.; Kolake, S.M.; Song, T.; Yeo, T.J.; Doo, S. A novel multistage support vector machine based approach for Lithium ion battery remaining useful life estimation. Appl. Energy 2015, 159, 285–297. [Google Scholar] [CrossRef]
- Yang, D.; Wang, Y.J.; Pan, R.; Chen, R.Y.; Chen, Z.H. State-of-health estimation for the lithium-ion battery based on support vector regression. Appl. Energy 2018, 227, 273–283. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory, 2nd ed.; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Price, K.; Storn, R.M.; Lampinen, J.A. Differential Evolution: A Practical Approach to Global Optimization, 1st ed.; Springer Science & Business Media: Berlin, Germany, 2006. [Google Scholar]
- Goebel, K.; Saha, B.; Saxena, A. Prognostics in battery health management. IEEE Trans. Instrum. Meas. 2008, 11, 33–40. [Google Scholar] [CrossRef]
- Li, X.Y.; Wang, Z.P.; Yan, J.Y. Prognostic health condition for lithium battery using the partial incremental capacity and Gaussian process regression. J. Power Sources 2019, 421, 56–67. [Google Scholar] [CrossRef]
- Orchard, M.; Tang, L.; Saha, B. Risk-sensitive particle-filtering-based prognosis framework for estimation of remaining useful life in energy storage devices. Stud. Inform. Control 2010, 19, 209–218. [Google Scholar] [CrossRef]
- Qin, T.C.; Zeng, S.K.; Guo, J.B.; Skaf, Z. A rest time-based prognostic framework for state of health estimation of lithium-ion batteries with regeneration phenomena. Energies 2016, 9, 896. [Google Scholar] [CrossRef]
- Tosun, N. Determination of optimum parameters for multi-performance characteristics in drilling by using grey relational analysis. Int. J. Adv. Manuf. Technol. 2006, 2528, 450–455. [Google Scholar] [CrossRef]
- Qin, T.C.; Zeng, S.K.; Guo, J.B. Robust prognostics for state of health estimation of lithium-ion batteries based on an improved PSO - SVR model. Microelectron. Reliab. 2015, 55, 1280–1284. [Google Scholar] [CrossRef]
- Weng, C.H.; Cui, Y.J.; Sun, J.; Peng, H. On-board state of health monitoring of lithium-ion batteries using incremental capacity analysis with support vector regression. J. Power Sources 2013, 235, 36–44. [Google Scholar] [CrossRef]
- Bole, B.; Kulkarni, C.S.; Daigle, M. Adaptation of an electrochemistry-based li-ion battery model to account for deterioration observed under randomized use. In Proceedings of the Annual Conference of The Prognostics and Health Management Society 2014, Fort Worth, TX, USA, 29 September–2 October 2014; Moffett Field Inc.: Santa Clara County, CA, USA, 2014. [Google Scholar]
| Battery Number | Conditions | ||||
|---|---|---|---|---|---|
| Charge Cutoff Voltage (V) | Discharge Cutoff Voltage (V) | Charging Current (A) | Discharge Current (A) | Temperature (°C) | |
| 05 | 4.2 | 2.7 | 1.5 | 2 | 24 |
| 06 | 4.2 | 2.5 | 1.5 | 2 | 24 |
| 07 | 4.2 | 2.2 | 1.5 | 2 | 24 |
| Features | Battery No. | ||
|---|---|---|---|
| 05 | 06 | 07 | |
| CCCTN and SOH | 0.7940 | 0.7862 | 0.8209 |
| CVCTN and SOH | 0.8091 | 0.7534 | 0.8274 |
| FSTN and SOH | 0.8543 | 0.7911 | 0.9037 |
| Cycle number and SOH | 0.5009 | 0.5015 | 0.5008 |
| Features | Battery No. | ||
|---|---|---|---|
| 05 | 06 | 07 | |
| CCCTN and CVCTN | 0.6818 | 0.6441 | 0.7101 |
| CCCTN and FSTN | 0.7868 | 0.8687 | 0.7490 |
| CVCTN and FSTN | 0.8169 | 0.6955 | 0.9219 |
| Battery No. | 05 | 06 | 07 | |||
|---|---|---|---|---|---|---|
| Criterion | MAPE (%) | RMSE | MAPE (%) | RMSE | MAPE (%) | RMSE |
| Proposed method | 0.45 | 0.0036 | 0.47 | 0.0057 | 0.38 | 0.0039 |
| 0.23 | 0.0024 | 0.98 | 0.0077 | 0.40 | 0.0041 | |
| 0.40 | 0.0033 | 1.29 | 0.0092 | 0.13 | 0.0029 | |
| 0.22 | 0.0023 | 1.19 | 0.0087 | 0.27 | 0.0033 | |
| Methods | 05 | 06 | 07 | |||
|---|---|---|---|---|---|---|
| MAPE (%) | RMSE | MAPE (%) | RMSE | MAPE (%) | RMSE | |
| GPR | 12.1 | 0.1303 | 27 | 0.2251 | 19.2 | 0.2070 |
| LGPFR | 23 | 0.0171 | 10.3 | 0.069 | 1.9 | 0.0159 |
| QGPFR | 1.9 | 0.015 | 7.7 | 0.0512 | 5.4 | 0.0552 |
| CLGPFR | 1.6 | 0.0136 | 10.2 | 0.0686 | 1.7 | 0.0173 |
| CQGPFR | 2.1 | 0.018 | 29 | 0.2044 | 2.6 | 0.0269 |
| SMK-GPR | 1.65 | 0.0138 | 10.6 | 0.0708 | 1.91 | 0.0188 |
| P-MGPR | 1.55 | 0.0136 | 2.96 | 0.0212 | 1.09 | 0.0114 |
| SE-MGPR | 1.38 | 0.012 | 2.93 | 0.0211 | 1.02 | 0.0107 |
| RTPF | 0.76 | 0.0068 | 1.25 | 0.0093 | 0.43 | 0.0044 |
| Proposed method | 0.23 | 0.0024 | 0.15 | 0.0055 | 0.13 | 0.0029 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Zhao, J.; Wang, H.; Yang, C. A New Lithium-Ion Battery SOH Estimation Method Based on an Indirect Enhanced Health Indicator and Support Vector Regression in PHMs. Energies 2020, 13, 830. https://doi.org/10.3390/en13040830
Liu Z, Zhao J, Wang H, Yang C. A New Lithium-Ion Battery SOH Estimation Method Based on an Indirect Enhanced Health Indicator and Support Vector Regression in PHMs. Energies. 2020; 13(4):830. https://doi.org/10.3390/en13040830
Chicago/Turabian StyleLiu, Zhengyu, Jingjie Zhao, Hao Wang, and Chao Yang. 2020. "A New Lithium-Ion Battery SOH Estimation Method Based on an Indirect Enhanced Health Indicator and Support Vector Regression in PHMs" Energies 13, no. 4: 830. https://doi.org/10.3390/en13040830
APA StyleLiu, Z., Zhao, J., Wang, H., & Yang, C. (2020). A New Lithium-Ion Battery SOH Estimation Method Based on an Indirect Enhanced Health Indicator and Support Vector Regression in PHMs. Energies, 13(4), 830. https://doi.org/10.3390/en13040830





