Numerical Simulations on the Application of a Closed-Loop Lake Water Heat Pump System in the Lake Soyang, Korea
Abstract
1. Introduction
2. The Status of the Surface Water Heat Pump System in Korea
3. Materials and Methods
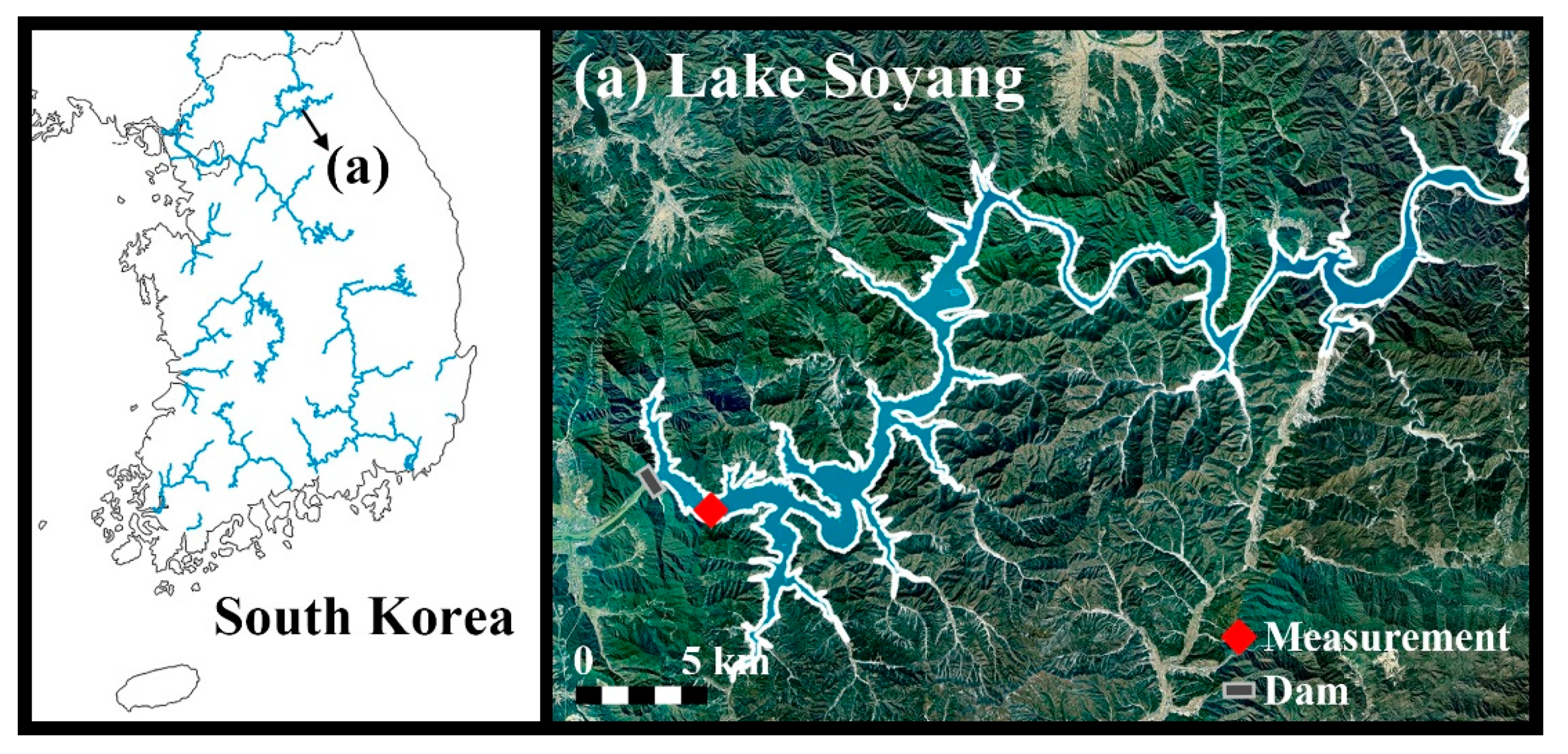
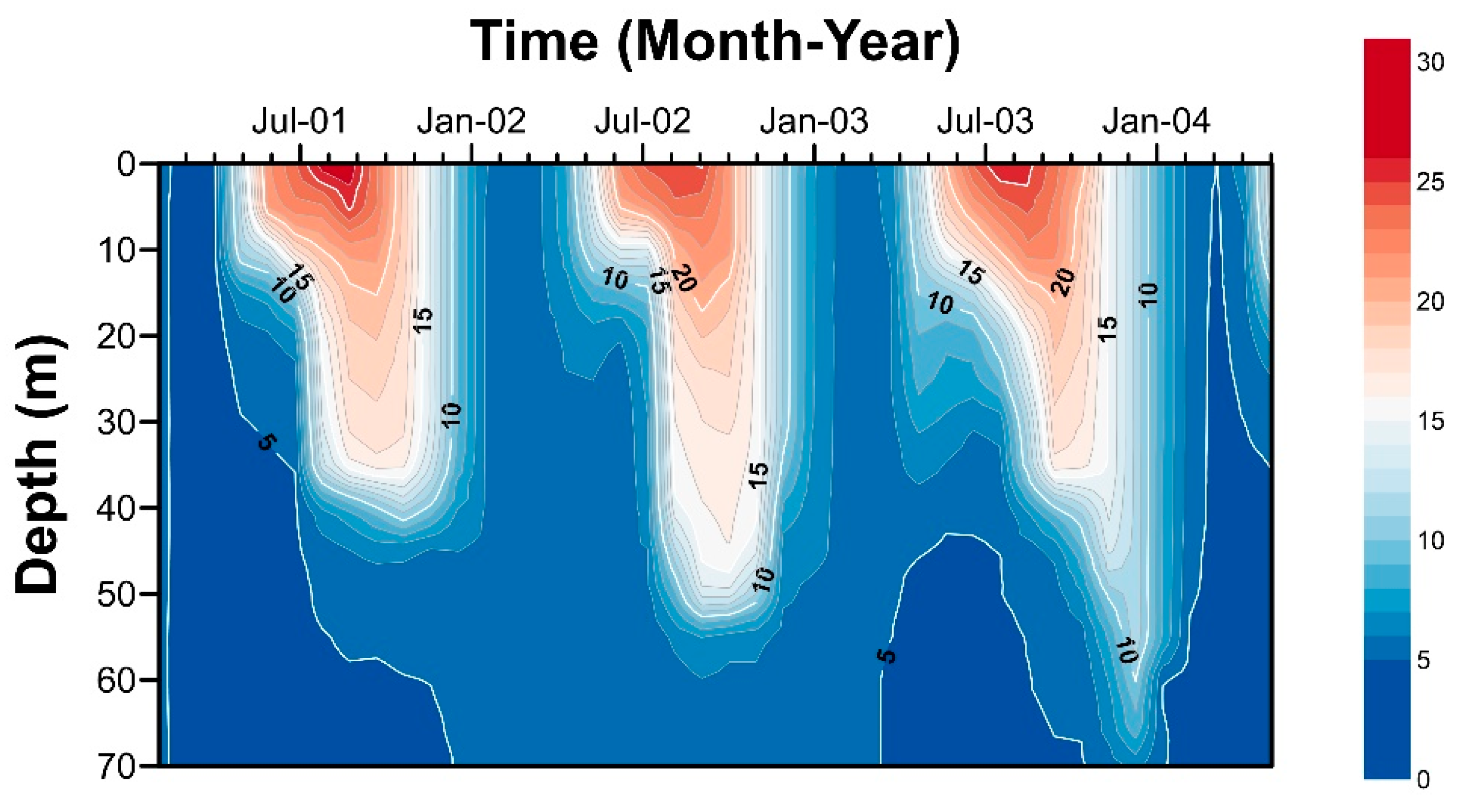
3.1. Lake Soyang and Its Temperature Profile
3.2. Computational Model
3.2.1. Flow Equation
3.2.2. Heat Transfer Equation
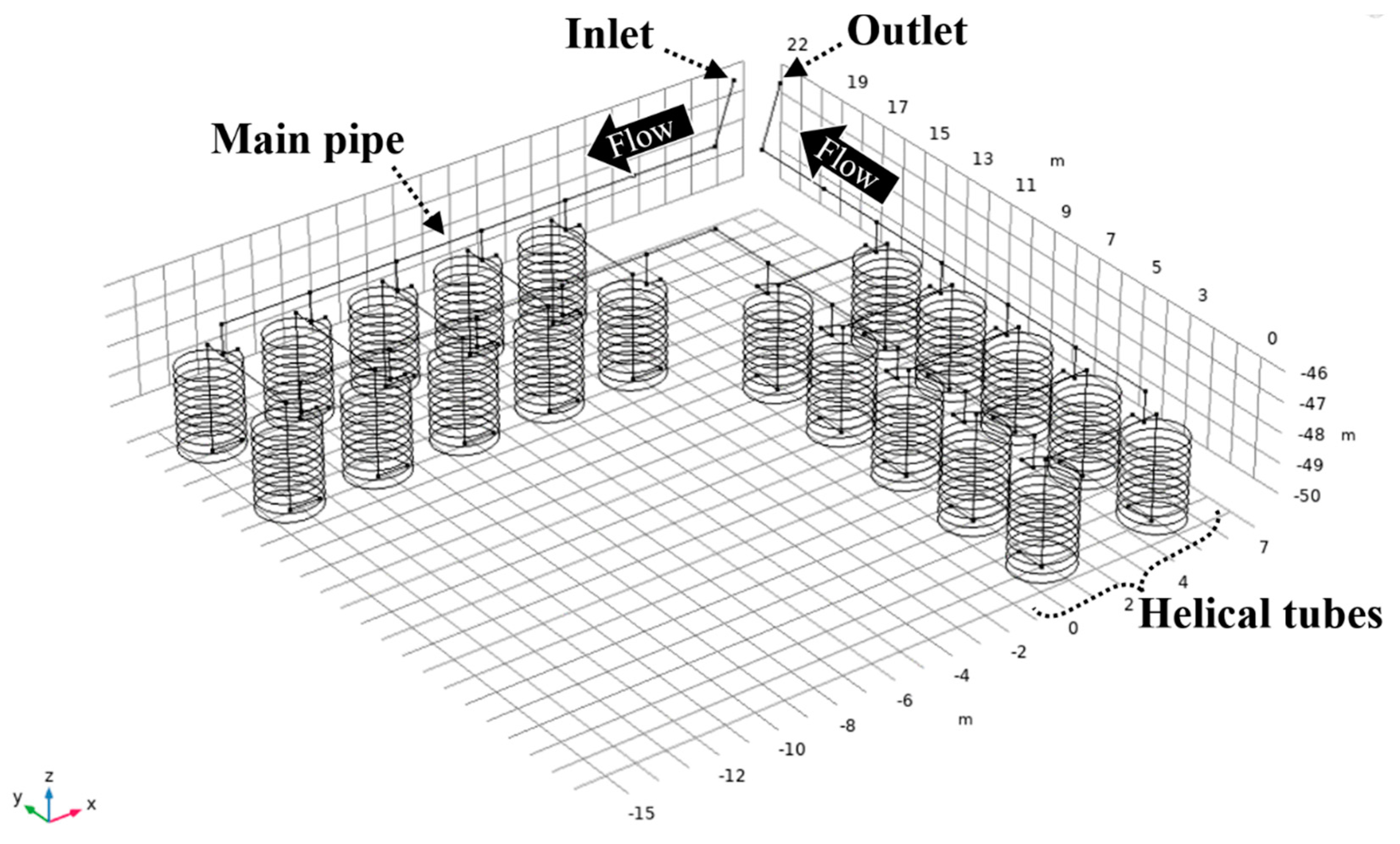
3.3. Model Setting and Assumptions
4. Results
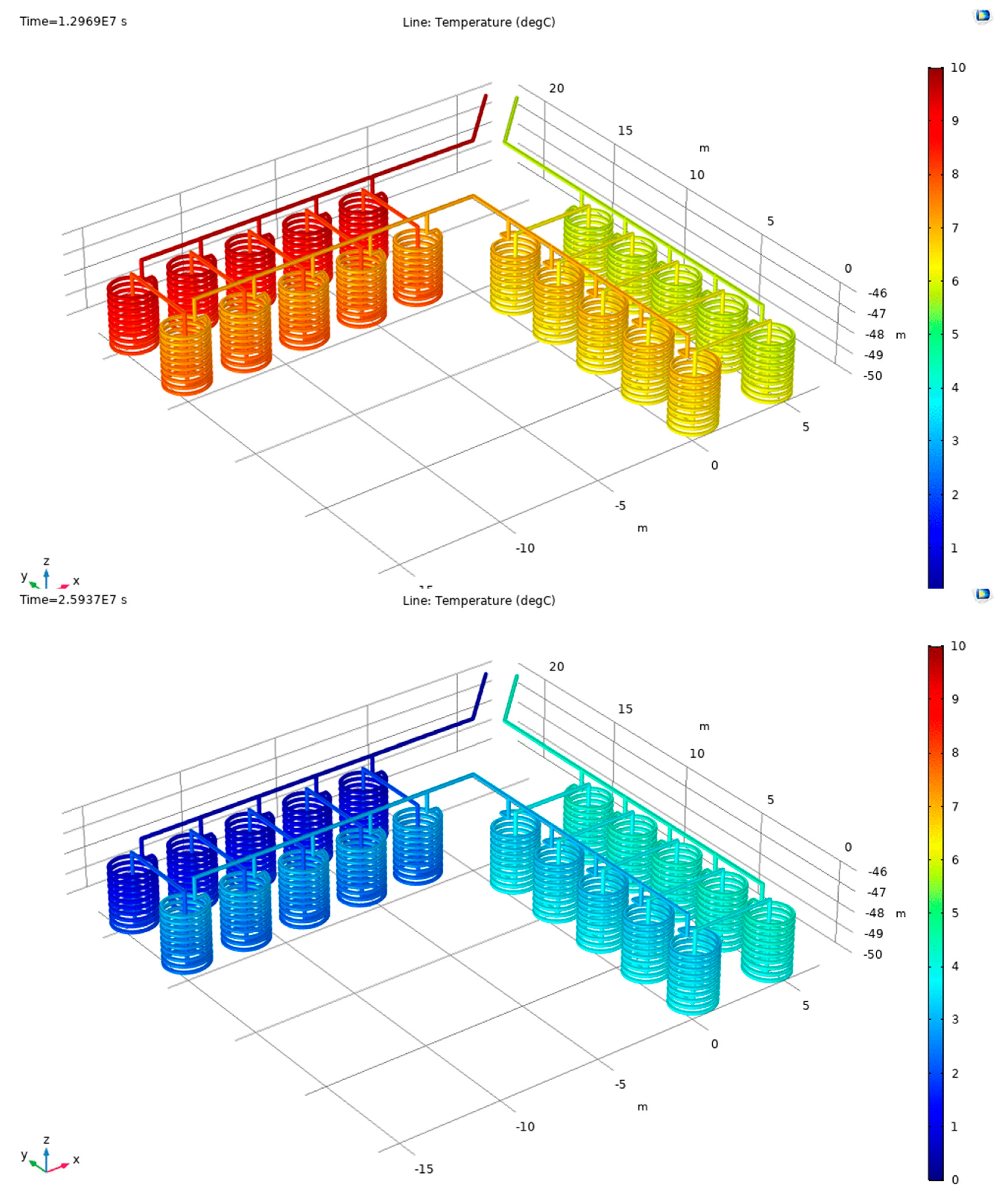
4.1. Modeling Procedure
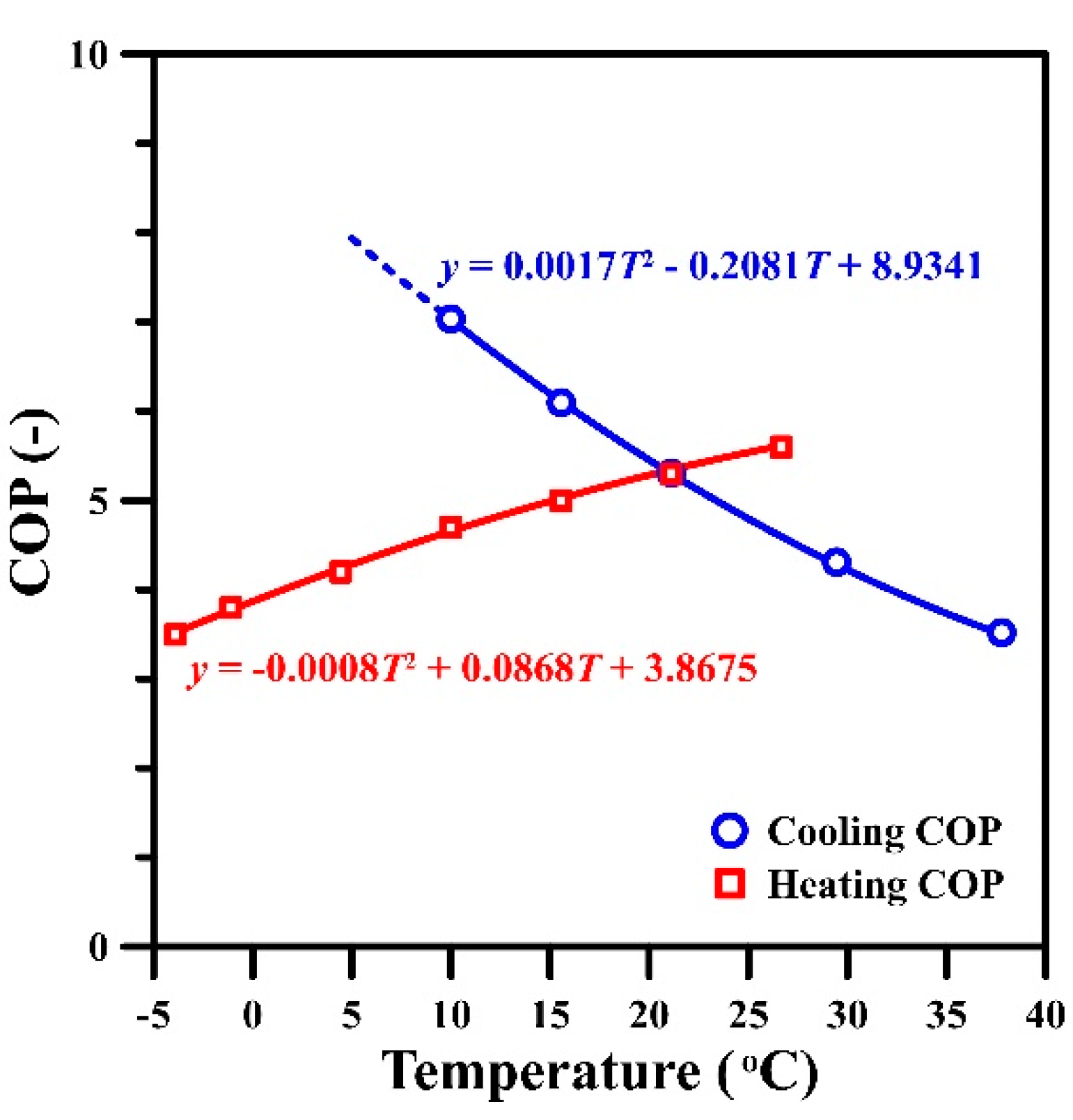
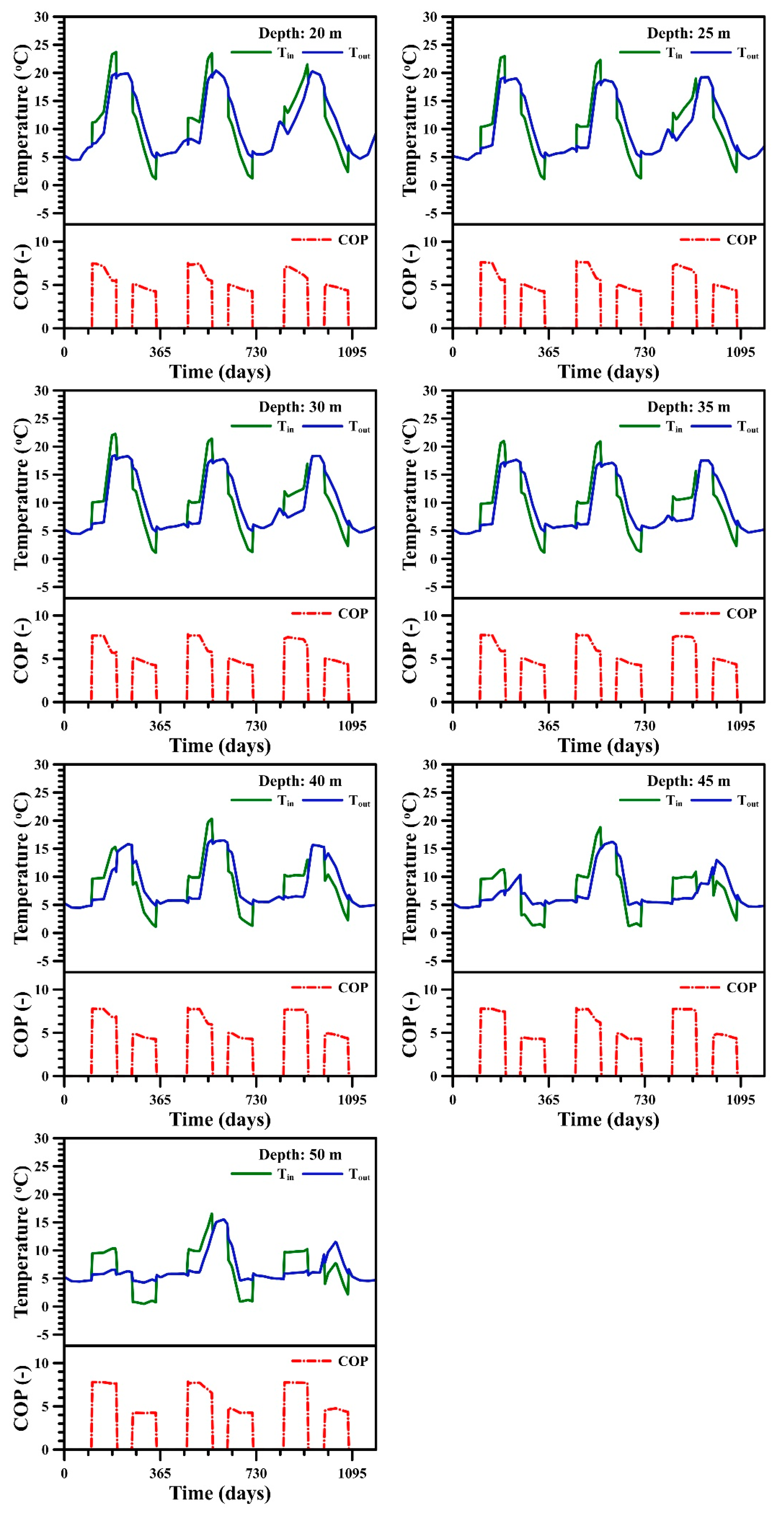
4.2. Installation Depth of Helical Tubes
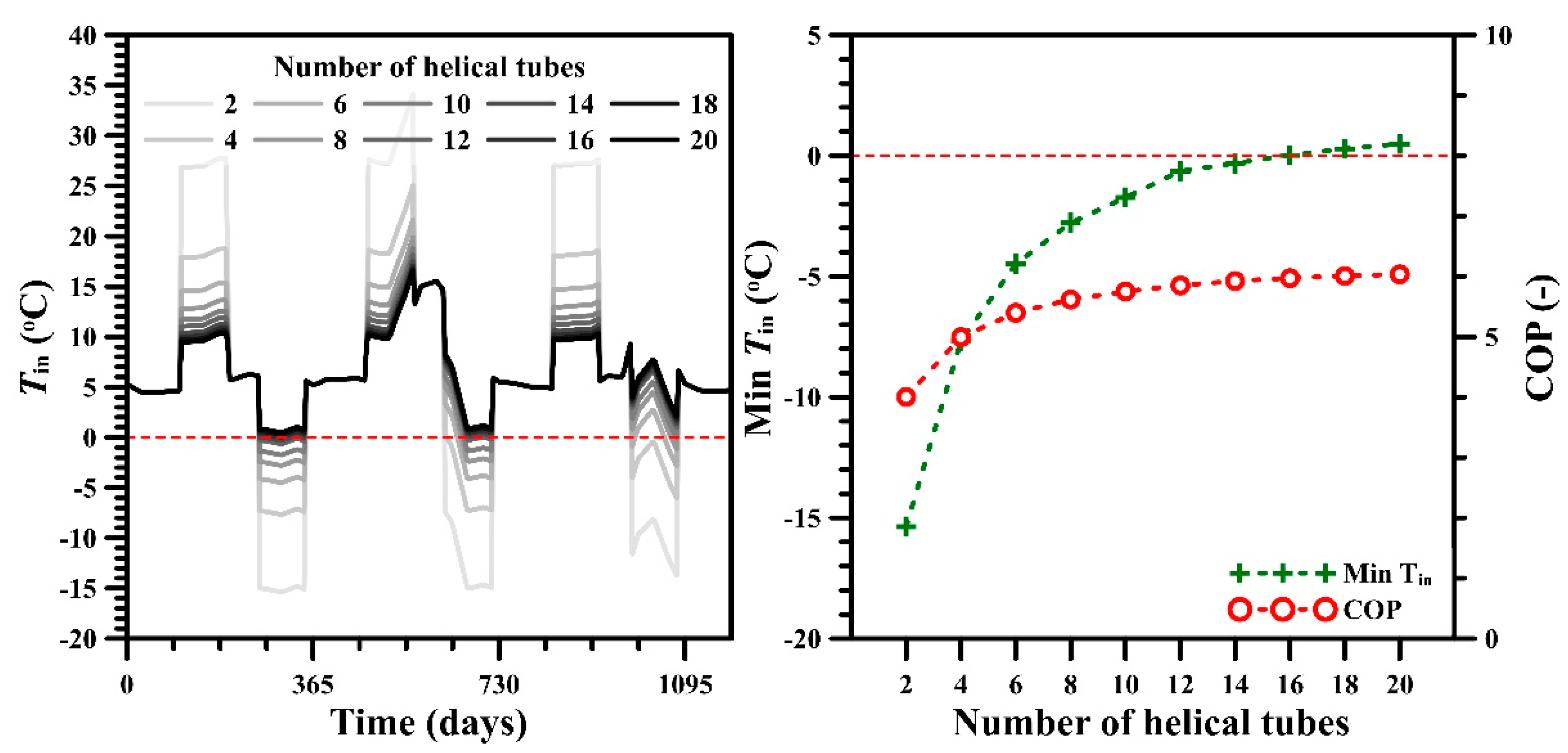
4.3. Number of Helical Tubes
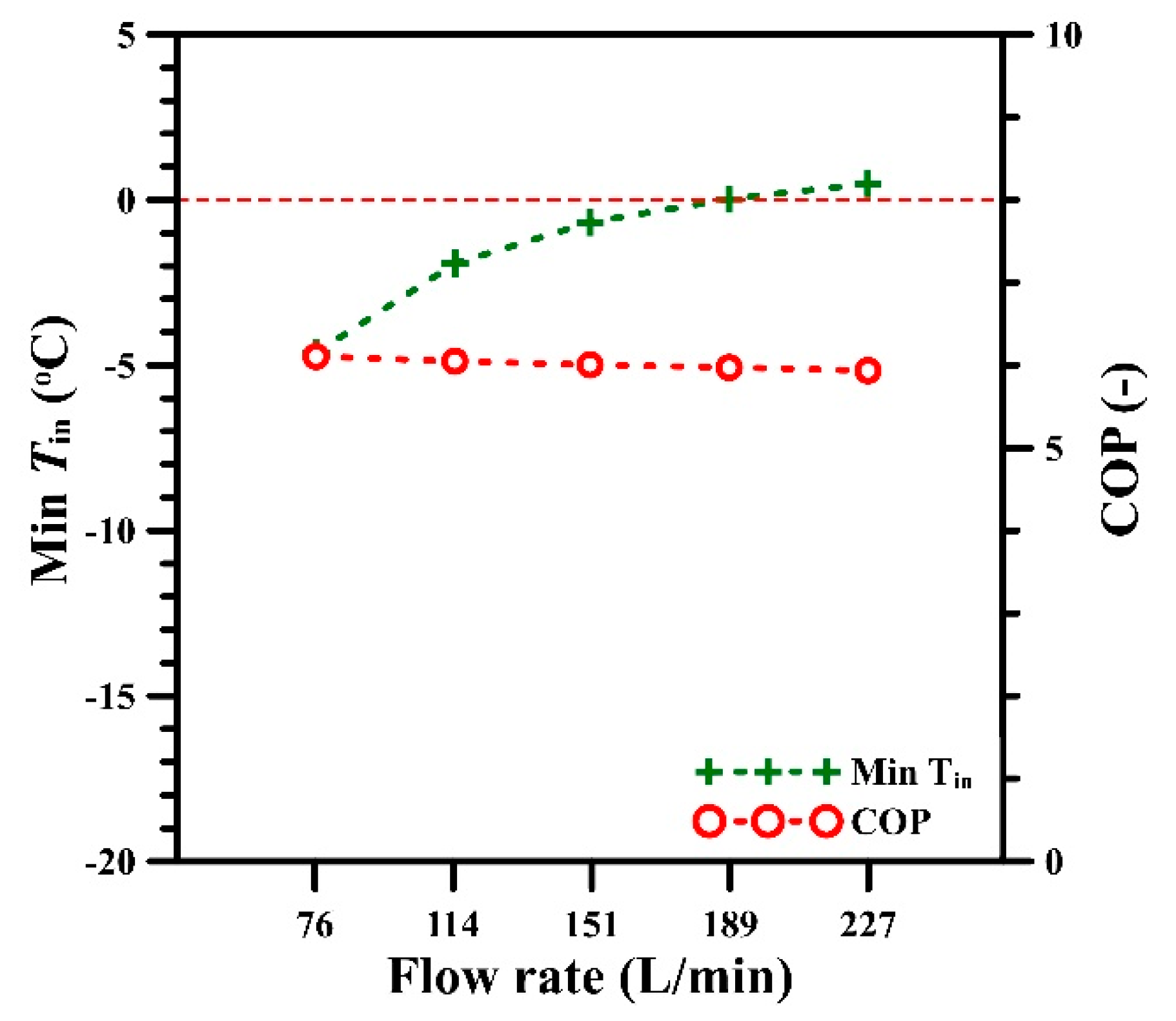
4.4. Flow Rate of the Heat-Carrier Fluid
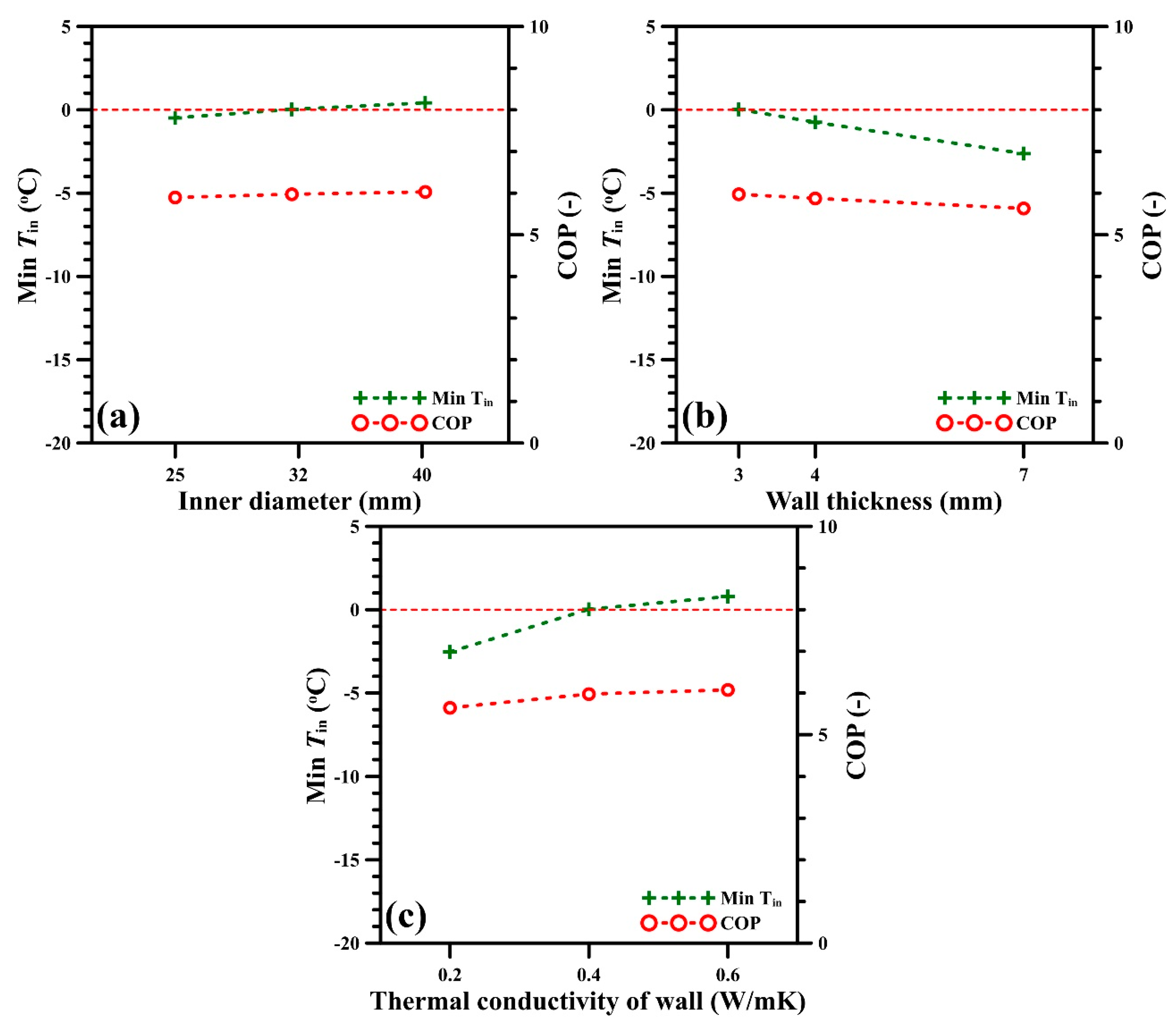
4.5. Properties of Helical Tubes
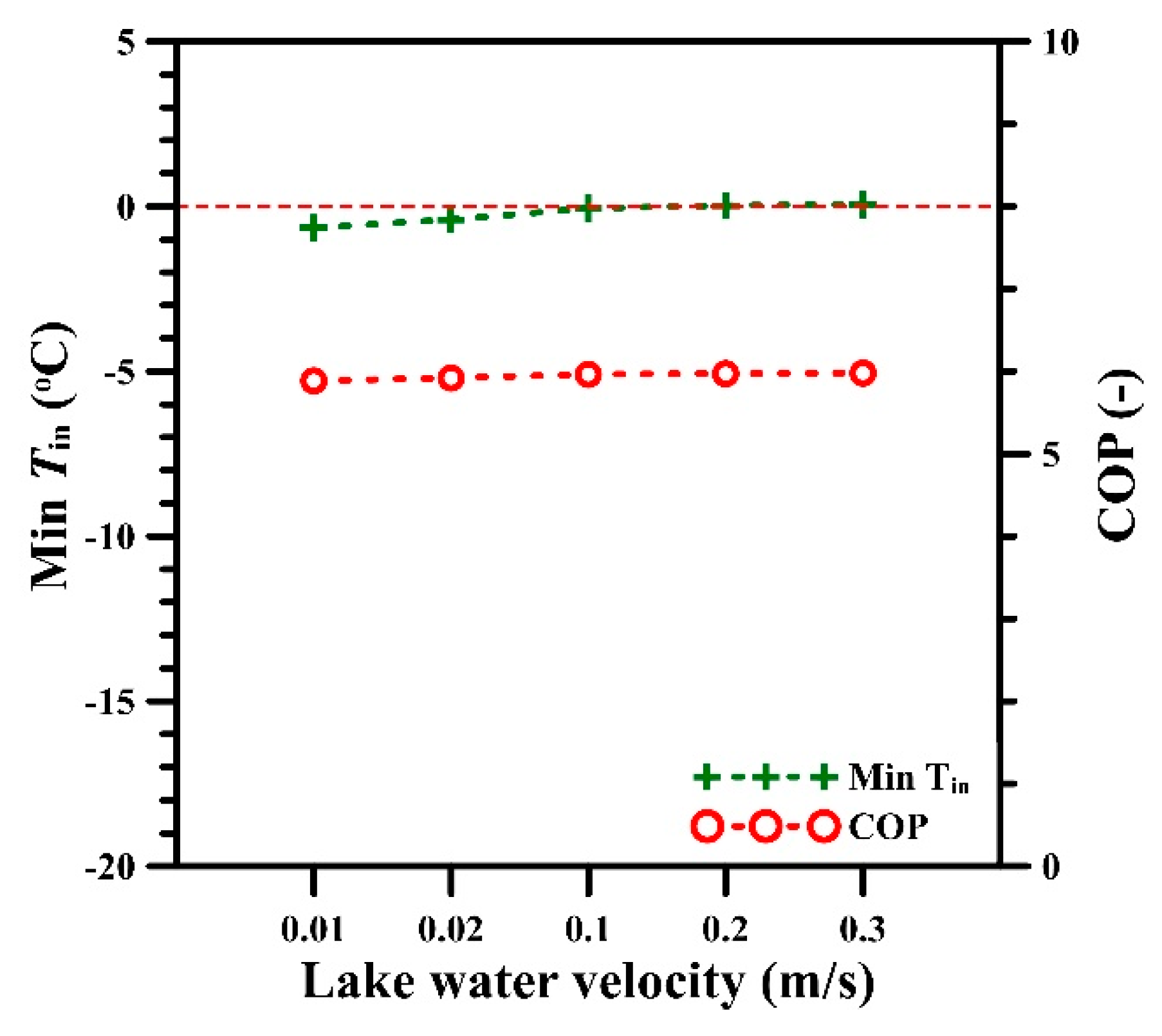
4.6. Flow Velocity in Lake
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ma, W.; Kim, M.K.; Hao, J. Numerical simulation modeling of a GSHP and WSHP system for an office building in the Hot Summer and Cold Winter Region of China: A Case Study in Suzhou. Sustainablity 2019, 11, 3282. [Google Scholar] [CrossRef]
- Spitler, J.D.; Mitchell, M.S. Surface water heat pump systems. In Advances in Ground-Source Heat Pump Systems; Rees, S.J., Ed.; Woodhead Publishing: Cambridge, UK, 2016; pp. 225–246. ISBN 9780081003220. [Google Scholar]
- Morton, A.C. Assessing the Performance of a Reservoir-Based Water Source Heat Pump. Master’s Thesis, Universtiy of Strathclyde Engineering, Glasgow, UK, 8 September 2013. [Google Scholar]
- Self, S.J.; Reddy, B.V.; Rosen, M.A. Geothermal heat pump systems: Status review and comparison with other heating options. Appl. Energy 2013, 101, 341–348. [Google Scholar] [CrossRef]
- Banks, D. An Introduction to Thermogeology: Ground Source Heating and Cooling; Wiley-Blackwell: Oxford, UK, 2012; ISBN 9781118447512. [Google Scholar]
- Gaudard, A.; Wüest, A.; Schmid, M. Using lakes and rivers for extraction and disposal of heat: Estimate of regional potentials. Renew. Energy 2019, 134, 330–342. [Google Scholar] [CrossRef]
- Yu, Y.; Olson, G. Ground Source Heat Pump Systems. In Handbook of Energy Systems in Green Buildings; Springe: Berlin/Heidelberg, Germany, 2018; pp. 393–472. ISBN 9783662491201. [Google Scholar]
- Mitchell, M.S.; Hansen, G.M.; Spitler, J.D. Experimental development of natural convection heat transfer correlations for spiral-helical surface water heat exchangers (1385-RP). Sci. Technol. Built Environ. 2018, 24, 714–725. [Google Scholar] [CrossRef]
- Zheng, W.; Zhang, H.; You, S.; Ye, T. The Thermal Characteristics of a Helical Coil Heat Exchanger for Seawater-source Heat Pump in Cold Winter. Procedia Eng. 2016, 146, 549–558. [Google Scholar] [CrossRef]
- Zhou, C.; Ni, L.; Yao, Y. Heat transfer analysis of multi-row helically coiled tube heat exchangers for surface water-source heat pump. Energy 2018, 163, 1032–1049. [Google Scholar] [CrossRef]
- Zhou, C.; Ni, L.; Ke, Y.; Yao, Y. Experimental study on the thermal performance of multi-row helically coiled tube heat exchanger for surface water-source heat pump. Appl. Therm. Eng. 2019, 149, 1274–1286. [Google Scholar] [CrossRef]
- Zhou, C.; Ni, L.; Lin, Z.; Yao, Y. Investigation on heat transfer and pressure drop characteristics of multi-row helically coiled tube heat exchanger for surface water-source heat pump. Int. J. Therm. Sci. 2019, 145. [Google Scholar] [CrossRef]
- Chiasson, A.D.; Spitler, J.D.; Rees, S.J.; Smith, M.D. Model for simulating the performance of a shallow pond as a supplemental heat rejecter with closed-loop ground-source heat pump systems. ASHRAE Trans. 2000, 106, 107–121. [Google Scholar]
- Büyükalaca, O.; Ekinci, F.; Yılmaz, T. Experimental investigation of Seyhan River and dam lake as heat source–sink for a heat pump. Energy 2003, 28, 157–169. [Google Scholar] [CrossRef]
- Schibuola, L.; Scarpa, M. Experimental analysis of the performances of a surface water source heat pump. Energy Build. 2016, 113, 182–188. [Google Scholar] [CrossRef]
- Zheng, W.; Ye, T.; You, S.; Zhang, H.; Zheng, X. Experimental Investigation of the Heat Transfer Characteristics of a Helical Coil Heat Exchanger for a Seawater-Source Heat Pump. J. Energy Eng. 2016, 142, 04015013. [Google Scholar] [CrossRef]
- Zheng, W.; Zhang, H.; You, S.; Ye, T. Numerical and experimental investigation of a helical coil heat exchanger for seawater-source heat pump in cold region. Int. J. Heat Mass Transf. 2016, 96, 1–10. [Google Scholar] [CrossRef]
- Kuyuk, A.; Ghoreishi-Madiseh, S.; Sasmito, A.; Hassani, F. Designing a Large-Scale Lake Cooling System for an Ultra-Deep Mine: A Canadian Case Study. Energies 2019, 12, 811. [Google Scholar] [CrossRef]
- Fernández-Seara, J.; Piñeiro-Pontevedra, C.; Dopazo, J.A. On the performance of a vertical helical coil heat exchanger. Numerical model and experimental validation. Appl. Therm. Eng. 2014, 62, 680–689. [Google Scholar] [CrossRef]
- Wu, Z.; You, S.; Zhang, H.; Fan, M.; Zheng, W.; Wang, Y.; Zhang, Y. Mathematical Modeling and Performance Analysis of Seawater Heat Exchanger in Closed-Loop Seawater-Source Heat Pump System. J. Energy Eng. 2019, 145, 04019012. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, G. Study on the application of closed-loop lake water heat pump systems for lakefront buildings in south China climates. J. Renew. Sustain. Energy 2014, 6, 033125. [Google Scholar] [CrossRef]
- MOTIE The 3rd Energy Master Plan (in Korean); Ministry of Trade, Industry and Energy (MOTIE): Sejong-si, Korea, 2019.
- KNREC. New & Renewable Energy Statistics 2018, 2019 ed.; Korea New & Renewable Energy Center (KNREC): Ulsan-si, Korea, 2019. (In Korean) [Google Scholar]
- K-water. Water for the Future; K-water: Daejeon-si, Korea, 2019. (In Korean) [Google Scholar]
- Chen, X.; Zhang, G.; Peng, J.; Lin, X.; Liu, T. The performance of an open-loop lake water heat pump system in south China. Appl. Therm. Eng. 2006, 26, 2255–2261. [Google Scholar] [CrossRef]
- Ramamoorthy, M.; Jin, H.; Chiasson, A.D.; Spitler, J.D. Optimal Sizing of Hybrid Ground-Source Heat Pump Systems That Use a Cooling Pond as a Supplemental Heat Rejecter—A system Simulation Approach. ASHRAE Trans. 2001, 107, 26–38. [Google Scholar]
- ME. A Study on the Improvement of Lake Environement Survey: Final Report; Ministry of Environment (ME): Sejong-si, Korea, 2013. (In Korean) [Google Scholar]
- Lee, H.; Han, H. Analysis of Lake Water Temperature and Seasonal Stratification in the Han River System from Time-Series of Landsat Images. Korean J. Remote Sens. 2005, 21, 253–271. (In Korean) [Google Scholar]
- Churchill, S.W. Friction-factor equation spans all fluid-flow regimes. Chem. Eng. 1977, 84, 91–92. [Google Scholar]
- Gnielinski, V. New Equations for Heat and Mass Transfer in Turbulent Pipe and Channel Flow. Int. Chem. Eng. 1976, 16, 359–368. [Google Scholar]
- Churchill, S.W.; Bernstein, M. A Correlating Equation for Forced Convection From Gases and Liquids to a Circular Cylinder in Crossflow. J. Heat Transf. 1977, 99, 300–306. [Google Scholar] [CrossRef]
| Parameters | Range of Value | Corresponding Chapter |
|---|---|---|
| Installation depth (m) | 20, 25, 30, 35, 40, 45, 50 * | 4.2 |
| Number of helical tubes | 2, 4, 6, 8, 10, 12, 14, 16 *, 18, 20 | 4.3 |
| Flow rate of heat-carrier fluid (L/min) | 75.71, 113.6, 151.4, 189.3 *, 227.1 | 4.4 |
| Inner diameter of tube (mm) | 25, 32 *, 40 | 4.5 |
| Tube wall thickness (mm) | 2.9 *, 4.0, 7.0 | 4.5 |
| Thermal conductivity of tube wall (W/mK) | 0.2, 0.4 *, 0.6 | 4.5 |
| Lake water velocity (m/s) | 0.01, 0.02, 0.1, 0.2 *, 0.3 | 4.6 |
| Installation Depth (m) | |||||||
|---|---|---|---|---|---|---|---|
| 20 | 25 | 30 | 35 | 40 | 45 | 50 | |
| Cooling COP | 6.69 | 6.94 | 7.09 | 7.21 | 7.39 | 7.54 | 7.63 |
| Heating COP | 4.67 | 4.67 | 4.67 | 4.66 | 4.59 | 4.50 | 4.42 |
| Total COP | 5.68 | 5.81 | 5.89 | 5.94 | 6.0 | 6.03 | 6.04 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, D.K.; Lee, Y. Numerical Simulations on the Application of a Closed-Loop Lake Water Heat Pump System in the Lake Soyang, Korea. Energies 2020, 13, 762. https://doi.org/10.3390/en13030762
Park DK, Lee Y. Numerical Simulations on the Application of a Closed-Loop Lake Water Heat Pump System in the Lake Soyang, Korea. Energies. 2020; 13(3):762. https://doi.org/10.3390/en13030762
Chicago/Turabian StylePark, Dong Kyu, and Youngmin Lee. 2020. "Numerical Simulations on the Application of a Closed-Loop Lake Water Heat Pump System in the Lake Soyang, Korea" Energies 13, no. 3: 762. https://doi.org/10.3390/en13030762
APA StylePark, D. K., & Lee, Y. (2020). Numerical Simulations on the Application of a Closed-Loop Lake Water Heat Pump System in the Lake Soyang, Korea. Energies, 13(3), 762. https://doi.org/10.3390/en13030762




