Tuning Techniques for Piezoelectric and Electromagnetic Vibration Energy Harvesters
Abstract
1. Introduction
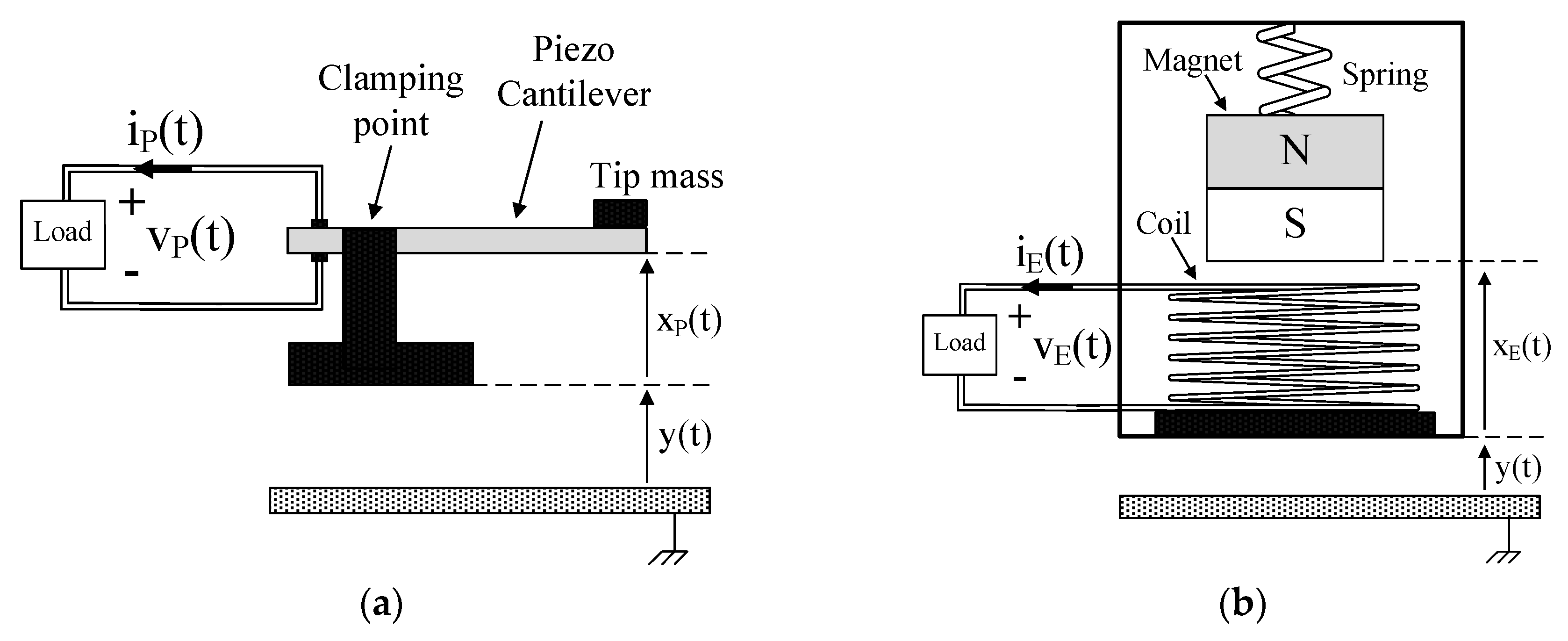
2. Piezoelectric and Electromagnetic Resonant Vibration Energy Harvesters
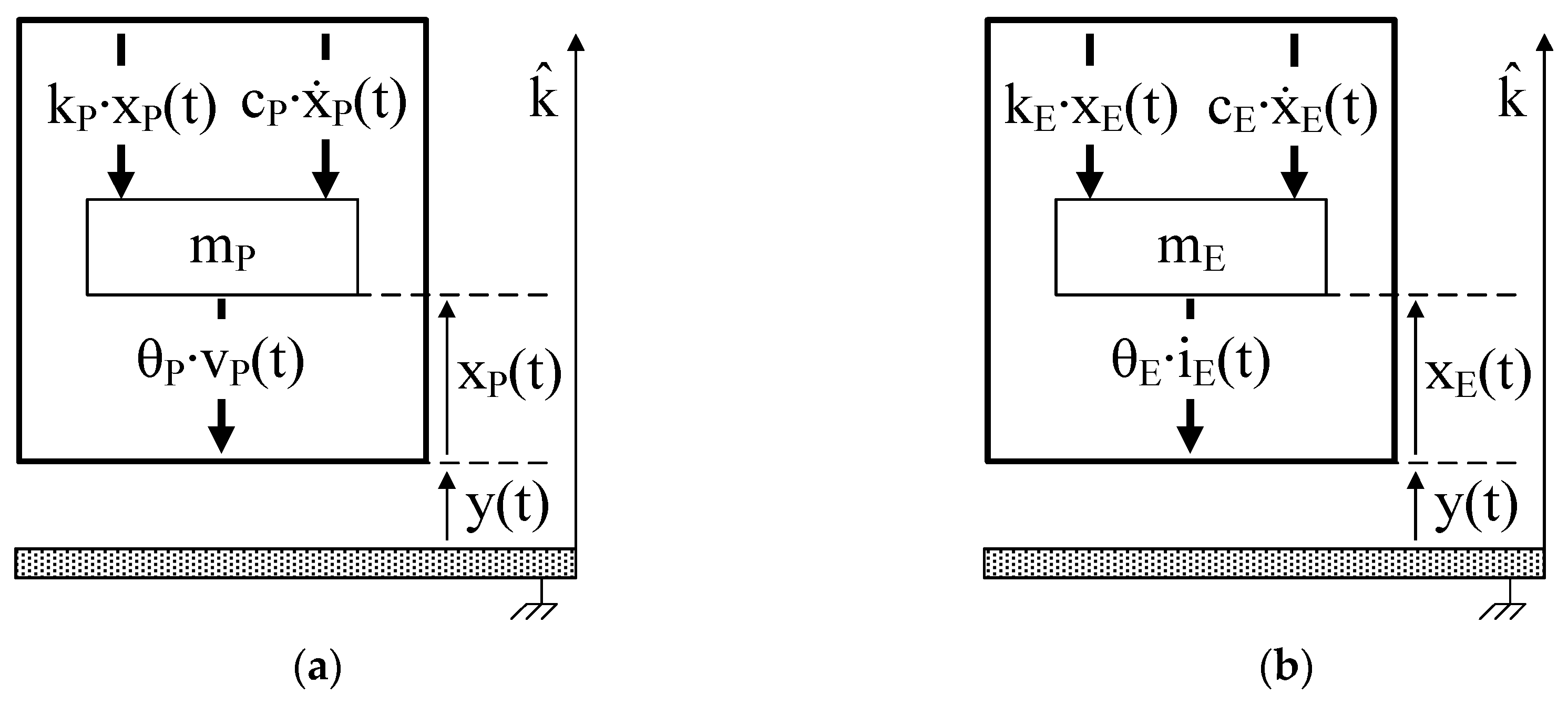
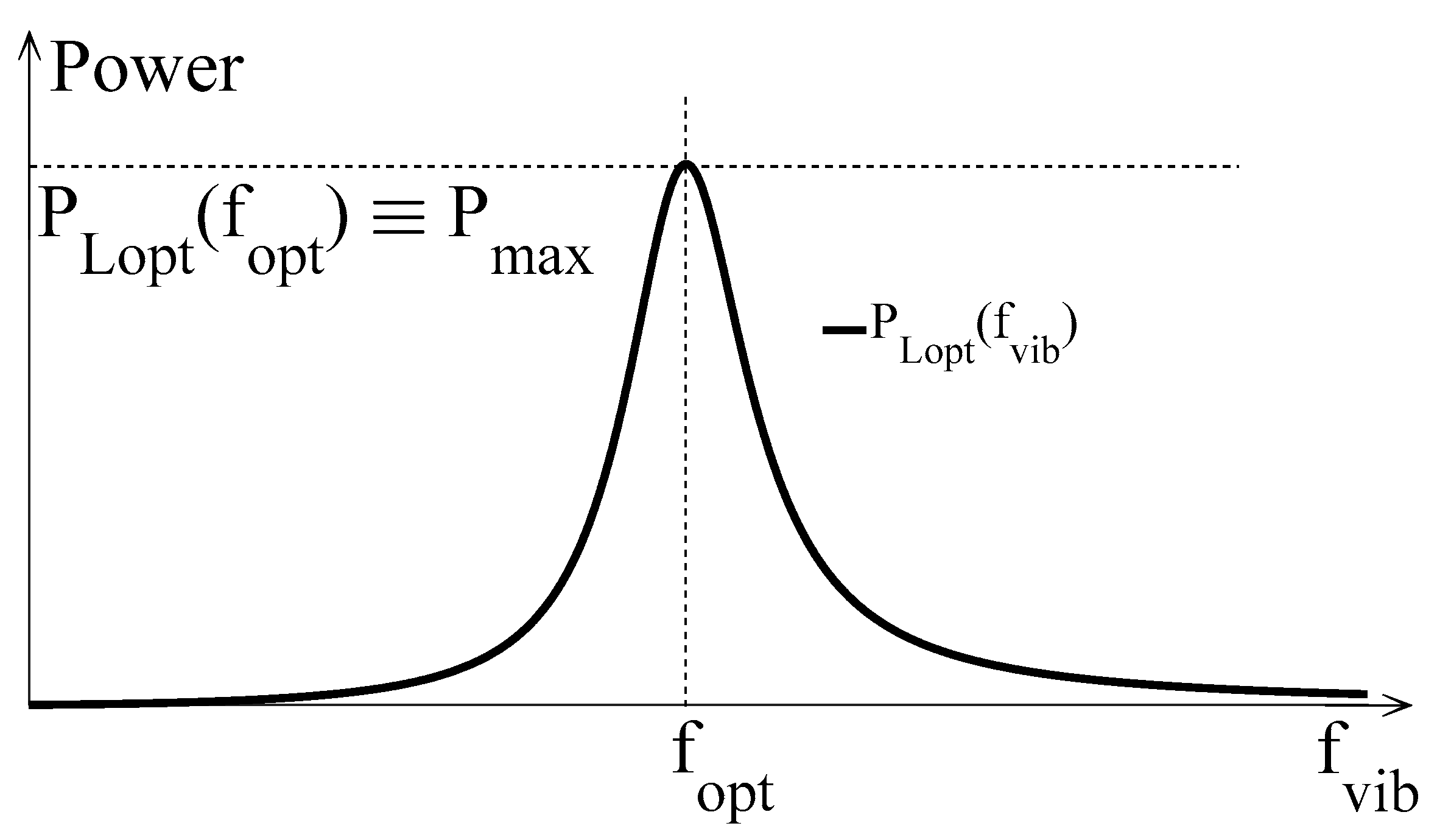
2.1. Modeling and Maximum Power Extraction
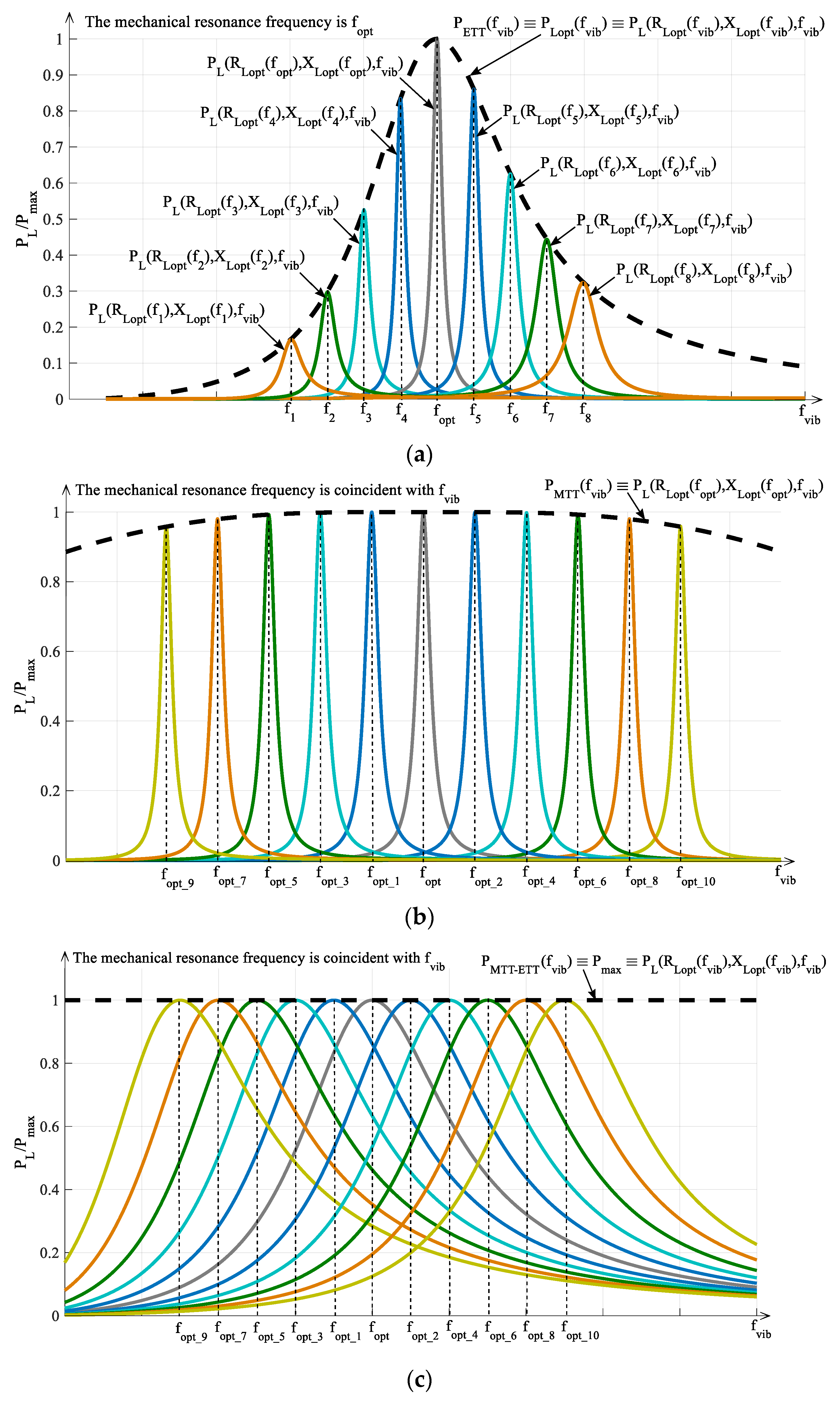
2.2. Definition of Tuning Techniques
3. Indicators for the Classification and Comparison of Mechanical Tuning Techniques
- Indicator Name: RVEH.
- Description: It indicates the type of RVEH to which the considered MTT is applied. If RVEH is “P” (“E”) it means that the considered MTT is applied to a P-RVEH (an E-RVEH). RVEH can be also equal to “Hybrid P/E” if the considered MTT is applied to a hybrid piezoelectric–electromagnetic RVEH.
- Indicator Name: Direction.
- Description: It indicates the oriented direction that, starting from the untuned resonance frequency, a MTT is able to exploit. In particular, if direction is “BOTH” the MTT is able to move the mechanical resonance frequency both in the increasing and in the decreasing direction. If instead direction is “RIGHT” (“LEFT”) the MTT is able to move the mechanical resonance frequency only in the increasing (decreasing) direction.
- Indicators Name: ΔfR and ΔfL.
- Description: These percentage indicators provide information concerning the range of frequency where the MTT can be applied with respect to the untuned mechanical resonance frequency. They are defined as followswhere fR (fL) is the maximum (minimum) achievable frequency in the right (left) direction starting from the untuned mechanical resonance frequency fopt. The definition of both indicators is obviously possible only for MTTs that can exploit both directions of tuning.
- Indicators Name: ΔPR and ΔPL.
- Description: These percentage indicators provide information concerning the reduction of the extracted power that is obtained at fR and fL with respect to fopt. They are defined as follows:where PR (PL) is the maximum extractable power in correspondence of fR (fL). Moreover, in this case, the definition of both indicators is obviously possible only for MTTs that can exploit both directions of tuning. Of course, in order to be able to compare MTTs, it is fair to provide also the amplitude Avib of the input acceleration.
- Indicator Name: Implementation.
- Description: It describes the way the considered MTT is implemented. In fact, the mechanical resonance frequency of an RVEH can be varied by acting on many different variables. Some of these are mechanical quantities, other are electrical quantities. Therefore, implementation can be “MECHANICAL” for mechanically implemented MTTs or “ELECTRICAL” for electrically implemented MTTs. In particular, in a mechanically implemented MTT the working principle of the tuning relies on the regulation of a mechanical variable (as an example a distance between magnets or the position of a clamp) even if such a variable is tuned by means of an electrical system (as an example an electrical actuator). What is important in this definition is the fundamental variable driving the working principle and not its particular implementation. Instead, in an electrically implemented MTT the operating principle of the tuning is based on the regulation of an electrical quantity (as an example the voltage of a piezoelectric actuator).
- Indicator Name: Actuation.
- Description: It indicates the way the considered MTT is actuated. In particular, if actuation is “MANUAL” the MTT needs the intervention of an operator that manually acts on the tuning mechanism. Instead, if it is “AUTOMATIC” the MTT adopts an actuator (as an example a motor) or an electrical signal in order to prevent the human intervention.
- Indicator Name: Control.
- Description: If control is equal to “OPEN LOOP” then the MTT needs a precharacterization of the RVEH (e.g., for the definition of a look-up table) and it is affected by errors due to any possible parameter change in the system. If control is equal to “CLOSED LOOP” then the MTT is more robust and does not need a precharacterization, but it needs sensors in order to implement the feedback circuitry and hence more energy is required for its operation. Obviously, the only type of actuation that can be controlled in a closed loop is the AUTOMATIC one.
- Indicator Name: Supply.
- Description: It provides a picture of the type of power demand characterizing the considered MTT. In particular, if supply is “PASSIVE”, the considered MTT needs a significant amount of power only to move the RVEH’s resonance frequency but it is able to indefinitely maintain the new resonance frequency value without any additional power consumption. In such a case, the control system energy consumption mainly depends on the energy required for the tuning step and, hence, on the rate of resonance frequency adjustments that the operating conditions require. If instead supply is “ACTIVE”, besides the initial power required in order to move the resonance frequency, the MTT continues to require power in order to maintain the new resonance frequency. If supply is “SEMI-ACTIVE”, the MTT needs an initial significant amount of power for moving the resonance frequency and it is able to maintain, only for a limited period of time, such a new value of resonance frequency without any other additional power demand. However, due to unavoidable continuous drifts of the resonance frequency, a periodic refresh is needed with additional power demands. It is worth noting that, the supply indicator can be defined only when the actuation indicator is equal to AUTOMATIC (without human intervention).
- Indicator Name: Tuning period.
- Description: This is a crucial indicator when considering the power consumption. The main requirement for a MTT is of course as low as possible power consumption. A MTT that consumes an average power greater than the harvested one is obviously useless in practice. In fact, the main purpose of a RVEH is to power both the MTT controller and the load in any vibrations’ conditions. The tuning period indicator provides the minimum period of time that is needed by the REVEH in order to store the amount of energy needed by the MTT controller for a given resonance frequency adjustment in the considered acceleration conditions. Obviously, in the presence of vibration frequency shifts, for a proper operation of a MTT the tuning period must be much shorter than the period of the vibration’s frequency shifts. The shorter the tuning period is, the faster the MTT will be able to react to vibrations’ frequencies changes. There are papers in which this aspect is not discussed at all. The tuning period indicator can be defined only when the actuation indicator is equal to AUTOMATIC.
- Indicator Name: Vibrations.
- Description: This indicator is focused on the type of vibrations that the considered MTT and the corresponding RVEH are able to exploit. In particular, the basic classification that is considered in this paper is between “SINUSOIDAL” and “NOT-SINUSOIDAL” vibrations. This is a crucial aspect from the practical point of view. Various vibration sources characterized by different harmonic contents exist in practical applications. Examples of vibration sources are walking people, moving trains or cars, and domestic or industrial working machines [84,85,86]. Sinusoidal vibrations are rarely encountered in real world applications. Even if vibrations in practical applications are usually periodic, random, or single event motions (e.g., impacts) [84,85,86], for simplicity reasons, most research papers focusing on RVEHs and in particular on MTTs deal with purely sinusoidal vibration sources.
4. Overview of Mechanical Tuning Techniques
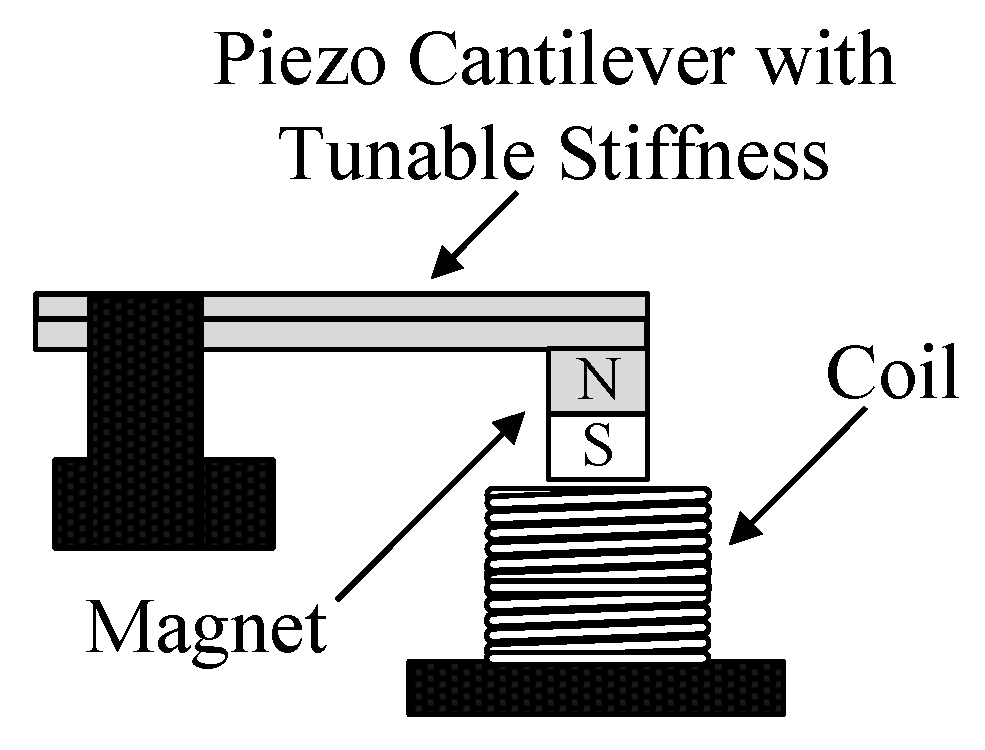
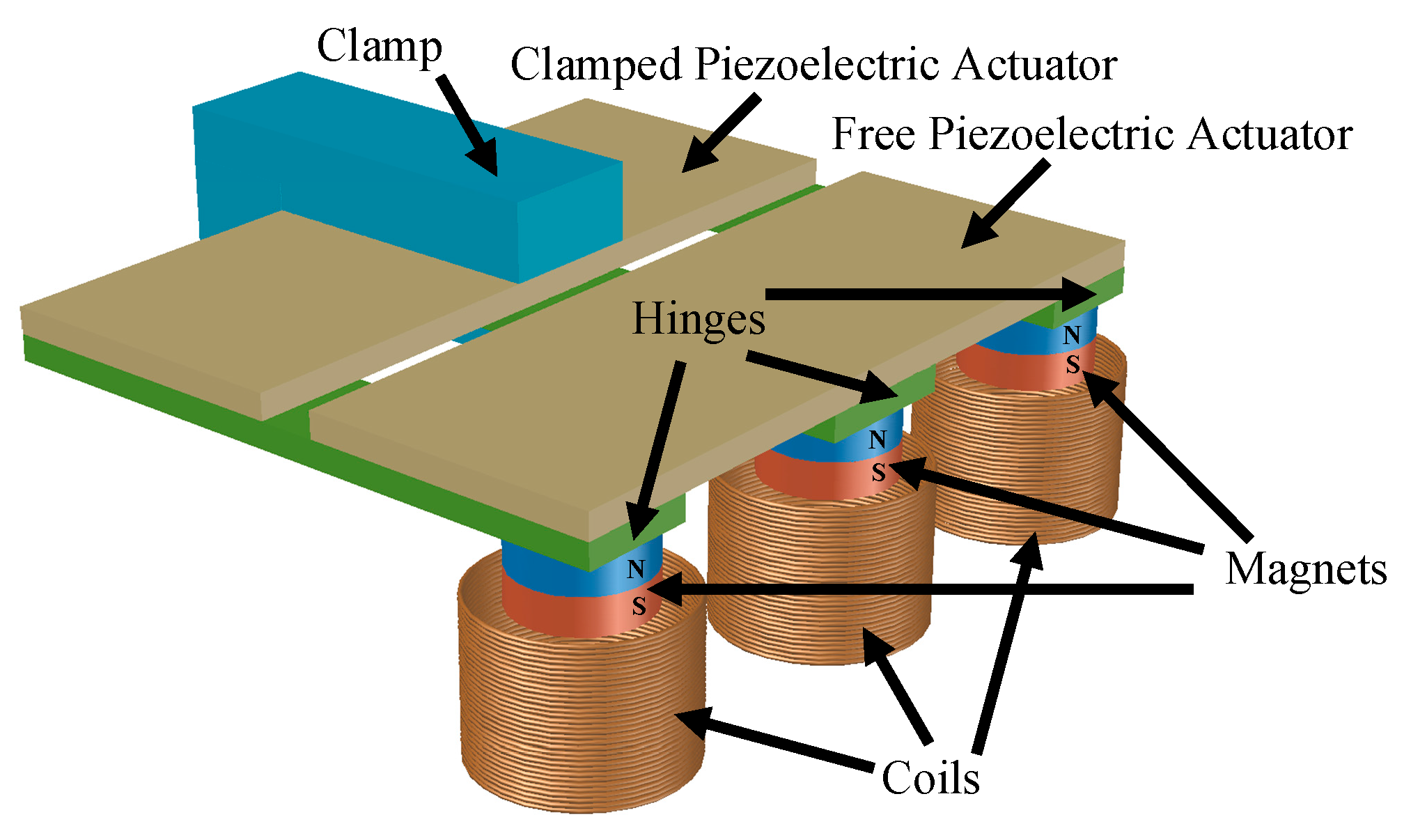
4.1. Magnetic Forces Based MTTs
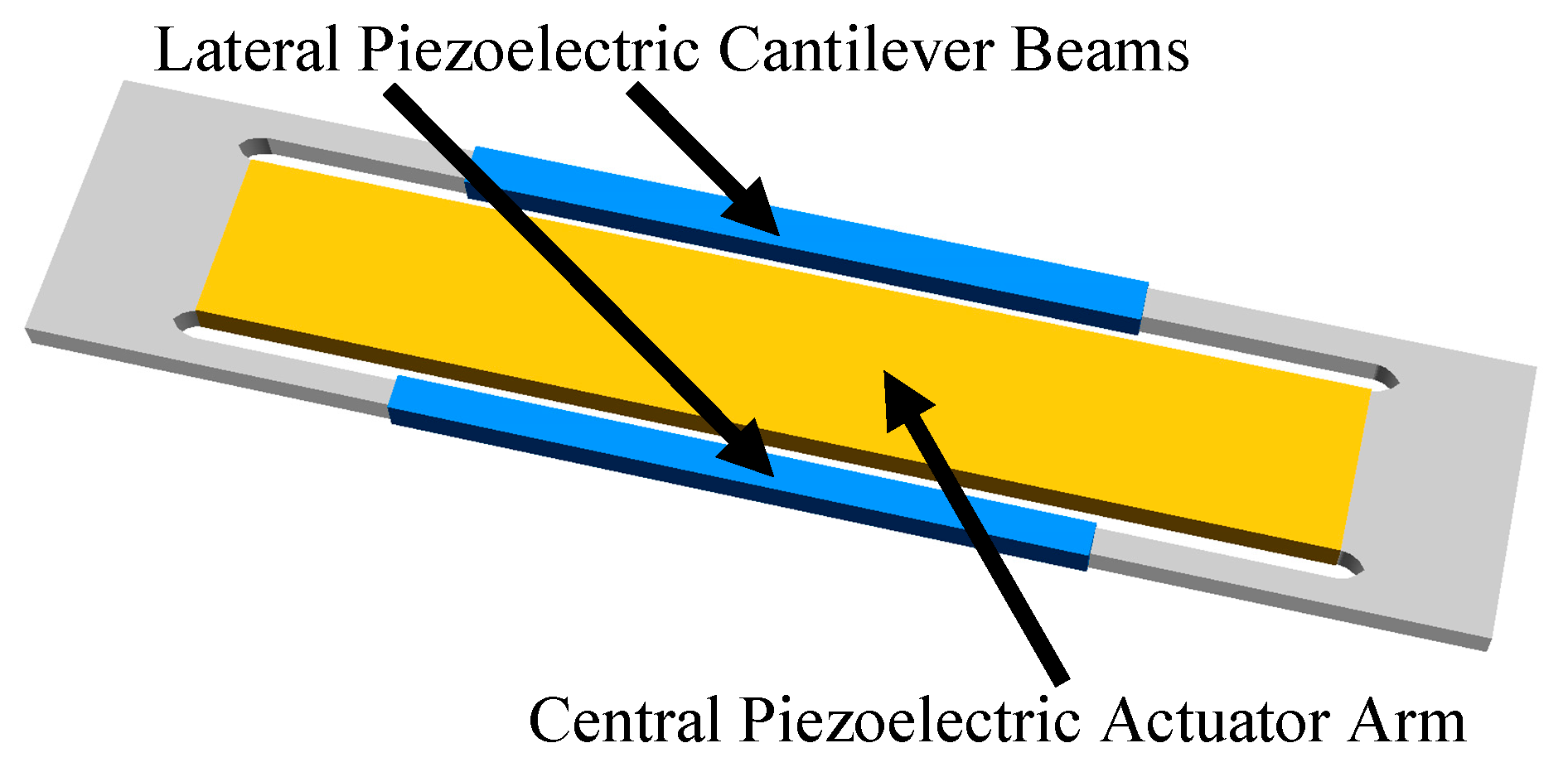
4.2. Piezoelectric Actuators Based MTTs
4.3. Axial Loads Based MTTs
4.4. Clamp Position Change Based MTTs
4.5. Variable Reluctance Based MTTs
4.6. Variable Center of Gravity Based MTTs
5. Discussions and Open Issues
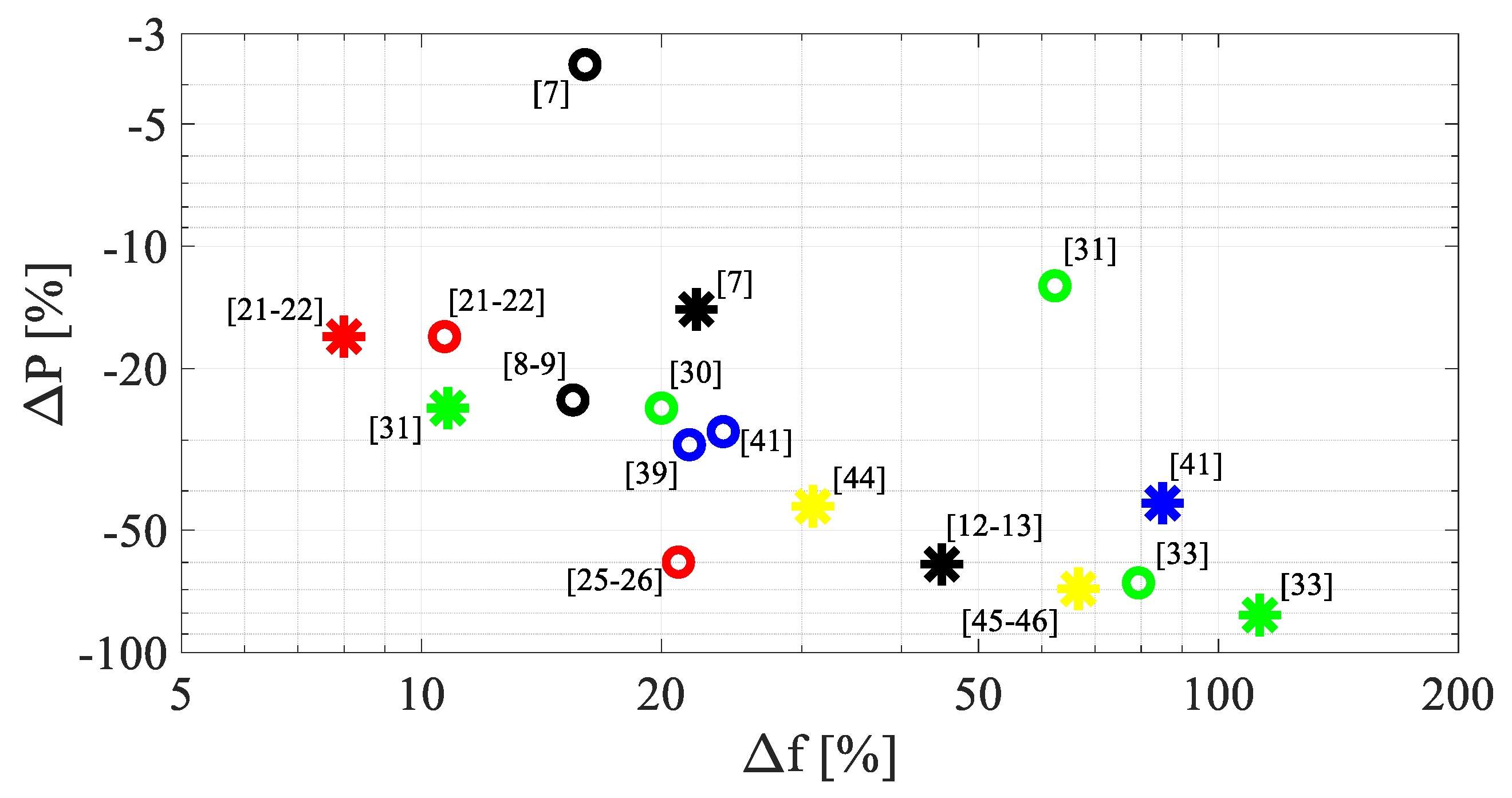
- First of all, it is possible to observe that, in all the papers focusing on MTTs, no attention at all is paid to ETTs. As it has been evidenced in Section 2, for the optimal exploitation of a RVEH both tuning techniques should be applied. Therefore, the need exists for a study of the joint application of both MTTs and ETTs. In addition, since in most papers reported in Figure 26 and Figure 27 a pure resistive load is considered, it is possible to state they are associated to underestimated results as their power performance is concerened.
- An important observation is worth noting. All the MTTs are based on the fact that RVEHs can be schematically represented (as discussed in Section 2.1) by means of spring-mass-damper systems. The mechanical resonance frequency of such systems (see (30) and (31)) depends on the values of the mass and of the stiffness and therefore it can be varied by acting on such two parameters values. In particular, for obvious reasons, it is easier to adopt a MTT that, during the RVEH operation, changes the stiffness rather than the value of the oscillating mass. In fact, nearly all the analyzed MTTs are based on the change of the stiffness. The application of a MTT for the increase of the resonance frequency by varying only the stiffness of the spring-mass-damper system is preferable also from another point of view. In fact, at least in principle, on the basis of (30) and (31), the increase of fres by means of the variation of the stiffness does not affect the maximum extractable power PMAX. Instead, the increase of fres by acting on the movable mass, requires the reduction of the value of such a mass with a consequent reduction of the maximum extractable power PMAX as shown in (32) and (33). It is worth noting instead that, in the case of application of a MTT for reducing fres, the variation of the moving mass (although unpractical) should be preferred with respect to that of the stiffness. In fact, at least in principle, on the basis of (32) and (33), the value of such a mass should be increased with a consequent increase of the maximum extractable power PMAX.
- From the analysis reported in Section 4 also another important aspect must be underlined. The tuning periods of the MTTs usually have too high values that can lead to questionable practical applicability of these techniques. In fact, a large tuning period means that a change in the frequency can be carried out only with a low speed, leading to quite slow MTTs that are able to track only vibrations characterised by relative slow dynamics. Therefore, an important objective for future research activities must be the reduction of the values of the tuning periods.
- It is clear that MTTs that are based on a closed-loop control are surely more robust and do not need a precharacterization of the system. However, they need sensors in order to implement the feedback circuitry and hence require much energy for their operation. Instead the MTTs that are based on an open-loop control require less energy but need a precharacterization of the system (e.g., for the definition of a LUT) and are less robust since they are affected by possible errors due to system parameters change. Trade-off solutions between closed-loop and open-loop adopting LUTs with “learning capability” seem to be very promising [25,26,38]. The MTTs that are more suitable for closed-loop controls are the piezoelectric actuators based MTTs since they can be simply controlled by acting on a voltage. In principle, it could be also possible to implement a MTT that is controlled in a closed-loop by acting on a current flowing in a proper coil in a magnetic forces based MTT. No system of this type has been proposed in the literature yet.
- A further aspect to underline is that, at the moment, all the MTTs are designed and tested in the case of purely sinusoidal vibrations. However, as stated in Section 3, purely sinusoidal vibrations are nearly impossible to be found in practical applications. Actual vibrations are usually periodic (with a fundamental component plus harmonics), random (with an energy content that is distributed over a wide frequency spectrum), or single event motions (as in the case of impacts) [84,85,86]. This is a crucial aspect and is an open issue for nearly all the RVEHs applications. In particular, as it can be observed from Section 4, many MTTs are based on the measurement of the vibration frequency. In the presence of purely sinusoidal vibrations such a task is quite simple. However, when the input vibrations are non-sinusoidal the task becomes much more complex and the detection of the vibration zero-crossings could mislead the MTT. A solution to such a problem could be a perturbative approach such as the one that is implemented in maximum power point tracking applications for RVEHs [98,100]. The perturbative approach could get rid of the measurement of the vibration frequency, since it could be based on the measurement of the extracted power and could adapt the RVEH’s resonance frequency in order to maximize such a power. Moreover, in this case the gap in the literature on such an important issue needs to be filled.
- Another important observation concerns the compliance of MTTs with miniaturization. In fact, miniaturization is of crucial importance in order to make RVEHs equipped with MTTs and suitable for wireless sensors networks or biosensors applications. Obviously, all the MTTs that are implemented by using cumbersome motors or mechanical actuators are not compatible with miniaturized systems and therefore further research on such a topic is necessary.
- Among all the analyzed MTTs, a very interesting property is the “passive self-tuning” capability that characterizes the variable center of gravity based MTT proposed in [45,46]. In particular, it has an auto-tune resonance frequency property due to the continuous change in the center of gravity following the vibration frequency change. This is a very important mechanical property that leads to a system that does not need any external control circuitry and its associated energy consumption. Such an interesting property could be the starting point for the future identification of other types of structures with auto-tuning capabilities.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Siang, J.; Lim, M.H.; Salman Leong, M. Review of vibration-based energy harvesting technology: Mechanism and architectural approach. Int. J. Energy Res. 2018, 42, 1866–1893. [Google Scholar] [CrossRef]
- Abdelkareem, M.A.A.; Xu, L.; Ahmed Ali, M.K.; Elagouz, A.; Mi, J.; Guo, S.; Liu, Y.; Zuo, L. Vibration energy harvesting in automotive suspension system: A detailed review. Appl. Energy 2018, 229, 672–699. [Google Scholar] [CrossRef]
- Luigi, C.; Massimo, V.; Yu, P.; Zuo, L. Maximizing the power extraction from train suspension energy harvesting system. In Proceedings of the ASME 2019 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Anaheim, CA, USA, 18–21 August 2019. Volume 8: 31st Conference on Mechanical Vibration and Noise. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, K.; Wang, D.; Chen, C.; Li, X. Energy conversion mechanism and regenerative potential of vehicle suspensions. Energy 2017, 119, 961–970. [Google Scholar] [CrossRef]
- Zuo, L.; Scully, B.; Shestani, J.; Zhou, Y. Design and characterization of an electromagnetic energy harvester for vehicle suspensions. Smart Mater. Struct. 2010, 19, 045003. [Google Scholar] [CrossRef]
- Balato, M.; Costanzo, L.; Vitelli, M. MPPT in wireless sensor nodes supply systems based on electromagnetic vibration harvesters for freight wagons applications. IEEE Trans. Ind. Electron. 2017, 64, 3576–3586. [Google Scholar] [CrossRef]
- Challa, V.R.; Prasad, M.G.; Shi, Y.; Fisher, F.T. A vibration energy harvesting device with bidirectional resonance frequency tunability. Smart Mater. Struct. 2008, 1, 15035. [Google Scholar] [CrossRef]
- Podder, P.; Constantinou, P.; Mallick, D.; Amann, A.; Roy, S. Magnetic tuning of nonlinear MEMS electromagnetic vibration energy harvester. J. Microelectromech. Syst. 2017, 26, 539–549. [Google Scholar] [CrossRef]
- Podder, P.; Constantinou, P.; Amann, A.; Roy, S. Frequency adjustable MEMS vibration energy harvester. J. Phys. Conf. Ser. 2016, 757, 012037. [Google Scholar] [CrossRef]
- Dong, L.; Prasad, M.G.; Fisher, F.T. Two-dimensional resonance frequency tuning approach for vibration-based energy harvesting. Smart Mater. Struct. 2016, 6, 65019. [Google Scholar] [CrossRef]
- Aboulfotoh, N.A.; Arafa, M.H.; Megahed, S.M. A self-tuning resonator for vibration energy harvesting. Sens. Actuators A Phys. 2013, 201, 328–334. [Google Scholar] [CrossRef]
- Zhu, D.; Roberts, S.; Tudor, M.J.; Beeby, S.P. Closed loop frequency tuning of a vibration-based micro-generator. In Proceedings of the PowerMEMS 2008 microEMS2008, Sendai, Japan, 9–12 November 2008; pp. 229–232. [Google Scholar]
- Zhu, D.; Roberts, S.; Tudor, M.J.; Beeby, S.P. Design and experimental characterization of a tunable vibration-based electromagnetic micro-generator. Sens. Actuators A Phys. 2010, 158, 284–293. [Google Scholar] [CrossRef]
- Al-Ashtari, W.; Hunstig, M.; Hemsel, T.; Sextro, W. Frequency tuning of piezoelectric energy harvesters by magnetic force. Smart Mater. Struct. 2012, 3, 35019. [Google Scholar] [CrossRef]
- Hoffmann, D.; Willmann, A.; Hehn, T.; Folkmer, B.; Manoli, Y. A self-adaptive energy harvesting system. Smart Mater. Struct. 2016, 3, 35013. [Google Scholar] [CrossRef]
- Hoffmann, D.; Willmann, A.; Folkmer, B.; Manoli, Y. Tunable vibration energy harvester for condition monitoring of maritime gearboxes. J. Phys. Conf. Ser. 2014, 557, 012099. [Google Scholar] [CrossRef]
- Mansour, M.O.; Arafa, M.H.; Megahed, S.M. Resonator with magnetically adjustable natural frequency for vibration energy harvesting. Sens. Actuators A Phys. 2010, 163, 297–303. [Google Scholar] [CrossRef]
- Chung, T.K.; Wang, C.M.; Yeh, P.C.; Liu, T.W.; Tseng, C.Y.; Chen, C.C. A three-axial frequency-tunable piezoelectric energy harvester using a magnetic-force configuration. IEEE Sens. J. 2014, 14, 3152–3163. [Google Scholar] [CrossRef]
- Li, M.; Wen, Y.; Li, P.; Yang, J. A magnetostrictive/piezoelectric laminate transducer based vibration energy harvester with resonance frequency tunability. In Proceedings of the 2011 IEEE Sensors Proceedings, Limerick, Ireland, 28–31 October 2011; pp. 1768–1771. [Google Scholar] [CrossRef]
- Davidson, J.R.; Mo, C. Piezoelectric energy harvesting with frequency tuning for ventilation system monitoring. Int. J. Eng. Sci. Innov. Technol. 2013, 5, 114–124. [Google Scholar]
- Wischke, M.; Masur, M.; Goldschmidtboeing, F.; Woias, P. Piezoelectrically tunable electromagnetic vibration harvester. In Proceedings of the 2010 IEEE 23rd International Conference on Micro Electro Mechanical Systems (MEMS), Hong Kong, China, 24–28 January 2010; pp. 1199–1202. [Google Scholar] [CrossRef]
- Wischke1, M.; Masur, M.; Goldschmidtboeing, F.; Woias, P. Electromagnetic vibration harvester with piezoelectrically tunable resonance frequency. J. Micromech. Microeng. 2010, 20, 035025. [Google Scholar] [CrossRef]
- Peters, C.; Maurath, D.; Schock, W.; Mezger, F.; Manoli, Y. A closed-loop wide-range tunable mechanical resonator for energy harvesting systems. J. Micromech. Microeng. 2009, 19, 094004. [Google Scholar] [CrossRef]
- Peters, C.; Maurath, D.; Schock, W.; Manoli, Y. Novel electrically tunable mechanical resonator for energy harvesting. In Proceedings of the PowerMEMS 2008, Sendai, Japan, 9–12 November 2008; pp. 253–256. [Google Scholar]
- Eichhorn, C.; Tchagsim, R.; Wilhelm, N.; Woias, P. A smart and self-sufficient frequency tunable vibration energy harvester. J. Micromech. Microeng. 2011, 21, 104003. [Google Scholar] [CrossRef]
- Eichhorn, C.; Tchagsim, R.; Wilhelm, N.; Goldschmidtboeing, F.; Woias, P. A compact piezoelectric energy harvester with a large resonance frequency tuning range. In Proceedings of the PowerMEMS 2010, Leuven, Belgium, 1–3 December 2010; pp. 207–211. [Google Scholar]
- Eichhorn, C.; Goldschmidtboeing, F.; Porro, Y.; Woias, P. A piezoelectric harvester with an integrated frequency-tuning mechanism. In Proceedings of the PowerMEMS, Washington, DC, USA, 1–4 December 2009; pp. 45–48. [Google Scholar]
- Eichhorn, C.; Tchagsim, R.; Wilhelm, N.; Biancuzzi, G.; Woias, P. An energy-autonomous self-tunable piezoelectric vibration energy harvesting system. In Proceedings of the 2011 IEEE 24th International Conference on Micro Electro Mechanical Systems, Cancun, Mexico, 23–27 January 2011; pp. 1293–1296. [Google Scholar]
- Cheng, Y.; Wu, N.; Wang, Q. An efficient piezoelectric energy harvester with frequency self-tuning. J. Sound Vib. 2017, 396, 69–82. [Google Scholar] [CrossRef]
- Leland, E.S.; Wright, P.K. Resonance tuning of piezoelectric vibration energy scavenging generators using compressive axial preload. Smart Mater. Struct. 2006, 15, 1413. [Google Scholar] [CrossRef]
- Morris, D.J.; Youngsman, J.M.; Anderson, M.J.; Bahr, D.F. A resonant frequency tunable, extensional mode piezoelectric vibration harvesting mechanism. Smart Mater. Struct. 2008, 17, 65021. [Google Scholar] [CrossRef]
- Eichhorn, C.; Goldschmidtboeing, F.; Woias, P. Bidirectional frequency tuning of a piezoelectric energy converter based on a cantilever beam. J. Micromech. Microeng. 2009, 19, 94006. [Google Scholar] [CrossRef]
- Eichhorn, C.; Goldschmidtboeing, F.; Woias, P. A frequency tunable piezoelectric energy converter based on a cantilever beam. In Proceedings of the PowerMEMS 2008, Sendai, Japan, 9–12 November 2008; pp. 309–312. [Google Scholar]
- Niri, E.D.; Salamone, S. A passively tunable mechanism for a dual bimorph energy harvester with variable tip stiffness and axial load. Smart Mater. Struct. 2012, 21, 125025. [Google Scholar] [CrossRef]
- Mounting Guidelines. Available online: https://support.piezo.com/article/126-mounting-guidelines (accessed on 18 January 2020).
- Piezoelectric Energy Harvesters. Available online: https://piezo.com/collections/piezoelectric-energy-harvesters?_=pf&pf_t_quantity=Quantity__1 (accessed on 18 January 2020).
- Yun, W.; He, H.; Xu, R. An analytical model for a piezoelectric vibration energy harvester with resonance frequency tunability. Adv. Mech. Eng. 2015, 7. [Google Scholar] [CrossRef]
- Huang, S.C.; Lin, K.A. A novel design of a map-tuning piezoelectric vibration energy harvester. Smart Mater. Struct. 2012, 21, 85014. [Google Scholar] [CrossRef]
- Ayala-Garcia, I.N.; Mitcheson, P.D.; Yeatman, E.M.; Zhu, D.; Tudor, J.; Beeby, S.P. Magnetic tuning of a kinetic energy harvester using variable reluctance. Sens. Actuators A Phys. 2013, 189, 266–275. [Google Scholar] [CrossRef]
- Beeby, S.P.; Torah, R.N.; Tudor, M.J.; Glynne-Jones, P.; Donnell Saha, C.R.; Roy, S. A micro electromagnetic generator for vibration energy harvesting. J. Micromech. Microeng. 2007, 17, 1257–1265. [Google Scholar] [CrossRef]
- Xia, H.; Chen, R.; Ren, L. Parameter tuning of piezoelectric–electromagnetic hybrid vibration energy harvester by magnetic force: Modeling and experiment. Sens. Actuators A Phys. 2017, 257, 73–83. [Google Scholar] [CrossRef]
- Mukherjee, A.G.; Mitcheson, P.D.; Wright, S.W.; Yeatman, E.M. Tuning resonant energy harvesters using a variable reluctance link. In Proceedings of the Technical Digest Power MEMS 2011, Soul, Korea, 23–27 January 2011; pp. 11–14. [Google Scholar]
- Wu, X.; Lin, J.; Kato, S.; Zhang, K.; Ren, T.; Liu, L. A frequency adjustable vibration energy harvester. In Proceedings of the PowerMEMS, Sendai, Japan, 9–12 November 2008; pp. 245–248. [Google Scholar]
- Schaufuss, J.; Scheibner, D.; Mehner, J. New approach of frequency tuning for kinetic energy harvesters. Sens. Actuators A Phys. 2011, 171, 352–360. [Google Scholar] [CrossRef]
- Chandwani, J.; Somkuwar, R.; Deshmukh, R. Multi-band piezoelectric vibration energy harvester for low-frequency applications. Microsyst Technol. 2019, 25, 3867–3877. [Google Scholar] [CrossRef]
- Somkuwar, R.; Chandwani, J.; Deshmukh, R. Wideband auto-tunable vibration energy harvester using change in centre of gravity. Microsyst Technol. 2018, 24, 3033–3044. [Google Scholar] [CrossRef]
- Kozinsky, I. Study of passive self-tuning resonator for broadband power harvesting. In Proceedings of the Power MEMS, Washington, DC, USA, 1–4 December 2009; pp. 388–389. [Google Scholar]
- Karadag, C.; Topaloglu, N. A self-sufficient and frequency tunable piezoelectric vibration energy harvester. ASME J. Vib. Acoust. 2016, 139. [Google Scholar] [CrossRef]
- Aboulfotoh, N.; Twiefel, J.; Krack, M.; Wallaschek, J. Experimental study on performance enhancement of a piezoelectric vibration energy harvester by applying self-resonating behavior. Energy Harvest. Syst. 2017, 4, 131–136. [Google Scholar] [CrossRef]
- Madinei, H.; Khodaparast, H.H.; Adhikari, S.; Friswell, M.I.; Fazeli, M. Adaptive tuned piezoelectric MEMS vibration energy harvester using an electrostatic device. Eur. Phys. J. Spec. Top. 2015, 224, 2703–2717. [Google Scholar] [CrossRef]
- Heit, J.; Christensen, D.; Roundy, S. A vibration energy harvesting structure, tunable over a wide frequency range using minimal actuation. In Proceedings of the ASME 2013 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, Snowbird, UT, USA, 16–18 September 2013; Volume 2: Mechanics and Behavior of Active Materials; Structural Health Monitoring; Bioinspired Smart Materials and Systems; Energy Harvesting. American Society of Mechanical Engineers: New York, NY, USA, 2013; Volume 2. [Google Scholar]
- Anup, P.; Batra, R.C. Beam-based vibration energy harvesters tunable through folding. J. Vib. Acoust. 2019, 141, 011003. [Google Scholar]
- Wang, X.; Chen, C.; Wang, N.; San, H.; Yu, Y.; Halvorsen, E.; Chen, X. A frequency and bandwidth tunable piezoelectric vibration energy harvester using multiple nonlinear techniques. Appl. Energy 2017, 190, 368–375. [Google Scholar] [CrossRef]
- Ibrahim, P.; Nassar, O.; Arafa, M.; Anis, Y. On adjusting the rotary inertia of a cantilever-type energy harvester for wideband operation. Procedia Eng. 2017, 199, 3422–3427. [Google Scholar] [CrossRef]
- Xie, L.; Du, R. Frequency tuning of a nonlinear electromagnetic energy harvester. ASME. J. Vib. Acoust. 2013, 136. [Google Scholar] [CrossRef]
- Lee, B.C.; Chung, G.S. Frequency tuning design for vibration-driven electromagnetic energy harvester. IET Renew. Power Gener. 2015, 9, 801–808. [Google Scholar] [CrossRef]
- Lee, B.C.; Chung, G.S. A novel frequency tuning design for vibration-driven electromagnetic energy harvester. In Proceedings of the 2015 IEEE SENSORS, Busan, Korea, 1–4 November 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Hassan, E.; Eugeni, M.; Gaudenzi, P. A review on mechanisms for piezoelectric-based energy harvesters. Energies 2018, 11, 1850. [Google Scholar]
- Yang, Z.; Zhou, S.; Zu, J.; Inman, D. High-performance piezoelectric energy harvesters and their applications. Joule 2018, 2, 642–697. [Google Scholar] [CrossRef]
- Liu, H.; Zhong, J.; Lee, C.; Lee, S.-W.; Lin, L. A comprehensive review on piezoelectric energy harvesting technology: Materials, mechanisms, and applications. Appl. Phys. Rev. 2018, 5, 041306. [Google Scholar] [CrossRef]
- Tan, Y.; Dong, Y.; Wang, X. Review of MEMS electromagnetic vibration energy harvester. J. Microelectromech. Syst. 2017, 26, 1–16. [Google Scholar] [CrossRef]
- Balato, M.; Costanzo, L.; Vitelli, M. Maximization of the extracted power in resonant electromagnetic vibration harvesters applications employing bridge rectifiers. Sens. Actuators A Phys. 2017, 263, 63–75. [Google Scholar] [CrossRef]
- Naifar, S.; Bradai, S.; Viehweger, C.; Kanoun, O. Survey of electromagnetic and magnetoelectric vibration energy harvesters for low frequency excitation. Measurement 2017, 106, 251–263. [Google Scholar] [CrossRef]
- Yasuyuki, N.; Uenishi, K. Electrostatic MEMS vibration energy harvesters inside of tire treads. Sensors 2019, 19, 890. [Google Scholar] [CrossRef]
- Balato, M.; Costanzo, L.; Vitelli, M. Closed-form analysis of switchless electrostatic vibration energy harvesters. In Proceedings of the Ecological Vehicles and Renewable Energies (EVER), 2015 Tenth International Conference on, Monte Carlo, Monaco, 31 March–2 April 2015; pp. 1–7. [Google Scholar] [CrossRef]
- Kempitiya, A.; Borca-Tasciuc, D.A.; Hella, M.M. Analysis and optimization of asynchronously controlled electrostatic energy harvesters. IEEE Trans. Ind. Electron. 2012, 59, 456–463. [Google Scholar] [CrossRef]
- Thomson, G.; Yurchenko, D.; Val, D.V.; Zhang, Z. Predicting energy output of a stochastic nonlinear dielectric elastomer generator. Energy Convers. Manag. 2019, 196, 1445–1452. [Google Scholar] [CrossRef]
- Thomson, G.; Lai, Z.; Val, D.V.; Yurchenko, D. Advantages of nonlinear energy harvesting with dielectric elastomers. J. Sound Vib. 2019, 442, 167–182. [Google Scholar] [CrossRef]
- Backman, G.; Lawton, B.; Morley, N.A. Magnetostrictive energy harvesting: Materials and design study. IEEE Trans. Magn. 2019. [Google Scholar] [CrossRef]
- Narita, F.; Fox, M. A review on piezoelectric, magnetostrictive, and magnetoelectric materials and device technologies for energy harvesting applications. Adv. Eng. Mater. 2018, 20, 1700743. [Google Scholar] [CrossRef]
- Yang, Z.; Nakajima1, K.; Onodera, R.; Tayama, T.; Chiba, D.; Narita, F. Magnetostrictive clad steel plates for high-performance vibration energy harvesting. Appl. Phys. Lett. 2018, 112, 073902. [Google Scholar] [CrossRef]
- Xu, L.; Jiang, T.; Lin, P.; Shao, J.; He, C.; Zhong, W.; Chen, X.; Wang, Z. Coupled Triboelectric Nanogenerator Networks for Efficient Water Wave Energy Harvesting. ACS Nano 2018, 12, 1849–1858. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.L.; Jiang, T.; Xu, L. Toward the blue energy dream by triboelectric nanogenerator networks. Nano Energy 2017, 39, 9–23. [Google Scholar] [CrossRef]
- Costanzo, L.; Lo Schiavo, A.; Vitelli, M. Power extracted from piezoelectric harvesters driven by non-sinusoidal vibrations. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 1291–1303. [Google Scholar] [CrossRef]
- Balato, M.; Costanzo, L.; Vitelli, M. Resonant electromagnetic vibration harvesters: Determination of the equivalent electric circuit parameters and simplified closed-form analysis for the identification of the optimal diode bridge rectifier DC load. Int. J. Electr. Power Energy Syst. 2017, 84, 111–123. [Google Scholar] [CrossRef]
- Al-Ashtari, W.; Hunstig, M.; Hemsel, T.; Sextro, W. Analytical determination of characteristic frequencies and equivalent circuit parameters of a piezoelectric bimorph. J. Intell. Mater. Syst. Struct. 2012, 23, 15–23. [Google Scholar] [CrossRef]
- Kong, C.S. A general maximum power transfer theorem. IEEE Trans. Educ. 1995, 38, 296–298. [Google Scholar] [CrossRef]
- Dhakar, L.; Liu, H.; Tay, F.E.H.; Lee, C. A new energy harvester design for high power output at low frequencies. Sens. Actuators A Phys. 2013, 199, 344–352. [Google Scholar] [CrossRef]
- Du, S.; Yu, J.; Seshia, A. Maximizing output power in a cantilevered piezoelectric vibration energy harvester by electrode design. J. Phys. Conf. Ser. 2015, 660, 012114. [Google Scholar] [CrossRef]
- Foisal, A.R.M.; Lee, B.; Chung, G. Fabrication and performance optimization of an AA size electromagnetic energy harvester using magnetic spring. In Proceedings of the Sensors 2011 IEEE, Limerick, Ireland, 28–31 October 2011; pp. 1125–1128. [Google Scholar] [CrossRef]
- Frank, G.; Woias, P. Characterization of different beam shapes for piezoelectric energy harvesting. J. Micromech. Microeng. 2008, 18, 104013. [Google Scholar]
- Ben Ayed, S.; Abdelkefi, A.; Najar, F.; Hajj, M.R. Design and performance of variable-shaped piezoelectric energy harvesters. J. Intell. Mater. Syst. Struct. 2014, 25, 174–186. [Google Scholar] [CrossRef]
- Muthalif, A.G.A.; Diyana Nordin, N.H. Optimal piezoelectric beam shape for single and broadband vibration energy harvesting: Modeling, simulation and experimental results. Mech. Syst. Signal Process. 2015, 54, 417–426. [Google Scholar] [CrossRef]
- Rahman, M.F.B.A.B.; Kok, S.L. Investigation of useful ambient vibration sources for the application of energy harvesting. In Proceedings of the 2011 IEEE Students Conference on Research and Development (SCOReD), Cyberjaya, Malaysia, 19–20 December 2011; pp. 391–396. [Google Scholar]
- Neri, I.; Neild, S.; Travasso, F.; Mincigrucci, R.; Vocca, H.; Orfei, F.; Gammaitoni, L. A real vibration database for kinetic energy harvesting application. J. Intell. Mater. Syst. Struct. 2012. [Google Scholar] [CrossRef]
- Petersen, D.; Howarda, C.; Sawalhi, N.; Ahmadia, A.M.; Singha, S. Analysis of bearing stiffness variations, contact forces and vibrations in radially loaded double row rolling element bearings with raceway defects. Mech. Syst. Signal Proc. 2015, 50–51, 139–160. [Google Scholar] [CrossRef]
- Zhu, D.; Tudor, M.J.; Beeby, S.P. Strategies for increasing the operating frequency range of vibration energy harvesters: A review. Meas. Sci. Technol. 2010, 21, 022001. [Google Scholar] [CrossRef]
- Yang, Z.; Zu, J.; Xu, Z. Reversible nonlinear energy harvester tuned by tilting and enhanced by nonlinear circuits. IEEE/ASME Trans. Mechatron. 2016, 21, 2174–2184. [Google Scholar] [CrossRef]
- Liu, H.; Gudla, S.; Hassani, F.A.; Heng, C.H.; Lian, Y.; Lee, C. Investigation of the nonlinear electromagnetic energy harvesters from hand shaking. IEEE Sens. J. 2015, 15, 2356–2364. [Google Scholar] [CrossRef]
- Andò, B.; Baglio, S.; Bulsara, A.R.; Marletta, V.; Pistorio, A. Experimental and theoretical investigation of a nonlinear vibrational energy harvester. Procedia Eng. 2015, 120, 1024–1027. [Google Scholar] [CrossRef]
- Li, C.; Wu, S.; Luk, P.C.K.; Gu, M.; Jiao, Z. Enhanced bandwidth nonlinear resonance electromagnetic human motion energy harvester using magnetic springs and ferrofluid. IEEE/ASME Trans. Mechatron. 2019, 24, 710–717. [Google Scholar] [CrossRef]
- Ullah, K.F. Review of non-resonant vibration based energy harvesters for wireless sensor nodes. J. Renew. Sustain. Energy 2016, 8, 044702. [Google Scholar]
- Mergen, T.N.; Ghayesh, H.; Arjomandi, M. Ambient vibration energy harvesters: A review on nonlinear techniques for performance enhancement. Int. J. Eng. Sci. 2018, 127, 162–185. [Google Scholar] [CrossRef]
- Haim, A.; Har-nes, I. Analysis and experimental validation of a piezoelectric harvester with enhanced frequency bandwidth. Materials 2018, 11, 1243. [Google Scholar] [CrossRef]
- Kazmierski, T.J.; Beeby, S. Energy Harvesting Systems; Springer: Berlin, Germany, 2014. [Google Scholar]
- Bowden, J.A.; Burrow, S.G.; Cammarano, A.; Clare, L.R.; Mitcheson, P.D. Switched-mode load impedance synthesis to parametrically tune electromagnetic vibration energy harvesters. IEEE/ASME Trans. Mechatron. 2015, 20, 603–610. [Google Scholar] [CrossRef]
- Costanzo, L.; Lo Schiavo, A.; Vitelli, M. Power maximization from resonant electromagnetic vibration harvesters feeding bridge rectifiers. Int. J. Circ. Theor. Appl. 2019, 47, 87–102. [Google Scholar] [CrossRef]
- Balato, M.; Costanzo, L.; Lo Schiavo, A.; Vitelli, M. Optimization of both perturb & observe and open circuit voltage mppt techniques for resonant piezoelectric vibration harvesters feeding bridge rectifiers. Sens. Actuators A Phys. 2018, 278, 85–97. [Google Scholar] [CrossRef]
- Kamali, S.H.; Moallem, M.; Arzanpour, S. A self-tuning vibration energy harvester with variable loads and maximum allowable displacement. Smart Mater. Struct. 2018, 27, 105015. [Google Scholar] [CrossRef]
- Costanzo, L.; Vitelli, M. Resonant electromagnetic vibration harvesters applications: Optimization of P&O MPPT technique parameters. In Proceedings of the Thirteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 10–12 April 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Du, S.; Jia, Y.; Do, C.D.; Seshia, A.A. An efficient sshi interface with increased input range for piezoelectric energy harvesting under variable conditions. IEEE J. Solid State Circuits 2016, 51, 2729–2742. [Google Scholar] [CrossRef]
- Rincón-Mora, G.A.; Yang, S. Tiny piezoelectric harvesters: Principles, constraints, and power conversion. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 63, 639–649. [Google Scholar] [CrossRef]
- Gu, L.; Livermore, C. Passive self-tuning energy harvester for extracting energy from rotational motion. Appl. Phys. Lett. 2010, 97, 081904. [Google Scholar] [CrossRef]
- Gu, L.; Livermore, C. Compact passively self-tuning energy harvesting for rotating applications. Smart Mater. Struct. 2012, 21, 015002. [Google Scholar] [CrossRef]
- Wang, Y.-J.; Chuang, T.-Y.; Yu, J.-H. Design and kinetic analysis of piezoelectric energy harvesters with self-adjusting resonant frequency. Smart Mater. Struct. 2017, 26, 095037. [Google Scholar]
- Alevras, P.; Theodossiades, S. Vibration energy harvester for variable speed rotor applications using passively self-tuned beams. J. Sound Vib. 2019, 444, 176–196. [Google Scholar] [CrossRef]
- Li, M.; Wen, Y.; Li, P.; Yang, J. A resonant frequency self-tunable rotation energy harvester based on magnetoelectric transducer. Sens. Actuators A 2013, 194, 16–24. [Google Scholar] [CrossRef]
- Kim, H.; Tai, W.C.; Zuo, L. Self-tuning stochastic resonance energy harvester for smart tires. In Proceedings of the SPIE 10595, Active and Passive Smart Structures and Integrated Systems XII, 105950U, Denver, CO, USA, 4–8 March 2018. [Google Scholar]


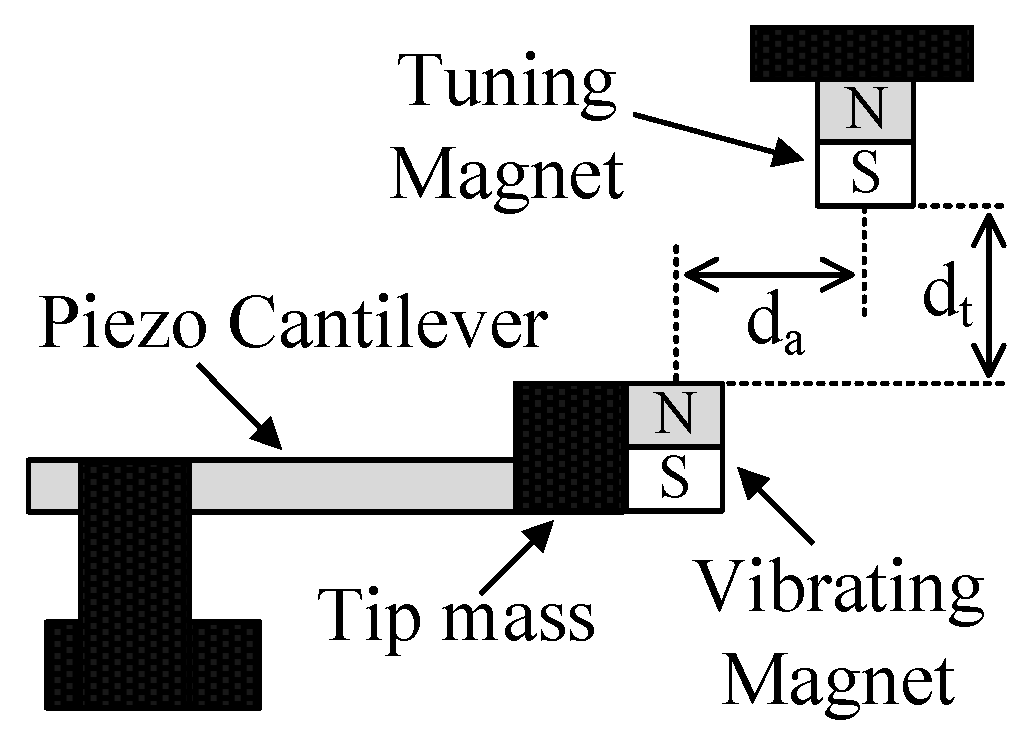
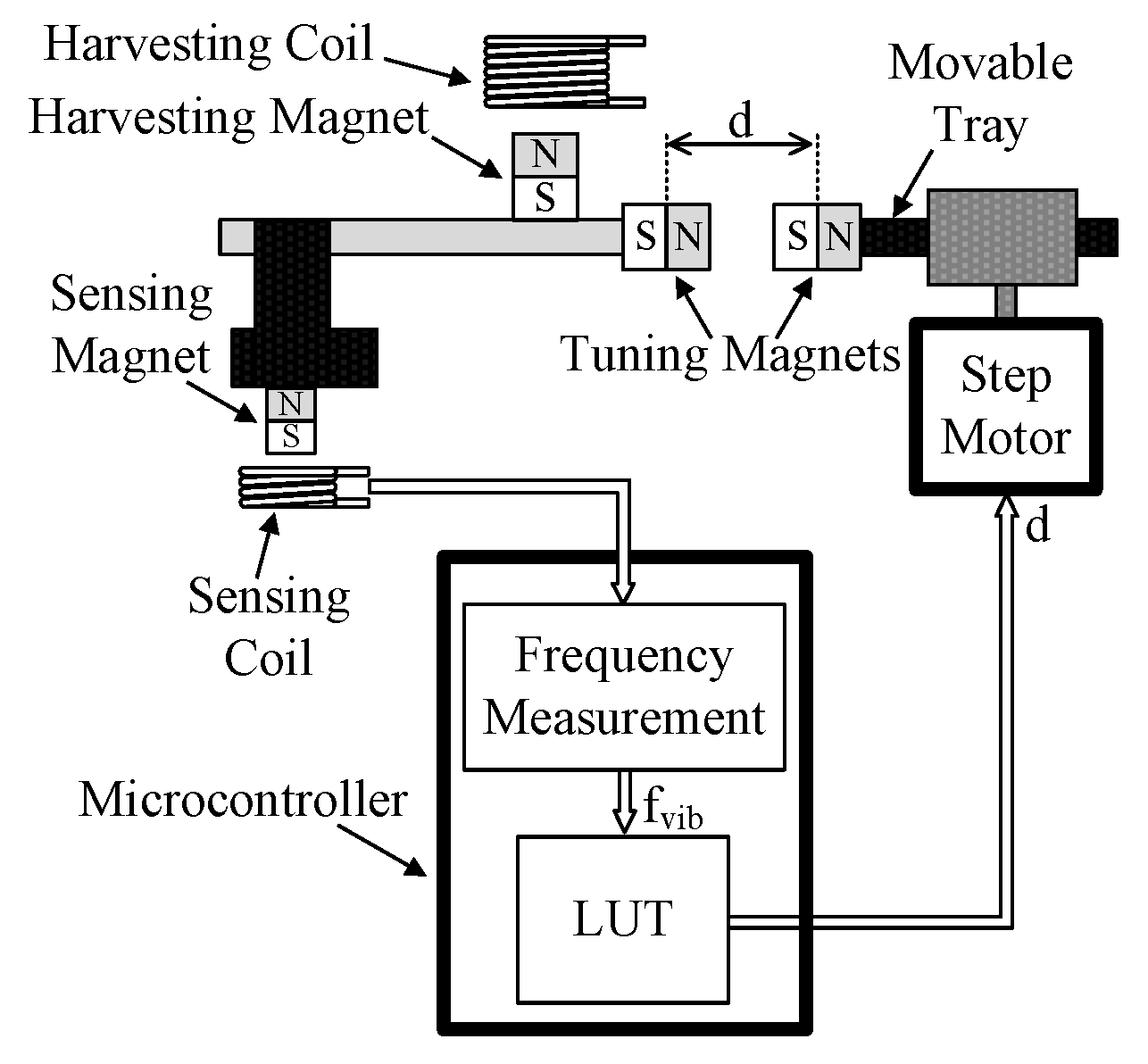
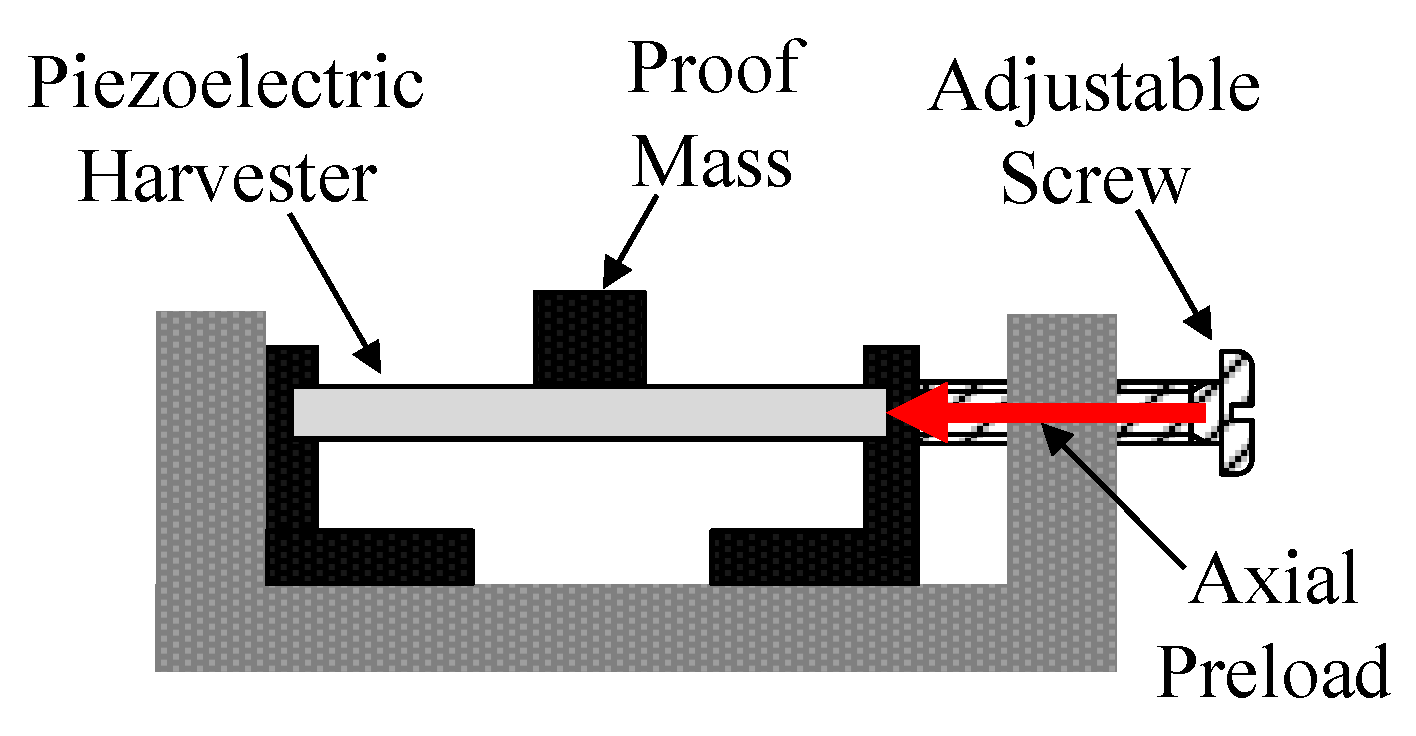
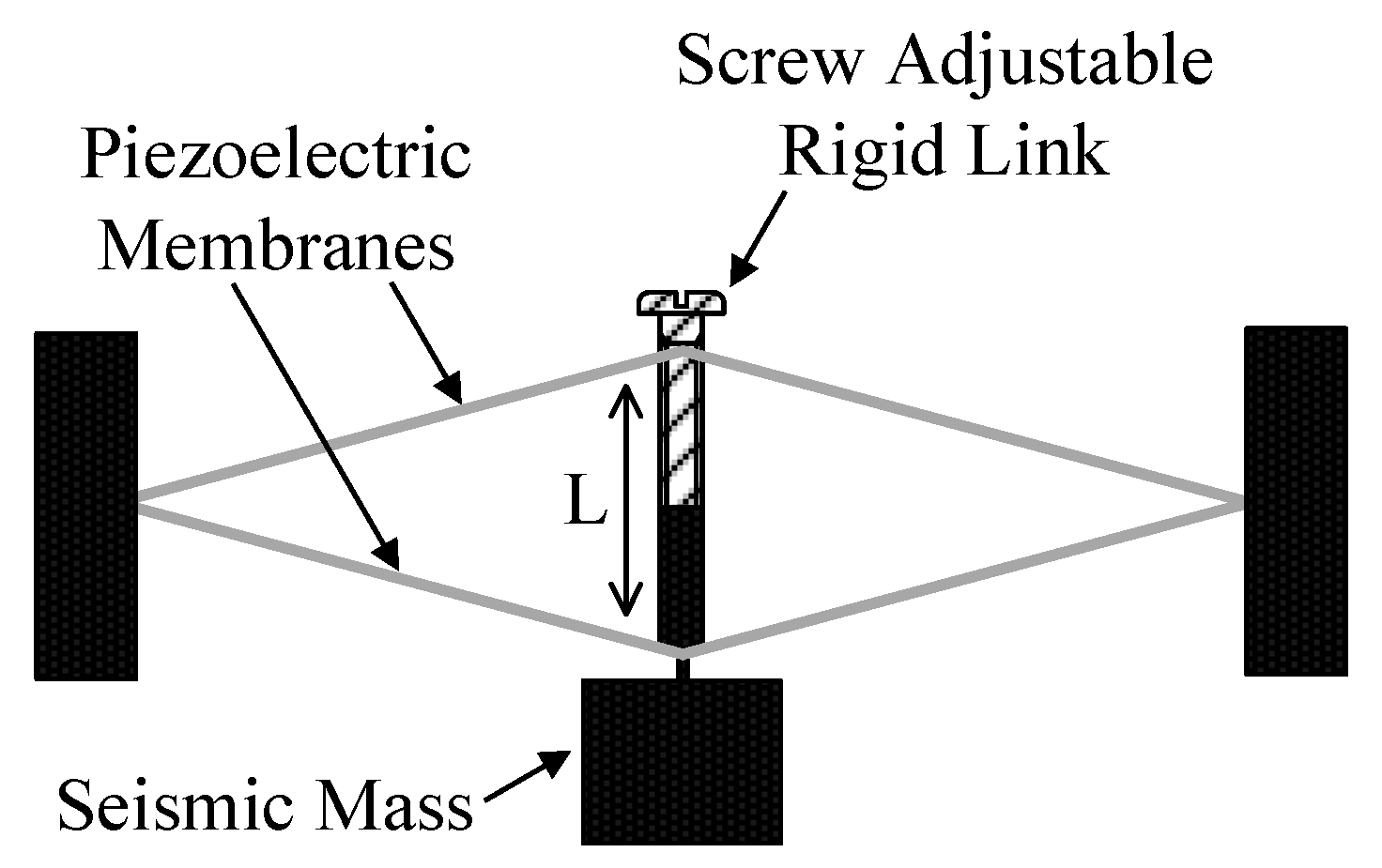
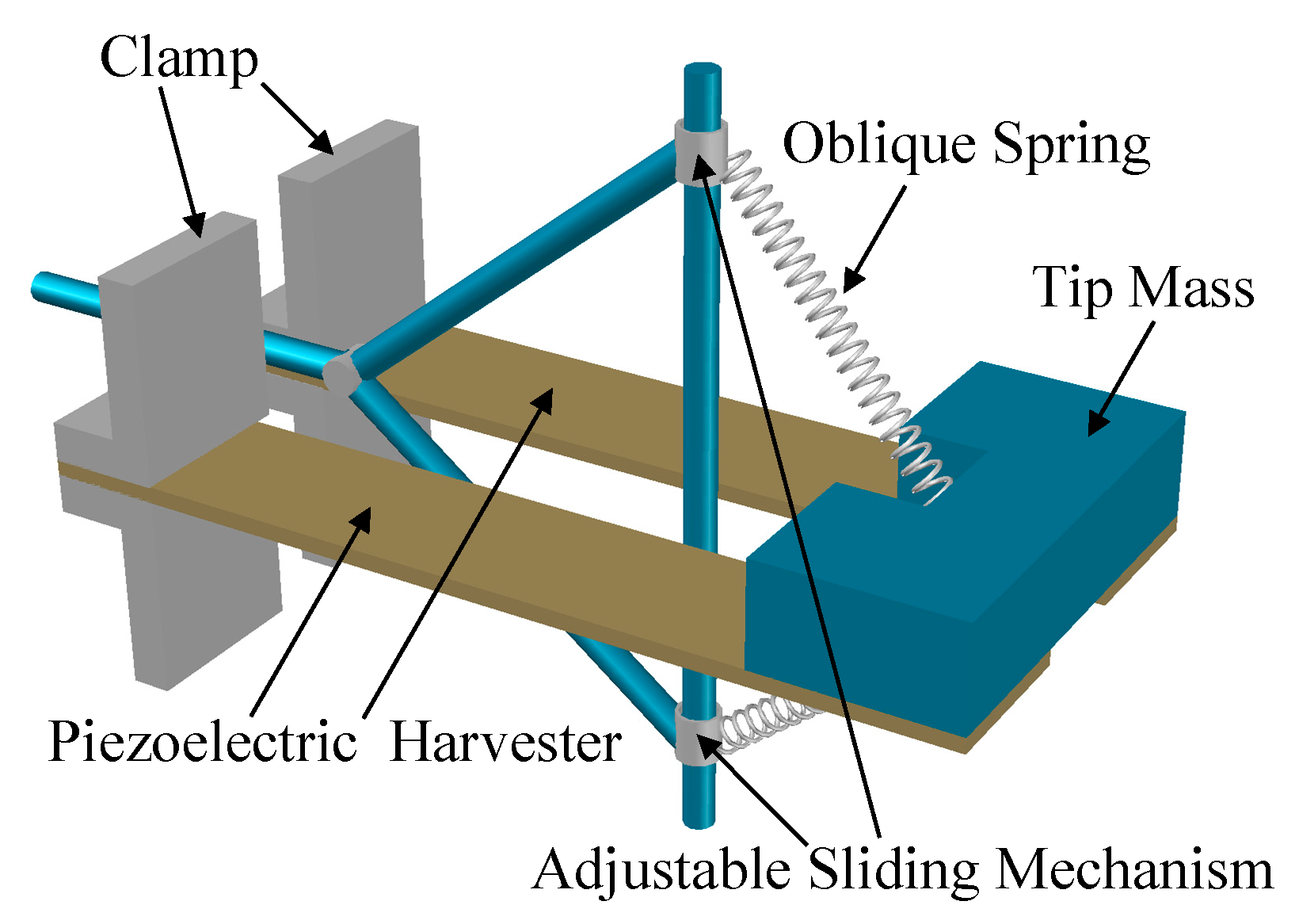
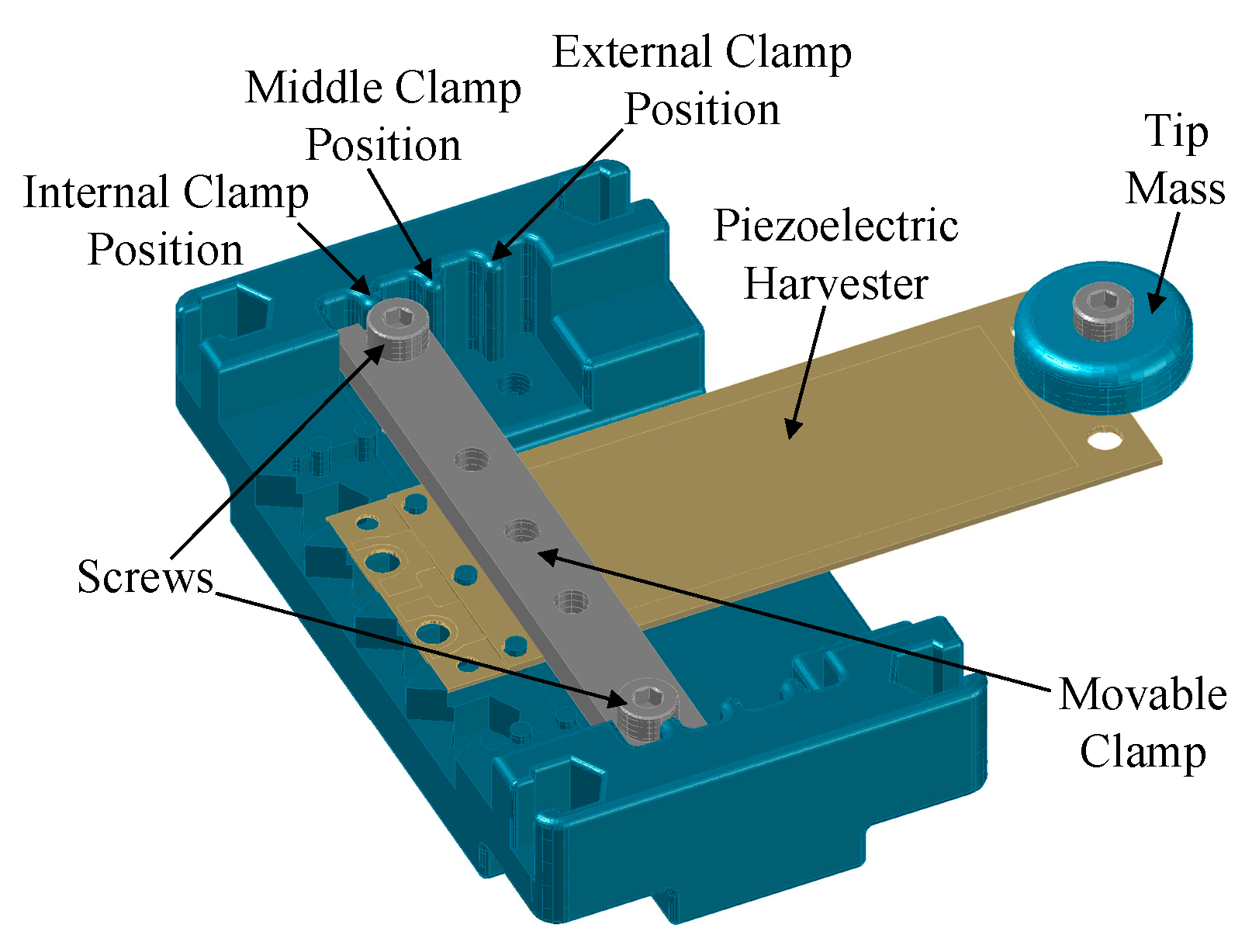
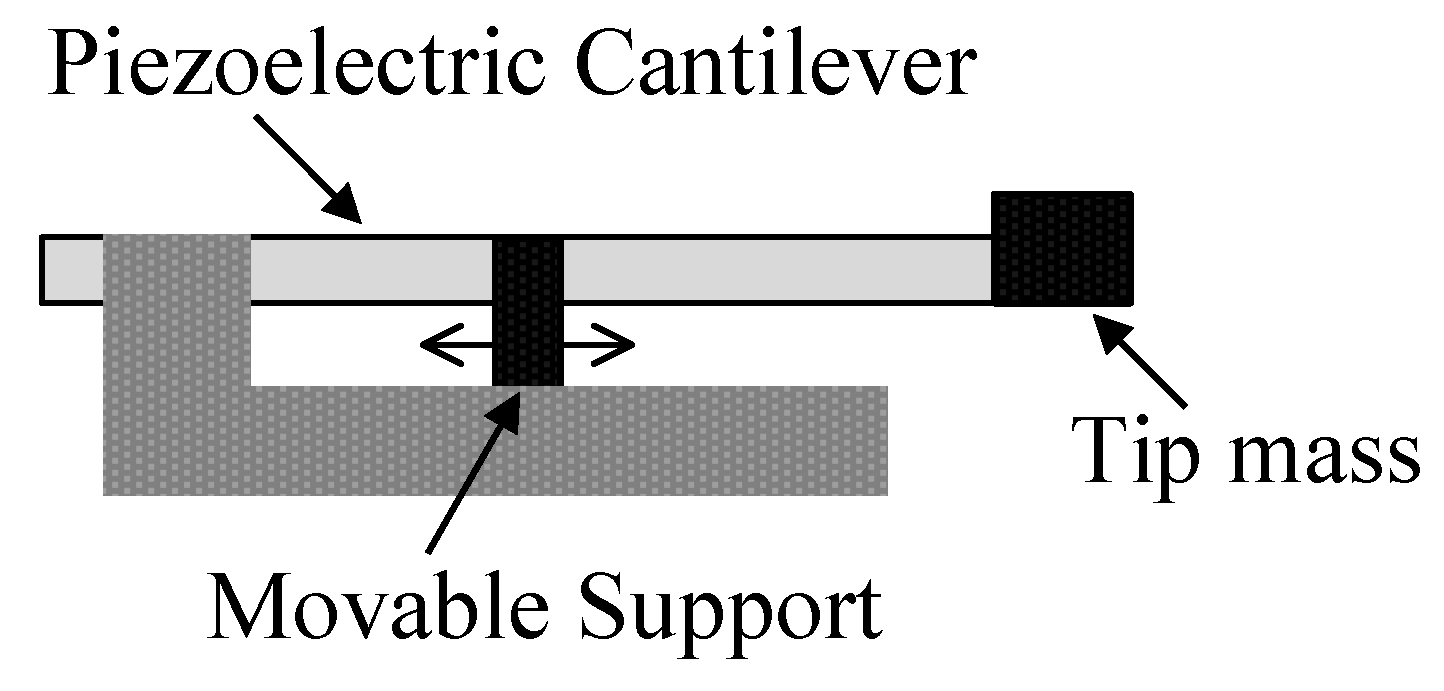
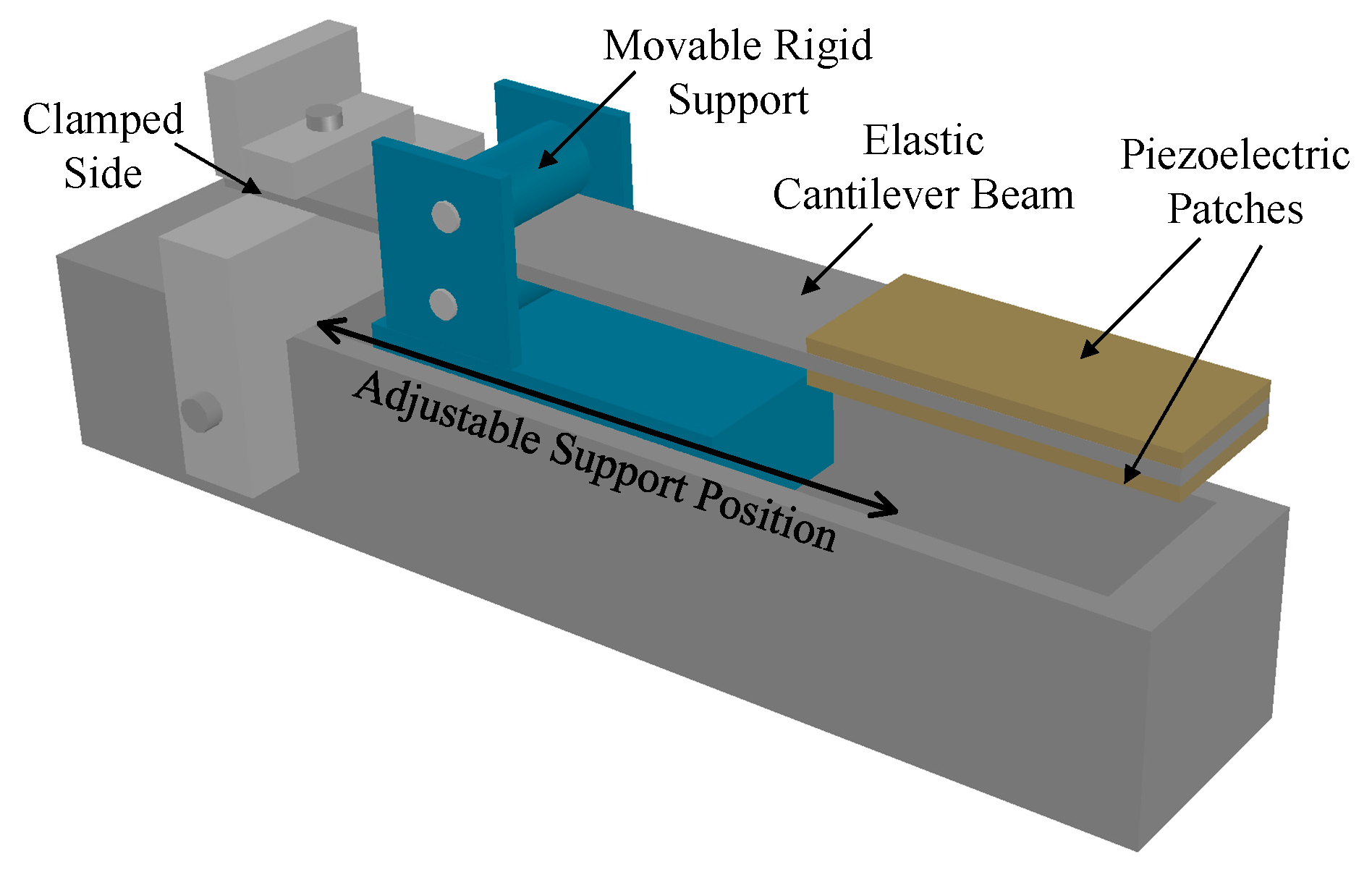

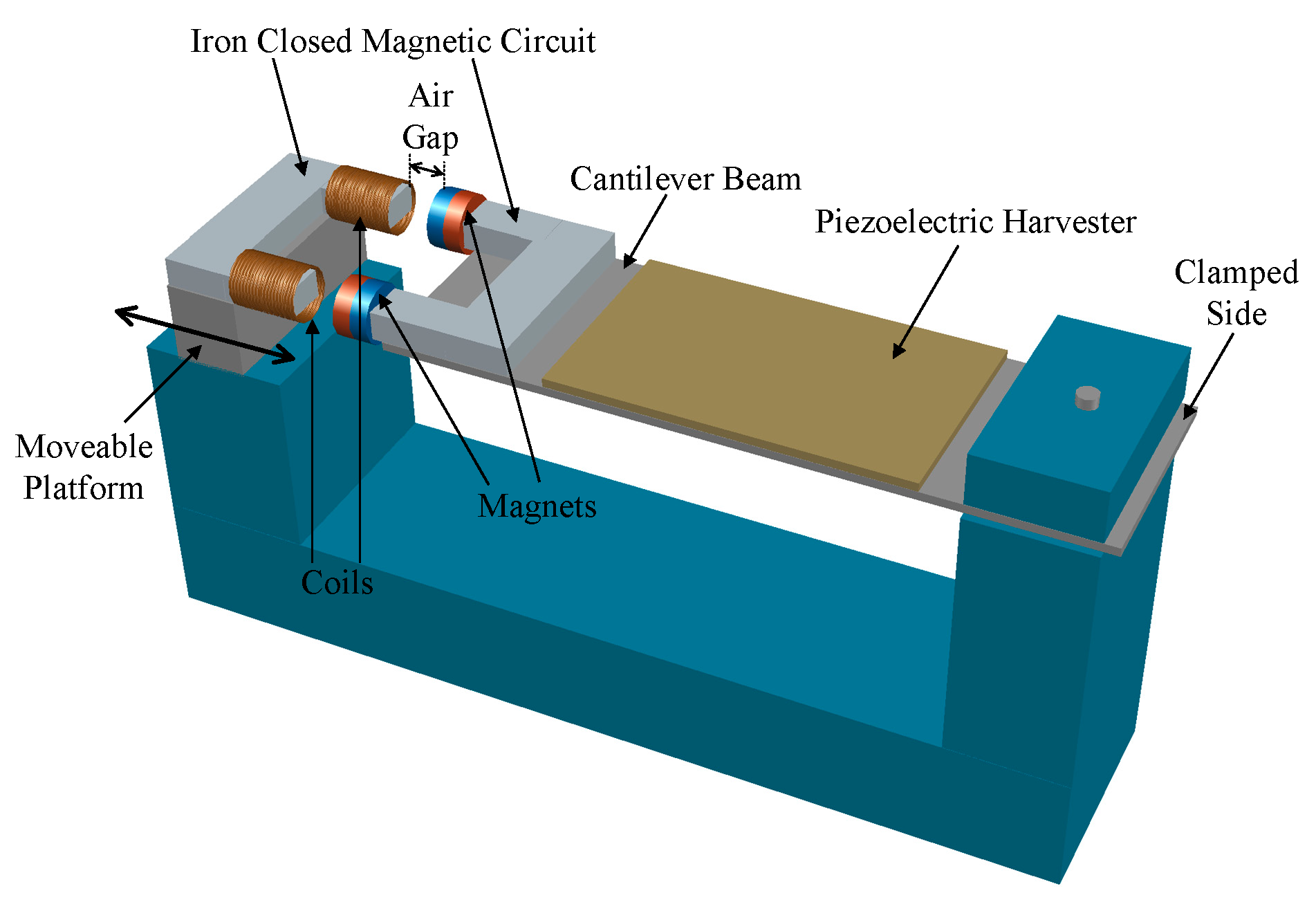

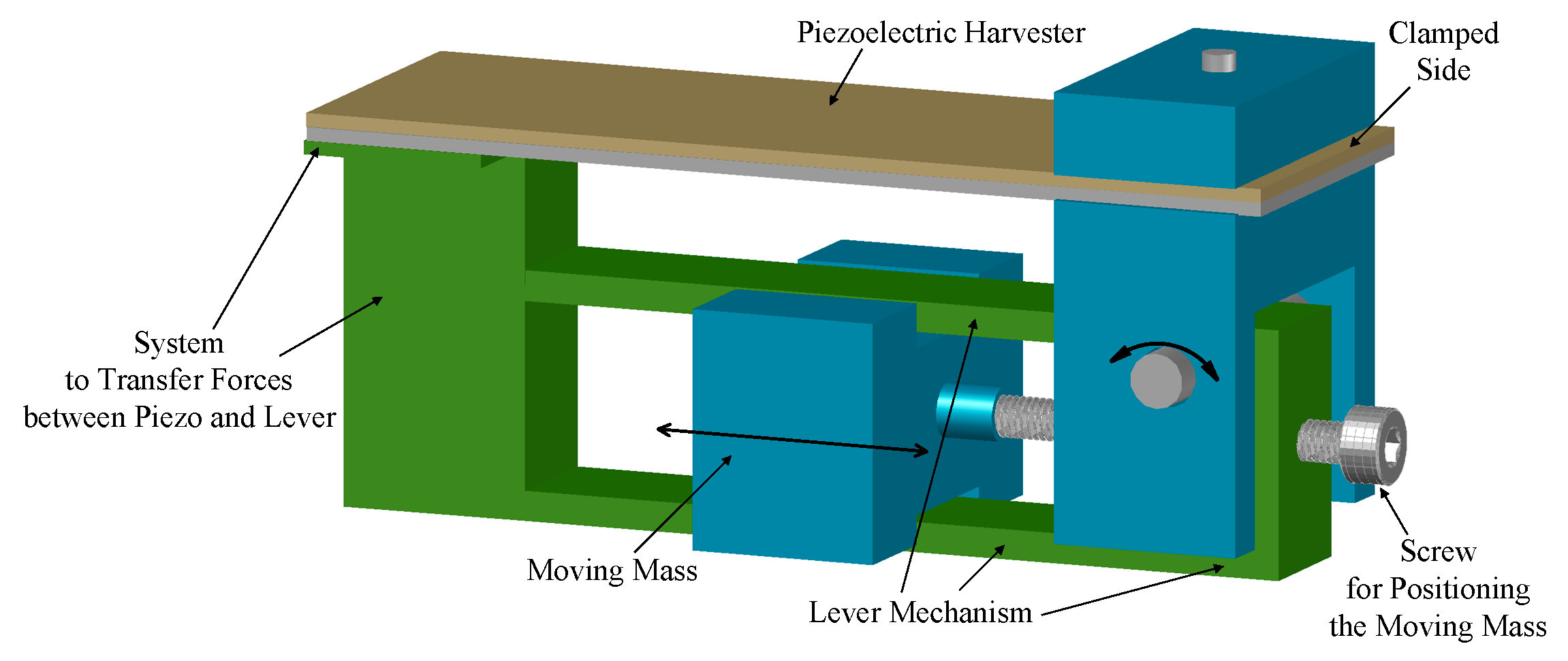
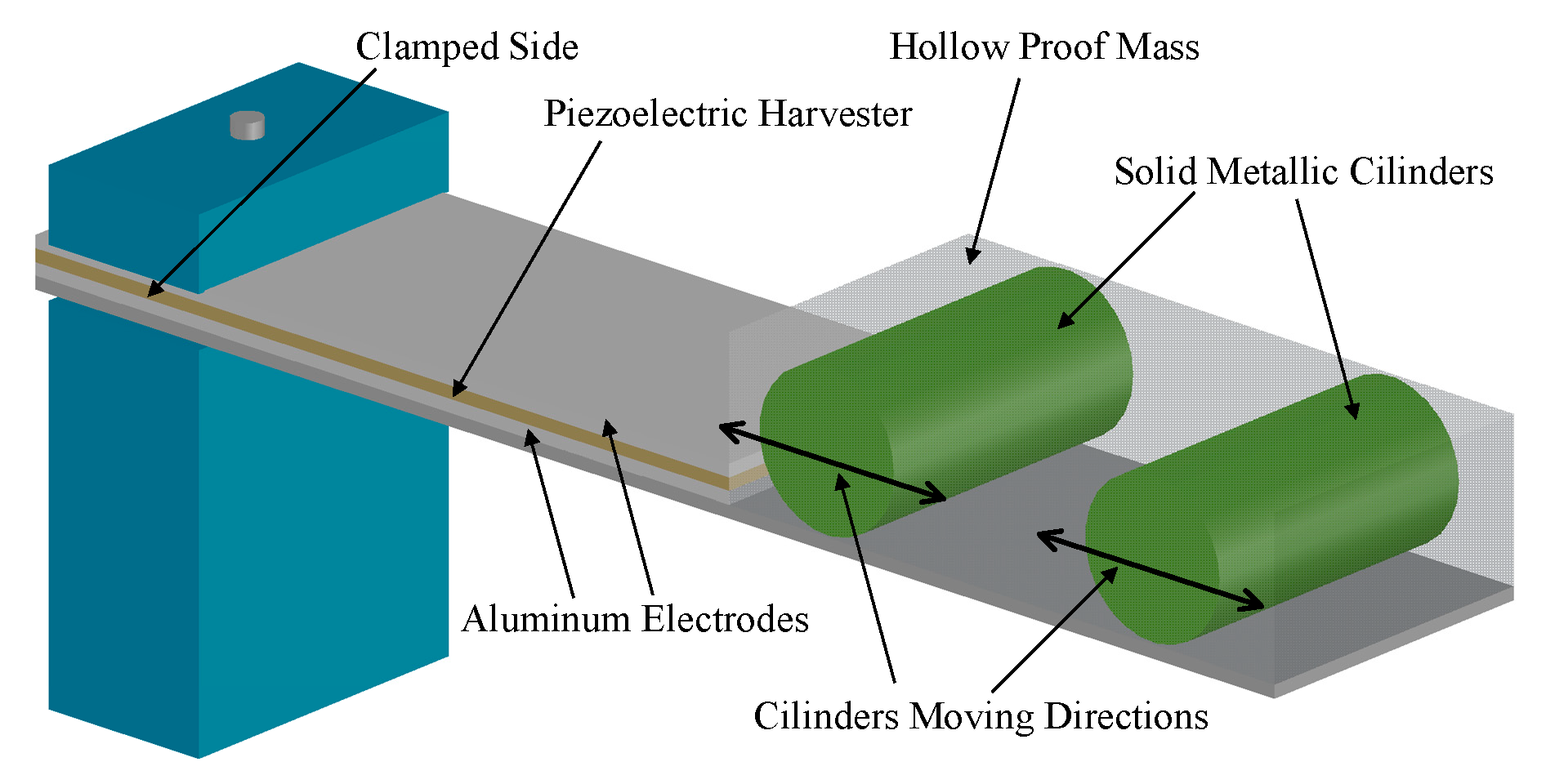

| MTT Name | Papers | Operating Principle Description |
|---|---|---|
| Magnetic Forces Based | [7,8,9,10,11,12,13,14,15,16,17,18,19,20] | They use the interaction between magnets with the aim of altering the stiffness of a RVEH, thus changing its mechanical resonance frequency. |
| Piezoelectric Actuators Based | [21,22,23,24,25,26,27,28,29] | The adjustment of the RVEH resonance frequency is implemented by changing the mechanical stiffness by using piezoelectric actuators. |
| Axial Loads Based | [30,31,32,33,34] | They exploit the fact that it is possible to vary the resonance frequency of an oscillating beam by means of axial loads. |
| Clamp Position Change Based | [35,36,37,38] | They tune the stiffness of a cantilever beam by changing the position of a clamp supporter placed along such a beam. |
| Variable Reluctance Based | [39,40,41,42] | They vary the force between two tuning magnets, and hence the stiffness of the structure, by means of the variation of the position of a magnetically permeable moveable flux guide placed between them. |
| Variable Center of Gravity Based | [43,44,45,46,47,48,49] | They exploit the fact that in a cantilever with a tip mass it is possible to change the resonance frequency of the structure by varying the position of the center of gravity. |
| Reference | [7] | [8,9] | [10] | [11] | [12,13] |
| RVEH | P | E | P | E | E |
| Direction | BOTH | LEFT | BOTH | RIGHT | RIGHT |
| fopt | 26.2 Hz | 223.1 Hz (2) | 61 Hz | 4.7 Hz | 67.6 Hz |
| ΔfR | 22.14% | 42.6% | 91.5% | 45% | |
| ΔfL | 16.03% | 15.5% | 16.4% | ||
| PMAX | 280 µW | 8.45 µW | NOT PROVIDED (3) | 800 µW | 156.6 µW |
| Avib | 80 mg | 125 mg | 10 mg | 60 mg | |
| ΔPR | −14.29% | NOT DEFINED (4) | −60.7% | ||
| ΔPL | −3.57% | −23.91% | |||
| Implementation | MECHANICAL | MECHANICAL | MECHANICAL | MECHANICAL | MECHANICAL |
| Actuation | MANUAL | MANUAL | MANUAL | AUTOMATIC | AUTOMATIC |
| Control | OPEN-LOOP | CLOSED-LOOP | |||
| Supply | PASSIVE | PASSIVE | |||
| Tuning Period | 320 s (1) | NOT PROVIDED | NOT PROVIDED | 217 s (5) | 230 s (6) |
| Vibrations | SINUSOIDAL | SINUSOIDAL | SINUSOIDAL | SINUSOIDAL | SINUSOIDAL |
| Reference | [21,22] | [23,24] | [25,26] |
| RVEH | E (1) | E | P |
| Direction | BOTH | BOTH | LEFT |
| fopt | 299 Hz | 78 Hz | 190 Hz |
| ΔfR | 8% | 14.1% | |
| ΔfL | 10.7% | 15.4% | 21% |
| PMAX | 60 µW | 1.4 mW | 50 μW |
| Avib | 1 g | NOT PROVIDED (3) | 0.6 g |
| ΔPR | −16.7% | NOT DEFINED (4) | |
| ΔPL | 16.7% | NOT DEFINED (4) | −60% |
| Implementation | ELECTRICAL | ELECTRICAL | ELECTRICAL |
| Actuation | MANUAL | AUTOMATIC | AUTOMATIC |
| Control | CLOSED-LOOP | OPEN-LOOP (6) | |
| Supply | SEMI-ACTIVE | SEMI-ACTIVE | SEMI-ACTIVE |
| Tuning Period | 20 s (2) | NOT PROVIDED (5) | 22.8 s (7) |
| Vibrations | SINUSOIDAL | SINUSOIDAL | SINUSOIDAL |
| Reference | [30] | [31] | [32,33] | [34] |
| RVEH | P | P | P | P |
| Direction | LEFT | BOTH | BOTH | BOTH |
| fopt | 250 Hz | 212 Hz | 380 Hz | 29.1 Hz |
| ΔfR | 10.8% | 4.5% | 112.6% (5) | |
| ΔfL | 20% | 62.3% | 23.2% | 79.4% (5) |
| PMAX | 400 μW | 40 μW (1) | NOT PROVIDED (4) | 368.9 μW (5) |
| Avib | 1 g | 0.35 g | 1 g | |
| ΔPR | −25% (2) | −80.8% (5) | ||
| ΔPL | −25% | −12.5% (3) | −67.3% (5) | |
| Implementation | MECHANICAL | MECHANICAL | MECHANICAL | MECHANICAL |
| Actuation | MANUAL | MANUAL | MANUAL | MANUAL |
| Control | ||||
| Supply | ||||
| Tuning Period | NOT PROVIDED | NOT PROVIDED | NOT PROVIDED | NOT PROVIDED |
| Vibrations | SINUSOIDAL | SINUSOIDAL | SINUSOIDAL | SINUSOIDAL |
| Reference | [37] | [38] |
| RVEH | P | P |
| Direction | BOTH | BOTH |
| fopt | 580 Hz (1) | 121 Hz (1) |
| ΔfR | 69% (2) | 48.8% |
| ΔfL | 60.3% (2) | 29.8% |
| PMAX | 22 μW (2) | NOT PROVIDED (4) |
| Avib | 0.1 g | |
| ΔPR | NOT DEFINED (3) | |
| ΔPL | NOT DEFINED (3) | |
| Implementation | MECHANICAL | MECHANICAL |
| Actuation | MANUAL | AUTOMATIC |
| Control | OPEN LOOP (5) | |
| Supply | PASSIVE | |
| Tuning Period | NOT PROVIDED | NOT PROVIDED |
| Vibrations | SINUSOIDAL | SINUSOIDAL |
| Reference | [39] | [41] | [42] |
| RVEH | E | Hybrid P-E | P |
| Direction | LEFT | BOTH | RIGHT |
| fopt | 63.6 Hz | 33.5 Hz | 102.5 Hz |
| ΔfR | 85.1% | 12.8% | |
| ΔfL | 21.7% | 23.9% | |
| PMAX | 166.2 µW | 2.78 mW | NOT PROVIDED (1) |
| Avib | 0.85 g | 0.3 g | |
| ΔPR | −42.9% | ||
| ΔPL | −30.8% | −28.6% | |
| Implementation | MECHANICAL | MECHANICAL | MECHANICAL |
| Actuation | MANUAL | MANUAL | MANUAL |
| Control | |||
| Supply | |||
| Tuning Period | NOT PROVIDED | NOT PROVIDED | NOT PROVIDED |
| Vibrations | SINUSOIDAL | SINUSOIDAL | SINUSOIDAL |
| Reference | [43] | [44] | [45,46] |
| RVEH | P | P | P |
| Direction | BOTH | RIGHT | RIGHT |
| fopt | 160 Hz (1) | 42 Hz (3) | 21 Hz (4) |
| ΔfR | 12.5% | 31% | 66.7% |
| ΔfL | 18.75% | ||
| PMAX | NOT PROVIDED (2) | 80 μW | 13.18 μW |
| Avib | 0.03 g | 1.4 g | |
| ΔPR | −43.7% | −69.7% | |
| ΔPL | |||
| Implementation | MECHANICAL | MECHANICAL | MECHANICAL |
| Actuation | MANUAL | MANUAL | AUTOMATIC |
| Control | OPEN LOOP | ||
| Supply | PASSIVE | ||
| Tuning Period | NOT PROVIDED | NOT PROVIDED | (5) |
| Vibrations | SINUSOIDAL | SINUSOIDAL | SINUSOIDAL |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costanzo, L.; Vitelli, M. Tuning Techniques for Piezoelectric and Electromagnetic Vibration Energy Harvesters. Energies 2020, 13, 527. https://doi.org/10.3390/en13030527
Costanzo L, Vitelli M. Tuning Techniques for Piezoelectric and Electromagnetic Vibration Energy Harvesters. Energies. 2020; 13(3):527. https://doi.org/10.3390/en13030527
Chicago/Turabian StyleCostanzo, Luigi, and Massimo Vitelli. 2020. "Tuning Techniques for Piezoelectric and Electromagnetic Vibration Energy Harvesters" Energies 13, no. 3: 527. https://doi.org/10.3390/en13030527
APA StyleCostanzo, L., & Vitelli, M. (2020). Tuning Techniques for Piezoelectric and Electromagnetic Vibration Energy Harvesters. Energies, 13(3), 527. https://doi.org/10.3390/en13030527