A Novel Porous Media Permeability Model Based on Fractal Theory and Ideal Particle Pore-Space Geometry Assumption
Abstract
1. Introduction
2. Mathematical Model
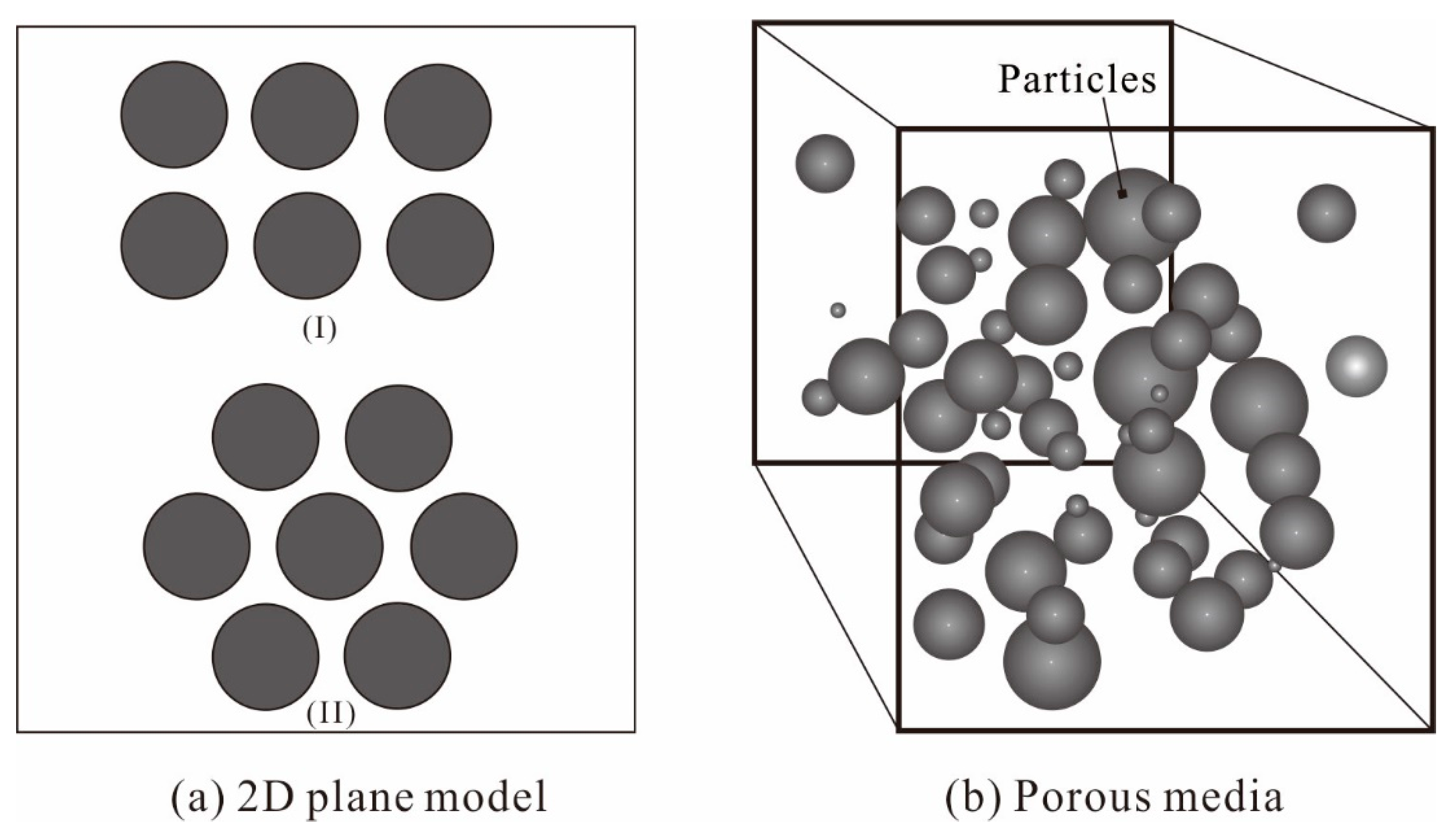
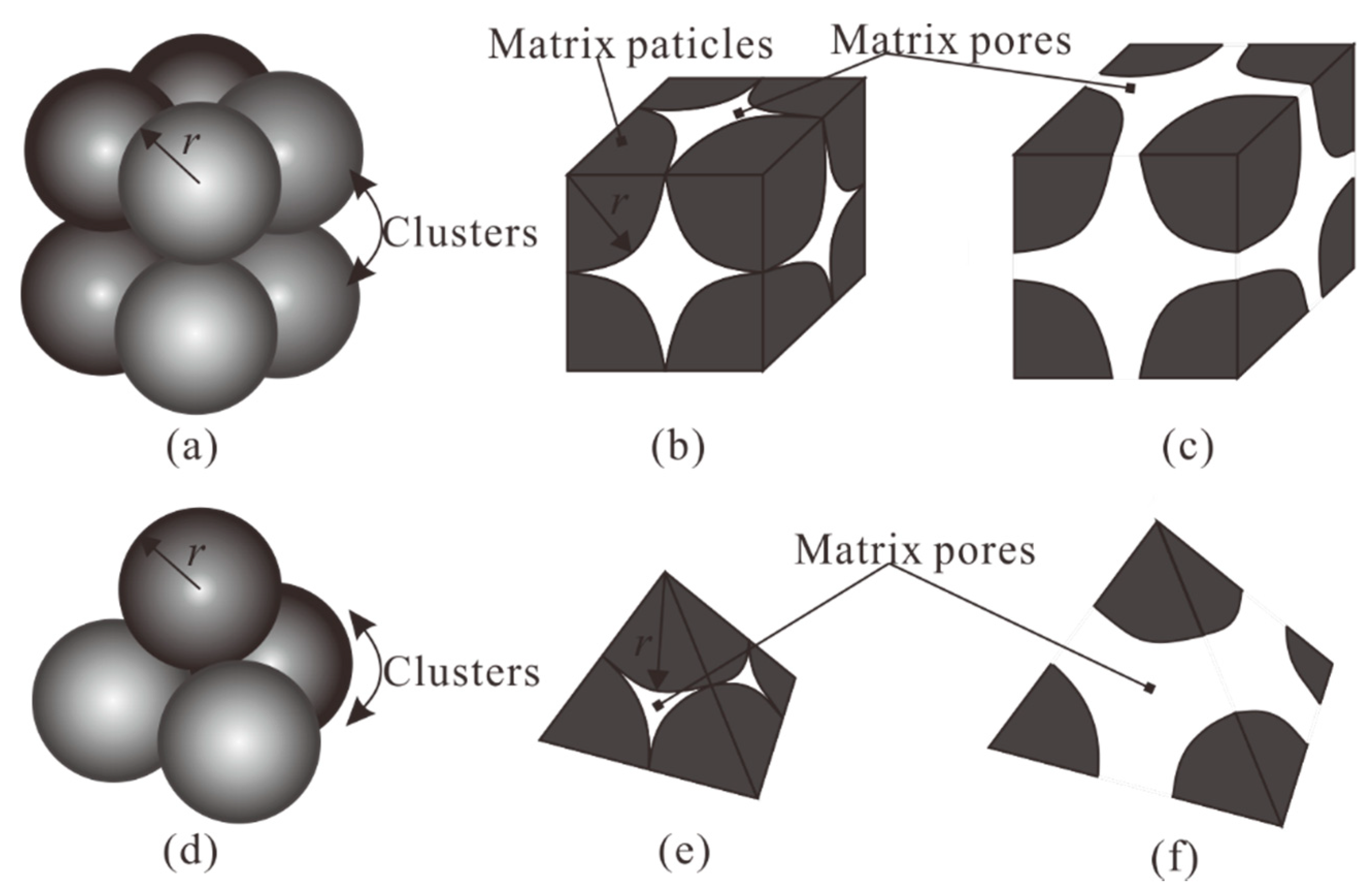
2.1. Fractal Characteristics of Spherical Particles Matrix
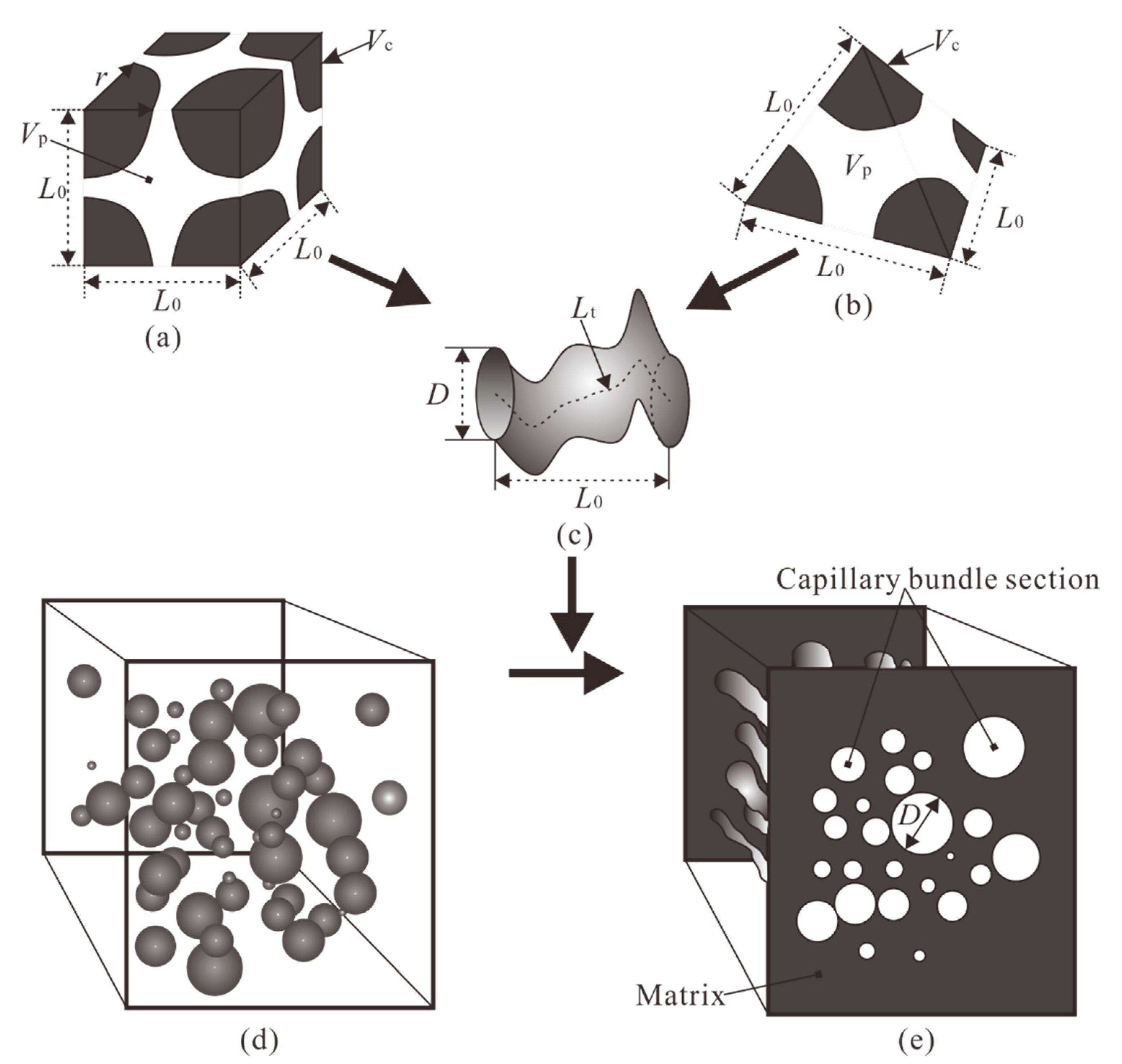
2.2. Fractal Capillary Bundle Model for Porous Media
2.3. Fractal Permeability Model for Porous Media
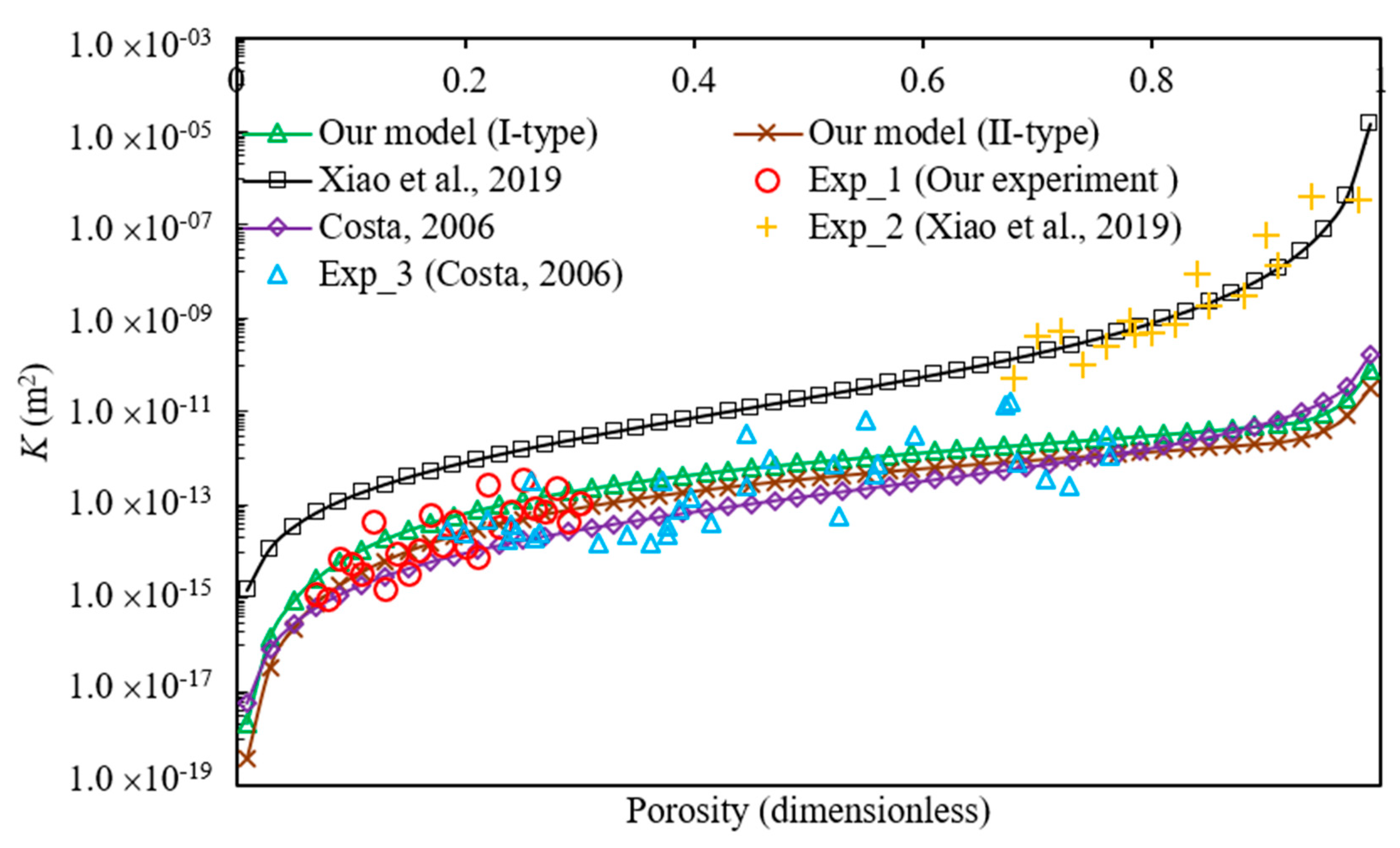
3. Model Validation
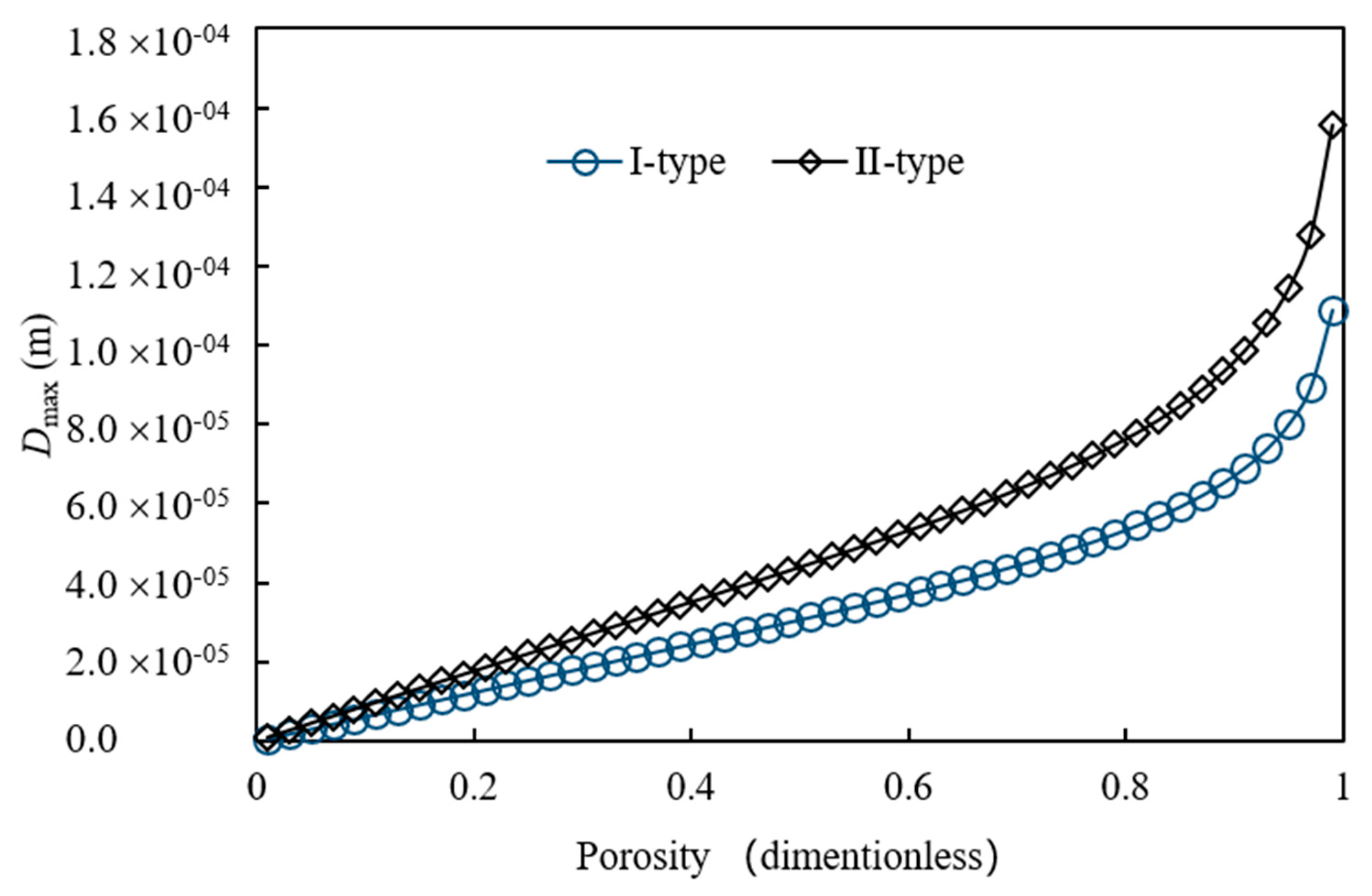
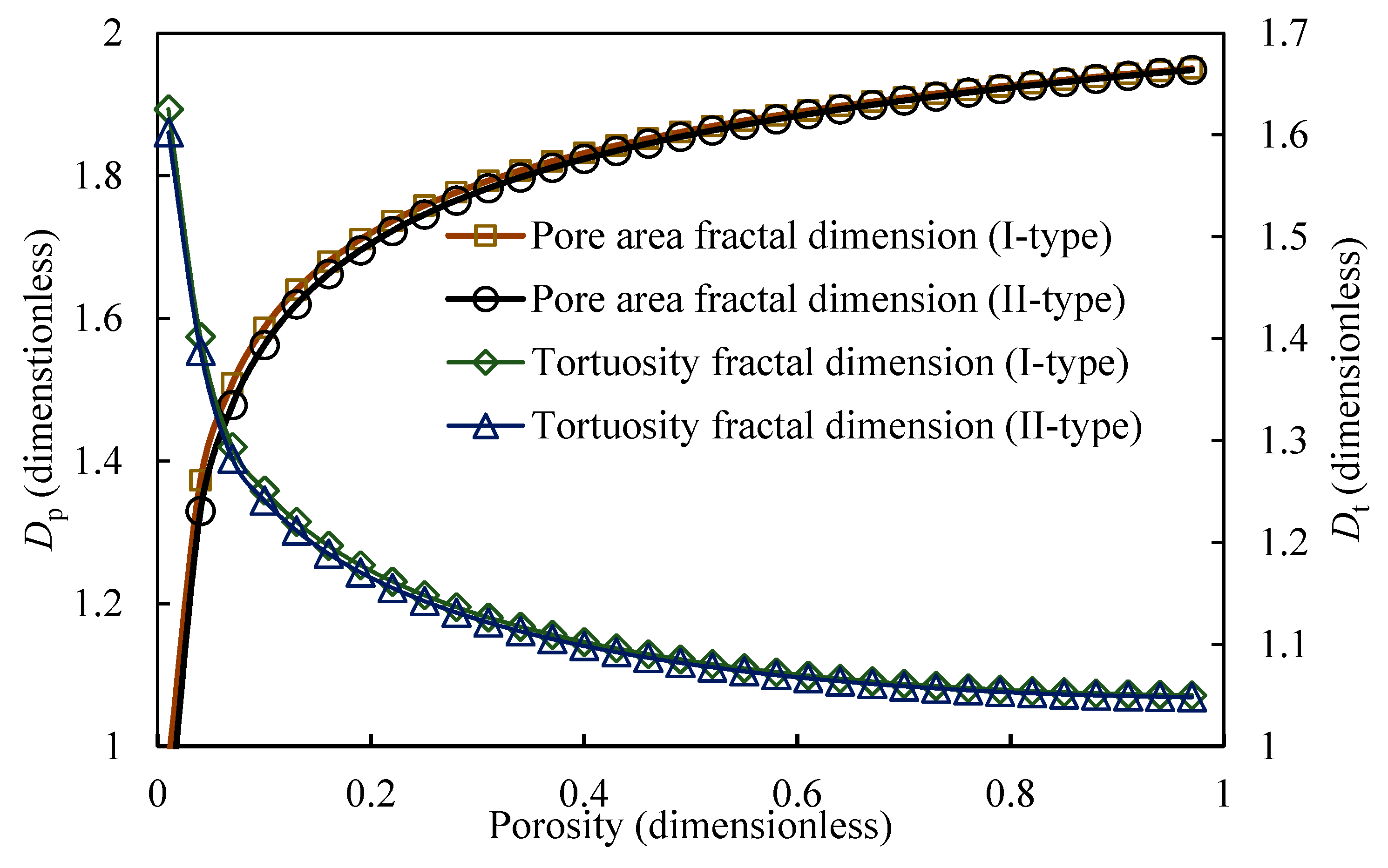
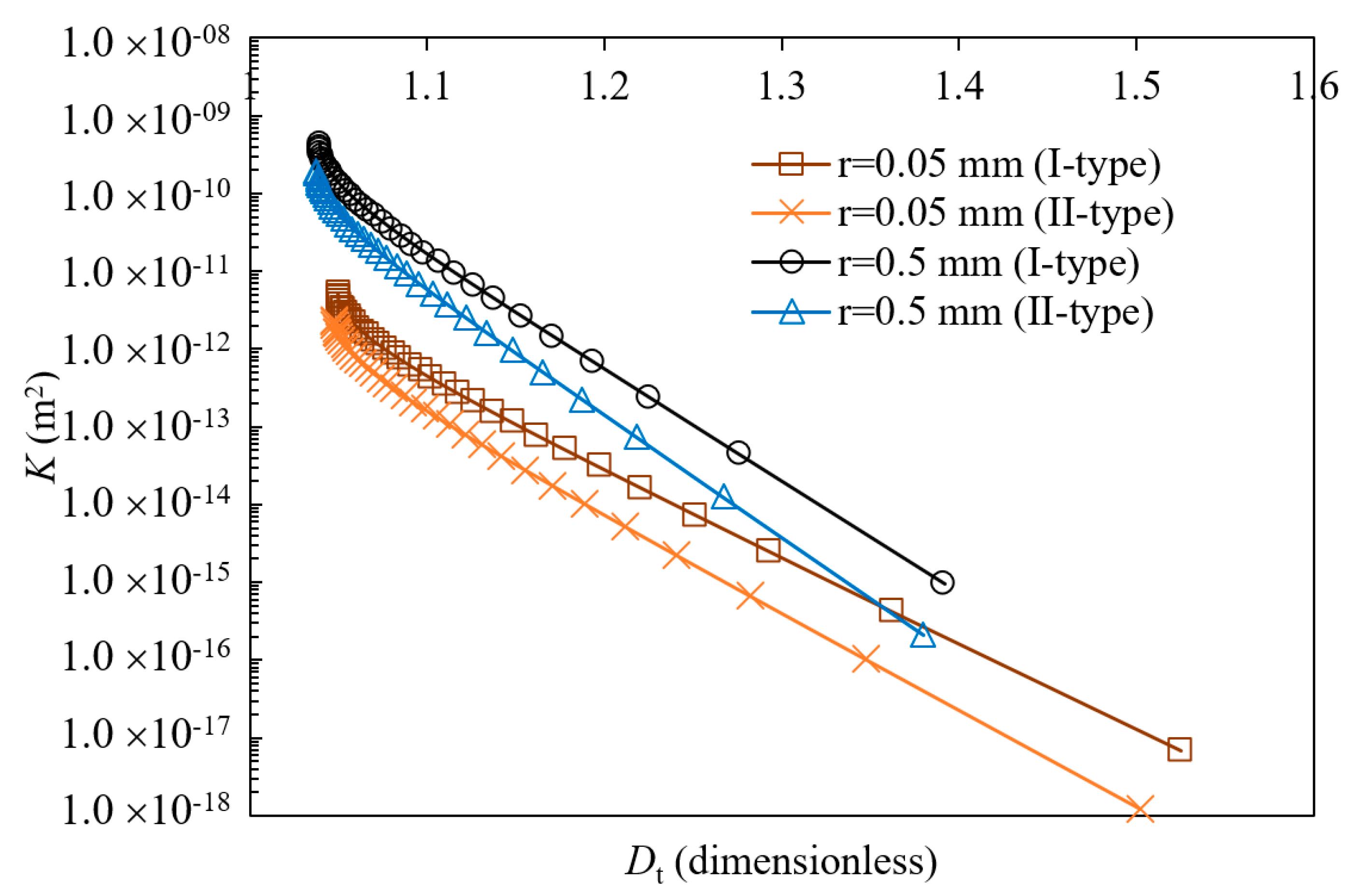
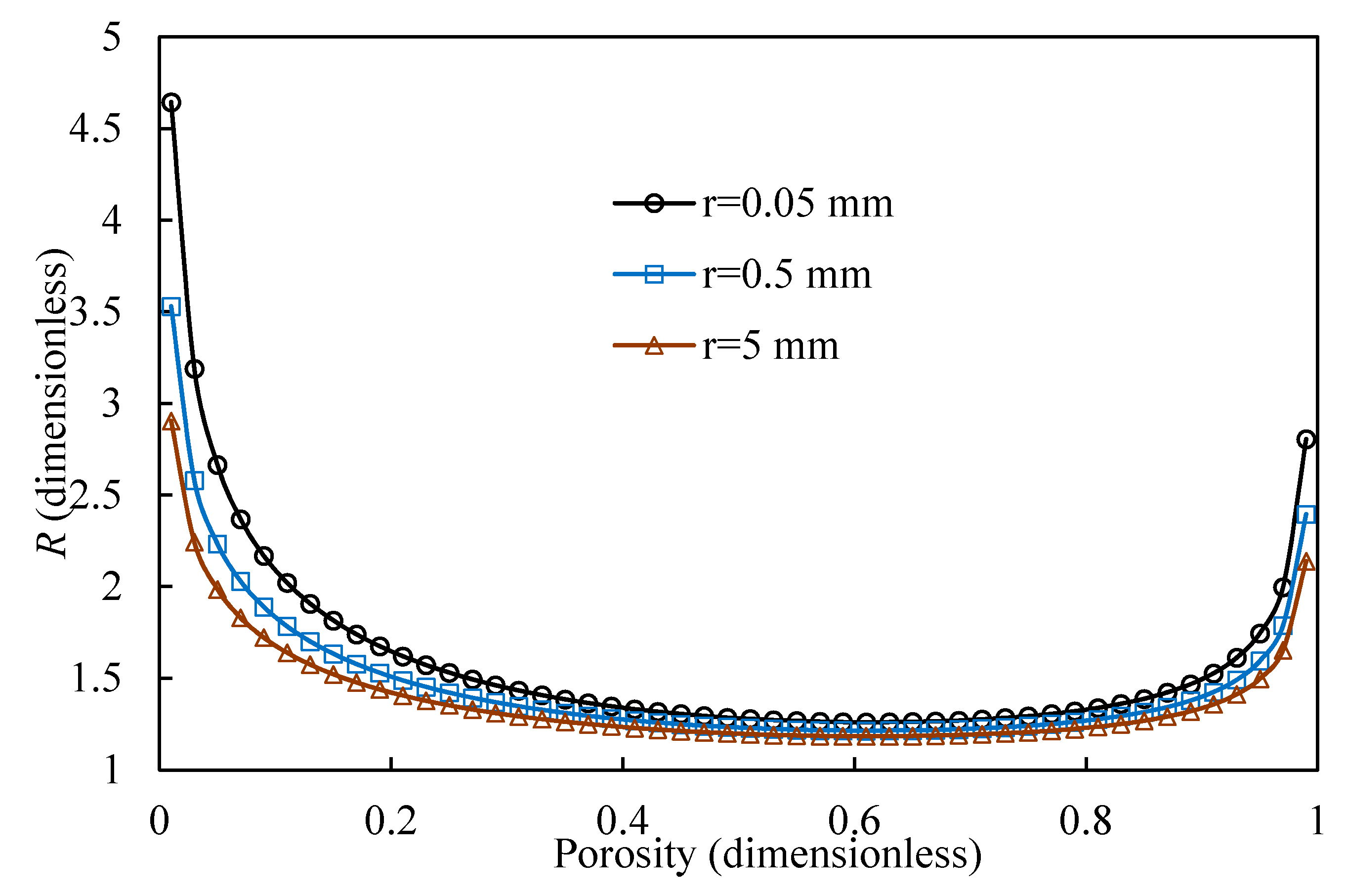
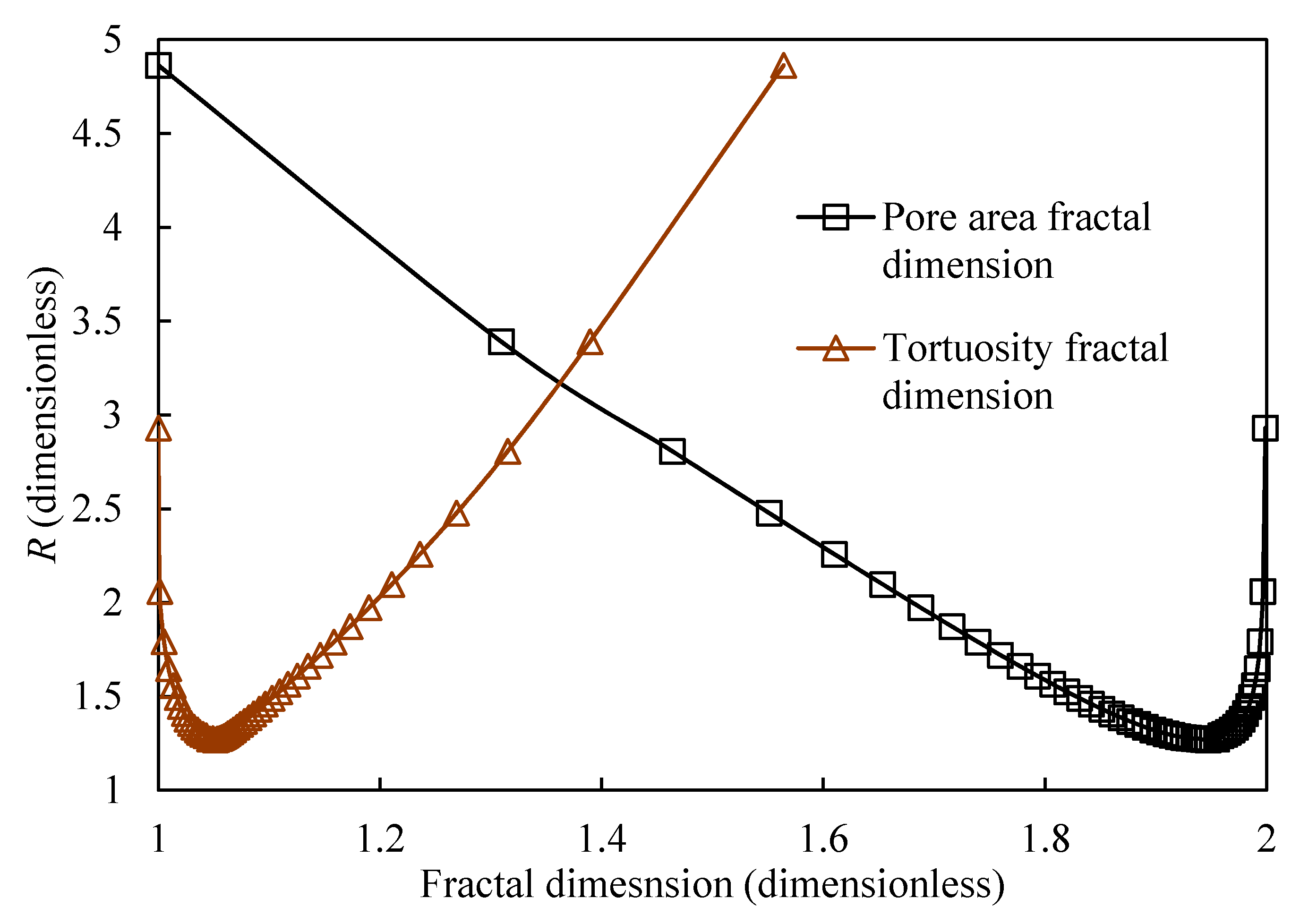
4. Results Discussion and Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mousavi, M.; Prodanovic, M.; Jacobi, D. New classification of carbonate rocks for process-based pore-scale modeling. SPE J. 2013, 18, 243–263. [Google Scholar] [CrossRef]
- Wu, K.; Chen, Z.X.; Li, X.F. Real gas transport through nanopores of varying cross-section type and shape in shale gas reservoirs. Chem. Eng. J. 2015, 281, 813–825. [Google Scholar] [CrossRef]
- Wu, K.; Chen, Z.X.; Li, X.F.; Guo, C.; Wei, M. A model for multiple transport mechanisms through nanopores of shale gas reservoirs with real gas effect-adsorption-mechanic coupling. Int. J. Heat Mass Transf. 2016, 93, 408–426. [Google Scholar] [CrossRef]
- Hosa, A.; Curtis, A.; Wood, R. Calibrating Lattice Boltzmann flow simulations and estimating uncertainty in the permeability of complex porous media. Adv. Water Resour. 2016, 94, 60–74. [Google Scholar] [CrossRef]
- Chen, Z.L.; Wang, N.T.; Sun, L.; Tan, X.H.; Deng, S. Prediction method for permeability of porous media with tortuosity effect based on an intermingled fractal units model. Int. J. Eng. Sci. 2017, 121, 83–90. [Google Scholar] [CrossRef]
- Pitchumani, R.; Ramakrishnan, B. A fractal geometry model for evaluating permeabilities of porous preforms used in liquid composite molding. Int. J. Heat Mass Transf. 1999, 42, 2219–2232. [Google Scholar] [CrossRef]
- Miguel, A.F.; Rosa, R.; Silva, A.M. Fractal geometry description of the permeability of a natural fissured rock. In Proceedings of the 9th International Congress on Deterioration and Conservation of Stone; Elsevier Science B.V.: Amsterdam, The Netherlands, 2000; Volume 1, pp. 595–600. [Google Scholar]
- Karacan, Q.; Halleck, P.M. A Fractal Model for Predicting Permeability around Perforation Tunnels Using Size Distribution of Fragmented Grains. J. Pet. Sci. Eng. 2003, 40, 159–176. [Google Scholar] [CrossRef]
- Dravis, J.J. Carbonate applied to hydrocarbon exploration and exploitation, HTC Intetnal report. Training course note. 2007. Available online: www.dravisinterests.com (accessed on 7 November 2009).
- Lucia, F.L. Petrophysical Parameters Estimated from Visual Descriptions of Carbonate Rocks: A Field Classification of Carbonate Pore Space. In Proceedings of the 1981 SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 5–7 October 1983. [Google Scholar]
- Wu, J.S. Analysis of Resistance for Flow Through Porous Media; Zhejiang University: Hangzhou, China, 2006. [Google Scholar]
- Gebart, B.R. Permeability of unidirectional reinforcements for RTM. J. Compos. Mater. 1992, 26, 1100–1133. [Google Scholar] [CrossRef]
- Othman, M.R.; Helwani, Z.; Martunus. Simulated fractal permeability for porous membranes. Appl. Math. Model. 2010, 34, 2452–2464. [Google Scholar] [CrossRef]
- Zhu, F.; Hu, W.X.; Cao, J.; Sun, F.; Liu, Y.; Sun, Z. Micro/nanoscale pore structure and fractal characteristics of tight gas sandstone: A case study from the Yuanba area, northeast Sichuan Basin, China. Mar. Pet. Geol. 2018, 98, 116–132. [Google Scholar] [CrossRef]
- Qin, X.; Cai, J.C.; Xu, P. A fractal model of effective thermal conductivity for porous media with various liquid saturation. Int. J. Heat Mass Transf. 2019, 128, 1149–1156. [Google Scholar] [CrossRef]
- Wang, Q.; Hu, Y.; Zhao, J.; Ren, L.; Zhao, C.; Zhao, J. Multiscale Apparent Permeability Model of Shale Nanopores Based on Fractal Theory. Energies 2019, 12, 3381. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, Q.; Hu, Y.; Ren, L.; Zhao, C. Numerical investigation of shut-in time on stress evolution and tight oil production. J. Pet. Sci. Eng. 2019, 179, 716–733. [Google Scholar] [CrossRef]
- Maik, N.K.; Sirisha, M.; Inani, A. Permeability characterization of polymer matrix composites by RTM/VARTM. Prog. Aerosp. Sci. 2014, 65, 22–40. [Google Scholar]
- Parnas, R.S.; Salem, A.J.; Sadiq, T.A.; Wang, H.P.; Advani, S.G. The interaction between micro-and macro-scopic flow in RTM preforms. Compos. Strcut. 1994, 27, 83–107. [Google Scholar] [CrossRef]
- Kozeny, J. Ueber kapillare leitung des wassers im boden. Sitzh. Akad. Wiss. Wein 1927, 136, 271–306. [Google Scholar]
- Carman, P.C. Fluid flow through granular beds. Trans. Inst. Chem. Eng. 1937, 15, 150–167. [Google Scholar] [CrossRef]
- Griffin, P.R.; Grove, S.M.; Russell, P.; Short, D.; Summerscales, J.; Guild, F.J.; Taylor, E. The effect of reinforcement architecture on the long-range flow in fibrous reinforcements. Compos. Manuf. 1995, 6, 221–235. [Google Scholar] [CrossRef]
- Khabbazi, A.E. Numerical and Analytical Characterization of Transport Properties for Single Phase Flows in Granular Porous Media; University of Toronto: Toronto, ON, Canada, 2015. [Google Scholar]
- Yu, B.M.; Lee, L.J.; Cao, H.Q. Fractal characters of pore microstructures of textile fabrics. Fractals 2001, 9, 155–163. [Google Scholar] [CrossRef]
- Xu, P.; Yu, B.M. Development a new form of permeability and Kozeny-Carman constant for homogeneous porous media by means of fractal geometry. Adv. Water Resour. 2008, 31, 74–81. [Google Scholar] [CrossRef]
- Xiao, B.Q.; Fan, J.T.; Ding, F. A fractal analytical model for the permeabilities of fibrous gas diffusion layer in proton exchange membrane fuel cells. Electrochem. Acta 2014, 134, 222–231. [Google Scholar] [CrossRef]
- Xiao, B.Q.; Wang, W.; Zhang, X.; Long, G.; Fan, J.T.; Chen, H.; Deng, L. A novel fractal solution for permeability and Kozeny-Carman constant of fibrous porous media made up of solid particles and porous fibers. Powder Technol. 2019, 349, 92–98. [Google Scholar] [CrossRef]
- Xiao, B.Q.; Fan, J.T.; Ding, F. A novel fractal model for relative permeability of gas diffusion layer in proton exchange membrane fuel cell with capillary pressure effect. Fractals 2019, 27, 1950012. [Google Scholar] [CrossRef]
- Shou, D.H.; Fan, J.; Ding, F. A difference-fractal model for the permeability of fibrous porous media. Phys. Lett. A 2010, 374, 1201–1204. [Google Scholar] [CrossRef]
- Zhang, L.Z. A fractal model for gas permeation through porous membranes. Int. J. Heat Mass Transf. 2012, 55, 1716–1723. [Google Scholar] [CrossRef]
- Zhu, Q.Y.; Xie, M.H.; Yang, J.; Li, Y. A fractal model for the coupled heat and mass transfer in porous fibrous media. Int. J. Heat Mass Transf. 2011, 54, 1400–1409. [Google Scholar] [CrossRef]
- Zhu, Q.Y.; Xie, M.H.; Yang, J.; Li, Y. Analytical determination of permeability of porous fibrous media with consideration of electro kinetic phenomena. Int. J. Heat Mass Transf. 2012, 9, 365–372. [Google Scholar]
- Costa, A. Permeability-porosity relationship: A reexamination of the Kozeny-Carman equation based on a fractal pore-space geometry assumption. Geophys. Res. Lett. 2005, 33, L02318. [Google Scholar] [CrossRef]
- Cihan, A.; Sukop, M.C.; Tyner, J.S.; Perfect, E.; Huang, H. Analytical predictions and lattice Boltzmann simulations of intrinsic permeability for mass fractal porous media. Vadose Zone J. 2009, 8, 187–196. [Google Scholar] [CrossRef]
- Garrison, J.R.; Pearn, W.C.; Vonrosenberg, D.U. The fractal menger sponge and Sierpinski carpet as models for reservoir rock/por systems: I. theory and image analysis of Sierpinski carpets. In Situ 1992, 16, 351–406. [Google Scholar]
- Garza-Lopez, R.A.; Naya, L.; Kozak, J.J. Tortuosity factor for permeant flow through a fractal solid. J. Chem. Phys. 2000, 112, 9956–9960. [Google Scholar] [CrossRef]
- Cihan, A.; Perfect, E.; Tyner, J.S. Water retention models for scale-variant and scale-invariant drainage of mass prefractal porous media. Vadose Zone J. 2007, 6, 786–792. [Google Scholar] [CrossRef]
- Atzeni, C.; Pia, G.; Sanna, U.; Spanu, N. A fractal model of the porous microstructure of earth-based materials. Constr. Build. Mater. 2008, 22, 1607–1613. [Google Scholar] [CrossRef]
- Pia, G.; Sanna, U. An intermingled fractal units model and method to predict permeability in porous rock. Int. J. Eng. Sci. 2014, 75, 31–39. [Google Scholar] [CrossRef]
- Pia, G.; Sanna, U. An intermingled fractal units model to evaluate pore size distribution influence on thermal conductivity values in porous materials. Appl. Therm. Eng. 2014, 65, 330–336. [Google Scholar] [CrossRef]
- Pia, G.; Sanna, U. Intermingled fractal units model and electrical equivalence fractal approach for prediction of thermal conductivity of porous materials. Appl. Therm. Eng. 2013, 61, 186–192. [Google Scholar] [CrossRef]
- Turcio, M.; Reyes, J.; Camacho, R.; Lira-Galeana, C.; Vargas, R.O.; Manero, O. Calculation of effective permeability for the BMP model in fractal porous media. J. Pet. Sci. Eng. 2013, 103, 51–60. [Google Scholar] [CrossRef]
- Bautista, F.; Santos, J.M.; Puig, J.E.; Manero, O. Understanding thixotropic and antithixotropic behavior of viscoelastc micellar solutions and liquid crystalline dispersions. I. the model. J. Non-Newton. Fluid Mech. 1999, 80, 93–113. [Google Scholar] [CrossRef]
- Miao, T.J.; Chen, A.; Zhang, L.W. A novel fractal model for permeability of damaged tree-like branching networks. Int. J. Heat Mass Transf. 2018, 127, 278–285. [Google Scholar] [CrossRef]
- Gostick, J.T.; Fowler, M.W.; Loannidis, M.A.; Pritzker, M.D.; Volfkovich, Y.M.; Sakars, A. Capillary pressure and hydrophilic porosity in gas diffusion layers for polymer electrolyte fuel cells. J. Power Sources 2006, 156, 375–387. [Google Scholar] [CrossRef]
- Shou, D.H.; Fan, J.; Ding, F. Hyfraulic permeability of fibrous porous media. Int. J. Heat Mass Transf. 2011, 54, 4009–4018. [Google Scholar] [CrossRef]
- Ju, Y.; Xi, C.; Zhang, Y.; Mao, L.T.; Gao, F.; Xie, H.P. Laboratory In Situ CT Observation of the Evolution of 3D Fracture Networks in Coal Subjected to Confining Pressures and Axial Compressive Loads: A Novel Approach. Rock Mech. Rock Eng. 2018, 51, 3361–3375. [Google Scholar] [CrossRef]
- Fan, W.P.; Sun, H.; Yao, J.; Fan, D.Y.; Zhang, K. A new fractal transport model of shale gas reservoirs considering multiple gas transport mechanisms, multi-scale and heterogeneity. Fractals 2018, 26, 1850096. [Google Scholar] [CrossRef]
- Yu, B.M.; Li, J.H. Some fractal characters of porous media. Fractals 2001, 9, 365–372. [Google Scholar] [CrossRef]
- Yun, M.J.; Yu, B.M.; Zhang, B.; Huang, M.T. A geometry model for tortuosity of stream tubes in porous media with spherical particles. Chin. Phys. Lett. 2005, 22, 1464–1467. [Google Scholar]
- Yun, M.J.; Yu, B.M.; Xu, P.; Wu, J.S. Geometrical models for tortuosity of streamlines in three-dimensional porous media. Can. J. Chem. Eng. 2006, 84, 301–309. [Google Scholar] [CrossRef]
- Kou, J.L.; Tang, X.M.; Zhang, H.Y.; Lu, H.J.; Wu, F.; Xu, Y.; Dong, Y. Tortuosity for streamlines in porous media. Chin. Phys. Rev. 2012, 21, 044701. [Google Scholar] [CrossRef]
- Daigle, H. Application of critical path analysis for permeability prediction in natural porous media. Adv. Water Resour. 2016, 96, 43–54. [Google Scholar] [CrossRef]
- Wheatcraft, S.W.; Tyler, S.W. An explanation of porous dispersivity in heterogeneous aquifers using concepts of fractal geometry. Water Resour. Res. 1988, 24, 566–578. [Google Scholar] [CrossRef]
- Sun, Z.; Shi, J.T.; Wu, L.; Zhang, T.; Feng, D.; Huang, L.; Shi, Y.; Ramachandean, H.; Li, X. An analytical model for gas transport through elliptical nanopores. Chem. Eng. Sci. 2019, 199, 199–209. [Google Scholar] [CrossRef]
- Cussler, E.L. Diffusion-Mass Transfer in Fluid Systems; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Skjeltorp, A.T.; Feder, A.A. (Eds.) Fractals in Physics; Elsevier: Amsterdam, The Netherlands, 1990. [Google Scholar]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Wang, Q.; Zhao, J.; Xie, S.; Jiang, H. A Novel Porous Media Permeability Model Based on Fractal Theory and Ideal Particle Pore-Space Geometry Assumption. Energies 2020, 13, 510. https://doi.org/10.3390/en13030510
Hu Y, Wang Q, Zhao J, Xie S, Jiang H. A Novel Porous Media Permeability Model Based on Fractal Theory and Ideal Particle Pore-Space Geometry Assumption. Energies. 2020; 13(3):510. https://doi.org/10.3390/en13030510
Chicago/Turabian StyleHu, Yongquan, Qiang Wang, Jinzhou Zhao, Shouchang Xie, and Hong Jiang. 2020. "A Novel Porous Media Permeability Model Based on Fractal Theory and Ideal Particle Pore-Space Geometry Assumption" Energies 13, no. 3: 510. https://doi.org/10.3390/en13030510
APA StyleHu, Y., Wang, Q., Zhao, J., Xie, S., & Jiang, H. (2020). A Novel Porous Media Permeability Model Based on Fractal Theory and Ideal Particle Pore-Space Geometry Assumption. Energies, 13(3), 510. https://doi.org/10.3390/en13030510




