Gasoline Demand Elasticities at the Backdrop of Lower Oil Prices: Fuel-Subsidizing Country Case
Abstract
1. Introduction
2. Literature Review
3. Theoretical Framework and Functional Specification
4. Econometric Methodology
Multiplicative Indicator Saturation (MIS) Approach
5. Data
6. Empirical Estimation Results
6.1. Unit Root Test Results
6.2. Long and Short-Run Estimation Results
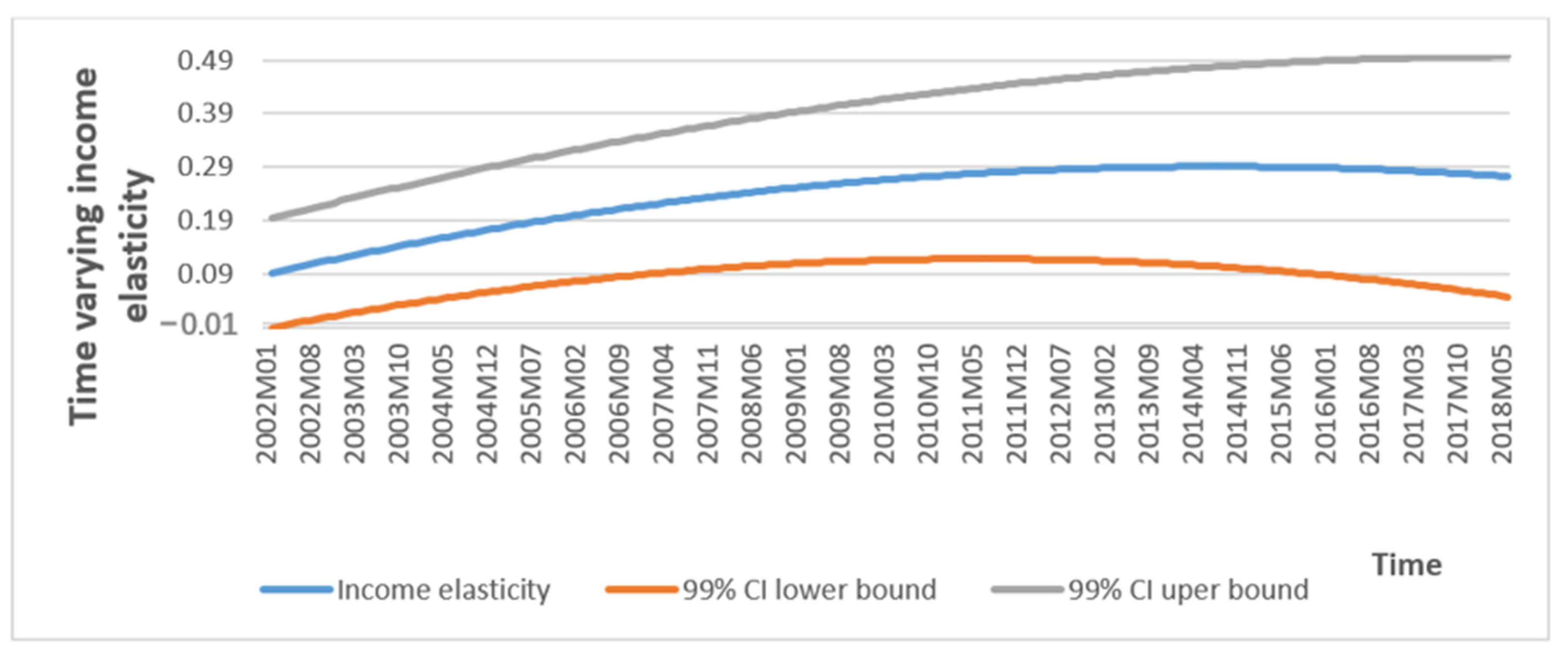
6.2.1. TVCC Estimation Results
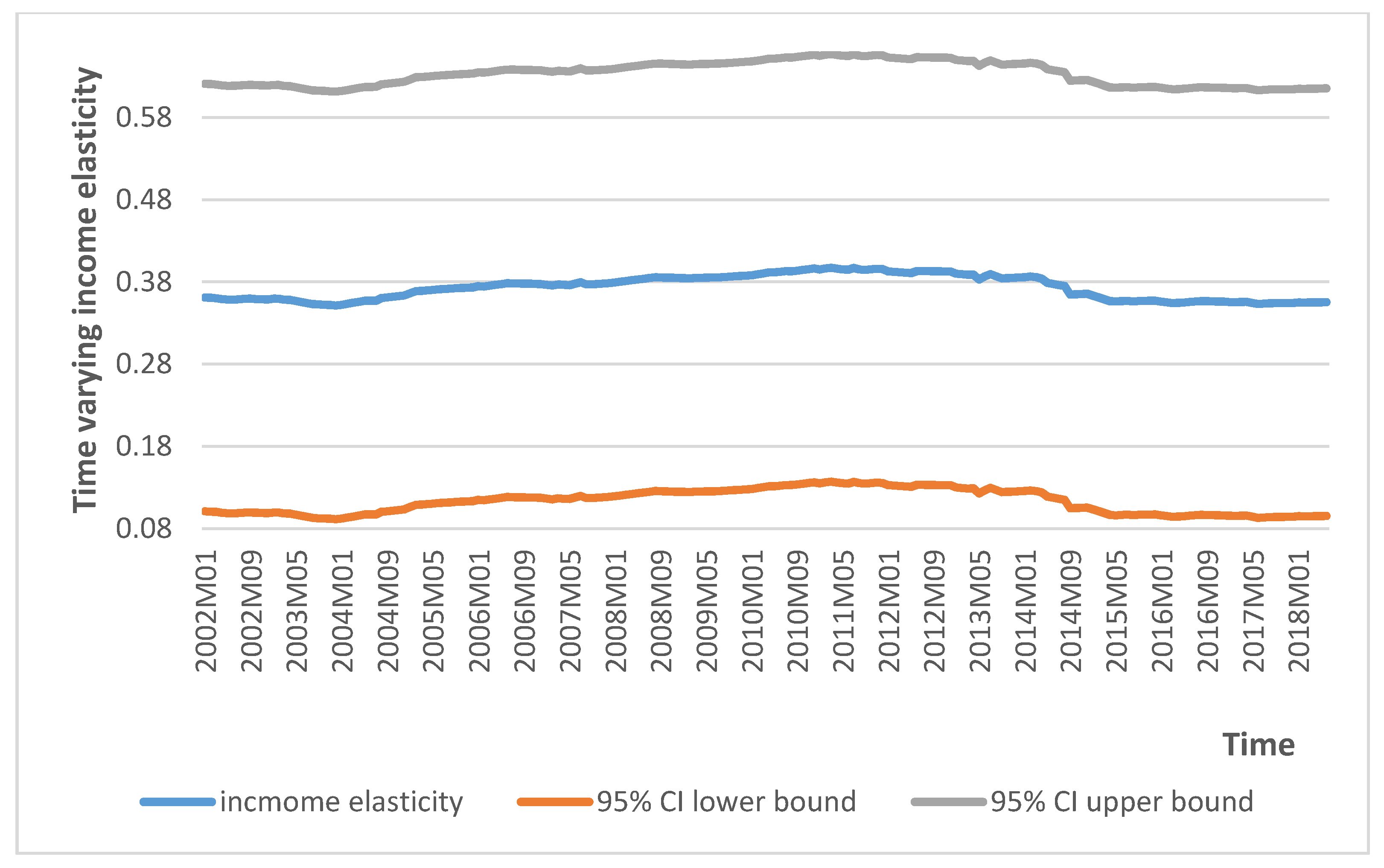
6.2.2. STSM Estimation Results
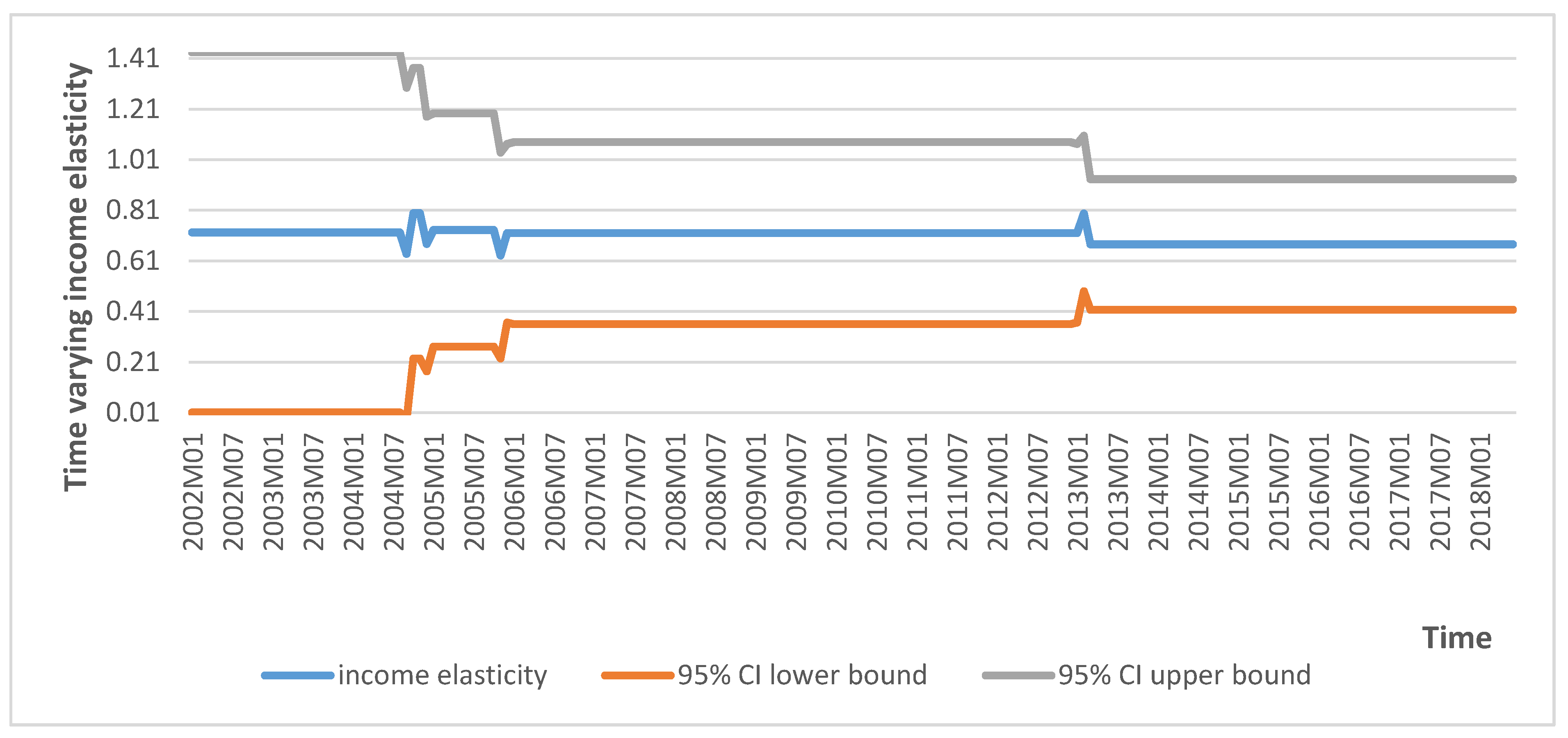
6.2.3. MIS Estimation Results
6.2.4. MIS Short-Run Results
7. Discussion of Empirical Results
8. Conclusions and Policy Insights
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Arzaghi, M.; Squalli, J. How price inelastic is demand for gasoline in fuel-subsidizing economies? Energy Econ. 2015, 50, 117–124. [Google Scholar] [CrossRef]
- The International Energy Agency-IEA. Available online: https://www.iea.org/weo/energysubsidies/ (accessed on 4 December 2020).
- SSCRA, State Statistical Committee of the Republic of Azerbaijan. 2019. Available online: https://www.stat.gov.az/source/transport/?lang=en (accessed on 2 May 2019).
- The International Energy Agency-IEA. World Energy Outlook. 2020. Available online: https://www.iea.org/reports/world-energy-outlook-2020 (accessed on 4 December 2020).
- GlobalPetrolPrices.com. 2020. Available online: https://www.globalpetrolprices.com/gasoline_prices/ (accessed on 4 December 2020).
- Park, J.Y.; Hahn, S.B. Cointegrating regressions with time varying coefficients. Econ. Theory 1999, 15, 664–703. [Google Scholar] [CrossRef]
- Hughes, J.; Christopher, K.; Daniel, S. Evidence of a Shift in the Short-Run Price Elasticity of Gasoline Demand. Energy J. 2008, 29, 93–114. [Google Scholar] [CrossRef]
- Bakhat, M.; Labandeira, X.; Labeaga, J.M.; López-Otero, X. Elasticities of transport fuels at times of economic crisis: An empirical analysis for Spain. Energy Econ. 2017, 68, 66–80. [Google Scholar] [CrossRef]
- Mukhtarov, S.; Mikayilov, J.I.; Humbatova, S.; Muradov, V. Do High Oil Prices Obstruct the Transition to Renewable Energy Consumption? Sustainability 2020, 12, 4689. [Google Scholar] [CrossRef]
- Totto, L.; Johnson, T.M. OPEC domestic oil demand: Product forecasts for 1985 and 1990. OPEC Rev. 1983, 7, 190–227. [Google Scholar] [CrossRef]
- Al-Sahlawi, M.A. Gasoline demand: The case of Saudi Arabia. Energy Econ. 1988, 10, 271–275. [Google Scholar] [CrossRef]
- Al-Faris, A.F. Income and price elasticities of gasoline demand in the organization of Arab Petroleum Exporting countries. J. Energy Dev. 1992, 17, 209–223. [Google Scholar]
- Eltony, M.N. An Econometric study of the demand for gasoline in the Gulf Co-operation Council countries. J. Energy Dev. 1994, 19, 265–273. [Google Scholar]
- Eltony, M.N. Demand for gasoline in the GCC: An application of pooling and testing procedures. Energy Econ. 1996, 18, 203–209. [Google Scholar] [CrossRef]
- Al-Faris, A.F. Demand for Oil Products in the GCC Countries. Energy Policy 1997, 25, 55–61. [Google Scholar] [CrossRef]
- Al-Sahlawi, M.A. The Demand for Oil Products in Saudi Arabia. OPEC Rev. 1997, 21, 33–38. [Google Scholar] [CrossRef]
- Alves, D.C.O.; Bueno, R.L.S. Short-run, long-run and cross elasticities of gasoline demand in Brazil. Energy Econ. 2003, 25, 191–199. [Google Scholar] [CrossRef]
- Cheung, K.-Y.; Thomson, E. The demand for gasoline in China: A cointegration analysis. J. Appl. Stat. 2004, 31, 533–544. [Google Scholar] [CrossRef]
- De Vita, G.; Endresen, K.; Hunt, L.C. An empirical analysis of energy demand in Namibia. Energy Policy 2006, 34, 3447–3463. [Google Scholar] [CrossRef]
- Polemis, M.L. Empirical assessment of the determinants of road energy demand in Greece. Energy Econ. 2006, 28, 385–403. [Google Scholar] [CrossRef]
- Akinboade, O.A.; Ziramba, E.; Kumo, W.L. The demand for gasoline in South Africa: An empirical analysis using co-integration techniques. Energy Econ. 2008, 30, 3222–3229. [Google Scholar] [CrossRef]
- Chakravorty, U.; Fesharaki, F.; Zhou, S. Domestic Demand for Petroleum in OPEC Countries. OPEC Rev. 2000, 24, 23–52. [Google Scholar] [CrossRef]
- Crotte, A.; Noland, R.B.; Graham, D.J. An analysis of gasoline demand elasticities at the national and local levels in Mexico. Energy Policy 2010, 38, 4445–4456. [Google Scholar] [CrossRef]
- Park, S.Y.; Zhao, G. An estimation of U.S. gasoline demand: A smooth time-varying cointegration approach. Energy Econ. 2010, 32, 110–120. [Google Scholar] [CrossRef]
- Liddle, B. The systemic, long-run relation among gasoline demand, gasoline price, income, and vehicle ownership in OECD countries: Evidence from panel cointegration and causality modeling. Transp. Res. Part D 2012, 17, 327–331. [Google Scholar] [CrossRef]
- Neto, D. Testing and estimating time-varying elasticities of Swiss gasoline demand. Energy Econ. 2012, 34, 1755–1762. [Google Scholar] [CrossRef]
- Dahl, C.A. Measuring global gasoline and diesel price and income elasticities. Energy Policy 2012, 41, 2–13. [Google Scholar] [CrossRef]
- Coyle, D.; DeBacker, J.; Prisinzano, R. Estimating the supply and demand of gasoline using tax data. Energy Econ. 2012, 34, 195–200. [Google Scholar] [CrossRef]
- Ben Sita, B.; Marrouch, W.; Abosedra, S. Short-run price and income elasticity of gasoline demand: Evidence from Lebanon. Energy Policy 2012, 46, 109–115. [Google Scholar] [CrossRef]
- Sene, S.O. Estimating the demand for gasoline in developing countries: Senegal. Energy Econ. 2012, 34, 189–194. [Google Scholar] [CrossRef]
- Al Yousef, N. Demand for oil products in OPEC countries: A panel cointegration analysis. Int. J. Energy Econ. Policy 2013, 3, 168. [Google Scholar]
- Burke, P.J.; Nishitateno, S. Gasoline prices, gasoline consumption, and new-vehicle fuel economy: Evidence for a large sample of countries. Energy Econ. 2013, 36, 363–370. [Google Scholar] [CrossRef]
- Baranzini, A.; Weber, S. Elasticities of gasoline demand in Switzerland. Energy Policy 2013, 63, 674–680. [Google Scholar] [CrossRef]
- Lin, C.-Y.C.; Prince, L. Gasoline price volatility and the elasticity of demand for gasoline. Energy Econ. 2013, 38, 111–117. [Google Scholar] [CrossRef]
- Ackah, I.; Adu, F. Modelling gasoline demand in Ghana: A structural time series analysis. Int. J. Energy Econ. Policy 2013, 4, 76–82. [Google Scholar]
- Scott, K.R. Rational Habits in Gasoline Demand. Energy Econ. 2012, 34, 1713–1723. [Google Scholar] [CrossRef]
- Hössinger, R.; Link, C.; Sonntag, A.; Stark, J. Estimating the price elasticity of fuel demand with stated preferences derived from a situational approach. Transp. Res. Part A Policy Pract. 2017, 103, 154–171. [Google Scholar] [CrossRef]
- Atalla, T.N.; Gasim, A.A.; Hunt, L.C. Gasoline demand, pricing policy, and social welfare in Saudi Arabia: A quantitative analysis. Energy Policy 2018, 114, 123–133. [Google Scholar] [CrossRef]
- Mikayilov, J.I.; Joutz, F.L.; Hasanov, F.J. Gasoline Demand in Saudi Arabia: Are the Price and Income Elasticities Constant? Environmental consequences of tourism: Do oil-exporting countries import more CO2 emissions? Energy Sources Part B Econ. Plan. Policy 2020, 15, 211–229. [Google Scholar] [CrossRef]
- Mousavi, M.H.; Ghavidel, S. Structural time series model for energy demand in Iran’s transportation sector. Case Stud. Transp. Policy 2019, 7, 423–432. [Google Scholar] [CrossRef]
- Mikayilov, J.I.; Mukhtarov, S.; Mammadov, J. Income and Price Elasticities of Gasoline Demand: An Empirical Analysis for Russia. ASERC J. Socio-Econ. Stud. 2019, 2, 3–12. [Google Scholar]
- Harvey, A.C. Forecasting, Structural Time Series Models and the Kalman Filter; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Ericsson, N.R. Detecting Crises, Jumps, and Changes in Regime; Working Paper; Federal Reserve Board of Governors: Washington, DC, USA, 2012.
- Castle, J.L.; Hendry, D.F.; Martinez, A.B. Evaluating forecasts, narratives and policy using a test of invariance. Econometrics 2017, 5, 39. [Google Scholar] [CrossRef]
- Castle, J.L.; Hendry, D.F. Modelling our Changing World 2029; Springer Publishing: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Koopman, S.J.; Shephard, N.; Doornik, J.A. Statistical algorithms for models in state space using SsfPack 2.2. Econom. J. 1999, 2, 113–166. [Google Scholar] [CrossRef]
- Commandeur, J.J.F.; Koopman, S.J. An Introduction to State Space Time Series Analysis; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Mikayilov, J.I.; Darandary, A.; Alyamani, R.; Hasanov, F.J.; Alatawi, H. Regional heterogeneous drivers of electricity demand in Saudi Arabia: Modeling regional residential electricity demand. Energy Policy 2020, 146, 111796. [Google Scholar] [CrossRef]
- Chang, Y.; Kim, C.K.; Miller, J.I.; Park, J.Y.; Park, S. Time-varying Long-run Income and Output Elasticities of Electricity Demand with an Application to Korea. Energy Econ. 2014, 46, 334–347. [Google Scholar] [CrossRef]
- Koopman, S.J.; Rutger, L.; Andrew, C.H. 1995–2018. STAMP 8.40 (C) [Software Package]. Available online: file:///C:/Program%20Files/OxMetrics8/doc/STAMP/index.html (accessed on 20 December 2020).
- Kitov, O.I.; Tabor, M.N. Detecting Structural Changes in Linear Models: A Variable Selection Approach Using Multiplicative Indicator Saturation; Unpublished Paper; University of Oxford: Oxford, UK, 2015. [Google Scholar]
- Doornik, J.A. Autometrics. In The Methodology and Practice of Econometrics; Castle, J.L., Shephard, N., Eds.; Oxford University Press: Oxford, UK, 2009; pp. 88–121. [Google Scholar]
- Doornik, J.A.; Hendry, D.F. Empirical Econometric Modelling Using PcGive: Volume I, 8th ed.; Timberlake Consultants Press: London, UK, 2018. [Google Scholar]
- Jodi-Oil. 2019. Available online: https://www.jodidata.org/oil/ (accessed on 2 May 2019).
- CBAR-the Central Bank of Republic of Azerbaijan. 2019. Available online: https://www.cbar.az/page-41/macroeconomic-indicators (accessed on 2 May 2019).
- The State Statistical Committee of the Republic of Azerbaijan-SSCRA. 2019. Available online: https://www.stat.gov.az/source/demoqraphy/ (accessed on 2 May 2019).
- Elliott, G.; Rothenberg, G.T.J.; Stock, J.H. Efficient Tests for an Autoregressive Unit Root. Econometrica 1996, 64, 813–836. [Google Scholar] [CrossRef]
- Kwiatkowski, D.; Phillips, P.C.B.; Schmidt, P.; Shin, Y. Testing the null hypothesis of stationarity against the alternative of a unit root: How sure are we that economic time series have a unit root? J. Econ. 1992, 54, 159–178. [Google Scholar] [CrossRef]
- Zivot, E.; Andrews, D.W.K. Further Evidence on the Great Crash, the Oil-Price Shock, and the Unit-Root Hypothesis. J. Bus. Econ. Stat. 1992, 10, 251. [Google Scholar] [CrossRef]
- Mackinnon, J.G. Numerical Distribution Functions for Unit Root and Cointegration Test. J. Appl. Econom. 1996, 11, 601–618. [Google Scholar] [CrossRef]
- Park, J.Y. Testing for unit roots and cointegration by variable addition. In Advances in Econometrics; Rhodes, G.F., Fomby, T.B., Eds.; JAI Press: Greenwich, UK, 1990; pp. 107–133. [Google Scholar]
- Ljung, G.M.; George EP Box. On a measure of lack of fit in time series models. Biometrika 1978, 65, 297–303. [Google Scholar] [CrossRef]
- Engle, R.F. Autoregressive conditional heteroscedasticity, with estimates of the variance of United Kingdom inflation. Econometrica 1982, 50, 987–1007. [Google Scholar] [CrossRef]
- Doornik, J.A.; Hansen, H. A Practical Test for Univariate and Multivariate Normality; Discussion Paper; Nuffield College: Oxford, UK, 1994. [Google Scholar]
- White, H. A heteroskedastic-consistent covariance matrix estimator and a direct test for heteroskedasticity. Econometrica 1980, 48, 817–838. [Google Scholar] [CrossRef]
- Ramsey, J.B. Tests for specification errors in classical linear least squares regression analysis. J. R. Stat. Soc. B 1969, 31, 350–371. [Google Scholar] [CrossRef]
- Nyblom, J.; Harvey, A.C. Tests of common stochastic trends. Econom. Theory 2000, 16, 176–199. [Google Scholar] [CrossRef]
- Nyblom, J.; Harvey, A.C. Testing Against Smooth Stochastic Trends. J. Appl. Econ. 2001, 16, 415–429. [Google Scholar] [CrossRef]
- Jarque, C.M.; Bera, A.K. A test for normality of observations and regression residuals. Int. Stat. Rev. 1987, 55, 163–172. [Google Scholar] [CrossRef]
- Harvey, A.C. The Econometric Analysis of Time Series; Philip Allan: Deddington, UK, 1981. [Google Scholar]
- Harvey, A.C. Time Series Models, 2nd ed.; Harvester Wheatsheaf: Hemel Hempstead, UK, 1993. [Google Scholar]
- Banerjee, A.; Dolado, J.J.; Galbraith, J.W.; Hendry, D.F. Co-Integration, Error Correction and the Econometric Analysis of Non-Stationary Data; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Campos, J.; Ericsson, N.R.; Hendry, D.F. Readings on General-to-Specific Modeling; Edward Elgar: Cheltenham, UK, 2005. [Google Scholar]
- IMF. International Monetary Fund. World Economic Outlook Database; IMF: Washington, DC, USA, 2018. [Google Scholar]
- CEIC. CEIC Data. 2019. Available online: https://cli.ceicdata.com (accessed on 20 December 2020).
- Caspian Barrel. 2019. Available online: http://caspianbarrel.org/az/2019/04/az-rbaycan-benzinin-alternativi/?fbclid=IwAR3_uPTa1lSl3hmYU7C8nV9l9oJPEnM0QSTnEqkkOVK2PIH6HaMkVVbXoXE (accessed on 2 May 2019).
- Havranek, T.; Kokes, O. Income elasticity of gasoline demand: A meta-analysis. Energy Econ. 2015, 47, 77–86. [Google Scholar] [CrossRef]
- Havranek, T.; Irsova, Z.; Janda, K. Demand for gasoline is more price-inelastic than commonly thought. Energy Econ. 2012, 34, 201–207. [Google Scholar] [CrossRef]
- Chang, Y.; Choi, Y.; Kim, C.S.; Miller, J.I.; Park, J.Y. Disentangling temporal patterns in elasticities: A functional coefficient panel analysis of electricity demand. Energy Econ. 2016, 60, 232–243. [Google Scholar] [CrossRef]


| Study | Country/Country Group | Period | Data Type | Methodology | Price Elasticity | Income Elasticity | ||
|---|---|---|---|---|---|---|---|---|
| SR | LR | SR | LR | |||||
| Totto and Johnson [10] | OPEC | 1970–1979 | T/A | MOLS | n/a | −0.09 | n/a | 1.02 to 1.26 |
| Al-Sahlawi [11] | KSA | 1970–1985 | T/A | OLS/PAM | −0.08 | −0.67 | 0.11 | 0.92 |
| Al-Faris [12] | KSA | 1970–1990 | T/A | OLS/PAM | −0.08 | −0.30 | 0.02 | 0.07 |
| Eltony [13] | GCC | 1975–1989 | T/A | CFE /PAM | −0.09 to −0.11 | −0.11 to −0.13 | 0.21 to 0.41 | 0.23 to 0.48 |
| Eltony [14] | GCC | 1975–1993 | T/A | CFE /PAM | −0.11 | −0.17 | 0.31 | 0.48 |
| Al-Faris [15] | KSA | 1970–1991 | T/A | OLS/PAM | −0.09 | −0.32 | 0.03 | 0.11 |
| Al-Sahlawi [16] | KSA | 1971–1995 | T/A | OLS/PAM | −0.16 | −0.80 | 0.30 | 1.50 |
| Alves et al. [17] | Brazil | 1974–1999 | T/A | OLS/ECM | −0.09 | −0.46 | 0.122 | 0.12 |
| Cheung and Thomson [18] | China | 1949–1999 | T/A | VECM | −0.19 | −0.56 | 1.64 | 0.97 |
| De Vita et al. [19] | Namibia | 1980–2002 | T/Q | ARDL | −0.79 | 0.96 | ||
| Polemis [20] | Greece | 1978–2003 | T/A | VECM | −0.10 | −0.38 | 0.36 | 0.79 |
| Akinboade et al. [21] | South Africa | 1978–2005 | T/A | ARDL | - 0.47 | 0.36 | ||
| Chakravorty et al. [22] | KSA | 1972–1992 | T/A | OLS/PAM | −0.08 | −0.52 | 0.10 | 0.66 |
| Crotte et al. [23] | Mexico | 1980–2006, 1993–2004 | T/A and P | GMM, OLS, FMOLS | −0.06 (OLS), −0.10 (FMOLS), −0.15 (GMM) | −0.06 (OLS), −0.29 (FMOLS), −0.39 (GMM) | 0.78 (OLS), 0.43(FMOLS), 047 (GMM) | 0.76 (OLS), 0.53(FMOLS), 1.19 (GMM) |
| Park and Zhao [24] | U.S. | 1976 −2008 | T/A | TVCC | −0.42 (M1), −0.66 for (M2). | 0.48 for (M1), 0.57 for (M2). | ||
| Liddle [25] | 14 OECD Countries | 1978–2005 | P/A | Panel DOLS and FMOLS, Panel Granger-causality | −0.16 | −0.43 | 0.28 | 0.34 |
| Neto [26] | Switzerland | 1973: Q1 to 2010: Q4 | T/Q | FMOLS/TVC | −0.17 | 0.69 | ||
| Dahl [27] | Panel of 120 countries, AZE included | Different time intervals | T/A and P | Review of previous studies (In some cases, the author employed different techniques to find the missed elasticities.) | n/a | −0.22 (AZE) | n/a | 1.27 (AZE) |
| Coyle et al. [28] | U.S. | 1990–2009 | T/Q | OLS, 3SLS | −0.08 | −0.06 a, −0.08 b | 0.41 | 0.36 a, 0.46 b |
| Ben Sita et al. [29] | Lebanon | 2000:M1–2010:M12 | T/M | Structural breaks | −0.62 | −0.30 | 0.31 | 1.14 |
| Sene [30] | Senegal | 1970 to 2008 | −0.12 | 0.46 | ||||
| Al Yousef [31] | THE KSA | 1980–2010 | P/A | Panel FMOLS & DOLS | n/a | −0.28 to −0.36 | n/a | 0.55 to 0.56 |
| Burke and Nishitaten [32] | 132 countries | 1995–2008 | P/A | PPOLS | n/a | −0.5 to −0.2 | n/a | 0.95 to 1.10 |
| Baranzini and Weber [33] | Switzerland | 1970–2008 | T/Q | ECM | −0.09 | −0.34 | 0.03 | 0.67 |
| Lin and Prince [34] | USA | 1990−2012 | T/M | OLS | −0.07 to −0.03 | −0.29 to −0.24 | 0.03 to 0.27 | 0.23 to 0.27 |
| Ackah and Adu [35] | Ghana | 1971–2010 | T/A | STSM | −0.01 | −0.07 | 0.713 | 5.13 |
| Scott [36] | 29 countries | 1990–2011 | P/A | FE 2SLS, PMGE | −0.05 to −0.20 | −0.74 to −0.19 | 0.25 to 0.28 | 0.82 to 1.09 |
| Arzaghi and Squalli [1] | 32 fuel-subsidizing Countries, AZE included | 1998–2010 | P/A | CFE, RE, FE /PAM | −0.05 | −0.25 | 0.16 | 0.81 |
| Hössinger et al. [37] | Austria | 2002M10–2011M12 | T/M | OLS | −0.14 | 0.18 | ||
| Atalla et al. [38] | KSA | 1981–2015 | T/A | STSM | −0.09 to −0.10 | −0.15 c, −0.09 d | insignificant | 0.15, 0.62 |
| Mikayilov et al. [39] | KSA | 1980–2017 | T/A | TVCC | −0.13 | −0.31 to −0.05 | insignificant | 0 to 0.15 |
| Mousavi and Ghavidel [40] | Iran | 1980–2016 | T/A | STSM | n/a | −0.24 to −0.17 | n/a | 0.38 to 0.48 |
| Mikayilov et al. [41] | Russia | 2002Q1–2018Q1 | T/Q | DOLS, FMOLS, CCR, STSM, TVCC | n/a | −0.17 | n/a | 0.78 |
| Elliott-Rothenberg-Stock DF-GLS Test (ERS) | Kwiatkowski-Phillips-Schmidt-Shin Test | ||||||
|---|---|---|---|---|---|---|---|
| Variables | Level | k | First Difference | k | Level | First Difference | |
| Intercept | 0.021 | 2 | −17.413 *** | 1 | 1.530 *** | 0.181 | |
| 1.048 | 1 | −2.448 ** | 6 | 1.392 *** | 0.572 * | ||
| −0.486 | 2 | −19.878 *** | 0 | 0.253 *** | 0.202 | ||
| Intercept and trend | −2.117 | 2 | 0.439 *** | ||||
| 0.048 | 2 | 0.415 *** | |||||
| −1.388 | 2 | 0.156 * | |||||
| Panel A | Panel B | ||||
|---|---|---|---|---|---|
| Variable Addition Test | TVC Significance Test | ||||
| Test Statistics | Test Statistics | ||||
| 3.50 | 149.33 | ||||
| Critical Values | |||||
| 1% | 5% | 10% | 1% | 5% | 10% |
| 13.18 | 9.49 | 7.78 | 9.21 | 5.99 | 4.61 |
| FC | Polynomials (p = 2) | FC | |||||
|---|---|---|---|---|---|---|---|
| Chosen terms | 1 | ||||||
| Corresponding coefficients of the chosen terms | |||||||
| (intercept) | Price | ||||||
| İncome | coefficients | −4.695 | 0.252 | 0.263 | −0.177 | −0.15 | |
| p-values | (0.000) | (0.017) | (0.016) | (0.096) | |||
| ect(−1) | dp(−1) | Constant Term | R_Square | Sigma | |
|---|---|---|---|---|---|
| −0.726 [0.0000] | −0.090 [0.0000] | −0.7070 to 0.438 | 0.739 | 0.069 | |
| Diagnostic tests’ results | |||||
| AR test | ARCH test | Normality test | Hetero test | Hetero X test | RESET test |
| 1.3743 [0.2192] | 0.43057 [0.8822] | 2.1657 [0.3386] | 0.76945 [0.6301] | 0.68131 [0.7252] | 0.080982 [0.9222] |
| Eigenvalues | Price | Income | Constant Term | R_Square | Prediction Error Variance: | ||
|---|---|---|---|---|---|---|---|
| 0.002466 | 2.71 × 10−19 | −8.470 × 10−22 | −0.117 [0.018] | 0.350 to 0.397 | −4.745 to −4.455 | 0.731 | 0.005 |
| Diagnostic tests’ results | |||||||
| Normality | H(56) | Q(24) | r(1) | r(24) | DW | ||
| 2.8288 [0.2431] | 0.40921 [0.9995] | 22.617 [0.0000] | −0.128 | −0.024 | 2.211 | ||
| ect(−1) | Dincome(−1) | Constant Term | R_Square | PREDICTION Error Variance: | |
|---|---|---|---|---|---|
| −0.784 [0.000] | 0.397 [0.005] | −0.370 to 0.569 | 0.888 | 0.006 | |
| Diagnostic tests’ results | |||||
| Normality | H(56) | Q(24) | r(1) | r(24) | DW |
| 1.6745 [0.4329] | 36.178 [0.0000] | 36.178 [0.0527] | −0.053 | 0.004 | 2.099 |
| Cointegration Test | p | Income | Constant Term | R_Square | Sigma |
|---|---|---|---|---|---|
| −44.717 [0.0000] | −0.190 [0.001] | 0.635 to 0.802 | −7.448 to −5.760 | 0.962 | 0.119 |
| Diagnostic tests’ results | |||||
| AR test | ARCH test | Normality test | Hetero test | Hetero X test | RESET test |
| 1.5508 [0.1535] | 0.59958 [0.7558] | 1.4682 [0.4799] | 0.69356 [0.8144] | 0.69693 [0.8645] | 1.8727 [0.1568] |
| ect(−1) | Dincome(−1) | Constant Term | R_Square | Sigma | |
|---|---|---|---|---|---|
| −0.741 [0.0000] | 0.332 [0.0114] | −0.885 to 0.590 | 0.672 | 0.077 | |
| Diagnostic tests’ results | |||||
| AR test | ARCH test | Normality test | Hetero test | Hetero X test | RESET test |
| 1.5150 [0.1652] | 1.5592 [0.1502] | 2.8067 [0.2458] | 1.2929 [0.2500] | 1.1727 [0.3153] | 0.13447 [0.8743] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mikayilov, J.I.; Mukhtarov, S.; Mammadov, J. Gasoline Demand Elasticities at the Backdrop of Lower Oil Prices: Fuel-Subsidizing Country Case. Energies 2020, 13, 6752. https://doi.org/10.3390/en13246752
Mikayilov JI, Mukhtarov S, Mammadov J. Gasoline Demand Elasticities at the Backdrop of Lower Oil Prices: Fuel-Subsidizing Country Case. Energies. 2020; 13(24):6752. https://doi.org/10.3390/en13246752
Chicago/Turabian StyleMikayilov, Jeyhun I., Shahriyar Mukhtarov, and Jeyhun Mammadov. 2020. "Gasoline Demand Elasticities at the Backdrop of Lower Oil Prices: Fuel-Subsidizing Country Case" Energies 13, no. 24: 6752. https://doi.org/10.3390/en13246752
APA StyleMikayilov, J. I., Mukhtarov, S., & Mammadov, J. (2020). Gasoline Demand Elasticities at the Backdrop of Lower Oil Prices: Fuel-Subsidizing Country Case. Energies, 13(24), 6752. https://doi.org/10.3390/en13246752







