Numerical Study on Anisotropic Influence of Joint Spacing on Mechanical Behavior of Rock Mass Models under Uniaxial Compression
Abstract
:1. Introduction
2. Particle Flow Modeling of the Jointed Specimens
2.1. Setup of the Jointed Specimens
2.2. Calibration of Micro-Properties in the Numerical Model
3. Quantities Defined at Different Scales
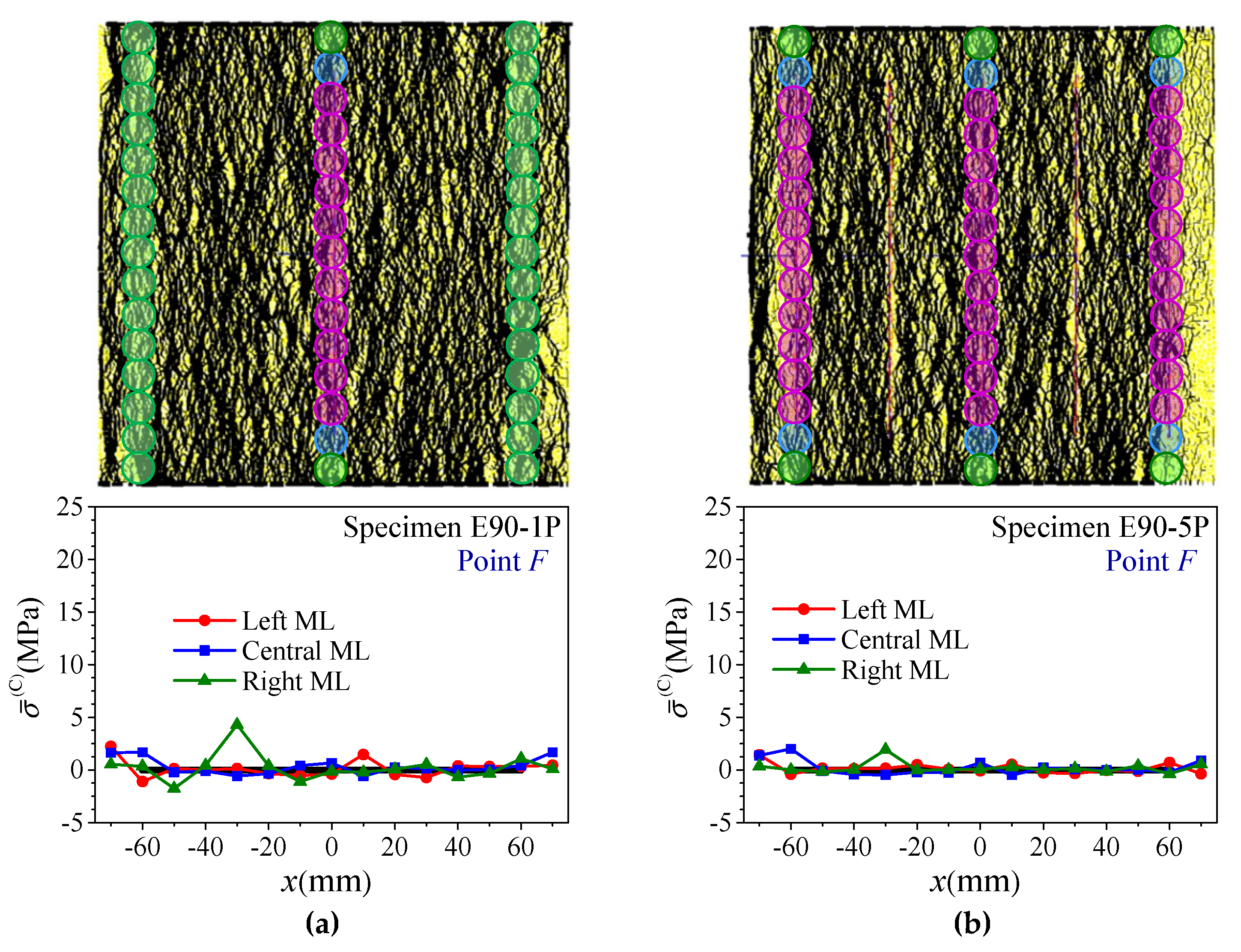
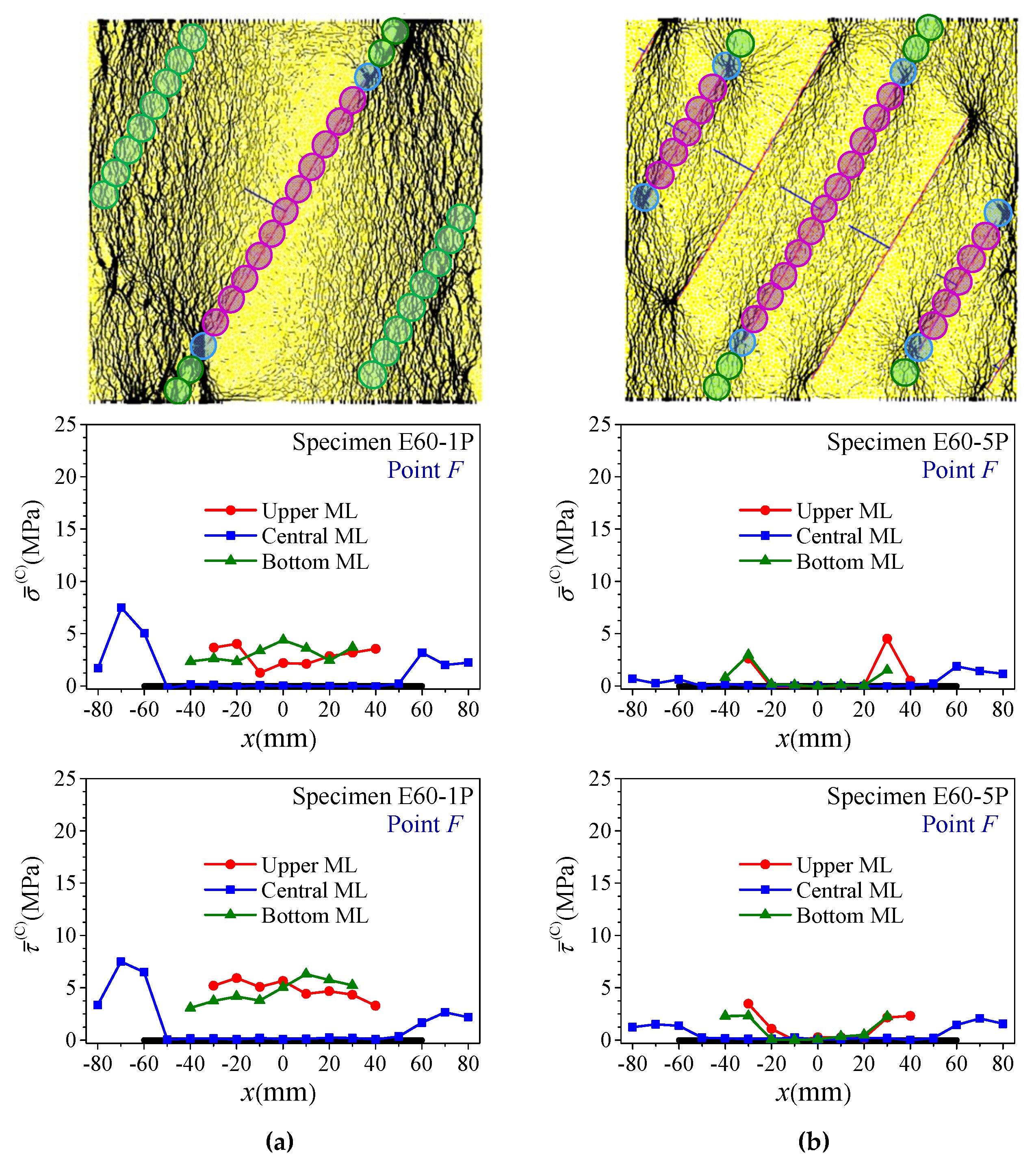
3.1. Quantities in the Local Measurement Circles
3.2. Quantities along the MLs
3.3. Quantities of the Whole Specimen
4. Results and Discussion
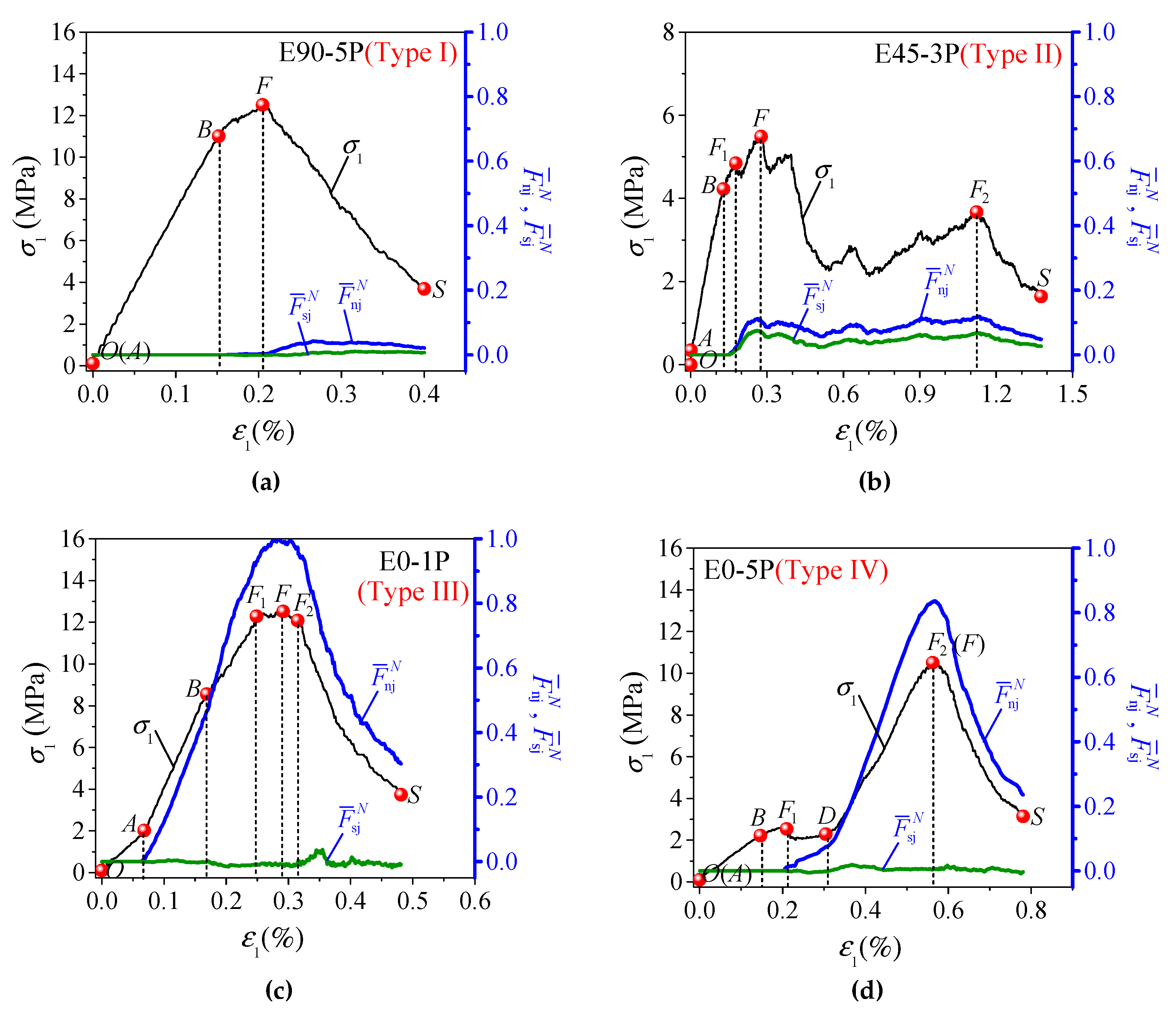
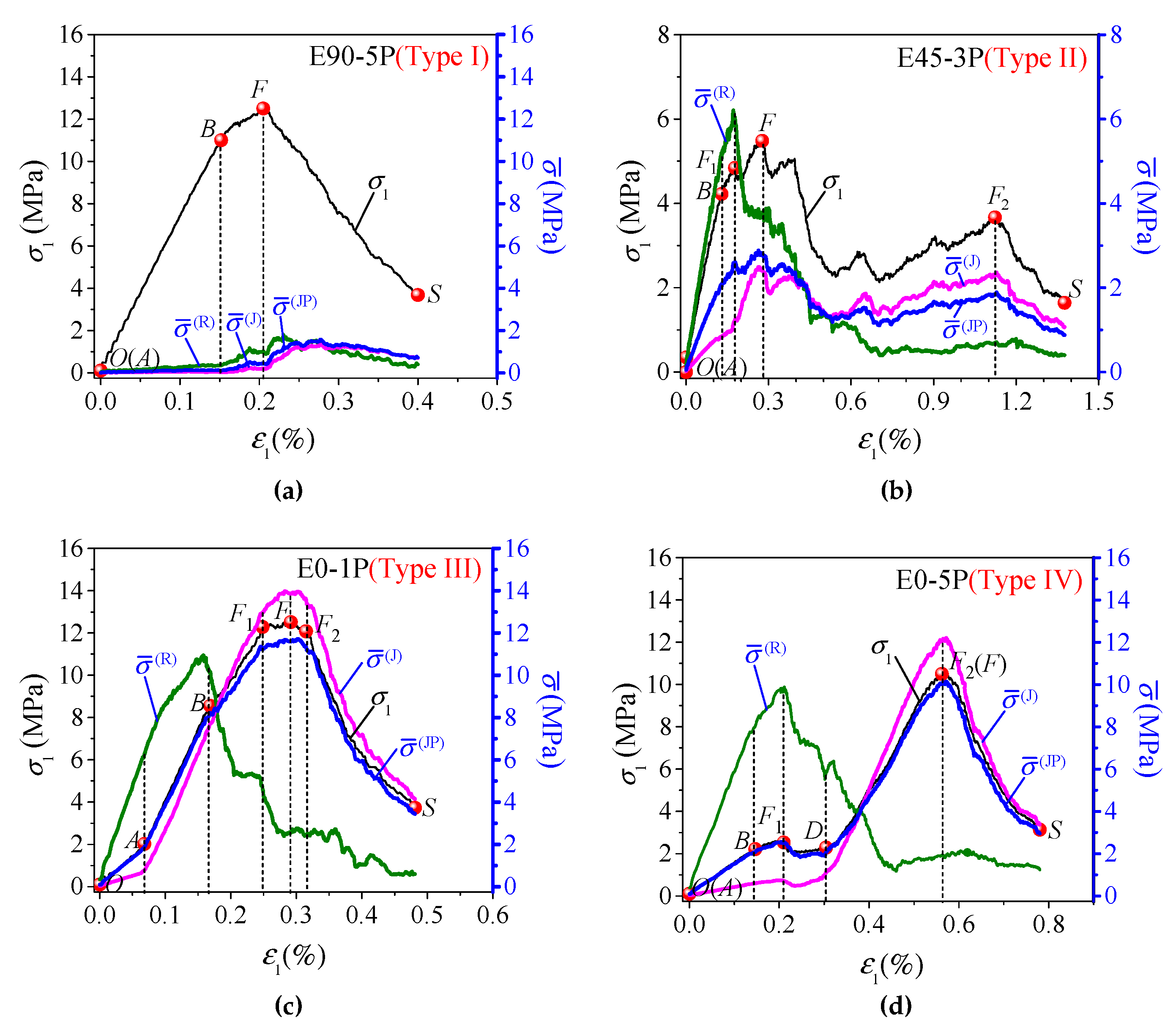
4.1. Macroscopic Mechanical Response of Jointed Specimens
4.2. Overall Response of the Joint System
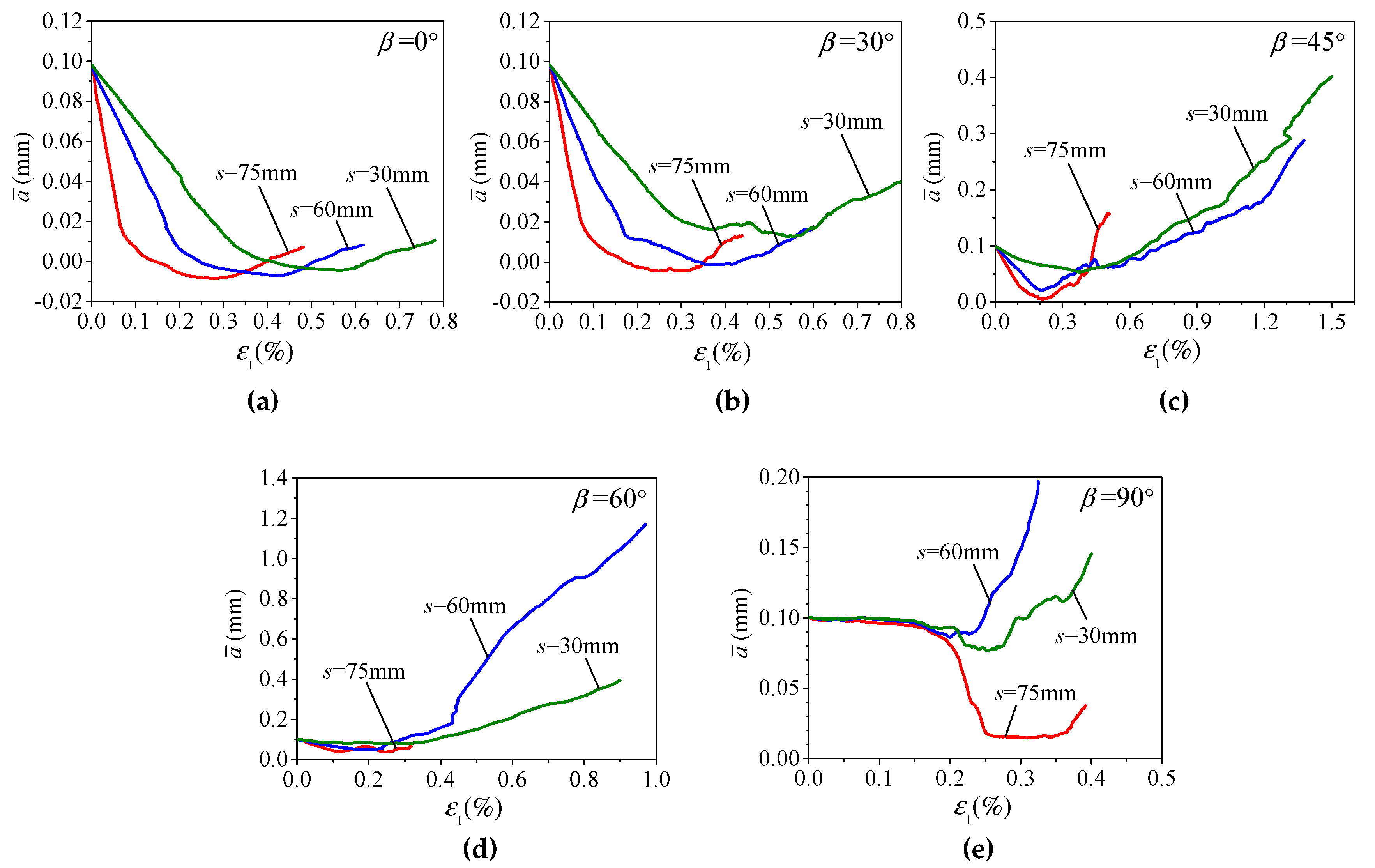
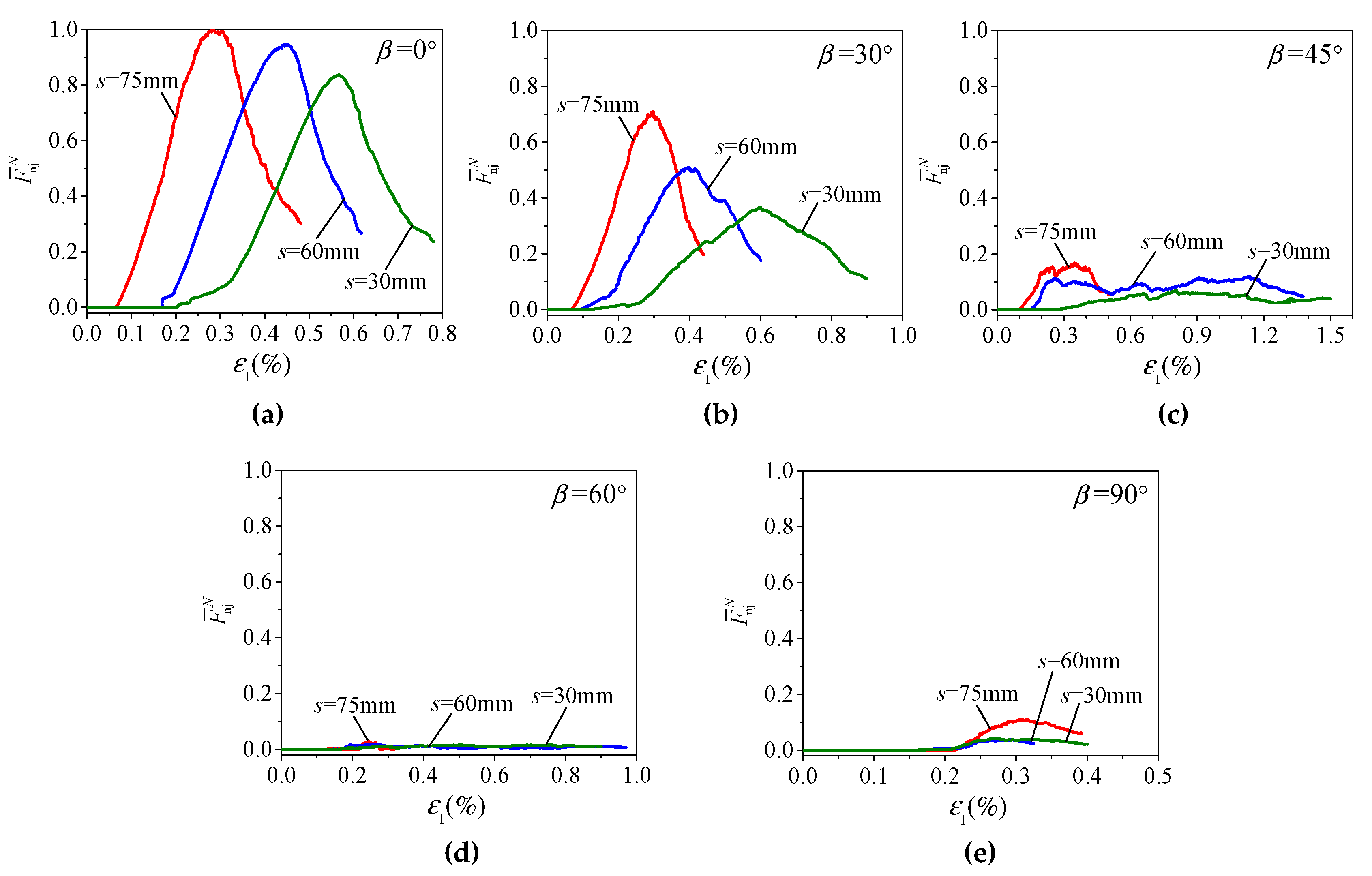
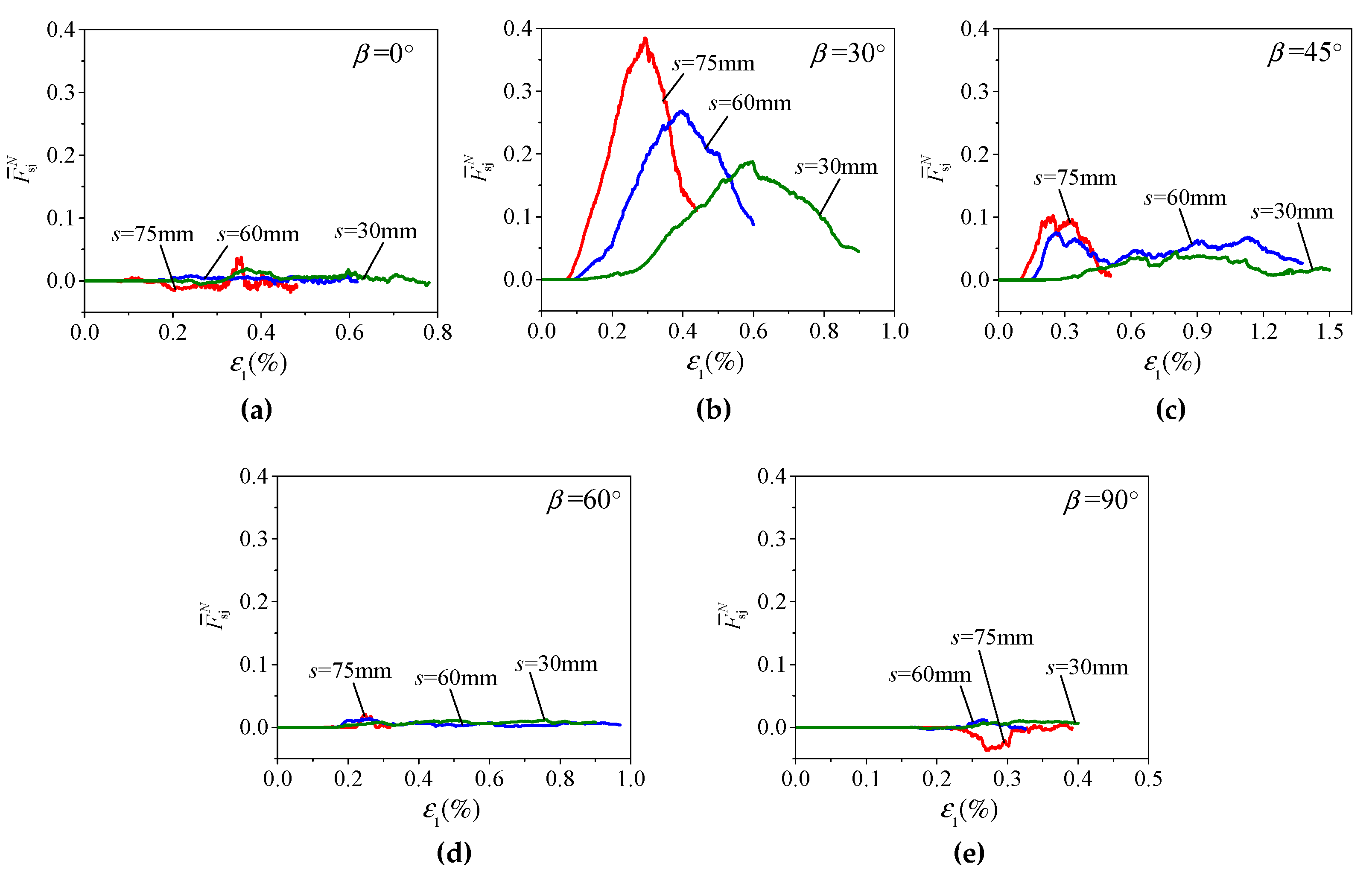
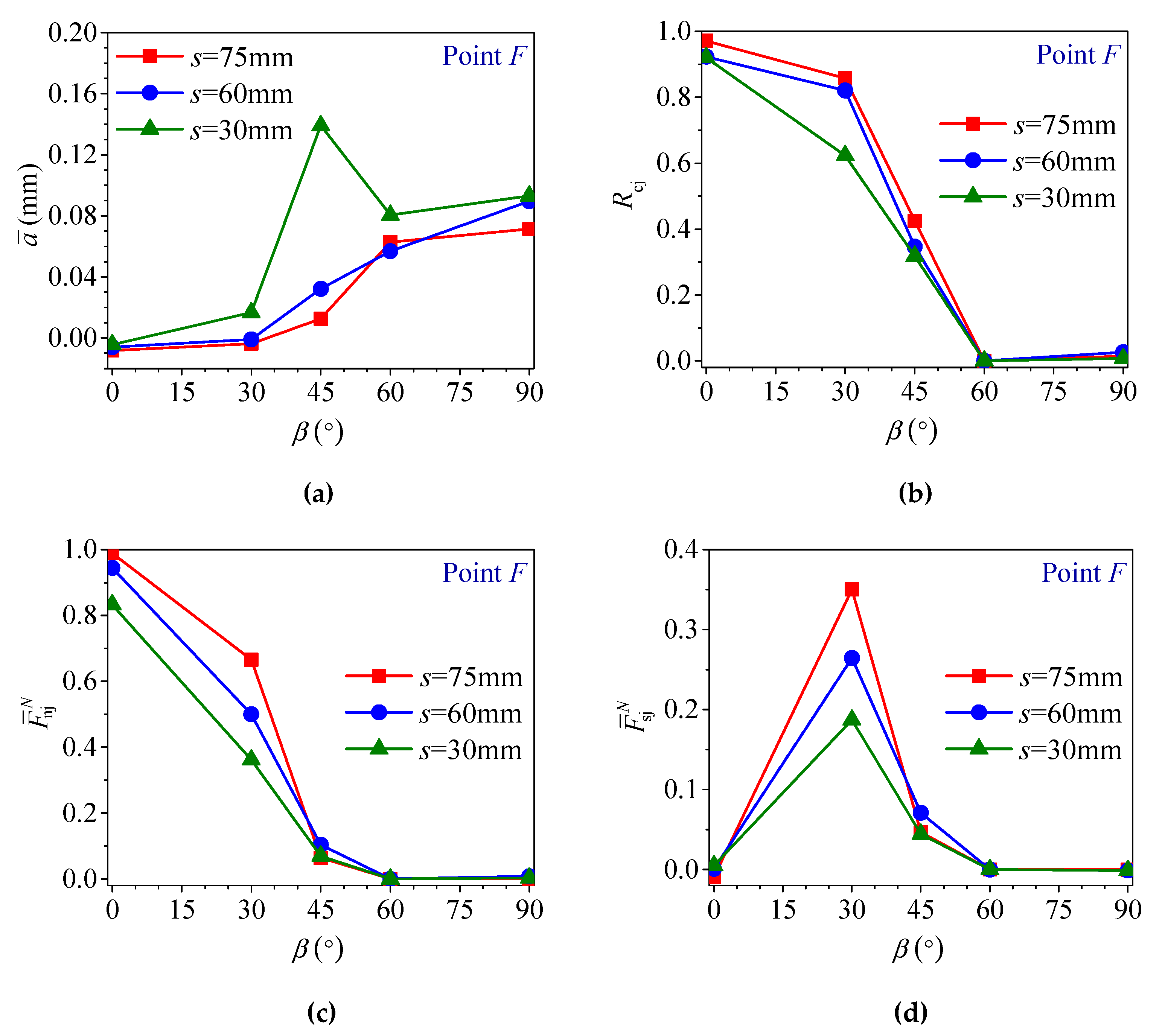
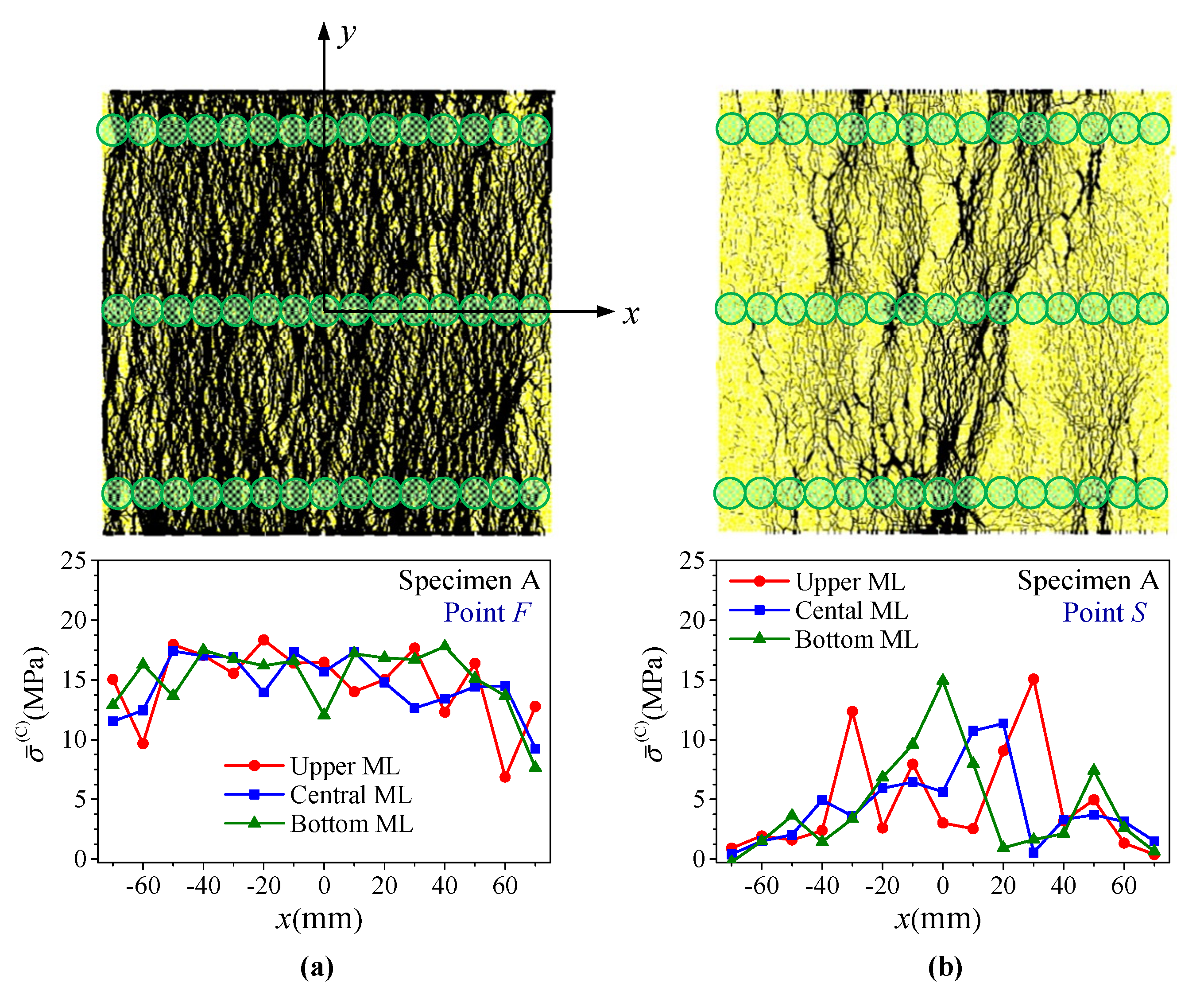
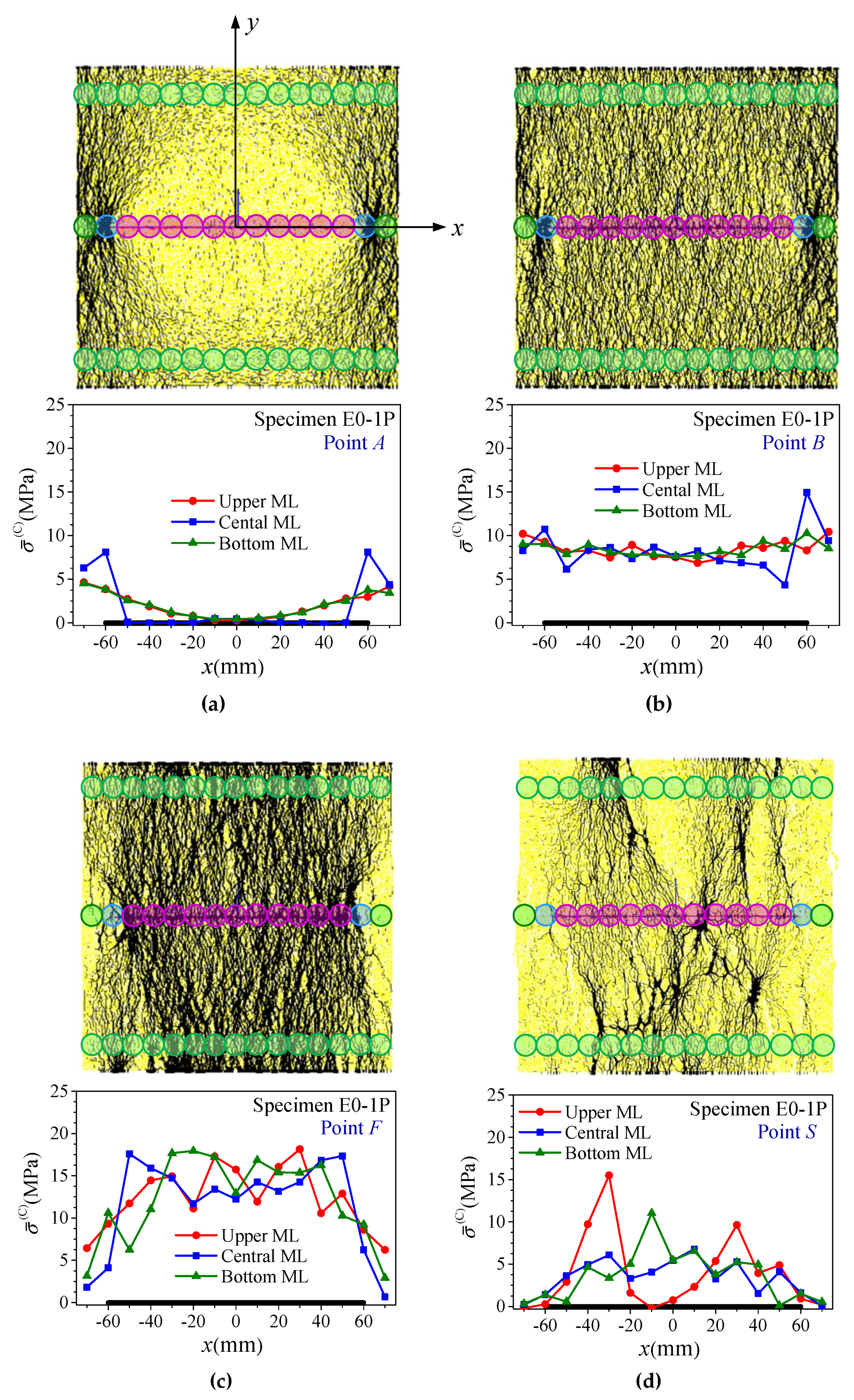
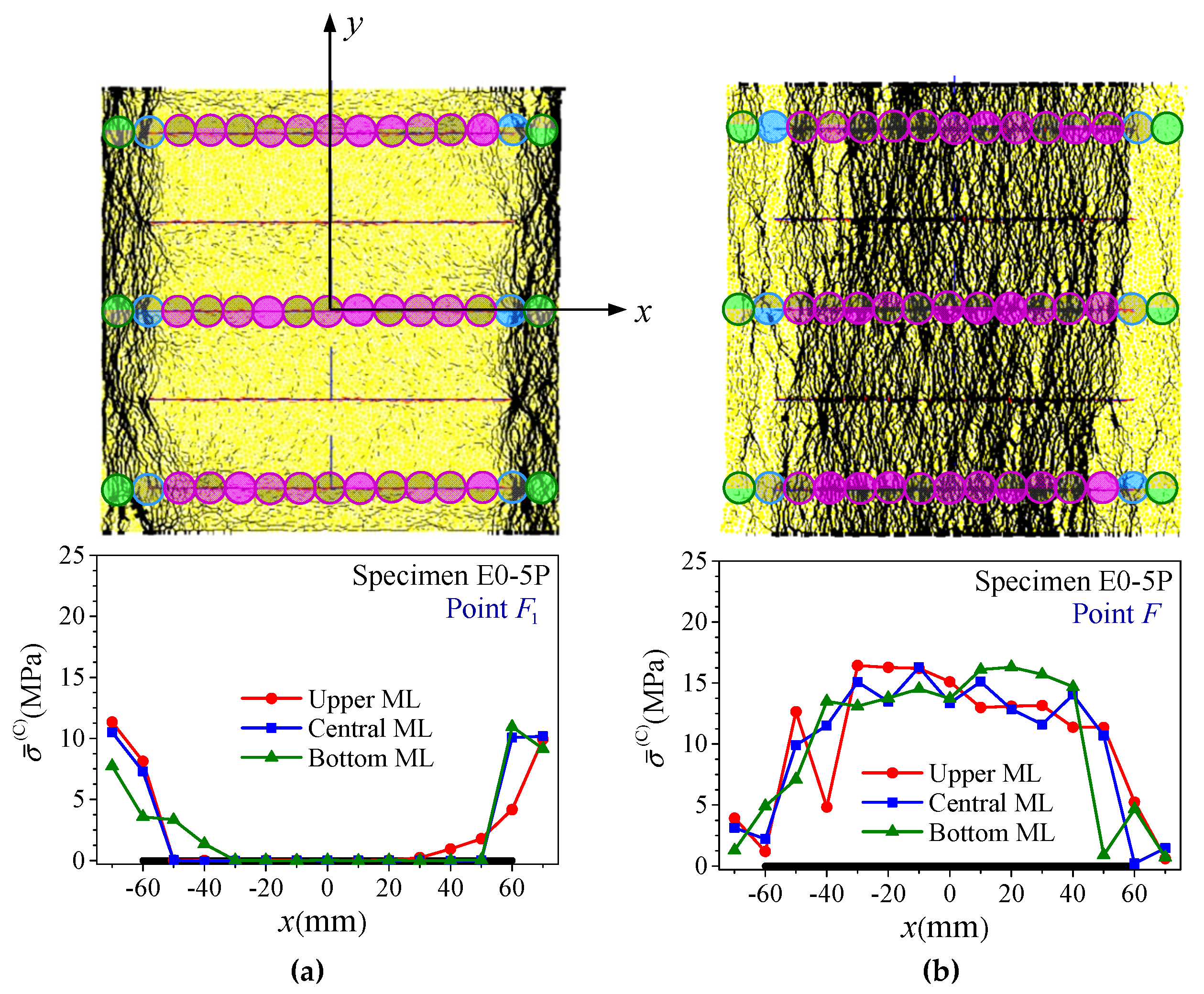
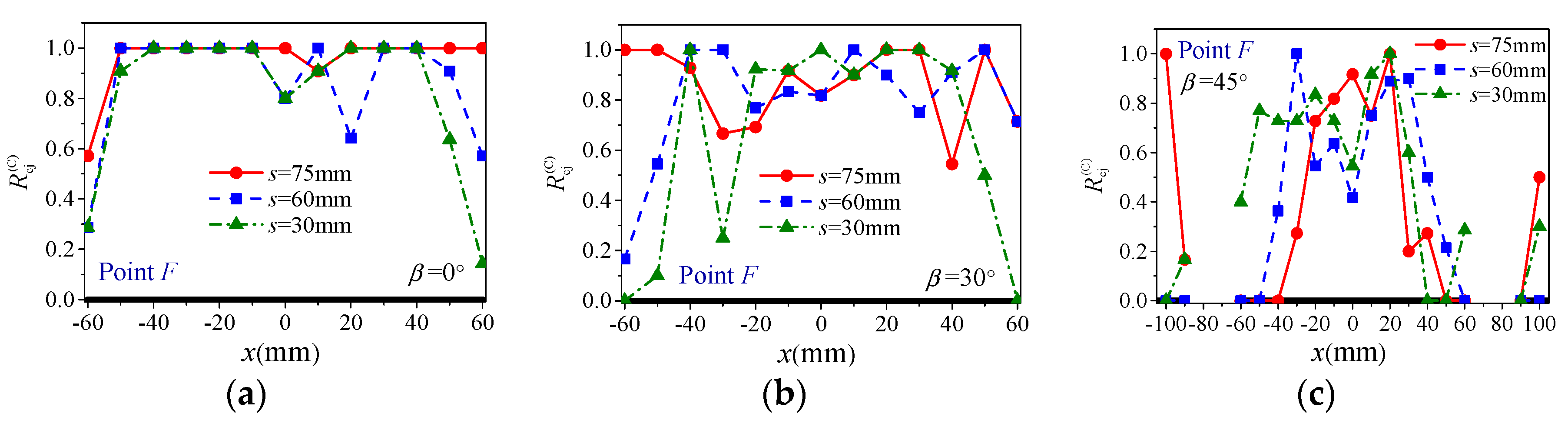
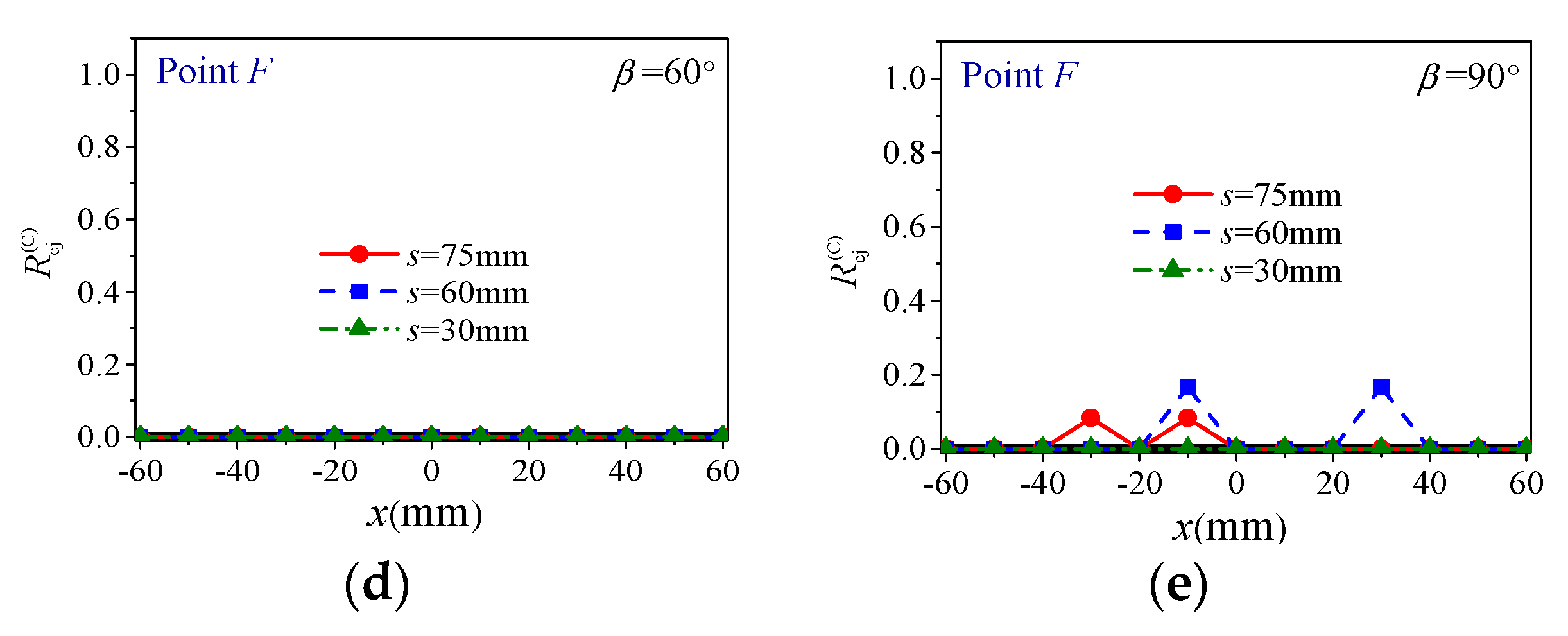
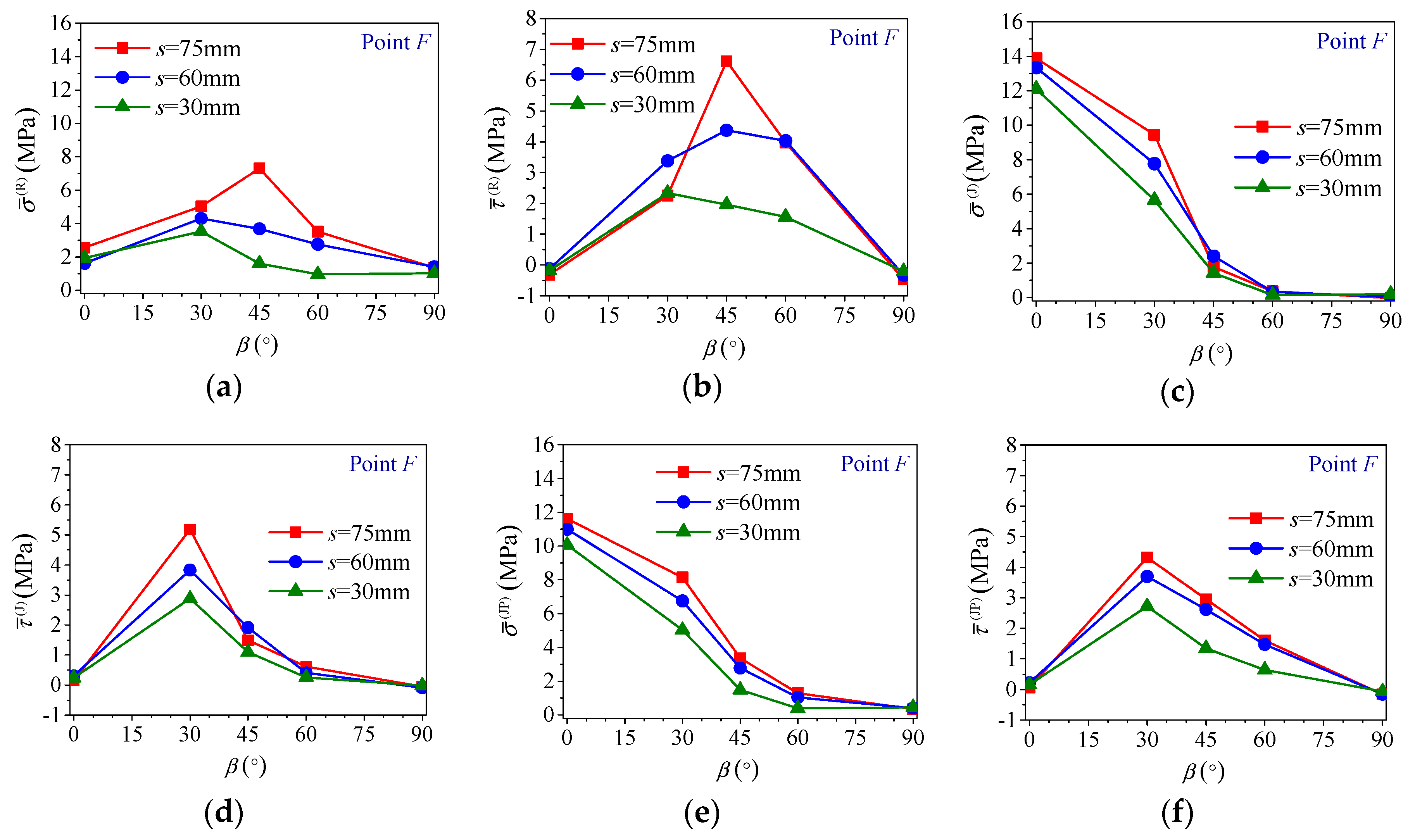
4.3. Response of Rock Bridges and Joints on the Joint Planes
4.4. Discussion on Anisotropic Damage Mechanisms
- For specimens with vertical joints (β = 90°), s has very little influence on their behavior. Since vertical joints are parallel to the loading direction, responses of joints are irrelevant to axial deformation and load transferring, leading to almost no alteration on the normalized Young’s modulus (EJR/ER) and the last peak strain (εf2) and slight increase in the normalized peak strength (σJR/σR) with s. The mechanical behavior of these specimens is the same as those of the intact specimen, i.e., Type I deformation behavior and failure mode A (axial cleavage).
- For specimens with β = 0° and 30°, s has salient influence on their behavior, especially on the deformability modulus. Before peak strength, gradual closure of most or the majority of originally open joints in these specimens contributes greatly to the increase in deformability, leading to rapid increase in EJR/ER with s. After peak strength, most or the majority of the joints closed entirely and the strengths of the joint system are mobilized fully or saliently, leading to Type III or IV deformation behavior and failure Mode B or C, and moderate increase in σJR/σR and decrease in εf2 with s.
- For specimens with β = 45° and 60°, s has significant influence on their behavior, especially on the strength and ductility. Before peak strength, gradual closure of minority of the joints or decreasing of joint aperture in these specimens, leads to salient increase in EJR/ER with s. At peak strength, some of the joints closed partially or none of them closed with slight mobilization or immobilization of joint strength, leading to the lowest strength in these specimens and fast increase in σJR/σR with s. After peak strength, shear failure of rock bridges and sliding along joint planes (failure Mode C or D) may lead to Type II deformation behavior and fast decrease in εf2 with s.
5. Conclusions
- In general, macroscopic behaviors of the jointed specimens, such as four types of deformation behaviors, four failure modes, strength, deformability modulus and ductility index, are dominated by the nonlinear response of joint system, especially the interaction between the joints and rock bridges on the joint planes.
- The response of joint system can be measured by evolution of the four joint response parameters, i.e., average aperture, ratio of closed number, and normalized average normal and shear forces of SJ contacts in the whole specimen (, , and ). The joint system may experience three stages, i.e., starting to close, closed and opening again. At peak strength, for each s, increases with β while and decrease with β, and the curves of -β are inverted V-shaped with the maxima at β = 30°; for a given β, decreases while , and increase with s;
- On the joint plane, the peak stresses of the two phases, i.e., the rock bridge phase and the joint phase, may not be reached at the same time. The interaction between the two phases on the central joint plane can be divided into three stages, i.e., (I) elastic deformation dominated stage (before the peak stress of the rock bridge phase), in which the rock bridge phase carries most of the load, (II) inelastic deformation developing stage (between the peak stress of the rock bridge phase and the last peak stress of the joint phase), in which the two phases carry the load together, and (III) residual deformation stage (after the last peak stress of the joint phase), in which the joint phase carries most of the load.
- The influence of s on specimen behavior is little for β = 90°, obvious for β = 0° or 30° and significant for β = 45° or 60°, and this can be related to their different damage mechanisms. For β = 90°, load transferring will not be interrupted by vertical joints and, therefore, s has very little influence on specimen behavior; for β = 0° or 30°, entire closure of the majority of pre-existing open joints and significant mobilization of joint strength leads to a fast increase in the normalized deformability modulus (EJR/ER) with s, and moderate increase in the normalized strength (σJR/σR) and decrease in the last peak strain (εf2,) with s; for β = 45° or 60°, strong interruption of load transferring by keeping open the majority, or all, of the joints with slight mobilization or immobilization of joint strength, leading to the lowest strength, salient increase in EJR/ER with s, and fast increase in σJR/σR and decrease in εf2 with s.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Deere, D.U.; Hendron, A.J.; Patton, F.D.; Cording, E.J. Design of surface and near surface constructions in rock. In Proceedings of the 8th US Symposium on Rock Mechanics, Minneapolis, MN, USA, 15–17 September 1967; pp. 237–302. [Google Scholar]
- Bieniawski, Z.T. Determining rock mass deformability: Experience from case histories. Int. J. Rock Mech. Min. Sci. 1978, 15, 237–247. [Google Scholar] [CrossRef]
- Barton, N.; Lien, R.; Lunde, J. Engineering classification of rock masses for the design of tunnel support. Rock Mech. 1974, 6, 189–236. [Google Scholar] [CrossRef]
- Hoek, E.; Kaiser, P.K.; Bawden, W.F. Support of Underground Excavations in Hard Rock; Balkema, Ed.; Taylor & Francis: Rotterdam, The Netherlands, 1995. [Google Scholar]
- Cai, M.; Kaiser, P.K.; Uno, H.; Tasaka, Y.; Minami, M. Estimation of rock mass deformation modulus and strength of jointed hard rock masses using the GSI system. Int. J. Rock Mech. Min. Sci. 2004, 41, 3–19. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E.T. Empirical strength criterion for rock masses. J. Soil Mech. Found Div. ASCE 1980, 106, 1013–1035. [Google Scholar]
- Hoek, E.; Brown, E.T. Practical estimates of rock mass strength. Int. J. Rock Mech. Min. Sci. 1997, 34, 1165–1186. [Google Scholar] [CrossRef]
- Cai, M.; Kaiser, P.K.; Tasaka, Y.; Minami, M. Determination of residual strength parameters of jointed rock masses using the GSI system. Int. J. Rock Mech. Min. Sci. 2007, 44, 247–265. [Google Scholar] [CrossRef]
- Bieniawski, Z.T. Engineering Rock Mass Classifications; John, W., Ed.; Butterworth-Heinemann: New York, NY, USA, 1989. [Google Scholar]
- Barton, N.; Bandis, S.; Bakhtar, K. Strength, deformation and conductivity coupling of rock joints. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1985, 22, 121–140. [Google Scholar] [CrossRef]
- Brown, E.T.; Trollope, D.H. Strength of a model of jointed rock. J. Soil Mech. Found Div. ASCE 1970, 96, 685–704. [Google Scholar]
- Einstein, H.H.; Hirschfeld, R.C. Model studies on mechanics of jointed rock. J. Soil Mech. Found Div. ASCE 1973, 99, 229–248. [Google Scholar]
- Tiwari, R.P.; Rao, K.S. Post failure behaviour of a rock mass under the influence of triaxial and true triaxial confinement. Eng. Geol. 2006, 84, 112–129. [Google Scholar] [CrossRef]
- Hayashi, M. Strength and dialatancy of brittle jointed mass—The extreme value stochastic and anisotropic failure mechanism. In Proceedings of the the first Congress of the International Society of Rock Mechanics, Lisbon, Portugal, 25 September–1 October 1966; Volume 1, pp. 295–302. [Google Scholar]
- Yang, Z.Y.; Chen, J.M.; Huang, T.H. Effect of joint sets on the strength and deformation of rock mass models. Int. J. Rock Mech. Min. Sci. 1998, 35, 75–84. [Google Scholar] [CrossRef]
- Lajtai, E.Z. Strength of discontinuous rock in shear. Geotechnique 1963, 19, 218–233. [Google Scholar] [CrossRef]
- Gehle, C.; Kutter, H.K. Breakage and shear behaviour of intermittent rock joints. Int. J. Rock Mech. Min. Sci. 2003, 40, 687–700. [Google Scholar] [CrossRef]
- Shen, B.; Stephansson, O.; Einstein, H.H.; Ghahreman, B. Coalescence of fractures under shear stress experiments. J. Geophys. Res. 1995, 100, 5975–5990. [Google Scholar] [CrossRef]
- Wong, R.H.C.; Chau, K.T. The coalescence of frictional cracks and the shear zone formation in brittle solids under compressive stresses. Int.J. Rock Mech. Min. Sci. 1997, 34, 366. [Google Scholar] [CrossRef]
- Chen, X.; Liao, Z.H.; Peng, X. Deformability characteristics of jointed rock masses under uniaxial compression. Int. J. Min. Sci. Technol. 2012, 22, 213–221. [Google Scholar] [CrossRef]
- Zhang, S.F. Study on the Mechanical Properties and Damage Mechanism of stratified Rock Masses under Uniaxial Compression. Master’s Thesis, School of Mechanics and Civil Engineering, China University of Mining & Technology, Beijing, China, 2016. [Google Scholar]
- Bobet, A.; Einstein, H.H. Fracture coalescence in rock-type materials under uniaxial and biaxial compression. Int. J. Rock Mech. Min. Sci. 1998, 35, 863–888. [Google Scholar] [CrossRef]
- Prudencio, M.; Van Sint Jan, M. Strength and failure modes of rock mass models with non-persistent joints. Int. J. Rock Mech. Min. Sci. 2007, 44, 890–902. [Google Scholar] [CrossRef]
- Zhang, H.Q.; Zhao, Z.Y.; Tang, C.A.; Song, L. Numerical study of shear behavior of intermittent rock joints with different geometrical parameters. Int. J. Rock Mech. Min. Sci. 2006, 43, 802–816. [Google Scholar] [CrossRef]
- Kulatilake, P.H.S.W.; Wang, S.; Stephansson, O. Effect of finite size joints on the deformability of jointed rock in three dimensions. Int. J. Rock Mech. Min. Sci. 1993, 30, 479–501. [Google Scholar] [CrossRef]
- Karami, A.; Stead, D. Asperity degradation and damage in the direct shear test: A hybrid FEM/DEM approach. Rock Mech. Rock Eng. 2008, 41, 229–266. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Ghazvinian, A.; Sarfarazi, V.; Schubert, W.; Blumel, M. A study of the failure mechanism of planar non-persistent open joints using PFC2D. Rock Mech. Rock Eng. 2012, 45, 677–693. [Google Scholar] [CrossRef]
- Fan, X.; Kulatilake, P.H.S.W.; Chen, X. Mechanical behavior of rock-like jointed blocks with multi-non-persistent joints under uniaxial loading: A particle mechanics approach. Eng. Geol. 2015, 190, 17–32. [Google Scholar] [CrossRef]
- Mas Ivars, D.; Pierce, M.E.; Darcel, C.; Reyes-Montes, J.; Potyondy, D.O.; Paul Young, R.; Cundall, P.A. The synthetic rock mass approach for jointed rock mass modelling. Int. J. Rock Mech. Min. Sci. 2011, 48, 219–244. [Google Scholar] [CrossRef]
- Bahaaddini, M.; Sharrock, G.; Hebblewhite, B.K. Numerical investigation of the effect of joint geometrical parameters on the mechanical properties of a non-persistent jointed rock mass under uniaxial compression. Comput. Geotech. 2013, 49, 206–225. [Google Scholar] [CrossRef]
- Bahaaddini, M.; Hagan, P.; Mitra, R.; Hebblewhite, B.K. Numerical study of the mechanical behavior of nonpersistent jointed rock masses. Int. J. Geomech. 2016, 16, 401–535. [Google Scholar] [CrossRef]
- Chiu, C.C.; Wang, T.T.; Weng, M.C.; Huang, T.H. Modeling the anisotropic behavior of jointed rock mass using a modified smooth-joint model. Int. J. Rock Mech. Min. Sci. 2013, 62, 14–22. [Google Scholar] [CrossRef]
- Barton, N.R.; Choubey, V. The shear strength of rock joints in theory and practice. Rock Mech. 1977, 10, 1–5. [Google Scholar] [CrossRef]
- Cheng, C.; Chen, X.; Zhang, S. Multi-peak deformation behavior of jointed rock mass under uniaxial compression: Insight from particle flow modeling. Eng. Geol. 2016, 213, 25–45. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, S.; Cheng, C. Numerical Study on Effect of Joint Strength Mobilization on Behavior of Rock Masses with Large Nonpersistent Joints under Uniaxial Compression. Int. J. Geomech. 2018, 18, 04018140. [Google Scholar] [CrossRef]
- Zanelato, E.B.; Alexandre, J.; de Azevedo, A.R.G.; Marvila, M.T. Evaluation of roughcast on the adhesion mechanisms of mortars on ceramic substrates. Mater. Struct. Constr. 2019, 52, 53. [Google Scholar] [CrossRef]
- Itasca Consulting Group. PFC2D Manual, Version 4.0; Itasca Consulting Group: Minneapolis, MN, USA, 2008. [Google Scholar]
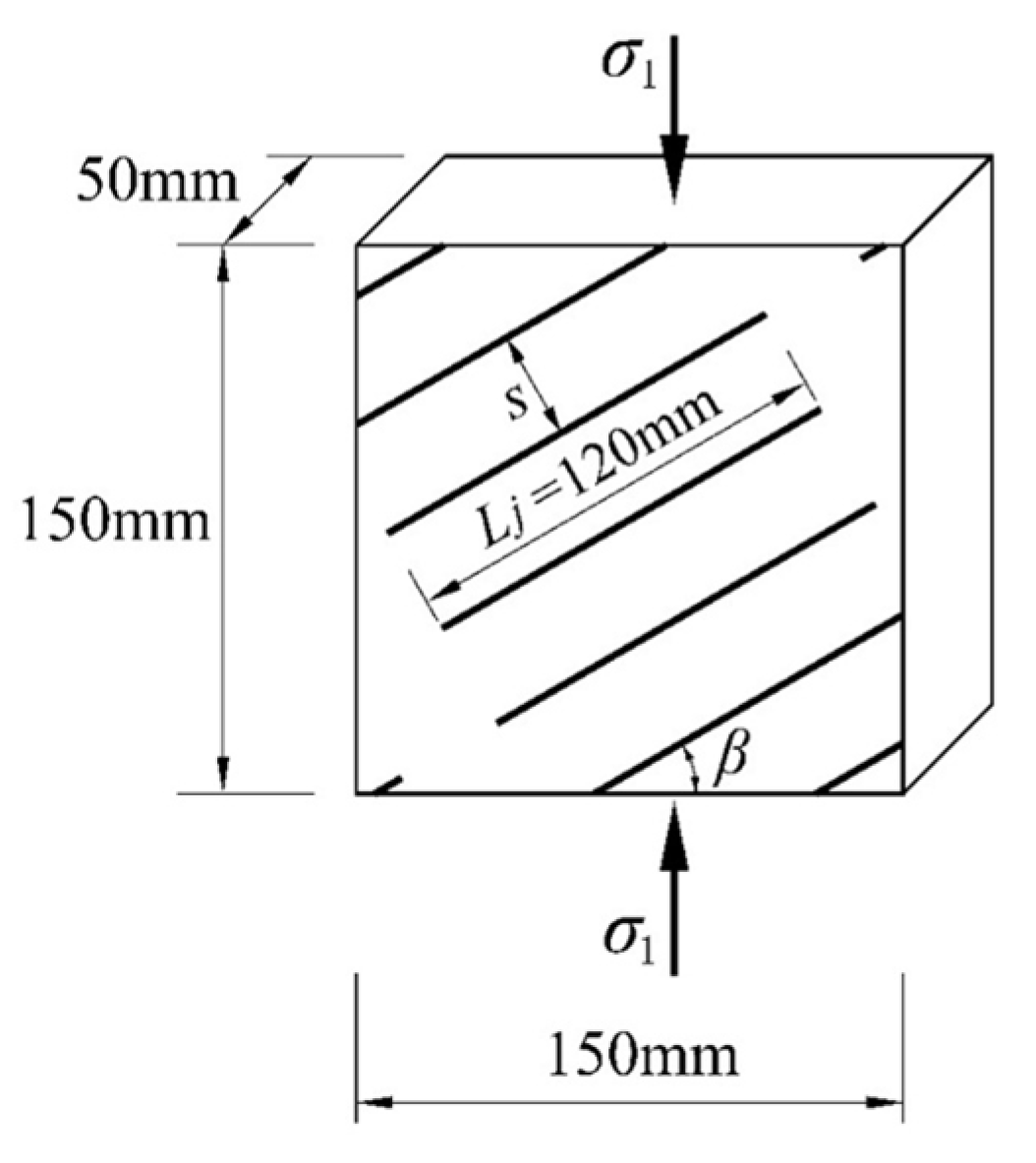

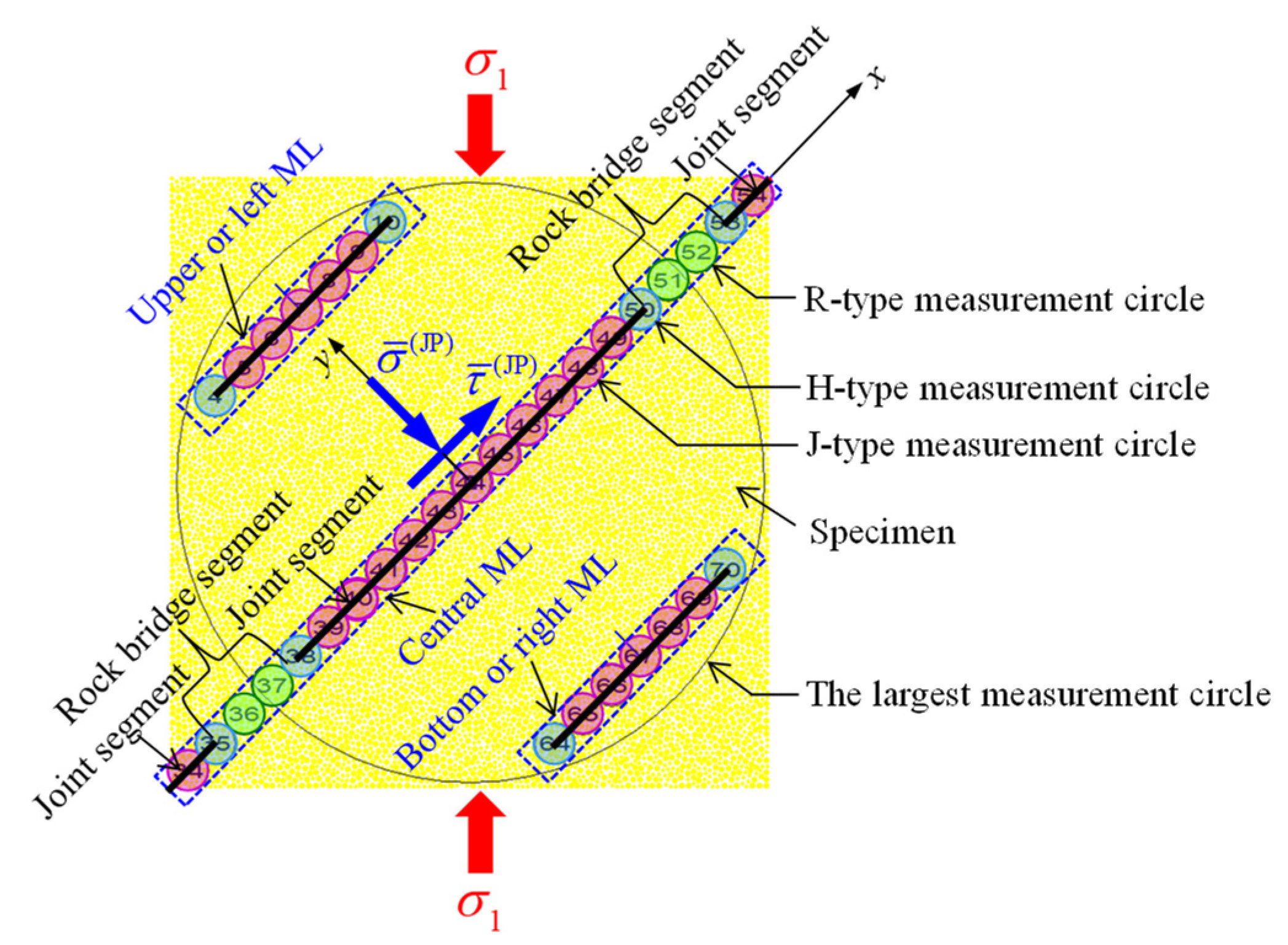
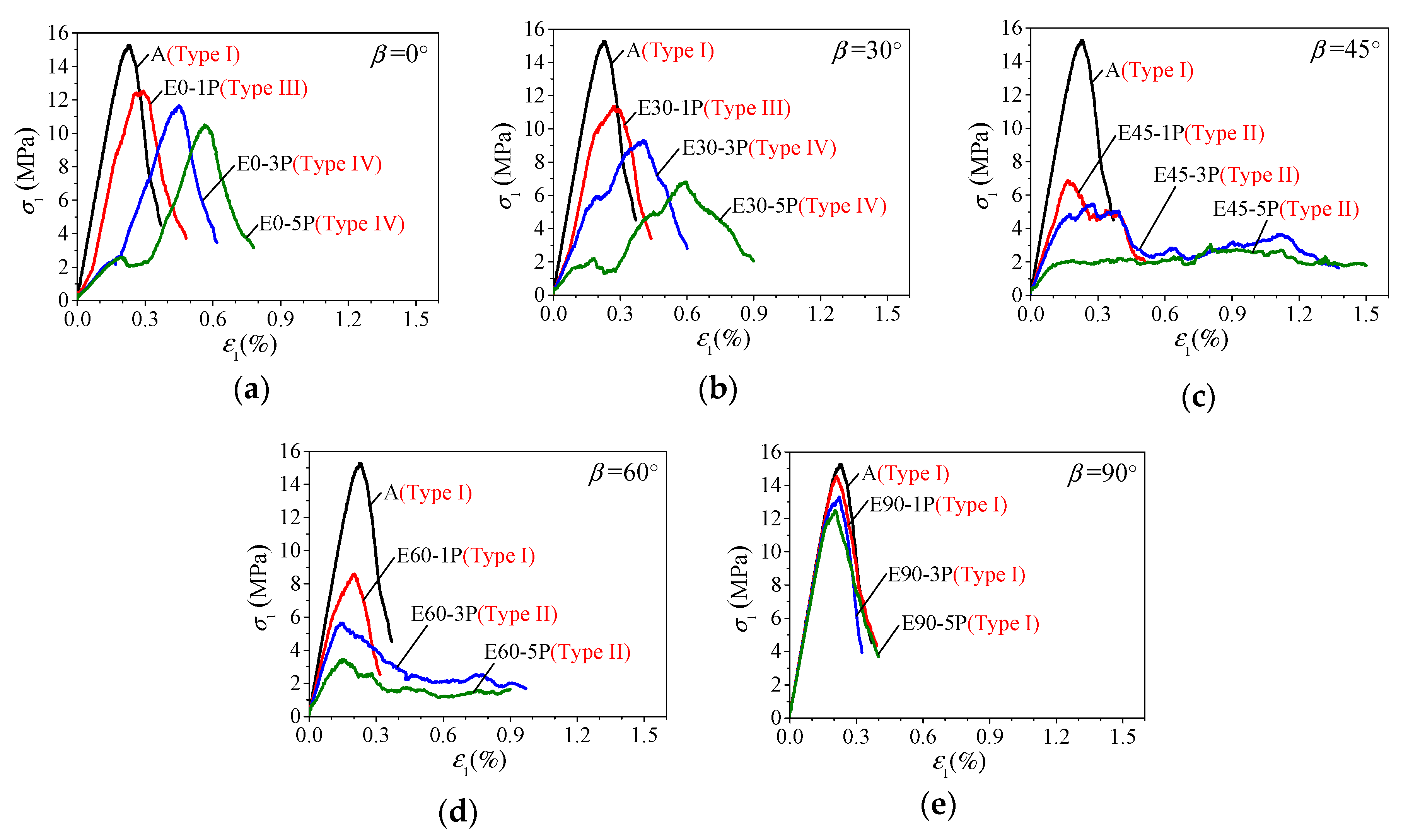


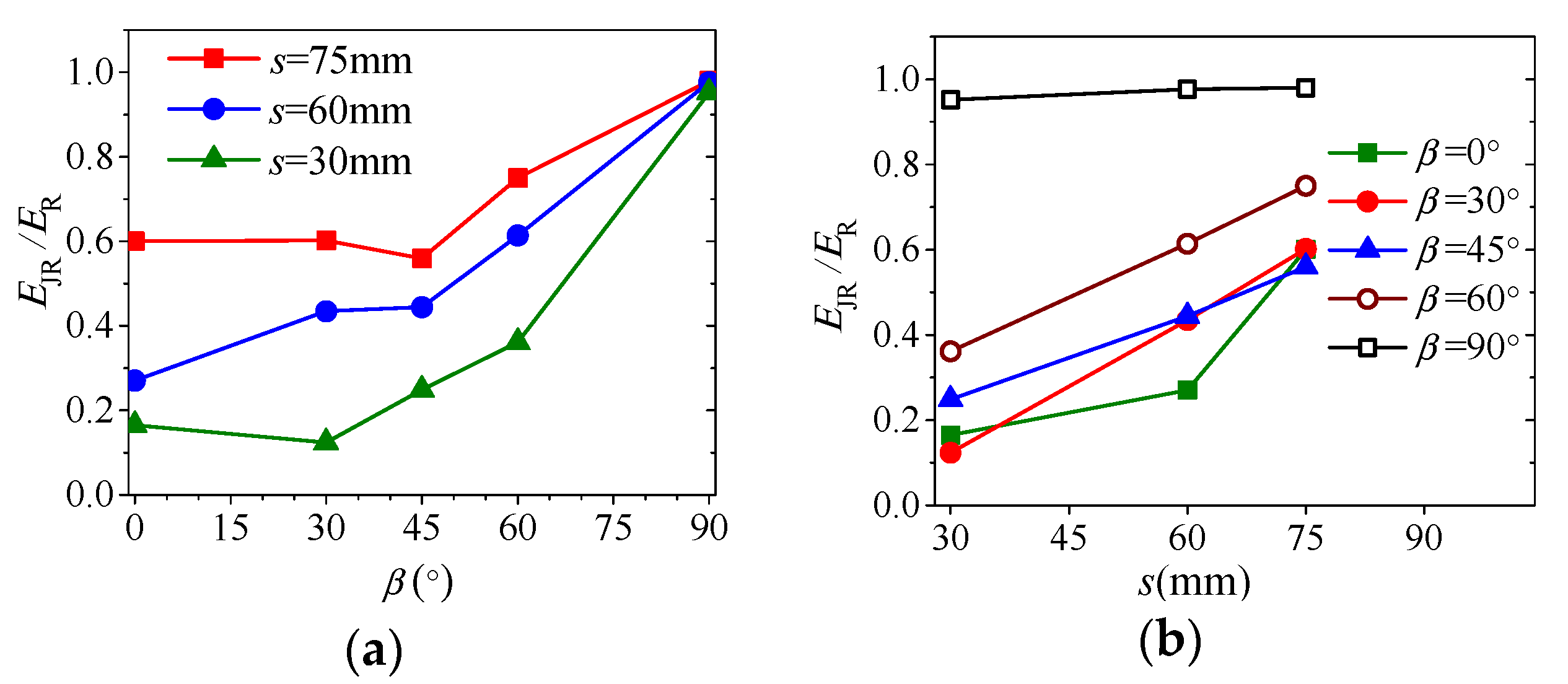




| No. | Specimen | Joint Inclination Angle β (°) | Joint Spacing s (mm) |
|---|---|---|---|
| 1 | A | – | 150 |
| 2 | E0-1P | 0 | 75 |
| 3 | E0-3P | 0 | 60 |
| 4 | E0-5P | 0 | 30 |
| 5 | E30-1P | 30 | 75 |
| 6 | E30-3P | 30 | 60 |
| 7 | E30-5P | 30 | 30 |
| 8 | E45-1P | 45 | 75 |
| 9 | E45-3P | 45 | 60 |
| 10 | E45-5P | 45 | 30 |
| 11 | E60-1P | 60 | 75 |
| 12 | E60-3P | 60 | 60 |
| 13 | E60-5P | 60 | 30 |
| 14 | E90-1P | 90 | 75 |
| 15 | E90-3P | 90 | 60 |
| 16 | E90-5P | 90 | 30 |
| Micro-Properties | Parameters | Value |
|---|---|---|
| Particle properties | Ball density ρmic (kg/m3) | 1158 |
| Minimum ball radius Rmin (mm) | 0.6 | |
| Ball radius ratio Rmax/Rmin | 1.66 | |
| Contact modulus Ec (GPa) | 6.0 | |
| Coefficient of friction μ | 0.5 | |
| Normal to shearing stiffness ratio kn/ks | 2.5 | |
| Parallel bond contacts properties | Bond modulus (GPa) | 6.0 |
| Normal bond strength (MPa) | 9.9 | |
| S.D. * normal bond strength (MPa) | 3.78 | |
| Shearing bond strength (MPa) | 48.0 | |
| S.D. shearing bond strength (MPa) | 19.8 | |
| Normal to shearing bond stiffness ratio / | 2.5 | |
| SJ contacts properties | Joint normal stiffness (N/m3) | 1.0 × 1012 |
| Joint shear stiffness (N/m3) | 1.0 × 1012 | |
| Joint friction angle φj (°) | 38 | |
| Joint dilation angle ψj (°) | 0 | |
| Initial joint aperture a0 (mm) | 0.10 |
| Macro Properties | Experimental | Numerical |
|---|---|---|
| UCS (MPa) | 15.10 | 15.27 |
| Young’s Modulus E (GPa) | 8.02 | 7.47 |
| Table | Stage | Normal Stresses of the Central ML | |||
|---|---|---|---|---|---|
| Type I (E90-5P) | OF | ||||
| FS |  |  | |||
| Type II (E45-3P) | OF1 | ||||
| F1F2 |  |  |  | ||
| F2S | |||||
| Type III (E0-1P) | OB | ||||
| BF1 | |||||
| F1F2 |  |  | |||
| F2S |  | ||||
| Type IV (E0-5P) | OF1 | ||||
| F1D | |||||
| DF2 |  | ||||
| F2S | |||||
 or
or  , and
, and  or
or  denote increasing, decreasing, unchanging, overall decreasing or increasing with oscillations, and increasing first then decreasing or decreasing first then increasing of the variable.
denote increasing, decreasing, unchanging, overall decreasing or increasing with oscillations, and increasing first then decreasing or decreasing first then increasing of the variable.Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Feng, Z.; Cheng, C. Numerical Study on Anisotropic Influence of Joint Spacing on Mechanical Behavior of Rock Mass Models under Uniaxial Compression. Energies 2020, 13, 6698. https://doi.org/10.3390/en13246698
Chen X, Feng Z, Cheng C. Numerical Study on Anisotropic Influence of Joint Spacing on Mechanical Behavior of Rock Mass Models under Uniaxial Compression. Energies. 2020; 13(24):6698. https://doi.org/10.3390/en13246698
Chicago/Turabian StyleChen, Xin, Zhongliang Feng, and Cheng Cheng. 2020. "Numerical Study on Anisotropic Influence of Joint Spacing on Mechanical Behavior of Rock Mass Models under Uniaxial Compression" Energies 13, no. 24: 6698. https://doi.org/10.3390/en13246698
APA StyleChen, X., Feng, Z., & Cheng, C. (2020). Numerical Study on Anisotropic Influence of Joint Spacing on Mechanical Behavior of Rock Mass Models under Uniaxial Compression. Energies, 13(24), 6698. https://doi.org/10.3390/en13246698






