Hoard or Exploit? Intergenerational Allocation of Exhaustible Natural Resources
Abstract
1. Introduction
2. Literature Review
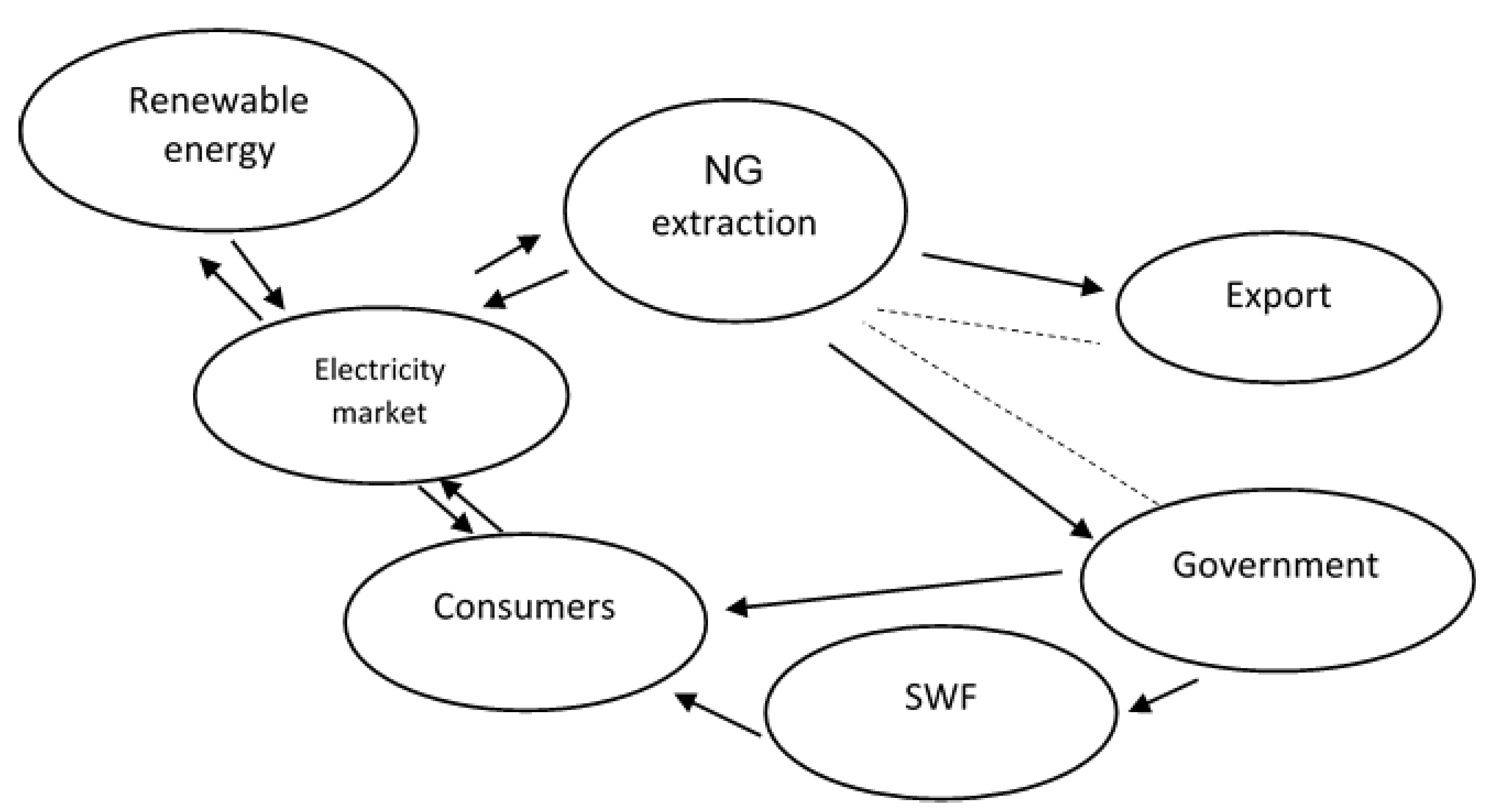
3. Model Specification
3.1. Electricity Consumers
3.2. Exhaustible Natural Resource-Extraction Sector
3.3. Government Transfers
3.4. Electricity Producers
3.5. Renewable Energy Sector
3.6. Equilibrium
4. Natural Gas in Israel
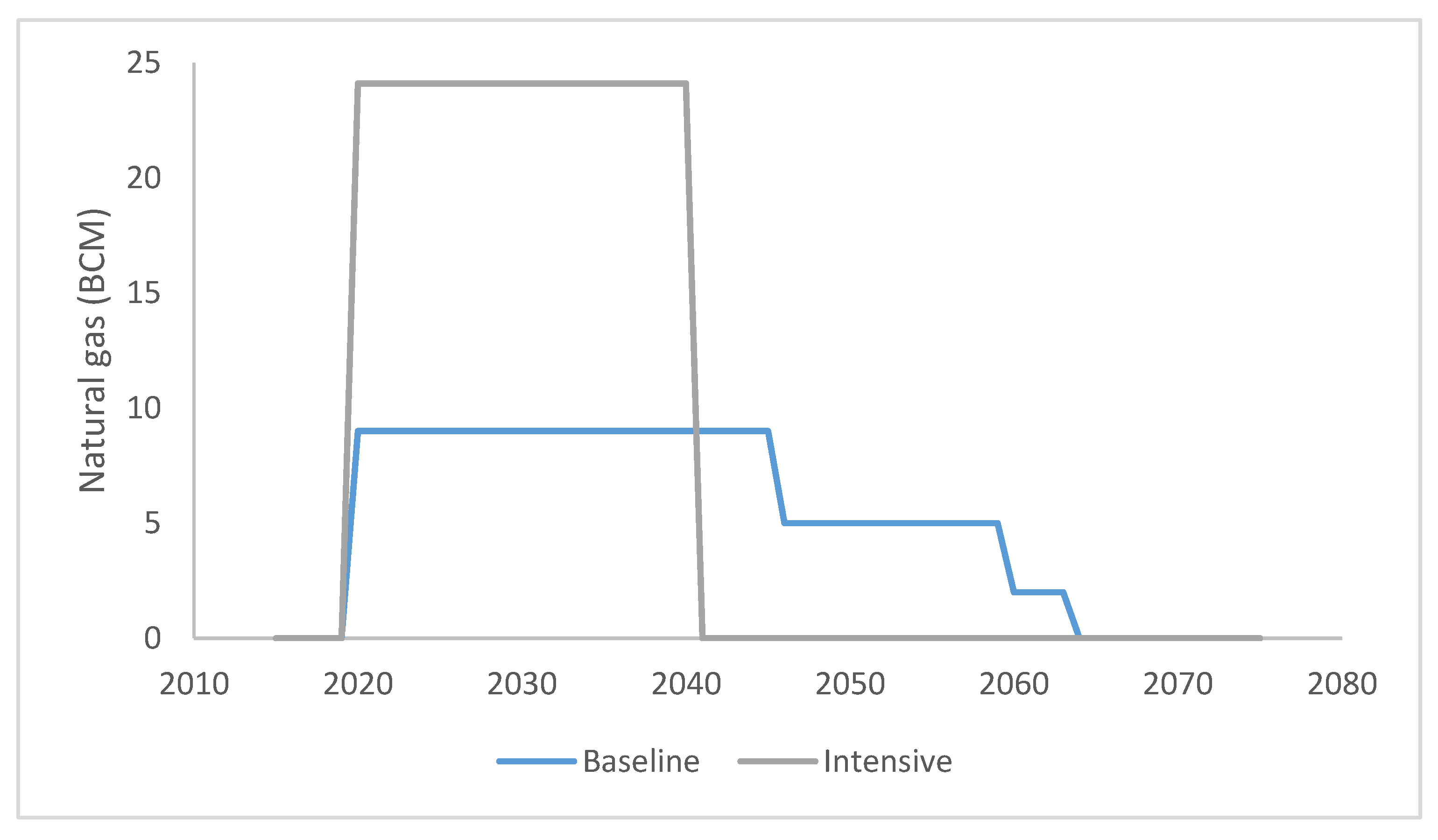
5. Extraction Scenarios
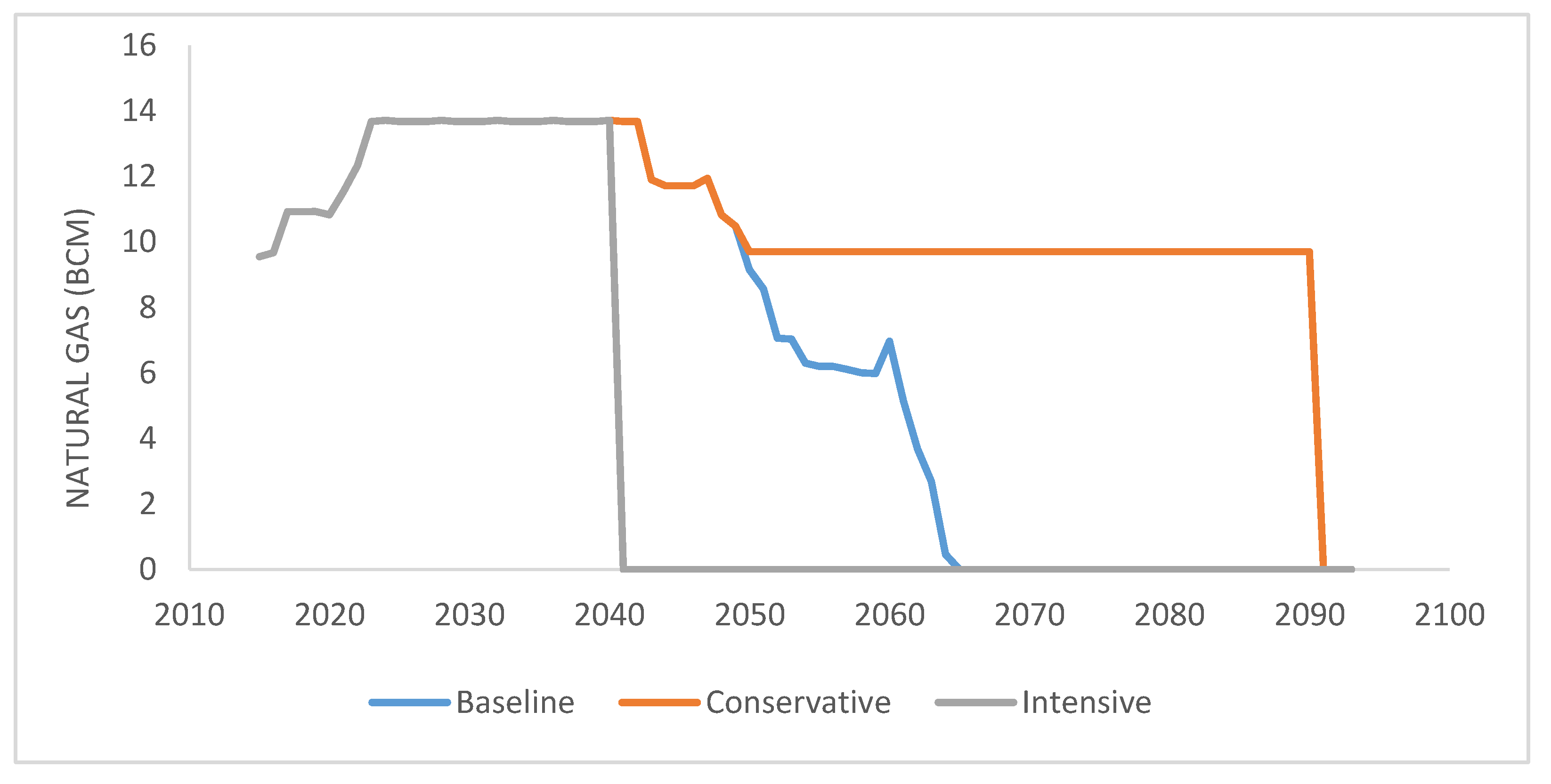
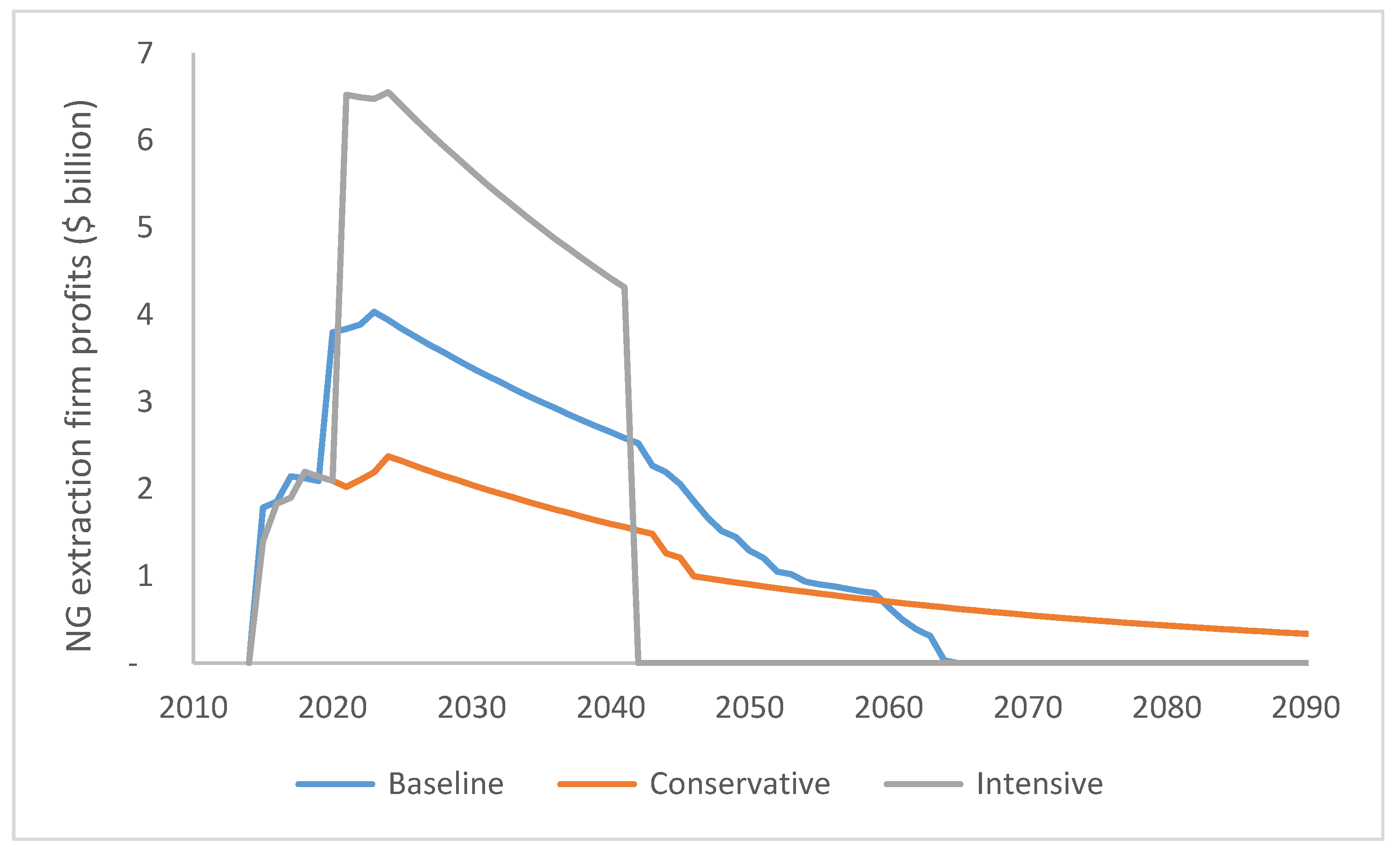
6. Results
6.1. Simulation Results
6.2. Simulation Results—Investing SWF in Improving Renewable Energy Productivity
7. Discussion
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ministry of Energy. Israeli Gas Opportunities; 2016. Available online: https://www.energy-sea.gov.il/English-Site/Pages/News%20And%20Media/ISRAELI%20GAS%20OPPORTUNITIES.pdf (accessed on 15 July 2017).
- Shaffer, B. Israel—New natural gas producer in the Mediterranean. Energy Policy 2011, 39, 5379–5387. [Google Scholar] [CrossRef]
- Liebes, I. Economic Implications of Natural Gas Exports: A Case Study Analysis for Israel; University of Haifa: Haifa, Israel, 2015. [Google Scholar]
- OECD economic survey—Israel 2016. Available online: http://www.oecd.org/economy/surveys/Israel-Overview-OECD-Economic-Survey-2016.pdf (accessed on 12 October 2016).
- Cohen, G. Israel Seeks Options to Export Huge Gas Reserves; Gulf Publishing Company: Houston, TX, USA, 2018; Available online: http://gasprocessingnews.com/features/201406/israel-seeks-options-to-export-huge-gas-reserves.aspx (accessed on 15 January 2019).
- Kneese, A.V.; Sweeney, J.B. Handbook of Natural Resource and Energy Economics; Elsevier: San Leandro, CA, USA, 2006; Volume 3. [Google Scholar]
- Dasgupta, P.S.; Heal, G.M. Economic Theory and Exhaustible Resources; Cambridge University Press: Cambridge, UK, 1979. [Google Scholar]
- Padilla, E. Intergenerational Equity and Stability. Ecol. Econ. 2002, 41, 69–83. [Google Scholar] [CrossRef]
- Solow, R.M. The Economics of Resources or the Resources of Economics. Am. Econ. Rev. 1974, 64, 1–14. [Google Scholar]
- Agnani, B.; Gutie´rrez, M.; Iza, A. Growth in overlapping generation economics with non-renewable resources. J. Environ. Econ. Manag. 2005, 50, 387–407. [Google Scholar] [CrossRef]
- Malthus, T.R. An Essay on the Principle of Population, as It Affects the Future Improvement of Society with Remarks on the Speculations of Mr. Godwin, M. Condorcet and Other Writers; Cosimo Inc.: New York, NY, USA, 1798. [Google Scholar]
- Hotelling, H. The Economics of Exhaustible Resources. J. Political Econ. 1931, 39, 137–175. [Google Scholar] [CrossRef]
- Solow, R.M. A Contribution to the Theory of Economic Growth. Q. J. Econ. 1956, 70, 56–94. [Google Scholar] [CrossRef]
- Hartwick, J.M. Intergenerational Equity and the Investment of Rents from Exhaustible Resources. Am. Econ. Rev. 1977, 67, 972–974. [Google Scholar]
- Samuelsson, P. An Exact Consumption- Loan Model of Interest with or without the Social Contrivance of Money. J. Political Econ. 1958, 66, 467–482. [Google Scholar] [CrossRef]
- Heal, G.M. The Optimal Use of Exhaustible Resources. In Handbook of Natural Resource and Energy Economics; Elsevier: San Leandro, CA, USA, 1993; Chapter 18; Volume 2, pp. 855–880. [Google Scholar]
- Stiglitz, J.E. Growth with Exhaustible Natural Resources: Efficient and Optimal Growth Paths. Rev. Econ. Stud. 1974, 41, 123–137. [Google Scholar] [CrossRef]
- Rowse, J. On ad valorem taxation of nonrenewable resource production. Resour. Energy Econ. 1997, 19, 221–239. [Google Scholar] [CrossRef]
- Howarth, R.; Norgaard, R. Intergenerational Transfers and the Social Discount Rate. Environ. Econ. Resour. 1993, 3, 337–358. [Google Scholar] [CrossRef]
- Benchekroun, H.; Withagen, C. The optimal depletion of exhaustible resources: A complete characterization. Resour. Energy Econ. 2011, 33, 612–636. [Google Scholar] [CrossRef]
- Haab, T.C.; McConnell, K.E. Valuing Environmental and Natural Resources—The Econometrics of Non-Market Valuation; Edward Elgar Publishing Inc.: Northampton, MA, USA, 2002. [Google Scholar]
- Lederman, D.; Maloney, W. Natural Resources Neither Curse nor Destiny; Stanford Univirsity Press: Palo Alto, CA, USA; The World Bank: Washington, DC, USA, 2007. [Google Scholar]
- Sachs, J.; Warner, A. The Curse of Natural Resources. Eur. Econ. Rev. 2001, 45, 827–838. [Google Scholar] [CrossRef]
- Nyambuu, U.; Semmler, W. Trends in the Extraction of Non-Renewable Resources: The Case of Fossil Energy. Econ. Modeling 2014, 37, 271–279. [Google Scholar] [CrossRef]
- Kotlikoff, L.; Polbin, A.; Zubarev, A. Will the Paris Accord Accelerate Climate Change? NBER Working Paper No. 22731; National Bureau of Economic Research: Cambridge, MA, USA, 2016; pp. 1–42. [Google Scholar]
- Aitzhanova, A.; Iskaliyeva, A.; Krishnaswamy, V.; Makauskas, D.; Razavi, H.; Sartip, A.R.; Urazaliyeva, A. A practical approach to oil wealth management: Application to the case of Kazakhstan. Energy Econ. 2015, 47, 178–188. [Google Scholar] [CrossRef]
- Kemp, M.C.; Long, N.V. The Under-Exploitation of Natural Resources: A Model with Overlapping Generation. Econ. Rec. 1979, 55, 214–221. [Google Scholar] [CrossRef]
- Lange, G.M.; Wodon, Q.; Carey, K. The Changing Wealth of Nation 2018—Building Sustainable Future; The World Bank: Washington, DC, USA, 2018. [Google Scholar]
- Holden, S. Avoiding the Resource Curse, the Case Norway; University of Oslo: Oslo, Norway, 2013. [Google Scholar]
- Barkhordar, Z.; Saboohi, Y. Assessing alternative options for allocating oil revenue in Iran. Energy Policy 2013, 63, 1207–1216. [Google Scholar] [CrossRef]
- Popper, S.W.; Berrebi, C.; Griffin, J.; Light, T.; Min, E.Y.; Crane, K. Natural Gas and Israel’s Energy Future- Near -Team Decisions from a Strategic Perspective. In RAND Environment, Energy and Economic Development; 2009; Available online: https://www.rand.org/pubs/monographs/MG927.html (accessed on 15 September 2017).
- Bahgat, G. Israel’s Energy Security: Regional Implications. Middle East Policy 2011, 1053, 25–35. [Google Scholar] [CrossRef]
- Shaffer, B. Israel’s Energy Resource Management Policy: Lessons for Small Markets. Energy Law J. 2016, 37, 331–350. [Google Scholar]
- Darbouche, H.; El-Katiri, L.; Fattouh, B. East Mediterranean Gas: What Kind of a Game-Changer? Oxford Institute for Energy Studies: Oxford, UK, 2012; NG71. [Google Scholar]
- Henderson, S. Natural Gas Export Options for Israel and Cyprus; GMF Paper Series; The German Marshall Fund of the United States: Washington, DC, USA, 2013. [Google Scholar]
- Fischhendler, I.; Nathan, D. In the name of energy security: The struggle over the exportation of Israeli natural gas. Energy Policy 2014, 70, 152–162. [Google Scholar] [CrossRef]
- Siddig, K.; Grethe, H. No more gas from Egypt? Modeling offshore discoveries and import uncertainty of natural gas in Israel. Appl. Energy 2014, 136, 312–324. [Google Scholar] [CrossRef]
- Cohen, G.; Korner, M. Israeli Oil & Gas Sector Economic and Geopolitical Aspects: Distinguish between the Impossible, the Potential and the Doable; Samuel Neaman Institute for National Policy Research: Haifa, Israel, 2016; pp. 1–30. [Google Scholar]
- Dagoumas, A.; Flouros, F. Energy Policy Formulation in Israel Following its Recent Gas Discoveries. Int. J. Energy Econ. Policy 2017, 7, 19–30. [Google Scholar]
- Palatnik, R.R.; Tavor, T.; Voldman, L. The Symptoms of Illness: Does Israel Suffer from “Dutch Disease”? Energies 2019, 12, 2752. [Google Scholar] [CrossRef]
- Ashwarya, S. Israel’s Mediterranean Gas: Domestic Governance, Economic Impact, and Strategic Implications; Routledge: Abingdon, UK, 2019. [Google Scholar]
- Fisher, I. The Theory of Interest; The Macmillan Company: New York, NY, USA, 1930. [Google Scholar]
- Andersen, J. The Dutch Disease and Intergenerational Welfare. Appl. Econ. 2013, 45, 465–476. [Google Scholar] [CrossRef]
- Klump, R.; McAdam, P.; Willman, A. Factor Substitution and Factor Augmenting Technical Progress in the United States: A Normalized Supply-Side System Approach. Rev. Econ. Stat. 2007, 89, 183–192. [Google Scholar] [CrossRef]
- Vousden, N. Basic Theoretical issues of Resource Depletion. J. Econ. Theory 1973, 6, 126–143. [Google Scholar] [CrossRef]
- Israel Electricity Company (IEC). Financial Statement; Israel Electricity Company (IEC): Haifa, Israel, 2019. [Google Scholar]
- The Israeli Petroleum Profits Tax Law. 2011. Available online: https://www.nevo.co.il/law_html/law01/500_479.htm (accessed on 21 September 2017).
- Hall, M. Future Conditions and Present Extraction: A Useful Method in Natural Resource Economics. Resour. Energy 1983, 5, 303–311. [Google Scholar]
- King, R.G.; Rebelo, T.R. Transitional Dynamics and Economic Growth in the Neoclassical model. Am. Econ. Rev. 1993, 83, 908–931. [Google Scholar]
- Brockway, P.; Heun, M.; Santos, J.; Barrett, J. Energy-Extended CES Aggregate Production: Current Aspects of Their Specification and Econometric Estimation. Energies 2017, 10, 202. [Google Scholar] [CrossRef]
- Van der Werf, E. Production functions for climate policy modeling: An empirical analysis. Energy Econ. 2008, 30, 2964–2979. [Google Scholar] [CrossRef]
- Sancho, F. Calibration of CES Functions for Real-World Multisectoral Modeling. Econ. Syst. Res. 2009, 21, 45–58. [Google Scholar] [CrossRef]
- Sajadifar, S.; Arakelyan, A.; Khiabani, N. The Linear Approximation of the CES Function to parameter estimation in CGE Modeling. In Proceedings of the International Conference -on Business and Economics Research (ICBER), Kuala Lumpur, Malaysia, 26–28 November 2010; pp. 1–10. [Google Scholar]
- Pelenc, J.; Ballet, J.; Dedeurwaerdere, T. Weak Sustainability versus Strong Sustainability. Brief for GSDR. 2015. Available online: https://sustainabledevelopment.un.org/content/documents/6569122-Pelenc-Weak%20Sustainability%20versus%20Strong%20Sustainability.pdf (accessed on 21 September 2017).
- Delek Drilling Financial Statements, December 2017. Available online: https://www.delekdrilling.com/investor-relations/financial-reports (accessed on 21 September 2017).
- Yagihashi, T.; Du, J. Intertemporal elasticity of substitution and risk aversion: Are they related empirically? Appl. Econ. 2015, 47, 1588–1605. [Google Scholar] [CrossRef][Green Version]
- Ministry of Environmental Protection Local Use of Natural Gas—Economic Analysis; 2015. Available online: https://www.sviva.gov.il/subjectsEnv/Economy/envecExternalities/Documents/Natural-gaz-Economic-Analysis.pdf (accessed on 16 October 2016).
- Fiscal Policy with Respect to Oil and Gas Resources in Israel. Sheshinski Committee’s Report. 2011. Available online: file:///C:/Users/home/Desktop/%D7%AA%D7%95%D7%90%D7%A8%20%D7%A9%D7%99%D7%9C%D7%99%D7%A9%D7%99/natural%20gas/CONCLUSIONS%20OF%20SHESHINSKI%20COMMITTEE%202011.pdf (accessed on 15 September 2017).
- Bank of Israel the Bank of Israel’s Reference to the Draft Outline Regarding the Development of the Gas Fields Discovered in the Economic Waters of Israel. 2015. Available online: https://www.boi.org.il/he/NewsAndPublications/PressReleases/Pages/01-12-2015-GovSpeechGas.aspx (accessed on 19 December 2016).
- The Electricity Authority in Israel (PUA) Map for Development of the Electricity Production Sector; 2018. Available online: https://www.gov.il/he/departments/general/mapat_derech (accessed on 25 February 2019).
- Kander, A.; Stern, D.I. Economic Growth and the Transition from Traditional to Modern Energy in Sweden; CAMA Centre for Applied Macroeconomic Analysis, Australian National University: Canberra, Australia, 2013. [Google Scholar]
- Evans, D.J.; Sezrs, H. Social discount rates for six major countries. Appl. Econ. Lett. 2004, 11, 557–560. [Google Scholar] [CrossRef]
- Eckstein, T.; Liefsetz, A. Strategy for Economic Growth; IDC Herzliya: Herzliya, Israel, 2017; Available online: https://www.idc.ac.il/he/research/aiep/documents/strategy_2018.pdf (accessed on 25 February 2019).
- Li, Q.; Pizer, A.P. Discounting for Public Cost-Benefit Analysis; NBER Working Papers; National Bureau of Economic Research: Cambridge, MA, USA, 2018; pp. 1–42. [Google Scholar]
- Israel Electricity Company (IEC). Investor Presentation; The Israeli electricity company: Haifa, Israel, 2017; Available online: https://www.iec.co.il/investors/DocLib2/IECnvestorPresentationFY2017Final_Hebrew.pdf (accessed on 29 October 2018).
| Reference | Aims | Methods | Key Findings |
|---|---|---|---|
| [31] | How big of a role should NG play in Israel’s energy balance? | Analyzing data from 2009 | A combination of demand management and utilization of several energy sources, particularly adding non-fossil fuel alternatives, enhances robustness; A strategy that rapidly enhances the use of NG in Israel can both be consistent with the interests of the Israeli population and provide security against various risks. |
| [32] | Analysis of potential effects of the Israeli windfall on its energy security and relations with its neighbors | Qualitative research | An overview of the Israeli NG sector |
| [2,33] | The process of establishing a management strategy for NG resources in Israel | Qualitative research | Israel’s policy decisions on its NG sector are highly influenced by two factors: lack of government involvement in establishing an infrastructure and the assurance of a competitive gas market. |
| [34] | Opportunities and challenges offered by East Mediterranean gas to countries (including Israel) and investors in the region | Qualitative research | East Mediterranean gas is more likely to be a game changer for local energy markets than for regional or international ones. LNG is the favored export option for Israel’s NG. |
| [35] | Israel NG export options | Literature review and analysis | Israel’s potential as a NG exporter, although important nationally, is small in global terms. |
| [36] | Insights into the energy security aspects related to NG discoveries in Israel | Analysis of various policy documents and seeking the use of the expression “energy security” | Numerous discursive means have been used to portray energy as an urgent existential issue for Israel, and to justify the framing of energy as a matter of national security. |
| [3] | Effects of the newly introduced NG resources on the Israeli economy | CGE | Initiating export of NG from the discovered reserves may have an overall beneficial impact across most key indicators. |
| [37] | To investigate the effect of reduced NG import from Egypt with the evolution of domestic gas production on the Israeli economy | Extended computable general equilibrium CGE model | Poor households will be more positively affected by domestic gas production than rich ones due to their composition of factor income and their higher expenditure shares for energy-intensive commodities. |
| [38] | To review the Israeli NG sector, focusing on economic and geopolitical aspects | Quantitative research | Recommendations were given on increasing the consumption of NG in the domestic market; expanding the gas-transmission system; encouraging the construction of distribution networks; providing infant industry protections to additional reservoirs and setting up a joint infrastructure to enable their connection and remove export barriers. |
| [39] | Identifying critical factors affecting energy policy formulation in Israel following the NG discoveries | Questionnaire/interviews with energy experts in Mediterranean countries. | Techno-economic and geopolitical factors are the most important factors in setting energy policy in the Israeli sector; in considering gas-export options, decisions should be based not only on economic and/or financial factors, but on political factors as well. |
| [5] | Aspects, conflicts, benefits, and challenges that may accrue in the Israeli economy as a result of the extraction, use, and export of NG | Analysis of various policy documents from the different parliamentary and extra-parliamentary committees | Provides a theoretical analysis of the Israeli NG sector based on geographical, as well as regional and economic concerns. |
| [40] | To examine whether strengthening of the Israeli currency in recent years is a symptom of “Dutch disease” | Event study approach; data from 2009–2017 | The classic symptom of Dutch disease is already in place in Israel, and gas-related news are found to have statistically significant impact and appreciate Israeli currency. |
| [41] | To examine the implications of Israel’s NG discoveries in the Eastern Mediterranean. | Qualitative research | The book presents a picture of history, politics, and conflicts that shape the economics of energy and NG in Israel. Including the challenges of energy economy in Israel; Israel’s relation with its neighbors in the Middle East; Dutch disease. |
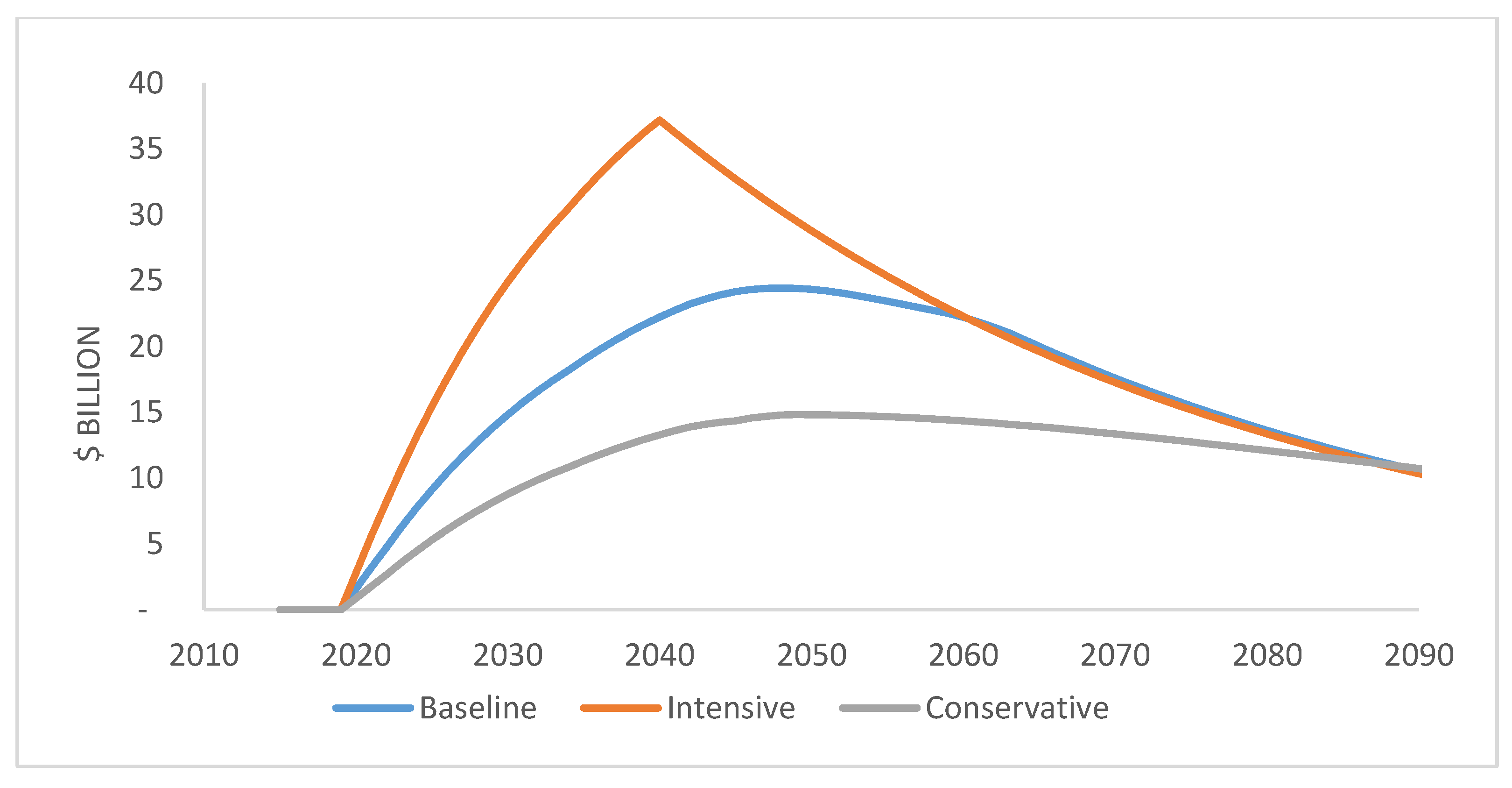
| Assumptions | Baseline Scenario | Conservative Scenario | Intensive Scenario |
|---|---|---|---|
| Export | Export of 9 BCM from 2020 to 2045, 5 BCM until 2059, and 2 BCM until field depletion in 2065, calculated based on Delek Drilling Financial Statements (2017) [55] | No export | Export of 20.24 BCM from 2020–2040. In this scenario, domestic NG use is equal to that in the baseline scenario. The excess amount of NG is destined for export and is distributed equally across the period 2020 to 2040. |
| Depletion | Tamar projected depletion by 2050. The other fields supply NG until 2065. | The NG will be depleted by 2090, calculated based [55]. Tamar field will be depleted by 2050, calculated based on Delek Drilling Financial Statements (2017) [55] NG-extraction amounts are similar to the baseline scenario for 2015–2065. The amounts are distributed equally across the years. | All NG reserves are depleted by 2040. NG-extraction amounts are similar to the baseline scenario for the years 2015–2040 in the domestic market. The rest is exported. |
| Financial data | Data on annual NG extraction, firm incomes, costs, royalties, government share of royalties, levy, income taxes, and corporate taxes are based on Delek Drilling Financial Statements (2017) [55]. | Data on firm incomes and levies are similar to the baseline scenario until 2050. For 2051–2090, the data equal the average over the 5 years before the specific year; for example, income tax in 2051 equals average annual income tax for 2044–2049. | Data on annual NG extraction, firm incomes, costs, royalties, government share of royalties, levy, income taxes, and corporate taxes are based on Delek Drilling Financial Statements (2017) [55]. |
| Levy | The levy is imposed on profits derived from the sale of NG pursuant to the Israeli Petroleum Profits Tax Law [56]. The levy follows a progressive R-Factor-based tax 1 starting at 20% and increasing to about 45%. The government take from the levy is transferred to the SWF. | ||
| Corporate tax | 10% corporate tax in accordance with the Israeli Petroleum Profits Tax Law [56] and the Ministry of environmental protection [57]. The income taxes are transferred to the government budget. | ||
| Royalties | Royalties of 24% of total cash flow; the government share of royalties is 11.5%, in accordance with the Sheshinski Committee [58] and the Israeli Petroleum Profits Tax Law [56]. The royalties are also transferred to the government budget. | ||
| Rate of return on SWF Investment (Same for all the scenarios) | 3% rate of return on SWF investment, based on Bank of Israel [59], who found that rates of return on investments vary between 1% and 5%. In the benchmark scenario, we assumed 3% and then we conducted a sensitivity analysis to see how changing this assumption might change the results. | ||
| Transfers to individuals (Same for all the scenarios) | The government transfers 3.5% of the SWF accumulated capital to the public between 2020 and 2034; in the following years, the government transfers an amount equal to the average rate of return for the previous 10 years multiplied by the accumulated capital, in accordance with the SWF Law of 2014. 3% rate of return on SWF investment. | ||
| Parameter | Description | Data Source | Range for Sensitivity Analysis |
|---|---|---|---|
| Cost of electricity generation by NG | [59] | $4.5–6.7/MMBTU | |
| Cost of electricity generation by renewable energy | [59] | ||
| Electricity tariff | [60] | ||
| 1 | The substitution parameter measures the percent change in the ratio of two inputs used in response to a percent change in their prices | [61] | |
| Individuals’ subjective discount rate | [62,63] | 0–0.045 | |
| Annual discount rate | [57,64] | 1.5–4.5% | |
| Productivity factor of NG | [65] | ||
| Productivity factor of renewable energy sources | [43] | See extension 1 in Section 5 |
| Baseline | Intensive | Conservative | |
|---|---|---|---|
| Period | 2015–2065 | 2015–2040 | 2015–2090 |
| Total income ($ billion) | 62.55 | 72.38 | 44.88 |
| Year | Baseline | Intensive | Conservative |
|---|---|---|---|
| 2015–2040 | 23 | 36 | 14 |
| 2041–2065 | 25 | 23 | 16 |
| 2066–2090 | 12 | 11 | 11 |
| 2090–2115 | 6 | 6 | 7 |
| Total | 66 | 76 | 48 |
| Source | Baseline | Intensive | Conservative |
|---|---|---|---|
| Net benefit ($ billion) 1 | 1194.7 | 1367.8 | 948.5 |
| SWF value ($ billion) | 124 | 153 | 85 |
| Total ($ billion) | 1318.7 | 1520.8 | 1033.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abu-Kalla, H.; Palatnik, R.R.; Ayalon, O.; Shechter, M. Hoard or Exploit? Intergenerational Allocation of Exhaustible Natural Resources. Energies 2020, 13, 6657. https://doi.org/10.3390/en13246657
Abu-Kalla H, Palatnik RR, Ayalon O, Shechter M. Hoard or Exploit? Intergenerational Allocation of Exhaustible Natural Resources. Energies. 2020; 13(24):6657. https://doi.org/10.3390/en13246657
Chicago/Turabian StyleAbu-Kalla, Hala, Ruslana Rachel Palatnik, Ofira Ayalon, and Mordechai Shechter. 2020. "Hoard or Exploit? Intergenerational Allocation of Exhaustible Natural Resources" Energies 13, no. 24: 6657. https://doi.org/10.3390/en13246657
APA StyleAbu-Kalla, H., Palatnik, R. R., Ayalon, O., & Shechter, M. (2020). Hoard or Exploit? Intergenerational Allocation of Exhaustible Natural Resources. Energies, 13(24), 6657. https://doi.org/10.3390/en13246657







