Abstract
The European Commission’s Target Model’s main objective is to integrate European electricity markets, leading to a single internal energy market and guaranteeing the instantaneous balance between electricity generation and demand. According to the target model for electricity trading, proposed by the European Network Transmission System Operators for Electricity (ENTSO-E), within each zone, electricity can be traded freely without taking into consideration network limitations. In contrast, for cross-border trading, the exchanges with other market areas are taken into account. Cross-border trade poses a further burden on the interconnection lines, resulting in increasing network congestion, which in turn restricts electricity trading. Thus, calculating the available capacity for trade has a significant ramification on the market. Today, the Available Transfer Capacity (ATC) mechanism dominates cross-border trading, but this methodology may be replaced by the Flow-Based (FB) approach across Europe. This paper investigates both approaches regarding the cross-border congestion management under the market coupling procedure. In our case study, the Southeast Europe (SEE) region is taken into consideration; it consists of both the FB and ATC approach in a five country (Greece, North Macedonia, Bulgaria, Serbia, and Romania) scenario. The purpose of our tests is to perform, compare, and evaluate the effectiveness of each method for the SEE region, while the main findings are the maximization of social welfare, better cross-border trading opportunities, and price convergence via the FB method.
1. Introduction
The energy market’s gradual integration across Europe has led to increased interest in cross-border electricity trading [1,2]. Despite this fact, the interconnection lines between the national transmission systems were originally designed to ensure stable operation and to render assistance in the case of system failures. In energy markets, the physical constraints of transmission systems will always be a factor that limits the energy flows [2,3]. Nevertheless, expanding the transmission systems with no limits is realistically unfeasible. Moreover, the upward trend towards the high penetration of renewable energy is also a key element that imposes the optimal use of transmission capacity. When renewable energy is integrated into the electricity system, the volume of renewable generation is often concentrated in places with advantageous geographical characteristics and weather conditions, such as wind and solar availability. To manage the difference between production and consumption, there is a need to transfer large quantities of electrical power across regions [4]. This situation creates the need to optimize the utilization of existing networks, while respecting the physical limits of power system [5,6] and also designing novel market solutions that will leverage the benefits of Renewable Energy Resources’ (RESs) integration within the electricity system [7]. From both the practical and economical points of view, new market models will propose solutions for congestion and for RES penetration near borders. These actions offer positive environmental and economic impacts at a pan-European level. However, all these manifold constraints should not only be addressed, but also be communicated by the energy market participants.
Electricity trading is conducted through different coordinated electricity markets. To this end, forward and future markets are successively combined with a day-ahead and intra-day market, concluding with a final real-time balancing market [4,8,9,10,11]. Historically, electricity markets were organized at the national level, and every country focused on self-sufficiency in terms of power supply. Hence, the target model for electricity trading proposed by ENTSO-E makes use of a zonal approach, based on a number of interconnected markets [12]. Within each market, electricity can be traded freely, without taking into consideration the physical limitations of the underlying electricity grid according to the ENTSO-E target model. Regarding the physical constraints, in every case, these should be respected, since the system security is the most important factor that shapes its operation. In most cases, there is sufficient transmission in order for the load requirements to be met. Nevertheless, even if internal congestion exists, there are no price differences within the market area. In contrast, for cross-border trade, the interconnection capacity with other zones takes into account the trading process. In that context, both cross-border trading methods take into account the physical infrastructure, but from a different perspective.
Cross-border trade leads to excessive pressure on the interconnection lines, resulting in increasing network congestion, which in turn restricts the electricity trade. Congestion refers to situations in which the demand for transferring the electrical power exceeds the limits of transmission system, i.e., situations in which unrestricted use of the network would pose a risk to the system’s security [5,6,13]. However, in the long term, the absence of cross-border trading or even the delay of interconnection expansion may lead to an increase in both CO emissions and generation costs [14]. According to the Capacity Allocation & Congestion Management (CACM)-Commission Regulation (EU) 2015/1222 of 24 July 2015, the term “congestion” can be classified into [15]:
- (a)
- “physical congestion”, which implies any network condition where forecasted or realized power flows violate the thermal limits of grid elements and the voltage stability or the angle stability limits of the power system, and
- (b)
- “structural congestion”, which implies congestion in the transmission system that can be unambiguously defined, is predictable, is geographically stable over time, and is frequently reoccurring under normal power system conditions.
To prevent overloading of the transmission system by cross-border energy transfers and the related risk to network security, a coordinated capacity calculation and allocation mechanism is required [5,6,13]. Coordination across different market areas is essential since electricity flows can not only be restricted by commercial agreements, but also follow the laws of physics. A coordinated capacity calculation mechanism ensures an efficient allocation of transmission capacity, since it balances the cross-border capacity fed into the market and the security of power supply [6,16,17]. The way in which the available capacity for trading is calculated is of great importance for the market. Today, the Available Transfer Capacity (ATC) mechanism is utilized. However, this methodology may be replaced by a Flow-Based (FB) approach across Europe.
In general terms, the capacity calculation procedure takes place in two different time frames:
- 1.
- Long-term capacity calculation for the year- and month-ahead market time frames is considered to be coordinated by the Transmission System Operators (TSOs) to ensure that capacity calculation is reliable and that optimal capacity is made available to the market [3,18]. Harmonized long-term across-the-region capacity allocation rules require the establishment of a single allocation mechanism at that regional level. Currently, capacity allocation is operated by Regional Coordination Centers (RCCs). A methodology for the allocation of long-term capacity in a coordinated manner between different long-term time frames within the respective region needs to be predefined. The solution for a common capacity calculation methodology must include mechanisms for operational security limits and contingencies. A common grid model methodology is agreed upon and established among the involved TSOs, while security analysis based on multiple scenarios is applied [13,19]. All involved TSOs in the region capacity calculation jointly develop a common set of scenarios to be used in the common grid model for each time frame. The following inputs are used for determining the allocation of forward capacity: (i) validated long-term capacity submitted by the RCC and capacities associated with the long-term transmission rights and (ii) bids submitted by market participants. It is up to the TSOs to commonly agree what percentage of the capacity should be allocated in the long term and what percentage in the short term. Further, after long-term allocations, the rest of the available capacity is subject to allocation on a short-term basis.
- 2.
- Short-term capacity calculation refers to the combination of day-ahead, intraday, and balancing time frames, where the available capacity needs to be calculated in a coordinated manner by the involved TSOs [3,8,9,20]. In that context, they should also use a common grid model including forecasts regarding generation, load, and network status for each hour. The available capacity then is calculated according to the “considered algorithm” (see the description in Section 2 and Section 3). The available cross-border capacity is one of the main inputs for the calculation process, in which all region bids and offers are collected and matched. One scenario per settlement period (market time unit) is developed for the day-ahead, for the intraday, and for the balancing capacity calculation time frames [20]. Each TSO in the capacity calculation region ensures that the capacity is recalculated within each market time frame based on the latest available information. The frequency of this recalculation takes into consideration efficiency and operational security [21].
The aforementioned “considered algorithm” used in the capacity calculation methodology is either a coordinated ATC algorithm or an FB algorithm.
The FB calculation algorithm is a method that takes into account that electricity can flow via different paths and optimizes the available capacity in highly interdependent grids [22,23]. The FB approach constitutes a capacity calculation method in which energy exchanges between market zones are constrained by Power Transfer Distribution Factors (PTDFs) and available margins on Critical Network Elements (CNEs) or Critical Branches (CBs) [13,24]. The FB approach could be used as a primary approach for day-ahead, intraday, and balancing capacity calculation, where the mathematical solution consists of the calculation of PTDFs and the calculation of available margins on CBs. The FB approach takes into account the physical constraints of the system and more specifically the CBs of the interconnected system. These CBs may be internal (lines that are declared as critical from each TSO) and/or interconnection lines. The FB approach is closer to the real capabilities of the system and thus offers more trading opportunities.
The coordinated ATC calculation algorithm is a method that takes into account that electricity can flow via different paths based on various predefined rules that ensure the safe and reliable operation of the interconnected electricity grid as considered safe and secure by interconnection partners. The coordinated ATC approach constitutes a capacity calculation method based on the principle of assessing and defining ex ante a maximum energy exchange between adjacent bidding zones. The ATC approach should only be applied in regions where capacity is less interdependent, and it can be shown that the FB approach would not bring added value [15]. Certainly, the ATC method provides an easier way to conduct cross-border trading. For the coordinated ATC approach, the rules for calculating capacity also consider the rules for efficiently sharing of the power flow capabilities of CBs across different bidding zone borders. The main purpose of these algorithms lies in allocating transfer capacity and electricity trading utilizing potential market opportunities via a market coupling procedure [16,25]. Of course, from a practical point of view, the algorithms are implemented in order to solve possible cross-border congestion. However, the ultimate objective of such a procedure is to use auctions of transfer capacity and a system-wide optimization of social welfare in order to determine the best possible market outcome, guaranteeing efficient utilization of the available transfer capacity [26].
Several approaches have been proposed for ATC computation. In [16], a comprehensive review of different approaches for ATC determination was presented. TSOs that participate in the trading have the responsibility to manage the actual physical flows, including transit flows. According to [5,13], congestions are solved on a “border-by-border” basis, while TSOs have to prioritize and allocate capacity to certain borders in order to manage the effect of transit flows and internal congestions. It should be noted that capacity calculation in a meshed grid becomes more and more complex, since transit flows are hard to predict [6,21].
Even though the FB approach adds more complexity to electricity market analyses and trading, the transmission capacities provided to the market come together with information on the physical flows on all CBs for each market zone [27]. Transit flows are monitored and overloads are managed directly by the market algorithm. The TSOs can provide the maximum capacity to the market, and the FB algorithm finds the optimal flow on all grid components by itself in terms of social welfare maximization. Because the TSO does not have to prioritize capacity on a “border-by-border” basis in advance, the solution domain, given by the FB method, is as large as or larger than the ATC domain [6,28].
In this paper, we investigate both algorithmic approaches. In general terms, the objective function is the same for ATC and FB, while the constraints differ. The objective in both methods is to maximize the social welfare of the electricity market. This differentiation is depicted in Figure 1 (where NP (Net Positions) = supply − demand).

Figure 1.
Formulation of the NTC and FB algorithm.
The FB algorithm, in most cases, leads to a better solution than the ATC, in terms of social welfare, price convergence, and trading opportunities. The reason behind this is the difference in the constraints, which lead to a wider solution space for the optimization problem. Thus, for a given level of safe operation, the boundaries of FB domain will always be located on or outside the boundaries of ATC domain.
Consequently, the main contributions of this paper are:
- –
- The maximization of total social welfare based on the ATC and FB capacity calculation approach.
- –
- Better trading opportunities to the market via the FB method and additional social welfare compared to the ATC.
- –
- A more effective use of transmission resources.
- –
- A better price convergence rate identified for the FB than for the ATC approach.
In particular, the case of the Southeast Europe (SEE) region is taken into consideration. The SEE region is selected as one of special interest. The main reasons behind this selection are:
- only basic steps in the market procedures were realized in the majority of the SEE countries [29],
- the cross-border trading has been until now based on bilateral agreements between the SEE countries,
- the market coupling especially via the FB approach has not yet been implemented in the SEE region, and
- the transmission network in the SEE region seems to have different characteristics in comparison with the Central and Western Europe meshed grid where the market coupling procedures are more mature.
Both the ATC and FB method are examined and tested for this region, as an extension of the work presented in [30], giving some valuable results. The scenario we examine encapsulates five countries (Greece, North Macedonia, Bulgaria, Serbia, and Romania). The data used as inputs were provided by the involved TSOs (ADMIE/IPTO, MEPSO, ESO, EMS, and Transelectrica) and the Regional Security Center of the SEE region (SCC), except the market data, which were simulated close to the real ones.
The rest of the paper is organized as follows: In Section 2 and Section 3, respectively, the ATC and FB approaches are given in detail. The market coupling procedure in the frame of an internal European electricity market is described as a system-wide optimization. In Section 4, some of the scenarios are tested for the SEE region. Section 5 includes the results for cross-border trading, using both aforementioned methods. Finally, in Section 6, some useful conclusions are drawn.
2. Available Transfer Capacity Method
In the ATC approach, the link between commercial exchanges and the physical features of the transmission system are simplified. The nodes of a bidding zone are grouped and replaced by one equivalent node; thus, only cross-border links are taken into account. Capacity allocation is conducted by TSOs ex ante the market clearing [5,31].
The ATC calculation method is based on heuristic rules and forecasts of the market outcome. Certainly, the ATC value determined for each cross-border link may be different for each flow direction of a line. ATC market coupling dominates the European electricity markets, except for Central Western Europe (where the FB market coupling is utilized) [12,32]. Although the market clearing algorithm is simple, the calculation of the ATC value itself is non-transparent for regulators. Moreover, the transmission capacity that is made available to the market seems to be a conservative estimation of the real one, since the ATC value needs to be excessively limited in order to prevent power system unbalances. The benefit of this approach is the fact that the ATC provides an easier way to conduct cross-border trading. The trade off, however, is the suboptimal solutions we have in the market clearing problem.
The Net Transfer Capacity (NTC) is the maximum exchange between two areas compatible with security standards applicable in both areas (N-1 criterion) and taking into account the technical uncertainties about the future network conditions. NTC may be allocated in different time frames to match the need for securing longer term trading and to provide space for shorter term trading, after extensive load flow studies performed by the TSOs. New information on weather, topology, etc., helps not only to distinguish the “already allocated” from the “still available” capacities, but also allows simulation of the coupling effects between NTCs across the ENTSO-E area or regions. This results in Notified Transmission Flows (NTF) that can be interpreted as the already occupied part of the NTC by the already accepted contracts at the studied time frame [16,25,31]. Then, TSOs evaluate the remaining ATC between systems. The ATC is “the transfer capacity remaining available between two interconnected areas for further commercial activity over and above already committed utilization of the transmission networks” [5,31]. The ATC for a specific time frame is finally given by the following equation:
where ATC stands for the Available Transmission Capacity and NTC represents the Net Transmission Capacity, while NTF represents the Notified Transmission Flows for this time frame. Since the optimal market outcome can be determined by a system-wide optimization of the social welfare, a suitable objective function and the required constraints are established. The term “social welfare” describes the sum of the consumer’s and producer’s surplus and the Congestion Rent (CR) [26,33]. The producer surplus represents the benefit to producers obtained from selling at a market price that is higher than the minimum at which they would be willing to sell [25,34]. The consumer surplus is the gain for the consumers as they can buy electricity at a price that is less than the maximum price that they are willing to pay. CR is the product of the price difference between two market areas and the limited energy trade between them, due to the scarce transmission capacity i.e., when market parties would like to exchange more power between the market areas than what is feasible. In the case of system-wide optimization, social welfare is not maximized for each individual market zone, but for all market zones [25,33]. Furthermore, the methodology presented above involves an optimization for a duration of one hour or an entire day. Thus, a suitable objective function can be formulated as follows, for each market area a and every hour t:
where N is the number of markets, stands for the price that the buyer is willing to pay for the accepted power quantity, is the price at which the seller is willing to sell for the accepted power quantity, represents the accepted quantity of the buy order, and is the accepted quantity of the sell order.
The basic constraints are:
where stands for each buy order (either partial or all or nothing buy order) that ranges between zero and , while represents the maximum quantity that is available for buy orders. Furthermore, stands for each sell order (either partial of all or nothing sell order) that ranges between zero and . Finally, represents the maximum quantity that is available for sell orders.
The nature of electricity markets stipulates that in each market zone, the sum of the demand accepted must match the sum of the supply volume accepted.
where stands for the sum buy order, stands for the sum of sell order, while represents the total power volume traded.
The balancing condition can be met by coupling N market areas by means of the exports or the imports into or out of neighboring market zones , which are then optimized.
where stands for each buy order and stands for for each sell order.
Possible energy transfers between the market zones must not exceed the maximum transfer capacity of the related interconnectors. This is depicted by further constraints, and in case of calculations with ATC values, where any export from a to b via interconnector must not exceed its maximum transfer capacity , for the relevant time interval t.
where represents each export from a to b, while stands for the maximum transfer capacity via .
3. Flow-Based Method
The FB market coupling procedure can be considered as a combination of the zonal approach of ATC method with the physical network limitations from the nodal one. In the FB approach, the network constraints are taken into consideration. Nevertheless, since the zonal approach is retained, the grid constraints need to be simplified. In other words, the capacity allocation happens partly ex ante the market clearing and partly simultaneously with the market clearing [13,28]. All CBs of the electricity grid are considered in the N-state and in critical N-1 states [24]. The commercial flow through a CB is limited by the Remaining Available Margin (RAM), while PTDFs contain the linear relationship between NPs and flows through CBs. The RAM and PTDF values are determined by the TSOs ex ante the market clearing. These parameters define the flow domain. Each boundary of the FB flow domain refers to the limit of a CB. By implementing the FB methodology, one creates market solutions closer to the physical reality, as well as respecting the operational security of the grid. As the physical characteristics of the grid are better represented in the FB approach than in the ATC method, the FB parameters can be determined in a less conservative way. Hence, the FB flow domain is, in most cases, larger than the ATC flow domain [6,32].
In that context, in the FB methodology, the physical laws of the network are integrated as part of the optimization problem in the form of optimization constraints. This denotes the main difference between the ATC and the FB algorithm. Thus, in the FB approach, the objective function of the optimization problem is similar to the ATC method with the additional physical constraints [13,17]. The additional constraints in the case of the FB algorithm are defined with the PTDF matrix and RAM values, related to the pairs of CBs/Critical Outages (COs) [23,33]. Equations (10) and (11) provide the additional network constraints:
where represents each buy order and each sell order and stands for the PDTF value calculated for each CB, for each capacity transfer from area z to area a, different for the import and export flow. Furthermore, represents the available margin flow on each CB, while RAM represents the maximum available margin flow on each CB.
To be more specific, the information on physical properties is used to describe how the power injection of one unit in one node will be allocated across the power grid. This is reflected in the sensitivity factors, the PTDFs. By including the PTDFs, one can obtain a better utilization of the system. The PTDFs are derived from the AC power flow equations through a DC power flow representation of the power grid. The final equation for calculating the PTDFs is presented in Equation (12):
where represents the PTDF value from node n to the line between nodes i and k. stands for the susceptance between node i and k with a negative sign, while and stand for the elements of the systems impedance matrix. By using the FB approach, the concept of borders disappears, and the physical properties reflected in the parameters determines the solution domain [22].
As mentioned previously, two additional parameters are deployed for the FB algorithm: the PTDFs and the RAM. The FB parameter calculation is started two days before the delivery day (D-2) and finished the day-ahead morning. Nevertheless, the day-ahead market outcome has to be known already to calculate the PTDFs and the RAM. This problem is addressed as follows: the PTDFs and the RAM are determined based on a forecast of the state of the power system at the moment of delivery (i.e., the D-2 congestion forecast). Then, these FB parameters are channeled to the day-ahead market clearing algorithm [32,35].
The second FB parameter is the RAM. The RAM is practically the line capacity that is available in the day-ahead market. The RAM procedure consists of two main steps. Firstly, the CBs and COs are determined. In the second step, the RAM is calculated for these CBs under the COs. For each CB, the highest power flow that is allowed, is determined based on the thermal limit of the line. The RAM is then calculated as the maximum allowable power flow limited by three factors [17,22,24]: (a) the reference flow caused by commercial trades outside the day-ahead power exchange (i.e., bilateral trades, forward markets, intra-day markets, and real-time balancing): these trades can be internal or external (within a market zone or between market zones); (b) the Final Adjustment Value (FAV): the FAV allows TSOs to take into consideration further information, such as an additional margin due to complex remedial actions or active topology control; the FAV can be positive or negative; (c) the Flow Reliability Margin (FRM): the FRM is a safety margin that needs to compensate for the approximations made in the FB method such as the assumptions for PTDFs, unintentional flow deviations due to load-frequency control, and the use of a linear grid model with a simplified topology.
4. The SEE Region Case Study
The case study of the SEE region is selected as one of special interest, where the market coupling procedures are still immature. Despite that the market coupling has been examined and implemented in Central and Western Europe, it remains under investigation for the SEE region. The scenario under consideration encapsulates five countries, namely Greece, North Macedonia, Bulgaria, Serbia, and Romania. Each country is a market, and each market is considered as a single bidding zone. Hourly and daily tests have taken place for a typical day (5th of June 2019). Here, it should be noted that even though our analysis considers a limited number of CBs (only the cross-border interconnection lines among the five countries for our tests), the results obtained provide some useful conclusions for the specific region and give clear answers regarding the applicability and efficiency of both cross-border trading methods.
4.1. Input Data
The complex nature of transmission system requires the supplied input data to be validated. This procedure is performed two days before delivery and encapsulates a set of tests, such as load flow analyses, voltage limits, and voltage stability assessment. The common grid model, which is a simplified network model, is derived as a combination of nodes and lines. Firstly, each TSO estimates the local base case for its own control area. Every TSO estimates its local base case based on a reference day, when the market outcome is known (i.e., a day in the past) with similar system conditions. The market outcome of the reference day is then updated with D-2 renewable generation forecasts, load forecasts, and outage schedules for generation units and grid elements. TSOs coordinate the NPs of the reference day, but each TSO applies a slightly different methodology to update the reference day [6,23,32].
Practically, a D-2 congestion forecast file is created by every TSO, giving a view of the expected power flows. In the ATC approach, this file is obtained for only two timestamps and contains at minimum the following information [6]:
- –
- Available grid topology and expected outages of components
- –
- Generating units and their estimated output levels and expected outages
- –
- Load forecast
- –
- Exchange programs
Next, all individual D-2 files are merged, leading to the so-called common base case. For the FB approach, the aforementioned input data have to be submitted in a 24 hour timestamp, since the FB algorithm is conducted for each hour.
In our case study, the market data (sell and buy bids) for each bidding zone are simulated very close to the real values, retrieving public data from the involved TSOs (ADMIE/IPTO, MEPSO, ESO, and EMS) [36]. The indicated values for transfer capacities can also be found on the ENTSO-E transparency platform. However, more updated data are obtained from the relevant TSOs and SCC. The network data used for both the ATC and FB method, i.e., ATC margins, AMF margins, PTDF values, and common grid model, are real and are provided by the involved TSOs and SCC for the entire SEE region.
4.2. Implementation Details
Viewing the objective function and constraints reveals that the procedure of market coupling and congestion management can be mapped as an optimization problem, which can be solved in closed form, using the algorithmic approach described earlier. For both the ATC and FB approach, a number of available standard solvers, which use linear programming, are utilized. The Yalmip toolbox in MATLAB is used for the optimization problem, while the proposed solver is the commercial CPLEX.
4.3. Expected Outputs
When a TSO provides the ATC constraints, it is necessary to make a choice in advance on how to split the capacity among its borders, even before the market participants’ bids are known. The results of the optimization performed, such as arising market clearing prices and energy transfers, as well as the acceptance of explicit capacity bids, can be examined on realistic reference systems [16,31]. By solving the problem with different possible ATC values, the market clearing prices and the maximized social welfare are obtained.
In the FB capacity calculation process, the FB parameters determine the transaction constraints considered in the market coupling algorithm. This means the parameters indicate all feasible NPs on CBs under consideration and without endangering the grid security. Moreover, sufficient cross-border transmission capacities are crucial in order for the expected price convergence to be achieved.
5. Results
The cross-border trading via the market coupling procedure is examined in three district scenarios for the SEE region. Hourly and daily tests are conducted for both the ATC and the FB method, verifying the result analysis given in the next subsection. For the reader’s convenience, here, the results are provided for a typical day (5th of June 2019) and a typical hour (i.e., 11:00 a.m.).
In the first scenario, the ATC method and the FB method are investigated for three countries of the region (Greece, North Macedonia, and Bulgaria). The results obtained by the optimization algorithms are recorded for the ATC method in Table 1 and for the FB method in Table 2. The outputs provided in Table 1 are the export and import flows “border-by-border” according the ATC approach, while the outputs recorded in Table 2 are the flows on each cross-border line for every market according to the FB approach. Furthermore, the total social welfare is recorded (Table 1 and Table 2) as derived from each method under the wide-area optimization frame. Moreover, the prices before and after the coupling procedure for each country are presented in Table 3.

Table 1.
Cross-border flows via the ATC method for the 3 country scenario.

Table 2.
Cross-border flows via the FB method for the 3 country scenario.

Table 3.
Market prices for the 3 countries.
In the second scenario, the ATC method and the FB method are investigated for four countries of the SEE region (Greece, North Macedonia, Bulgaria, and Serbia). The results obtained by the optimization algorithms are recorded for the ATC method in Table 4 and for the FB method in Table 5. As mentioned before, the outputs provided in these tables are the export and import flows on the borders (ATC approach) or on the cross-border lines for each market (FB approach). The total social welfare is also given for both approaches (Table 4 and Table 5), while the prices for each country are presented in Table 6.

Table 4.
Cross-border flows via the ATC method for the 4 country scenario.

Table 5.
Cross-border flows via the FB method for the 4 country scenario.

Table 6.
Market prices for the 4 countries.
In the third step, the methods are implemented for a five country scenario, namely Greece, Bulgaria, N. Macedonia, Serbia, and Romania. The relevant results are recorded in Table 7, Table 8 and Table 9.

Table 7.
Cross-border flows via the ATC method for the 5 country scenario.

Table 8.
Cross-border flows via the FB method for the 5 country scenario.

Table 9.
Market prices for the 5 countries.
In all cases, all results obtained were derived by the optimization algorithms and the relevant constraints that were formulated in Section 2 and Section 3. The overall approach (common for the ATC and FB method) is considered as a wide-area optimization, resulting in optimal total social welfare for the entire region, for all the markets and all participants of each market together. Therefore, as the results indicate, the market coupling procedure defines the cross-border trading flows and the final prices not taking into account each market separately.
In Figure 2 and Figure 3, an overall view of the cross-border trading conducted with the ATC and the FB method among the five countries is presented. The internal electricity price for each country after trading is denoted within the boxes. As one can observe, all the prices tend to converge to a mean value, mainly in the results obtained by the FB market coupling. The arrows connecting the countries represent the energy flows between them due to the trading procedure. These optimal exports and imports are calculated via the ATC and FB optimization algorithm, respectively, taking into consideration the wide-area social welfare to be optimized. These flows are given here aggregated in each border direction, while for the FB approach, they are recorded on each CB (see Table 8).
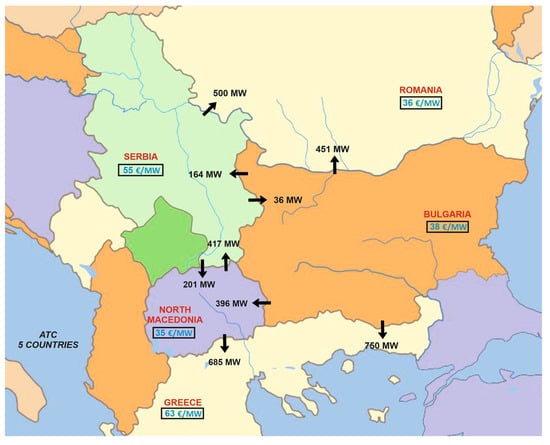
Figure 2.
Cross-border trading with the ATC method for the five countries.
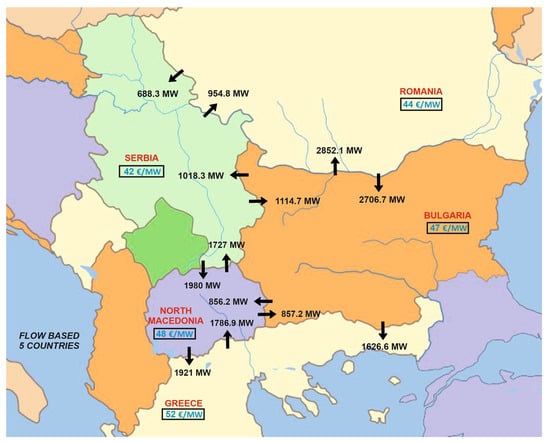
Figure 3.
Cross-border trading with the flow-based method for the five countries.
Results Analysis
The case study investigates the efficiency and the applicability for both the ATC and FB approach in a specific region of SEE regarding (i) maximization of the social welfare, (ii) better trading opportunities, and (iii) price convergence. To quantify these points in order to assess the results and draw some valuable conclusions, we consider three indexes, namely the social welfare (Equation (13)), power traded (Equation (14)), and the price convergence (Equation (15)) index. The definitions of these three indexes follow:
- (1)
- Social welfare index:
- (2)
- Price traded index:where c represents the countries participating in the cross-border trading and l the interconnection lines.
- (3)
- Price convergence index:where is the price vector of the countries involved in the cross-border trading.
To further analyze the results of the cross-border trading via market coupling for the three scenarios in the SEE region, we calculate the indexes’ values, presented in Figure 4, Figure 5 and Figure 6.
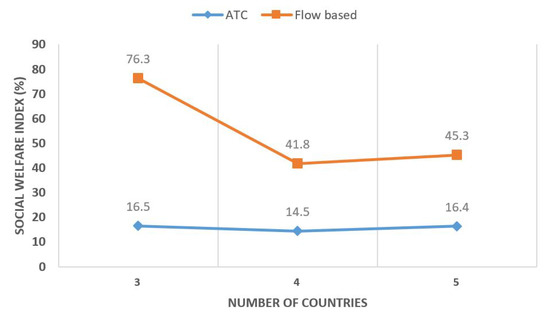
Figure 4.
Social welfare index for different number of countries.
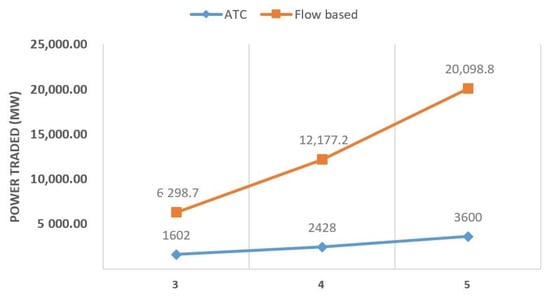
Figure 5.
Volume of power traded for different number of countries.
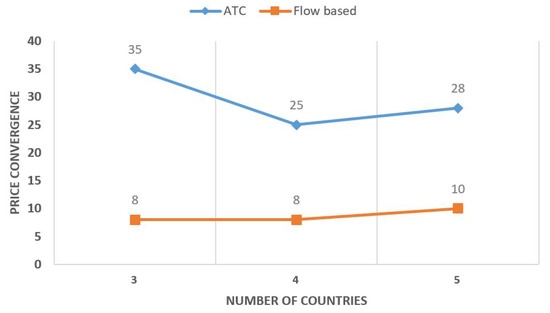
Figure 6.
Price convergence index for different number of countries.
Figure 4 illustrates the social welfare index that is calculated for the three different scenarios encapsulating three, four, and five countries and for both methods, respectively. As is obvious, this index significantly increases since the cross-border trading is based on the FB market coupling.
Figure 5 depicts the volume of power traded for the different scenarios and for both the ATC and FB method. One can observe an important increase in the overall traded electricity via the FB approach compared with the one obtained via the ATC method for different numbers of countries.
In Figure 6, the price convergence index is presented for the tested scenarios. One can observe that the prices converge clearly better via the FB method for three, four, and five countries. The price convergence index is of great importance since the wide-area optimization is realized for both approaches for the entire region, resulting in similar final prices for all markets involved.
Consequently, as was expected, there is significant difference in the social welfare achieved via the two methods for the three scenarios tested. Clearly, better trading opportunities are achieved by the FB approach since the volume of traded power is higher. In all cases, it is obvious that the best price convergence is achieved via the FB method.
To further evaluate these conclusions, some results on a daily basis are obtained, since the previous scenarios were examined for the aggregated markets’ bids of a typical day (5 June 2019). In Figure 7, the total daily social welfare is presented for all scenarios and methods. One can observe the differences between the daily social welfare obtained by the ATC and the FB market coupling. The conclusion is the significant increase of daily social welfare with the FB approach. The daily total social welfare for the case of uncoupled markets is also presented in Figure 7. As expected, the more the countries are coupled, the more the overall welfare gain is. Certainly, in all the examined scenarios, the FB approach seems superior to the ATC one.
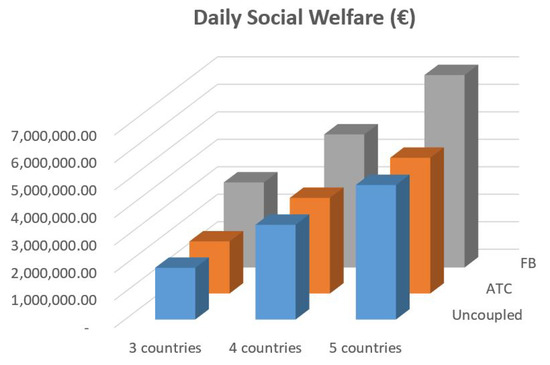
Figure 7.
Total daily social welfare for different number of countries and cross-border trading method.
6. Conclusions
In this paper, the deployment of cross-border trading towards an internal European electricity market is considered. Our scenarios incorporate the market coupling and congestion management for the SEE region. The problem is formulated under mathematical terms as an optimization problem, by a common objective function for both the ATC and FB approaches. The main difference is found in the constraints established. As previously noticed, the objective function of the optimization problem is the same for both the ATC and FB approaches; the main difference is found in the linear constraints of the problem formulation.
The FB method leads to a more efficient use of the transmission grid. In the ATC method, TSOs themselves calculate the capacity values based on forecasts and historical data, while the FB method allows TSOs to gain the impact of trading in terms of physical flows on the network. Under the FB market coupling, the market decides how transmission capacity is allocated over market parties. More capacity and more trading opportunities are offered to the market, resulting in an overall welfare gain and enhanced price convergence. However, the necessary input data TSOs have to provide are more complex and affect the outcome of the market clearing algorithm, while the capacity calculation process is less straightforward.
Our tests verify the theoretical benefits that the FB approach brings to the cross-border trading. Even though our case study is limited to a five country scenario, some useful conclusions are extracted. Firstly, the FB approach leads to better trading opportunities and better utilization of the interconnection lines. Secondly, the total social welfare is increased, and finally, the internal energy prices decrease due to the cross-border trading. Those results guarantee the effectiveness of the FB method in the SEE region.
7. Future Work
As future work, the authors will realize a sensitivity analysis for both methods, expanding the analysis to more countries and expanding the time horizon. Various scenarios are under test, and more CBs from the involved countries will be included and for extended time intervals. Moreover, the authors will consider comparing the price convergence index with the one obtained by the Granger causality connectivity analysis [37].
Author Contributions
The paper was a collaborative effort among the authors. The authors contributed collectively to the theoretical analysis, modeling, simulation, and manuscript preparation. All authors read and agreed to the published version of the manuscript.
Funding
This research is supported by the EU H2020 project CROSSBOW (Grant Agreement No. 773430; http://crossbowproject.eu/).
Acknowledgments
The authors would like to thank all the involved TSOs namely ADMIE/IPTO, MEPSO, EMS, ESO, and Transelectrica, for providing all the necessary data to conduct our experiments. Moreover, the authors would like to thank SCC for their help throughout the experiments and the data provision.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SEE | Southeast Europe |
| RES | Renewable Energy Resources |
| ENTSO-e | European Network Transmission System Operators for Electricity |
| CACM | Capacity Allocation and Congestion Management |
| CR | Congestion Rent |
| FB | Flow Based |
| RCC | Regional Control Center |
| SCC | Security Center of the SEE region |
| TSO | Transmission System Operator |
| NTC | Net Transfer Capacity |
| NTF | Notified Transmission Flows |
| ATC | Available Transfer Capacity |
| CB | Critical Branch |
| CO | Critical Outages |
| CNE | Critical Network Element |
| PTDF | Power Transfer Distribution Factor |
| RAM | Remaining Available Value |
| FAV | Final Adjustment Value |
| FRM | Flow Reliability Margin |
| D-2 | Day 2 before delivery |
| NP | Net Position |
References
- Kannavou, M.; Zampara, M.; Capros, P. Modelling the EU internal electricity market: The PRIMES-IEM Model. Energies 2019, 12, 2887. [Google Scholar] [CrossRef]
- Newbery, D.; Strbac, G.; Viehoff, I. The benefits of integrating European electricity markets. Energy Policy 2016, 94, 253–263. [Google Scholar] [CrossRef]
- Puka, L.; Szulecki, K. The politics and economics of cross-border electricity infrastructure: A framework for analysis. Energy Res. Soc. Sci. 2014, 4, 124–134. [Google Scholar] [CrossRef]
- Lam, L.H.; Ilea, V.; Bovo, C. European day-ahead electricity market coupling: Discussion, modeling, and case study. Electr. Power Syst. Res. 2018, 155, 80–92. [Google Scholar] [CrossRef]
- The European Network of Transmission System Operators for Electricity (ENTSOE). Definitions of Transfer Capacities in Liberalized Electricity Markets; ENTSOE: Brussels, Belgium, 2001. [Google Scholar]
- Leuven, K. Cross-border electricity trading: Towards flow-based market coupling. Eifact Sheet 2015, 2, 1–5. [Google Scholar]
- Borowski, P.F. Zonal and Nodal Models of energy market in European Union. Energies 2020, 13, 4182. [Google Scholar] [CrossRef]
- Biskas, P.N.; Chatzigiannis, D.I.; Bakirtzis, A.G. European electricity market integration with mixed market designs—Part I: Formulation. IEEE Trans. Power Syst. 2013, 29, 458–465. [Google Scholar] [CrossRef]
- Biskas, P.N.; Chatzigiannis, D.I.; Bakirtzis, A.G. European electricity market integration with mixed market designs—Part II: Solution algorithm and case studies. IEEE Trans. Power Syst. 2013, 29, 466–475. [Google Scholar] [CrossRef]
- Kath, C. Modeling intraday markets under the new advances of the cross-border intraday project (XBID): Evidence from the German intraday market. Energies 2019, 12, 4339. [Google Scholar] [CrossRef]
- Nobis, M.; Schmitt, C.; Schemm, R.; Schnettler, A. Pan-European CVaR-Constrained Stochastic Unit Commitment in Day-Ahead and Intraday Electricity Markets. Energies 2020, 13, 2339. [Google Scholar] [CrossRef]
- Weber, A.; Graeber, D.; Semmig, A. Market coupling and the CWE project. Z. Energiewirtsch. 2010, 34, 303–309. [Google Scholar] [CrossRef][Green Version]
- The European Network of Transmission System Operators for Electricity (ENTSOE). Methodology: Flow-Based Market Coupling, Brussels; ENTSOE: Brussels, Belgium, 2018. [Google Scholar]
- Ritter, D.; Meyer, R.; Koch, M.; Haller, M.; Bauknecht, D.; Heinemann, C. Effects of a Delayed Expansion of Interconnector Capacities in a High RES-E European Electricity System. Energies 2019, 12, 3098. [Google Scholar] [CrossRef]
- The European Commission. Commission Regulation (EU) 2015/1222 of 24 July 2015, establishing a guideline on capacity allocation and congestion management. Off. J. Eur. Union 2015, L197, 24–72. [Google Scholar]
- Mohammed, O.O.; Mustafa, M.W.; Mohammed, D.S.S.; Otuoze, A.O. Available transfer capability calculation methods: A comprehensive review. Int. Trans. Electr. Energy Syst. 2019, 29, e2846. [Google Scholar] [CrossRef]
- Bjorndal, E.; Bjorndal, M.H.; Cai, H. Flow-based market coupling in the european electricity market–a comparison of efficiency and feasibility. In NHH Department of Business and Management Science Discussion Paper; NHH: Bergen, Norway, 2018. [Google Scholar]
- Spodniak, P.; Collan, M.; Makkonen, M. On long-term transmission rights in the Nordic electricity markets. Energies 2017, 10, 295. [Google Scholar] [CrossRef]
- See, P.C.; Fosso, O.B.; Wong, K.Y.; Molinas, M. An approach for establishing a common grid model for flow-based market mechanism simulations. CSEE J. Power Energy Syst. 2019, 5, 374–381. [Google Scholar]
- Doorman, G.L.; Van Der Veen, R. An analysis of design options for markets for cross-border balancing of electricity. Util. Policy 2013, 27, 39–48. [Google Scholar] [CrossRef]
- Oggioni, G.; Smeers, Y. Market failures of Market Coupling and counter-trading in Europe: An illustrative model based discussion. Energy Econ. 2013, 35, 74–87. [Google Scholar] [CrossRef]
- Energinet.dk; Svenska Kraftnät; Fingrid; Statnett SF. Methodology and concepts for the Nordic Flow-Based Market Coupling Approach; Technical Report; Energinet.dk: Fredericia, Denmark; Svenska Kraftnät: Sundbyberg, Sweden; Fingrid: Helsinki, Finland; Statnett SF.: Oslo, Norway, 2014. [Google Scholar]
- Amprion Gmbh. Flow Based Market Coupling—Development of the Market and Grid Situation; Technical Report; Amprion GmbH: Dortmund, Germany, 2018. [Google Scholar]
- Wyrwoll, L.; Kollenda, K.; Müller, C.; Schnettler, A. Impact of Flow-Based Market Coupling Parameters on European Electricity Markets. In Proceedings of the 2018 53rd International Universities Power Engineering Conference (UPEC), Glasgow, UK, 4–7 September 2018; pp. 1–6. [Google Scholar]
- Haubrich, H.; Hinüber, G.; Mirbach, T.; Tersteegen, B. Technical Issues Regarding Open Market Coupling-Omc; RWTH Aachen University: Aachen, Germany, 2006. [Google Scholar]
- Gómez, P.M. Benefits of market coupling in terms of social welfare. In Regulation and Investments in Energy Markets; Elsevier: Amsterdam, The Netherlands, 2016; pp. 185–198. [Google Scholar]
- Kristiansen, T. The flow based market coupling arrangement in Europe: Implications for traders. Energy Strategy Rev. 2020, 27, 100444. [Google Scholar] [CrossRef]
- Sőrés, P.; Divényi, D.; Raisz, D. Flow-based capacity calculation method used in electricity market coupling. In Proceedings of the 2013 10th International Conference on the European Energy Market (EEM), Stockholm, Sweden, 27–31 May 2013; pp. 1–7. [Google Scholar]
- Koltsaklis, N.; Dagoumas, A. Policy Implications of Power Exchanges on Operational Scheduling: Evaluating EUPHEMIA’s Market Products in Case of Greece. Energies 2018, 11, 2715. [Google Scholar] [CrossRef]
- Makrygiorgou, D.I.; Andriopoulos, N.L.; Dikaiakos, C.; Papaioannou, G.P. Cross-border trading via market coupling in South East Europe region. In Proceedings of the 2020 17th International Conference on the European Energy Market (EEM), Stockholm, Sweden, 16–18 September 2020; pp. 1–6. [Google Scholar]
- The European Network of Transmission System Operators for Electricity (ENTSOE). Net Transfer Capacities (NTC) and Available Transfer Capacities (ATC) in The Internal Market of Electricity in Europe (IEM); Technical Report; ENTSOE: Brussels, Belgium, 2000. [Google Scholar]
- Van den Bergh, K.; Boury, J.; Delarue, E. The flow-based market coupling in central western europe: Concepts and definitions. Electr. J. 2016, 29, 24–29. [Google Scholar] [CrossRef]
- Energy Community. Market Coupling Simulator for South East Europe; Technical Report; Energy Community Center: Bellaire, TX, USA, 2014. [Google Scholar]
- Meeus, L.; Vandezande, L.; Cole, S.; Belmans, R. Market coupling and the importance of price coordination between power exchanges. Energy 2009, 34, 228–234. [Google Scholar] [CrossRef]
- Poplavskaya, K.; Totschnig, G.; Leimgruber, F.; Doorman, G.; Etienne, G.; De Vries, L. Integration of day-ahead market and redispatch to increase cross-border exchanges in the European electricity market. Appl. Energy 2020, 278, 115669. [Google Scholar] [CrossRef]
- ENTSO-E Transparency Platform. Available online: https://transparency.entsoe.eu/ (accessed on 8 March 2020).
- Papaioannou, G.P.; Dikaiakos, C.; Kaskouras, C.; Evangelidis, G.; Georgakis, F. Granger Causality Network Methods for Analyzing Cross-Border Electricity Trading between Greece, Italy, and Bulgaria. Energies 2020, 13, 900. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).