Multidisciplinary Design Optimization for a Solar-Powered Exploration Rover Considering the Restricted Power Requirement
Abstract
1. Introduction
2. Modeling of the Operational Environment
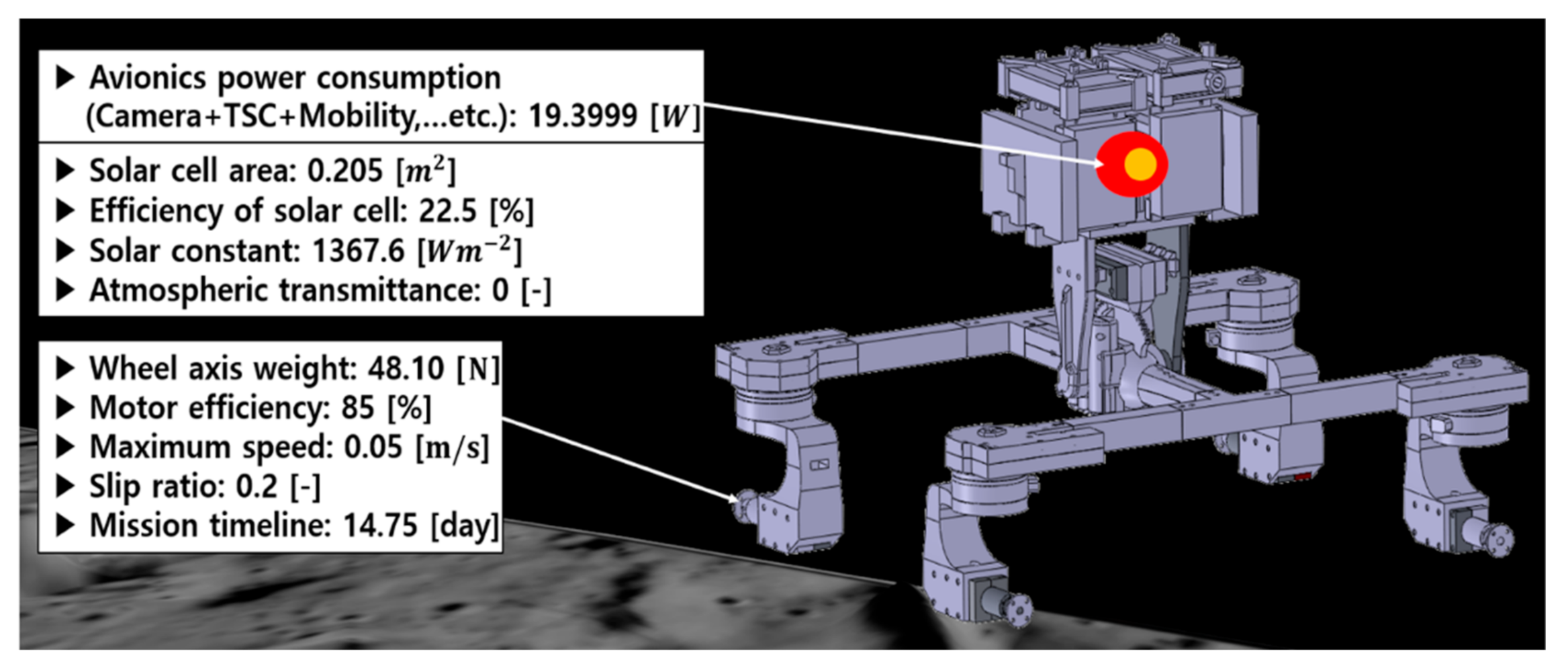
2.1. Power Acquisition Model
2.2. Modeling of Terrain Characteristics in Lunar Simulant
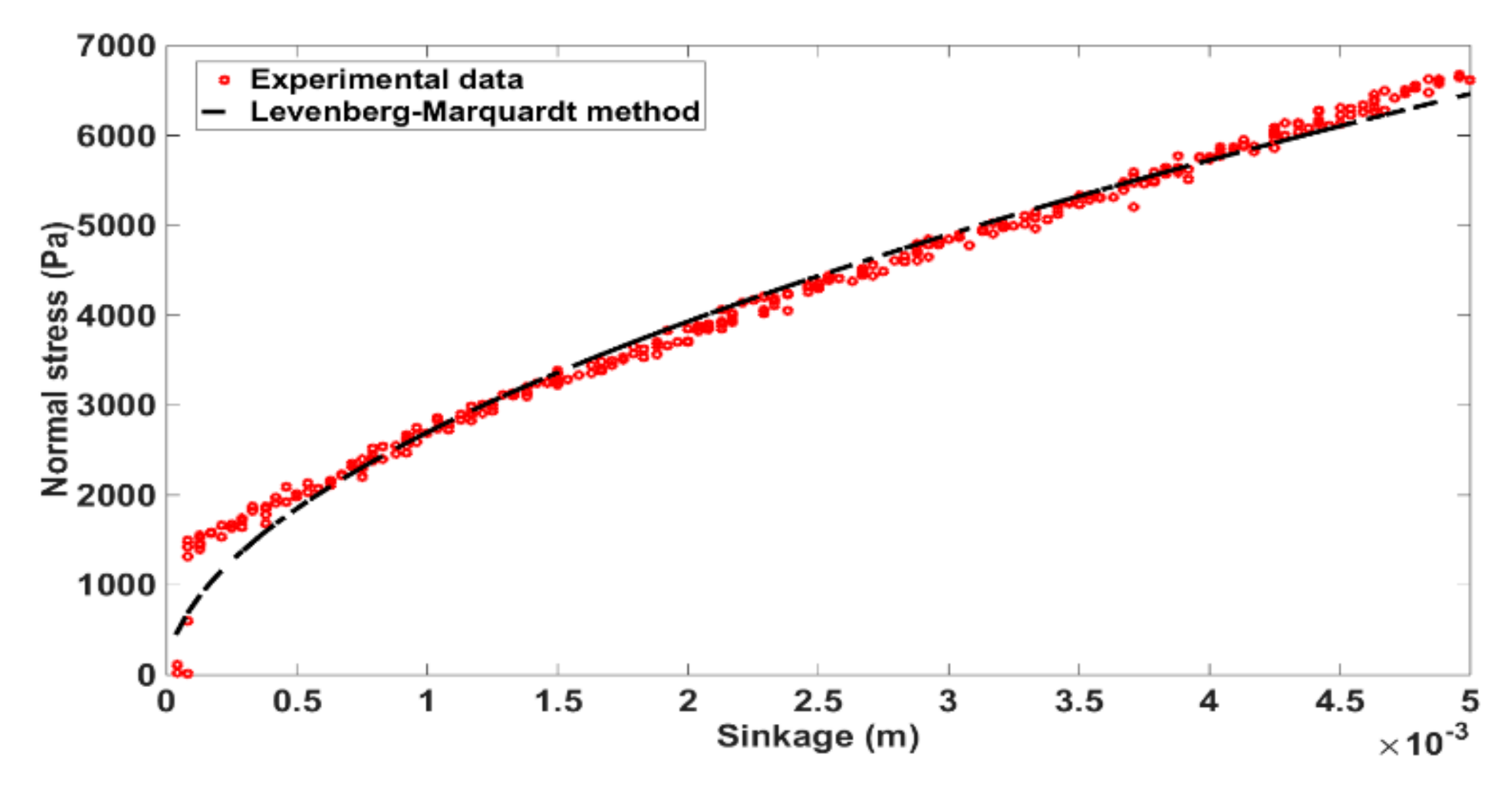
2.2.1. Pressure-Sinkage Relationship Associated with Normal Stress Component
2.2.2. Mohr–Coulomb Failure Criterion/Janosi–Hanamoto Model Associated with Shear Stress Component
3. Multi-Body Dynamics Simulation Tool Based on the Wheel-terrain Interaction Model
3.1. Wheel-Terrain Interaction Model
3.2. MBD Simulation Tool Based on Wheel-Terrain Interaction
| number of limbs, | |
| inertia matrices for the entire system composed by the inertia property of each body | |
| position/orientation of the base body, | |
| articulated joint angles, | |
| non-linear velocity-dependent term, | |
| gravity term, | |
| forces exerted on the base body, | |
| joint articulated torque, | |
| external forces/torques acting on the wheel, | |
| [38]. |
| Algorithm 1 Multi-Body Dynamics Simulation Based on the Wheel-Terrain Interaction Model |
|
4. Multi-Objective Design Optimization Based on Operational Environment in Accordance with the Target Landing Site
4.1. System-Level Requirements
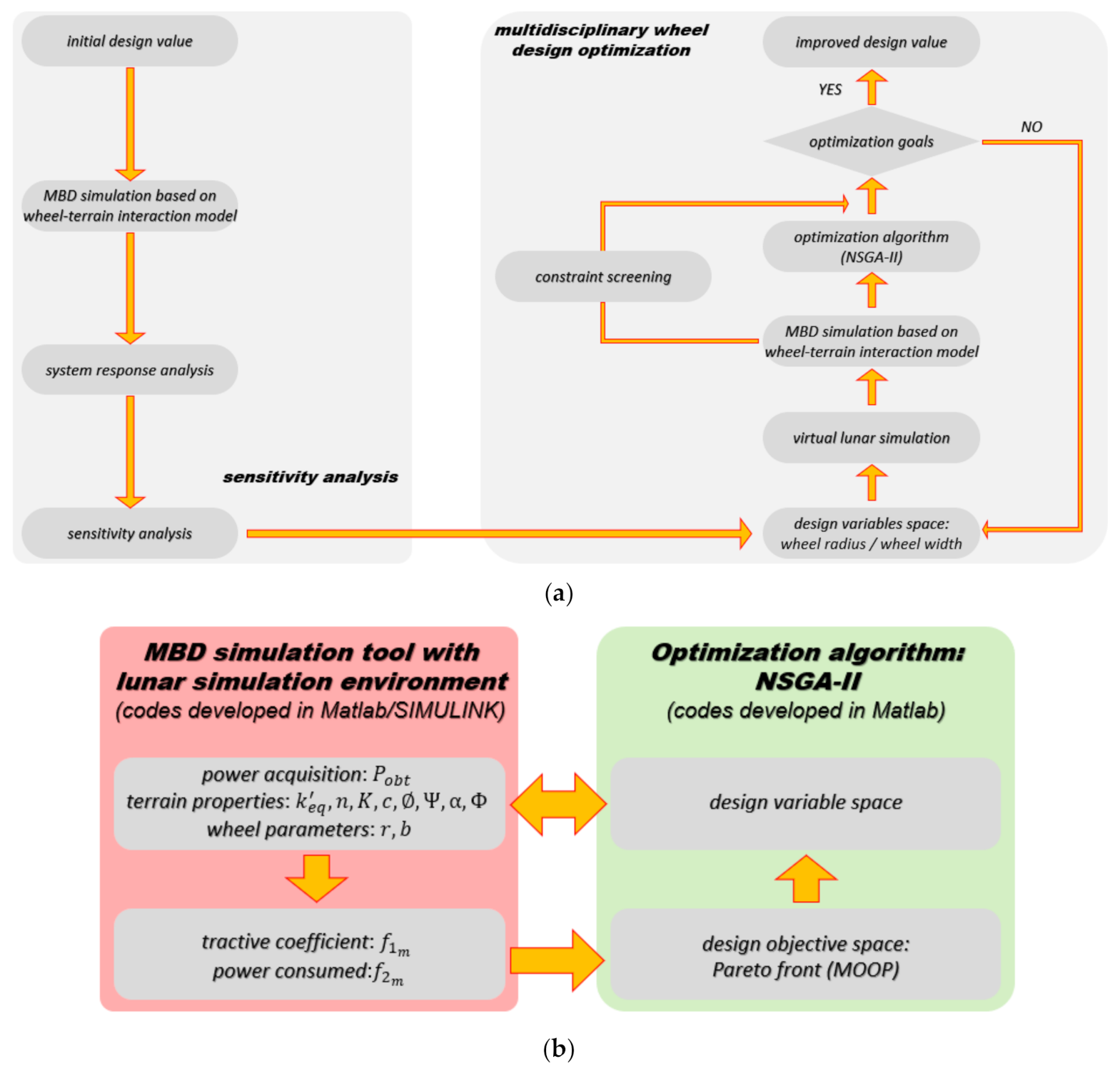
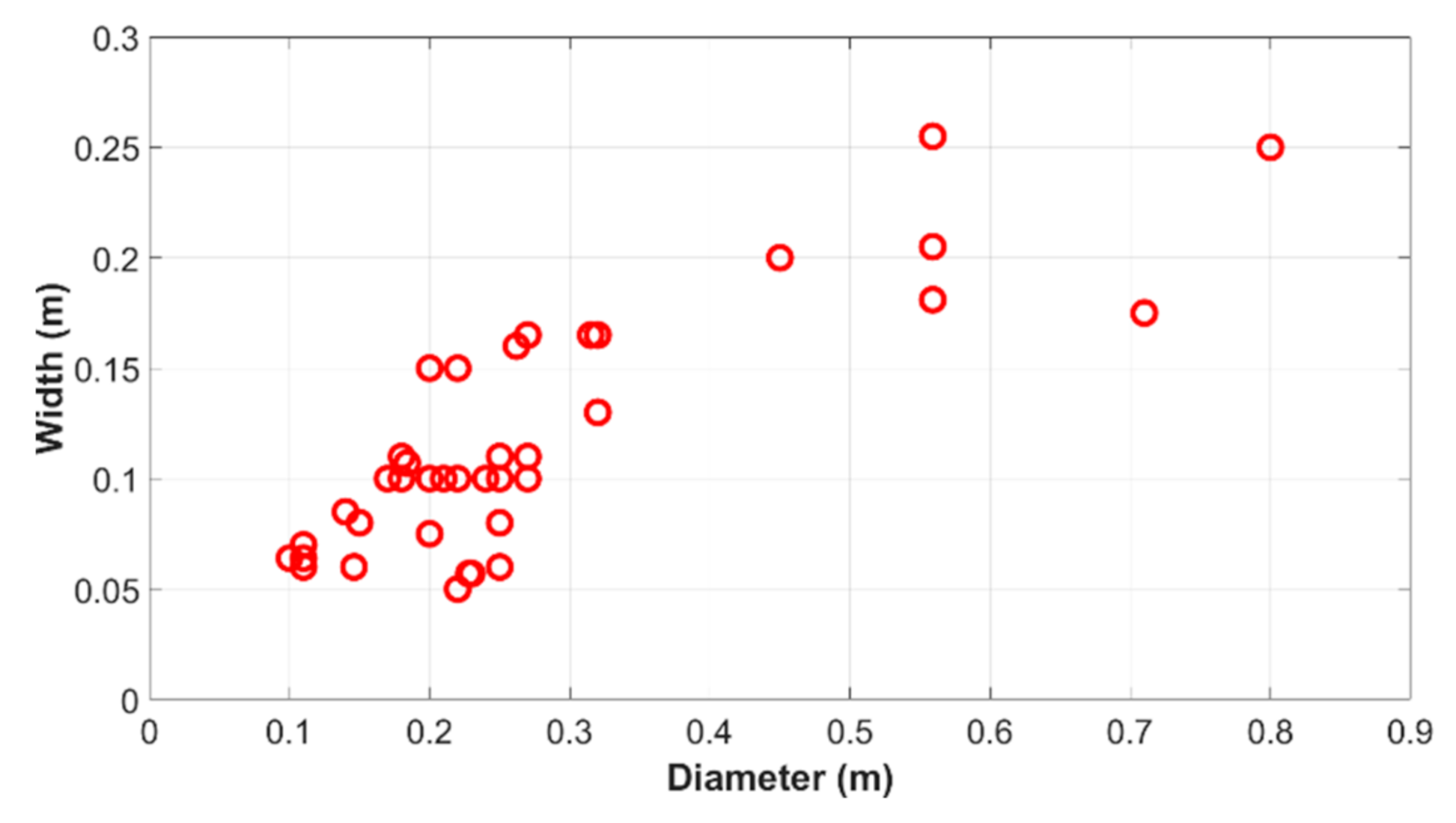
4.2. Wheel Parameter Sensitivity Analysis via Developed MBD Simulation Tool
4.3. Multi-Objective Wheel Design Optimization
4.3.1. Objective Function
4.3.2. Constraint Condition
4.3.3. Optimization Algorithm
4.3.4. Optimization Procedure
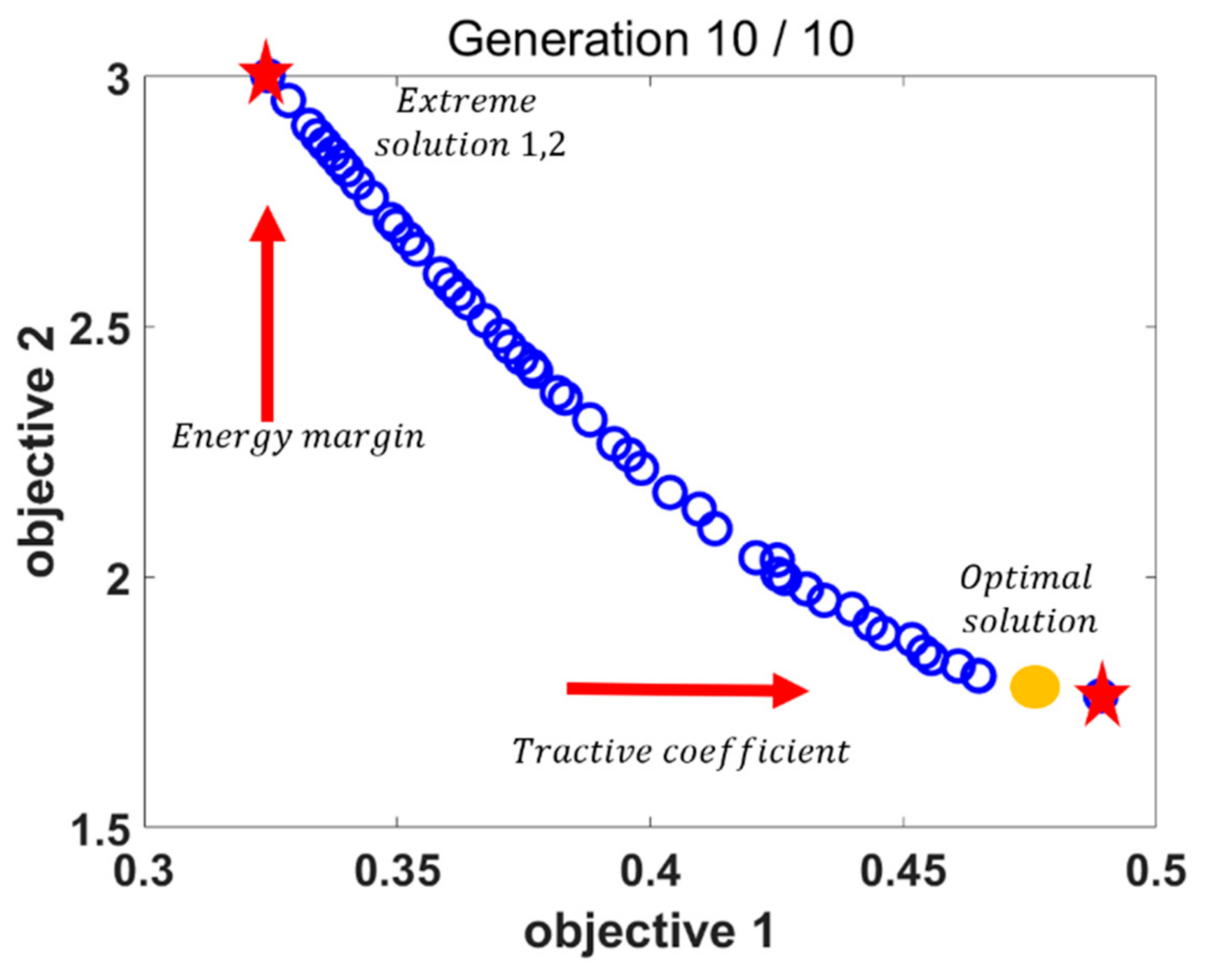
4.3.5. Results of Multi-Objective Optimization Problem with NSGA-II
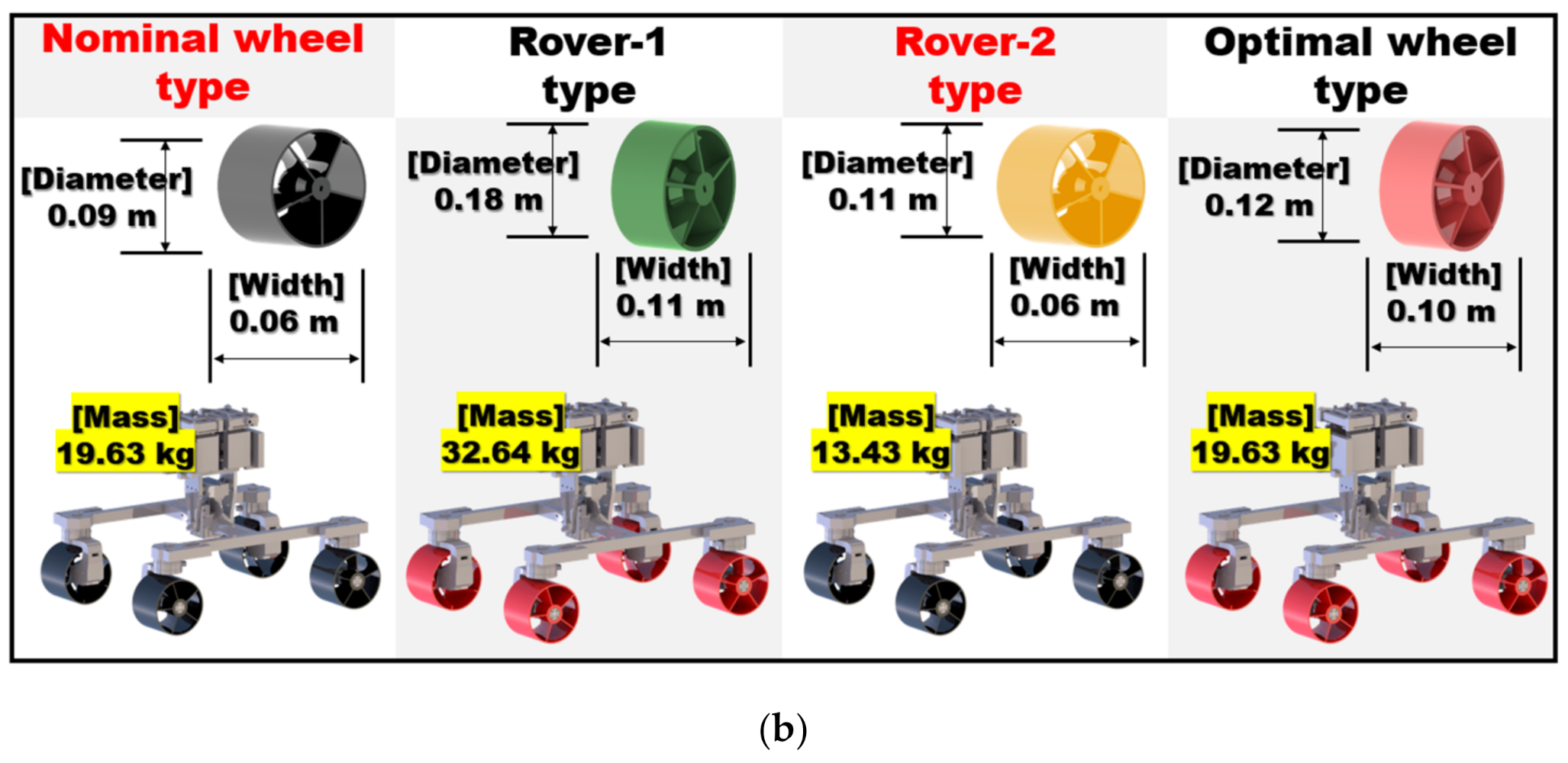
5. Performance Evaluation of Optimal Design Results
5.1. Case Study: Scenario-Based Dynamic Analysis
5.1.1. Rover Model and MBD Simulation Procedure
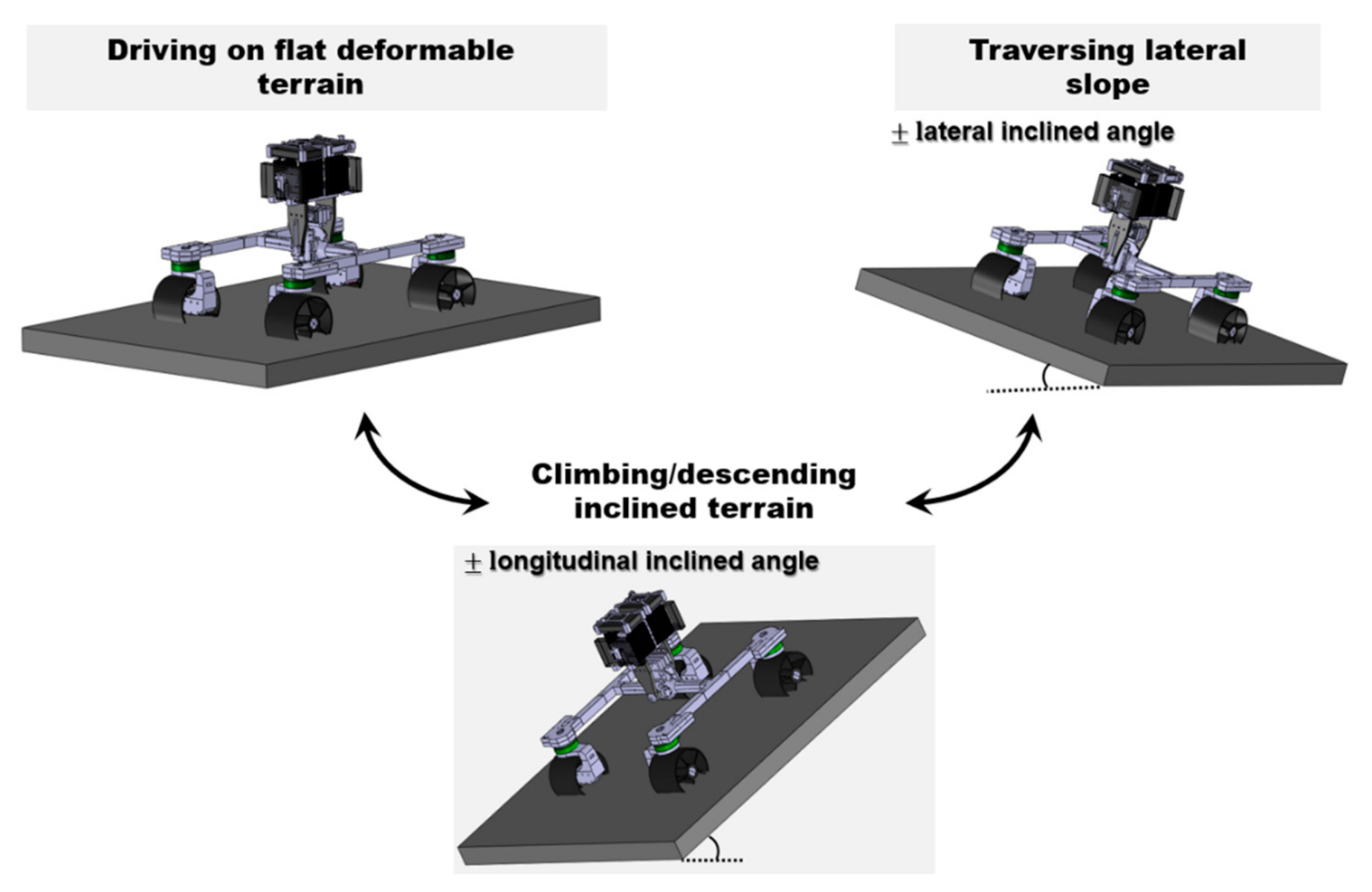
5.1.2. Case Study: Driving over Flat Deformable Terrain
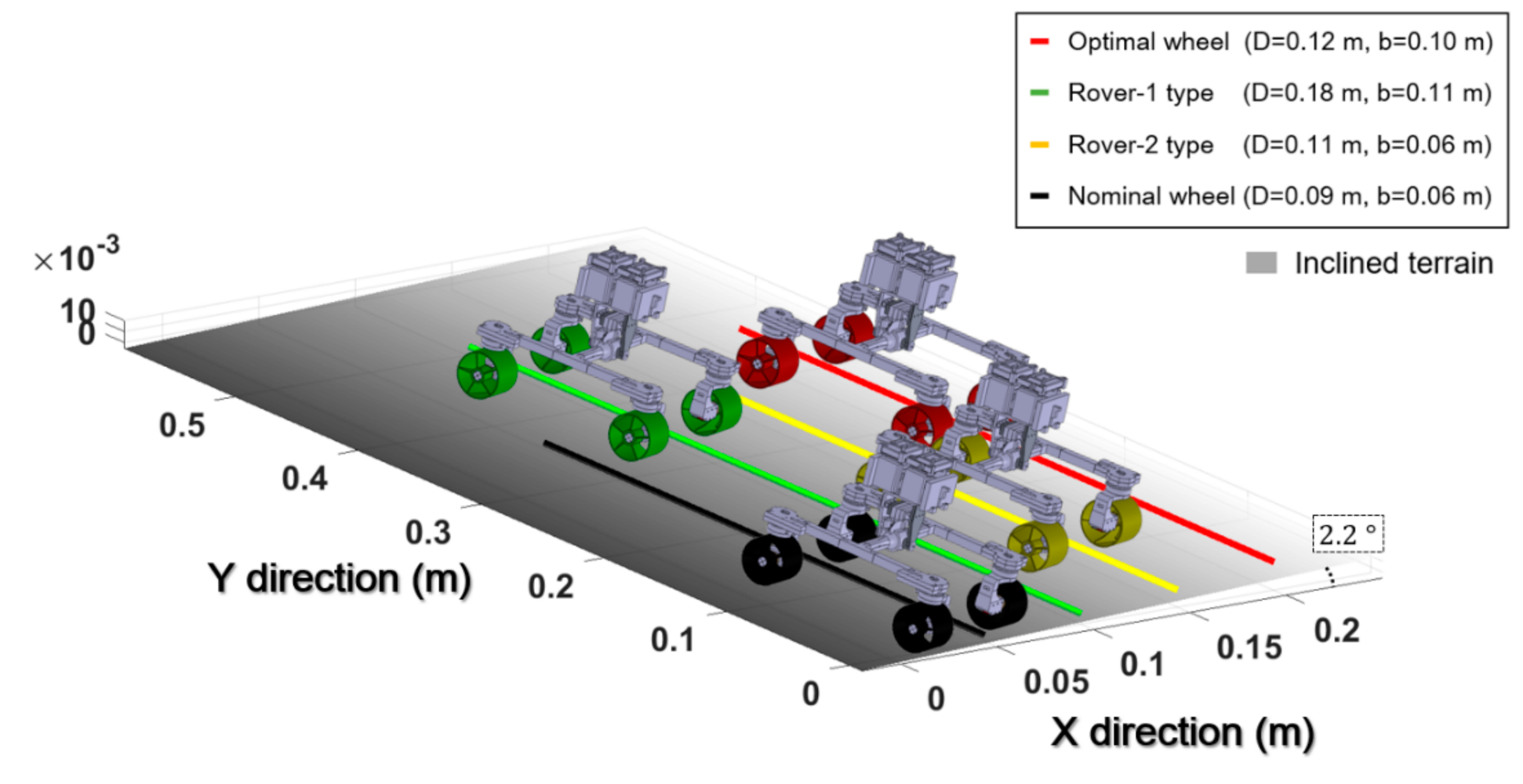
5.1.3. Case Study: Climbing Slope at 2.2° Inclined Terrain
5.1.4. Case Study: Traversing on 2.2° Side Slope
5.2. Experimental Verification
5.2.1. Single Wheel Testbed and Experimental Procedure
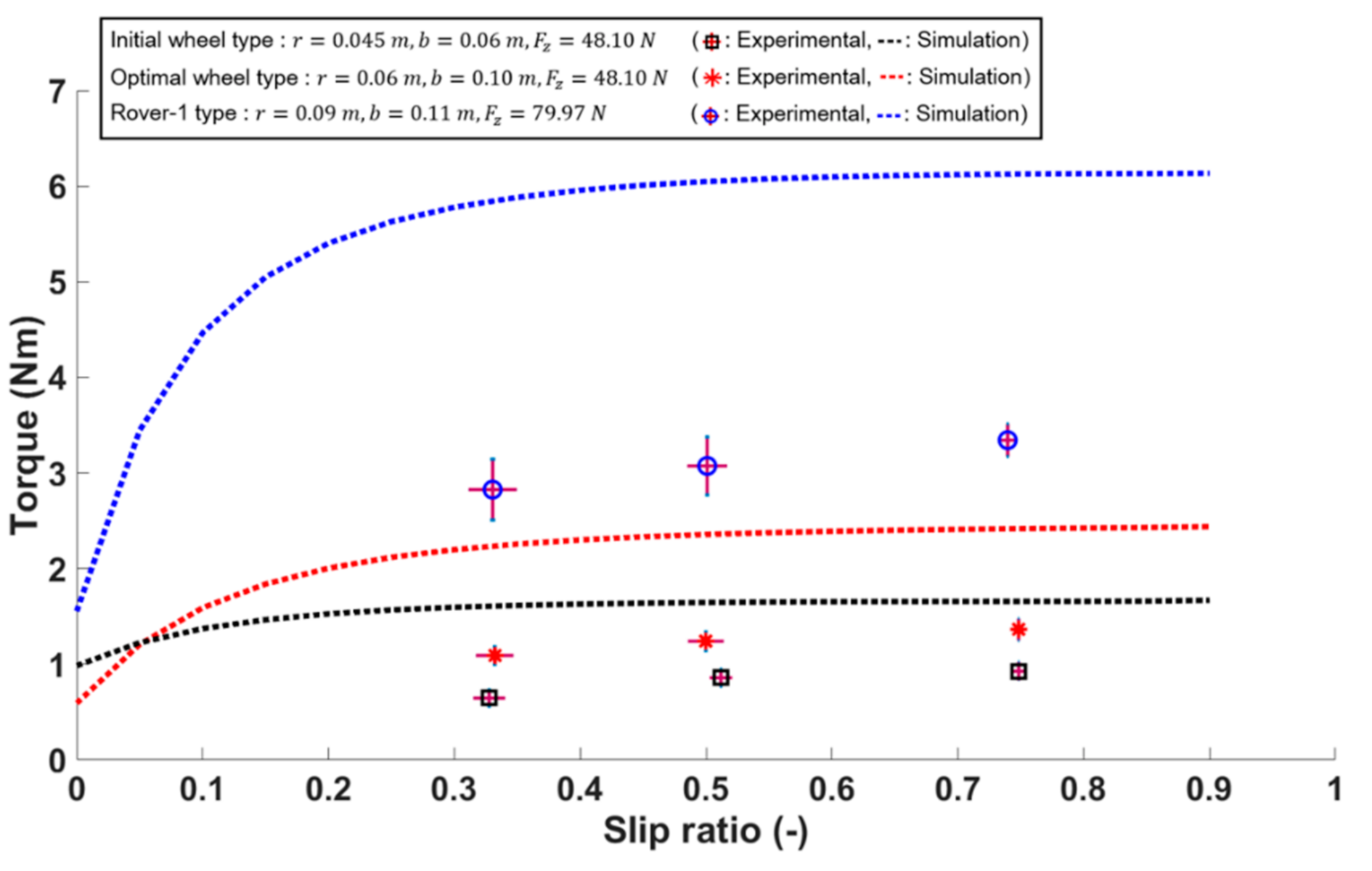
5.2.2. Results of Experimental Verification
5.2.3. Discussion
6. Conclusions
- The modeling of solar power acquisition and terrain characteristics on the Moon for predicting the operational environment of the exploration rover is described.
- An MBD simulation tool based on the rover wheel-terrain interaction model, which can deal with the longitudinal/lateral dynamic behavior of exploration rover with the path following the controller on a given digital elevation model map, is developed.
- Via sensitivity analysis with regard to the wheel geometry parameters, the dominant design parameter is selected, and a multi-objective wheel design optimization method integrating the developed simulation environments and NSGA-II is created over various dynamic states. With the use of MOOP based on the NSGA-II method, an optimal design point that considers both tractive coefficient and energy consumption is obtained.
- Numerical/experimental verification using a single wheel testbed were conducted to convincingly validate the derived optimization results and simulation environment. Compared to the comparative group, the optimized design was enhanced by −71% in terms of the sinkage (associated with the immobility), +398% in terms of tractive coefficient (associated with the tractive capability), and −57.9% in terms of the driving resistance torque (associated with power condition).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Weatherred, C.J.; Bendix Corporation; Bendix Systems Division. Lunar Surface Mobility Systems Comparison and Evolution (MOBEV). Final Presentation Report, NASA-CR-92641; University of Michigan Press: Ann Arbor, MI, USA, 1966. [Google Scholar]
- Zhang, P.; Deng, Z.; Hu, M.; Gao, H. Mobility Performance Analysis of Lunar Rover Based on Terramechanics. In Proceedings of the Advanced Intelligent Mechatronics, AIM 2008, IEEE/ASME International Conference on IEEE, Xi’an, China, 2–5 July 2008; pp. 1201–1225. [Google Scholar]
- Taghavifar, H.; Mardani, A. Evaluating the effect of tire parameters on required drawbar pull energy model using adaptive neuro-fuzzy inference system. Energy 2015, 85, 5865–5893. [Google Scholar] [CrossRef]
- Bekker, G. Theory of Land Locomotion: The Mechanics of Vehicle Mobility; University of Michigan Press: Ann Arbor, MI, USA, 1956. [Google Scholar]
- Bekker, G. Introduction to Terrain-Vehicle Systems; University of Michigan Press: Ann Arbor, MI, USA, 1969. [Google Scholar]
- Wong, J.; Reece, A.R. Prediction of rigid wheel performance based on analysis of soil-wheel stresses, Part I. Performance of driven rigid wheels. J. Terramechanics 1967, 4, 81–98. [Google Scholar] [CrossRef]
- Wong, J.; Reece, A.R. Prediction of rigid wheel performance based on analysis of soil-wheel stresses, Part II. Performance of towed rigid wheels. J. Terramechanics 1967, 4, 7–25. [Google Scholar] [CrossRef]
- Wong, J. Theory of Ground Vehicles, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Wong, J. Terramechanics and Off-Road Engineering, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Ding, L.; Yang, H.; Gao, H.; Li, N.; Deng, Z.; Gua, J.; Li, N. Terramechanics-based modeling of sinkage and moment for in-situ steering wheels of mobile robots on deformable terrain. Mech. Mach. Theory 2017, 116, 14–33. [Google Scholar] [CrossRef]
- Iagnemma, K.; Kang, S.; Brooks, C.; Dubowsky, S. Multi-Sensor Terrain Estimation for Planetary Rovers. In Proceedings of the 8th International Symposium on Artificial Intelligence, Robotics, and Automation in Space, I-SAIRAS, Nara, Japan, 19–23 May 2003. [Google Scholar]
- Ishigami, G.; Miwa, A.; Nagatani, K.; Yoshida, K. Terramechanics-based model for steering maneuver of planetary exploration rovers on loose soil. J. Field Robot. 2007, 24, 233–250. [Google Scholar] [CrossRef]
- Iagnema, K.; Kang, S.; Shibly, H.; Dubowsky, S. Online terrain parameter estimation for wheeled mobile robots with application to planetary rovers. IEEE Trans. Robot. 2004, 20, 921–927. [Google Scholar] [CrossRef]
- Ishigami, G. Terramechanics-Based Analysis and Control for Lunar/Planetary Exploration Robots. Ph.D. Thesis, Tohoku University, Sendai, Japan, 2008. [Google Scholar]
- Flippo, D. Design and Analysis of Rover Wheel Testbed. Ph.D. Thesis, University of Oklahoma, Oklahoma, OK, USA, 2009. [Google Scholar]
- Irani, R. Dynamic Terramechanic Model for Lightweight Wheeled Mobile Robots. Ph.D. Thesis, The University of Dalhousie, Halifax, NS, Canada, 2011. [Google Scholar]
- Chen, B.; Wang, R.; Jia, Y.; Guo, L.; Yang, L. Design of a high performance suspension for lunar rover based on evolution. Acta Astronaut. 2009, 64, 925–934. [Google Scholar] [CrossRef]
- Leite, A.C.; Schäfer, B. Mass, Power and Static Stability Optimization of a 4-Wheeled Planetary Exploration Rover. In Proceedings of the 2nd International Conference on Engineering Optimization, Lisbon, Portugal, 6–9 September 2010. [Google Scholar]
- Ebrahimi, S.; Mardani, A. Expanding scissor-based UGV for large obstacles climbing. Mech. Based Des. Struct. Mach. 2019, 47, 20–36. [Google Scholar] [CrossRef]
- Mardani, A.; Ebrahimi, S.; Alipour, K. 6AP wheel: A new transformable robotic wheel for traction force improvement and halting avoidance of a UGV on soft terrains. Mech. Based Des. Struct. Mach. 2020. [Google Scholar] [CrossRef]
- Sim, B.-S.; Kim, K.-J.; Yu, K.-H. Development of Body Rotational Wheeled Robot and Its Verification of Effectiveness. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May 2020. [Google Scholar]
- Alamdari, A.; Krovi, V.N. Design of articulated leg-wheel subsystem by kinetostatic optimization. Mech. Mach. Theory 2016, 100, 222–234. [Google Scholar] [CrossRef]
- Kim, D.; Hong, H.; Kim, H.S.; Kim, J. Optimal design and kinetic analysis of a stair-climbing mobile robot with rocker-bogie mechanism. Mech. Mach. Theory 2012, 50, 90–108. [Google Scholar] [CrossRef]
- Papantoniou, V.; Skevakis, S.; Katelouzos, A.; Papantoniou, A.; Kapellos, K.; Papadopoulos, E.; van Winnendael, M. Use of Flexible Variable Stiffness Wheels for High Speed Lunar and Planetary Exploration Rovers and Their Potential Impact on the Cost of Transport. In Proceedings of the I-SAIRAS, Pasadena, CA, USA, 18–21 October 2020. [Google Scholar]
- Sutoh, M.; Yusa, J.; Ito, T.; Nagatani, K.; Yoshida, K. Traveling performance evaluation of planetary rovers on loose soil. J. Field Robot. 2012, 29, 648–662. [Google Scholar] [CrossRef]
- Ding, L.; Gao, H.; Li, Y.; Liu, G.; Deng, Z. Improved explicit-form equations for estimating dynamic wheel sinkage and compaction resistance on deformable terrain. Mech. Mach. Theory 2015, 86, 235–264. [Google Scholar] [CrossRef]
- Ghotbi, B.; González, F.; Kövecses, J.; Angeles, J. Mobility evaluation of wheeled robots on soft terrain: Effect of internal force distribution. Mech. Mach. Theory 2016, 100, 259–282. [Google Scholar] [CrossRef]
- Baratta, M.; Genta, G.; Laurenzano, D.; Misul, D. Exploring the surface of the Moon and Mars: What kind of ground vehicles are required? Acta Astronaut. 2019, 154, 204–213. [Google Scholar] [CrossRef]
- Edwin, L.E.; Denhart, J.D.; Gemmer, T.R.; Ferguson, S.M.; Mazzoleni, A.P. Performance analysis and technical feasibility assessment of a transforming roving-rolling explorer rover for Mars exploration. J. Mech. Des. 2014, 136. [Google Scholar] [CrossRef]
- Delgado-Bonal, A.; Martín-Torres, F.J.; Vázquez-Martín, S.; Zorzano, M.P. Solar and wind exergy potentials for Mars. Energy 2016, 102, 550–558. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes; John Wiley & Sons: New Jersey, NJ, USA, 2013. [Google Scholar]
- Lee, J.-S.; Yu, K.-H. Optimal path planning of solar-powered UAV using gravitational potential energy. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1442–1451. [Google Scholar] [CrossRef]
- Sutoh, M.; Otsuki, M.; Wakabayashi, S.; Hoshino, T.; Hashimoto, T. The right path: Comprehensive path planning for lunar exploration rovers. IEEE Robot. Autom. Mag. 2015, 22, 22–33. [Google Scholar] [CrossRef]
- Ryu, B.-H.; Wang, C.-C.; Chang, I. Development and geotechnical engineering properties of KLS-1 lunar simulant. J. Aerosp. Eng. 2017, 31, 1–11. [Google Scholar] [CrossRef]
- Ryu, B.-H.; Baek, Y.; Kim, Y.-S.; Chang, I. Basic study for a Korean lunar simulant (KLS-1) development. J. Korean Geotech. Soc. 2015, 31, 53–63. [Google Scholar] [CrossRef][Green Version]
- Jia, Z.; Smith, W.; Peng, H. Fast analytical models of wheeled locomotion in deformable terrain for mobile robots. Robotica 2012, 31, 35–53. [Google Scholar] [CrossRef]
- Hegedus, E. A simplified method for the determination of bulldozing resistance. Land Locomot. Res. Lab. Army Tank Automot. Command Rep. 1960, 61, 1–29. [Google Scholar]
- Yoshida, K.; Wilcox, B. Space Robots and Systems. In Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1031–1063. [Google Scholar]
- Ishigami, G.; Miwa, A.; Yoshida, K. Steering Trajectory Analysis of Planetary Exploration Rovers Based on All-Wheel Dynamics Model. In Proceedings of the Eighth International Symposium on Artificial Intelligence, Robotics and Automation in Space, Munich, Germany, 5–8 September 2005; pp. 121–128. [Google Scholar]
- Inotsume, H.; Sutoh, M.; Nagaoka, K.; Nagatani, K.; Yoshida, K. Modeling, analysis, and control of an actively reconfigurable planetary rover for traversing slopes covered with loose soil. J. Field Robot. 2013, 30, 875–896. [Google Scholar] [CrossRef]
- Inotsume, H. Analysis of Angle of Attack for Efficient Slope Ascent by Rovers. Master’s Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 2015. [Google Scholar]
- Kim, K.-J.; Guerra Padilla, G.E.; Sim, B.-S.; Yu, K.-H. Path planning and following based on the Fast Marching Method (FMM)/feedback control for lunar exploration rover on Digital Elevation Model (DEM). J. Inst. Control Robot. Syst. 2019, 25, 1109–1115. [Google Scholar] [CrossRef]
- Berkelman, P.; Easudes, J.; Martin, M.C.; Rollins, E.; Silberman, J. Design of a Day/Night Lunar Rover. Technical Report, Robotics Institute Technical Report CMU-RI-TR-95-24; Carnegie Mellon University: Pittsburgh, PA, USA, 1995. [Google Scholar]
- Della Torre, A.; Finzi, A.E.; Genta, G.; Curti, F.; Schirone, L.; Capuuano, G.; Sacchetti, A.; Vukman, I.; Mailland, F.; Monchieri, E.; et al. AMALIA mission lunar rover-the conceptual design of the team ITALIA rover, candidate for the Google Lunar X Prize Challenge. Acta Astronaut. 2010, 67, 961–978. [Google Scholar] [CrossRef]
- Yoshida, K.; Britton, N.; Walker, J. Development and field testing of MoonRaker: A four-wheel rover in minimal design. In Proceedings of the 12th International Symposium on Artificial Intelligence, Robotics and Automation in Space, Montreal, QC, Canada, 17–19 June 2013. [Google Scholar]
- Pitre, R. Systematic Structural Optimization of a Next Generation Lunar Rover Chassis. Master’s Thesis, Queen’s University, Ontario, ON, Canada, 2015. [Google Scholar]
- Zhao, J.; Huang, J.; Qiao, L.; Xiao, Z.; Huang, Q.; Wang, J.; He, Q.; Xiao, L. Geologic characteristics of the Chang’E-3 exploration region. Sci. China Phys. Mech. Astron. 2014, 57, 569–576. [Google Scholar] [CrossRef]
- Pin, F.G.; Oblow, E.M.; Horwedel, J.E.; Lucius, J.L. ADGEN: An Automated Adjoint Code Generator for Large-Scale Sensitivity Analysis. No. CONF-871101-4; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1987. [Google Scholar]
- Cardile, D. System of Systems Conceptual Design Methodology for Space Exploration. Ph.D. Thesis, Politecnico di Torino, Torino, Italy, 2013. [Google Scholar]
- Carletti, N. Planetary Rover Mobility on Loose Soil: Terramechanics Theory for Side Slip Prediction and Compensation. Master’s Thesis, Politecnico di Milano, Milano, MI, Italy, 2016. [Google Scholar]
- Callina, A.; Krenn, R.; Schäfer, B. On the treatment of soft soil parameter uncertainties in planetary rover mobility simulations. J. Terramechanics 2016, 63, 33–47. [Google Scholar]
- Guo, J.; Gao, H.; Ding, L.; Guo, T.; Deng, Z. Linear normal stress under a wheel in skid for wheeled mobile robots running on sandy terrain. J. Terramechanics 2017, 70, 49–57. [Google Scholar] [CrossRef]
- Irani, R.A.; Bauer, R.J.; Warkentin, A. Modeling a Single-Wheel Testbed for Planetary Rover Applications. In Proceedings of the ASME 2010 Dynamic Systems and Control Conference DSCC 2010, Cambridge, MA, USA, 12–15 September 2010; pp. 181–188. [Google Scholar]
- Ishigami, G.; Kewlani, G.; Iagnemma, K. Statistical Mobility Prediction for Planetary Surface Exploration Rovers in Uncertain Terrain. In Proceedings of the IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 4–8 May 2010; pp. 588–593. [Google Scholar]
- Kaveh-Moghaddam, N. Experimental Investigation of Lunar Prototype Wheel Traction Performance on Deformable Terrain. Master’s Thesis, McGill University, Montreal, QC, Canada, 2010. [Google Scholar]
- Kinugasa, T.; Kuwagi, K.; Leadbeater, T.W.; Gargiuli, J.; Parker, D.J.; Seville, J.P.; Yoshida, K.; Amano, H. Three-dimensional dynamic imaging of sand particles under wheel via gamma-ray camera system. J. Terramechan. 2015, 62, 5–17. [Google Scholar] [CrossRef]
- Michaud, S.; Schneider, A.; Bertrand, R.; Lamon, P.; Siegwart, R.; Winnendael, M.V.; Schiele, A. SOLERO: Solar-Powered Exploration Rover. In Proceedings of the 7th ESA Workshop on Advanced Space Technologies for Robotics and Automation (ASTRA), Noordwijk, The Netherlands, 19–21 November 2002. [Google Scholar]
- Moreland, S.; Skonieczny, K.; Inotsume, H.; Wettergreen, D. Soil Behavior of Wheels with Grousers for Planetary Rovers. In Proceedings of the Aerospace Conference, BigSky, MT, USA, 3–10 March 2012; pp. 1–8. [Google Scholar]
- Otsuki, M.; Otsu, K.; Sugimura, S.; Oya, T.; Honda, T.; Murakami, R.; Kubota, T. Development of Planetary Exploration Rover with Advanced Mobility and Intelligence. In Proceedings of the International Symposium on Artificial Intelligence, Robotics and Automation in Space, Saint-Hubert, QC, Canada, 17–19 June 2014. [Google Scholar]
- Skonieczny, K.; Moreland, S.J.; Wettergreen, D. A Grouser Spacing Equation for Determining Appropriate Geometry of Planetary Rover Wheels. In Proceedings of the IEEE/RSJ International Conference on IEEE, Intelligent Robots and Systems (IROS), Algarve, Portugal, 7–12 October 2012; pp. 5065–5070. [Google Scholar]
- Smith, W.; Melanz, D.; Senatore, C.; Iagnemma, K.; Peng, H. Comparison of discrete element method and traditional modeling methods for steady-state wheel-terrain interaction of small vehicles. J. Terramechan. 2014, 56, 61–75. [Google Scholar] [CrossRef]
- Thüer, T. Mobility Evaluation of Wheeled All-Terrain Robots. Ph.D. Thesis, ETH Zurich, Zürich, Switzerland, 2009. [Google Scholar]
- Xiao, W.; Zhang, Y. Design of manned lunar rover wheels and improvement in soil mechanics formulas for elastic wheels in consideration of deformation. J. Terramechanics 2016, 65, 61–71. [Google Scholar] [CrossRef]
- Yoshida, K.; Mizuno, N.; Ishigami, G.; Miwa, A. Terramechanics-Based Analysis for Slope Climbing Capability of a Lunar/Planetary Rover. In Proceedings of the 24th International Symposium on Space Technology and Science, Miyazaki, Japan, 30 May–6 June 2004. [Google Scholar]
- Yoshikawa, H.; Oda, T.; Nonaka, K.; Sekiguchi, K. Modeling and Simulation of Wheel Driving Systems Based on Terramechanics for Planetary Exploration Rover Using Modelica. In Proceedings of the 12th International Modelica Conference, Prague, Czech Republic, 15–17 May 2017; pp. 901–907. [Google Scholar]
- Zhou, F.; Arvidson, R.E.; Bennett, K.; Trease, B.; Lindemann, R.; Bellutta, P.; Iagnemma, K.; Senatore, C. Simulations of mars rover traverses. J. Field Robot. 2014, 31, 141–160. [Google Scholar] [CrossRef]
- Liu, H.; Lei, Y.; Fu, Y.; Li, X. Multi-objective optimization study of regenerative braking control strategy for range-extended electric vehicle. Appl. Sci. 2020, 10, 1789. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Sutha, S.; Thyagarajan, T. Eigenstructure Assignment Based Multiobjective Dynamic State Feedback Controller Design for MIMO System Using NSGA-II. In Proceedings of the 2010 International Conference on Modelling, Identification and Control, Kayama, Japan, 17–19 July 2020; pp. 870–875. [Google Scholar]
- Kallio, S.; Siroux, M. Energy analysis and exergy optimization of photovoltaic-thermal collector. Energies 2020, 13, 5106. [Google Scholar] [CrossRef]
- Fang, L.; Qin, S.; Xu, G.; Li, T.; Zhu, K. Simultaneous optimization for hybrid electric vehicle parameters based on multi-objective genetic algorithms. Energies 2011, 4, 532–544. [Google Scholar] [CrossRef]
- Zeng, L.; Hu, J.; Pan, D.; Shao, X. Automated design optimization of a mono tiltrotor in hovering and cruising states. Energies 2020, 13, 1155. [Google Scholar] [CrossRef]
- Jayakumar, P.; Melanz, D.; MacLennan, J.; Senatore, C.; Iagnemma, K. Stochastic Modeling and Uncertainty Cascade of Soil Bearing and Shearing Characteristics for Light-Weight Vehicle Applications. In Proceedings of the 7th Americas Regional Conference of the ISTVS 2013, Tampa, FL, USA, 15 September 2013. [Google Scholar]
- Meirion-Griffith, G.; Spenko, M. A modified pressure-sinkage model for small, rigid wheels on deformable terrains. J. Terramechanics 2011, 48, 149–155. [Google Scholar] [CrossRef]
- Kim, K.-J.; Sim, B.-S.; Yu, K.-H. Stochastic Identification of Terrain Parameter for Lunar Exploration Rover Using a Bayesian Approach. In Proceedings of the 17th international conference on control, Automation and Systems, Jeju, Korea, 18–21 October 2017. [Google Scholar]
- Zhang, R.; Pang, H.; Dong, W.; Li, T.; Liu, F.; Zhang, H.; Li, J. Three-dimensional discrete element method simulation system of the interaction between irregular structure wheel and lunar soil simulant. Adv. Eng. 2020, 148, 102873. [Google Scholar] [CrossRef]











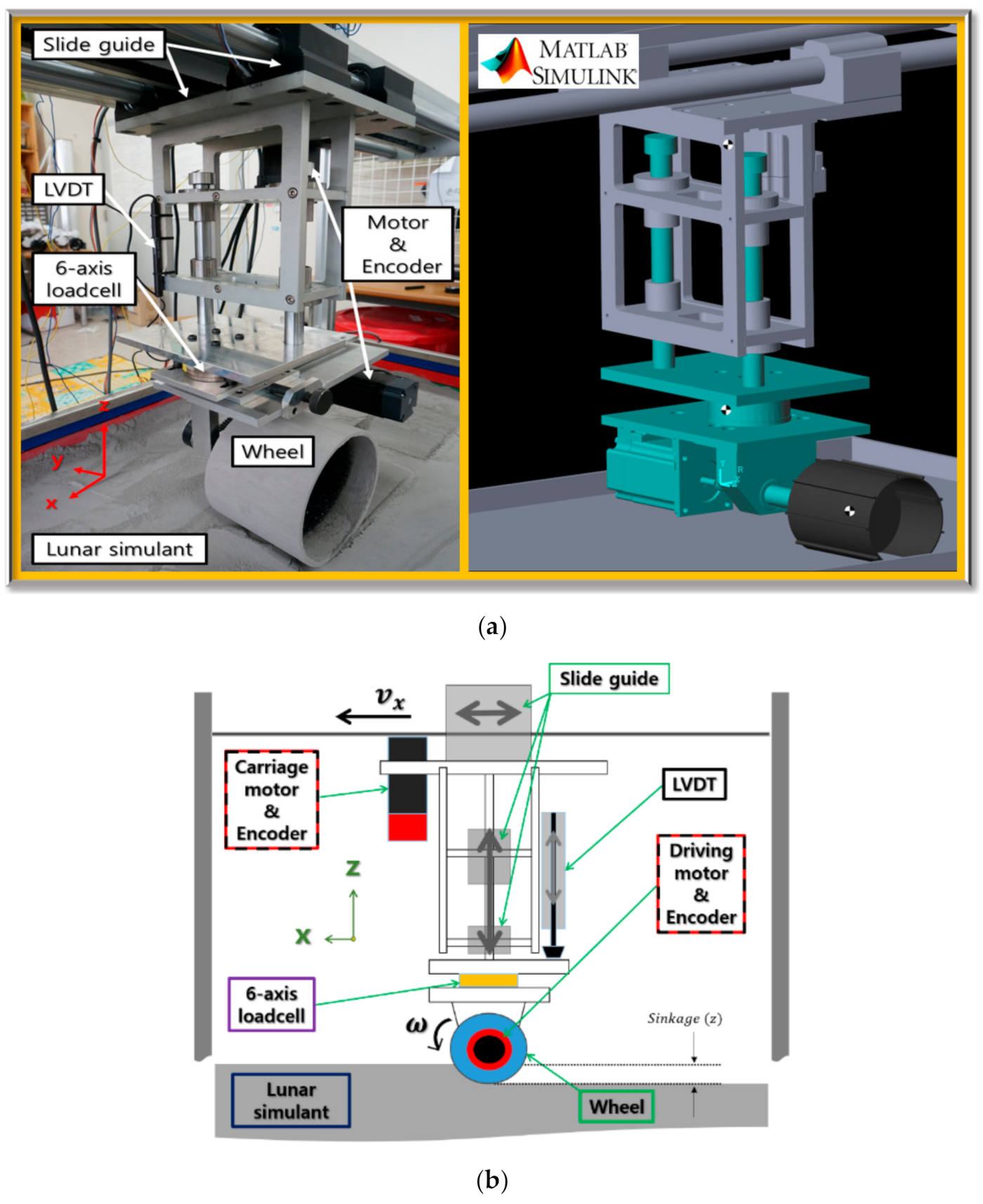



| Parameter | Description | Unit | Value |
|---|---|---|---|
| relative density | |||
| sinkage exponent | |||
| pressure-sinkage modulus | |||
| cohesion | |||
| friction angle | |||
| shear deformation modulus |
| Lunokhod | Yutu | Polaris (Google Lunar X Prize) | Moonraker (Google Lunar X Prize) | Amalia (Google Lunar X Prize) | |
|---|---|---|---|---|---|
| Mass (kg) | 840 | 140 | 149 | 8.424 | 30.9 |
| Mission location (-) | Sea of Rains (38.24 35.01 | Lacus Mortis (44.95 26.61 | Moon’s Pole | Marius Hills (13.0 306.2 | Lunar Equatorial |
| Mission timeline (day) | 116 | 90 | 14 | ||
| Thermal control (-) | Yes | Yes | Yes | ||
| Considered temperature range (℃) | −180 to +50 | to +120 | to +200 | −150 to +150 | |
| Power source (-) | Solar | Solar + Pu238 | Solar | Solar | Solar |
| Solar cell area ( | 4 | 3.6 | 0.22 | 0.36 or more | |
| Power consumption (W) | 50 | 30 | 250 | 24.2 | 73.8 |
| Number of wheels (-) | 8 | 6 | 4 | 4 | 4 |
| Suspension type (-) | Custom-machined rocker-bogie | Rocker-bogie | Passive rocker | Roll axis swing arms | Roll axis swing arms |
| Maximum speed (m/s) | 0.22 | 0.056 | 0.41 | 0.045 | 0.014 |
| Distance (km) | 39 | 0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, K.-J.; Yu, K.-H. Multidisciplinary Design Optimization for a Solar-Powered Exploration Rover Considering the Restricted Power Requirement. Energies 2020, 13, 6652. https://doi.org/10.3390/en13246652
Kim K-J, Yu K-H. Multidisciplinary Design Optimization for a Solar-Powered Exploration Rover Considering the Restricted Power Requirement. Energies. 2020; 13(24):6652. https://doi.org/10.3390/en13246652
Chicago/Turabian StyleKim, Kun-Jung, and Kee-Ho Yu. 2020. "Multidisciplinary Design Optimization for a Solar-Powered Exploration Rover Considering the Restricted Power Requirement" Energies 13, no. 24: 6652. https://doi.org/10.3390/en13246652
APA StyleKim, K.-J., & Yu, K.-H. (2020). Multidisciplinary Design Optimization for a Solar-Powered Exploration Rover Considering the Restricted Power Requirement. Energies, 13(24), 6652. https://doi.org/10.3390/en13246652





