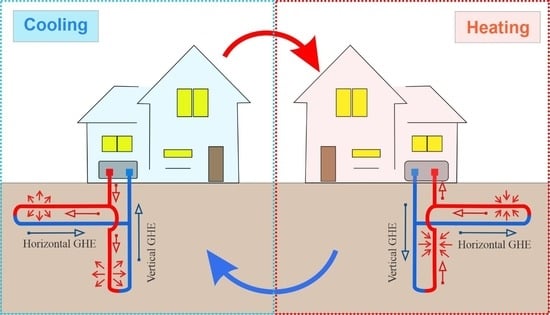
Mathematical Modelling and Operational Analysis of Combined Vertical–Horizontal Heat Exchanger for Shallow Geothermal Energy Application in Cooling Mode
Abstract
1. Introduction
2. Development of a Combined Horizontal–Vertical Geothermal Heat Exchanger Model
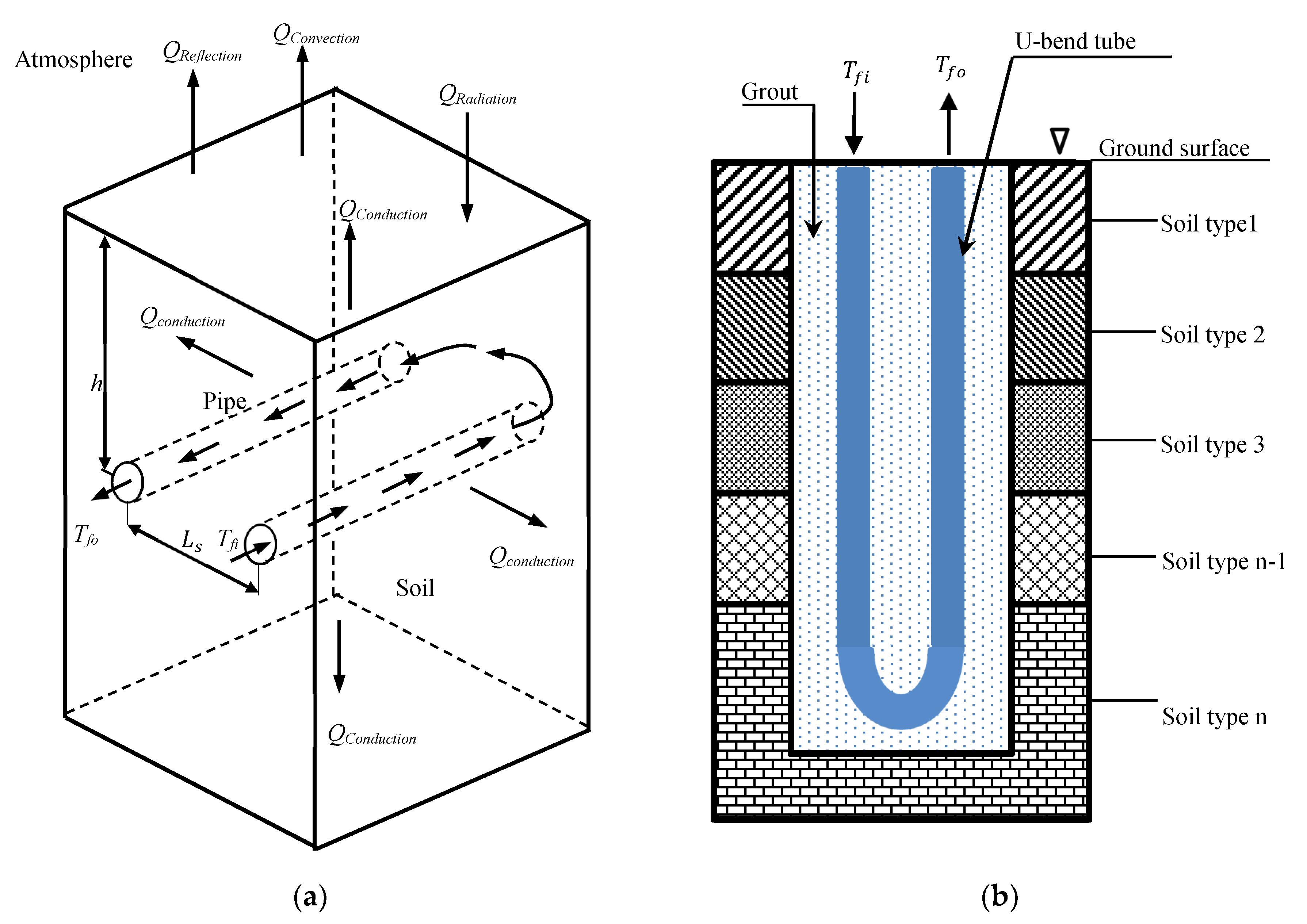
2.1. Physical Model
2.2. Mathematical Model
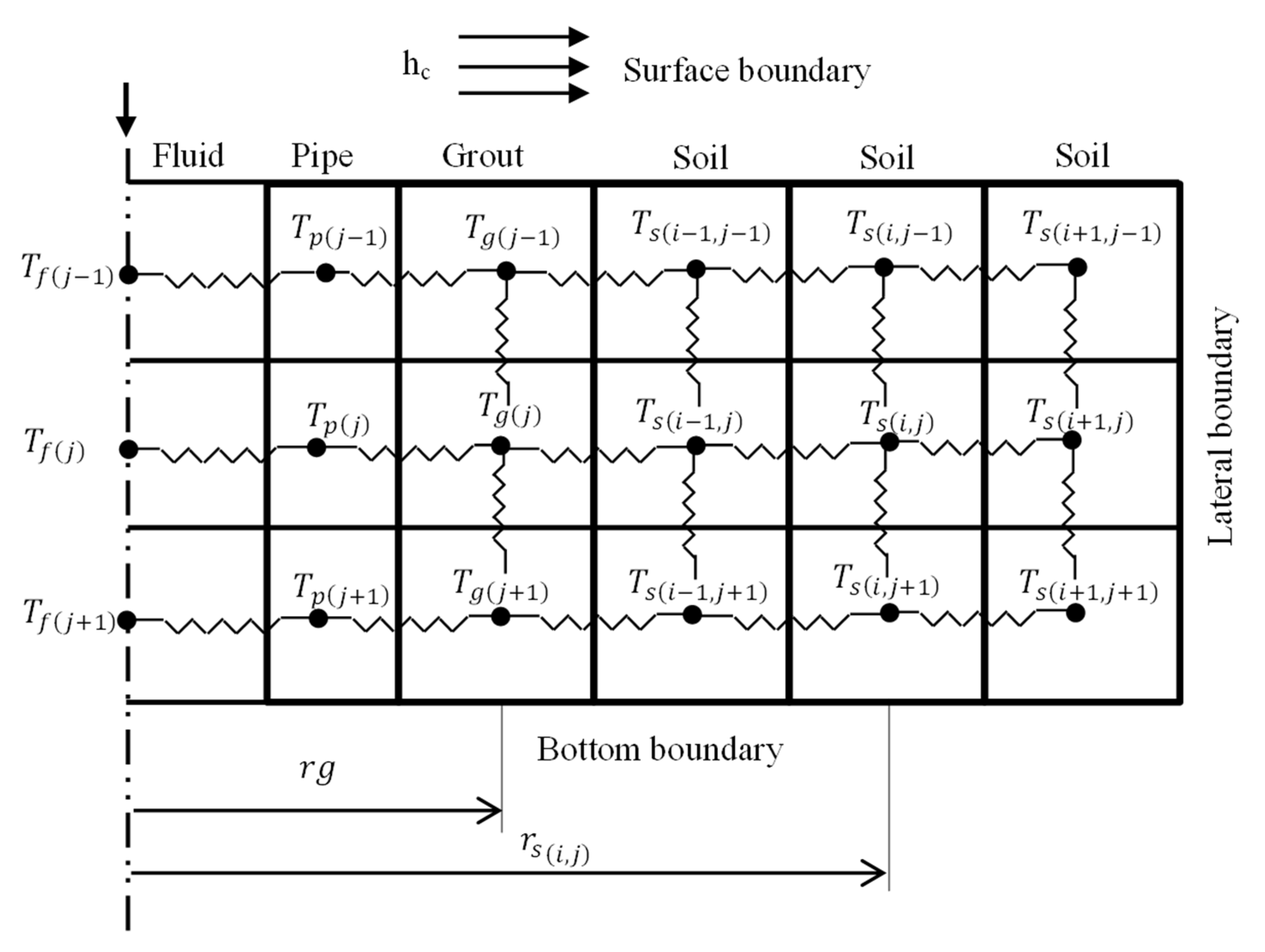
2.2.1. Governing Equation of the Soil
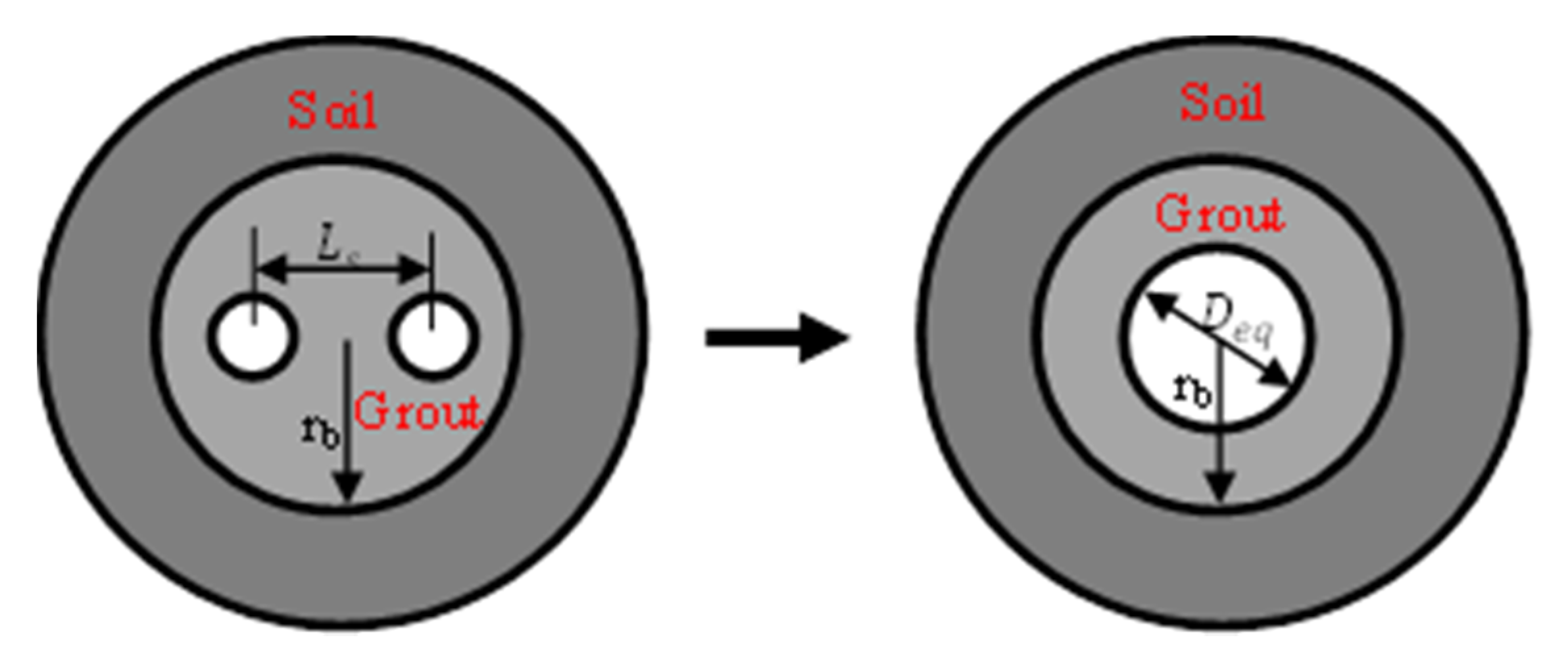
2.2.2. Governing Equation of the Temperature Exchange in the Grout for the Vertical GHE
2.2.3. Governing Equation of the Pipe
2.2.4. Governing Equation of the Fluid
2.2.5. The Initial and Boundary Conditions
- The initial conditions are:
- The boundary conditions of the computational domain of the horizontal GHE are:
- The boundary conditions of the computational domain of the vertical GHE are:
3. A Hypothetical Case Study
4. Results and Discussion
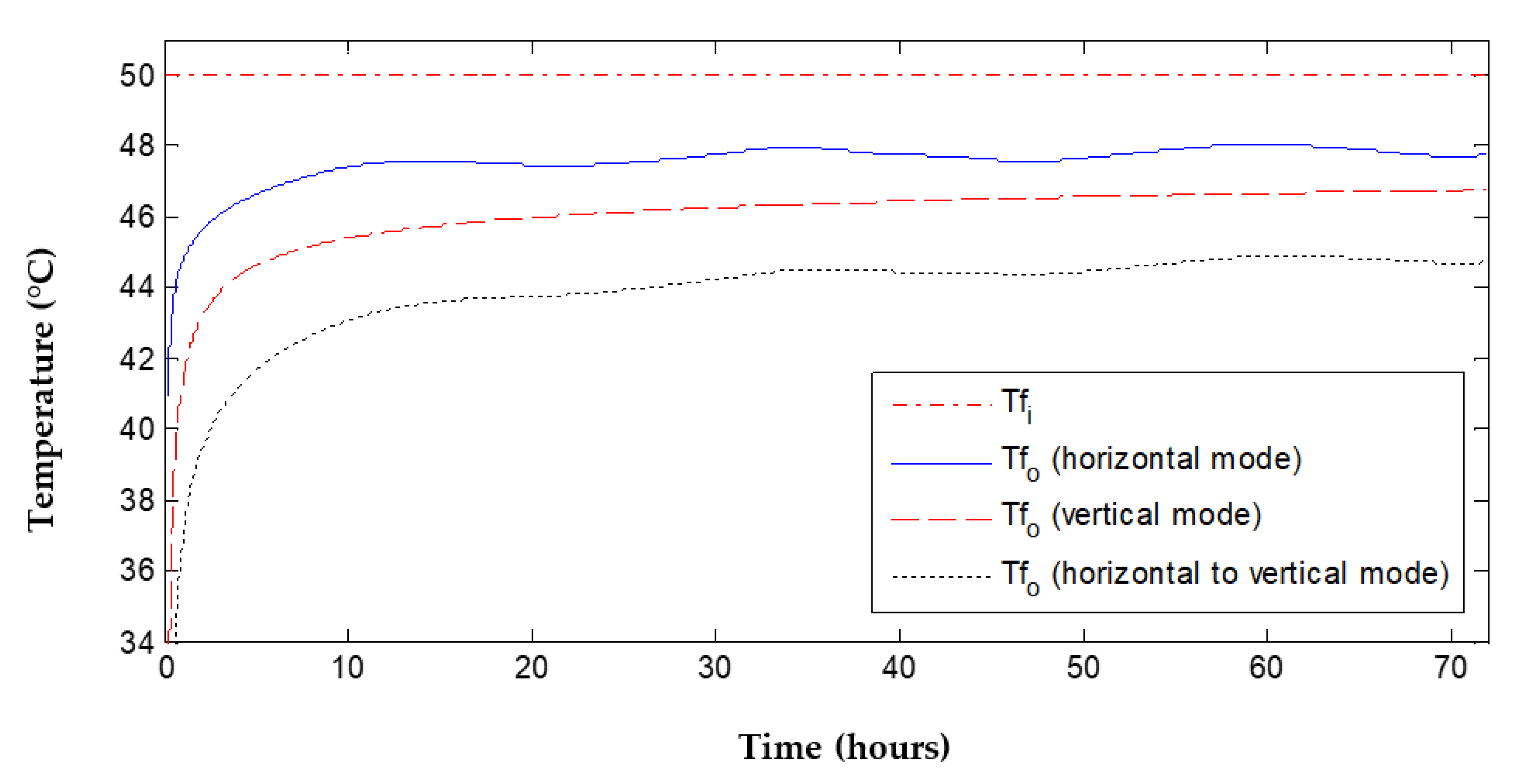
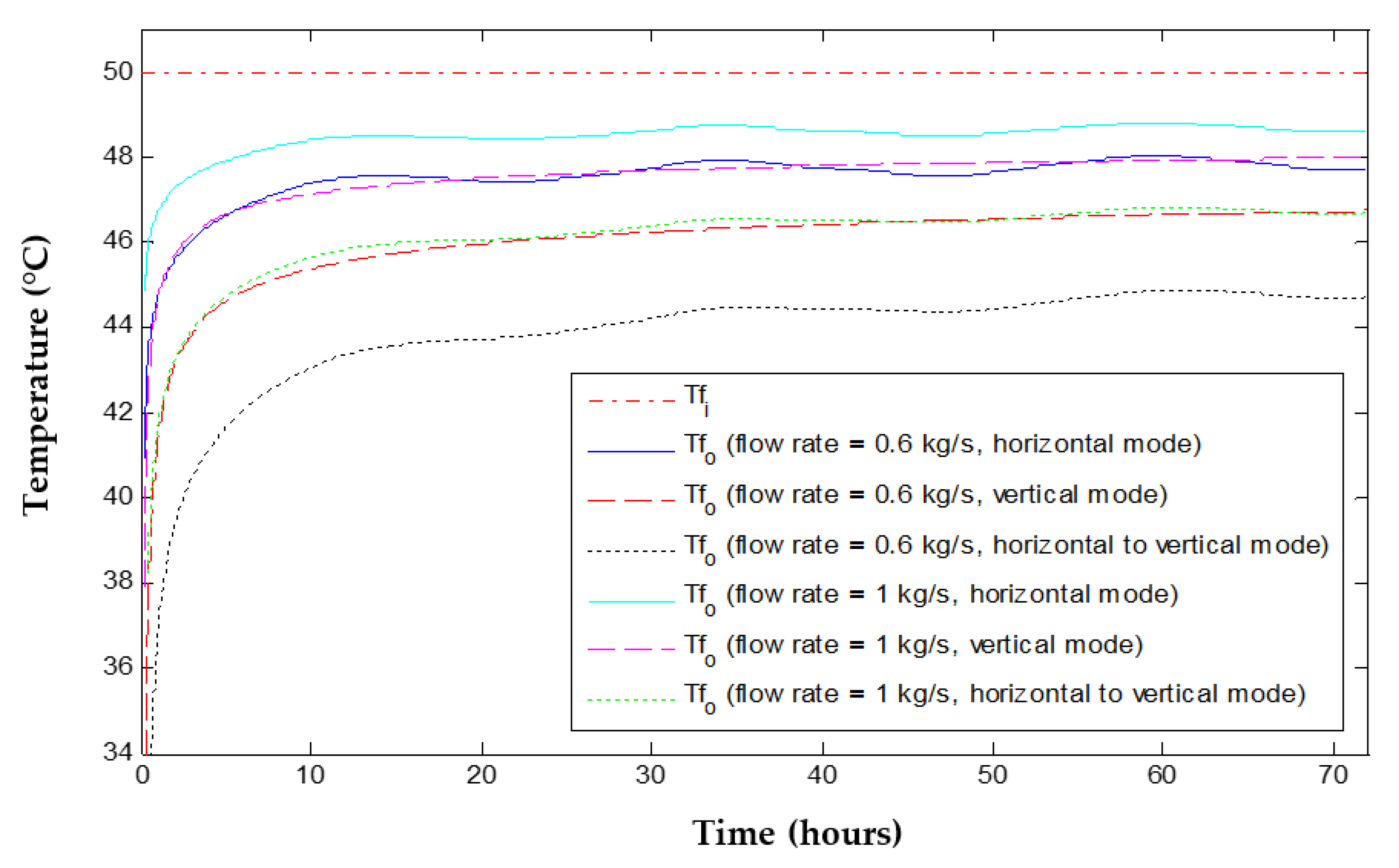
4.1. Continuous Operation
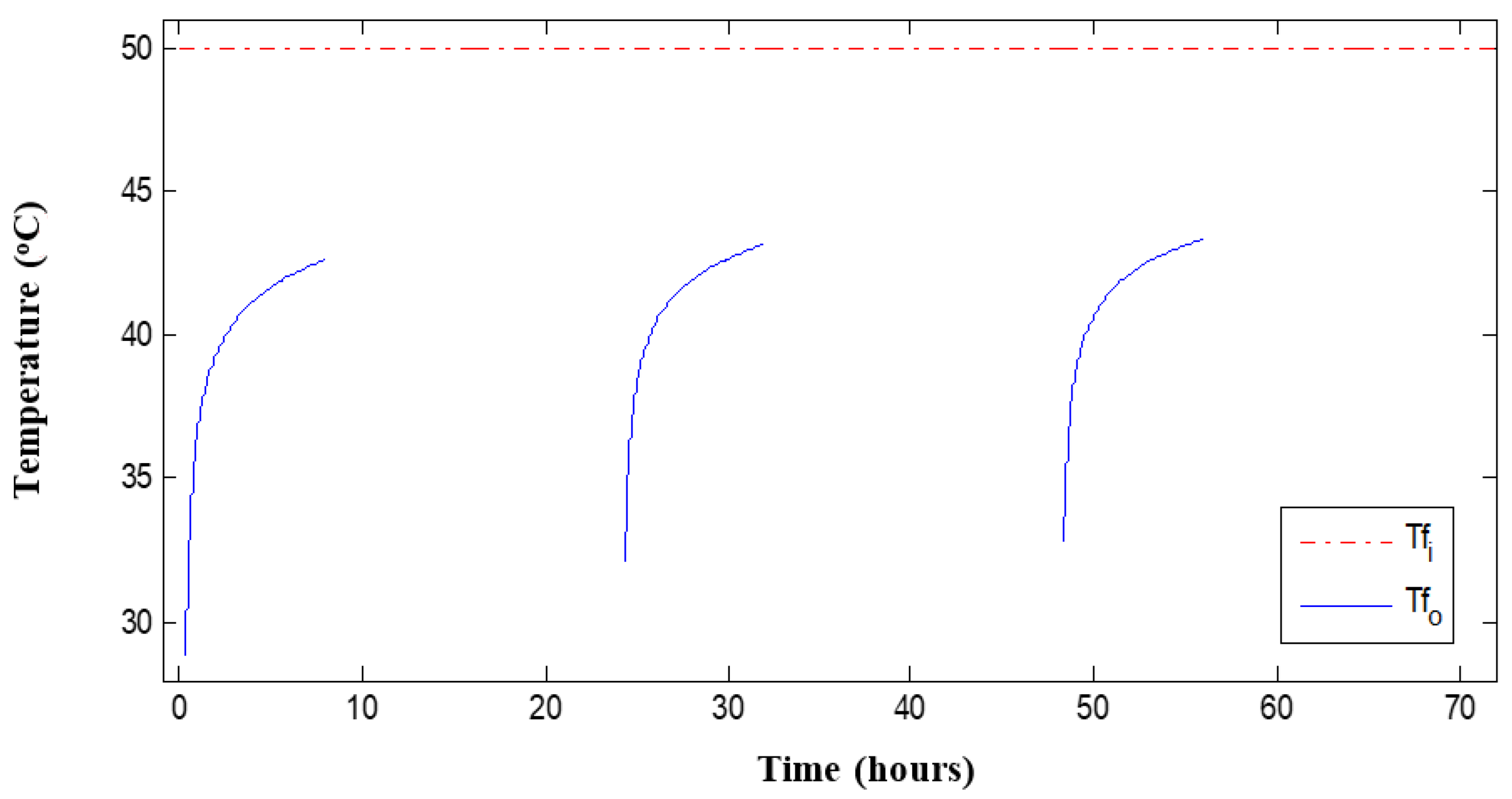
4.2. Intermittent Operation
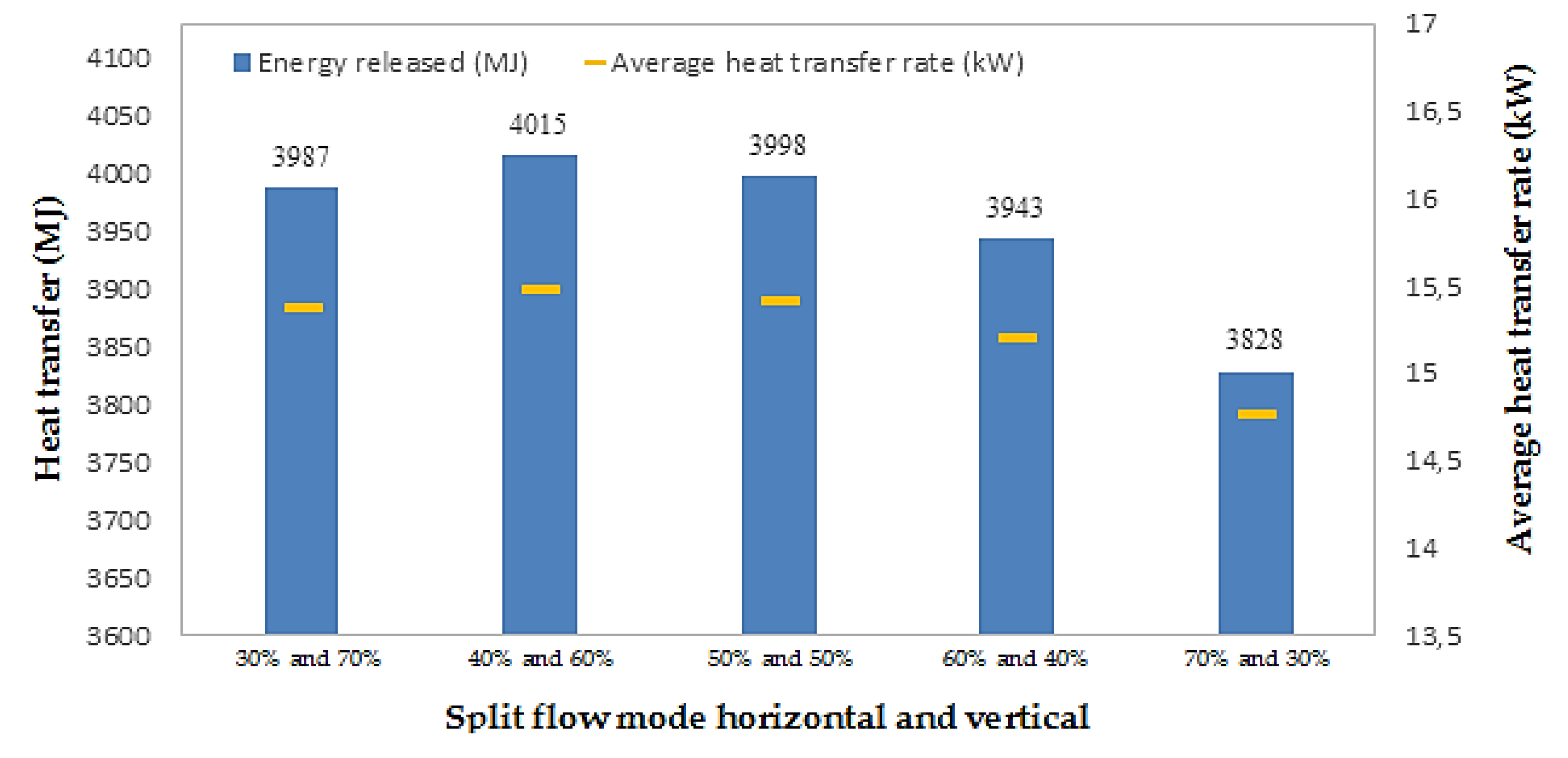
4.3. Split Flow Operation
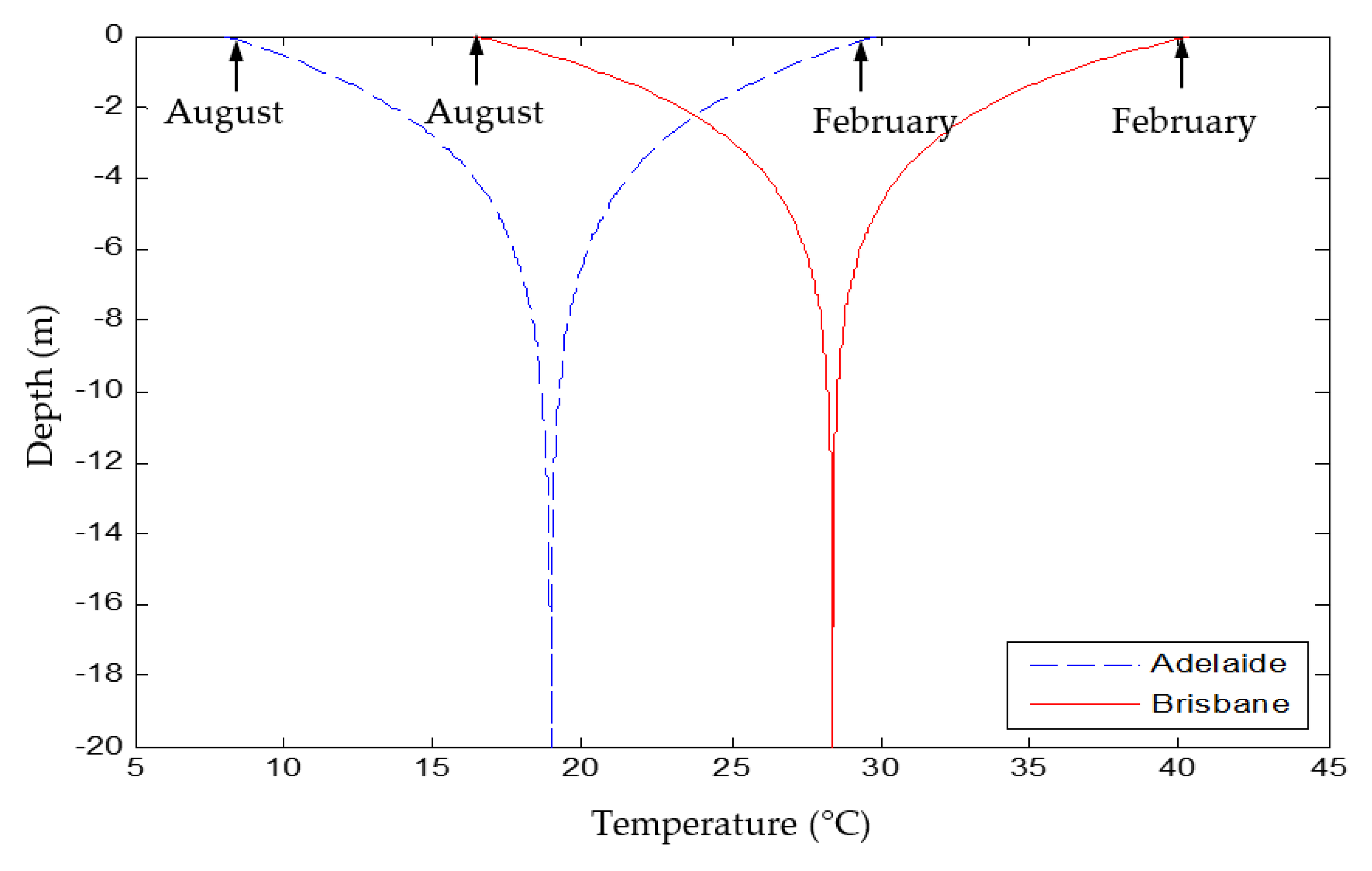
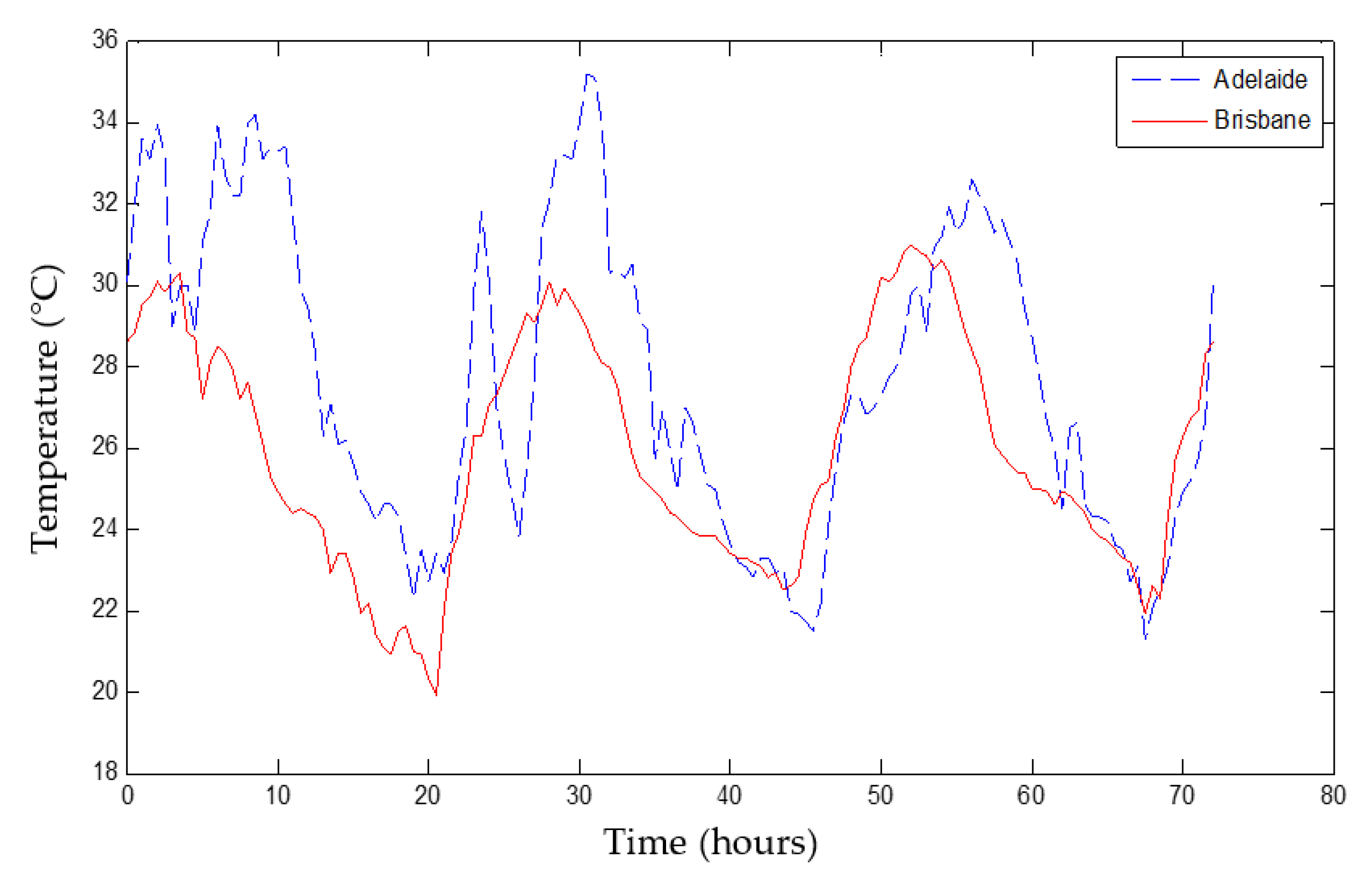
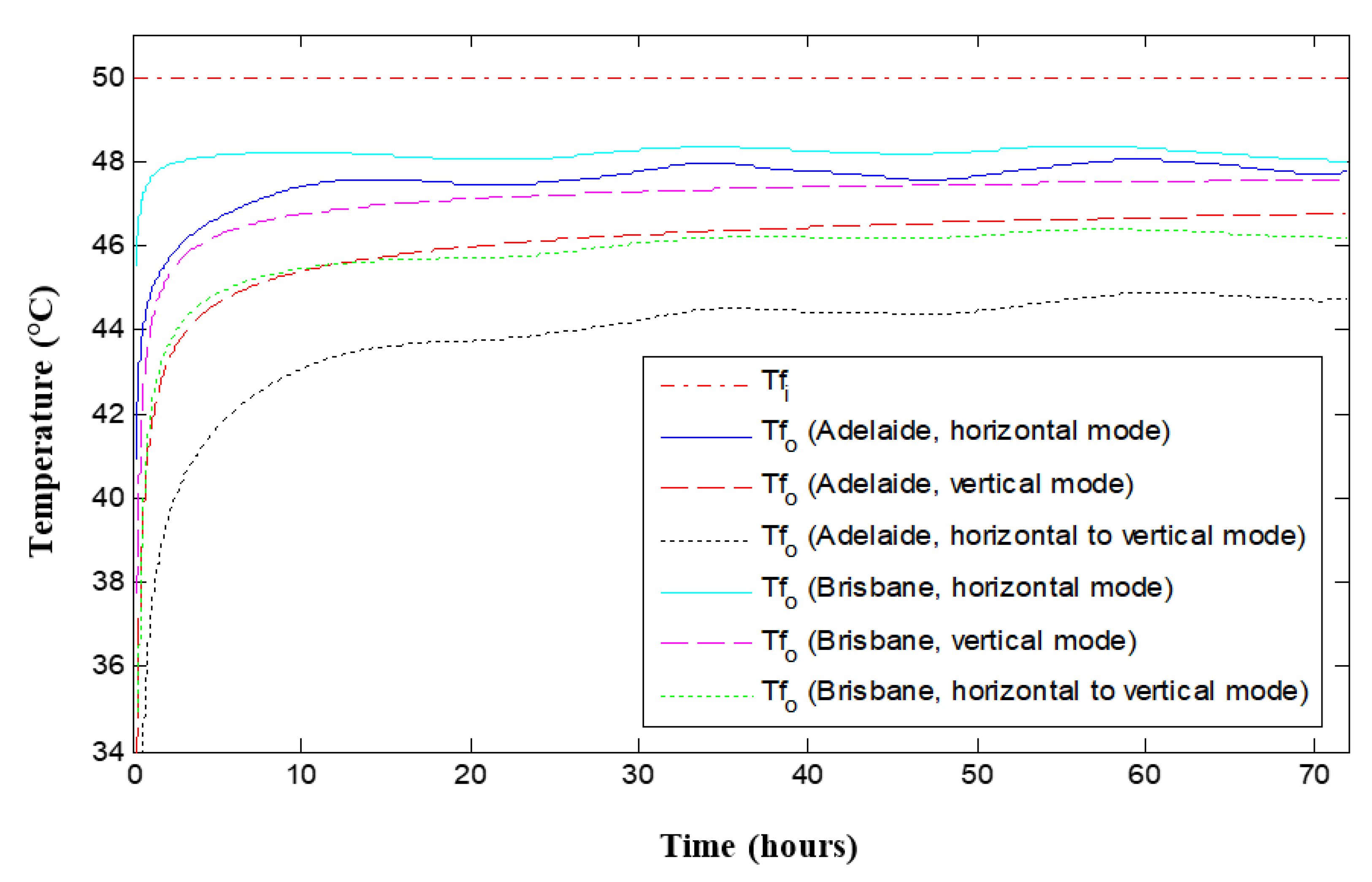
4.4. Climate Condition
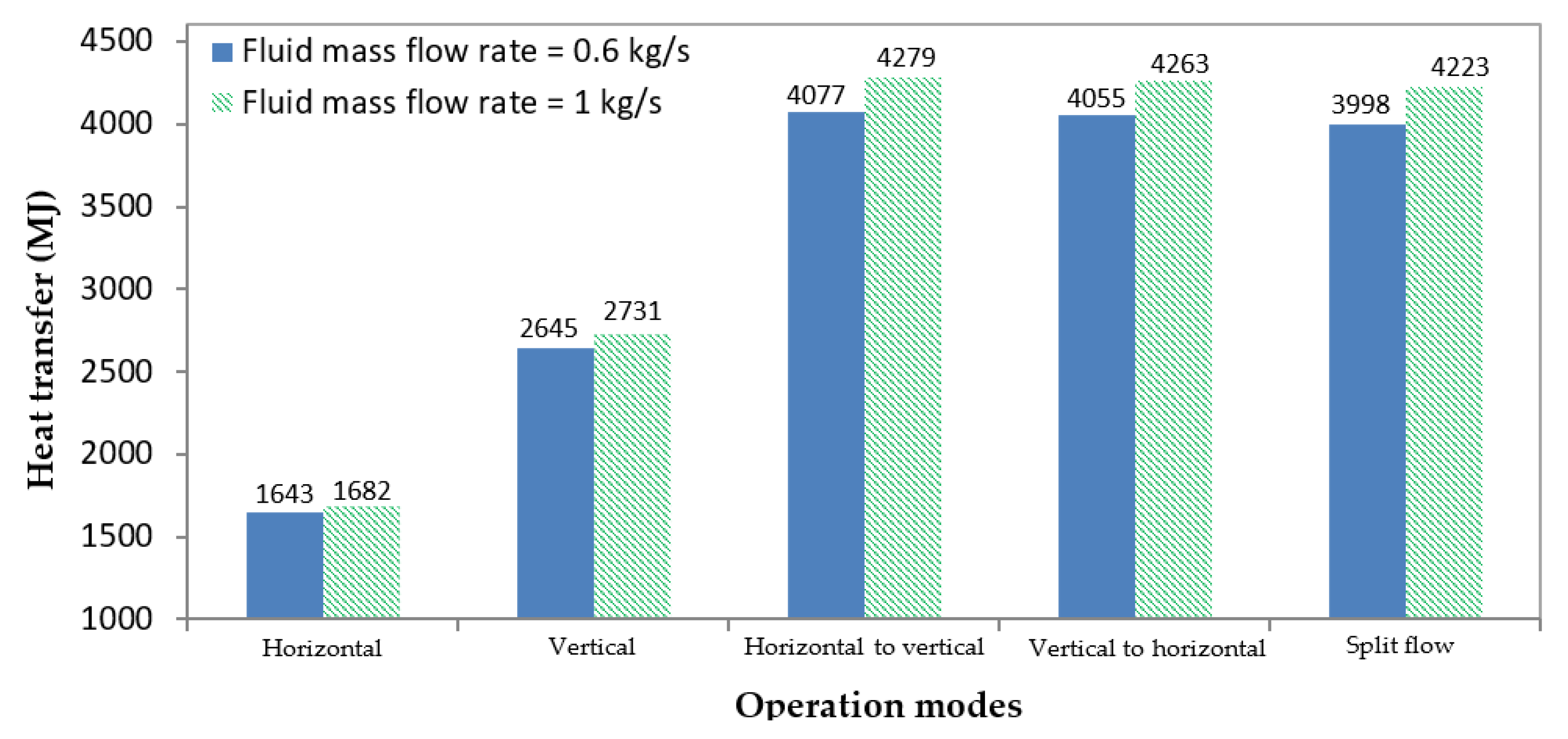
4.5. Variations of the Fluid Mass Flow Rate
5. Conclusions
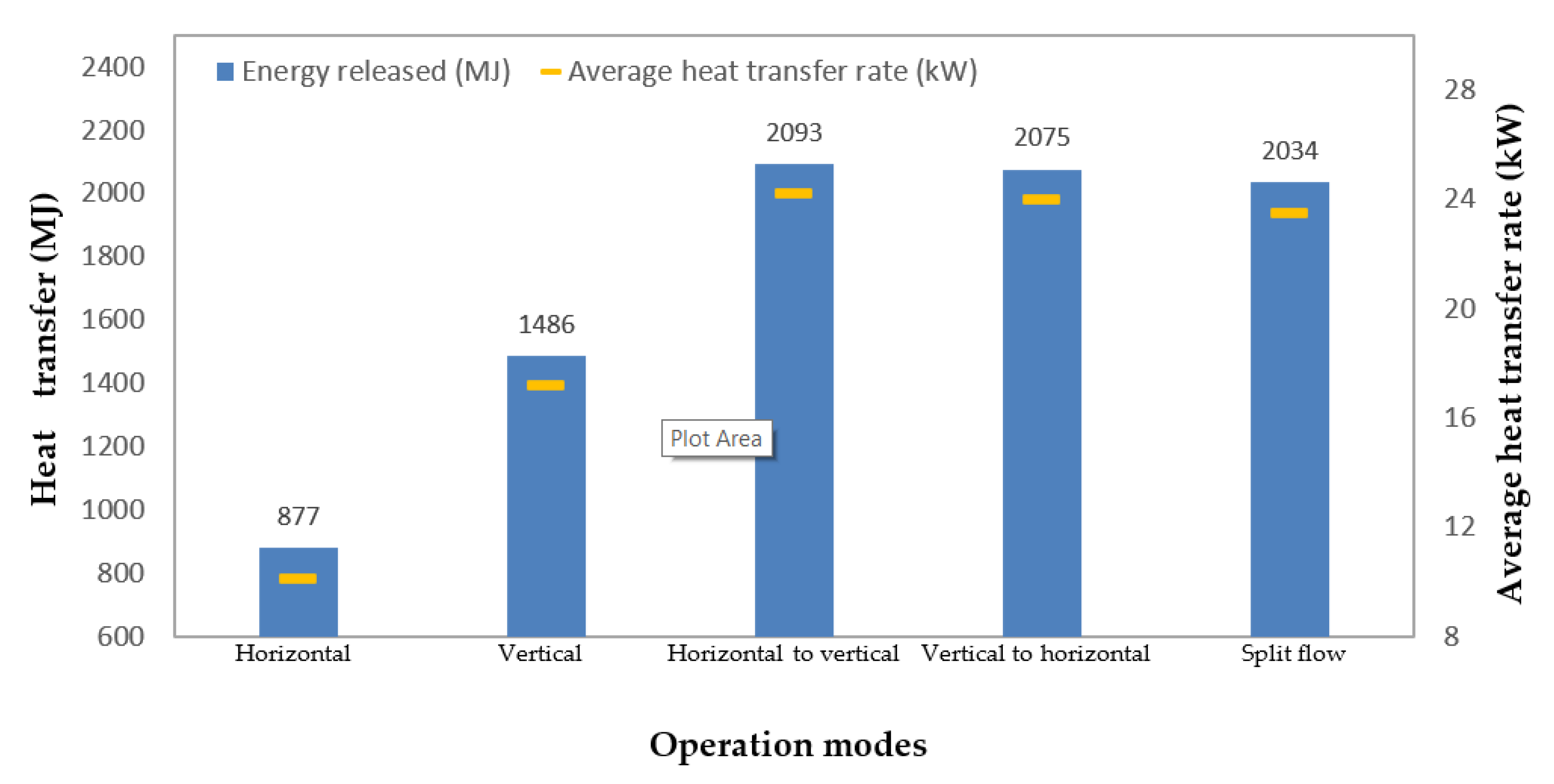
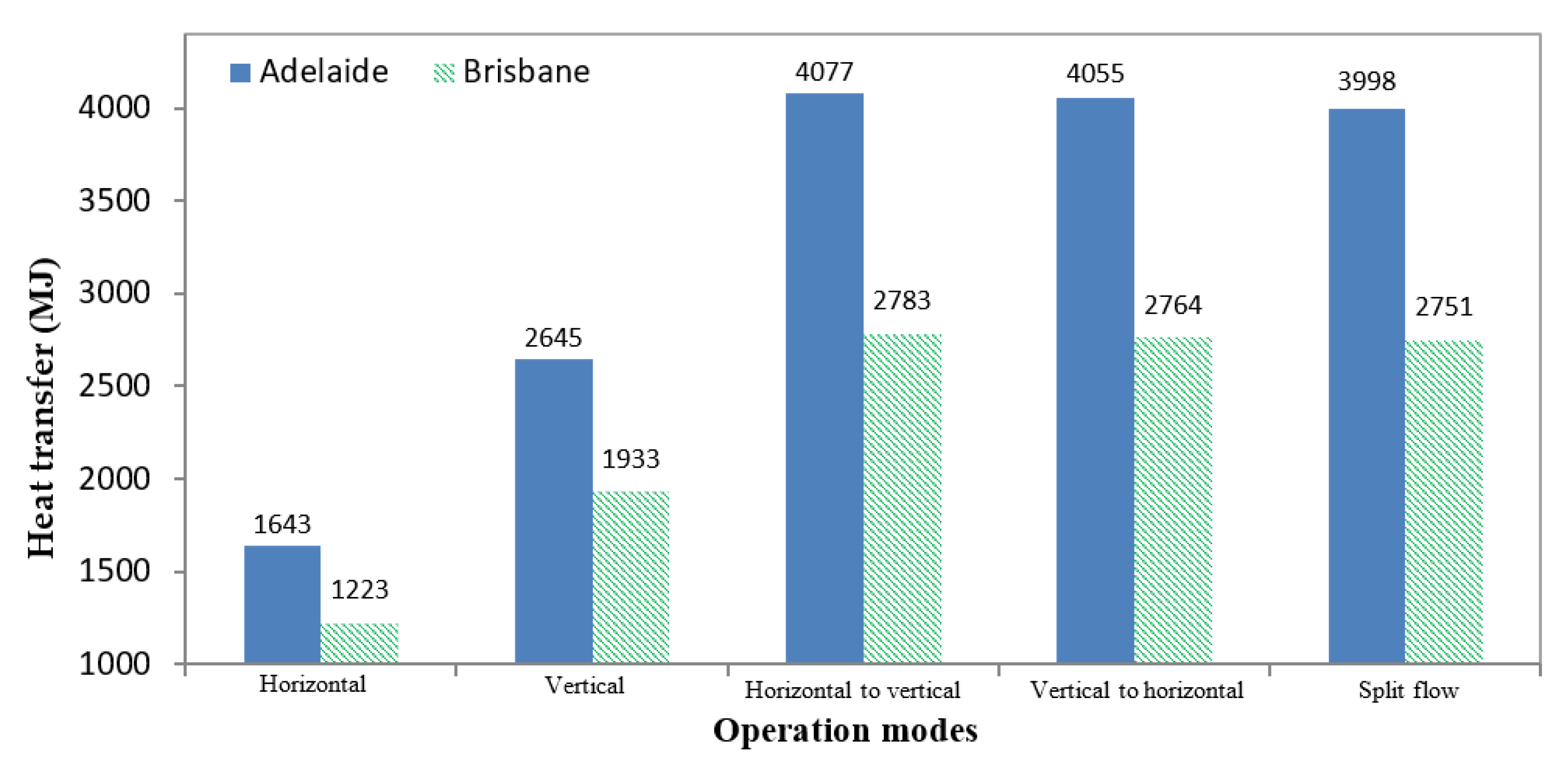
- With the same length of the pipe system, the vertical GHE could release more energy than the horizontal GHE, as the initial soil temperature (in summer) at a deeper layer was lower than that at a shallow region;
- When the GHE operated in combined modes, the amount of energy released by the GHE was increased, as the contact area, where heat was exchanged with the surrounding soil, was increased;
- The series operations (horizontal to vertical or vertical to horizontal) of the GHE could release more energy than could be done in the split mode. The difference in the fluid velocity in the split flow and series modes contributed to the amount of energy released by the GHE;
- The intermittent operation of the GHE might be conducted to cope with cyclic thermal loading. The intermittent operation could benefit the performance of the GHE as the degradation of the ground temperature during the operation of the GHE was largely recovered during the system shut down.
- In the split flow mode, the ratio of the fluid mass flow rate did not significantly affect the amount of energy released by the GHE. The GHE with a ratio of mass flow rate of 40% horizontal and 60% vertical releases the highest amount of energy in the split flow operational mode.
- Climate conditions had a significant effect on the GHE’s performance. The GHE installed in a temperate climate, corresponding to Adelaide’s conditions, could release more energy than the same installation located in a subtropical climate, such as Brisbane. This was due to the difference in the initial soil temperature.
- Increasing the fluid mass flow rate could enhance the amount of energy released by the GHE as the fluid mass flow rate affected the coefficient of the convective heat transfer of the working fluid.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| area of the pipe (m2) | grout temperature (K) | ||
| amplitude of the annual air temperature (K) | average annual air temperature (°C) | ||
| fluid specific heat (J/kg K) | pipe temperature (K) | ||
| soil specific heat (J/kg K) | ground temperature at a given depth x on calendar day t (°C) | ||
| pipe specific heat (J/kg K) | inlet fluid temperature (K) | ||
| internal pipe diameter (m) | outlet fluid temperature | ||
| equivalent diameter of the pipe (m) | final temperature of the mixed fluids (K) | ||
| convective heat transfer coefficient of fluid (W/(m2 K)) | soil temperature (K) | ||
| soil heat source (W/m3) | outlet temperature of the horizontal GHE (K) | ||
| soil thermal conductivity (W/(m K)) | outlet temperature of the vertical GHE (K) | ||
| grout thermal conductivity (W/(m K)) | velocity of the working fluid (m/s) | ||
| vegetation coefficient ( = 1 for bare ground, = 0.22 for year round full vegetation cover) | volume of the pipe’s wall (m3) | ||
| centre to centre distance between two legs of the U pipe | soil depth (cm) | ||
| fluid mass flow rate (kg/s) | axial distance of grout domain (m) | ||
| fluid mass flow rate (kg/s) | soil diffusivity (m2/s) | ||
| fluid mass flow rate in the horizontal GHE (kg/s) | grout diffusivity (m2/s) | ||
| fluid mass flow rate in the vertical GHE (kg/s) | fluid density (kg/m3) | ||
| Q | energy released by the GHE (J) | pipe density (kg/m3) | |
| Convective heat transfer on the ground surface (W) | soil density (kg/m3) | ||
| Convective heat transfer on the inner pipe surface (W) | time period (s) | ||
| radius of soil domain (m) | local site variable for the ground temperature (K) | ||
| radius of the borehole | fluid density (kg/m3) | ||
| time period (s) | soil temperature difference in summer and winter (K) | ||
| phase of air temperature wave (day) | radial increment (m) | ||
| calendar day, where 1 January = 1 and so forth | distance in the direction parallel to the pipe (m) | ||
| fluid temperature (K) | Courant number |
References
- Sliwa, T.; Gonet, A. Theoretical Model of Borehole Heat Exchanger. J. Energy Resour. Technol. 2004, 127, 142–148. [Google Scholar] [CrossRef]
- Florides, G.; Christodoulides, P.; Pouloupatis, P. Single and double U-tube ground heat exchangers in multiple-layer substrates. Appl. Energy 2013, 102, 364–373. [Google Scholar] [CrossRef]
- Zhai, X.; Qu, M.; Yu, X.; Yang, Y.; Wang, R. A review for the applications and integrated approaches of ground-coupled heat pump systems. Renew. Sustain. Energy Rev. 2011, 15, 3133–3140. [Google Scholar] [CrossRef]
- Dai, L.; Li, S.; Duanmu, L.; Li, X.; Shang, Y.; Dong, M. Experimental performance analysis of a solar assisted ground source heat pump system under different heating operation modes. Appl. Therm. Eng. 2015, 75, 325–333. [Google Scholar] [CrossRef]
- Kjellsson, E.; Hellström, G.; Perers, B. Optimization of systems with the combination of ground-source heat pump and solar collectors in dwellings. Energy 2010, 35, 2667–2673. [Google Scholar] [CrossRef]
- Ozgener, O.; Hepbasli, A. Experimental performance analysis of a solar assisted ground-source heat pump greenhouse heating system. Energy Build. 2005, 37, 101–110. [Google Scholar] [CrossRef]
- Yang, W.; Sun, L.; Chen, Y. Experimental investigations of the performance of a solar-ground source heat pump system operated in heating modes. Energy Build. 2015, 89, 97–111. [Google Scholar] [CrossRef]
- Zajacs, A.; Lalovs, A.; Borodinecs, A.; Bogdanovics, R. Small ammonia heat pumps for space and hot tap water heating. Energy Procedia 2017, 122, 74–79. [Google Scholar] [CrossRef]
- Park, H.; Lee, J.S.; Kim, W.; Kim, Y. Performance optimization of a hybrid ground source heat pump with the parallel configuration of a ground heat exchanger and a supplemental heat rejecter in the cooling mode. Int. J. Refrig. 2012, 35, 1537–1546. [Google Scholar] [CrossRef]
- Man, Y.; Yang, H.; Wang, J. Study on hybrid ground-coupled heat pump system for air-conditioning in hot-weather areas like Hong Kong. Appl. Energy 2010, 87, 2826–2833. [Google Scholar] [CrossRef]
- Wang, S.; Liu, X.; Gates, S. Comparative study of control strategies for hybrid GSHP system in the cooling dominated climate. Energy Build. 2015, 89, 222–230. [Google Scholar] [CrossRef]
- Sagia, Z.; Rakopoulos, C.D.; Kakaras, E. Cooling dominated Hybrid Ground Source Heat Pump System application. Appl. Energy 2012, 94, 41–47. [Google Scholar] [CrossRef]
- Fan, R.; Gao, Y.; Hua, L.; Deng, X.; Shi, J. Thermal performance and operation strategy optimization for a practical hybrid ground-source heat-pump system. Energy Build. 2014, 78, 238–247. [Google Scholar] [CrossRef]
- Canelli, M.; Entchev, E.; Sasso, M.; Yang, L.; Ghorab, M. Dynamic simulations of hybrid energy systems in load sharing application. Appl. Therm. Eng. 2015, 78, 315–325. [Google Scholar] [CrossRef]
- Zhu, N.; Hu, P.; Lei, Y.; Jiang, Z.; Lei, F. Numerical study on ground source heat pump integrated with phase change material cooling storage system in office building. Appl. Therm. Eng. 2015, 87, 615–623. [Google Scholar] [CrossRef]
- Wu, W.; Li, X.; You, T.; Wang, B.; Shi, W. Combining ground source absorption heat pump with ground source electrical heat pump for thermal balance, higher efficiency and better economy in cold regions. Renew. Energy 2015, 84, 74–88. [Google Scholar] [CrossRef]
- You, T.; Shi, W.; Wang, B.; Wu, W.; Li, X. A new ground-coupled heat pump system integrated with a multi-mode air-source heat compensator to eliminate thermal imbalance in cold regions. Energy Build. 2015, 107, 103–112. [Google Scholar] [CrossRef]
- Li, X.; Lyu, W.; Ran, S.; Wang, B.; Wu, W.; Yang, Z.; Jiang, S.; Cui, M.; Song, P.; You, T.; et al. Combination principle of hybrid sources and three typical types of hybrid source heat pumps for year-round efficient operation. Energy 2020, 193, 116772. [Google Scholar] [CrossRef]
- Hou, G.; Taherian, H.; Li, L.; Fuse, J.; Moradi, L. System performance analysis of a hybrid ground source heat pump with optimal control strategies based on numerical simulations. Geothermics 2020, 86, 101849. [Google Scholar] [CrossRef]
- Allaerts, K.; Coomans, M.; Salenbien, R. Hybrid ground-source heat pump system with active air source regeneration. Energy Convers. Manag. 2015, 90, 230–237. [Google Scholar] [CrossRef]
- Sofyan, S.E.; Hu, E.; Kotousov, A.; Kotousov, A. A new approach to modelling of a horizontal geo-heat exchanger with an internal source term. Appl. Energy 2016, 164, 963–971. [Google Scholar] [CrossRef]
- Sofyan, S.E.; Hu, E.; Kotousov, A.; Riayatsyah, T.M.I.; Khairil; Hamdani. A new approach to modelling of seasonal soil temperature fluctuations and their impact on the performance of a shallow borehole heat exchanger. Case Stud. Therm. Eng. 2020, 22, 100781. [Google Scholar] [CrossRef]
- Sofyan, S.E.; Hu, E.; Kotousov, A. Modelling of a Horizontal Geo Heat Exchanger with an Internal Source Term Approach. Energy Procedia 2014, 61, 104–108. [Google Scholar] [CrossRef]
- Baggs, S.A. Remote prediction of ground temperature in Australian soils and mapping its distribution. Sol. Energy 1983, 30, 351–366. [Google Scholar] [CrossRef]
- Gu, Y.; O’Neal, D.L. Development of an equivalent diameter expression for vertical U-tube used in ground-coupled heat pumps. ASHRAE Trans. 1998, 104, 347–355. [Google Scholar]
- Zima, W.; Dziewa, P. Modelling of liquid flat-plate solar collector operation in transient states. Proc. Inst. Mech. Eng. Part A J. Power Energy 2011, 225, 53–62. [Google Scholar] [CrossRef]
- Geoserver, S.A.R.I. Soil Association Map. Available online: https://sarigbasis.pir.sa.gov.au/WebtopEw/ws/plans/sarig1/image/DDD/200471-235 (accessed on 4 October 2020).
- Prangnell, J.; McGowan, G. Soil temperature calculation for burial site analysis. Forensic Sci. Int. 2009, 191, 104–109. [Google Scholar] [CrossRef]
- Australian Government Bureau of Meteorology. Climate Data Online. Available online: http://www.bom.gov.au/climate/data/?ref=ftr (accessed on 4 October 2020).




| Parameters | Value | Unit | Parameters | Value | Unit |
|---|---|---|---|---|---|
| Horizontal GHE | - | - | Circulation fluid (water) | - | - |
| Total pipe length (L) | 200 | m | Inlet water temperature () | 50 | °C |
| Burial depth (h) | 0.25 | m | Flow rate () | 0.6 | kg/s |
| Pipe internal diameter () | 0.04 | m | Specific heat () | 4188 | J/kg K |
| Pipe outer diameter () | 0.044 | m | Density () | 980 | kg/m3 |
| Centre distance between pipe () | 0.28 | m | Soil type in Adelaide: layered old dune sands [27] | - | - |
| Distance of soil domain in x direction (z) | 0.14 | m | Thermal conductivity () | 1.3 | W/m K |
| Distance of soil domain in y direction (z) | 1.5 | m | Specific heat () | 1140 | J/kg K |
| Vertical GHE | - | - | Density () | 1500 | kg/m3 |
| Total pipe length (L) | 200 | m | Soil type in Brisbane: clay [28] | - | - |
| Borehole depth (h) | 100 | m | Thermal conductivity () | 1.1 | W/m K |
| Borehole diameter () | 0.15 | m | Specific heat () | 1500 | J/kg K |
| Soil domain diameter () | 4 | m | Density () | 1300 | kg/m3 |
| Pipe internal diameter () | 0.04 | m | Grout (vertical GHE) | ||
| Pipe outer diameter () | 0.044 | m | Thermal conductivity () | 2 | W/m K |
| Centre distance between pipes () | 0.07 | m | Specific heat () | 1140 | J/kg K |
| Density () | 1500 | kg/m3 | |||
| Wind speed (Adelaide) | 4.9 | m/s | |||
| Wind speed (Brisbane) | 3.8 | m/s |
| Parameter | Adelaide | Unit | Brisbane | Unit |
|---|---|---|---|---|
| Average annual air temperature (Tm) | 16.45 | °C | 25.4 | °C |
| Amplitude of the annual air temperature (As) | 11.9 | °C | 11.2 | °C |
| The local site variable for the ground temperature (∆Tm) | 2.5 | °C | 3 | °C |
| Vegetation coefficient () | 1 | - | 1 | - |
| Soil thermal diffusivity (α) | 0.76 | 10−2 cm−2 s−1 | 0.55 | 10−2 cm−2 s−1 |
| Phase of air temperature wave (t0) | 10 (10 January) | day | 19 (19 January) | Day |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sofyan, S.E.; Hu, E.; Kotousov, A.; Riayatsyah, T.M.I.; Thaib, R. Mathematical Modelling and Operational Analysis of Combined Vertical–Horizontal Heat Exchanger for Shallow Geothermal Energy Application in Cooling Mode. Energies 2020, 13, 6598. https://doi.org/10.3390/en13246598
Sofyan SE, Hu E, Kotousov A, Riayatsyah TMI, Thaib R. Mathematical Modelling and Operational Analysis of Combined Vertical–Horizontal Heat Exchanger for Shallow Geothermal Energy Application in Cooling Mode. Energies. 2020; 13(24):6598. https://doi.org/10.3390/en13246598
Chicago/Turabian StyleSofyan, Sarwo Edhy, Eric Hu, Andrei Kotousov, Teuku Meurah Indra Riayatsyah, and Razali Thaib. 2020. "Mathematical Modelling and Operational Analysis of Combined Vertical–Horizontal Heat Exchanger for Shallow Geothermal Energy Application in Cooling Mode" Energies 13, no. 24: 6598. https://doi.org/10.3390/en13246598
APA StyleSofyan, S. E., Hu, E., Kotousov, A., Riayatsyah, T. M. I., & Thaib, R. (2020). Mathematical Modelling and Operational Analysis of Combined Vertical–Horizontal Heat Exchanger for Shallow Geothermal Energy Application in Cooling Mode. Energies, 13(24), 6598. https://doi.org/10.3390/en13246598