Abstract
Current transportation systems contributed to one quarter to the Greenhouse Gases (GhG) emissions and the mobility demand increases continuously. The transportation infrastructure design has to be optimized to mitigate these emissions. The methodology “Sloop” (acronym for Slope Optimization) has recently been set up to optimize the longitudinal road profile with respect to a Global Warming Potential (GWP) criterion calculated for both the construction and operational phases while incorporating accurate vehicle models. This paper proposes a customized optimization strategy that significantly improves the Sloop methodology. From an initial longitudinal profile generated by road designers, our algorithm identifies the optimized profile in terms of GWP. This optimization step is complex due to the large number of degrees of freedom, along with various constraints to obtaining a feasible solution and the computational cost of the operational phase assessment. The most stringent constraint entails connecting the profile with the existing road (i.e., a constraint on the final profile altitude). We have developed a specific algorithm based on the Sequential Quadratic Programming (SQP) method; this algorithm takes into account the quasi-quadratic nature of the constraint on the final altitude. In a real case study, our algorithm outputs a profile whose GWP assessment saves 4% compared to the GWP assessment of the initial profile. The benefit of our specific protocol for treating the final altitude constraint is demonstrated in this example. By means of this new efficient and open-box algorithm, profile evolution at each iteration is analyzed to determine the most sensitive degrees of freedom, and the sensitivity of the optimization with respect to the main construction parameters and traffic assumptions are conducted. The results are consistent and stable.
1. Introduction
According to [1], “only an acceleration in structural changes to the way the world produces and consumes energy can break the Greenhouse Gases (GhG) emissions trend for good”. Knowing that emissions from transport amounted to one quarter of the GhG emissions in 2016 and that the mobility demand increases year after year [2], all new transportation infrastructure project have to be optimized to mitigate these emissions.
Within the eco-design framework, a methodology called PEAM (for Project Energy Assessment Method) was specifically developed to assess transportation projects according to the geometry of the infrastructure taking into account construction and operation phases i.e., the planned traffic impact. PEAM was then applied to either evaluate High-Speed Line projects [3], road speed-sectioning [4] or to assess the longitudinal profile i.e., slopes of road project [5].
Researchers specialized in vehicle fuel consumption have pointed out the importance of slopes traversed on fuel consumption, from the seminal investigations of Webb in 1952 [6] to recent papers of [7,8,9], yet their logic still treats slopes as constant. The construction phase has long been a subject of research, dating back to the mathematician Monge in 1781 [10]. Most research conducted on such assessments has focused on the construction and maintenance phases since these steps are monitored by road builder [11,12]. Most of the advanced research in this field of road design, e.g., [13,14], account for the influence of slopes on traffic-related fuel consumption by use of an average slope in a statistical model. This modeling set-up only provides a rough approximation of reality, depending on the domain of validity inherent in the statistical model. In a recent work [15], the authors emphasize the necessity of an accurate model of vehicles to assess the effect of slopes on fuel consumption. An optimization of the road profile is proposed based only on fuel consumption with a profile finally difficult to build.
In [5], the authors implement a local optimization called Sloop for Slope Optimization. The starting point is a profile proposed on the drawing board. The objective function is the global warming potential (GWP) of both the construction and operation phases i.e., the traffic GhG emission. The degrees of freedom in this optimization process pertain to the longitudinal road profile. The operational phase is evaluated by simulating traffic over a 10-years period. The traffic simulation is implemented by means of vehicle dynamic models associated with an engine model in a free-flow regime. The construction phase is evaluated by examining the earthworks, which are estimated by computing 3D geometric variations between the natural terrain and the longitudinal profile. The optimization was carried out with a black-box algorithm (i.e., the toolbox optimization from Matlab©) as a proof of concept of the methodology.
Sloop faces a major limitation since the optimization step becomes highly complicated by the use of such precise models. This paper proposes an efficient open-box optimization algorithm specially tailored for this problem which paves the way to the development of an efficient tool for the practitioners.
This paper focuses on the optimization step of the methodology, in ensuring:
- the optimization problem is fully described;
- the choice of the algorithm is justified;
- the algorithm is described and specially tailored for the problem.
By means of this new efficient and open-box algorithm, we analyze the sensitivity of
- the evaluation model with respect to the parameters of the longitudinal profiles;
- the optimization with respect to the main construction parameters and traffic assumptions.
The optimization problem will be completely described, in terms of degrees of freedom, constraints, and objective function in Section 2 and Section 3. Section 4 constitutes the core of the paper by justifying, describing and adapting the optimization algorithm. Section 5 will then present a case study whose highlights and limitations will be discussed in Section 6. The last section concludes this paper by offering some leads for handling the limitations of our approach.
2. Degrees of Freedom: Parameters of the Longitudinal Profile Model
Our algorithm minimizes the GWP of a road by choosing a feasible longitudinal profile. This section displays the equations of such a profile. Equations of this type depend on the degrees of freedom parameters, which also serve as the optimization problem input. To obtain a feasible solution, the degrees of freedom are constrained. The corresponding constraints are listed in the second part of this section.
2.1. Road Longitudinal Profile
The longitudinal profile is modeled as illustrated in Figure 1. It is constituted of a sequence of straight lines connected by circular arcs. The following set of road-specific equations describes this model.
where denotes the longitudinal slope of the straight line k, , are the abscissa and altitude of the point of the intersection of straight line k and straight line . , are internal variables coming from the computation of the circle connecting this straight line k to the next straight line.
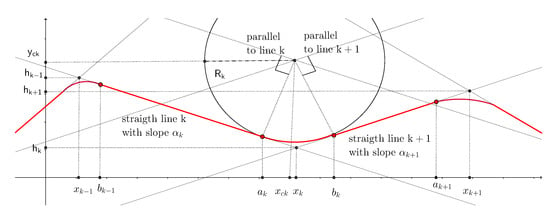
Figure 1.
Longitudinal profile (in red) modeled as a sequence of straight lines connected by circular arcs (adapted from [5]).
is the equation of the circle, with radius , that connects straight line k to straight line . This circle is tangent to straight line k at the point with abscissa and it is tangent to the straight line at the point with abscissa . By virtue of these equations, the derivative of is continuous. Road designers often use circular arc to “smooth” the profile: large radii ( > 10,000 m) tend to be chosen: circular arcs cannot be neglected in the longitudinal profile model.
The center of the circle, whose coordinates are , lies at the intersection of the parallels at a distance of the straight lines k and . is the projection of the center’s circle on the straight lines k. is the projection of the center on the straight line . The following equations specify this construction, where is the solution to the following system of equations.
is the offset of the straight line k ( for ). These equations have been written under the assumption that the circle is above the straight lines i.e., the curve is locally convex as it is the case presented on Figure 1. In the concave case, and have to be subtracted.
After solving this system of equations, () can be computed as intersection of line () and the perpendicular to this line passing through the center of the circle. Solutions to this double system of equations are:
which
The sign of the last equation must be adapted when the curve is locally concave. The case when one line is vertical has not been treated since it is unrealistic for a road context (the road is at least continuous i.e., without step).
The boundary conditions model the connection with the existing road: , , , , , , . is the longitudinal slope of the existing road before , which is the beginning of the profile to optimize, is the longitudinal slope of the existing road after , which is the end of the profile to optimize.
The degrees of freedom are: , , , with to and , , .
The other variables are dependent from these degrees of freedom. is calculated from , and . , are computed with the equation of circle as mentioned above.
2.2. Constraints
The degrees of freedom cannot evolve freely. Each degree of freedom is first bounded by rules expressed in the road standards. For example, the slope cannot exceed a certain threshold for safety reasons: a loaded truck should not decelerate too strongly [16]. The degrees of freedom must also be restricted in order to model a road that can actually be built: feasible slopes depends on the type of materials due to the stability of embankment, the road project must be tied to the existing road. To specify these before the construction, the road is built virtually in a sequence from the beginning to the end of the profile i.e., from to n. Some of these constraints are linear, which can be taken into account relatively easily, while others are nonlinear.
2.2.1. Linear Constraints
The intersection of both straight lines k and has to be located after the previous intersection, as ensured by the following inequality:
with k varying from 1 to n. Moreover, the last intersection must be far enough from the beginning of the actual road to link both straight lines by a circle with a compatible radius. This is expressed by the following inequality where is set by the optimization process user ( has to be set before the end of the studied profile, ).
Two consecutive straight lines have to be different in order to generate an intersection point.
is chosen to ensure a reasonable intersection point.
Activation of this constraint serves as a signal to stakeholders that the road profile can be simplified by considering one ramp with the same slope instead of two ramps with two different slopes. Activation of an inequality means that this inequality becomes a strict equality during an iteration of the optimization algorithm.
2.2.2. Non-Linear Constrains
In order to build the road, it is essential that (see Figure 1):
These inequalities are nonlinear because and depend non linearly on and .
The profile needs to be connected to the existing road, which implies that the profile assumes prescribed values on the boundary. According to the previous subsection, these boundary conditions are expressed as:
These constraints penalize heavily the optimization problem as
- they are nonlinear;
- they are equality constraints, hence they must be taken into account at each iteration of the optimization process.
Since the constraints are specified as if the road were being built sequentially, the constraint is automatically satisfied. According to our model, the derivative is also automatically continuous. On the other hand, the constraint must be added to the problem. Given that the optimization process begins with a compatible solution, respecting this constraint merely entails considering that the derivative of this constraint equal zero in the direction of the descent, which means that the gradient of this constraint has to be computed. Our model (see Figure 2 to support this analysis), therefore yields:
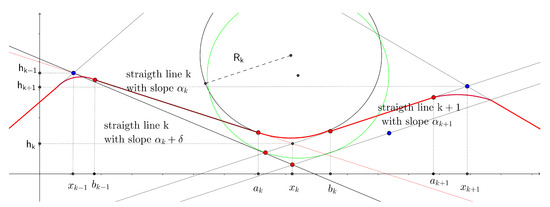
Figure 2.
Longitudinal initial and modified profiles when one slope is modified.
Except for the derivative according to the last radius , which is computed with Equation (4).
It turns out that the constraint is quadratic as the second derivatives are constant except for the degree of freedom . This “ almost quadratic ” property will be utilized in order to simplify the optimization problem.
3. Objective Function
Starting from a feasible road longitudinal profile, the objective function outputs the GWP of the road. This function is the sum of two independent assessments:
- the assessment of the construction phase;
- the assessment of the operation phase.
3.1. Construction
The GWP assessment of the construction phase has been fully described in [5]. Let’s recall herein the main features to provide an overview.
Knowing a longitudinal profile, a 3D model of the road sub-grade, which supports the pavement layers, is calculated. Earthworks are required to transform the natural terrain into this sub-grade road. Different longitudinal profiles imply significant differences in excavation quantities. On the other hand, these longitudinal profiles do not lead to significant changes to the pavement layers. Their widths and lengths mainly depend on traffic levels. Therefore, road pavement layers have not been taken into account in the optimization process.
Earthworks include the following tasks: raw material extraction, transportation, and deposit as fill (in the case of reuse) or storage as a final deposit [17]. Assessment of Earthworks includes an estimate of the fuel consumed by earthworks equipment (bulldozer, scraper, dump truck) during each task. Soil treatment also needs to be quantified. The consumed fuel depends on the earth movements which are estimated from volume differences between the natural ground level and the road project longitudinal profile. The GhG emissions is assessed using the software ECORCE M, which features an extensive database relative to earthworks equipment [18].
3.2. Volume Computation
The longitudinal profile of the project, denoted , and the natural soil profile, , are altitudes relative to the metric point, i.e., distance ; they are discretized every meters. For each point on these discretized profiles, the difference in altitude is computed and multiplied by the road infrastructure width, , to yield a surface area measure. In turn, this surface area is multiplied by the segment length, , to obtain a volume. Embankments with a given transverse slope, , are added along each side of this volume as displayed in Figure 3.
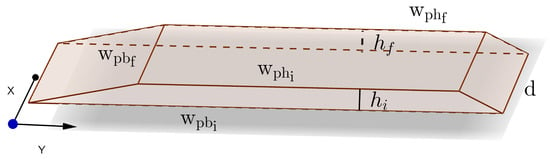
Figure 3.
Elementary earthmoving Volume, X is the longitudinal direction, Y is the transverse direction by [5].
An elementary volume, is computed for each point on the discretized profiles.
3.3. Assessment of Ghg Emissions from the Volume Computation
Starting from these volumes, the GWP are estimated by taking into account the raw material extraction, the transportation between excavation and embankment, the laying of materials, and the quicklime treatment of natural soil.
GWP is calculated with the following equations:
() is the GWP per cubic meter for the fill (the cutting spread in a final deposit).
where is the GWP per cubic meter to extract the materials. is the GWP to transport one cubic meter of materials over one kilometer. is the average distance between cut and fill, is the GWP to spread one cubic meter of materials, is the GWP associated with one cubic meter of quicklime, is the quicklime rate of treated embankment materials, is the quicklime rate of treated materials stored in the final deposit and lastly is the average distance between cut and final deposit.
is the GWP required by additional material in the case of a negative balance between fills and cuts (i.e., for a work site with a material deficit).
The optimization process includes as part of the objective function to be minimized.
For organizational purposes, a work site is in a state of either materials deficit or surplus. It becomes too complicated to switch the organization from one type of work site to another. For this reason, if the work site is in a state of surplus for the proposed profile, the following nonlinear inequality gets added to the optimization problem:
The inverse inequality would be added in the case of a work site with a materials deficit.
3.4. Operations
A traffic simulation model has been used to assess the operational cost (see [5] for more details). Different classes of vehicles are modeled from small passenger cars to heavy-duty vehicles. Both diesel and gasoline-powered engines are considered for passenger cars. An average vehicle model has been developed to represent the fuel consumption of the entire class of like vehicles. Fuel consumption is obviously dependent on the slope and the speed, which is limited by the applicable speed limit or the vehicle’s capabilities. The vehicle models have been developed under the customized Matlab/Simulink© library, called VEHLIB [19]. Fuel consumption is derived working backwards from wheel forces to the engine through component sub-models. The chassis model describes the aerodynamic and rolling resistance forces used to solve the fundamental dynamic principle. Wheel forces are then known and relayed to the engine shaft using a power model composed of ratios and efficiencies of the final gear and gearbox. If needed, a clutch model may also be involved (at low speed). A specific fuel consumption map is then used to assess engine fuel consumption, which then gets transposed into GWP (CO2 emissions).
4. Optimization
The previous section presented the methodology employed to assess the cost, in GWP, of a road longitudinal profile. This section will demonstrate how to derive an optimal profile that minimizes GWP. The mathematical formulation is as follows:
where is the objective function of the longitudinal profile , in accordance with the previous section. summarizes the non linear inequalities described in Section 2.2.1 and the inequality added in the construction phase (Equation (16))
4.1. Choice of Algorithm
The following discussion presents the features of this optimization problem. The choice of a suitable algorithm will then be justified.
- Optimization type The problem is a finite dimensional nonlinear optimization with various linear and nonlinear inequalities and one nonlinear equality.
- Global/Local optimization The optimized profile cannot be too dissimilar from the initial profile for economic and mechanical reasons: earth movements are costly, embankments too large are not stable. The optimization is rather local.
- Initial solution An initial designed profile is available; it is considered feasible to the extent that it satisfies the constraints.
- Smoothness We analyze this mathematical property for the objective function and for the constraints.
- The objective function is relatively smooth as the sum of two smooth functions, i.e.:
- The construction assessment is based on a volume computation. This function has continuous derivatives of all orders ().
- The operational assessment is the sum of the fuel consumption of various vehicles rolling virtually on the road. This sum numerically regularizes the integrand. However, the integrand is not as smooth as the construction cost. For example, a slight change in slope can lead to a drop in engine efficiency that locally alters the consumption or can lead to mechanical braking, which changes overall fuel consumption on the road. This function is at least .
- The nonlinear constraints stem from geometric considerations; they are .
- Computational burden The construction assessment and nonlinear constraints do not require a large amount of computational operations since they rely on simple geometric analysis. On the other hand, the operational assessment requires the simulation of vehicle dynamics, which is a computation time-consuming task.
- Nearly quadratic equality According to Section 2.2.2, the equality constraint on altitude is nearly quadratic. Given that such a constraint must be verified at each iteration, an efficient algorithm needs to take advantage of this property.
This type of optimization is classically solved by sequential quadratic programming (SQP) [20,21,22]. SQP is a local optimization solver starting from an initial solution; however, SQP exhibits certain weaknesses as regards this specific problem. The following discussion will list these weaknesses and our solutions to mitigate them.
- Generic SQP algorithms do not take the quadratic equality constraints into account. We have developed a dedicated solution to take advantage of this feature.
- SQP imposes that the cost function and constraints can be continuously differentiated twice (), whereas the operational assessment is at least . At each iteration, we verify that the quadratic approximation of the Lagrangian is validated by comparing this approximation with the actual value of the objective function.
- SQP requires a computation of the Hessian of the Lagrangian and then of the Hessian of the objective function. The numerical computation of this Hessian is not straightforward because:
- -
- the number of inputs may be high;
- -
- the computation of the operational assessment is time-consuming.
We have approximated the Hessian by means of the BFGS (Broyden-Fletcher-Goldfarb-Shanno) method [21,22].
4.2. Description of the Algorithm
Our algorithm is an SQP with BFGS approximation adapted to our specific equality constraint.
Sqp Algorithm
We have followed [23] for a practical implementation of SQP, including the BFGS approximation of the Hessian. To simplify the presentation, optimization problem (17) is reformulated:
SQP is an iterative algorithm starting from an initial profile:
with is the descent increment; it is computed according to a two-step process.
- by the descent direction solving the Karush Kuhn Tucker (KKT) conditions [24] of the quadratic optimization with linear equality constraints. The quadratic program is as follows:with is the Lagrangian of the non linear optimization problem. is the Lagrange’s multiplier at step k. is the Hessian according to x and error is the gradient operator. The corresponding KKT conditions are:The linear equalities include:
- the linear approximation of the non linear equality constraint on the altitude;
- the linear approximation of the active inequalities, i.e., the inequalities, numbered l, which are saturated and hence become equalities, .
This step requires to compute the gradient and hessian of the objective function and constitutes the main computational cost of the algorithm. The gradient is computed numerically by centered finite difference; this requires simulations of traffic. We have applied the BFGS approximation to compute the hessian according to the equations given in [23] so as to avoid to carrying out traffic simulations in order to compute the Hessian by finite difference. - by reducing the length of the increment with being accommodated:
- activation of one non active linear inequality;
- activation of one non active linearized nonlinear inequality;
- an increment can respect linearized nonlinear inequalities while not respecting the nonlinear inequalities themselves. In this case, the increment’s length is reduced until the inequalities are validated, with this reduction factor being due to the linear approximation of non linear constrains;
- along the same line, a reduced increment can output a solution that fails to respect the linear approximation of the non linear equality on altitude. In this case, a reduced factor is computed, as will be described in the next subsection;
- if the reduced increment yields a solution which increases the objective, the increment is again reduced until the objective decreases with this reduction factor being due to the quadratic approximation of the cost;
4.3. Adaptation of Sqp to the Nonlinear Equality on Altitude
In our particular study, the nonlinear equality constraint of the optimization problem (17) is a sequence of straight lines and circle arcs, which means that this constraint is in fact quadratic equality constraint as described in Section 2.2.1 except for the last parameter .
Numerically, the constraint on altitude is written as follows:
where is the tolerance and . is the reduction factor of the descent which yields the profile to be rendered consistent with the altitude constraint.
Let’s consider that is quadratic, thus yielding:
if this last inequality is not true when , then would have to be reduced. Let’s now suppose that the has been exceeded, then provides the solution to the second-order equation:
The calculation is straightforward. The equation is symmetrical if has been exceeded. This equation thus directly yields the reduction factor of the increment. This solution is much more effective than when ignoring the quadratic property of this constraint, as it is the case with a generic algorithm. A generic algorithm actually guesses and approximates iteratively, in requiring at each iteration the longitudinal profile computation. Since the profile is nearly quadratic and as a result of numerical error, this factor might need to be reduced as well by another reduction factor in order to numerically respect the altitude constraint (this second reduction factor is denoted ).
5. Results
5.1. Case Study
Our case study is a road project built prior to our study. Its construction and traffic data have been fully described in [5]. We will recall herein the key points necessary to understanding the article.
The project is an 8.7-km long, 2 × 2-lane road within the French national highway network; the optimized portion of the project extends 4.75 km in length. The entire section was covered by the same asphalt pavement mix. All technical data (earthworks, pavement structure) required to assess GWP during construction work were collected from the relevant road authorities.
Construction Phase Parameters
During the construction phase, the GhG emitted to extract, spread, transport and treat are indicated, according to Equations (12) and (13) plus the parameters given in Table 1.

Table 1.
Values of the parameters used to assess the construction phase adapted from [5].
The site specific parameters are: average distance between cut and fill (), average distance between cut and final deposit (), average quicklime rate of the material treated for fill () and the quicklime rate for the final deposit, set at 0% given the absence of treatment (). These numbers are accurate because dedicated experiments were carried out in 2012 as part of the national TERDOUEST project (funded by the French National Research Agency). This site had a material surplus: inequality constraint (16) is added to the optimization problem.
5.2. Simulation Parameters of the Operations Phase
Traffic was measured on a daily basis. Table 2 displays its composition. The average daily traffic equaled approx. 7000 vehicles in both directions. We decided to consider the traffic as stable, in terms of trend in the number of vehicles over 25 years. Different traffic assumptions can be tested by using the new algorithm presented in this paper. The variation of the optimization with respect to traffic assumptions is analyzed in Section 5.5.

Table 2.
Measured traffic for the different vehicle categories (t: metric ton) adapted from [5].
To simulate this traffic, we divided it into vehicle classes. In each class, dynamic models were introduced to represent the vehicle behavior. In France, diesel engines represent roughly 70% of all passenger cars, and nearly 100% in trucks and vans. Moreover, the “diesel personal car” class was split into three categories, modeled by a given vehicle type (small, medium or large), as available in the VEHLIB base. These models were calibrated using data from vehicles that had been tested and characterized at Ifsttar. The heavy-duty vehicle characteristics were provided by the CEREMA-Lyon Institute. The number of vehicles was determined by calibration with the data obtained from CEREMA-Lyon during the traffic measurement campaign. Table 3 lists the technical characteristics of the various vehicles used for this assessment:

Table 3.
Vehicle data (t: metric ton) adapted from [5].
- number of vehicles/day in each direction over the studied part of the road;
- mass of each type of vehicle (including load and passengers);
- product of the drag coefficient and the front surface area, denoted ;
- tire rolling resistance coefficients, () represents the constant part () the part proportional to vehicle speed.
5.3. Optimized Profiles
Figure 4 displays the initial and optimized profiles, along with the natural terrain. The initial profile has been designed manually by specialists in eco-design in adopting the same objective as for the algorithm, i.e.: mitigation of GWP during both the construction and operational phases. For this reason, the profile is smooth, meaning that slopes are limited. Let’s begin with this profile in order to verify whether the algorithm can find a better profile than that optimized by specialists.
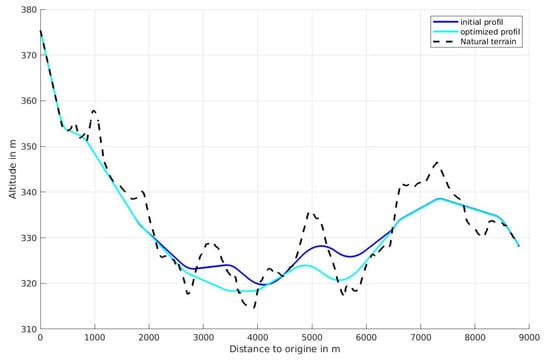
Figure 4.
Optimized profile.
This profile is denoted ; its length equals 4.75 km. Since the actual road is divided into six subsections the profile is also divided into six subsections (). The number of degrees of freedom is therefore 19, according to the formulation of the simplified optimization problem (see Equation (17)), i.e.:
- 6 abscissas defining the intersection points between two consecutive straight lines; the displacements of abscissas are limited to +/− 100 m in order to obtain a profile not to far from the initial.
- 6 slopes, one per section; Slopes can vary from −5.3% to 5.3%. These bounds are set in order to ensure stability of the embankment.
- 7 radii for the circle linking the sections, since the two radii of the two extremities are also degrees of freedom; Radii vary from +/− 2000 m around the initial radii in order to keep a profile relatively smooth.
- The tolerance on the altitude constrain is +/− 0.1 m. This step with a maximum height of 10 cm is easily flattened during construction.
According to Figure 4, the optimized profile has a simpler shape and is significantly below the initial profile.
Figure 5 presents the profile derived by the algorithm at various iterations. For the sake of clarity, we have not drawn any iterations that fail to provide graphical information on the algorithm’s evolution.
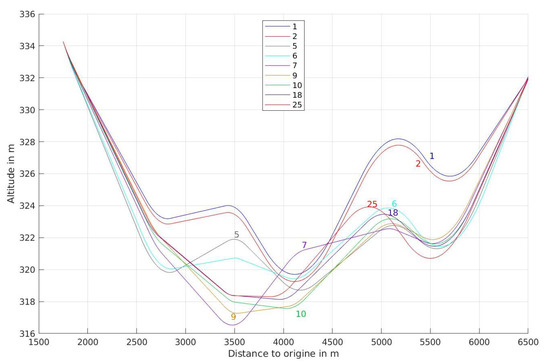
Figure 5.
Iteration process.
Table 4 shows the evolution in emissions stemming from the construction and operation phases. Each iteration gives the reduction factors limiting the length of the descent increment. The final reduction factor is the product of the following reduction factors, which are to be applied sequentially (the explanation of these reduction factors is given in the Section 4.2):

Table 4.
Evolution of cost and reduction factor at each iteration.
- : activation of one inactive linear inequality;
- : activation of one inactive linearized non linear inequality;
- : linear approximation of the non linear equality constraints;
- : compatibility of the quadratic approximation of the altitude constraint ( is the solution of Equation (24));
- : quadratic approximation of the altitude constraint;
- : quadratic approximation of the objective function.
These reduction factors are set to 1 when inactive. For example, if multiplying the 5 first reduction factors yields a solution that decreases the objective function then . For the sake of clarity, reduction factors , , have already multiplied to display a single synthetic factor in the table. is the difference in altitude between the initial profile and the profile computed by the algorithm. We have set a tolerance of m, which implies that .
The first row of the table provides the assessment of the initial solution. The construction cost accounts for less than 8% of the overall cost. The bottom row of the table displays the difference in the optimized solution relative to the initial solution. A GWP savings of about 4% has been gained: the GWP of the operational phase is stable, while the construction phase GWP has been halved.
According to this table, the algorithm first finds a solution that decreases the construction cost of the initial solution and then refines this solution (Iterations 2 to 4). After this first exploratory step, distinct profiles are identified whose construction phase assessment shows a significantly smaller GWP but whose operational phase emissions exert a greater impact (Iterations 5 and 6). Next, the algorithm proposes distinct profiles whose the operational phase emissions is lowered by smoothing the slopes (Iterations 7 to 9) but the emissions due to the construction increase. Iteration 10 refines the output of the last iteration to decrease the construction cost. Iterations 11 through 16 do not substantially improve the objective function, as the constraint on altitude is bounded by the upper limit of the tolerance interval (), which serves to limit the descent ( is small). Then, the algorithm determines other profiles that decrease the construction emissions (Iterations 17 to 18) then decrease the traffic emissions (Iteration 19) before ultimately refining the solution (Iterations 20 to 25).
5.4. Sensitivity Analysis
5.4.1. With Optimization Variables
One of the interests of an open-box algorithm is to be able to analyze each iteration of the algorithm. We can thus relate the variations of the objective function to the variations of the degrees of freedom. A sensitivity analysis of the objective function with respect to the degrees of freedom of the optimization is performed by using this method.
Table 5 shows the iterations whose the variations in traffic and construction emissions were the largest: these are iterations 2, 5 and 7. The first row of the table provides the assessment of the initial solution. The first 4 lines present the 6 variations of the intersection points between two consecutive straight lines. The following 4 lines shows the variations for the 6 slopes. The last lines displays the variations for the 7 radii.

Table 5.
Sensitivity of cost function depending on optimization variables.
Major variations in GhG emissions occur at iteration 5 (variation of 851 and −2838 Mteq CO2 for the traffic and construction, respectively). They correspond to significant variations for the slopes (variation from 0.18 to 0.54%). The variation of the other parameters are not significant (maximum variation of 2 m for the intersection points and 5 m for the radii). If this result is confirmed on various case studies, the optimization could be simplified by considering only slopes.
5.4.2. On Construction Parameters
The purpose of this section is to estimate the influence of the variation of the construction phase parameters on the Sloop solution. Table 1 displays the main parameters. According to Equations (12) to (15), the influence of these parameters are linear on the cost construction. If this influence were important, Sloop solution could be totally different. To test this assumption, we performed 4 optimizations, one by parameter, by increasing each parameter by 5%.
Table 6 displays this sensitivity analysis. The column Parameter specifies the parameter that is modified. The first two lines correspond to the optimization with the initial values of the parameters. Profile init is the starting point of the optimization. Profile opt is the profile optimized. By subtracting the cost of initial profile of each change of parameter (101,223; 101,232; 101,226; 101,552 Mteq CO2) to the cost of initial profile when the parameters are fixed to their initial values (101,210 Mteq CO2), we observe that only the change of has a significant impact on the cost function with an increase of 0.4%. This is consistent with the practitioners of Life Cycle Analysis who underline the influence of Lime on GWP [5]. A comparison of the cost of the profile optimized (97,848 Mteq CO2) with the profile optimized computed with the initial value (97,505 Mteq CO2) shows a small difference (0.35%) consistent with our expectations: as the cost of construction increased relatively to the operation cost, the optimization process focuses more its effort on the construction cost (3717 Mteq CO2 when the parameter changes and 3917 Mteq CO2 in the initial scenario). The costs of the profile optimized when the other parameters change do not differ significantly with the profile optimized with the initial values (difference < 0.06%).

Table 6.
Sensitivity analysis on construction parameters.
5.5. Evolution of Vehicle Fleet Scenario
The scenario proposed to develop and test our model is based on the fleet measured in 2018 in France. At that time, the part of electrical vehicle were negligible. This scenario called scenario 0 assumes that the share of electrical vehicle will remain negligible in the next 25 years. This scenario is not realistic except to demonstrate the feasibility of Sloop. With the algorithm presented in this paper, practitioners will be able to test different scenarios and to analyze the results. This subsection is an example of this approach and gives a first idea of the sensitivity of the fleet composition on the results.
Two scenarios including electrical vehicles have been added. As for the internal combustion engine vehicle, the electrical vehicles have been separated in different classes: small, medium and large classes for the passengers cars and Mini-truck and van for the duty vehicle. Their characteristics are presented by Table 7. The first scenario (scenario 1) is optimistic, the second scenario (scenario 2) is a medium way between scenario 0 and scenario 1. In these scenarios, the global number of vehicle remains the same along the next 25 years. The number of electrical vehicle increases with a linear rate from 0 (the first year) to a maximum which is different according to the scenario 1 or 2. Conversely, the number of diesel vehicle decreases following a linear rate to reach a certain part of the passengers and duty vehicle in 25 years. In scenario 1, the diesel passengers cars completely disappear in 25 years, and 50% of passengers cars will be electric. Thus 50% remain gasoline cars. For duty vehicles (Mini-truck and van), 50% become electric and replace the diesel cars. In scenario 2, a quater of passengers cars and duty vehicles are electrified in 25 years. 50% of diesel passengers cars disappear. Table 8 presents the number of vehicles per days for the first year and in 25 years for the two scenarios. A key point, when considering electrical vehicle, is the energetic mix of the country which is highly influenced by the mode of production of electricity. We consider in this study a GWP of 75 gCO2 per kW·h, mean value for the French electrical mix highly composed of nuclear electricity [25]. It is clear that the results are influenced by this value for others countries.

Table 7.
Electrical vehicle data.

Table 8.
Vehicle number in scenarios 1 and 2.
Figure 6 shows the optimized profiles according to scenarios 0, 1 and 2. The curves of the 3 scenarios are close to one another, but not identical. Globally, Figure 6 shows that the profile is not highly influenced par the introduction of electrical vehicle for this particular case study. This is confirmed by Table 9 that presents the gains between initial and optimized solution according to the 3 scenarios.
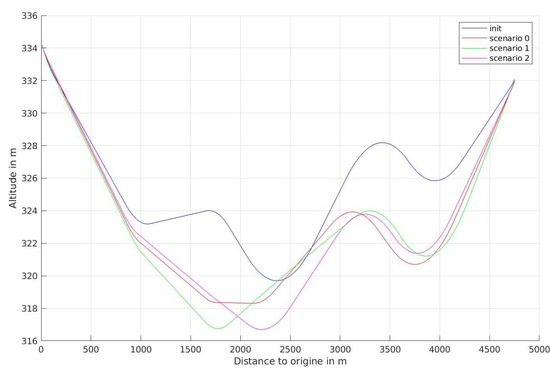
Figure 6.
Optimized profiles for different scenarios.

Table 9.
Optimal cost for different scenarios.
6. Discussion
- Since vehicle consumption accounts for roughly 90% of GHG emissions, we anticipated finding an optimized profile with milder slopes than the initial profile because, in this case, consumption would be lower. However, the optimized profile proved to have steeper slopes. This finding can be explained by the fact that the ramps remain sufficiently mildly inclined so as to not significantly modify engine efficiency and not trigger braking. If consumption remains rather stable, the algorithm will minimize construction-related emissions, which are largely due to the lime treatment of embankments as underlined by the sensitivity analysis. For this reason, the optimized profile minimizes the embankment while holding vehicle consumption stable. Yet an optimization that only takes construction into account would output a profile with a steep ramp, as is the case for Iteration 5 in Table 4 in order to avoid the embankment. In this case, the traffic-related emissions increase significantly.
- As expected, according to Table 4, the nearly quadratic constraint on the altitude often limits the descent during several iterations: lies below 1 for two thirds of the iterations and in half of the iterations, is the appropriate reduction factor of the increment to validate the altitude constraint ( and ), a finding that underscores the benefit of taking this property into account by the algorithm under the real-world scenario.
- This algorithm explores various feasible profiles with distinct features, thus providing stakeholders with different possibilities. They can refine one of the proposed profiles if deemed relevant. For example, given that the optimized solution includes two successive slopes very close to one another, stakeholders can propose a simpler profile to replace these two successive ramps by just one ramp. In its practical implementation, our algorithm takes this special case into account by automatically equalizing successive slopes when they are nearly equal. This type of ad hoc procedure is not robust (i.e., a discontinuity is artificially created) and difficult to tune (e.g., how to numerically define what constitutes “nearly equal” successive slopes?).
- This last point suggests a limitation of the algorithm, which depends on the number of slopes defined in the initial profile by road designers. An alternative would be to directly optimize the profile in an infinite dimensional space through the use of variational methods. The optimized solution would then be approximated by lines and circles in order to transform this optimized, but not necessarily feasible, solution into a longitudinal road profile that can indeed be built. Research along these lines is currently underway; this approach does not guarantee a feasible solution.
- The degrees of freedom are different in nature and are expressed in different units: angles, abscissa, radii. The implementation of the optimization algorithm does not directly use them: a scaling is first performed.
- The optimization with just a single criterion oversimplifies the problem. One perspective would call for a multi-criteria optimization in order to propose to stakeholders a set of efficient solutions (a Pareto front). It should be noted that stakeholders already have a feasible profile at each iteration in using our algorithm.
- Our vehicle consumption models are more sensitive to slope than the usual models used in environmental assessment. However, they do not take into account the specific deformation of the tire on uphill slopes as described in the article [26]. This phenomenon depends on the tire pressure which is not taken into account in our model. This is a point of improvement in our modeling.
- Our case study does not include civil engineering structures such as bridges or tunnels. Our methodology is based on Project Energy Assessment Method (PEAM) and PEAM also models civil engineering structures as mentioned in [3], so there are no theoretical limits to include civil engineering structures in our methodology. Implementation can be complicated because the construction cost function may not be continuous. We plan to implement them according to users’ requests.
7. Conclusions
Sloop is a methodology that optimizes a road’s longitudinal profile according to GWP criteria. Its solution entails a customized sequential quadratic program starting from an initially designed road profile. At each iteration, a quadratic optimization problem is solved. The length of the descent increment often depends on a linear approximation of the nonlinear constraint that models the project’s connection to the existing road. We have utilized the quasi-quadratic property of this constraint to approximate this length. During an application of our algorithm to a real-world example, this approximation was activated in two thirds of iterations. In comparison with a black-box optimization software, stakeholders access a feasible solution at each iteration of the algorithm and are then aware of the cause of descent increment limitation, allowing them to ultimately simplify the road model if deemed relevant. By using this property, we have been able to demonstrate that slopes were the most sensitive degrees of freedom for the road project studied. This finding will be used to simplify the optimization on the next studied cases. Using this new efficient algorithm, different scenarios of traffic evolution and a sensitivity analysis with respect to the main parameters of constructions were carried out. Results are consistent and demonstrate the stability of the optimization. One limitation of the proposed algorithm is its dependence on the initial number of ramps established in the initial design. Two solutions are envisaged to overcome this limitation. The simplest way would be to present a meta level analysis of the algorithm to the stakeholders that exposes the cause of this descent step limitation, in offering them insights into modifying this initial number of ramps. The second, more elegant solution would entail reformulating the problem within the variational analysis framework without the guarantee to obtain a feasible solution. An open-source software based on this paper is currently under development in order to popularize Sloop among practitioners.
Author Contributions
Both authors contributed to all phases of this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors would like to thank Mohammed Bouteldja and the CEREMA-Lyon Institute’s team for establishing the heavy-duty vehicle characteristics in order to derive an accurate estimation of fuel consumption.
Conflicts of Interest
The authors declare no conflict of interest.
References
- IEA. World Energy Outlook 2020—Analysis. 2020. Available online: https://www.iea.org/reports/world-energy-outlook-2020 (accessed on 1 December 2020).
- FIT. ITF Transport Outlook 2019; OECD Publishing: Paris, France, 2019. [Google Scholar] [CrossRef]
- Bosquet, R.; Jullien, A.; Vandanjon, P.O.; Dauvergne, M.; Sanchez, F. Eco-design model of a railway: A method for comparing the energy consumption of two project variants. Transp. Res. Part D Transp. Environ. 2014, 33, 111–124. [Google Scholar] [CrossRef]
- Coiret, A.; Deljanin, E.; Vandanjon, P.O. Vehicle energy savings by optimizing road speed-sectioning. Eur. Transp. Res. Rev. 2020, 41, 1–15. [Google Scholar] [CrossRef]
- Vandanjon, P.O.; Vinot, E.; Cerezo, V.; Coiret, A.; Dauvergne, M.; Bouteldja, M. Longitudinal profile optimization for roads within an eco-design framework. Transp. Res. Part D Transp. Environ. 2019, 67, 642–658. [Google Scholar] [CrossRef]
- Webb, C. The Effect of Gradient on Fuel Consumption and Speed of a Road Vehicle. Proc. Inst. Mech. Eng. Part E 1952, 3, 104–117. [Google Scholar] [CrossRef]
- Wyatt, D.W.; Li, H.; Tate, J.E. The impact of road grade on carbon dioxide (CO2) emission of a passenger vehicle in real-world driving. Transp. Res. Part D Transp. Environ. 2014, 32, 160–170. [Google Scholar] [CrossRef]
- Ragione, L.D.; Giovanni, M. The Influence of Road Gradient in an Integrated Approach of Real Driving Cycles and Emissions Factors Model. Transp. Res. Procedia TRA-2016 2016, 14, 3179–3188. [Google Scholar] [CrossRef]
- Costagliola, M.A.; Costabile, M.; Prati, M.V. Impact of road grade on real driving emissions from two Euro 5 diesel vehicles. Appl. Energy 2018, 231, 586–593. [Google Scholar] [CrossRef]
- Monge, G. Mémoire sur la théorie des déblais et des remblais. In Histoire de l’Académie Royale Des Sciences; Imprimerie Royale: Paris, France, 1781; pp. 666–705. [Google Scholar]
- Inyim, P.; Pereyra, J.; Bienvenu, M.; Mostafavi, A. Environmental assessment of pavement infrastructure: A systematic review. J. Environ. Manag. 2016, 176, 128–138. [Google Scholar] [CrossRef] [PubMed]
- Santos, J.; Ferreira, A.; Flintsch, G.; Cerezo, V. A multi-objective optimisation approach for sustainable pavement management. Struct. Infrastruct. Eng. 2018, 14. [Google Scholar] [CrossRef]
- Jha, M.K.; Schonfeld, P.M.; Jong, J.C.; Kim, E. Intelligent Road Design; WIT Press: Southampton, UK, 2006; ISBN 978-1-84564-003-3. [Google Scholar]
- Kang, M.W.; Jha, M.K.; Schonfeld, P. Applicability of highway alignment optimization models. Transp. Res. Part C Emerg. Technol. 2011, 21, 257–286. [Google Scholar] [CrossRef]
- Ferreira, H.; Rodrigues, C.M.; Pinho, C. Impact of Road Geometry on Vehicle Energy Consumption and CO2 Emissions: An Energy-Efficiency Rating Methodology. Energies 2020, 13, 119. [Google Scholar] [CrossRef]
- AASHTO. A Policy on Geometric Design of Highway and Streets; Technical Report; American Association of State Highway and Transportation Officials: Washington, DC, USA, 1994. [Google Scholar]
- Capony, A.; Muresan, B.; Dauvergne, M.; Auriol, J.C.; Ferber, V.; Jullien, A. Monitoring and environmental modeling of earthwork impacts: A road construction case study. Resour. Conserv. Recycl. 2013, 74, 124–133. [Google Scholar] [CrossRef]
- Jullien, A.; Dauvergne, M.; Proust, C. Road LCA: The dedicated ECORCE tool and database. Int. J. Life Cycle Assess. 2015, 20, 655–670. [Google Scholar] [CrossRef]
- Vinot, E.; Scordia, J.; Trigui, R.; Jeanneret, B.; Badin, F. Model simulation, validation and case study of the 2004 THS of Toyota Prius. Int. J. Veh. Syst. Model. Test. 2008, 3, 139–167. [Google Scholar] [CrossRef]
- Wilson, R. A Simplicial Method for Convex Programming; Harvard University: Cambridge, MA, USA, 1963. [Google Scholar]
- Nocedal, J.; Wright, S. Numerical Optimization, 2nd ed.; Springer Series in Operations Research and Financial Engineering; Springer: New York, NY, USA, 2006. [Google Scholar]
- Gill, P.E.; Wong, E. Sequential quadratic programming methods. In Mixed Integer Nonlinear Programming; Springer: New York, NY, USA, 2012; pp. 147–224. [Google Scholar]
- Hansen, E.L.; Volcker, C. Numerical Algorithms for Sequential Quadratic Optimization. Master’s Thesis, Informatics and Mathematical Modelling, Technical University of Denmark, Lyngby, Denmark, 2007. [Google Scholar]
- Boltyanski, V.; Martini, H.; Soltan, V. Geometric Methods and Optimization Problems; Springer Science & Business Media: New York, NY, USA, 2013; Volume 4. [Google Scholar]
- ADEME. Agency for Ecological Transition. 2020. Available online: https://www.bilans-ges.ademe.fr/ (accessed on 2 December 2020).
- Sina, N.; Nasiri, S.; Karkhaneh, V. Effects of resistive loads and tire inflation pressure on tire power losses and CO2 emissions in real-world conditions. Appl. Energy 2015, 157, 974–983. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).