Modelling of the Dynamic Young’s Modulus of a Sedimentary Rock Subjected to Nonstationary Loading
Abstract
1. Introduction
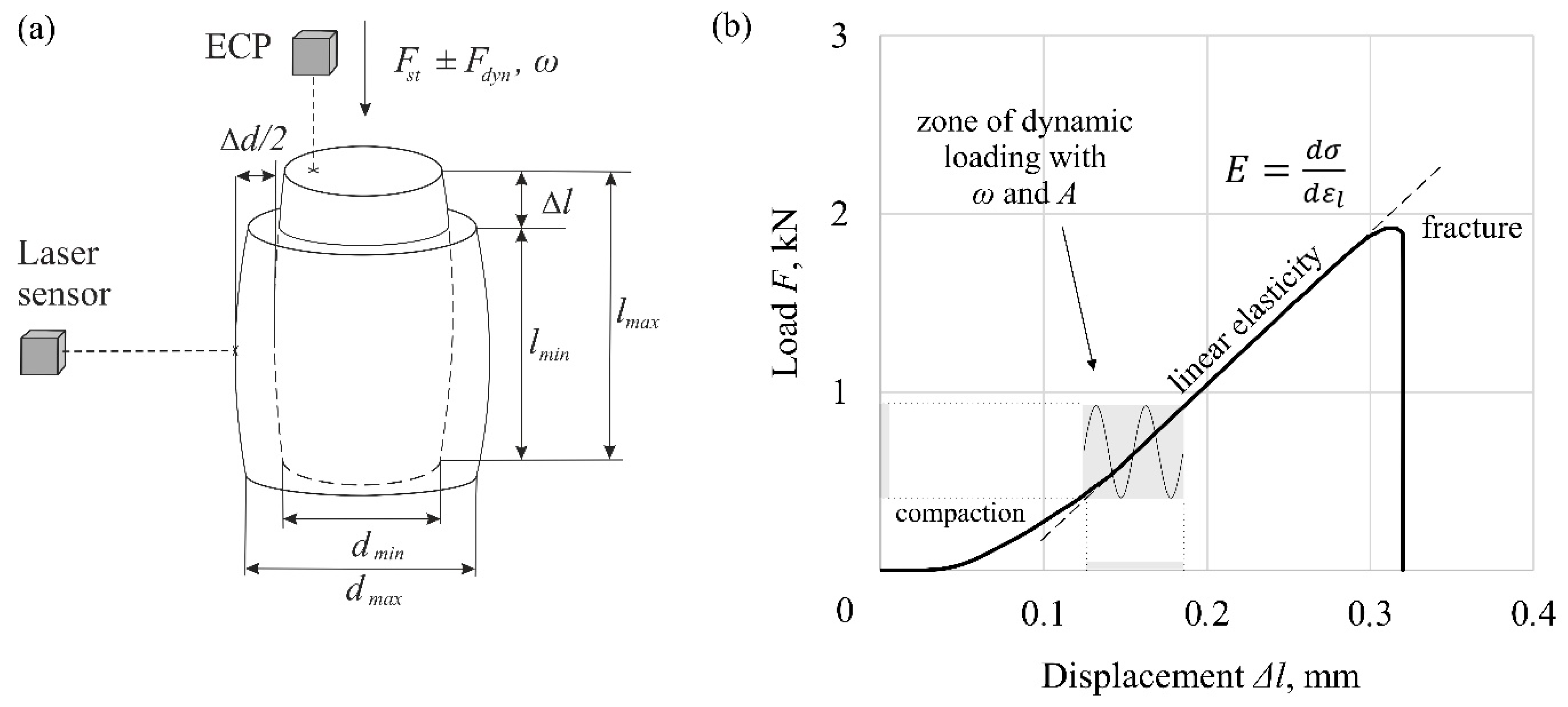
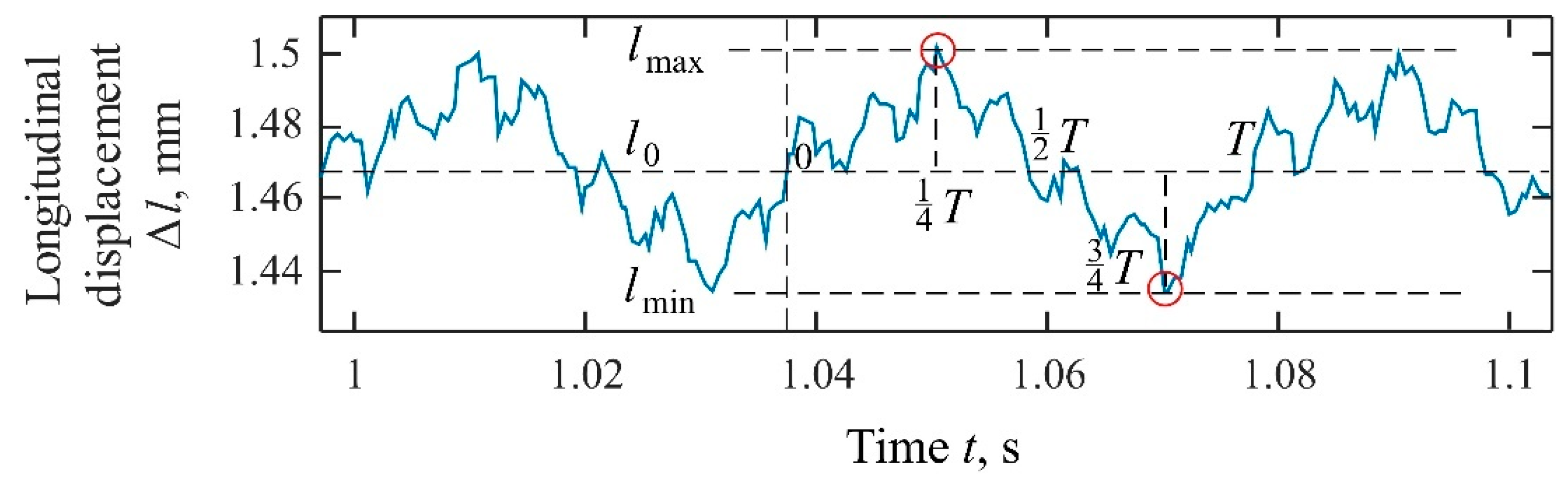
2. Description of the Experiment
3. Model Formulation
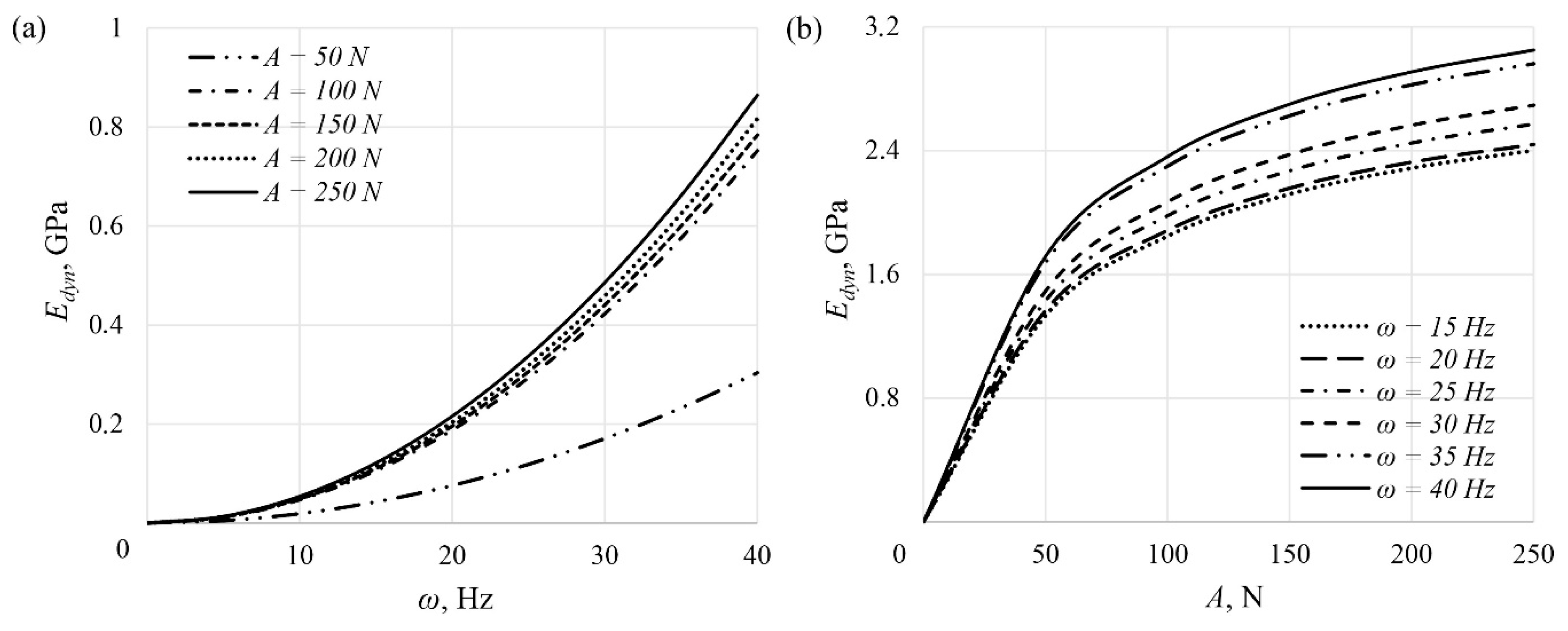
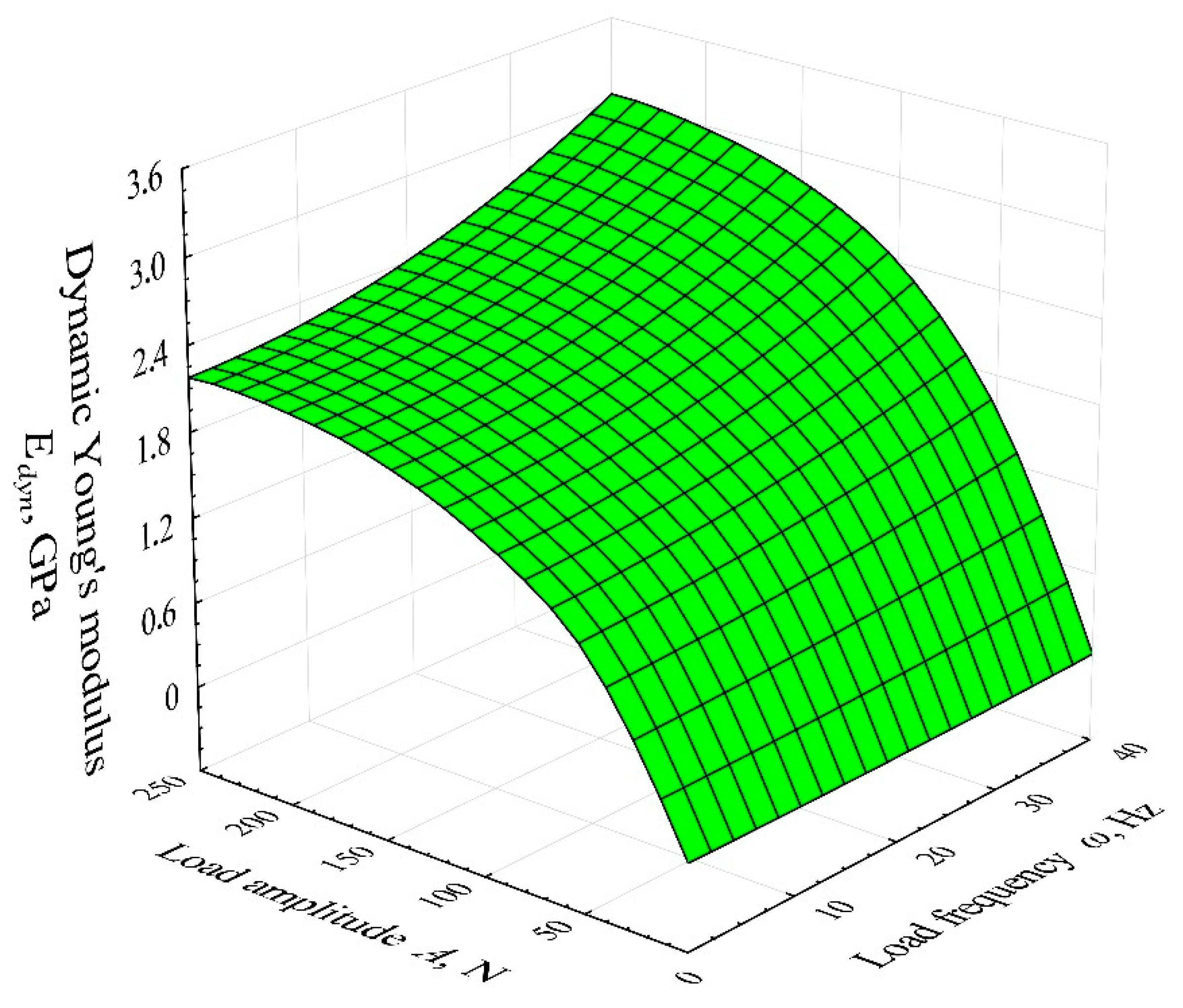
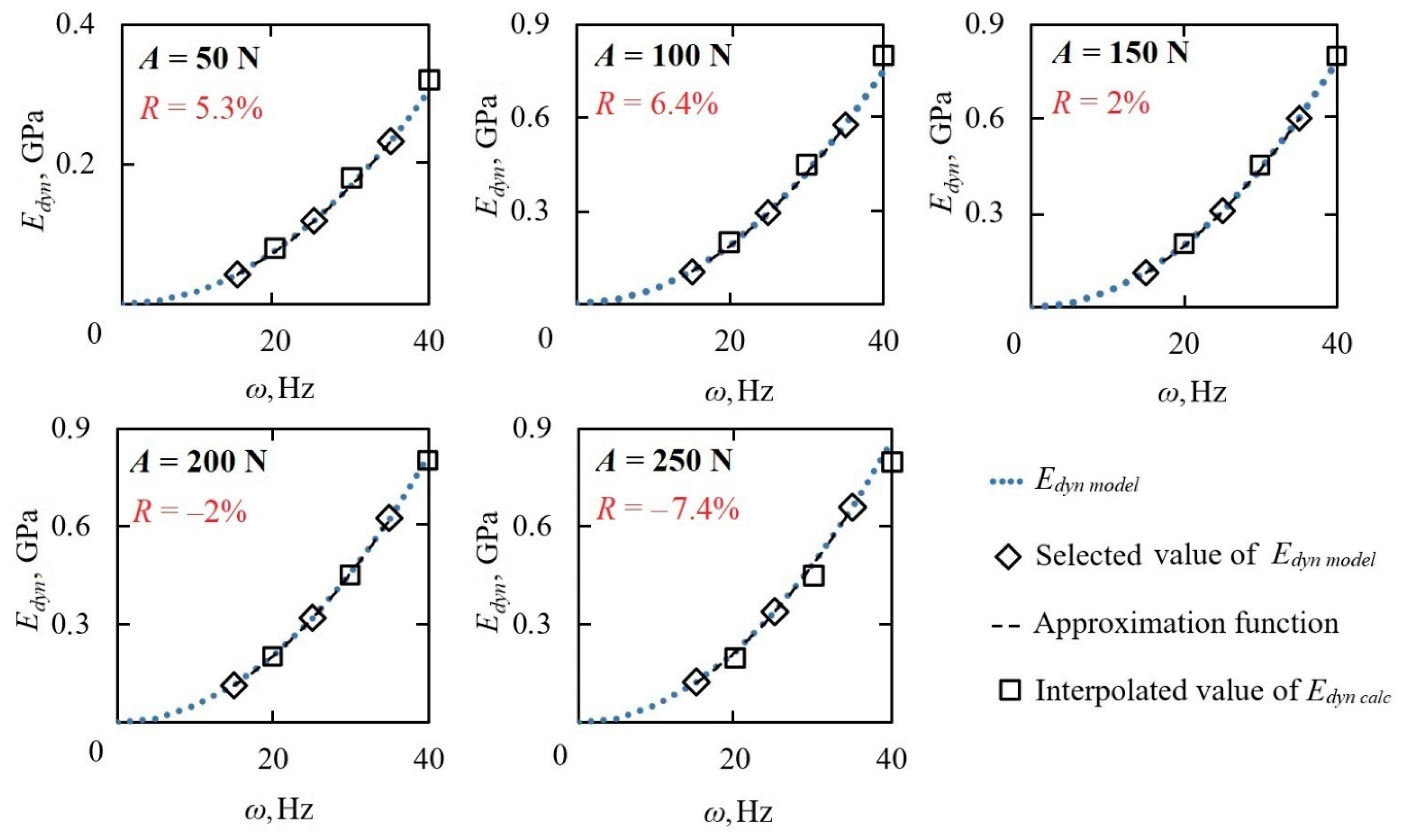
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
List of Symbols
| A | Amplitude of the dynamic load, N |
| dmax | Maximum value of sample’s diameter, m |
| dmin | Minimum value of sample’s diameter, m |
| Edyn calc | Calculated dynamic component of the Young’s modulus, Pa |
| Edyn model | Model dynamic component of the Young’s modulus, Pa |
| Edyn | Dynamic component of the Young’s modulus, Pa |
| Fst | Static preload, N |
| g | Gravity, m/s2 |
| k | Stiffness |
| l | Sample length, m |
| l0 | Sample length in the preloaded state, m |
| lmax | Maximum sample length, m |
| lmin | Minimum sample length, m |
| m | Mass, m |
| R | Percentage deviation |
| S | Cross-section area of the sample, m2 |
| T | Period, s |
| t | Time, s |
| u | Displacement, m |
| umax | Maximum displacement, m |
| umin | Minimum displacement, m |
| α | Coefficient linking external and natural frequencies |
| Δd | Transverse displacement, m |
| Δl | Longitudinal displacements, m |
| εl | Longitudinal strain |
| π | Ratio of a circle’s circumference to its diameter |
| σ | Stress, Pa |
| ω | External frequency, Hz |
| Ω | Natural frequency, Hz |
References
- Muir, T.G.; Cormack, J.M.; Slack, C.M.; Hamilton, M.F. Elastic softening of sandstone due to a wideband acoustic pulse. J. Acoust. Soc. Am. 2020, 147, 1006–1014. [Google Scholar] [CrossRef] [PubMed]
- Peng, K.; Zhou, J.; Zou, Q.; Song, X. Effect of loading frequency on the deformation behaviours of sandstones subjected to cyclic loads and its underlying mechanism. Int. J. Fatigue 2020, 131, 105349. [Google Scholar] [CrossRef]
- Rivière, J.; Shokouhi, P.; Guyer, R.A.; Johnson, P.A. A set of measures for the systematic classification of the nonlinear elastic behavior of disparate rocks. J. Geophys. Res. Solid Earth 2015, 120, 1587–1604. [Google Scholar] [CrossRef]
- Lozovyi, S.; Bauer, A. Static and dynamic stiffness measurements with Opalinus Clay. Geophys. Prospect. 2019, 67, 997–1019. [Google Scholar] [CrossRef]
- Yin, S.; Xie, R. Experimental analysis of dynamic and static mechanical properties of deep thick anhydrite cap rocks under high-stress conditions. Carbonates Evaporites 2018, 34, 807–823. [Google Scholar] [CrossRef]
- Sone, H.; Zoback, M.D. Mechanical properties of shale-gas reservoir rocks—Part 1: Static and dynamic elastic properties and anisotropy. Geophysics 2013, 78, D381–D392. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, L.; Han, D.-H.; Qin, X.; Ren, J.; Wei, Q. Micro-mechanical analysis of the effects of stress cycles on the dynamic and static mechanical properties of sandstone. Int. J. Rock Mech. Min. Sci. 2020, 134, 104431. [Google Scholar] [CrossRef]
- Petrie, E.S.; Jeppson, T.N.; Evans, J.P. Predicting rock strength variability across stratigraphic interfaces in caprock lithologies at depth: Correlation between outcrop and subsurface. Environ. Geosci. 2012, 19, 125–142. [Google Scholar] [CrossRef]
- Nazari Ostad, M.; Niri, M.E.; Darjani, M. 3D modeling of geomechanical elastic properties in a carbonate-sandstone reservoir: A comparative study of geostatistical co-simulation methods. J. Geophys. Eng. 2018, 15, 1419–1431. [Google Scholar] [CrossRef]
- Zuo, J.-P.; Wei, X.; Shi, Y.; Liu, C.; Li, M.; Wong, R.H.C. Experimental study of the ultrasonic and mechanical properties of a naturally fractured limestone. Int. J. Rock Mech. Min. Sci. 2020, 125, 104162. [Google Scholar] [CrossRef]
- Li, X.B.; Lok, T.S.; Zhao, J. Dynamic characteristics of granite subjected to intermediate loading rate. Rock Mech. Rock Eng. 2005, 38, 21–39. [Google Scholar] [CrossRef]
- Szewczyk, D.; Bauer, A.; Holt, R.M. A new laboratory apparatus for the measurement of seismic dispersion under deviatoric stress conditions. Geophys. Prospect. 2016, 64, 789–798. [Google Scholar] [CrossRef]
- Szewczyk, D.; Holt, R.M.; Bauer, A. The impact of saturation on seismic dispersion in shales—laboratory measurements. Geophysics 2018, 83, 15–34. [Google Scholar] [CrossRef]
- Batzle, M.L.; Han, D.-H.; Hofmann, R. Fluid mobility and frequency-dependent seismic velocity—Direct measurements. Geophysics 2006, 71, N1–N9. [Google Scholar] [CrossRef]
- Pimienta, L.; Fortin, J.; Guéguen, Y. Bulk modulus dispersion and attenuation in sandstones. Geophysics 2015, 80, A25–A30. [Google Scholar] [CrossRef]
- Gong, F.; Di, B.; Wei, J.; Ding, P.; Tian, H.; Han, J. A study of the anisotropic static and dynamic elastic properties of transversely isotropic rocks. Geophysics 2019, 84, C281–C293. [Google Scholar] [CrossRef]
- Bagde, M.N.; Petroš, V. Fatigue properties of intact sandstone samples subjected to dynamic uniaxial cyclical loading. Int. J. Rock Mech. Min. Sci. 2005, 42, 237–250. [Google Scholar] [CrossRef]
- Aghaei Araei, A.; Razeghi, H.R.; Ghalandarzadeh, A.; Hashemi Tabatabaei, S. Effects of loading rate and initial stress state on stress-strain behavior of rock fill materials under monotonic and cyclic loading conditions. Sci. Iran. 2012, 19, 1220–1235. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, T.; Wu, S.; Tang, H.; Xin, P.; Liang, C. Dynamics stress–strain behavior of Tianshui soils. Landslides 2017, 14, 323–335. [Google Scholar] [CrossRef]
- ASTM Standard D3999-91. Standard D3999-91. Standard test methods for the determination of the modulus and damping properties of soils using the cyclic triaxial apparatus. In Annual Book of ASTM Standard; ASTM International: West Conshohocken, PA, USA, 2003. [Google Scholar]
- Riabokon, E.P. Laboratory study on the effect of elastic wave treatment on geomechanical and capillary properties of clastic reservoirs. Neftyanoe Khozyaystvo—Oil Ind. 2020, 4, 54–57. [Google Scholar] [CrossRef]
- Wiercigroch, M.; Riabokon, E.P.; Guzev, M.A.; Turbakov, M.S.; Kobiakov, D.V. Experimental studies on static and dynamic loading of heterogeneous rocks. In Proceedings of the XLVIII International Conference Advanced Problems in Mechanics, Saint Petersburg, Russia, 21–26 June 2020; p. 55. [Google Scholar]
- Lomakin, E.V. Mechanics of media with stress-state dependent properties. Phys. Mesomech. 2007, 10, 255–264. [Google Scholar] [CrossRef]
- Myasnikov, V.P.; Sadovskii, V.M. Variational principles of the theory of the limiting equilibrium of media with different strengths. J. Appl. Math. Mech. 2004, 68, 437–446. [Google Scholar] [CrossRef]
- Min, K.-B.; Jing, L. Stress dependent mechanical properties and bounds of Poisson’s ratio for fractured rock masses investigated by a DFN-DEM technique. Int. J. Rock Mech. Min. Sci. 2004, 41, 1–6. [Google Scholar] [CrossRef]
- Makarov, P.V. Evolutionary nature of structure formation in lithospheric material: Universal principle for fractality of solids. Russ. Geol. Geophys. 2007, 48, 558–574. [Google Scholar] [CrossRef]
- Grayeli, R.; Mortazavi, A. Discontinuous deformation analysis with second-order finite element meshed block. Int. J. Numer. Anal. Methods Geomech. 2006, 30, 1545–1561. [Google Scholar] [CrossRef]
- Sadovskii, V.M.; Sadovskaya, O.V. Supercomputer modeling of wave propagation in blocky media accounting fractures of interlayers. Adv. Struct. Mater. 2020, 122, 379–398. [Google Scholar] [CrossRef]
- Liu, G.-Y.; Xu, W.-J.; Govender, N.; Wilke, D.N. A cohesive fracture model for discrete element method based on polyhedral blocks. Powder Technol. 2020, 359, 190–204. [Google Scholar] [CrossRef]
- Chanyshev, A.I.; Belousova, O.E. A method to describe hierarchical block structure of rock mass, considering nonuniformity of mechanical properties. J. Min. Sci. 2017, 53, 441–448. [Google Scholar] [CrossRef]
- Wang, W.; Chen, S. 3D elasto-visco-plastic hierarchical block element method for rock mass. Yanshilixue Yu Gongcheng Xuebao/Chin. J. Rock Mech. Eng. 2003, 22, 525–531. [Google Scholar]
- Li, J.; Chen, W.; Shi, C.; Wang, M. Calculation method of irreversible displacement region radius based on block hierarchical structure under large-scale underground explosion. Baozha Yu Chongji/Explos. Shock Waves 2018, 38, 1271–1277. [Google Scholar] [CrossRef]
- Oparin, V.N.; Tanaino, A.S. Canonical ranking of sizes of structural units in rocks classifications. J. Min. Sci. 2009, 45, 551–562. [Google Scholar] [CrossRef]
- Nikafshan Rad, H.; Jalali, Z.; Jalalifar, H. Prediction of rock mass rating system based on continuous functions using Chaos-ANFIS model. Int. J. Rock Mech. Min. Sci. 2015, 73, 1–9. [Google Scholar] [CrossRef]
- Müller, L. Rock Mechanics; Springer: Wien, Austria; New York, NY, USA, 1982. [Google Scholar]
- Brocato, M. A continuum model of close packing granular materials for the study of rock filled gabions. Int. J. Solids Struct. 2020, 187, 38–47. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid II. Higher frequency range. J. Acoust. Soc. Am. 1956, 28, 179–191. [Google Scholar] [CrossRef]
- O’Connell, R.J.; Budiansky, B. Viscoelastic properties of fluid-saturated cracked solids. J. Geophys. Res. 1977, 82, 5719–5735. [Google Scholar] [CrossRef]
- Mavko, G.; Nur, A. Melt squirt in the asthenosphere. J. Geophys. Res. 1975, 80, 1444–1448. [Google Scholar] [CrossRef]
- Murphy, W.F., III; Winkler, K.W.; Kleinberg, R.L. Acoustic relaxation in sedimentary rocks: Dependence on grain contacts and fluid saturation. Geophysics 1986, 51, 757–766. [Google Scholar] [CrossRef]
- Johnston, D.H.; Toksoz, M.N.; Timur, A. Attenuation of seismic waves in dry and saturated rocks—II. Mechanisms. Geophysics 1979, 44, 691–711. [Google Scholar] [CrossRef]
- Endres, A.L.; Knight, R.J. Incorporating pore geometry and fluid pressure communication into modeling the elastic behavior of porous rocks. Geophysics 1997, 62, 106–115. [Google Scholar] [CrossRef]
- Dvorkin, J.; Nur, A. Dynamic poroelasticity: A unified model with the squirt and the Biot mechanisms. Geophysics 1993, 58, 524–533. [Google Scholar] [CrossRef]
- Pride, S.R.; Berryman, J.G. Linear dynamics of double-porosity dual-permeability materials. I. Governing equations and acoustic attenuation. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2003, 68, 366031–3660310. [Google Scholar] [CrossRef] [PubMed]
- Chapman, M.; Zatsepin, S.V.; Crampin, S. Derivation of a microstructural poroelastic model. Geophys. J. Int. 2002, 151, 427–451. [Google Scholar] [CrossRef]
- Mikhaltsevitch, V.; Lebedev, M.; Gurevich, B. A laboratory study of the elastic and anelastic properties of the sandstone flooded with supercritical CO2 at seismic frequencies. Energy Procedia 2014, 63, 4289–4296. [Google Scholar] [CrossRef]
- Spencer, J.W., Jr. Stress relaxations at low frequencies in fluid-saturated rocks: Attenuation and modulus dispersion. J. Geophys. Res. 1981, 86, 1803–1812. [Google Scholar] [CrossRef]
- Winkler, K.W. Frequency dependent ultrasonic properties of high-porosity sandstones. J. Geophys. Res. 1983, 88, 9493–9499. [Google Scholar] [CrossRef]
- Zhang, Q.B.; Zhao, J. A review of dynamic experimental techniques and mechanical behaviour of rock materials. Rock Mech. Rock Eng. 2014, 47, 1411–1478. [Google Scholar] [CrossRef]
- Ožbolt, J.; Sharma, A.; Reinhardt, H.-W. Dynamic fracture of concrete—Compact tension specimen. Int. J. Solids Struct. 2011, 48, 1534–1543. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Shang-Ping, B.; Ravindra, G. Fracture of rock: Effect of loading rate. Eng. Fract. Mech. 1993, 45, 393–398. [Google Scholar] [CrossRef]
- Tutuncu, A.N.; Podio, A.L.; Gregory, A.R.; Sharma, M.M. Nonlinear viscoelastic behavior of sedimentary rocks, Part I: Effect of frequency and strain amplitude. Geophysics 1998, 63, 184–194. [Google Scholar] [CrossRef]
- Saksala, T. On the strain rate sensitivity of coarse-grained rock: A mesoscopic numerical study. Rock Mech. Rock Eng. 2019, 52, 3229–3240. [Google Scholar] [CrossRef]
- Denoual, C.; Hild, F. A damage model for the dynamic fragmentation of brittle solids. Comput. Methods Appl. Mech. Eng. 2000, 183, 247–258. [Google Scholar] [CrossRef]
- Jaeger, J.C.; Cook, N.G.W.; Zimmerman, R.W. Laboratory testing of rocks. In Fundamentals of Rock Mechanics, 4th ed.; Blackwell Publishing: Malden, MA, USA, 2007; pp. 145–167. [Google Scholar]
- Goldstein, H.; Poole, C., Jr.; Safko, J. Classic Mechanics, 3rd ed.; Addison Wesley: San Francisco, CA, USA, 2002. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guzev, M.; Riabokon, E.; Turbakov, M.; Kozhevnikov, E.; Poplygin, V. Modelling of the Dynamic Young’s Modulus of a Sedimentary Rock Subjected to Nonstationary Loading. Energies 2020, 13, 6461. https://doi.org/10.3390/en13236461
Guzev M, Riabokon E, Turbakov M, Kozhevnikov E, Poplygin V. Modelling of the Dynamic Young’s Modulus of a Sedimentary Rock Subjected to Nonstationary Loading. Energies. 2020; 13(23):6461. https://doi.org/10.3390/en13236461
Chicago/Turabian StyleGuzev, Mikhail, Evgenii Riabokon, Mikhail Turbakov, Evgenii Kozhevnikov, and Vladimir Poplygin. 2020. "Modelling of the Dynamic Young’s Modulus of a Sedimentary Rock Subjected to Nonstationary Loading" Energies 13, no. 23: 6461. https://doi.org/10.3390/en13236461
APA StyleGuzev, M., Riabokon, E., Turbakov, M., Kozhevnikov, E., & Poplygin, V. (2020). Modelling of the Dynamic Young’s Modulus of a Sedimentary Rock Subjected to Nonstationary Loading. Energies, 13(23), 6461. https://doi.org/10.3390/en13236461




