Deep Reinforcement Learning Based Optimal Route and Charging Station Selection

Abstract

This paper proposes an optimal route and charging station selection (RCS) algorithm based on model-free deep reinforcement learning (DRL) to overcome the uncertainty issues of the traffic conditions and dynamic arrival charging requests. The proposed DRL based RCS algorithm aims to minimize the total travel time of electric vehicles (EV) charging requests from origin to destination using the selection of the optimal route and charging station considering dynamically changing traffic conditions and unknown future requests. In this paper, we formulate this RCS problem as a Markov decision process model with unknown transition probability. A Deep Q network has been adopted with function approximation to find the optimal electric vehicle charging station (EVCS) selection policy. To obtain the feature states for each EVCS, we define the traffic preprocess module, charging preprocess module and feature extract module. The proposed DRL based RCS algorithm is compared with conventional strategies such as minimum distance, minimum travel time, and minimum waiting time. The performance is evaluated in terms of travel time, waiting time, charging time, driving time, and distance under the various distributions and number of EV charging requests.

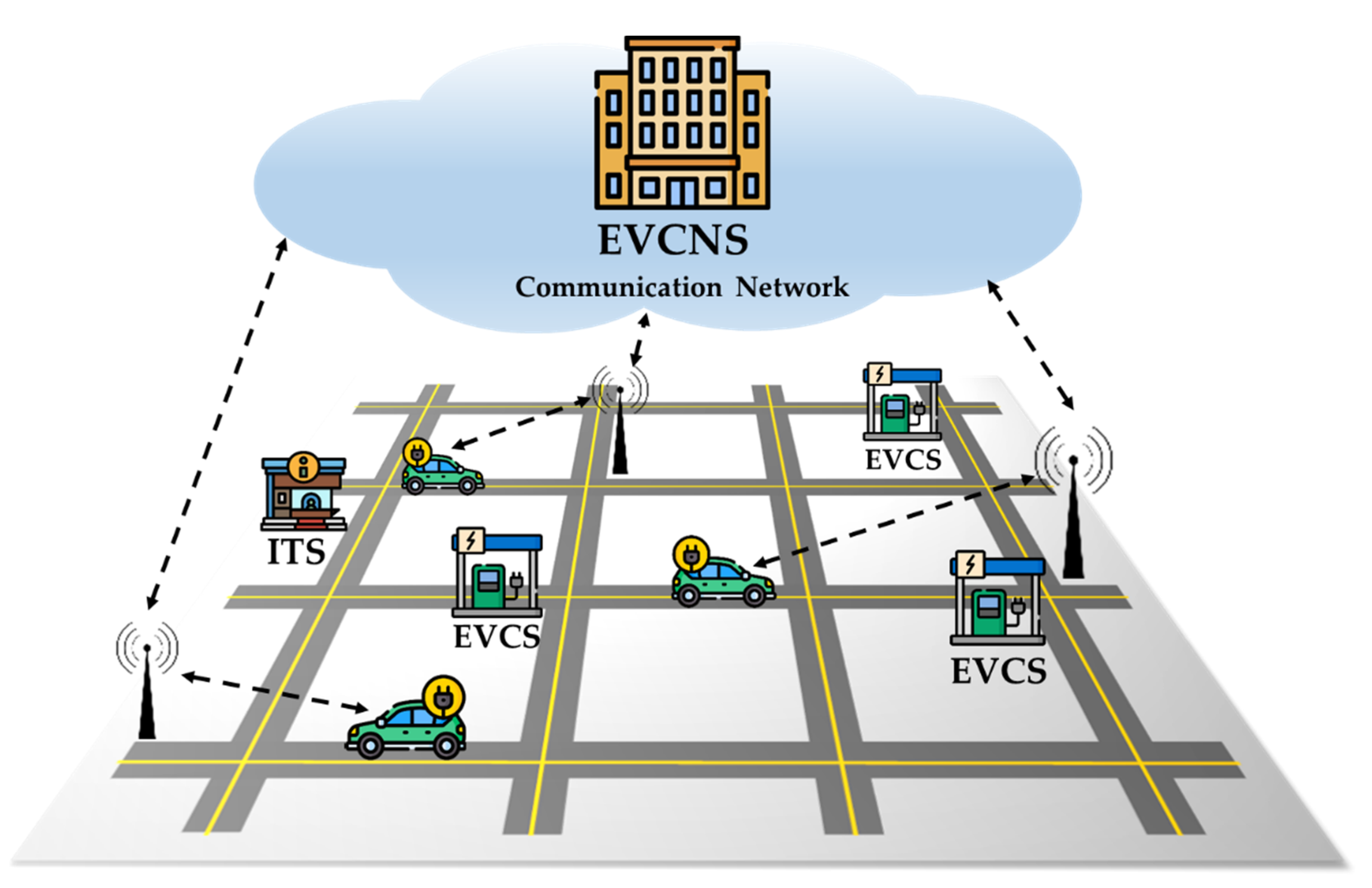
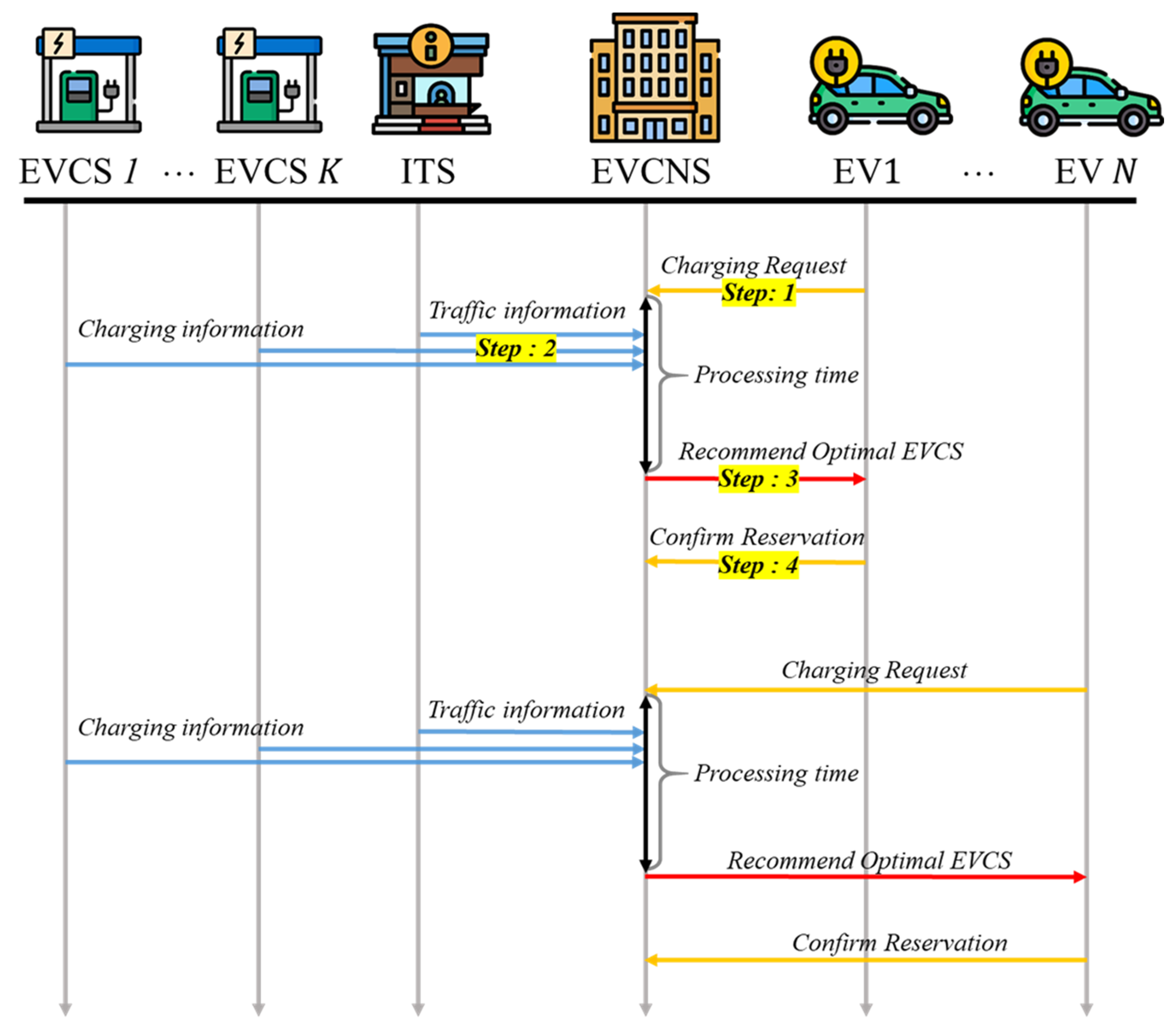
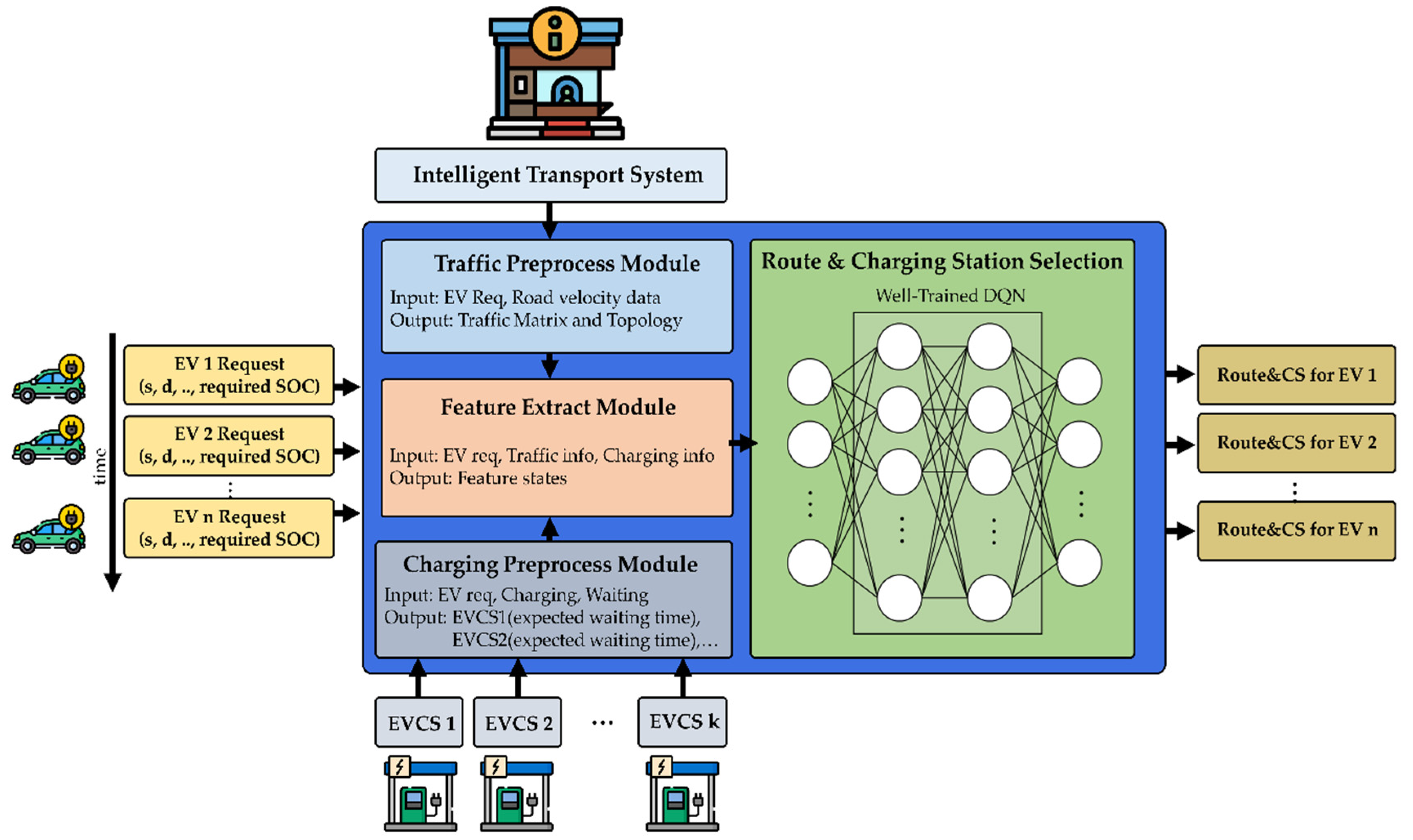
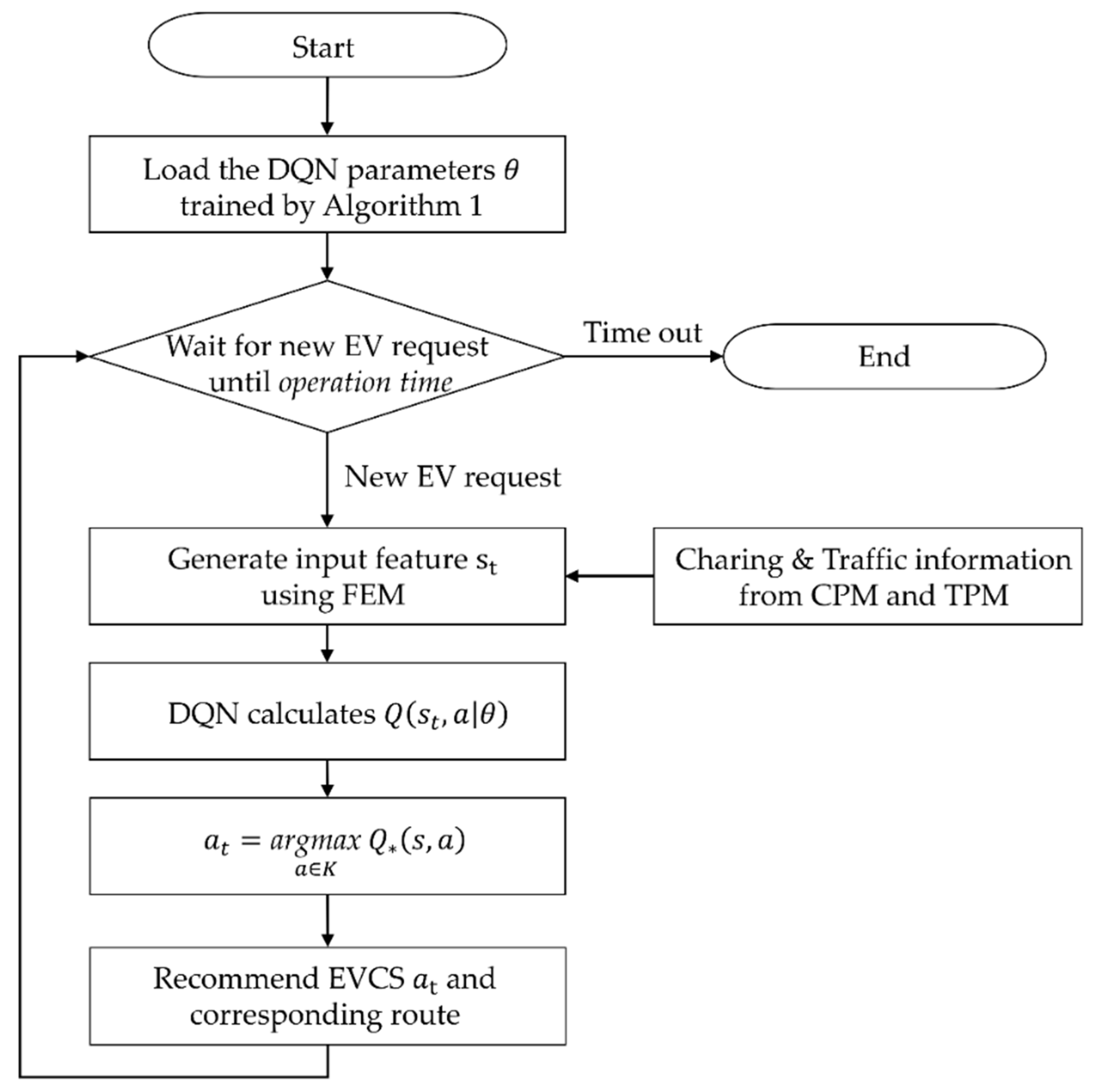
1. Introduction

In recent years, electric vehicles (EV) are considered a promising eco-friendly means of transportation that alleviate the environmental pollution problems caused by the use of traditional fossil fuel sources [1]. Although EVs aim to provide zero fossil fuel consumption and emits no greenhouse gases, the additional charging power generated by the increase in the use of EVs may be concentrated in a specific time period, depending on the user’s charging patterns, which significantly result in high peak demand. The required amount of charging electricity for EVs will increase power losses, voltage fluctuations and grid overloads, making the operation of power plants inefficient and negatively affecting the stability and reliability of the power grid [2]. The electric vehicle charging stations (EVCS) are playing an important role in recharging EVs. These EVCSs buy power from the power grid at a lower price and then sell power to EVs at a higher price in order to make a profit [3]. Compared with home charging, the charging stations could offer lower charging prices because of the lower rate of purchasing from the wholesale market. In order to support the grid integration of EVs and alleviate the high peak demand issues, hourly rates (day-ahead pricing or real-time rates) are widely used to move loads and stabilize the power systems.

The grid integration of electric vehicles and charging/discharging capabilities of the charging stations have received much attention in different applications including vehicle-to-home (V2H), vehicle-to-vehicle (V2V), and vehicle-to-grid (V2G). In V2H, a single electric vehicle is connected to a single home/building for charging/discharging based on the home/building control scheme. In V2V, multiple electric vehicles are able to transfer energy to a local grid or other electric vehicles using bidirectional chargers. In V2G, a large number of electric vehicles can be connected to a grid for charging/discharging such as parking lots and fast charging stations [4,5].

Many studies have proposed different charging schemes for scheduling and optimizing the operation of EVs. These methods aim to mitigate power peaks using dynamic electricity prices. However, most studies determine the charging time and the charging speed when EVs are parking at home and parking lots for a long time. However, EV users may need the charging service while driving for a short mileage due to limited EV battery capacity. Therefore, an electric vehicle navigation system (EVNS) will play an important role to recommend the appropriate route and charging station for charging, taking into account user preferences such as the driving time, the charging price, and the charging wait time [6,7,8,9,10,11].

Authors in [6] proposed an integrated EV navigation system (EVNS) based on a hierarchical game approach considering the impact of the transportation system and the power system. The proposed system consists of a power system operating center (PSOC), charging stations, an EVNS, and EV terminals. The competition between charging stations has been modeled as a non-cooperative game approach. Authors in [7] proposed a charging navigation strategy and an optimal EV route selection based on real-time crowdsensing using a central control center. The control center is collecting information from EV drivers such as the real-time traffic information (vehicle speed and location) while charging stations are uploading charging station information. Authors in [8] proposed an electric vehicle navigation system (EVNS) based on autonomic computing and a hierarchical architecture over vehicle ad-hoc network (VANET). The proposed architecture consists of EVs, charging stations and a traffic information center (TIC). The main functions of TIC are monitoring, analysis, planning and execution. Authors in [9] proposed an integrated rapid charging navigation system based on an intelligent transport system (ITS) center, a power system control center (PSCC), charging stations and EV terminals. The EV terminal determines the best route based on the broadcasted data from the ITS center (status of the traffic system and the power the grid) without any uplink data from the EV side that ensure driver privacy. Authors in [11] proposed a hybrid charging management framework for optimal choice between battery charging/swapping stations for urban EV taxis. The main entities are EVs, charging stations, battery-swapping stations, and a global controller. The global controller is a central entity that receives real-time information from charging/swapping stations and accurately determine the optimal station for supporting the EV taxi charging. However, the above methods are performed in a deterministic environment and do not consider the uncertainties due to the dynamically changing traffic conditions and waiting time of the charging stations. The randomness of the traffic conditions and the charging waiting time can have a significant impact on the performance of the route and charging station selection schemes. In addition, EV charging requests that arrive dynamically according to EV user’s behavior patterns are also another important factor. Therefore, dealing effectively with the uncertainty of unknown future states to select the appropriate route and charging station presents a very considerable challenge. Reinforcement learning can be applied to complex decision-making problems, as reinforcement learning does not rely on prior knowledge of uncertainty.

Deep reinforcement learning (DRL) is a combination of reinforcement learning (decision-making ability) and deep learning (perception function) which is able to address the challenging problems of sequential decision-making. Under a stochastic environment and uncertainty, most of the decision-making problems can be modeled by the Markov decision process (MDP). The MDP is a basic formulation for reinforcement learning, which provides a framework for optimal decision making under uncertainty. The DRL can be divided into two categories: model-based methods and model-free methods. To evaluate the decision behavior, the DRL uses the reward function [12,13,14,15]. With respect to charging navigation of electric vehicle on the move, the main challenges are the location of the electric vehicle (the selected route and charging station are different based on electric vehicle location), charging mode (slow/fast charging), battery state of charge (the travel distance is proportional to remain battery status). Other factors include the randomness of user behaviors, traffic conditions, waiting time at the charging station, and charging prices [16,17,18,19,20,21,22].

Most studies using Reinforcement Learning are studied for the purpose of energy management and cost minimization in EVs, charging stations, and smart buildings [16,17,18,19,20,21]. There are few studies for charging station selection. To minimize charging cost and time, the EV charging navigation using reinforcement learning is proposed in [22]. The proposed system selects the optimum route and charging station without prior knowledge of traffic conditions, charging price, and charging waiting time. However, the proposed system only considers the route from the starting point to the charging station and can significantly increase complexity in the large-size network due to the extraction of features using optimization techniques from inter-node movements. In addition, the impact between EVs serviced by the navigation system and the uncertainty of future EV charging requests was not considered.

In this paper, we propose an optimal route and charging station selection (RCS) algorithm based on model-free deep reinforcement learning. The proposed RCS algorithm minimizes the total travel time with the uncertainty of the traffic conditions and dynamic arrival charging requests. We formulate this RCS problem as a Markov decision process (MDP) model with unknown transition probability. The proposed deep reinforcement learning (DRL) based RCS algorithm learns the optimal RCS policy by the DQN through repeated trial and error. To obtain the feature states for each EVCS, we present the traffic preprocess module, charging preprocess module, and feature extract module. The energy consumption model and link cost function are defined. The performance of the proposed DRL based RCS algorithm is compared to the conventional strategies in terms of travel time, waiting time, charging time, driving time, and distance under the various distributions and number of EV charging requests. The novelty and attribution of the paper are as follows:

• Model-free deep reinforcement learning based optimal route and charging station selection (RCS) algorithm is proposed to overcome the uncertainty issues of the traffic conditions and dynamic arrival EV charging requests.
• The RCS problem is formulated by the Markov Decision Process (MDP) model with unknown transition probabilities.
• The performance of the proposed DRL based RCS algorithm is compared to the conventional algorithms in terms of travel time, waiting time, charging time, driving time, and distance under the various distributions and number of EV charging requests.

The rest of this paper is organized as follows. In Section 2, we discuss the related work. In Section 3, we proposed EV charging navigation system architecture and deep reinforcement learning-based RCS algorithm. Various simulations are carried out in Section 4 to prove the effectiveness and benefits of the proposed approach. Finally, conclusions are drawn in Section 5.

2. Related Work

Generally, the electric vehicle system consists of two main layers: the physical infrastructure layer (electric vehicles, charging stations, transformers, electric feeders, etc.) and the cyber infrastructure layer (IoT devices, sensor nodes, meters, monitoring devices, etc.) [5]. There are many challenges associated with the charging/discharging of the electric vehicles considering many sources of uncertainties and the interaction among different domains including electric vehicles, charging stations, the electric power grid, communication networks, and the electricity market. Deep reinforcement learning has received much attention and is considered as a promising tool to address the aforementioned challenges.

With respect to the electric power grid, authors in [12] introduced the applications of deep reinforcement learning in the power system such as operational control, electricity market, demand response, and energy management. With respect to communications and networking, authors in [13] presented the applications of the deep reinforcement learning approach to address many emerging issues such as data rate control, data offloading, dynamic network access, wireless catching, network security, etc. In [14], the authors presented the application of deep reinforcement learning for the future IoT systems, called autonomous IoT (AIoT), where the environment has been divided into three layers: the perception layer, the network layer, and the application layer. In [15], the application of deep reinforcement learning for cyber security has been presented to solve the security problem with the presence of threats/cyber-attacks.

A comprehensive review of the application of reinforcement learning for autonomous building energy management has been presented in [16]. Reinforcement learning has been applied to different tasks such as appliance scheduling, electric vehicle charging, water heather control, HVAC control, lighting control, etc. In [17], the authors presented a reinforcement learning for scheduling the energy consumption of smart home appliances and distributed energy resources (electric vehicle and energy storage system). The energy consumptions of home appliances and distributed energy resources are scheduled in a continuous action space using the actor-centric deep reinforcement learning method. Authors in [18] proposed a reinforcement learning-based energy management system for a smart building with a renewable energy source, energy storage system, and vehicle-to-grid station to minimize the total energy cost. The energy management system has been modeled using the Markov decision process describing the state space, transition probability, action space, and reward function.

Authors in [19] proposed a model-free real-time electric vehicle charging scheduling based on deep reinforcement learning. The scheduling problem of EV charging/discharging has been formulated as a Markov decision process (MDP) with unknown transition probability. The proposed architecture consists of two networks: a representation network for extracting the discriminative features from electricity prices and a Q network for optimal action-value function. Authors in [20] proposed model-free coordination of EV charging with reinforcement learning to coordinate a group of charging stations. The work focused on load flattening/load shaving (minimizing the load and spreading out the consumption equally over time). Authors in [21] proposed a reinforcement learning approach for scheduling EV charging in a single public charging station with random arrival and departure time. The pricing and the scheduling problem have been formulated as a Markov decision process. The system was able to optimize the total charging rates of electric vehicles and fulfill the charging demand before departure. Authors in [22] proposed a deep reinforcement learning for EV charging navigation with the aim to minimize charging cost (at charging station) and total travel time. The proposed system adaptively learns the optimal strategy without any prior knowledge of system data uncertainties (traffic condition, charging prices, and waiting time at charging stations).

Most of the above-mentioned studies are aimed at managing energy and minimizing costs in EVs, charging stations and smart buildings [16,17,18,19,20,21]. In [22], The proposed system selects the optimum route and charging station without prior knowledge of traffic condition, charging price, and charging waiting time. Due to the extraction of features using optimization techniques from inter-node movements, the proposed system can significantly increase complexity to calculate the feature states in the large-size network. In addition, the uncertainty in future EV charging requests was not considered because the MDP model was designed from a single EV perspective.

Table 1. Summary of literature review for main entities of electric vehicle navigation system.

Ref.	Contributions	Main Entities	Decision
[6]	An integrated EV charging navigation system based on a hierarchical game approach	EV terminals, EVCS, power system operation center (PSOC), and EVNS	EVs decide when to charge and which EVCS should be selected
[7]	EV route selection and charging navigation based on crowd sensing	Electric vehicles, charging stations, decision making center	The decision making center send charging navigation decisions & route selection to EVs
[8]	Electric vehicle navigation system based on vehicular ad-hoc networks (VANETS)	EVs, charging stations, traffic information center	The traffic information center analyzes the traffic information and plans routes accordingly
[9]	Rapid charging navigation strategy based on real time traffic data and status of the power grid	EVs, charging stations, ITS center, power system control center (PSCC)	The ITS and PSCC do not require data from EV side to take decision. EV owners are not required to upload information
[11]	Hybrid charging management framework for optimal choice between battery charging and swapping for urban EV taxi	Electric taxi, charging station, Battery swapping station, Global controller	The global controller selects a proper charging/swapping station as well as enabling charging reservation
[22]	EV charging navigation based on deep reinforcement learning,	EVs, Charging stations, ITS center	EV driver decides based on received EVCS charging price, waiting time and road velocity
Current work	EV navigation algorithm based on deep reinforcement learning,	EVs, charging stations, ITS center, and EVNS control center	The EVNS selects send charging navigation decisions & route selection to EVs

provides a summary of the literature review for the main entities of EVNS. It can be observed that the main entities in our system are EVs, charging stations, ITS center, and EVNS control center.

Table 2. Summary of literature review of main objectives and challenges of reinforcement learning for different electric vehicle applications.

Ref.	Objective	EV Problem	Method	Challenges
[18]	Min. Operation energy cost	Charging/discharging schedules of Building	RL, Q-Learning	Unknown future information (load, energy prices, and amount of energy generation)
[19]	Min. Charging cost	Charging/discharging schedules of EV	DRL, DQN, LSTM	Randomness in traffic conditions, user’s commuting behavior, and the pricing process
[20]	Min. Cost of charging a group of EVs	EV charging scheduling of EVCSs	RL, fitted Q-iteration	Curse of dimensionality due to the continuity and scale of the state and action spaces
[21]	Max. Profit of EVCS	Optimal pricing and charging scheduling	RL, SARSA	Random EV arrivals and departures
[22]	Min. Total cost of an EV	Navigate an EV to EVCS	DRL, DQN	Uncertainty in traffic conditions, charging price, and waiting time
Current work	Min. Total travel time of multiple EVs	Navigate multiple EVs to destination via EVCS	DRL, DQN	Uncertainty in traffic conditions, randomly arrival requests

provides a comparison between our work and other related work for the main objectives and challenges of reinforcement learning.

3. DRL Based Route and Charging Station Selection Algorithm

In this section, we define the overall architecture of EV charging navigation system (EVCNS) and propose the deep reinforcement learning (DRL) based optimal route and charging station selection (RCS) algorithm.

3.1. System Architecture

The overall architecture of the proposed EVCNS is illustrated in Figure 1. It consists of four main elements: electric vehicles (EVs), electric vehicle charging stations (EVCS), intelligent transport system (ITS) center, and EVNS center. The detailed description of each element is given below.

3.1.1. Electric Vehicle (EV)

This study considers the scenario where EVs are on-the-move and regularly check the battery state-of-charge (SoC). If the current SoC is below a threshold value or the EV driver wants to charge, the EV can request the EVCNS center to recommend an appropriate charging station for charging considering the EV’s current location and the final destination.

3.1.2. Electric Vehicle Charging Station (EVCS)

The EVCSs are usually distributed around the city at different locations. Each EVCS consists of parking spots with charging poles. All EVCSs send their information such as current charging price, number of charging EVs, number of waiting EVs to the EVCNS center. Based on the received information, the EVCNS center is able to calculate the expected waiting time and charging time at each EVCS.

3.1.3. Intelligent Transport System (ITS) Center

The ITS center is an advanced management system for transportation which aims to monitor the real-time traffic condition in order to reduce traffic congestion. The information on road traffic conditions such as the number of vehicles on the road and the average velocity are collected using different monitoring devices (IoT sensors, CCTV, roadside units (RSU), etc.) [7,8]. The ITS center updates real-time information on the average road speed to the EVNS center.

3.1.4. Electric Vehicle Charging Navigation System (EVCNS) Center

The EVCNS center is a centralized system that communicates with all entities (EVs, EVCSs and ITS center) using wired/wireless communication networks. The EVCNS enables the selection of the optimal route and the appropriate EVCS for the charging request based on the real-time received information from EVs, EVCSs and ITS center. The detailed operation and description of the EVCNS are described in Section 3.3.

3.2. System Operation

A typical information flow among EVs, EVCSs, ITS center and EVCNS center is shown in Figure 2. Note that, different communication technologies including wired/wireless technologies could be used for data transmission among different entities.

• Step 1: The EV which needs a charging service is requesting for the route & charging station selection service from the EVCNS center. The EV request is transmitted to the EVCNS center through wireless communication technologies.
• Step 2: The EVCNS center is continuously receiving the monitoring information of EVCSs (number of charging vehicles, number of waiting vehicles, etc.) and the road traffic condition (road states, average velocity, etc.) from the ITS center.
• Step 3: Based on the received information from EVCSs and ITS center, the EVCNS center recommends the optimal route & charging station for the requested EV.
• Step 4: The EV confirms the recommended charging station and sends a confirmation message for reservation information to the EVCNS center. The EVCNS center stores the reservation information for the next charging requests.

3.3. Electric Vehicle Charging Navigation System

The EVCNS consists of four main modules: traffic preprocess module (TPM), charging preprocess module (CPM), feature extract module (FEM), and route & charging station selection module (RCSM), as shown in Figure 3.

3.3.1. Traffic Preprocess Module (TPM)

The main function of the TPM is to create and manage traffic matrix and network topology using the received monitoring data by ITS such as center average velocity and road conditions, and the EV charging request. This traffic matrix and the network topology made in the TPM are used as inputs to the feature extract module (FEM).

The network topology can be denoted by a directed graph $G=\left(V,E\right)$, where $V=\left\{1,2,3,\cdots N\right\}$ is a set of vertices and $E=\left\{l_{ij}\right|i,j=1,2,3,\dots ,N\}$ is a set of edges. Each node represents an intersection or end point of the road where $l_{ij}\in E$ is expressed as the road between node $i$ and $j$. The average road velocity $v_{ij}^t$ between node $i$ and $j$ at time step $t$ is managed as the traffic matrix. The traffic network can be modeled as a weighted directed graph, assigning weight to each link. This weight can be variously defined, but in this paper, we aim to minimize the total travel time of EVs, so the weight is defined as follow:

$$w_{ij}^t=\frac{d_{ij}}{v_{ij}^t},$$

(1)

where $w_{ij}^t$ is the weight value of $l_{ij}$ and $d_{ij}$ is the distance of $l_{ij}$. In other words, the weight value means the time required to pass through the $l_{ij}$. When weights are applied for all links, we can obtain the shortest time path using Dijkstra algorithm, which is used to find the least cost path problem [23]. Thus, the TPM provides the traffic matrix and network topology to the FEM by updating and maintaining traffic information collected from the ITS center in real time.

3.3.2. Charging Preprocess Module (CPM)

The main function of the CPM is to communicate with all EVCSs distributed around the city. The received information from EVCSs includes charging status data such as number of charging EVs and number of waiting EVs. This information is used by CPM to calculate the available charging time and waiting time for all EVCSs. In addition, the available charging time and expected waiting time are used for the FEM. This information is updated periodically, as soon as EV’s requests arrive.

The CPM manages the charging reservations to estimate charging waiting time for future EV charging requests. The expected waiting time at each EVCS k is expressed as ${\tau }_{wait}^k$. This charging waiting time can be obtained using the algorithm to obtain the expected charging waiting time from Ref. [24]. The algorithm can estimate the expected waiting time for the charging request based on past information of EV charging reservations.

3.3.3. Feature Extract Module (FEM)

The FEM takes inputs from TPM, CPM and EVs. The FEM extracts the feature state of a request for each EVCS, such as expected driving time, driving distance, arrival time, and charging time. The output of the FEM is the input to the route & charging station selection module (RCSM). These feature states are used to represent states used in the Markov decision process (MDP) model.

Each EV charging request randomly arrives at the EVNS center during the time horizon $T$. The EV charging request consists of the following tuple: $CR=\left\{P_s,P_d,SO{C}_{cur},SO{C}_{req}\right\}$, where $P_s$ is the initial position, $P_d$ is the location of the destination, $SO{C}_{cur}$ is the current battery state of charge, and $SO{C}_{req}$ is the required SOC. In order to extract the features of the expected arrival time, the charging time, and the charge amount of EVs, the route for each charging station from the current position of the EV must first be selected. To find the shortest time path for each EVCS, the above-mentioned Dijkstra algorithm and the weighted graph are considered. Based on that route, the estimated arrival time to each charging station and the expected total driving time required to the final destination are calculated. The values calculated here are expected values based on the current traffic condition without any prior knowledge that will vary in the future. It is also possible to calculate the expected charge of EV by using the path to the specific EVCS. Note that each feature state is extracted based on the current time information.

We define energy consumption and time models of EVs. The energy consumption and time model are used to represent the states of EVCSs and traffic conditions.

$$e_l=ϵd_l, \forall l\in E,$$

(2)

where $e_l$, $ϵ$ and $d_l$ are energy consumption of link $l$, energy consumption rate (kW/km), and distance of link $l$, respectively.

When the EV arrives at EVCS k, the $SO{C}_{arr}^k$ is given as follows:

$$SO{C}_{arr}^k=SO{C}_{cur}-{{\displaystyle \sum }}_{\forall l\in L_f^k}\frac{e_l}{E_{max}}, 0<SO{C}_{arr}^k<SO{C}_{req}, \forall k\in K,$$

(3)

where $L_f^k$ is the set of links from origin to EVCS $k$ and $E_{max}$ is the maximum battery capacity of EVs.

From Equations (2) and (3), the estimated charging amount energy $E_{ch}^k$ at EVCS k can be calculated by the following Equation (4).

$$E_{ch}^k=\left(SO{C}_{req}-SO{C}_{arr}^k\right)\times E_{max}, \forall k\in K$$

(4)

The charging time ${\tau }_{ch}^k$ at EVCS k is also estimated by using Equation (5) based on the estimated charging amount.

$${\tau }_{ch}^k=\frac{E_{ch}^k}{\eta \mu }, \forall k\in K$$

(5)

where $\eta$ is the charging efficiency and $\mu$ is the charging power of EVCS. We assume that the charging poles of all charging stations provide the same charging power.

Similar to Equation (1), driving time ${\tau }_l^t$ to move a link l at time step t is represented by $d_l/v_l^t$. Therefore, the total driving time ${\mathsf{\tau }}_{drive}^k$ of route $L^k$ from the origin to the destination via the EVCS k is as shown in Equation (6).

$${\tau }_{drive}^k={\displaystyle \sum }_{\forall l\in L^k}{\tau }_l^t, \forall k\in K$$

(6)

Expected arrival time ${\tau }_{arr}^k$ at EVCS k can be calculated as follows:

$${\tau }_{arr}^k={\tau }_r+{\displaystyle \sum }_{\forall l\in L_f^k}{\tau }_l^t, \forall k\in K$$

(7)

where ${\tau }_r$ is the charging request time and ${\displaystyle \sum }_{\forall l\in L_f^k}{\tau }_l^t$ is the driving time to EVCS k.

Therefore, the total estimated travel time for the EV charging request is as follows:

$${\tau }_{tr}^k={\tau }_{drive}^k+{\tau }_{wait}^k+{\tau }_{ch}^k, \forall k\in K$$

(8)

where the estimated travel time is determined by the EVNS upon arrival of the charging request and is not the actual value. This value is used as the reward function of the MDP in the training of DQN.

The feature states for each EVCS can be obtained from the above formulations. Note that these values are the estimated values based on the information of current time step. It is difficult to use all information about the environment as a feature state under the curse of dimensionality. Therefore, the current environment is defined using the estimated values for each EVCS as reduced feature states.

3.3.4. Route & Charging Station Selection Module (RCSM)

The function of the RCSM is to make a decision for the optimal route and the EVCS for each EV charging request using a well-trained Deep Q Network (DQN). Due to the curse of dimensionality, it is difficult to use Q-learning with the table look-up method for large-scale problems in real-world scenarios. In this work, we use the DQN to approximate the optimal action-value function. The feature states of each charging station extracted from the FEM and the charging request information of the EV are concatenated as state $s_t$ at time step $t$. The state $s_t$ concatenated feature vector is used as an input to that DQN. We deal with the training process and details of DQN in detail in Section 3.4.

3.4. Deep Q Network for Route and Charging Station Selection

3.4.1. Markov Decision Process Modeling

In this section, we formulate the route and charging station selection problem as a Markov Decision Process (MDP) model without the unknown transition probability. The MDP is a classical formalization of a sequential decision-making problem. The MDP is characterized by a finite state space, a finite set of actions, transition probability, and a reward function associated with the transition. In view of the EVNS, the EV charging request that arrives dynamically in the operation time is modeled as MDP in a stochastic environment. The MDP is defined as a set of states, actions, transition probability, and reward function.

• System States: The state including the arrived EV charge request $C{R}_t$ and information for each EVCS is represented as ${\mathrm{s}}_{\mathrm{t}}$, as given in Equation (9), where $A{T}_t, W{T}_t,D{T}_t, D_t$ are the set of expected arrival time, waiting time, driving time, and driving distance for each EVCS, respectively. The EV charge request $C{R}_t$ consists of the starting point $P_s$, the destination location $P_d$, the request time ${\tau }_r$, the request time interval $\Delta t$, the current SOC, $SO{C}_{cur}$, and the required SOC, $SO{C}_{req}$, as given in Equation (10). Since the charging requests arrive dynamically, the time difference $\Delta t$ between the past request and the current request is provided as an additional feature. We assume that a fixed number of EV charge requests $C{R}_t$ arrive within the operation time T because the possible status is infinite when the $C{R}_t$ continues to arrive. The set of expected waiting time, driving time, and driving distance represents the expected values for each EVCS selection, which is to reduce the number of rapidly increasing dimensions to represent the current environment.

  $$s_t=\left\{C{R}_t,A{T}_t,W{T}_t,D{T}_t,D_t\right\}$$

  (9)

  $$C{R}_t=\left\{P_s,P_d,{\tau }_r,\Delta t,SO{C}_{cur},SO{C}_{req}\right\}$$

  (10)

  $$A{T}_t=\left\{{\tau }_{arr}^1,{\tau }_{arr}^2,\dots ,{\tau }_{arr}^k\right\}, \forall k\in K$$

  (11)

  $$W{T}_t=\left\{{\tau }_w^1,{\tau }_w^2,\dots ,{\tau }_w^k\right\}, \forall k\in K$$

  (12)

  $$D{T}_t=\left\{{\tau }_{drive}^1,{\tau }_{drive}^2,\dots ,{\tau }_{drive}^k\right\}, \forall k\in K$$

  (13)

  $$D_t=\left\{d_w^1,d_w^2,\dots ,d_w^k\right\}, \forall k\in K$$

  (14)
• Action and Transition Probability: The EVNS can take an action for each state $s_t$. This action represents an index of EVCS and includes the route planned corresponding EVCS k from $P_s$ to $P_d$ via an EVCS k using the FEM. The action space is the set of K.

  $$a_t \in \left\{1,2,\dots ,k\right\}$$

  (15)

  The function $P\left(s_{t+1}|s_t,a_t\right)$ is transition probability from $s_t$ to $s_{t+1}$ by the agent taking an action $a_t$. Without accurate models of the environment and prior knowledge of uncertainty, it is difficult to define the transfer probability. Therefore, in this work, transition probability is learned using model-free deep reinforcement learning approach with unknown transition probability. The learning process is to learn the policy that maximizes cumulative rewards through repeated trial and error.
• Reward: The reward function is divided into two parts, one for terminal state and one for non-terminal state. Where the terminal state indicates when operation time T expired. If it is not a terminal state, the reward is defined as the expected travel time that can be obtained by selecting action $a_t$ with the corresponding EVCS, even if the EV chooses the EVCS, because the actual travel time has not been revealed due to the real-time traffic conditions and the charging behavior of other EVs. In terminal state, the actual travel time of all EV requests is revealed, and the difference between actual travel time and expected travel time is defined as the reward. The reward function is formulated as

  $$r_t=\{\begin{array}{c}\hspace{1em}-{\tau }_{tr}^a\hspace{1em}\hspace{1em},t\ne T\\ - {\displaystyle \sum }_{n \in N_{CR}}{\tau }_{tr, n}^{true}-{\tau }_{tr, n}^{ept} , t=T\end{array} ,$$

  (16)

  where ${\tau }_{tr,n}^{true}$ is the actual travel time for charging request n, ${\tau }_{tr,n}^{ept}$ is the expected travel time for charging request n. The reward function has negative values in both cases. The reinforcement learning aims to maximize cumulative rewards. Therefore, it is defined as a negative value to minimize travel time.
• Action-Value Function: The action-value function denotes $Q_{\pi }\left(s,a\right)$, which is the expected total summation of future rewards for using action $a$ in a certain state $s$ following a policy $\pi$.

  $$Q_{\pi }\left(s,a\right)=E_{\pi }[{{\displaystyle \sum }}_{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}|s_t=s,a_t=a]$$

  (17)

  where $\mathsf{\gamma }$ is the discount factor, $0 < \gamma < 1$, which balances the importance between the immediate reward and future rewards. The objective of the EVCS selection problem based on the DQN is to find an optimal policy $\pi$ to maximize the cumulative rewards or minimize total travel time. The optimal action-value function is shown as follow:

  $$Q_{*}\left(s,a\right)=\underset{\pi }{\max }{Q}_{\pi }\left(s,a\right)$$

  (18)

3.4.2. Training of DQN

The objective of training DQN is to find the optimal action-value function. To get the optimal action-value function, we use the Deep Q-learning based on Bellman optimal equation. We use the fixed target-network and experience replay buffer [25,26].

The Algorithm 1 summarizes the procedures of the DRL based EVNS with DQN. Firstly, the DQN parameters $\theta$ is initialized randomly. The target network $\overline{\theta }$ is initialized by $\theta$ and an empty experience buffer is generated to store samples given by $\left(s_t,a_t,r_r,s_{t+1}\right)$. The training of DQN is carried out through M episodes. For each epoch, we assume that $N_{CR}$ charging requests are dynamically arrived at EVNS within operation time. The DQN takes an action $a_t$ based on $\epsilon$-greedy strategy. Then EVNS recommends an EVCS indexed $a_t$. The DQN obtains immediate $r_t$ and $s_{t+1}$ is generated with new arrived $C{R}_{t+1}$ from the environment. We store the experience sample $\left(s_t,a_t,r_r,s_{t+1}\right)$ in the experience replay buffer. Here we use training threshold $\psi$ to train after a certain number of samples have been accumulated. The target action-value $y_t$ is calculated as Equation (19). The Q-learning update uses the loss function of Equation (20). The loss function is minimized by updating the Q network parameter $\theta$ using gradient decent as Equation (21). If the number of samples in the buffer is larger than $\psi$, then the gradient descent step is performed to update the DQN parameters using mini-batch with random samples. After that, the target network is updated after every B training sessions on the DQN. The training of DQN is illustrated in Algorithm 1 and the training process are present by Figure 4.

$$y_t=r_{t+1}+\gamma \underset{a^{\prime }}{\max }Q\left(s_{t+1},a^{\prime }|\overline{\theta }\right)$$

(19)

$$L\left({\theta }_t\right)={{\displaystyle \sum }}_{i=1}^F\left[(y_t - Q{(s,a|{\theta }_t)}^2\right]$$

(20)

$${\theta }_{t+1}={\theta }_t+\alpha \nabla L\left({\theta }_t\right)$$

(21)

Algorithm 1. Training process of DQN.

Randomly initialize DQN parameters $\theta$. Initialize target network parameters $\overline{\theta }=\theta$. foreach epoch = 1 to M do Generate the initial state $s_0$ foreach$CR$ = 1 to $N_{CR}$ do Take an action $a_t$ based on $\mathsf{\epsilon }$-greedy Execute action $a_t$ and then obtain reward $r_t$ and $s_{t+1}$ Store $sample\left(s_t,a_t,r_t,s_{t+1}\right)$ in experience replay buffer if$\psi >N_{sp}$do $y_t=r_{t+1}+\gamma \underset{a^{\prime }}{\max }Q\left(s_{t+1},a^{\prime }|\overline{\theta }\right)$ Perform a gradient descent step on $(y_t–Q{\left(s_t,a_t|\theta \right)}^2$ using sample batch Update DQN parameters $\theta$ using (21) Update target-network every $\mathrm{B}$ steps, $\overline{\theta }=\theta$

3.4.3. EVCS Selection Using Trained DQN

For dynamically arrived charging requests, the EVCS selection using well-trained DQN by Algorithm 1 works as shown in Figure 5 and Algorithm 2. Firstly, the trained DQN parameters are loaded. A charging request arrives within the operation time, an input feature vector for the request is generated using the FEM. The feature vector is used as the input of DQN, then DQN calculates $Q_{*}\left(s_t,a|\theta \right)$ as the output. The action with the maximum Q is selected. The selected action represents the index of EVCS and the corresponding path is also recommended.

Algorithm 2. Route & Charging Station Selection.

Load the DQN parameters $\mathsf{\theta }$ trained by Algorithm 1. foreach$CR=1$ to $N_{CR}$ do Generate input feature vector using FEM DQN calculates action-value $Q_{*}\left(s_t,a|\theta \right)$ $a_t=\underset{a\in K}{argmax} Q_{*}\left(s,a\right)$ Recommend EVCS $a_t$ and corresponding route

4. Performance Evaluation

In this section, we give a detailed description of the environment and training parameters setting for the simulations. The performance of the proposed algorithm has been evaluated with the conventional charging station selection strategies.

4.1. Simulation and Training Setup

This work considers electric vehicles with a maximum battery capacity of 54.75 kWh [27]. The initial SoC and required SoC of EVs are configured using a uniform distribution. The charging power of EVCS is 60 kW [9] and the energy consumption rate is 0.16kW/h [28], as shown in

Table 3. Simulation parameters.

Parameter	Value
Max. Battery capacity	54.75 kWh
Initial SOC	Uniform (0.2, 0.4)
Required SOC	0.9
Energy consumption rate	0.16 kW/km
Number of EVCS	3
Number of charging pole	2
Charging power	60 kW
Charging efficiency	0.9
Number of nodes	39
Number of links	134

. The network topology consists of 39 nodes and 134 links [22]. We assume that the three EVCS are scattered at the network topology. The roads are divided into three categories according to the maximum speed limits. The speed limits of each category are 60 km/h, 80 km/h, and 120 km/h, respectively. The average speed of each load is randomly generated between $\left(v_{max}\times 0.7,v_{max}\right)$ and updated every 5 min.

The simulation is performed in a variety of environments in order to show the efficiency and flexibility of the proposed algorithm. For example, we considered varying the number of different EV charging requests and the distribution of arrival time for the EV charging requests [29]. The arrival time of EV charging requests is randomly generated according to the uniform distribution and the normal distribution. The EV charging requests arrive between 360 and 1200 min for the uniform distribution. The mean of the normal distribution is 600 min and the standard deviation is 200 min. The two distributions are shown in Figure 6.

The simulation code is written in Python with TensorFlow [30]. The training environment is on a computer with i7-6700 CPU and GTX 970. The DQN consists of an input layer with 18 nodes, three hidden layers with 800 nodes, and the output layer size is 3. The training parameters of the proposed model are given in

Table 4. Training parameters.

Parameter	Value	Parameter	Value
Number of epochs, M	7000	Target Net. update period, $B$	10
Discount factor, $\gamma$	0.99	Batch size, $F$	256
Learning rate, $\alpha$	0.01	Training threshold, $\psi$	5000

. The convergence of cumulative rewards during the training process is shown in Figure 7. Up to the first 50 epochs, the experience is stored in the replay buffers according to random policy and subsequently learned by the $\epsilon$-greedy strategy. Figure 7 shows convergence in 6000 epochs. The training time is about 7 h.

4.2. Performance Evaluation

The proposed DRL based algorithm is evaluated and compared with three conventional benchmarking strategies. The Benchmarking strategies are summarized in

Table 5. Benchmarking strategies.

Objective	EVCS Selection Function
Min. Distance	$\underset{k\in K}{argmin}\left({\displaystyle \sum }_{l\in L^k}{d}_l\right)$
Min. Travel Time	$\underset{k\in K}{argmin}\left(T_{drive}^k+T_{waiting}^k+T_{ch}^k\right)$
Min. Waiting time	$\underset{k\in K}{argmin}\left(T_{waiting}^k\right)$

.

• First, the Minimum Distance (MD) strategy aims to minimize the traveled distance, therefore, the charging time and waiting time at the charging station are not considered. This approach is used as a benchmarking strategy [6,27,31].
• Second, the Minimum Travel Time (MTT) strategy aims at minimizing the total travel time, including driving, waiting, and charging time, similar to the proposed algorithm. The strategy selects the EVCS and corresponding route that takes a minimum travel time [24].
• Third, the Minimum Waiting Time (MWT) strategy aims to select an EVCS with a minimum waiting time [24,32]. The MWT selects a corresponding route with minimum driving time.

The total travel time of EVs represents the total trip time including the driving, charging, and waiting time from source to the destination via an EVCS. Figure 8 shows the average travel time of EV charging requests according to different strategies with various distributions of EV requests. This result was carried out under scenarios in which 100 requests are generated according to uniform and normal distributions. The proposed DRL based algorithm shows the best performance with the lowest average total travel time. Compared with MTT, MWT and MD strategies in the uniform distribution case, DRL shows performance improvements of about 4%, 20% and 30%, respectively. In the normal distribution scenario, where EV charging requests occur intensively at certain times, the ability to reduce total travel time by 5%, 20% and 29% for DRLs is also identified.

The MTT strategy selects the route and an EVCS with the least total travel time when EV charging requests arrive. Although MTT and the proposed algorithm have the same objective, it can be seen that the proposed algorithm can efficiently select the appropriate route and EVCSs for dynamically arrived EV charging requests. In particular, showing shorter waiting times with similar results in other factors means that the policy to select the optimal route and EVCS has been well trained. In the normal distribution scenario, the wait time for all strategies is increased because EV requests are gathered at a specific time. The proposed DRL showed improvements over other strategies, even in a scenario where many requests occur at a certain time, such as the rush hour. Therefore, the proposed DRL has the ability to select the optimal route and EVCS flexibly and efficiently for future unknown EV charging requests.

In addition, the performance of the proposed DRL algorithm is also analyzed for the number of EV charging requests. As with the above scenarios, we set the number of EV charging requests occurring during the day to 80, 100, 120, and 140, depending on each distribution. Figure 9 and Figure 10 show the total distance and travel time according to different numbers of EV charging requests.

In Figure 9, we can observe that the proposed DRL selects a longer path compared to MD but the total travel distance of MTT is similar. The MWT can select the EVCSs with minimum waiting time by selecting long-distance EVCSs, which increases total driving distance and time. From the perspective of total travel time, it can be confirmed that the influence of waiting time is greater than driving distance and driving time.

Figure 10 shows the total travel time of each strategy under the different number of EV charging requests. The total travel time of all strategies is increased as the number of EVs charging requests increases, but the proposed DRL in all scenarios showed the lowest total travel time. From the above results, we have confirmed that the proposed DRL has well learned the policy of selecting the optimal route and EVCS regardless of the distribution or number of EV charging requests. Therefore, the proposed well-trained DRL based algorithm showed the potential capacity to provide the optimal route and EVCSs selection for minimizing total travel time in stochastic environments where the distribution and number of future EV charging requests according to EV user behavior patterns are unknown.

5. Conclusions

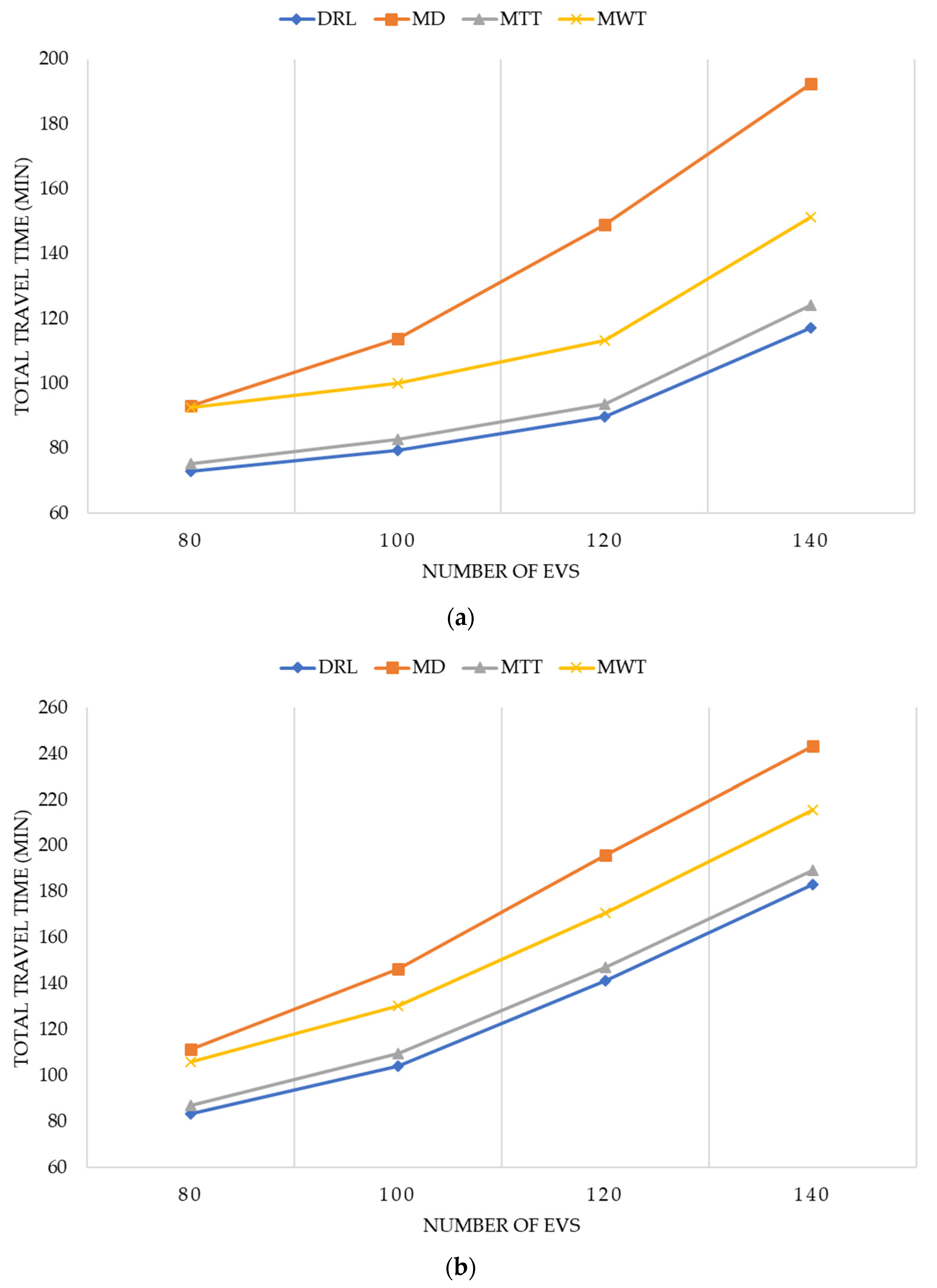
This paper proposed a framework for an electric vehicle charging navigation system (EVCNS) which aims to select the optimal route and electric vehicle charging station (EVCS). The proposed architecture consists of four main elements: EVs, EVCSs, an intelligent transport system (ITS) center, and an EVCNS center. The EVCNS includes four main modules: traffic preprocess module (TPM), charging preprocess module (CPM), feature extract module (FEM), and route & charging station selection module (RCSM). The TPM module receives traffic information from the ITS center such as the average road velocity where the data are processed in order to define the road traffic matrix and the network topology. The CPM module communicates with EVCSs and received information such as the number of charging vehicles, number of waiting vehicles. The FEM module extracts the feature state from inputs (TPM, CPM and EVs), and feeds it to the route & charging station selection module (RCSM). The RCSM makes the decision based on a well-trained Deep Q Network to select the optimal route and the charging station for each EV charging request. The performance of the proposed algorithm is compared with conventional strategies including minimum distance strategy, minimum travel time strategy, and minimum waiting time strategy in terms of travel time, waiting time, charging time, driving time, and distance under the various distributions and number of EV charging requests. The results showed that the proposed well-trained DRL based route and charging station selection algorithm improved the performance by about 4% to 30% compared to conventional strategies. The proposed well-trained DRL based algorithm showed the potential capacity to provide the optimal route and charging station selection for minimizing total travel time in real-world environments where the distribution and number of future EV charging requests according to EV user behavior patterns are unknown. Future work would consider applying the proposed algorithm for a real scenario with actual EV user behavior patterns.