Author Contributions
Conceptualization, Y.J.; methodology, Z.Z., Y.J., and L.Z.; software, G.H. and G.J.; validation, G.H. and G.J.; formal analysis, G.H.; investigation, G.H.; resources, G.H.; data curation, G.H.; writing—original draft preparation, G.H.; writing—review and editing, G.H., G.J. and Y.J.; visualization, G.H.; supervision, Y.J. and L.Z.; project administration, Z.Z., L.Z. and Y.J.; funding acquisition, Z.Z., L.Z. and Y.J. All authors have read and agreed to the published version of the manuscript.
Figure 1.
Numerical simulation procedure.
Figure 1.
Numerical simulation procedure.
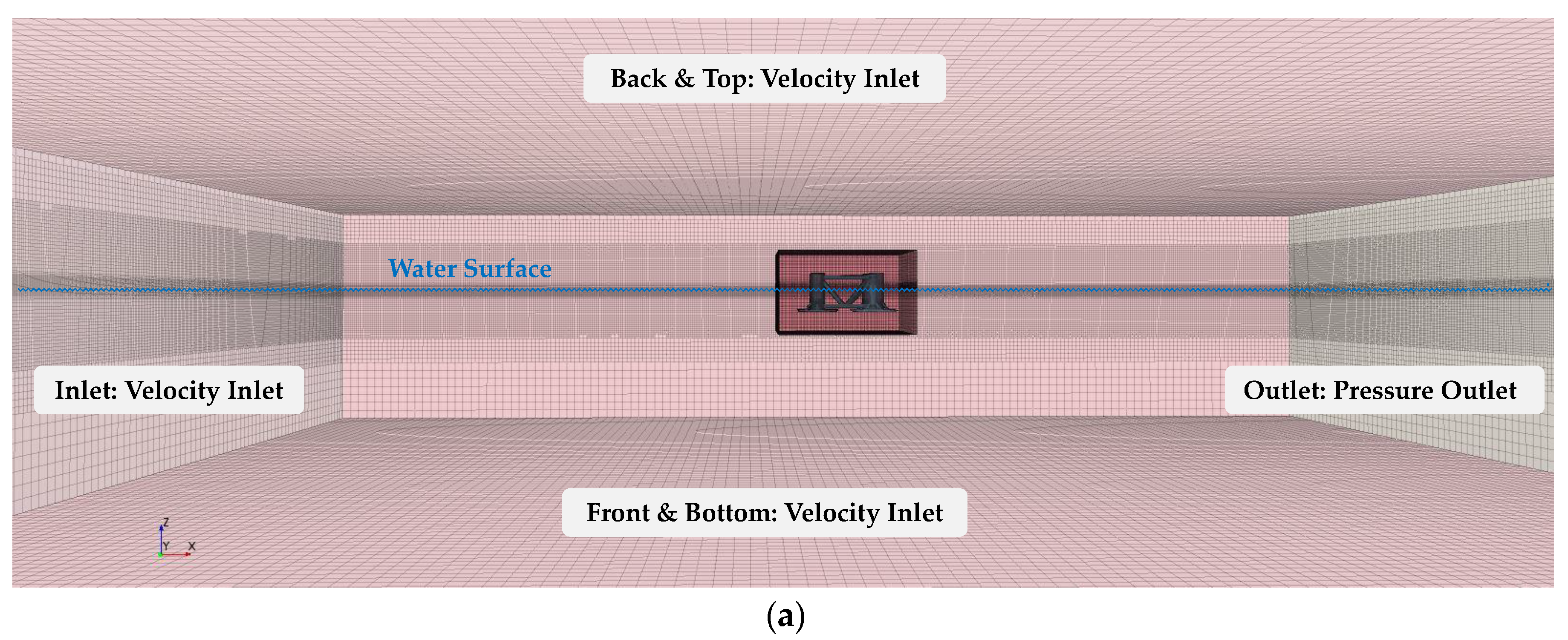
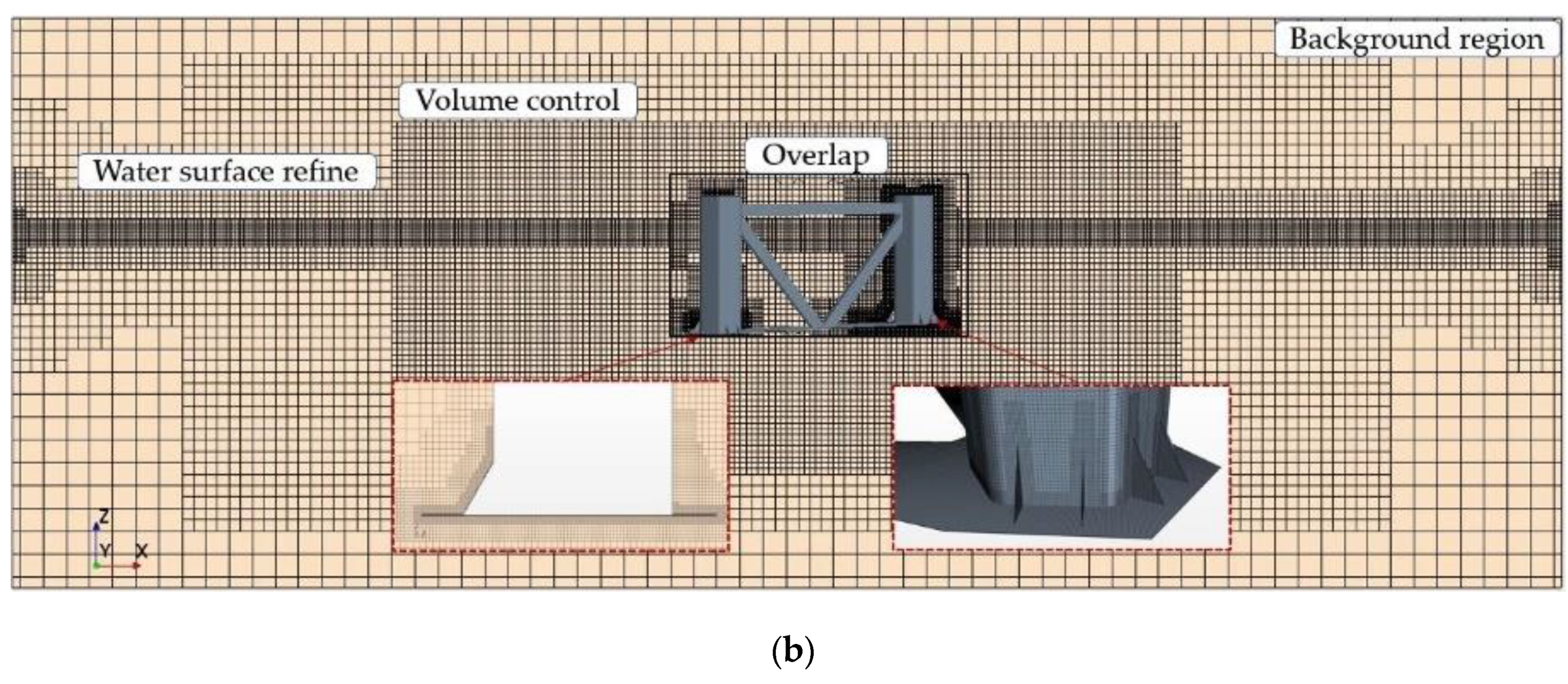
Figure 2.
The whole fluid domain: (a) Boundary conditions in CFD, (b) Mesh distribution in xz-plane and close-up view of mesh around heave plate.
Figure 2.
The whole fluid domain: (a) Boundary conditions in CFD, (b) Mesh distribution in xz-plane and close-up view of mesh around heave plate.
Figure 3.
(a) WindFloat-type platform and (b) HexaSemi WADAM models.
Figure 3.
(a) WindFloat-type platform and (b) HexaSemi WADAM models.
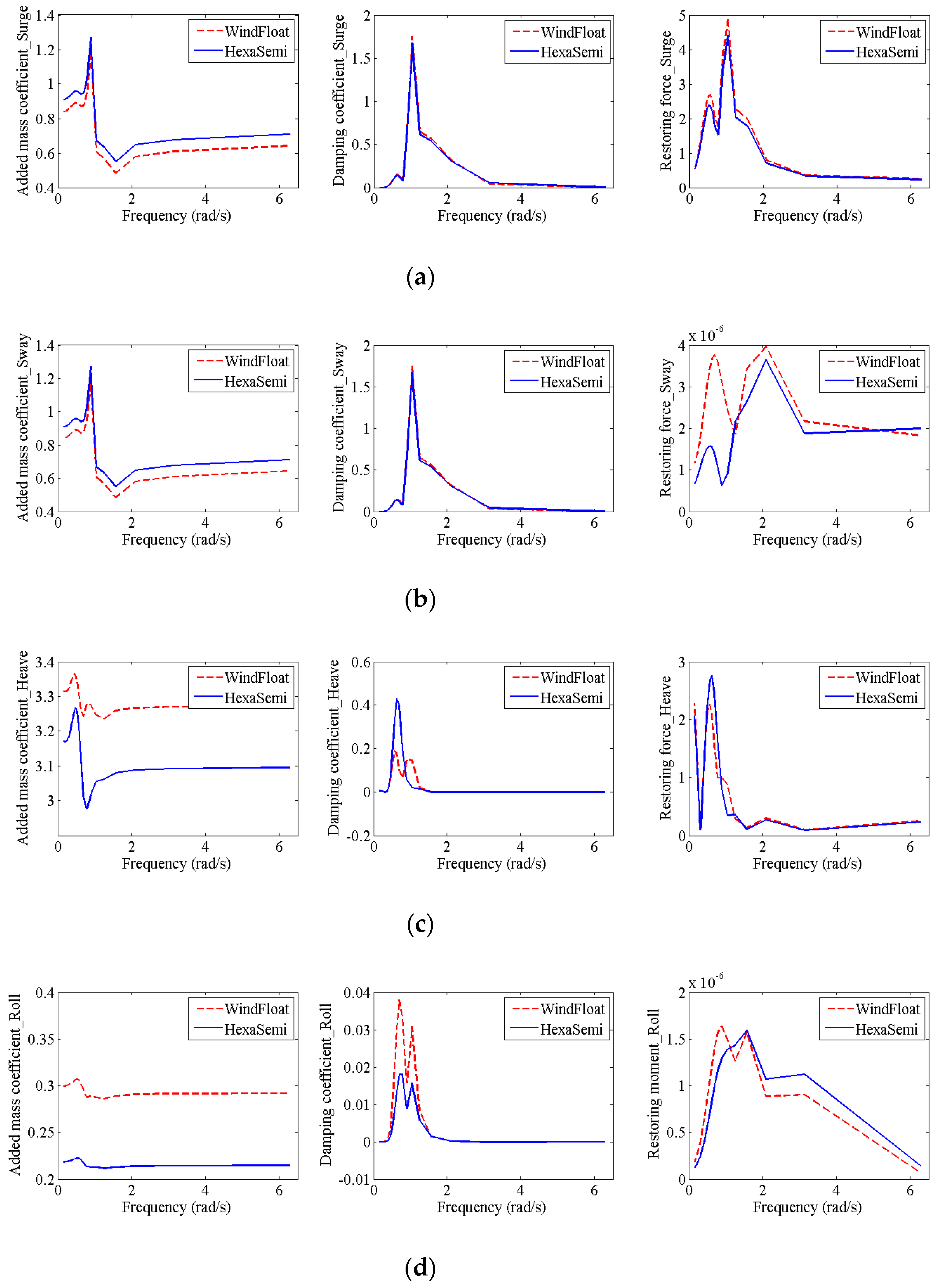
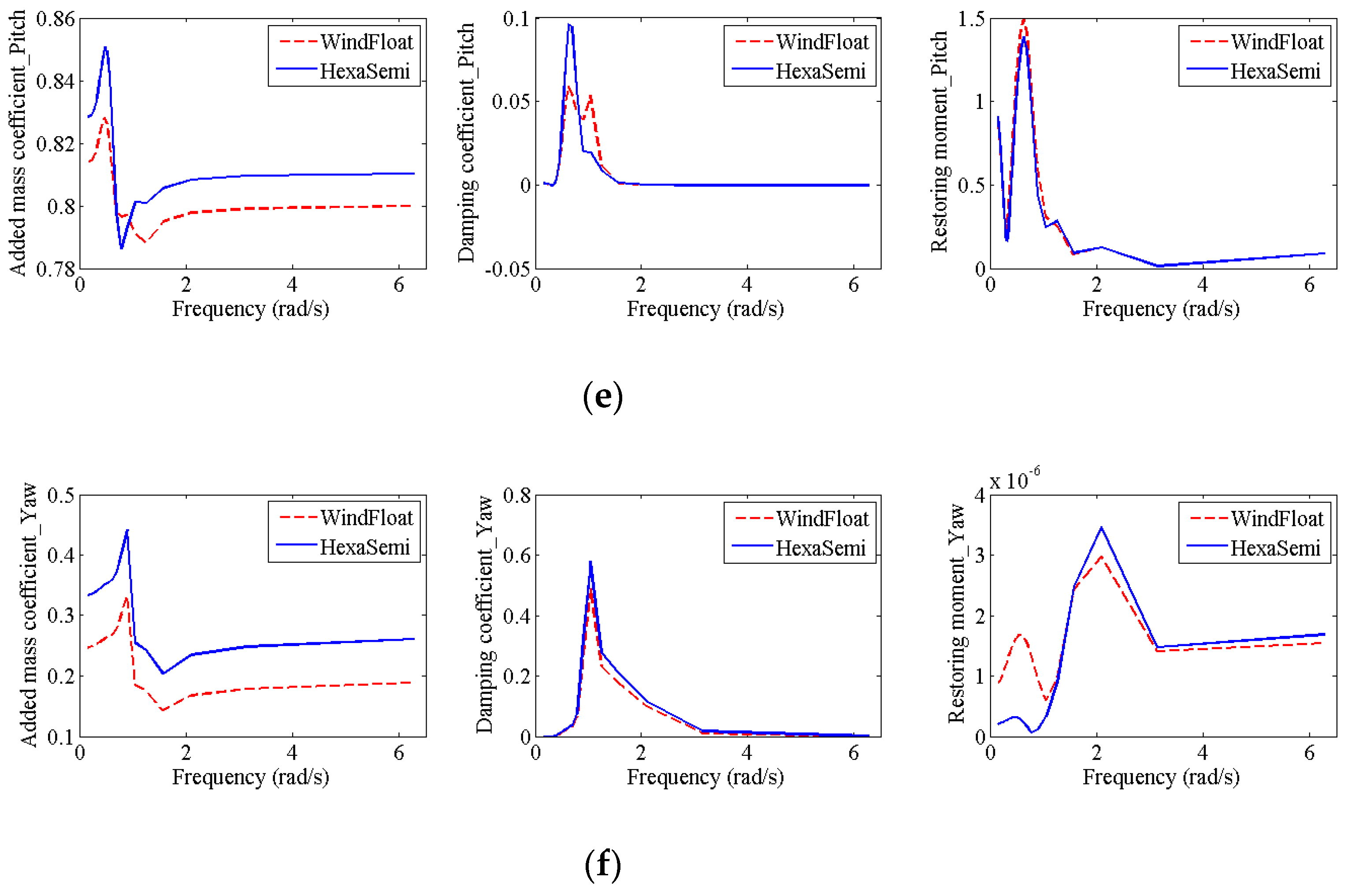
Figure 4.
The comparisons of hydrodynamic coefficients in all six DOFs: (a) surge, (b) sway, (c) heave, (d) roll, (e) pitch, (f) yaw.
Figure 4.
The comparisons of hydrodynamic coefficients in all six DOFs: (a) surge, (b) sway, (c) heave, (d) roll, (e) pitch, (f) yaw.
Figure 5.
The total circumferences of (a) WindFloat-type platform and (b) HexaSemi.
Figure 5.
The total circumferences of (a) WindFloat-type platform and (b) HexaSemi.
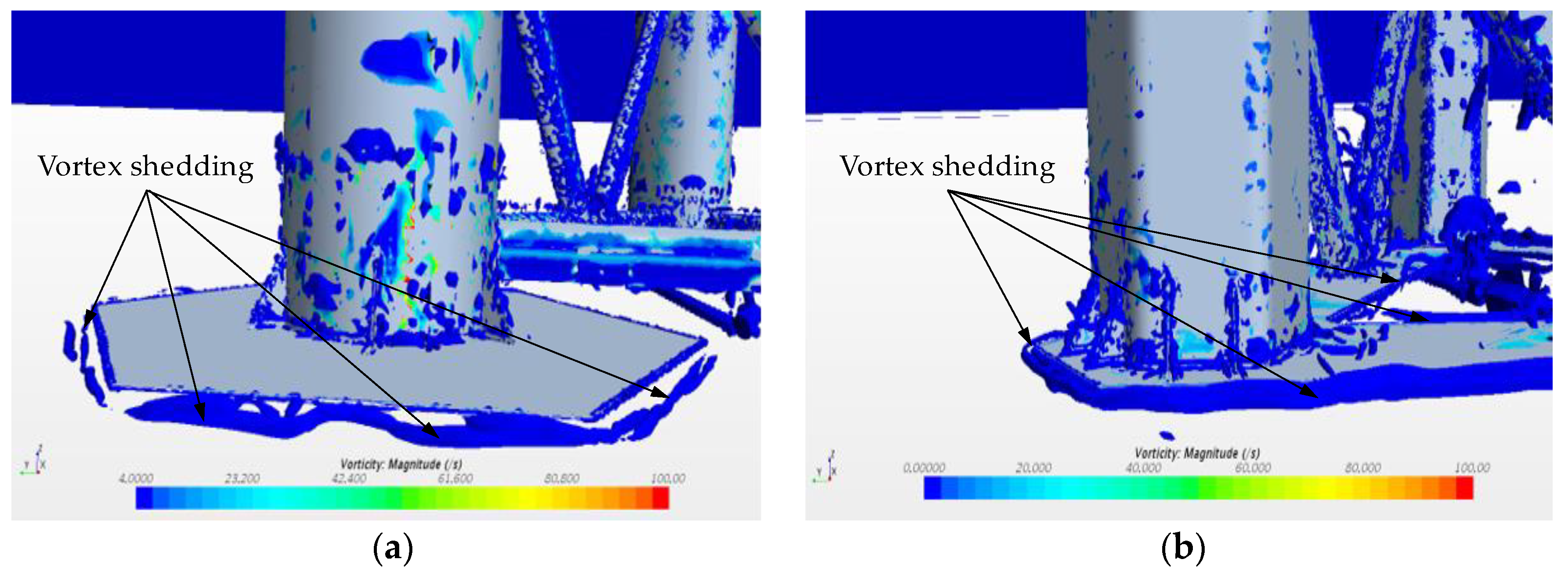
Figure 6.
The vorticity of (a) WindFloat-type platform and (b) HexaSemi.
Figure 6.
The vorticity of (a) WindFloat-type platform and (b) HexaSemi.
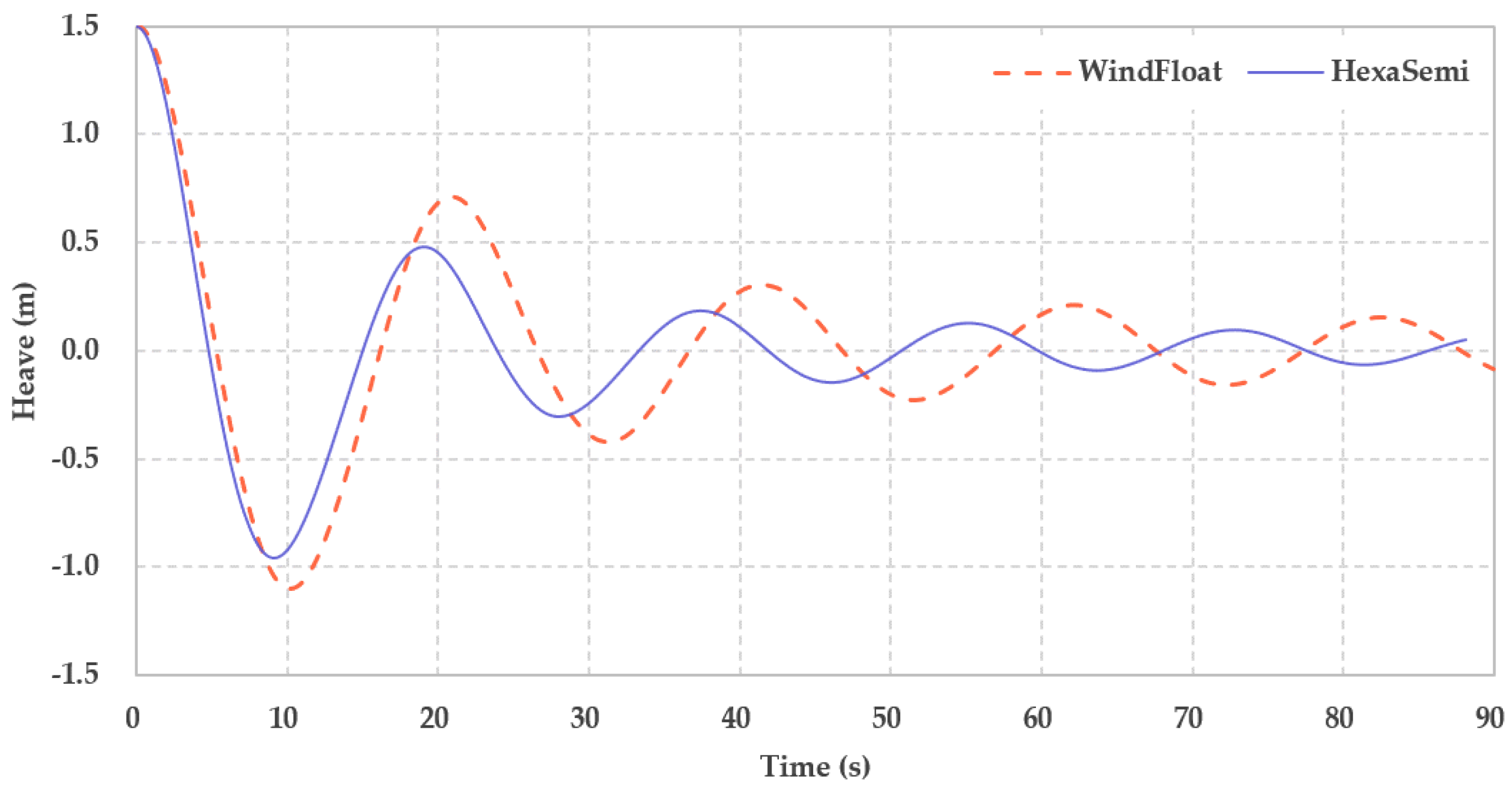
Figure 7.
Free decay curves of heaving (WindFloat-type platform and HexaSemi).
Figure 7.
Free decay curves of heaving (WindFloat-type platform and HexaSemi).
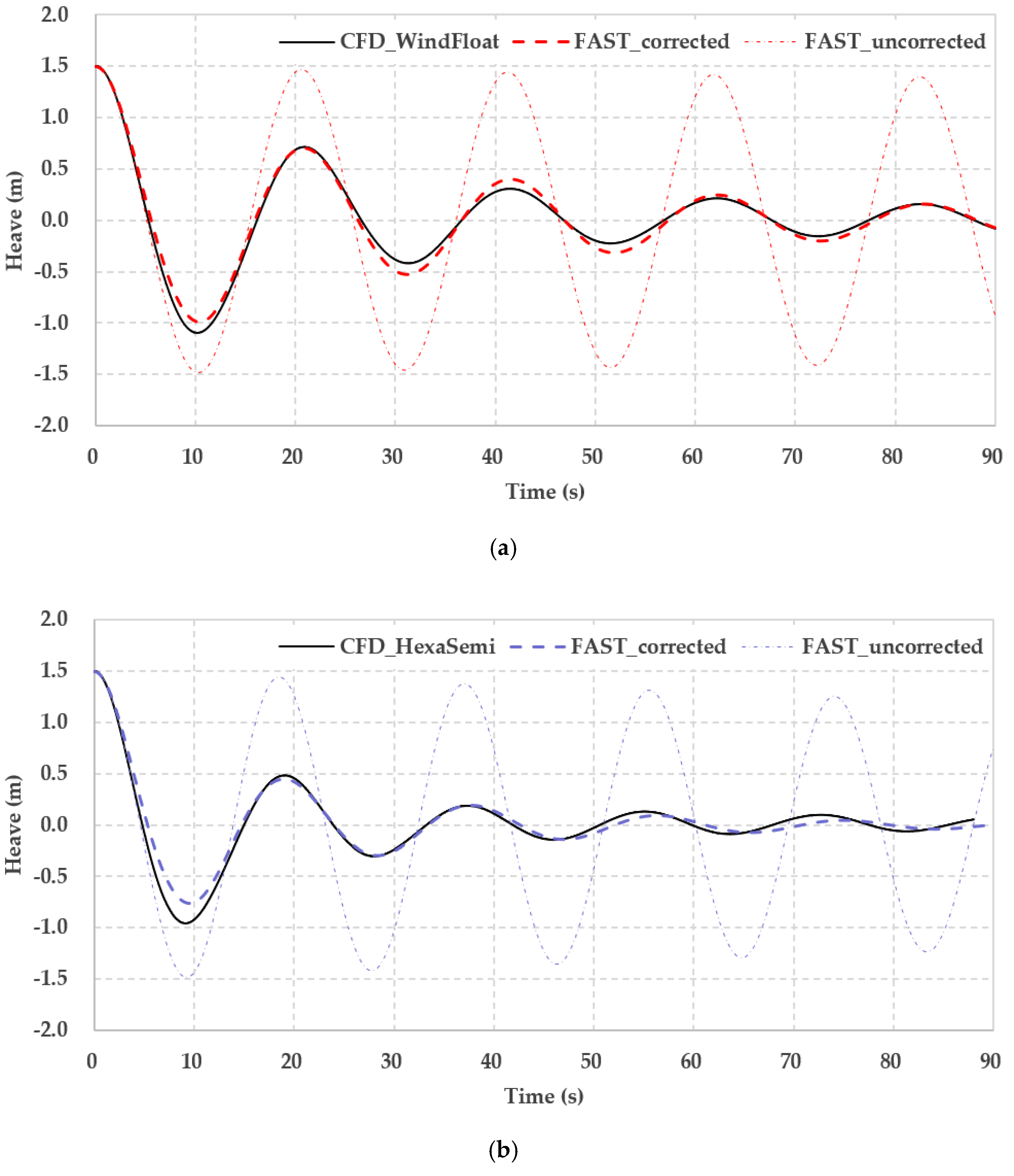
Figure 8.
Three heave-decay simulations of (a) the WindFloat-type platform and (b) HexaSemi.
Figure 8.
Three heave-decay simulations of (a) the WindFloat-type platform and (b) HexaSemi.
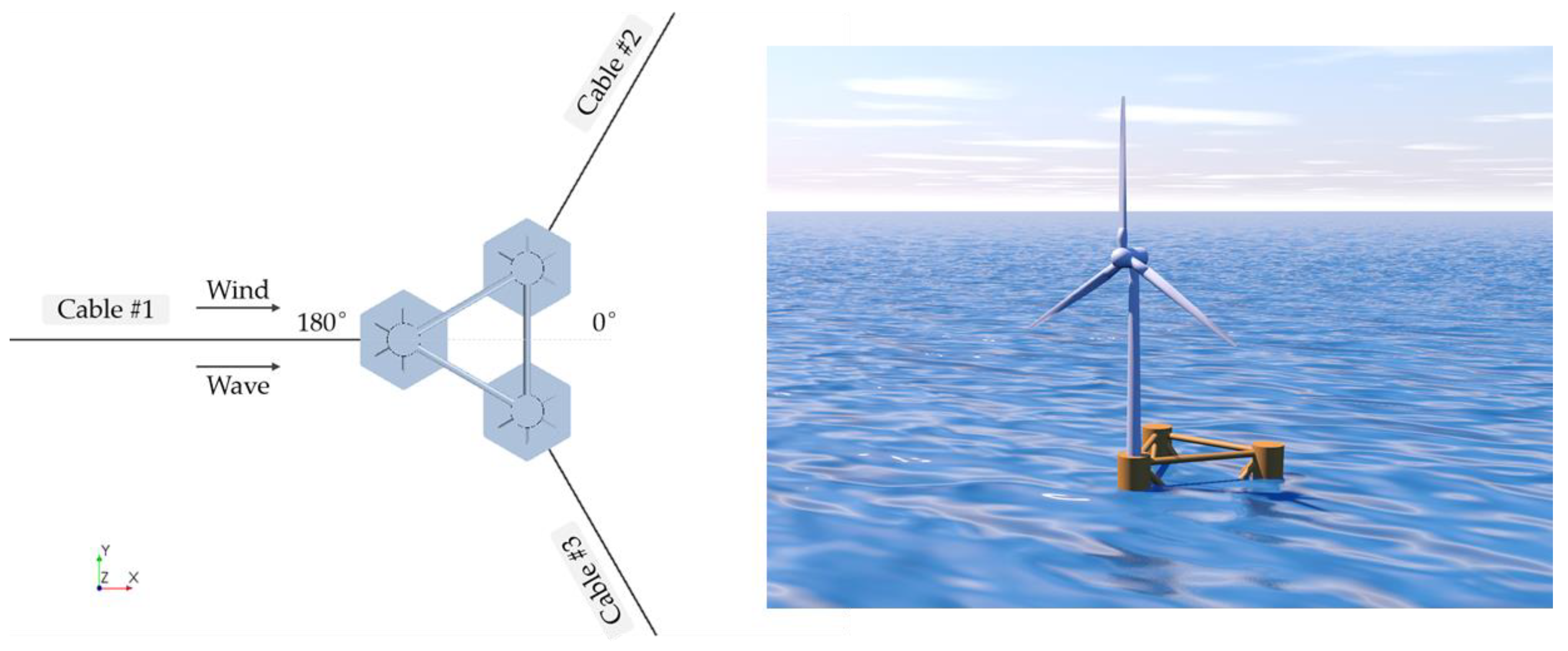
Figure 9.
Illustration of the mooring system (left) and panorama of FOWT (right).
Figure 9.
Illustration of the mooring system (left) and panorama of FOWT (right).
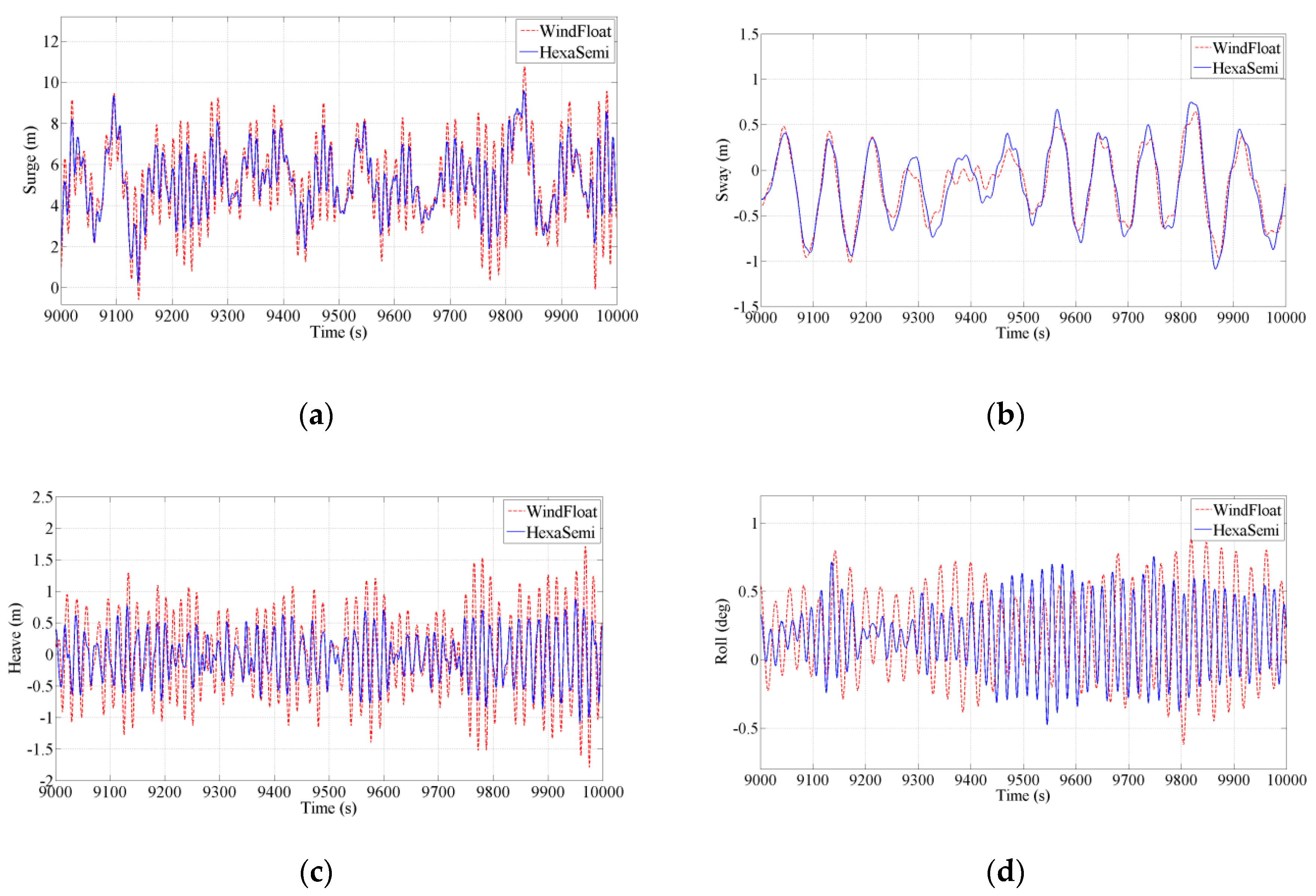
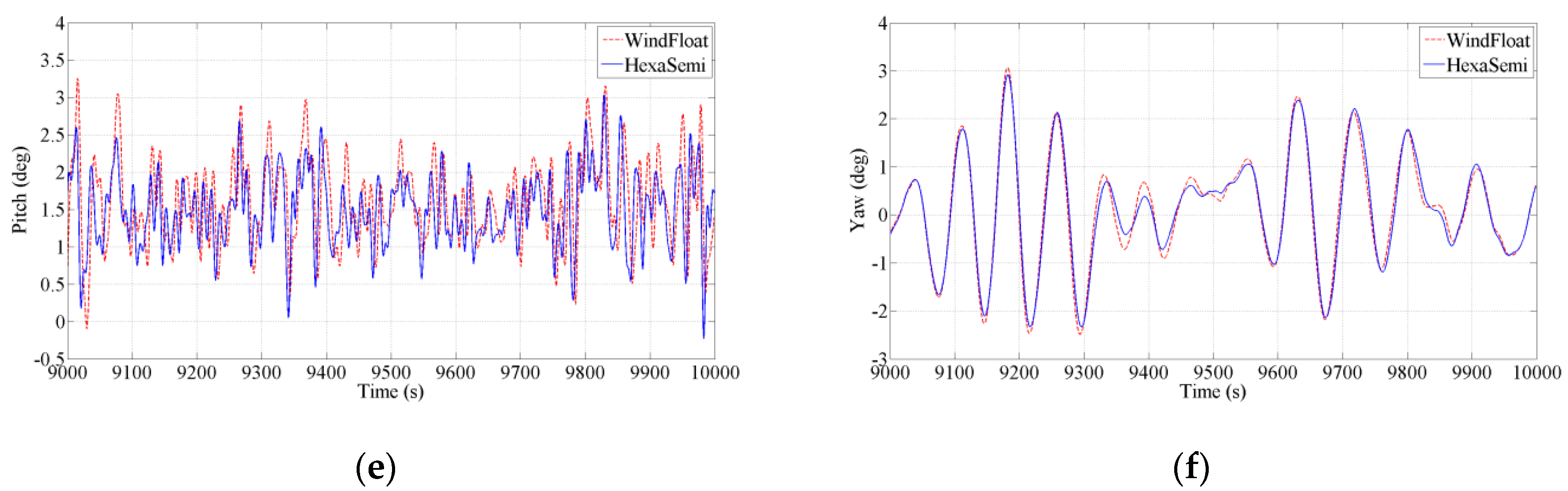
Figure 10.
6-DOFs motion response under the operational condition: (a) surge, (b) sway, (c) heave, (d) roll, (e) pitch, (f) yaw.
Figure 10.
6-DOFs motion response under the operational condition: (a) surge, (b) sway, (c) heave, (d) roll, (e) pitch, (f) yaw.
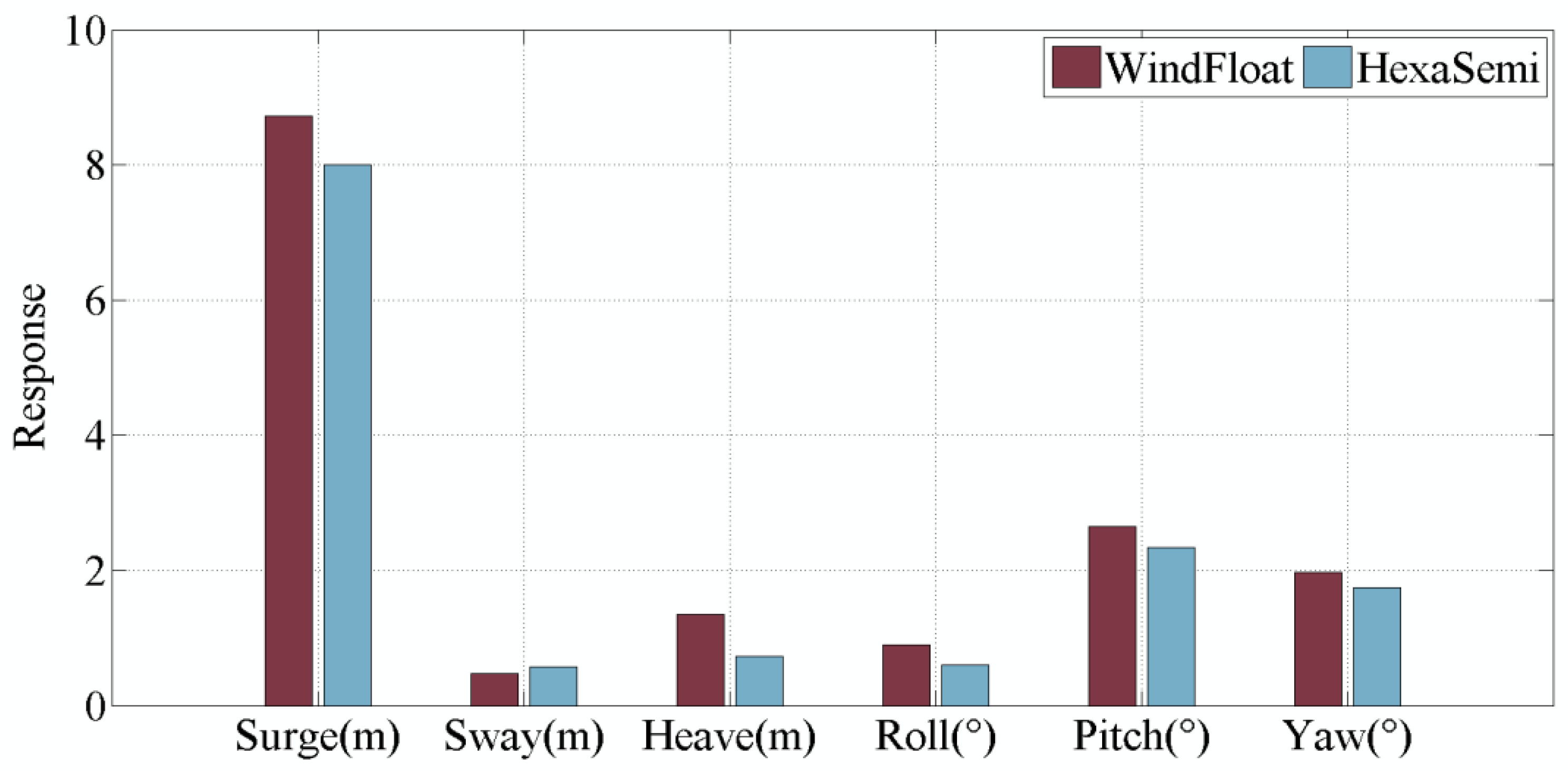
Figure 11.
Comparison of 6-DOFs significant responses between the WindFloat-type platform and HexaSemi under the operational condition.
Figure 11.
Comparison of 6-DOFs significant responses between the WindFloat-type platform and HexaSemi under the operational condition.
Figure 12.
6-DOFs motion spectrum under the operational condition: (a) surge, (b) sway, (c) heave, (d) roll, (e) pitch, (f) yaw.
Figure 12.
6-DOFs motion spectrum under the operational condition: (a) surge, (b) sway, (c) heave, (d) roll, (e) pitch, (f) yaw.
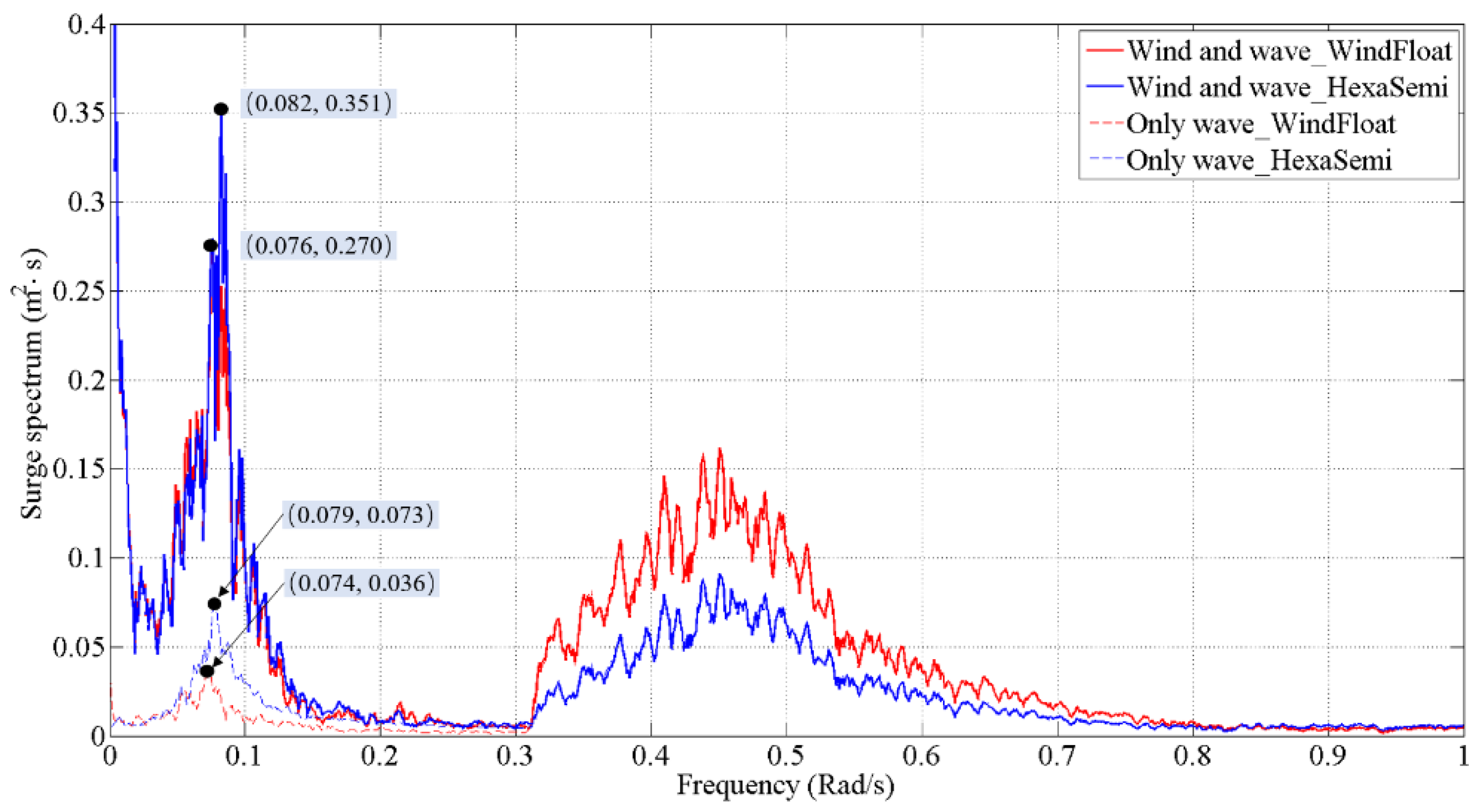
Figure 13.
Comparison of surge spectrum under wind and wave induced condition and only wave induced condition.
Figure 13.
Comparison of surge spectrum under wind and wave induced condition and only wave induced condition.
Figure 14.
6-DOFs motion response under the storm condition: (a) surge, (b) sway, (c) heave, (d) roll, (e) pitch, (f) yaw.
Figure 14.
6-DOFs motion response under the storm condition: (a) surge, (b) sway, (c) heave, (d) roll, (e) pitch, (f) yaw.
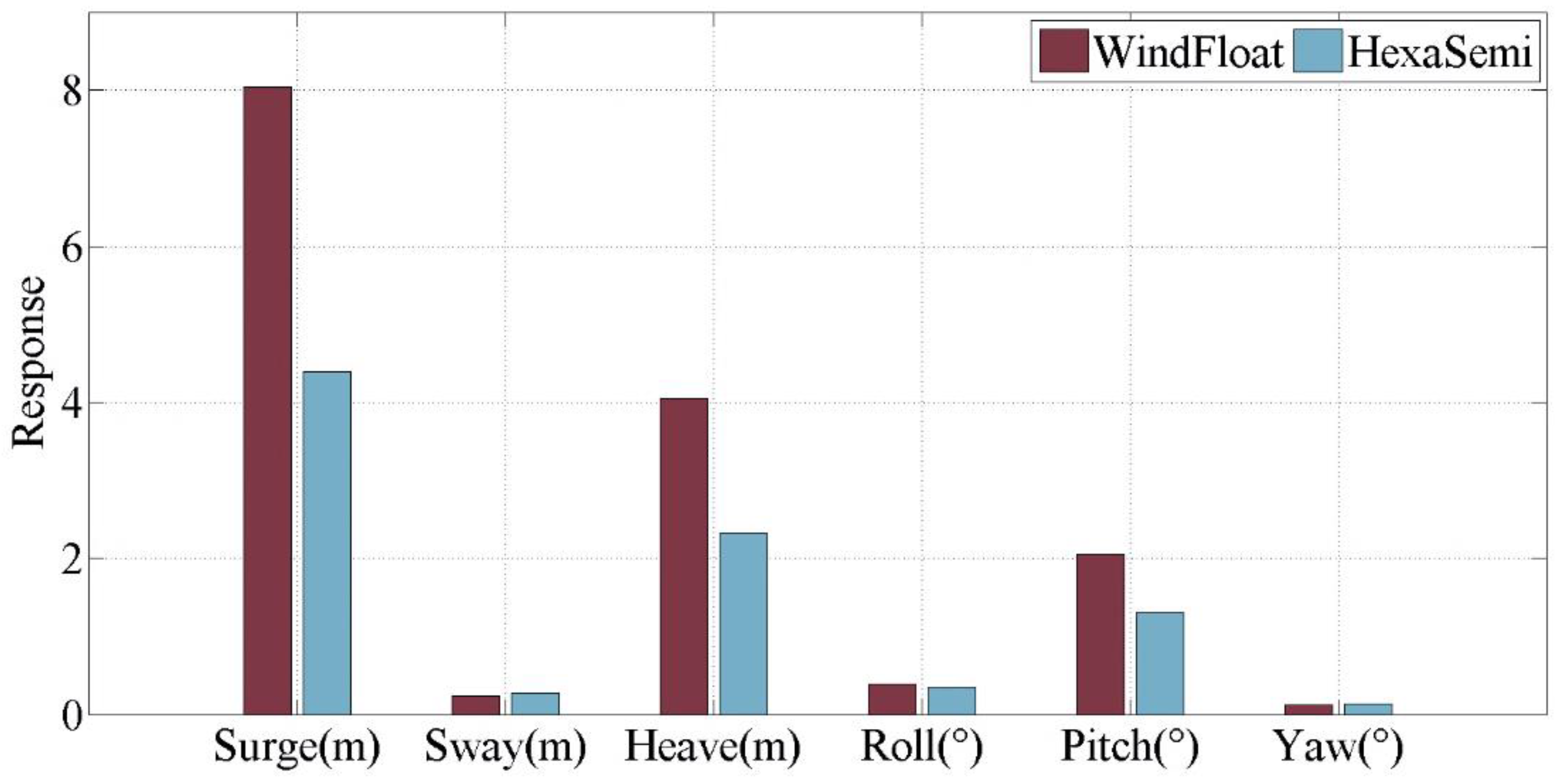
Figure 15.
Comparison of 6-DOFs significant responses between the WindFloat-type platform and HexaSemi under a storm condition.
Figure 15.
Comparison of 6-DOFs significant responses between the WindFloat-type platform and HexaSemi under a storm condition.
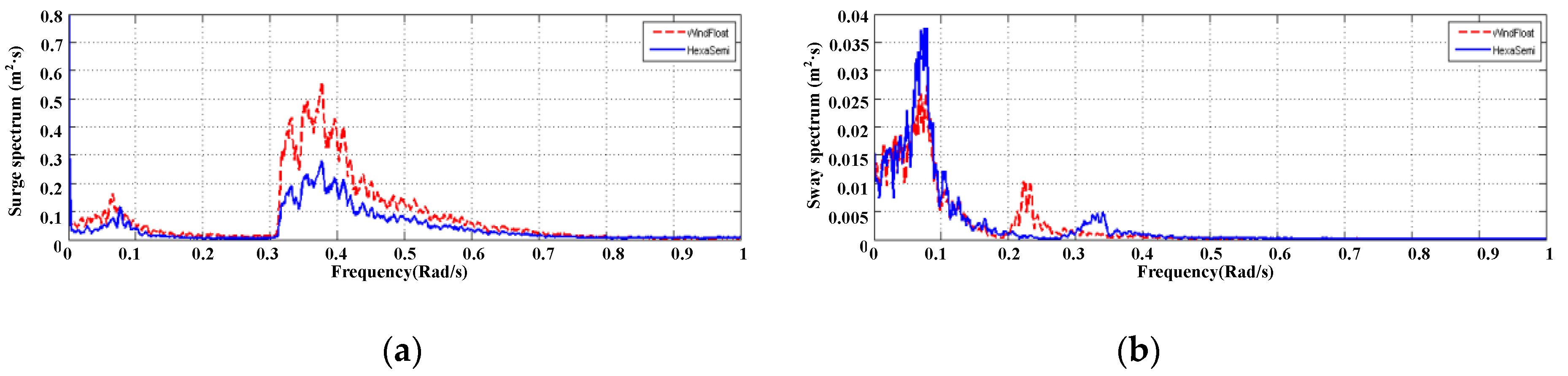
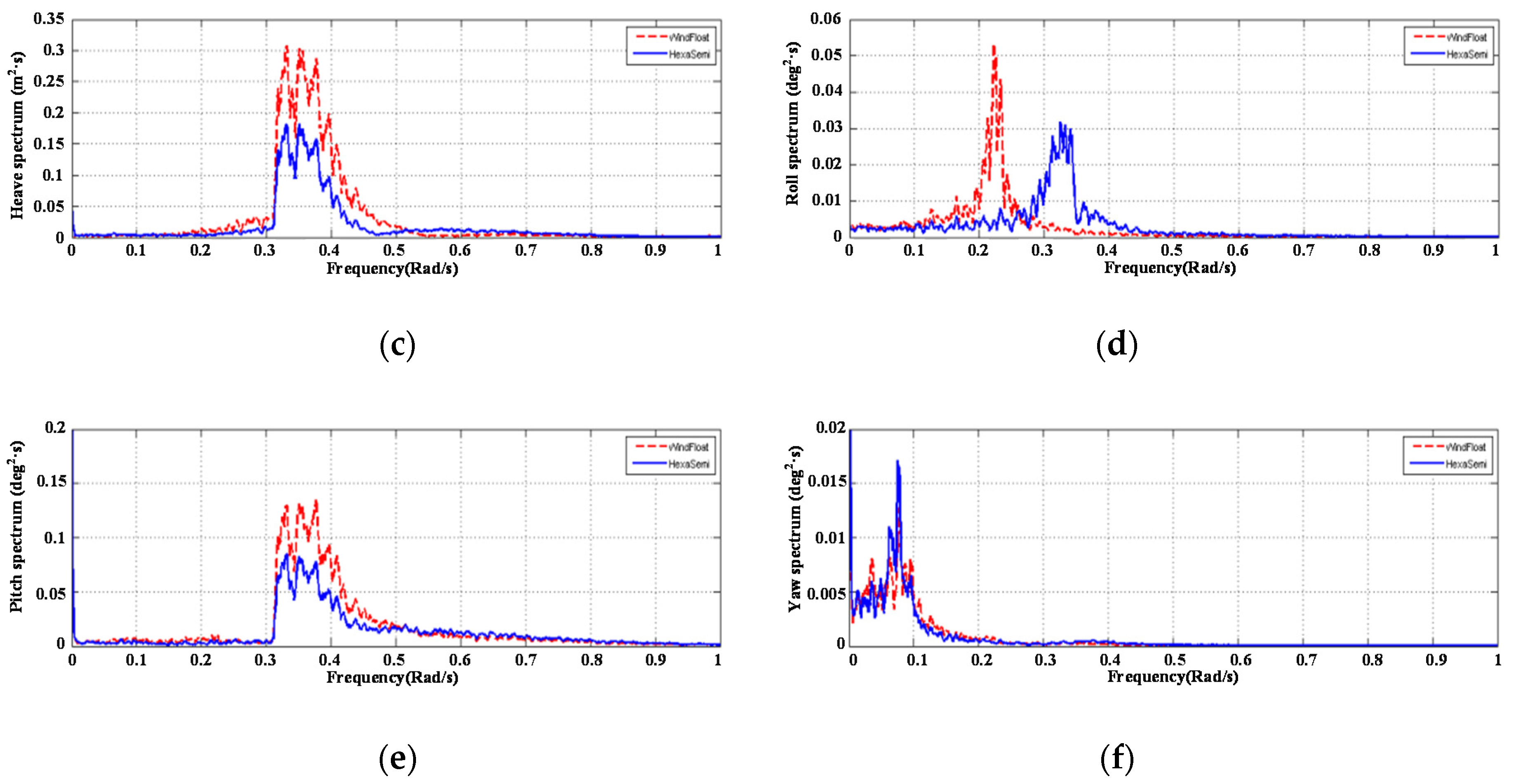
Figure 16.
6-DOFs motion spectrum under the storm condition: (a) surge, (b) sway, (c) heave, (d) roll, (e) pitch, (f) yaw.
Figure 16.
6-DOFs motion spectrum under the storm condition: (a) surge, (b) sway, (c) heave, (d) roll, (e) pitch, (f) yaw.
Table 1.
Main Parameters of the WindFloat-type platform-type platform.
Table 1.
Main Parameters of the WindFloat-type platform-type platform.
| Parameter | Value |
|---|
| Height of column (m) | 33.600 |
| Column diameter (m) | 10.700 |
| Thickness of heave plate (m) | 0.030 |
| Length of heave plate edge (m) | 15.629 |
| Column center to center (m) | 56.400 |
| Pontoon diameter (m) | 2.200 |
| Bracing diameter (m) | 2.038 |
| Operating draft (m) | 22.900 |
| Height of CG (m) | 29.800 |
| Height of buoyancy center (m) | 10.904 |
| Displacement/Tonnage (t) | 7247.928 |
| Moment of inertia about CG (kg·m2) | [4.250 × 109, 4.250 × 109, 7.056 × 109] |
Table 2.
Main Parameters of HexaSemi.
Table 2.
Main Parameters of HexaSemi.
| Parameter | Value |
|---|
| Height of hexagonal prism (m) | 33.600 |
| Length of hexagonal prism edge (m) | 5.884 |
| Thickness of heave plate (m) | 0.030 |
| Length of heave plate edge (m) | 8.771 |
| Breadth of heave plate (m) | 10.228 |
| Prism center to center (m) | 56.400 |
| Breadth of pontoon (m) | 2.000 |
| Height of pontoon (m) | 3.000 |
| Operating draft (m) | 22.900 |
| Height of CG (m) | 29.800 |
| Height of buoyancy center (m) | 11.377 |
| Displacement/Tonnage (t) | 7247.894 |
| Moment of inertia about CG (kg·m2) | [4.250 × 109, 4.250 × 109, 7.056 × 109] |
Table 3.
Total linear and quadratic heave damping of the two platforms.
Table 3.
Total linear and quadratic heave damping of the two platforms.
| Damping | WindFloat-Type | HexaSemi |
|---|
| Total linear heave damping (N/(m/s)) | 4.289 × 105 | 9.126 × 105 |
| Total quadratic heave damping (N/(m/s)2) | 1.242 × 107 | 1.295 × 107 |
Table 4.
The attenuation rate of heave free decay curves of the two platforms.
Table 4.
The attenuation rate of heave free decay curves of the two platforms.
| | Initial Height (m) | 1st Period(m) | 2nd Period(m) | 3rd Period(m) |
|---|
| WindFloat-type | 1.50 | 0.71 | 0.30 | 0.21 |
| Attenuation rate 1 | | 52.7% | 80.0% | 86.0% |
| HexaSemi | 1.50 | 0.48 | 0.18 | 0.13 |
| Attenuation rate 2 | | 68.0% | 88.0% | 91.3% |
Table 5.
Additional linear and quadratic heave damping of the two platforms.
Table 5.
Additional linear and quadratic heave damping of the two platforms.
| DOFs | Damping | WindFloat-Type | HexaSemi |
|---|
| Heave | Additional linear damping (N/(m/s)) | 1.08 × 106 | 9.65 × 105 |
| Additional quadratic damping (N/(m/s)2) | 4.23 × 106 | 4.20 × 106 |
| Pitch | Additional linear damping (N·m/(rad/s)) | 2.41 × 109 | 1.80 × 109 |
| Additional quadratic damping (N·m /(rad/s)2) | 3.20 × 109 | 3.00 × 109 |
| Roll | Additional linear damping (N·m/(rad/s)) | 2.39 × 109 | 2.70 × 109 |
| Additional quadratic damping (N·m /(rad/s)2) | 5.81 × 109 | 5.92 × 109 |
Table 6.
Specific parameters of the two load cases.
Table 6.
Specific parameters of the two load cases.
| Sea State | Irregular Wave | Turbulent Wind |
|---|
| Hs (m) | Tp (s) | V (m/s) |
|---|
| Operational condition | 7.45 | 13.60 | 14.54 |
| Storm condition | 15.18 | 16.96 | 34.40 |
Table 7.
Mooring line properties.
Table 7.
Mooring line properties.
| Parameter | Value |
|---|
| Diameter of line (mm) | 76.6 |
| Mass density (kg·m−1) | 126.5 |
| Extensional stiffness (kN) | 5.45 × 105 |
| Fairlead to foundation center/ (m) | 37.72 |
| Fairlead below water surface (m) | 10 |
| Anchor below water surface (m) | 200 |
| Anchor to foundation center (m) | 834.27 |
| Unstretched mooring line length (m) | 835.35 |
Table 8.
6-DOF motion statistics of WindFloat-type platform under a storm condition.
Table 8.
6-DOF motion statistics of WindFloat-type platform under a storm condition.
| | Surge (m) | Sway (m) | Heave (m) | Roll (deg) | Pitch (deg) | Yaw (deg) |
|---|
| Mean | 0.1959 | 0.0078 | 0.0250 | −0.0020 | 0.1035 | 0.0560 |
| Max. | 14.060 | 0.5896 | 5.6180 | 0.6938 | 3.7400 | 0.2855 |
| Min. | −16.190 | −0.8282 | −5.4770 | −0.8008 | −3.4410 | −0.1232 |
| Range | 30.250 | 1.4178 | 11.095 | 1.4946 | 7.1810 | 0.4087 |
| Std. | 4.1295 | 0.1843 | 2.1839 | 0.2157 | 1.0022 | 0.0624 |
Table 9.
6-DOF motion statistics of HexaSemi under a storm condition.
Table 9.
6-DOF motion statistics of HexaSemi under a storm condition.
| | Surge(m) | Sway(m) | Heave(m) | Roll(deg) | Pitch(deg) | Yaw(deg) |
|---|
| Mean | 0.4334 | 0.0092 | 0.0306 | −0.0021 | 0.1052 | 0.0553 |
| Max. | 7.7790 | 0.7056 | 3.3800 | 0.6250 | 2.3830 | 0.2762 |
| Min. | −7.3880 | −0.7509 | −3.2020 | −0.6032 | −2.2180 | −0.1134 |
| Range | 15.167 | 1.4565 | 6.5820 | 1.2282 | 4.6010 | 0.3896 |
| Std. | 2.0716 | 0.2200 | 1.2346 | 0.1945 | 0.6293 | 0.0674 |
Table 10.
Mooring cable tension statistics.
Table 10.
Mooring cable tension statistics.
| Model | WindFloat-Type Platform | HexaSemi |
|---|
| Cable # | 1 | 2 | 3 | 1 | 2 | 3 |
|---|
| Mean(kN) | 1313 | 1271 | 1271 | 1302 | 1262 | 1261 |
| Max. (kN) | 2620 | 1695 | 1700 | 1827 | 1443 | 1435 |
| Min. (kN) | 689 | 1047 | 1045 | 938 | 1123 | 1119 |
| Range(kN) | 1931 | 648 | 655 | 889 | 320 | 316 |
| Std. (kN) | 252 | 78 | 78 | 125 | 38 | 38 |