Wind Resource Assessment and Economic Viability of Conventional and Unconventional Small Wind Turbines: A Case Study of Maryland †
Abstract
1. Introduction
2. Literature Review
3. Data Collection
4. A Brief Review of Baltimore City Climate
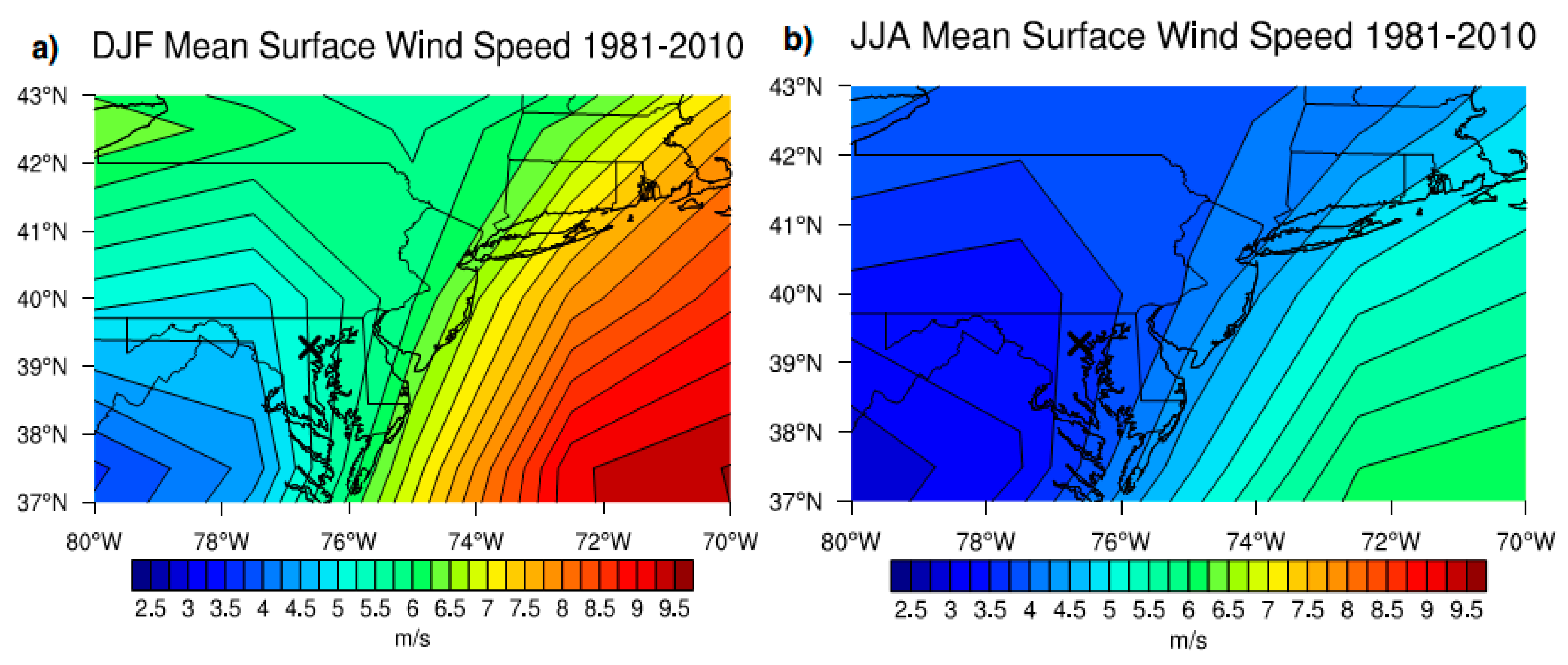
4.1. Seasonal Variability
4.2. Inter-Site Variability
5. Analysis Procedure
6. Results and Discussion
6.1. Wind Patterns
6.2. Performance Evaluation of Weibull Parameter Estimation Methods
6.3. Wind Power and Energy Densities
7. Implications of the Study: Integrating Wind Energy Harvesting Technologies in the Built Environment
7.1. Conventional Wind Energy Systems
7.2. Unconventional/Modern Wind Energy Systems
8. Conclusions
- (a)
- There is a maximum 43% probability for having wind speeds larger than 3 m/s. Results are consistent with the NREL residential wind power classification. Spatial and seasonal variability among sites makes it suitable for non-grid connected electrical and mechanical applications.
- (b)
- The strongest and weakest wind power and energy density values were observed at UMBC, Padonia, and Essex sites, respectively. Higher wind speeds at UMBC compared to other sites could be related to its position above the Fall Line, along the Piedmont Plateau, while weaker winds in Essex are related to stagnation from the persistence of a local bay breeze circulation.
- (c)
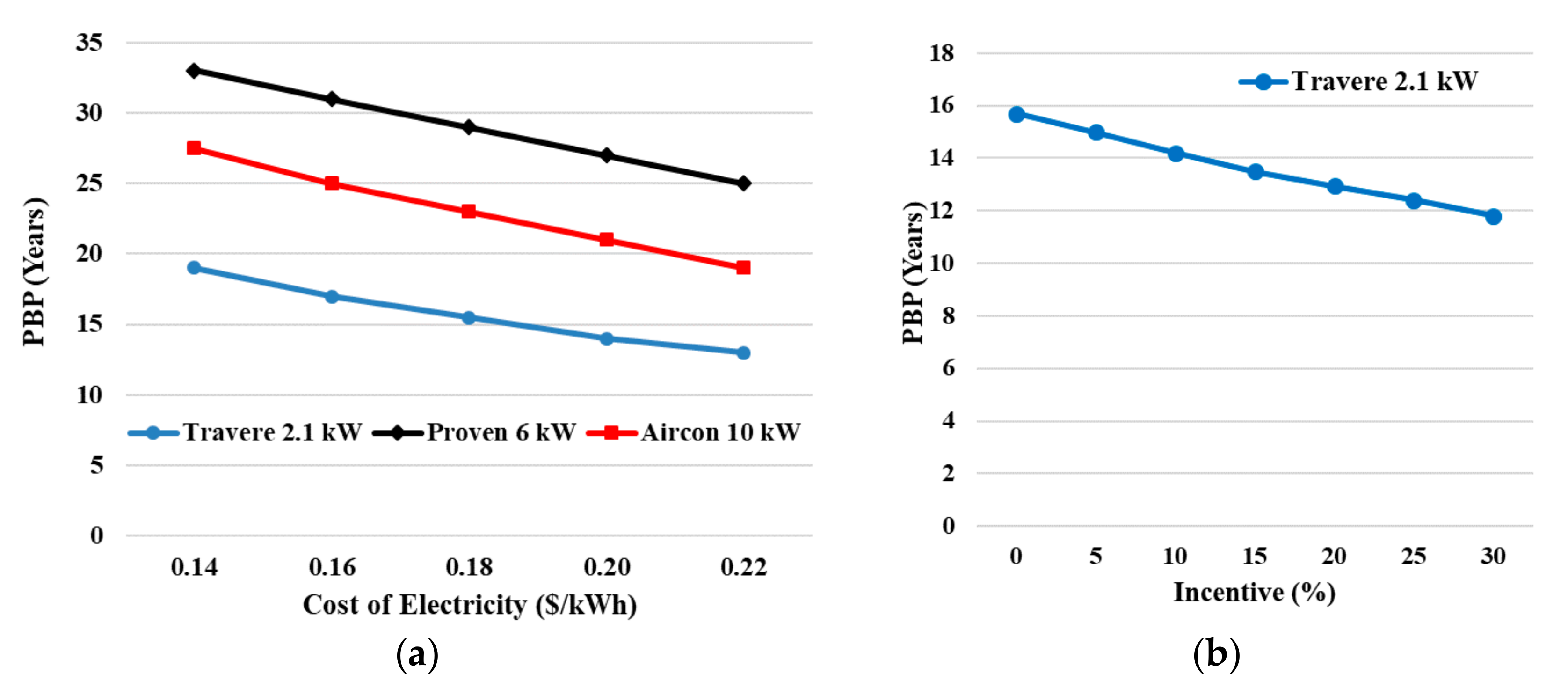
- Among examined distributed wind energy solutions, including conventional HAWTs, an annual CF of 11% with an electricity production of 1990 kWh is feasible. Economic analysis showed that it has the lowest PBP, which changes from 19 years to 13 years when the electricity price increases from $0.14/kWh to $0.22/kWh, respectively. Government incentives improve the economic feasibility.
- (d)
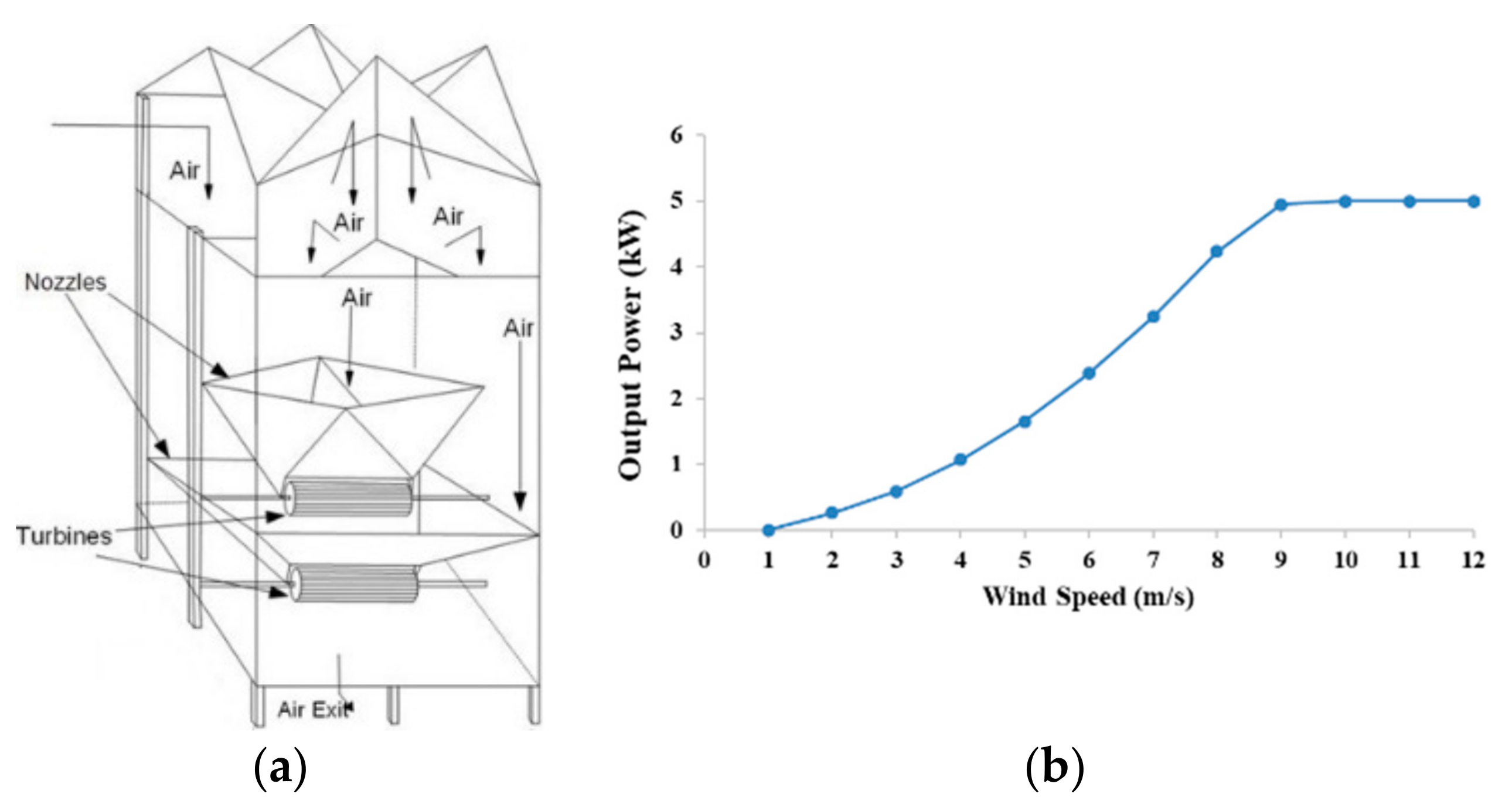
- Employment of modern wind harvesting machines in Baltimore City, a low-wind speed region, supports extending the use of wind energy for power generation.
- (e)
- Limitations and future work: While significant work has been performed on optimizing performance parameters of turbines, more research on the impact of wind gust, turbulence intensity, ease of manufacturing, and cost on airfoil/rotor designs are required. In addition, both spatial and temporal metrological analysis from macroscale to building scales should be conducted to better understand the urban physics and pertinent parameters in optimizing wind harnessing technologies; these include employing both computational and experimental fluid dynamic analysis of a studied site.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- IRENA. Global Energy Transformation: A Roadmap to 2050; International Renewable Energy Agency: Abu Dhabi, UAE, 2018; ISBN 978-92-9260-059-4. Available online: https://www.irena.org/publications/2018/Apr/Global-Energy-Transition-A-Roadmap-to-2050 (accessed on 15 July 2020).
- US Department of Energy (DOE); Energy Information Administration (EIA). Annual Energy Outlook 2050. 2020. Available online: https://www.eia.gov/outlooks/aeo/pdf/AEO2020%20Full%20Report.pdf (accessed on 15 July 2020).
- US Department of Energy (DOE). Wind Vision: A New Era for Wind Power in the United States. 2020. Available online: http://energy.gov/eere/wind/wind-vision (accessed on 15 July 2020).
- Goudarzi, N.; Zhu, W.D. A review on the development of the wind turbine generators across the world. Int. J. Dyn. Control 2013, 1, 192–202. [Google Scholar] [CrossRef]
- Lee, J.A.; Doubrawa, P.; Xue, L.; Newman, A.J.; Daxl, C.; Scott, G. Wind resource assessment for Alaska’s offshore region: Validation of a 14-year high-resolution WRF data set. Energies 2019, 12, 2780. [Google Scholar] [CrossRef]
- Dorrell, J.; Lee, K. The cost of wind: Negative economic effects of global wind energy development. Energies 2020, 13, 3667. [Google Scholar] [CrossRef]
- Poore, R.; Lettenmaier, T. Alternative Design Study Report: WindPACT Advanced Wind Turbine Drive Train Designs Study; NREL/SR-500-33196; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2003. [Google Scholar]
- Polinder, H.; Van Der Pijl, F.F.A.; De Vilder, G.-J.; Tavner, P.J. Comparison of Direct-Drive and Geared Generator Concepts for Wind Turbines. IEEE Trans. Energy Convers. 2006, 21, 725–733. [Google Scholar] [CrossRef]
- Goudarzi, N.; Zhu, W.D. Offshore and onshore wind energy conversion: The potential of a novel multiple-generator drivetrain. Key Eng. Mater. 2013, 569–570, 644–651. [Google Scholar] [CrossRef]
- Mikhail, A.; Petch, D. Clipper Liberty series: Advanced low wind speed technology. Paper Presented in California Wind Energy Collaborative Forum, Davis, CA, USA, 14 December 2005. [Google Scholar]
- Goudarzi, N.; Zhu, W.D.; Bahari, H. An assessment of the potential of a novel ducted turbine for harvesting wind power. J. Intell. Mater. Syst. Struct. 2014, 26, 1059–1070. [Google Scholar] [CrossRef]
- Wu, J.; Wang, J.; Chi, D. Wind energy potential assessment for the site of Inner Mongolia in China. Renew. Sustain. Energy Rev. 2013, 21, 215–228. [Google Scholar] [CrossRef]
- Goudarzi, N.; Zhu, W.D.; Delgado, R.; Pe, A. An assessment on the wind energy potential and possible solutions for power generation in Baltimore County in Maryland, USA. In Proceedings of the ASME 4th Joint US-European Fluid Engineering Division Summer Meeting, Chicago, IL, USA, 3–7 August 2014. [Google Scholar]
- Keyhani, A.; Ghasemi-Varnamkhasti, M.; Khanali, M.; Abbaszadeh, R. An assessment of wind energy potential as a power generation source in the capital of Iran, Tehran. Energy 2010, 35, 188–201. [Google Scholar] [CrossRef]
- Hamouda, Y.A. Wind energy in Egypt: Economic feasibility for Cairo. Renew. Sustain. Energy Rev. 2012, 16, 3312–3319. [Google Scholar] [CrossRef]
- Zhou, J.Y.; Erdem, E.; Li, G.; Shi, J. Comprehensive evaluation of wind speed distribution models: A case study for North Dakota sites. Energy Convers. Manag. 2010, 51, 1449–1458. [Google Scholar] [CrossRef]
- Kiss, P.; Jánosi, I.M. Comprehensive empirical analysis of ERA-40 surface wind speed distribution over Europe. Energy Convers. Manag. 2008, 49, 2142–2151. [Google Scholar] [CrossRef]
- Seguro, J.V.; Lambert, T.W. Modern estimation of the parameters of the Weibull wind speed distribution for wind energy analysis. J. Wind. Eng. Ind. Aerodyn. 2000, 85, 75–84. [Google Scholar] [CrossRef]
- Ülgen, K.; Hepbasli, A. Determination of Weibull parameters for wind energy analysis of Izmir, Turkey. Int. J. Energy Res. 2002, 26, 495–506. [Google Scholar] [CrossRef]
- Chang, T.P. Performance comparison of six numerical methods in estimating Weibull parameters for wind energy application. Appl. Energy 2011, 88, 272–282. [Google Scholar] [CrossRef]
- Available online: http://www.geonames.org/maps/google_39.25441_-76.70974.html (accessed on 15 July 2020).
- National Renewable Energy Laboratory (NREL). Wind Research, Wind Resource Assessment. Available online: http://www.nrel.gov/wind/resource_assessment.html (accessed on 15 July 2020).
- Hughes, W.K.; Williams, H.D.; Brenner, L.; Speakes-Backman, K. Ten-Year Plan (2012–2021) of Electric Companies in Maryland. Maryland Department of Natural Resources, 2013. Available online: http://webapp.psc.state.md.us/intranet/Reports/TYP2021.pdf (accessed on 15 July 2020).
- U.S. Environmental Protection Agency. Ambient Air Monitoring Network Plan for Calendar Year 2017. Maryland Department of the Environment: Baltimore, MD, USA, 2016. Available online: http://www.mde.state.md.us/programs/Air/AirQualityMonitoring/Documents/MDNetworkPlanCY2017.pdf (accessed on 15 July 2020).
- Emeis, S. Wind Energy Meteorology: Atmospheric Physics for Wind Power Generation; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-642-30522-1. [Google Scholar]
- Fırtın, E.; Güler, Ö.; Akdağ, S.A. Investigation of wind shear coefficients and their effect on electrical energy generation. Appl. Energy 2011, 88, 4097–4105. [Google Scholar] [CrossRef]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained—Theory, Design, and Application; John Wiley and Sons: Amherst, MA, USA, 2009; ISBN 0-471-49972-2. [Google Scholar]
- Miller, S.T.K.; Keim, B.D.; Talbot, R.W.; Mao, H. Sea breeze: Structure, forecasting, and impacts. Rev. Geophys. 2003, 41, 1–31. [Google Scholar] [CrossRef]
- Segal, M.; Avissar, R.; McCumber, M.C.; Pielke, R.A. Evaluation of Vegetation Effects on the Generation and Modification of Mesoscale Circulations. J. Atmos. Sci. 1988, 45, 2268–2293. [Google Scholar] [CrossRef]
- Civerolo, K.L.; Sistla, G.; Rao, S.T.; Nowak, D.J. The effects of land use in meteorological modeling: Implications for assessment of future air quality scenarios. Atmos. Environ. 2000, 34, 1615–1621. [Google Scholar] [CrossRef]
- Hoskins, B.J. Dynamical processes in the atmosphere and the use of models. Q. J. R. Meteorol. Soc. 1983, 109, 1–21. [Google Scholar] [CrossRef]
- Cook, K.H.; Held, I.M. The Stationary Response to Large-Scale Orography in a General Circulation Model and a Linear Model. J. Atmos. Sci. 1992, 49, 525–539. [Google Scholar] [CrossRef][Green Version]
- Schär, C.; Smith, R.B. Shallow-Water Flow Past Isolated Topography. Part I: Vorticity Production and Wake Formation. J. Atmos. Sci. 1993, 50, 1373–1400. [Google Scholar] [CrossRef][Green Version]
- Grubišić, V.; Smith, R.B.; Schär, C. The Effect of Bottom Friction on Shallow-Water Flow Past an Isolated Obstacle. J. Atmos. Sci. 1995, 52, 1985–2005. [Google Scholar] [CrossRef][Green Version]
- Richter, I.; Mechoso, C.R. Orographic influences on the annual cycle of Namibian stratocumulus clouds. Geophys. Res. Lett. 2004, 31, 1–4. [Google Scholar] [CrossRef]
- Buermann, W.; Dong, J.; Zeng, X.; Myneni, R.B.; Dickinson, R.E. Evaluation of the Utility of Satellite-Based Vegetation Leaf Area Index Data for Climate Simulations. J. Clim. 2001, 14, 3536–3550. [Google Scholar] [CrossRef]
- Seaman, L.N. Meteorological modeling for air-quality assessments. Atmos. Environ. 2000, 34, 2231–2259. [Google Scholar] [CrossRef]
- Klink, K. Trends in mean monthly maximum and minimum surface wind speeds in the coterminous United States, 1961 to 1990. Clim. Res. 1999, 13, 193–205. [Google Scholar] [CrossRef]
- Balling, R.C., Jr.; Cerveny, R.S. Long-Term Associations between Wind Speeds and the Urban Heat Island of Phoenix, Arizona. J. Clim. Appl. Meteorol. 1987, 26, 712–716. [Google Scholar] [CrossRef]
- Bornstein, R.D.; Johnson, D.S. Urban-rural wind velocity differences. Atmos. Environ. 1977, 11, 597–604. [Google Scholar] [CrossRef]
- Lee, D. The influence of atmospheric stability and the urban heat island on urban-rural wind speed differences. Atmos. Environ. 1979, 13, 1175–1180. [Google Scholar] [CrossRef]
- Stauffer, R.M.; Thompson, A.M. Bay breeze climatology at two sites along the Chesapeake bay from 1986–2010: Implications for surface ozone. J. Atmos. Chem. 2013, 72, 355–372. [Google Scholar] [CrossRef]
- Loughner, C.P.; Allen, D.J.; Pickering, K.E.; Zhang, D.-L.; Shou, Y.-X.; Dickerson, R.R. Impact of fair-weather cumulus clouds and the Chesapeake Bay breeze on pollutant transport and transformation. Atmos. Environ. 2011, 45, 4060–4072. [Google Scholar] [CrossRef]
- Martins, D.K.; Stauffer, R.M.; Thompson, A.M.; Halliday, H.S.; Kollonige, D.W.; Joseph, E.; Weinheimer, A.J. Ozone correlations between mid-tropospheric partial columns and the near-surface at two mid-Atlantic sites during the DISCOVER-AQ campaign in July 2011. J. Atmos. Chem. 2013, 72, 373–391. [Google Scholar] [CrossRef] [PubMed]
- Irwin, J.S. A theoretical variation of the wind profile power-law exponent as a function of surface roughness and stability. Atmos. Environ. 1979, 13, 191–194. [Google Scholar] [CrossRef]
- Bailey, H.; McDonald, L. Wind Resource Assessment Handbook; AWS Scientific Inc: Albany, NY, USA, 1997. [Google Scholar]
- Johnson, G.L. Wind Energy Systems. Electronic Edition. 2006. Available online: http://www.pssurvival.com/ps/windmills/Wind_Energy_Systems_Johnson_2001.pdf (accessed on 15 July 2020).
- Mohammadi, K.; Alavi, O.; Mostafaeipour, A.; Goudarzi, N.; Jalilvand, M. Assessing different parameters estimation methods of Weibull distribution to compute wind power density. Energy Convers. Manag. 2016, 108, 322–335. [Google Scholar] [CrossRef]
- Justus, C.G. Winds and Wind System Performance; Franklin Institute Press: Philadelphia, PA, USA, 1978. [Google Scholar]
- IEC. International Standard IEC 61400-1: Wind Turbines—Part 1: Design Requirements; International Electrotechnical Commission: Geneva, Switzerland, 2005. [Google Scholar]
- Elliot, D.L.; Schwartz, M.N. Wind Energy Potential in the United States, PNL-SA-23109; Pacific Northwest Laboratory: Richmond, WA, USA, 1993; NTIS No. DE94001667. [Google Scholar]
- Mohammadi, K.; Mostafaeipour, A.; Sedaghat, A.; Shamshirband, S.; Petković, D. Application and economic viability of wind turbine installation in Lutak, Iran. Environ. Earth Sci. 2016, 75, 1–16. [Google Scholar] [CrossRef]
- Christiner, M.; Dobbins, R.; Ndegwa, A.; Sivak, J. Rooftop Wind Turbine Feasibility in Boston, Massachusetts. Master’s Thesis, Worcester Polytechnic Institute, Worcester, MA, USA, 2010. [Google Scholar]
- Singh, R.K.; Ahmed, M.R. Blade design and performance testing of a small wind turbine rotor for low wind speed applications. Renew. Energy 2013, 50, 812–819. [Google Scholar] [CrossRef]
- Kishore, R.A.; Coudron, T.; Priya, S. Small-scale wind energy portable turbine (SWEPT). J. Wind. Eng. Ind. Aerodyn. 2013, 116, 21–31. [Google Scholar] [CrossRef]
- Goudarzi, N.; Zhu, W.D.; Bahari, H. Numerical simulation of a fluid flow inside a novel ducted wind turbine. In Proceedings of the ASME 4th Joint US-European Fluids Engineering Division Summer Meeting, Chicago, IL, USA, 3–7 August 2014. [Google Scholar]
- Catalogue of European Urban Wind Turbine Manufacturers. Available online: http://www.urbanwind.net/pdf/Catalogue_Final.pdf (accessed on 15 July 2020).
- Bakhshi, R.; Sandborn, P.A. A Return on Investment Model for the Implementation of New Technologies on Wind Turbines. IEEE Trans. Sustain. Energy 2017, 9, 284–292. [Google Scholar] [CrossRef]
- Bruck, M.; Sandborn, P.; Goudarzi, N. A Levelized Cost of Energy (LCOE) model for wind farms that include Power Purchase Agreements (PPAs). Renew. Energy 2018, 122, 131–139. [Google Scholar] [CrossRef]
- EIA. Electric Power Monthly. Available online: https://www.eia.gov/electricity/monthly/epm_table_grapher.php?t=epmt_5_6_a. (accessed on 15 July 2020).
- Bahariaenergy. Available online: https://www.baharienergy.com/ (accessed on 15 July 2020).

| UMBC | Padonia | Essex | |
|---|---|---|---|
| RPE | 2.3–10.5% | 0.2–11% | 3–11% |
| MAPE | 7.62% | 4.46% | 8% |
| MABE | 2.91 W/m2 | 1.11 W/m2 | 1.06 W/m2 |
| RMSE | 3.19 W/m2 | 2.48 W/m2 | 1.30 W/m2 |
| Season | Power Density (W/m2) | Energy Density (kWh/m2) | ||||||
|---|---|---|---|---|---|---|---|---|
| UMBC | ||||||||
| Winter | 3.35 | 2.09 | 1.68 | 3.75 | 2.17 | 6.01 | 53.79 | 38.38 |
| Spring | 3.04 | 1.71 | 1.86 | 3.40 | 2.26 | 5.03 | 35.43 | 25.84 |
| Summer | 2.40 | 1.30 | 1.95 | 2.69 | 1.86 | 3.86 | 16.22 | 11.95 |
| Fall | 2.73 | 1.51 | 1.92 | 3.06 | 2.20 | 5.35 | 24.84 | 18.48 |
| Padonia | ||||||||
| Winter | 3.145 | 1.978 | 1.663 | 3.522 | 2.007 | 5.699 | 36.684 | 30.446 |
| Spring | 2.446 | 1.517 | 1.679 | 2.740 | 1.599 | 4.370 | 17.556 | 13.655 |
| Summer | 1.923 | 1.131 | 1.783 | 2.154 | 1.354 | 3.291 | 7.557 | 5.814 |
| Fall | 2.613 | 1.756 | 1.526 | 2.927 | 1.463 | 5.059 | 34.100 | 25.142 |
| Essex | ||||||||
| Winter | 2.337 | 1.478 | 1.652 | 2.617 | 1.477 | 4.258 | 20.740 | 14.821 |
| Spring | 1.903 | 1.076 | 1.872 | 2.132 | 1.404 | 3.164 | 9.422 | 6.874 |
| Summer | 1.571 | 0.841 | 1.978 | 1.760 | 1.227 | 2.514 | 4.918 | 3.575 |
| Fall | 1.970 | 1.272 | 1.799 | 2.206 | 1.382 | 3.380 | 13.637 | 10.067 |
| Wind Turbine | Rated Power (kW) | Cut-in Speed (m/s) | Rated Speed (m/s) | Cut-Out Speed (m/s) | Rotor Diameter (m) |
|---|---|---|---|---|---|
| Travere 2.1 | 2.1 | 2.5 | 8 | 60 | 6 |
| Proven WT 6000 | 6 | 2.5 | 12 | none | 5.5 |
| Aircon 10 | 10 | 2.5 | 11 | 32 | 7.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goudarzi, N.; Mohammadi, K.; St. Pé, A.; Delgado, R.; Zhu, W. Wind Resource Assessment and Economic Viability of Conventional and Unconventional Small Wind Turbines: A Case Study of Maryland. Energies 2020, 13, 5874. https://doi.org/10.3390/en13225874
Goudarzi N, Mohammadi K, St. Pé A, Delgado R, Zhu W. Wind Resource Assessment and Economic Viability of Conventional and Unconventional Small Wind Turbines: A Case Study of Maryland. Energies. 2020; 13(22):5874. https://doi.org/10.3390/en13225874
Chicago/Turabian StyleGoudarzi, Navid, Kasra Mohammadi, Alexandra St. Pé, Ruben Delgado, and Weidong Zhu. 2020. "Wind Resource Assessment and Economic Viability of Conventional and Unconventional Small Wind Turbines: A Case Study of Maryland" Energies 13, no. 22: 5874. https://doi.org/10.3390/en13225874
APA StyleGoudarzi, N., Mohammadi, K., St. Pé, A., Delgado, R., & Zhu, W. (2020). Wind Resource Assessment and Economic Viability of Conventional and Unconventional Small Wind Turbines: A Case Study of Maryland. Energies, 13(22), 5874. https://doi.org/10.3390/en13225874







