1. Introduction
Permanent magnet synchronous motors (PMSMs) are now widely employed in rail transit vehicles, industrial servo drives and other domains because of their high efficiency, power factor and power density. It is important to obtain accurate parameters for high-performance control and fault diagnosis. In particular, maximum torque per ampere (MTPA) control, which is based on motor parameters such as flux and
dq-axis inductances, is the most common method to maximize the efficiency of the system. Therefore, accurate flux and
dq-axis inductances are essential to ensure the accuracy of system output under MTPA control. However, these parameters are affected by temperature and operating conditions. Flux and resistance are mainly affected by temperature [
1], while inductances are mainly affected by the current [
2]. Hence, many methods have been proposed to estimate the inductance and calculate the flux linkage of PMSMs.
Offline parameter identification methods for PMSMs are mainly used for the initial setting of motor parameters. For example, a step input signal was injected to calculate the flux and identify the inductances in [
3,
4]. In [
5], the fundamental components of phase voltages and currents are acquired by fast Fourier transform (FFT) in order to identify the inductance. This type of method can identify relatively accurate motor parameters, but the identification process often requires complex data acquisition and fails to reflect the variation of parameters caused by temperature differences.
Numerous studies have focused on real-time parameter identification [
6,
7,
8,
9,
10,
11,
12,
13]. In [
6], resistance and inductance were identified by fixing the flux to a nominal value. In [
7], a
d-axis current injection method was used to identify the resistance and flux for the first time. The method in [
8] achieved good results in resistance and flux identification, but failed to identify the inductance. In [
9], a recursive least squares (RLS) algorithm was proposed to identify the flux and
dq-axis inductances. In [
10], an extended Kalman filter (EKF) was employed to identify the resistance and flux. This type of method is mostly based on steady-state voltage equations. However, it is rank-deficient to identify more than two parameters using one set of steady-state equations, and the results are greatly influenced by inaccurate nominal or initial parameters. In [
9,
11], the authors proposed that injecting a signal into a
d-axis current could solve the rank deficiency problem in multiparameter identification, but this resulted in nonnegligible perturbation in the torque. In addition to the proposals in these studies, other methods were introduced in [
12,
13] which used a sinusoidal
d-axis current injection based on dynamic equations, but this resulted in torque ripple during identification.
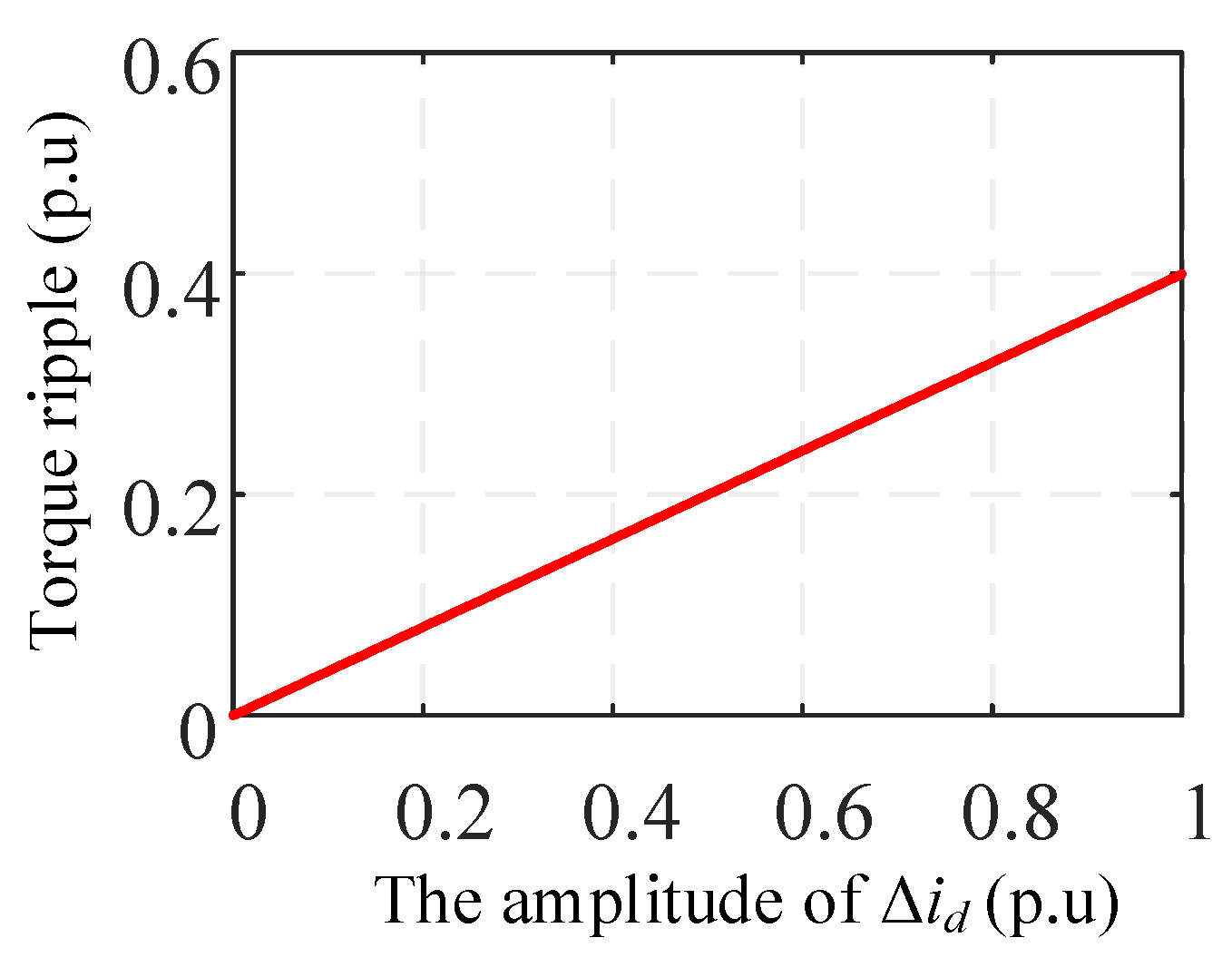
In this paper, a novel and simple method is proposed for real-time multiparameter identification of salient-pole PMSMs, especially in systems where the motor working conditions do not change frequently, such as rail transit systems. During the steady state operation process of the motor, a temporary steady state is designed for the simultaneous estimation of flux, resistance and dq-axis inductances. The torque ripple during the state transition process is so negligible that it has little effect on the speed control system, especially in a rail transit system with large inertia. In addition, the error caused by the variation of inductances is analyzed, and the better shift direction of the state transition process is calculated. The use of mean sampling instead of RLS means that there are no complicated matrix calculations in this algorithm. Thus, the identification process is very simple and needs minimal computation compared with other methods. Simulation and experimental results validate the good performance of the proposed method.
3. Error Analysis
3.1. Theoretical Error
The feasibility of the proposed method is analyzed in
Section 2. The performance of the method is influenced by parameter variations, and analyzing the error caused by these variations can improve the accuracy of identification.
Since the interval between two steady states is short, the temperature can be considered not to change during the identification process. Therefore, the flux and resistance, which are mainly affected by temperature, can be assumed to be constant during identification. However, in practice, the inductance changes with the current. The inductances, which are set to be constant in the derivations of Equations (2)–(14), result in theoretical errors. In order to simplify the analysis, it is assumed that the
dq-axis inductances can be denoted as a linear function of the
dq-axis currents [
15,
16,
17], as given below.
where the subscript
x denotes the
xth steady state and the subscript 0 denotes the value at zero current.
α and
β are both positive values that stand for the self-saturation constants.
Substituting Equation (15) into Equation (2) yields Equation (16):
This can be simplified according to the original derivation process as
The theoretical error of the parameters in the first steady state is shown in (18):
Under the traction condition, iq > 0, id < 0. △iq, △id and △idq are of the same polarity. Therefore, it is easy to deduce that Rs1err > 0 and Lq1err < 0, and that Ld1err and ψf1err are determined by the relative size between α and β. Among these values, only Rs1err is positively related to speed.
3.2. Influence of Torque Variation on Theoretical Error
According to Equation (18), it can be known that the theoretical error is quite complex because it is related to id1, iq1, id2 and iq2. However, iq1, id2 and iq2 can all be expressed by id1. Therefore, in order to perform a qualitative analysis of theoretical error, Equation (18) needs to be simplified, and can be expressed by id1.
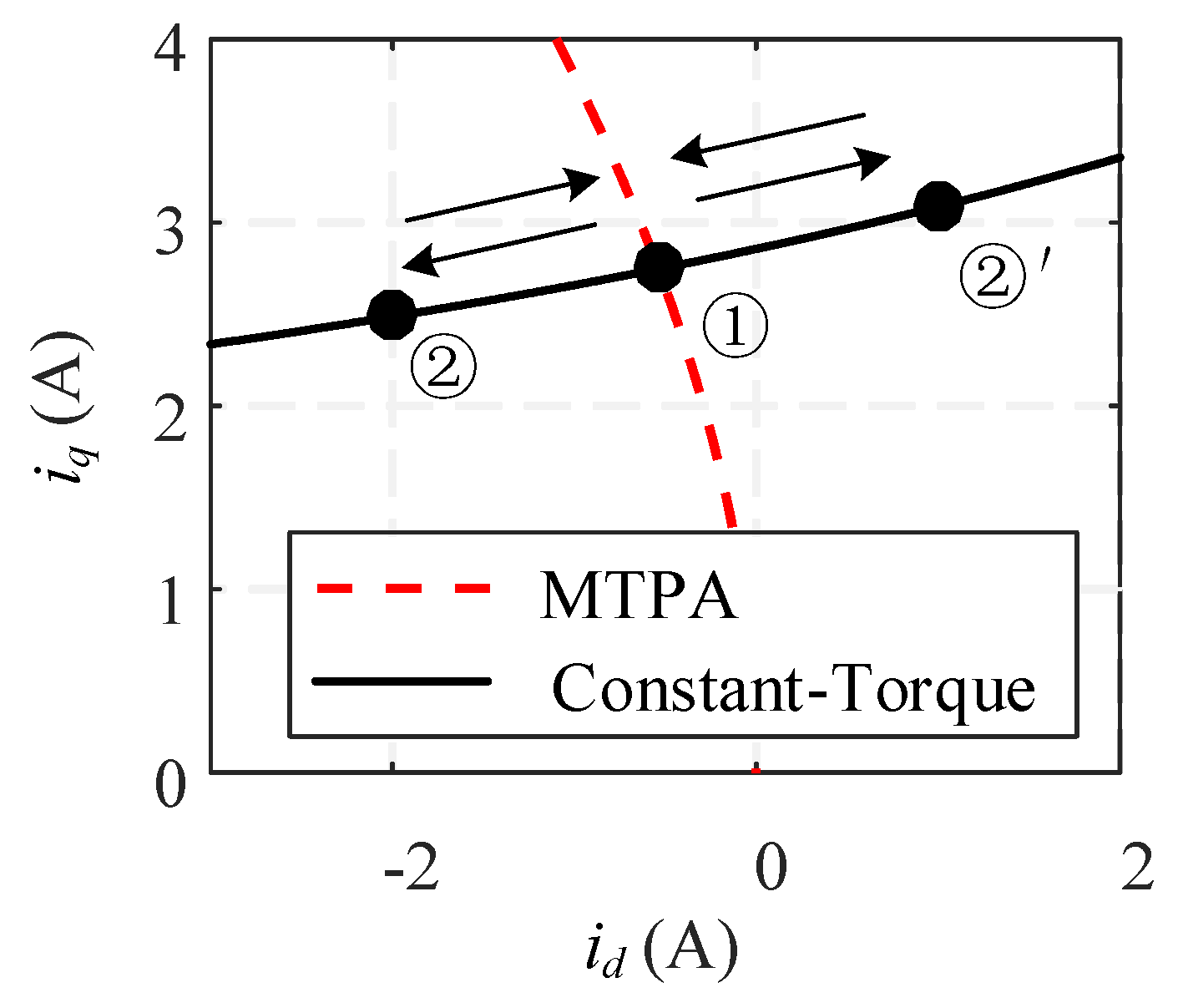
The constant torque curve in
Figure 2 is given by
Equation (19) can be expanded into a first-order Taylor expansion at
id = 0 as
where
k and
b are positive coefficients including the motor parameters and torque command. They are both positively related to torque command.
c is a positive value and is only related to the parameters.
The constant torque curve can be approximated as a straight line on which points (
id1,
iq1) and (
id2,
iq2) are located. Equation (21) can be obtained from Equation (20).
The MTPA curve can be approximated as a straight line passing through the origin and perpendicular to the constant torque curve. The point (
id1,
iq1) is located on this line such that Equation (22) can be obtained as
Therefore,
iq1,
id2 and
iq2 can be expressed by
id1 as Equation (23):
Substituting Equations (21) and (22) into Equation (19) yields Equation (24).
The derivative of
T*
ewith respect to
id1 is given in
Thus,
T*
eis negatively related to
id1. Substituting Equation (23) into Equation (18) yields Equation (26).
where
In order to deduce the relationship between theoretical error and torque, the derivative of Equation (26) with respect to
id1 is given in
where
Coefficient
c is much less than 1 because the reluctance torque is much less than the synchronous torque in PMSMs. Thus, there exist the following relationships in Equation (28).
It is easy to deduce that
dRs1err/
did1 < 0 and
dLq1err/
did1 > 0.
Ld1err and
ψf1err should be derived in more detail.
Ld1err is positively related to
id1 when
α and
β satisfy Equation (31).
ψf1err is positively related to
id1 when
α and
β satisfy Equation (32).
It can be verified that
α is much smaller than
β for the majority of PMSMs and that the motor described in this paper satisfies Equations (31) and (32). Therefore
where − denotes a negative value and + denotes a positive value. Since
did1/
dTe < 0, the conclusion is as follows:
In conclusion, only Rs1err is positively related to torque while the other values are negatively related to torque.
3.3. Comparison of Errors Due to the Left and Right Shifts
The shift direction of the operating point, which can be to the left or right, is analyzed here in order to minimize the theoretical error. Define △
id = −
I < 0 when the shift direction is left and △
id =
I > 0 when the shift direction is right. Substituting the different △
id into Equation (26) and then subtracting the left shift error from the right shift error yields Equation (35)
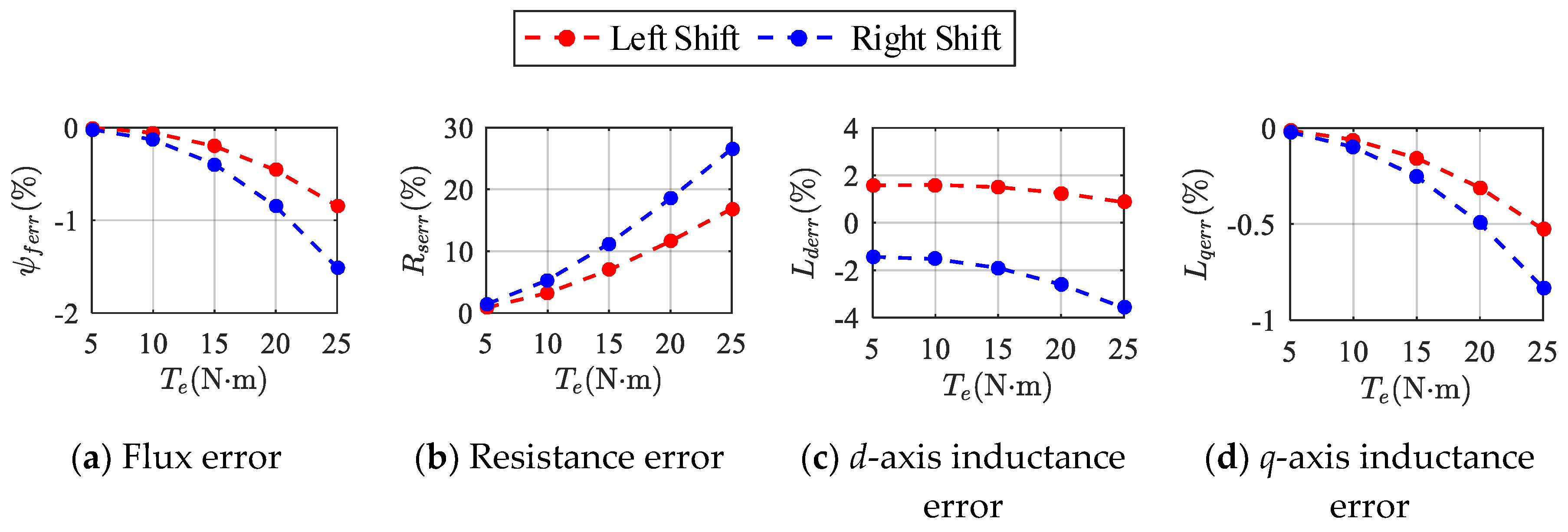
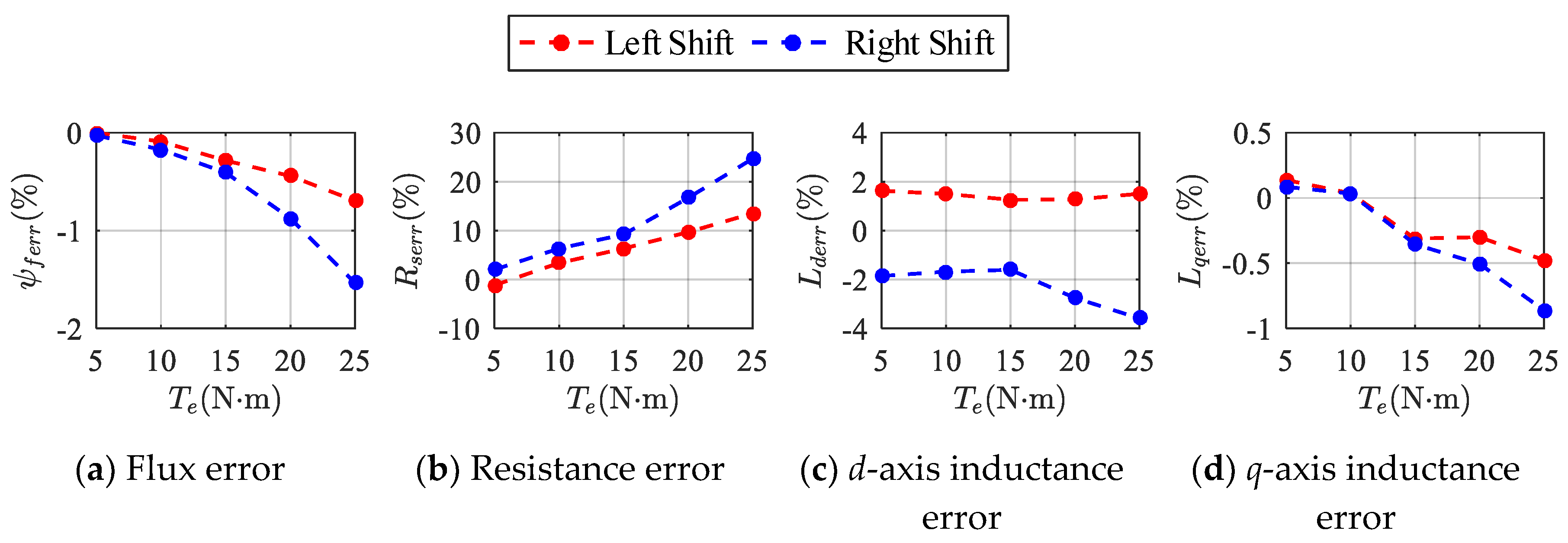
In order to analyze Equation (35) more intuitively, by combining it with the conclusion discussed above, we can plot the curves of the errors with increasing torque at 40 Hz, as shown in
Figure 4. The percentage of the relative error is defined with reference to the reference parameter, as shown below
As can be seen from
Figure 4, it is obvious that only
Rs1err increases with increasing torque, while the other values show the opposite tendency. Furthermore, the right shift curve of
Rs1err is always above the left shift curve, while the other values again show the opposite. In short, the magnitude of the left shift error is always smaller than the right one. For the braking condition, the same conclusion can also be obtained. In this case, it is recommended to identify parameters using left shift mode. Although
Rs1err is quite large, its influence on torque control performance is usually so small that it can be ignored.
4. Simulation and Experimental Results of the Proposed Method
The proposed multiparameter identification method was verified through the simulation and experimental platforms of a 3 kW salient-pole PMSM. The experimental platform was as shown in
Figure 5. The DSP(TMS320F28335)-based vector control system was employed to implement the proposed method.
In order to reduce the influence of nonideal factors such as initial position angle error, control delay and dead zones, we first had to compensate these factors in the experiment.
Considering the variability of the inductances, the second step was to obtain accurate reference parameters for the PMSM using offline measurement methods. For instance,
Ld (
Lq) was measured under the condition of different
id (
iq) while
iq (
id) = 0. The results are shown in
Table 1.
4.1. Simulation Results for Left and Right Shifts of the Operating Point with Different Torques
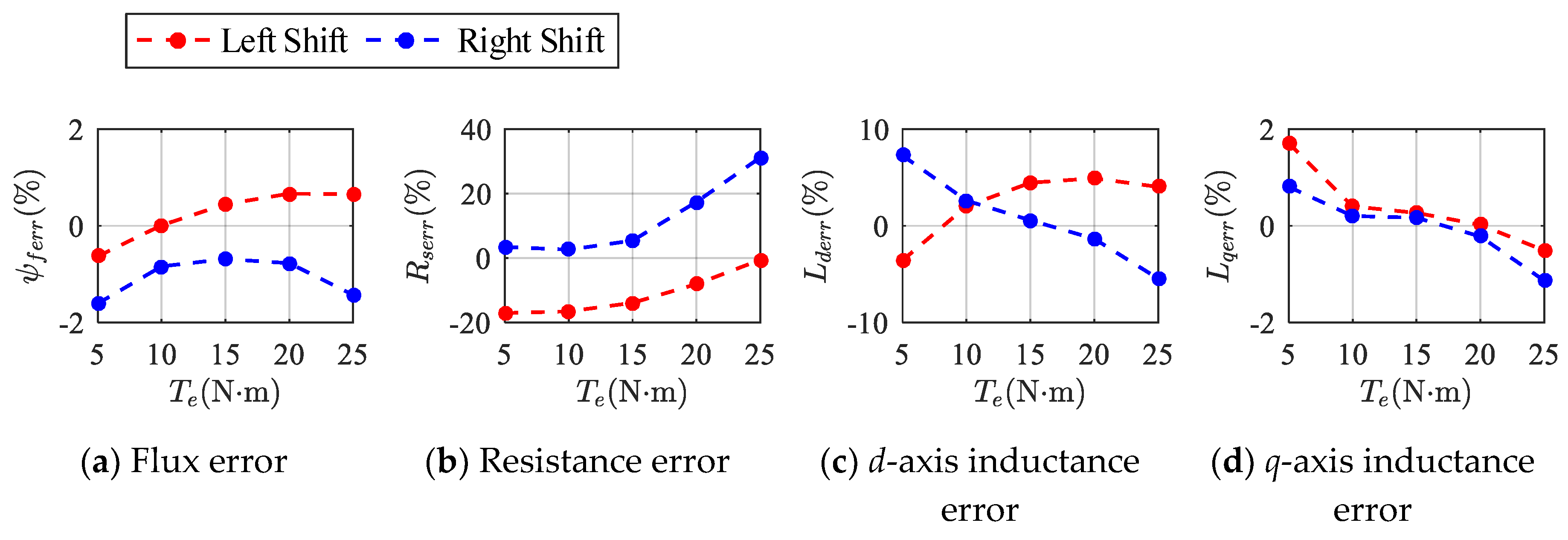
For the simulation, the proposed method was validated on a test motor operating at 40 Hz with load torques of 5, 10, 15, 20 and 25 N·m, respectively. The value of the △id was ±2 A. Nonideal factors such as temperature change and inverter nonlinearity were not considered in the simulation.
Figure 6 shows the simulation results of all four parameters. They are exactly the same as the theoretical results because the simulation environment was largely ideal. Therefore, the simulation verified the accuracy of the above theoretical analysis.
4.2. Experimental Results for Left and Right Shifts of the Operating Point with Different Torques
The experimental conditions were the same as those of the simulation except that there were nonideal factors that were difficult to compensate in the experiment, such as temperature, switching delay and switch voltage drop [
18,
19].
Figure 7 shows the experimental results for all four parameters. There are similarities between experimental results and the simulation results. For example, the variation trend of the parameter error was similar when the torque was more than 10 N·m. However, there were also large differences when the torque was 5 and 10 N·m because the pressure drop on parameters such as (
ωeLdid) was not large enough compared to the voltage errors caused by nonideal factors. The smaller the torque, the smaller the currents, and the greater the influence of voltage errors on the identification result, according to the voltage equations.
The resistance error, which reached between −20% and 30%, was the largest of the four parameter errors and was quite different from the simulation result. The reason is that the identification equation for resistance can be approximated as △ud/△id, and therefore resistance is more sensitive to voltage errors. If there is a 0.5 V voltage error, the resulting identification of resistance error is 10%. Apart from this, the errors for the other parameters, which were kept within 5%, met the accuracy requirements for vector control.
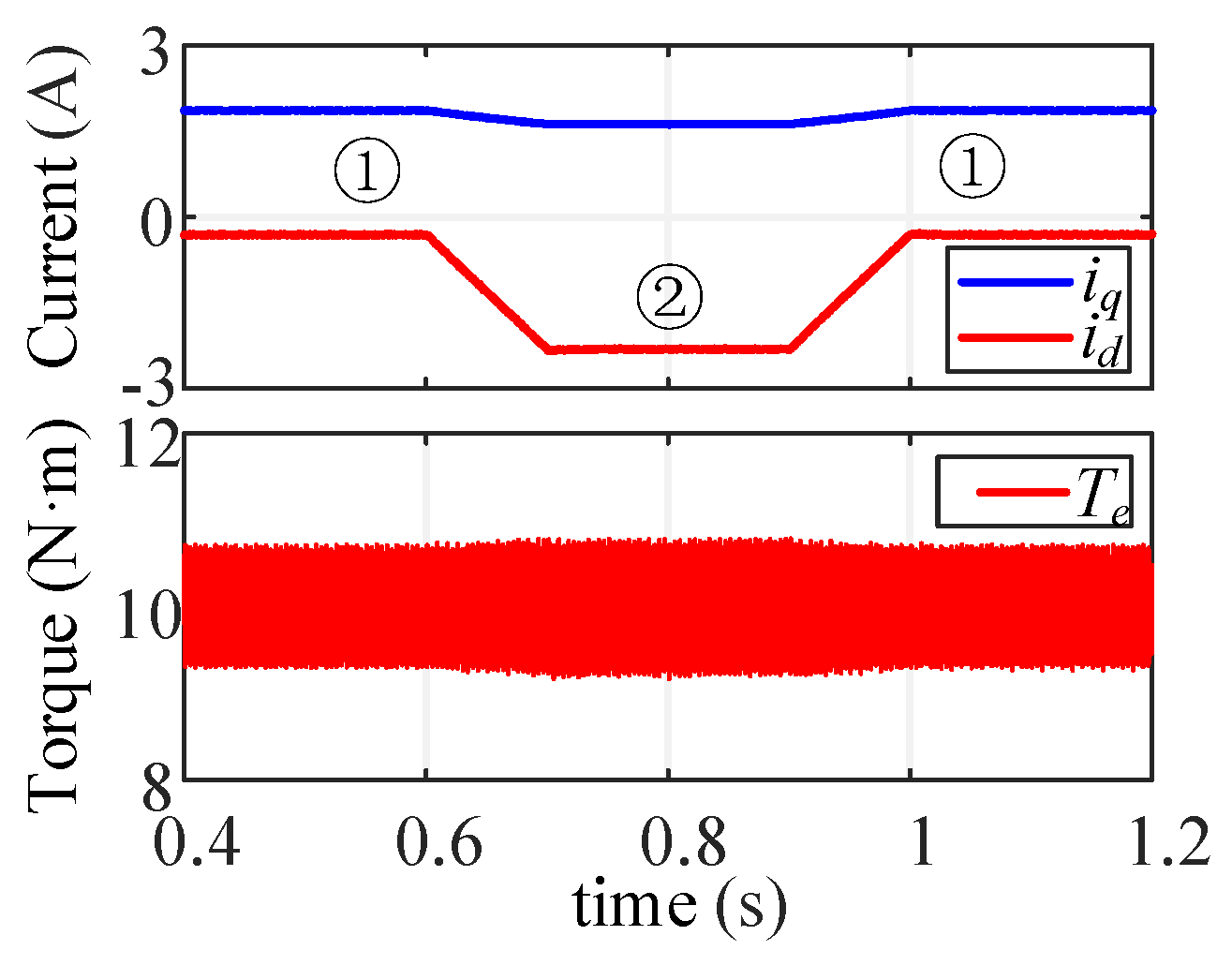
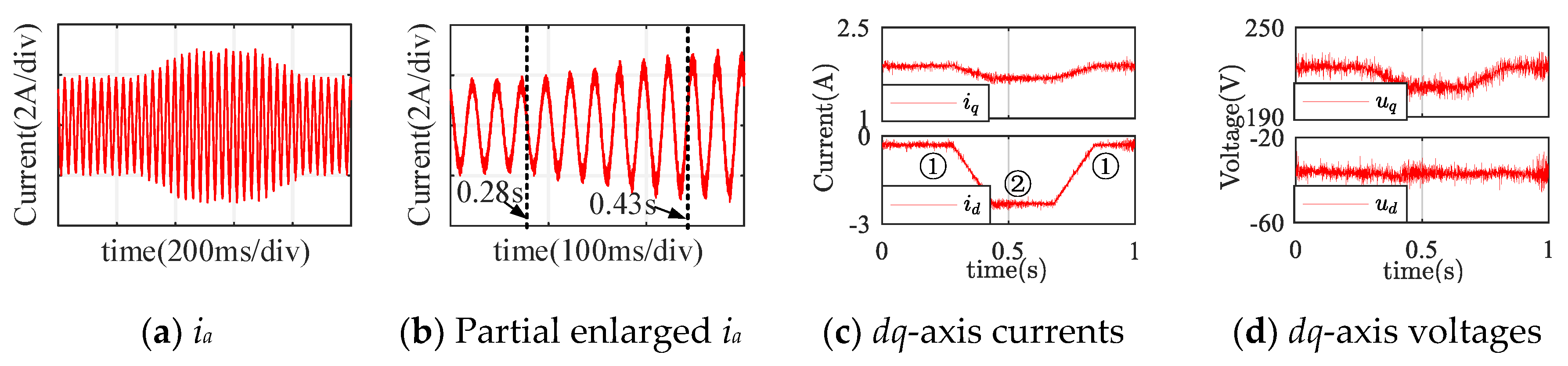
Figure 8 shows the waveforms of currents and voltages with a load torque of 10 N·m using left shift mode. The motor worked in the first steady state up to 0.28 s. The operating point moved left from 0.28 to 0.43 s and reached the second steady state at 0.43 s. During this period, the amplitude of
ia increased uniformly. The temporary operating point returned to the normal operating point along the original path from 0.68 to 0.83 s and reached the original steady state at 0.83 s. The
dq-axis voltages contained a certain degree of higher harmonics.
4.3. Experimental Results for Different Speeds
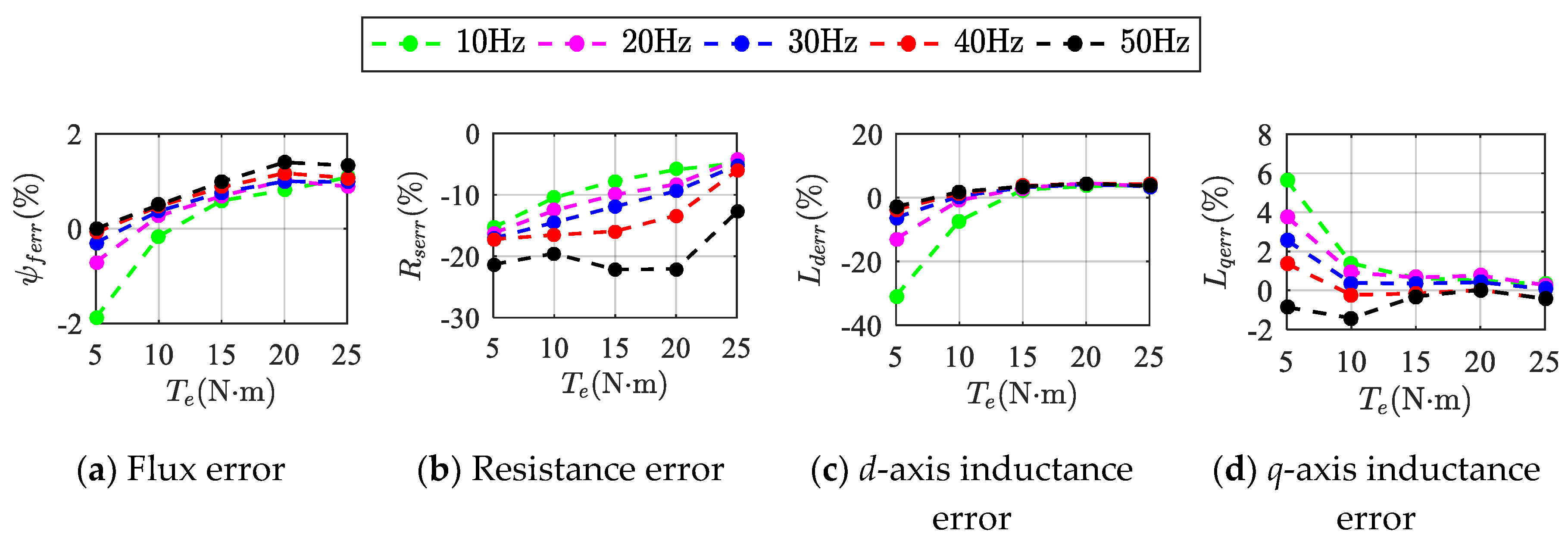
Figure 9 shows the experimental results for different speeds using left shift mode. The magnitude of
Rs1err increased with increasing speed. One reason has already been mentioned above. The identification equation of
Rs can be approximated as △
ud/△
id, which is not related to speed. However, the voltage errors, which were caused by nonideal factors and related to speed, resulted in increasing
Rs1err. Other errors, which were inversely proportional to the rotor speed according to Equation (12), decreased with increasing speed.
Ld1err was about −30% with a load torque of 5 N·m at 10 Hz because the voltage due to
Ld (
ωeLdid) was much smaller than that of
ψf (
ωeψf) in the
q-axis voltage equation. Thus,
Ld was more sensitive to the voltage error than
ψf. In conclusion, the higher the speed, the more accurate the identification will be.
4.4. Identification Results with Inaccurate Initial Parameters
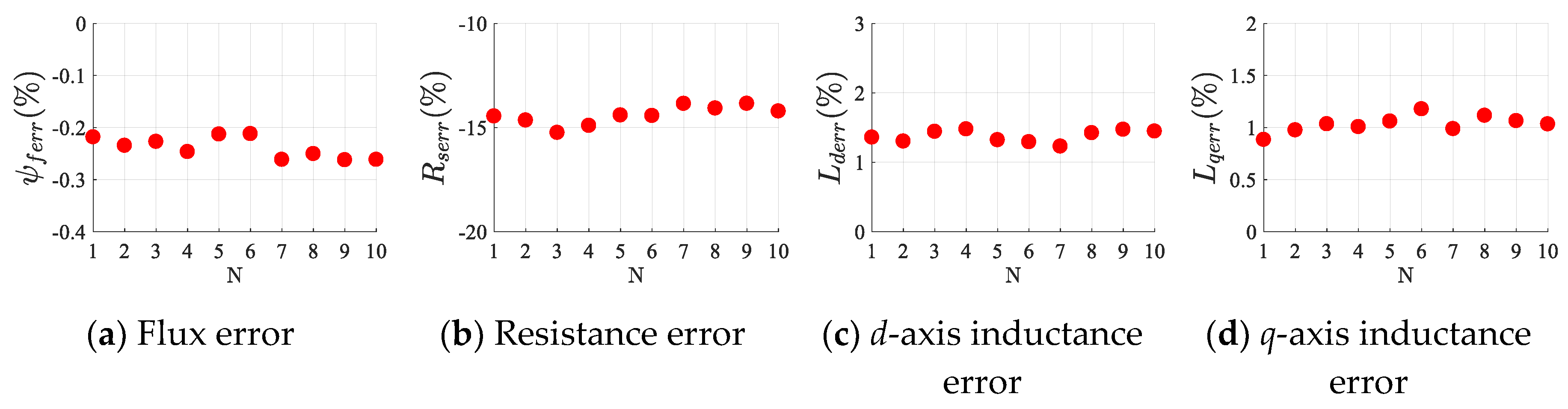
For the purpose of verifying the influence of inaccurate initial parameters on this method, the initial parameters of the motor, with reference to the reference parameters, were set according to Equation (37). Simultaneously, the identified parameters were applied to the vector control system. The algorithm was executed ten times with a load torque of 10 N·m at 40 Hz. The results are shown in
Figure 10.
The experimental results indicate that the inaccuracy of the initial parameters had no effect on this identification method. The reason for this is that the existence of the Proportion-Integral (PI) regulator kept the voltage constant at the steady state. Therefore, the identification result, which is based on the voltage, could be approximated as a constant value.
5. Conclusions
In this paper, a novel and simple method was designed for the real-time multiparameter identification of salient-pole PMSMs. Based on the steady-state equations of a salient-pole PMSM, a second steady state was constructed to meet full-rank conditions and minimize the torque ripple. The proposed error analysis method is applicable to the linear inductance model. The better shift direction of the operating point was designed to decrease identification errors using the results of error analysis. The simulation and experimental results indicate that this method can effectively identify flux and inductance at different loads and speeds. Furthermore, it does not need the nominal value of any parameter. Moreover, the computation of the proposed algorithm was much less-intensive than other real-time algorithms. However, the identification results were influenced by nonideal factors, especially for the resistance. We will carry out further investigations on the compensation algorithm to improve the identification accuracy in the future.