Abstract
Ocean wave energy is a broadly accessible renewable energy source; however, it is not fully developed. Further studies on wave energy converter (WEC) technologies are required in order to achieve more commercial developments. In this study, four CETO6 spherical WEC arrangements have been investigated, in which a fully submerged spherical converter is modelled. The numerical model is applied using linear potential theory, frequency-domain analysis, and irregular wave scenario. We investigate a parametric study of the distance influence between WECs and the effect of rotation regarding significant wave direction in each arrangement compared to the pre-defined layout. Moreover, we perform a numerical landscape analysis using a grid search technique to validate the best-found power output of the layout in real wave models of four locations on the southern Australian coast. The results specify the prominent role of the distance between WECs, along with the relative angle of the layout to dominant wave direction, in harnessing more power from the waves. Furthermore, it is observed that a rise in the number of WECs contributed to an increase in the optimum distance between converters. Consequently, the maximum exploited power from each buoy array has been found, indicating the optimum values of the distance between buoys in different real wave scenarios and the relative angle of the designed layout with respect to the dominant in-site wave direction.
1. Introduction
Wave energy is expected to contribute towards the development of a carbon-free electricity generation. The theoretical computation of wave energy potential over the oceans is projected to be in the order of 1–10 TW [1], which can cover the current global energy demand [2]. This tremendous potential has attracted attention from research societies, which have proved that harnessing electric power from ocean waves is possible [3,4]. Wave energy converters (WEC) are planned to be stationed in an array constituted of many converters -similar to offshore wind turbines. The initial developments of the analytical modeling of hydrodynamic forces on submerged buoys can be found in [5]. However, it has been further developed since then. The next stage of studies was focused on enhancing the design and power take off system of a single buoy [6]. The next studies bring the idea of WEC’s array by conducting a comparative study on different configurations [7]. The proceeding research phase concentrated on finding the optimal value for WEC’s array parameters (such as optimal position or layout) using either numerical, parametric or optimisation-based solutions [8,9,10,11], as this story falls in this category. The position of converters in the array which is scattered through the array has a direct relationship with the performance of the array because hydrodynamic interactions between them can be constructive or destructive. These interactions depend on the configuration of the array. Consequently, this is the main reason to investigate these interactions in order to apply them to reinforce the total power output. There are many relevant publications with this subject by several R&D units across Europe in the past by the pioneering works [12,13,14,15,16], and it is still an interesting research field, as several investigations have been published recently [17,18,19,20]. Furthermore, the identification of techno-economically feasible decarbonisation paths and sustainability transitions have been investigated by [21,22,23]. Some of the related research projects that considered the performance of arrays or converters’ distance were undertaken by [9,24,25,26] and the effects of nonlinear mooring forces via a time-domain analysis and the influence of interactions between WECs are well described in [27,28], respectively. Table 1 demonstrates a brief survey of some of the recent literature on the various aspects of WECs including layouts, PTO and design optimisation. Some of the mentioned research has used hindcast wave models; however, different layout configurations were considered regarding real wave scenarios in this study.

Table 1.
A briefly survey some of the recent literature on the layout, Power Take-Off (PTO) parameters and design optimisation of wave energy converters.
The CETO6 is a fully-submerged point absorber wave energy converter that is manufactured, installed, and updated by Carnegie Clean Energy Ltd. The prospective location of the WECs array is off the coast of Albany due to its exposure to open ocean wave conditions [58]. This study has been conducted based on the numerical simulation of this converter’s array. Our concentration is particularly on the arrangement optimisation of WEC arrays and shows the effectiveness of the inter-distance among WECs to produce more power. In order to establish an array of WECs, an optimal layout is chosen to maximise the power conversion; however, the number of WECs is a significant factor. We evaluate various numbers of WECs as an array, arrangements and separations, and report the performance of the layouts using q-factor, power of each converter and total power output. The distances between the WECs, and the array size are constrained, which is a more realistic approach for studying WEC arrays. Finally, a landscape numerical analysis is performed with regard to evaluating the position effect of each WEC in the array’s power output using a grid search approach.
It should be noticed that such research has not been investigated in the mentioned real wave scenarios (Perth, Adelaide, Sydney, and Tasmania) regarding this parametric study. Therefore, the main motivation of this study is to evaluate the output performance of the simulated CETO6 arrays to find a suitable layout with optimal distance, and the rotation angle to the dominant wave direction in these specific case studies. Moreover, the investigation coverage is more comprehensive than in other research studies by exploiting wave power using a ten-degree resolution covering the whole area of study, compared to, Bozzi et al. [24] presented the implementation and evaluation of a few numbers of WEC separation distances (5, 10, 20 and 30 buoy diameters) and incident wave directions ( apart).
This paper is structured into five sections. Section 2 presents a brief description of the hydrodynamic WEC array interaction model, modeling the wave climate and the equations used to compute the produced power. Section 3 expresses the layout assessment routine and presents the strategy to explore the optimal position of the WECs in the array. Section 4 discusses the array layout investigation results in terms of performance and optimal array layout solutions. Subsequently, Section 5 summarises the principal finding of the paper.
2. Numerical Modelling
2.1. Wave Energy Converter
In this study, a CETO6 wave energy converter with a three-tethered mooring system is considered which has a fully submerged spherical buoy attached to the seabed by the tethers, as shown in Figure 1. This model is developed in MATLAB and was modified in 2020 [59]. The WEC details are: buoy radius = 5 (m), submergence depth = 3 (m), water depth = 50 (m), buoy mass = 376 (t), buoy volume = 523.6 (m), tether angle = 55 (degree), PTO stiffness = 2.7 × 10 (N/m), PTO damping= 1.3 × 10 (Ns/m).
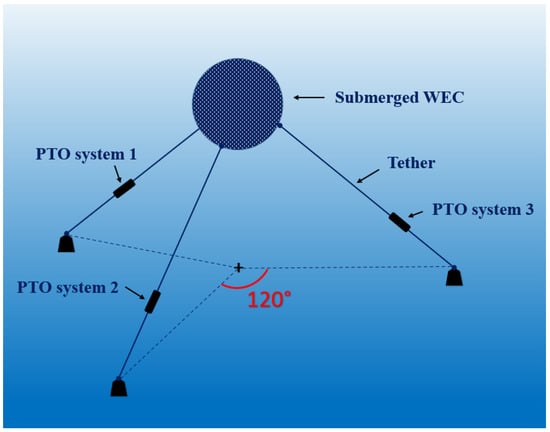
Figure 1.
Schematic representation of the CETO6 modelled point absorber wave energy converter (adapted from [60]).
This buoy, which is floating at sea, moves in six degrees of motion. However, due to the converter’s spherical shape, its displacement is in three degrees of freedom which are surge, heave, and sway. Based on these degrees, the motion equation can be written on the frequency domain.
where is the mooring force, is the hydro-static force resulting from buoyancy, W is the body weight, represents added mass and wave damping forces, force resulted by PTO system is , represents the vertical components of the wave exciting force and is the vertical viscous drag force [61]. This equation is used in order to describe a time-domain response of the WECs in waves, and can be rewritten as:
where m is a buoy mass, is the infinite-frequency added mass coefficient, C is the hydro-static stiffness, is the radiation impulse response function, is the wave excitation force, is the load force exerted on the buoy from the power take-off system [62]. Free surface elevation height results from a linear superposition consisting of some wave characteristics in irregular waves. This is usually determined by a wave spectrum which describes the distribution of energy in a vast number of wave frequencies. Significant wave height and peak period are utilized as the basic identification of the wave in the spectrum. The irregular excitation force can be calculated as the real part of an integral term across all wave frequencies as follows.
where R denotes the real part of the equation, is the excitation vector consists of amplitude and phase of the wave, S is the wave spectrum, is the stochastic phase angle, represents water elevation and is the element of force vector [48]. The load force of PTO is modeled as a linear spring-damper system.
where in Equation (4) and are control parameters which represent stiffness and damping of PTO and in Equation (5) u is the Heaviside step function, and are the hard stop spring coefficients, and and are the stroke limits which are related to the nominal position of the converter. It is important to note that, for computing useful absorbed energy, the effect of this force is not considered [63].
In order to calculate the energy produced by each buoy, the sum of three forces is necessary: wave excitation , force of radiation , and power take off force . The scattered irregular waves are included in the wave field when computing the excitation force. Furthermore, the stiffness and damping parameters of the PTO system at the end of each tether along with hydrodynamical parameters are taken in order to compute the total power output of an array. To calculate the average power absorbed by the array, several variables have to be taken in to account, as follows.
where is the average power absorbed by the array in a regular wave of unit amplitude, is the irregular wave spectrum which is calculated with the Bretschneider spectrum and represents the directional spreading spectrum, particularly for this site which is come from the wave rose [64]. is the wave frequency and is the power function of each submerged buoy defined by Equation (7).
where is the response amplitude operator (RAO) of the productive degree of freedom of the buoy obtained by solving the equation of motion from Equation (2), and is the Power Take-Off (PTO) damping. The wave angle is based on the [40], which can be calculated by equation (2) at the beginning of this section. The array at a certain test site is generated by total mean annual power , and to calculate that, the contribution of energy absorption from a wave climate in each state can be summarized as:
where is a number of chosen sea state, is the significant wave height and is the peak wave period for each sea state, represents the probability of occurrence of sea state which stems from the wave scatter diagram and is a power which the array produces in the nth sea state [40]. Significant wave height and peak wave period are statistics of a sea state which can refer to the condition of the ocean/sea surface. To calculate in irregular waves, it is necessary to sum all power contributions in each frequency and significant wave direction.
2.2. Wave Resource
According to previous works [40,45], four different sea sites were chosen for this study. The wave height directional distribution (wave rose) can be seen in Figure 2, at the chosen locations (as an example, the wave condition at the Sydney site is shown). The wave rose shows that the significant wave directions are from 15 degrees to 190 degrees, where 90 percent of the incident waves travelled. Consequently, the dominant wave direction is from the south.
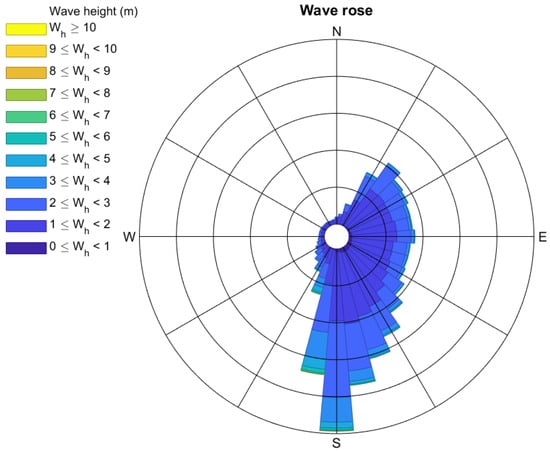
Figure 2.
The wave rose plot at Sydney.
Each array is constrained by the maximum area and the minimum distance between WECs. Firstly the minimum separation between buoys has to be 50 m to provide a safe pass for vessels. Secondly, although the area grows by increasing the number of buoys, it has to be constrained within the area , where [45].
The Bretschneider spectrum is used for modeling irregular waves in this study. This spectrum is a modified Pierson-Moskowitz spectrum which is based on significant wave height and peak period. These two parameters are highly dependent on wind speed and its direction [65].
where and are the significant wave height and the frequency of the peak wave period, respectively.
2.3. Array Interaction Criteria
The optimal designs of the array for four different locations in Australia use power matrices of various configurations (i.e., different layout geometry, WEC distance and relative angles regarding dominant wave direction wave directions). To be more precise, the goal is to select the best site for each layout configuration with the optimal separation among WECs and rotation angle, namely, the one that provides the highest annual energy output per each converter. For this aim, based on the number of WECs, different layouts can be deployed with various orientations and separation among converters. Note that there are certain constraints for distances, and this depends on the number of WECs. Similarly, the number of converters in an array allows configurations to be chosen. Hence, it is crucial to measure the effectiveness of interactions between converters by the q-factor coefficient. The q-factor is shown to be an important evaluation criterium such that if , then it has a positive effect on the total energy of an array; otherwise, the interactions are destructive.
where is the power that an isolated WEC generates, N is the number of converters [41]. As Equation (10) indicates, there is a direct relationship between q-factor and power output of each array; however, both of them have to be studied separately, due to different objectives of finding optimal values for each parameter. The maximum feasible amount of q-factor is investigated to achieve the best constructive effects of interactions of buoys in an array. On the flip side, since the power output of a WEC array plays a significant role in the assessment of the system’s response to energy consumption needs in coastal areas, this parameter is considered along with the q-factor. The equation below calculates the mean q-factor by considering the number of converters, variety of wave directions and allowable distance within a 5 m interval.
where is the direction of wave n 10-degrees resolution, except when N is 5, the interval changes to 9 degrees ranging from 0–63 degrees and l is the maximum allowable distance between buoys within the area. This mean q-factor coefficient will be considered to find the best location for the max q-factor over different angles and distances.
3. Layout Assessment Routine
According to the mentioned equations in Section 2, the following outcomes are obtained. Four different layouts are considered regarding the number of buoys, and they are thoroughly described in detail. By looking at the mentioned literature, it is evident that using more converters results in more potential destructive interaction. Specifically, the q-factor may decrease when the number of buoys rises to greater than five [54]. Therefore, we decided to choose the five buoy layout as the maximum complexity for the model; however, evaluating the larger wave farm characteristics is a part of our future research plan. Furthermore, the symmetric design is proposed for the layouts based on the following reasons: (i) To find a single variable to handle, the buoy-buoy distance must remain constant for each configuration. Thus, the symmetric configuration fulfills this requirement in our assessment, like in previous studies [66]. (ii) To cover the whole area of study in power absorption assessment process, the array rotates 10 degrees, regarding the dominant wave direction, in each evaluation. The asymmetric effect of the array configuration rules out the duplicate assessment, resulting in less computational cost.
In the first step, There are two buoys in this array, and one line connecting them. The dominant wave direction indicates the direction in which most waves travel. However, in the calculation of power output from each buoy or an array, the significant wave directions are used. These are directions from where 90 percent of the waves are traveling. Furthermore, the resolution size of the evaluation is 15 degrees, by which we detect the dominant direction of the waves.
The dominant wave direction is obtained by considering one-third of the maximum waves in the wave rose. The angle between dominant wave direction and a hypothetical line is considered to be alpha (), which is clearly illustrated in Figure 3. The interval of alpha is chosen to be tested every 10 degrees; therefore, there would be 18 different alpha ranging from 0 to 170 degrees. This range has been considered to prevent the extra calculation of results that have already been calculated. When there are three buoys to consider in an array, one of the most common geometries is the equilateral triangle. If some lines are used for connecting these buoys, angles between vertexes of the triangle will be 60. There is a line from this converter perpendicular to the line, which connects the two other buoys. The angle between the dominant wave direction and this perpendicular line is alpha, shown in Figure 3, and this parameter has twelve degrees from 0 to 110, which changes every 10 degrees. A regular quadrilateral is taken into account to configure four buoys. To describe alpha in this layout, firstly, the dominant wave direction needs to be determined. Secondly, a hypothetical line should be drawn from one converter to the furthest one. For example, if the converters are numbered clockwise and the closest buoy to the front wave is buoy number one, the line should be drawn from 1 to 3, exactly like in Figure 3. Finally, the angle between this line and dominant wave direction is alpha, and the range of this is from 0 to 80 degrees, which has nine different amounts with equal intervals.
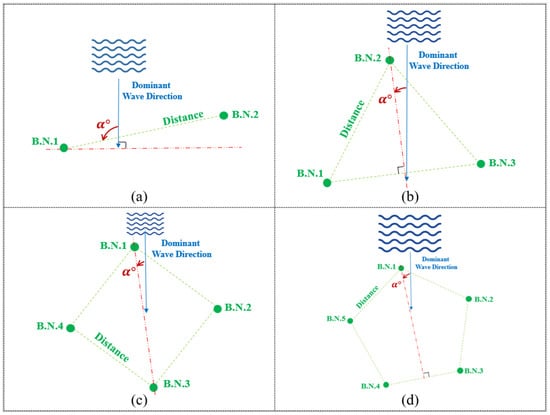
Figure 3.
Layout Setup of (a) 2 buoys array (linear), (b) 3 buoys array (triangle-shape), (c) 4 buoys array (square-shape) and (d) 5 buoys array (pentagon-shape), with regard to dominant wave direction.
In this layout, five similar converters form an array are shown in the shape of a regular pentagon. The dominant wave direction is illustrated in Figure 3 with a blue arrow. Converters are numbered clockwise, and the first number starts from the closest buoy to the front wave. As shown in Figure 3, each converter has the longest distance with two buoys. In this case, the furthest converter to buoy number 1 is number 3 and 4. If a perpendicular line is drawn from the first converter to the connecting line between furthest converters, the angle between the dominant wave direction and the perpendicular line represents alpha. The range for alpha is from 0 to 63 in 9-degree intervals, so there are eight alphas to test in this layout. Distances are also assumed to change every five meters between the allowable period. In the end, three measurements, which are the power output of each buoy, array power, and q-factor, are taken in each step for all layouts, separately. The details of all results are discussed comprehensively in Section 5.
4. Results and Discussions
This section represents the results of different array layouts when the number of buoys rises from 2 to 5 in considered locations on the Australian coast. The results demonstrate the sensitivity of the array power and the q-factor due to the changes in buoy-buoy distance and rotation angle. It is worth mentioning that there are 16 conditions in this study, which will be discussed in detail as follows. To choose the optimal degree in this section, one of the most important variables is alpha, whose optimum value leads to the average maximum amount of the power output.
4.1. Sensitivity of Two-Buoy Array Performance to Distance
Figure 4 shows the sensitivity analysis of the array power output to the different buoy-buoy distances. It can be seen that Tasmania has the most wave array power, which is almost 0.534 Mw where the is 80 degrees and the buoy-buoy distance is 160 m. The 60-degree angle line, which has the most average power, rises with a sinusoidal trend from the beginning to 200 m. Then, it increases gradually. The second location is Sydney, which has a considerable array power. Although its array power is 0.218 Mw, which is far less than Tasmania, the maximum average array power occurs in 130 degrees with a similar trend to the mentioned location. The maximum power that Sydney’s layout determines is achievable when the distance is around 400 m. Adelaide and Perth are similar in terms of the array power range, which is roughly from 0.18 to 0.196 Mw. As the green line in these figures shows, when the rotation angle and buoy-buoy distance are 40 degrees and 165 m, respectively, both reach the highest array power. The maximum average of array power can be witnessed in 20 degrees in Adelaide and 30 in Perth. In the two mentioned sites, it is apparent that figure lines follow different trends. To compare, when is 20 degrees, and buoy-buoy distance is 100 m, the first peak of the array power is observed in Adelaide. Next, it falls until the distance goes over 150 m. The first peak in Perth happens when the distance is near 60 m. Then, it remains unchanged for the next 60 m. After significant growth, it reaches around 0.194 Mw with 160 m buoy-buoy distance. Overall, it is remarkable that the maximum power can be harnessed in three locations when the distance is 160 m.
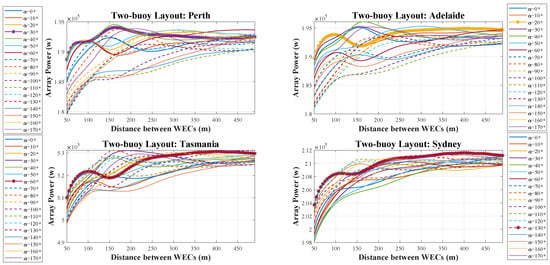
Figure 4.
Array power of the two-buoy layout over different distances in four wave models.
4.2. Sensitivity of Three-Buoy Array Performance to Distance
It can be seen that in Figure 5, the most obvious inferred outcome is that, the longer distance between WECs leads to more extracted power output. However, widening the area might not be proficient because the line only rises 0.2 Mw by increasing the distance from 250 to 500 m. The maximum harnessed power output can be seen when is 10 degrees, except in Sydney, which is 110. The range of array power is quite narrow in the mentioned locations, where only a 0.05 Mw gap can be witnessed among 12 tested angles. The main reason for obtaining the similar results among different angles’ experiments can be explained as follows. Where the three converters are placed in equilateral triangle geometry, there would always be two buoys in the zone of radiation. Therefore, the changes in cannot produce considerable effects. By comparing the power output of WECs over the changes of distances, we can see the same overall trend has been followed in all studied locations. A sharp rise in array power can be achieved by increasing the distance up to 100 m, followed by a gradual rise by increasing the distance up to the maximum allowed size. It can be mentioned that differences between maximum distance in each layout relate to the area constraints, which have already been discussed in Section 2.
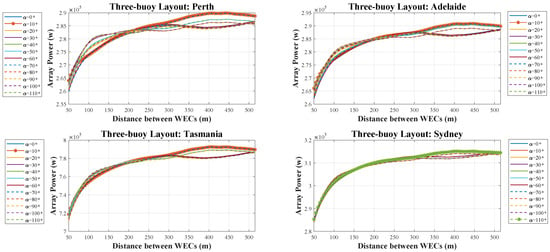
Figure 5.
Array power of the three-buoy layout over different distances in four wave models.
4.3. Sensitivity of Four-Buoy Array Performance to Distance
The geometry chosen for four converters is a square shape. values in this layout range from 0 to 80 degrees with 10-degree intervals. The highest harnessed array power is 1.05 Mw in Tasmania, while the lowest one observed in the Perth layout is around 0.387 Mw. Turning to the rotation angle, for Perth and Sydney, the angle is 40 degrees to extract the maximum average array power; however, for Tasmania and Adelaide, is 0 and 80 degrees in order of appearance. Considering the distances between WECs, it is interesting that where the buoy-buoy distance is between 150 and 200 m, the maximum wave array power can be exploited in Perth, Adelaide, and Tasmania. However, in Sydney, it seems that in this , the array power evens off after reaching the highest amount. Hence, the minimum distance between WECs is more cost beneficial for considering layout design 160 m of distance takes into account. In contrast, in Adelaide and Tasmania, a 160 or 170-m distance seems to be the best distance between converters. This amount is a bit greater in Perth, where the highest array power is firstly seen in the 180-m distance (Figure 6).
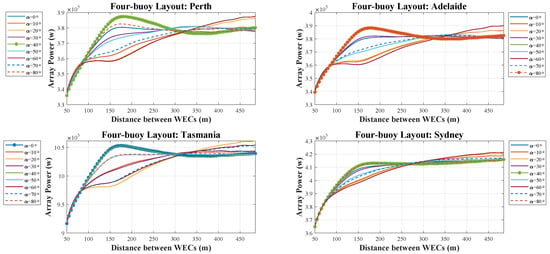
Figure 6.
Array power of the four-buoy layout over different distances in four wave models.
4.4. Sensitivity of Five-Buoy Array Performance to Distance
In this study, the configuration of five converters is chosen as a regular pentagon array. This is because there is no difference between each WEC, and the range of rotation angles is restricted to be between 0 and 63 with eight different angles. The maximum averaged array power in all four case studies is witnessed when the is either 18 or 63 degrees. To be more precise, in Tasmania and Perth, the is 18 degrees, and for the other two, it is 63 degrees. Also, it is evident that when the distance is between 200 and 250 m, the maximum power output is harnessed in all wave scenarios; and the optimal choice can be found in the mentioned range consequently. As Figure 7 shows, the trend of all case studies are similar, except in the 18-degree’s line in Tasmania and Perth, where the array power reduces gradually after the peak, instead of leveling at the peaks power. By comparing this result with recent similar studies, we can see the same trend of absorbed power by raising the distance between WECs in each layout up to an optimal value, after which the results were roughly stable [54,67].
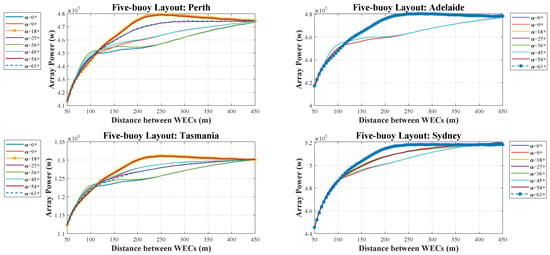
Figure 7.
Array power of the five-buoy layout over different distances in four wave models.
4.5. Sensitivity Analysis of q-Factor to the Relative Angle of Rotation
The interaction of converters is measured with a well-known parameter called q-factor. A sensitivity analysis has done by monitoring the q-factor distribution over different rotation angles of the WECs in each layout. Since the interaction of the buoys in each layout could be constructive or destructive, the q-factor is calculated per 5 m of distance between converters. Figure 8, Figure 9, Figure 10 and Figure 11 show the distribution of results of calculated q-factors over different relative angles in a box chart, describing the values as they spread across the entire range. In each angle, there is a box that reveals the amount of fifty percent of q-factor results. Also, the middle line indicates the mean value of all results. The other amounts of q-factor, which are far from the mean values (i.e., the greatest 25 percent and the least 25 percent of the results), are shown by two lines located above and below the rectangular box.
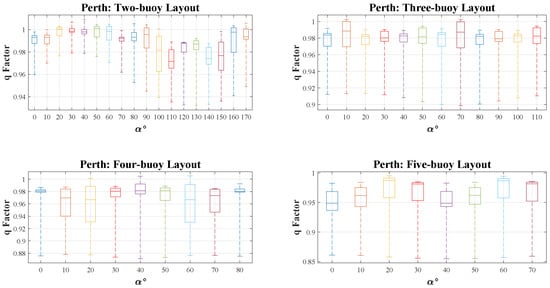
Figure 8.
q-factor results distribution and mean value per five meters of the Wave Energy Converters (WECs)’ distance over rotation angle due to significant wave direction in the Perth wave model. (Fifty percent of results near the mean value are plotted in a box, the range of other results is shown by a dashed line).
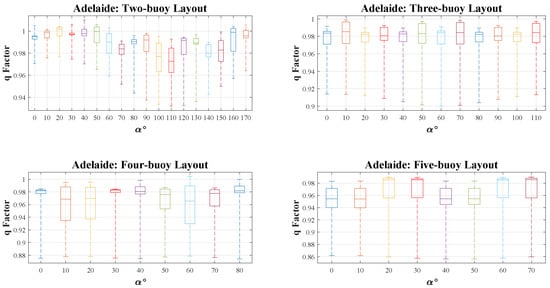
Figure 9.
The q-factor results distribution and mean value every five meters of WECs’ distance over rotation angle due to the significant wave direction in the Adelaide wave model. (Fifty percent of results near the mean value are plotted in a box, the range of the other results is shown by a dashed line).
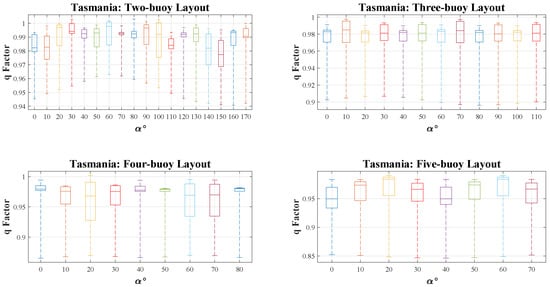
Figure 10.
The q-factor results distribution and mean value per five meters of WECs’ distance over rotation angle due to significant wave direction in Tasmania wave model. (Fifty percent of results near the mean value are plotted in a box, the range of other results are shown by a dashed line).
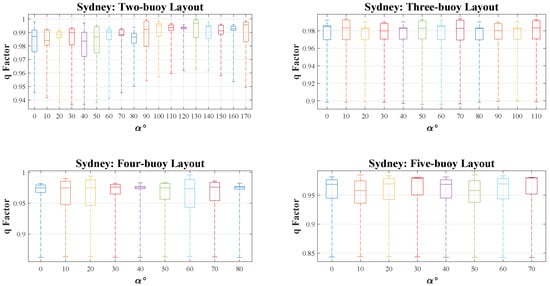
Figure 11.
q-factor results distribution and mean value per five meters of WECs’ distance over rotation angle due to significant wave direction in the Sydney wave model. (Fifty percent of results near the mean value are plotted in a box, the range of the other results is shown by a dashed line).
There is a lot of similarity between Adelaide and Perth in terms of their q-factors, but Sydney and Tasmania have different trends. In both Adelaide and Perth, as Figure 8 and Figure 9 show in two-buoy layout, a fluctuating pattern is witnessed which indicates the importance of the rotation angle of the array power with respect to the dominant wave direction. Thus, when is between 30 and 40 degrees, the highest q-factor is achieved, and the layout design process should be followed by choosing the best buoy-buoy distance in the mentioned angle. The distinction between q-factors in the three-buoy layout is negligible due to the effects of dominant wave direction on the equilateral triangle layout, in which one converter affects two others by radiated waves. The maximum q-factor can be seen in the 30 and 40 degrees area. In the four-buoy layout, when is 40 degrees, the q-factor is around 1 in both locations. Among the 9 discussed dominant wave directions, the highest q-factors are seen when is 20, 40, or 60 degrees, and the average q-factor in each direction is a bit over 0.96. In the five-buoy layout, it is clear that the average q-factors are between 0.95 and 0.98, and the highest q-factors happen when is either 20, 30, 60, or 70 degrees, and the range of q-factors is from 0.85 to 0.98. It is important to note that in the mentioned degrees, q-factors are mostly close to the highest amount because the average line is on top of each box.
In Tasmania, due to the symmetry between WECs and small effects of changing in q-factor for the three-buoy and five-buoy layout, changes are not considerable. The average q-factor in each rotation angle is approximately 0.98 and 0.96, respectively. When is between 40 and 90 degrees in the two-buoy layout, q-factors in each distance are between 0.95 and 1.005. The maximum averaged array power occurs at 20 degrees. In the four-buoy layout, maximum q-factors are observed in four rotation angles, which are 0, 20, 40, and 60 degrees. Further details can be found in Figure 10.
Looking at Sydney in Figure 11, in the two-buoy layout, it is evident that maximum q-factors happen when is either between 110 and 120 degrees or 130 and 140. One of the distinctions compared to the mentioned locations is that the lowest q-factor is seen at 40 degrees. In the three-buoy and four-buoy layout, the average q-factor in each is around 0.98 and 0.97, respectively, and its changes are not recognizable in all 12 tested angles. The q-factors in the five-buoy layout ranged from 0.84 to 0.98. The closest q-factor values to 1 are found at 10 and 50 degrees. Moreover, it can be inferred that when is 30 or 70 degrees, the related q-factors are near 0.98. These results would help further feasibility studies of the WECs’ array analysis by presenting the possible range of achievable q-factors in Perth, Adelaide, Tasmania, and Sydney ports.
4.6. Landscape Analysis
Figure 12, Figure 13, Figure 14 and Figure 15 reveal the power for each buoy in four different layouts. Overall, it is inferred that the asymmetry in arrays makes the power more predictable in each distance and rotation angle. The illustrated plots in this section indicate four kinds of buoy layout for each area in Adelaide, Tasmania, Sydney, and Perth. For each layout, the Colour-bar presents the amount of total power per buoy. This amount has been shown in the form of a contour. In general, there is a similar pattern for studied locations by considering the configuration of the arrays. The maximum amount of extracted energy is more likely to be found in the 5-buoy layout. Moreover, the power of each converter in the center area is not considerable, and the maximum amounts of the exploited energy found for higher buoy-buoy distances. The asymmetry of these energy distributions is high as well, but Perth is an exception. To observe abrupt changes, an increase in the resolution of distance and angles are needed. Take the 2-buoy layout in Adelaide as another example of non-asymmetric layout; the distribution of the incident waves over different angles implied such non-asymmetric contour of exploited energy. The reason behind the asymmetry in other layouts would be that by increasing the number of buoys, possible shadowing effects proportional to each rotation angle occur in every layout. In some placements of the 2-buoy layout, as the array experiences different rotation angles, the buoys may see the same dominant wave direction; however, in some angles, the shadowing effect of one buoy over the other can play a crucial role in reducing the energy. This shadowing effect of buoys to each other becomes more drastic, as the number of buoys increases because, in each angle, there is more chance of interaction between at least two buoys. To describe blue spots it should be noted that in this research, the minimum separation between buoys is considered to be 50 m. Then, by assessing the different angles, the configuration of the array rotates over the center point, such that the lowest amounts of energy may be witnessed in the middle of the figures by interpolation.
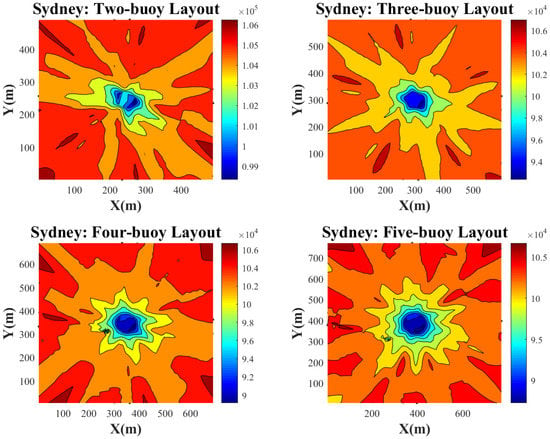
Figure 12.
Exploited energy distribution of the WECs array over entire area in Sydeny wave scenario.
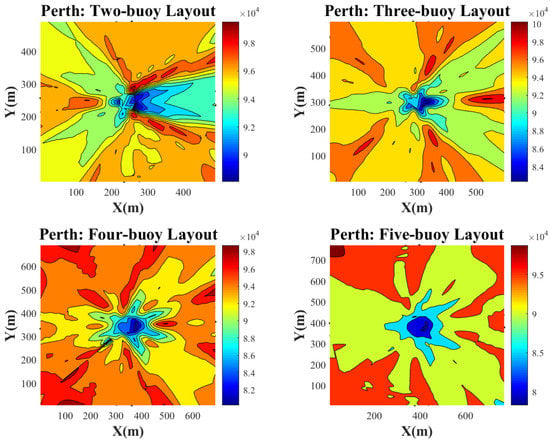
Figure 13.
Exploited energy distribution of the WECs array over the entire area in the Perth wave scenario.
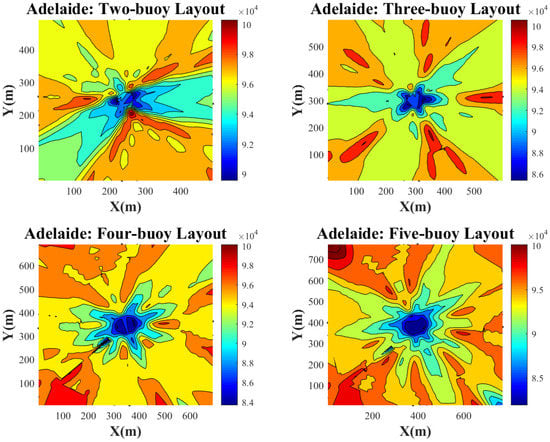
Figure 14.
Exploited energy distribution of the WECs array over the entire area in the Adelaide wave scenario.
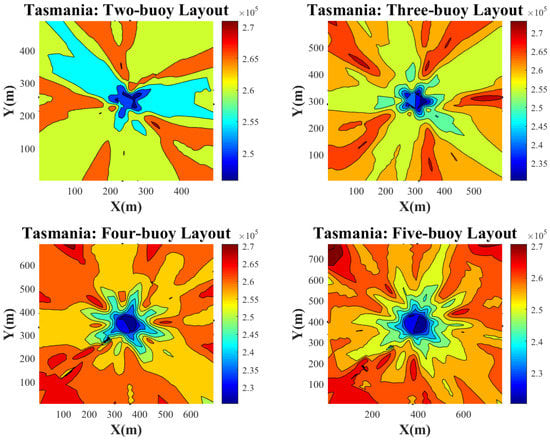
Figure 15.
Exploited energy distribution of the WECs array over the entire area in the Tasmania wave scenario.
Taking a look at Figure 12, it is interesting that the order of maximum power for each layout is around 0.1 to 0.105 Mw in most areas. However, this range increases in the two-buoy layout, so more areas with dark red colour can be seen. In this figure, asymmetry in each layout is more evident than in the other locations.
There are many similarities between Adelaide and Perth in Figure 13 and Figure 14. For instance, in a two-buoy layout, their contour has resemblance, and the range of power is identical. Furthermore, more power is extracted in Perth based on these plots. To compare the four-buoy layout, Adelaide has more symmetrical power distribution, and the chance of reaching 1 power is more in Adelaide in general. Finally, there is a small difference between choosing Perth or Adelaide as the installation site among the other surveyed sites.
The highest amount of power can be exploited from converters in Tasmania, which is obvious in Figure 15. Although seemingly green areas in the two-buoy layout cover the majority of the zone, the power that belongs to the green areas is very close to the other layouts of the orange ones. The chance of extracting over 0.27 Mw power is seen in the five-buoy and four-buoy layouts. It is worth considering the three-buoy layout power when the x axis is over 250 m, which reveals the potential of this layout under certain conditions. Likewise, when the y axis is less than 150 or more than 350, this potential is met.
4.7. Interaction Based Layout Selection
Figure 16 shows the maximum and mean value of the q-factors in a given number of buoys in each wave model. The most significant observations inferred from Figure 16 are addressed as follows. The maximum q-factor in Tasmania and Sydney is less than in the other locations because of the lack of constructive interactions to compare to the other layouts. The mean q-factors are also higher in Perth and Adelaide in all locations for the same reason. Turning to the maximum q-factor, it is apparent that the highest constructive interactions in the two-buoy layout occur in Adelaide. However, in Sydney’s wave scenario, installing buoys, whether separately or in an array, is almost the same because the q-factor equals 1 in the best-case scenario. Although this amount is over 1 in all locations of the four buoy layout, Sydney is an exception. In the three-buoy layout and five-buoy layout, only the q-factor of Perth is more than 1. It is worth considering that the latter has the least maximum q-factor. These results confirm results from previous studies on the decrease of q-factor after increasing the number of WECs arrays, specifically after incorporating more than five buoys [54]. Turning to the mean q-factor, it is evident that by increasing the number of buoys, this variable decreases, and a reduction of almost 0.07 is seen by adding a buoy. Also, this measure is observed to be a trend because constructive interactions are more likely to be seen in Perth and Adelaide. These interactions will occur if the , buoy-buoy distance, and the geometry of layout are appropriately chosen.
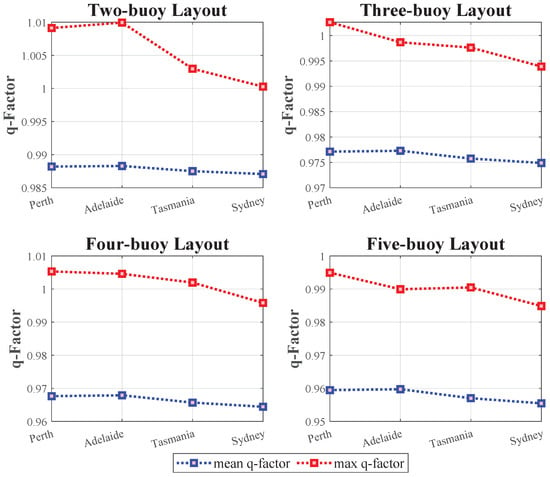
Figure 16.
Comparison of maximum and mean q-factor in different wave scenarios in each layout.
Finally, it has to be noticed that further details and numbers are written in Table 2, which enables a comparison between each location. The bold numbers in Table 2 represent constructive interactions between converters. Therefore, in those cases, installing an array is more efficient.

Table 2.
Best solutions related to maximum q-factor in each wave scenario.
5. Conclusions
Investigating for an appropriate arrangement an array layout constitutes a complicated problem in wave energy projects. Wave energy converters can reinforce each other to provide more power output in the form of an array if the distance among them is efficiently adjusted and the arrangement of the layout appropriately defined. In this paper, we analyzed the CETO6-project WECs separation in an array with different numbers of devices and arrangements. In order to assess the impact of various wave models, we perform and compare all numerical analyses in four real wave scenarios including the Sydney, Perth, Adelaide, and Tasmania sea sites. According to the numerical analysis, there is a direct relationship between the number of converters and optimal inter-distance among them and also relative angle to the significant wave direction. Greater separation between converters leads to more array harnessed power output. However, the most exploited energy can be achieved in 2 buoy layout with a 165 m buoy-buoy distance. A sensitivity analysis has revealed that the q-factor distribution differed due to different rotation angles of the WECs array. Moreover, the maximum q-factor output analysis showed that results in a two-buoy layout in all scenarios, tree-buoy layout in Perth and four-buoy layout in all scenarios (excluding Tasmania) are far higher than the other locations’ q-factor, and this parameter is almost the same in the five-buoy layout sea sites. However, the landscape analysis-approved maximum amount in terms of the extracted net power output was found in the 5-buoy layout in the Tasmania wave scenario.
Author Contributions
Conceptualization, E.A.; Data curation, D.G., M.M.N., M.N.; Formal analysis, E.A., D.G., F.A.; Investigation, E.A., D.G., F.A., M.M.N. and M.N.; Methodology, E.A., D.G., F.A., M.M.N. and M.N.; Resources, M.N.; Supervision, D.A.G., F.A.; Validation, E.A., D.G., F.A., and M.M.N.; Visualization, E.A., D.G., and F.A.; Writing—original draft, E.A., D.G., M.M.N. and M.N.; Writing—review & editing, M.N. and D.A.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by ODYSSEA project that received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 727277.
Acknowledgments
The authors would like to express their gratitude to ODYSSEA project that received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 727277. Furthermore, the authors would like to appreciate Nataliia Surgiienko from the University of Adelaide due to publishing the MATLAB source code of the wave energy simulator. This work has been supported by the High Performance Computing Research Center (HPCRC)—Amirkabir University of Technology under Contract No. ISI-DCE-DOD-Cloud-700101-4504.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| WEC | Wave Energy Converter |
| PTO | Power Take-off |
| PSO | Particle Swarm Optimisation |
| GA | Genetic Algorithm |
| EA | Evolutionary Algorithms |
| DE | Differential Evolution |
| GWO | Gray Wolf Optimiser |
| ML | Machine Learning |
References
- Barstow, S.; Mørk, G.; Mollison, D.; Cruz, J. The wave energy resource. In Ocean Wave Energy; Springer: Berlin/Heidelberg, Germany, 2008; pp. 93–132. [Google Scholar]
- (US) EIA; Government Printing Office. International Energy Outlook 2016, with Projections to 2040; Government Printing Office: Washington, DC, USA, 2016.
- Clément, A.; McCullen, P.; Falcão, A.; Fiorentino, A.; Gardner, F.; Hammarlund, K.; Lemonis, G.; Lewis, T.; Nielsen, K.; Petroncini, S.; et al. Wave energy in Europe: Current status and perspectives. Renew. Sustain. Energy Rev. 2002, 6, 405–431. [Google Scholar] [CrossRef]
- Antonio, F.d.O. Wave energy utilization: A review of the technologies. Renew. Sustain. Energy Rev. 2010, 14, 899–918. [Google Scholar]
- Linton, C. Radiation and diffraction of water waves by a submerged sphere in finite depth. Ocean Eng. 1991, 18, 61–74. [Google Scholar] [CrossRef]
- Babarit, A. On the park effect in arrays of oscillating wave energy converters. Renew. Energy 2013, 58, 68–78. [Google Scholar] [CrossRef]
- Babarit, A.; Hals, J.; Muliawan, M.; Kurniawan, A.; Moan, T.; Krokstad, J. Numerical Estimation of Energy Delivery from a Selection of Wave Energy Converters—Final Report; Report; Ecole Centrale de Nantes & Norges Teknisk-Naturvitenskapelige Universitet: Nantes, France, 2011. [Google Scholar]
- Göteman, M.; Engström, J.; Eriksson, M.; Isberg, J.; Leijon, M. Methods of reducing power fluctuations in wave energy parks. J. Renew. Sustain. Energy 2014, 6, 043103. [Google Scholar] [CrossRef]
- Göteman, M.; Engström, J.; Eriksson, M.; Isberg, J. Optimizing wave energy parks with over 1000 interacting point-absorbers using an approximate analytical method. Int. J. Mar. Energy 2015, 10, 113–126. [Google Scholar] [CrossRef]
- Giassi, M.; Castellucci, V.; Göteman, M. Economical layout optimization of wave energy parks clustered in electrical subsystems. Appl. Ocean Res. 2020, 101, 102274. [Google Scholar] [CrossRef]
- Neshat, M.; Sergiienko, N.Y.; Amini, E.; Majidi Nezhad, M.; Astiaso Garcia, D.; Alexander, B.; Wagner, M. A New Bi-Level Optimisation Framework for Optimising a Multi-Mode Wave Energy Converter Design: A Case Study for the Marettimo Island, Mediterranean Sea. Energies 2020, 13, 5498. [Google Scholar] [CrossRef]
- Budal, K. Theory for absorption of wave power by a system of interacting bodies. J. Ship Res. 1977, 21, 248–254. [Google Scholar]
- Evans, D. A theory for wave-power absorption by oscillating bodies. J. Fluid Mech. 1976, 77, 1–25. [Google Scholar] [CrossRef]
- Budal, K. Interacting Point Absorbers with Controlled Motion; Pascal Academic Press: London, UK, 1980. [Google Scholar]
- Thomas, G.; Evans, D. Arrays of three-dimensional wave-energy absorbers. J. Fluid Mech. 1981, 108, 67–88. [Google Scholar] [CrossRef]
- Simon, M. Multiple scattering in arrays of axisymmetric wave-energy devices. Part 1. A matrix method using a plane-wave approximation. J. Fluid Mech. 1982, 120, 1–25. [Google Scholar] [CrossRef]
- Castro, F.A.; Chiang, L.E. Design optimization and experimental validation of a two-body Wave Energy Converter with adjustable Power Take-Off parameters. Energy Sustain. Dev. 2020, 56, 19–32. [Google Scholar] [CrossRef]
- Neshat, M.; Alexander, B.; Wagner, M. A hybrid cooperative co-evolution algorithm framework for optimising power take off and placements of wave energy converters. Inf. Sci. 2020, 534, 218–244. [Google Scholar] [CrossRef]
- Bonovas, M.I.; Anagnostopoulos, I.S. Modelling of operation and optimum design of a wave power take-off system with energy storage. Renew. Energy 2020, 147, 502–514. [Google Scholar] [CrossRef]
- Calvário, M.; Gaspar, J.; Kamarlouei, M.; Hallak, T.; Soares, C.G. Oil-hydraulic power take-off concept for an oscillating wave surge converter. Renew. Energy 2020, 159, 1297–1309. [Google Scholar] [CrossRef]
- Tronchin, L.; Manfren, M.; Nastasi, B. Energy analytics for supporting built environment decarbonisation. Energy Procedia 2019, 157, 1486–1493. [Google Scholar] [CrossRef]
- Mazzoni, S.; Ooi, S.; Nastasi, B.; Romagnoli, A. Energy storage technologies as techno-economic parameters for master-planning and optimal dispatch in smart multi energy systems. Appl. Energy 2019, 254, 113682. [Google Scholar] [CrossRef]
- Nastasi, B. Hydrogen policy, market, and R&D projects. In Solar Hydrogen Production; Elsevier: Amsterdam, The Netherlands, 2019; pp. 31–44. [Google Scholar]
- Bozzi, S.; Giassi, M.; Miquel, A.M.; Antonini, A.; Bizzozero, F.; Gruosso, G.; Archetti, R.; Passoni, G. Wave energy farm design in real wave climates: The Italian offshore. Energy 2017, 122, 378–389. [Google Scholar] [CrossRef]
- De Andrés, A.; Guanche, R.; Meneses, L.; Vidal, C.; Losada, I. Factors that influence array layout on wave energy farms. Ocean Eng. 2014, 82, 32–41. [Google Scholar] [CrossRef]
- Engström, J.; Eriksson, M.; Göteman, M.; Isberg, J.; Leijon, M. Performance of large arrays of point absorbing direct-driven wave energy converters. J. Appl. Phys. 2013, 114, 204502. [Google Scholar] [CrossRef]
- Vicente, P.C.; Falcão, A.d.O.; Justino, P.A. A time domain analysis of arrays of floating point-absorber wave energy converters including the effect of nonlinear mooring forces. In Proceedings of the ICOE’2010—3rd International Conference on Ocean Energy, Bilbao, Spain, 6–8 October 2010. [Google Scholar]
- Yang, S.; Ringsberg, J.; Johnson, E. Analysis of interaction effects between WECs in four types of wave farms. In Proceedings of the 3rd International Conference on Renewable Energies Offshore (RENEW 2018), Lisbon, Portugal, 8–10 October 2018; pp. 647–658. [Google Scholar]
- Sergiienko, N.Y.; Neshat, M.; da Silva, L.S.; Alexander, B.; Wagner, M. Design optimisation of a multi-mode wave energy converter. arXiv 2020, arXiv:2001.08966. [Google Scholar]
- Neshat, M.; Alexander, B.; Sergiienko, N.Y.; Wagner, M. Optimisation of Large Wave Farms Using a Multi-Strategy Evolutionary Framework. In Proceedings of the 2020 Genetic and Evolutionary Computation Conference, GECCO’20, Cancún, Mexico, 14 June 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 1150–1158. [Google Scholar] [CrossRef]
- Jusoh, M.; Ibrahim, M.; Daud, M.; Yusop, Z.; Albani, A.; Rahman, S.; Mohad, S. Parameters estimation of hydraulic power take-off system for wave energy conversion system using genetic algorithm. In Proceedings of the International Conference on Sustainable Energy and Green Technology, Bangkok, Thailand, 11–14 December 2019; Volume 463, p. 012129. [Google Scholar]
- Rodríguez, C.A.; Rosa-Santos, P.; Taveira-Pinto, F. Hydrodynamic optimization of the geometry of a sloped-motion wave energy converter. Ocean Eng. 2020, 199, 107046. [Google Scholar] [CrossRef]
- M’zoughi, F.; Bouallègue, S.; Garrido, A.J.; Garrido, I.; Ayadi, M. Water cycle algorithm–based airflow control for oscillating water column—Based wave energy converters. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2020, 234, 118–133. [Google Scholar] [CrossRef]
- Chen, M. Hydrodynamic Analysis and Optimization of a Hinged-Type Wave Energy Converter-SeaWEED. Ph.D. Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, 2020. [Google Scholar]
- Liu, Z.; Wang, Y.; Hua, X. Prediction and optimization of oscillating wave surge converter using machine learning techniques. Energy Convers. Manag. 2020, 210, 112677. [Google Scholar] [CrossRef]
- Izquierdo-Pérez, J.; Brentan, B.M.; Izquierdo, J.; Clausen, N.E.; Pegalajar-Jurado, A.; Ebsen, N. Layout Optimization Process to Minimize the Cost of Energy of an Offshore Floating Hybrid Wind–Wave Farm. Processes 2020, 8, 139. [Google Scholar] [CrossRef]
- Esmaeilzadeh, S.; Alam, M.R. Shape optimization of wave energy converters for broadband directional incident waves. Ocean Eng. 2019, 174, 186–200. [Google Scholar] [CrossRef]
- Lyu, J.; Abdelkhalik, O.; Gauchia, L. Optimization of dimensions and layout of an array of wave energy converters. Ocean Eng. 2019, 192, 106543. [Google Scholar] [CrossRef]
- Kelly, M.; Alam, M.R. Shape Optimization of a Submerged Pressure Differential Wave Energy Converter for Load Reductions. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Glasgow, UK, 9–14 June 2019; American Society of Mechanical Engineers: New York, NY, USA, 2019; Volume 58899, p. V010T09A030. [Google Scholar]
- Neshat, M.; Alexander, B.; Sergiienko, N.; Wagner, M. New insights into position optimisation of wave energy converters using hybrid local search. Swarm Evol. Comput. 2020, 59, 100744. [Google Scholar] [CrossRef]
- Neshat, M.; Abbasnejad, E.; Shi, Q.; Alexander, B.; Wagner, M. Adaptive neuro-surrogate-based optimisation method for wave energy converters placement optimisation. In Proceedings of the International Conference on Neural Information Processing, Sydney, Australia, 12–15 December 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 353–366. [Google Scholar]
- Jabrali, A.; Khatyr, R.; Naciri, J.K. Viscous effects and energy recovery optimization for freely floating and bottom fixed wave energy converters. Int. J. Renew. Energy Res. 2019, 9, 290–300. [Google Scholar]
- Wang, L.; Ringwood, J.V. Geometric optimization of a hinge-barge wave energy converter. In Proceedings of the 13th European Wave and Tidal Energy Conference, Naples, Italy, 1–6 September 2019; p. 1389. [Google Scholar]
- Faraggiana, E.; Masters, I.; Chapman, J. Design of an optimization scheme for the WaveSub array. In Advances in Renewable Energies Offshore, Proceedings of the 3rd International Conference on Renewable Energies Offshore (RENEW), Lisbon, Portugal, 8–10 October 2018; Soares, G., Ed.; Taylor & Francis Group: London, UK, 10 October 2019; pp. 633–638. [Google Scholar]
- Neshat, M.; Alexander, B.; Sergiienko, N.Y.; Wagner, M. A Hybrid Evolutionary Algorithm Framework for Optimising Power Take off and Placements of Wave Energy Converters. In Proceedings of the Genetic and Evolutionary Computation Conference, GECCO’19, Prague, Czech Republic, 14 July 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 1293–1301. [Google Scholar] [CrossRef]
- Vatchavayi, S.R. Heuristic Optimization of Wave Energy Converter Arrays. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 2019. [Google Scholar]
- Amini, E. Locating and Evaluating the Oscillating Surge Wave Energy Converter Using Grey Wolf Optimizer Algorithm and WEC-Sim Toolbox. Ph.D. Thesis, University of Tehran, Tehran, Iran, 2019. [Google Scholar]
- Amini, E.; Naeeni, S.T.O.; Ghaderi, P. Investigating Wave Energy Potential in Southern Coasts of the Caspian Sea and Evaluating the Application of Gray Wolf Optimizer Algorithm. arXiv 2019, arXiv:1912.13201. [Google Scholar]
- Sharp, C.; DuPont, B. Wave energy converter array optimization: A genetic algorithm approach and minimum separation distance study. Ocean Eng. 2018, 163, 148–156. [Google Scholar] [CrossRef]
- Neshat, M.; Alexander, B.; Wagner, M.; Xia, Y. A detailed comparison of meta-heuristic methods for optimising wave energy converter placements. In Proceedings of the Genetic and Evolutionary Computation Conference, Kyoto, Japan, 15–19 July 2018; ACM: New York, NY, USA, 2018; pp. 1318–1325. [Google Scholar]
- Fang, H.W.; Feng, Y.Z.; Li, G.P. Optimization of Wave Energy Converter Arrays by an Improved Differential Evolution Algorithm. Energies 2018, 11, 3522. [Google Scholar] [CrossRef]
- Arbonès, D.R.; Sergiienko, N.Y.; Ding, B.; Krause, O.; Igel, C.; Wagner, M. Sparse incomplete lu-decomposition for wave farm designs under realistic conditions. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Coimbra, Portugal, 8–12 September 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 512–524. [Google Scholar]
- Abdelkhalik, O.; Darani, S. Optimization of nonlinear wave energy converters. Ocean Eng. 2018, 162, 187–195. [Google Scholar] [CrossRef]
- Giassi, M.; Göteman, M. Layout design of wave energy parks by a genetic algorithm. Ocean Eng. 2018, 154, 252–261. [Google Scholar] [CrossRef]
- Göteman, M.; Engström, J.; Eriksson, M.; Isberg, J. Fast modeling of large wave energy farms using interaction distance cut-off. Energies 2015, 8, 13741–13757. [Google Scholar] [CrossRef]
- López-Ruiz, A.; Bergillos, R.J.; Raffo-Caballero, J.M.; Ortega-Sánchez, M. Towards an optimum design of wave energy converter arrays through an integrated approach of life cycle performance and operational capacity. Appl. Energy 2018, 209, 20–32. [Google Scholar] [CrossRef]
- Borgarino, B.; Babarit, A.; Ferrant, P. Impact of wave interactions effects on energy absorption in large arrays of wave energy converters. Ocean Eng. 2012, 41, 79–88. [Google Scholar] [CrossRef]
- Carnegie Clean Energy Limited (formerly Carnegie Wave Energy). Carnegie CETO 6 Technology. Available online: https://arena.gov.au/projects/carnegie-ceto-6-technology/ (accessed on 15 July 2020).
- Sergiienko, N. Wave Energy Converter (WEC) Array Simulator. 2020. Available online: https://www.mathworks.com/matlabcentral/fileexchange/71840-wave-energy-converter-wec-array-simulator (accessed on 27 July 2020).
- Sergiienko, N.Y.; Cazzolato, B.S.; Ding, B.; Arjomandi, M. An optimal arrangement of mooring lines for the three-tether submerged point-absorbing wave energy converter. Renew. Energy 2016, 93, 27–37. [Google Scholar] [CrossRef]
- Nolte, J.D.; Ertekin, R. Wave power calculations for a wave energy conversion device connected to a drogue. J. Renew. Sustain. Energy 2014, 6, 013117. [Google Scholar] [CrossRef]
- Cummins, W.E. The Impulse Response Function and Ship Motions; Report; DTIC Document: Rockville, MD, USA, 1962.
- Sergiienko, N.; Cazzolato, B.; Ding, B.; Hardy, P.; Arjomandi, M. Performance comparison of the floating and fully submerged quasi-point absorber wave energy converters. Renew. Energy 2017, 108, 425–437. [Google Scholar] [CrossRef]
- Flavià, F.F.; Babarit, A.; Clément, A.H. On the numerical modeling and optimization of a bottom-referenced heave-buoy array of wave energy converters. Int. J. Mar. Energy 2017, 19, 1–15. [Google Scholar] [CrossRef]
- Zwolan, P.; Czaplewski, K. Sea waves models used in maritime simulators. Zesz. Nauk. Morska W Szczecinie 2012, 104, 186–190. [Google Scholar]
- Chen, W.; Gao, F.; Meng, X.; Fu, J. Design of the wave energy converter array to achieve constructive effects. Ocean Eng. 2016, 124, 13–20. [Google Scholar] [CrossRef]
- De Andres, A.; Maillet, J.; Hals Todalshaug, J.; Möller, P.; Bould, D.; Jeffrey, H. Techno-Economic Related Metrics for a Wave Energy Converters Feasibility Assessment. Sustainability 2016, 8, 1109. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).