Black Start Restoration of Islanded Droop-Controlled Microgrids
Abstract
1. Introduction
- Propose a systematic black start formulation for the sequential restoration of islanded droop-controlled microgrids. To the best of the authors’ knowledge, this is the first systematic black start restoration formulation considering droop as the primary control.
- Show how to coordinate multiple grid-supporting (master/droop) and grid following (or PQ) DGs to dynamically configure microgrid instead of the multiple microgrids commonly considered in other systematic formulations. Coordination of the grid-supporting DGs to form a single microgrid, when possible, can help improve load balancing, resilience, redundancy, and better utilization of the DGs.
- Propose a zero-dispatch synchronization scheme for the grid-supporting DGs during the sequential build-up of the islanded microgrid and show how this can be mathematically composed into the restoration formulation.
- Validate the restoration approach through detailed electromagnetic transient program (EMTP) simulation in PSCAD and highlight some of the observations from the simulation such as restoration modeling limitations and suggestions on how these limitations can be solved.
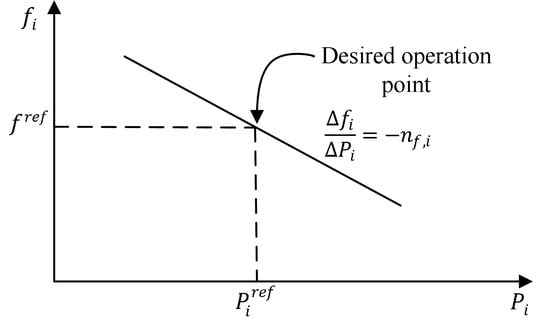
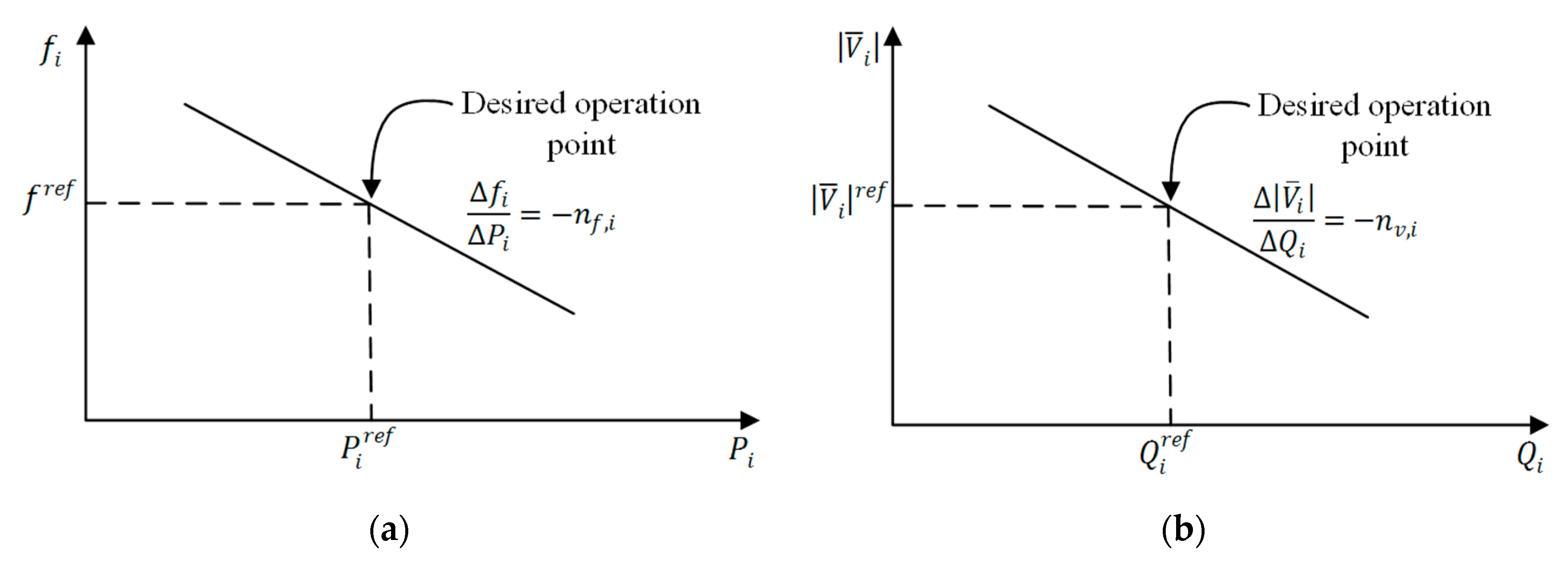
2. Droop Control Basics and Reference Operation
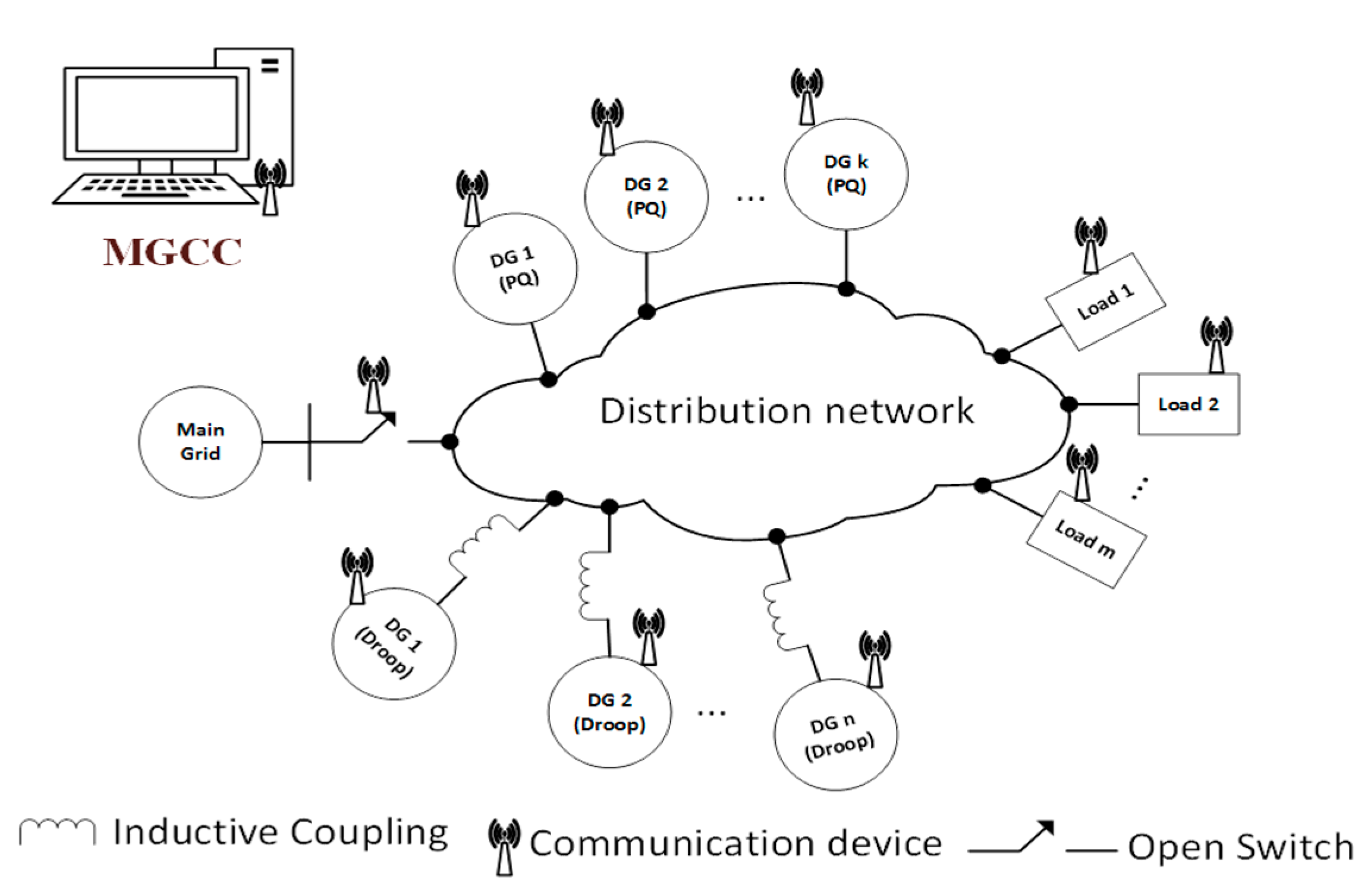
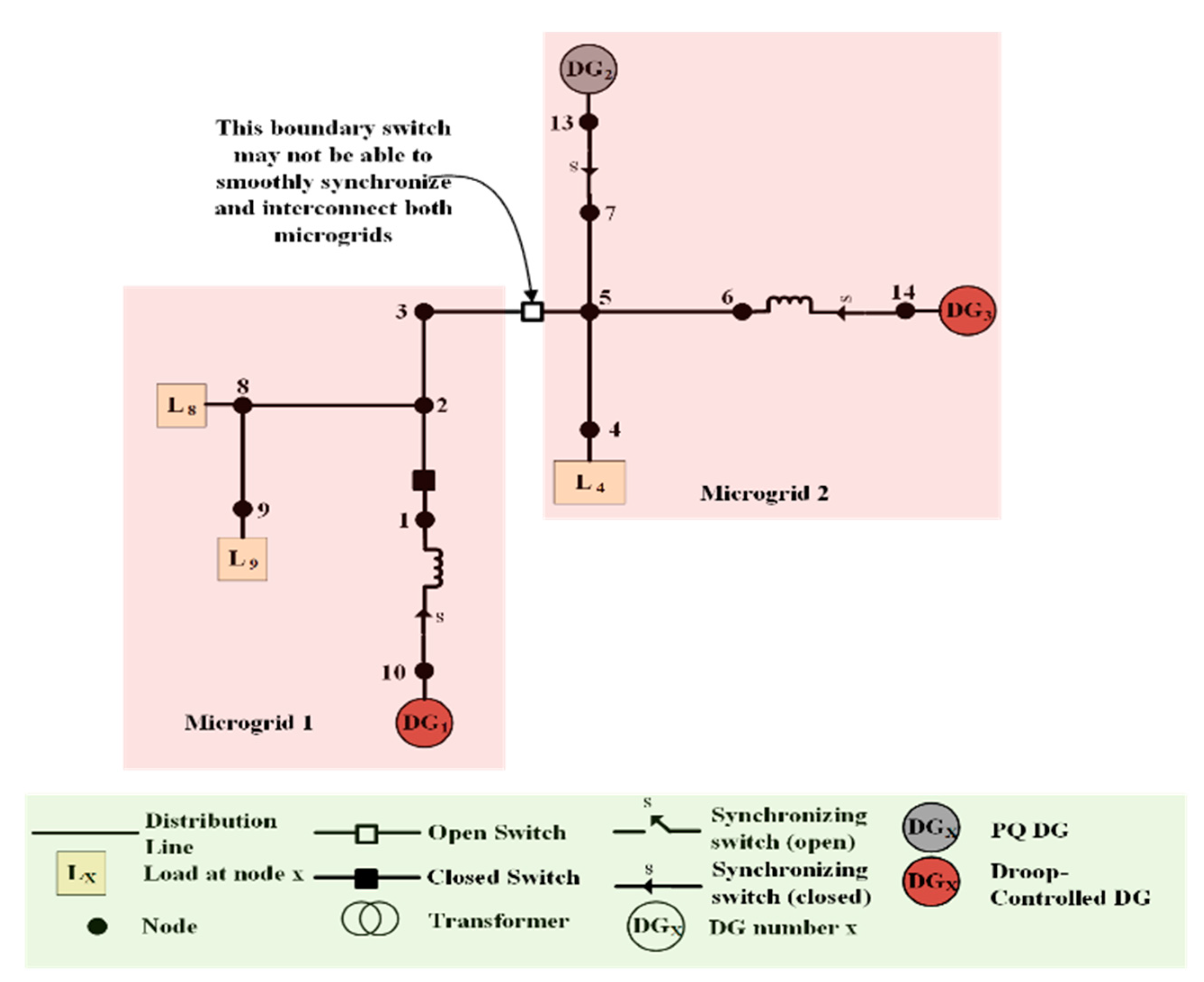
3. Description of Islanded Microgrid to be Restored
4. Formulation of Black Start Restoration for Droop-Controlled Microgrid
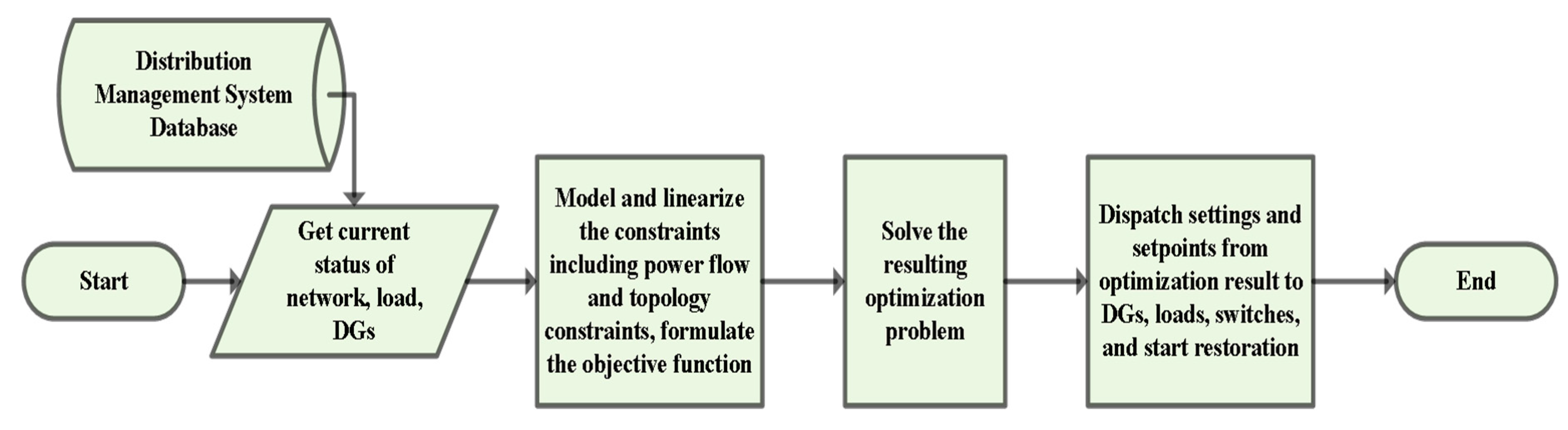
4.1. Overview of the Black Start Process
4.1.1. Step 1, 2, and 3
4.1.2. Step 4 and 5
4.2. Objective Function
4.3. Initial Sequencing Constraints
4.4. Connectivity Constraints
- Whenever a DG is energized, then that DG’s node must have been energized in the same or previous time step as the DG energization time step (Equation (7))
- Once any DG, branch, or load is energized, it cannot be de-energized (EQUATIONS (8), (11), and (14) respectively)
- Both nodes of an energized switchable branch must be energized (Equation (9)) and the status of non-switchable branches are the same with its two nodes (Equation (10))
- A switchable load can only be energized once its node is energized (Equation (12)) and a non-switchable load is automatically energized when its node is energized (Equation (13))
4.5. Synchronization Enhancing Constraints
- At most one droop-controlled DG can be newly connected to the system per time step (Equation (15))
- “Freeze” the status/settings of every other element at any time step that a droop-controlled DG is synchronized to the system. This means that:
- No additional load is restored at a synchronization time step (Equation (16)).
- The status and dispatch settings of PQ DGs should remain the same as the previous time step just before the synchronization step (Equations (17)–(19)).
- The active and reactive power reference settings of all droop DGs should remain the same as the previous time step just before the synchronization step, and the DG that is about to be synchronized to the system should do at zero power reference settings (Equations (20) and (21)). Equations (20) and (21) also ensure that the synchronized DG is connected with a zero reference power since its reference power at the previous step would be set to zero according to the DG operation constraints.
- The status of all branches should remain the same as the previous time step just before the synchronization step except for one branch that can connect the synchronizing DG to the system, that is, only the branch that connects the DG to the system is allowed to change from “OFF” to “ON” (Equation (22)) if it was not already energized.
4.6. Power Flow Constraints
4.6.1. Kirchhoff’s Current Law (KCL) at each Node
4.6.2. Current Injection at Each Node
4.6.3. Current Injection at Droop Nodes
4.6.4. Current Injection at Load Node
4.6.5. Current Injection at PQ DG Nodes
4.7. DG and System Operating Constraints
4.7.1. Phase Voltage Unbalance Rate Constraint (PVUR)
4.7.2. Voltage Limit Constraint
4.7.3. DG Power Unbalance Constraints
4.7.4. Nominal System Load Unbalance Index (NSLUI) Constraints
4.7.5. DG Output Constraints
4.7.6. Ramp Rate Constraints
4.8. Topology and Sequencing Constraints
5. Example Case Study and Discussions
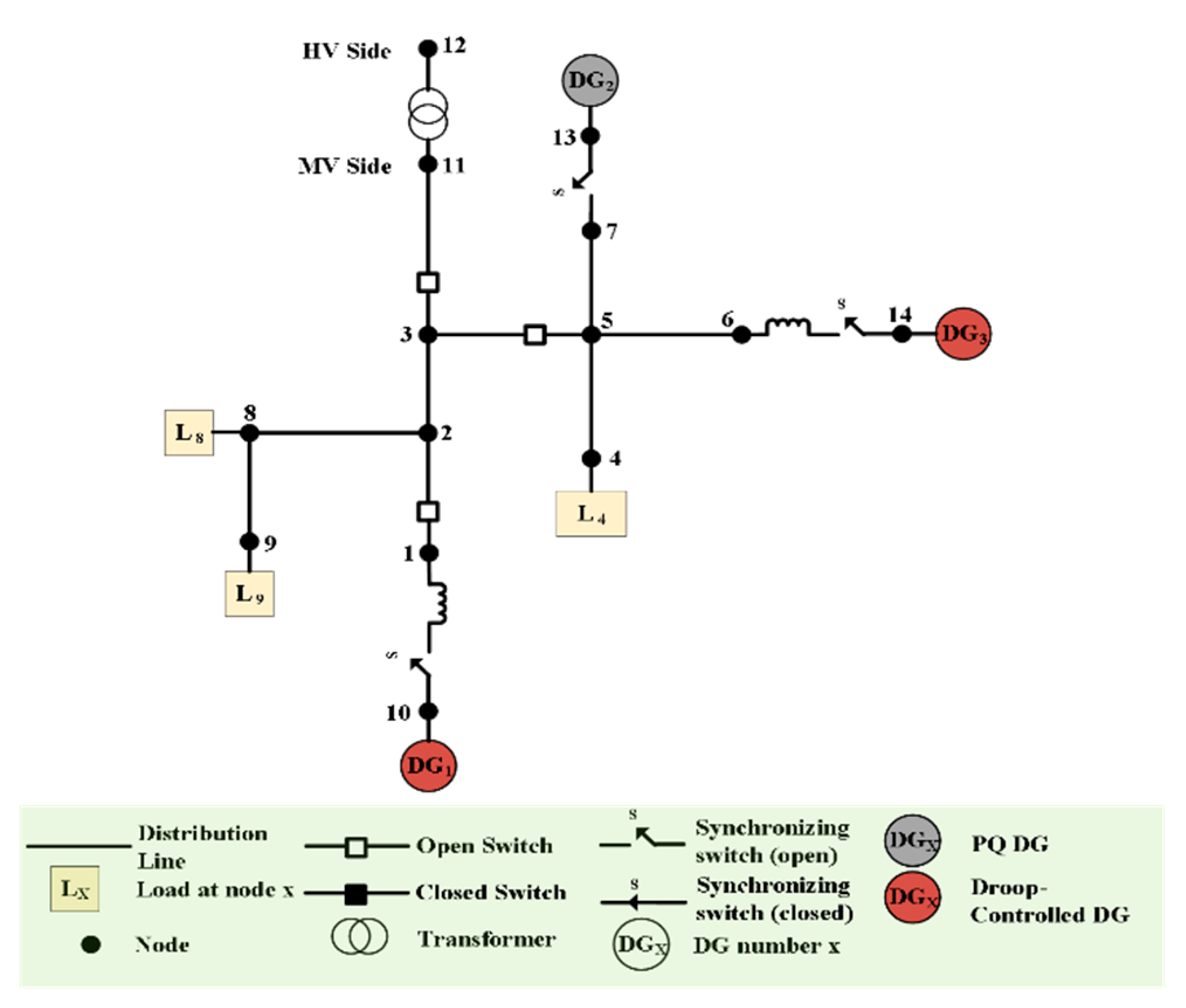
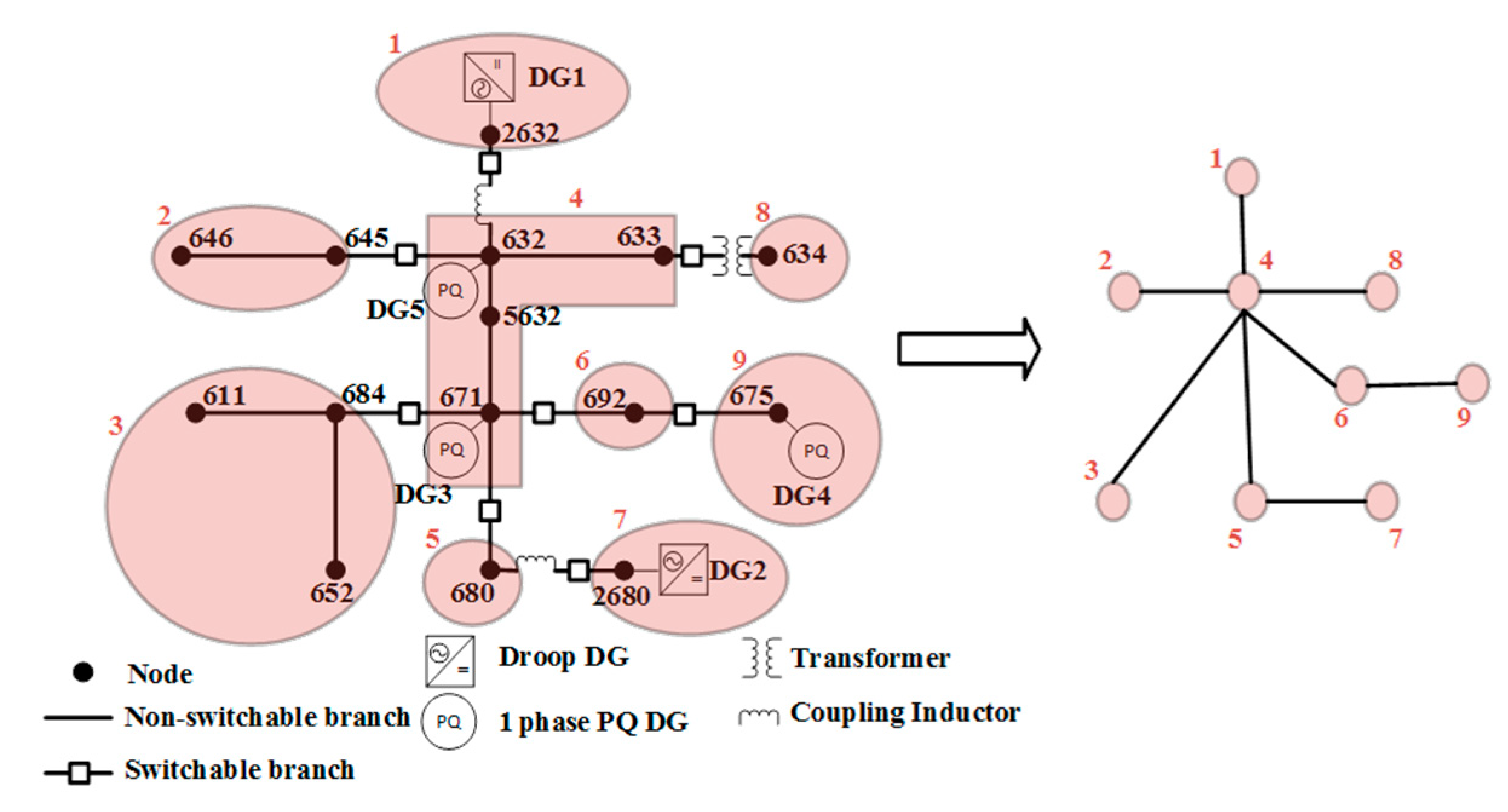
5.1. Description of the Test System
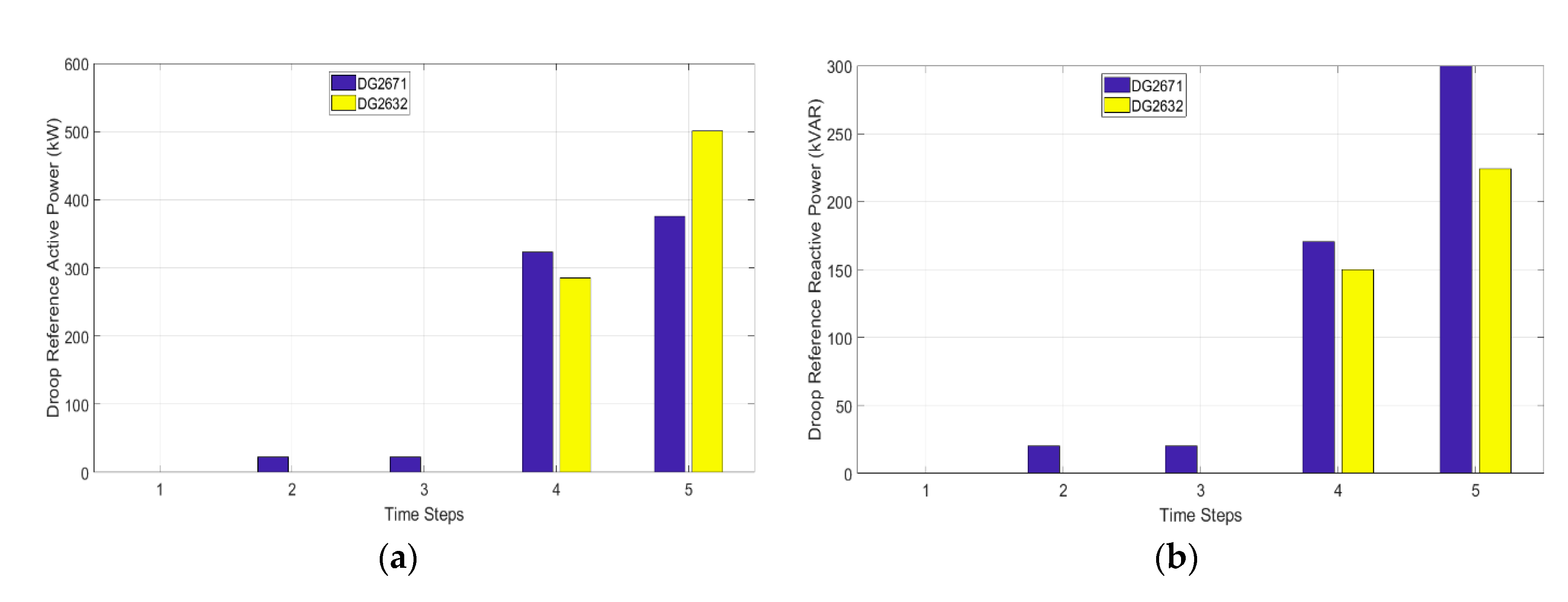
5.2. Restoration Solution
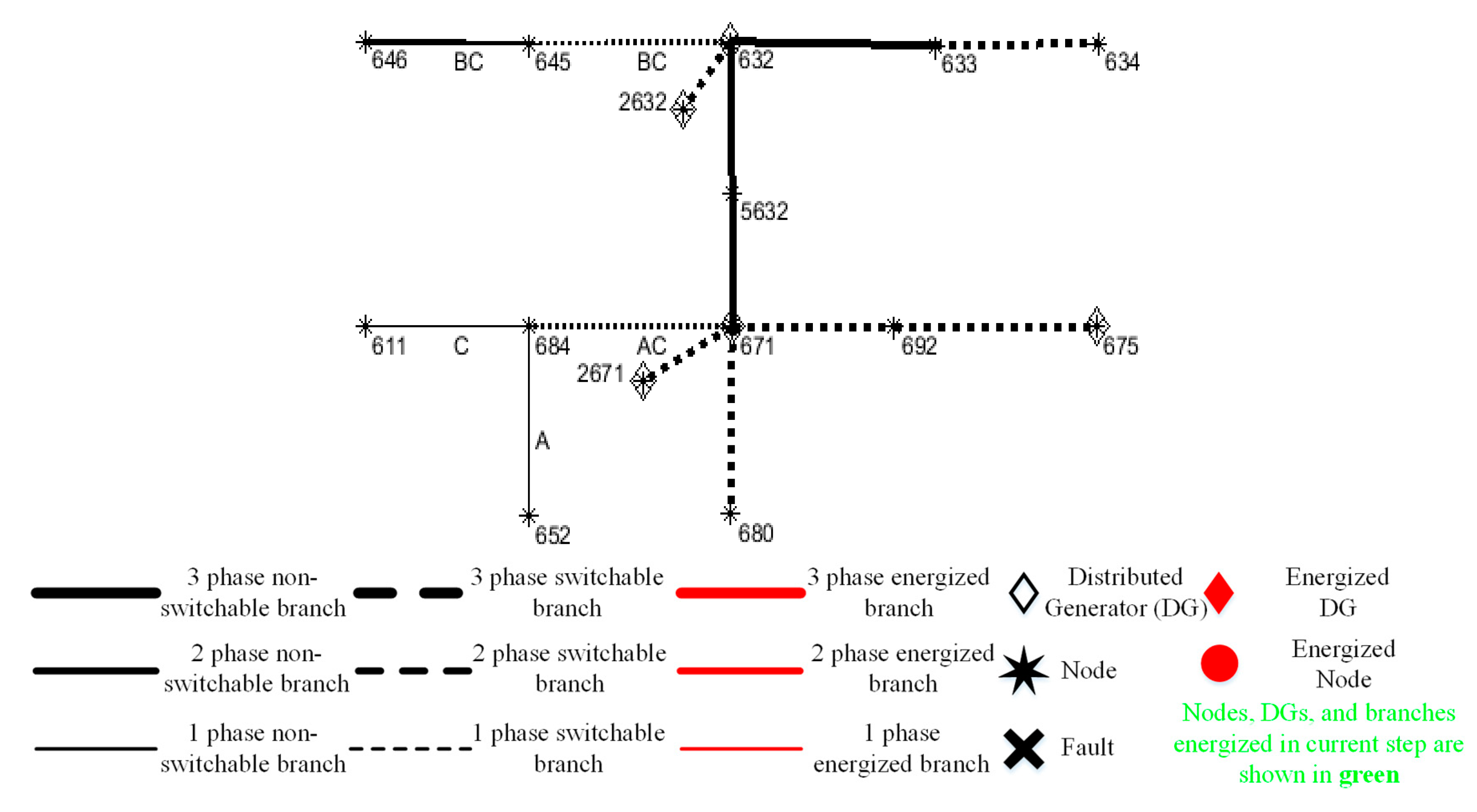
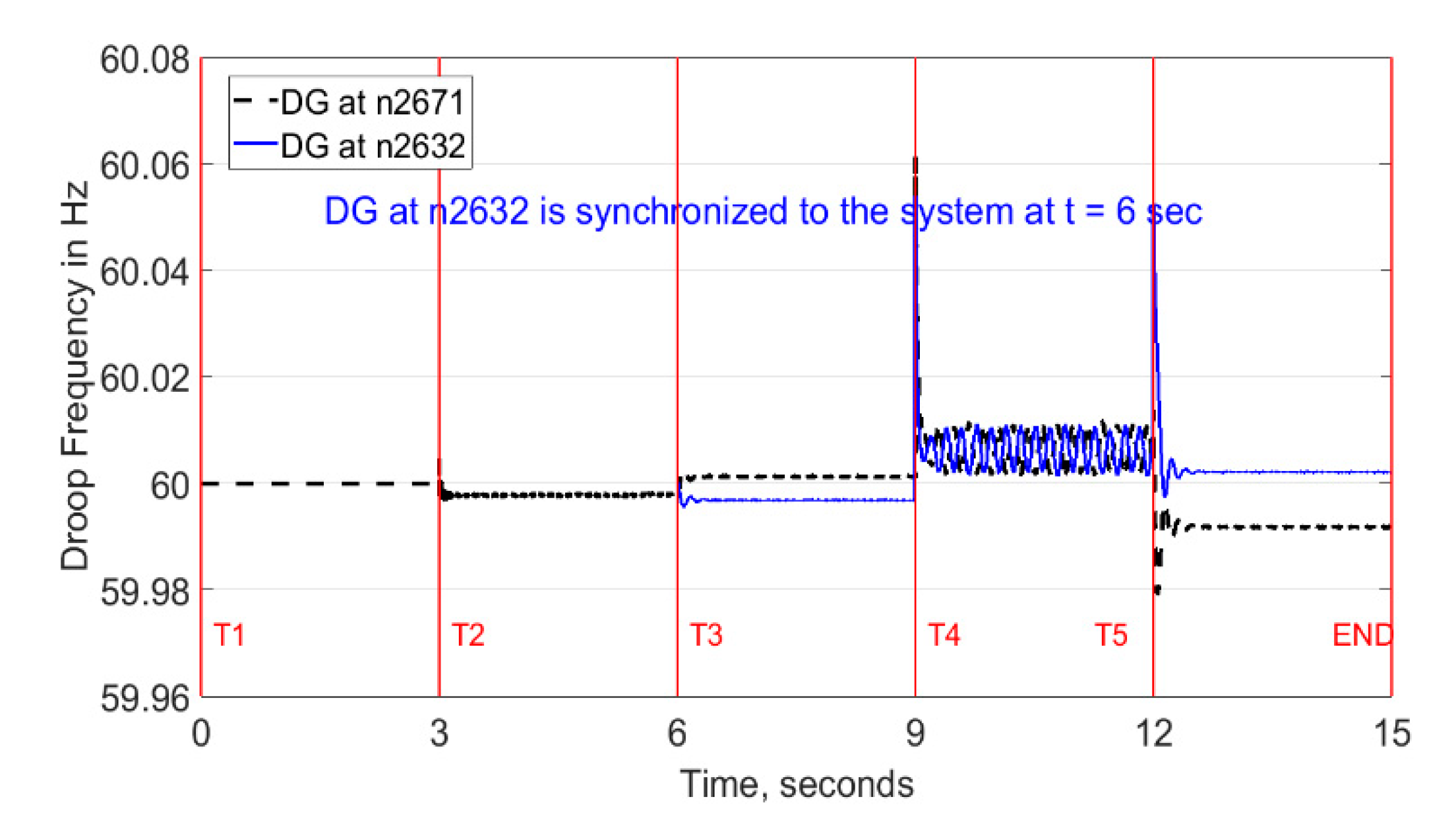
5.3. Solution Verification Using PSCAD Simulation as Benchmark
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Hussain, A.; Bui, V.-H.; Kim, H.-M. Microgrids as a resilience resource and strategies used by microgrids for enhancing resilience. Appl. Energy 2019, 240, 56–72. [Google Scholar] [CrossRef]
- Teimourzadeh, S.; Tor, O.B.; Cebeci, M.E.; Bara, A.; Oprea, S.V. A three-stage approach for resilience-constrained scheduling of networked microgrids. J. Mod. Power Syst. Clean Energy 2019, 7, 705–715. [Google Scholar] [CrossRef]
- Cohn, L. California Microgrids Flex Their Skills During Blackouts. 2020. Available online: https://microgridknowledge.com/california-blackouts-microgrids-flexible-load/ (accessed on 15 September 2020).
- Merchant, E.F. As Hurricane Season Approaches, More Microgrids Crop Up in Puerto Rico. Available online: https://www.greentechmedia.com/articles/read/as-hurricane-season-approaches-more-microgrids-cropping-up-in-puerto-rico (accessed on 4 June 2018).
- Cohn, L. Microgrid Kept Power On Even as the California Wildfires Caused Outages. Available online: https://microgridknowledge.com/islanded-microgrid-fires/ (accessed on 29 November 2017).
- Peters, A. New Microgrids Are Helping Australia Get Power Back after the Fires. Available online: https://www.fastcompany.com/90465605/new-microgrids-are-helping-australia-get-power-back-after-the-fires (accessed on 15 September 2020).
- Farrokhabadi, M.; Cañizares, C.A.; Simpson-Porco, J.W.; Nasr, E.; Fan, L.; Mendoza-Araya, P.A.; Tonkoski, R.; Tamrakar, U.; Hatziargyriou, N.; Lagos, D.; et al. Microgrid Stability Definitions, Analysis, and Examples. IEEE Trans. Power Syst. 2020, 35, 13–29. [Google Scholar] [CrossRef]
- Farrokhabadi, M.; König, S.; Cañizares, C.A.; Bhattacharya, K.; Leibfried, T. Battery Energy Storage System Models for Microgrid Stability Analysis and Dynamic Simulation. IEEE Trans. Power Syst. 2018, 33, 2301–2312. [Google Scholar] [CrossRef]
- Chandorkar, M.C.; Divan, D.M.; Adapa, R. Control of parallel connected inverters in standalone AC supply systems. IEEE Trans. Ind. Appl. 1993, 29, 136–143. [Google Scholar] [CrossRef]
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodríguez, P. Control of Power Converters in AC Microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Brabandere, K.D.; Bolsens, B.; Keybus, J.V.d.; Woyte, A.; Driesen, J.; Belmans, R. A Voltage and Frequency Droop Control Method for Parallel Inverters. IEEE Trans. Power Electron. 2007, 22, 1107–1115. [Google Scholar] [CrossRef]
- Guo, W.; Mu, L. Control principles of micro-source inverters used in microgrid. Prot. Control Mod. Power Syst. 2016, 1, 5. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J. Self-Healing Resilient Distribution Systems Based on Sectionalization Into Microgrids. IEEE Trans. Power Syst. 2015, 30, 3139–3149. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Y.; He, J.; Liu, C.; Schneider, K.P.; Hong, M.; Ton, D.T. Coordinating Multiple Sources for Service Restoration to Enhance Resilience of Distribution Systems. IEEE Trans. Smart Grid 2019. [Google Scholar] [CrossRef]
- Chen, C.; Wang, J.; Qiu, F.; Zhao, D. Resilient Distribution System by Microgrids Formation After Natural Disasters. IEEE Trans. Smart Grid 2016, 7, 958–966. [Google Scholar] [CrossRef]
- Chen, B.; Chen, C.; Wang, J.; Butler-Purry, K.L. Sequential Service Restoration for Unbalanced Distribution Systems and Microgrids. IEEE Trans. Power Syst. 2018, 33, 1507–1520. [Google Scholar] [CrossRef]
- Chen, B.; Chen, C.; Wang, J.; Butler-Purry, K.L. Multi-Time Step Service Restoration for Advanced Distribution Systems and Microgrids. IEEE Trans. Smart Grid 2018, 9, 6793–6805. [Google Scholar] [CrossRef]
- Gilani, M.A.; Kazemi, A.; Ghasemi, M. Distribution system resilience enhancement by microgrid formation considering distributed energy resources. Energy 2020, 191, 116442. [Google Scholar] [CrossRef]
- Fu, L.; Liu, B.; Meng, K.; Dong, Z.Y. Optimal Restoration of An Unbalanced Distribution System into Multiple Microgrids Considering Three-Phase Demand-Side Management. IEEE Trans. Power Syst. 2020. [Google Scholar] [CrossRef]
- Lopes, J.A.P.; Moreira, C.L.; Madureira, A.G. Defining control strategies for MicroGrids islanded operation. IEEE Trans. Power Syst. 2006, 21, 916–924. [Google Scholar] [CrossRef]
- Katiraei, F.; Iravani, M.R.; Lehn, P.W. Micro-grid autonomous operation during and subsequent to islanding process. IEEE Trans. Power Deliv. 2005, 20, 248–257. [Google Scholar] [CrossRef]
- Che, L.; Khodayar, M.; Shahidehpour, M. Only Connect: Microgrids for Distribution System Restoration. IEEE Power Energy Mag. 2014, 12, 70–81. [Google Scholar] [CrossRef]
- Nuschke, M. Development of a microgrid controller for black start procedure and islanding operation. In Proceedings of the 2017 IEEE 15th International Conference on Industrial Informatics (INDIN), Emden, Germany, 24–26 July 2017; pp. 439–444. [Google Scholar]
- Vandoorn, T.L.; Vasquez, J.C.; Kooning, J.D.; Guerrero, J.M.; Vandevelde, L. Microgrids: Hierarchical Control and an Overview of the Control and Reserve Management Strategies. IEEE Ind. Electron. Mag. 2013, 7, 42–55. [Google Scholar] [CrossRef]
- Kaur, A.; Kaushal, J.; Basak, P. A review on microgrid central controller. Renew. Sustain. Energy Rev. 2016, 55, 338–345. [Google Scholar] [CrossRef]
- Bassey, O.; Butler-Purry, K.L.; Chen, B. Dynamic Modeling of Sequential Service Restoration in Islanded Single Master Microgrids. IEEE Trans. Power Syst. 2020, 35, 202–214. [Google Scholar] [CrossRef]
- Simpson-Porco, J.W.; Dörfler, F.; Bullo, F. Droop-controlled inverters are Kuramoto oscillators. IFAC Proc. Vol. 2012, 45, 264–269. [Google Scholar] [CrossRef]
- Saadat, H. Power System Analysis McGraw-Hill Series in Electrical Computer Engineering; Mcgraw-Hill College: New York, NY, USA, 1999. [Google Scholar]
- Ahmadi, H.; Martı´, J.R.; von Meier, A. A Linear Power Flow Formulation for Three-Phase Distribution Systems. IEEE Trans. Power Syst. 2016, 31, 5012–5021. [Google Scholar] [CrossRef]
- Williams, H.P. Model Building in Mathematical Programming; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Bassey, O. Control and Black Start Restoration of Islanded Microgrids; Texas A&M University: College Station, TX, USA, 2020. [Google Scholar]
- Renmu, H.; Ma, J.; Hill, D.J. Composite load modeling via measurement approach. IEEE Trans. Power Syst. 2006, 21, 663–672. [Google Scholar] [CrossRef]
- IEEE Standard Test Procedure for Polyphase Induction Motors and Generators in IEEE Std 112-2017 (Revision of IEEE Std 112-2004); IEEE: New York, NY, USA, 2018; pp. 1–115.
- Pillay, P.; Manyage, M. Definitions of voltage unbalance. IEEE Power Eng. Rev. 2001, 21, 50–51. [Google Scholar] [CrossRef]
- Peng, L.; Bai, D.; Kang, Y.; Chen, J. Research on three-phase inverter with unbalanced load. In Proceedings of the Applied Power Electronics Conference and Exposition (APEC’04), Anaheim, CA, USA, 22–26 February 2004; Volume 121, pp. 128–133. [Google Scholar]
- Bassey, O.; Butler-Purry, K.L. Modeling Single-Phase PQ Inverter for Unbalanced Power Dispatch in Islanded Microgrid. In Proceedings of the 2019 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 7–8 February 2019; pp. 1–6. [Google Scholar]
- Adibi, M.; Clelland, P.; Fink, L.; Happ, H.; Kafka, R.; Raine, J.; Scheurer, D.; Trefny, F. Power System Restoration—A Task Force Report. IEEE Trans. Power Syst. 1987, 2, 271–277. [Google Scholar] [CrossRef]
- Lavorato, M.; Franco, J.F.; Rider, M.J.; Romero, R. Imposing Radiality Constraints in Distribution System Optimization Problems. IEEE Trans. Power Syst. 2012, 27, 172–180. [Google Scholar] [CrossRef]
- Lofberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation (IEEE Cat. No.04CH37508), New Orleans, LA, USA, 2–4 September 2004; pp. 284–289. [Google Scholar]
- Gurobi Optimization. Available online: http://www.gurobi.com/ (accessed on 15 September 2020).
- Baran, M.E.; Wu, F.F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 1989, 4, 1401–1407. [Google Scholar] [CrossRef]
- Gan, L.; Low, S.H. Convex relaxations and linear approximation for optimal power flow in multiphase radial networks. In Proceedings of the 2014 Power Systems Computation Conference, Wroclaw, Poland, 18–22 August 2014; pp. 1–9. [Google Scholar]
- Bassey, O.; Butler-Purry, K.L.; Chen, B. Active and Reactive Power Sharing in Inverter Based Droop-Controlled Microgrids. In Proceedings of the 2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 4–8 August 2019; pp. 1–5. [Google Scholar]
- Barklund, E.; Pogaku, N.; Prodanovic, M.; Hernandez-Aramburo, C.; Green, T.C. Energy Management in Autonomous Microgrid Using Stability-Constrained Droop Control of Inverters. IEEE Trans. Power Electron. 2008, 23, 2346–2352. [Google Scholar] [CrossRef]








| Sets | |
| The number of elements in set A | |
| Set of branches, switchable and damaged branches, set of switchable branches between bus blocks | |
| Set of all DGs, subset of black start DGs, subset of droop-controlled DGs, subset of damaged DGs, subset of PQ DGs | |
| Set of loads, subset of switchable loads, and subset of damaged load | |
| Set of time steps and | |
| Set of phase nodes, nodes, bus blocks, | |
| Binary Decision Variables (1–Energized, 0–Not Energized) | |
| Energization status of node at time step , energization status of bus block at time step | |
| Energization status of DG at time step | |
| Energization status of line at time step, , where respectively | |
| Energization status of load at time step | |
| Continuous Decision Variables | |
| Used as subscript or superscript to denote variable or parameter in phase a, b or c respectively | |
| , | Active and reactive power output of PQ DG at step and phase |
| , | Real and imaginary part of three-phase nodal voltage vector of node at step |
| , | Real and imaginary part of nodal voltage of node at step and phase |
| Voltage droop co-efficient of DG , at step | |
| Frequency droop co-efficient of DG , at step | |
| Droop reference active and reactive power output of DG at step , | |
| Nominal active and reactive power demand of load , phase , at time step | |
| Parameters | |
| A large number chosen deliberately to manipulate the constraint equations | |
| time interval between restoration steps and is assumed to be a constant value for all intervals | |
| Maximum absolute value of differential active and reactive power output of DG for each time step (DG ramp rate) | |
| Minimum and maximum active power output of DG | |
| Minimum and maximum reactive power output of DG | |
| Nominal active and reactive power value of load , phase , at time step (fixed to the same value for all time steps and is independent of whether the load has been restored or not) | |
| Impedance of line between nodes and , and | |
| Shunt admittance between nodes and | |
| Label | Node | Type | (Hz) | Per Phase BaseMVA | Per Phase baseKV | Pu Coupling X | Pmax (KW) | Pmin (KW) | Qmax (KVAR) | Qmin (KVAR) | Phase | Status | Blackstart | Ramp Rate % |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DG1 | 2671 | Droop | 60 | 1 | 2.4018 | 0.5 | 600 | 0 | 300 | −50 | ABC | 1 | 1 | 50 |
| DG2 | 2632 | Droop | 60 | 1 | 2.4018 | 0.5 | 600 | 0 | 300 | −50 | ABC | 1 | 1 | 50 |
| DG3 | 671 | PQ | NA | NA | 2.4018 | NA | 200 | 0 | 120 | 0 | C | 1 | 0 | 50 |
| DG4 | 675 | PQ | NA | NA | 2.4018 | NA | 200 | 0 | 120 | 0 | A | 1 | 0 | 50 |
| DG5 | 632 | PQ | NA | NA | 2.4018 | NA | 200 | 0 | 120 | 0 | B | 1 | 0 | 50 |
| Node | Config | P(a/B/C) KW | Q(A/B/C) KVAR | Turn-On Step |
|---|---|---|---|---|
| 611 | Y | 0/0/85 | 0/0/40 | 4 |
| 634 | Y | 83/60/30 | 55/45/15 | 4 |
| 645 | Y | 0/82/0 | 0/62.5/0 | 4 |
| 646 | D | 0/115/0 | 0/66/0 | 5 |
| 652 | Y | 100/0/0 | 55/0/0 | 5 |
| 671 | D | 110/90/90 | 60/50/50 | 4 |
| 671 | Y | 2.835/11/19.5 | 1.665/6.335/11.35 | 2 |
| 675 | Y | 100/34/70 | 45/30/40 | 5 |
| 692 | D | 0/0/85 | 0/0/75.5 | Off |
| 5632 | Y | 5.665/22/39 | 3.335/12.665/22.65 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bassey, O.; Butler-Purry, K.L. Black Start Restoration of Islanded Droop-Controlled Microgrids. Energies 2020, 13, 5996. https://doi.org/10.3390/en13225996
Bassey O, Butler-Purry KL. Black Start Restoration of Islanded Droop-Controlled Microgrids. Energies. 2020; 13(22):5996. https://doi.org/10.3390/en13225996
Chicago/Turabian StyleBassey, Ogbonnaya, and Karen L. Butler-Purry. 2020. "Black Start Restoration of Islanded Droop-Controlled Microgrids" Energies 13, no. 22: 5996. https://doi.org/10.3390/en13225996
APA StyleBassey, O., & Butler-Purry, K. L. (2020). Black Start Restoration of Islanded Droop-Controlled Microgrids. Energies, 13(22), 5996. https://doi.org/10.3390/en13225996